Spatiotemporal Changes in Air Temperature and Precipitation Extremes over Iran
Abstract
:1. Introduction
2. Data and Methods
2.1. Data Description
2.2. Extreme Precipitation and Air Temperature Indices
2.3. Trend Analysis
2.3.1. Mann-Kendall Test
2.3.2. Correlation Analysis
2.3.3. Quantile Regression
3. Results and Discussion
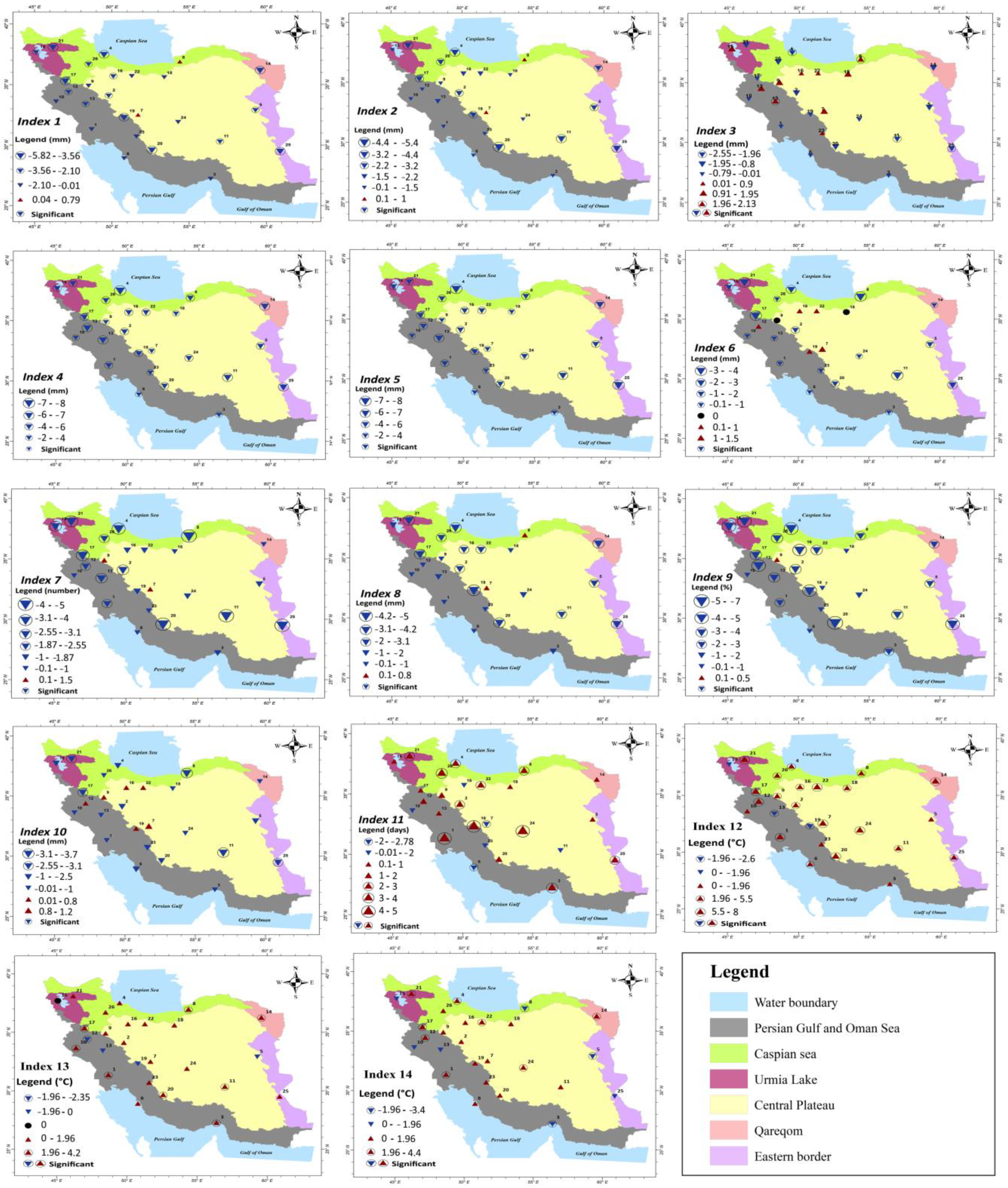
3.1. Spatiotemporal Precipitation Trend by the Mann–Kendall Test
3.2. Spatiotemporal Air Temperature Trend by Mann-Kendall Test
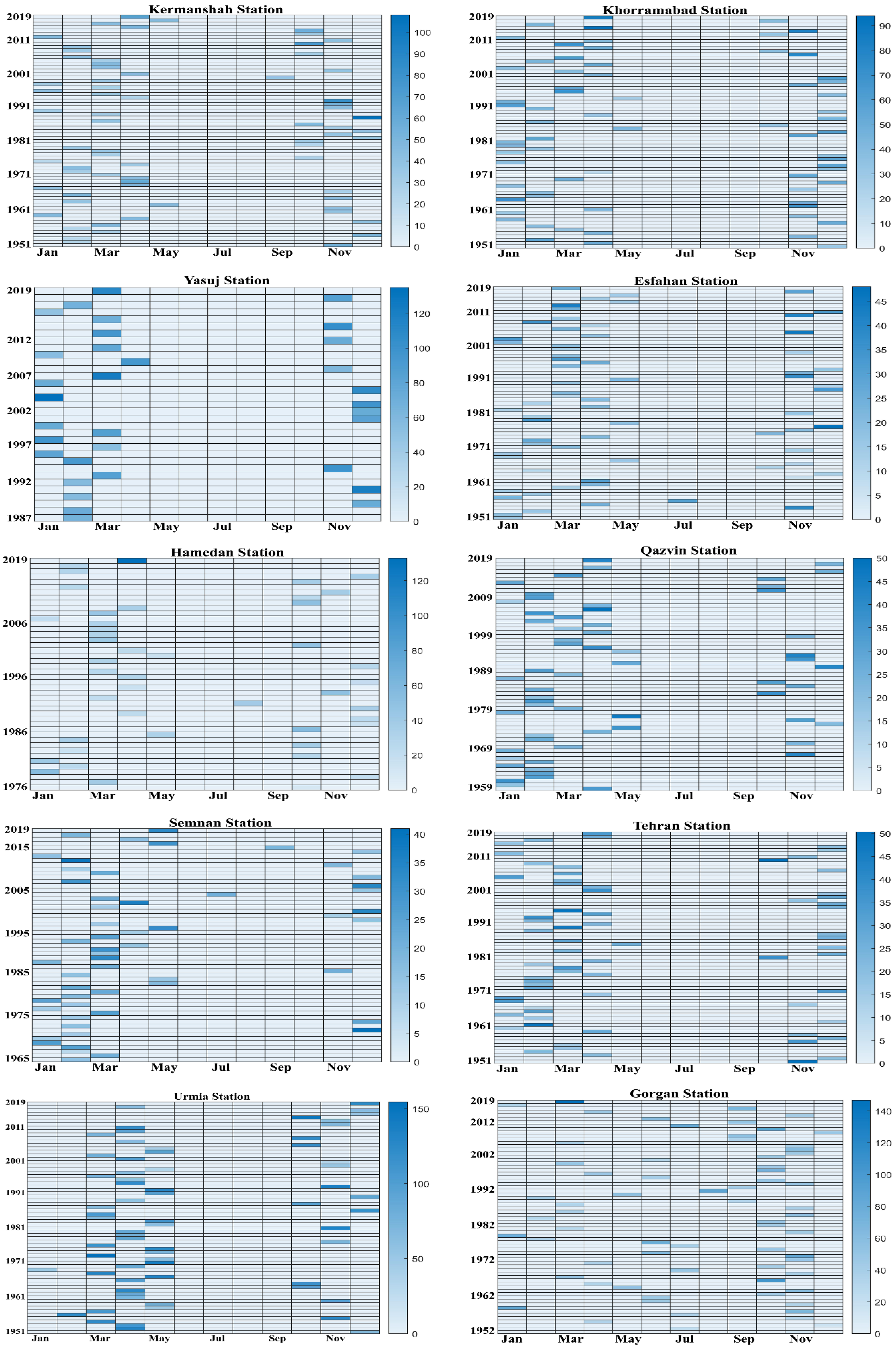
3.3. Maximum Daily Precipitation Analysis
3.4. Quantile Regression Results
3.4.1. Temporal Precipitation Trend Analysis
3.4.2. Precipitation Assessment with Increased Air Temperature
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Balling, R.C.; Keikhosravi Kiany, M.S.; Sen Roy, S.; Khoshhal, J. Trends in Extreme Precipitation Indices in Iran: 1951–2007. Adv. Meteorol. 2016, 2016, 2456809. [Google Scholar] [CrossRef] [Green Version]
- Zwiers, F.W.; Alexander, L.V.; Hegerl, G.C.; Knutson, T.R.; Kossin, J.P.; Naveau, P.; Nicholls, N.; Schär, C.; Seneviratne, S.I.; Zhang, X. Climate Extremes: Challenges in Estimating and Understanding Recent Changes in the Frequency and Intensity of Extreme Climate and Weather Events. In Climate Science for Serving Society: Research, Modeling and Prediction Priorities; Asrar, G.R., Hurrell, J.W., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 339–389. [Google Scholar]
- Zhang, Q.; Xu, C.-Y.; Tao, H.; Jiang, T.; Chen, Y.D. Climate changes and their impacts on water resources in the arid regions: A case study of the Tarim River basin, China. Stoch. Environ. Res. Risk Assess. 2010, 24, 349–358. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.-Y.; Zhang, Z.; Chen, Y.D.; Liu, C.-l.; Lin, H. Spatial and temporal variability of precipitation maxima during 1960–2005 in the Yangtze River basin and possible association with large-scale circulation. J. Hydrol. 2008, 353, 215–227. [Google Scholar] [CrossRef]
- Wright, D.B.; Samaras, C.; Lopez-Cantu, T. Resilience to Extreme Rainfall Starts with Science. Bull. Am. Meteorol. Soc. 2021, 102, E808–E813. [Google Scholar] [CrossRef]
- Asfaw, A.; Simane, B.; Hassen, A.; Bantider, A. Variability and time series trend analysis of rainfall and temperature in northcentral Ethiopia: A case study in Woleka sub-basin. Weather. Clim. Extrem. 2018, 19, 29–41. [Google Scholar] [CrossRef]
- Bohlinger, P.; Sorteberg, A. A comprehensive view on trends in extreme precipitation in Nepal and their spatial distribution. Int. J. Climatol. 2018, 38, 1833–1845. [Google Scholar] [CrossRef]
- Hajani, E.; Rahman, A.; Ishak, E. Trends in extreme rainfall in the state of New South Wales, Australia. Hydrol. Sci. J. 2017, 62, 2160–2174. [Google Scholar] [CrossRef]
- Jiang, P.; Yu, Z.; Gautam, M.R.; Acharya, K. The Spatiotemporal Characteristics of Extreme Precipitation Events in the Western United States. Water Resour. Manag. 2016, 30, 4807–4821. [Google Scholar] [CrossRef]
- Jung, I.-W.; Bae, D.-H.; Kim, G. Recent trends of mean and extreme precipitation in Korea. Int. J. Climatol. 2011, 31, 359–370. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Easterling, D.R.; Redmond, K.; Hubbard, K. Temporal variations of extreme precipitation events in the United States: 1895–2000. Geophys. Res. Lett. 2003, 30, 291–305. [Google Scholar] [CrossRef]
- Li, W.; Duan, L.; Luo, Y.; Liu, T.; Scharaw, B. Spatiotemporal Characteristics of Extreme Precipitation Regimes in the Eastern Inland River Basin of Inner Mongolian Plateau, China. Water 2018, 10, 35. [Google Scholar] [CrossRef] [Green Version]
- Machekposhti, K.H.; Sedghi, H.; Telvari, A.; Babazadeh, H. Modeling climate variables of rivers basin using time series analysis (case study: Karkheh River basin at Iran). Civ. Eng. J. 2018, 4, 78–92. [Google Scholar] [CrossRef] [Green Version]
- Mishra, A.K.; Singh, V.P. Changes in extreme precipitation in Texas. J. Geophys. Res. Atmos. 2010, 115, 29. [Google Scholar] [CrossRef]
- Peng, Y.; Zhao, X.; Wu, D.; Tang, B.; Xu, P.; Du, X.; Wang, H. Spatiotemporal Variability in Extreme Precipitation in China from Observations and Projections. Water 2018, 10, 1089. [Google Scholar] [CrossRef] [Green Version]
- Rajeevan, M.; Bhate, J.; Jaswal, A.K. Analysis of variability and trends of extreme rainfall events over India using 104 years of gridded daily rainfall data. Geophys. Res. Lett. 2008, 35, 6. [Google Scholar] [CrossRef]
- Wan, L.; Zhang, X.P.; Ma, Q.; Zhang, J.J.; Ma, T.Y.; Sun, Y.P. Spatiotemporal characteristics of precipitation and extreme events on the Loess Plateau of China between 1957 and 2009. Hydrol. Process. 2014, 28, 4971–4983. [Google Scholar] [CrossRef]
- Zhai, P.; Zhang, X.; Wan, H.; Pan, X. Trends in Total Precipitation and Frequency of Daily Precipitation Extremes over China. J. Clim. 2005, 18, 1096–1108. [Google Scholar] [CrossRef]
- Donat, M.G.; Lowry, A.L.; Alexander, L.V.; O’Gorman, P.A.; Maher, N. More extreme precipitation in the world’s dry and wet regions. Nat. Clim. Change 2016, 6, 508–513. [Google Scholar] [CrossRef]
- Craig, C.A.; Feng, S. A temporal and spatial analysis of climate change, weather events, and tourism businesses. Tour. Manag. 2018, 67, 351–361. [Google Scholar] [CrossRef]
- Mahmood, R.; Jia, S.; Zhu, W. Analysis of climate variability, trends, and prediction in the most active parts of the Lake Chad basin, Africa. Sci. Rep. 2019, 9, 6317. [Google Scholar] [CrossRef]
- Nkemelang, T.; New, M.; Zaroug, M. Temperature and precipitation extremes under current, 1.5 °C and 2.0 °C global warming above pre-industrial levels over Botswana, and implications for climate change vulnerability. Environ. Res. Lett. 2018, 13, 065016. [Google Scholar] [CrossRef] [Green Version]
- Tolika, K.; Anagnostopoulou, C.; Velikou, K.; Vagenas, C. A comparison of the updated very high resolution model RegCM3_10km with the previous version RegCM3_25km over the complex terrain of Greece: Present and future projections. Theor. Appl. Climatol. 2016, 126, 715–726. [Google Scholar] [CrossRef]
- Groisman, P.Y.; Knight, R.W.; Karl, T.R. Heavy Precipitation and High Streamflow in the Contiguous United States: Trends in the Twentieth Century. Bull. Am. Meteorol. Soc. 2001, 82, 219–246. [Google Scholar] [CrossRef]
- Vincent, L.A.; Mekis, É. Changes in Daily and Extreme Temperature and Precipitation Indices for Canada over the Twentieth Century. Atmosphere-Ocean 2006, 44, 177–193. [Google Scholar] [CrossRef] [Green Version]
- Min, S.-K.; Zhang, X.; Zwiers, F.W.; Hegerl, G.C. Human contribution to more-intense precipitation extremes. Nature 2011, 470, 378–381. [Google Scholar] [CrossRef]
- Westra, S.; Alexander, L.V.; Zwiers, F.W. Global Increasing Trends in Annual Maximum Daily Precipitation. J. Clim. 2013, 26, 3904–3918. [Google Scholar] [CrossRef] [Green Version]
- Westra, S.; Fowler, H.J.; Evans, J.P.; Alexander, L.V.; Berg, P.; Johnson, F.; Kendon, E.J.; Lenderink, G.; Roberts, N.M. Future changes to the intensity and frequency of short-duration extreme rainfall. Rev. Geophys. 2014, 52, 522–555. [Google Scholar] [CrossRef] [Green Version]
- Ahani, H.; Kherad, M.; Kousari, M.R.; Rezaeian-Zadeh, M.; Karampour, M.A.; Ejraee, F.; Kamali, S. An investigation of trends in precipitation volume for the last three decades in different regions of Fars province, Iran. Theor. Appl. Climatol. 2012, 109, 361–382. [Google Scholar] [CrossRef]
- Farhangi, M.; Kholghi, M.; Chavoshian, S.A. Rainfall trend analysis of hydrological subbasins in Western Iran. J. Irrig. Drain. Eng. 2016, 3, 70–73. [Google Scholar] [CrossRef]
- Hekmatzadeh, A.A.; Kaboli, S.; Torabi Haghighi, A. New indices for assessing changes in seasons and in timing characteristics of air temperature. Theor. Appl. Climatol. 2020, 140, 1247–1261. [Google Scholar] [CrossRef]
- Kaboli, S.; Hekmatzadeh, A.A.; Darabi, H.; Haghighi, A.T. Variation in physical characteristics of rainfall in Iran, determined using daily rainfall concentration index and monthly rainfall percentage index. Theor. Appl. Climatol. 2021, 144, 507–520. [Google Scholar] [CrossRef]
- Modarres, R.; de Paulo Rodrigues da Silva, V. Rainfall trends in arid and semi-arid regions of Iran. J. Arid Environ. 2007, 70, 344–355. [Google Scholar] [CrossRef]
- Modarres, R.; Sarhadi, A. Rainfall trends analysis of Iran in the last half of the twentieth century. J. Geophys. Res. Atmos. 2009, 114, 9. [Google Scholar] [CrossRef]
- Mohammadi, B. Trend Analysis of annual rainfall over Iran. Geogr. Environ. Plan. 2011, 22, 95–106. [Google Scholar]
- Raziei, T.; Arasteh, P.D.; Saghafian, B. Annual rainfall trend in arid and semi-arid regions of Iran. In Proceedings of the ICID 21st European Regional Conference, Frankfurt, Germany; Slubice, Polan, 15–19 May 2005; pp. 15–19. [Google Scholar]
- Soltani, S.; Saboohi, R.; Yaghmaei, L. Rainfall and rainy days trend in Iran. Clim. Change 2012, 110, 187–213. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P.H. Temporal variability of precipitation over Iran: 1966–2005. J. Hydrol. 2011, 396, 313–320. [Google Scholar] [CrossRef]
- Alijani, B. Time series analysis of daily rainfall variability and extreme events. In Proceedings of the 10th International Meeting on Statistical Climatology, Beijing, China, 20 August 2007. [Google Scholar]
- Ma, S.; Zhou, T.; Dai, A.; Han, Z. Observed Changes in the Distributions of Daily Precipitation Frequency and Amount over China from 1960 to 2013. J. Clim. 2015, 28, 6960–6978. [Google Scholar] [CrossRef]
- Durocher, M.; Burn, D.H.; Mostofi Zadeh, S.; Ashkar, F. Estimating flood quantiles at ungauged sites using nonparametric regression methods with spatial components. Hydrol. Sci. J. 2019, 64, 1056–1070. [Google Scholar] [CrossRef]
- Ahmed, K.; Sachindra, D.A.; Shahid, S.; Iqbal, Z.; Nawaz, N.; Khan, N. Multi-model ensemble predictions of precipitation and temperature using machine learning algorithms. Atmos. Res. 2020, 236, 104806. [Google Scholar] [CrossRef]
- Douglas, E.M.; Vogel, R.M.; Kroll, C.N. Trends in floods and low flows in the United States: Impact of spatial correlation. J. Hydrol. 2000, 240, 90–105. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann–Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Partal, T.; Kahya, E. Trend analysis in Turkish precipitation data. Hydrol. Process. 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S. Changes of Pan Evaporation in the West of Iran. Water Resour. Manag. 2011, 25, 97–111. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendal, M. Rank Correlation Methods; Charles Griffin: London, UK, 1975. [Google Scholar]
- Yue, S.; Pilon, P. A comparison of the power of the t test, Mann-Kendall and bootstrap tests for trend detection/Une comparaison de la puissance des tests t de Student, de Mann-Kendall et du bootstrap pour la détection de tendance. Hydrol. Sci. J. 2004, 49, 21–37. [Google Scholar] [CrossRef]
- von Storch, H.; Navarra, A. Analysis of Climate Variability: Applications of Statistical Techniques: Proceedings of an Autumn School Organized by the Commision of the European Community on Elba from October 30 to November 6, 1993; Springer: Berlin/Heidelberg, Germany, 1995; Volume 2. [Google Scholar]
- Kendall, M.G.; Stuart, A.J.L. The Advanced Theory of Statistics; Charles Griffin & Co.: London, UK, 1968; Volume 3. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Chamaillé-Jammes, S.; Fritz, H.; Murindagomo, F. Detecting climate changes of concern in highly variable environments: Quantile regressions reveal that droughts worsen in Hwange National Park, Zimbabwe. J. Arid Environ. 2007, 71, 321–326. [Google Scholar] [CrossRef]
- Malekinezhad, H.; Zare-Garizi, A. Regional frequency analysis of daily rainfall extremes using L-moments approach. Atmósfera 2014, 27, 411–427. [Google Scholar] [CrossRef] [Green Version]
- Raziei, T.; Daryabari, J.; Bordi, I.; Modarres, R.; Pereira, L.S. Spatial patterns and temporal trends of daily precipitation indices in Iran. Clim. Chang. 2014, 124, 239–253. [Google Scholar] [CrossRef]
- Dhorde, A.G.; Zarenistanak, M.; Kripalani, R.H.; Preethi, B. Precipitation analysis over southwest Iran: Trends and projections. Meteorol. Atmos. Phys. 2014, 124, 205–216. [Google Scholar] [CrossRef]
- Alavinia, S.H.; Zarei, M. Analysis of spatial changes of extreme precipitation and temperature in Iran over a 50-year period. Int. J. Climatol. 2021, 41, E2269–E2289. [Google Scholar] [CrossRef]
- Rahimi, M.; Fatemi, S.S. Mean versus Extreme Precipitation Trends in Iran over the Period 1960–2017. Pure Appl. Geophys. 2019, 176, 3717–3735. [Google Scholar] [CrossRef]
- Fathian, F.; Ghadami, M.; Haghighi, P.; Amini, M.; Naderi, S.; Ghaedi, Z. Assessment of changes in climate extremes of temperature and precipitation over Iran. Theor. Appl. Climatol. 2020, 141, 1119–1133. [Google Scholar] [CrossRef]
- Rahimzadeh, F.; Asgari, A.; Fattahi, E. Variability of extreme temperature and precipitation in Iran during recent decades. Int. J. Climatol. 2009, 29, 329–343. [Google Scholar] [CrossRef]
- Asgari, A.; Rahimzadeh, F.; Mohammadian, N.; Fattahi, E. Trend Analysis of Extreme Precipitation Indices Over Iran. Iran-Water Resour. Res. 2007, 3, 42–55. [Google Scholar]
- Alpert, P.; Ben-Gai, T.; Baharad, A.; Benjamini, Y.; Yekutieli, D.; Colacino, M.; Diodato, L.; Ramis, C.; Homar, V.; Romero, R.; et al. The paradoxical increase of Mediterranean extreme daily rainfall in spite of decrease in total values. Geophys. Res. Lett. 2002, 29, 31-1–31-4. [Google Scholar] [CrossRef] [Green Version]
- Ahmadi, F.; Nazeri Tahroudi, M.; Mirabbasi, R.; Khalili, K.; Jhajharia, D. Spatiotemporal trend and abrupt change analysis of temperature in Iran. Meteorol. Appl. 2018, 25, 314–321. [Google Scholar] [CrossRef] [Green Version]
- Saboohi, R.; Soltani, S.; Khodagholi, M. Trend analysis of temperature parameters in Iran. Theor. Appl. Climatol. 2012, 109, 529–547. [Google Scholar] [CrossRef]
- Murray, V.; Ebi, K.L. IPCC Special Report on Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation (SREX). J. Epidemiol. Community Health 2012, 66, 759. [Google Scholar] [CrossRef]
- Groisman, P.Y.A.; Karl, T.R.; Easterling, D.R.; Knight, R.W.; Jamason, P.F.; Hennessy, K.J.; Suppiah, R.; Page, C.M.; Wibig, J.; Fortuniak, K.; et al. Change. In Weather and Climate Extremes: Changes, Variations and a Perspective from the Insurance Industry; Karl, T.R., Nicholls, N., Ghazi, A., Eds.; Springer: Dordrecht, The Netherlands, 1999; pp. 243–283. [Google Scholar]
- Degefu, M.A.; Bewket, W. Variability and trends in rainfall amount and extreme event indices in the Omo-Ghibe River Basin, Ethiopia. Reg. Environ. Change 2014, 14, 799–810. [Google Scholar] [CrossRef]
- Porto de Carvalho, J.R.; Assad, E.D.; de Oliveira, A.F.; Silveira Pinto, H. Annual maximum daily rainfall trends in the Midwest, southeast and southern Brazil in the last 71 years. Weather Clim. Extrem. 2014, 5–6, 7–15. [Google Scholar] [CrossRef] [Green Version]
- Ghenim, A.N.; Megnounif, A. Variability and Trend of Annual Maximum Daily Rainfall in Northern Algeria. Int. J. Geophys. 2016, 2016, 6820397. [Google Scholar] [CrossRef]
- Chen, F.; Chen, H.; Yang, Y. Annual and seasonal changes in means and extreme events of precipitation and their connection to elevation over Yunnan Province, China. Quat. Int. 2015, 374, 46–61. [Google Scholar] [CrossRef]
- Guan, Y.; Zheng, F.; Zhang, X.; Wang, B. Trends and variability of daily precipitation and extremes during 1960–2012 in the Yangtze River Basin, China. Int. J. Climatol. 2017, 37, 1282–1298. [Google Scholar] [CrossRef]
- Mei, C.; Liu, J.; Chen, M.-T.; Wang, H.; Li, M.; Yu, Y. Multi-decadal spatial and temporal changes of extreme precipitation patterns in northern China (Jing-Jin-Ji district, 1960–2013). Quat. Int. 2018, 476, 1–13. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, W.; Liang, S.; Wang, S. Spatiotemporal Variations of Extreme Precipitation Events in the Jinsha River Basin, Southwestern China. Adv. Meteorol. 2020, 2020, 3268923. [Google Scholar] [CrossRef]

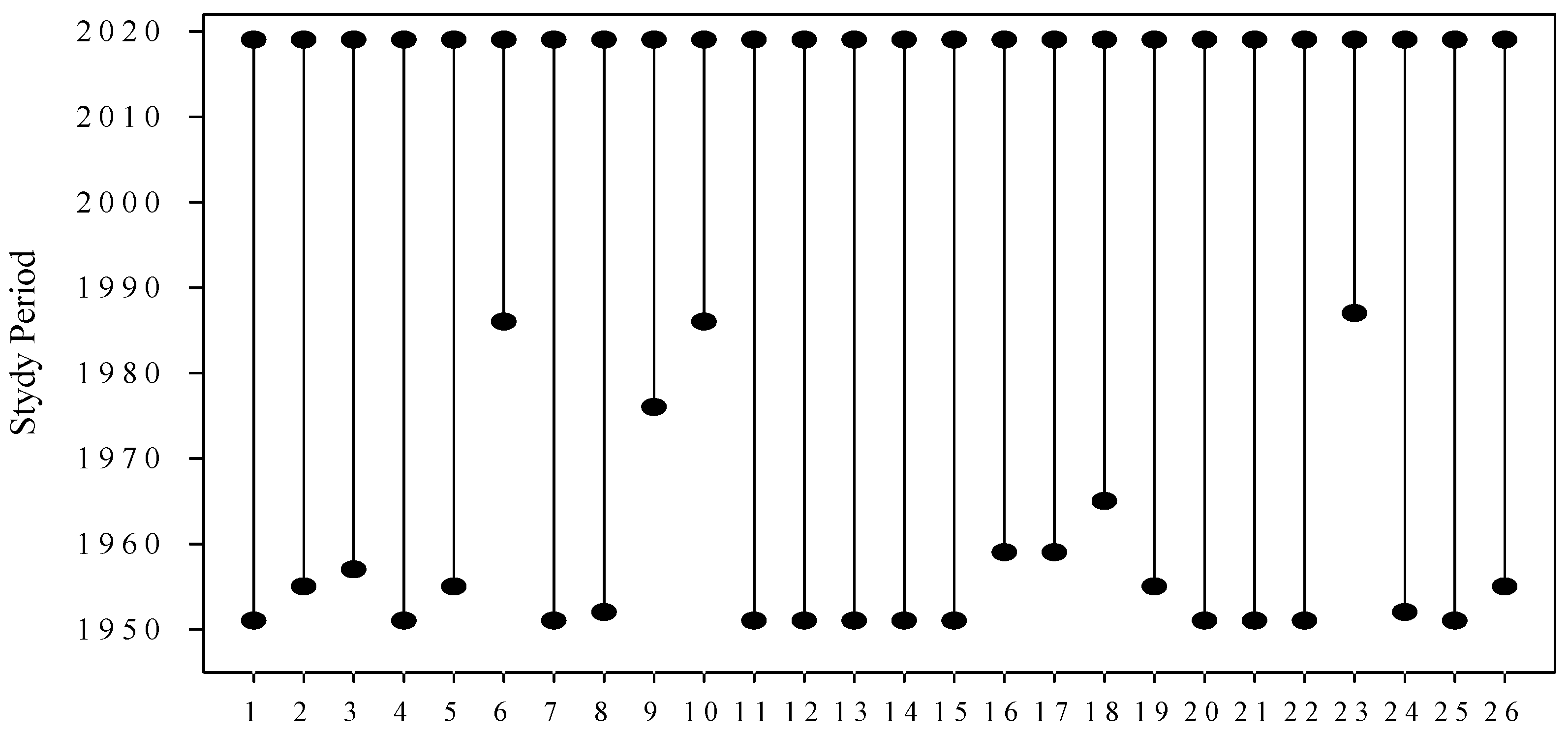

| No. | Station | Longitude (E) | Latitude (N) | Altitude (m) | River Basin |
|---|---|---|---|---|---|
| 1 | Ahvaz | 48.7 | 31.3 | 22.5 | Persian Gulf and Oman Sea |
| 2 | Arak | 49.8 | 34.1 | 1702.8 | Central Plateau |
| 3 | Bandar Abbas | 56.4 | 27.2 | 9.8 | Persian Gulf and Oman Sea |
| 4 | Bandar Anzali | 49.5 | 37.5 | −23.6 | Caspian Sea |
| 5 | Birjand | 59.3 | 32.9 | 1491.0 | Central Plateau |
| 6 | Bushehr | 50.8 | 28.9 | 8.4 | Persian Gulf and Oman Sea |
| 7 | Isfahan | 51.7 | 32.5 | 1550.4 | Central Plateau |
| 8 | Gorgan | 54.4 | 36.9 | 0.0 | Caspian Sea |
| 9 | Hamedan | 48.5 | 34.9 | 1740.8 | Central Plateau |
| 10 | Ilam | 46.4 | 33.6 | 1337.0 | Persian Gulf and Oman Sea |
| 11 | Kerman | 57.0 | 30.3 | 1754.0 | Central Plateau |
| 12 | Kermanshah | 47.2 | 34.4 | 1318.5 | Persian Gulf and Oman Sea |
| 13 | Khorramabad | 48.3 | 33.4 | 1147.8 | Persian Gulf and Oman Sea |
| 14 | Mashhad | 59.6 | 36.2 | 999.2 | Qareqom |
| 15 | Urmia | 45.1 | 37.7 | 1328.0 | Lake Urmia |
| 16 | Qazvin | 50.1 | 35.7 | 1279.1 | Central Plateau |
| 17 | Sanandaj | 47.0 | 35.3 | 1373.4 | Persian Gulf and Oman Sea |
| 18 | Semnan | 53.4 | 35.6 | 1127.0 | Central Plateau |
| 19 | Shahrekord | 50.8 | 32.3 | 2048.9 | Persian Gulf and Oman Sea |
| 20 | Shiraz | 52.6 | 29.6 | 1488.0 | Central Plateau |
| 21 | Tabriz | 46.2 | 38.1 | 1361.0 | Lake Urmia |
| 22 | Tehran | 51.3 | 35.7 | 1191.0 | Central Plateau |
| 23 | Yasuj | 51.6 | 30.7 | 1816.3 | Persian Gulf and Oman Sea |
| 24 | Yazd | 54.3 | 31.9 | 1230.2 | Central Plateau |
| 25 | Zahedan | 60.9 | 29.5 | 1370.0 | Eastern Border |
| 26 | Zanjan | 48.5 | 36.7 | 1659.4 | Caspian Sea |
| Indices | Definition | Unit |
|---|---|---|
| Index 1 | The maximum 3-h precipitation | mm |
| Index 2 | The maximum 6-h precipitation | mm |
| Index 3 | The maximum 24-h precipitation | mm |
| Index 4 | The average 3-h precipitation | mm |
| Index 5 | The average 6-h precipitation | mm |
| Index 6 | The average 24-h precipitation | mm |
| Index 7 | The number of 3-h precipitation above 95% quantile | number |
| Index 8 | The average of extreme 3-h precipitation | mm |
| Index 9 | The ratio of the 3-h extreme precipitation to annual precipitation | % |
| Index 10 | The annual precipitation | mm |
| Index 11 | The number of wet days | days |
| Index 12 | The average annual temperature | °C |
| Index 13 | The maximum annual temperature | °C |
| Index 14 | The minimum annual temperature | °C |
| Basin | Stations | Index 1 | Index 2 | Index 3 | Index 4 | Index 5 | Index 6 | Index 7 | Index 8 | Index 9 | Index 10 | Index 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| The Persian Gulf and Oman Sea | Ahvaz | −1.163 | −0.86 | −0.178 | −5.63 | −5.64 | −0.664 | −2.46 | −0.326 | −2.82 | −0.628 | 4.397 |
| Bandar Abas | −1.531 | −1.44 | −0.419 | −3.67 | −3.67 | −0.616 | −1.855 | −1.383 | −2.399 | −0.627 | 3.857 | |
| Bushehr | −0.666 | −1.28 | −0.387 | −2.81 | −2.81 | −0.563 | −0.899 | −0.418 | −0.697 | −1.224 | −2.616 | |
| Ilam | −0.847 | −1.32 | −0.565 | −2.31 | −2.31 | −0.830 | −0.328 | −0.771 | −0.415 | −0.474 | −1.202 | |
| Kermanshah | −2.181 | −1.2 | 1.27 | −6.01 | −6.01 | 0.108 | −1.977 | −0.927 | −4.42 | 0.025 | 1.425 | |
| Khorramabad | −2.458 | −1.67 | 2.048 | −6.34 | −6.34 | −0.927 | −2.735 | −1.466 | −3.636 | −0.751 | 0.098 | |
| Sanandaj | −4.394 | −3.1 | −0.361 | −6 | −6 | −3.310 | −3.419 | −4.108 | −3.989 | −2.889 | 0.641 | |
| Shahrekord | −4.235 | −2.4 | −0.476 | −5.15 | −5.16 | 0.549 | −1.591 | −4.942 | −5.023 | 0.753 | 4.438 | |
| Yasuj | −1.195 | −0.76 | 0.387 | −2.09 | −2.06 | −0.852 | −0.265 | −0.418 | −0.232 | −1.348 | −0.637 | |
| Central Plateau | Arak | −3.503 | −3.1 | −1.140 | −5.55 | −5.08 | −1.636 | −2.847 | −2.923 | −3.702 | −1.285 | 2.634 |
| Birjand | −3.083 | −2.3 | −1.411 | −5.28 | −5.23 | −1.111 | −1.796 | −2.37 | −2.689 | −1.058 | 0.799 | |
| Isfahan | 0.312 | 0.74 | 1.892 | −3.71 | −3.71 | 1.31 | 0.561 | 0.355 | −0.338 | 1.11 | −2.78 | |
| Hamedan | −1.455 | −1.32 | 1.275 | −3.26 | −3.26 | 0 | 1.313 | −0.233 | 0.355 | 0.354 | 1.144 | |
| Kerman | −2.478 | −3.4 | −2.095 | −6.96 | −6.95 | −3.361 | −4.208 | −2.964 | −3.762 | −3.289 | −0.845 | |
| Qazvin | −2.414 | −1.92 | 0.666 | −5.08 | −5.07 | 0.653 | −1.063 | −2.453 | −4.188 | 0.777 | −0.473 | |
| Semnan | −0.0874 | −0.26 | 1.82 | −3.62 | −3.61 | 0 | −0.118 | −0.705 | −0.508 | −0.716 | 0.029 | |
| Shiraz | −5.822 | −5.1 | −1.583 | −5.70 | −5.70 | −1.253 | −4.023 | −3.773 | −6.442 | −1.273 | 1.861 | |
| Tehran | −1.504 | −1.73 | 0.658 | −5.24 | −5.25 | 0.419 | −1.796 | −2.14 | −3.299 | 0.57 | 2.176 | |
| Yazd | −1.444 | −1.37 | −0.349 | −4.06 | −4.06 | −0.397 | −1.107 | −1.49 | −1.906 | −0.153 | 4.723 | |
| Urmia Lake | Urmia | −2.138 | −0.99 | 1.135 | −5.75 | −5.57 | −1.238 | −3.053 | −1.575 | −4.822 | −1.212 | 0.466 |
| Tabriz | −4.108 | −3.4 | −1.705 | −5.79 | −5.78 | −3.308 | −3.605 | −3.5 | −4.113 | −2.543 | 2.436 | |
| Caspian sea | Bandar Anzali | −3.926 | −3.7 | −2.160 | −7.25 | −7.26 | −2.056 | −3.828 | −4.133 | −5.023 | −1.818 | 2.529 |
| Gorgan | 0.556 | 0.86 | 2.123 | −5.48 | −5.48 | −3.431 | −4.097 | 0.606 | −2.478 | −3.701 | 2.982 | |
| Zanjan | −2.763 | −2.9 | −0.912 | −5.57 | −5.57 | −0.888 | −2.540 | −2.69 | −3.572 | −0.379 | 3.885 | |
| Eastern border | Zahedan | −3.789 | −3.6 | −2.551 | −7 | −7 | −2.989 | −4.716 | −3.64 | −4.784 | −2.853 | 2.805 |
| Qareqom | Mashhad | −3.925 | −2.7 | −0.886 | −6.34 | −6.34 | −0.16 | −0.90 | −3.73 | −2.988 | −0.16 | 0.819 |
| Stations | Index 1 | Index 2 | Index 3 | Index 4 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Quantile Re. | 0.1 | 0.25 | 0.5 | 0.75 | 0.9 | 0.1 | 0.25 | 0.5 | 0.75 | 0.9 | 0.1 | 0.25 | 0.5 | 0.75 | 0.9 | 0.1 | 0.25 | 0.5 | 0.75 | 0.9 |
| Ahvaz | −10.53 | −5.41 | −6.45 | −25.81 | −13.04 | −15.56 | −3.92 | 0 | −27.86 | −20.91 | −6.67 | 0 | 0 | −25 | 11.4 | −0.18 | −0.16 | −0.35 | −0.48 | −0.67 |
| Bandar Abas | 0.71 | −7.69 | −12.5 | −32 | 11.11 | −5.26 | −10.53 | −25 | −22.4 | 27.78 | 1.05 | −4.35 | −11.11 | −4.35 | 55.5 | −0.11 | −0.21 | −0.26 | −0.37 | −0.34 |
| Bushehr | −44.44 | −46.15 | −27.59 | −132 | −46.15 | 1.04 | −34.78 | −40.4 | −21.7 | −93.5 | −18.52 | 1.75 | 2.44 | −50.56 | −105 | −0.44 | −0.4 | −0.45 | −0.76 | 0.03 |
| Ilam | −18.18 | −20 | −8.27 | −0.33 | 2.77 | −15 | −18.52 | −42.1 | 2.82 | 175 | −56.67 | −41.18 | 0 | 95 | 74.5 | −0.54 | −0.53 | −0.67 | −0.6 | −0.78 |
| Kermanshah | −5.26 | 0 | −16.67 | −18.42 | −13.21 | −9.37 | 2.94 | −22.7 | −18.2 | −16 | 14.81 | 16.38 | 3.18 | 0 | 9.34 | −0.3 | −0.28 | −0.44 | −0.88 | −1.19 |
| Khorramabad | −3.45 | −12.12 | −15.63 | −17.19 | 11 | −10 | −18.64 | −13.5 | −8.75 | 11.9 | 8.33 | 7.31 | 3.92 | 27.27 | 49.2 | −0.54 | −0.56 | −0.71 | −1.04 | −1.04 |
| Sanandaj | −13.64 | −25 | −26.1 | −30.6 | −37.5 | 1.06 | −27.5 | −23 | −23.2 | −23.5 | 0.04 | −6.37 | −7.35 | −2.56 | 17.3 | −0.3 | −0.64 | −0.9 | −1.18 | −0.11 |
| Shahrekord | −5.56 | −9.09 | −19.1 | −27.3 | −34.04 | −12.2 | −13.64 | −17.8 | −26.3 | −22.9 | −1.14 | 0.62 | −9.26 | 2.22 | 2.82 | −0.19 | −0.29 | −0.38 | −0.59 | −0.74 |
| Yasuj | −14.29 | −26.3 | −21.05 | 0 | −29.03 | −16 | −20 | −37.5 | −6.86 | 16.13 | −10 | 3.47 | 4.16 | 5.11 | 5.5 | −0.73 | −1.01 | −0.87 | −0.4 | −0.67 |
| Arak | −5.26 | −22.7 | −24.39 | −34.4 | −30.15 | 23.02 | 14.63 | −19.1 | −24.4 | −38.6 | −18.75 | −18.9 | −7.41 | 6.67 | −5.08 | −0.3 | −0.49 | −0.53 | −0.84 | −0.73 |
| Birjand | −4 | −6.9 | −15.4 | −13.89 | −22.22 | −6.52 | −7.69 | −10.8 | 1.21 | −22.2 | −5.82 | −7.89 | −7.41 | 16.67 | −11.4 | −0.8 | −0.22 | −0.3 | −0.36 | −0.39 |
| Esfahan | 6.25 | 0 | 2.99 | −3.45 | −0.22 | 2 | 3.57 | 4.35 | 5.56 | −5.56 | 7.27 | 3.92 | 16.13 | 13.56 | 22.4 | −0.06 | −0.07 | −0.16 | −0.24 | −0.24 |
| Hamedan | 2.9 | 6.67 | −0.17 | −4.55 | 1.66 | 29.09 | 13.58 | −3.45 | −25 | 2.01 | 26.2 | 1.39 | 16.8 | −2.78 | 5.88 | 0 | −0.04 | −0.35 | −0.67 | −0.41 |
| Kerman | −4.55 | −4.44 | −6.67 | −15 | −16.67 | 0 | −11.11 | −19 | −26 | −27 | −1.58 | −3.7 | −10 | −18.72 | −15 | −0.09 | −0.25 | −0.29 | −0.35 | −0.4 |
| Qazvin | 0.65 | −4 | −11.11 | −14.29 | −14.81 | −4.88 | −3.48 | −6.67 | −15 | −20 | 10.45 | 5.45 | 7.14 | 0.03 | 8.62 | −0.23 | −0.23 | −0.46 | −0.51 | −0.6 |
| Semnan | 3.7 | 0 | −2.44 | −10 | 5.56 | 5 | 4.35 | 2.42 | 3.57 | 6.38 | 3.23 | 9.55 | 0 | 14.32 | 18.9 | −0.12 | −0.09 | −0.13 | −0.32 | −0.47 |
| Shiraz | −17.9 | −23.4 | −33.3 | −46.8 | −47.3 | −14.58 | −25 | −41 | −74 | −100 | 1.91 | −14.31 | −9.14 | −29.55 | −75 | −0.32 | −0.26 | −0.51 | −0.73 | −1 |
| Tehran | 0 | −2.44 | −6.9 | −6.45 | −4.55 | 0 | −1.03 | −7.81 | −24 | −16 | 6.38 | 3.33 | 2.89 | −5.38 | 0 | −0.16 | −0.21 | −0.28 | −0.39 | −0.52 |
| Yazd | −4 | −4.17 | −6.12 | −7.69 | −14.29 | −3 | −4.84 | −4 | −14 | −12.7 | 2.08 | −3.11 | 0.69 | 0 | −11.2 | −0.04 | −0.06 | −0.08 | −0.14 | −0.18 |
| Urmia | 0 | −15.2 | −9.09 | −6.9 | −10 | −12.64 | −7.27 | 0 | −5.56 | 2 | −4.28 | −1.96 | 17.39 | 13.31 | 21.5 | −0.49 | −0.52 | −0.57 | −0.63 | −0.59 |
| Tabriz | −9.7 | −11.1 | −13.64 | −16.3 | −21.8 | −12.12 | −11.11 | −14.7 | −10.7 | −16.2 | −5.26 | −12.94 | −6.67 | −5.16 | 12 | −0.38 | −0.47 | −0.49 | −0.56 | −0.76 |
| Bandar Anzali | −29.27 | −31.29 | −52.63 | −145 | −242 | −27.78 | −46.15 | −96 | −161 | 12.65 | −11.86 | −13.33 | −19.57 | −87.76 | 12.6 | −1.99 | −2.48 | −2.72 | −3.39 | −4.59 |
| Gorgan | 4 | 3.57 | 2.63 | 8.7 | 3.39 | 27.27 | 8.33 | 8.16 | 2.63 | 2.94 | 25.93 | 22.11 | 26.67 | 27.27 | 18.1 | −0.27 | −0.67 | −1.13 | −1.32 | −1.6 |
| Zanjan | −9.52 | 7.69 | −14.7 | −13.04 | −17.19 | −4.65 | −10.87 | −16 | −14.8 | −24.5 | −4.06 | −8.78 | −7.67 | −17.4 | −14.2 | −0.25 | −0.37 | −0.54 | −0.68 | −0.78 |
| Zahedan | −10.53 | −13.3 | −17.6 | −20.41 | −20.45 | −10.87 | −14 | −26 | −17.6 | −13.4 | −13.54 | −13.33 | −11.22 | −16.64 | −17.6 | −0.13 | −0.17 | −0.18 | −0.25 | −0.25 |
| Mashhad | −10.26 | −13.1 | −15 | −16.7 | −18.4 | −10.26 | −11.82 | −12.7 | −20 | −22.4 | 0 | −6.86 | −3.17 | −10.34 | −8.33 | −0.29 | −0.21 | −0.36 | −0.39 | −0.48 |
| Stations | Index 5 | Index 6 | Index 7 | Index 8 | ||||||||||||||||
| Quantile Re. | 0.1 | 0.25 | 0.5 | 0.75 | 0.9 | 0.1 | 0.25 | 0.5 | 0.75 | 0.9 | 0.1 | 0.25 | 0.5 | 0.75 | 0.9 | 0.1 | 0.25 | 0.5 | 0.75 | 0.9 |
| Ahvaz | 0.35 | −0.31 | −0.69 | −0.97 | −1.28 | 0.07 | 0.02 | −0.09 | −0.15 | −0.21 | −1.89 | −3.85 | −5.2 | −2.38 | 0.25 | −1.47 | 2.59 | 3.11 | 7.14 | 8.11 |
| Bandar Abas | −0.21 | −0.42 | −0.52 | −0.73 | −0.67 | −0.06 | −0.27 | −0.02 | 0.04 | −0.27 | 0 | −2.27 | −2.13 | −1.79 | 0 | 2.17 | −3.1 | −1.9 | −13.77 | 3.12 |
| Bushehr | −0.88 | −0.8 | −0.9 | −1.53 | 0.07 | −0.97 | −0.44 | 0.04 | −0.37 | −0.2 | −3.7 | −7.14 | −4.76 | −0.12 | 0 | −4.17 | 1.3 | 0.7 | 25.61 | 10.51 |
| Ilam | −1.09 | −1.06 | −1.35 | −0.12 | −1.56 | −0.91 | −0.68 | −1.04 | −1.6 | 0.12 | 0 | 0.29 | 0 | −7.14 | −6.12 | −1.98 | −3.6 | −0.69 | 1.27 | 1.66 |
| Kermanshah | −0.62 | −0.56 | −0.88 | −1.76 | −2.39 | 0.31 | 0.24 | −0.3 | −0.5 | −0.85 | 0 | −2.04 | −2.63 | −6.9 | −14 | −1.15 | −3.52 | 0.07 | −0.7 | −2.29 |
| Khorramabad | −1.08 | −1.13 | −1.42 | −2.09 | −2.07 | −0.06 | −0.27 | −0.32 | −0.46 | 0.11 | −5.6 | −6.7 | −4.76 | −5.13 | −5.71 | −7.1 | −3.45 | −3.19 | 0.81 | −1.69 |
| Sanandaj | −0.61 | −1.28 | −0.18 | −2.36 | −0.22 | 0.13 | −0.57 | −0.57 | −1.23 | −0.99 | 0 | −9.7 | −11 | −15 | −12.5 | −6.8 | −7.4 | −8.3 | −8.9 | −12 |
| Shahrekord | −0.39 | −0.59 | −0.76 | −1.18 | −1.48 | 0.13 | 0.16 | 0.16 | −0.02 | −0.09 | 0 | 0 | −3.77 | −8.34 | −6.67 | −3.49 | −7.7 | −9.3 | −12 | −15 |
| Yasuj | −1.46 | −2.02 | −1.74 | −0.81 | −1.35 | −1.56 | −2.12 | −0.16 | −0.66 | 0.17 | −5.88 | −10 | 0 | 0 | 1.49 | 3.06 | −3.57 | −1.96 | −4.48 | −14.25 |
| Arak | −0.59 | −0.99 | −1.07 | −1.68 | −1.47 | −0.05 | 0.21 | 0.38 | −0.09 | −0.18 | −4.17 | −4.98 | −6.67 | −5.77 | −9.84 | −3.75 | −4.02 | −6.43 | −9.6 | −5.98 |
| Birjand | −0.15 | −0.43 | −0.59 | −0.72 | −0.78 | −0.07 | −0.05 | −0.01 | −0.01 | −0.22 | 0 | −1.69 | −2.86 | −5.13 | −5.08 | −2.19 | −3.03 | −2.79 | −5.72 | −4.04 |
| Esfahan | −0.12 | −0.13 | −0.3 | −0.48 | −0.48 | 0.15 | 0.15 | 0.07 | 0.13 | 0.08 | 1.92 | 0 | 0 | 1.75 | 0 | 1.15 | 0 | 0 | −1.75 | −2.98 |
| Hamedan | 0 | −0.08 | −0.7 | −1.35 | −0.82 | 0.32 | −0.15 | −0.25 | −0.62 | 0.43 | 6.25 | 11.5 | 5.56 | 7.69 | 0.55 | 5 | 1.02 | −2.69 | −6.67 | −7.5 |
| Kerman | −0.18 | −0.5 | −0.58 | −0.7 | −0.8 | −0.22 | −0.2 | −0.24 | −0.32 | −0.43 | −2.04 | −5.2 | −4.7 | −5.7 | −11 | −0.89 | −1.19 | −1.11 | −2.27 | −2.73 |
| Qazvin | −0.46 | −0.47 | −0.92 | −1.02 | −1.2 | 0.21 | 0.4 | 0.02 | −0.08 | −0.5 | −2.86 | 0 | −8.33 | −3.23 | −14.63 | −2.31 | −5.1 | −2.66 | −0.38 | 2.38 |
| Semnan | −0.24 | −0.17 | −0.27 | −0.64 | −0.93 | 0.01 | 0.11 | −0.03 | −0.06 | −0.34 | 1.96 | 0 | 2.27 | −3.33 | −4.17 | 0.67 | −1.73 | 0.99 | −5 | −3.74 |
| Shiraz | −0.65 | −0.52 | −1.02 | −1.45 | −2 | −0.48 | 0.16 | −0.3 | −0.4 | −1.36 | −4.3 | −4.08 | −6.7 | −7.1 | −16 | −7.5 | −6.5 | −11 | −14 | −22.7 |
| Tehran | −0.32 | −0.41 | −0.56 | −0.78 | −1.05 | 0.1 | 0.06 | 0.07 | 0.1 | −0.31 | −1.72 | 0 | −4.62 | −7.84 | −9.6 | −1.27 | −2.47 | −2.28 | −1.78 | −4.62 |
| Yazd | −0.08 | −0.13 | −0.17 | −0.28 | −0.36 | 0.01 | −0.02 | 0 | −0.05 | 0.1 | 0 | −1.72 | 0 | −2.7 | 0 | −1.48 | −2.04 | −2.54 | −3.95 | 3.7 |
| Urmia | −0.99 | −1.04 | −1.15 | −1.27 | −1.19 | −0.34 | −0.09 | −0.39 | −0.3 | 0.1 | −10 | −9.1 | −8.7 | −8 | −3.28 | −2.31 | −5.1 | −2.66 | −0.38 | 2.38 |
| Tabriz | −0.76 | −0.95 | −0.97 | −1.12 | −1.53 | −0.27 | −0.25 | −0.33 | −0.29 | −0.62 | −5.6 | −7.1 | −7.27 | −5.71 | −12.1 | −1.8 | −2.97 | −2.56 | −3.99 | −3.09 |
| Bandar Anzali | −3.97 | −4.95 | −5.44 | −6.78 | −9.19 | −0.07 | −0.05 | −0.19 | −0.01 | −0.22 | −5.26 | −8.51 | −19 | −14.3 | −15.22 | −10 | −12 | −14 | −28 | −27 |
| Gorgan | −0.54 | −1.34 | −2.26 | −2.63 | −0.32 | −0.23 | −0.76 | −0.48 | −0.82 | −1.12 | 0 | −8.33 | −11 | −12 | −15.6 | 2.52 | 1.68 | 4.2 | −1.65 | 0.36 |
| Zanjan | −0.5 | −0.73 | −1.07 | −1.37 | −1.55 | 0.07 | 0.06 | −0.07 | −0.2 | −0.51 | −5.13 | −5.41 | −4.76 | −9.76 | −14.3 | −2.5 | −3.11 | −4 | −2.59 | −3.49 |
| Zahedan | −0.27 | −0.34 | −0.36 | −0.51 | −0.51 | −0.14 | −0.21 | −0.2 | −0.14 | −0.31 | −4.1 | −4.1 | −4.5 | −5.4 | −3.4 | −2.08 | −1.6 | −4.78 | −6.41 | −6.67 |
| Mashhad | −0.58 | −0.42 | −0.73 | −0.78 | −0.97 | 0 | 0.07 | −0.12 | −0.11 | −0.17 | −2.04 | −3.23 | −0.00 | −1.52 | −0.00 | −3.51 | −4.3 | −4.3 | −2.56 | −5.45 |
| Stations | Index 9 | Index 10 | Index 11 | |||||||||||||||||
| Quantile Re. | −0.3 | −0.4 | −0.4 | −0.22 | −0.4 | 5.23 | −11.3 | −5.53 | −54.7 | −61 | 32.69 | 50 | 34.9 | 38.5 | 25.1 | |||||
| Ahvaz | 0 | −0.7 | −0.41 | −0.29 | −0.05 | −21.2 | −21.7 | −6.69 | 4.02 | −99.9 | 11.54 | 17.1 | 15.6 | 20 | 15.25 | |||||
| Bandar Abas | −0.68 | −0.89 | −0.45 | 0.14 | 0.38 | −115 | 3.42 | −18.8 | −291 | −719 | −29.1 | −23.1 | −38 | −33.3 | −46.1 | |||||
| Bushehr | −0.04 | 0.21 | −0.16 | −0.02 | −0.06 | 21.24 | −246 | 30.07 | 429.3 | 41.52 | −2.74 | −44.4 | −26.9 | −81.5 | −6.45 | |||||
| Ilam | −0.01 | −0.2 | −0.3 | −0.24 | −0.13 | 87.98 | 78.97 | −134 | −316 | −437 | 31.82 | 10.81 | 4.55 | 24.53 | 20 | |||||
| Kermanshah | −0.3 | −0.18 | −0.3 | −0.3 | −0.25 | 16.88 | 5.53 | −89.8 | 21.16 | 41.32 | 7.46 | −1.69 | 14.29 | −11.1 | −4.55 | |||||
| Khorramabad | −0.19 | −0.3 | −0.5 | −0.4 | −0.5 | 13.92 | −168 | −195 | −428 | −160 | 17.5 | 10.53 | 12.5 | 0 | 2.94 | |||||
| Sanandaj | −0.12 | −0.3 | −0.4 | −0.5 | −0.6 | 45.58 | 81.34 | 47.83 | −6 | 22.92 | 43.5 | 53.8 | 36.8 | 5 | 37.3 | |||||
| Shahrekord | −0.04 | −0.24 | −0.23 | 0.34 | 0.2 | −392 | 30.6 | 42.12 | −844 | −619 | 36.84 | 0 | −9.09 | −40.9 | −13.3 | |||||
| Yasuj | −0.5 | −0.3 | −0.4 | −0.4 | −0.41 | 9.84 | −75.1 | −15.1 | −89.4 | −188 | 32.5 | 31 | 36.4 | 4.35 | 27.27 | |||||
| Arak | −0.05 | −0.3 | −0.3 | −0.5 | −0.4 | −26.7 | −7.87 | −54.3 | −30.5 | 11.16 | 7.14 | 8.33 | 0 | −5.45 | −9.62 | |||||
| Birjand | 0.23 | 0.08 | −0.05 | 0.08 | −0.14 | 50.51 | 48.29 | 26.05 | 28.89 | 34.04 | −10.6 | −7.41 | −17 | 2.46 | −42 | |||||
| Esfahan | 0.4 | 0.32 | 0.15 | −0.24 | −0.15 | 10.07 | 12.84 | −31.2 | 18.8 | 80.63 | 23.65 | 31.25 | 4.55 | 31.25 | 44.44 | |||||
| Hamedan | −0.27 | −0.4 | −0.3 | −0.4 | −0.5 | −33.3 | −74 | −83.5 | −90.3 | −155 | 0 | 6.9 | −8.7 | −10.3 | −29.7 | |||||
| Kerman | −0.17 | −0.2 | −0.3 | −0.4 | −0.4 | 78.21 | 13.07 | 58.9 | 14.84 | −42 | 3.57 | −22.7 | 0 | −2.44 | −11.1 | |||||
| Qazvin | 0.07 | −0.08 | −0.03 | −0.24 | −0.19 | 20.3 | 39.51 | −12.2 | −23.2 | 11.65 | 0 | −6.67 | 0 | 4.55 | −15 | |||||
| Semnan | −0.6 | −0.7 | −0.5 | −0.8 | −0.7 | −16.6 | 42.61 | 123.1 | −144 | −492 | 20.51 | 24.1 | 13.24 | 5.88 | 13.79 | |||||
| Shiraz | −0.05 | −0.11 | −0.4 | −0.4 | −0.3 | 39.57 | 39.82 | 25.32 | 33.33 | −82.2 | 25.81 | 15.38 | 21.05 | 22.73 | 9.76 | |||||
| Tehran | 0 | −0.31 | −0.5 | −0.31 | −0.09 | 5.88 | 20.76 | −2.1 | 3.85 | −29.9 | 30.6 | 34.7 | 29.3 | 27.27 | 18.42 | |||||
| Yazd | −0.4 | −0.3 | −0.3 | −0.3 | −0.05 | −113 | −36.6 | −149 | −110 | 36.56 | 20.83 | 6.67 | 12.24 | 3.47 | −16.4 | |||||
| Urmia | −0.2 | −0.3 | −0.3 | −0.2 | −0.14 | −97 | −91.1 | −127 | −106 | −161 | 34.1 | 39.2 | 13.79 | 18.87 | 22.5 | |||||
| Tabriz | −0.2 | −0.3 | −0.4 | −0.5 | −0.4 | −21.2 | −21.8 | −606 | −519 | −128 | 18.18 | 24.07 | 34.8 | 27.8 | 59.3 | |||||
| Bandar Anzali | 0.26 | −0.11 | −0.3 | −0.16 | −0.3 | −84.2 | −287 | −176 | −219 | −38.4 | 7.14 | 31.82 | 47.2 | 35.1 | 6.44 | |||||
| Gorgan | −0.5 | −0.5 | −0.3 | 0.23 | −0.4 | 30.23 | 34.48 | −0.28 | −92.4 | −187 | 50.94 | 55.6 | 55.8 | 5 | 55.6 | |||||
| Zanjan | −0.8 | −0.8 | −0.7 | −0.6 | −0.6 | 1.58 | −76. | −79 | −70.2 | −87.6 | 2.26 | 14.71 | 20.4 | 22.6 | 26.3 | |||||
| Zahedan | −0.37 | −0.3 | −0.2 | −0.19 | −0.3 | 3.97 | 24.43 | −42.1 | −41.5 | 17.36 | 23.5 | 3.54 | 4 | 4.44 | −6.9 | |||||
| Mashhad | −0.3 | −0.4 | −0.4 | −0.22 | −0.4 | 5.23 | −11.3 | −5.53 | −54.7 | −61 | 32.69 | 50 | 34.9 | 38.5 | 25.1 | |||||
| Stations | Index 1 | Index 3 | Index 10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Quantile Re. | 0.1 | 0.25 | 0.5 | 0.75 | 0.9 | 0.1 | 0.25 | 0.5 | 0.75 | 0.9 | 0.1 | 0.25 | 0.5 | 0.75 | 0.9 |
| Ahvaz | −1.08 | −0.833 | −3.076 | −0.625 | −0.6 | 0.408 | 0.454 | −1.42 | −1.66 | 1.47 | −5.01 | −11.89 | −14.10 | −27.90 | −28.66 |
| Bandar Abas | 1.57 | 2.173 | 1 | 4.7 | 3.84 | 3.71 | 2.12 | 1.81 | 5.5 | 8.48 | −0.212 | −0.218 | −0.067 | 0.04 | −0.99 |
| Bushehr | −0.333 | −1.39 | −1.02 | −2.11 | −1.2 | −0.20 | −2.54 | −3.15 | −2.22 | 1.66 | −1.15 | 0.0342 | −0.187 | −2.91 | −7.19 |
| Ilam | −1 | −2.38 | −2.7 | −2.08 | 21.57 | −4.52 | −3.33 | −2.21 | −3 | 23.75 | −9.61 | −50.93 | −69.99 | −14.81 | 26.34 |
| Kermanshah | 3.3 × 10−6 | −9 | −11 | −4.9 × 10−7 | 4 | −11 | −6.66 | −7.01 | −5 | 3 | −30.42 | −20.62 | −43.5 | −54.5 | −76.1 |
| Khorramabad | −25 | −10 | 2.5 | −39.9 | −5 | −17.5 | −5 | 12.5 | −40 | 45 | −20.11 | −15.73 | 5 | 21.81 | −7.51 |
| Sanandaj | 0.322 | 0.6 | 0.833 | 1.8 | 0.5 | 0.97 | 1.7 | 2.27 | 2.78 | 3.72 | 27.95 | −10.36 | −24.6 | −20.94 | −47.7 |
| Shahrekord | 2.5 | 1.36 | 1.76 | 0.6 | −1 | 2.66 | 2.28 | 1.25 | 1.2 | 1.42 | −1.83 | −31.1 | −35.31 | −56.15 | −22.58 |
| Yasuj | −1.66 | −1.5 | 0.937 | −5.7 × 10−9 | −4 | −1.07 | 1.56 | 1.87 | 4.83 | −10.2 | −141.1 | −179 | −58.91 | −68.16 | −71.39 |
| Arak | −0.625 | −0.769 | 1.052 | 2.619 | 0.8 | −1.5 | −2 × 10−7 | 1.4 | 0.25 | 3 × 10−7 | 0.09 | −0.75 | −0.151 | −0.894 | −1.87 |
| Birjand | 0.669 | 0.357 | 0.357 | −2.03 × 10−8 | −1 | 1.6 | 0.833 | 0.466 | 0.56 | 1.25 | −0.267 | −0.078 | −0.543 | −0.305 | 0.111 |
| Esfahan | 1 | 1.4 × 10−7 | −1.5 | −0.62 | 2.6 × 10−7 | 1 | 1.11 | −0.93 | 0.933 | 0.66 | −7.90 | −23.3 | −16.52 | −24.62 | −18.33 |
| Hamedan | −0.62 | −9.4 × 10−11 | 5.2 × 10−6 | 0.41 | 0.76 | −1.8 | 2 | 1.66 | 1.25 | −3.33 | −46.05 | −25.78 | −7.087 | −15.54 | 4.86 |
| Kerman | −0.045 | −0.044 | −0.067 | −15 | −0.16 | 0.25 | −0.57 | −0.25 | −1 × 10−7 | −0.71 | −12.55 | −16.8 | −15.5 | −18.94 | −9.37 |
| Qazvin | −0.45 | −1.5 × 10−7 | −0.434 | −0.909 | −2 | −1.73 | −0.45 | 6 × 10−7 | 2 × 10−8 | 0.83 | −20.25 | −10.79 | −17.9 | −40.27 | −48 |
| Semnan | 0.357 | −1.29 × 10−7 | 1.5 × 10−8 | −2 | −1.42 | −1 | −0.87 | −1.55 | −3 | −0.33 | −8.28 | −23.63 | −26.2 | −27.76 | −31.39 |
| Shiraz | −1.42 | −1 | −3.84 | −7.94 | −9.5 | 1.16 | −3.21 | −3.75 | −8.2 | −14 | −3.13 | −13.44 | −41.6 | −45.39 | −87.3 |
| Tehran | −1 × 10−7 | −2.5 × 10−7 | −1.53 | −1.5 | −4.28 | −0.5 | −0.15 | −1.15 | −3.33 | −5.25 | 13.38 | −8.11 | −21.8 | −20.39 | −16.25 |
| Yazd | −2.8 × 10−8 | 0.434 | 0.384 | −0.5 | −0.714 | 1 | 1.22 | −0.15 | −0.57 | −2.1 | −3.59 | −5.40 | −5.92 | −8.99 | −2.4 |
| Urmia | −1 × 10−8 | 2.6 × 10−7 | 1.33 | 1.66 | 5.5 | 2.5 | 1.5 | 0.38 | 0.28 | 3.67 | −24.11 | −9 | 0.56 | −12.42 | 5.41 |
| Tabriz | −0.937 | −0.294 | −0.416 | −0.555 | −1.8 | −0.78 | −0.5 | −0.25 | −0.94 | −1.66 | −33.2 | −21.4 | −27 | −26.95 | −12.80 |
| Bandar Anzali | −102.64 | −145.7 | −196.3 | −263.78 | −395.18 | 0.285 | 0.909 | 1.38 | 7.5 | 12.5 | −102.6 | −145 | −196 | −263.7 | −395 |
| Gorgan | 33.58 | 44.44 | 1.94 | −12.04 | −46.76 | 1.25 | 1.27 | 0.454 | −1 | 1.2 × 10−8 | 33.58 | 44.44 | 1.94 | −12.04 | −46.7 |
| Zanjan | −14.90 | −16.71 | −18.66 | −24.46 | −19.91 | −0.48 | −0.227 | −0.52 | 0.626 | 1 | −14.90 | −16.71 | −18.66 | −24.46 | −19.91 |
| Zahedan | −4.89 | −8.98 | −10.35 | −13.66 | −11.53 | −1 | −0.5 | −1.66 | −1 | 1.66 | −4.89 | −8.98 | −10.35 | −13.66 | −11.53 |
| Mashhad | −2.27 | −5.54 | −11.66 | −13.32 | −26.35 | −0.66 | −0.37 | −1.11 | −1.5 | −2.62 | −2.27 | −5.54 | −11.66 | −13.32 | −26.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamali, M.; Gohari, A.; Motamedi, A.; Haghighi, A.T. Spatiotemporal Changes in Air Temperature and Precipitation Extremes over Iran. Water 2022, 14, 3465. https://doi.org/10.3390/w14213465
Jamali M, Gohari A, Motamedi A, Haghighi AT. Spatiotemporal Changes in Air Temperature and Precipitation Extremes over Iran. Water. 2022; 14(21):3465. https://doi.org/10.3390/w14213465
Chicago/Turabian StyleJamali, Mohammad, Alireza Gohari, Armita Motamedi, and Ali Torabi Haghighi. 2022. "Spatiotemporal Changes in Air Temperature and Precipitation Extremes over Iran" Water 14, no. 21: 3465. https://doi.org/10.3390/w14213465








