Budyko-Type Models and the Proportionality Hypothesis in Long-Term Water and Energy Balances
Abstract
:1. Introduction
2. Budyko-Type Functional Relationships
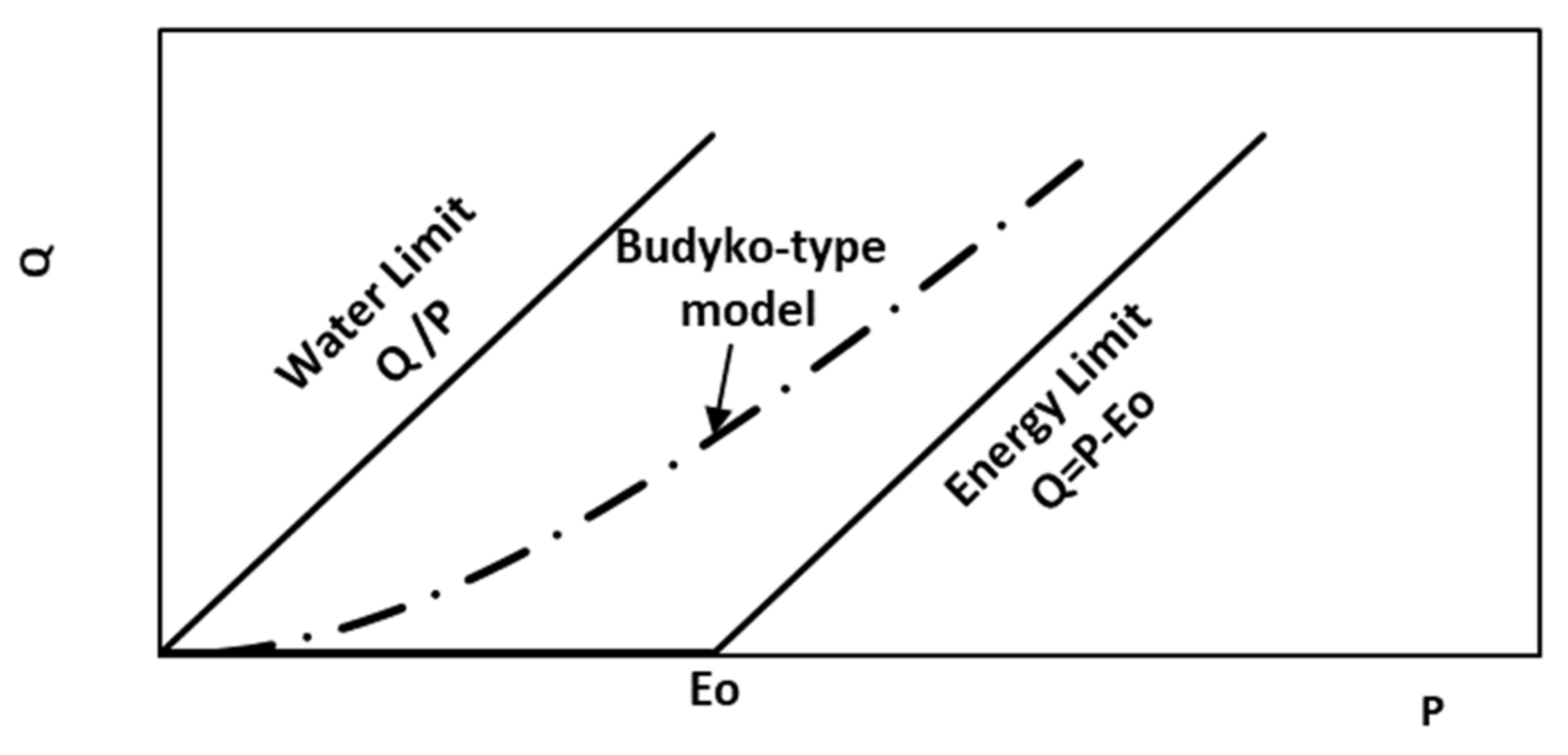
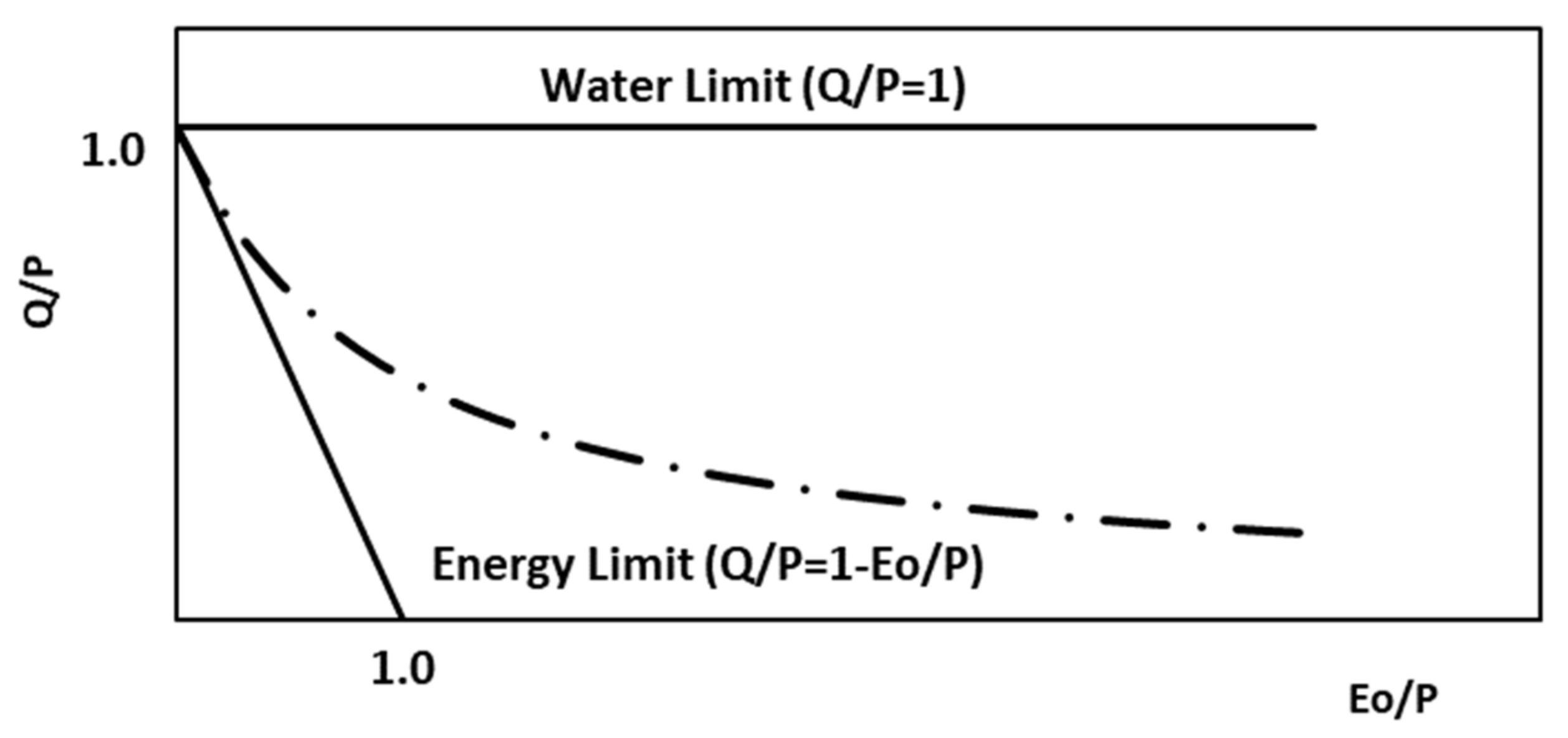
2.1. Budyko Hypothesis and Representation Diagrams
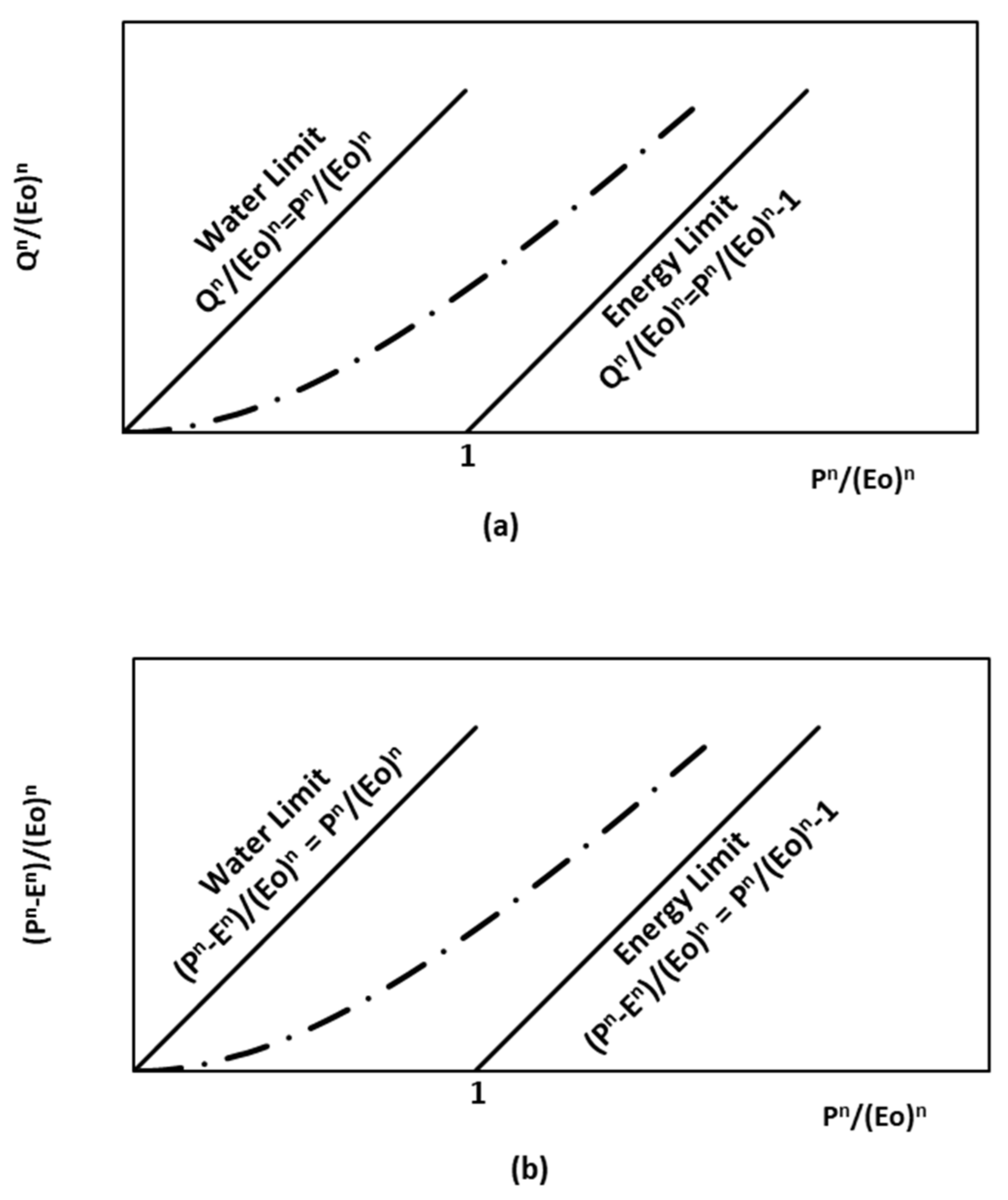
2.2. Budyko-Type Functional Relationships
3. Derivation of Selected Budyko-Type Models
4. Budyko-Type Models in the P–Q Space
4.1. Model TMPHCY
4.2. Model SZ
4.3. Model Z
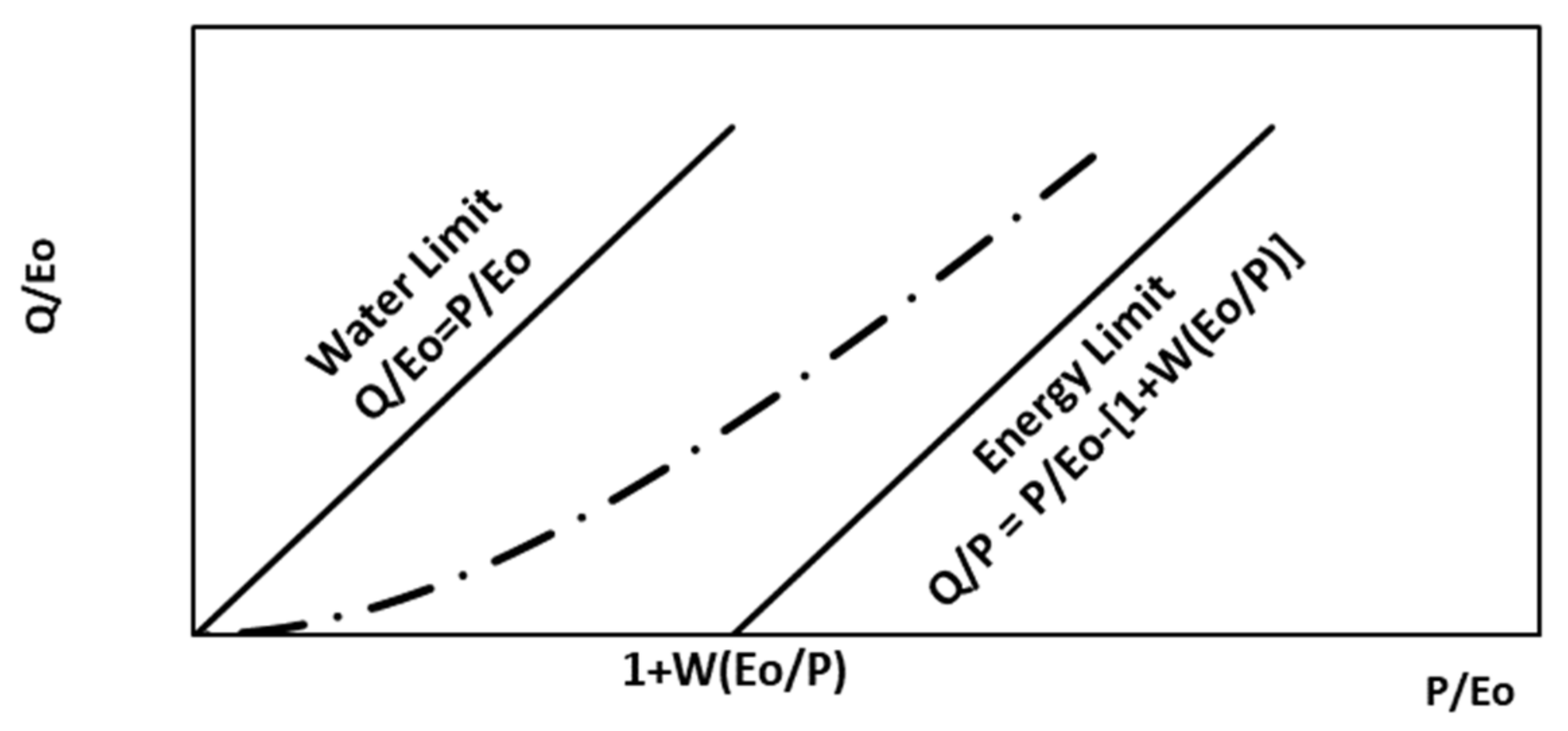
4.4. Model WT
4.5. Non Proportionality Hypothesis Models
5. An Expolinear Model of the P–Q Relationship
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Unit | Description |
| P | mm | Precipitation |
| E | mm | Actual evapotranspiration. The E symbol in hydrology is commonly used for Evaporation, but we change it in line with common notations in Budyko type models |
| Q | mm | Runoff |
| E0 | mm | Potential evapotranspiration. Symbol changed as used in common hydrology practice |
| m, k, n, W, ε, ω, α, b, f, d | - | Fitting parameters of the Budyko type models |
Appendix A
Appendix A.1. Proportionality Hypothesis of the CN-SCS Method
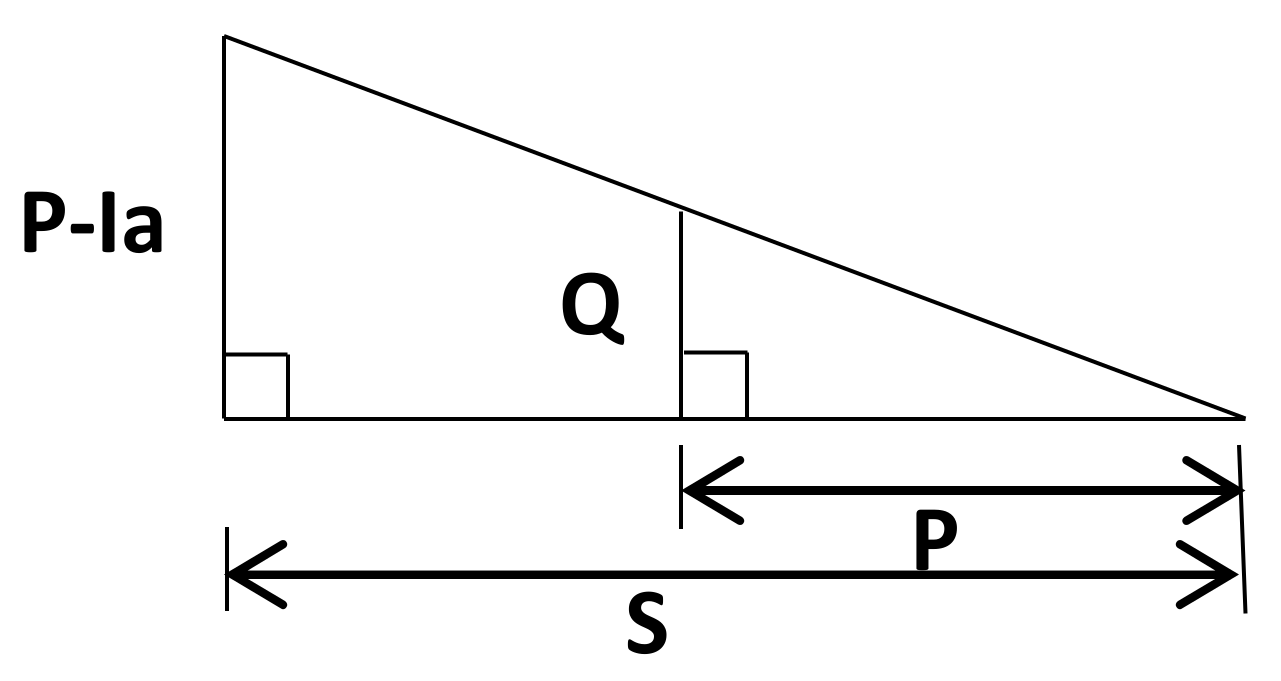
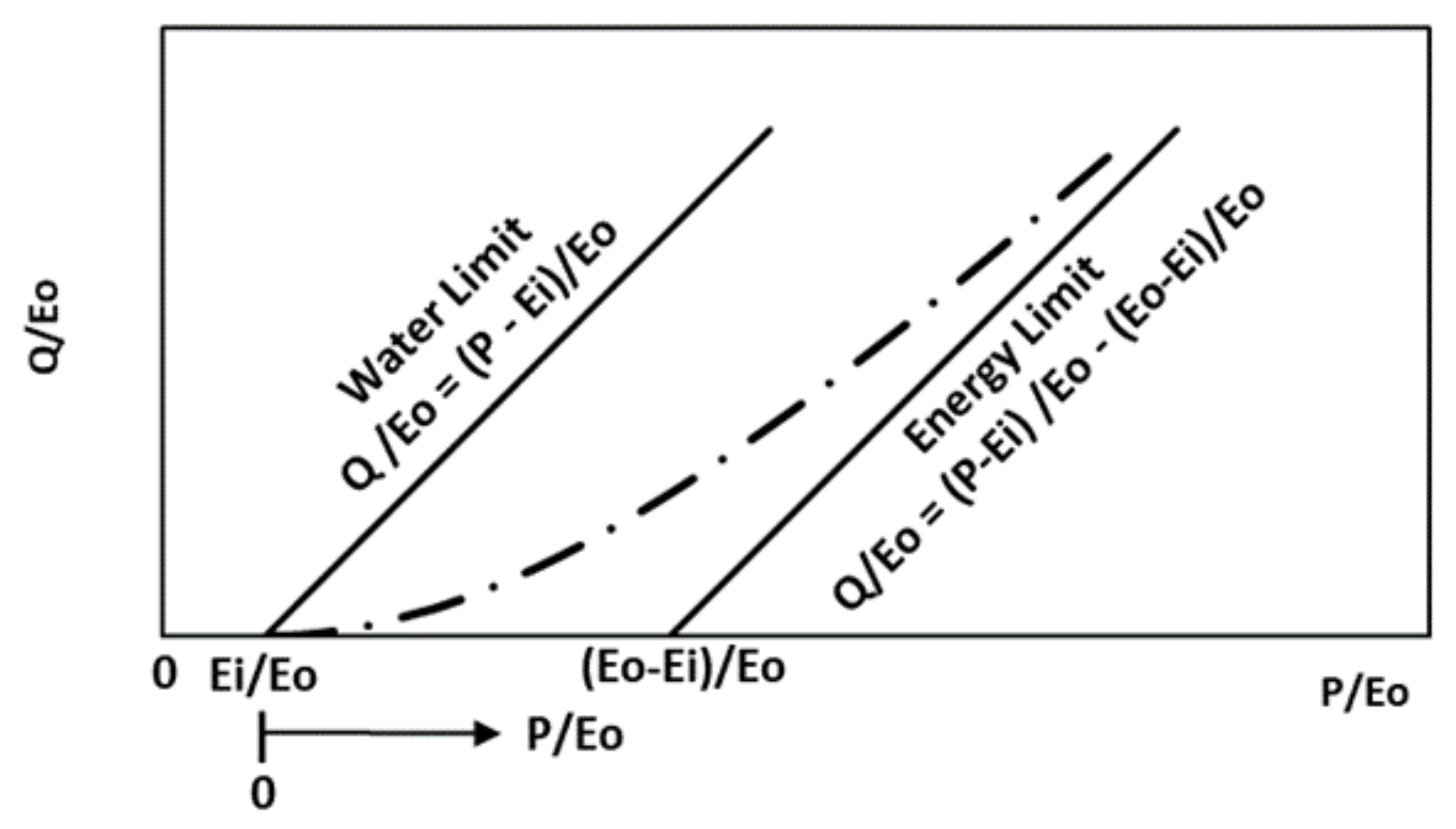
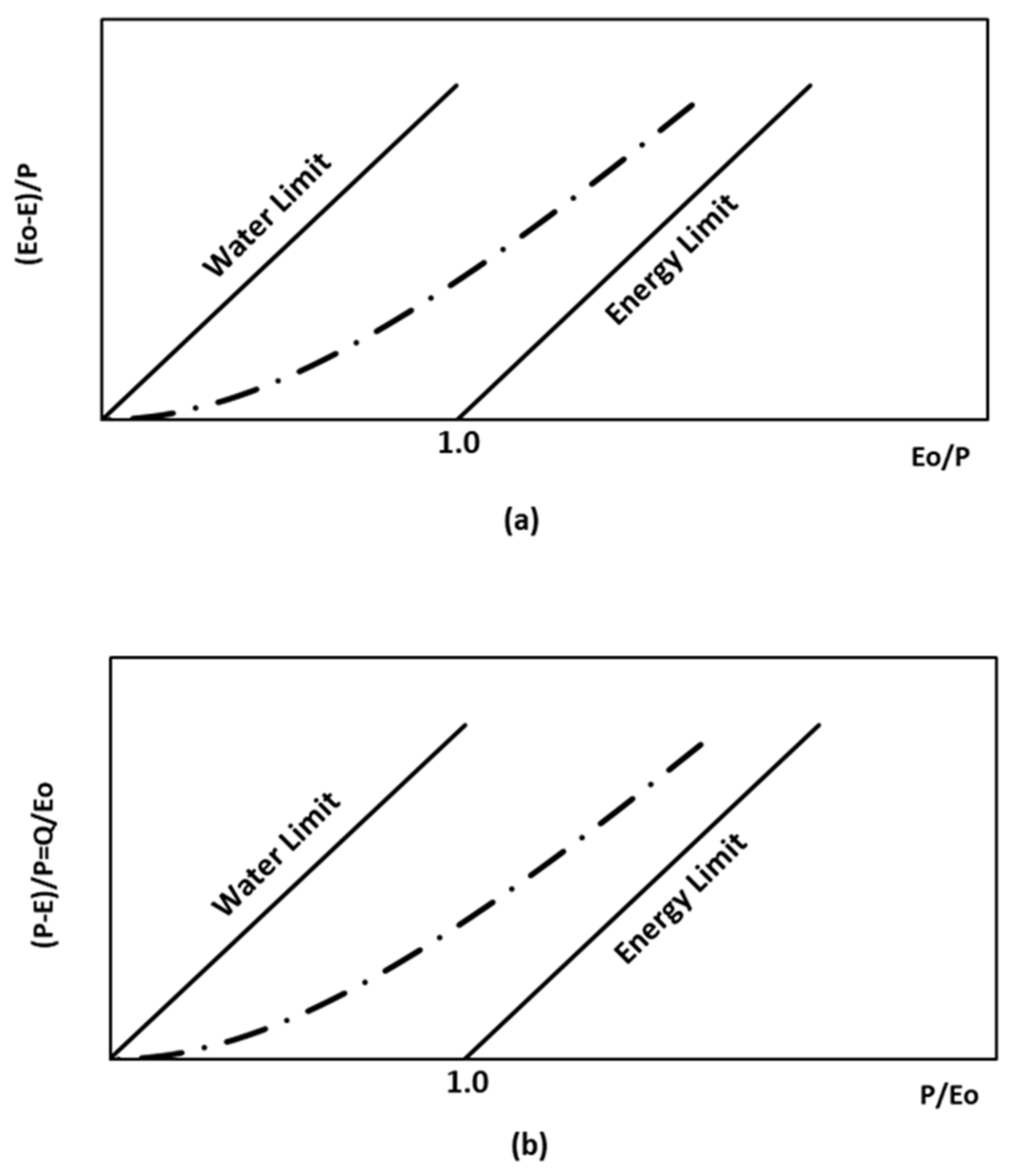
Appendix A.2. P-Q Space Limits
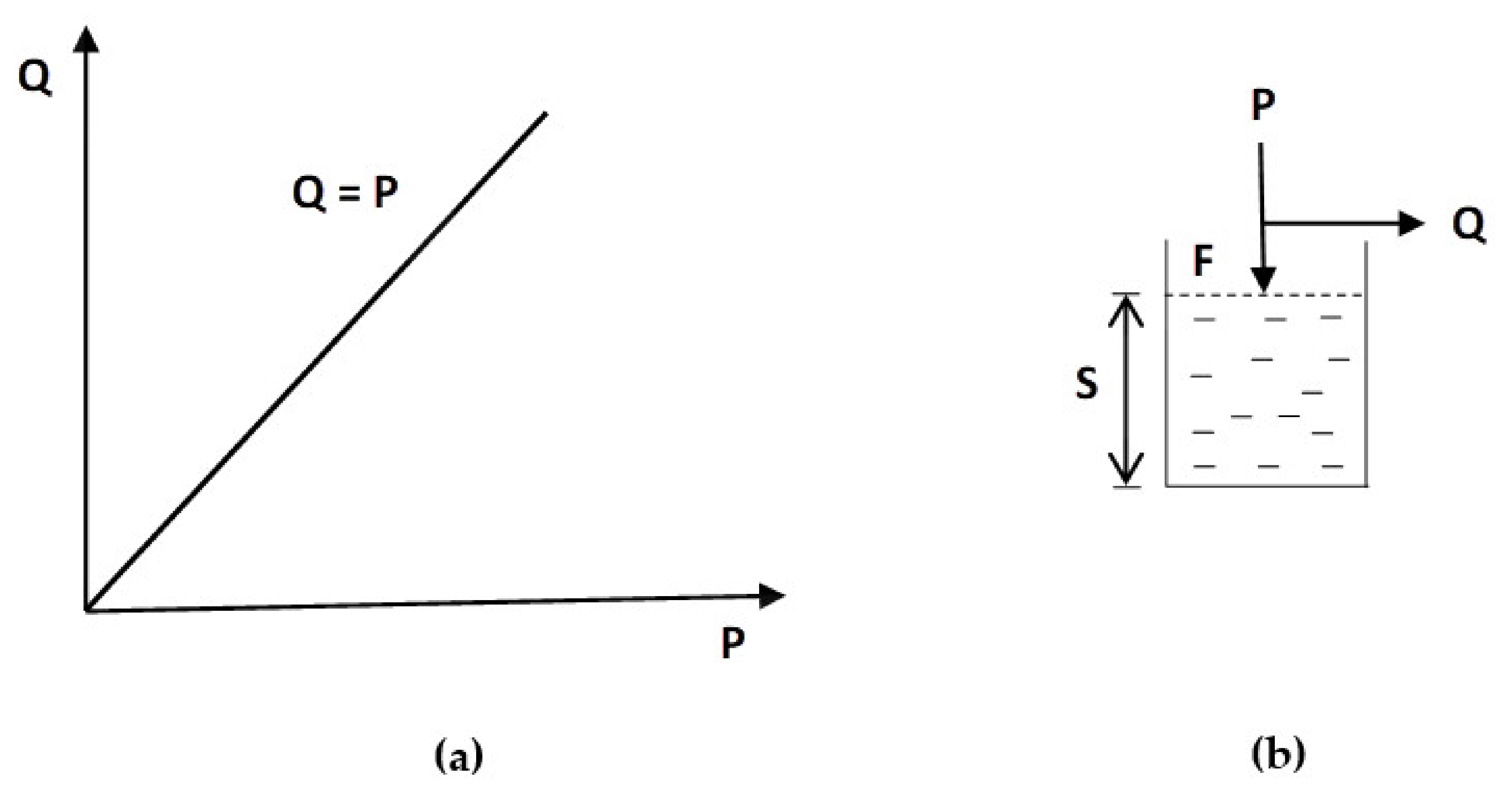

Appendix A.3. Case Ia = 0
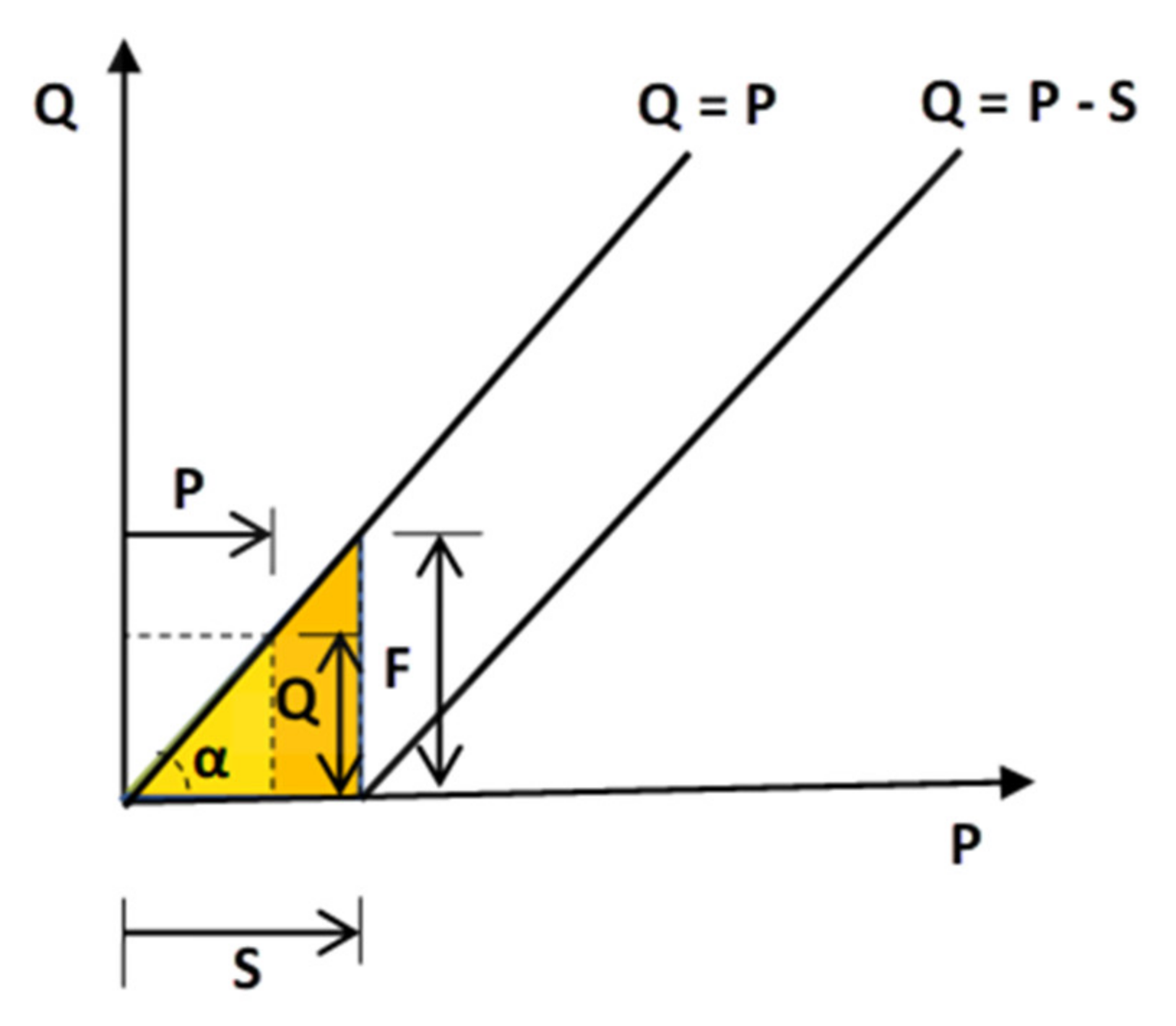
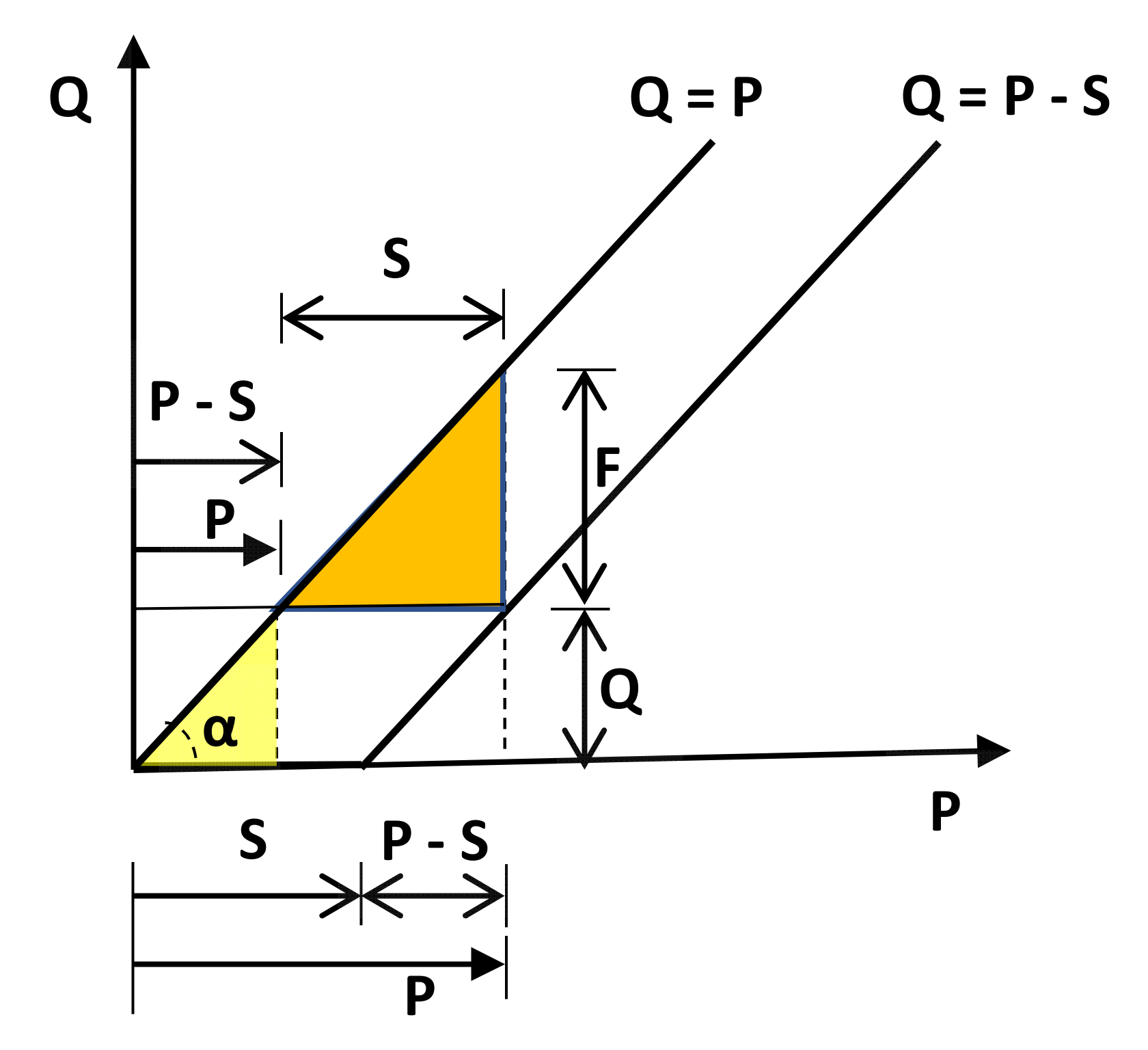
Appendix A.4. Case Ia > 0 and Different Origins of P and S
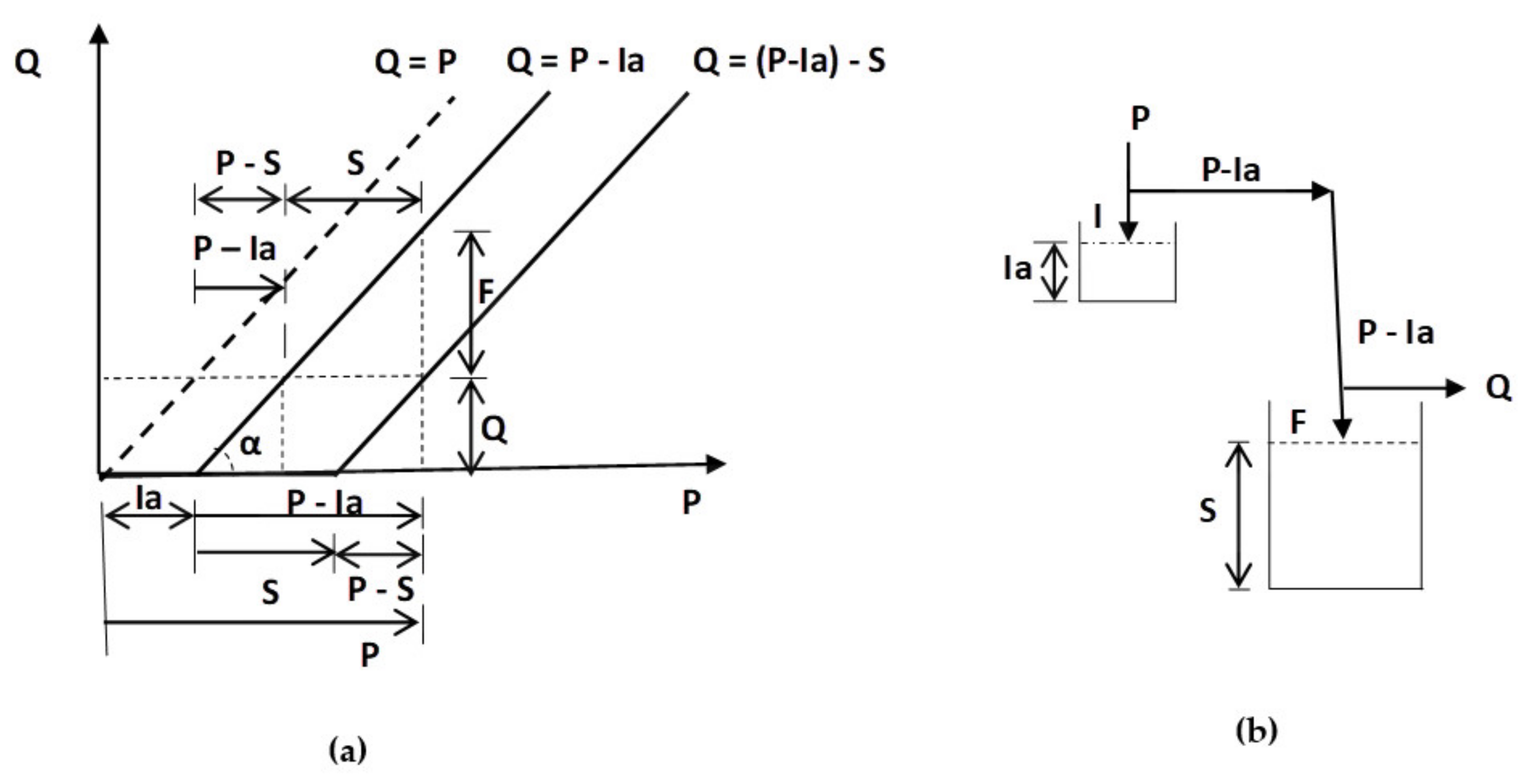
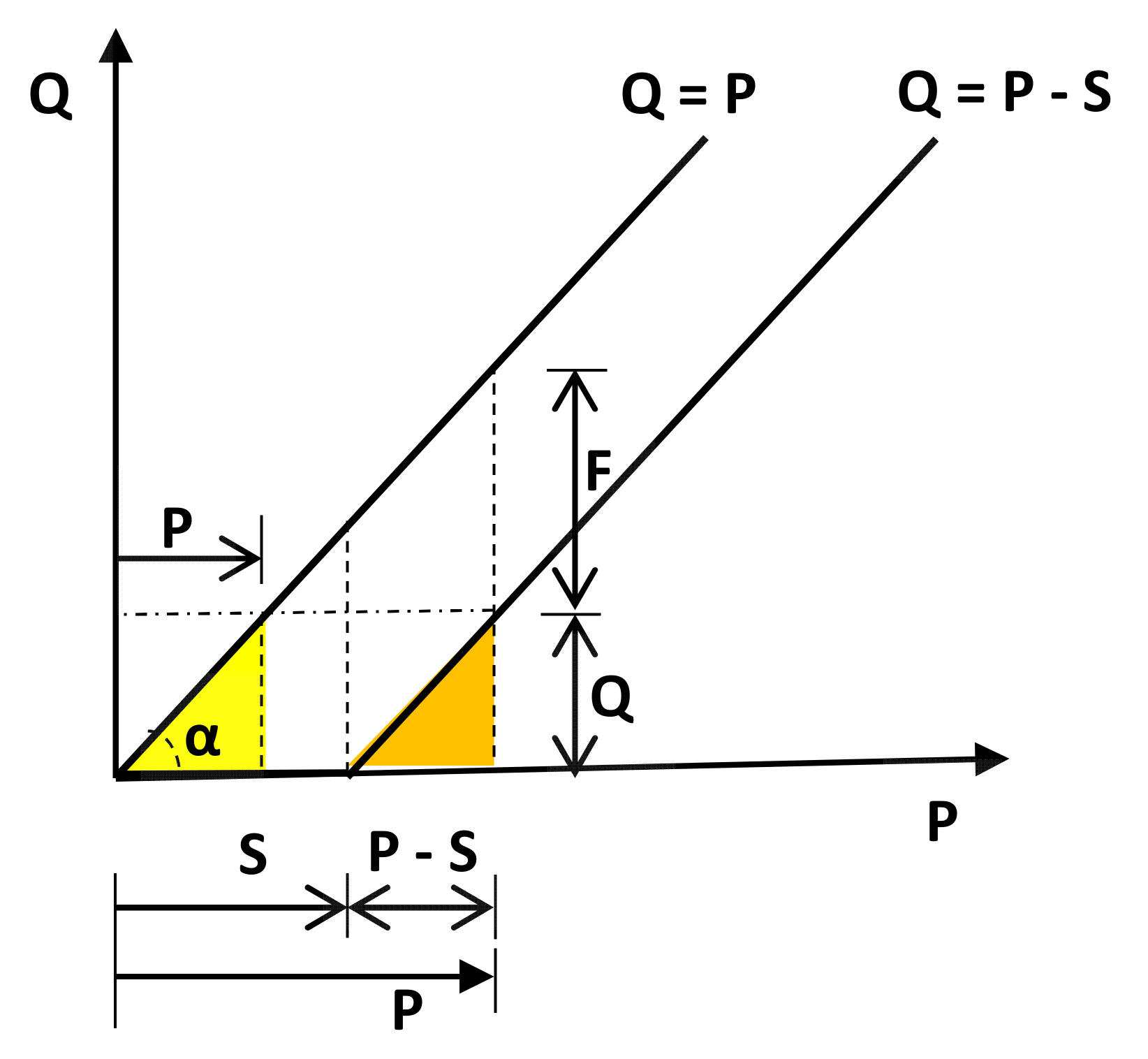
Appendix A.5. Case Ia > 0 and Equal Origins of P and S
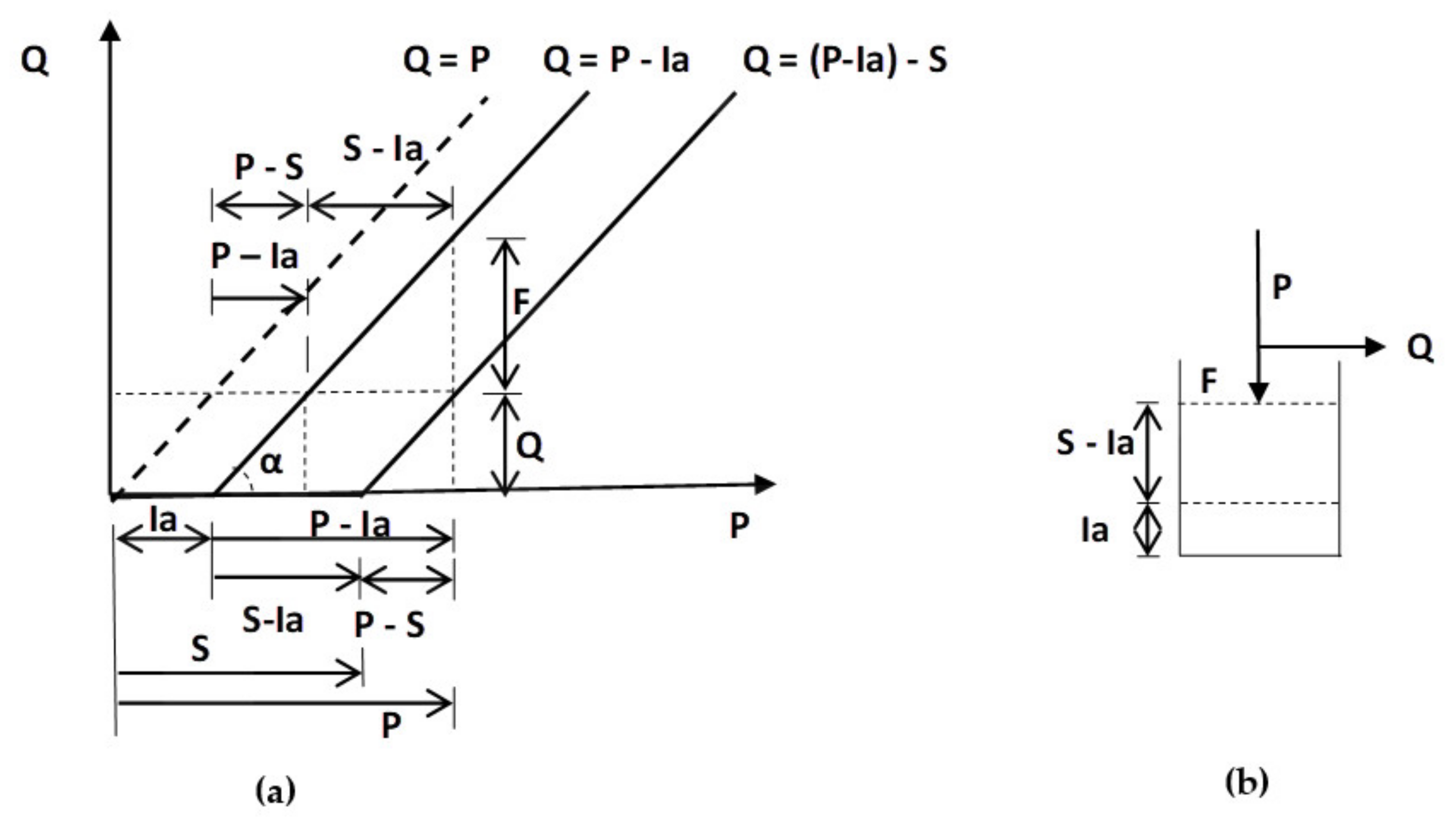
Appendix A.6. General Discussion
Appendix A.7. Historical Context
References
- Klemeš, V. Conceptualization and scale in hydrology. J. Hydrol. 1983, 65, 1–23. [Google Scholar] [CrossRef]
- Sivapalan, M.; Blöschl, G.; Zhang, L.; Vertessy, R. Downward approach to hydrological prediction. Hydrol. Process. 2003, 17, 2101–2111. [Google Scholar] [CrossRef]
- Littlewood, I.G.; Croke, B.F.W.; Jakeman, A.J.; Sivapalan, M. The role of ‘top-down’ modelling for Prediction in Ungauged Basins (PUB). Hydrol. Process. 2003, 17, 1673–1679. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model Development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Hartman, C.; Troch, P.A. What makes Darwinian hydrology “Darwinian”? Asking a different kind of question about landscapes. Hydrol. Earth Syst. Sci. 2014, 18, 417–433. [Google Scholar] [CrossRef] [Green Version]
- Budyko, M.I. The Heat Balance of the Earth’s Surface; National Weather Service, U.S. Department of Commerce: Washington, DC, USA, 1958; pp. 144–155. [Google Scholar]
- Wang, C.; Wang, S.; Fu, B. Advances in hydrological modelling with the Budyko framework: A review. Prog. Phys. Geogr. 2016, 40, 409–430. [Google Scholar] [CrossRef]
- Fu, B.P. On the calculation of the evaporation from land surface. Sci. Atmos. Sin. 1981, 51, 23–31. Available online: https://en.cnki.com.cn/Article_en/CJFDTOTAL-DQXK198101002.htm (accessed on 13 February 2021). (In Chinese).
- Sposito, G. Understanding the Budyko equation. Water 2017, 9, 236. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Yang, D.; Lei, Z.; Sun, F. New analytical derivation of the mean annual water-energy balance equation. Water Resour. Res. 2008, 44, W03410. [Google Scholar] [CrossRef]
- Zhang, L.; Hickel, K.; Dawes, W.R.; Chiew, F.H.S.; Western, A.W.; Briggs, P.R. A rational function approach for estimating mean annual evapotranspiration. Water Resour. Res. 2004, 40, W02502. [Google Scholar] [CrossRef]
- Zhou, S.; Yu, B.; Huang, Y.; Wang, G. The complementary relationship and generation of the Budyko functions. Geophys. Res. Lett. 2015, 42, 1781–1790. [Google Scholar] [CrossRef]
- Klemeš, V. Dilettantism in hydrology: Transition or destiny? Water Resour. Res. 1986, 22, 177S–188S. [Google Scholar] [CrossRef]
- Dooge, J.C.I. Hydrological models and climate change. J. Geophys. Res. 1992, 97, 2677–2686. [Google Scholar] [CrossRef]
- Lhomme, J.P.; Moussa, R. Matching the Budyko functions with the complementary evaporation relationship: Consequences for the drying power of the air and the Priestley-Taylor coefficient. Hydrol. Earth Syst. Sci. 2016, 20, 4857–4865. [Google Scholar] [CrossRef]
- Andréassian, V.; Perrin, C. On the ambiguous interpretation of the Turc-Budyko nondimensional graph. Water Resour. Res. 2012, 48, W10601. [Google Scholar] [CrossRef]
- Carmona, A.M.; Sivapalan, M.; Yaeger, M.A.; Poveda, G. Regional patterns of interannual variability of catchment water balances across the continental U.S.: A Budyko framework. Water Resour. Res. 2014, 50, 9177–9193. [Google Scholar] [CrossRef]
- Mouelhi, S. Vers una Chaîne Coherente de Modelès Pluie-Débit Conceptuels Globaux pas Temps Pluriannuel, Annuel, Mensual et Journalier. Thèse de Doctorat, École Nationale du Génie Rural, des Eaux et Forêts, Paris, France, 2003. Available online: https://pastel.archives-ouvertes.fr/tel-00005696/document (accessed on 19 February 2021).
- Schreiber, P. Über die Beziehungen zwischen dem Niederschlag und der Wasserführung der Flüsse in Mitteleuropa. Meteorolog. Z. 1904, 21, 441–452. [Google Scholar]
- Ol’dekop, E.M. On evaporation from the surface of river basins. T. Meteorol. Obs. 1911, 4, 200. (In Russian) [Google Scholar]
- Fraedrich, K. A parsimonious stochastic water reservoir: Schreiber´s 1904 equation. J. Hydrometeorol. 2010, 11, 575–578. [Google Scholar] [CrossRef]
- Fraedrich, K.; Sielmann, F. An equation of state for land surface climates. Int. J. Bifurc. Chaos 2011, 21, 3577–3587. [Google Scholar] [CrossRef]
- Budyko, M.I. Climate and Life, 1st ed.; Academic Press: Orlando, FL, USA, 1974; p. 508. [Google Scholar]
- Oudin, L.; Andréassian, V.; Lerat, J.; Michel, C. Has land cover a significant impact on mean annual streamflow? An international assessment using 1508 catchments. J. Hydrol. 2008, 357, 303–316. [Google Scholar] [CrossRef]
- Paz, F.; Marín, M.I.; López, E.; Zarco, A.; Bolaños, M.A.; Oropeza, J.L.; Martínez, M.; Palacios, E.; Rubiños, E. Elements for developing an operational hydrology with remote sensing: Soil-vegetation mixture. Ing. Hidraul. Mex. 2009, 24, 69–80. (In Spanish) [Google Scholar]
- Mouelhi, S. Existe-t-il une relation entre les modelès pluie-débit au pas de temps pluriannual? Rev. Sci. Eau 2011, 24, 193–206. [Google Scholar] [CrossRef] [Green Version]
- Choudhury, B.J. Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model. J. Hydrol. 1999, 216, 99–110. [Google Scholar] [CrossRef]
- Hsuen-Chun, Y. A composite method for estimating annual actual evapotranspiration. Hydrol. Sci. J. 1988, 33, 345–356. [Google Scholar] [CrossRef]
- Mezentsev, V.S. More on the calculation of average total evaporation. Meteorol. Gidrol. 1955, 5, 24–26. (In Russian) [Google Scholar]
- Pike, J.G. The estimation of annual runoff from meteorological data in a tropical climate. J. Hydrol. 1964, 2, 116–123. [Google Scholar] [CrossRef]
- Turc, L. Le bilan D’eau Des Sols. Relation Entre la Précipitation, L’évaporation et L’écoulement. Ann. Agron. 1954, 5, 491–569. Available online: https://www.persee.fr/docAsPDF/jhydr_0000-0001_1955_act_3_1_3278.pdf (accessed on 26 February 2021).
- Sharif, H.O.; Crow, W.; Miller, N.L.; Wood, E.F. Multidecadal high-resolution hydrological modeling of the Arkansas-Red River basin. J. Hydrometeorol. 2007, 8, 1111–1127. [Google Scholar] [CrossRef]
- Zhang, L.; Dawes, W.R.; Walker, G.R. Response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar] [CrossRef]
- Wang, D.; Tang, Y. A one parameter Budyko model for water balance captures emergent behaviour in Darwinian hydrologic models. Geophys. Res. Lett. 2014, 41, 4567–4577. [Google Scholar] [CrossRef] [Green Version]
- Tixeront, J. Prévision des apports des cours d’eau. In Proceedings of the Symposium Eau de Surface Tenu à L’occasion de l’Assemblée Générale de Berkeley de L’U. G.G. I., Berkeley, CA, USA, 19–31 August 1963. [Google Scholar]
- Porporato, A.; Daly, E.; Rodriguez-Iturbe, I. Soil water balance and ecosystem response to climate change. Am. Nat. 2004, 164, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Iturbe, I.; Porporato, A.; Ridolfi, L.; Isham, V.; Coxi, D.R. Probabilistic modelling of water balance at a point: The role of climate, soil and vegetation. Proc. Royal Soc. Lond. A 1999, 455, 3789–3805. [Google Scholar] [CrossRef]
- Sankarasubramanian, A.; Vogel, R.M. Annual hydroclimatology of the United States. Water Resour. Res. 2002, 38, 1083. [Google Scholar] [CrossRef]
- Fernandez, W.; Vogel, R.M.; Sankarasubramanian, A. Regional calibration of a watershed model. Hydrol. Sci. J. 2000, 45, 689–707. [Google Scholar] [CrossRef]
- Gerrits, A.M.J.; Savenije, H.H.G.; Veling, E.J.M.; Pfister, L. Analytical derivation of the Budyko curve based on rainfall characteristics and a simple evaporation model. Water Resour. Res. 2009, 45, W04403. [Google Scholar] [CrossRef]
- Porada, P.; Kleidon, A.; Schymanski, S.J. Entropy production of soil hydrological processes and its maximization. Earth Syst. Dynam. 2011, 2, 179–190. [Google Scholar] [CrossRef] [Green Version]
- Andréassian, V.; Sari, T. Technical note: On the puzzling similarity of two water balance formulas—Turc-Mezentsev vs Tixeront-Fu. Hydrol. Earth Syst. Sci. 2019, 23, 2339–2350. [Google Scholar] [CrossRef] [Green Version]
- Lebecherel, L.; Andréassian, V.; Perrin, C. On regionalizing the Turc-Mezentsev water balance formula. Water Resour. Res. 2013, 49, 7508–7517. [Google Scholar] [CrossRef]
- Kenney, B.C. Beware of spurious self-correlations! Water Resour. Res. 1982, 18, 1041–1048. [Google Scholar] [CrossRef]
- Berghuijs, W.R.; Gnann, S.J.; Woods, R.A. Unanswered questions on the Budyko framejork. Hydrol. Process. 2020, 34, 5699–5703. [Google Scholar] [CrossRef]
- Paz, F. Myths and Fallacies about the Curve Number Hydrological Method of the SCS/NRCS. Agrociencia 2009, 43, 521–528. Available online: https://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1405-31952009000500007 (accessed on 23 March 2021).
- United States Department of Agriculture; Natural Resources Conservation Service. SCS National Engineering Handbook, Section 4, Hydrology. 1972. Available online: https://directives.sc.egov.usda.gov/OpenNonWebContent.aspx?content=18383.wba (accessed on 12 March 2021).
- Natural Resources Conservation Service; United States Department of Agriculture. Estimation of Direct Runoff from Storm Rainfall. In Part 630 Hydrology. National Engineering Handbook; (210-VI-NEH, July 2004); United States Department of Agriculture: Washington, DC, USA, 2004; p. 79. Available online: https://directives.sc.egov.usda.gov/OpenNonWebContent.aspx?content=17752.wba (accessed on 13 April 2021).
- Carmona, A.M.; Poveda, G.; Sivapalan, M.; Vallejo-Bernal, S.M.; Bustamante, E. A scaling approach to Budyko’s framework and the complementary relationship of evapotranspiration in humid environments: Case study of the Amazon River basin. Hydrol. Earth Syst. Sci. 2016, 20, 589–603. [Google Scholar] [CrossRef] [Green Version]
- Mishra, S.K.; Singh, V.P. Another look at SCS-CN method. J. Hydrol. Eng. 1999, 4, 257–264. [Google Scholar] [CrossRef]
- Chen, X.; Alimohammadi, N.; Wang, D. Modeling interanual variability of seasonal evaporation and storage change based on the extended Budyko framework. Water Resour. Res. 2013, 49, 6067–6078. [Google Scholar] [CrossRef] [Green Version]
- Du, C.; Sun, F.; Yu, J.; Lin, X.; Chen, Y. New interpretation of the role of water balance in an extended Budyko hypothesis in arid regions. Hydrol. Earth Syst. Sci. 2016, 20, 393–409. [Google Scholar] [CrossRef] [Green Version]
- Ponce, V.M.; Shetty, A.V. A conceptual model of catchment water balance. 1. Formulation and calibration. J. Hydrol. 1995, 173, 27–40. [Google Scholar] [CrossRef]
- Chen, X.; Wang, D. Modeling seasonal surface runoff and base flow based on the generalized proportionality hypothesis. J. Hydrol. 2015, 527, 367–379. [Google Scholar] [CrossRef]
- Sivapalan, M.; Yaeger, M.A.; Harman, C.J.; Xu, X.; Troch, P.A. Functional model of water balance variability at the catchment scale: 1. Evidence of hydrologic similarity and space-time symmetry. Water Resour. Res. 2011, 47, W02522. [Google Scholar] [CrossRef]
- L’vovich, M.I. World Water Resources and Their Future; American Geophysical Union: Washington, DC, USA, 1979; Volume 197, p. 415. [Google Scholar]
- Bagrov, N. On multi-year average of evapotranspiration from land surface. Meteorog. I Gidrol. 1953, 10, 20–25. (In Russian) [Google Scholar]
- Goudriaan, J.; van Laar, H. Modelling Potential Crop Growth Processes: Textbook with Exercises. Current Issues in Production Ecology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994; Volume 2, p. 238. [Google Scholar]
- Paz, F.; Marín-Sosa, M.I.; Martínez-Menes, M. Modelo expo-lineal de la precipitación-escurrimiento en lotes experimentales de largo plazo en cultivos de maíz. Tecnol. Cienc. Agua. 2013, 5, 85–97. [Google Scholar]
- Paz, F.; López Bautista, E.; Marín Sosa, M.I. Validación del modelo expo-lineal precipitación-escurrimiento en un simulador de Lluvia. Terra Latinoam. 2017, 35, 329–341. [Google Scholar]
- Beven, K. Prophecy, reality and uncertainty in distributed hydrological modelling. Adv. Water Resour. 1993, 16, 41–51. [Google Scholar] [CrossRef]
- Mockus, V. Estimation of Total (and Peak Rates of) Surface Runoff for Individual Storms. Exhibit A in Appendix B. Interim Survey Report Grand (Neosho) River Watershed; United States Department of Agriculture: Washington, DC, USA, 1949; p. 51. [Google Scholar]
- Boughton, W.C. A mathematical model for relating run-off to rainfall with daily data. Civ. Engr. Trans. Inst. Engrs. 1966, CE8, 83–97. [Google Scholar]
- Kohler, M.A.; Richards, M.M. Multicapacity basin accounting for pree4dicting runoff from storm precipitation. J. Geophys. Res. 1962, 67, 5187–5197. [Google Scholar] [CrossRef]
- Klemeš, V. A hydrological perspective. J. Hydrol. 1988, 100, 3–28. [Google Scholar] [CrossRef]
- Pilgrim, D.H.; Cordery, I. Flood runoff. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill, Inc.: New York, NY, USA, 1993; pp. 9.1–9.39. [Google Scholar]
- Mishra, S.K.; Singh, V.P. Soil Conservation Service Curve Number (SCS-CN) Methodology, 1st ed.; Springer-Science+Business Media, B.V.: Dordrecht, The Netherlands, 2003; p. 515. [Google Scholar]
- Boughton, W.C. Evaluating partial areas of watershed runoff. J. Irrig. Drain. Eng. 1987, 113, 356–366. [Google Scholar] [CrossRef]
- Rallison, R.E.; Miller, N. Past, present, and future SCS runoff procedure. In Rainfall-Runoff Relationship; Singh, V.P., Ed.; Water Resources Publications: Littleton, CO, USA, 1982; pp. 353–364. [Google Scholar]
- Mockus, V. Estimation of direct runoff from storm rainfall. In Section 4: Hydrology, National Engineering Handbook; United States Department of Agriculture: Washington, DC, USA, 1972; NEH Notice 4-102 SCS; p. 27. [Google Scholar]
- Mockus, V.; Ferris, O. Personal communication. 1964. [Google Scholar]
- Mockus, V.; Schwab, G.O. Personal communication. 1963. [Google Scholar]
- Mockus, V.; Ogrosky, H.O. Personal communication. 1962. [Google Scholar]
- Ponce, V.M. Notes of My Conversation with Vic Mockus. 1996. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paz Pellat, F.; Garatuza Payán, J.; Salas Aguilar, V.; Velázquez Rodríguez, A.S.; Bolaños González, M.A. Budyko-Type Models and the Proportionality Hypothesis in Long-Term Water and Energy Balances. Water 2022, 14, 3315. https://doi.org/10.3390/w14203315
Paz Pellat F, Garatuza Payán J, Salas Aguilar V, Velázquez Rodríguez AS, Bolaños González MA. Budyko-Type Models and the Proportionality Hypothesis in Long-Term Water and Energy Balances. Water. 2022; 14(20):3315. https://doi.org/10.3390/w14203315
Chicago/Turabian StylePaz Pellat, Fernando, Jaime Garatuza Payán, Víctor Salas Aguilar, Alma Socorro Velázquez Rodríguez, and Martín Alejandro Bolaños González. 2022. "Budyko-Type Models and the Proportionality Hypothesis in Long-Term Water and Energy Balances" Water 14, no. 20: 3315. https://doi.org/10.3390/w14203315
APA StylePaz Pellat, F., Garatuza Payán, J., Salas Aguilar, V., Velázquez Rodríguez, A. S., & Bolaños González, M. A. (2022). Budyko-Type Models and the Proportionality Hypothesis in Long-Term Water and Energy Balances. Water, 14(20), 3315. https://doi.org/10.3390/w14203315




