Characterization of the Propagation of Meteorological Drought Using the Copula Model
Abstract
:1. Introduction
- Evaluation of the relationship between meteorological drought by SPI and agricultural drought by SMI (or hydrological drought by SRI) in Andong Dam basin and Hapcheon Dam basin through correlation analysis;
- Estimation of propagation time from meteorological drought to agricultural (or hydrological) drought;
- Estimation of the probability of propagation from various severity (weak, moderate, severe, extreme) to agricultural (or hydrological) drought using the Copula-based conditional probability distribution method;
- Attempt to classify seasonal propagation characteristics by performing this analysis on a seasonal basis.
2. Materials and Methods
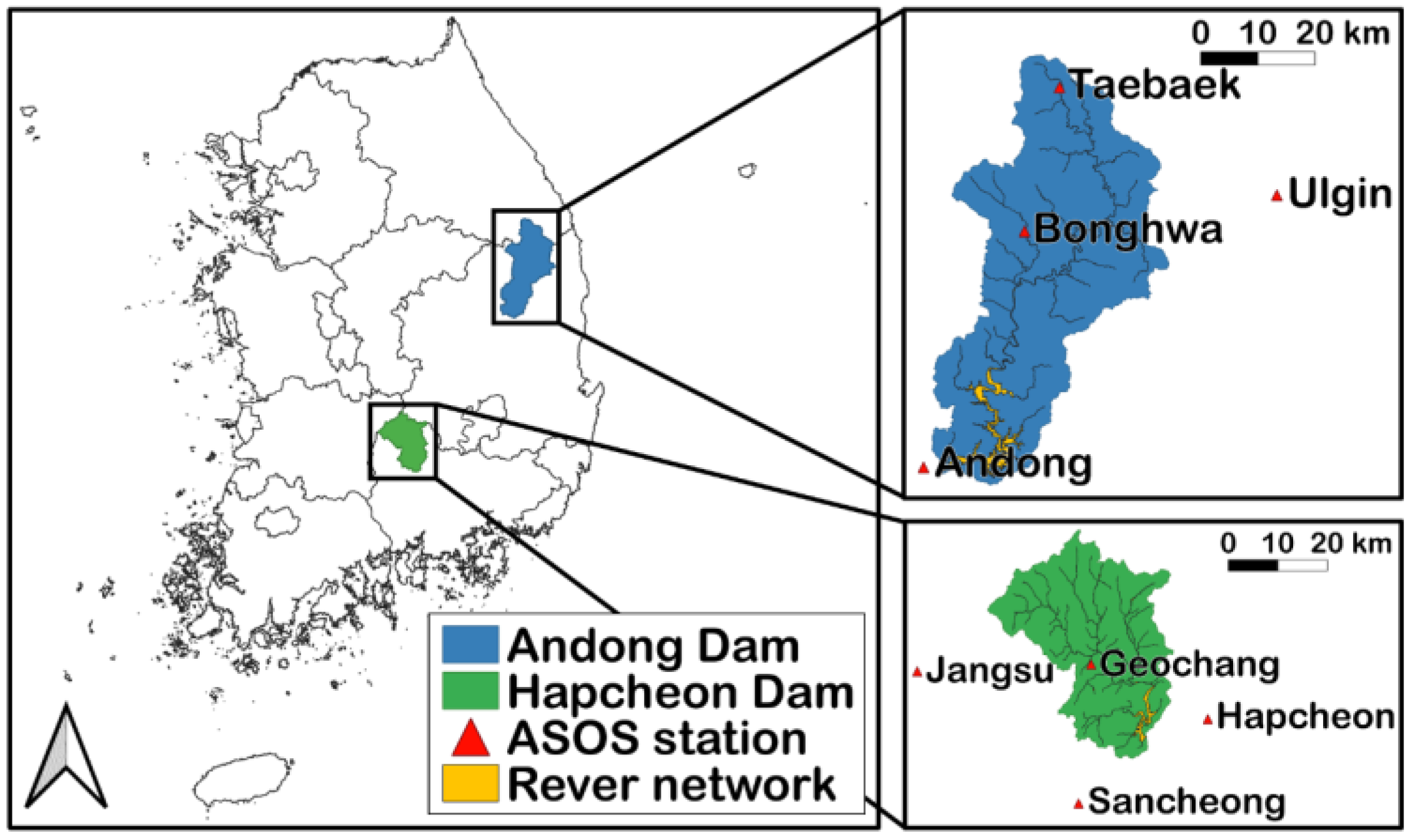
2.1. Data and Research Areas
2.2. Monthly Soil Moisture Simulation Model
2.3. Drought Index
- Weak drought (−1 to −0.5);
- Normal drought (−1.5 to −1);
- Severe drought (−2 to −1.5);
- Extreme drought (−2 or less).
2.4. Drought Propagation Time
2.5. Copula Model between Meteorological and Agricultural (or Hydrological) Drought Propagation
3. Results and Discussion
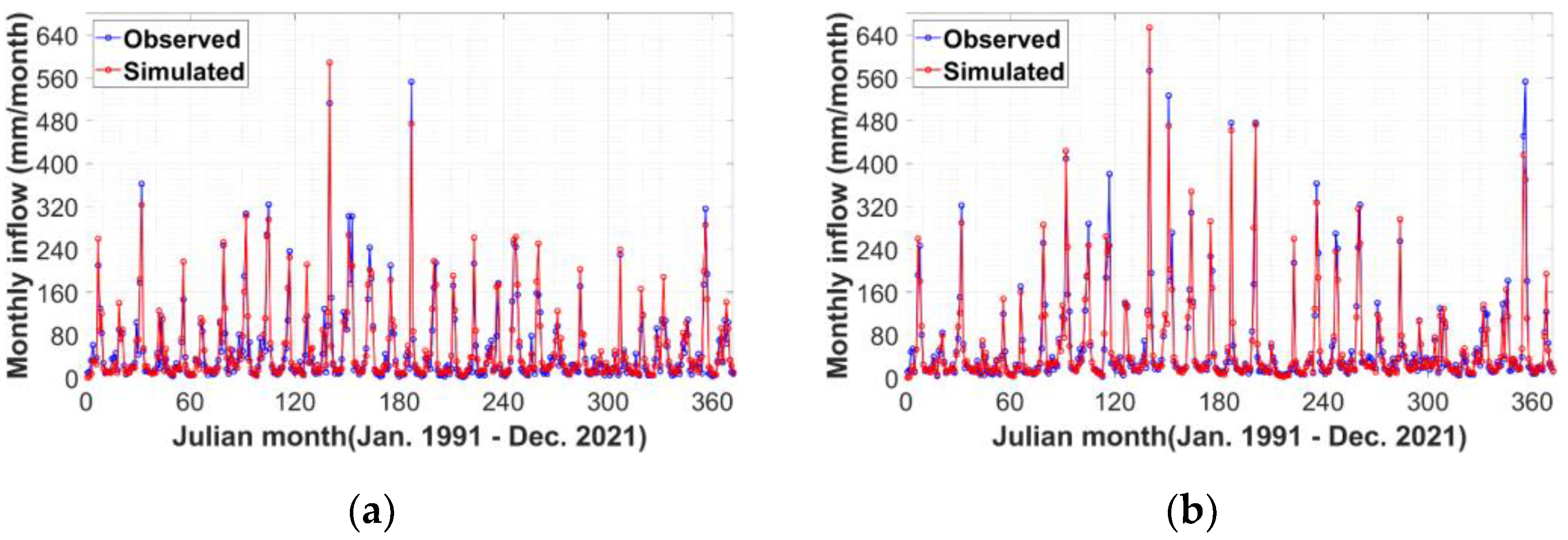
3.1. Soil Moisture Simulation
3.2. Meteorological Drought Propagation Time and Correlation with Other Types of Drought
3.3. Propagation of Drought Severity
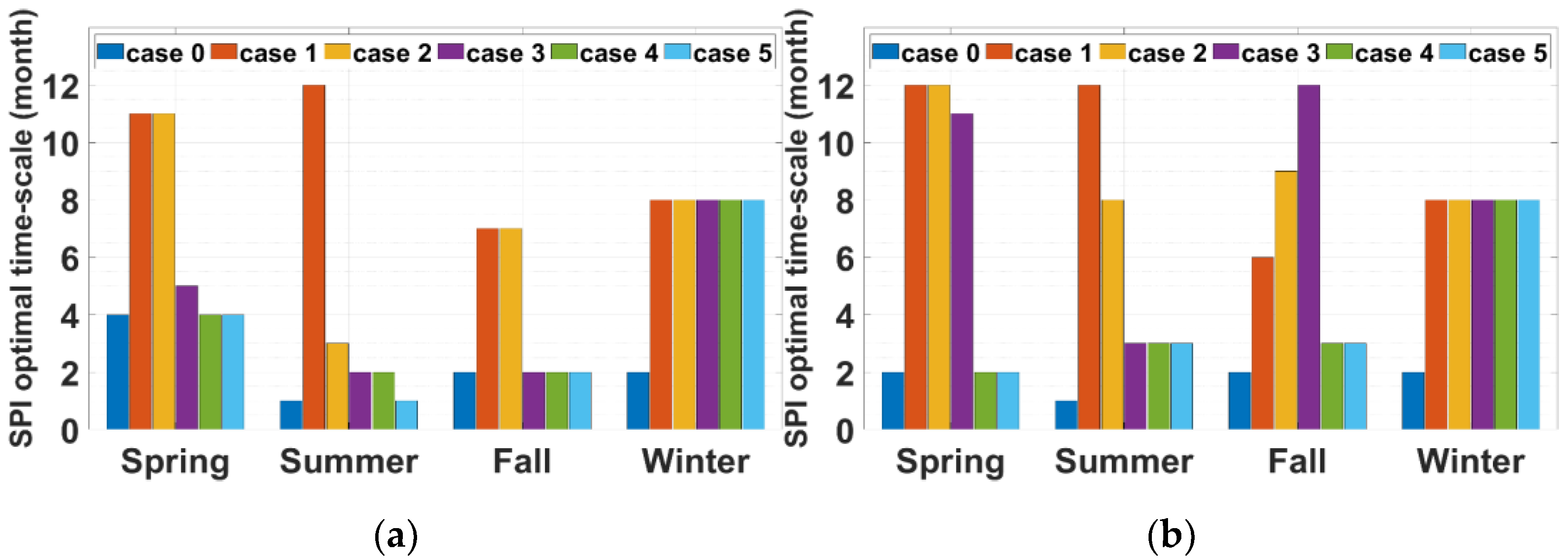
3.4. Changes in Drought Propagation Characteristics by Multipurpose Dam
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dai, A. Drought under global warming: A review. WIREs Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef] [Green Version]
- Gampe, D.; Zscheischler, J.; Reichstein, M.; O’Sullivan, M.; Smith, W.; Sitch, S.; Buermann, W. Increasing impact of warm droughts on northern ecosystem productivity over recent decades. Nat. Clim. Chang. 2021, 11, 772–779. [Google Scholar] [CrossRef]
- Lesk, C.; Coffel, E.; Winter, J.; Ray, D.; Zscheischler, J.; Seneviratne, S.; Horton, R. Stronger temperature–moisture couplings exacerbate the impact of climate warming on global crop yields. Nat. Food 2021, 2, 683–691. [Google Scholar] [CrossRef]
- Chiang, F.; Mazdiyasni, O.; AghaKouchak, A. Evidence of anthropogenic impacts on global drought frequency, duration, and intensity. Nat. Commun. 2021, 12, 2754. [Google Scholar] [CrossRef] [PubMed]
- Watson, P.; Spaulding, A.; Koukoula, M.; Anagnostou, E. Improved quantitative prediction of power outages caused by extreme weather events. Weather Clim. Extrem. 2022, 37, 100487. [Google Scholar] [CrossRef]
- Naumann, G.; Cammalleri, C.; Mentaschi, L.; Feyen, L. Increased economic drought impacts in Europe with anthropogenic warming. Nat. Clim. Chang. 2021, 11, 485–491. [Google Scholar] [CrossRef]
- Samaniego, L.; Thober, S.; Kumar, R.; Wanders, N.; Rakovec, O.; Pan, M.; Zink, M.; Sheffield, J.; Wood, E.; Marx, A. Anthropogenic warming exacerbates European soil moisture droughts. Nat. Clim. Chang. 2018, 8, 421–426. [Google Scholar] [CrossRef] [Green Version]
- Iglesias, V.; Travis, W.; Balch, J. Recent droughts in the United States are among the fastest-developing of the last seven decades. Weather Clim. Extrem. 2022, 37, 100491. [Google Scholar] [CrossRef]
- Trenberth, K.; Dai, A.; van der Schrier, G.; Jones, P.; Barichivich, J.; Briffa, K.; Sheffield, J. Global warming and changes in drought. Nat. Clim. Chang. 2014, 4, 17–22. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Huschke, R.E. Glossary of Meteorology, 1st ed.; American Meteorological Society: Boston, MA, USA, 1959; p. 638. [Google Scholar]
- Rosenberg, N.J. Drought in the Great Plains: Research on Impacts and Strategies, 1st ed.; Water Resources Publications: Littleton, CO, USA, 1979; p. 225. [Google Scholar]
- Yevjevich Vujica, H.W.A.; Salas, J.D. Drought Research Needs, 1st ed.; Water Resources Publications: Littleton, CO, USA, 1977; p. 276. [Google Scholar]
- Zeng, J.; Zhang, R.; Tang, J.; Liang, J.; Li, J.; Zeng, Y.; Li, Y.; Zhang, Q.; Shui, W.; Wang, Q. Ecological sustainability assessment of the carbon footprint in Fujian Province, southeast China. Front. Earth Sci. 2020, 15, 12–22. [Google Scholar] [CrossRef]
- Yu, M.; Cho, Y.; Kim, T.; Chae, H. Analysis of drought propagation using hydrometeorological data: From meteorological drought to agricultural drought. J. Korea Water Resour. Assoc. 2017, 51, 195–205. [Google Scholar]
- Van Loon, A.F.; Tijdeman, E.; Wanders, N.; van Lanen, H.A.J.; Teuling, A.J.; Uijlenhoet, R. How climate seasonality modifies drought duration and deficit. J. Geophys. Res. Atmos. 2014, 119, 4640–4656. [Google Scholar] [CrossRef]
- Ma, F.; Luo, L.; Ye, A.; Duan, Q. Drought Characteristics and propagation in the semiarid Heihe River basin in northwestern China. J. Hydrometeor. 2019, 20, 59–77. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, S.; Huang, Q.; Leng, G.; Fang, W.; Wang, L.; Wang, H. Propagation thresholds of meteorological drought for triggering hydrological drought at various levels. Sci. Total Environ. 2020, 712, 136502. [Google Scholar] [CrossRef] [PubMed]
- Seo, J.; Won, J.; Choi, J.; Lee, J.; Kim, S. A copula model to identify the risk of river water temperature stress for meteorological drought. J. Environ. Manag. 2022, 311, 114861. [Google Scholar] [CrossRef] [PubMed]
- Yoo, J.; So, B.; Lee, J.; Kim, T. Analysis of drought propagation from meteorological to hydrological drought considering spatio-temporal moving pattern of drought events. J. Korean Soc. Civ. Eng. 2020, 40, 135–143. [Google Scholar]
- Joseph, S.; Sahai, A.K.; Goswami, B.N. Eastward propagating MJO during boreal summer and Indian monsoon droughts. Clim. Dyn. 2009, 32, 1139–1153. [Google Scholar] [CrossRef] [Green Version]
- Eltahir, E.A.B.; Yeh, P.J.F. On the asymmetric response of aquifer water level to floods and droughts in Illinois. Water Resour. Res. 1999, 35, 1199–1217. [Google Scholar] [CrossRef] [Green Version]
- Barker, L.J.; Hannaford, J.; Chiverton, A.; Svensson, C. From meteorological to hydrological drought using standardised indicators. Hydrol. Earth Syst. Sci. 2016, 20, 2483–2505. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Zhang, X.; Wang, X.; Hao, Z.; Singh, V.P.; Hao, F. Propagation from meteorological drought to hydrological drought under the impact of human activities: A case study in northern China. J. Hydrol. 2019, 579, 124147. [Google Scholar] [CrossRef]
- Han, Z.; Huang, S.; Huang, Q.; Leng, G.; Wang, H.; Bai, Q.; Zhao, J.; Ma, L.; Wang, L.; Du, M. Propagation dynamics from meteorological to groundwater drought and their possible influence factors. J. Hydrol. 2019, 578, 124102. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, S.; Huang, Q.; Wang, H.; Fang, W.; Yang, Y.; Wang, L. Assessing socioeconomic drought based on an improved Multivariate Standardized Reliability and Resilience Index. J. Hydrol. 2019, 568, 904–918. [Google Scholar] [CrossRef]
- Won, J.; Seo, J.; Kim, S. A copula model integrating atmospheric moisture demand and supply for vegetation vulnerability mapping. Sci. Total Environ. 2022, 812, 151464. [Google Scholar] [CrossRef] [PubMed]
- Mo, K.C. Drought onset and recovery over the United States. J. Geophys. Res. Atmos. 2011, 116, D20106. [Google Scholar] [CrossRef]
- Wu, G.; Chen, J.; Shi, X.; Kim, J.S.; Xia, J.; Zhang, L. Impacts of global climate warming on meteorological and hydrological droughts and their propagations. Earth’s Future 2022, 10, e2021EF002542. [Google Scholar] [CrossRef]
- Bloomfield, J.P.; Marchant, B.P. Analysis of groundwater drought building on the standardised precipitation index approach. Hydrol. Earth Syst. Sci. 2013, 17, 4769–4787. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhang, B. The responses of natural vegetation dynamics to drought during the growing season across China. J. Hydrol. 2019, 574, 706–714. [Google Scholar] [CrossRef]
- Grillakis, M.G. Increase in severe and extreme soil moisture droughts for Europe under climate change. Sci. Total Environ. 2019, 660, 1245–1255. [Google Scholar] [CrossRef] [PubMed]
- Apurv, T.; Sivapalan, M.; Cai, X. Understanding the role of climate characteristics in drought propagation. Water Resour. Res. 2017, 53, 9304–9329. [Google Scholar] [CrossRef] [Green Version]
- Keyantash, J.A.; Dracup, J.A. An aggregate drought index: Assessing drought severity based on fluctuations in the hydrologic cycle and surface water storage. Water Resour. Res. 2004, 40, W09304. [Google Scholar] [CrossRef] [Green Version]
- Gevaert, A.I.; Veldkamp, T.I.E.; Ward, P.J. The effect of climate type on timescales of drought propagation in an ensemble of global hydrological models. Hydrol. Earth Syst. Sci. 2018, 22, 4649–4665. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, X.; Hao, Z.; Singh, V.P.; Hao, F. Characterization of agricultural drought propagation over China based on bivariate probabilistic quantification. J. Hydrol. 2021, 598, 126194. [Google Scholar] [CrossRef]
- Chen, N.; Li, R.; Zhang, X.; Yang, C.; Wang, X.; Zeng, L.; Tangf, S.; Wanga, W.; Li, D.; Niyogig, D. Drought propagation in Northern China Plain: A comparative analysis of GLDAS and MERRA-2 datasets. J. Hydrol. 2020, 588, 125026. [Google Scholar] [CrossRef]
- Lorenzo-Lacruz, J.; Vicente-Serrano, S.M.; González-Hidalgo, J.C.; López-Moreno, J.I.; Cortesi, N. Hydrological drought response to meteorological drought in the Iberian Peninsula. Clim. Res. 2013, 58, 117–131. [Google Scholar] [CrossRef] [Green Version]
- Haslinger, K.; Koffler, D.; Schöner, W.; Laaha, G. Exploring the link between meteorological drought and streamflow: Effects of climate-catchment interaction. Water Resour. Res. 2014, 50, 2468–2487. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, Q.; Huang, S.; Leng, G.; Zheng, X.; Fang, W.; Deng, M.; Song, S. Elucidating the effects of mega reservoir on watershed drought tolerance based on a drought propagation analytical method. J. Hydrol. 2021, 598, 125738. [Google Scholar] [CrossRef]
- Xing, Z.; Ma, M.; Zhang, X.; Leng, G.; Su, Z.; Lv, J.; Yu, Z.; Yi, P. Altered drought propagation under the influence of reservoir regulation. J. Hydrol. 2021, 603, 127049. [Google Scholar] [CrossRef]
- Ji, U.; Hwang, M.; Yeo, W.; Lim, K. Risk Assessment and potentiality analysis of soil loss at the Nakdong River watershed using the land use map, revised universal soil loss equation, and landslide risk map. J. Korea Water Resour. Assoc. 2012, 45, 617–629. [Google Scholar] [CrossRef] [Green Version]
- Open MET Data Portal. Available online: https://data.kma.go.kr (accessed on 22 March 2022).
- Water Resources Management Information System. Available online: http://www.wamis.go.kr (accessed on 5 April 2022).
- Thomas, H.A. Improved Methods for National Water Assessment, Water Resources Contract: WR15249270; Final report; Harvard Water Resources Group: Washington, DC, USA, 1981; p. 59. [Google Scholar]
- Won, J.; Choi, J.; Lee, O.; Kim, S. Copula-based Joint Drought Index using SPI and EDDI and its application to climate change. Sci. Total Environ. 2020, 744, 140701. [Google Scholar] [CrossRef] [PubMed]
- Won, J.; Son, Y.; Lee, S.; Kang, L.; Kim, S. Evaluation of utilization of satellite remote sensing data for drought monitoring. Korean J. Remote Sens. 2021, 37, 1803–1818. [Google Scholar]
- McKee, T.; Doesken, N.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Hayes, M.; Svoboda, M.; Wall, N.; Widhalm, M. The Lincoln declaration on drought indices: Universal meteorological drought index Recommended. Bull. Am. Meteor. Soc. 2011, 92, 485–488. [Google Scholar] [CrossRef] [Green Version]
- Kao, S.C.; Govindaraju, R.S. A copula-based joint deficit index for droughts. J. Hydrol. 2010, 380, 121–134. [Google Scholar] [CrossRef]
- Ionita, M.; Scholz, P.; Chelcea, S. Assessment of droughts in Romania using the Standardized Precipitation Index. Nat. Hazards 2016, 81, 1483–1498. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Li, P.; Huang, Q.; Leng, G.; Hou, B.; Ma, L. The propagation from meteorological to hydrological drought and its potential influence factors. J. Hydrol. 2017, 547, 184–195. [Google Scholar] [CrossRef]
- Huang, S.; Huang, Q.; Chang, J.; Leng, G.; Xing, L. The response of agricultural drought to meteorological drought and the influencing factors: A case study in the Wei River Basin China. Agric. Water Manag. 2015, 159, 45–54. [Google Scholar] [CrossRef]
- Ryu, J.S.; Ahn, J.; Kim, S. An application of drought severity-area- duration curves using copulas-based joint drought index. J. Korea Water Resour. Assoc. 2012, 45, 1043–1050. [Google Scholar] [CrossRef] [Green Version]
- Sklar, M. Fonctions de repartition an dimensions et leurs marges. Publ. De L’institut De Stat. De L’université De Paris 1959, 8, 229–231. [Google Scholar]
- Salvadori, G.; De Michele, C. Frequency analysis via copulas: Theoretical aspects and applications to hydrological events. Water Resour. Res. 2004, 40, W12511. [Google Scholar] [CrossRef]
- Akaike, H. Information Theory and an Extension of the Maximum Likelihood Principle, 1st ed.; Akadémiai Kiadó: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Sadegh, M.; Ragno, E.; AghaKouchak, A. Multivariate Copula Analysis Toolbox (MvCAT): Describing dependence and underlying uncertainty using a B ayesian framework. Water Resour. Res. 2017, 53, 5166–5183. [Google Scholar] [CrossRef]
- Vrugt, J.; Gupta, H.; Bouten, W.; Sorooshian, S. A shuffled complex evolution metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters. Water Resour. Res. 2012, 39, 1201. [Google Scholar] [CrossRef] [Green Version]
- Green, C.H.; Tomer, M.D.; Di Luzio, M.; Arnold, J.G. Hydrologic evaluation of the soil and water assessment tool for a lager tile-drained watershed in Iowa. Trans. Am. Soc. Agric. Biol. Eng. 2006, 49, 413–422. [Google Scholar]
- Patil, S.D.; Stieglitz, M. Comparing spatial and temporal transferability of hydrological model parameters. J. Hydrol. 2015, 525, 409–417. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.; Lee, J.; Kim, S. Utilization of the long short-term memory network for predicting streamflow in ungauged basins in Korea. Ecol. Eng. 2022, 182, 106699. [Google Scholar] [CrossRef]
- Maity, R.; Suman, M.; Verma, N. Drought prediction using a wavelet based approach to model the temporal consequences of different types of droughts. J. Hydrol. 2016, 539, 417–428. [Google Scholar] [CrossRef]
- Milly, P.C.D. Potential evaporation and soil moisture in general circulation models. J. Clim. 1992, 5, 209–226. [Google Scholar] [CrossRef]
- Qian, Y.; He, F.; Wang, W. Seasonality, rather than nutrient addition or vegetation types, influenced short-term temperature sensitivity of soil organic carbon decomposition. PLoS ONE 2016, 11, e0153415. [Google Scholar] [CrossRef]












| Basin | Parameters | |||
|---|---|---|---|---|
| a | b | c | d | |
| Andong Dam | 0.88209 | 194.0413 | 0.075125 | 0.60503 |
| Hapcheon Dam | 0.94594 | 287.4673 | 0.149630 | 0.51401 |
| Basin | Calibration | Validation | ||||
|---|---|---|---|---|---|---|
| NSE | KGE | NSE | KGE | |||
| Andong Dam | 0.89268 | 0.88595 | 0.91163 | 0.90374 | 0.89368 | 0.86295 |
| Hapcheon Dam | 0.93364 | 0.93266 | 0.96607 | 0.92641 | 0.92491 | 0.91494 |
| Seasons | Conditions for SPI | Agricultural Drought Probability | |||
|---|---|---|---|---|---|
| SMI ≤ −0.5 (0.30854) | SMI ≤ −1.0 (0.15866) | SMI ≤ −1.5 (0.06681) | SMI ≤ −2.0 (0.02275) | ||
| Spring | SPI ≤ −0.5 | 0.74407 | 0.44797 | 0.20291 | 0.07136 |
| SPI ≤ −1.0 | 0.87116 | 0.62950 | 0.33033 | 0.12622 | |
| SPI ≤ −1.5 | 0.93710 | 0.78448 | 0.50648 | 0.23040 | |
| SPI ≤ −2.0 | 0.96777 | 0.88023 | 0.67659 | 0.38632 | |
| Summer | SPI ≤ −0.5 | 0.80175 | 0.49478 | 0.21591 | 0.07373 |
| SPI ≤ −1.0 | 0.96220 | 0.79868 | 0.41196 | 0.14328 | |
| SPI ≤ −1.5 | 0.99716 | 0.97834 | 0.79826 | 0.33660 | |
| SPI ≤ −2.0 | 0.99990 | 0.99918 | 0.98845 | 0.79823 | |
| Fall | SPI ≤ −0.5 | 0.75084 | 0.46268 | 0.21111 | 0.07347 |
| SPI ≤ −1.0 | 0.89977 | 0.67017 | 0.36173 | 0.13796 | |
| SPI ≤ −1.5 | 0.97496 | 0.85905 | 0.58736 | 0.27629 | |
| SPI ≤ −2.0 | 0.99636 | 0.96209 | 0.81135 | 0.50583 | |
| Winter | SPI ≤ −0.5 | 0.78375 | 0.47978 | 0.21427 | 0.07368 |
| SPI ≤ −1.0 | 0.93302 | 0.71304 | 0.38121 | 0.14111 | |
| SPI ≤ −1.5 | 0.98955 | 0.90532 | 0.63956 | 0.29705 | |
| SPI ≤ −2.0 | 0.99926 | 0.98404 | 0.87229 | 0.56599 | |
| Seasons | Conditions for SPI | Agricultural Drought Probability | |||
|---|---|---|---|---|---|
| SMI ≤ −0.5 (0.30854) | SMI ≤ −1.0 (0.15866) | SMI ≤ −1.5 (0.06681) | SMI ≤ −2.0 (0.02275) | ||
| Spring | SPI ≤ −0.5 | 0.75082 | 0.45188 | 0.20416 | 0.07164 |
| SPI ≤ −1.0 | 0.87878 | 0.63847 | 0.33502 | 0.12760 | |
| SPI ≤ −1.5 | 0.94287 | 0.79562 | 0.51712 | 0.23533 | |
| SPI ≤ −2.0 | 0.97162 | 0.88985 | 0.69106 | 0.39772 | |
| Summer | SPI ≤ −0.5 | 0.81541 | 0.49373 | 0.21585 | 0.07373 |
| SPI ≤ −1.0 | 0.96016 | 0.75457 | 0.39726 | 0.14270 | |
| SPI ≤ −1.5 | 0.99687 | 0.94343 | 0.69071 | 0.31438 | |
| SPI ≤ −2.0 | 0.99992 | 0.99519 | 0.92319 | 0.62591 | |
| Fall | SPI ≤ −0.5 | 0.72532 | 0.46231 | 0.21214 | 0.07356 |
| SPI ≤ −1.0 | 0.89905 | 0.71249 | 0.38913 | 0.14200 | |
| SPI ≤ −1.5 | 0.97974 | 0.92411 | 0.70885 | 0.32264 | |
| SPI ≤ −2.0 | 0.99761 | 0.99031 | 0.94745 | 0.70816 | |
| Winter | SPI ≤ −0.5 | 0.70020 | 0.42121 | 0.19344 | 0.06897 |
| SPI ≤ −1.0 | 0.81912 | 0.57238 | 0.29934 | 0.11627 | |
| SPI ≤ −1.5 | 0.89339 | 0.71087 | 0.44039 | 0.19898 | |
| SPI ≤ −2.0 | 0.93537 | 0.81085 | 0.58433 | 0.31773 | |
| Seasons | Conditions for SPI | Hydrological Drought Probability | |||
|---|---|---|---|---|---|
| SRI ≤ −0.5 (0.30854) | SRI ≤ −1.0 (0.15866) | SRI ≤ −1.5 (0.06681) | SRI ≤ −2.0 (0.02275) | ||
| Spring | SPI ≤ −0.5 | 0.70590 | 0.41580 | 0.18539 | 0.06449 |
| SPI ≤ −1.0 | 0.80860 | 0.53602 | 0.25856 | 0.09319 | |
| SPI ≤ −1.5 | 0.85617 | 0.61402 | 0.31949 | 0.12017 | |
| SPI ≤ −2.0 | 0.87458 | 0.64992 | 0.35290 | 0.13657 | |
| Summer | SPI ≤ −0.5 | 0.71034 | 0.42757 | 0.19583 | 0.06961 |
| SPI ≤ −1.0 | 0.83149 | 0.58540 | 0.30655 | 0.11870 | |
| SPI ≤ −1.5 | 0.90439 | 0.72799 | 0.45520 | 0.20612 | |
| SPI ≤ −2.0 | 0.94401 | 0.82781 | 0.60529 | 0.33276 | |
| Fall | SPI ≤ −0.5 | 0.70104 | 0.41278 | 0.18415 | 0.06408 |
| SPI ≤ −1.0 | 0.80274 | 0.53040 | 0.25556 | 0.09210 | |
| SPI ≤ −1.5 | 0.85045 | 0.60692 | 0.31477 | 0.11824 | |
| SPI ≤ −2.0 | 0.86907 | 0.64230 | 0.34721 | 0.13405 | |
| Winter | SPI ≤ −0.5 | 0.66748 | 0.39166 | 0.17524 | 0.06112 |
| SPI ≤ −1.0 | 0.76167 | 0.49251 | 0.23545 | 0.08472 | |
| SPI ≤ −1.5 | 0.80932 | 0.55914 | 0.28393 | 0.10568 | |
| SPI ≤ −2.0 | 0.82893 | 0.59081 | 0.31034 | 0.11804 | |
| Seasons | Conditions for SPI | Hydrological Drought Probability | |||
|---|---|---|---|---|---|
| SRI ≤ −0.5 (0.30854) | SRI ≤ −1.0 (0.15866) | SRI ≤ −1.5 (0.06681) | SRI ≤ −2.0 (0.02275) | ||
| Spring | SPI ≤ −0.5 | 0.75852 | 0.44743 | 0.19778 | 0.06845 |
| SPI ≤ −1.0 | 0.87011 | 0.59962 | 0.29239 | 0.10540 | |
| SPI ≤ −1.5 | 0.91342 | 0.69437 | 0.37571 | 0.14356 | |
| SPI ≤ −2.0 | 0.92834 | 0.73503 | 0.42158 | 0.16792 | |
| Summer | SPI ≤ −0.5 | 0.74385 | 0.44784 | 0.20287 | 0.07135 |
| SPI ≤ −1.0 | 0.87092 | 0.62921 | 0.33018 | 0.12617 | |
| SPI ≤ −1.5 | 0.93691 | 0.78412 | 0.50614 | 0.23024 | |
| SPI ≤ −2.0 | 0.96764 | 0.87991 | 0.67612 | 0.38596 | |
| Fall | SPI ≤ −0.5 | 0.68647 | 0.40367 | 0.18035 | 0.06283 |
| SPI ≤ −1.0 | 0.78502 | 0.51375 | 0.24671 | 0.08886 | |
| SPI ≤ −1.5 | 0.83291 | 0.58590 | 0.30102 | 0.11262 | |
| SPI ≤ −2.0 | 0.85207 | 0.61970 | 0.33070 | 0.12683 | |
| Winter | SPI ≤ −0.5 | 0.59161 | 0.34921 | 0.16238 | 0.05924 |
| SPI ≤ −1.0 | 0.67912 | 0.43964 | 0.22331 | 0.08760 | |
| SPI ≤ −1.5 | 0.74991 | 0.53031 | 0.29883 | 0.12958 | |
| SPI ≤ −2.0 | 0.80343 | 0.61094 | 0.38052 | 0.18475 | |
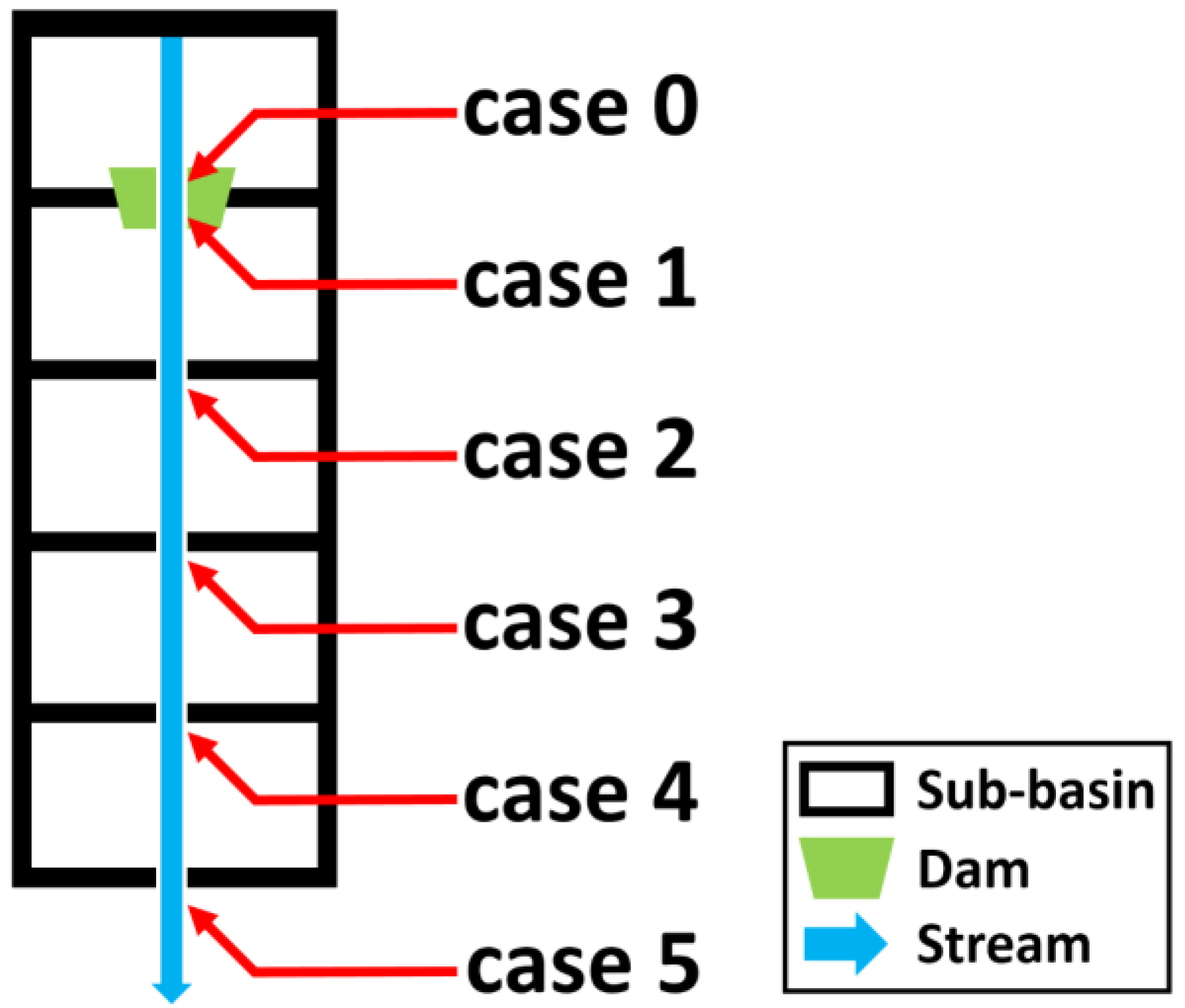
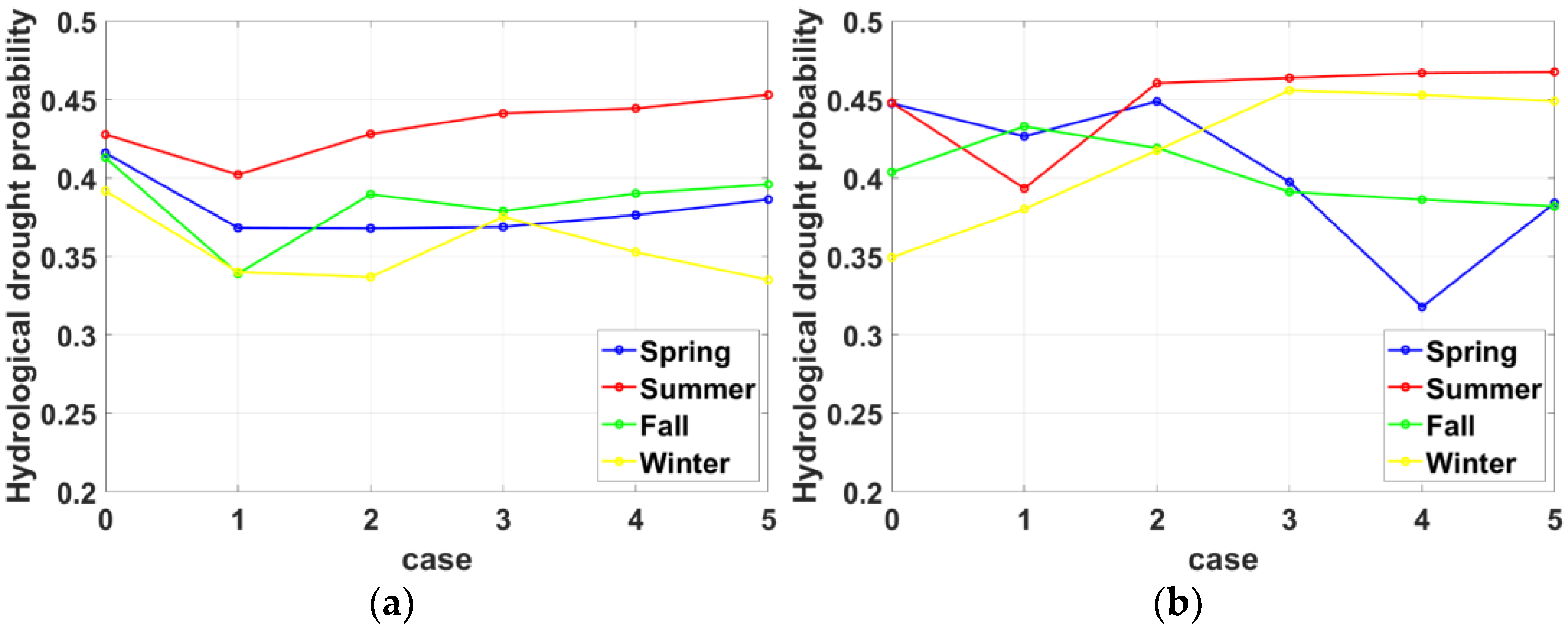
| Case | Input Data |
|---|---|
| Case 0 | Dam inflow |
| Case 1 | Dam outflow |
| Case 2 | Dam inflow + Dam outflow |
| Case 3 | Dam inflow × 2 + Dam outflow |
| Case 4 | Dam inflow × 3 + Dam outflow |
| Case 5 | Dam inflow × 4 + Dam outflow |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, H.; Won, J.; Kang, S.; Kim, S. Characterization of the Propagation of Meteorological Drought Using the Copula Model. Water 2022, 14, 3293. https://doi.org/10.3390/w14203293
Jung H, Won J, Kang S, Kim S. Characterization of the Propagation of Meteorological Drought Using the Copula Model. Water. 2022; 14(20):3293. https://doi.org/10.3390/w14203293
Chicago/Turabian StyleJung, Haeun, Jeongeun Won, Shinuk Kang, and Sangdan Kim. 2022. "Characterization of the Propagation of Meteorological Drought Using the Copula Model" Water 14, no. 20: 3293. https://doi.org/10.3390/w14203293
APA StyleJung, H., Won, J., Kang, S., & Kim, S. (2022). Characterization of the Propagation of Meteorological Drought Using the Copula Model. Water, 14(20), 3293. https://doi.org/10.3390/w14203293







