Study on Multi-Objective Optimization of Sponge Facilities Combination at Urban Block Level: A Residential Complex Case Study in Nanjing, China
Abstract
:1. Introduction
2. Methodology
2.1. The Multi-Objective Optimization Model
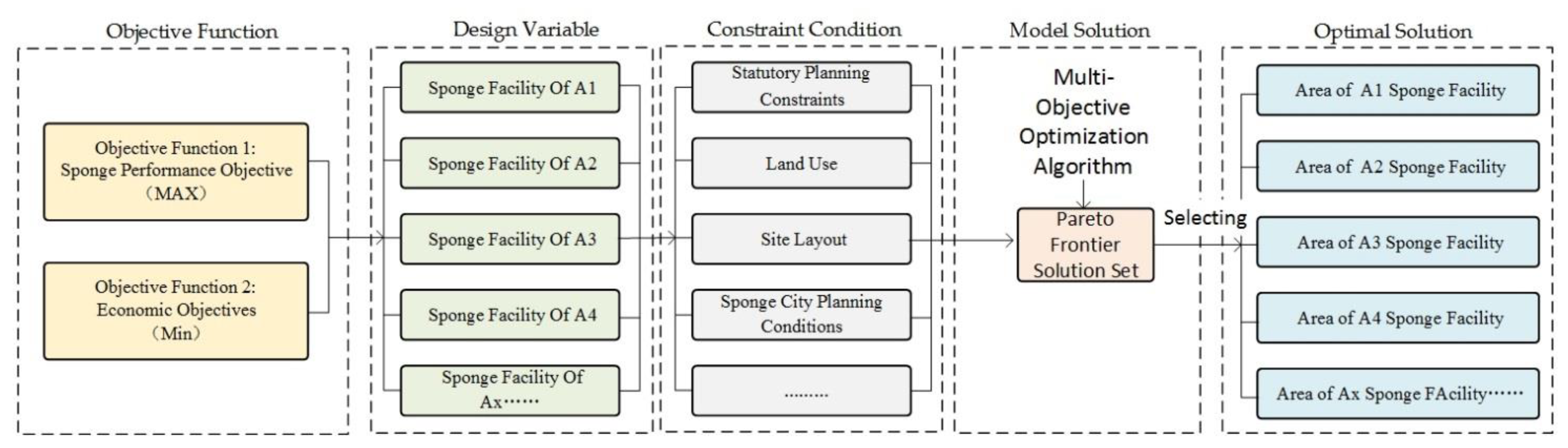
2.2. Model Framework
- First, determine the sponge city design objective functions under different site conditions.
- Second, determine the number of design variables and constraints, while obtaining model constants such as sponge capacity attributes and economic cost per unit sponge facility.
- Again, establish a list of multi-objective optimization model for sponge facilities combination.
- Finally, the optimization algorithm is used to solve the model list to obtain the Pareto solution set, and the optimal solution for the combination of sponge facilities is selected according to the project situation.
2.3. Model Components
2.3.1. The Objective Functions
- Rainwater infiltration and storage effect
- Rainwater harvesting and utilization effect
- Runoff pollution removal effect
2.3.2. The Decision Variables
2.3.3. The Constraints
- (1)
- Constraints of the total area
- (2)
- Constraints of the site green space ratio
- (3)
- Runoff Control Constraints for Sponge City Construction
- (4)
- Constraints of the Site Building Density Rate
- (5)
- Constraints of the Hard Surface Area
- (6)
- Constraints of the Water Surface Rate
- (7)
- Non-negative Constraints
2.3.4. The Constants
2.4. Model Solution
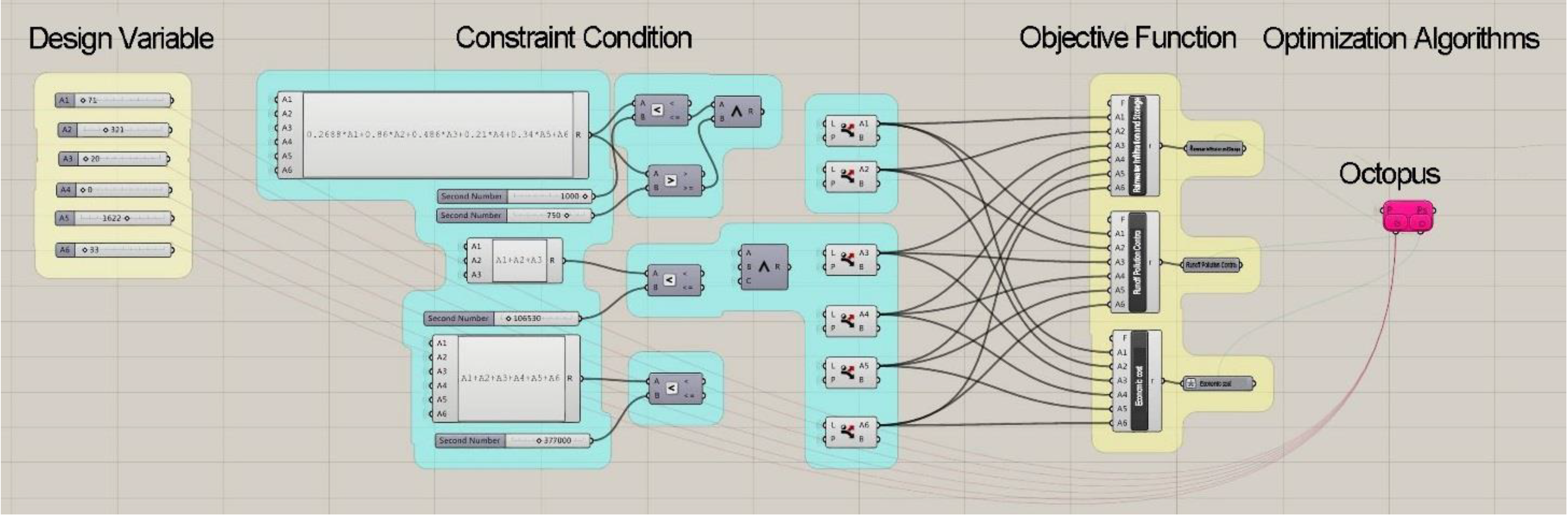
2.4.1. Algorithms
2.4.2. Software Tools
3. Case Study
3.1. Overview of the Study Area
3.1.1. Location
3.1.2. Weather
3.1.3. Underlying Surface
3.1.4. Planning and Policy Status
3.1.5. Sponge City Scale Control Requirements
3.2. Optimization Objectives
3.3. Constraint Settings
3.4. Model List
4. Results
4.1. Parameter Settings
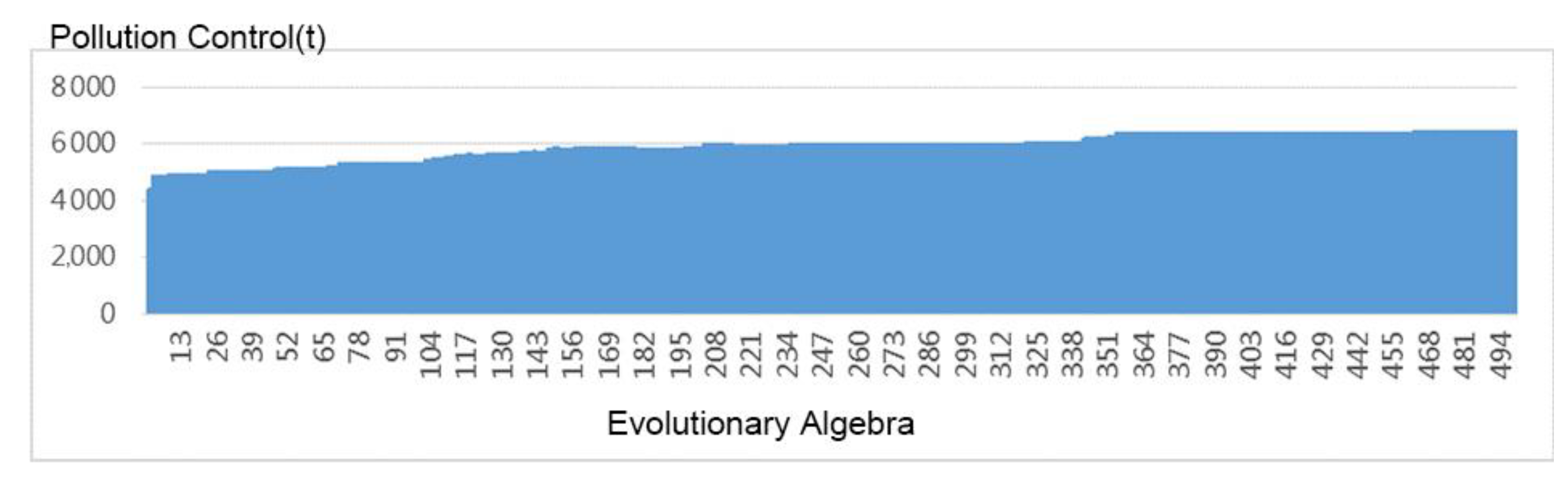
4.2. Validity Verification
4.3. Analysis of the Results
4.3.1. Optimal Solution for Rainwater Infiltration, Storage and Economic Objectives
4.3.2. Optimal Solution for Runoff Pollution Control and Economic Objectives
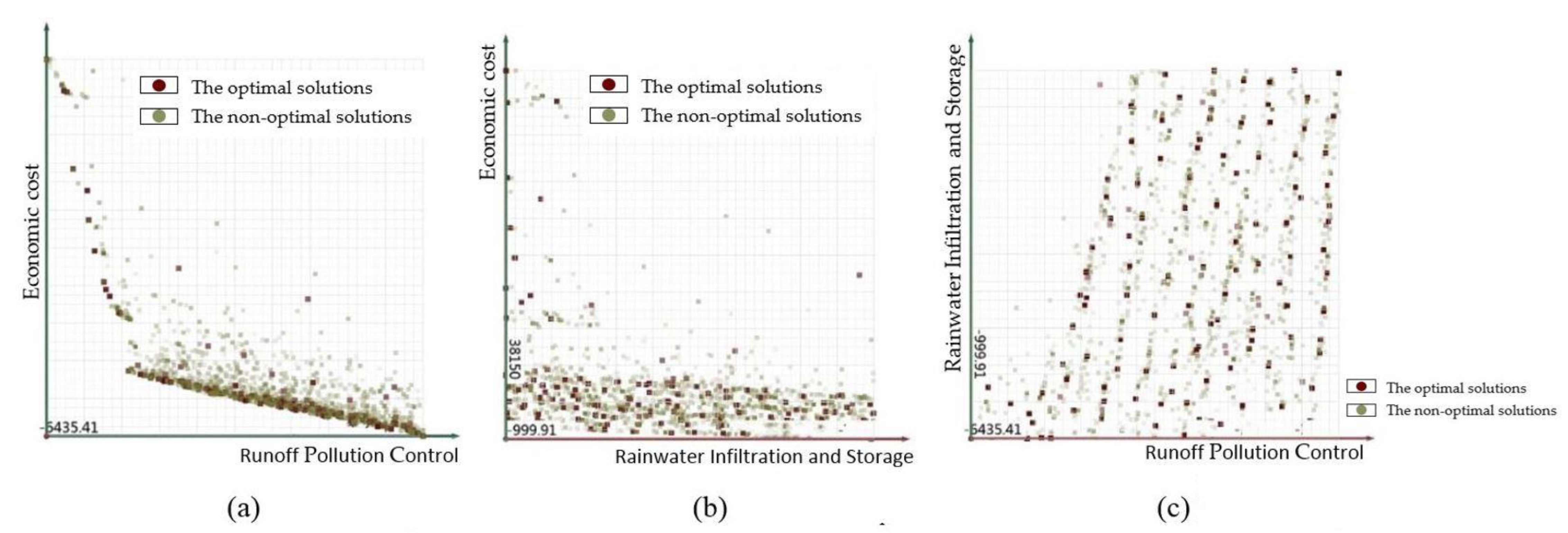
4.3.3. Optimal Solution for All Objectives
4.3.4. Target Interval Selection and Priority for Specific Facility Types
5. Discussion
5.1. Comparison of Algorithms
5.2. Selecting Software Tools
5.3. Comparison with Related Research
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Scheme | Constants | Description of Constants | Unit |
|---|---|---|---|
| 1 | s | Infiltration storage capacity per unit area of facility | m3 |
| 3 | r | Water collected per unit area of facility | m3 |
| 4 | p | Runoff pollution removal per unit area of facility | t |
| 5 | e | Facility cost per unit area of facility | Yuan/m2 |
| Materials | Grain Size (mm) | Weight (%) | Permeability Coefficient K (m/s) |
|---|---|---|---|
| Clay | - | - | <5.7 × 10−8 |
| Silty clay | - | - | 5.7 × 10−8 ~ 1.16 × 10−6 |
| Powdered soil | - | - | 1.16 × 10−6 ~ 5.79 × 10−6 |
| Silt | >0.075 | >50 | 5.79 × 10−6 ~ 1.16 × 10−5 |
| Fine sandy clay | >0.075 | >85 | 1.16 × 10−5 ~ 5.79 × 10−5 |
| Medium sand | >0.25 | >50 | 5.79 × 10−5 ~ 2.31 × 10−4 |
| Homogenised medium sand | - | - | 4.05 × 10−4 ~ 5.79 × 10−4 |
| Coarse sand | >0.50 | >50 | 2.31 × 10−4 ~ 5.79 × 10−4 |
| Round gravel | >2.00 | >50 | 5.79 × 10−4 ~ 1.16 × 10−3 |
| Pebbles | >20.0 | >50 | 1.16 × 10−3 ~ 5.79 × 10−3 |
| Slightly fractured rock | - | - | 2.31 × 10−4 ~ 6.94 × 10−4 |
| Rocks with many fissures | - | - | >6.94 × 10−4 |
| Type of Soil | K (mm/h) | ψ (mm) | Φ (Fractions) | FC (Fractions) | WP (Fractions) |
|---|---|---|---|---|---|
| Sandy Soil | 120.4 | 4.9022 | 0.437 | 0.062 | 0.024 |
| Loamy Sandy Soil | 29.972 | 6.096 | 0.437 | 0.105 | 0.047 |
| Sandy Loamy Soil | 10.922 | 10.9982 | 0.453 | 0.190 | 0.085 |
| Loamy Soil | 3.302 | 8.89 | 0.463 | 0.232 | 0.116 |
| Silty Loamy Soil | 6.604 | 16.9926 | 0.501 | 0.284 | 0.135 |
| Sandy Clay Loam Soil | 1.524 | 21.9964 | 0.398 | 0.244 | 0.136 |
| Clay Loamy Soil | 1.016 | 21.0058 | 0.464 | 0.310 | 0.187 |
| Chalky Clay Loam Soil | 1.016 | 27.0002 | 0.471 | 0.342 | 0.210 |
| Sandy Clay Soil | 0.508 | 24.003 | 0.430 | 0.321 | 0.221 |
| Chalky Clay Soil | 0.508 | 29.0068 | 0.479 | 0.371 | 0.251 |
| Clay Soil | 0.254 | 32.004 | 0.475 | 0.378 | 0.265 |
| Name of coefficient | Horizontal green space | Horizontal Green Space with Water Storage Modules | Water-storing Sunken Green Space | Permeable Hard Surface | Designed Water Body for Water Storage | Green Roof |
|---|---|---|---|---|---|---|
| K | 65 | 85 | 60 | 85 | 0 | 75 |
| P | Annual average SS of stormwater runoff from urban areas | |||||
| Serial Number | Types of Sponge Facilities | Rource of Values | Unit Area Cost (yuan/m2) | Notes |
|---|---|---|---|---|
| 1 | Horizontal green space | Technical Guide for Sponge City Construction | 30–50 | |
| 2 | Horizontal green space with water storage modules | Prices in Nanjing | 800–1200 | Depth of 0.8–1 m |
| 3 | Water-storing sunken green space | Technical Guide for Sponge City Construction | 40–50 | Average depth 100–200 mm |
| 4 | Permeable hard surface | Technical Guide for Sponge City Construction | 60–200 | |
| 5 | Designed water body for water storage | Prices in Nanjing | 80 | Average depth 1 m |
| 6 | Green roof | Technical Guide for Sponge City Construction | 100–300 |
References
- Yang, D.; Yang, Y.; Xia, J. Hydrological cycle and water resources in a changing world: A review. Geogr. Sustain. 2021, 2, 115–122. [Google Scholar] [CrossRef]
- Zhang, J.; Song, X.; Wang, G.; He, R.; Wang, X. Development and challenges of urban hydrology in a changing environment: I: Hydrological response to urbanization. Adv. Water Sci. 2014, 25, 594–605. [Google Scholar]
- Liu, J.; Shao, W.; Xiang, C.; Mei, C.; Li, Z. Uncertainties of urban flood modeling: Influence of parameters for different underlying surfaces. Environ. Res. 2019, 182, 108929. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.N.; Xie, M.K. Being both Opposite and Complementary: Urban Road Sponge System Practice Based on Digital Technology—Taking Nanjing Tianbao Street Ecological Road as the Example. Chin. Landscape Archit. 2017, 33, 5–13. [Google Scholar]
- Hamidi, A.; Ramavandi, B.; Sorial, G.A. Sponge City—An emerging concept in sustainable water resource management: A scientometric analysis. Resour. Environ. Sustain. 2021, 5, 100028. [Google Scholar] [CrossRef]
- Yin, D.; Xu, C.; Jia, H.; Yang, Y.; Sun, C.; Wang, Q.; Liu, S. Sponge City Practices in China: From Pilot Exploration to Systemic Demonstration. Water 2022, 14, 1531. [Google Scholar] [CrossRef]
- Gao, J.; Li, J.; Li, Y.; Xia, J.; Lv, P. A Distribution Optimization Method of Typical LID Facilities for Sponge City Construction. Ecohydrol. Hydrobiol. 2020, 21, 13–22. [Google Scholar] [CrossRef]
- Li, Q.; Wang, F.; Yu, Y.; Huang, Z.; Li, M.; Guan, Y. Comprehensive performance evaluation of LID practices for the sponge city construction: A case study in Guangxi, China. J. Environ. Manag. 2019, 231, 10–20. [Google Scholar] [CrossRef]
- Zhang, K.; Chui, T.F.M. A comprehensive review of spatial allocation of LID-BMP-GI practices: Strategies and optimization tools. Sci. Total Environ. 2017, 621, 915–929. [Google Scholar] [CrossRef]
- George’s County, Maryland Department of Environmental Resources Programs and Planning Division. Low Impact Development Design Strategies: An Integrated Design Approach; U.S. Environmental Protection Agency: Washington, DC, USA, 1999. [Google Scholar]
- Brown, R.A.; Line, D.E.; Hunt, W.F. LID Treatment Train: Pervious Concrete with Subsurface Storage in Series with Bioretention and Care with Seasonal High Water Tables. J. Environ. Eng. 2012, 138, 689–697. [Google Scholar] [CrossRef]
- Jia, H.; Wang, X.; Ti, C.; Zhai, Y.; Field, R.; Tafuri, A.N.; Cai, H.; Yu, S.L. Field monitoring of a LID-BMP treatment train system in China. Environ. Monit. Assess. 2015, 187, 373. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Hong, J.; Jia, H.; Liang, S.; Xu, T. Life cycle environmental and economic assessment of a LID-BMP treatment train system: A case study in China. J. Clean. Prod. 2017, 149, 227–237. [Google Scholar] [CrossRef]
- Lee, J.G.; Selvakumar, A.; Alvi, K.; Riverson, J.; Zhen, J.X.; Shoemaker, L.; Lai, F.-H. A watershed-scale design optimization model for stormwater best management practices. Environ. Modell. Software 2012, 37, 6–18. [Google Scholar] [CrossRef]
- Xu, T.; Jia, H.; Wang, Z.; Mao, X.; Xu, C. SWMM-based methodology for block-scale LID-BMPs planning based on site-scale multi-objective optimization: A case study in Tianjin. Front. Environ. Sci. Eng. 2017, 11, 48–59. [Google Scholar] [CrossRef]
- Zhang, Z.; Gu, J.; Zhang, G.; Ma, W.; Zhao, L.; Ning, P.; Shen, J. Design of urban runoff pollution control based on the Sponge City concept in a large-scale high-plateau mountainous watershed: A case study in Yunnan, China. J. Water Clim. Chang. 2021, 12, 201–222. [Google Scholar] [CrossRef] [Green Version]
- Jiang, C.; Li, J.; Gao, J.; Lv, P.; Yao, Y.; Li, H. Advances in research of optimal rainwater infrastructure configuration in sponge city construction. J. Hydroelectr. Eng. 2021, 40, 19–29. [Google Scholar]
- Sun, H.; Li, L.; Tian, Y.; Zhang, T.; Zuo, W.; Cai, G.; Zhang, F. Sponge city planning and design based on multi-objective optimization and comprehensive evaluation. Acta Sci. Circumstantiae. 2020, 40, 3605–3614. [Google Scholar]
- She, L.; Wei, M.; You, X.-Y. Multi-objective Layout Optimization for Sponge City by Annealing Algorithm and Its Environmental Benefits Analysis. Sustain. Cities Soc. 2021, 66, 102706. [Google Scholar] [CrossRef]
- Hou, J.; Zhu, M.; Wang, Y.; Sun, S. Optimal spatial priority scheme of urban LID-BMPs under different investment periods. Landsc. Urban Plan. 2020, 202, 103858. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, C.; Xu, T.; Jia, H.; Zhang, X.; Chen, Z.; Yin, D. Integrating socioecological indexes in multiobjective intelligent optimization of green-grey coupled infrastructures. Resour. Conserv. Recycl. 2021, 174, 105801. [Google Scholar] [CrossRef]
- Yu, Y.; Zhou, Y.; Guo, Z.; van Duin, B.; Zhang, W. A new LID spatial allocation optimization system at neighborhood scale: Integrated SWMM with PICEA-g using MATLAB as the platform. Sci. Total Environ. 2022, 831, 154843. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Hamlett, J.M.; Reed, P.; Yong, T. Multi-Objective Optimization of Low Impact Development Designs in an Urbanizing Watershed. Open J. Optim. 2013, 2, 95–108. [Google Scholar] [CrossRef] [Green Version]
- Mytilinou, V.; Kolios, A.J. A multi-objective optimization approach applied to offshore wind farm location selection. J. Ocean Eng. Mar. Energy 2017, 3, 265–284. [Google Scholar] [CrossRef] [Green Version]
- Branke, J.; Deb, K.; Miettinen, K.; Sowiński, R. Multiobjective Optimization: Interactive and Evolutionary Approaches; Branke, J., Ed.; Springer: Berlin, Germany, 2008. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; Ross, S., Weber, R., Eds.; John Wiley & Sons: New York, NY, USA, 2001; p. 15. [Google Scholar]
- Beijing University of Civil Engineering and Architecture. Technical Guide for Sponge City Construction; The Ministry of Housing and Urban-Rural Development; China Architecture & Building Press: Beijing, China, 2015; pp. 49–53. [Google Scholar]
- Eiben, A.E.; Smith, J.E. Multiobjective Evolutionary Algorithms. In Introduction to Evolutionary Computing; Natural Computing Series; Springer: Berlin, Germany, 2015. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength pareto evolutionary algorithm. Tech. Rep. Gloriastrasse. 2001, 103, 95–100. [Google Scholar]
- Roudsari, M.S.; Pak, M. Ladybug: A parametric environmental plugin for grasshopper to help designers create an environmentally-conscious design. In Proceedings of the BS 2013: 13th Conference of the International Building Performance Simulation Association, Chambéry, France, 26–28 August 2013. [Google Scholar]
- Shan, R. In Integrating Genetic Algorithm with Rhinoceros and Grasshopper in Whole Building Energy Simulation. In Proceedings of the Grand Renewable Energy 2014, Tokyo, Japan, 27 July–1 August 2014. [Google Scholar]
- Shi, X.; Yang, W. Performance-driven architectural design and optimization technique from a perspective of architects. Autom. Constr. 2013, 32, 125–135. [Google Scholar] [CrossRef]
- Cubukcuoglu, C.; Nourian, P.; Sariyildiz, S.; Tasgetiren, M.F. A discrete event simulation procedure for validating programs of requirements: The case of hospital space planning. SoftwareX 2020, 12, 100539. [Google Scholar] [CrossRef]
- Bahdad, A.A.S.; Fadzil, S.F.S.; Onubi, H.O.; BenLasod, S.A. Sensitivity analysis linked to multi-objective optimization for adjustments of light-shelves design parameters in response to visual comfort and thermal energy performance. J. Build. Eng. 2021, 44, 102996. [Google Scholar] [CrossRef]
- Lakhdari, K.; Sriti, L.; Painter, B. Parametric optimization of daylight, thermal and energy performance of middle school classrooms, case of hot and dry regions. Build. Environ. 2021, 204, 108173. [Google Scholar] [CrossRef]
- Toutou, A.; Fikry, M.; Mohamed, W. The parametric based optimization framework daylighting and energy performance in residential buildings in hot arid zone. Alexandria Eng. J. 2018, 57, 3595–3608. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, Y.; Hou, J.; Jia, H. Decision-Making Framework for GI Layout Considering Site Suitability and Weighted Multi-Function Effectiveness: A Case Study in Beijing Sub-Center. Water 2022, 14, 1765. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China; General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. Technical Code for Rainwater Management and Utilization of Building and Sub-District, 1st ed.; China Architecture & Building Press: Beijing, China, 2017; pp. 8–9. [Google Scholar]
- Rawls, W.J.; Brakensiek, D.L.; Miller, N. Green-ampt Infiltration Parameters from Soils Data. J. Hyd. Engr. 1983, 109, 62–70. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Construction of the People’s Republic of China. Technical Guide for Sponge City Construction: Technical Guide for Sponge City Construction, 1st ed.; China Architecture & Building Press: Beijing, China, 2014; p. 46. [Google Scholar]






| Elements of the Model | Description |
|---|---|
| Decision variables | Constructing a choice of options for describing the characteristics of a system (process) in a mathematical model, where each different set of values taken for the design variables corresponds to a solution value for the problem. |
| Constants | Known constants to be considered in model construction. |
| Objectives | A function constructed according to the objective problem to be solved, usually requiring a maximum or minimum value. |
| Constraints | Constraints that need to be met to establish decision variables. |
| S/N | Name | Description | Section Illustration |
|---|---|---|---|
| 1 | Horizontal Green Space Without Water Storage Modules | Low cost, low infiltration and runoff pollution control, low stormwater storage capacity |  |
| 2 | Horizontal Green Space With Water Storage Modules | Infiltration and runoff pollution control advantages of horizontal green space, but space saving, high rainwater harvesting efficiency and high cost |  |
| 3 | Sunken Green Space | Low cost with a certain volume of water storage and pollution control function for rainwater runoff, but the actual storage volume is insufficient |  |
| 4 | Permeable Hard Surface | Effective stormwater infiltration and runoff pollution control, insufficient stormwater storage capacity and high costs. |  |
| 5 | Green Roof | Only be used on building roofs, with less scope for application and higher costs. |  |
| 6 | Designed Water Body | High rainwater storage capacity, low pollution control and low cost of construction. |  |
| Serial Number | Design Variable Symbol | Description | Unit |
|---|---|---|---|
| 1 | A1 | Area of horizontal green space | m2 |
| 2 | A2 | Area of horizontal green space with water storage modules | m2 |
| 3 | A3 | Area of water-storing sunken green space | m2 |
| 4 | A4 | Area of permeable hard surface | m2 |
| 5 | A5 | Area of designed water body for water storage | m2 |
| 6 | A6 | Area of green roof | m2 |
| Serial Number | Underlying Surface Classification | Planning Indicators (m2) |
|---|---|---|
| 1 | Total site area | 377,133 |
| 2 | Area of building area | 41,260 |
| 3 | Area of road and open space | 229,343 |
| 4 | Area of green space | 106,530 |
| 5 | Area of water surface | 9600 |
| Planning Control Index | Annual Runoff Control Rate (%) | Design Rainfall Amount (mm) | Surface Source Pollution Control Rate (%) | Rainfall Field Control Rate (%) | Design of Storage Volumes (m3) |
|---|---|---|---|---|---|
| Values | 79.52 | 29.7 | 55 | 87.3 | 750–1000 |
| Design Variables | A1: Area of horizontal green space | |||
| A2: Area of horizontal green space with water storage module | ||||
| A3: Area of water-storing sunken green space | ||||
| A4: Area of permeable hard surface | ||||
| A5: Area of designed water body for water storage | ||||
| A6: Area of green roof | ||||
| Objective Functions | Overall objective function | Sub-objectives | Formula | Description |
(Maximum sponge efficiency and lowest economic cost) | Rainwater infiltration and storage objective | Max (x) = n = 6 | The larger the rainwater infiltration storage capacity the better the objective | |
Runoff pollution control objective | = | The greater the runoff pollution removal capacity the better the objective. | ||
Economic objective | = | The lower the economic cost, the better the objective. | ||
| Constraints | Constraints of the total area | A1 + A2 + A3 + A4 + A5 + A6 ≤ 377,000 | ||
| Constraints of the site green space ratio | A1 + A2 + A3 ≤ 106,530 | |||
| Runoff Control Constraints for Sponge City Construction | 1.7248A1 + 2.764A2 + 2.39A3 + 1.89A4 + 0.34A5 + 1.344A6 ≥ 750 | |||
| Constraints of the hard surface area | A4 ≤ 229,343 | |||
| Constraints of the Site Building Density Rate | A6 ≤ 41,260 | |||
| Constraints of the Water Surface Rate | A5 ≤ 9600 | |||
| Optimization Algorithms | The Strength Pareto Evolutionary Algorithm-2 (SPEA-2) | |||
| Optimization Objective | Objective Values | Area of Sponge Facilities (m2) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Rainwater Infiltration and Storage Volumes (m3) | Runoff Pollution Control (t) | Economic Costs (yuan) | A1 | A2 | A3 | A4 | A5 | A6 | |
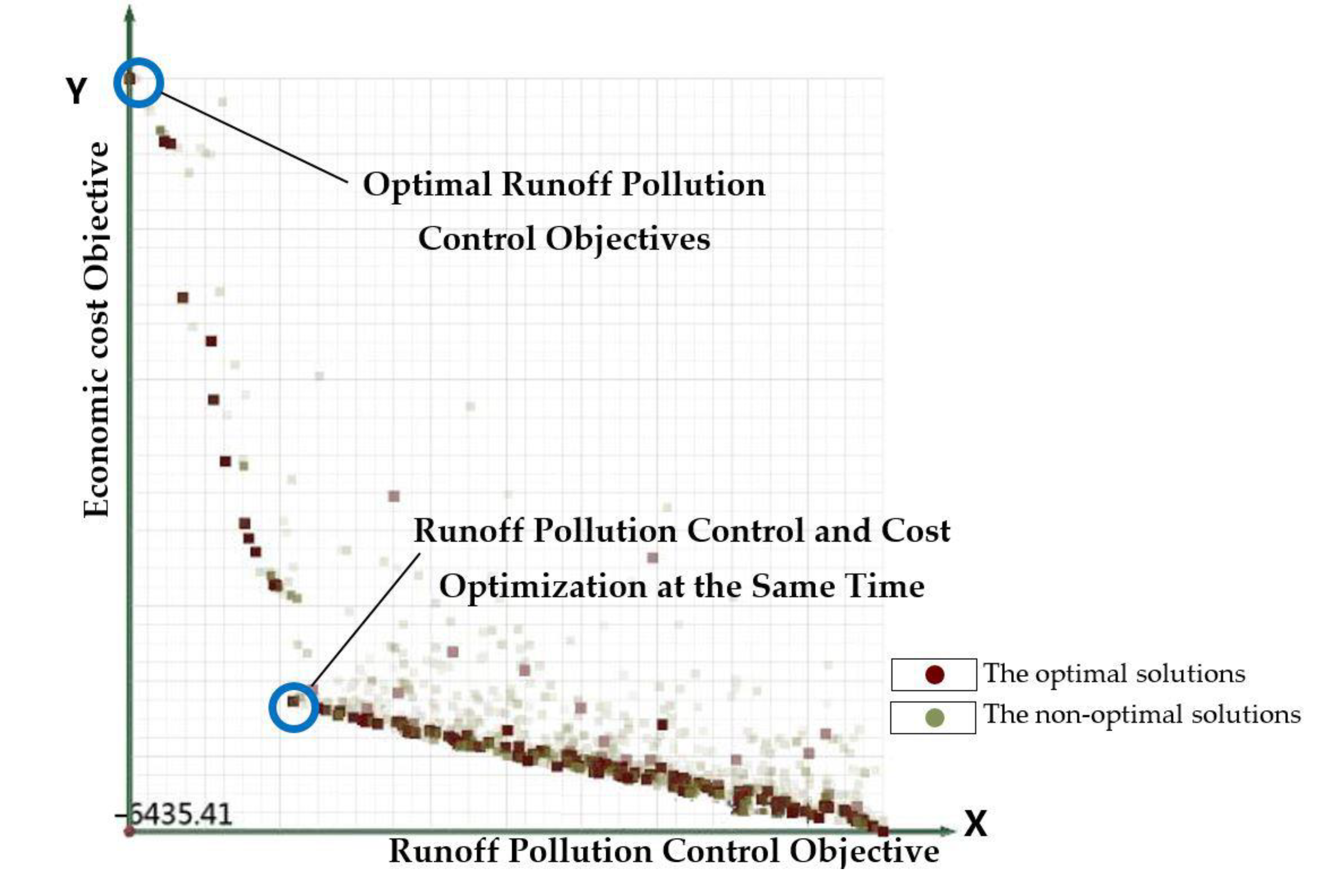
| Optimal runoff pollution control (regardless of economic factors) | 999 | 6435 | 453,730 | 2173 | 0 | 4 | 1938 | 2 | 6 |
| Optimal runoff pollution control and lowest economic cost | 995 | 5258 | 109,340 | 3579 | 0 | 1 | 1 | 0 | 33 |
| S/N | Facility Combination Solution | Area for Various Types of Facilities (m2) | Rainwater Infiltration and Storage Volumes (t) | Runoff Pollution Control (t) | Economic Costs (yuan) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | A5 | A6 | |||||
| 1 | Solution 1 | 3579 | 0 | 1 | 1 | 9 | 34 | 999 | 5260 | 110,110 |
| 2 | Solution 2 | 3243 | 1 | 1 | 365 | 11 | 46 | 999 | 5400 | 174,590 |
| 3 | Solution 3 | 2905 | 0 | 4 | 5 | 2 | 202 | 986 | 4517 | 98,890 |
| 4 | Solution 4 | 2131 | 0 | 2 | 43 | 10 | 405 | 991 | 3723 | 93,820 |
| S/N | Facility Combination Solution | Area for Various Types of Facilities (m2) | Rainwater Infiltration and Storage Volumes (m3) | Runoff Pollution Control (t) | Economic Costs (yuan) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | A5 | A6 | |||||
| 1 | Maximum Area of A1 | 3632 | 0 | 19 | 2 | 2 | 13 | 999 | 5345 | 112,450 |
| 2 | Maximum Area of A2 | 209 | 439 | 345 | 719 | 138 | 165 | 999 | 5400 | 174,590 |
| 3 | Maximum Area of A3 | 1101 | 9 | 1330 | 19 | 43 | 18 | 986 | 4208 | 209,770 |
| 4 | Maximum Area of A4 | 2131 | 0 | 2 | 43 | 10 | 405 | 991 | 3723 | 93,820 |
| 5 | Maximum Area of A5 | 809 | 10 | 708 | 100 | 858 | 105 | 999 | 4946 | 568,780 |
| 6 | Maximum Area of A6 | 3300 | 0 | 21 | 2 | 0 | 975 | 999 | 6400 | 450,570 |
| S/N | Facility Combination Solution | Area for Various Types of Facilities (m2) | Rainwater Infiltration and Storage Volumes (m3) | Runoff Pollution Control (t) | Economic Costs (yuan) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | A5 | A6 | |||||
| 1 | Solution 1 | 2197 | 0 | 241 | 1 | 399 | 15 | 858 | 3678 | 127,712 |
| 2 | Solution 2 | 2261 | 1 | 233 | 754 | 336 | 3 | 999 | 5011 | 275,823 |
| 3 | Solution 3 | 2259 | 1 | 204 | 237 | 459 | 4 | 917 | 4083 | 177,862 |
| 4 | Solution 4 | 2203 | 1 | 175 | 22 | 636 | 8 | 907 | 3590 | 143,711 |
| References | Objectives | Scale | Methodology | Tools | Highlights |
|---|---|---|---|---|---|
| Te Xu, Haifeng Jia et al. (2017) [15] | LID-BMPs planning, LID-BMP chain layout optimization | Block-scale, site-scale | Multi-objective optimization | SWMM-based methodology, NSGA-II algorithm | Coupling MOEA to SWMM and LID-BMP chain layout, optimization was combined with block-scale scenario analysis |
| Kun Zhang, Ting Fong May Chui (2018) [9] | selected, designed, and allocated for LID-BMP-GI | From site to catchment scale | Strategic planning cycle | Spatial allocation optimization tools (SAOTs) | Spatial allocation of LID-BMP-GI practices is illustrated. Strategic planning cycle |
| Yang Yu, Yongchao Zhou et al. (2022) [22] | LID spatial allocation optimization | Neighborhood scale | Integrated hydrological computing enginean with optimization algorithm | SWMM &MATLAB, PICEA-g algorithm | LID spatial allocation optimization couples SWMM & MATLAB, PICEA-g algorithm |
| Joong Gwang Lee, Ariamalar Selvakumar et al. (2012) [14] | SUSTAIN-based approach to optimising applications in BMPs | Watershed-scale | Optimization module | SUSTAIN, NSGA-II algorithm | Details of the SUSTAIN model |
| Zijing Liu, Haifeng Jia et al. (2022) [38] | Decision-making framework for GI layout | City scale | An adaptive GI layout decisionmaking System | Arcgis | Considering Site Suitability and Weighted Multi-Function Effectiveness: |
| Jingwei Hou, Moyan Zhu et al. (2020) [20] | Optimal spatial priority scheme of urban LID-BMPs | City scale | Multi-objective model | ArcMap, ADEA (Adaptive differential evolution algorithm) | Includes different investment periods |
| Zijing Liu, Changqing Xu et al. (2022) [21] | Multiobjective optimization of green-grey coupled infrastructures | Block-scale | Multiobjective evaluation framework, Intelligent optimization algorithm | SWMM NSGA-II algorithm | Integrating socioecological indexes, Grey-green infrastructure coupling |
| Our works | Sponge facilities combination | Block-scale | Multi-objective optimization | Octopus, Grasshopper, SPEA-2 | Six typical sponge facilities, Application of Grasshopper with SPEA-2 algorithm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, M.; Cheng, Y.; Dong, Z. Study on Multi-Objective Optimization of Sponge Facilities Combination at Urban Block Level: A Residential Complex Case Study in Nanjing, China. Water 2022, 14, 3292. https://doi.org/10.3390/w14203292
Xie M, Cheng Y, Dong Z. Study on Multi-Objective Optimization of Sponge Facilities Combination at Urban Block Level: A Residential Complex Case Study in Nanjing, China. Water. 2022; 14(20):3292. https://doi.org/10.3390/w14203292
Chicago/Turabian StyleXie, Mingkun, Yuning Cheng, and Zengchuan Dong. 2022. "Study on Multi-Objective Optimization of Sponge Facilities Combination at Urban Block Level: A Residential Complex Case Study in Nanjing, China" Water 14, no. 20: 3292. https://doi.org/10.3390/w14203292






