Experimental Study on Microchannel with Addition of Microinserts Aiming Heat Transfer Performance Improvement
Abstract
:1. Introduction
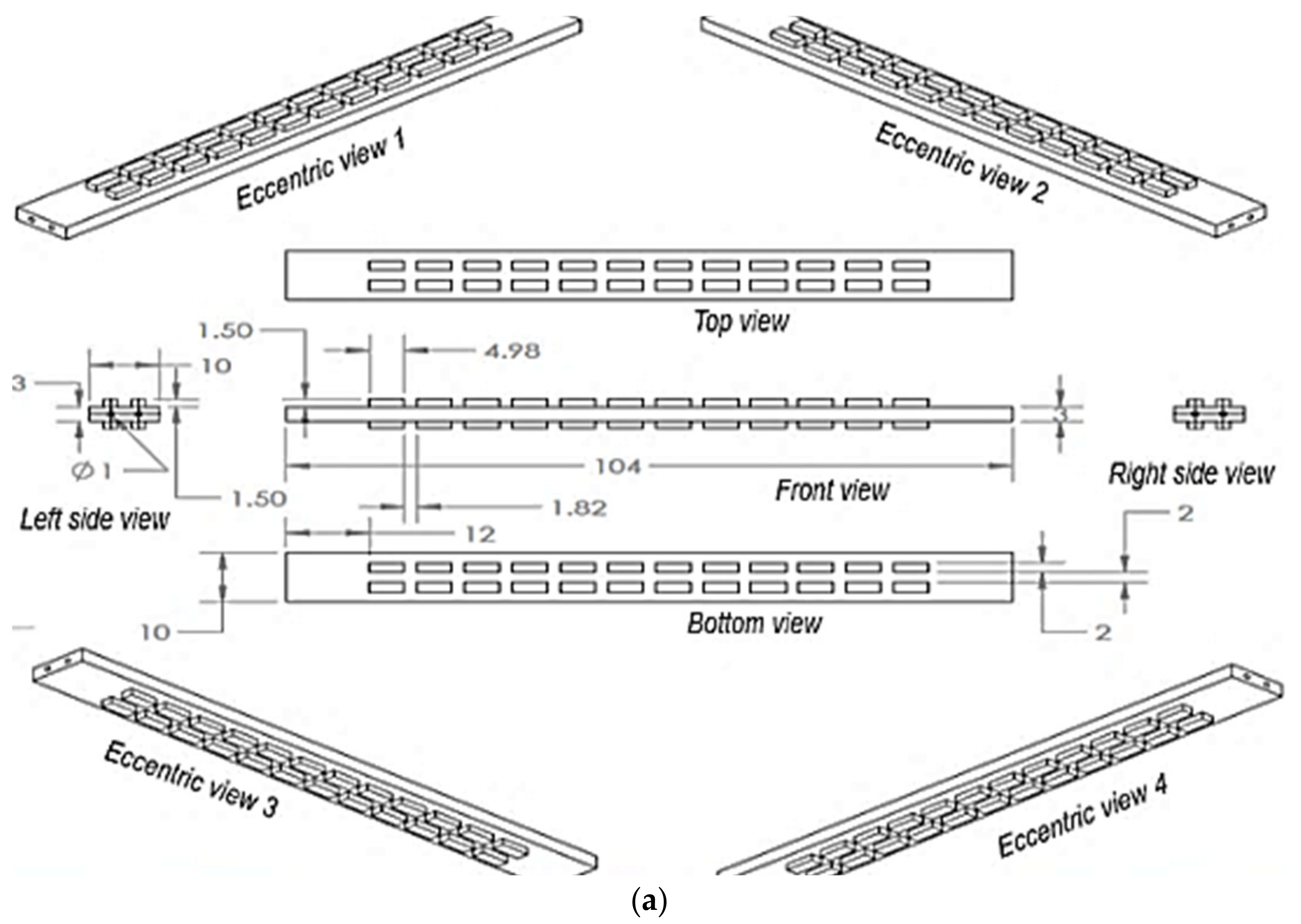
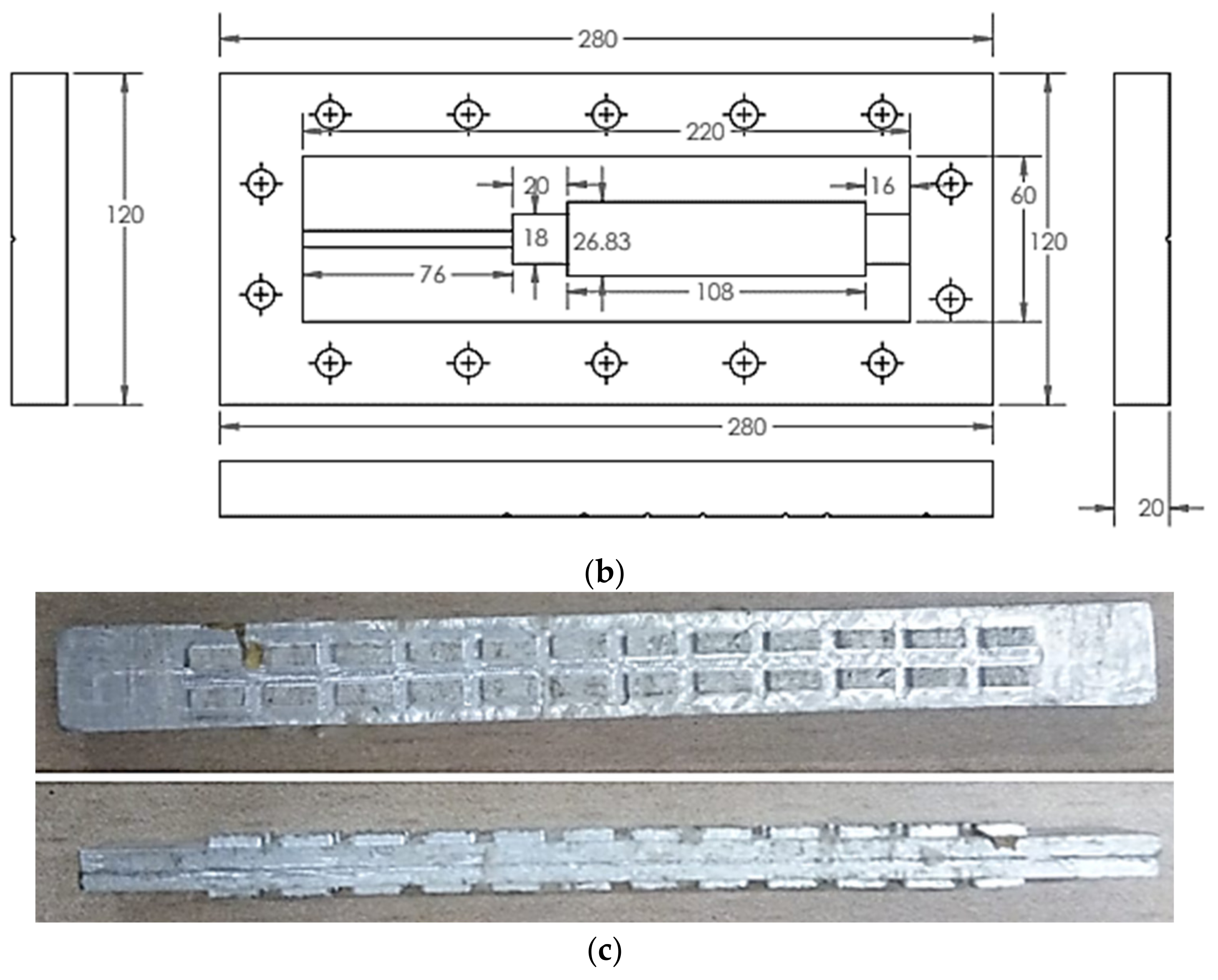
2. Experiment
2.1. Experimental Set-Up
2.2. Scaling Parameters and Uncertainty
3. Results and Discussion
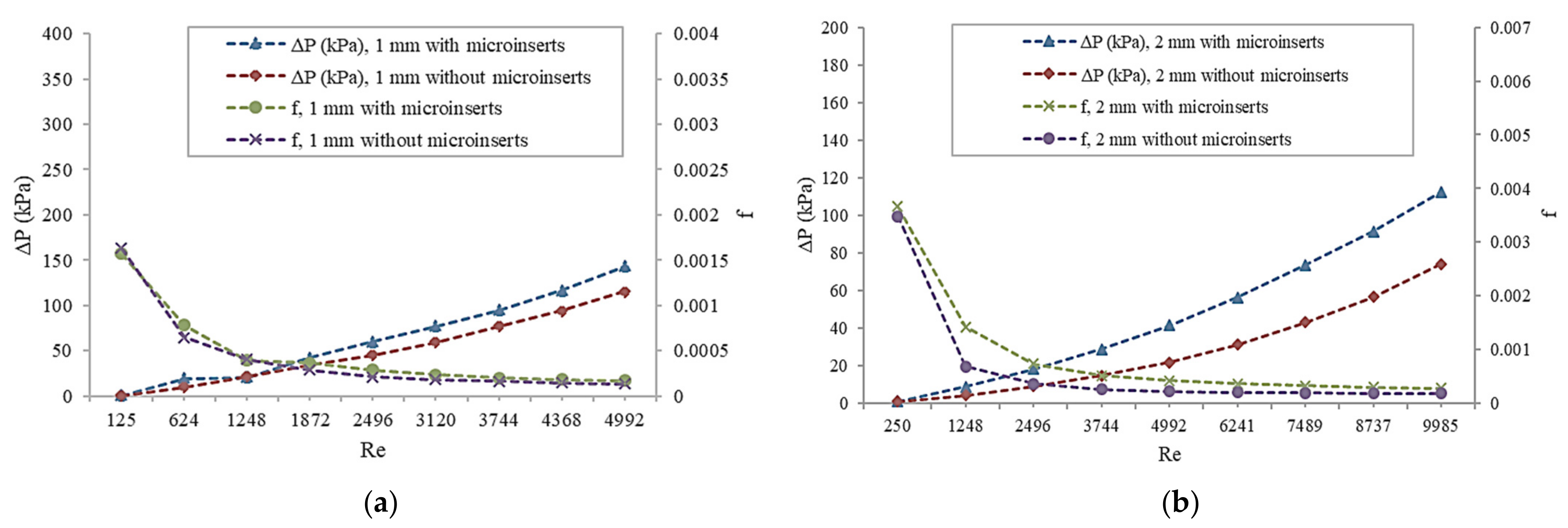
3.1. Pressure Drop Characteristics
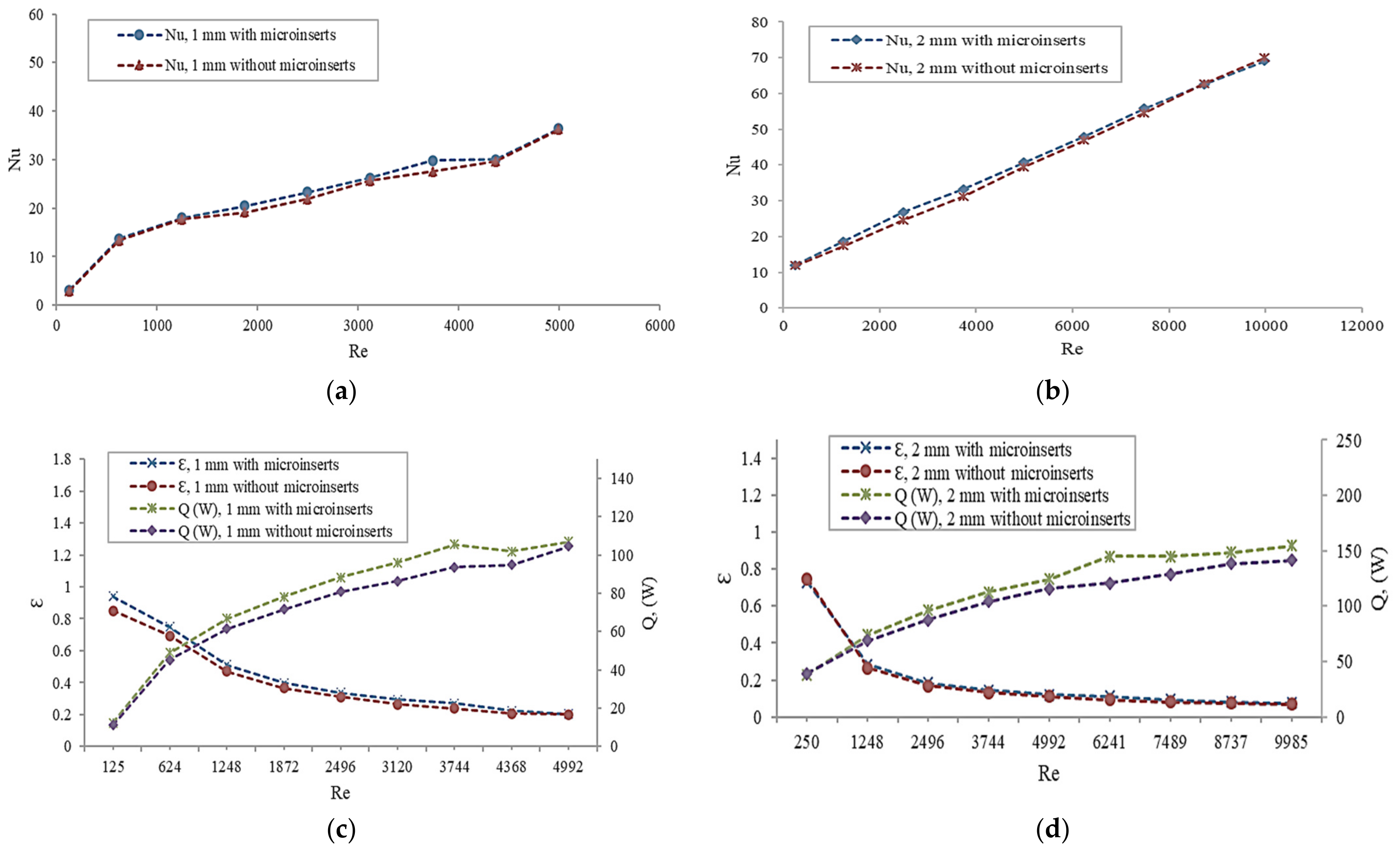
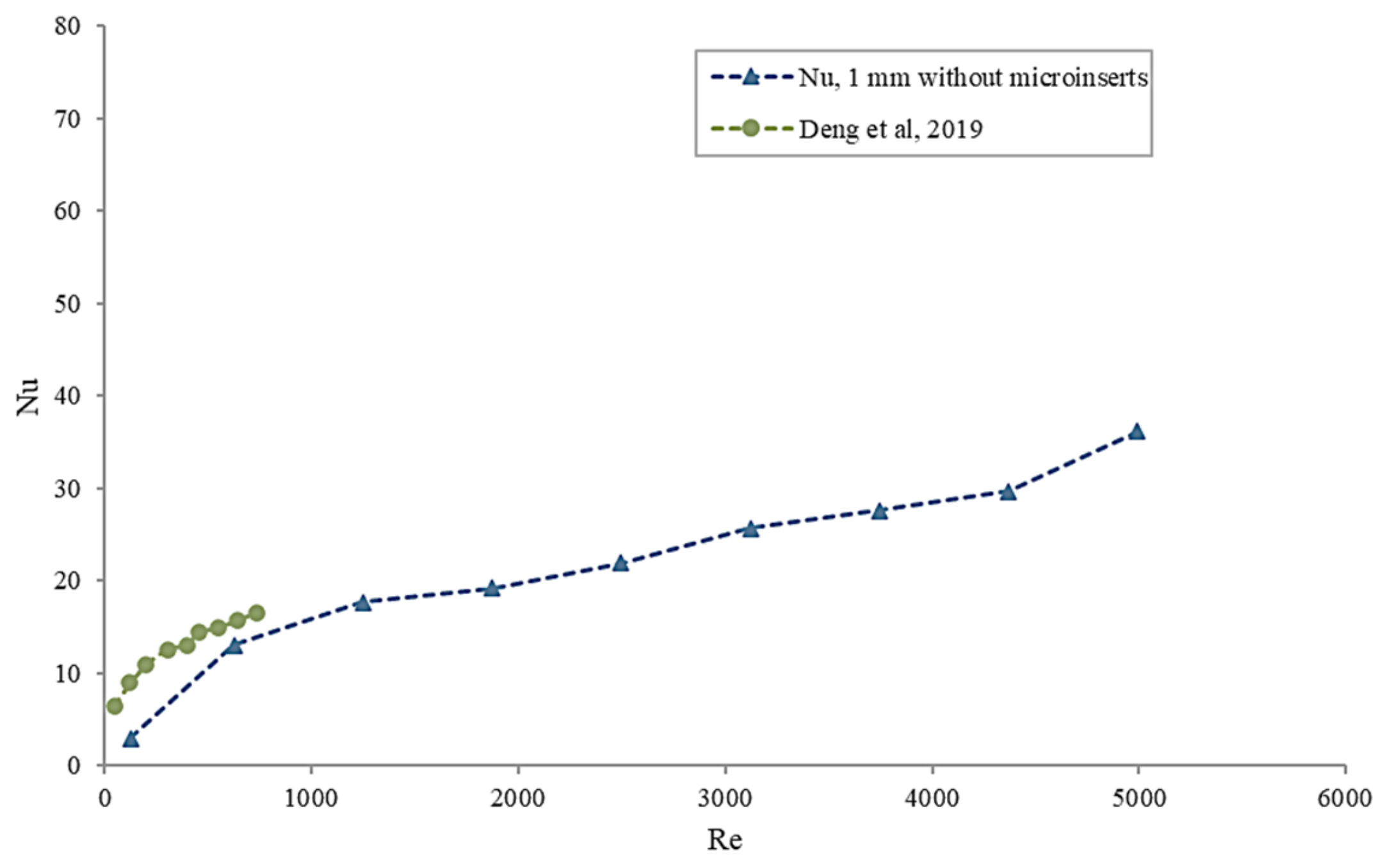
3.2. Heat Transfer Characteristics
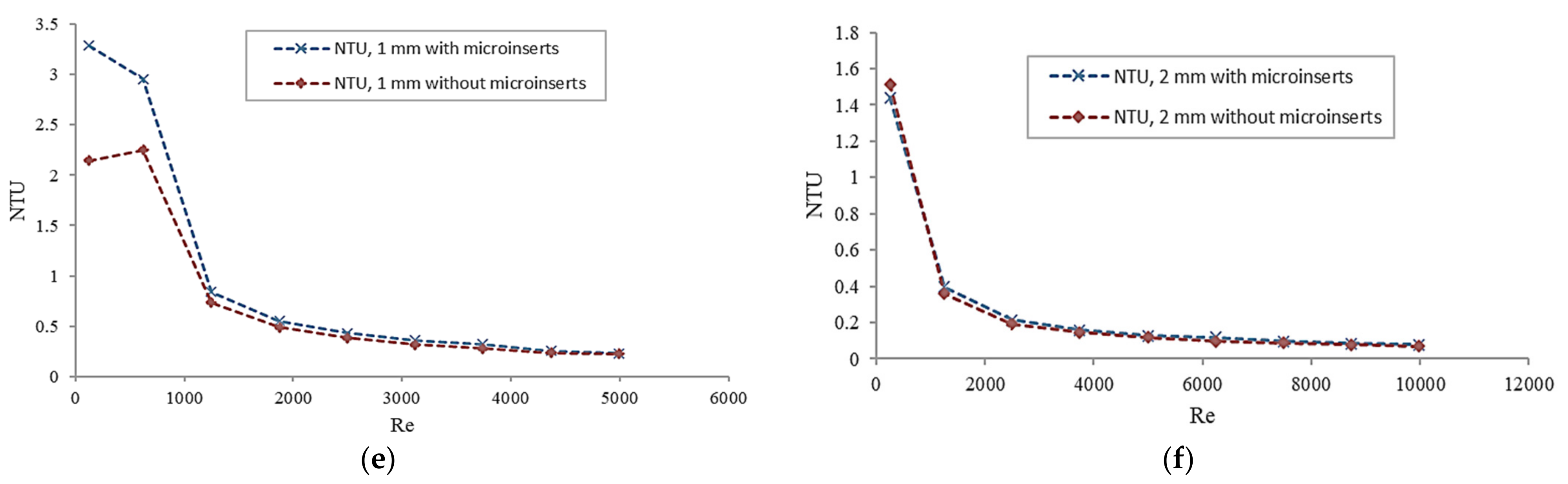
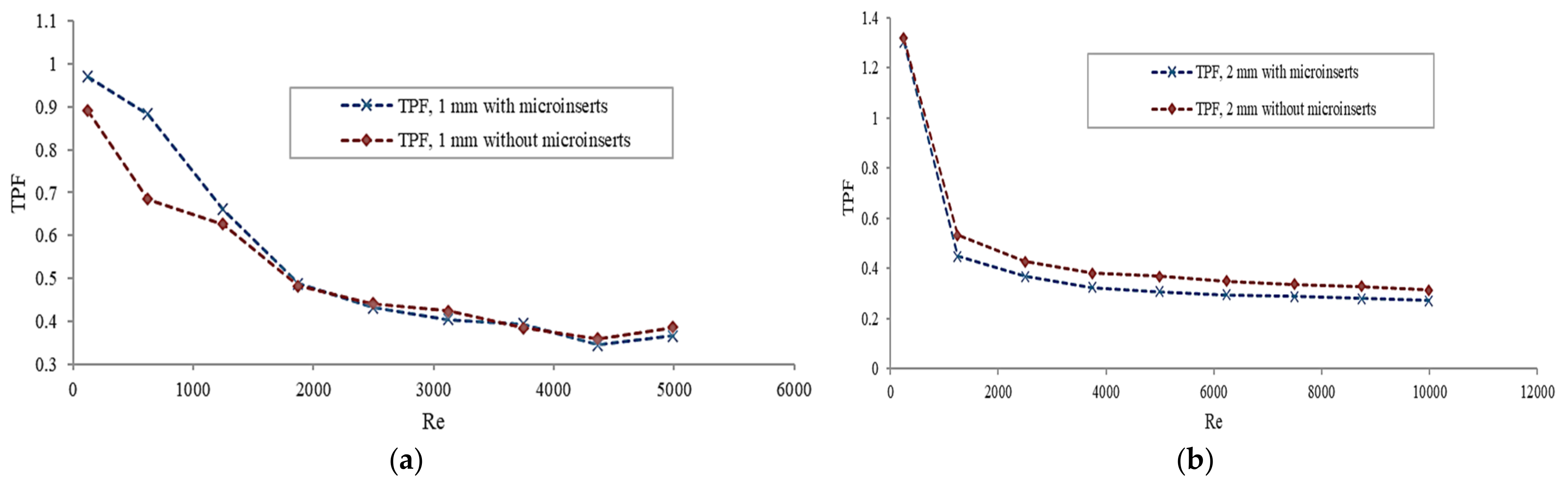
3.3. Overall Performance Evaluation
4. Conclusions
- The microinserts in the channel resulted in higher fluid outlet temperatures, causing lower base temperature when compared with the channel without microinserts.
- Microinserts performed in enhanced heat transfer, however, also caused a larger pressure drop. Pressure drops of the channel with microinserts were increased by a factor of 1.01–1.32 and 1.05–2.08, corresponding to 1 mm and 2 mm, respectively. The presence of microinserts resulted in increased flow resistance. It was obvious that temperature-dependent thermo-physical properties influenced the flow resistance.
- The heat transfer coefficients, effectiveness, NTU, and Nu of channels with microinserts were found to be increased, as compared to that of the channel without microinserts. The values of Nu were found to be larger by a factor of 1.01–1.08 in the case of the 1 mm and 1–1.07 for 2 mm channel sizes. It is indicated that the thermal performance of channels with microinserts improved. Microinserts effectively enhanced the heat transfer performance for both channel sizes.
- The performance evaluation criteria were employed to assess the overall performance of different channels. The results obtained by this method concluded that the overall performance of the channel with microinserts is better than that for the channel without microinserts for both channel sizes. It was found that microinserts result in the best overall performance at a lower Reynolds number. At a higher Reynolds number, microinserts improve the overall performance only marginally.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | Descriptions | Unit |
| As | Contact surface area of the fluid and microchannel | mm2 |
| cp | Specific heat of water | J/kg-K |
| Dh | Hydraulic diameter | mm |
| f | Friction factor | |
| H | Height of the microchannel | mm |
| h | Heat transfer coefficient | W/m2-K |
| kf | Thermal conductivity of fluid | J/s-m-K |
| Ks | Solid thermal conductivity | J/s-m-K |
| L | Length of the microchannel | mm |
| m | Mass | kg |
| Nu | Nusselt number | |
| p | Pressure | Pa |
| Re | Reynolds Number | |
| T | Temperature | K |
| TPF | Thermal performance factor | |
| U | Fluid velocity | m/s |
| W | Width of the microchannel | mm |
| Δp | Pressure difference | |
| ΔT | Temperature difference | |
| Greek symbols | ||
| ρ | Fluid density | kg/m3 |
| µ | Dynamic viscosity | Pa-s |
| Subscript | ||
| f | Fluid | |
| s | Solid |
References
- Gao, J.; Hu, Z.; Yang, Q.; Liang, X.; Wu, H. Fluid flow and heat transfer in microchannel heat sinks: Modelling review and recent progress. Therm. Sci. Eng. Prog. 2022, 29, 101203. [Google Scholar] [CrossRef]
- Ameel, T.A.; Warrington, R.O.; Wegeng, R.S.; Drost, M.K. Miniaturization technologies applied to energy systems. Energy Convers. Manag. 1997, 38, 969–982. [Google Scholar] [CrossRef]
- Dixit, T.; Ghosh, I. Review of micro- and mini-channel heat sinks and heat exchangers for single phase fluids. Renew. Sustain. Energy Rev. 2015, 41, 1298–1311. [Google Scholar] [CrossRef]
- Abdoli, A.; Jimenez, G.; Dulikravich, G.S. Thermo-fluid analysis of micro pin-fin array cooling configurations for high heat fluxes with a hot spot. Int. J. Therm. Sci. 2015, 90, 290–297. [Google Scholar] [CrossRef]
- Sohel Murshed, S.M.; Nieto de Castro, C.A. A critical review of traditional and emerging techniques and fluids for electronics cooling. Renew. Sustain. Energy Rev. 2017, 78, 821–833. [Google Scholar] [CrossRef]
- Pan, X.; Hong, X.; Xu, L.; Li, Y.; Yan, M.; Mai, L. On-chip micro/nano devices for energy conversion and storage. Nano Today 2019, 28, 100764. [Google Scholar] [CrossRef]
- Alihosseini, Y.; Zabetian, M.; Mohammad, T.; Heyhat, M. Thermo-hydraulic performance of wavy microchannel heat sink with oblique grooved finned. Appl. Therm. Eng. 2021, 189, 116719. [Google Scholar] [CrossRef]
- Tuckerman, D.B.; Pease, R.F.W. High-Performance Heat Sinking for VLSI. IEEE Electron Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Asadi, M.; Gongnan, X.; Sunden, B. A review of heat transfer and pressure drop characteristics of single and two-phase microchannels. Int. J. Heat Mass Transf. 2014, 79, 34–53. [Google Scholar] [CrossRef]
- Mansoor, M.M.; Wong, K.C.; Siddique, M. Numerical investigation of fluid flow and heat transfer under high heat flux using rectangular micro-channels. Int. Commun. Heat Mass Transf. 2012, 39, 291–297. [Google Scholar] [CrossRef]
- Qu, W.; Mudawar, I. Analysis of three-dimensional heat transfer in micro-channel heat sinks. Int. J. Heat Mass Transf. 2002, 45, 3973–3985. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Z.; Gao, J. Influence of geometric parameters on flow and heat transfer performance of micro-channel heat sinks. Appl. Therm. Eng. 2016, 107, 870–879. [Google Scholar] [CrossRef]
- Xia, G.D.; Jiang, J.; Wang, J.; Zhai, Y.L.; Ma, D.D. Effects of different geometric structures on fluid flow and heat transfer performance in microchannel heat sinks. Int. J. Heat Mass Transf. 2015, 80, 439–447. [Google Scholar] [CrossRef]
- Gawali, B.S.; Swami, V.B.; Thakre, S.D. Theoretical and experimental investigation of heat transfer characteristics through a rectangular microchannel heat sink. Int. J. Innov. Res. Sci. Eng. Technol. 2014, 3, 15631–15640. [Google Scholar] [CrossRef]
- Alfaryjat, A.A.; Mohammed, H.A.; Adam, N.M.; Ariffin, M.K.A.; Najafabadi, M.I. Influence of geometrical parameters of hexagonal, circular and rhombus microchannel heat sinks on the thermohydraulic characteristics. Int. Commun. Heat Mass Transf. 2014, 52, 121–131. [Google Scholar] [CrossRef]
- Chiu, H.C.; Jang, J.H.; Yeh, H.W.; Wu, M.S. The heat transfer characteristics of liquid cooling heat sink containing microchannels. Int. J. Heat Mass Transf. 2011, 54, 34–42. [Google Scholar] [CrossRef]
- Huang, H.; Wu, H.; Zhang, C. An experimental study on flow friction and heat transfer of water in sinusoidal wavy silicon microchannels. J. Micromechanics Microengineering 2018, 28, 55003. [Google Scholar] [CrossRef]
- Chai, L.; Wang, L. Thermal-hydraulic performance of interrupted microchannel heat sinks with different rib geometries in transverse microchambers. Int. J. Therm. Sci. 2018, 127, 201–212. [Google Scholar] [CrossRef] [Green Version]
- Khoshvaght-Aliabadi, M.; Sahamiyan, M. Performance of nanofluid flow in corrugated minichannels heat sink. Energy Convers. Manag. 2016, 108, 297–308. [Google Scholar] [CrossRef]
- Ma, D.D.; Xia, G.D.; Li, Y.F.; Jia, Y.T.; Wang, J. Effects of structural parameters on fluid flow and heat transfer characteristics in microchannel with offset zigzag grooves in sidewall. Int. J. Heat Mass Transf. 2016, 101, 427–435. [Google Scholar] [CrossRef]
- Deng, D.; Wan, W.; Tang, Y.; Shao, H.; Huang, Y. Experimental and numerical study of thermal enhancement in reentrant copper microchannels. Int. J. Heat Mass Transf. 2015, 91, 656–670. [Google Scholar] [CrossRef]
- Sui, Y.; Lee, P.S.; Teo, C.J. An experimental study of flow friction and heat transfer in wavy microchannels with rectangular cross section. Int. J. Therm. Sci. 2011, 50, 2473–2482. [Google Scholar] [CrossRef]
- Zeng, L.; Deng, D.; Zhong, N.; Zheng, G. Thermal and flow performance in microchannel heat sink with open-ring pin fins. Int. J. Mech. Sci. 2021, 200, 106445. [Google Scholar] [CrossRef]
- Khoshvaght-Aliabadi, M.; Deldar, S.; Hassani, S.M. Effects of pin-fins geometry and nanofluid on the performance of a pin-fin miniature heat sink (PFMHS). Int. J. Mech. Sci. 2018, 148, 442–458. [Google Scholar] [CrossRef]
- Khoshvaght-Aliabadi, M.; Hassani, S.M.; Mazloumi, S.H. Performance enhancement of straight and wavy miniature heat sinks using pin-fin interruptions and nanofluids. Chem. Eng. Process. Process Intensif. 2017, 122, 90–108. [Google Scholar] [CrossRef]
- Yeom, T.; Simon, T.; Zhang, T.; Zhang, M.; North, M.; Cui, T. Enhanced heat transfer of heat sink channels with micro pin fin roughened walls. Int. J. Heat Mass Transf. 2016, 92, 617–627. [Google Scholar] [CrossRef] [Green Version]
- Siu-Ho, A.; Qu, W.; Pfefferkorn, F. Experimental study of pressure drop and heat transfer in a single-phase micro pin-fin heat sink. ASME J. Electron Packag. 2007, 129, 479–487. [Google Scholar] [CrossRef]
- Peles, Y.; Koşar, A.; Mishra, C.; Kuo, C.; Schneider, B. Forced convective heat transfer across a pin fin micro heat sink. Int. J. Heat Mass Transf. 2005, 48, 3615–3627. [Google Scholar] [CrossRef]
- Datta, A.; Sharma, V.; Sanyal, D.; Das, P. A conjugate heat transfer analysis of performance for rectangular microchannel with trapezoidal cavities and ribs. Int. J. Therm. Sci. 2019, 138, 425–446. [Google Scholar] [CrossRef]
- Bahiraei, M.; Mazaheri, N.; Rizehvandi, A. Application of a hybrid nanofluid containing graphene nanoplatelet-platinum composite powder in a triple-tube heat exchanger equipped with inserted ribs. Appl. Therm. Eng. 2019, 149, 588–601. [Google Scholar] [CrossRef]
- Wang, G.; Qian, N.; Ding, G. Heat transfer enhancement in microchannel heat sink with bidirectional rib. Int. J. Heat Mass Transf. 2019, 136, 597–609. [Google Scholar] [CrossRef]
- Kumar, S.R.; Singh, S. CFD analysis for heat transfer and fluid flow in microchannel heat sink with micro inserts. Mater. Today Proc. 2021, 46 Pt 20, 11213–11216. [Google Scholar] [CrossRef]
- Kumar, S.R.; Singh, S. Numerical Analysis for Augmentation of Thermal Performance of Single-Phase Flow in Microchannel Heat Sink of Different Sizes with or without Micro-Inserts. Fluids 2022, 7, 149. [Google Scholar] [CrossRef]
- Feng, Z.; Luo, X.; Guo, F.; Li, H.; Zhang, J. Numerical investigation on laminar flow and heat transfer in rectangular microchannel heat sink with wire coil inserts. Appl. Therm. Eng. 2017, 116, 597–609. [Google Scholar] [CrossRef]
- Khoshvaght-Aliabadi, M.; Nozan, F. Water cooled corrugated minichannel heat sink for electronic devices Effect of corrugation shape. Int. Commun. Heat Mass Tran. 2016, 76, 188–196. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, Y.; Wang, C.C.; Xie, G. Comparative study for convective heat transfer of counter-flow wavy double-layer microchannel heat sinks in staggered arrangement. Appl. Therm. Eng. 2018, 137, 228–237. [Google Scholar] [CrossRef]
- Ali, A.M.; Ron, A.; Kadhim, H.T.; Angelino, M.; Gao, S. Thermo-hydraulic performance of a circular microchannel heat sink using swirl flow and nanofluid. Appl. Therm. Eng. 2021, 191, 116817. [Google Scholar] [CrossRef]
- Xie, G.; Liu, J.; Liu, Y.; Sunden, B.; Zhang, W. Comparative study of thermal performance of longitudinal and transversal-wavy microchannel heat sinks for electronic cooling. J. Electron. Packag. 2013, 135, 21008. [Google Scholar] [CrossRef]
- Khoshvaght-Aliabadi, M.; Arani-Lahtari, Z. Forced convection in twisted minichannel (TMC) with different cross section shapes: A numerical study. Appl. Therm. Eng. 2016, 93, 101–112. [Google Scholar] [CrossRef]
- Chatterjee, R.; Duryodhan, V.S.; Agrawal, A. Impact of aspect ratio and thermophysical properties on heat transfer behavior in spiral microchannel. Int. J. Therm. Sci. 2022, 172 Pt A, 107335. [Google Scholar] [CrossRef]
- Khalesi, J.; Sarunac, N. Numerical analysis of flow and conjugate heat transfer for supercritical CO2 and liquid sodium in square microchannels. Int. J. Heat Mass Transf. 2019, 132, 1187–1199. [Google Scholar] [CrossRef]
- Kumar, P. Numerical investigation of fluid flow and heat transfer in trapezoidal microchannel with groove structure. Int. J. Therm. Sci. 2019, 136, 33–43. [Google Scholar] [CrossRef]
- Liang, J.; Engelbrecht, K.; Nielsen, K.K.; Loewe, K.; Vieyra, H.; Barcza, A.; Bahl, C.R.H. Performance assessment of a triangular microchannel active magnetic regenerator. Appl. Therm. Eng. 2021, 186, 116519. [Google Scholar] [CrossRef]
- Abdollahi, A.; Norris, S.E.; Sharma, R.N. Fluid flow and heat transfer of liquid-liquid Taylor flow in square microchannels. Appl. Therm. Eng. 2020, 172, 115123. [Google Scholar] [CrossRef]
- He, W.; Mashayekhi, R.; Toghraie, D.; Akbari, O.A.; Li, Z.; Tlili, I. Hydrothermal performance of nanofluid flow in a sinusoidal double layer microchannel in order to geometric optimization. Int. Commun. Heat Mass Transf. 2020, 117, 104700. [Google Scholar] [CrossRef]
- Yan, Y.Y.; Lin, T.F. Condensation heat transfer and pressure drop of refrigerant R134a in a small pipe. Int. J. Heat Mass Transf. 1999, 42, 697–708. [Google Scholar] [CrossRef]
- Liu, D.; Ling, X.; Peng, H.; Li, J.; Duan, L. Experimental and numerical analysis on heat transfer performance of slug flow in rectangular microchannel. Int. J. Heat Mass Transfer. 2020, 147, 118963. [Google Scholar] [CrossRef]
- Derakhshanpour, K.; Kamali, R.; Eslami, M. Effect of rib shape and fillet radius on thermal-hydrodynamic performance of microchannel heat sinks: A CFD study. Int. Commun. Heat Mass Transf. 2020, 119, 104928. [Google Scholar] [CrossRef]
- Khalesi, J.; Sarunac, N.; Razzaghpanah, Z. Supercritical CO2 conjugate heat transfer and flow analysis in a rectangular microchannel subject to uniformly heated substrate wall. Therm. Sci. Eng. Prog. 2020, 19, 100596. [Google Scholar] [CrossRef]
- Alfaryjat, A.A.; Mohammed, H.A.; Adam, N.M.; Stanciu, D.; Dobrovicescu, A. Numerical investigation of heat transfer enhancement using various nanofluids in hexagonal microchannel heat sink. Therm. Sci. Eng. Prog. 2018, 5, 252–262. [Google Scholar] [CrossRef]
- Ma, H.; Duan, Z.; Ning, X.; Su, L. Numerical investigation on heat transfer behavior of thermally developing flow inside rectangular microchannels. Case Stud. Therm. Eng. 2021, 24, 100856. [Google Scholar] [CrossRef]
- Meyari, M.; Salehi, Z.; Zarghami, R.; Saeedipour, M. Numerical investigation of particle separation in Y-shaped bifurcating microchannels. Particuology 2021, 56, 142–151. [Google Scholar] [CrossRef]
- Ling, W.; Zhou, W.; Liu, C.; Zhou, F.; Yuan, D.; Huang, J. Structure and geometric dimension optimization of interlaced microchannel for heat transfer performance enhancement. Appl. Therm. Eng. 2020, 170, 115011. [Google Scholar] [CrossRef]
- Rabiei, S.; Khosravi, R.; Bahiraei, M.; Raziei, M.; Hosseini, A.A. Thermal and hydraulic characteristics of a hybrid nanofluid containing graphene sheets decorated with platinum through a new wavy cylindrical microchannel. Appl. Therm. Eng. 2020, 181, 115981. [Google Scholar] [CrossRef]
- Saha, S.K.; Agrawal, A.; Soni, Y. Heat transfer characterization of rhombic microchannel for H1 and H2 boundary conditions. Int. J. Therm. Sci. 2017, 111, 223–233. [Google Scholar] [CrossRef]
- Wang, C.S.; Wei, T.C.; Shen, P.Y.; Liou, T.M. Lattice Boltzmann study of flow pulsation on heat transfer augmentation in a louvered microchannel heat sink. Int. J. Heat Mass Transfer. 2020, 148, 119139. [Google Scholar] [CrossRef]
- Abdollahi, P.; Karimi-Sabet, J.; Moosavian, M.A.; Amini, Y. Microfluidic solvent extraction of calcium: Modeling and optimization of the process variables. Sep. Purif. Technol. 2020, 231, 115875. [Google Scholar] [CrossRef]
- Jahromi, P.F.; Karimi-Sabet, J.; Amini, Y.; Fadaei, H. Pressure-driven liquid-liquid separation in Y-shaped microfluidic junctions. Chem. Eng. J. 2017, 328, 1075–1086. [Google Scholar] [CrossRef]
- Jahromi, P.F.; Karimi-Sabet, J.; Amini, Y. Ion-pair extraction-reaction of calcium using Y-shaped microfluidic junctions: An optimized separation approach. Int. Commun. Heat Mass Transf. 2018, 334, 2603–2615. [Google Scholar]
- Marsousi, S.; Karimi-Sabet, J.; Moosavian, M.A.; Amini, Y. Liquid-liquid extraction of calcium using ionic liquids in spiral microfluidics. Chem. Eng. J. 2019, 356, 492–505. [Google Scholar] [CrossRef]
- Omar, P.J.; Gaur, S.; Dikshit, P.K.S. Conceptualization and development of multi-layered groundwater model in transient condition. Appl. Water Sci. 2021, 11, 162. [Google Scholar] [CrossRef]
- Omar, P.J.; Kumar, V. Land surface temperature retrieval from TIRS data and its relationship with land surface indices. Arab. J. Geosci. 2021, 14, 1–14. [Google Scholar] [CrossRef]
- Omar, P.J.; Shivhare, N.; Dwivedi, S.B.; Dikshit, P.K.S. Identification of soil erosion-prone zone utilizing geo-informatics techniques and WSPM model. Sustain. Water Resour. Manag. 2022, 8, 66. [Google Scholar] [CrossRef]
- Sadeghi, A.; Amini, Y.; Saidi, M.H.; Chakraborty, S. Numerical modeling of surface reaction kinetics in electrokinetically actuated microfluidic devices. Anal. Chim. Acta 2014, 838, 64–75. [Google Scholar] [CrossRef]
- Sadeghi, A.; Amini, Y.; Saidi, M.H.; Yavari, H. Shear-Rate-Dependent Rheology Effects on Mass Transport and Surface Reactions in Biomicrofluidic Devices. AIChE J. 2015, 61, 1912–1924. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, C.; Jiaqiang, E.; Mao, X.; Yu, Z. Research on modeling and parameter sensitivity of flow and heat transfer process in typical rectangular microchannels: From a data-driven perspective. Int. J. Therm. Sci. 2022, 172 Pt B, 107356. [Google Scholar] [CrossRef]
- Zhu, Q.; Su, R.; Xia, H.; Zeng, J.; Chen, J. Numerical simulation study of thermal and hydraulic characteristics of laminar flow in microchannel heat sink with water droplet cavities and different rib columns. Int. J. Therm. Sci. 2022, 172, 107319. [Google Scholar] [CrossRef]
- Webb, R.L. Performance evaluation criteria for use of enhanced heat transfer surfaces in heat exchanger design. Int. J. Heat Mass Transf. 1981, 24, 715–726. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, S.R.; Singh, S. Experimental Study on Microchannel with Addition of Microinserts Aiming Heat Transfer Performance Improvement. Water 2022, 14, 3291. https://doi.org/10.3390/w14203291
Kumar SR, Singh S. Experimental Study on Microchannel with Addition of Microinserts Aiming Heat Transfer Performance Improvement. Water. 2022; 14(20):3291. https://doi.org/10.3390/w14203291
Chicago/Turabian StyleKumar, Shailesh Ranjan, and Satyendra Singh. 2022. "Experimental Study on Microchannel with Addition of Microinserts Aiming Heat Transfer Performance Improvement" Water 14, no. 20: 3291. https://doi.org/10.3390/w14203291
APA StyleKumar, S. R., & Singh, S. (2022). Experimental Study on Microchannel with Addition of Microinserts Aiming Heat Transfer Performance Improvement. Water, 14(20), 3291. https://doi.org/10.3390/w14203291





