Two-Phase Flow Modeling for Bed Erosion by a Plane Jet Impingement
Abstract
:1. Introduction
- The impinging region. It is characterized by a stagnation point on the jet axis at the wall with a deflexion of flow streamlines [21].
2. Laboratory Experiments
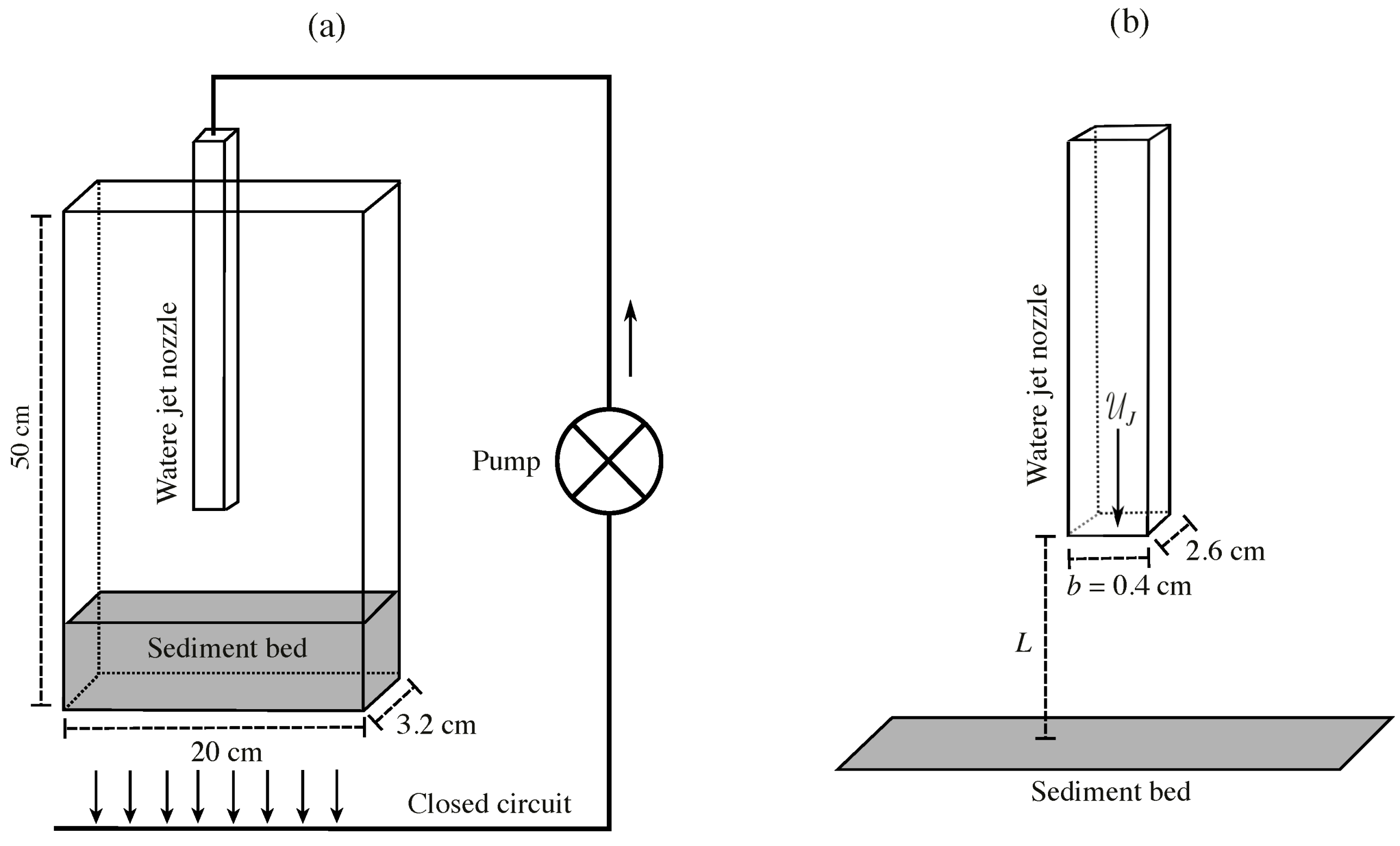
2.1. Experimental Setup
2.2. Measure of the Crater Dimensions
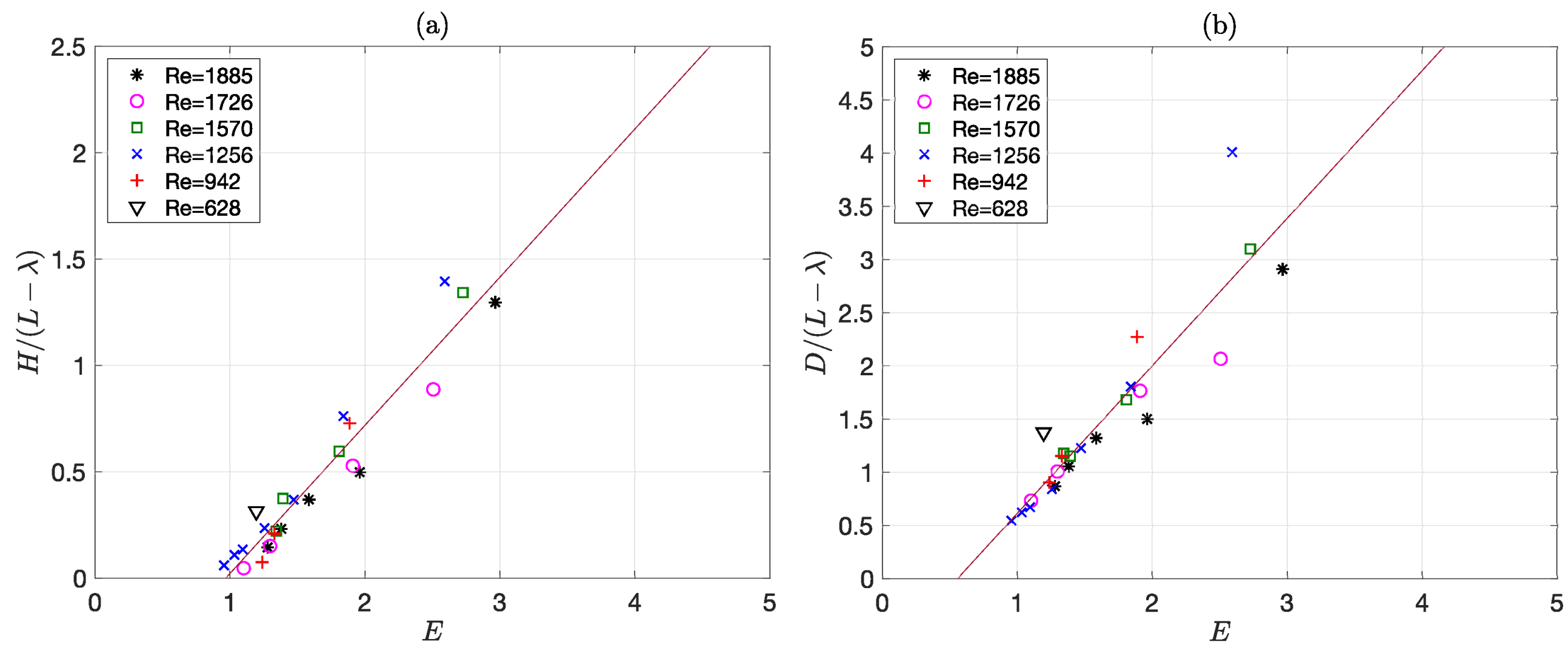
2.3. Experimental Results
3. Mathematical Model
3.1. Governing Equations
3.2. A Unified Momentum Equation for the Solid Phase
Solid-Like Model
3.3. Solid-Liquid Transition of the Granular Phase
3.4. Numerical Technique
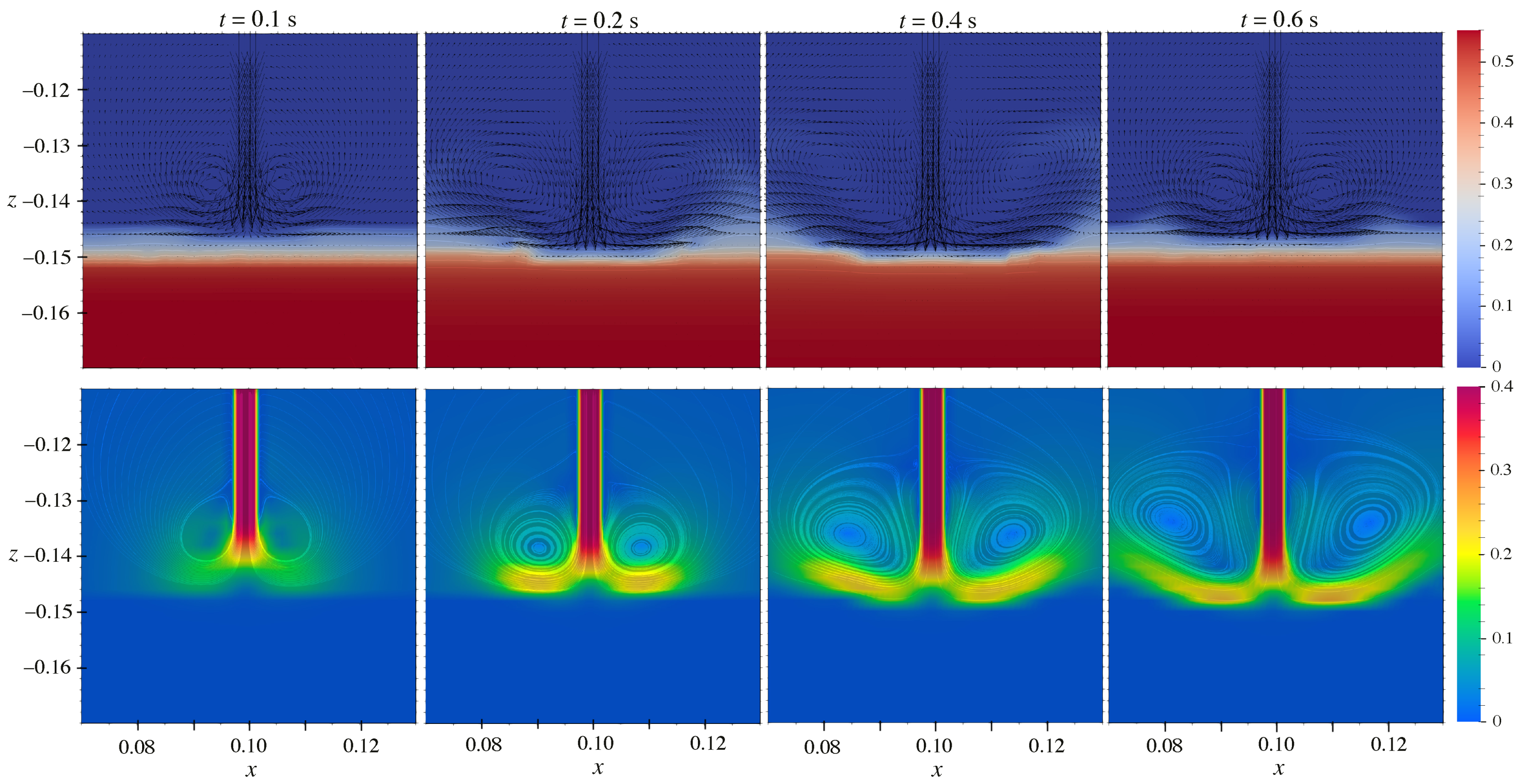
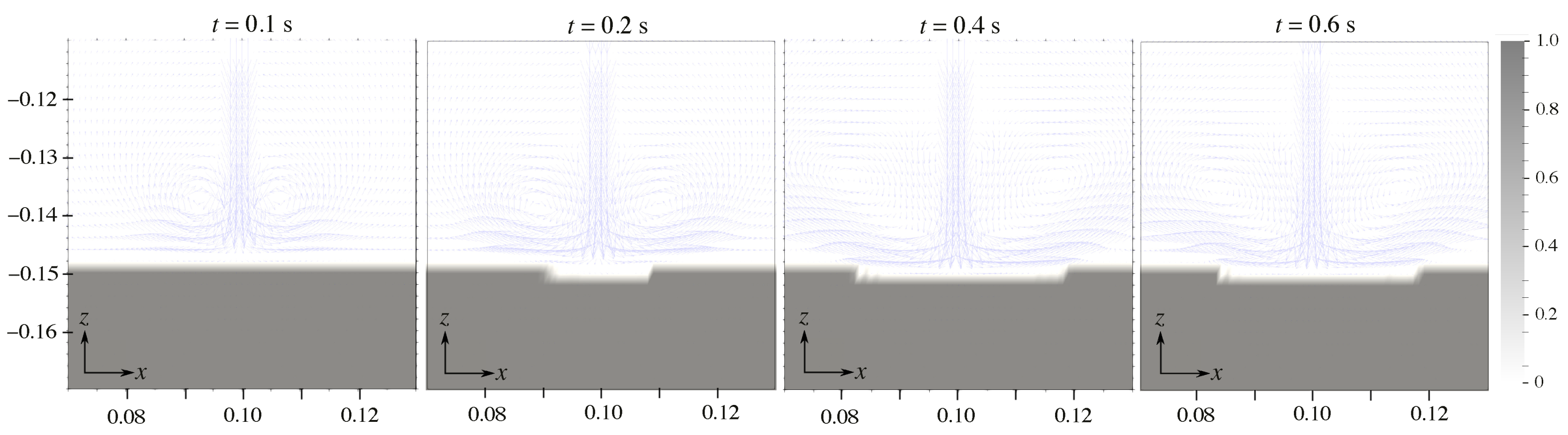
4. Numerical Results
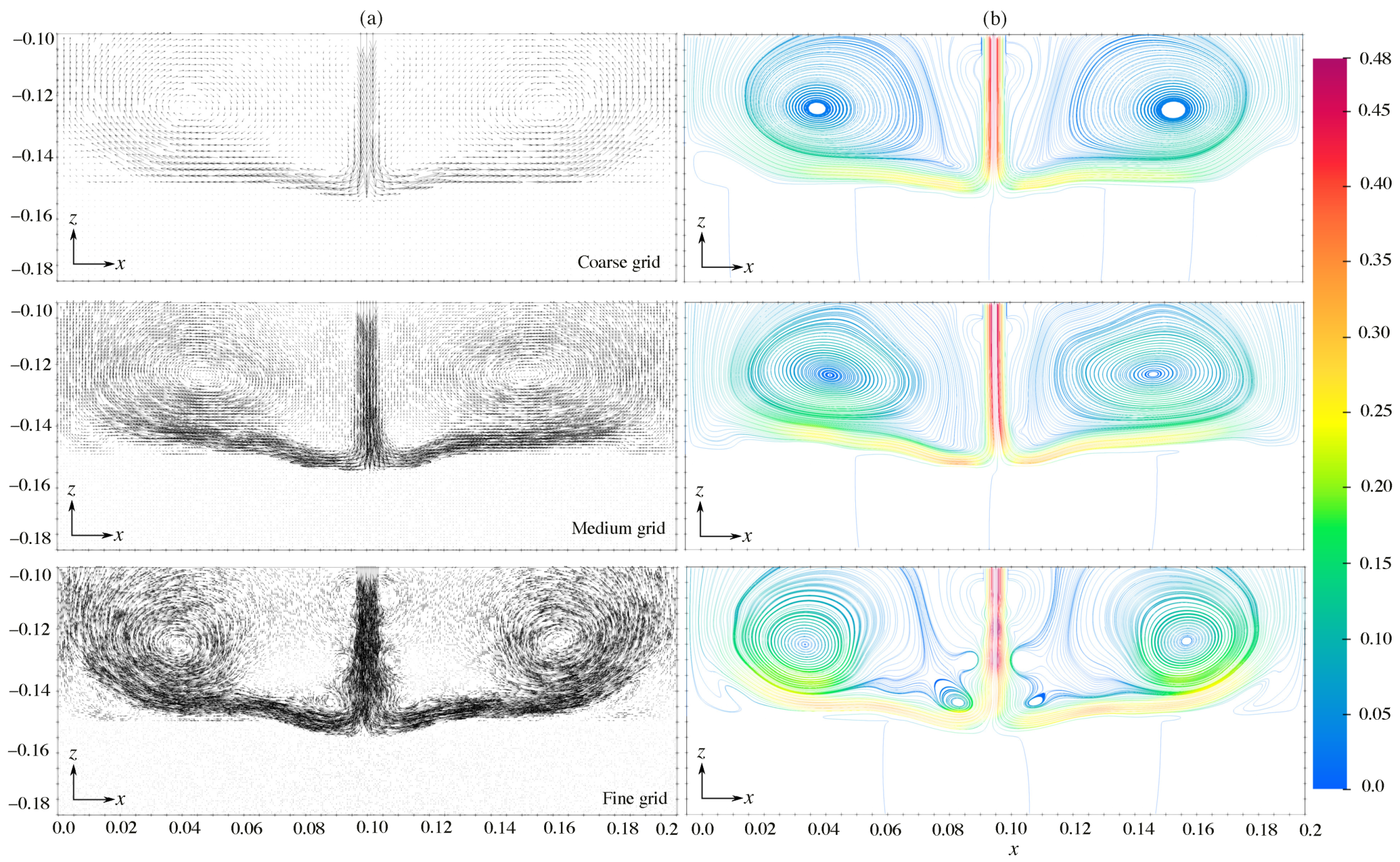
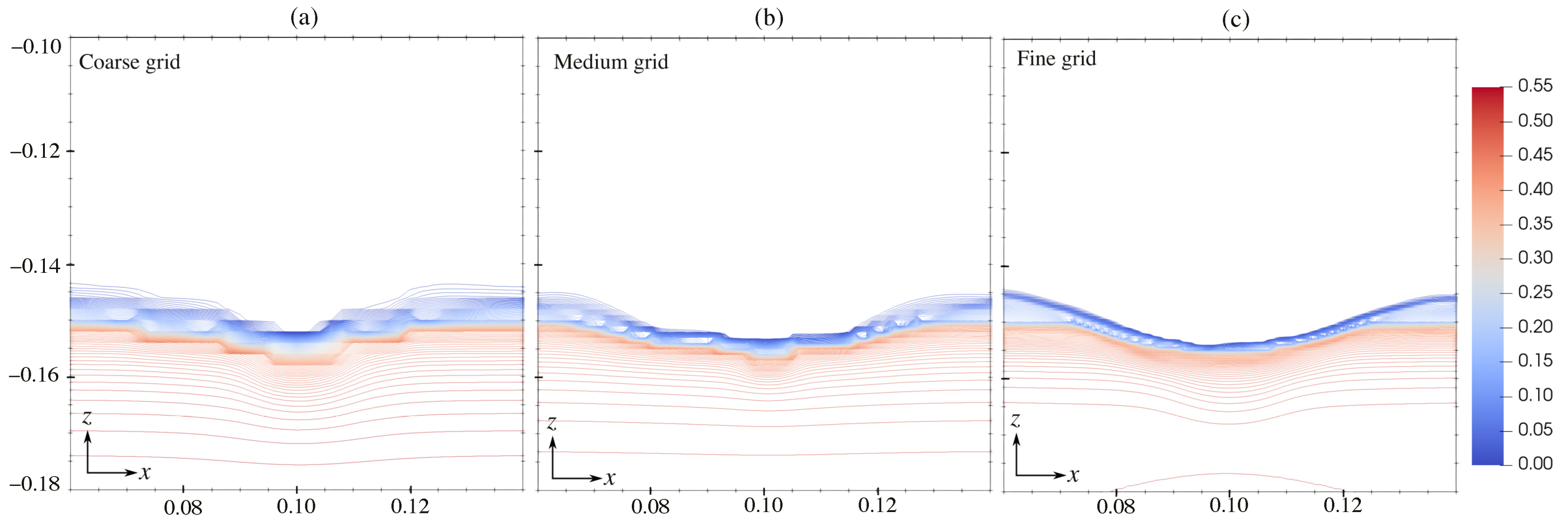
4.1. Original and Unified Model
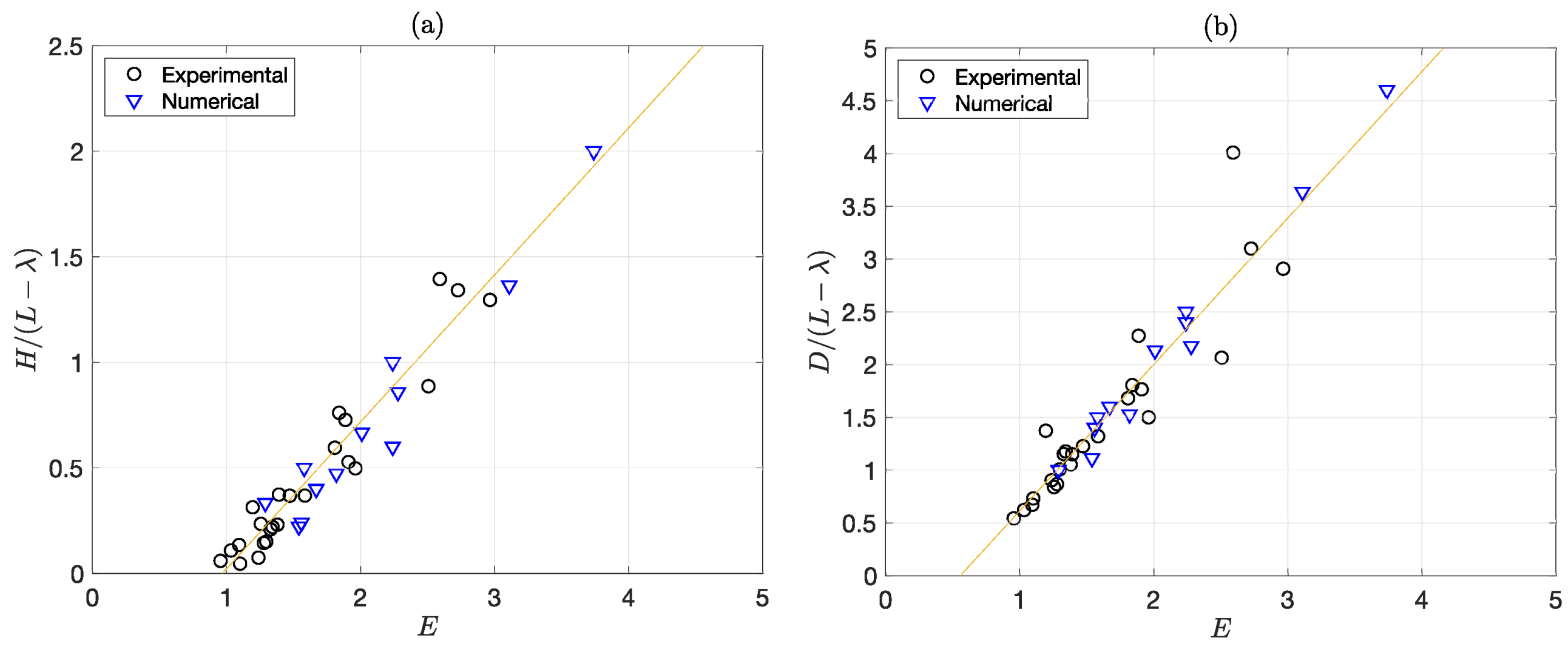
4.2. Crater Size Predictions
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two Dimensional |
| 3D | Three Dimensional |
| JET | Jet Erosion Test |
| WID | Water Injection Dredging |
| CFD | Computational Fluid Dynamics |
| MPI | Message Passing Interface |
| SOR | Successive Over Relaxation |
| GPU | Graphics Processing Unit |
| TVD | Total Variation Diminishing |
| PMMA | Polymethyl Methacrylate |
References
- Metzger, P.T.; Latta, R.C.; Schuler, J.M.; Immer, C.D. Craters formed in granular beds by impinging jets of gas. AIP Conf. Proc. 2009, 1145, 767–770. [Google Scholar]
- Metzger, P.T.; Immer, C.D.; Donahue, C.M.; Vu, B.T.; Latta, R.C.; Deyo-Svendsen, M. Jet-induced cratering of a granular surface with application to lunar spaceports. J. Aerosp. Eng. 2009, 22, 24–32. [Google Scholar] [CrossRef] [Green Version]
- Rouse, H. Criteria for similarity in the transportation of sediment. In Proceedings of the 1st Hydraulics Conference, Bulletin 20, State University of Iowa, Iowa City, IA, USA, 12–15 June 1939; pp. 33–49. [Google Scholar]
- Hanson, G.J.; Cook, K.R. Apparatus, test procedures, and analytical methods to measure soil erodibility in situ. Appl. Eng. Agric. 2004, 20, 455–462. [Google Scholar] [CrossRef]
- Hanson, G.J.; Hunt, S.L. Lessons learned using laboratory JET method to measure soil erobibility of compacted soils. Appl. Eng. Agric. 2007, 23, 305–312. [Google Scholar] [CrossRef]
- Perng, A.T.H.; Capart, H. Underwater sand bed erosion and internal jump formation by a travelling plane jets. J. Fluid. Mech. 2008, 595, 1–43. [Google Scholar] [CrossRef] [Green Version]
- Kobus, H.; Leister, P.; Westrich, B. Flow field and scouring effects of steady and pulsating jets impinging on a movable bed. J. Hydr. Res. 1979, 17, 175–192. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Beltaos, S. Erosion by impinging circular turbulent jets. Procs. ASCE J. Hydr. Div. 1977, 103, 1191–1205. [Google Scholar] [CrossRef]
- Aderibigbe, O.O.; Rajaratnam, N. Erosion of loose beds by submerged circular impinging vertical turbulent jets. J. Hydraulic Res. 1996, 34, 19–33. [Google Scholar] [CrossRef]
- Badr, S.; Gauthier, G.; Gondret, P. Crater jet morphology. Phys. Fluids 2016, 28, 033305. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Mazurek, K.A. Erosion of Sand by Circular Impinging Water Jets with Small Tailwater. J. Hydr. Eng. 2003, 129, 225–229. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Mazurek, K.A. Impingement of circular turbulent jets on rough boundaries Impact des jets turbulents sur des parois rugueuses. J. Hydr. Res. 2005, 43, 688–694. [Google Scholar] [CrossRef]
- Mazurek, K.A.; Gheisi, A.R. Assessment of the Erodibility of a Cohesive Soil using a Submerged Circular Turbulent Impinging Jet. In Proceedings of the 33rd IAHR Congress, Vancouver, BC, Canada, 9–14 August 2009. [Google Scholar]
- Sutherland, B.R.; Dalziel, S. Bedload transport by a vertical jet impinging upon sediments. Phys. Fluids 2014, 26, 035103. [Google Scholar] [CrossRef]
- Badr, S.; Gauthier, G.; Gondret, P. Erosion threshold of a liquid immersed granular bed by an impinging plane liquid jet. Phys. Fluids 2014, 26, 023302. [Google Scholar] [CrossRef] [Green Version]
- Beltaos, S.; Rajaratnam, N. Plane turbulent impinging jets. J. Hydr. Res. 1973, 11, 29–59. [Google Scholar] [CrossRef]
- Rajaratnam, N. Erosion by plane turbulent jets. J. Hydr. Res. 1981, 19, 339–358. [Google Scholar] [CrossRef]
- Phares, D.; Smedley, G.; Flagan, R. The wall shear stress produced by a normal impingement of a jet on a flat surface. J. Fluid Mech. 2000, 418, 351–375. [Google Scholar] [CrossRef] [Green Version]
- Tritton, D.J. Physical Fluid Dynamics, 2nd ed.; Springer: Oxford, UK, 1988. [Google Scholar]
- Pope, S.B. Turbulent Flows, 1st ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Donalson, C.D.; Snedeker, R.S. A study of free jet impingement. Part 1. Mean properties of free and impinging jets. J. Fluid Mech. 1971, 45, 281–319. [Google Scholar] [CrossRef]
- Glauert, M.B. The wall jet. J. Fluid Mech. 1956, 1, 625–643. [Google Scholar] [CrossRef]
- Launder, B.E.; Rodi, W. The turbulent wall: Measurements and modeling. Ann. Rev. Fluid Mech. 1983, 15, 429–459. [Google Scholar] [CrossRef]
- Magyari, E.; Keller, B. The algebraically decaying wall jet. Eur. J. Mech. B Fluids 2004, 23, 601–605. [Google Scholar] [CrossRef]
- Weidner, K.; Petrie, J.; Diplas, P.; Nam, S.; Gutierrez, M.; Ellenberg, M. Numerical simulation of jet test and associated soil erosion. In Proceedings of the 6th International Conference on Scour and Erosion, ICSE6, Paris, France, 27–31 August 2012. [Google Scholar]
- Mercier, F.; Bonelli, S.; Anselmet, F.; Pinettes, P.; Courivaud, J.R.; Fry, J.J. On the numerical modelling of the Jet Erosion Test. In Proceedings of the 6th International Conference on Scour and Erosion, ICSE6, Paris, France, 27–31 August 2012. [Google Scholar]
- Wang, T.; Song, B. Study on deepwater conductor jet excavation mechanism in cohesive soil. Appl. Ocean Res. 2019, 82, 225–235. [Google Scholar] [CrossRef]
- Kuang, S.B.; LaMarche, C.Q.; Curtis, J.S.; Yu, A.B. Discrete particle simulation of jet-induced cratering of a granular bed. Powder Technol. 2013, 239, 319–336. [Google Scholar] [CrossRef]
- Benseghier, Z.; Cuéllar, P.; Luu, L.H.; Delenne, J.Y.; Bonelli, S.; Philippe, P. Relevance of free jet model for soil erosion by impinging jets. J. Hydraul. Eng. 2020, 146, 04019047. [Google Scholar] [CrossRef]
- Benseghier, Z.; Cuéllar, P.; Luu, L.H.; Bonelli, S.; Philippe, P. A parallel GPU-based computational framework for the micromechanical analysis of geotechnical and erosion problems. Comput. Geotech. 2020, 120, 103404. [Google Scholar] [CrossRef]
- Boyaval, S.; Caboussat, A.; Mrad, A.; Picasso, M.; Steiner, G. A semi-Lagrangian splitting method for the numerical simulation of sediment transport with free surface flows. Comput. Fluids 2018, 172, 384–396. [Google Scholar] [CrossRef]
- Qian, Z.D.; Hu, X.Q.; Huai, W.X.; Xue, W.Y. Numerical simulation of sediment erosion by submerged jets using an Eulerian model. Sci. China Technol. Sci. 2010, 53, 3324–3330. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhao, M.; Wang, C.; Ge, T. Numerical study of sand scour with a modified Eulerian model based on incipient motion theory. Mar. Georesour. Geotechnol. 2018, 36, 818–826. [Google Scholar] [CrossRef]
- Uh Zapata, M.; Pham Van Bang, D.; Nguyen, K.D. Parallel simulations for a 2D x/z two-phase flow fluid-solid particle model. Comput. Fluids 2018, 173, 103–110. [Google Scholar] [CrossRef]
- Wang, B.; van Rhee, C.; Nobel, A.; Keetels, G. Modeling the hydraulic excavation of cohesive soil by a moving vertical jet. Ocean Eng. 2021, 227, 108796. [Google Scholar] [CrossRef]
- Greenshields, C.J.; Weller, H.G. A unified formulation for continuum mechanics applied to fluid-structure interaction in flexible tubes. Int. J. Numer. Meth. Engng. 2005, 64, 1575–1593. [Google Scholar] [CrossRef]
- Chua, L.P.; Lua, A.C. Measurements of a confined jet. Phys. Fluids 1998, 10, 3137–3144. [Google Scholar] [CrossRef]
- Midi, G.D.R. On dense granular flows. Eur. Phys. J. E 2004, 14, 341–365. [Google Scholar] [CrossRef] [Green Version]
- Loiseleux, T.; Gondret, P.; Rabaud, M.; Doppler, D. Onset of erosion and avalanche for an inclined granular bed sheared by a continuous laminar flow. Phys. Fluids 2005, 17, 103304. [Google Scholar] [CrossRef]
- Drew, D.A.; Lahey, R.T. Analytical Modelling of Multiphase Flow, in Particulate Two-Phase Flow; Roco, M.C., Ed.; Butterworth-Heinemann: Boston, MA, USA, 1993. [Google Scholar]
- Barbry, N.; Guillou, S.; Nguyen, K.D. Une approche diphasique pour le calcul du transport sédimentaire en milieux estuariens. C.R. Acad. Sci. IIb 2000, 328, 793–799. [Google Scholar] [CrossRef]
- Nguyen, K.D.; Guillou, S.; Chauchat, J.; Barbry, N. A two-phase numerical model for suspended-sediment transport in estuaries. Adv. Water Resour. 2009, 32, 1187–1196. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Levy, F.; Van Bang, D.P.; Nguyen, K.D.; Guillou, S.; Chauchat, J. Simulation of dredged sediment releases into homogeneous water using a two-phase model. Adv. Water Resour. 2012, 48, 102–112. [Google Scholar] [CrossRef]
- Lundgren, T. Slow flow through stationary random beds and suspensions of spheres. J. Fluid. Mech. 1972, 51, 273–299. [Google Scholar] [CrossRef]
- Graham, A.L. On the viscosity of suspensions of solid spheres. Appl. Sci. Res. 1981, 37, 275–286. [Google Scholar] [CrossRef]
- Chauchat, J.; Guillou, S. On turbulence closures for two-phase sediment-laden flow models. J. Geophys. Res. 2008, 113, C11017. [Google Scholar] [CrossRef] [Green Version]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and non-spherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Guillou, S.; Barbry, N.; Nguyen, K.D. Calcul numérique des ondes de surface par une méthode de projection et un maillage eulérien adaptatif. C.R. Acad. Sci. IIb 2000, 328, 875–881. [Google Scholar]
- Uh Zapata, M.; Zhang, W.; Marois, L.; Hammouti, A.; Pham Van Bang, D.; Nguyen, K.D. Two-phase experimental and numerical studies on scouring at the toe of vertical seawall. Eur. J. Mech. B Fluids 2022, 93, 13–28. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical solution of the Navier–Stokes equations. Math. Comp. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Guillou, S.; Nguyen, K.D. An improved technique for solving two-dimensional shallow water problems. Int. J. Num. Meth. Fluids 1999, 29, 465–483. [Google Scholar] [CrossRef]




| Mean Velocity | Reynolds Number | Impingement Distance | Crater Width | Crater Depth | Mean Velocity | Reynolds Number | Impingement Distance | Crater Width | Crater Depth |
|---|---|---|---|---|---|---|---|---|---|
| (m/s) | Re | L (m) | D (m) | H (m) | (m/s) | Re | L (m) | D (m) | H (m) |
| 0.471 | 1885 | 0.145 | 0.015 | 0.091 | 0.314 | 1256 | 0.111 | 0.007 | 0.044 |
| 0.471 | 1885 | 0.130 | 0.020 | 0.095 | 0.314 | 1256 | 0.103 | 0.008 | 0.042 |
| 0.471 | 1885 | 0.084 | 0.022 | 0.067 | 0.314 | 1256 | 0.088 | 0.011 | 0.040 |
| 0.471 | 1885 | 0.059 | 0.025 | 0.057 | 0.314 | 1256 | 0.075 | 0.013 | 0.043 |
| 0.471 | 1885 | 0.036 | 0.025 | 0.034 | 0.314 | 1256 | 0.062 | 0.017 | 0.040 |
| 0.471 | 1885 | 0.108 | 0.025 | 0.090 | 0.314 | 1256 | 0.051 | 0.015 | 0.045 |
| 0.431 | 1726 | 0.159 | 0.005 | 0.087 | 0.314 | 1256 | 0.041 | 0.021 | 0.050 |
| 0.431 | 1726 | 0.125 | 0.012 | 0.086 | 0.235 | 942 | 0.068 | 0.002 | 0.025 |
| 0.431 | 1726 | 0.079 | 0.020 | 0.069 | 0.235 | 942 | 0.064 | 0.005 | 0.028 |
| 0.431 | 1726 | 0.063 | 0.020 | 0.047 | 0.235 | 942 | 0.052 | 0.008 | 0.027 |
| 0.431 | 1726 | 0.042 | 0.025 | 0.050 | 0.235 | 942 | 0.039 | 0.011 | 0.024 |
| 0.392 | 1570 | 0.106 | 0.014 | 0.078 | 0.235 | 942 | 0.032 | 0.011 | 0.019 |
| 0.392 | 1570 | 0.101 | 0.023 | 0.071 | 0.235 | 942 | 0.020 | 0.012 | 0.012 |
| 0.392 | 1570 | 0.076 | 0.021 | 0.061 | 0.235 | 942 | 0.009 | 0.020 | 0.019 |
| 0.392 | 1570 | 0.056 | 0.021 | 0.049 | 0.157 | 628 | 0.053 | 0.004 | 0.018 |
| 0.392 | 1570 | 0.034 | 0.022 | 0.032 | 0.157 | 628 | 0.041 | 0.006 | 0.016 |
| 0.392 | 1570 | 0.020 | 0.024 | 0.035 | 0.157 | 628 | 0.029 | 0.007 | 0.016 |
| Mean Velocity | Impingement Distance | Jet Width | Jet-Bed Distance | Reynolds Number | Erosion Parameter | Crater Width | Crater Depth |
|---|---|---|---|---|---|---|---|
| (m/s) | L (mm) | b (mm) | Re | E | D (mm) | H (mm) | |
| 0.18 | 40 | 4 | 10 | 720 | 2.24 | 12 | 3 |
| 0.18 | 50 | 4 | 12.5 | 720 | 1.29 | 15 | 5 |
| 0.28 | 50 | 4 | 12.5 | 1120 | 2.01 | 32 | 10 |
| 0.28 | 60 | 4 | 15 | 1120 | 1.56 | 35 | 6 |
| 0.30 | 40 | 4 | 10 | 1200 | 3.74 | 23 | 10 |
| 0.30 | 60 | 4 | 15 | 1200 | 1.67 | 40 | 10 |
| 0.37 | 46 | 4 | 11.5 | 1480 | 3.11 | 40 | 15 |
| 0.37 | 80 | 4 | 20 | 1480 | 1.54 | 50 | 10 |
| 0.28 | 70 | 6 | 11.66 | 1680 | 2.28 | 38 | 15 |
| 0.28 | 80 | 6 | 13.33 | 1680 | 1.82 | 42 | 13 |
| 0.18 | 80 | 8 | 10 | 1440 | 2.24 | 25 | 10 |
| 0.18 | 90 | 8 | 11.25 | 1440 | 1.58 | 30 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham Van Bang, D.; Uh Zapata, M.; Gauthier, G.; Gondret, P.; Zhang, W.; Nguyen, K.D. Two-Phase Flow Modeling for Bed Erosion by a Plane Jet Impingement. Water 2022, 14, 3290. https://doi.org/10.3390/w14203290
Pham Van Bang D, Uh Zapata M, Gauthier G, Gondret P, Zhang W, Nguyen KD. Two-Phase Flow Modeling for Bed Erosion by a Plane Jet Impingement. Water. 2022; 14(20):3290. https://doi.org/10.3390/w14203290
Chicago/Turabian StylePham Van Bang, Damien, Miguel Uh Zapata, Georges Gauthier, Philippe Gondret, Wei Zhang, and Kim Dan Nguyen. 2022. "Two-Phase Flow Modeling for Bed Erosion by a Plane Jet Impingement" Water 14, no. 20: 3290. https://doi.org/10.3390/w14203290






