Runoff Estimation Using Advanced Soft Computing Techniques: A Case Study of Mangla Watershed Pakistan
Abstract
:1. Introduction
2. Materials and Methods
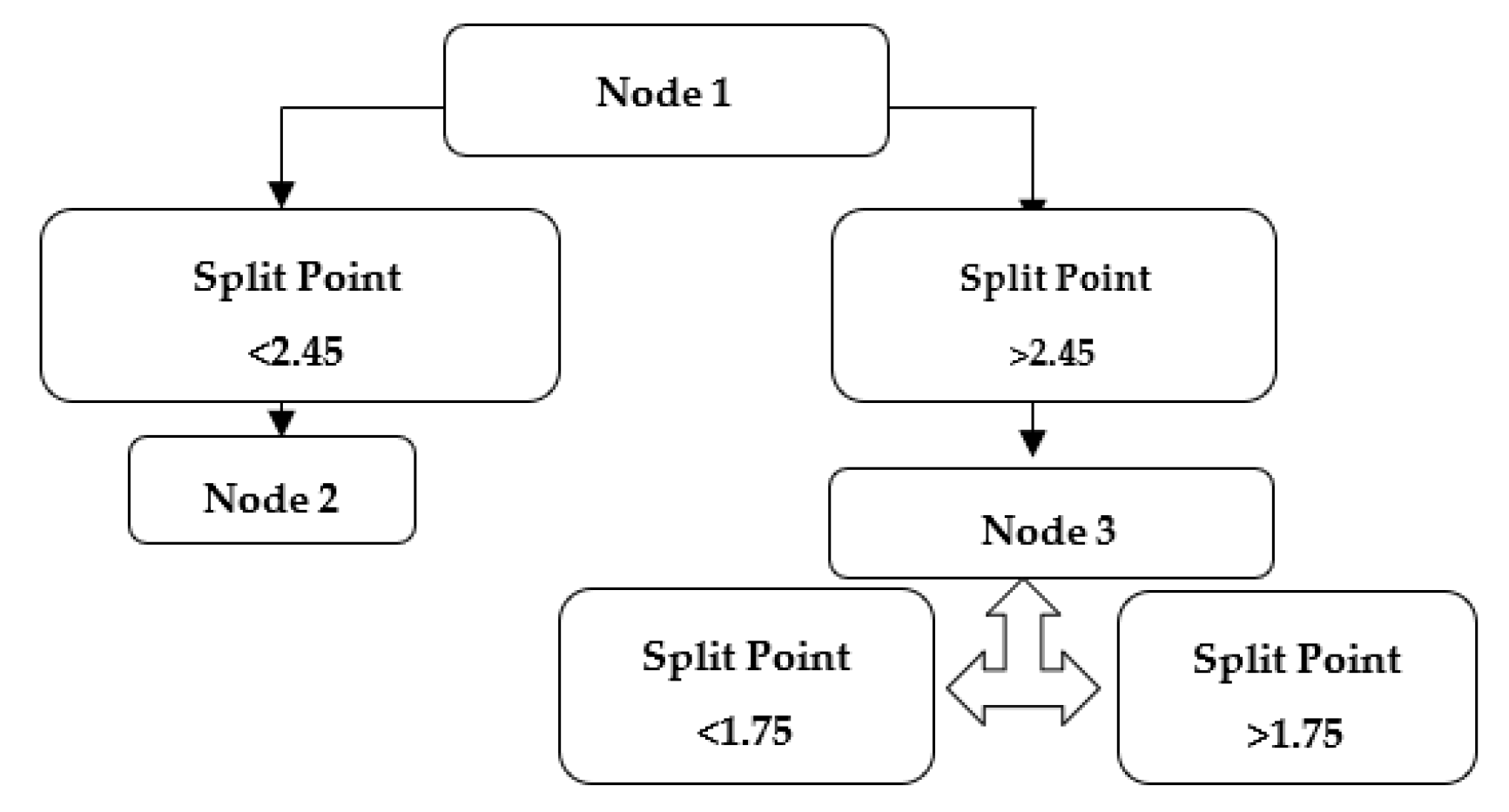
2.1. Single Decision Trees (SDTs)
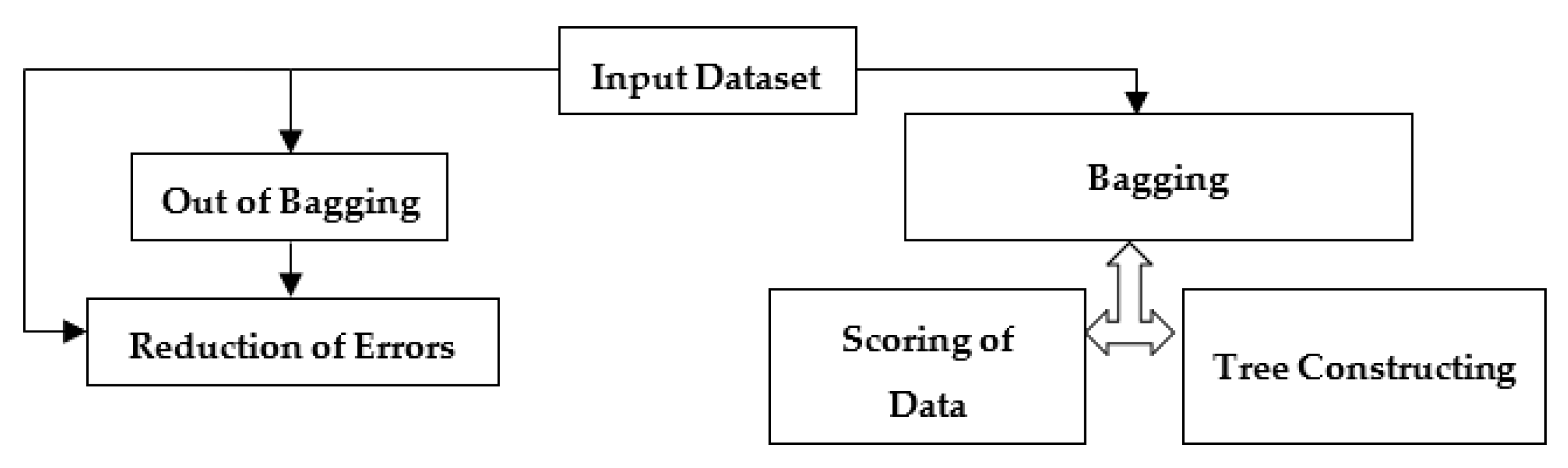
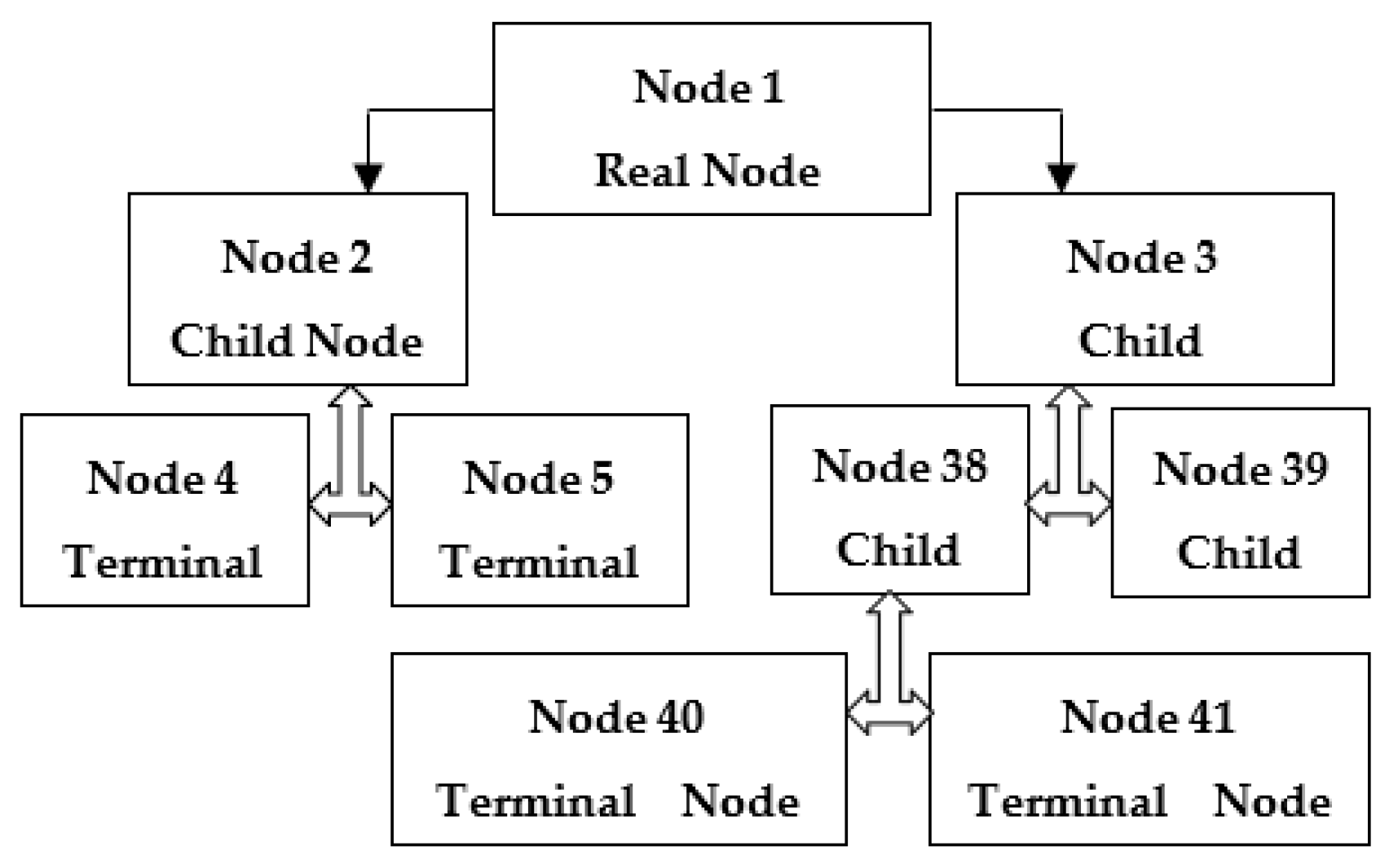
2.2. Decision Tree Forests (DTFs)
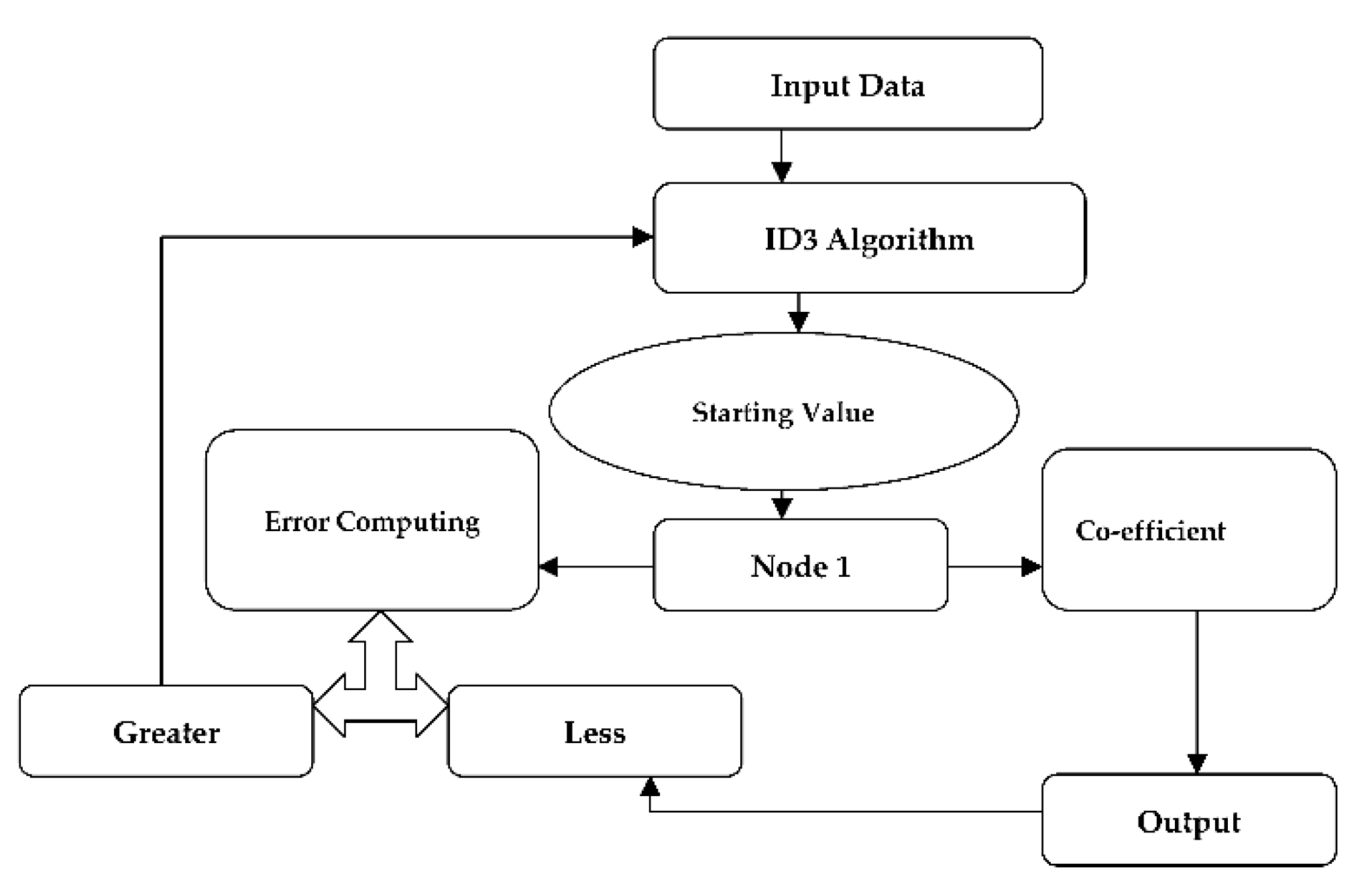
2.3. Tree Boost (TB)
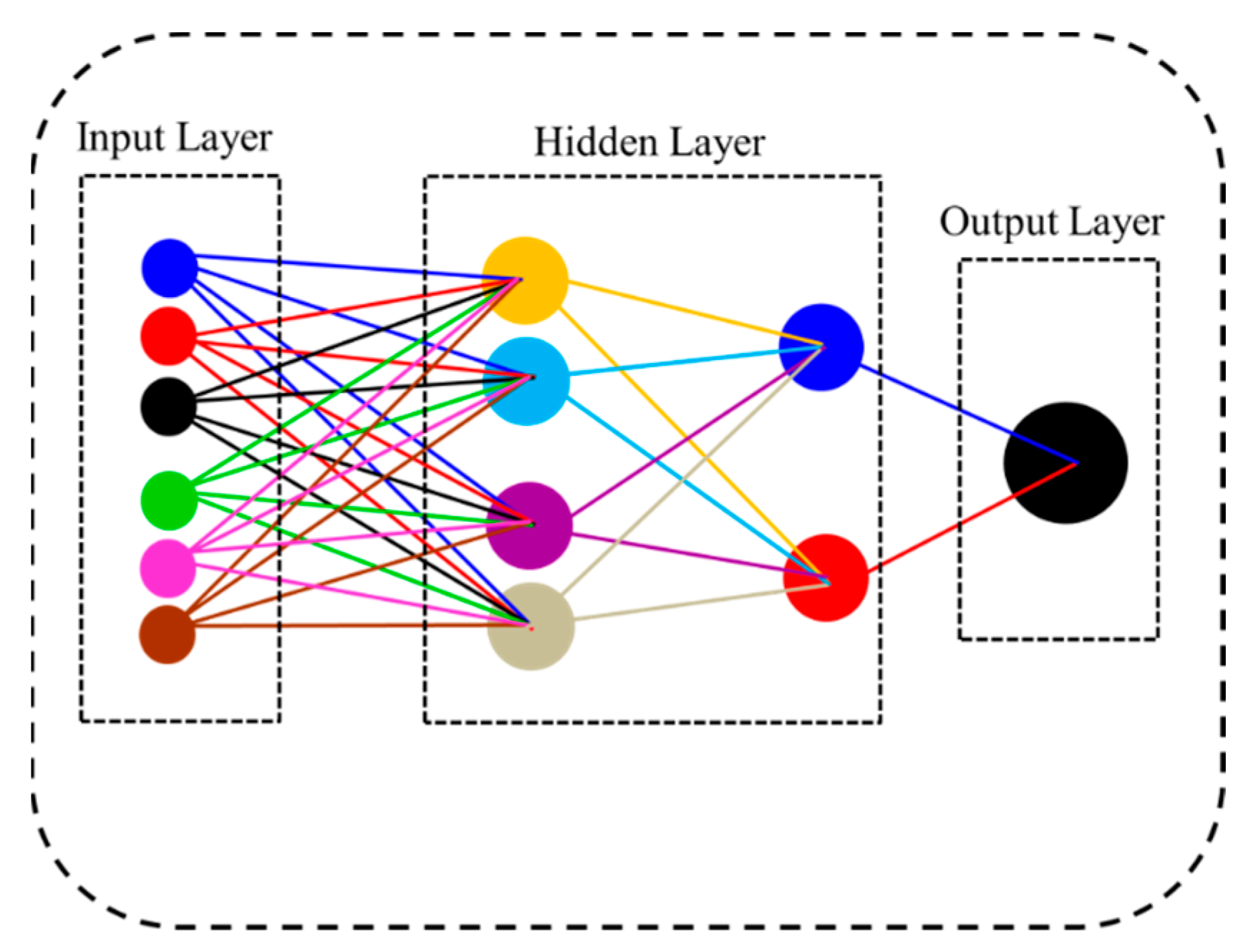
2.4. Multi-Layer Perceptron (MLP)
2.5. Study Area
2.6. Dataset
2.7. Performance Evaluation
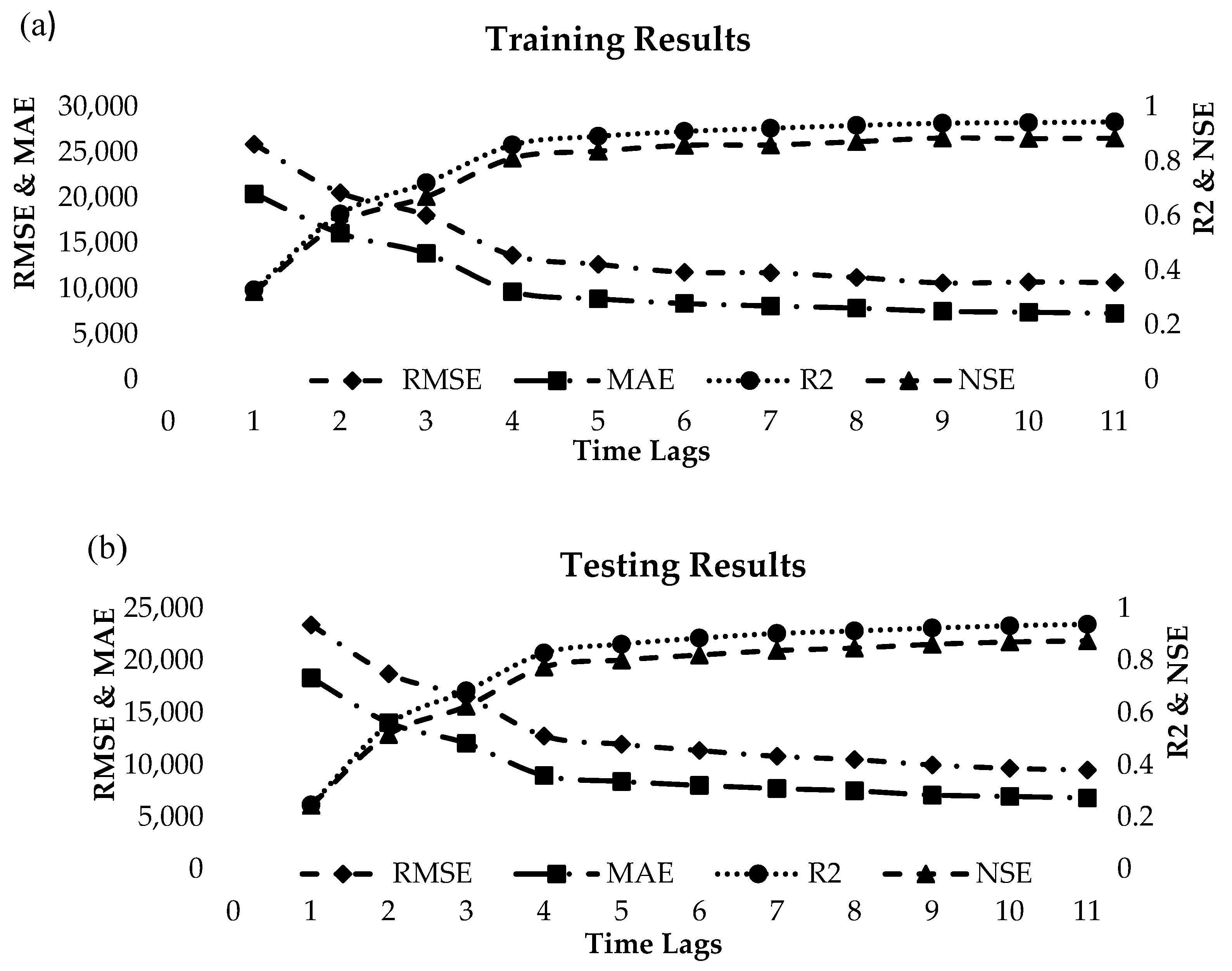
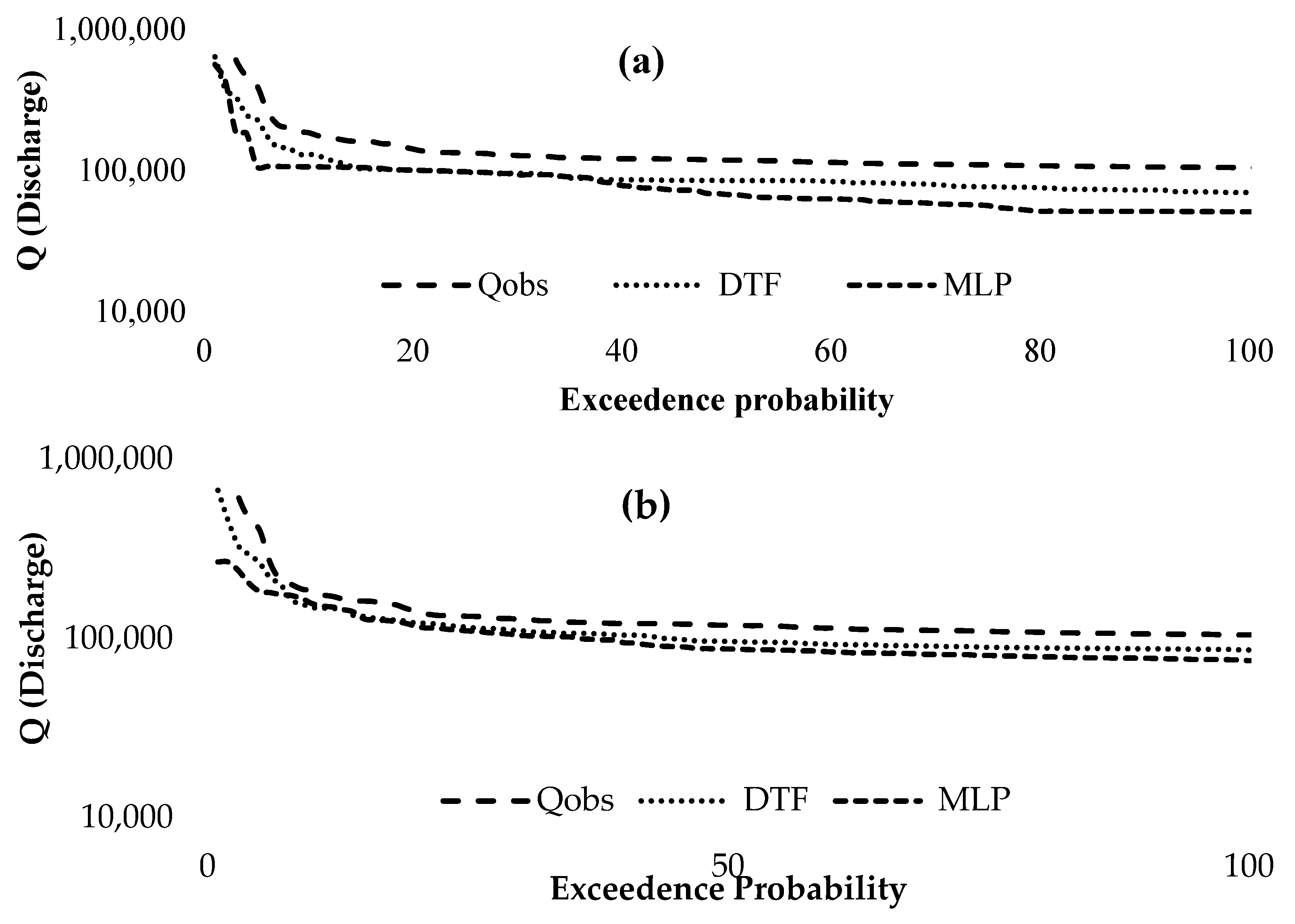
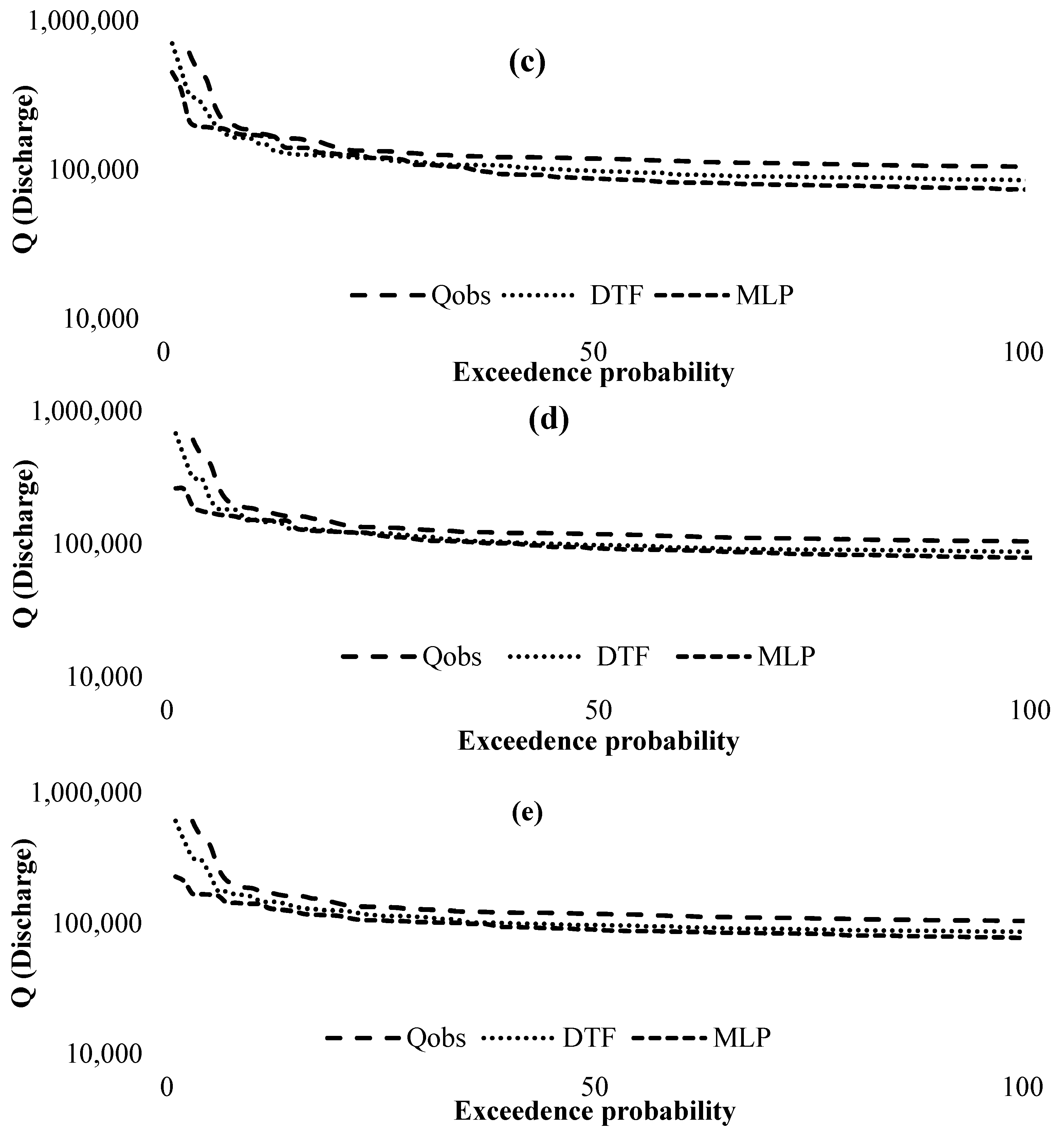
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TB | Tree Boost |
| DTFs | Decision tree forests |
| SDTs | Single decision trees |
| MLP | Multilayer perceptron |
| RMSE | Root means square error |
| MAE | Mean absolute error |
| R2 | Coefficient of determination |
| NSE | Nash–Sutcliffe efficiency |
| FDCs | Flow duration curves |
| ANN | Artificial neural network |
| ANFIS | Adaptive neuro-fuzzy inference system |
| GP | Genetic programming |
| GEP | Gene expression programming |
| SVM | Support vector machine |
| BPA | Back-propagation algorithm |
| RGA | Real-coded genetic algorithm |
| SOM | Self-organizing map |
| MCS | Monte Carlo simulation |
| SORM | Simplified order reliability method |
| FORM | First-order reliability method |
| ME | misclassification error |
| km2 | Square kilometers (area) |
| MAF | Million acre feet (storage capacity) |
| MW | Megawatts (electric power) |
| °C | Degrees Celsius (temperature) |
| Inches | Precipitation |
References
- Nawaz, Z.; Li, X.; Chen, Y.; Guo, Y.; Wang, X. Temporal and Spatial Characteristics of Precipitation and Temperature in Punjab, Pakistan. Water 2019, 11, 1916. [Google Scholar] [CrossRef] [Green Version]
- Fahad, S.; Wang, J. Climate change, vulnerability, and its impacts in rural Pakistan: A review. Environ. Sci. Pollut. Res. 2020, 27, 1334–1338. [Google Scholar] [CrossRef] [PubMed]
- Asadi, S.; Shahrabi, J.; Abbaszadeh, P.; Tabanmehr, S. A new hybrid artificial neural networks for rainfall–runoff process modeling. Neurocomputing 2013, 121, 470–480. [Google Scholar] [CrossRef]
- Waqas, M.; Saifullah, M.; Hashim, S.; Khan, M.; Muhammad, S. Evaluating the Performance of Different Artificial Intelligence Techniques for Forecasting: Rainfall and Runoff Prospective. In Weather Forecasting; IntechOpen: London, UK, 2021; p. 23. [Google Scholar]
- Gholami, V.; Sahour, H. Simulation of rainfall-runoff process using an artificial neural network (ANN) and field plots data. Theor. Appl. Climatol. 2022, 147, 87–98. [Google Scholar] [CrossRef]
- Solomatine, D.; See, L.M.; Abrahart, R.J. Data-driven modelling: Concepts, approaches and experiences. In Practical Hydroinformatics; Abrahart, R.J., See, L.M., Solomatine, D.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 17–30. [Google Scholar]
- Shoaib, M.; Shamseldin, A.Y.; Melville, B.W.; Khan, M.M. A comparison between wavelet based static and dynamic neural network approaches for runoff prediction. J. Hydrol. 2016, 535, 211–225. [Google Scholar] [CrossRef]
- Verma, R. ANN-based Rainfall-Runoff Model and Its Performance Evaluation of Sabarmati River Basin, Gujarat, India. Water Conserv. Sci. Eng. 2022, 1–8. [Google Scholar] [CrossRef]
- Nourani, V.; Baghanam, A.H.; Adamowski, J.; Kisi, O. Applications of hybrid wavelet–Artificial Intelligence models in hydrology: A review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. The Cross-Section of Expected Stock Returns. J. Financ. 1992, 47, 427–465. [Google Scholar] [CrossRef]
- Jang, J.-S.R. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Koza, J.R. Evolution of subsumption using genetic programming. In Toward a Practice of Autonomous Systems: Proceedings of the First European Conference on Artificial Life; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Savic, D.A.; Walters, G.A.; Davidson, J.W. A genetic programming approach to rainfall-runoff modelling. Water Resour. Manag. 1999, 13, 219–231. [Google Scholar] [CrossRef]
- Joachims, T. Text categorization with Support Vector Machines: Learning with many relevant features. In Machine Learning: ECML-98; Springer: Berlin/Heidelberg, Germany, 1998; pp. 137–142. [Google Scholar]
- Shoaib, M.; Shamseldin, A.Y.; Melville, B.W. Comparative study of different wavelet based neural network models for rainfall–runoff modeling. J. Hydrol. 2014, 515, 47–58. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Kisi, O.; Rajaee, T. Performance of radial basis and LM-feed forward artificial neural networks for predicting daily watershed runoff. Appl. Soft Comput. 2013, 13, 4633–4644. [Google Scholar] [CrossRef]
- Srinivasulu, S.; Jain, A. A comparative analysis of training methods for artificial neural network rainfall–runoff models. Appl. Soft Comput. 2006, 6, 295–306. [Google Scholar] [CrossRef]
- Setiono; Hadiani, R. Analysis of Rainfall-runoff Neuron Input Model with Artificial Neural Network for Simulation for Availability of Discharge at Bah Bolon Watershed. Procedia Eng. 2015, 125, 150–157. [Google Scholar] [CrossRef] [Green Version]
- Elsafi, S.H. Artificial Neural Networks (ANNs) for flood forecasting at Dongola Station in the River Nile, Sudan. Alex. Eng. J. 2014, 53, 655–662. [Google Scholar] [CrossRef]
- Farajzadeh, J.; Fard, A.F.; Lotfi, S. Modeling of monthly rainfall and runoff of Urmia lake basin using "feed-forward neural network" and "time series analysis" model. Water Resour. Ind. 2014, 7–8, 38–48. [Google Scholar] [CrossRef] [Green Version]
- Napolitano, G.; See, L.; Calvo, B.; Savi, F.; Heppenstall, A. A conceptual and neural network model for real-time flood forecasting of the Tiber River in Rome. Phys. Chem. Earth Parts A/B/C 2010, 35, 187–194. [Google Scholar] [CrossRef]
- Waqas, M.; Shoaib, M.; Saifullah, M.; Naseem, A.; Hashim, S.; Ehsan, F.; Ali, I.; Khan, A. Assessment of Advanced Artificial Intelligence Techniques for Streamflow Forecasting in Jhelum River Basin. Pak. J. Agric. Res. 2021, 33, 580–598. [Google Scholar] [CrossRef]
- Rajurkar, M.; Kothyari, U.; Chaube, U. Modeling of the daily rainfall-runoff relationship with artificial neural network. J. Hydrol. 2004, 285, 96–113. [Google Scholar] [CrossRef]
- Shamseldin, A.Y. Application of a neural network technique to rainfall-runoff modelling. J. Hydrol. 1997, 199, 272–294. [Google Scholar] [CrossRef]
- Shin, M.-J.; Guillaume, J.H.A.; Croke, B.F.W.; Jakeman, A.J. A review of foundational methods for checking the structural identifiability of models: Results for rainfall-runoff. J. Hydrol. 2015, 520, 1–16. [Google Scholar] [CrossRef]
- Tokar, A.S.; Johnson, P.A. Rainfall-Runoff Modeling Using Artificial Neural Networks. J. Hydrol. Eng. 1999, 4, 232–239. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W.; Fan, C. Prediction of rainfall time series using modular artificial neural networks coupled with data-preprocessing techniques. J. Hydrol. 2010, 389, 146–167. [Google Scholar] [CrossRef] [Green Version]
- Devak, M.; Dhanya, C.; Gosain, A. Dynamic coupling of support vector machine and K-nearest neighbour for downscaling daily rainfall. J. Hydrol. 2015, 525, 286–301. [Google Scholar] [CrossRef]
- He, Z.; Wen, X.; Liu, H.; Du, J. A comparative study of artificial neural network, adaptive neuro fuzzy inference system and support vector machine for forecasting river flow in the semiarid mountain region. J. Hydrol. 2014, 509, 379–386. [Google Scholar] [CrossRef]
- Kisi, O.; Cimen, M. A wavelet-support vector machine conjunction model for monthly streamflow forecasting. J. Hydrol. 2011, 399, 132–140. [Google Scholar] [CrossRef]
- Kundu, S.; Khare, D.; Mondal, A. Future changes in rainfall, temperature and reference evapotranspiration in the central India by least square support vector machine. Geosci. Front. 2017, 8, 583–596. [Google Scholar] [CrossRef]
- Noori, R.; Karbassi, A.R.; Moghaddamnia, A.; Han, D.; Zokaei-Ashtiani, M.H.; Farokhnia, A.; Gousheh, M.G. Assessment of input variables determination on the SVM model performance using PCA, Gamma test, and forward selection techniques for monthly stream flow prediction. J. Hydrol. 2011, 401, 177–189. [Google Scholar] [CrossRef]
- Rasouli, K.; Hsieh, W.W.; Cannon, A.J. Daily streamflow forecasting by machine learning methods with weather and climate inputs. J. Hydrol. 2012, 414–415, 284–293. [Google Scholar] [CrossRef]
- Keskin, M.E.; Taylan, D.; Terzi, Ö. Adaptive neural-based fuzzy inference system (ANFIS) approach for modelling hydrological time series. Hydrol. Sci. J. 2006, 51, 588–598. [Google Scholar] [CrossRef]
- Shoaib, M.; Shamseldin, A.Y.; Melville, B.W.; Khan, M.M. Runoff forecasting using hybrid Wavelet Gene Expression Programming (WGEP) approach. J. Hydrol. 2015, 527, 326–344. [Google Scholar] [CrossRef]
- Quinlan, J.R. Simplifying decision trees. Int. J. Man-Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef] [Green Version]
- Preis, A.; Ostfeld, A. A coupled model tree–genetic algorithm scheme for flow and water quality predictions in watersheds. J. Hydrol. 2008, 349, 364–375. [Google Scholar] [CrossRef]
- Etemad-Shahidi, A.; Mahjoobi, J. Comparison between M5′ model tree and neural networks for prediction of significant wave height in Lake Superior. Ocean Eng. 2009, 36, 1175–1181. [Google Scholar] [CrossRef]
- Xu, M.; Watanachaturaporn, P.; Varshney, P.K.; Arora, M.K. Decision tree regression for soft classification of remote sensing data. Remote Sens. Environ. 2005, 97, 322–336. [Google Scholar] [CrossRef]
- Deo, R.C.; Kisi, O.; Singh, V.P. Drought forecasting in eastern Australia using multivariate adaptive regression spline, least square support vector machine and M5Tree model. Atmos. Res. 2017, 184, 149–175. [Google Scholar] [CrossRef] [Green Version]
- Clay, D.E.; Alverson, R.; Johnson, J.M.; Karlen, D.L.; Clay, S.; Wang, M.Q.; Bruggeman, S.; Westhoff, S. Crop Residue Management Challenges: A Special Issue Overview. Agron. J. 2019, 111, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Sherrod, P.H. DTREG Predictive Modeling Software; DTREG: Brentwood, TN, USA, 2003; Available online: http://www.dtreg.com (accessed on 30 December 2003).
- Sherrod, P. Classification and Regression Trees and Support Vector Machines for Predictive Modeling and Forecasting; DTREG: Brentwood, TN, USA, 2006; Available online: http://www.DTREG.com/DTREG.pdf (accessed on 30 December 2006).
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting (With discussion and a rejoinder by the authors). Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- McGarry, K.; Wermter, S.; MacIntyre, J. Knowledge extraction from radial basis function networks and multilayer perceptrons. In Proceedings of the IJCNN’99, International Joint Conference on Neural Networks (Cat. No.99CH36339), Washington, DC, USA, 10–16 July 1999; IEEE: Piscataway, NJ, USA, 1999. [Google Scholar]
- Mahmood, R.; Babel, M.S. Evaluation of SDSM developed by annual and monthly sub-models for downscaling temperature and precipitation in the Jhelum basin, Pakistan and India. Theor. Appl. Climatol. 2012, 113, 27–44. [Google Scholar] [CrossRef]
- Jacquin, A.P.; Shamseldin, A.Y. Development of rainfall–runoff models using Takagi–Sugeno fuzzy inference systems. J. Hydrol. 2006, 329, 154–173. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Tayyab, M.; Ahmad, I.; Sun, N.; Zhou, J.; Dong, X. Application of Integrated Artificial Neural Networks Based on Decomposition Methods to Predict Streamflow at Upper Indus Basin, Pakistan. Atmosphere 2018, 9, 494. [Google Scholar] [CrossRef] [Green Version]
- Sharma, V.; Mishra, V.D.; Joshi, P.K. Implications of climate change on streamflow of a snow-fed river system of the Northwest Himalaya. J. Mt. Sci. 2013, 10, 574–587. [Google Scholar] [CrossRef] [Green Version]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Archer, D.; Fowler, H. Using meteorological data to forecast seasonal runoff on the River Jhelum, Pakistan. J. Hydrol. 2008, 361, 10–23. [Google Scholar] [CrossRef]
- Babur, M.; Babel, M.S.; Shrestha, S.; Kawasaki, A.; Tripathi, N.K. Assessment of Climate Change Impact on Reservoir Inflows Using Multi Climate-Models under RCPs—The Case of Mangla Dam in Pakistan. Water 2016, 8, 389. [Google Scholar] [CrossRef] [Green Version]
- Hayat, H.; Akbar, T.A.; Tahir, A.A.; Hassan, Q.K.; Dewan, A.; Irshad, M. Simulating Current and Future River-Flows in the Karakoram and Himalayan Regions of Pakistan Using Snowmelt-Runoff Model and RCP Scenarios. Water 2019, 11, 761. [Google Scholar] [CrossRef]
- Searcy, J.K. Flow-Duration Curves; US Government Printing Office: Washington, DC, USA, 1959. [Google Scholar]

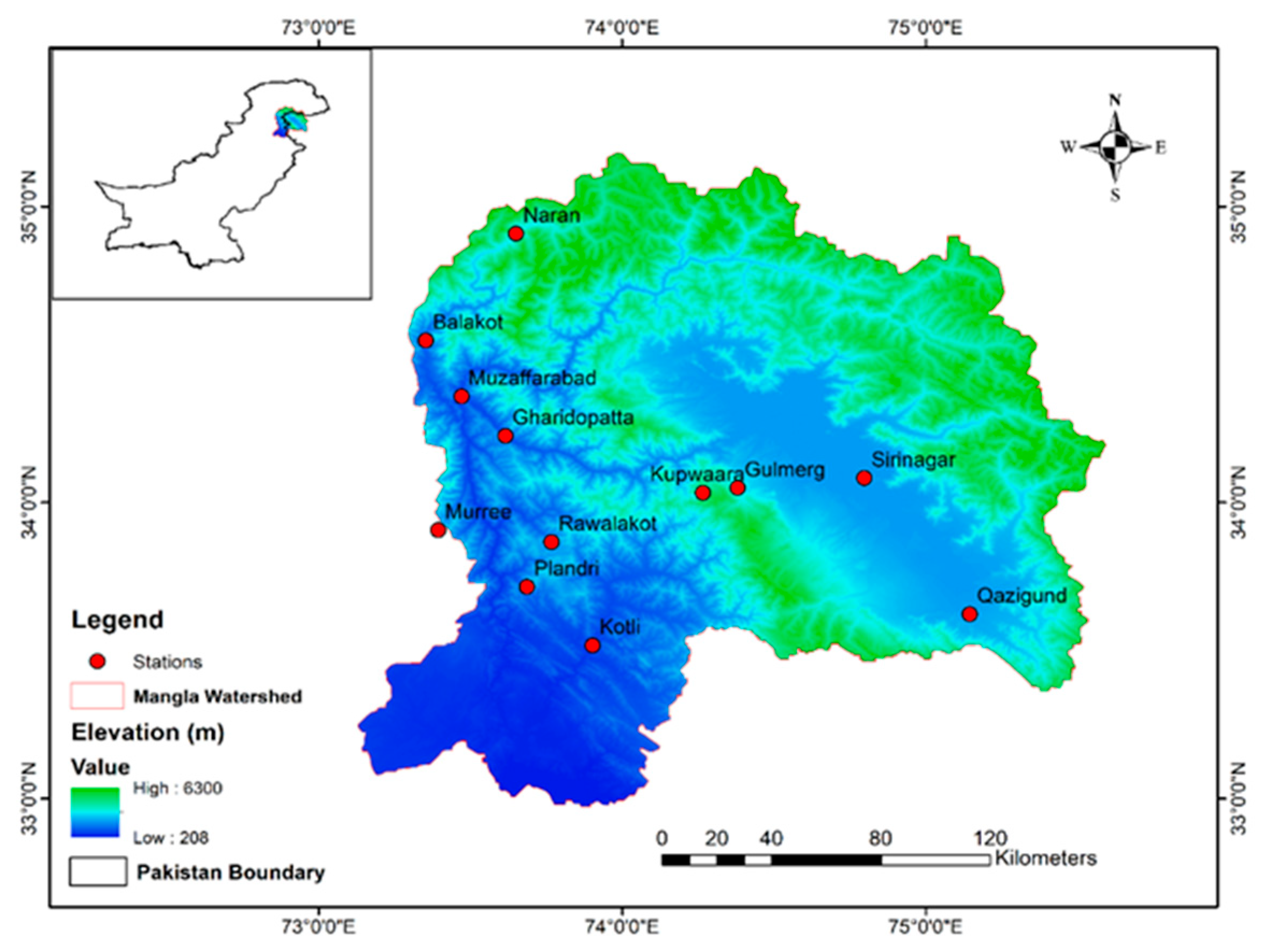
| Name of Station | Elevation (MSL) in Meters | Latitude | Longitude | Mean Yearly Precipitation (Inches) | Mean Yearly Temperature (°C) | Country |
|---|---|---|---|---|---|---|
| Naran | 2409 | 34.909° N | 73.6507° E | 1.83 | 19 | Pakistan |
| Balakot | 975 | 34.548° N | 73.3532° E | 48.7 | 25.1 | Pakistan |
| Muzaffarabad | 679 | 34.359° N | 73.47105° E | 45.67 | 27.6 | Pakistan |
| Gharidopatta | 817 | 34.225° N | 73.6154° E | 3.85 | 25.9 | Pakistan |
| Murree | 2291.2 | 33.907° N | 73.3943° E | 5.91 | 17.7 | Pakistan |
| Plandri | 1400 | 33.715° N | 73.6861° E | 5.91 | 21.8 | Pakistan |
| Kotli | 3000 | 33.518° N | 73.9022° E | 5.48 | 28.5 | Pakistan |
| Rawlakot | 1638 | 33.866° N | 73.7666° E | 19.99 | 24.7 | Pakistan |
| Kupwaara | 1522 | 34.033° N | 74.266° E | 42.00 | 13.9 | India |
| Qazigund | 1670 | 33.624° N | 75.145° E | 3.30 | 27.0 | India |
| Gulmerg | 2650 | 34.05° N | 74.38° E | 67.1 | 4.1 | India |
| Sirinagar | 5000 | 34.083° N | 74.797° E | 32.5 | 11.8 | India |
| Input Combinations | AIC |
|---|---|
| P(t) | 4.5432 |
| P(t), P(t-1) | 4.2015 |
| P(t), P(t-1), P(t-2) | 4.1534 |
| P(t), P(t-1), P(t-2), P(t-3) | 3.9812 |
| P(t), P(t-1), P(t-2), P(t-3), P(t-4) | 3.9678 |
| P(t), P(t-1), P(t-2), P(t-3), P(t-4), P(t-5) | 3.9561 |
| P(t), P(t-1), P(t-2), P(t-3), P(t-4), P(t-5), P(t-6) | 3.8911 |
| P(t), P(t-1), P(t-2), P(t-3), P(t-4), P(t-5), P(t-6), P(t-7) | 3.6582 |
| P(t), P(t-1), P(t-2), P(t-3), P(t-4), P(t-5), P(t-6), P(t-7), P(t-8) | 3.5121 |
| P(t), P(t-1), P(t-2), P(t-3), P(t-4), P(t-5), P(t-6), P(t-7), P(t-8), P(t-9) | 3.3140 |
| P(t), P(t-1), P(t-2), P(t-3), P(t-4), P(t-5), P(t-6), P(t-7), P(t-8), P(t-9), P(t-10) | 3.1480 |
| Training Results with P(t) | Testing Results with P(t) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | R2 | NSE | RMSE | MAE | Model | R2 | NSE | RMSE | MAE |
| DTFs | 0.329 | 0.322 | 25,905.668 | 20,441.804 | DTFs | 0.247 | 0.245 | 23,431.452 | 18,356.359 |
| SDTs | 0.072 | 1.000 | 30,319.632 | 21,709.896 | SDTs | 0.116 | 0.116 | 25,354.221 | 19,403.642 |
| TB | 0.169 | 0.164 | 28,804.129 | 20,771.767 | TB | 0.118 | 0.093 | 25,975.933 | 18,769.243 |
| MLP | 0.145 | 0.144 | 29,107.893 | 21,653.686 | MLP | 0.163 | 0.163 | 24,671.509 | 19,676.838 |
| Training Results with P(t-1) | Testing Results with P(t-1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | R2 | NSE | RMSE | MAE | Model | R2 | NSE | RMSE | MAE |
| DTFs | 0.607 | 0.573 | 20,552.859 | 16,087.144 | DTFs | 0.555 | 0.517 | 18,743.686 | 14,051.887 |
| SDTs | 0.283 | 0.283 | 26,655.355 | 20,296.326 | SDTs | 0.143 | 0.143 | 24,957.492 | 18,966.122 |
| TB | 0.247 | 0.234 | 27,574.589 | 19,787.896 | TB | 0.179 | 0.157 | 24,902.517 | 17,934.826 |
| MLP | 0.202 | 0.201 | 28,125.942 | 21,264.919 | MLP | 0.150 | 0.149 | 24,873.708 | 19,182.440 |
| Training Results with P(t-2) | Testing Results with P(t-2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | R2 | NSE | RMSE | MAE | Model | R2 | NSE | RMSE | MAE |
| DTFs | 0.721 | 0.670 | 18,066.618 | 13,873.521 | DTFs | 0.684 | 0.625 | 16,512.014 | 12,073.647 |
| SDTs | 0.307 | 0.307 | 26,196.097 | 19,778.782 | SDTs | 0.180 | 0.180 | 24,422.021 | 18,304.985 |
| TB | 0.254 | 0.242 | 27,432.893 | 19,339.867 | TB | 0.185 | 0.159 | 24,930.989 | 17,685.465 |
| MLP | 0.214 | 0.214 | 27,899.405 | 20,915.020 | MLP | 0.138 | 0.137 | 25,058.222 | 19,672.974 |
| Training Results with P(t-3) | Testing Results with P(t-3) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | R2 | NSE | RMSE | MAE | Model | R2 | NSE | RMSE | MAE |
| DTFs | 0.861 | 0.812 | 13,654.807 | 9663.240 | DTFs | 0.829 | 0.776 | 12,776.157 | 8996.971 |
| SDTs | 0.312 | 0.312 | 26,105.991 | 19,558.401 | SDTs | 0.184 | 0.184 | 24,360.689 | 18,264.990 |
| TB | 0.257 | 0.246 | 27,367.762 | 19,095.066 | TB | 0.203 | 0.167 | 24,850.153 | 17,518.771 |
| MLP | 0.217 | 0.217 | 27,850.550 | 20,693.155 | MLP | 0.164 | 0.160 | 24,717.335 | 19,418.675 |
| Training Results with P(t-4) | Testing Results with P(t-4) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | R2 | NSE | RMSE | MAE | Model | R2 | NSE | RMSE | MAE |
| DTFs | 0.892 | 0.838 | 12,669.483 | 8868.312 | DTFs | 0.863 | 0.803 | 11,980.313 | 8415.763 |
| SDTs | 0.294 | 0.294 | 26,447.197 | 19,776.773 | SDTs | 0.200 | 0.200 | 24,118.012 | 18,123.016 |
| TB | 0.267 | 0.257 | 27,152.242 | 18,731.501 | TB | 0.298 | 0.288 | 22,771.702 | 16,219.624 |
| MLP | 0.214 | 0.214 | 27,906.102 | 20,439.615 | MLP | 0.144 | 0.144 | 24,957.346 | 19,268.403 |
| Training Results with P(t-5) | Testing Results with P(t-5) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | R2 | NSE | RMSE | MAE | Model | R2 | NSE | RMSE | MAE |
| DTFs | 0.910 | 0.859 | 11,802.909 | 8361.152 | DTFs | 0.886 | 0.822 | 11,381.253 | 8046.244 |
| SDTs | 0.296 | 0.296 | 26,405.846 | 19,680.738 | SDTs | 0.201 | 0.201 | 24,107.606 | 18,224.162 |
| TB | 0.317 | 0.310 | 26,148.224 | 18,184.550 | TB | 0.281 | 0.267 | 23,123.848 | 16,485.957 |
| MLP | 0.234 | 0.234 | 27,556.290 | 20,657.409 | MLP | 0.161 | 0.160 | 24,719.766 | 19,027.579 |
| Training Results with P(t-9) | Testing Results with P(t-9) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | R2 | NSE | RMSE | MAE | Model | R2 | NSE | RMSE | MAE |
| DTFs | 0.943 | 0.884 | 10,728.798 | 7399.087 | DTFs | 0.934 | 0.871 | 9672.249 | 6975.412 |
| SDTs | 0.302 | 0.302 | 26,299.122 | 19,562.380 | SDTs | 0.216 | 0.216 | 23,882.899 | 17,811.067 |
| TB | 0.293 | 0.274 | 26,855.594 | 18,116.157 | TB | 0.375 | 0.359 | 21,614.152 | 15,211.614 |
| MLP | 0.230 | 0.230 | 27,622.395 | 19,999.241 | MLP | 0.117 | 0.089 | 25,938.759 | 20,903.000 |
| Training Results with P(t-10) | Testing Results with P(t-10) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | R2 | NSE | RMSE | MAE | Model | R2 | NSE | RMSE | MAE |
| DTFs | 0.945 | 0.885 | 10,671.543 | 7273.468 | DTFs | 0.940 | 0.876 | 9511.740 | 6840.659 |
| SDTs | 0.325 | 0.325 | 25,870.455 | 19,120.118 | SDTs | 0.217 | 0.217 | 23,867.600 | 17,791.516 |
| TB | 0.351 | 0.339 | 25,613.232 | 17,437.303 | TB | 0.325 | 0.308 | 22,469.118 | 15,777.656 |
| MLP | 0.215 | 0.214 | 27,903.246 | 20,319.296 | MLP | 0.145 | 0.144 | 24,965.553 | 19,058.321 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Humphries, U.W.; Ali, R.; Waqas, M.; Shoaib, M.; Varnakovida, P.; Faheem, M.; Hlaing, P.T.; Lin, H.A.; Ahmad, S. Runoff Estimation Using Advanced Soft Computing Techniques: A Case Study of Mangla Watershed Pakistan. Water 2022, 14, 3286. https://doi.org/10.3390/w14203286
Humphries UW, Ali R, Waqas M, Shoaib M, Varnakovida P, Faheem M, Hlaing PT, Lin HA, Ahmad S. Runoff Estimation Using Advanced Soft Computing Techniques: A Case Study of Mangla Watershed Pakistan. Water. 2022; 14(20):3286. https://doi.org/10.3390/w14203286
Chicago/Turabian StyleHumphries, Usa Wannasingha, Rashid Ali, Muhammad Waqas, Muhammad Shoaib, Pariwate Varnakovida, Muhammad Faheem, Phyo Thandar Hlaing, Hnin Aye Lin, and Shakeel Ahmad. 2022. "Runoff Estimation Using Advanced Soft Computing Techniques: A Case Study of Mangla Watershed Pakistan" Water 14, no. 20: 3286. https://doi.org/10.3390/w14203286







