Physical Modeling of the Scour Volume Upstream of a Slit Weir Using Uniform and Non-Uniform Mobile Beds
Abstract
:1. Introduction
2. Materials and Methods
Dimensional Analysis
3. The Experimental Work
4. Results
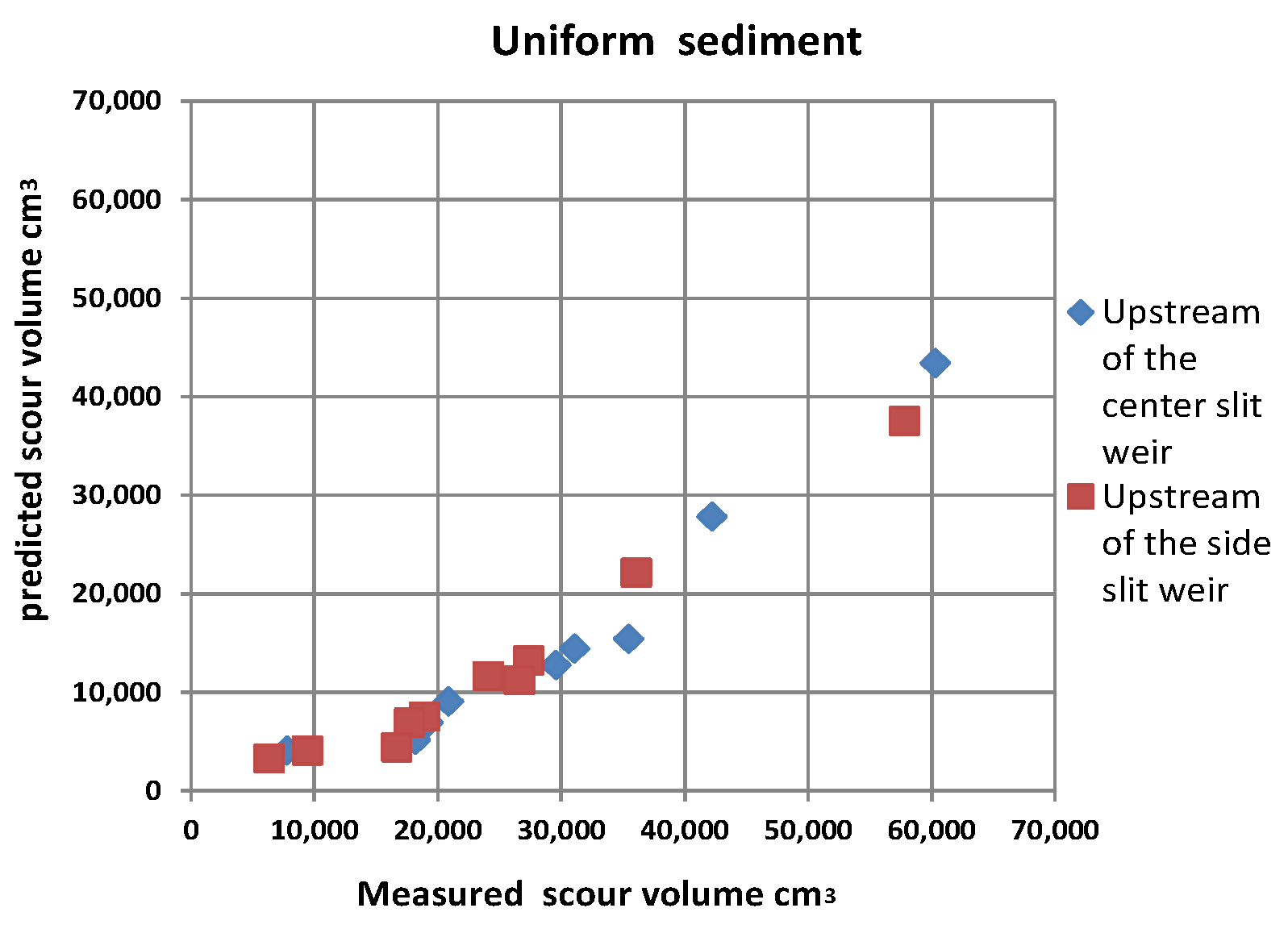
4.1. Clear Water Scour
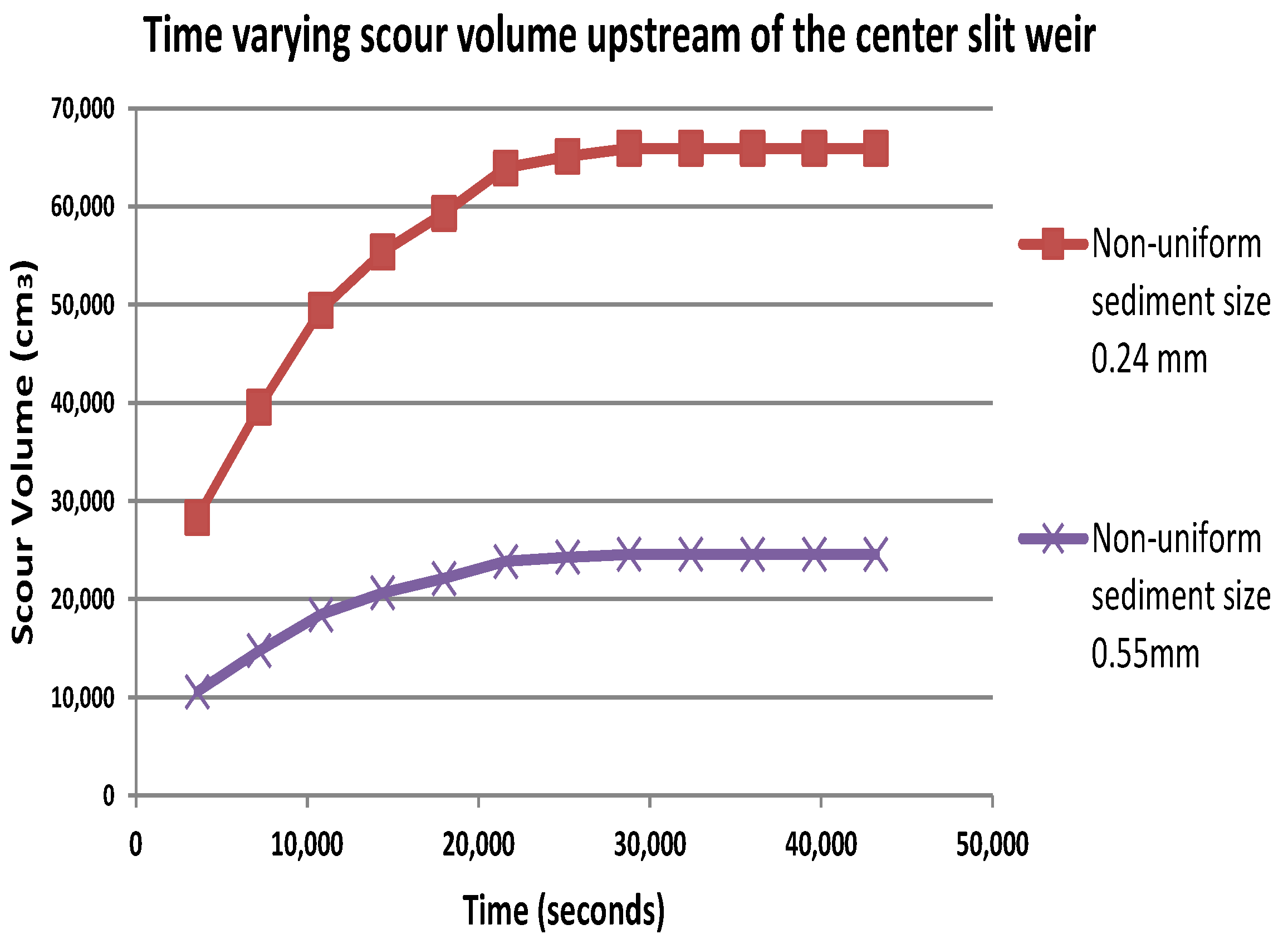
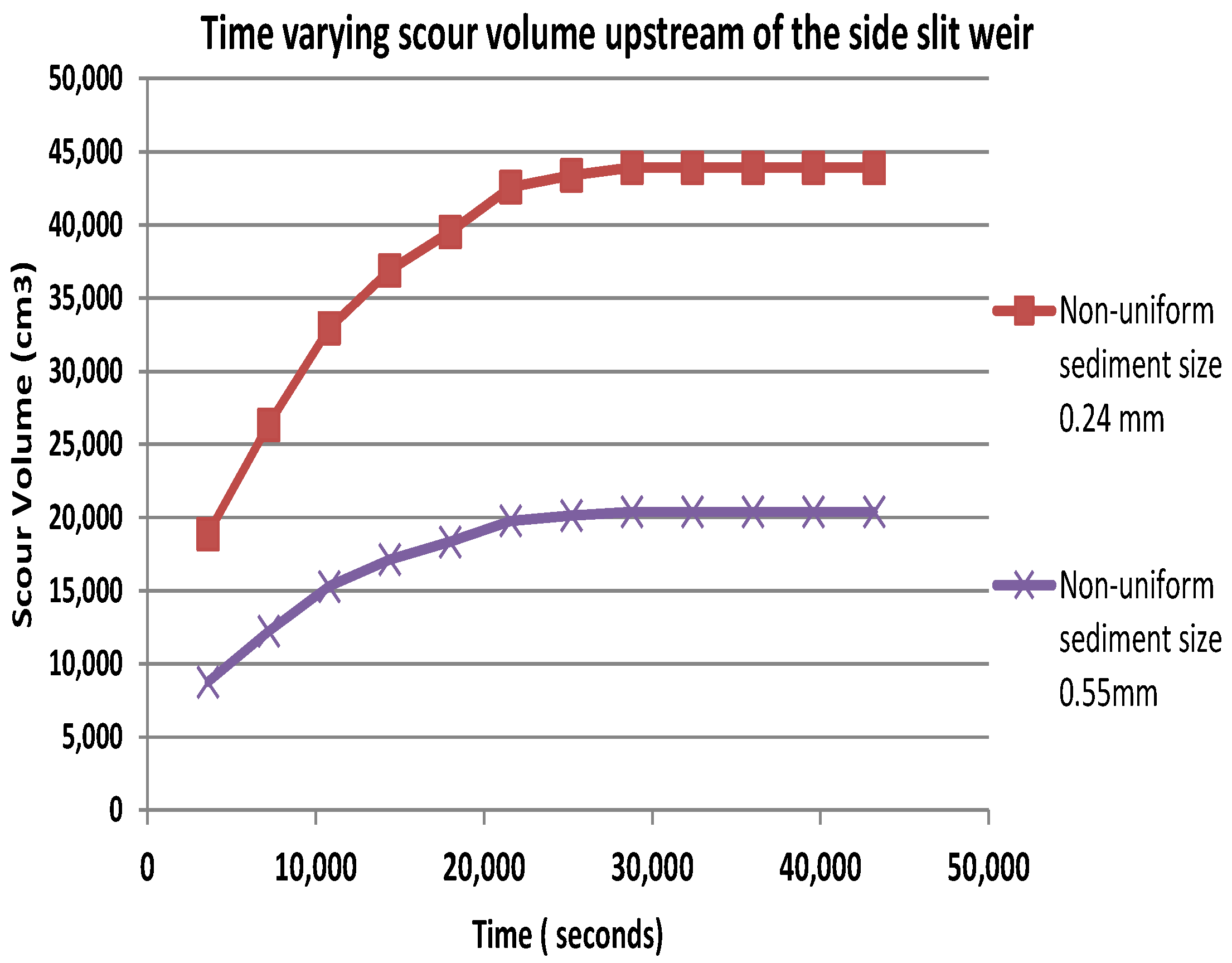
4.2. Equilibrium Scour Time
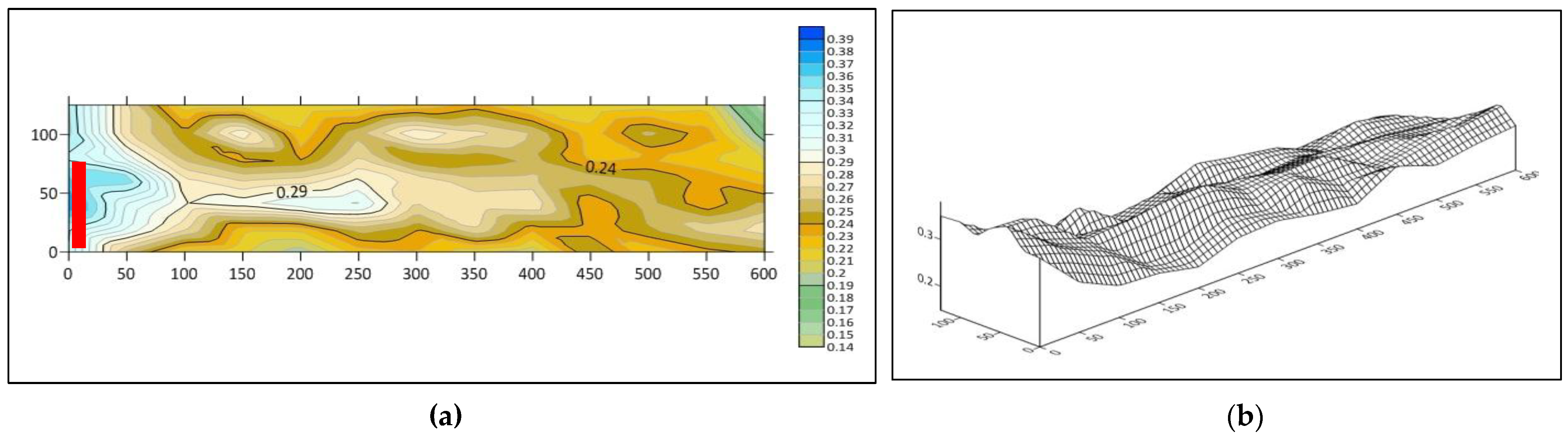
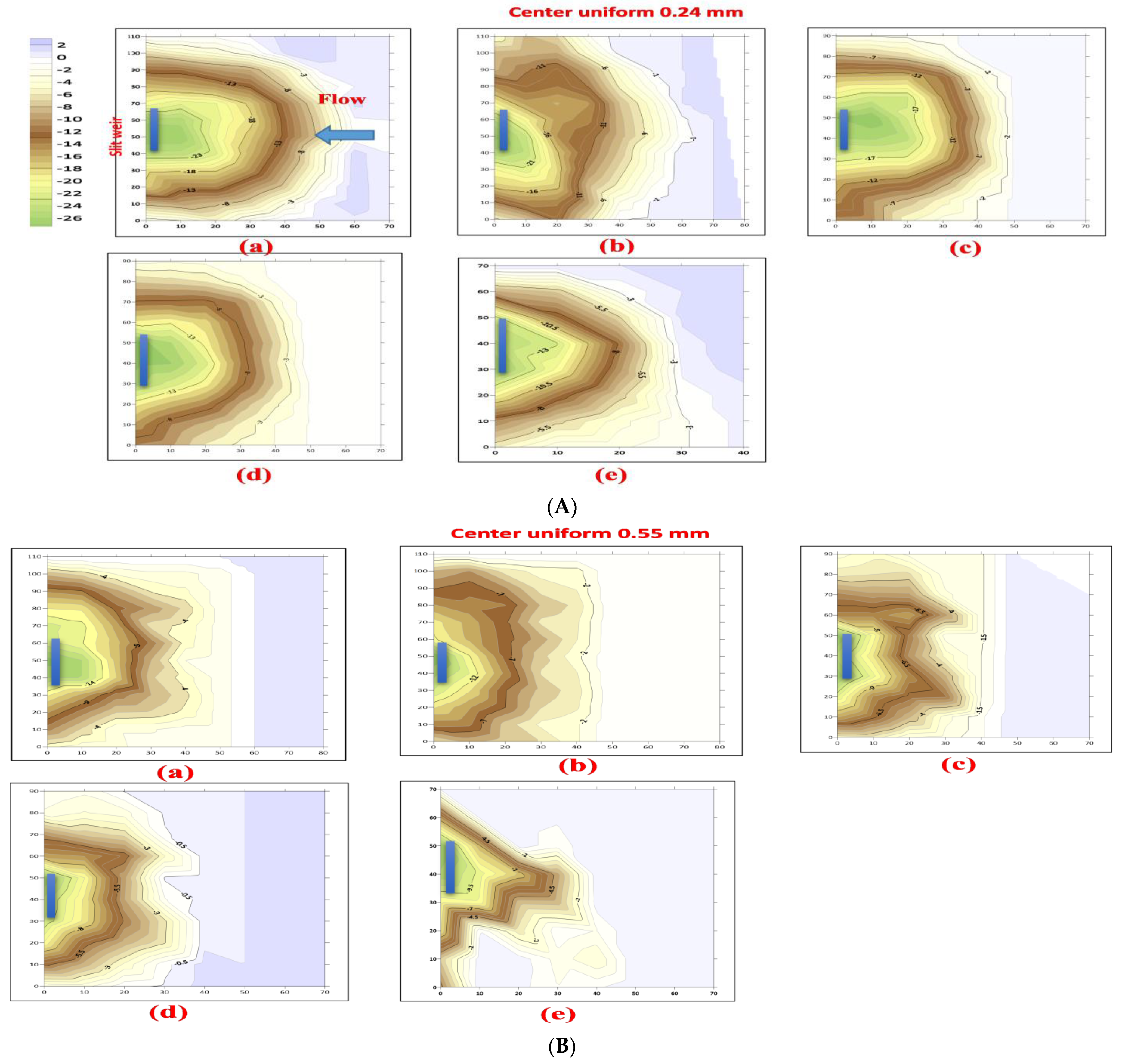
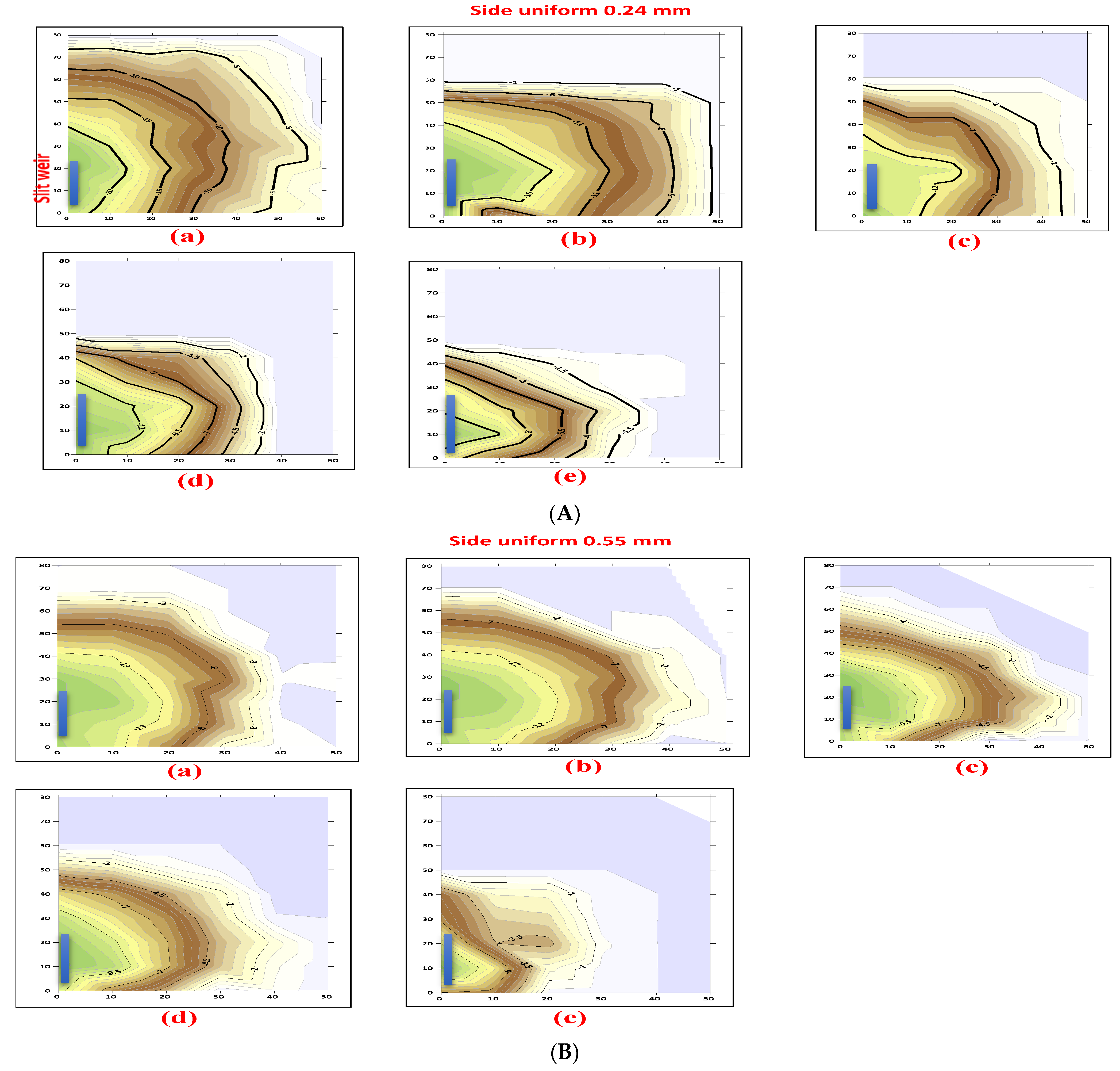
4.3. Mechanism of Scour Hole Development and Velocity Distribution
5. Conclusions
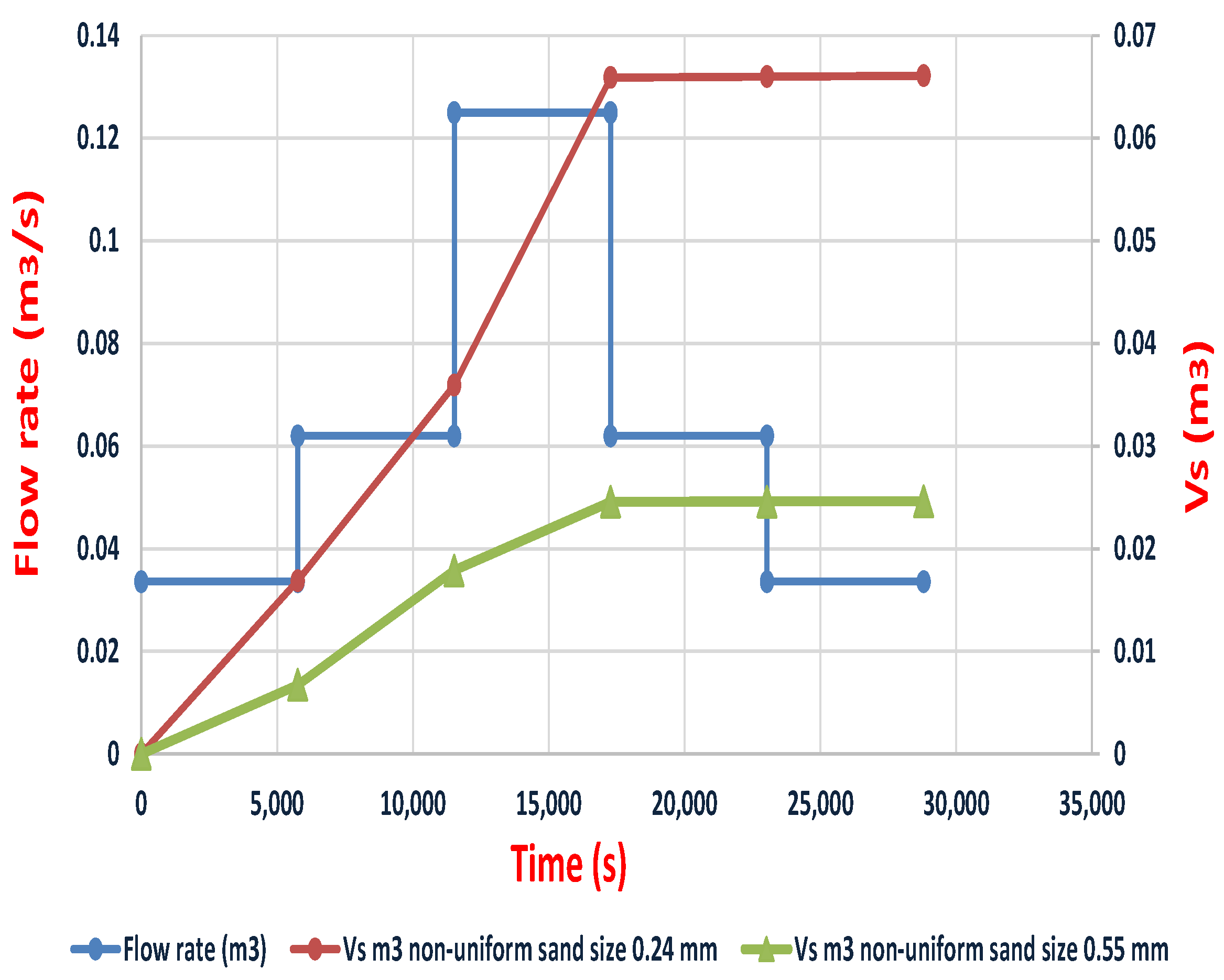
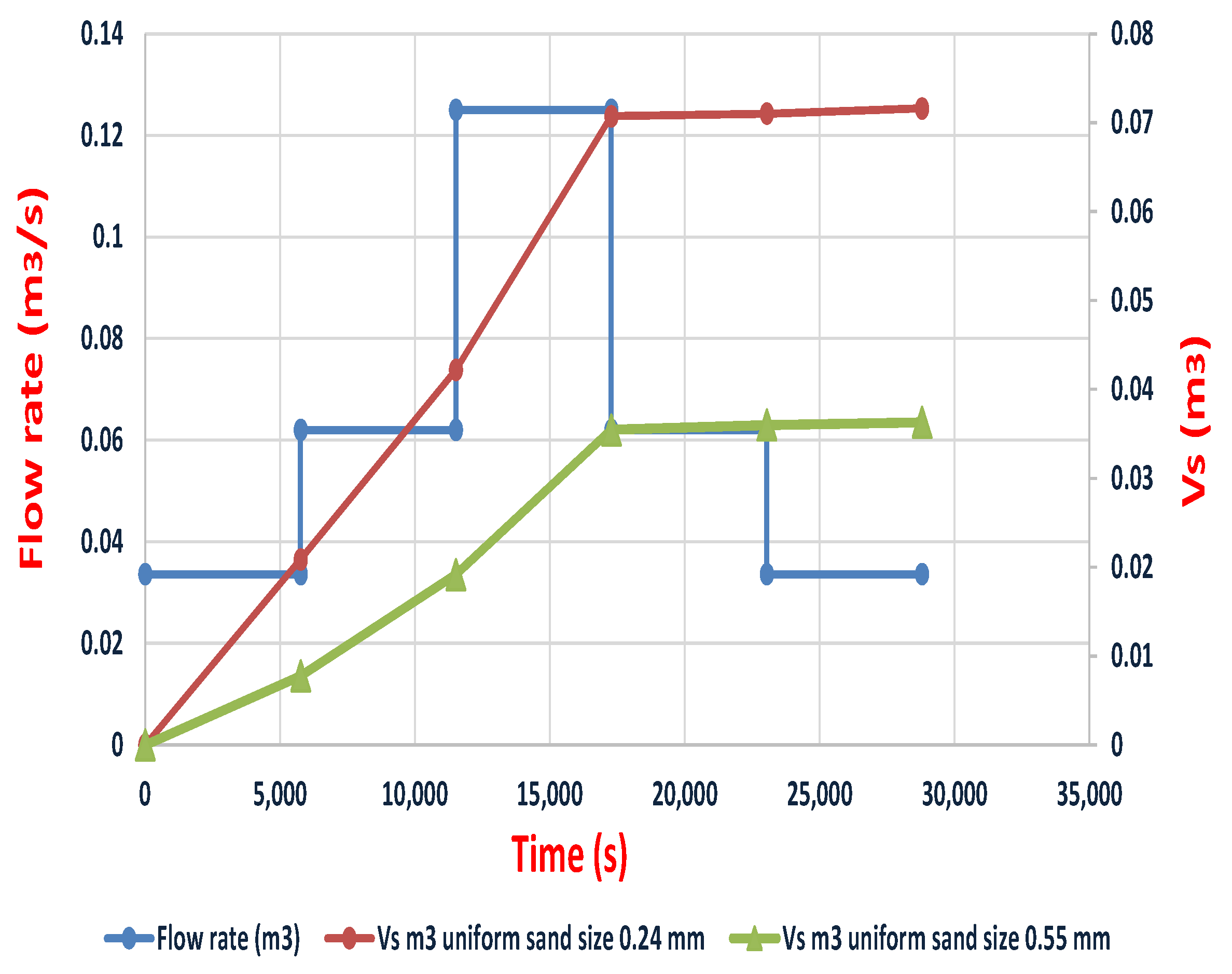
- The flow rate had a major impact on the resulting scour volume. Thus, when the flow rate increased from 34 L/s to 125 L/s, the scour volume increased 4 times for a uniform sand of size d50 = 0.24 mm at the center slit weir, and it was 3.25 when the slit was located at the side. For non-uniform sediment, the increment was 4 times for the same sand size at the center slit weir and three times at the side slit weir. The value of the increment in scour volume for uniform sediment with a median size of d50 = 0.55 mm was four times at the center slit weir. In addition, the scour volume became 4.3 times larger than the value predicted with the minimum flow rate with the side slit weir. In addition, the difference for non-uniform sediment with a sand size of d50 = 0.55 mm was 4 times at the center slit weir and 4.5 when the slit was at side of the weir.
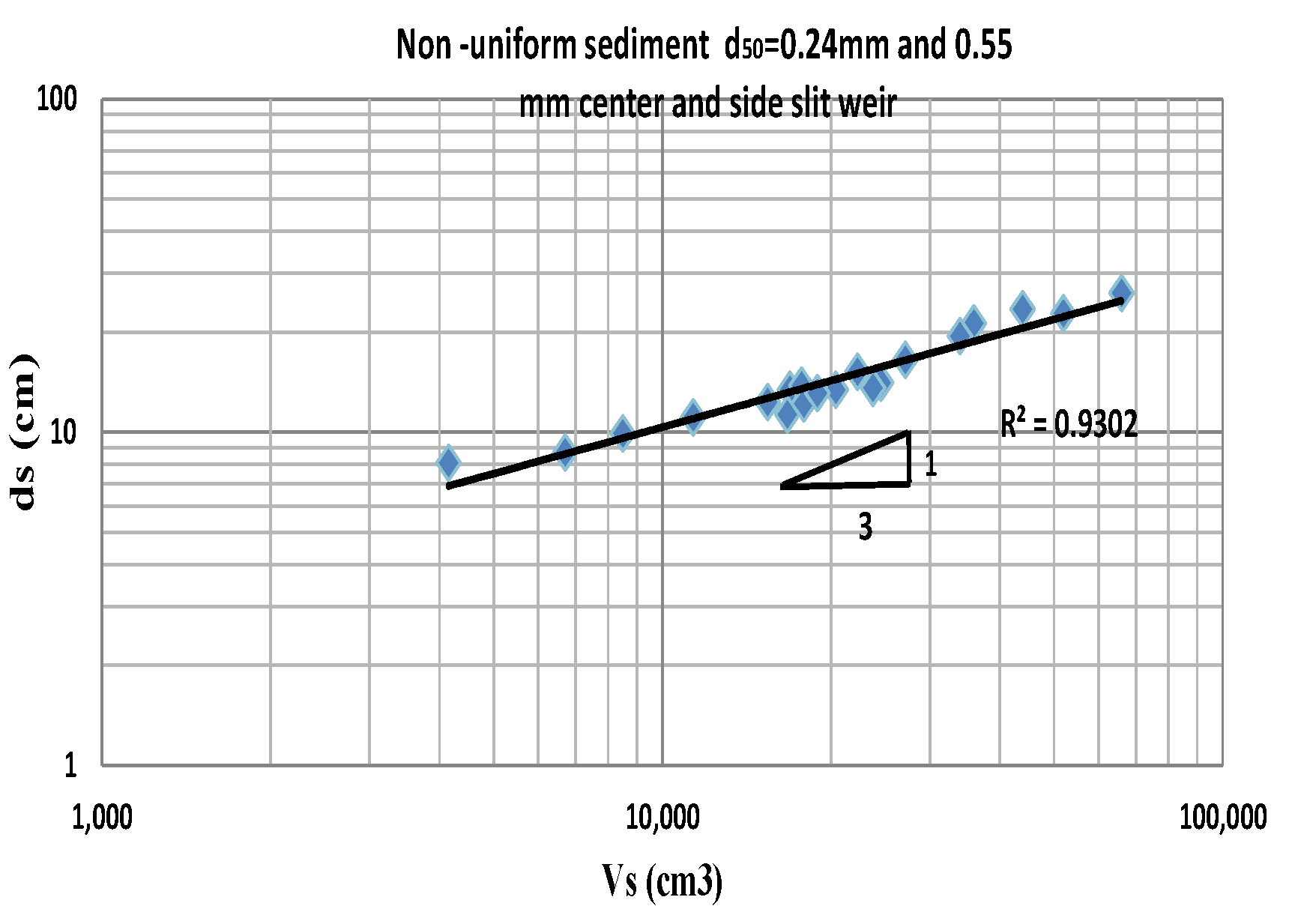
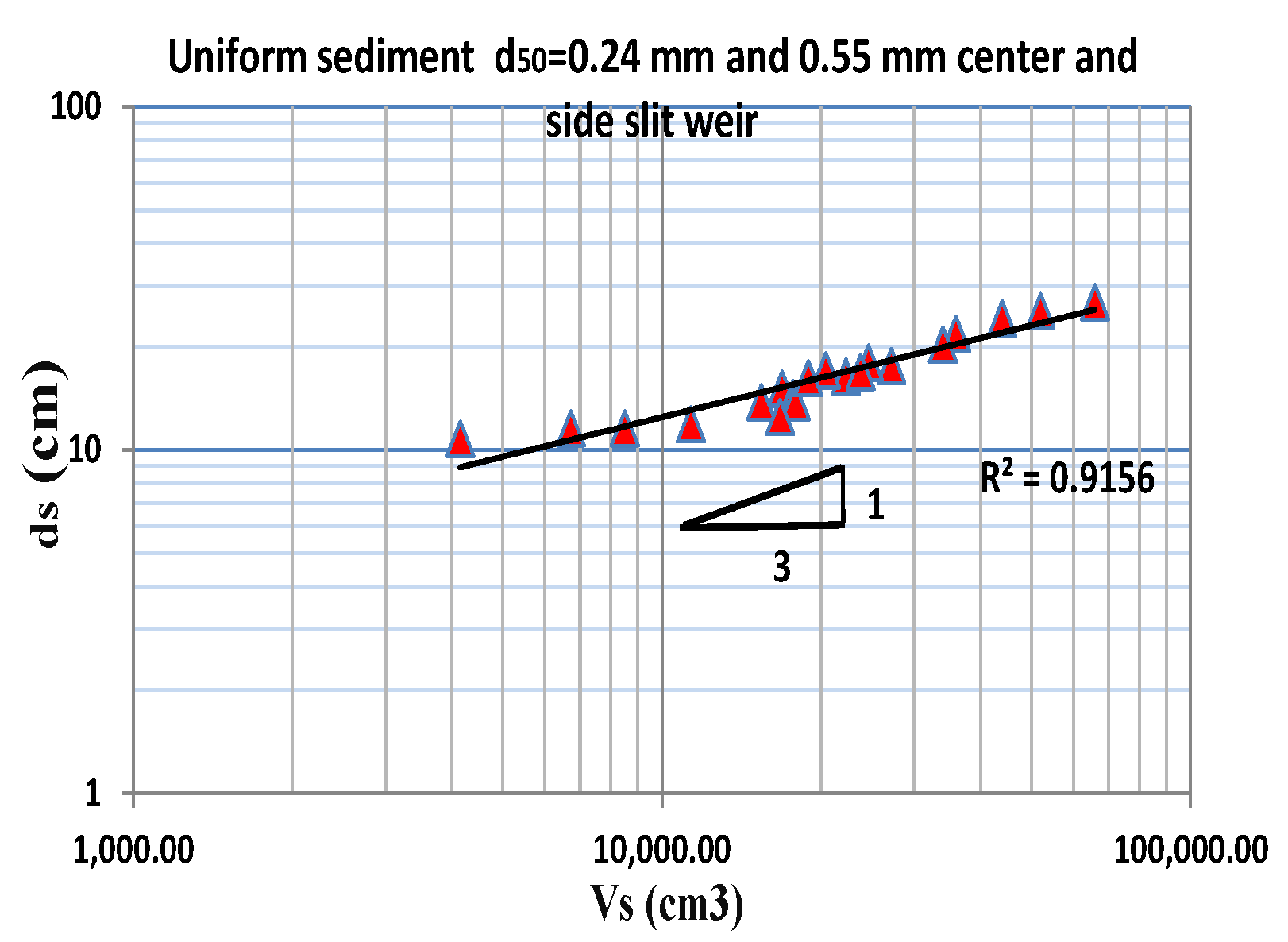
- The effect of the median particle size played an essential role in the scour volume upstream of the slit weir. However, the scour volume was recorded as 2 times higher when adopting a sediment particle size of 0.24 mm compared to the values measured with a sediment size of 0.55 mm for uniform sediment at the center and side slit weirs. In addition, the difference was 3 times for non-uniform sediment when the slit was at the center of the weir and by 2 at the side slit weir.
- The influence of sand uniformity was investigated in this research for the same sand median size. The scour volume resulted in a higher value with uniform sediment compared to the value obtained with non-uniform ones by 25% when the sediment size was 0.24 mm and 30% with d50 = 0.55 mm.
- The experimental work shows that the slit location had a governing impact on the scour volume. Higher values were recorded when the slit was positioned at the center of the weir, and the observed increment was 1.25 in the measured scour volume at the center slit weir compared to the values obtained when the slit was located at the side of the weir under the same conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| d50 | Median particle size |
| ds | Scour depth |
| Vs | Scour volume |
| hs | Slit weir height |
| hw | Weir height |
| g | Gravity acceleration |
| μ | Dynamic viscosity |
| ρ | Water density |
| ρs | Sediment density |
| B | Flume width |
| bs | Slit weir width |
| v | Flow velocity |
| va | Armor velocity |
| vc | Sediment entrainment critical velocity |
| Q | Flow rate |
| y | Flow water depth |
References
- Tundu, C.; Tumbare, M.J.; Kileshye Onema, J.-M. Sedimentation and its impacts/effects on river system and reservoir water quality: Case study of Mazowe catchment, Zimbabwe. Proc. Int. Assoc. Hydrol. Sci. 2018, 377, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Ara, Z.; Zakwan, M. Reservoir sedimentation analysis: A case study. In Proceedings of the 5th National Conference on Water, Environment & Society (NCWES-2018), JNTU, Hyderabad, India, 4–6 June 2018; pp. 247–252. [Google Scholar]
- Jaiswal, D.; Pandey, J. Impact of heavy metal on activity of some microbial enzymes in the riverbed sediments: Ecotoxicological implications in the Ganga River (India). Ecotoxicol. Environ. Saf. 2018, 150, 104–115. [Google Scholar] [CrossRef] [PubMed]
- Ota, K.; Sato, T. Experimental and numerical study of the local scour caused by sediment releasing through a dam gate. J. JSCE 2015, 3, 184–190. [Google Scholar] [CrossRef] [Green Version]
- Ota, K.; Sato, T.; Nakagawa, H. 3D numerical model of sediment transport considering transition from bed-load motion to suspension—Application to a scour upstream of a cross-river structure. J. JSCE 2016, 4, 173–180. [Google Scholar] [CrossRef] [Green Version]
- Ota, K.; Sato, T.; Arai, R.; Nakagawa, H. Local scour upstream of a slit weir: Ordinary differential equation–based model under steady and unsteady flow conditions. J. Hydraul. Eng. 2017, 143, 4016073. [Google Scholar] [CrossRef]
- Ota, K.; Sato, T.; Nakagawa, H.; Kawaike, K. Three-dimensional simulation of local scour around a weir-type structure: Hybrid euler-lagrange model for bed-material load. J. Hydraul. Eng. 2017, 143, 4016096. [Google Scholar] [CrossRef]
- Nkad, N.Z.; Mohammad, T.A.; Mohammed, H. Experimental Investigations on Scour Volume Upstream of a Slit Weir. Pertanika J. Sci. & Technol. 2022, 30, 1927–1947. [Google Scholar]
- Guan, D.; Melville, B.W.; Friedrich, H. Live-bed scour at submerged weirs. J. Hydraul. Eng. 2015, 141, 4014071. [Google Scholar] [CrossRef]
- Guan, D.; Melville, B.W.; Friedrich, H. Local scour at submerged weirs in sand-bed channels. J. Hydraul. Res. 2016, 54, 172–184. [Google Scholar] [CrossRef]
- Wang, L.; Melville, B.W.; Guan, D. Effects of upstream weir slope on local scour at submerged weirs. J. Hydraul. Eng. 2018, 144, 4018002. [Google Scholar] [CrossRef]
- Wang, L.; Melville, B.W.; Guan, D.; Whittaker, C.N. Local scour at downstream sloped submerged weirs. J. Hydraul. Eng. 2018, 144, 4018044. [Google Scholar] [CrossRef]
- Gaudio, R.; Marion, A.; Bovolin, V. Morphological effects of bed sills in degrading rivers. J. Hydraul. Res. 2000, 38, 89–96. [Google Scholar] [CrossRef]
- Marion, A.; Tregnaghi, M.; Tait, S. Sediment supply and local scouring at bed sills in high-gradient streams. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Unger, J.; Hager, W.H. Down-flow and horseshoe vortex characteristics of sediment embedded bridge piers. Exp. Fluids 2007, 42, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Najafzadeh, M.; Barani, G.-A. Experimental study of local scour around a vertical pier in cohesive soils. Sci. Iran. 2014, 21, 241–250. [Google Scholar]
- Ghodsi, H.; Najafzadeh, M.; Khanjani, M.J.; Beheshti, A. Effects of different geometric parameters of complex bridge piers on maximum scour depth: Experimental study. J. Waterw. Port Coast. Ocean. Eng. 2021, 147, 4021021. [Google Scholar] [CrossRef]
- Amini, A.; Hamidi, S.; Shirzadi, A.; Behmanesh, J.; Akib, S. Efficiency of artificial neural networks in determining scour depth at composite bridge piers. Int. J. River Basin Manag. 2021, 19, 327–333. [Google Scholar] [CrossRef]
- Zumrawi, M.M.E.; Abusim, H.A. A Study on Scour Failure at Bridge Foundation. Univ. Khartoum Eng. J. 2020, 9, 12–17. [Google Scholar]
- Truce, B.A. Estimation of Clear-Water Local Scour at Pile Groups Using Genetic Expression Programming (GEP) and Multivariate Adaptive Regression Splines (MARS); University of Hawaiʻi at Mānoa: Honolulu, HI, USA, 2017. [Google Scholar]
- Dey, S.; Barbhuiya, A.K. Velocity and turbulence in a scour hole at a vertical-wall abutment. Flow Meas. Instrum. 2006, 17, 13–21. [Google Scholar] [CrossRef]
- Dey, S.; Barbhuiya, A.K. 3D flow field in a scour hole at a wing-wall abutment. J. Hydraul. Res. 2006, 44, 33–50. [Google Scholar] [CrossRef]
- Abdollahpour, M.; Dalir, A.H.; Farsadizadeh, D.; Gualtieri, C. Experimental study on erosion and sedimentation patterns downstream of a W-weir in a sinusoidal mild bend. Water 2017, 9, 638. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Liu, Z.; Wang, T.; Fu, H.; Li, J.; Xia, Q.; Guo, Y. Discharge capacity evaluation and hydraulic design of a piano key weir. Water Supply 2019, 19, 871–878. [Google Scholar] [CrossRef]
- Khalili, M.; Honar, T. Discharge coefficient of semi-circular labyrinth side weir in subcritical flow. Water SA 2017, 43, 433–441. [Google Scholar] [CrossRef]
- Powell, D.N.; Khan, A.A. Scour upstream of a circular orifice under constant head. J. Hydraul. Res. 2012, 50, 28–34. [Google Scholar] [CrossRef]
- Lauchlan, C. Experimental investigation of bed-load and suspended-load transport over weirs. J. Hydraul. Res. 2004, 42, 551–558. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, Y.; Yang, Y.; Shi, B.; Wu, X. Scale model experiment on local scour around submarine pipelines under bidirectional tidal currents. J. Mar. Sci. Eng. 2021, 9, 1421. [Google Scholar] [CrossRef]
- Fathi-Moghadam, M.; Emamgholizadeh, S.; Bina, M.; Ghomeshi, M. Physical modelling of pressure flushing for desilting of non-cohesive sediment. J. Hydraul. Res. 2010, 48, 509–514. [Google Scholar] [CrossRef]
- Featherstone, R.E.; Nalluri, C. Civil Engineering Hydraulics: Essential Theory with Worked Examples; Colllins Professional and Technical Books: London, UK, 1982; ISBN 0-00-383245-7. [Google Scholar]
- Melville, B.W.; Coleman, S.E. Bridge Scour; Water Resources Publication, LLC: Highlands Ranch, CO, USA, 2011; ISBN 1-887-201-18-1. [Google Scholar]
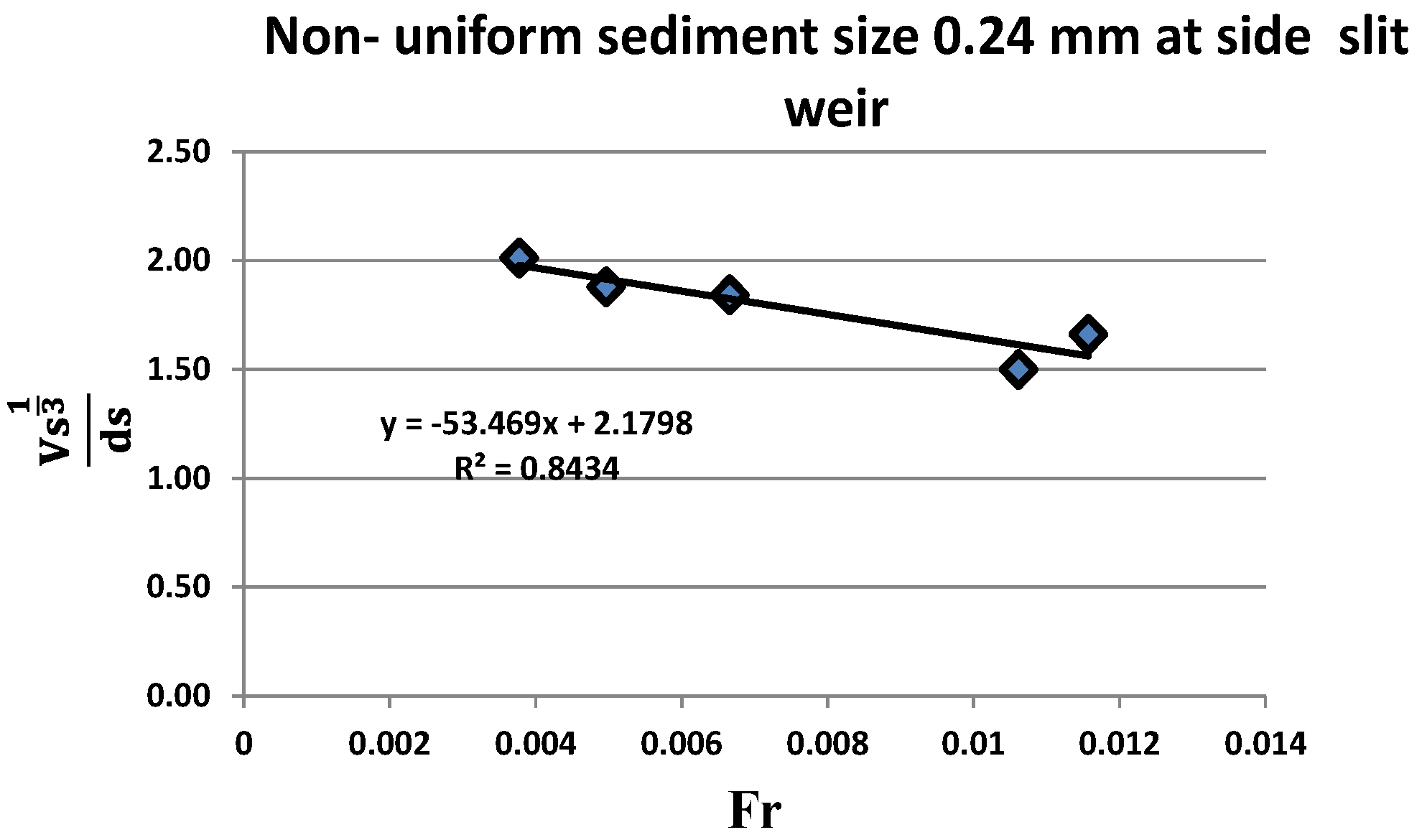
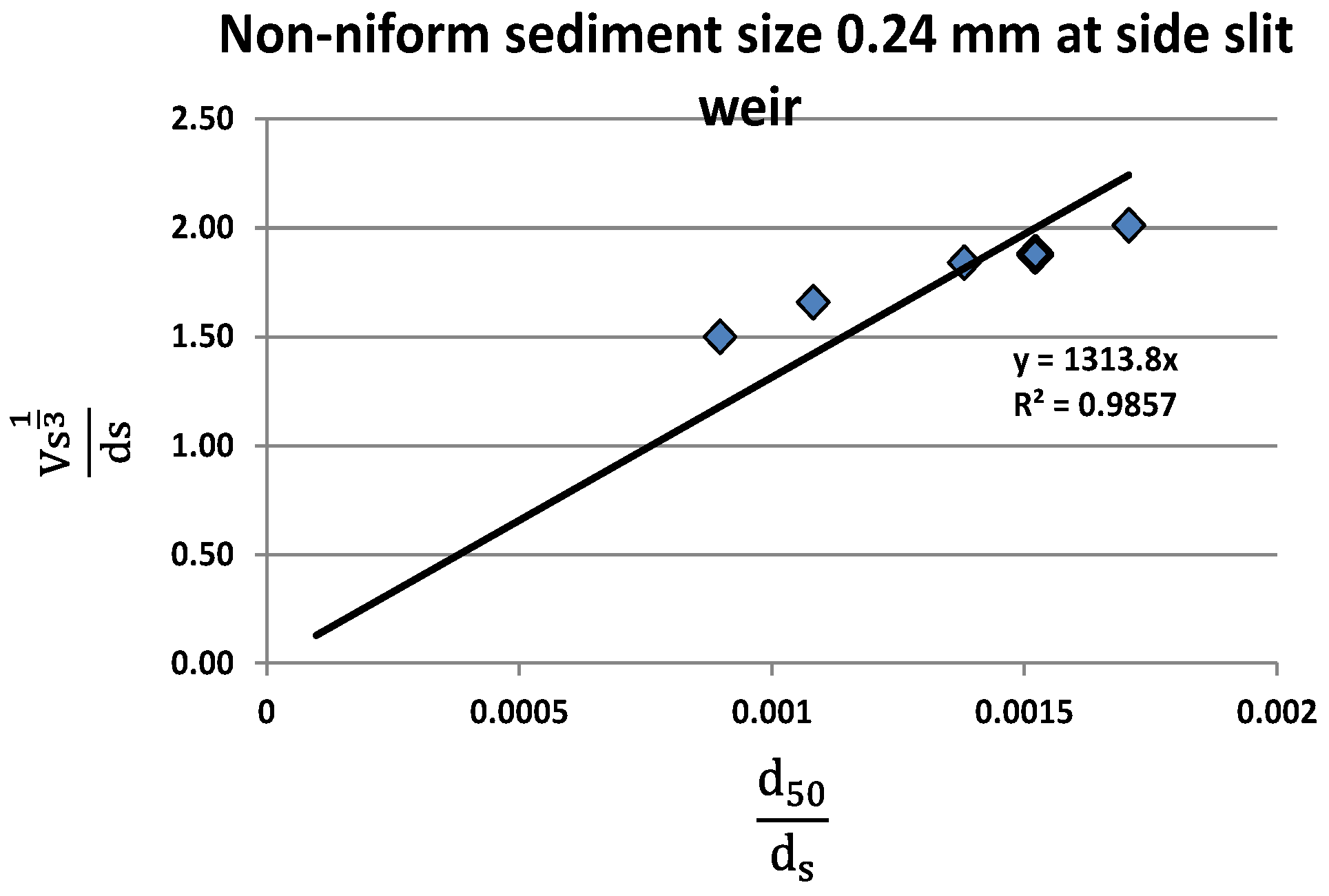
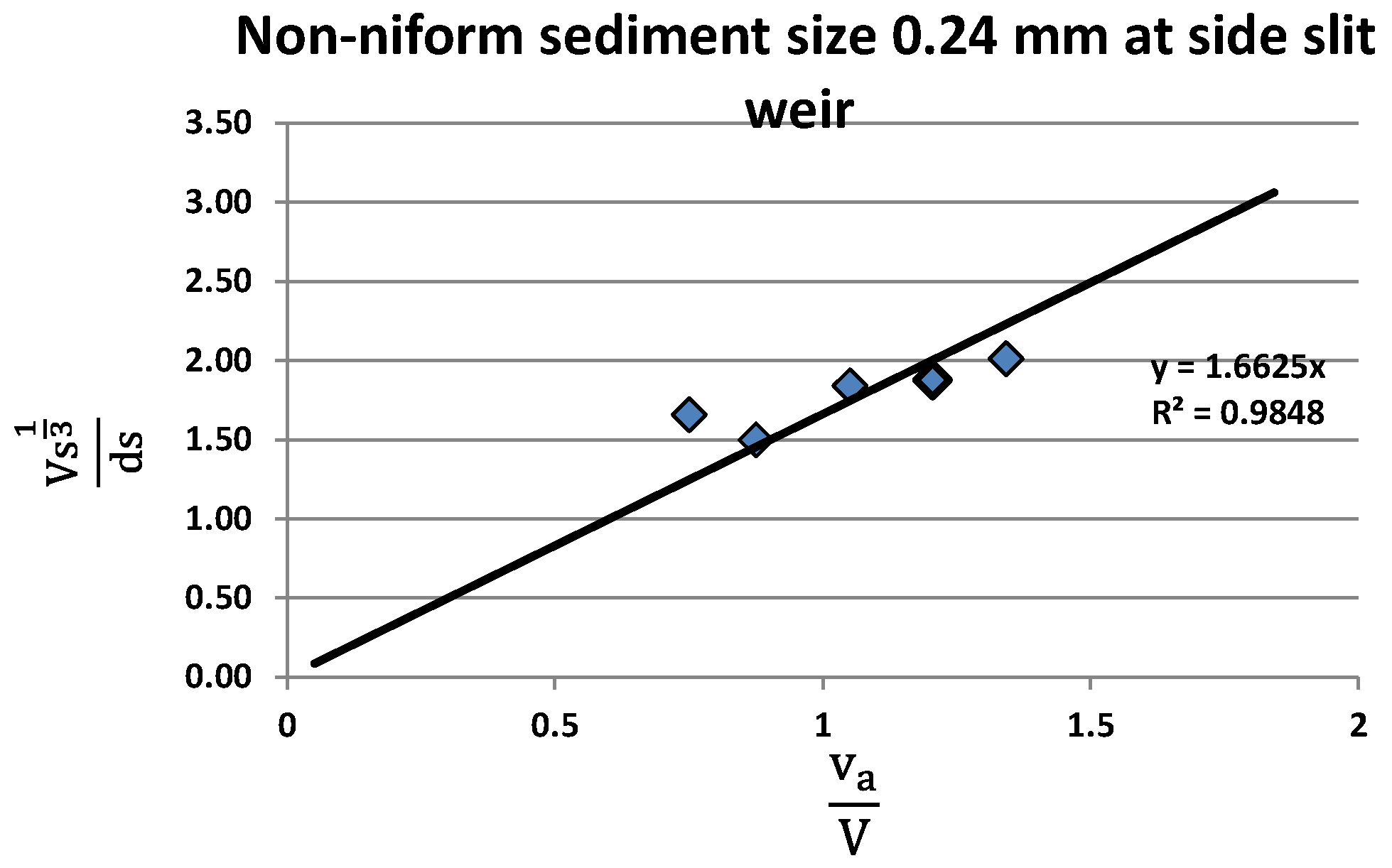
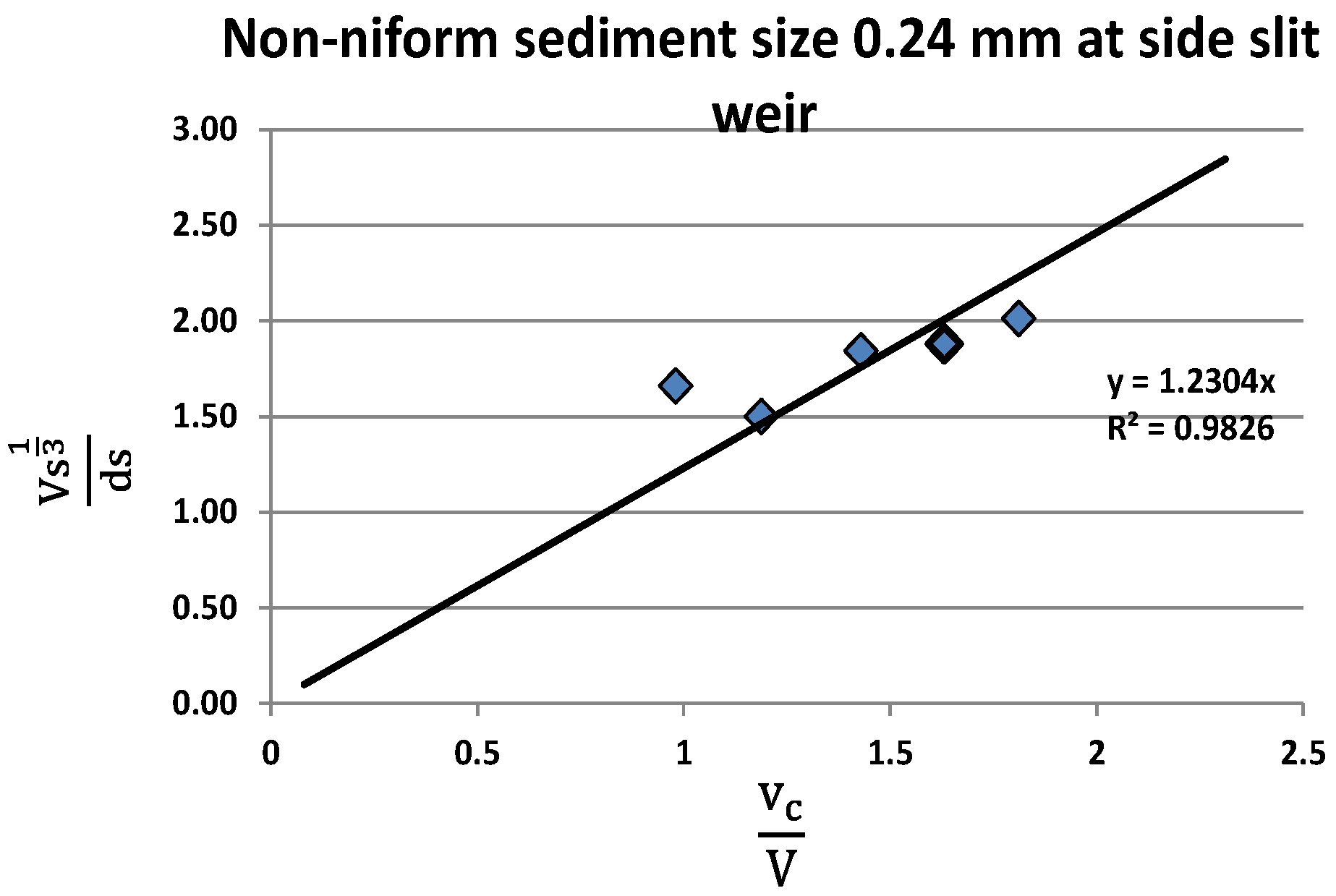
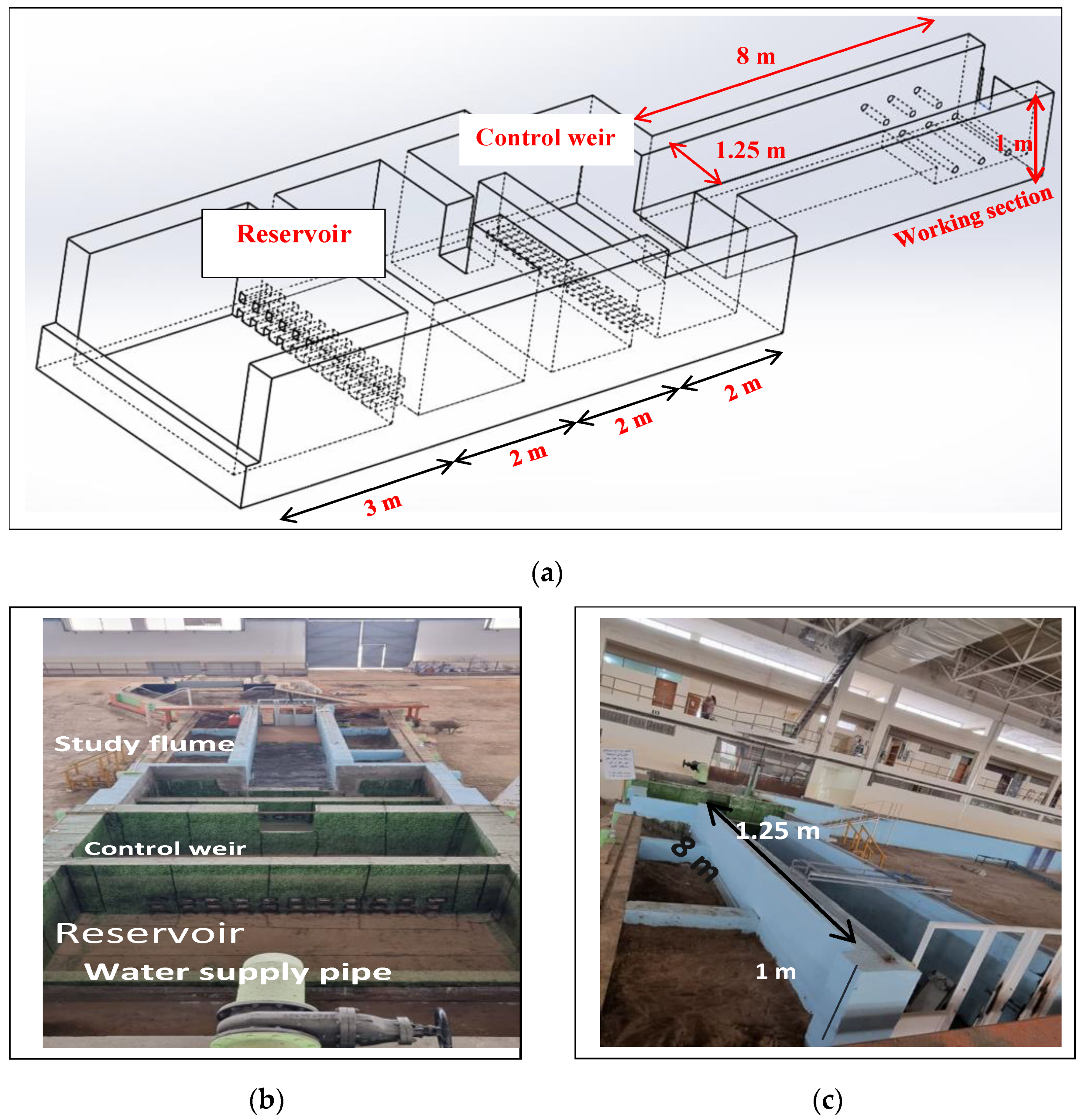













| Author | Nature of Study | Main Findings |
|---|---|---|
| Scour development upstream and around slit weirs | ||
| Ota and Sato [4] | Sediment releasing through a dam gate | Simulated the scour process around a slit weir experimentally and numerically by a 3D numerical analysis based on Reynolds-averaged Navier–Stokes (RANS) equations coupled with the VOF method and the k-ꭃ SST turbulence closure model. |
| Ota [5] | 3D numerical model for a scour around a slit weir | Updated the study of Ota and Sato (2015) to reproduce the resulting scour around a slit weir. |
| Ota [6] | Ordinary differential equation model for the scour upstream of a slit weir | Investigation of time varying scour volume and maximum scour depth generating upstream of a slit weir under steady and unsteady conditions by adopting an ordinary differential-equation-based model. |
| Ota [7] | 3D simulation for the scour upstream of a slit weir | Suggested 3D hybrid Euler–Lagrange model for a bed-material load considering transitions between the bed load and suspended load to accurately reproduce the scour around the slit weir. |
| Nkad [8] | Scour volume upstream of a slit weir | The scour volume and maximum scour depth were investigated experimentally on the upstream side of a slit weir under steady flow, clear-water scour conditions and non-uniform sedimentation. |
| Scour development upstream and downstream of a submerged weir | ||
| Guan [9,10] | Scour investigation upstream and downstream of a submerged weir | The scour was investigated experimentally upstream and downstream of submerged weirs within live-bed scour conditions. New equations, including the effects of sediment size, flow intensity and weir geometry are proposed for the prediction of equilibrium scour depths, and a new design method is given for estimating the maximum scour depths at the weir. |
| Wang [11,12] | Local scour at the submerged weir | Experimentally studied the effect of different slopes downstream and upstream of a submerged weir on the scour within numerous scenarios for fine and coarse sediments under clear and live-bed scour conditions. The study presents a new technique for investigating the maximum scour depth and the correlation between average and maximum scour depth. |
| Local scour at bed sill | ||
| Gaudio [13] | Local scour downstream of a bed sill | Experimentally studied the influence of morphology on the scour downstream of a bed sill within a gravel bed with a classical dimensional analysis. The study presents numerical formulas for estimating scour depth, scour hole length and the location of the maximum scour depth. |
| Marion [14] | Local scour at the bed still in high-gradient streams | Experimentally predicted the effect of steady releases of sedimentation under clear water conditions on scour depth and shape, created at the toe of the bed sills. |
| Scour around bridge piers | ||
| Hager [15] | Horseshoe vortex of sediment-embedded bridge piers | Experimentally investigated the flow features around a circular bridge pier. The study presents novel data for numerical simulations. |
| Najafzadeh [16] | Local scour around a vertical pier in cohesive soils | An experimental work was carried out to predict the maximum scour depth generated around bridge piers under various governing parameters. The study presents a general scour depth equation and compares it with an empirical scour depth equation, and both are in good agreement. |
| Ghodsi [17] | The geometric effect of complex bridge piers on the maximum scour depth | Eighty-two laboratory tests within six physical models were adopted to study pier geometry as the affecting parameter the on maximum scour depth. A dimensional analysis was carried out, and the study results clarify that each individual parameter impacts the maximum scour depth. |
| Amini, Magdi and Truce [18,19,20] | Bridge scour | The majority of published studies are focused on bridge scour. |
| Scour around different weir types and sediment-release techniques | ||
| Dey and Barbhuiya [21,22] | Flow field in scour hole at a vertical and wing wall abutment | An experimental study was conducted to investigate the local scour and 3D flow parameters in a vertical and wing wall abutment within a clear water scour. |
| Abdollahpour [23] | Erosion and sedimentation downstream of a W-weir | Experimentally studied the effect of a W-weir structure on the erosion and sedimentation of a sinusoidal channel. |
| Liu [24] | Piano key weir | The PKW performance was evaluated and analyzed with new formulas for efficient discharge release. |
| Khalili and Honar [25] | Simi-circular labyrinth side weir | An experimental study was conducted, evaluating a semi-circular labyrinth side weir to investigate the effect of the structure geometry on the flow intensity coefficients. |
| Powell and Khan [26] | Scour upstream of a circular orifice | Investigated the sediment transport mechanism and the scour area, depth and shape upstream of a circular orifice. The investigation was conducted under steady flow conditions with different sediment sizes and heads on the orifice. |
| Lauchlan [27] | Sediment transportation over weirs | Sediment transport was experimentally predicted with steep-slope weirs and dikes, including both the bed load and the suspended load. |
| Zhang [28] | Local scour around submarine pipelines | An experimental work is proposed with empirical equations for accurate live bed scour predictions around submarine pipelines. |
| Fathi-Moghadam [29] | Desilting of non-cohesive sediment | An experimental work is presented with numerical equations used to predict the scour cone depth and volume generated throughout the flushing process from dam intake. |
| No. | Weir Location | Weir Dimensions Width (cm) × Height (cm) | Q (L/s) | Sediment Type | d50 (mm) | No. of Runs |
|---|---|---|---|---|---|---|
| Steady condition | ||||||
| 1 | Center | 25 × 60 | 125.0, 95.0, 62.0, 50.0, and 34.0 | Uniform | 0.24 | 5 |
| 2 | Center | 25 × 60 | 125.0, 95.0, 62.0, 50.0, and 34.0 | Uniform | 0.55 | 5 |
| 3 | Center | 25 × 60 | 125.0, 95.0, 62.0, 50.0, and 34.0 | Non- uniform | 0.24 | 5 |
| 4 | Center | 25 × 60 | 125.0, 95.0, 62.0, 50.0, and 34.0 | Non- uniform | 0.55 | 5 |
| 5 | Side | 25 × 60 | 125.0, 95.0, 62.0, 50.0, and 34.0 | Uniform | 0.24 | 5 |
| 6 | Side | 25 × 60 | 125.0, 95.0, 62.0, 50.0, and 34.0 | Uniform | 0.55 | 5 |
| 7 | Side | 25 × 60 | 125.0, 95.0, 62.0, 50.0, and 34.0 | Non- uniform | 0.24 | 5 |
| 8 | Side | 25 × 60 | 125.0, 95.0, 62.0, 50.0, and 34.0 | Non- uniform | 0.55 | 5 |
| Unsteady condition | ||||||
| 9 | Center | 25 × 60 | 125.0, 62.0, 34.0 | Uniform and non- uniform | 0.24 | 2 |
| 10 | Center | 25 × 60 | 125.0, 62.0, 34.0 | Uniform and non- uniform | 0.55 | 2 |
| Total number of test runs | 44 | |||||
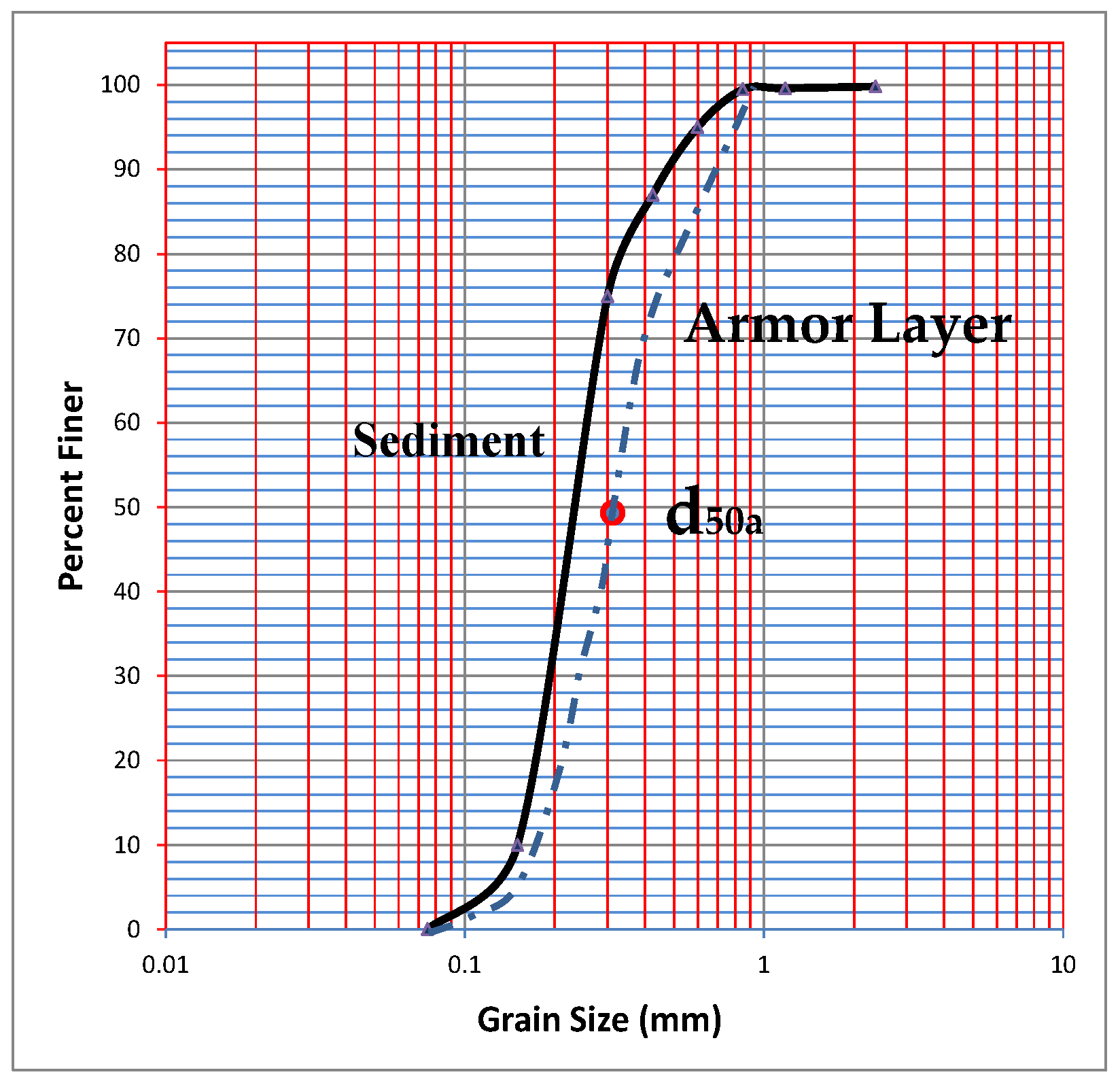
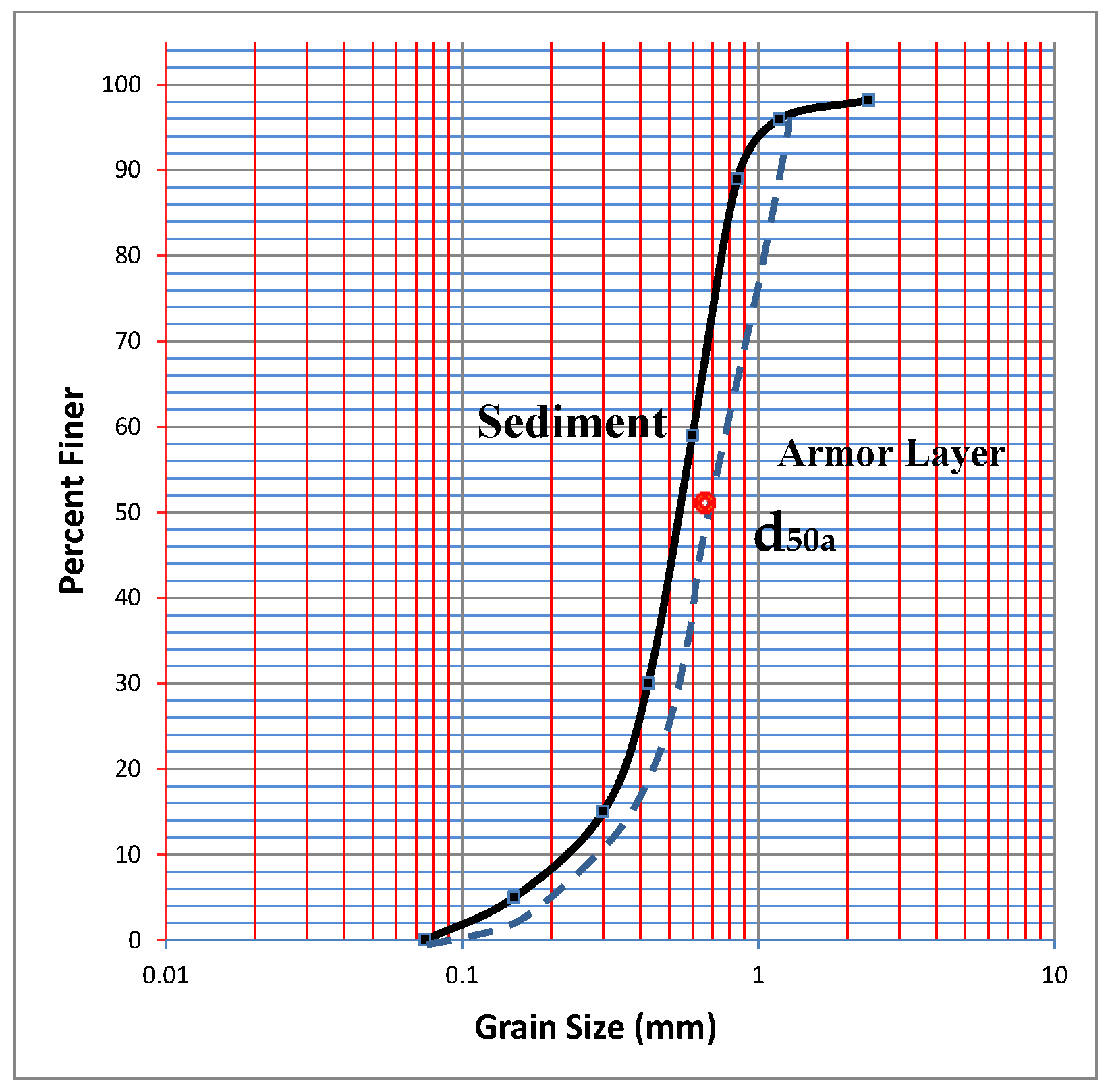
| Sand Type | d84 (mm) | d50 (mm) | d16 (mm) | σg | dmax (mm) | d50a (mm) | Bulk Density (kg/m3) |
|---|---|---|---|---|---|---|---|
| Uniform sand | 0.28 | 0.24 | 0.17 | 1.28 | 0.3 | - | 1349 |
| Uniform sand | 0.72 | 0.55 | 0.45 | 1.26 | 0.8 | - | 1436 |
| Non- uniform sand | 0.4 | 0.24 | 0.16 | 1.55 | 0.5 | 0.3 | 1315 |
| Non- uniform sand | 0.81 | 0.55 | 0.31 | 1.6 | 0.9 | 0.5 | 1518 |
| No. | Scenario | Side Opening d50 = 0.24 mm | Center Opening d50 = 0.24 mm | ||
|---|---|---|---|---|---|
| Flat crest | Uniform sand | Non-uniform sand | Uniform sand | Non-uniform sand | |
| Scour hole dimensions (x × y) cm | Scour hole dimensions (x × y) cm | Scour hole dimensions (x × y) cm | Scour hole dimensions (x × y) cm | ||
| 1 | Q = 125 L/s | 60 × 70 | 50 × 70 | 60 × 110 | 57 × 110 |
| 2 | Q = 95 L/s | 40 × 50 | 40 × 50 | 56 × 110 | 47 × 110 |
| 3 | Q = 62 L/s | 40 × 50 | 40 × 50 | 42 × 90 | 40 × 80 |
| 4 | Q = 50 L/s | 40 × 40 | 40 × 40 | 53 × 90 | 40 × 70 |
| 5 | Q = 34 L/s | 40 × 40 | 32 × 40 | 40 × 70 | 35 × 60 |
| No. | Scenario | Side Opening d50 = 0.55 mm | Center Opening d50 = 0.55 mm | ||
|---|---|---|---|---|---|
| Flat crest | Uniform sand | Non-uniform sand | Uniform sand | Non-uniform sand | |
| Scour hole dimensions (x × y) cm | Scour hole dimensions (x × y) cm | Scour hole dimensions (x × y) cm | Scour hole dimensions (x × y) cm | ||
| 1 | Q = 125 L/s | 37 × 70 | 26 × 70 | 40 × 100 | 40 × 100 |
| 2 | Q = 95 L/s | 37 × 70 | 25 × 60 | 40 × 100 | 35 × 100 |
| 3 | Q = 62 L/s | 36 × 50 | 25 × 60 | 40 × 90 | 35 × 90 |
| 4 | Q = 50 L/s | 36 × 50 | 24 × 50 | 40 × 90 | 32 × 90 |
| 5 | Q = 34 L/s | 32 × 50 | 21 × 50 | 32 × 70 | 24 × 70 |
| Gaudio [13] | Marion [14] | Guan [10] | Wang [11] | Ota [6] | Nkad [8] | This Study | |
|---|---|---|---|---|---|---|---|
| Type of structure | Bed sills | Bed sills | Submerged weir | Submerged weir | Slit weir | Slit weir | Slit weir |
| Flowrate L/s | 45–81 | 18, 22, 26 | 15–86 | 12–89.3 | 7.2 | 2.6–8 | 34–125 |
| Sediment size d50 mm | 4.1, 8.5/uniform | 8.7 uniform | 0.26, 0.85 uniform | 0.26, 0.85 uniform | 0.22, 0.77, 1/uniform | 0.3, 0.7 non- uniform | 0.24, 0.55 uniform and non- uniform |
| Number of tests | 19 | 48 | 37 | 62 | 33 | 6 | 44 |
| Flume dimensions m | 2.44 wide and 0.6 deep | 10 long, 0.5 wide and 0.5 deep | 12 long, 0.44 wide and 0.58 deep | 12 long, 0.44 wide and 0.38 deep | 10.5 long, 0.5 wide and 0.35 deep | 12 long, 0.3 wide and 0.3 deep | 8 long, 1.25 wide and 1 deep |
| Bed slope% | 0.0120–0.0018 | 0.042–0.041 | 0.0009–0.008 | 0.0004–0.0074 | Flat bed | Flat bed with ramp of 1:10 | Flat bed |
| Flow depth cm | 9–14 | - | 12–17.4 | 15–18 | 3.6–18 | 11.1–21.1 | 18–38 |
| Flow velocity m/s | 0.69–0.921 | Specific energy = water depth + 7.8–10.1 | 0.281–1.124 | 0.185–1.166 | 0.13 | 0.05–0.240 | 0.15–0.26 |
| Fr | 0.64–0.95 | 1.06–1.44 | 0.13–0.88 | 0.13–0.89 | 0.17 | 0.04–0.16 | 0.112–0.148 |
| Maximum scour depth cm | 25.8 | 28.8 | 15.5 | 16.5 | 9.2 | 4.2 | 27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamdan, R.K.; Al-Adili, A.; Mohammed, T.A. Physical Modeling of the Scour Volume Upstream of a Slit Weir Using Uniform and Non-Uniform Mobile Beds. Water 2022, 14, 3273. https://doi.org/10.3390/w14203273
Hamdan RK, Al-Adili A, Mohammed TA. Physical Modeling of the Scour Volume Upstream of a Slit Weir Using Uniform and Non-Uniform Mobile Beds. Water. 2022; 14(20):3273. https://doi.org/10.3390/w14203273
Chicago/Turabian StyleHamdan, Ruaa Khalid, Aqeel Al-Adili, and Thamer Ahmed Mohammed. 2022. "Physical Modeling of the Scour Volume Upstream of a Slit Weir Using Uniform and Non-Uniform Mobile Beds" Water 14, no. 20: 3273. https://doi.org/10.3390/w14203273
APA StyleHamdan, R. K., Al-Adili, A., & Mohammed, T. A. (2022). Physical Modeling of the Scour Volume Upstream of a Slit Weir Using Uniform and Non-Uniform Mobile Beds. Water, 14(20), 3273. https://doi.org/10.3390/w14203273






