1. Introduction
Long-distance water transfer project is an important approach to effectively solve the water shortage problem in large- and medium-sized cities [
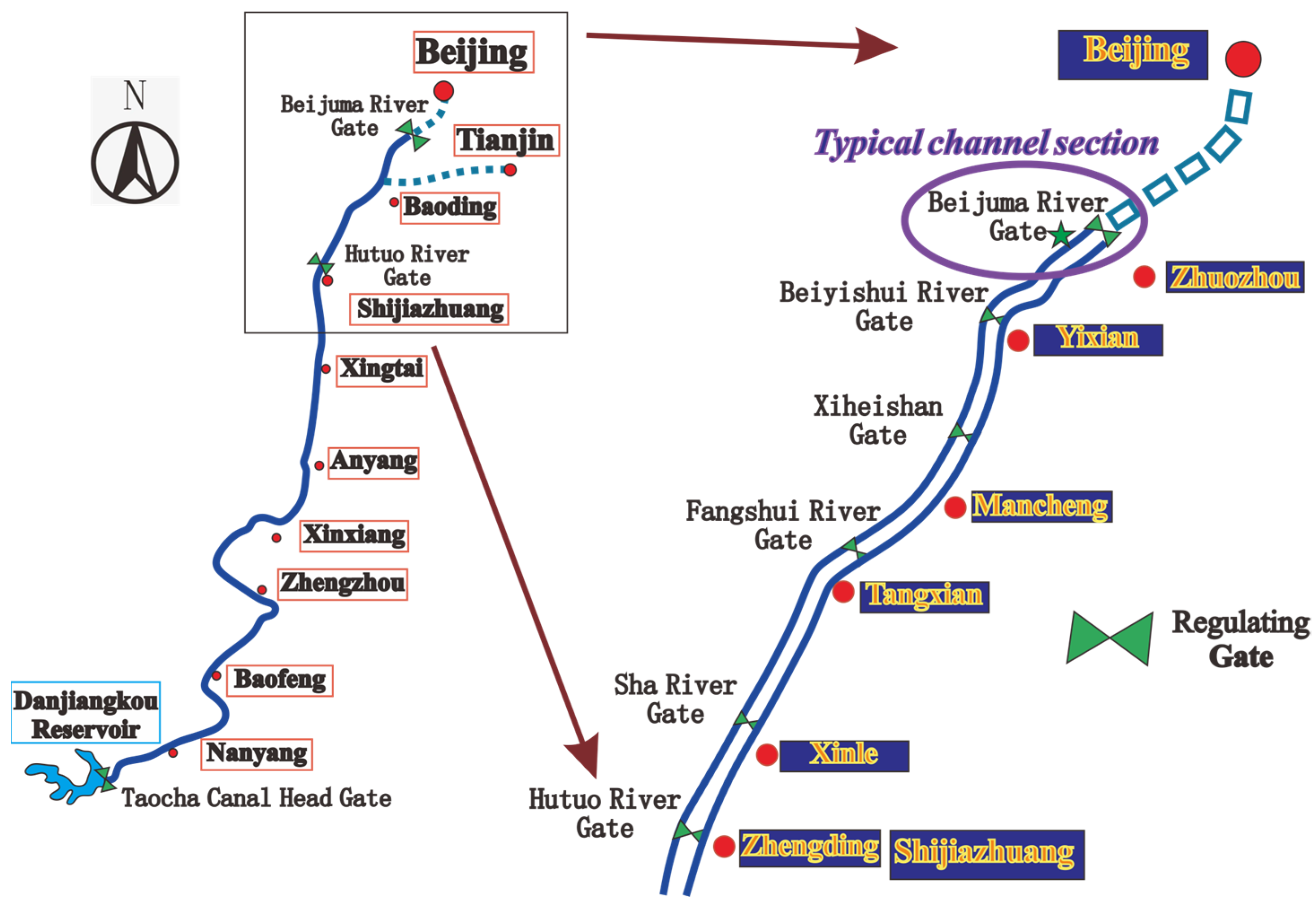
1]. The total length of the main canal of the Middle Route of the South-to-North Water Transfer Project is 1267 km, as shown in
Figure 1. Water is transported from the Danjiangkou Reservoir in the Hanjiang River to the North China Plain [
2]. The purpose of this water transfer project is to transfer water to Henan Province, Hebei Province, and the cities of Beijing and Tianjin. The average annual amount of transferred water is 9.5 billion m
3 [
3]. Since the start of the operation of this water transfer project in 2014, given the strong coupling of cascaded channels, it has been difficult to keep water levels at all gates along the route being stable. The cross-section of the main canal has a trapezoidal shape, with a bottom width range from 7.0 to 26.5 m. Along the water transfer route, there are no lakes or reservoirs for water detention, indicating the importance of safety operation of this project [
4]. The main canal of this water transfer line is spanned from the place located at the north latitude of 33° to the north latitude of 40°. During winter periods, the temperature in northern China such as in Beijing is generally low. As a consequence, the formation of ice cover in the water transfer cannel creates a big ice problem [
5].
During an ice-covered flow condition, the characteristics of river hydraulics have been dramatically changed compared to that under an open flow condition. An ice cover adds an extra boundary to the flow, which leads to considerable changes in the velocity profile, flow rate, bed shear stress distribution, and water temperature [
6]. Water temperature is greatly affected by thermal factors and environmental variables [
7]. Under the influence of air temperature, flow and boundary conditions during a winter period [
8], water temperature is affected by the hydraulic response to the channel or the complex process of water transport during an ice-covered period. In the meantime, water temperature is an important physical factor affecting the change of river ice regime [
9]. Therefore, water temperature is often used as one of important indicators for forecasting river ice regime [
10]. To avoid the development and formation of an ice jam during winter periods, the water temperature during the water transfer process should be carefully controlled [
11].
Boyd et al. [
12] calculated and analyzed the peak temperature and duration of each supercooling event by observing the water temperature of three controlled rivers, Kananaskis, North Saskatchewan and Peace Rivers in Alberta, Canada. They pointed out that the water supercooling process is the key condition for the formation of suspended ice and anchor ice in rivers in cold regions. Osterkamp et al. [
13] measured the temperature of water in the Goldstream Creek and Chatanika River in Alaska during the formation of frazil ice particles that forms in turbulent water. Frazil ice particles in flowing water are essential for the development of ice pans which may lead to the development of ice jams and cause disaster [
14]. The correlation between the cooling rate of a river and the heat loss of the water surface has been calculated for the periods before and during the formation of frazil ice. It was found that the core of frazil ice in the river was cold organic matter, soil particles or a combination of these substances, which could enter the river through the mass exchange process of the air–water interface. The degree of supercooling of the observed river was given. McFarlane et al. [
15] compared five different methods for calculating sensible heat flux and latent heat flux based on air temperature, relative humidity, air pressure, wind speed and wind direction, short-wave and long-wave radiation for the Dauphin River in Manitoba. By calculating the heat balance of the river, the supercooling phenomenon of the river was predicted. They claimed that the solar radiation is an important factor in the heat budget of water bodies. Wang et al. [
16] pointed out that both temperature field and velocity field of flowing water during an ice-covered period are essential for studying the formation and evolution of frazil ice. By applying the Navier–Stokes equations and energy equation for flow under an ice cover, the velocity field and temperature field of flowing water have been analyzed. It is found that the temperature field of water body is mainly affected by heat conduction on the surface of ice cover and convective heat transfer on the riverbed. Yang [
17] developed both linear and non-linear models for calculating heat exchange between water and atmosphere based on meteorological data including solar radiation, long-wave radiation, evaporation and convective heat exchange. The one-dimensional model for simulating temperature of flowing water in an open channel is developed. The model is verified and applied along some typical channel reaches of the Middle Route of the South-to-North Water Transfer Project (MR-SNWTP).
Field observations along the main canal of the MR-SNWTP indicate that, with the decrease in air temperature and water temperature in winter, frazil ice appears and ice pans form. An ice cover will be gradually developed on water surface of the MR-SNWTP. After the MR-SNWTP is covered by ice, both the growth of ice cover thickness and the decrease in water temperature slowed down. During the stable ice-covered period, the water temperature was low with some minor fluctuations. With the increase in air temperature in spring, river ice starts to melt, and the water temperature begins to rise as well [
18]. Since the change of water temperature is also an indicator of the complex nonlinear evolution process of an ice cover during winter periods, the machine learning method with advantages in dealing with nonlinear problems can be considered to predict the trend of water temperature [
19]. Sun et al. [
20] used the machine learning method to predict the river breakup time and peak flow of the Athabasca River in Fort McMurray, Canada. Their results show that the inclusion of certain inputs in the optimal models can reveal some hints for the potential mechanism on river ice from the data-driven perspective. Seidou et al. [
21] applied the artificial neural network and the lake ice thermodynamic model to the study ice cover thickness of several lakes and reservoirs in Canada. It is found that, in case of scarce or less data available for use, result using the artificial neural network has higher prediction accuracy. Guo et al. [
22] used the improved back propagation (BP) neural network method to predict the river-breakups in the Heilongjiang and improved the prediction accuracy by integrating multiple factors affecting water temperature and development of ice conditions. The commonly used data-driven prediction models include multiple regression, projection pursuit, and cloud model. These prediction models have achieved a series of results in different engineering cases [
23]. The traditional multiple regression model is difficult to accurately describe the complex relationship between independent variables and dependent variables. When the process is highly random, the prediction accuracy is often low. The machine learning models such as projection pursuit and cloud model possess the nonlinear mapping and adaptive ability, and their computational efficiency and prediction accuracy are improved compared to the traditional multiple regression models. However, because the goal of train samples for these models is to minimize the fitting error, it is easy to create problems such as overfitting or local optimality. The support vector machine (SVM) is an algorithm based on the statistical learning theory of small samples, which can be used to solve nonlinear and high dimension problems [
24]. Wang et al. [
25] predicted the water level during an ice-jammed period by means of the BP neural network and the support vector machine. Their results show that the prediction accuracy using the support vector machine method is higher than that using the BP neural network in case that the sample is small. The principal component analysis (PCA) method can be used to extract independent and effective information from features, which is a statistical analysis method to reduce the input dimension [
26]. Ren et al. [
27] used the PCA method to eliminate redundant information and effectively analyzed the main factors affecting water temperature in the upper reach of the Yellow River. The identification of the heat balance state of water body in the channel during a winter period has the characteristics of nonlinear process and high dimension, which is in line with the characteristics of the machine learning method. However, no research work has been reported regarding the heat balance of a water body during an ice-covered period.
In summary, the seasonal change of water temperature in rivers affects the formation of river ice. Results of daily field observations at channel cross-sections in winters may be affected by ice conditions in the MR-SNWTP. The heat balance of water body in rivers during a winter period is more complicated. The sluice gate for flow control located in Beijuma of the MR-SNWTP is the junction point of the water transfer channel from an open channel to the culvert, and its location is shown in
Figure 1. This channel cross-section of the MR-SNWTP was chosen in this study since relatively more field observation data are available and the temperature in this region is relatively low. Additionally, this cross-section is vulnerable to the ice problem during winter periods. In this study, the machine learning method is used to study the heat balance and water temperature at this cross-section of the MR-SNWTP.
2. Methodology
The change of temperature follows the principle of energy conservation [
28], and the main parameters used in the water temperature model are shown in
Table 1.
The general equation for describing temperature of water in an open channel is as follows:
Equation (1) is a mathematical model for describing water temperature field [
29]. Symbols in Equation are explained in
Table 1. From left to right of Equation (1), it is the time term, the convection term, the diffusion term, and the source term, respectively.
For a channel with a regular cross-section similar to ghat of the MR-SNWTP, the temperature gradient along the flow direction is small, and the diffusion term can often be ignored. Combined with the continuity equation of the flow, by assuming the flow is incompressible with the fixed specific heat capacity, Equation (1) can be simplified. In the presence of an ice cover on water surface (either partially or fully covered), both the boundary conditions and flow conditions for the model have been changed, resulting in a significant impact on the water temperature [
30]. The exchange of heat occurs between the atmosphere, ice cover and water, which is related to the coverage of ice cover on water surface. Therefore, the equation for describing temperature of water can be rewritten as follows:
where
Ni represents the extent that the cross-section is covered by ice. When an ice cover is present in a channel, the heat transfer of the water body is closely related to the heat loss of the ice body. The above equations characterize the physical mechanism of the heat transfer of the water body during a winter period [
31].
The heat exchange between atmosphere and water is affected by weather conditions, solar radiation and wind speed. In late fall or early winter, with the decrease in air temperature, cooling intensity will be increased. Therefore, heat loss from water body results in the decrease in water temperature until the water surface is covered by an ice cover which is normally formed by frazil ice particle and ice pans in rivers. After the entire water surface is covered by ice, the water temperature continues to fluctuate and drop, and the water temperature gradient at the front of the ice sheet is large. During the stable ice-covered period, with the decrease in air temperature, the thickness of the ice cover gradually increases, and the heat exchange between water and air decreases. During this stable ice-covered period, the water temperature can reach a dynamic equilibrium condition with some minor fluctuations. In the spring, with the increase in the air temperature and solar radiation, an ice-covered river undergoes the thermodynamic breakup process (ice cover melting process). The water body gradually absorbs heat and results in the increase in temperature of water body. Since the MR-SNWTP is 1267 km long and spans a latitude difference of 7°, there will be some changes in the temperature of water body along the MR-SNWTP. The change of air temperature and that of water temperature has an obvious nonlinear relationship. The continuous change of meteorological elements in winter and spring affects the relevant parameters in Equation (2).
Equations (1) and (2) show the relationship between the change of water temperature and other factors. Since the parameters in these equations vary with various factors including the environmental variables, the analytical solution of these equations will be very complicated. The hydrodynamic process also affects the heat balance of the water body. When the flow velocity is high enough, shore ice along channel banks is normally difficult to be developed. Additionally, the relatively larger flow velocity during a freeze-up period is likely to cause the incoming ice pans/floes to be entrained and submerged under the sheet ice cover to form an ice jam. During the break-up period, the surface of the entire channel (together with pools) is grouped into the open channel section, ice-cover melting section and the fully ice-covered section. Along the melting section of the channel, ice cover becomes soft and loose with a lot of pores. Under the influence of hydrodynamic force, this loose ice cover is gradually eroded, and the wavy-shaped surface appears on the bottom of an ice cover, which eventually causes the ice cover to be melted, broken, and transported downstream. The hydrodynamics of the flowing water and the ice dynamics affect the heat transfer of water and changes of water temperature.
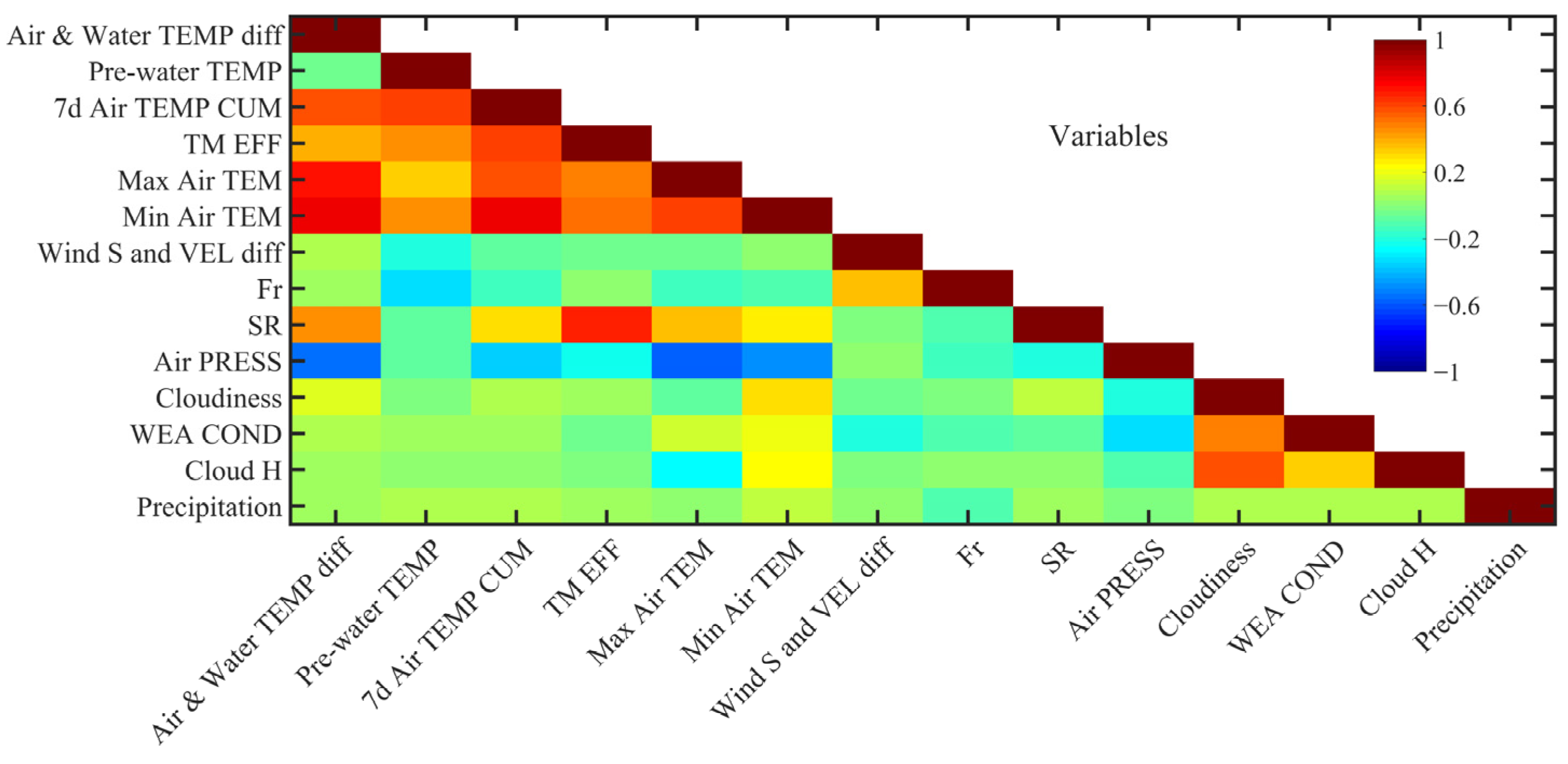
By taking the thermal and dynamic factors that affect the change of temperature of water body as the input features, an SVM-based discriminant model for water heat balance is established to assess the heat loss and heat gain of water body. In this study, data were obtained through on-site observations. Among them, the observed data for water flow conditions at some cross-sections near the control gate have been acquired from the management department of the MR-SNWTP. The temperature sensor and flow velocity meter have been used to collect data for describing water flow conditions, which were measured 4 times every day. The meteorological data were acquired from the meteorological station which was setup by considering the locations for observations of the water flow. The number of daily measurements of meteorological data is consistent with that of for water flow. The daily average approach is adopted to form a dataset for subsequent analysis. These environmental variables have different effects on the latent heat flux and the sensible heat flux, which are correlated to the heat balance. The correlation analysis of each characteristic data has been carried out, and the correlation matrix of the measured dataset is established. The calculated correlation coefficient is presented in
Figure 2. The corresponding thermal factors and dynamic factors are abbreviated to better express the figure. These factors include: the temperature difference between air and water (Air and Water TEMP diff), the previous water temperature (Pre-water TEMP), the cumulated seven-day average daily air temperature (7d Air TEMP CUM), the time effect (TM EFF), the maximum air temperature (Max Air TEMP), the minimum air temperature (Min Air TEMP), the difference between wind speed and water velocity (Wind S and VEL diff), the flow Froude number of water flow (Fr), the solar radiation (SR), the air pressure (Air PRESS), the cloudiness (Cloudiness), the weather conditions (WEA COND), the cloud height (Cloud H), and the precipitation (Precipitation).
In
Figure 2, the correlation coefficient of 1 indicates that the two features are completely linear positive correlated; the correlation coefficient of −1 indicates that the two features are completely linear negative correlation; and the correlation coefficient of 0 indicates that the two features are independent. It can be seen from
Figure 2 that there is a certain degree of correlation among the influencing features, that is, there is information overlap between the input features. The commonly used methods for data dimension reduction include single-factor analysis, grey system analysis, set pair analysis, analytic hierarchy process and principal component analysis. Results of single-factor analysis have polarization problem. The dimension reduction methods based on grey system theory, set pair analysis theory and analytic hierarchy process are controversial in the selection of index weight, and the application of the model automatic calculation is limited. The core idea of the PCA method is to reduce the high-dimensional associated features to a few unrelated features, and to reflect the original information as much as possible. The PCA method can be used to process the standardized sample data, extract the main information of input variables, and improve the accuracy of classification based on comprehensive consideration of various influencing factors [
32]. To ensure that the data have the same importance as the input scale, the daily average dataset of the selected measured parameters and measurement records are pre-processed by the standardized method, and the covariance matrix
S is calculated according to Equation (3):
where
n is the number of sample data, and
X is the normalized sample matrix. By solving the characteristic equation,
m non-negative features
λk (
k = 1, 2, ⋯,
m) of the covariance matrix
S are obtained and arranged in the order of
λ1 >
λ2 > ⋯ >
λm > 0. The corresponding orthogonal unit eigenvector
µk is solved, and the formula of principal component calculation is as follows:
In Equation (4),
Zk represents the
kth principal component (
k ≤
m), and the contribution rate
vi of the
ith principal component is calculated using Equation (5):
The upper limit of machine learning effect is controlled by the available data. The standardized input data are divided into training and verification sets. To reduce the difference introduced by different sample division, the model is trained by the cross-validation method. For the part of training set, it is divided equally and one of them is selected as the test set, and the rest is used as the training set to complete the cross-validation process.
The SVM algorithm is based on the principle of minimization of structural risk. Regarding the classification of samples, the sample dataset is set as
Zi =
[
Zi1;
Zi2],
yi is the corresponding label of
Zi. The heat gain of water body is labeled as “+1”, and the heat loss of water body is labeled as “−1”. The hyperplane formula for the sample classification is expressed in Equation (6), and the classification decision function is described as Equation (7) [
33]:
where
w = (
w1;
w2; ⋯;
wm) is the weight vector corresponding to
Z,
b is the displacement term which determines the distance between the hyperplane and the origin. The sign ( ) represents the sign function. The Lagrangian function for solving this problem can be described as Equation (8):
where
α = (
α1;
α2; ⋯;
αp) is a Lagrangian operator,
αi > 0. By solving Equation (8) and substituting it into Equations (7) and (9) is obtained:
The standardized sample data are inseparable in the original space. To solve this problem, the standardized sample data are mapped and transformed in the original space, and the value of the transformed space inner product function can be transformed into the value directly calculated using the kernel function. The calculation formula is as follows:
where
η (
Zi) and
η (
Zh) are the mapping transformation functions of the original space; and
k (
Zi,
Zh) is the kernel function. When meteorological data are relatively complete, based on the observed thermal-hydrodynamic data about winter ice-water regime of the MR-SNWTP, the heat budget process of water body and the mutual feedback relationship of the related parameters are identified.
3. Analysis of Heat Budget of Water Body
The MR-SNWTP delivers water from the low latitude to high latitude. In winter, it is necessary to identify the influence of both thermal and dynamic factors of flowing water on the heat balance of flowing water in the main canal of the MR-SNWTP. The key to the study is how to consider the influence of temperature, solar radiation, cloud cover, precipitation, wind speed and other factors on the heat balance process of flowing water.
The supercooling process caused by heat loss of water body is a critical process for ice formation in channels. Hence, it is proposed to use environmental variables to predict the correct direction of water temperature change. Then, by considering the difference between calculation accuracy and complexity, the parameter adjustment algorithm was selected to assess the heat balance state of water body. The cumulative temperature during a certain time period is often used for analyzing river ice hydrology [
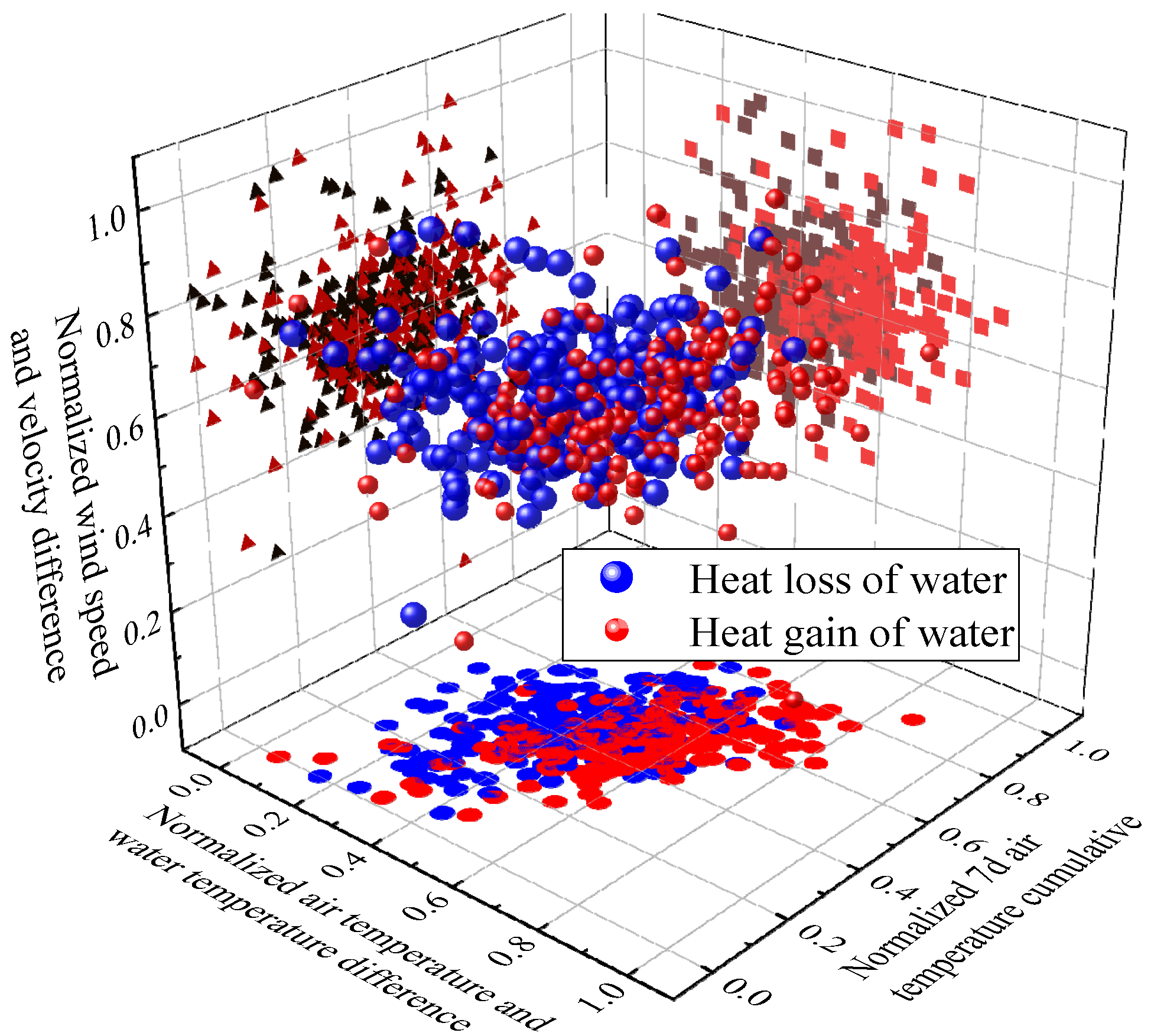
34]. The difference between air temperature and water temperature, the cumulative air temperature, and wind speed and velocity gradient were selected for analyzing the impact these factors on the heat balance of water body, as shown in
Figure 3.
It can be seen from
Figure 3 that, under condition of the heat balance of water body, both thermal factors and dynamic factors contribute to the heat transfer of water body, and it is difficult to use a linear segmentation to directly separate the heat transfer caused by thermal factors from that by dynamic factors. This is the characteristics of the heat budget of water body in river during a winter period. It has also become difficult to accurately calculate the heat exchange of flowing water in winter by using both theoretical equations and numerical simulation. Due to the mixing process of flowing water and latent heat from the phase transition from liquid water to solid ice, the heat balance state of water body cannot be simply expressed as a good linear function of either dynamic or thermal condition. In the case of being linearly inseparable, the samples in the low-dimensional space are mapped to a high-dimensional feature space by using a nonlinear mapping function to make it to be linear. Then, it is possible to use the linear algorithm to analyze the nonlinearity of samples in the high-dimensional feature space, and the optimal classification hyperplane can be found in this feature space. The so-called optimal classification surface not only requires to correctly separate the categories, but also needs to maximize the classification interval. The purpose for correctly separation of categories is to ensure that the empirical risk is minimized. Actually, the maximum classification interval is to minimize the confidence range in the generalization bound.
Considering the complexity and coupling of the water heat budget process, the Gaussian radial basis function (RBF) is used as the kernel function of the support vector machine:
In Equation (11),
Zi and
Zh represent different input characteristics, and
γ is the Gaussian kernel bandwidth parameter. By introducing the multiplier
, and the penalty parameter
C, a slack variable
ε needs to be added to the threshold to reduce the error of the dual problem. The slack variable represents that the error term whose deviation is less than
ε is not penalized, we can get:
The parameter C represents the degree of punishment for prediction errors. The larger the C value, the more the model does not allow prediction errors. If the C value is too large, the model will make fewer errors in the training data process and easily cause overfitting. On the contrary, if the C value is too small, the model will easily ignore the prediction error, which will lead to a poor performance of the model. The value of γ will influence the range of the Gaussian function corresponding to each supporting vector. The weight of high-order features decays very fast, so that, the larger the γ value, the less the support vectors; the smaller the γ value, the more the support vectors. The number of support vectors will affect the speed of the training and prediction process. The parameters C and γ jointly determine the prediction results of the model. Appropriate selection of their optimal combination can lead to the good generalization ability and fitting effect of the model.
The selection of values of parameters in the kernel function is the key to the calculation accuracy. Thus, the optimization of parameters is needed to determine the values of
C and
γ. The commonly used methods for parameter adjustment include the grid search (GS) method, the particle swarm optimization (PSO) method, and the genetic algorithm (GA) method. The grid search method is to use the search data to form a grid space, and then obtain the value for each grid point using the exhaustive method. The concept about the PSO method is that each particle contains two attributes of speed and position, each particle contains a fitness value determined by the objective function and knows the best position and the current position found by itself until now. In the whole group, the best target position found by all individuals is also known by each particle. How each individual particle proceeds to the next position is determined by the parallel search of the population. The GA method is a random search method by means of the evolutionary process of the biological world. Its main characteristics is to directly operate the data to be optimized. It can automatically obtain and guide the optimized search space, adaptively adjust the search direction, and has strong robustness. As mentioned above, the heat exchange of water body during an ice-covered period is a complex process and affected by many factors, which can be expressed as:
where
Tw−h represents the historical conditions of water temperature;
Ta−s represents air temperature conditions including daily maximum, minimum, average temperature and cumulative temperature during a period;
Tt represents the time-effect factor. Since the variation of water temperature approximately shows a periodic function and it fluctuates around the average annual water temperature, both sin (2π
Tday/
Tyear) and cos (2π
Tday/
Tyear) are selected to reflect the time-effect
Tt; where
Tday is the date count of the year (note: 1 January is 1, etc.); and
Tyear is the number of annual dates;
δv represents the component gradient of wind speed and flow velocity in the flow direction, which has an important influence on the heat transfer process;
Fr is the flow Froude number;
P is the average daily pressure;
Ra is the solar radiation;
Rel is the daily average relative humidity;
Rp is the average daily precipitation;
N is cloud amount;
Hc is the cloud height. These parameters have either direct or indirect impact on the change of water temperature. Results of field observation showed that the changes of water temperature are compatible with the simulations of the collected data. If
g > 0, it indicates that the water body absorbs heat and the water temperature rises; if
g < 0, water body loses heat and water temperature drops. After standardizing parameters in Equation (10) based on data measured at the typical survey stations, the PCA was used to extract the first principal component and the second principal component as the input of the SVM. The cumulative contribution rate of each principal component output by using the PCA is shown in
Table 2.
According to the cumulative contribution rate of each principal component in
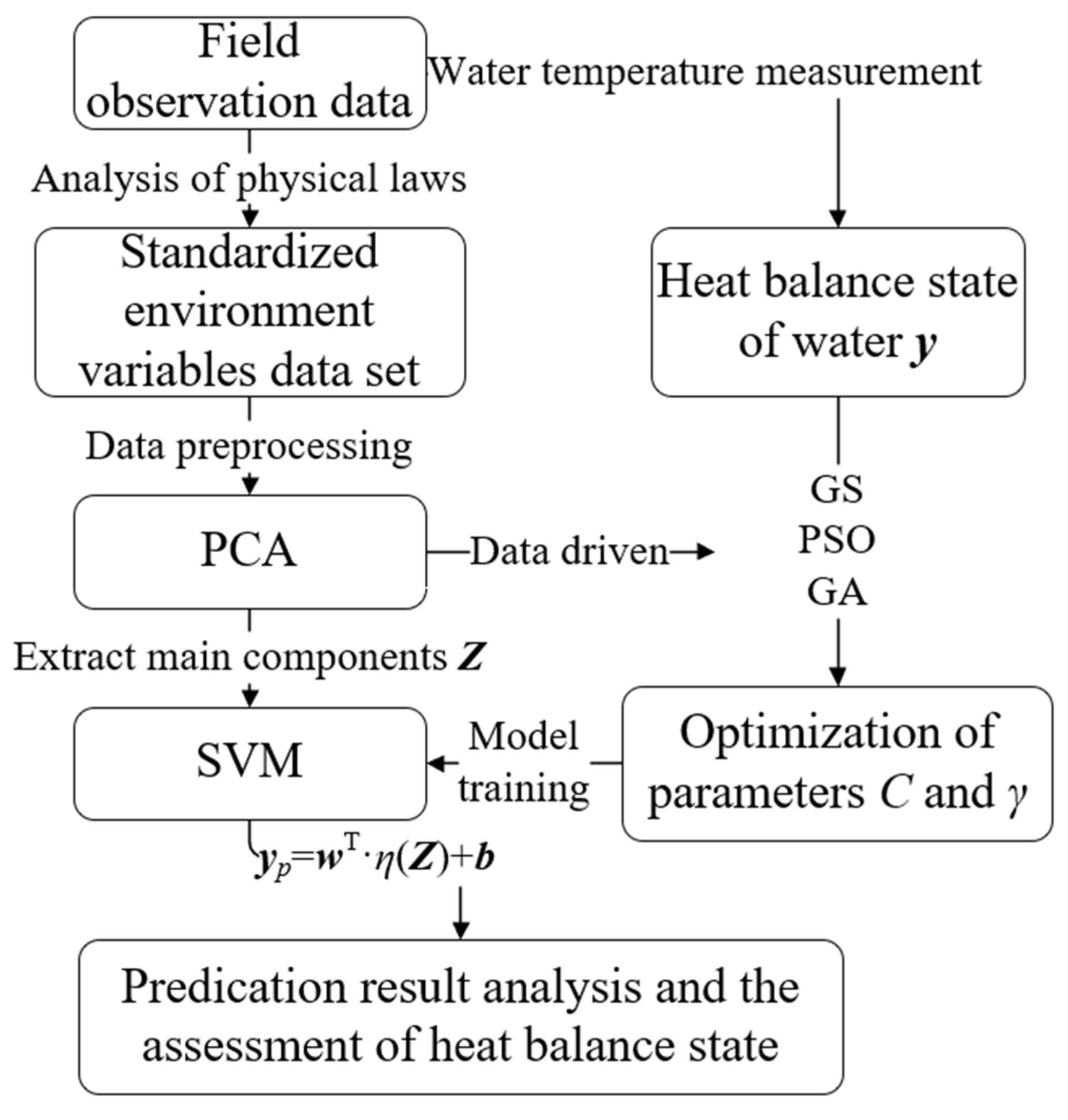
Table 2, results showed that the result for the first two principal components can explain more than 50% of the information for original data; the information for the first five principal components can explain more than 80% of the information for original data; the information for the first seven principal components can explain more than 90% of the information for original data. With respect to the prediction of water temperature and heat balance state, based on the data measured at the typical survey section during six winters from 2015 to 2021, the measured data from 2015 to 2020 are used as the training samples to establish the model and optimize the model parameters, but the measured data from 2020 to 2021 are used as the verification samples to test the capacity for generalization of the model. The flow chart for calculation for the assessment of heat balance state is shown in
Figure 4.
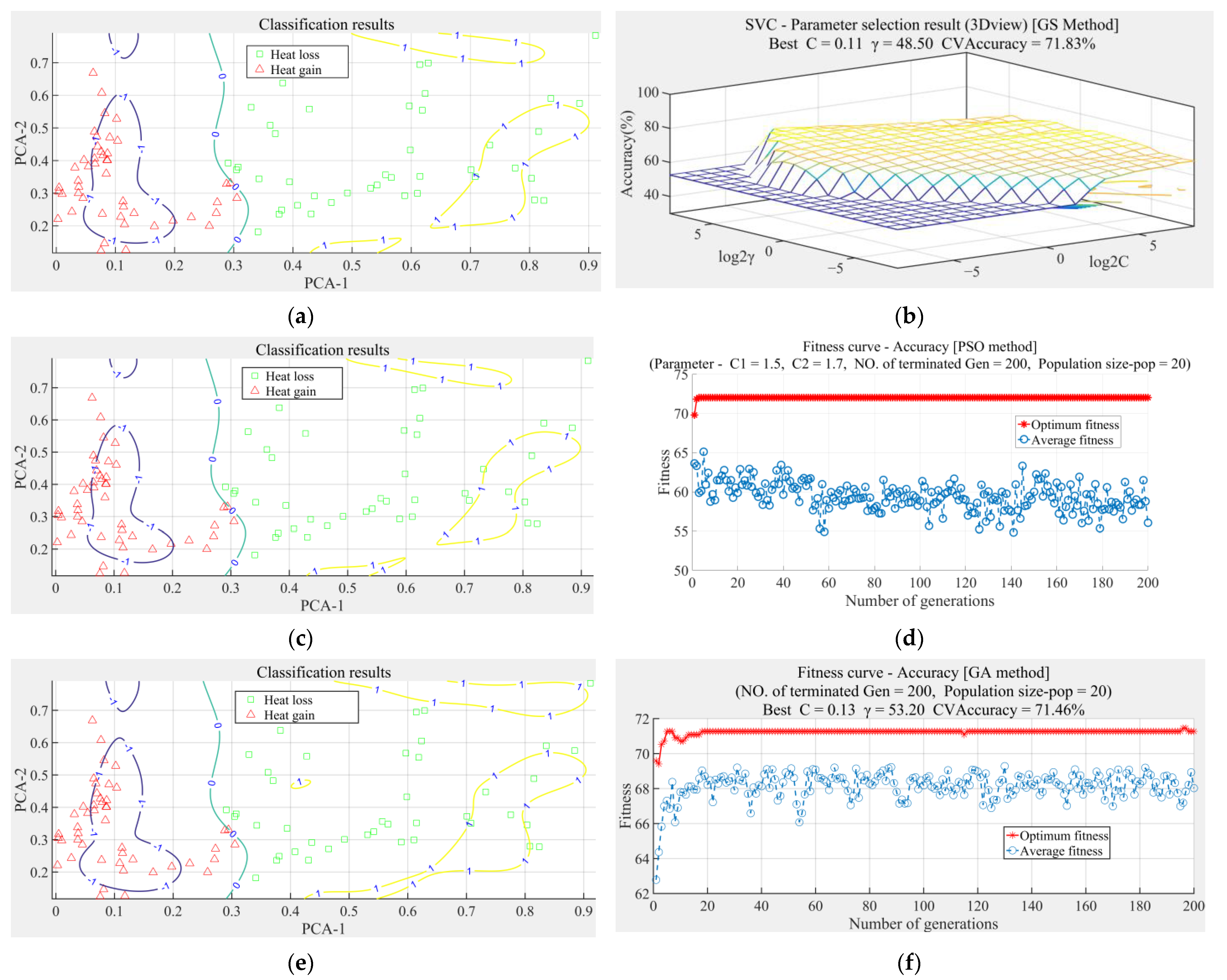
Since the annual accumulated negative temperature of the training sample varies in a certain range, it can be used to describe different winter characteristics. During the winter period of 2019~2020, the Huinanzhuang pumping station (on the Beijuma River) was under maintenance. The measured data for water transport in the Beiyishui River during an ice-covered period are used to act as the observation data of the typical survey section, so that the training set also has a certain coverage on the hydraulic characteristics. PCA-1 is selected as the first axis and PCA-2 as the second axis. By applying the GS, PSO and GA methods, results of prediction of classification are generated (
Figure 5), and the corresponding parameter values are shown in
Table 3. When the direction of water temperature change (heat gain vs. heat loss) is correctly identified, it is classified as a successful prediction.
In
Figure 5, log
2C and log
2γare the logarithms of parameters
C and
γ, respectively. According to the calculation process of Equations (3) and (4), the composition of the principal components includes all the influencing factors, and the contribution of each factor is different. Due to the different features of various algorithms, the combination of parameters
C and
γ obtained by the optimization also fluctuates within a certain range. It can be seen from
Figure 5 that the generated nonlinear partition hyperplane can better distinguish the heat budget of water body. In the prediction model, 63 out of the 89 classified data were predicted correctly, and the accuracy reached at 70.79%. From the number of iterations, the GS method has fewer iterations with a higher optimization efficiency. In view of the cross-validation rate, the GA algorithm performs well in the model training, and the number of the support vectors is less. By observing the execution time of the algorithm, with respect to the operation management of water transfer process, the calculation time consumed using these three algorithms is within the acceptable range, and the time need using the GA algorithm is slightly higher. Furthermore, by selecting the first five principal components in order to adequately reflect the influence of the original correlation factors, the SVM is used to predict the heat balance state of water body. The prediction results are summarized in
Table 4.
With the increases in the number of principal components extracted, the contribution of each component in the model also increases accordingly. It can be seen from
Table 4 that the comprehensive impact factor formed by more principal components can reflect more information about the original data, and the prediction accuracy of the model can be further improved. It has been found that the prediction results by means of two bionic algorithms, namely the PSO and GA methods, are better than those using the GS method. Results showed that the number of support vectors generated by the PSO algorithm is less. From
Table 3 and
Table 4, once can see that there are differences in computational performance using different approaches. When the number of input data are increased, the time of iterations also increases. This study is concerned with the exploration of the heat balance state of the MR-SNWTP. In practical application, different parameters for describing the performance need to be trade-off according to the actual situation of the project. Among these three methods, the times of iterations using the GA algorithm is relatively small, and the cross-validation rate of this method is convenient and outstanding. This means that the GA algorithm method is clearly suitable for the parameter optimization process of the SVM model in this study. The changes of water temperature have been well predicted by means of the proposed method together with the state of water heat balance.
According to the classification results of the model, the prediction results showed that water body began to absorb heat from 13 January 2021. At this time, the air temperature began to maintain above 0 °C with the highest air temperature of about 5 °C when the weather became sunny with sufficient solar radiation and relative low humidity. On 17 January 2021, the main channel of the Beijuma River survey section eventually broke up. After the breakup of the channel along this survey section, due to the release of latent heat from the upstream inflow and ice, the water body experienced a repeatedly heat gain -heat loss process. By 21 January 2021, the main channel was eventually opened, and the water body continued to absorb heat, causing the water temperature to rise. Additionally, then, the remaining shore ice vanished. As a machine learning method, the SVM model can mine the potential knowledge information of the data and complete the classification and prediction of the data according to the features of datasets. In this study, the feasibility of the proposed approach has been verified by using results of the actual water transfer project. Result of this study can provide reference for engineers in water resources engineering. To apply it, by replacing the input data and the value of the kernel parameters, the trend of variation of water temperature can be identified, and the state of water heat budget can be classified. The proposed method in this study can be promising for controlling ice problems in channels for water transfer in cold regions and can provide the operation guidelines for a river system under an ice-covered flow condition in winter.