Prediction for the Influence of Guide Vane Opening on the Radial Clearance Sediment Erosion of Runner in a Francis Turbine
Abstract
:1. Introduction
2. Mathematical and Geometrical Models
2.1. Mathematical Model
2.1.1. Governing Equations
2.1.2. Lagrangian Tracking of Particle Motion
2.1.3. Erosion Model
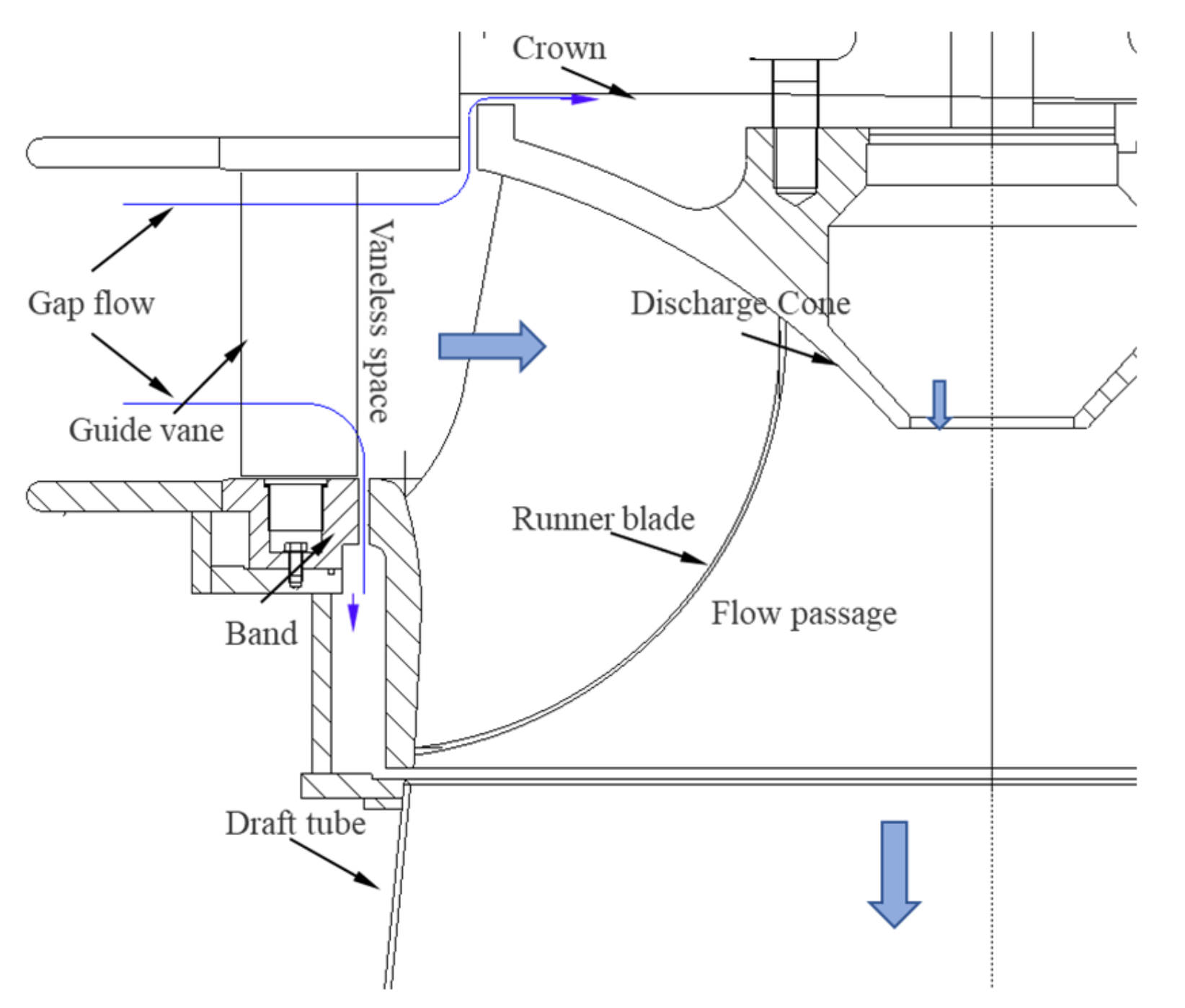
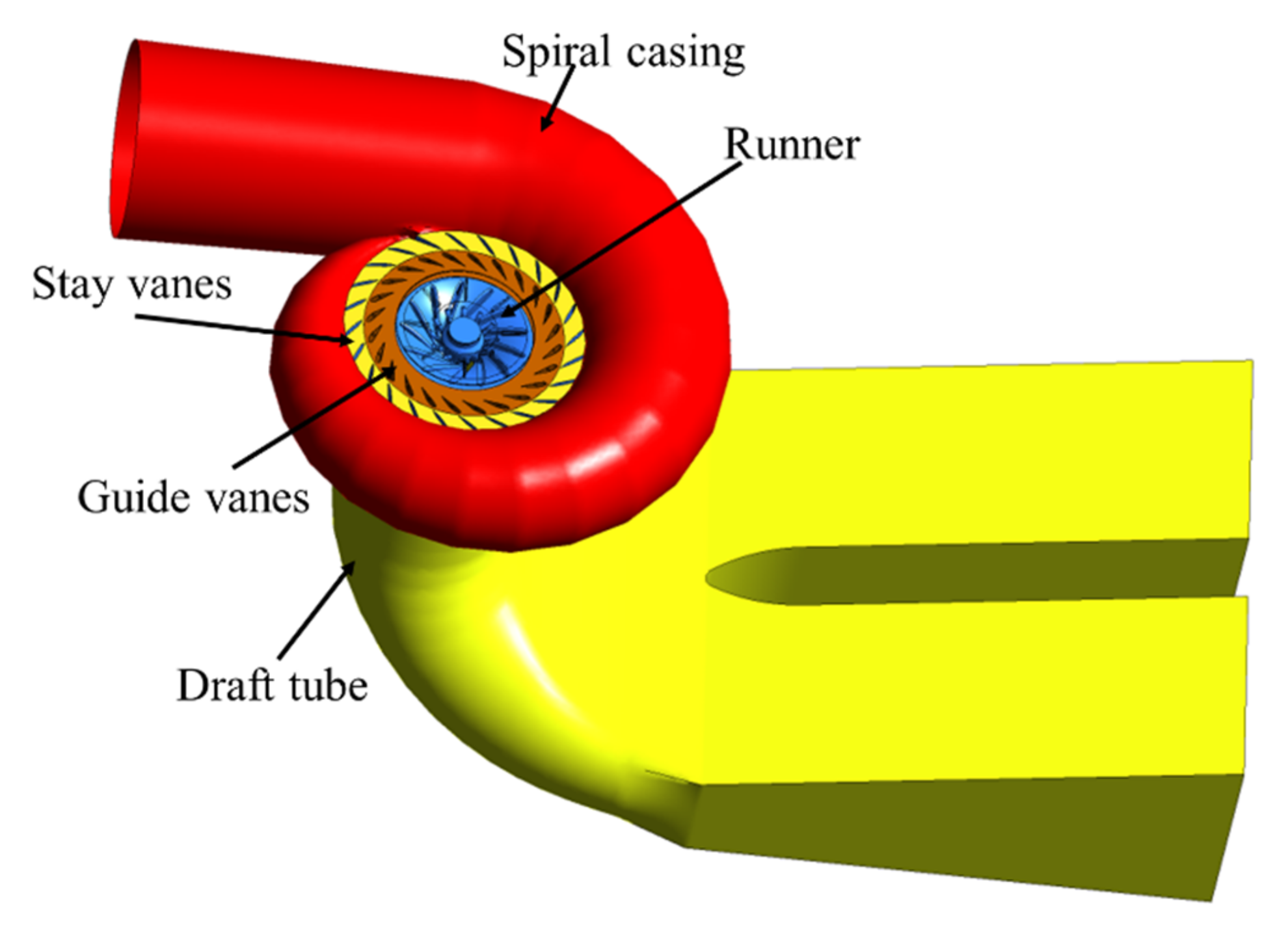
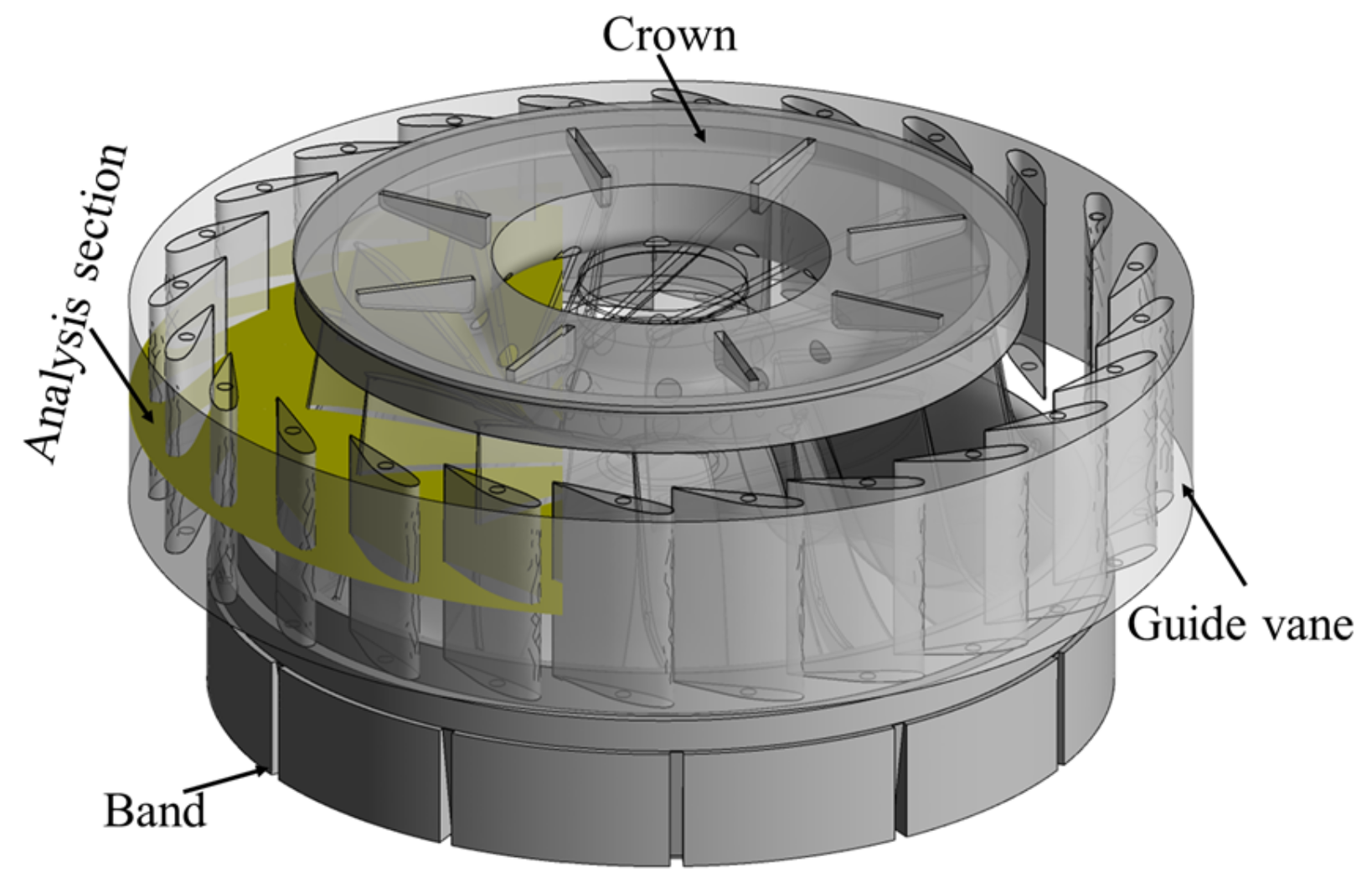
2.2. Simulation Geometry Model
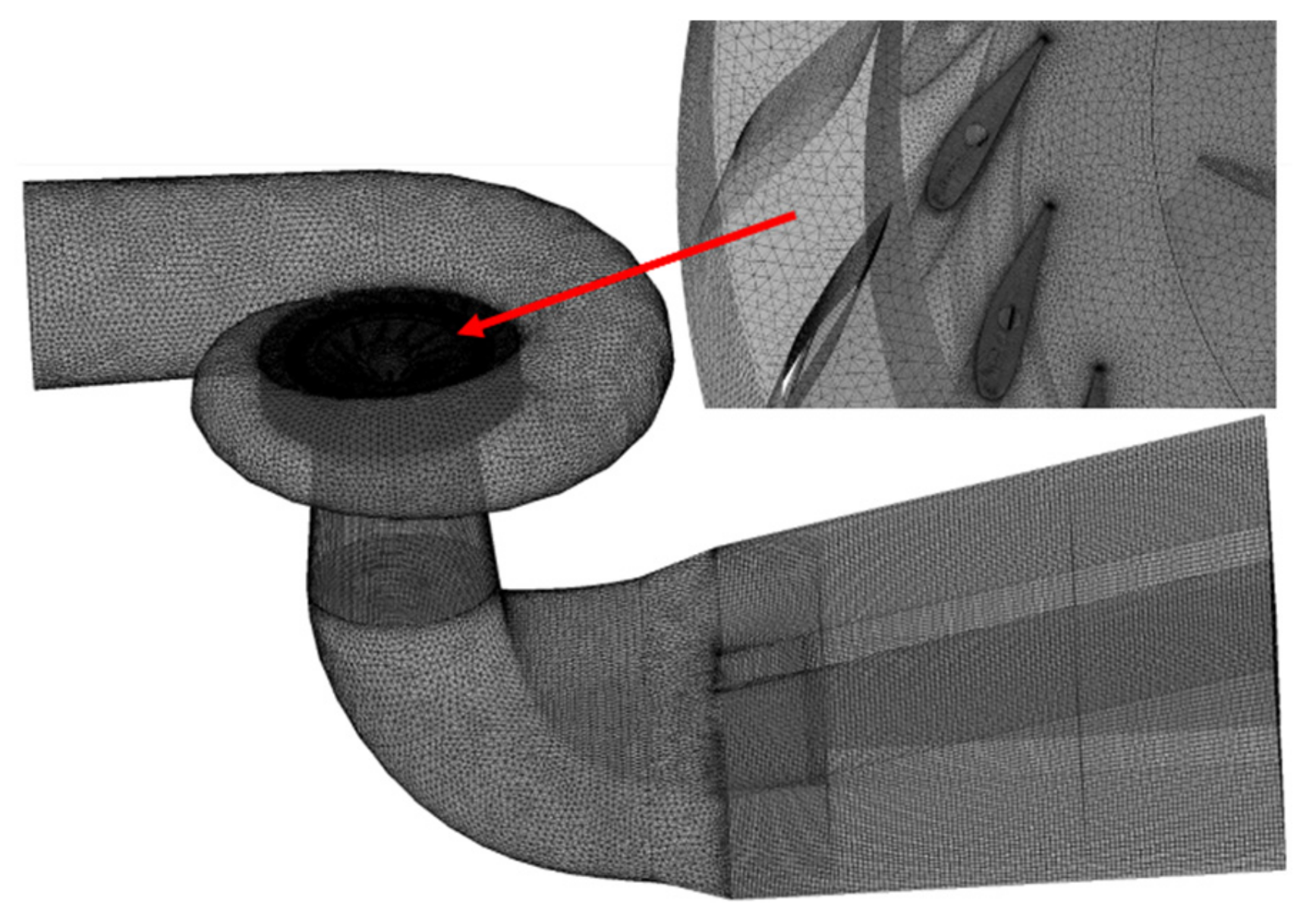
2.2.1. Geometric Model Set Up
2.2.2. Parameter Setting in Calculation Model
- (1)
- Boundary conditions
- (2)
- Calculation parameters
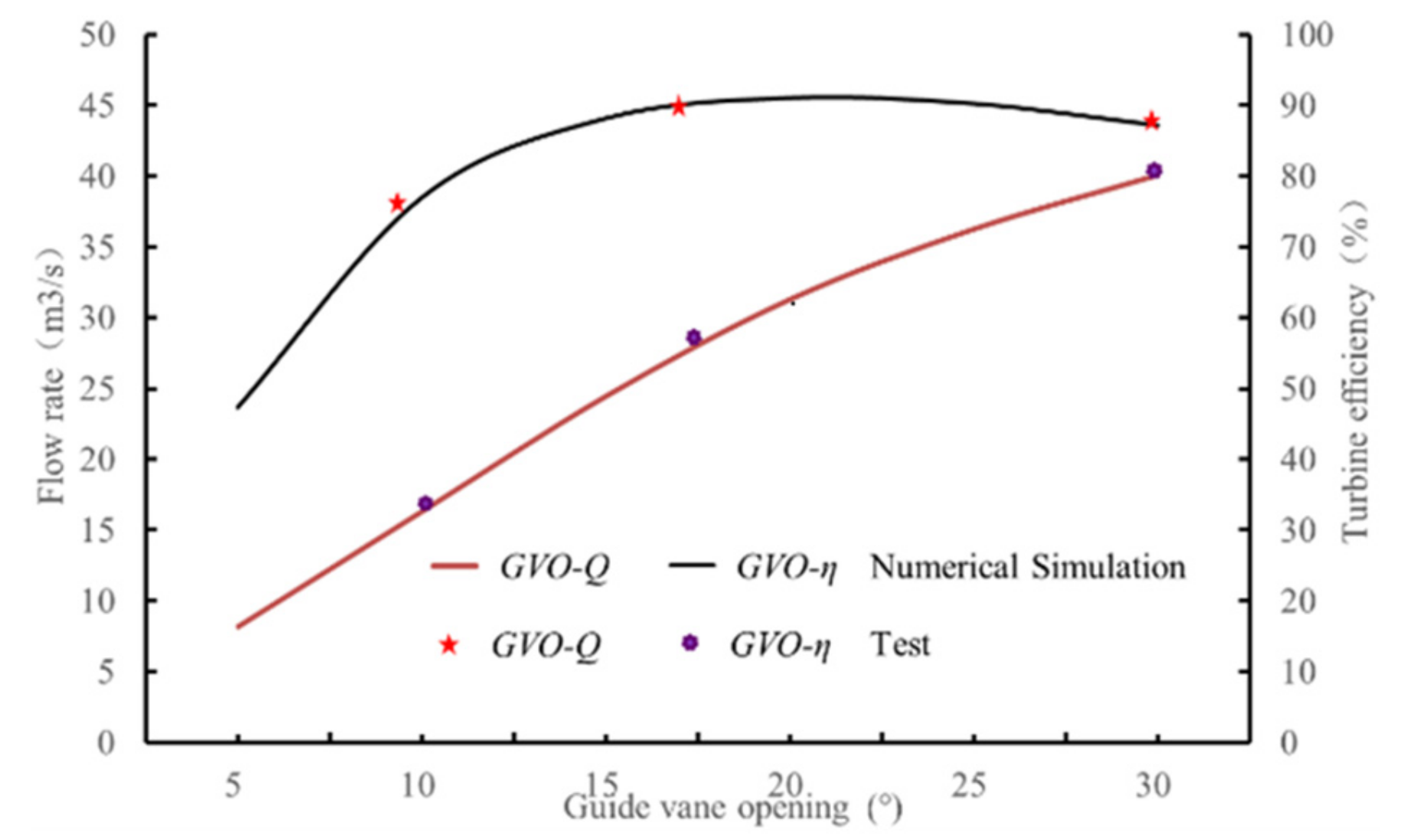
2.3. Reliability Verification of Calculation Model
3. Result Analysis
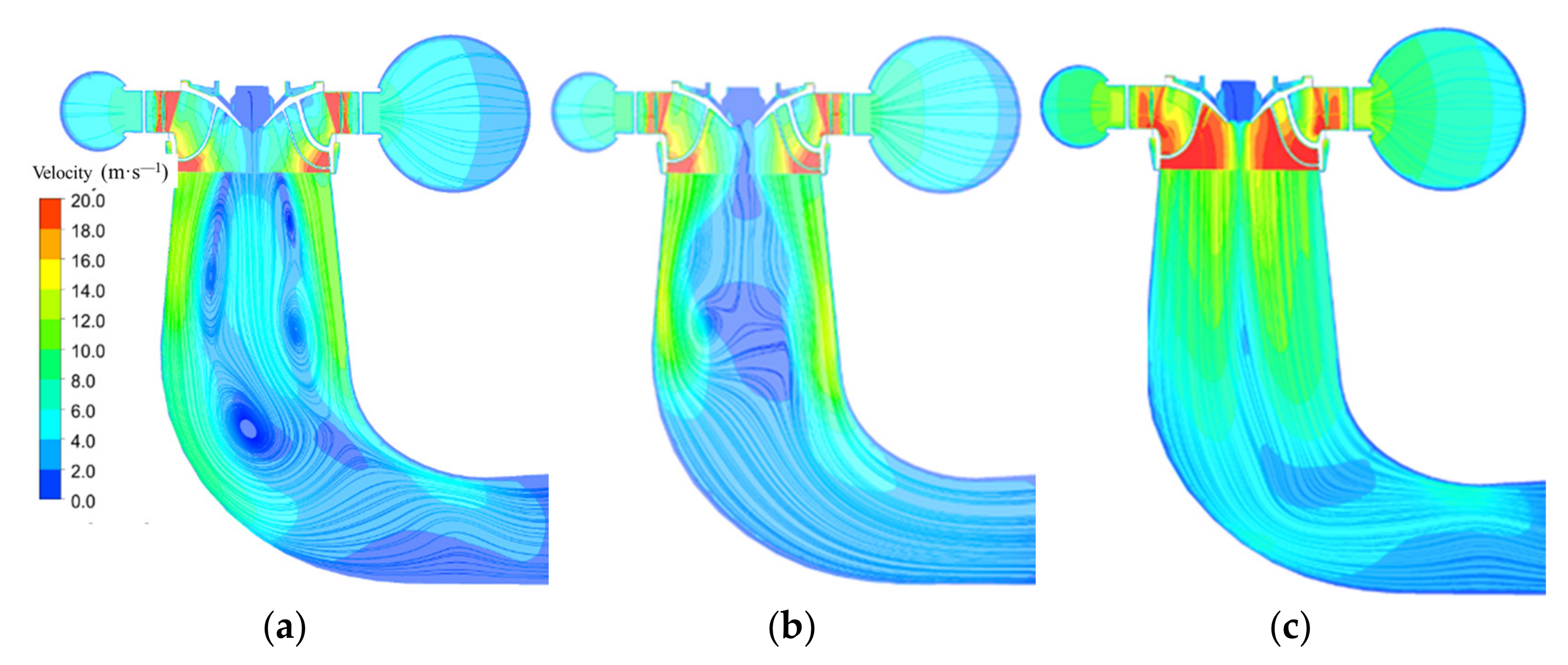
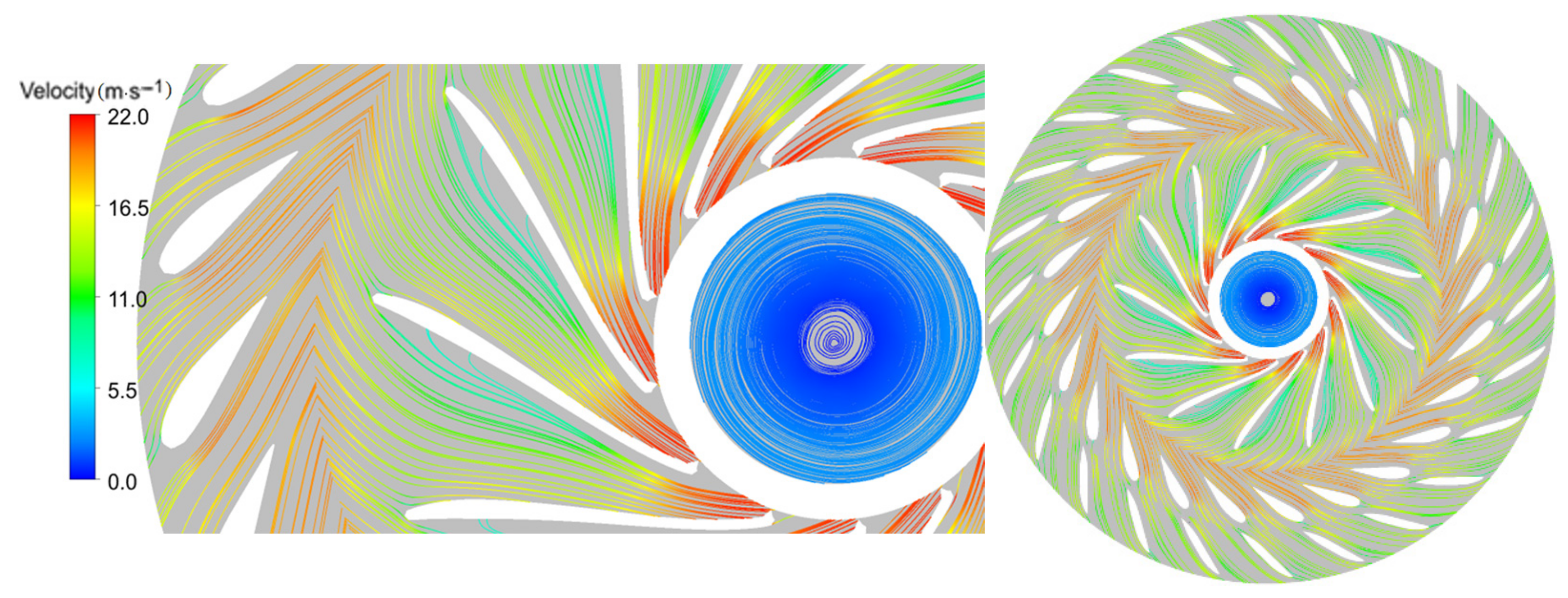
3.1. Flow Pattern of Turbine under Different Openings
3.2. Sediment Distribution at Different Guide Vane Openings
3.3. Sediment Erosion Distribution of Guide Vane and Runner Blade Wall
4. Conclusions
- (1)
- The increase in guide vane opening has an important effect on the particle motion in the runner. With the increase in guide vane opening, the velocity of sediment particles increases, and the impact velocity on the guide vane and runner wall increases. The particles have more energy to destroy the wall structure of the runner and blade. The smaller the opening, the higher the sediment concentration in the runner and guide vane channel. In the low-velocity region of the vortex return center, more particles are separated from the main flow into the vortex center of the channel and away from the runner wall. This is consistent with the flow change law in the runner and guide vane.
- (2)
- The opening of the guide vane affects the flow in the hydraulic turbine channel. When the opening of the guide vane is small, the velocity triangle of the water flow at the inlet of the blade head completely deviates from the design velocity triangle of the hydraulic turbine, the velocity loop of the water flow out of the guide vane cannot meet the velocity loop required by the runner blade, and the relative velocity angle of the water flow entering the runner is larger than the inlet angle of the runner blade, resulting in the water flow hitting the pressure surface of the runner blade at a large angle, and the flow phenomenon occurs at the head of the runner blade. The separated flow loses the restriction of the blade and forms a blade passage vortex in the runner.
- (3)
- The overall sediment erosion in the hydraulic turbine unit with the optimal opening is the smallest, and the erosion rate increases under a small opening and a large opening. The wear of the guide vane and the runner inlet head is mainly impact wear, and the sediment erosion on the outlet wall is mainly frictional wear. The sediment erosion in the unit channel is most serious under a large opening. The long-term wear of the runner inlet and guide vane outlet will cause the loss of local structure, increase the radial clearance of the runner, increase the clearance leakage, increase the vibration of the unit, and reduce the efficiency.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, T.S.; Cha, K.S. Comparative analysis of the influence of labyrinth seal configuration on leakage behavior. J. Mech. Sci. Technol. 2009, 23, 2830–2838. [Google Scholar] [CrossRef]
- Takaffoli, M.; Papini, M. Numerical simulation of solid particle impacts on Al6061-T6 part I: Three-dimensional representation of angular particles. Wear 2012, 292, 100–110. [Google Scholar] [CrossRef]
- Song, X.; Liu, C.; Wang, Z. Prediction on the pressure pulsation induced by the free surface vortex based on experimental investigation and Biot-Saval Law. Ocean Eng. 2022, 250, 110934. [Google Scholar] [CrossRef]
- Song, X.; Luo, Y.; Wang, Z. Numerical prediction of the influence of free surface vortex air- entrainment on pump unit performance. Ocean Eng. 2022, 256, 111503. [Google Scholar] [CrossRef]
- Cheng, X.; Dong, F.; Yang, C. The influence of particle diameter on friction loss intensity and collision wear loss intensity along blades of centrifugal pump. J. Lanzhou Univ. Technol. 2015, 41, 44. [Google Scholar]
- Song, X.; Liu, C. Experiment study of the floor-attached vortices in pump sump using V3V. Renew. Energy 2021, 164, 752–766. [Google Scholar] [CrossRef]
- Matsumura, T.; Shirakashi, T.; Usui, E. Identification of Wear Characteristics in Tool Erosion model of Cutting Process. Int. J. Mater. Form. 2008, 1, 555–558. [Google Scholar] [CrossRef]
- Koirala, R.; Thapa, B.; Neopane, H.P.; Zhu, B. A review on flow and sediment erosion in guide vanes of Francis turbines. Renew. Sustain. Energy Rev. 2017, 75, 1054–1065. [Google Scholar] [CrossRef]
- Qian, Z.; Gao, Y.; Zhang, K.; Huai, W.; Wu, Y. Influence of dynamic seals on silt abrasion of the impeller ring in a centrifugal pump. Proc. Inst. Mech. Eng. Part A J. Power Energy 2013, 227, 557–566. [Google Scholar] [CrossRef]
- Zhang, Y.; Qian, Z.; Ji, B.; Wu, Y. A review of microscopic interactions between cavitation bubbles and particles in silt-laden flow. Renew. Sustain. Energy Rev. 2016, 56, 303–318. [Google Scholar] [CrossRef]
- Smirnov, P.E.; Menter, F.R. Sensitization of the SST turbulence model to rotation and curvature by applying the Spalart–Shur correction term. J. Turbomach. 2009, 131, 041010. [Google Scholar] [CrossRef]
- Guo, B.; Xiao, Y.; Rai, A.K.; Zhang, J.; Liang, Q. Sediment-laden flow and erosion modeling in a Pelton turbine injector. Renew. Energy 2020, 162, 30–42. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Xianbei, H.; Qiang, G.; Baoyun, Q. Prediction of Air-Entrained Vortex in Pump Sump: Influence of Turbulence Models and Interface-Tracking Methods. J. Hydraul. Eng. 2020, 146, 04020010. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar]
- Zeise, B.; Liebich, R.; Prölß, M. Simulation of fretting wear evolution for fatigue endurance limit estimation of assemblies. Wear 2014, 316, 49–57. [Google Scholar] [CrossRef]
- Shrestha, U.; Chen, Z.; Park, S.H.; Do Choi, Y. Numerical studies on sediment erosion due to sediment characteristics in Francis hydro turbine. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 042001. [Google Scholar] [CrossRef]
- Shen, Z.; Chu, W.; Li, X. Sediment erosion in the impeller of a double-suction centrifugal pump—A case study of the Jingtai Yellow River Irrigation Project, China. Wear 2019, 422–423, 269–279. [Google Scholar] [CrossRef]
- Gautam, S.; Neopane, H.P.; Thapa, B.S.; Chitrakar, S.; Zhu, B. Numerical Investigation of the Effects of Leakage Flow From Guide Vanes of Francis Turbines using Alternative Clearance Gap Method. J. Appl. Fluid Mech. 2020, 13, 1407–1419. [Google Scholar]
- Song, X.J.; Liu, C. Experimental investigation of floor-attached vortex effects on the pressure pulsation at the bottom of the axial flow pump sump. Renew. Energy 2020, 145, 2327–2336. [Google Scholar] [CrossRef]
- Fan, M.; Li, Y.; Ji, P. Energy Characteristics of Full Tubular Pump Device with Different Backflow Clearances Based on Entropy Production. Appl. Sci. 2021, 11, 3376. [Google Scholar]
- Zhao, W.; Egusquiza, M.; Estevez, A. Valentín Improved damage detection in Pelton turbines using optimized condition indicators and data-driven techniques. Struct. Health Moni. 2020, 20, 3239–3251. [Google Scholar]
- Karakas, E.S.; Watanabe, H.; Aureli, M.; Evrensel, C.A. Cavitation Performance of Constant and Variable Pitch Helical Inducers for Centrifugal Pumps: Effect of Inducer Tip Clearance. J. Fluids Eng. 2020, 142, 1–19. [Google Scholar] [CrossRef]
- Cao, J.; Luo, Y.; Presas, A.; Ahn, S.H.; Wang, Z.; Huang, X.; Liu, Y. Influence of rotation on the modal characteristics of a bulb turbine unit rotor. Renew. Energ. 2022, 187, 887–895. [Google Scholar] [CrossRef]
- Takaffoli, M.; Papini, M. Numerical simulation of solid particle impacts on Al6061-T6 Part II: Materials removal mechanisms for impact of multiple angular particles. Wear 2012, 296, 648–655. [Google Scholar] [CrossRef]
- Zhu, Y.; Lu, J.; Liao, H.; Wang, J.; Fan, B.; Yao, S. Research on cohesive sediment erosion by flow: An overview. Sci. China Ser. E Technol. Sci. 2008, 51, 2001–2012. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Z.; Song, X.; Zhang, A.; Shao, F.; Wang, Z. Prediction for the Influence of Guide Vane Opening on the Radial Clearance Sediment Erosion of Runner in a Francis Turbine. Water 2022, 14, 3268. https://doi.org/10.3390/w14203268
Jin Z, Song X, Zhang A, Shao F, Wang Z. Prediction for the Influence of Guide Vane Opening on the Radial Clearance Sediment Erosion of Runner in a Francis Turbine. Water. 2022; 14(20):3268. https://doi.org/10.3390/w14203268
Chicago/Turabian StyleJin, Zhiqiang, Xijie Song, Anfu Zhang, Feng Shao, and Zhengwei Wang. 2022. "Prediction for the Influence of Guide Vane Opening on the Radial Clearance Sediment Erosion of Runner in a Francis Turbine" Water 14, no. 20: 3268. https://doi.org/10.3390/w14203268



