1. Introduction
The Sustainable Development Goals (SDGs) adopted by the United Nations in 2015 set forth a basis to pursue the sustainable development of coastal cities that have long been an important gathering place for the global population and economic growth [
1]. As coastal areas are becoming increasingly dependent on ocean resources, leading ocean core competencies, and playing an essential role in a certain region [
2], the creation of global maritime capital has significant implications for the sustainable development of coastal areas. In 2017, China proposed to build global maritime capitals in cities such as Shenzhen and Shanghai. Subsequently, eight cities in China have successively put forward the vision of building and developing global maritime capitals, including two municipalities (Shanghai and Tianjin), one provincial capital (Guangzhou), four sub-provincial cities (Shenzhen, Dalian, Qingdao, Ningbo) and one prefecture-level city (Zhoushan).
However, coastal cities are at a higher risk of being affected by marine disasters such as storm surges, red tides and waves than other cities [
3]. Under global warming, the interaction imbalance between the atmosphere and the ocean represented by ENSO (El Nino and Southern Oscillation) occurs frequently, and the intensity and frequency of marine disasters are further enhanced. It seriously limits the sustainable development of maritime finance and trade, the governance of the maritime industry and marine culture in coastal cities. Therefore, the construction of a global maritime capital must take into account the management of maritime catastrophes. Vulnerability refers to the propensity to be adversely affected and encompasses a variety of indexes including adaptive capacity, sensitivity and exposure [
4]. Vulnerability assessment is an important component of disaster risk management and an effective tool to formulate policies and guide priority disaster reduction measures [
5,
6]. However, recent research has started to shift from disaster vulnerability to resilience, as resilience is recognized as an optimistic and practical expression of engagement in emergencies [
7,
8,
9]. The importance of research on disaster resilience has been recognized by international organizations and cooperation treaties. In 2010, the United Nations Office for Disaster Risk Reduction (UNDRR) launched the “Cities are Resilient” campaign to encourage cities to join in building resilience [
10]. In addition, the Sendai Framework for Disaster Risk Reduction 2015–2030 emphasized the restoration capacity of disasters through the implementation of inclusive and integrated social, economic, institutional, technological, educational and political measures [
11]. The SDGs also emphasized building community resilience to natural disasters, with a focus on local planning and management [
12].
Many conceptual frameworks have been proposed for the assessment of disaster resilience. Mayunga proposed a capital-based approach and constructed a conceptual framework of Community Disaster Resilience Index (DRI) that includes social, economic, demographic, material and natural capitals [
13]; Cutter et al. argued that disaster resilience has multiple dimensions, including physical, social, institutional, economic, and ecological factors, and proposed a Baseline Resilience Indicator for Communities (BRIC) based on the theoretical framework of the Disaster Resilience of Place (DROP) model [
7,
8]; Joerin et al. assessed the physical, social and economic resilience of individuals through a Climate-related Disaster Community Resilience Framework (CDCRF) [
14]; Yoon et al. proposed the Community Disaster Resilience Index (CDRI), measured by human, social, economic, environmental, and institutional factors, for the comprehensive disaster resilience of the entire country of South Korea [
15]; Lam et al. and Cai et al. proposed the Resilience Inference Measurement (RIM) model to assess and validate community resilience to coastal hazard in the Caribbean and Mississippi regions [
16,
17]. In addition, scholars have conducted several studies on different types of hazards, such as multiple hazards [
18,
19,
20,
21], hurricanes [
22], floods [
4,
23,
24] and earthquakes [
25]. However, a unified framework and model for disaster resilience assessment is still lacking [
9]. A widely adopted resilience model is based on the capital division model to divide the study unit’s resilience, according to different components such as demographic, economic, social, and material capitals, which are necessary to develop a sustainable economy [
13]. The more capital the research unit has, the more resilient it is, which emphasizes the research unit’s capacity and its stakeholders’ ability to adapt. A capital perspective can provide policy makers with a clearer picture of resilience actions and strategies [
21].
Current assessment methods for disaster resilience mainly include tool evaluation models, scorecard models and indicator evaluation models [
26,
27,
28]. Compared to the previous two approaches, indicator-based evaluation can summarize complex or multifaceted problems into a simple form that is easy to understand [
9,
15] and help to compare longitudinal or transverse results [
7]. Since disaster resilience is an abstract, multidimensional and interdisciplinary concept [
15], the indicator evaluation model is more commonly used in this research area [
7,
13]. However, as a complex nonlinear system at the intersection of nature and socio-economics, disaster resilience assessments based on the indicator system approach continue to be controversial in terms of quantification and assessment methods. The controversial portion mainly involves determining subjective or objective weights and aggregation techniques for compensatory or non-compensatory resilience indices [
27,
28]. In addition, there are fewer articles on the identification of the key influencing factors of disaster resilience. Some references have used regression methods to identify key factors affecting disaster resilience [
15,
17,
22]. However, as a comprehensive problem, the large number of influencing factors involved in disaster resilience is prone to have the curse of dimensionality, and problems such as multiple co-linearities in the regression process are difficult to solve. Machine learning, on the other hand, has inherent advantages in overcoming the curse of dimensionality and nonlinear problems through information mining and is also outstanding in assessment accuracy. Among them, random forest (RF), as an integrated learning method, is insensible to multicollinearity and is not susceptible to overfitting. It has a fast-learning process, does not require normalization of variable units, and has good tolerance for aberrations and noises [
29,
30]. It is also possible to identify critical indicators of the fitted results based on the RF model, which is beneficial for subsequent improvement work [
31]. Researchers have attempted to apply RF to flood disasters and have achieved good assessment results [
32]. However, to the best of our knowledge, the use of RF models in marine disaster resilience is very limited.
Based on this, our study constructed and measured the Chinese Coastal Marine Disaster Resilience Index (CMDRI), and then applied the RF model to assess marine disaster resilience and identified the key influencing factors of CMDRI for eight coastal cities in China that are proposed to build a global maritime capital. Finally, multiple evaluation indicators such as MAE, MAPE, R2, RMSE and a five-fold cross-validation were used to compare and validate the reasonableness and reliability of the RF assessment results. The contributions of this study arethe following: firstly, the innovative construction and measurement of the CMDRI for Chinese coastal cities complements and expands the research content in the field of disaster resilience, taking into account the characteristics of major marine disasters suffered by Chinese coastal cities; secondly, we applied the RF model for the first time to the evaluation of marine disaster resilience and the identification of key factors, which solves previous problems such as ambiguity in assessing complex nonlinear systems and the curse of dimensionality, and has significant academic value.
This paper is divided into five parts.
Section 1 is the introduction and
Section 2 depicts the construction of CMDRI and data sources.
Section 3 describes the research methods used in this paper. Details on the main empirical results and discussions are conducted in
Section 4. The last section is the conclusion and future research needs.
2. Construction of Coastal Marine Disaster Resilience Index (CMDRI) and Data Sources
The term “resilience” is often used in the same way as the concept of “bouncing back” that reflects its Latin root, “resiliere” [
33]. The concept of resilience was introduced into ecology by Holling in 1973 to describe the behavior of dynamic systems that stay stable despite disturbances and changes [
34]. Subsequently, Timmerman in 1981 introduced the concept of resilience into the field of natural disasters, defining it as the ability of a system to absorb disaster disturbances and recover from disaster events [
35]. Since then, the study of disaster resilience has been valued by scholars and experts in the fields of socio-economics, environmental change and disaster [
36]. The definition of resilience varies depending on the goals of the study. The UNDRR and National Research Council (NRC) defined it as the ability of a system, community or society exposed to hazards to resist, absorb, accommodate and recover from the effects of a hazard in a timely and efficient manner, including through the preservation and restoration of its essential basic structures and functions [
37,
38]. This definition has been identified as the most appropriate definition for resilience [
39]. Cutter et al. defined resilience as the ability of individuals or communities to adapt through resistance or change to achieve and sustain their survival and functioning, and the social aspect less formally involves the ability of individuals to recover with minimal disruption [
7]. Mayunga proposed a capital-based approach and viewed resilience as the ability of communities and their built environment to quickly mitigate, prepare, respond to and recover from disasters and adapt to new situations while learning from past disasters [
13]. Lam et al. defined resilience by including both aspects of vulnerability to hazards and adaptive capacity over time. In their view, resilience is the ability to successfully prepare, plan, absorb, recover from, and adapt to adverse events [
16].
Although many researchers have given the definition of disaster resilience, there is still a lack of consensus on the selection of disaster resilience indicators. The main reason behind this is the different nature of socio-economic systems and organizational environments of research units [
7]. However, these indicators can be converted from one region to another based on data availability and understanding [
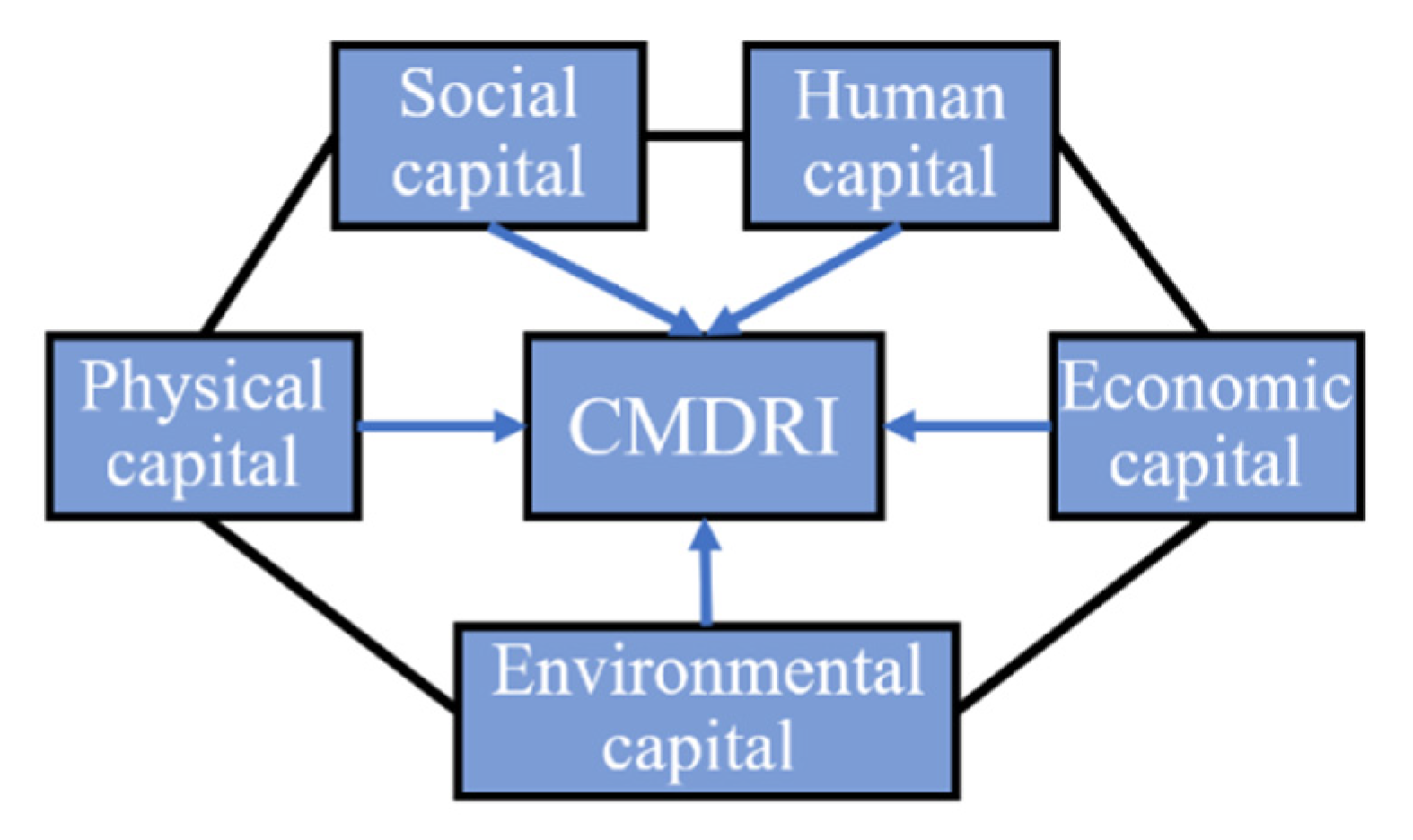
9]. With reference to the existing literature, this study defines coastal marine disaster resilience as “the ability of coastal cities to rapidly mitigate, prepare, respond and recover from, and adapt to new disaster situations while learning from past marine disasters”. Based on the capital perspective, human, social, economic, physical and environmental capitals were selected [
8,
15,
22,
36,
37,
40] to construct the framework of Coastal Marine Disaster Resilience Index (CMDRI), as shown in
Figure 1. Combined with the characteristics of marine disasters in coastal cities and data availability, 34 capacity indicators and 18 sub-dimensions were selected, covering five capitals of disaster resilience (
Table 1). The existing literature also contains indicators of other dimensions, such as cultural indicators (organizational beliefs, religions, etc.). However, considering the coastal city scale and the data unavailability, they were not included in this study [
28].
Human capital refers to the innate, derived or accumulated capacity of human beings to cooperate effectively with other forms of capital to sustain all aspects of economic production and life during all phases of a disaster [
41]. This study uses four components to measure the characteristics associated with disaster phases: demographics, gender structure, age structure, and educational attainment. Social capital is defined primarily as the social structures and networks that promote collective action [
36], with a general emphasis on coordination and cooperation in the mutual interest. This study of social capital refers to the characteristics of information, communication and the capacity of social assistance organizations, mainly to improve resilience during disasters and in post-disaster reconstruction [
15]. Economic capital is commonly defined as the financial resources that people use to support themselves [
36]. It comprises principally the level and diversity of the economy, the level of investment, employment and foreign trade. Among them, economic diversity means that the urban economy should not rely on the development of a single industry that is more affected by the marine disaster. Otherwise, it is difficult to quickly recover from the final stages of the catastrophe. This study reflects the proportion of other industries that have eliminated industries that are easily impacted by marine disasters, such as transportation, accommodation and tourism [
8]. Economic capital measures the ability of cities to withstand financial disruptions caused by damage and losses from marine disasters. Cities with more robust economic and financial resources have greater resilience.
In this study, physical capital is defined as the overall built environment [
36] that helps people sustain their livelihoods, including basic physical capital, critical physical capital, housing conditions for residents, and the number of schools, libraries, and hotel establishments that can provide temporary shelter services in a disaster event. Physical capital is critical to the effective functioning of cities, especially during evacuations, to ensure that people have the resources and support they need in an emergency. Environmental characteristics in terms of resources and atmospheric and geographic factors are also considered in measuring resilience to marine hazards [
32]. Environmental capital is essential for the maintenance of all life forms, including human life [
41]. Storm surges, red tides, and waves are the major marine hazards experienced in China’s coastal areas. Therefore, this study innovatively included the disaster-causing factors and geographic conditions that lead to the major marine hazards to the environmental capital, such as wastewater discharge, rainfall, sea level height elevations and coastal line data. In addition, natural resources such as green area cover were also included to measure the impact of urban hazard mitigation.
The data in this paper came from the statistical yearbooks, the national economic and social development bulletins of eight coastal cities, the China Marine Disaster Bulletin, the China Sea Level Bulletin, and the China Economic and Social Development Statistical Database. The indicators reflecting the age structure and education attainment do not have annual data. This paper linearly interpolated according to the results of each city’s fifth, sixth and seventh population census bulletins. The urban elevation data were obtained from the China geographic information resource catalog service system (
http://www.webmap.cn/ (accessed on 20 August 2022)), based on ArcGIS software (Release 10.7, Environmental Systems Research Institute, Redlands, CA, USA) for unified processing after spatial statistics. Some data were calculated based on statistical data, and the missing data were supplemented with the mean value method.
5. Conclusions
The frequent outbreak of marine disasters in the context of global warming poses a serious threat to the sustainable development of coastal areas and the construction of global maritime capitals. Marine and coastal management and marine disaster resilience assessment of maritime capitals have become the research focus. For eight coastal cities in China that propose to build global maritime capital, this paper innovates by constructing and calculating the CMDRI for China’s coastal cities, evaluating marine disaster resilience and identifying key factors first using the RF model. The results show that:
- (1)
The overall level of CMDRI in each city is at a steady increase, with the highest level in Shenzhen and the relatively lowest level in Zhoushan throughout the all years. With the exception of Zhoushan, the remaining cities have achieved an increase in CMDRI grades during 2000–2019. Shenzhen, Shanghai and Guangzhou belong to the southeast coastal region with relatively high CMDRI, while Dalian, located in the Yellow Bohai Sea region, is relatively lower than Tianjin and Qingdao.
- (2)
In the identification of key factors, coastline length, the population burdened by each employed person, coverage rate of urban green area, number of beds in health facilities, total import and export, total fixed asset investment and the percentage of population with high school education and above are the indicator factors ranked high in the importance of evaluation results. Economic and human capitals are the most essential urban capital in the identification of key factors, followed by physical and social capitals, with environmental capital having the smallest share.
- (3)
Compared to SVM and LR models, the fitting accuracy and generalization ability of the RF model are better than other models. In addition, the RF model has better stability in the assessment process, and the results are more reasonable. The RF performs well in assessing and identifying the CMDRI, and the developed method can be transferred to other fields of disaster resilience and regional sustainability assessment.
Determining the level of city resilience to marine hazards and key factors will provide strategic direction for emergency policymakers to reduce the negative impacts of disasters. According to the results, managers of coastal cities can make full use of location advantages to develop the economy and attract labor power. Specifically, the following suggestions are proposed: (1) reduce the burden of the employed population while improving the quality of the population; (2) enhance the level of urban trade and investment; (3) strengthen the city’s medical help capacity and the level of urban green area; (4) pay attention to the supervision and warning of marine disasters in cities with long coastlines, such as Zhoushan and Dalian. This study provides a reference for coastal cities to incorporate marine disaster resilience into disaster risk management plans. Improving the key factors of CMDRI and ensuring rapid regulation will have a significant and long-lasting driving effect and jointly promote the improvement of marine disaster resilience in coastal cities for the smooth construction of global maritime capital. There will be other coastal cities considered for the construction of global maritime capital. This study has proved that the CMDRI has good city adaptability and can be applied to other coastal cities in China to assess marine disaster resilience. At the same time, our results are also of practical value for other coastal areas around the world that rely on marine resources but often suffer from marine disasters, such as the Caribbean and the Mediterranean regions. By identifying the level of disaster resilience and key impact factors, research results will have excellent references for marine disaster management and the sustainable development of coastal cities.
Finally, further studies could improve the potential limitations of this study. Due to the inconsistencies in the timing length and statistical caliber of the statistical data in various cities, some indicators referring to organizational beliefs, disaster warning capabilities and so on could not be included in the study. However, with the continuous improvement of marine disaster monitoring, socioeconomic development, and the utilization of predictive modeling, such as grey models [
48], it will be possible to break through data availability limitations and consider an appropriate increase in indicators of the marine disaster resilience system.