Online Storage Technology of the Separate Sewage System: Demonstration Study in a Typical Plain River Network City
Abstract
:1. Introduction
2. Methodology
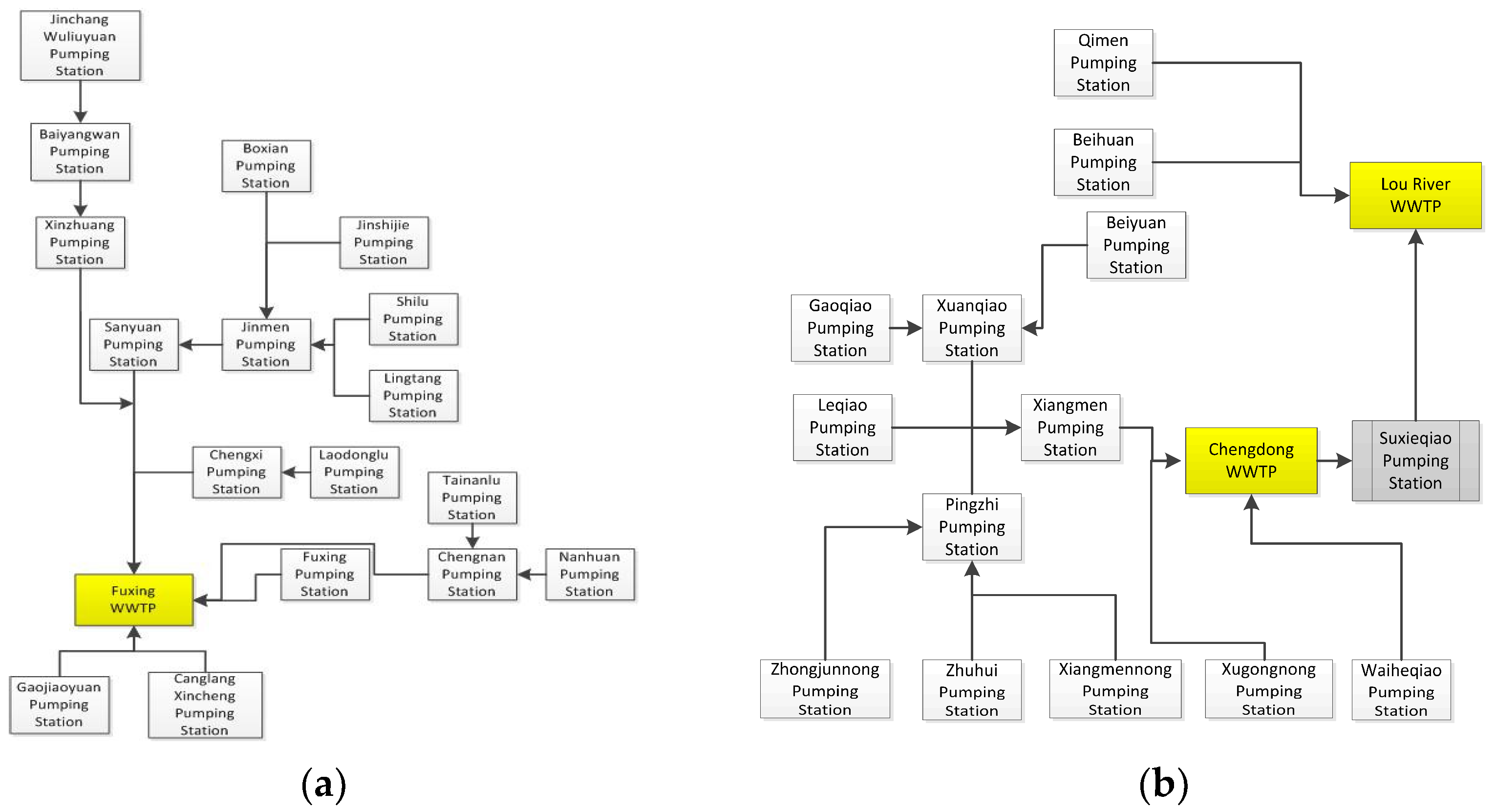
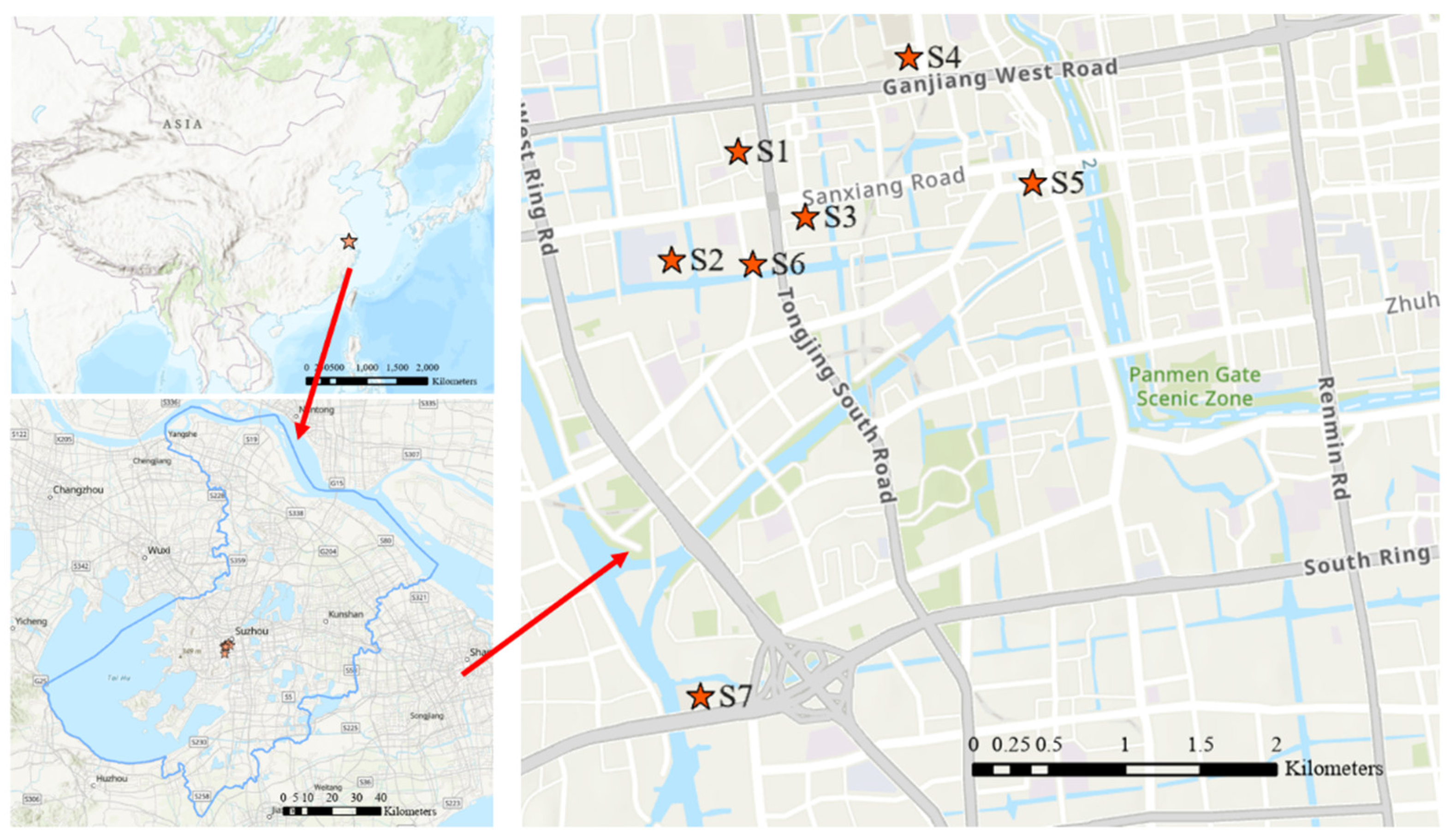
2.1. Site Description
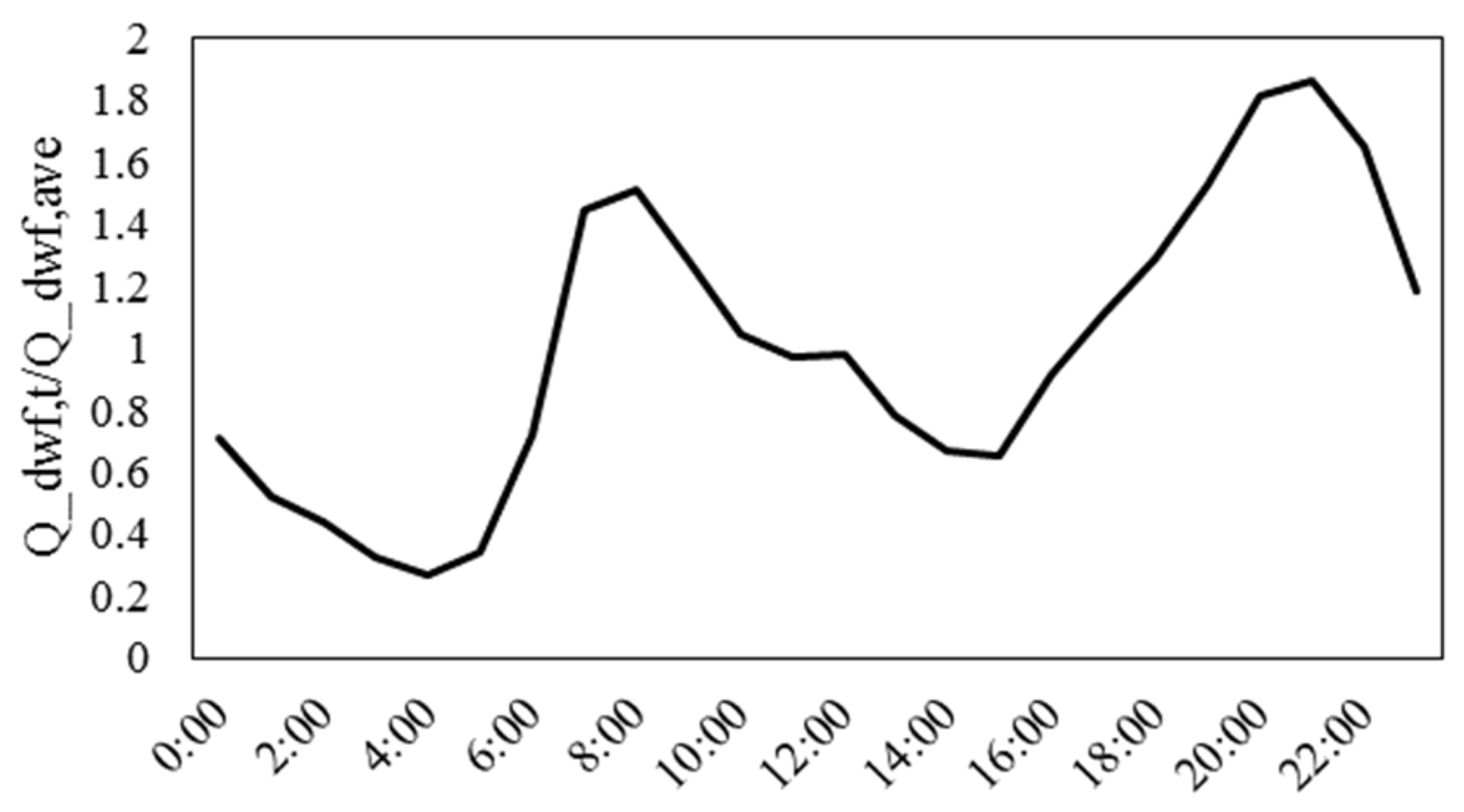
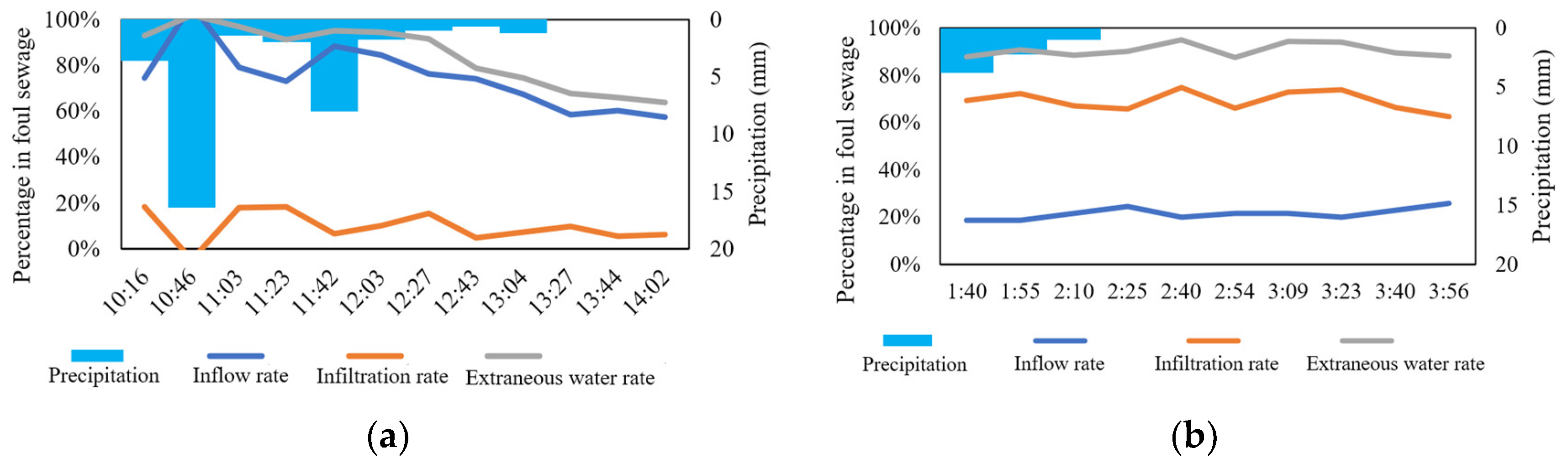
2.2. I/I Quantification
2.3. SWMM-Based Analysis of Storage Capacity
- (1)
- Base Model-Hydraulic Module
- (2)
- Infiltration Module
- (3)
- Inflow module
- (4)
- Storage capacity evaluation
2.4. Rule-Based Control Strategy for Online Storage Scheduling
- The pumping stations are classified according to their importance of the service area and ground elevation. Commercial, residential areas, and areas with low ground elevation (prone to flooding) are listed as critical protection areas; industrial areas away from the city center, logistics areas, and areas with high ground elevation are listed as general areas.
- When there is an increase in the I/I induced by rainfall, priority is given to ensuring the normal operation of pumping stations in critical areas, increasing the conveying amount of water and avoiding sewage overflow in these areas. For general areas, reduce the conveying amount of water from pumping stations, alleviating the pressure of their water load on pumping stations in downstream critical areas.
- The pre-emptying rule before rainfall. Suppose the weather forecast indicates that a rainfall event will occur. In that case, the sewage plant and the pumping station intake can be increased in advance for pre-emptying of the pipe network to cope with the upcoming rainfall event.
- Water-level balancing rules of lateral pumping stations under rainfall. Under rainfall, a pumping station (called “pumping station A”) exceeds its critical water level, in addition to flow restriction upstream, the water-level balance of lateral pumping stations (other pumping stations that converge to the same downstream pumping station) can also be carried out. Suppose the water level of the lateral pumping station B is below the critical level. In that case, the flow of pumping station B can be reduced (using the storage room of the pipeline system when the critical level has not been reached). In contrast, the flow of pumping station A can be increased to ensure that the total flow is relatively stable to better achieve the level balance between pumping stations A and B, making full use of the storage room of different pumping stations.
- Limit water-level protection rules. Set the limit levels (including the minimum and maximum values) for each pumping station. When the level is lower than the minimum value, all pumps must be forced off; a pump (or multiple pumps) must be forced on when the level is higher than the maximum value.
- Flow restoration rules after rainfall. After rainfall, if all other downstream pumping stations and the front pond of the sewage plant have returned to their normal level range, the pumping station can be released from the rain flow restriction and return to dry-season level control mode. Executing judgment on individual pumping stations allows all pumping stations to gradually return to the dry-season control mode. However, it should be noted that in order to avoid unstable pumping station operation, when cutting back to dry-season control mode, instead of starting multiple pumps (not including those previously switched on), only one pump should be switched on for a certain period of time, followed by the next pump.
- In accordance with the above principles, changes in water levels at the pumping stations and complaints of sewage overflow in their service areas are monitored during rainfall, and the operation of pumping stations is scheduled based on manual experiences and storage capacities evaluated from Section 2.3.
- (1)
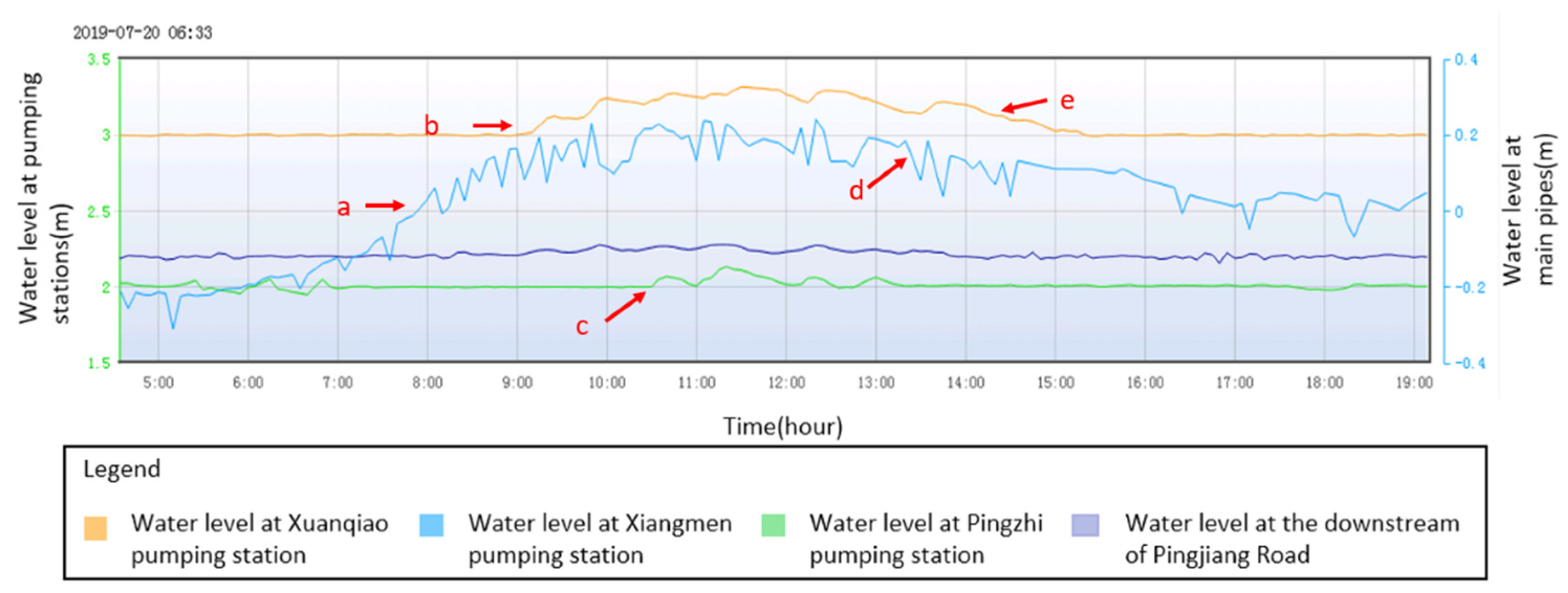
- If the rising rate and duration of water level at the Xiangmen pumping station exceed a specific value, indicating the flow amount of influent is large. According to particular rules, the pump-control water level is increased up to the maximum limit to maximize online storage capacity at this level.
- (2)
- At the same time, calculate and assess the storage capacities of the two upstream pumping stations of Xuanqiao and Pingzhi and their corresponding pipes in their service areas. Prioritize the reduction of water conveyance from the Xuanqiao pumping station in accordance with its importance and storage capacity to reduce the pressure of rising water levels at the downstream Xiangmen pumping station.
- (3)
- If the water level of the Xiangmen pumping station is still rising, reduce the amount of water conveyed from the Pingzhi pumping station. Conversely, when the peak flow has passed and the water level at Xiangmen pumping station tends to be normal, the pumping stations will gradually return to their original operating state in order.
3. Results and Discussion
3.1. I/I Quantification
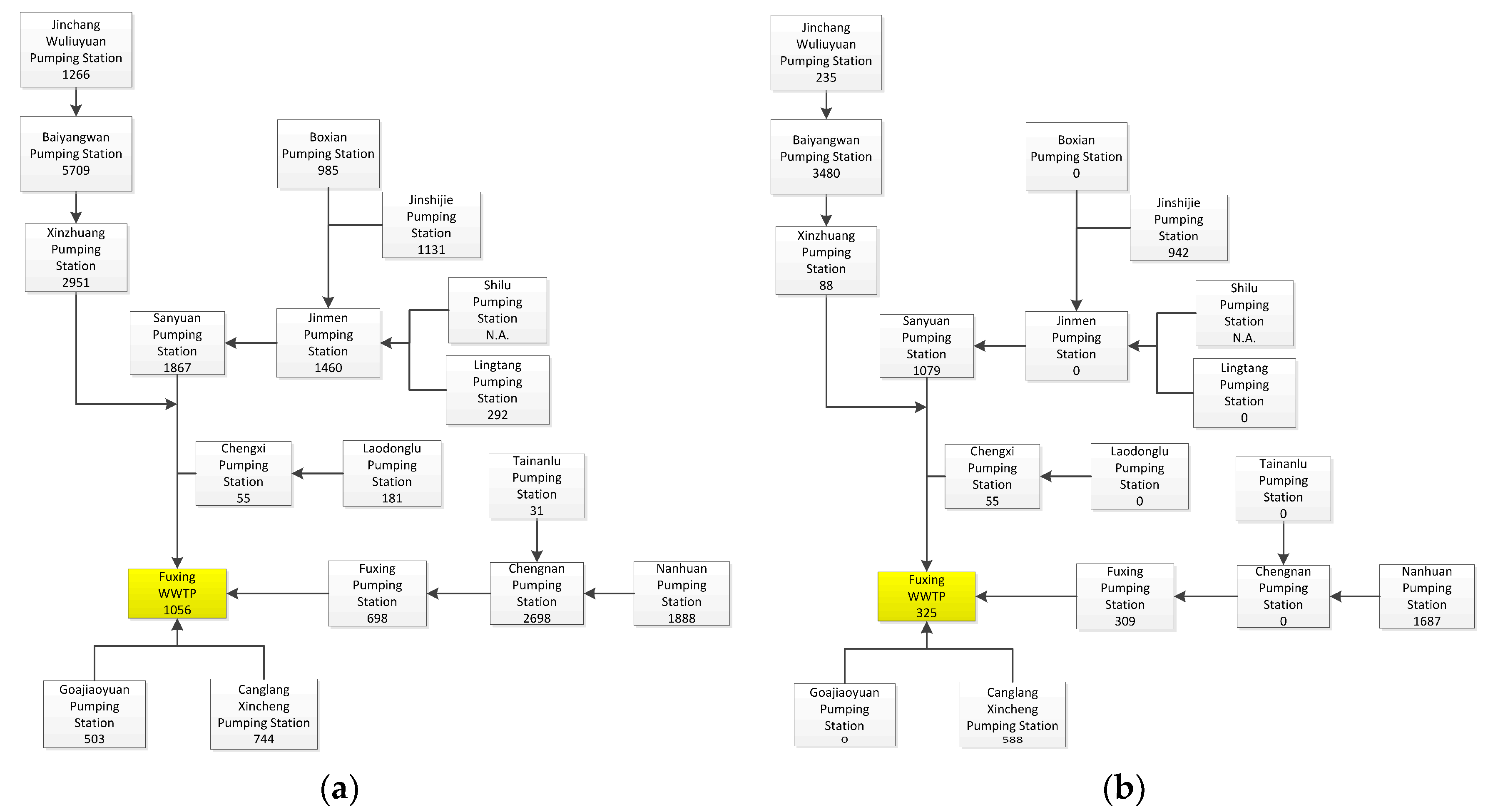
3.2. SWMM Model and Storage Capacity Evaluation
3.3. Effects of Rule-Based Control Strategy
- The peak-time water level and duration are significantly reduced. Compared with 2020, the average duration of peak hours during daytime is reduced by 3 h, and the highest water level is reduced by 56 cm. The average duration of peak hours at night is reduced by 1 h, and the highest level is reduced by 55 cm. The design cooperative control mode reduces the duration of peak hours and the highest level and fully guarantees the safety of the pipe network operation.
- The storage capacity of the pipe network has increased significantly. After implementation, the storage capacity was increased by 198 and 293% during the day and night, separately.
- The number of pump starts and stops was reduced by 96%. The number of frequent starts and stops before commissioning was 15.8 times/day; after commissioning, the number of frequent starts and stops was 0.6 times/day, an overall decrease of 96% compared to the same period in the previous year. The number of frequent starts and stops of the sewage pumping station has been significantly reduced, which has a positive effect on the pump-life extension and the reduction of energy consumption of the pumping station.
- In terms of energy consumption per unit in the pumping stations, the average unit consumption before was 0.037 kWh/m3 and after was 0.032 kWh/m3, a 12.2% overall decrease compared to the same period in 2020.
- Inflow fluctuations of the sewage plant were reduced by 30%. Through pre-drainage during the usual period, staggered conveyance and discharge during the peak period utilizing full use of the sewage network storage room make the influent flow to plants water relatively balanced, ensuring a stable sewage plant operation and effluent quality.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liang, S.; Liu, Y.; Dong, X. Evaluation of the current drainage system in China and some policy advice. Water Wastewater Engineering 2018, 44, 132–140. [Google Scholar]
- Jenssen Sola, K.; Bjerkholt, J.T.; Lindholm, O.G.; Ratnaweera, H. Infiltration and Inflow (I/I) to wastewater systems in Norway, Sweden, Denmark, and Finland. Water 2018, 10, 1696. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Wang, L.; Yi, H.; Li, H. Quantification of Groundwater Infiltration into Urban Drainage Networks Based on Marker Species Approach. J. Tongji Univ. (Nat. Sci.) 2016, 44, 593–599. [Google Scholar]
- Weiss, G.; Brombach, H.; Haller, B. Infiltration and inflow in combined sewer systems: Long-term analysis. Water Sci. Technol. 2002, 45, 11–19. [Google Scholar] [CrossRef]
- Ertl, T.; Spazierer, G.; Wildt, S. Estimating groundwater infiltration into sewerages by using the moving minimum method—A survey in Austria. In Proceedings of the 11th International Conference on Urban Drainage, Edinburgh, UK, 31 August–5 September 2008. [Google Scholar]
- Gasperi, J.; Cladière, M.; Rocher, V.; Moilleron, R. Combined sewer overflow quality and EU Water Framework Directive. Urban Waters 2009, 1, 124–128. [Google Scholar]
- Council, D.C.; Council, D.L.C.; Council, F.C.; Council, K.C.; Council, M.C.; Council, W.C. Greater Dublin Strategic Drainage Study. Dublin. New Development Policy–Technical Guidance Document. 2005; pp. 1–5.
- Kracht, O.; Gujer, W. Quantification of infiltration into sewers based on time series of pollutant loads. Water Sci. Technol. 2005, 52, 209–218. [Google Scholar] [CrossRef] [PubMed]
- Bareš, V.; Krejčí, P.; Stránský, D.; Sýkora, P. Long-term monitoring of infiltration/inflow based on diurnal variation of pollutant mass flux. In Proceedings of the 11th International Conference on Urban Drainage, Edinburgh, UK, 31 August–5 September 2008. [Google Scholar]
- Liu, X.H.; Zhang, J.S.; Goulven, I. Groundwater Infiltration in Shenzhen Drainage System. China Water Wastewater 2013, 29, 77–79. [Google Scholar]
- Tian, L.; Zhang, S.F.; Shi, Z.B. Evaluation on Ground Water Infiltration Capacity into Shanghai Sewerage System. China Water Wastewater 2013, 19, 12–15. [Google Scholar]
- García, L.; Barreiro-Gomez, J.; Escobar, E.; Téllez, D.; Quijano, N.; Ocampo-Martínez, C. Modeling and real-time control of urban drainage systems: A review. Adv. Water Resour. 2015, 85, 120–132. [Google Scholar] [CrossRef] [Green Version]
- Garofalo, G.; Giordano, A.; Piro, P.; Spezzano, G.; Vinci, A. A distributed real-time approach for mitigating CSO and flooding in urban drainage systems. J. Netw. Comput. Appl. 2017, 78, 30–42. [Google Scholar] [CrossRef]
- Lund, N.S.V.; Borup, M.; Madsen, H.; Mark, O.; Mikkelsen, P.S. CSO Reduction by Integrated Model Predictive Control of Stormwater Inflows: A Simulated Proof of Concept Using Linear Surrogate Models. Water Resour. Res. 2020, 56, e2019WR026272. [Google Scholar] [CrossRef]
- Lund, N.S.V.; Falk, A.K.V.; Borup, M.; Madsen, H.; Steen Mikkelsen, P. Model predictive control of urban drainage systems: A review and perspective towards smart real-time water management. Crit. Rev. Environ. Sci. Technol. 2018, 48, 279–339. [Google Scholar] [CrossRef]
- Mullapudi, A.; Lewis, M.J.; Gruden, C.L.; Kerkez, B. Deep reinforcement learning for the real time control of stormwater systems. Adv. Water Resour. 2020, 140, 103600. [Google Scholar] [CrossRef]
- Saliba, S.M.; Bowes, B.D.; Adams, S.; Beling, P.A.; Goodall, J.L. Deep Reinforcement Learning with Uncertain Data for Real-Time Stormwater System Control and Flood Mitigation. Water 2020, 12, 3222. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, L.; Zhang, X.; Xue, A. Fuzzy Optimal Control of Sewage Pumping Station with Flow Concentration. In Proceedings of the International Conference on Computer Science, Environment, Ecoinformatics, and Education, Wuhan, China, 21–22 August 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 259–266. [Google Scholar]
- Hou, S.; Li, D.; Xi, Y.; Cen, L. Energy-saving optimization of urban drainage system based on pump performance. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015; pp. 308–313. [Google Scholar]
- Choukri, L.; Lasri, R.; Bouhorma, M. Application of Fuzzy Logic in Energy Efficiency for one Pumping Systems. In Proceedings of Proceedings of the 2nd International Conference on Computing and Wireless Communication Systems, Larache, Morocco, 14–16 November 2017; pp. 1–6. [Google Scholar]
- Fecarotta, O.; Carravetta, A.; Morani, M.C.; Padulano, R. Optimal pump scheduling for urban drainage under variable flow conditions. Resources 2018, 7, 73. [Google Scholar] [CrossRef]
- Huang, M. Strategy Research on Intelligent Optimal Coordinated Discharge of Urban Sewage Based on Flow. Master’s Thesis, Tongji University, Shanghai, China, 2010. [Google Scholar]
- Song, C.F.; Zhou, W.D.; Wang, X.H. Optimal Schedule CPN Model for Regional Drainage Pump Station. Comput. Eng. 2011, 37, 240–244. [Google Scholar]
- Chen, L.L.; Xia, Y.Y.; Wang, X.H. Flow predictable optimal scheduling control of sewage discharge system. Appl. Mech. Mater. 2012, 121, 848–852. [Google Scholar] [CrossRef]
- Zhuan, X.; Xia, X. Optimal operation scheduling of a pumping station with multiple pumps. Appl. Energy 2013, 104, 250–257. [Google Scholar] [CrossRef]
- Zhang, Q. Research on Risk Assessment of Urban Sewage Pipeline and Optimal Operation of Sewage Pumping Station. Master’s Thesis, Hefei University of Technology, Hefei, China, 2019. [Google Scholar]
- Zhang, Q.; Guo, H. Circulation Differences in Anomalous Rainfall over the Yangtze River and Huaihe River Valleys in Summer. Chin. J. Atmos. Sci. 2014, 38, 656–669. [Google Scholar]
- Yao, Y. Performance Assessment of Urban Drainage System based on Quantification of Inflow and Infiltration. Master’s Thesis, Tsinghua University, Beijing, China, 2019. [Google Scholar]
- APHA. Standard Methods for the Examination of Water and Wastewater; American Public Health Association: Washington, DC, USA, 2005. [Google Scholar]
- Zhang, Q.; Luo, Z.; Lu, W.; Harald, Z.; Zhao, Y.; Tang, J. Using water isotopes and hydrogeochemical evidences to characterize groundwater age and recharge rate in the Zhangjiakou area, North China. J. Geogr. Sci. 2020, 30, 935–948. [Google Scholar] [CrossRef]
- Yao, P.; Zheng, L.; Liao, X.; Jin, H.; He, B. An efficient graph accelerator with parallel data conflict management. In Proceedings of the 27th International Conference on Parallel Architectures and Compilation Techniques, Limassol, Cyprus, 1–4 November 2018; pp. 1–12. [Google Scholar]




| Indicator | Statistical Type | Source of Sewage | Upstream Mixed Sewage | Downstream Mixed Sewage | Infiltration | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Residents | Productive Service | S1 | S2 | S3 | S5 | S6 | S7 | Groundwater | ||
| TN | Range | 51.9~109.0 | 17.9~31.6 | 4.9~28.0 | 15.7~51.3 | 35.8~99.6 | 8.0~44.0 | 22.4~59.2 | 27.5~58.1 | 1.1~3.5 |
| Average | 69.3 | 23.9 | 13.3 | 27.4 | 60.7 | 17.6 | 37.4 | 43.3 | 2.5 | |
| Standard deviation | 17.0 | 6.0 | 8.2 | 11.6 | 19.4 | 11.6 | 10.2 | 9.9 | 0.8 | |
| Coefficient of variation | 0.25 | 0.25 | 0.62 | 0.42 | 0.32 | 0.66 | 0.27 | 0.23 | 0.31 | |
| Electric conductivity | Range | 756~1743 | 998~1274 | 670~793 | 752~1172 | 790~1229 | 632~1040 | 624~995 | 908~1233 | 690~739 |
| Average | 1156 | 1110 | 728 | 889 | 955 | 778 | 761 | 1012 | 714 | |
| Standard deviation | 242 | 126 | 41 | 132 | 119 | 129 | 122 | 101 | 21 | |
| Coefficient of variation | 0.21 | 0.11 | 0.06 | 0.15 | 0.12 | 0.17 | 0.16 | 0.1 | 0.03 | |
| 18O | Range | −3.55~−3.44 | −3.57~−3.33 | −4.57~−3.74 | −4.05~−3.49 | −4.02~−2.83 | −5.17~−4.20 | −4.74~−4.44 | −4.27~−3.82 | −6.23~−5.31 |
| Average | −3.50 | −3.48 | −4.09 | −3.83 | −3.64 | −4.74 | −4.59 | −4.00 | −5.72 | |
| Standard deviation | 0.04 | 0.12 | 0.25 | 0.17 | 0.32 | 0.31 | 0.09 | 0.13 | 0.38 | |
| Coefficient of variation | 0.01 | 0.03 | 0.06 | 0.04 | 0.09 | 0.06 | 0.02 | 0.03 | 0.07 | |
| 2H | Range | −27.55~−27.05 | −28.02~−26.74 | −33.25~−27.31 | −30.00~−26.67 | −29.44~−20.69 | −38.56~−31.06 | −32.26~−30.50 | −31.79~−29.44 | −40.29~−30.71 |
| Average | −27.29 | −27.47 | −30.31 | −28.56 | −26.40 | −35.55 | −31.14 | −30.51 | −36.05 | |
| Standard deviation | 0.14 | 0.57 | 1.64 | 1.30 | 2.59 | 2.50 | 0.58 | 0.67 | 4.25 | |
| Coefficient of variation | 0.01 | 0.02 | 0.05 | 0.05 | 0.10 | 0.07 | 0.02 | 0.02 | 0.12 | |
| Spatial Hierarchy | Typical Plots | Service Area of Pumping Station | Service Area of WWTP | |||
|---|---|---|---|---|---|---|
| Monitoring points | S1 | S2 | S3 | S5 | S6 | S7 |
| Hourly average infiltration rate (%) | 27 | 15 | 8 | 55 | 48 | 22 |
| Hourly average infiltration flow (L/s) | 0.63 | 0.65 | 0.20 | 22.14 | 188.55 | 415.31 |
| Maximum hourly infiltration rate and flow | 2.61 | 2.05 | 2.52 | 1.36 | 1.13 | 1.59 |
| Area Names | Xinzhuang | Sanyuan | Chengxi | Chengnan | Jiaoyuyuan | Fuxing |
|---|---|---|---|---|---|---|
| Parameter a | 0.0663 | 0.0700 | 0.0463 | 0.0997 | 0.0302 | 0.3948 |
| Parameter b | 0.5490 | 0.5266 | 0.6885 | 0.4722 | 0.5197 | 0.4824 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, X.; Xu, G.; Ding, Y.; Zeng, S.; You, L.; Jiang, J.; Zhang, H. Online Storage Technology of the Separate Sewage System: Demonstration Study in a Typical Plain River Network City. Water 2022, 14, 3194. https://doi.org/10.3390/w14203194
Dai X, Xu G, Ding Y, Zeng S, You L, Jiang J, Zhang H. Online Storage Technology of the Separate Sewage System: Demonstration Study in a Typical Plain River Network City. Water. 2022; 14(20):3194. https://doi.org/10.3390/w14203194
Chicago/Turabian StyleDai, Xiaohu, Guozhong Xu, Yongwei Ding, Siyu Zeng, Lan You, Jianjun Jiang, and Hao Zhang. 2022. "Online Storage Technology of the Separate Sewage System: Demonstration Study in a Typical Plain River Network City" Water 14, no. 20: 3194. https://doi.org/10.3390/w14203194
APA StyleDai, X., Xu, G., Ding, Y., Zeng, S., You, L., Jiang, J., & Zhang, H. (2022). Online Storage Technology of the Separate Sewage System: Demonstration Study in a Typical Plain River Network City. Water, 14(20), 3194. https://doi.org/10.3390/w14203194






