1. Introduction
The appropriate selection of an effective calculation tool constitutes the first action to be explored and pursued in order to obtain, as far as possible, a correct forecast of the evolution of possible impacting natural phenomena for the territory under observation. Several simplified methods have been proposed in the literature to evaluate the annual balances of water flows in river basins [
1]. However, the approaches commonly used are based on the elaboration of experimental data expressed through empirical formulas. Obviously, the feasibility of using more advanced mathematical-numerical tools would be desirable. The most advanced approaches, based on the balance equations of physics are pursued by computational fluid dynamics (CFD). CFD relies on solving Navier–Stokes flow equations, including turbulence [
2,
3,
4,
5], the results of which are, consequently, very complex from a mathematical point of view. Therefore, to avoid at least the further complexity of the geometric domain discretization, the meshless approach has been proposed and adopted. In this context, the smoothed particle hydrodynamics (SPH) method appears to be quite well established [
6,
7,
8].The mistaken was that Reduced complexity models (RCM), to which, for example, the cellular automata (CA) approach belongs [
9,
10], represent an important alternative to CFD, suitable to be applied on a large area and over relevant time scales (climate evolution as well), both at reach and at catchment scale. Therefore, for the study of the phenomena considered here, a suitable compromise can be found in approaches capable of simplifying the CFD technique, such as the widely used, simplified but effective ‘Shallow Water’ approach [
11,
12,
13,
14,
15], as implemented in the RiverFlow2D calculation code [
16] that was chosen to perform the simulations discussed in the following sections. The use of the GPU and, therefore, of parallel computing even on simple workstations and laptops, (by consequence not necessarily on very less accessible hardware such as supercomputers) was fundamental to fill the gap between two conflicting requirements. That is, the need for reasonable computation time and the need to use more realistic and advanced mathematical-numerical models than semiempirical or very simplified models such as CA, as well as for the study of phenomenology that evolve over a period of one year on a spatial scale of a river basin, similar to the selected test case. The results discussed in this article, which can be improved in the extension of this type of study and with more powerful but still accessible hardware, have demonstrated the concrete possibility of carrying out these types of simulations. The options available in RiverFlow2D allow the inclusion of various topic models that are useful for civil protection, from debris flow simulations to urban floods and, through the option of parallel computing accessible on desktop and laptop (GPU), also for a possible early-warning system [
17,
18,
19].
The objective of the study discussed in this paper was to model the surface water flow dynamics of the Pescara River Basin, located in Abruzzo (Central Italy) and selected as a well representative test case of medium-sized fluvial basins. The territory is equipped with experimental measurement stations and has been studied over the years through several geological campaigns which have produced numerous available data. Detailed parametric sensitivity approaches, regarding some leading parameters that are difficult to be directly measured [
20], were employed. The related assumed values, although reasonably justifiable from the physical point of view, were essentially used to calibrate the simulations. First, an extensive bibliographic analysis was conducted to have an appropriate geological knowledge of the study area [
21] while also consulting the data relating to the hydrogeological balance [
22,
23,
24,
25]; something which is necessary to quantify the dynamics of surface waters within the basin. The available stations network consists of 11 pluviometers distributed over the entire basin area, whose data are then processed by using the Horton’s semiempirical model [
26], whose parameter values in turn were selected from the literature, based on soil grain size, morphology and incidence of vegetation [
27,
28]. Evapotranspiration was also included, but in a simplified way, as detailed in
Section 2.3.3., to reduce the number of parameters to be calibrated and, consequently, to more easily face the problem of computation time, which was very demanding despite the parallel approach. The inflow to the Pescara River basin was included considering the monitored data of the measurement stations, especially those at Pescara-Maraone and Tirino-Madonnina as main contributions. Minor water inventory sources, poorly defined not only during the reference periods for calibration and validation, but also currently, were not included. For example, the impact of snow occurrence and melting modalities (temperatures rising, rain events, etc.) [
29] were not explicitly considered. However, in the calibration step, the not completely known contributions were included by adjusting some parameters, as detailed below. Accordingly, only reliable contributions were considered. In a subsequent phase, using the QGIS software, the morphological digital model of the basin under study, based on a 10 × 10 m DTM, was processed. ‘Shape files’ were created containing information relating to the area such as the perimeter of the basin area and the location of the 11 pluviometric stations defining their influence area by the Voronoy polygon technique. Subsequently these ‘shape files’ were inserted and processed on the River Flow 2D dedicated graphic user interface SMS, thus proceeding with the construction of the conceptual model, containing all the necessary information (perimeter of the study area, flow boundary conditions, Manning’s [
30] roughness coefficient, rainfall distribution) with the related infiltration and evaporation rate as well. Once the conceptual model was acquired, the Delanuay [
31,
32] numerical tessellation of the selected DTM was performed through an unstructured mesh approach, based on linear triangular elements, applying the meshing tool accompanying the Riverflow2D computer code.
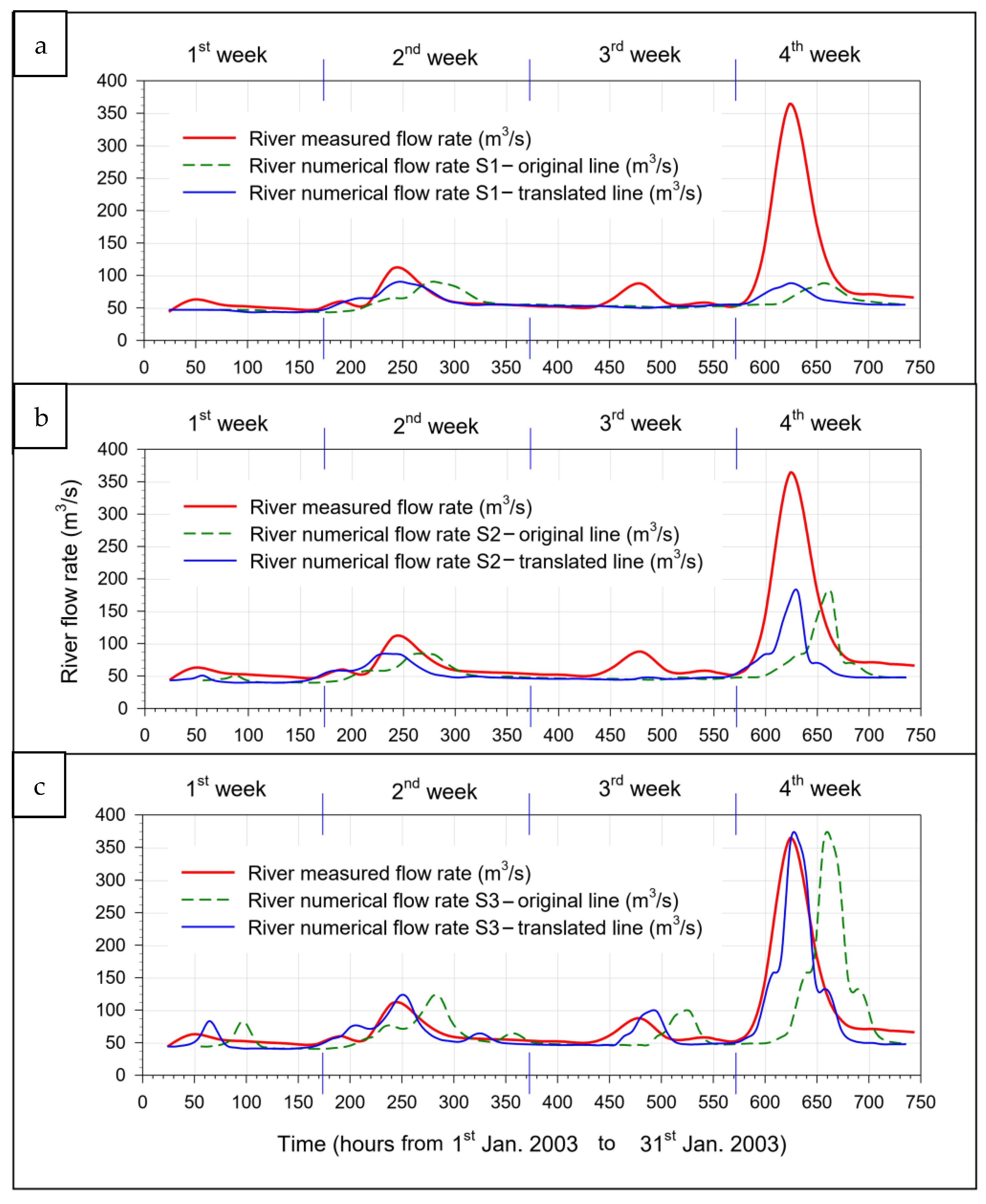
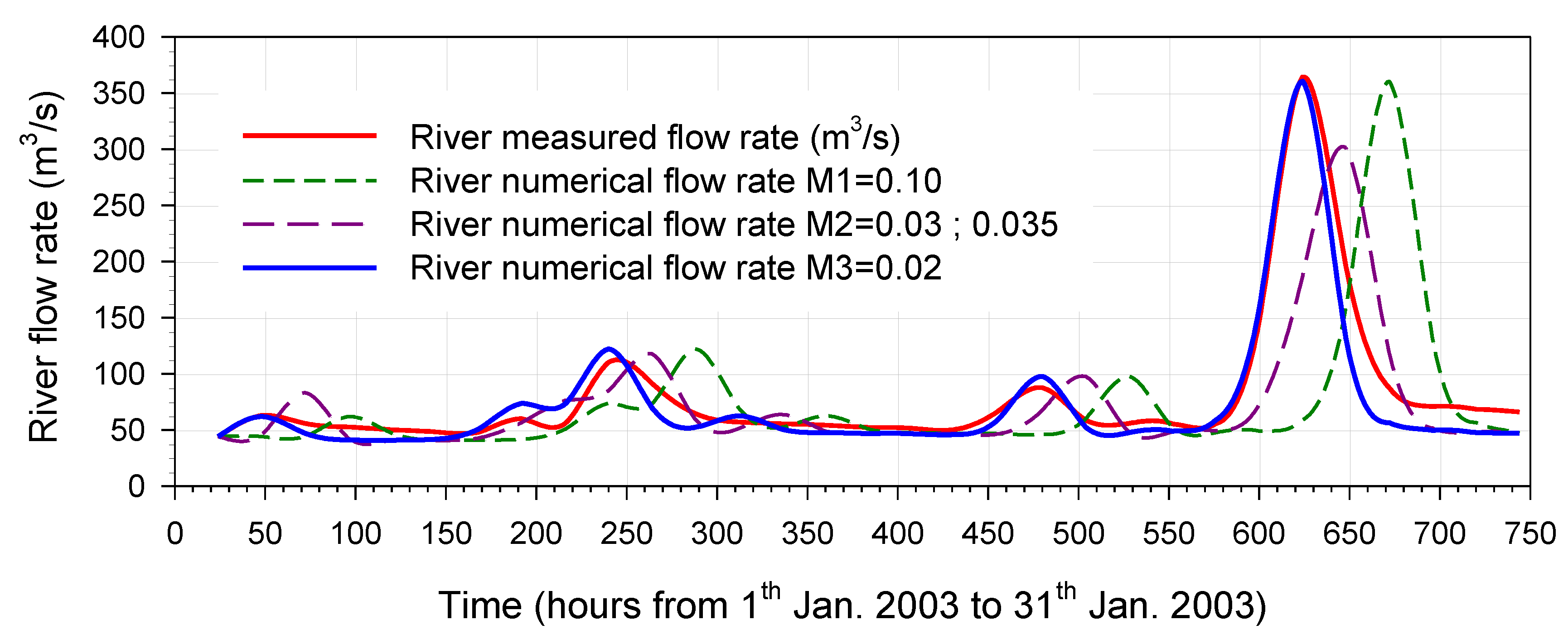
To satisfy two conflicting requirements, namely the need for both numerical accuracy (high number of tessellation elements) and a less excessive execution time, the identification of an appropriate, balanced numerical discretization of the spatial domain was essential. Subsequently, after an accurate analysis of the regional annals, some complete time series, whose experimental data were consistent with each other, were identified. Therefore, once the mesh was generated, the calibration process was carried out on the basis of the experimental data of one month, measured in January 2003, while three semesters, two belonging to the full year 2000 and the third belonging to the first half of the year 2007 were selected for validation. In this work, in particular, we analyzed the impact that the infiltration-evapotranspiration rate and the Manning number have on the numerical results of the selected model and how the computation time can be reduced through the use of the GPU.
3. Results and Discussion
After the calibration step, some simulations were performed to validate the feasibility of the discussed approach. The parameters identified through calibration may vary depending on the year chosen and the different seasons of the year. However, in this paper we considered all parameters constant over time. The effectiveness of the procedure will be demonstrated in the validation step. Of course, further analysis could refine the methodology.
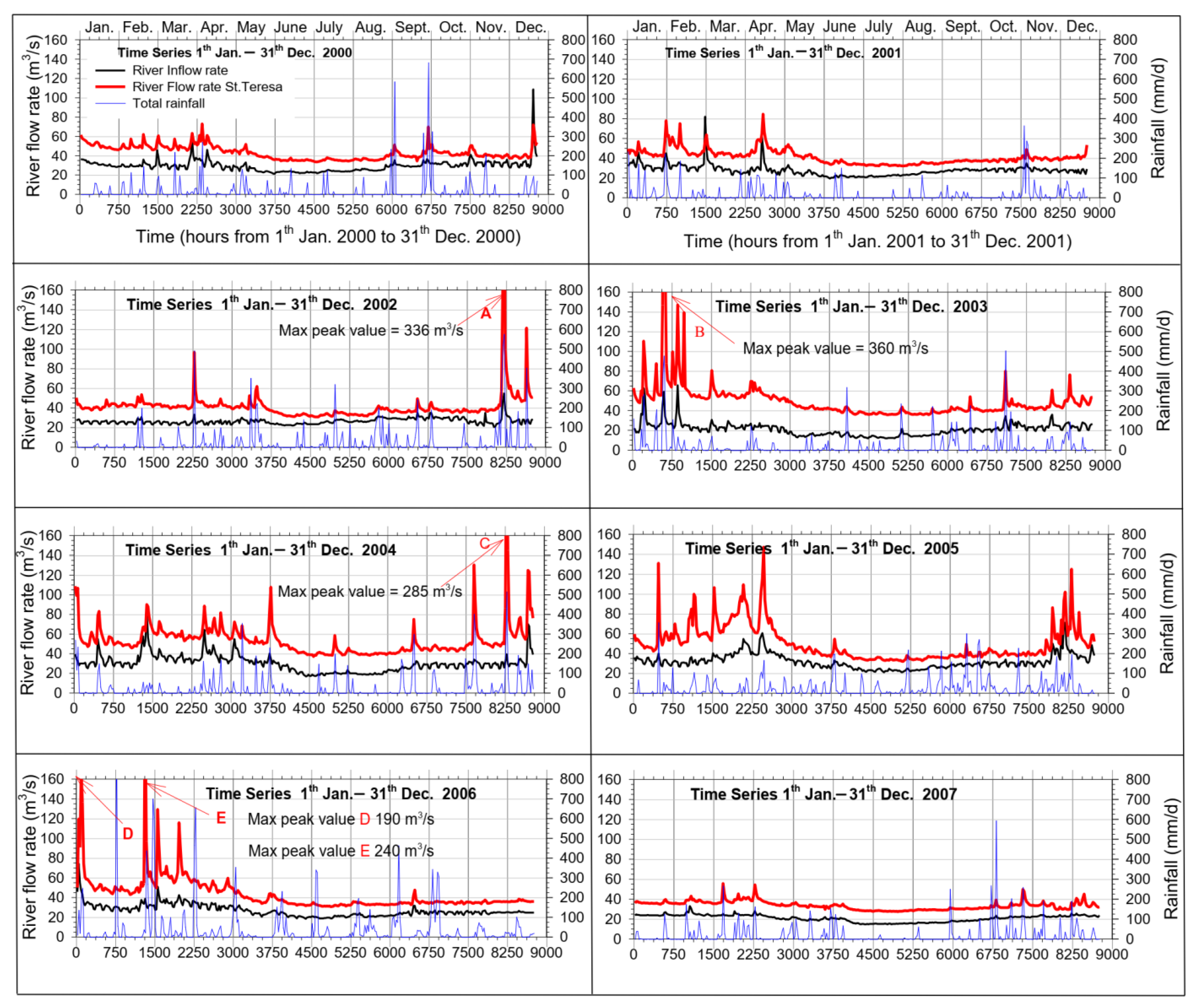
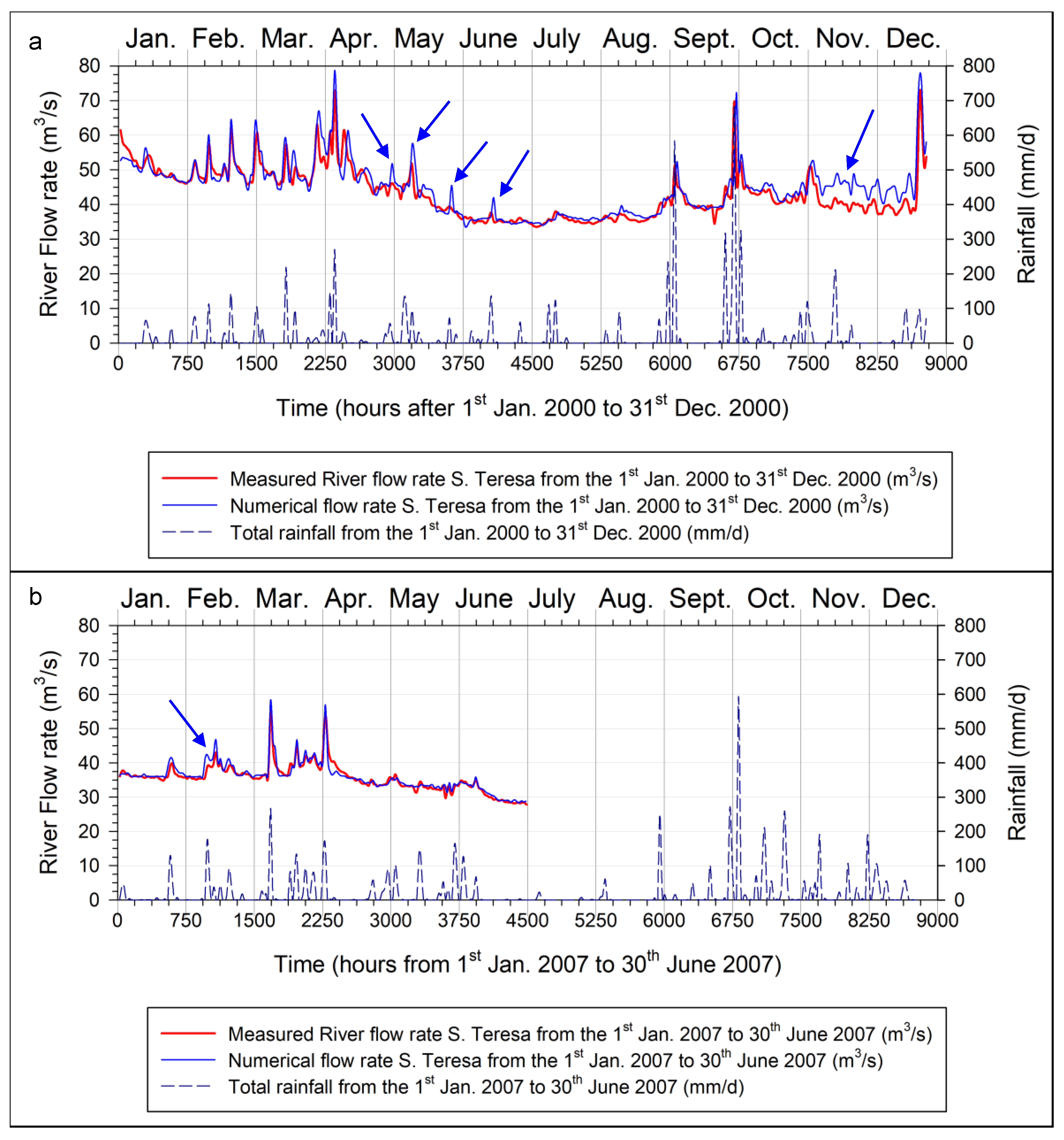
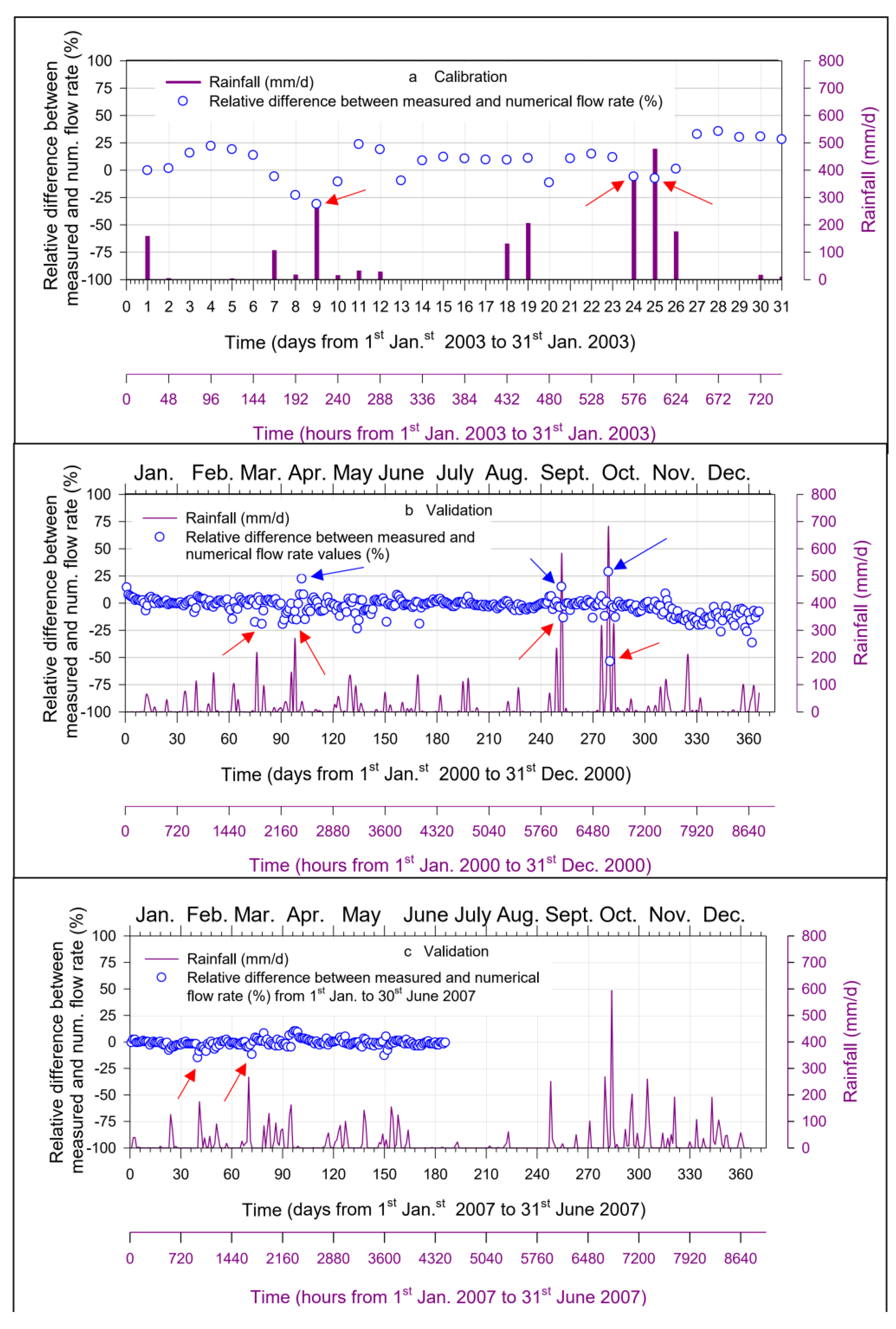
The validation of the process certainly had to cover a wide time interval, therefore the two semesters of the year 2000 and the first semester of the year 2007 were selected, i.e., respectively before and after the calibration year 2003. As previously observed, from a first remark of
Figure 2, a systematic discrepancy emerges between the inflow data at the entrance to the basin (flow rate measured at Pescara-Maraone summed to the measurements at Tirino-Madonnina; black line) and those detected at Santa Teresa. The origin of these kind of anomalies are not yet completely known. However, to balance the water flow correctly, the inlet flow had to be synthetically increased. As a result, 18 m
3/s were added to the base-flow of the 2000 time series, while 14 m
3/s was added to the base-flow of the 2007 time series.
Figure 7 shows the good match between the measured values and the numerical values predicted after calibrating the model and adjusting adequately the input, as described above.
Regarding the year 2000, the simulations for the period of November to mid-December overestimate the measured values, while the peak of mid-December is well simulated, even if the predicted value persists to be slightly higher. The blue arrows show some peaks resulting from the numerical model, which, however, do not match adequately the measured actual values, although in correspondence some not negligible rainfall events occurred. The reasons, in these cases, could be attributed to the measuring instruments, management of the hydropower plant and/or to an inadequate input distribution of rainfall, whose measurements were localized and not diffused.
To quantify the deviations between the numerically predicted values and the measured values, some statistical analyses were carried out.
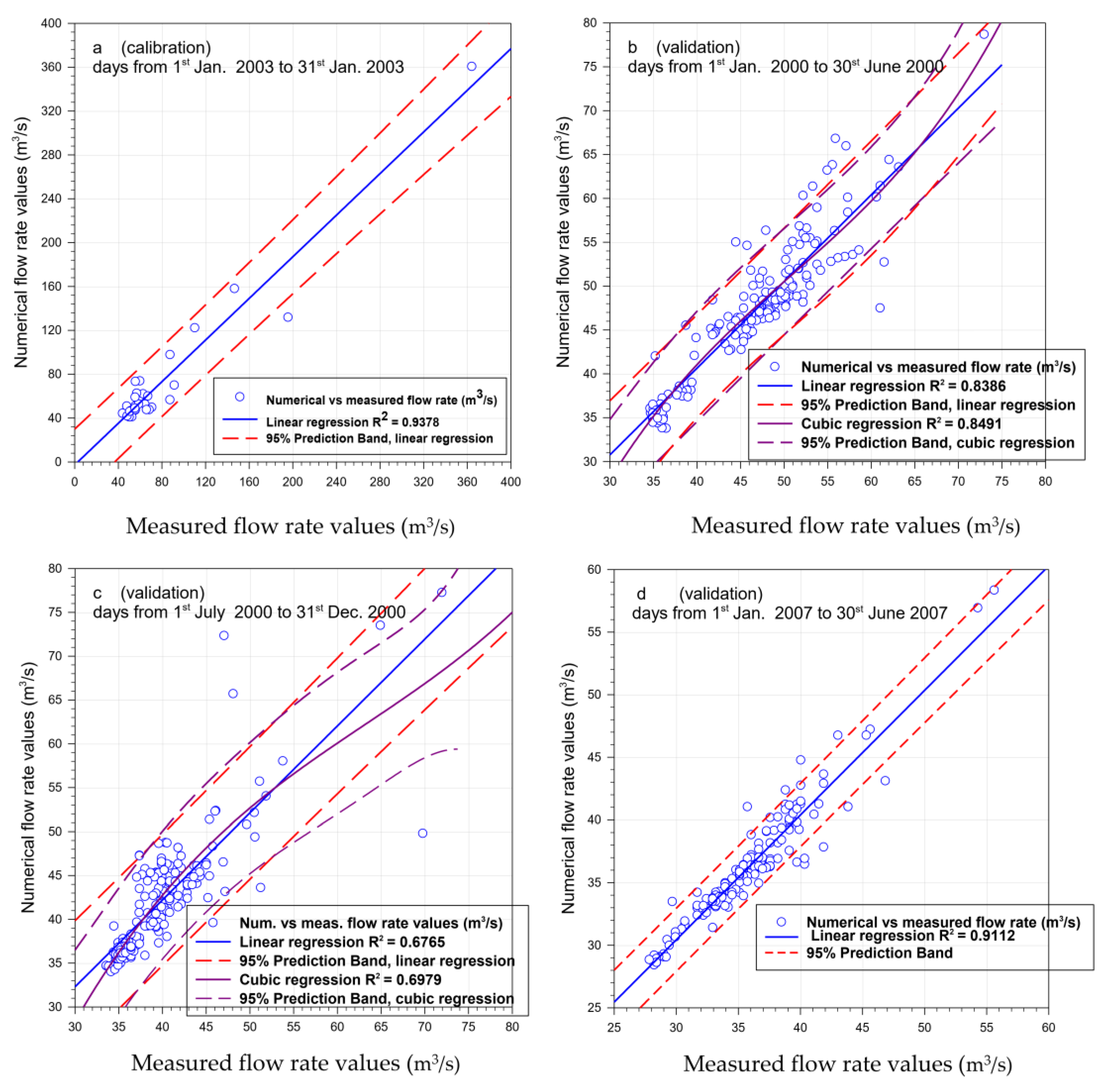
Figure 8 shows the linear correlations for the simulations regarding the calibration (
Figure 8a) and the validation of the first half of 2007(
Figure 8a,d), while both linear and cubic regression the validation processes relating to year 2000 (
Figure 8b,c). By the calibration step a rather high value of
, equal to
, was gained (
Figure 8a).
The validation step, performed by adopting the physical parameters already calibrated, indicated that the simulations of the first half of the two selected years showed a better correspondence with the measured values (
year 2000,
Figure 8b;
year 2007,
Figure 8d) compared to the only second half considered (
year 2000,
Figure 8c). On the other hand, this circumstance may not be surprising since the calibration step considered only the month of January, therefore belonging to the first half of the year. Evidently, for the second half of the year, the need for a different calibration could emerge. By means of cubic correlation, slightly better values were obtained (
first semester year 2000,
Figure 8b;
second semester year 2007,
Figure 8c). In this case,
indicates the degree of reliability (from 0 to 1) of the hypotheses, the assumptions, the applied modeling and the numerical description of the territory for obtaining a correct correspondence between the values of the flow water predicted numerically and measured values.
Moreover, the validation carried out shows that the predictions of the flow rate were particularly satisfactory for the first two semesters of the year 2000 () and 2007 (), while the matching was quite satisfactory for the second half of the year 2000 (). This observation will also provide further indications to direct future investigations.
The regression provides global indications. However, it does not indicate nor describe which are the distributions of the deviations. In this regard, the following index has been introduced:
where
is the acronymous of ‘Relative Difference between Measured and Numerical values’,
measured flow rate,
numerically predicted flow rate.
Accordingly,
Figure 9a shows the deviations related to calibration, while
Figure 9b,c indicate the deviations resulting from the validation step.
A first inspection reveals that the most important deviations are observed at higher rainfall peaks for both calibration and validation, highlighted in the figures by red and blue arrows. Furthermore, it appears that the predicted values overestimated the measured values (negative RDMN), specifically when more intense rain peaks are observed, apart from some exceptions (three events, during 2000, blue arrows in
Figure 9b). This characteristic of the applied model certainly satisfies the safety requirements, but could be too conservative, leading to dangerous announcement of false flood alarms.
As already highlighted above, the reasons of these circumstances should be explored both by a mathematical-phenomenological level (important phenomena could have been excluded or the numerical discretization of the territory may not have been sufficiently adequate) and by rain gauges network and measuring instruments levels.
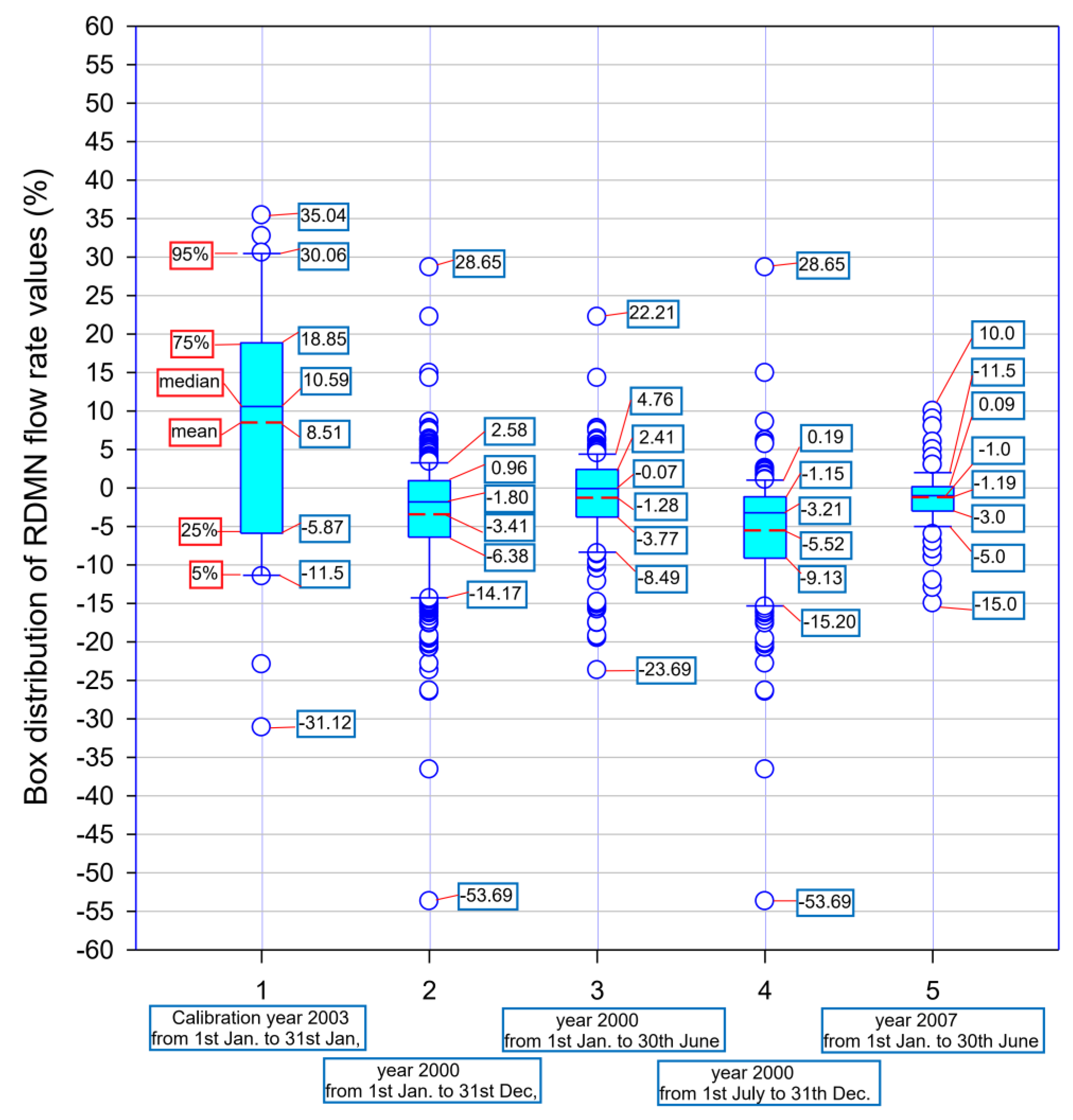
To better visualize the details of the distributions of the deviations,
Figure 10 shows the box plots that highlight the quartiles, the medians, the average values, the minimum and maximum values. The distribution spread is highlighted through the range between the first quartile to the third quartile (
, maximum for calibration
, minimum
) for the validation of the first half of 2007. The resulting average was positive for calibration, while all negative for validations (
calibration, January 2003;
validation, first semester 2000;
validation, second semester 2000;
validation first semester 2007). It is also noted that the smallest average deviation surveyed was obtained for the validation of the first half of year 2007.
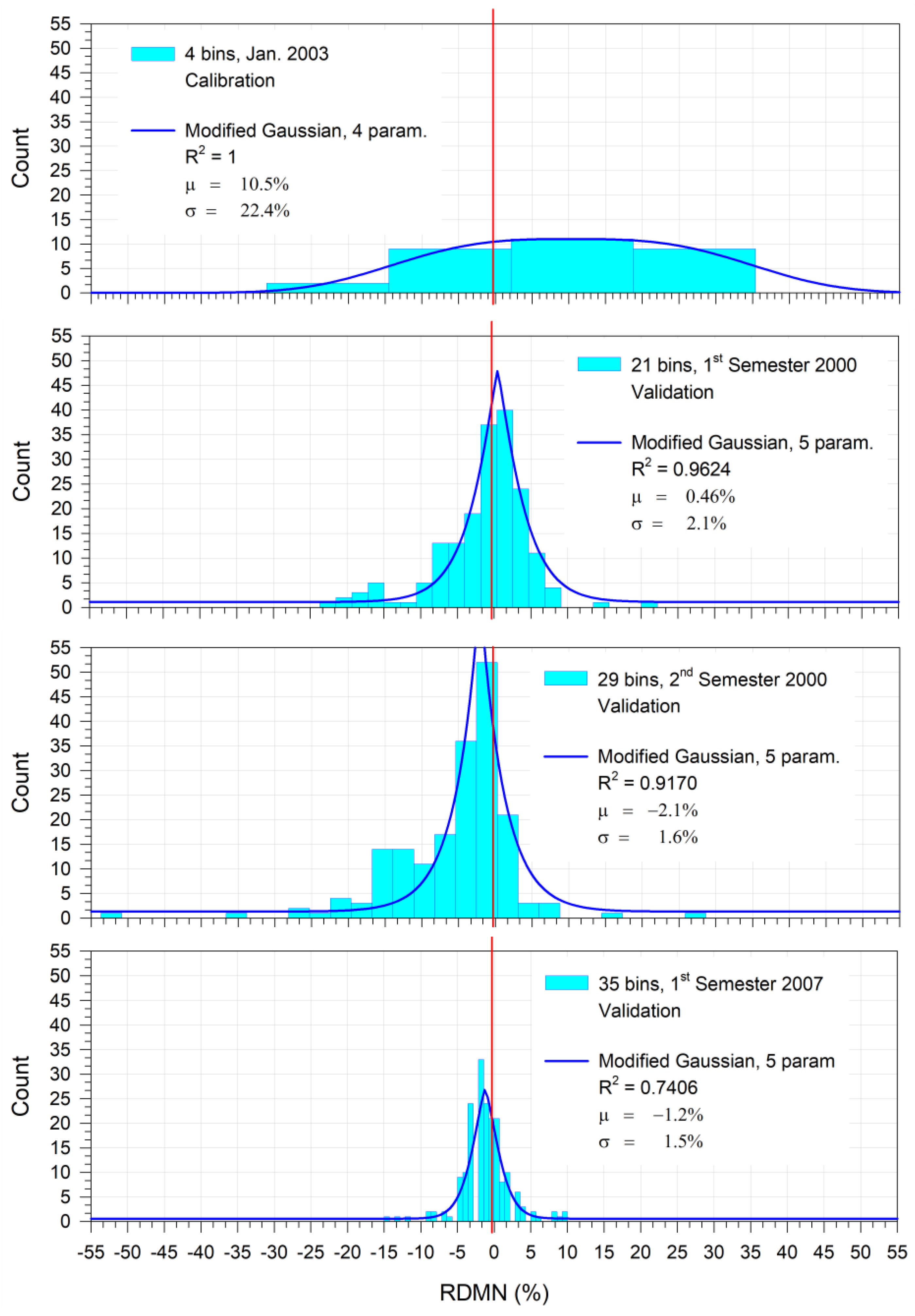
In order to get a better visualization of the RDMN distribution, by means of histograms, the Freedman–Diaconis rule [
33], which not only considers the sample size, but also considers the spread of the sample, was selected:
where (referred to
Figure 10):
stands for third quartile
,
stands for the first quartile
,
stands for sample size and
, respectively the maximum and minimum values of the elements belonging to the sample. Furthermore, the representation by means of histogram could identify analytic functions that can possibly describe the statistical distribution under consideration. Accordingly, from
Figure 10 and Equation (10), the
Table 1 follows.
The following are the selected functions:
where
,
,
,
,
are parameters numerically identified by one-way ANOVA test [
34].
It is worth underlining that the values of the statistical parameters obtained with the technique shown in
Figure 11 can be compared with the results obtained by constructing the box plots shown in
Figure 10.
4. Conclusions
Despite the considerable complexity of the studied phenomena, the identified approach based on the ‘shallow water modelling’, an advanced mathematical-numerical model able to reproduce reality in almost the best possible way, proved to be feasible to simulate well the behavior of the surface water flow and the hydrological balance of a catchment area similar to the Pescara basin, selected as a test case. The discussed modeling can also be a useful integrative tool in designing further hydrogeological experimental campaigns, over the different seasons, with different weather conditions, aimed to acquire a more robust water basin inventory. It is worth underlining that one of the important objectives of the work was to verify the possibility of using a valid and advanced modeling tool to explore the consistency of all available data and to identify which of them should be subjected to further investigations, also by an experimental point of view. The results, shown in the graphs and in the discussion, were remarkably encouraging.
On the other hand, from the inspection of
Figure 7 and in particular from
Figure 9, the emergence of statistical outliers in correspondence to intense rainfall rates has suggested the need for further investigations in order to improve not only the mathematical-numerical model selected, but also the analysis and methods of acquiring experimental data. This point is particularly important as the current climate change and its developments evolve, and lead to further occurrences of extreme events such as very violent rainfalls, which are limited in time and would need specific models.
Therefore, in short, based on the results and in the face of different needs (suggestions for further measurement campaigns, management of the territory, etc.) we could define the quality of the applied modeling between good and very good.
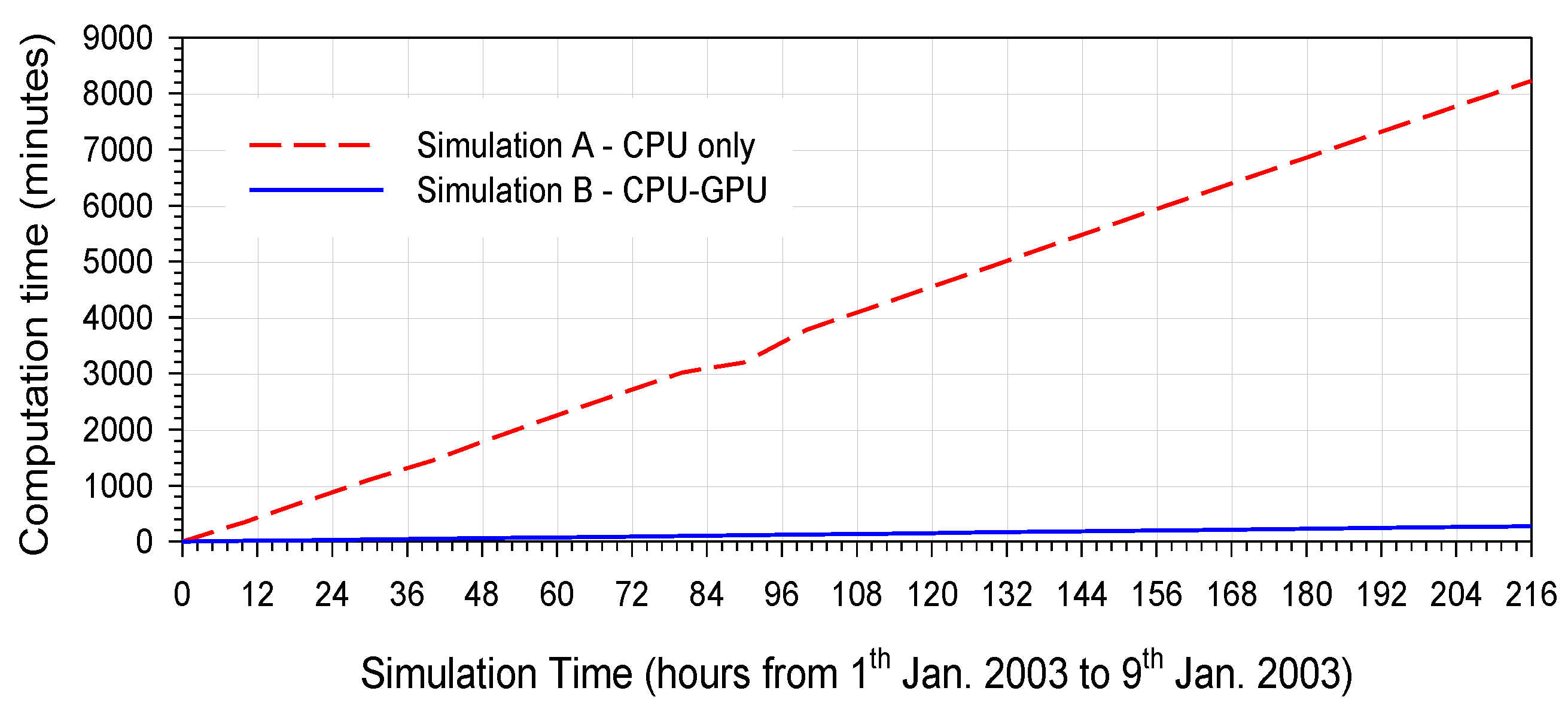
Of course, the simulation of a complex phenomenology affecting a large area, within a period of one year or more, combined with the necessity of an accurate level of numerical discretization of the topography, appears to be very demanding in terms of calculation time, when only CPU platforms are employed. The use of parallel computing, even if on desktop or laptop hardware, revealed mandatory to perform parametric simulations on such large spatial scales and over long periods of time in, not only satisfactory, but acceptable computation times. By taking advantage of the GPU processors, computation times were made about 30 times faster by the hardware available to us. A simulation re-quiring 30 days running only on CPU hardware would be performed in only 1 day by the inclusion of the parallel calculation (CPU + GPU). Of course, a more powerful hardware, like Tesla Nvidia GPU Card A100, in accordance with what is discussed in this study, would be more suitable allowing us to reduce the computation time even more.
A detailed description of the hydrology, rainfall, water sources, flow rate input, were also fundamental information. In our paper, the data were acquired from the documentation made available by the Regione Abruzzo and subsequently analyzed, processed, and introduced into the model.
The numerical outcomes were strongly affected by the correct calibration of the spatial discretization, the Manning’s roughness coefficient and the infiltration-evapotranspiration rate. The simplified inclusion of the evapotranspiration effect as an adjustment of the actual parameter values of the selected infiltration model to obtain the match between the numerical simulations and the experimental results, proved to be effective.
Many calibration tests were performed covering 744 h of January 2003, compared successfully with the experimental measurements obtained from the available annals. So, a further outcome of this work was achieved by understanding and identifying how the different parameters of the selected model affected and could affect quantitatively the simulated phenomena.
Then, the validation simulations involved three semesters, the entire year 2000 and the first half of 2007. A more detailed morphological digital model would have been desirable, to perform more accurate numerical simulations of the phenomena.
Moreover, the concentration time of the basin was numerically estimated in about 22 h, consistent with the actual value. The application of the CPU-GPU allows us to simulate a transient of this duration in about 30 min (22/48 = 0.46 h, on our hardware). Accordingly, another important outcome of this study is certainly the possible utilization of the developed model as a part of an early warning system of floods.
A further consideration emerged from this study. The selected hydrographic basin may not coincide with a possible larger hydrogeological basin that could contain it. There is an aquifer–river exchange, in which the river feeds the aquifer up-stream, while downstream the aquifer feeds the river, and this is certainly a topic to be studied and deepened in future research activities that can clarify the lack of water inventory between the flow rate at the mouth of the Pescara river and the main tributaries identified.
Another important opportunity, not discussed in depth in this paper, would also be the water management of the area, for example irrigation and the impact of hydroelectric plants.
The developed model so far, based on GPU, on an advanced numerical approach, and on hardware such as a simple workstation and laptop, could be useful not only for the validation of the available data, such as for the water balance of a river basin, but also as a basis for applications in sediment transport, influence (or instabilities) of hydric structures such as dams or bridles, debris flow phenomena [
7,
8,
17], transport of pollutants, floods [
18,
19,
35] and many other aspects involved in ‘Mitigation Projects of Territory Risk’ and could therefore, by consequence, be useful in the context of the public territory management (‘Civil Protection’ in Italy).
This will surely be a starting point for future works, including also further analysis over other years, on other fluvial basins, aimed at providing more exhaustive validation of the model.