Wave Climate and Trends for the Marine Experimental Station of Capo Tirone Based on a 70-Year-Long Hindcast Dataset
Abstract
1. Introduction
2. Materials and Methods
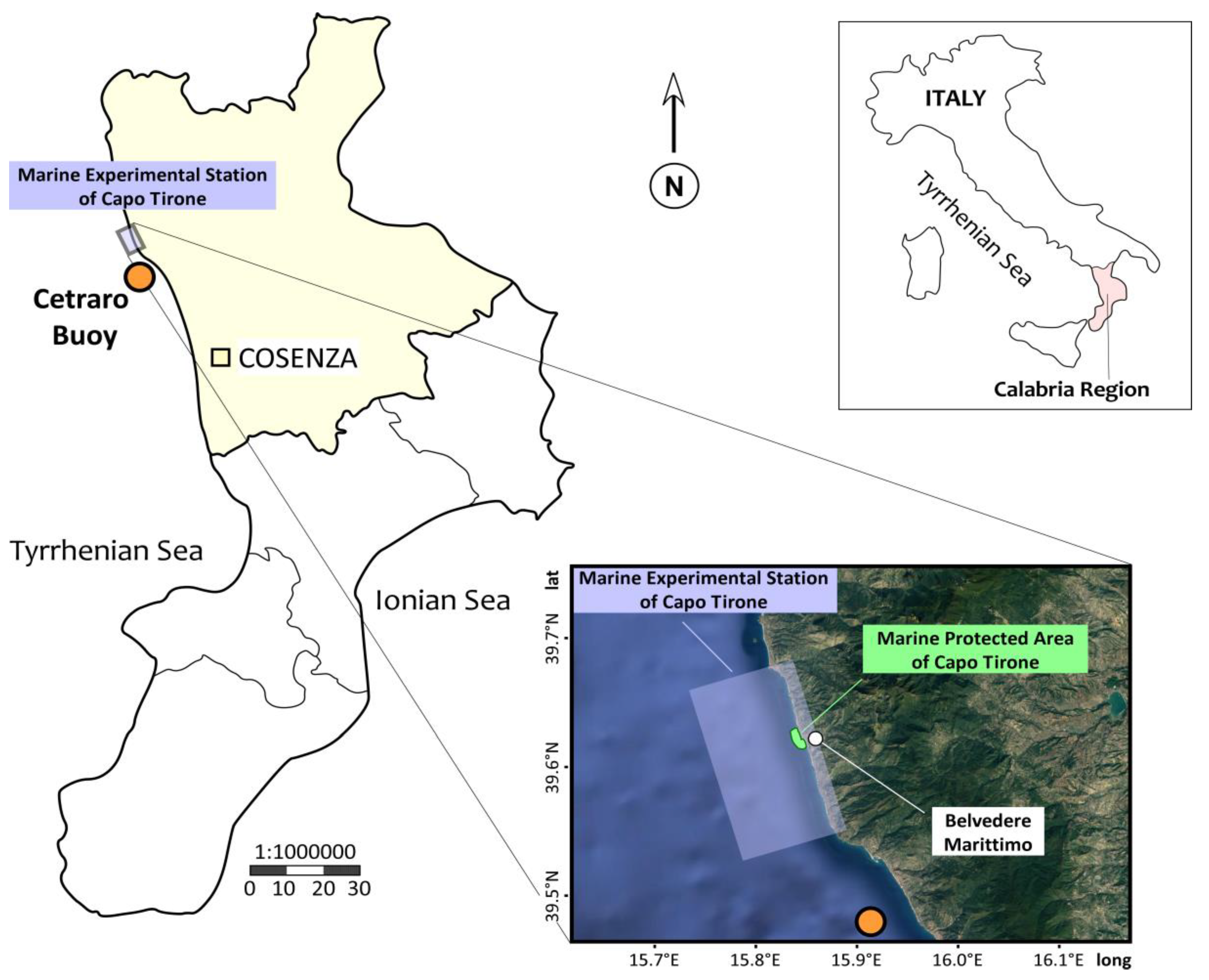
2.1. The Study Area
The Marine Experimental Station of Capo Tirone
2.2. Dataset
2.2.1. Cetraro Buoy Dataset
2.2.2. ERA5 Hindcast
2.2.3. WAM Model
2.2.4. MIKE Hydrodynamical Model
2.3. Methods
2.3.1. ERA5 Validation
2.3.2. WAM–ERA5 Difference
3. Results and Discussion
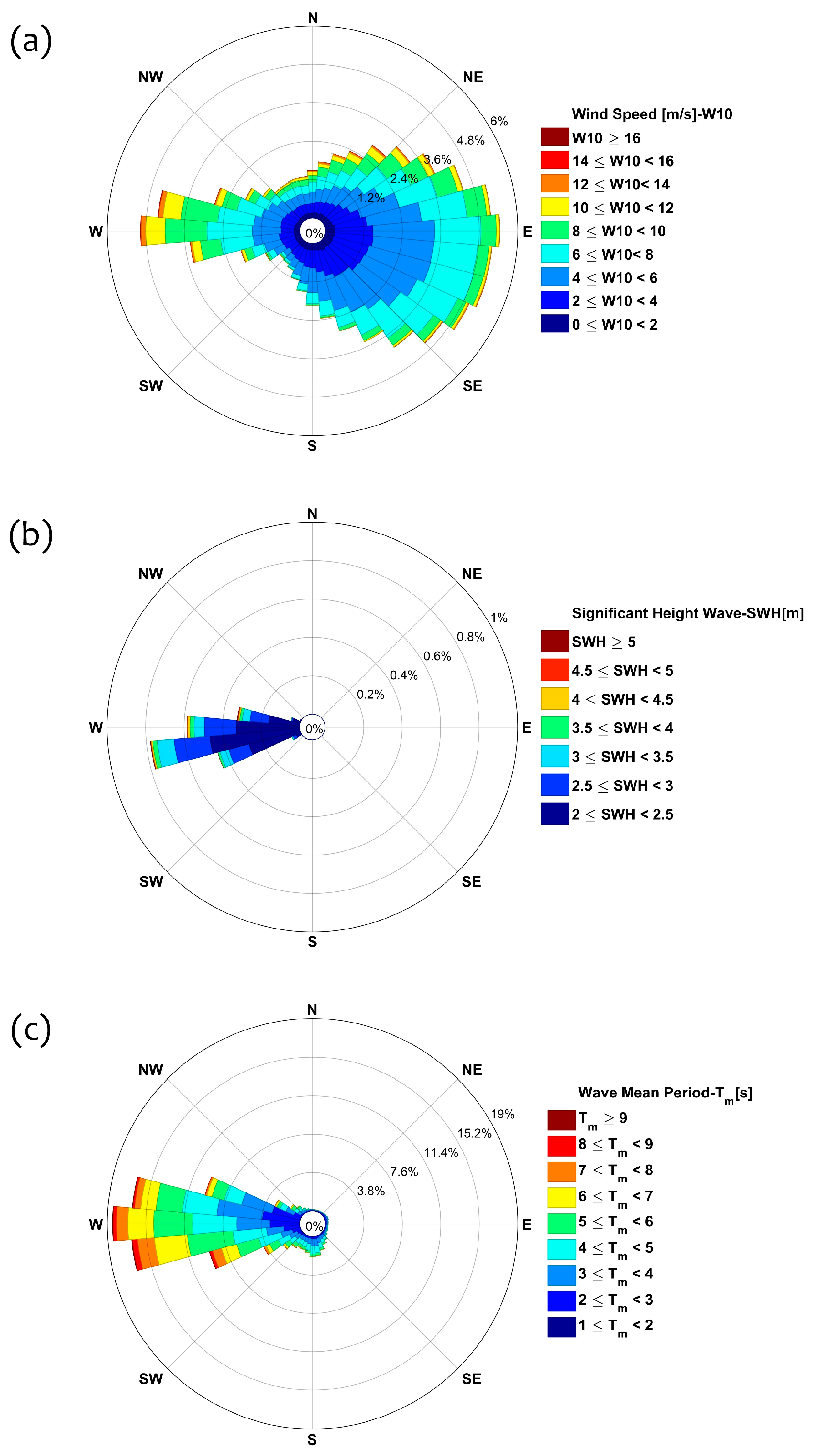
3.1. Off-Shore Wind and Wave Climatology
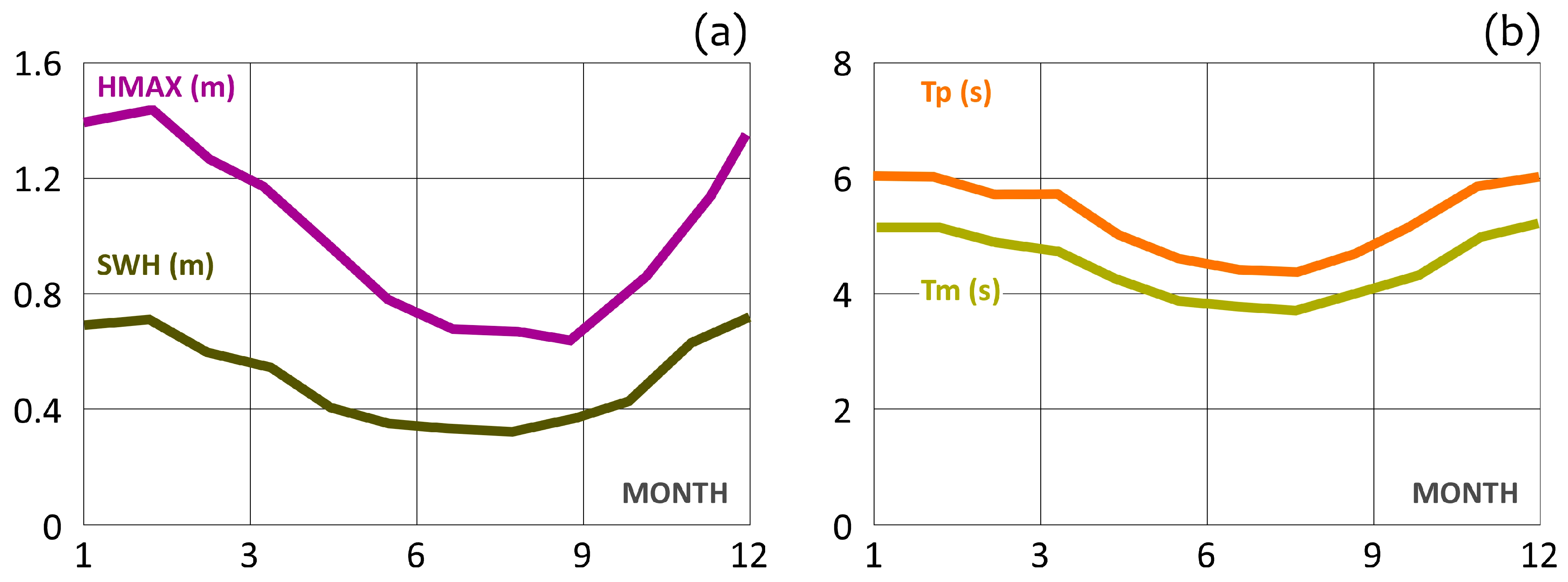
3.1.1. Seasonal Variability
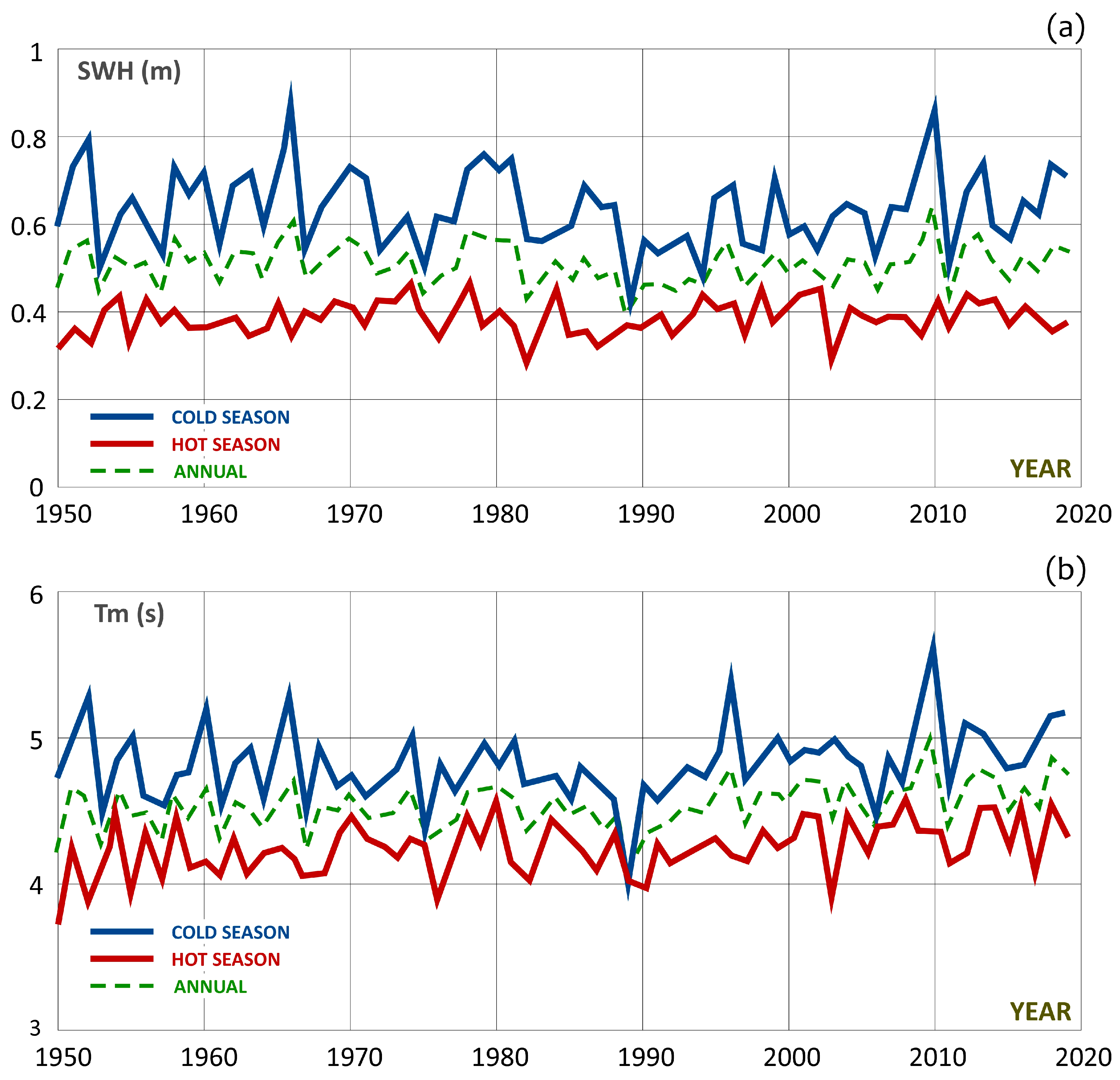
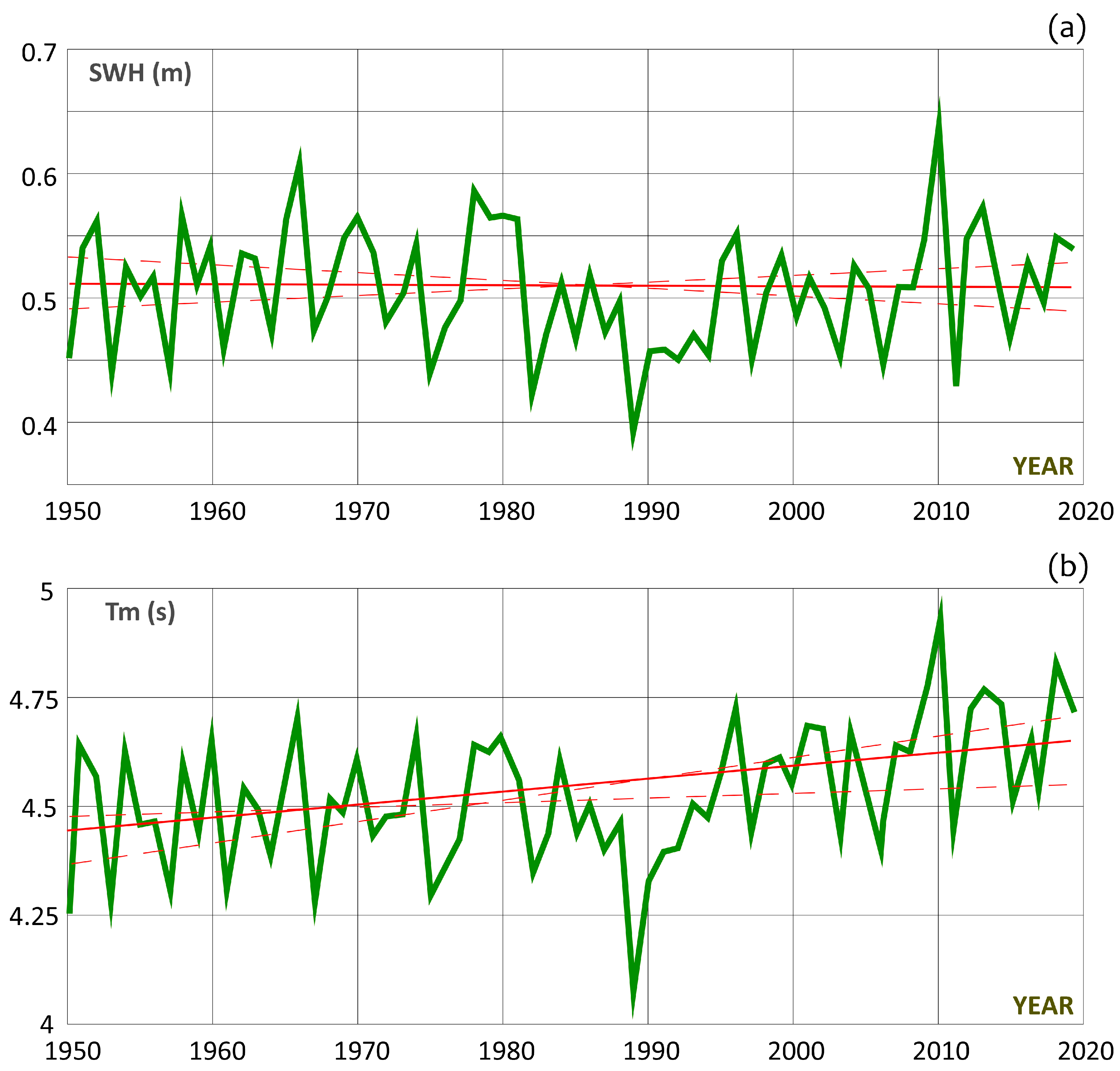
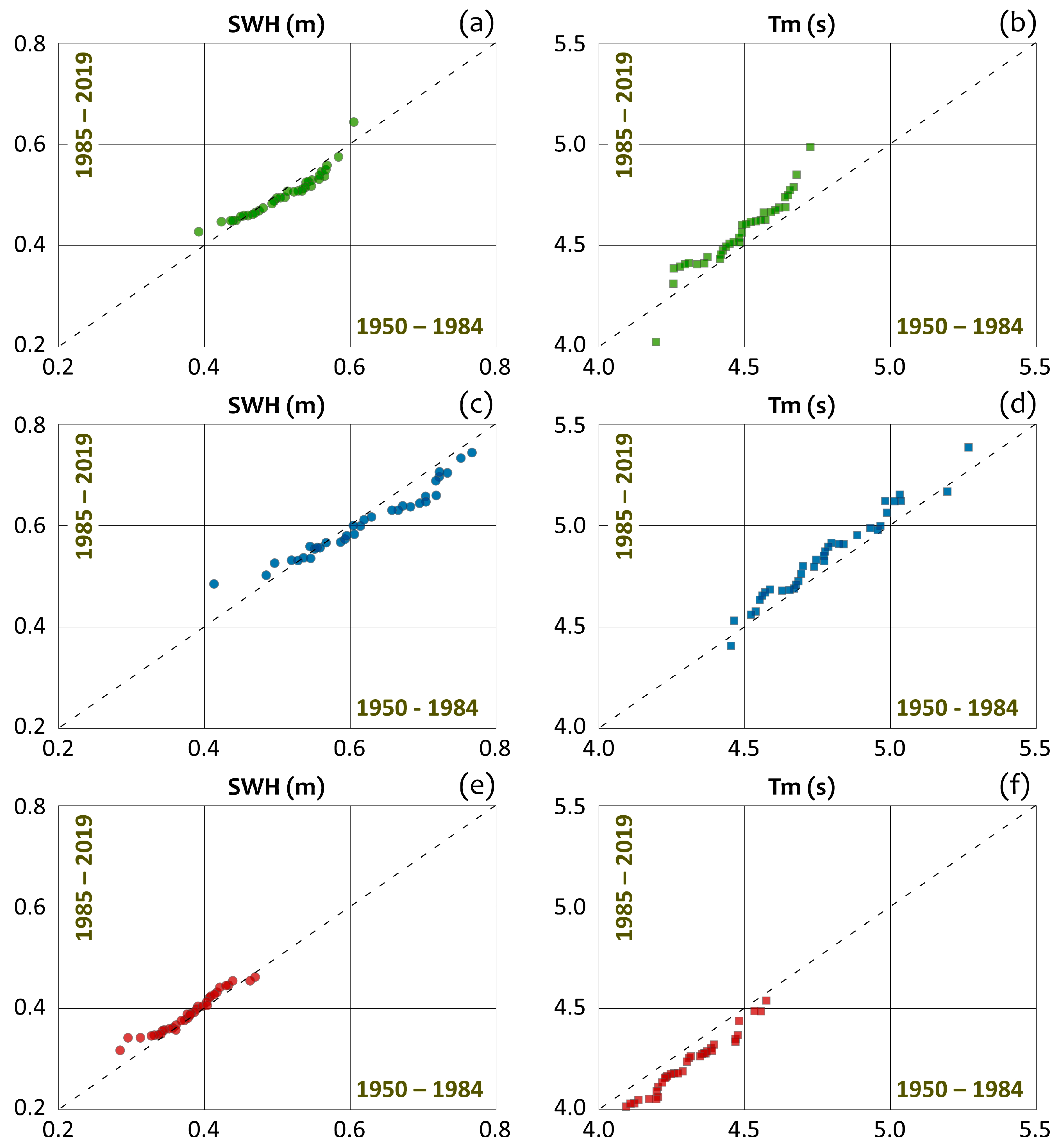
3.1.2. Trend Analysis
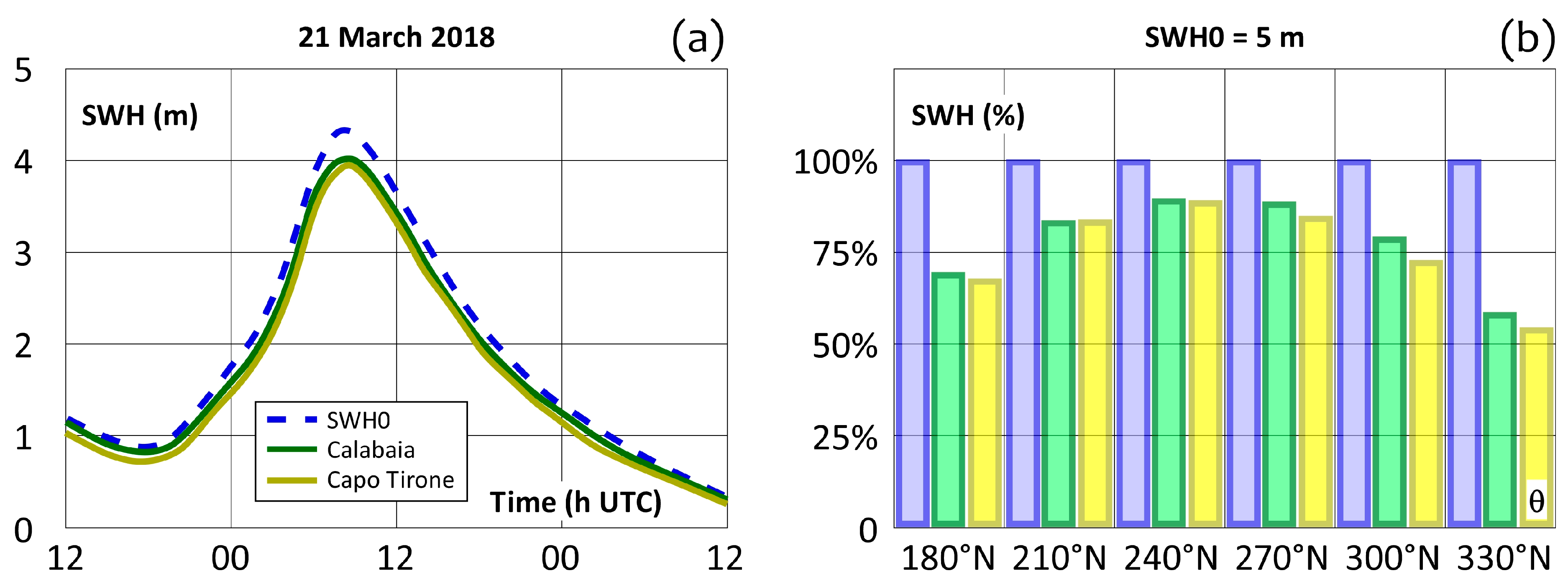
3.2. Nearshore Wave Analysis
4. Conclusions
- -
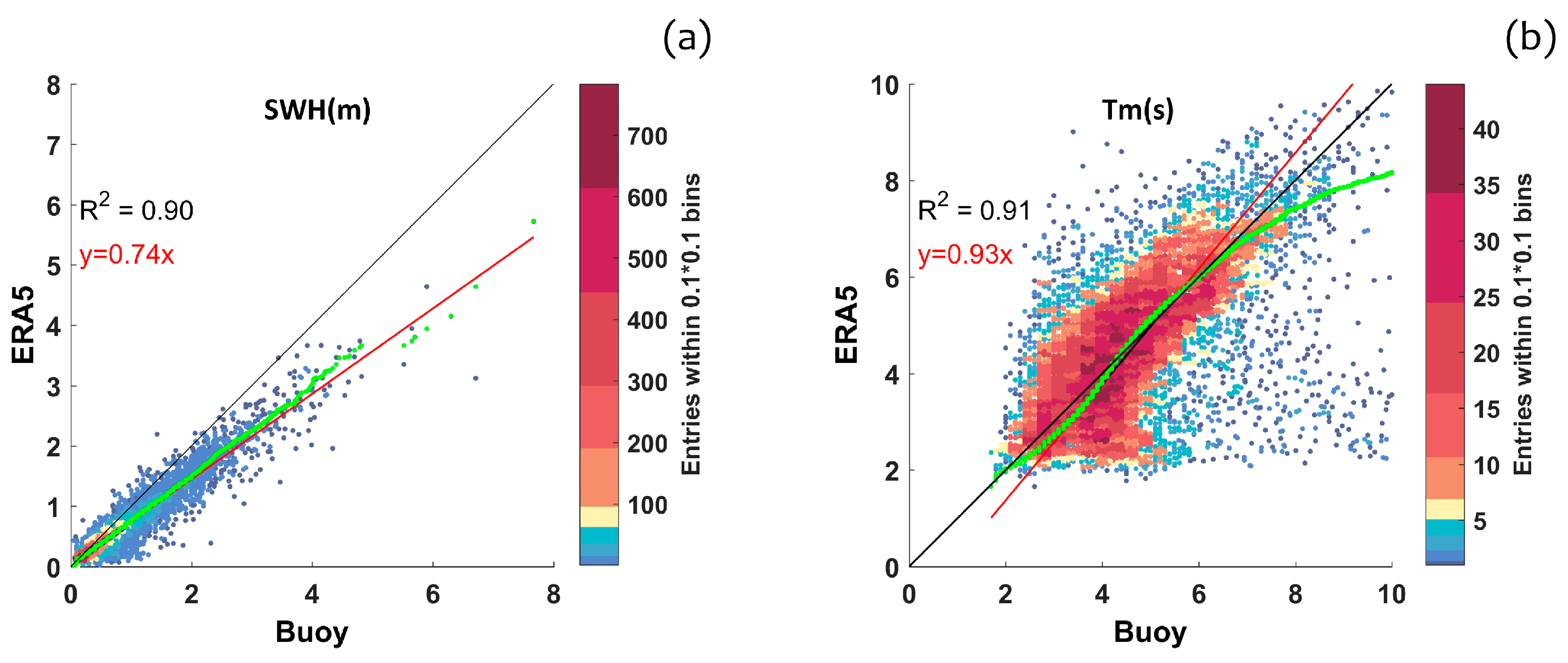
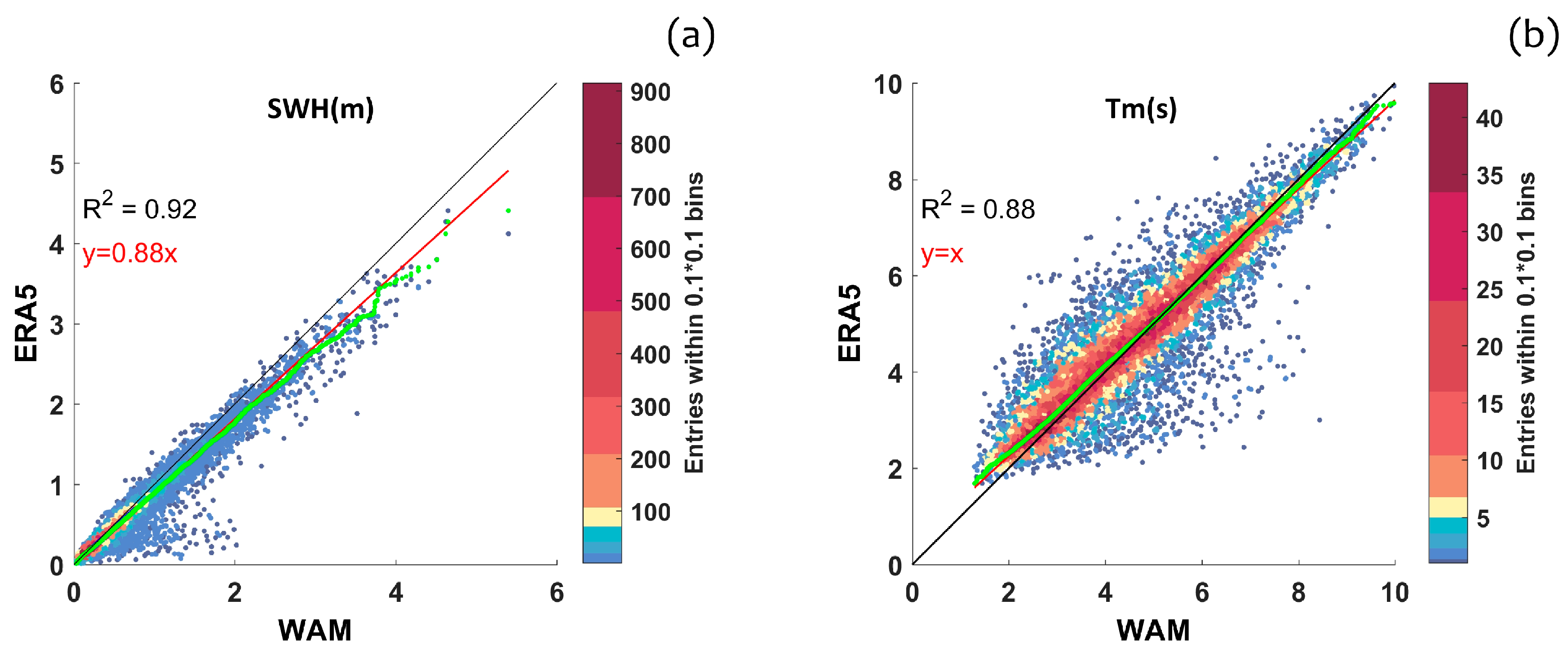
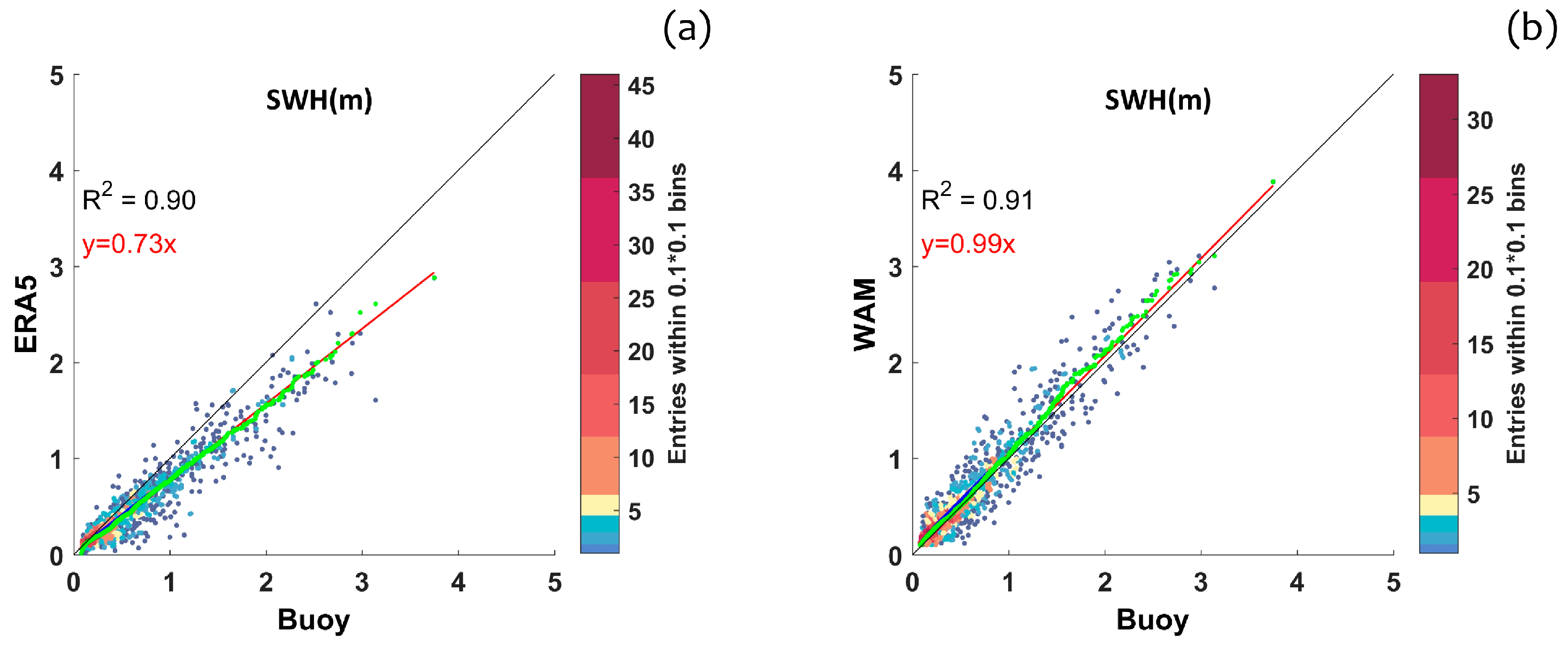
- beside a general underestimation of wave height and period, ERA5 showed satisfactory results, accurately estimating the wave climate in the Southern Tyrrhenian Sea. Typical values of the average monthly bias were −0.15 m (wave height) and −0.13 s (wave period), with correlation coefficients R2 of about 0.9. The WAM model evidenced a smaller negative bias than ERA5, compared to the buoy data, proving to be a fundamental tool to counterbalance the recent lack of data at the Cetraro buoy;
- -
- the 70-year long ERA5 dataset showed that the offshore wave climate at Capo Tirone was characterized by a mean significant wave height of about 0.5 m. The mean maximum wave height and peak period exceeded 1.2 m and 6 s, respectively, corresponding to the major storms occurring in the winter. Furthermore, the results evidenced a clear seasonality for both the wave height and wave period and a strong interannual variability;
- -
- -
- nearshore wave modeling provided instructive insight into the spatial variability of the wave climate. The location in front of Calabaia is considered most suitable for buoy deployment and for further wave climate monitoring at the Marine Experimental Station of Capo Tirone.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
| Bias | Arithmetic Mean Value of the Errors |
| CBS | Coastal Boundary Section |
| DJF | Winter (December–February) |
| ERA5 | ECMWF Reanalysis v5 |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| HMAX | Maximum Wave Height |
| IFS41r2 | ECMWF Integrated Forecast System model |
| ITA | Innovative Trend Analysis |
| JJA | Summer (June–August) |
| LBS | Lateral Boundary Section |
| MAE | Mean Absolute Error |
| MAM | Spring (March–May) |
| MESCT | Marine Experimental Station of Capo Tirone |
| MIKE | MIKE 21-3 Coupled Model FM |
| MK | Mann-Kendall test |
| R2 | Correlation Coefficient |
| RMSE | Root Mean Square Error |
| RON | Italian National Sea Wave Measurement Network |
| SBS | Seaward Boundary Section |
| SCI_CT | Marine Protected Area of Capo Tirone |
| SD | Standard Deviation |
| SI | Scatter Index |
| SON | Autumn (September–November) |
| SSE | Sen’s Slope Estimator |
| SWH | Significant Wave Height |
| Tm | Mean Wave Period |
| Tp | Peak Wave Period |
| WAM | WAve Model |
| W10 | 10 m Wind Speed |
| θ | Wave Direction |
| θWind | Wind Direction |
References
- OECD. Marine Protected Areas: Economics, Management and Effective Policy Mixes; OECD Publishing: Paris, France, 2017. [Google Scholar] [CrossRef]
- Roumasset, J.K.; Brooks, K. Valuing Indirect Ecosystem Services: The Case of Tropical Watersheds. Environ. Dev. Econ. 2002, 7, 701–714. [Google Scholar] [CrossRef]
- Jorve, J.; Kordas, R.; Anderson, K.; Nelson, J.; Picard, M.; Harley, C. Climate Change: Coastal Marine Ecosystems. Encycl. Nat. Resour. Air 2014. [Google Scholar] [CrossRef]
- Costanza, R.; d’Arge, R.; de Groot, R.; Farber, S.; Brasso, M.; Hannon, B.; Limburg, K.; Naeem, S.; O’Neill, R.V.; Paruelo, J.; et al. The value of the world’s ecosystem services and natural capital. Nature 1997, 387, 253–260. [Google Scholar] [CrossRef]
- Hoegh-Guldberg, O.; Bruno, J.F. The impact of climate change on the world’s marine ecosystems. Science 2010, 328, 1523–1528. [Google Scholar] [CrossRef] [PubMed]
- Hoozemans, F.M.J.; Marchand, M.; Pennekamp, H.A. A Global Vulnerability Analysis: Vulnerability Assessment for Population, Coastal Wetlands and Rise Production on a Global Scale, 2nd ed.; Delft Hydraulics: Delft, The Netherlands, 1993. [Google Scholar]
- Tol, R.S.J. The double trade-off between adaptation and mitigation for sea level rise: An application of FUND. Mitig. Adapt. Strateg. Glob. Chang. 2007, 5, 741–753. [Google Scholar] [CrossRef]
- Vafeidis, A.T.; Nicholls, R.J.; McFadden, L.; Tol, R.S.J.; Spencer, T.; Grashoff, P.S.; Boot, G.; Klein, R.J.T. A new global coastal database for impact and vulnerability analysis to sea-level rise. J. Coast. Resour. 2008, 24, 917–924. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Marinova, N.; Lowe, J.A.; Brown, S.; Vellinga, P.; de Gusmão, D.; Hinkel, J.; Tol, R.S.J. Sea-level rise and its possible impacts given a ‘beyond 4 degrees C world’ in the twenty-first century. Philos. Trans. R. Soc. 2011, 369, 161–181. [Google Scholar] [CrossRef]
- Mel, R. Exploring the partial use of the Mo. S.E. system as effective adaptation to rising flood frequency of Venice. Nat. Hazards Earth Syst. Sci. 2021, 21, 3629–3644. [Google Scholar] [CrossRef]
- Mel, R.; Carniello, L.; Viero, D.P.; Defina, A.; D’Alpaos, L. The first operations of Mo. S.E. system to prevent the flooding of Venice: Insights on the hydrodynamics of a regulated lagoon. Estuar. Coast. Shelf Sci. 2021, 261, 107547. [Google Scholar] [CrossRef]
- Jena, B.K.; Rajkumar, J.; Avula, A.; Jossia, K.; Murthy, M. Simulated wave climate and variability over the North Indian Ocean. Curr. Sci. 2020, 118, 11. [Google Scholar] [CrossRef]
- Lee, Y.H.; Shindell, D.T.; Faluvegi, G.; Pinder, R.W. Potential impact of a US climate policy and air quality regulations on future air quality and climate change. Atmos. Chem. Phys. 2016, 16, 5323–5342. [Google Scholar] [CrossRef]
- Giorgi, F.; Bi, X.; Pal, J. Mean, interannual variability and trends in a regional climate change experiment over Europe. II: Climate change scenarios (2071–2100). Clim. Dyn. 2004, 23, 839–858. [Google Scholar] [CrossRef]
- Vecchi, G.A.; Wittemberg, A.T. El Niño and our future climate: Where do we stand? Wiley Interdiscip. Rev. Clim. Chang. 2010, 1, 260–270. [Google Scholar] [CrossRef]
- Pasaric, M.; Orlic, M. Meteorological forcing of the Adriatic: Present vs. projected climate conditions. Geofizika 2004, 21, 69–87. [Google Scholar]
- Conte, D.; Lionello, P. Storm surge distribution along the Mediterranean coast: Characteristics and evolution. Procedia-Soc. Behav. Sci. 2014, 120, 110–115. [Google Scholar] [CrossRef]
- Bellafiore, D.; Bucchignani, E.; Gualdi, S.; Carniel, S.; Djurdjevic, V.; Umgiesser, G. Assessment of meteorological climate models as inputs for coastal studies. Ocean Dyn. 2012, 62, 555–568. [Google Scholar] [CrossRef]
- Bolanos-Sanchez, R.; Sanchez-Arcilla, A.; Cateura, J. Evaluation of two atmospheric models for wind-wave modelling in the NW Mediterranean. J. Mar. Syst. 2007, 65, 336–353. [Google Scholar] [CrossRef]
- Yang, Z.; García-Medina, G.; Wu, W.C.; Wang, T.; Ruby Leung, L.; Castrucci, L.; Mauger, G. Modeling analysis of the swell and wind-sea climate in the Salish Sea. Estuar. Coast. Shelf Sci. 2019, 224, 289–300. [Google Scholar] [CrossRef]
- Gippius, F.; Myslenkov, S.A. Black Sea’s wind wave climate with a focus on coastal regions. Ocean. Eng. 2020, 218, 108199. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions. Model description and validation. J. Geophys. Res.-Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Campos, R.M.; Alves, J.H.G.M.; Soares, C.G.; Guimaraes, L.G.; Parente, C.E. Extreme wind-wave modeling and analysis in the south Atlantic Ocean. Ocean Model. 2018, 124, 75–93. [Google Scholar] [CrossRef]
- Mulligan, R.P.; Bowen, A.J.; Hay, A.E.; van der Westhuysen, A.J.; Battjes, J.A. Whitecapping and wave field evolution in a coastal bay. J. Geophys. Res.-Ocean. 2008, 113. [Google Scholar] [CrossRef]
- Gedan, K.B.; Silliman, B.R.; Bertness, M.D. Centuries of human-driven change in saltmarsh ecosystems. Annu. Rev. Mar. Sci. 2009, 1, 117–141. [Google Scholar] [CrossRef] [PubMed]
- Liquete, C.; Zulian, G.; Delgado, I.; Stips, A.; Maes, J. Assessment of coastal protection as an ecosystem service in Europe. Ecol. Indic. 2013, 30, 205–217. [Google Scholar] [CrossRef]
- Mel, R.; Sterl, A.; Lionello, P. High resolution climate projection of storm surge at the Venetian coast. Nat. Hazards Earth Syst. Sci. 2013, 13, 1135–1142. [Google Scholar] [CrossRef][Green Version]
- Nayak, S.; Bhaskaran, P.K.; Venkatesan, R.; Dasgupta, S. Modulation of local windwaves at Kalpakkam from remote forcing effects of Southern Ocean swells. Ocean. Eng. 2013, 64, 23–35. [Google Scholar] [CrossRef]
- Mel, R.; Lionello, P. Storm surge ensemble prediction for the city of Venice. Weather Forecast. 2014, 29, 1044–1057. [Google Scholar] [CrossRef]
- Bendoni, M.; Mel, R.; Solari, L.; Lanzoni, S.; Francalanci, S.; Oumeraci, H. Insights into lateral marsh retreat mechanism through localized field measurements. Water Resour. Res. 2016, 52, 1446–1464. [Google Scholar] [CrossRef]
- Albarakati, A.M.A.; Aboobacker, V.M. Wave transformation in the nearshore waters of Jeddah, west coast of Saudi Arabia. Ocean Eng. 2018, 163, 599–608. [Google Scholar] [CrossRef]
- Finotello, A.; Marani, M.; Carniello, L.; Pivato, M.; Roner, M.; Tommasini, L.; D’alpaos, A. Control of wind-wave power on morphological shape of salt marsh margins. Water Sci. Eng. 2020, 13, 45–56. [Google Scholar] [CrossRef]
- Mel, R.; Carniello, L.; D’Alpaos, L. How long the Mo. S.E. barriers will be effective in protecting all the urban settlements in the Venice lagoon? The wind setup constraint. Coast. Eng. 2021, 168, 103923. [Google Scholar] [CrossRef]
- Scarascia, L.; Lionello, P. Global and regional factors contributing to the past and future sea level rise in the northern Adriatic Sea. Glob. Planet. Chang. 2013, 106, 51–63. [Google Scholar] [CrossRef]
- Pranzini, E.; Wetzel, A.; Williams, A. Aspects of coastal erosion and protection in Europe. J. Coast. Conserv. 2015, 19, 445–459. [Google Scholar] [CrossRef]
- Pytharoulis, I.; Craig, G.C.; Ballard, S.P. The hurricane-like Mediterranean cyclone of January 1995. Meteorol. Appl. 2000, 7, 261–279. [Google Scholar] [CrossRef]
- Davolio, S.; Miglietta, M.M.; Moscatello, A.; Pacifico, F.; Buzzi, A.; Rotunno, R. Numerical forecast and analysis of a tropical-like cyclone in the Ionian Sea. Nat. Hazard. Earth Syst. Sci. 2009, 9, 551–562. [Google Scholar] [CrossRef]
- Miglietta, M.M.; Laviola, S.; Malvaldi, A.; Conte, D.; Levizzani, V.; Price, C. Analysis of tropical-like cyclones over the Mediterranean Sea through a combined modeling and satellite approach. Geophys. Res. Lett. 2013, 40, 2400–2405. [Google Scholar] [CrossRef]
- Lionello, P.; Sanna, A. Mediterranean wave climate variability and its links with NAO and Indian Monsoon. Clim. Dyn. 2005, 25, 611–623. [Google Scholar] [CrossRef]
- Galanis, G.; Hayes, D.; Zodiatis, G.; Chu, P.C.; Kuo, Y.H.; Kallos, G. Wave height characteristics in the Mediterranean Sea by means of numerical modeling, satellite data, statistical and geometrical techniques. Mar. Geophys. Res. 2012, 33, 1–15. [Google Scholar] [CrossRef][Green Version]
- Pomaro, A.; Cavaleri, L.; Lionello, P. Climatology and trends of the Adriatic Sea wind waves: Analysis of a 37-year long instrumental data set. Int. J. Climatol. 2017, 37, 4237–4250. [Google Scholar] [CrossRef]
- Caloiero, T.; Aristodemo, F.; Algieri-Ferraro, D. Trend analysis of significant wave height and energy period in southern Italy. Theor. Appl. Climatol. 2019, 138, 917–930. [Google Scholar] [CrossRef]
- Caloiero, T.; Aristodemo, F.; Algieri-Ferraro, D. Changes of Significant Wave Height, Energy Period and Wave Power in Italy in the Period 1979–2018. Environ. Sci. Proc. 2020, 2, 3. [Google Scholar] [CrossRef]
- Trigo, R.M.; Osborn, T.J.; Corte-Real, J.M. The North Atlantic Oscillation influence on Europe: Climate impacts and associated physical mechanisms. Clim. Res. 2002, 20, 9–17. [Google Scholar] [CrossRef]
- Maiolo, M.; Mel, R.A.; Sinopoli, S. A stepwise approach to beach restoration at Calabaia Beach. Water 2020, 12, 2677. [Google Scholar] [CrossRef]
- Maiolo, M.; Mel, R.A.; Sinopoli, S. A simplified method for an evaluation of the submerged breakwaters effect on the wave damping: The case study of Calabaia Beach. J. Mar. Sci. Eng. 2020, 8, 510. [Google Scholar] [CrossRef]
- Maiolo, M.; Carini, M.; Pantusa, D.; Capano, G.; Bonora, M.A.; Lo Feudo, T.; Sinopoli, S.; Mel, R.A. History and heritage of coastal protection in the southern Tyrrhenian area. Ital. J. Eng. Geol. Environ. 2020, 2. [Google Scholar] [CrossRef]
- Erdik, T.; Beji, S. Wave climate in the sea of Marmara. In Oil Spill Along the Turkish Straits Sea Area; Turkish Marine Research Foundation: Istanbul, Turkey, 2018. [Google Scholar]
- Foti, G.; Barbaro, G.; Bombino, G.; Fiamma, V.; Puntonieri, P.; Minniti, F.; Pezzimenti, C. Shoreline changes near river mouth: Case study of Sant’Agata River (ReggioCalabria, Italy). Eur. J. Remote Sens. 2019, 52, 102–112. [Google Scholar] [CrossRef]
- De Falco, G.; Molinaroli, E.; Baroli, M.; Bellacicco, S. Grain size and compositional trends of sediments from Posidonia oceanica meadows to beach shore, Sardinia, western Mediterranean. Estuar. Coast. Shelf Sci. 2003, 58, 299–309. [Google Scholar] [CrossRef]
- Bellotti, P.; Caputo, C.; Davoli, L.; Evangelista, S.; Pugliese, F. Coastal protections in Tyrrhenian Calabria (Italy): Morphological and sedimentological feedback on the vulnerable area of belvedere Marittimo. Geogr. Fis. Din. Quat. 2009, 32, 3–14. [Google Scholar]
- Federico, S.; Bellecci, C. Sea storms hindcast around Calabrian coasts: Seven cases study. Il Nuovo Cim. C 2004, 2, 179–203. [Google Scholar] [CrossRef]
- Bossolasco, M. L’Erosione del litorale di Belvedere Marittimo. Geofis. Pura Appl. 1939, 1, 47–51. [Google Scholar] [CrossRef]
- Maiolo, M.; Versace, P.; Natale, L.; Irish, J.; Pope, J.; Frega, F.A. Comprehensive study of the Tyrrhenian shoreline of the Province of Cosenza. In Proceedings of the Giornate Italiane di Ingegneria Costiera V Edizione (AIPCN 2000) 2000, Reggio Calabria, 11–13 October 2000. [Google Scholar]
- Cavaleri, L.; Abdalla, S.; Benetazzo, A.; Bertotti, L.; Bidlot, J.R.; Breivik, Ø.; Carniel, S.; Jensen, R.E.; Portilla-Yandun, J.; Rogers, W.E.; et al. Wave modelling in coastal and inner seas. Prog. Oceanogr. 2018, 167, 164–233. [Google Scholar] [CrossRef]
- Bencivenga, M.; Nardone, G.; Ruggiero, F.; Calore, D. The Italian Data Buoy Network (RON). WIT Trans. Eng. Sci. 2012, 74, 305. [Google Scholar] [CrossRef]
- Fairley, I.; Williams, H.; Horrillo-Caraballo, J.; Thompson, I.; Masters, I.; Reeve, D.; Karunarathna, H.; Faraggiana, E.; Thompson, D. An analysis of the wave climate in South Wales. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Hersbach, H.; Dee, D. ERA5 Reanalysis Is in Production; ECMWF Newsletter; ECMWF: Reading, UK, 2016. [Google Scholar]
- Hersbach, H.; de Rosnay, P.; Bell, B. Operational global reanalysis: Progress, future directions and synergies with NWP. Re-Anal. Proj. Rep. Ser. 2018, 27, 1–63. [Google Scholar]
- Nogueira, M. Inter-comparison of ERA-5, ERA-interim and GPCP rainfall over the last 40 years: Process-based analysis of systematic and random differences. J. Hydrol. 2020, 583, 124632. [Google Scholar] [CrossRef]
- Johannsen, F.; Ermida, S.; Martins, J.; Trigo, I.F.; Nogueira, M.; Dutra, E. Cold bias of ERA5 summertime daily maximum land surface temperature over Iberian Peninsula. Remote Sens. 2019, 11, 2570. [Google Scholar] [CrossRef]
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-de-pison, F.K.; Sanz-Garcia, A. Evaluation of global horizontal irradiance estimates from ERA5 and COSMO-REA6 reanalyses using ground and satellite-based data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- Ramon, J.; Lledo, L.; Torralba, V.; Soret, A.; Doblas-Reyes, F.J. What global reanalysis best represents near-surface winds? Q. J. R. Meteorol. Soc. 2019, 145, 3236–3251. [Google Scholar] [CrossRef]
- WAMDI Group. The WAM model—A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar] [CrossRef]
- Federico, S.; Lo Feudo, T.; Bellecci, C.; Arena, F. Impact of wind field horizontal resolution on sea waves hindcast around Calabrian coasts. Il Nuovo Cim. C 2006, 29, 147–165. [Google Scholar] [CrossRef]
- Roe, P.L. Approximate Riemann Solvers, Parameter Vectors, and Difference Schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Jawahar, P.; Kamath, H.A. High-Resolution Procedure for Euler and Navier-Stokes Computations on Unstructured Grids. J. Comput. Phys. 2000, 164, 165–203. [Google Scholar] [CrossRef]
- Anastasiau, K.; Chan, C.T. Solution of the 2D shallow water equations using the finite-volume method on unstructured triangular meshes. Int. J. Numer. Methods Fluids 1997, 24, 1225–1245. [Google Scholar] [CrossRef]
- Danish Hydraulics Institute. MIKE 21 & MIKE 3 Flow Model FM–Hydrodynamic and Transport Module, Scientific Documentation; DHI: Hørsholm, Denmark, 2017. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Oxford University Press: New York, NY, USA, 1975. [Google Scholar]
- Kundzewicz, Z.W.; Robson, A. 2000 Detecting Trend and Other Changes in Hydrological Data. World Climate Program Data and Monitoring. WMO/TD-No. 1013. Available online: https://library.wmo.int/index.php?lvl=notice_display&id=11628#.Yd0KoFkRVPZ (accessed on 22 November 2021).
- De Leo, F.; De Leo, A.; Besio, G.; Briganti, R. Detection and quantification of trends in time series of significant wave heights: An application in the Mediterranean. Sea Ocean Eng. 2020, 202, 107155. [Google Scholar] [CrossRef]
- Şen, Z. Innovative Trend Analysis Methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Cavaleri, L.; Bertotti, L. Accuracy of the modelled wind and wave fields in enclosed seas. Tellus A Dyn. Meteorol. Oceanogr. 2004, 56, 167–175. [Google Scholar] [CrossRef]
- Morucci, S.; Picone, M.; Nardone, G.; Arena, G. Tides and waves in the Central Mediterranean Sea. J. Oper. Oceanogr. 2016, 9, s10–s17. [Google Scholar] [CrossRef]
- Klein-Tank, A.M.G.; Können, G.P. Trends in Indices of Daily Temperature and Precipitation Extremes in Europe 1946–99. J. Clim. 2003, 16, 3665–3680. [Google Scholar] [CrossRef]
- Vitale, D.; Rana, G.; Pietro, S. Trends Analysis of Daily Data from a Site in the Capitanata Plain (Southern Italy). Ital. J. Agron. 2010, 5, 133–144. [Google Scholar] [CrossRef]
- Haktanir, T.; Citakoglu, H. Trend, Independence, Stationarity, and Homogeneity Tests on Maximum Rainfall Series of Standard Durations Recorded in Turkey. J. Hydrol. Eng. 2014, 19, 05014009. [Google Scholar] [CrossRef]
- Kisi, O. An innovative method for trend analysis of monthly pan evaporations. J. Hydrol. 2015, 527, 1123–1129. [Google Scholar] [CrossRef]
- Pasqua, A.A.; Bruno, C.; Guardia, S.; Valente, E.; Petrucci, O. La Mareggiata del 21 Marzo 2018 Sulla Costa Tirrenica Calabrese; Consiglio Nazionale delle Ricerche–IRPI: Perugia, Italy, 2018; ISBN 978-88-95172-08-8. [Google Scholar]
- Sun, Y.J.; Perrie, W.; Toulany, B. Simulation of wave-current interactions under hurricane conditions using an unstructured-grid model: Impacts on ocean waves. J. Geophys. Res.-Ocean. 2018, 123, 3739–3760. [Google Scholar] [CrossRef]
- Gong, W.P.; Chen, Y.Z.; Zhang, H.; Chen, Z.Y. Effects of wave-current interaction on salt intrusion during a typhoon event in a highly stratified estuary. Estuar. Coasts 2018, 41, 1904–1923. [Google Scholar] [CrossRef]
- Wargula, A.; Raubenheimer, B.; Elgar, S.; Chen, J.L.; Shi, F.Y.; Traykovski, P. Tidal flow asymmetry owing to inertia and waves on an unstratified, shallow ebb shoal. J. Geophys. Res.-Ocean. 2018, 123, 6779–6799. [Google Scholar] [CrossRef]


| 10,857 Data | Significant Wave Height SWH (m) | Wave Mean Period Tm (s) | Wave Mean Direction Θ (deg) | |||
|---|---|---|---|---|---|---|
| ERA5 | Buoy | ERA5 | Buoy | ERA5 | Buoy | |
| Mean | 0.52 m | 0.67 m | 4.6 s | 4.7 s | 252° | 240° |
| Variance | 0.22 m2 | 0.40 m2 | 2.1 s2 | 2.4 s2 | // | // |
| St. Deviation | 0.46 m | 0.62 m | 1.4 s | 1.5 s | // | // |
| Median | 0.33 m | 0.50 m | 4.4 s | 4.3 s | 263° | 261° |
| 10th percentile | 0.13 m | 0.14 m | 2.7 s | 3.0 s | 181° | 131° |
| 90th percentile | 1.08 m | 1.43 m | 6.6 s | 6.5 s | 264° | 261° |
| BIAS | −0.15 m | −0.13 s | 12° | |||
| MAE | 0.19 m | 0.96 s | 34° | |||
| RMSE | 0.28 m | 1.44 s | 67° | |||
| SI | 0.42 | 0.33 | 0.30 | |||
| R2 | 0.90 | 0.91 | 0.70 | |||
| 14,607 Data | Significant Wave Height SWH (m) | Wave Mean Period Tm (s) | Wave Mean Direction Θ (deg) | |||
|---|---|---|---|---|---|---|
| ERA5 | WAM | ERA5 | WAM | ERA5 | WAM | |
| Mean | 0.55 m | 0.62 m | 4.7 s | 4.6 s | 254° | 253° |
| Variance | 0.25 m2 | 0.32 m2 | 2.3 s2 | 2.7 s2 | // | // |
| St. Deviation | 0.50 m | 0.57 m | 1.5 s | 1.6 s | // | // |
| Median | 0.38 m | 0.43 m | 4.5 s | 4.5 s | 266° | 270° |
| 10th percentile | 0.14 m | 0.16 m | 2.8 s | 2.6 s | 187° | 176° |
| 90th percentile | 1.17 m | 1.30 m | 6.8 s | 6.8 s | 289° | 296° |
| BIAS | −0.07 m | 0.07 s | 1° | |||
| MAE | 0.09 m | 0.39 s | 14° | |||
| RMSE | 0.15 m | 0.59 s | 37° | |||
| SI | 0.25 | 0.13 | 0.15 | |||
| R2 | 0.92 | 0.88 | 0.61 | |||
| SWH | Winter | Spring | Summer | Fall | Annual |
|---|---|---|---|---|---|
| Mean | 0.71 m | 0.52 m | 0.33 m | 0.48 m | 0.51 m |
| Variance | 0.020 m2 | 0.008 m2 | 0.002 m2 | 0.008 m2 | 0.002 m2 |
| St. Deviation | 0.140 m | 0.089 m | 0.039 m | 0.088 m | 0.048 m |
| Median | 0.70 m | 0.53 m | 0.34 m | 0.47 m | 0.51 m |
| 10th percentile | 0.53 m | 0.40 m | 0.29 m | 0.37 m | 0.45 m |
| 90th percentile | 0.88 m | 0.62 m | 0.38 m | 0.58 m | 0.56 m |
| Max | 0.99 m | 0.76 m | 0.43 m | 0.76 m | 0.64 m |
| Tm | Winter | Spring | Summer | Fall | Annual |
|---|---|---|---|---|---|
| Mean | 5.20 s | 4.65 s | 3.83 s | 4.43 s | 4.52 s |
| Variance | 0.148 s2 | 0.088 s2 | 0.040 s2 | 0.111 s2 | 0.027 s2 |
| St. Deviation | 0.384 s | 0.296 s | 0.200 s | 0.333 s | 0.165 s |
| Median | 5.27 s | 4.67 s | 3.84 s | 4.41 s | 4.51 s |
| 10th percentile | 4.73 s | 4.22 s | 3.62 s | 4.04 s | 4.31 s |
| 90th percentile | 5.66 s | 5.06 s | 4.03 s | 4.92 s | 4.73 s |
| Max | 5.99 s | 5.32 s | 4.31 s | 5.26 s | 4.99 s |
| Period | Test Z | Significance | A |
|---|---|---|---|
| Jan | 0.1521 | // | 0.00030 |
| Feb | −1.0443 | // | −0.00154 |
| Mar | 1.1964 | // | 0.00142 |
| Apr | −0.3650 | // | −0.00025 |
| May | 1.2624 | // | 0.00091 |
| Jun | 0.4157 | // | 0.00017 |
| July | 0.8314 | // | 0.00036 |
| Aug | −2.2104 | SS | −0.00087 |
| Sep | 1.2978 | // | 0.00070 |
| Oct | −0.5171 | // | −0.00043 |
| Nov | 0.3853 | // | 0.00042 |
| Dec | −0.4157 | // | −0.00065 |
| DJF | −0.96 | // | −0.00067 |
| MAM | 1.38 | // | 0.00082 |
| JJA | −0.67 | // | −0.00018 |
| SON | 0.48 | // | 0.00030 |
| ANNUAL | −0.13 | // | −0.00005 |
| Period | Test Z | Significance | A |
|---|---|---|---|
| Jan | 0.0406 | // | 0.00011 |
| Feb | 0.5779 | // | 0.00217 |
| Mar | −0.1115 | // | −0.00032 |
| Apr | 1.2066 | // | 0.00426 |
| May | 1.3485 | // | 0.00373 |
| Jun | 2.1293 | SS | 0.00577 |
| July | 1.8758 | S | 0.00421 |
| Aug | 1.5108 | // | 0.00342 |
| Sep | −1.0342 | // | −0.00186 |
| Oct | 2.4537 | SS | 0.00620 |
| Nov | 0.9937 | // | 0.00407 |
| Dec | 1.4296 | // | 0.00443 |
| DJF | 0.06 | // | 0.00009 |
| MAM | 2.58 | SS | 0.00473 |
| JJA | 1.65 | S | 0.00212 |
| SON | 3.02 | SSS | 0.00579 |
| ANNUAL | 3.10 | SSS | 0.00304 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lo Feudo, T.; Mel, R.A.; Sinopoli, S.; Maiolo, M. Wave Climate and Trends for the Marine Experimental Station of Capo Tirone Based on a 70-Year-Long Hindcast Dataset. Water 2022, 14, 163. https://doi.org/10.3390/w14020163
Lo Feudo T, Mel RA, Sinopoli S, Maiolo M. Wave Climate and Trends for the Marine Experimental Station of Capo Tirone Based on a 70-Year-Long Hindcast Dataset. Water. 2022; 14(2):163. https://doi.org/10.3390/w14020163
Chicago/Turabian StyleLo Feudo, Teresa, Riccardo Alvise Mel, Salvatore Sinopoli, and Mario Maiolo. 2022. "Wave Climate and Trends for the Marine Experimental Station of Capo Tirone Based on a 70-Year-Long Hindcast Dataset" Water 14, no. 2: 163. https://doi.org/10.3390/w14020163
APA StyleLo Feudo, T., Mel, R. A., Sinopoli, S., & Maiolo, M. (2022). Wave Climate and Trends for the Marine Experimental Station of Capo Tirone Based on a 70-Year-Long Hindcast Dataset. Water, 14(2), 163. https://doi.org/10.3390/w14020163









