1. Introduction
Recent changes in climatic conditions have increased the incidence of flooding worldwide. Flood warnings are based on the predicted height of the flood, and most previous research in flood height prediction has been based on radar echo maps and hydrological models [
1,
2,
3].
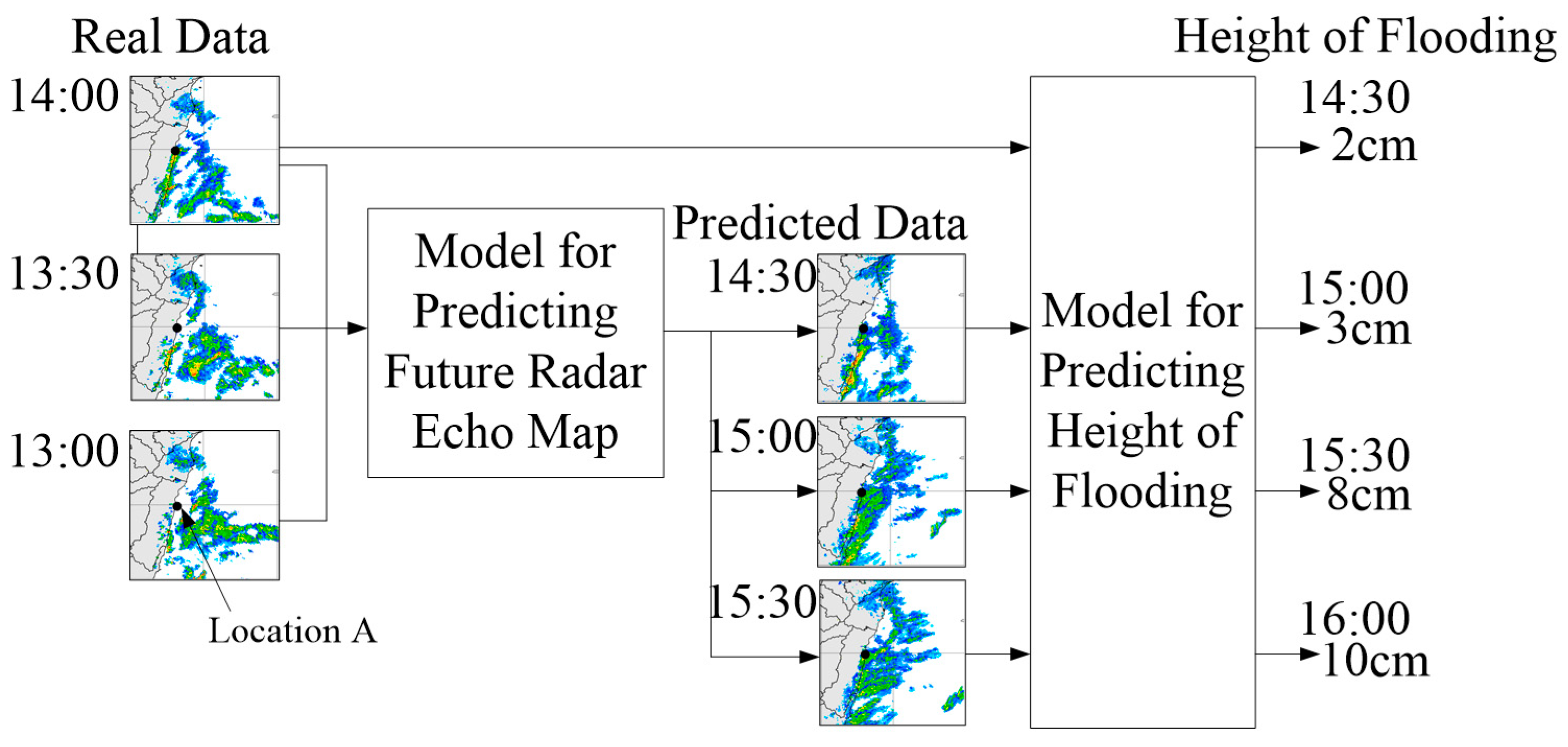
Figure 1 illustrates the concept underlying this type of research. Suppose that the current time is 13:00, 1 January 2022, and the Central Weather Bureau has trained a model for location A. Using the radar echo map for time
t as an input, the model outputs a prediction for the height of flooding at location A at time
t + 30 min. In this way, it is possible to use radar echo maps from 13:00, 13:30, and 14:00 to simulate radar echo maps indicating the conditions predicted for 14:30, 15:00, and 15:30. Using the actual radar echo map from 14:00 and the predicted radar echo maps from 14:30 to 15:30 as inputs, it is then possible to predict the height of flooding in location A for every half hour between 14:30 and 16:00.
Scholars have developed a variety of hydrological models to illustrate the correlation between radar echo maps and flood height. Mecklenburg et al. [
1] constructed a model to simulate radar echo maps for use in predicting flood height. Using the Hydrog model and data of two flood events in the Czech Republic, Šálek et al. [
2] confirmed that radar echo maps can indeed be used to make accurate predictions pertaining to flood events. Novák et al. [
3] demonstrated that tracking radar echoes via correlation-based quantitative forecasts of precipitation provide flood predictions of high accuracy. To improve the accuracy of flood predictions, Yoon [
4] developed a blending model involving six commonly used quantitative precipitation forecasts as inputs for the StormWater Management Model and Grid-based Inundation Analysis Model.
The methods outlined above have no doubt proven effective in the prediction of flooding events; however, they have two notable shortcomings: (1) Establishing hydrological models requires considerable professional knowledge and extensive measurement data, and updating can only be performed by teams of highly specialized individuals. Most scholars are unable to acquire and/or apply the data or verify the correctness of their predictions. (2) Collecting all of the data required to make flood height predictions for all locations would require considerable time and increase the likelihood that important factors are inadvertently overlooked.
Many scholars have begun applying deep learning models (DLMs) to radar echo maps. Chen et al. [
5] developed an extended model based on convolutional long short-term memory to predict future radar echo maps. Yin et al. [
6] used DLMs to fill occluded areas in radar echo maps. Singh et al. [
7] modified part of the long short-term memory structure to enable high-precision precipitation nowcasting using radar echo maps. Yin et al. [
8] performed high-precision strong convection nowcasting based on the convolutional gated recurrent unit. Yan et al. [
9] used a dual-channel neural network to make short-term predictions of precipitation. Previous experience indicates that DLMs have two fundamental benefits: (1) DLMs do not require professional knowledge and depend entirely on historical data, such that the building and updating process is relatively simple. (2) DLMs automate the process of finding patterns in inputs and outputs, thereby making it possible to obtain a more comprehensive collection of factors (far exceeding what can be achieved using conventional approaches) with a corresponding increase in accuracy. To the best of our knowledge, this is the first paper to address the use of radar echo maps and DLMs for the prediction of flood height.
It should be noted that using CNNs to formulate flood height predictions directly from radar echo maps would be highly inefficient. Discrete CNNs would be required to deal with the flood conditions specific to every site within large regions or the entire country. Furthermore, CNN operations would have to be completed in short intervals (e.g., 10 min or 1 h), thereby necessitating the use of expensive high-end servers. Our primary objective in the current study was to reduce the cost of operating DLMs without undermining prediction accuracy.
Previous attempts to reduce the operating cost of DLMs can be divided into two approaches: (1) methods aimed at simplifying the model structure while maintaining the dimensions of the input data, and (2) methods aimed at reducing the input dimensions without simplifying the model structure. The first approach reduces computational cost by deleting the layers, neurons, or weights that contribute least to the output. Han et al. [
10] deleted weight values and Li et al. [
11] deleted entire filter layers. Molchanov et al. [
12] used the Taylor expansion to explore the influence of each filter layer on the loss function in order to identify filter layers for deletion. Luo et al. [
13] implemented a similar approach using a greedy algorithm. Note that the first approach is effective in reducing the computational cost of DLMs; however, a lack of compatibility with many graphics processing units means that this approach is ill-suited to many practical online applications. The second approach involves training a DLM and then disassembling it to obtain key factors for use as inputs for machine learning models or deep learning models with limited input dimensionality. The fact that these models employ only the most important factors for modeling means that their prediction accuracy does not deviate considerably from that of the original DLM. In the scheme proposed by Sani et al. [
14], the key factors are contained in the output of the last pooling layer after training. Mohammad et al. [
15] developed a set of mathematical theories by which to disassemble the trained DLM to obtain the key factors. These studies confirmed that the key factors identified by the DLM could be used to perform high-precision motion recognition using a low-cost model. Chen and Lee [
16] pointed out that the use of complex mathematical conversion is a waste of computational resources. They developed a radius base function long short-term memory model to simplify the disassembly process. Furthermore, the key factors selected using their method match the input of the original model, thereby eliminating the extra step of converting model inputs into key factors. They went on to demonstrate that their key factors could be used to achieve prediction accuracy on par that of deep learning from any machine learning model, with presumably far lower computational overhead.
In the current study, we adopted an approach similar to the scheme described in [
16]. Briefly, a DLM is trained using a radar echo map as the input and flood height as the output. From the trained DLM, key grid cells are extracted (i.e., key factors in [
16]) for use as inputs in other lightweight models. Finally, only the lightweight models are used in online applications in order to reduce the computational cost.
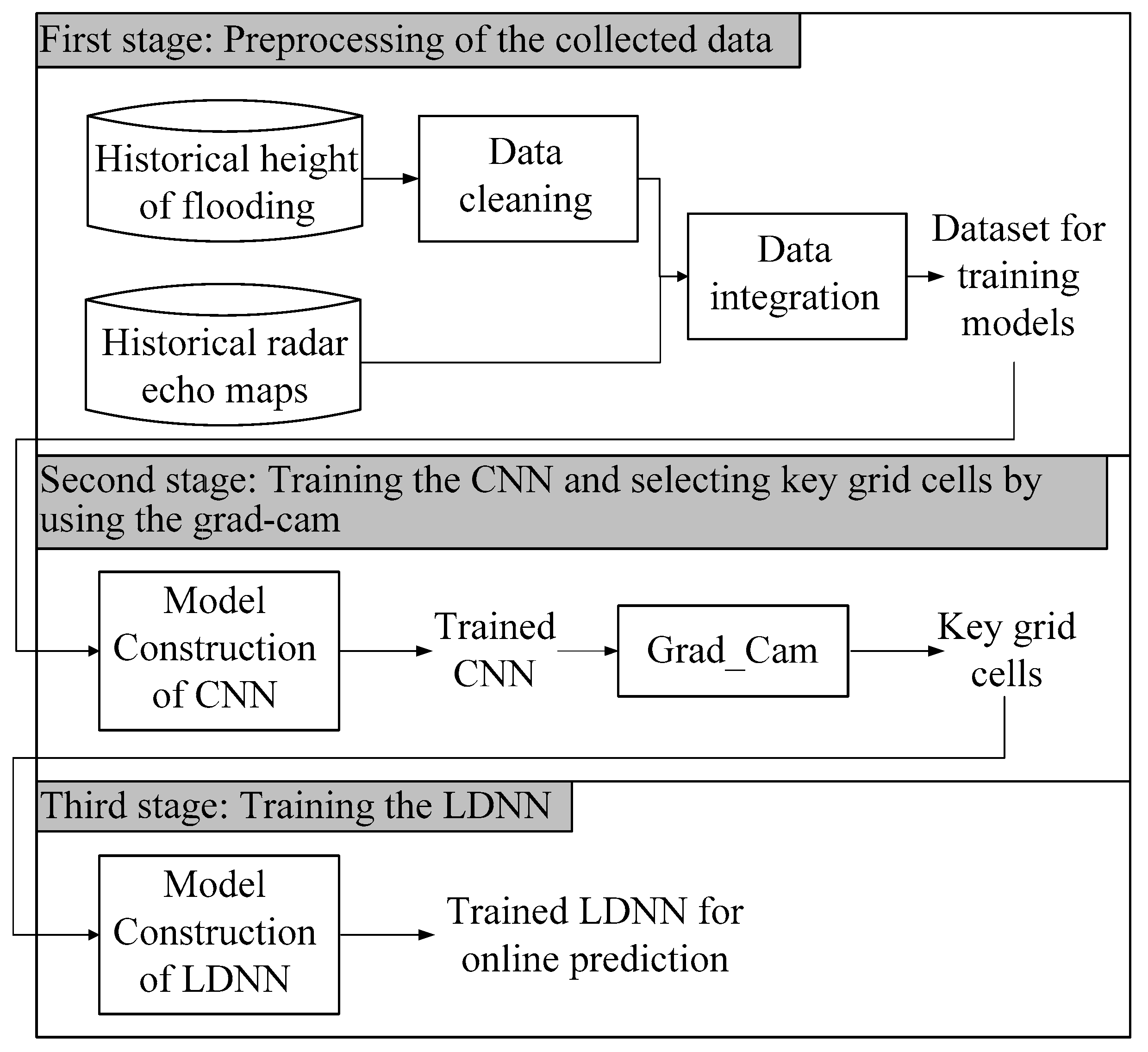
Figure 2 presents a flow chart of the proposed scheme. Note that even when using the proposed scheme to make flood predictions for a large number of locations simultaneously, the computational demands are far lower than those imposed by a DLM. Note also that this approach greatly increases the cost of building lightweight models; however, we disregarded the cost of model building due to the fact that model rebuilding or updating is required only for long-term predictions (quarterly or yearly). The methods outlined in [
16] are inapplicable to our scheme, because the model input in that study is an independent data dimension, whereas the model input in this study is a radar echo map divided into a grid with strong dependence among adjacent grid cells.
In the current study, we employed a convolutional neural network (CNN) in conjunction with the Grad-Cam package for the extraction of key grid cells from radar echo maps (representing regions with the greatest impact on flooding) for use as inputs into another DLM, as shown in
Figure 2. This approach makes it possible to reduce the number of input dimensions with a corresponding reduction in computational overhead. This, in turn, should make it possible to make multiple simultaneous predictions of flood height over large areas. Note that we selected a CNN for this research because the model input is a radar echo map comprising a large number of grid cells, and the model output is a single value (flood height) associated with the target place. CNNs are among the most effective models for predicting single output values from grid input data. After inputting data (in grid format) into the trained CNN, back propagation is used to identify the key cells (i.e., those of greatest relevance of the output value). The Grad-Cam package is an accessory widely used with CNNs. He et al. [
17] used a CNN with Grad-Cam to select factors that are important in the detection of lung cancer. Li et al. [
18] used Grad-Cam to optimize channel selection in a CNN for EEG-based intention recognition. Marsot et al. [
19] combined a CNN with Grad-Cam to optimize facial recognition in a porcine model. Combining a CNN with Grad-Cam is a reasonable approach to analyzing radar echo maps; however, our grid input differs fundamentally from the inputs in previous papers. The grid cells in this paper represent distinct geographic locations, which do not vary. The grid inputs in most previous studies were derived from images, such that the entity represented by the grid cell tended to vary. Thus, we had to modify the means by which Grad-Cam is used for the extraction of key factors. In the end of this work, we will conduct experiments using actual radar echo maps and historical flooding records to confirm that the proposed CNN–Grad-Cam framework can indeed identify the grid cells with the greatest influence on flood heights in multiple locations. Our results confirmed that using only the key grid cells to build a DLM reduced computational overhead, while maintaining accuracy close to that of the original CNN.
The fact that our model is based primarily on the key features of DLM means that as long as relevant inputs are available, a lightweight model can be established without the need for hydrological knowledge. However, this type of system cannot be used when input–output correlation is poor, when all input dimensions that affect the output value are unavailable, or when the reproducibility of historical data is not good. In real-world scenarios, flood height can be affected by other factors, such as the tides, upstream rainfall, and flood discharge from reservoirs. In such situations, the exclusive use of radar echo maps would be unlikely to achieve accurate predictions in areas adjacent to the sea or rivers. Additionally, when flood conditions in low-lying areas are controlled by pumps, DLM cannot be used to establish an effective predictive model, let alone a lightweight model. Therefore, we recommend applying the proposed model to relatively simple environments, such as places where the flooding situation is predominantly affected by rainfall or terrain. Note that such environments are very common in most rural and even urban locations. In this paper, we consider only the relationship between radar echo maps and flood height, such that the CNN is used primarily for first-stage modeling. CNNs provide good modeling results when using data in a grid format (e.g., a map grid), but poor modeling results when grid-format data and single data are input together. In the future, we will develop extended versions of this model to overcome the limitations of conventional CNNs.
Section 2 presents an overview of the relevant literature. The proposed algorithm is presented in
Section 3. Simulation experiments are outlined in
Section 4. Conclusions and future work are discussed in
Section 5.
3. Algorithms
Figure 3 illustrates the three-stage computational framework proposed in this paper. Our aim is to predict the flood height in grid cell A. The first stage involves data pre-processing, aimed at sorting out the historical flood records pertaining to cell A and finding the radar echo map for the corresponding time point. The second stage involves training a CNN using the radar echo map identified in the previous stage (as the input) and the flood height of A (as the output). After training the CNN, Grad-Cam is used to find the grid cells that are key to estimating flood height in area A. The final stage involves using the key grid cells as input into a lightweight deep neural network (LDNN) for modeling and prediction. In the following subsection, we discuss the collection, cleaning, and integration of flood-related data and radar echo maps. We then introduce the CNN architecture, after which we describe how Grad-Cam is used to identify key grid cells. In the final subsection, we introduce the LDNN used in this paper.
3.1. Collection, Cleaning, and Integration of Flood-Related Data and Radar Echo Maps
In this section, we introduce the methods used in the collection and formatting of flood-related data. We also introduce the radar echo maps and discuss the means by which the data are assembled into a data set applicable to the CNN. Flood-related data from sensors is returned as a value representing the flood height at steady intervals. Assuming that the sensor is set up in grid cell A, the first time the sensor collects data is
t1, and a value is returned after every interval
t. We then represent the flood height value of
n consecutive returns as H
A = [
hA(
t1),
hA(
t2), …,
hA(
tn)], where
ti =
ti−1 +
t. The value of
t ranges from 10 min to 12 h. Due to network instability, external sensors are prone to missing H
A values. Cleaning and augmenting H
A values involves two sub-steps. The first sub-step involves obtaining a reasonable range of flood heights for grid cell A, based on historical data from the weather bureau. We then check whether the H
A values fall within that range, and mark any missing values or values outside that range. The second sub-step involves determining whether to change or discard the marked values, based on the timespan to the previous sub-step. If the duration of the marked value is less than 24 h, then Equation (1) is used to fill in the value in accordance with the situation at that time of day.
where
a represents the time of the previous marked value,
b represents the number of consecutively marked values, and
c represents the data inserted for the
cth record. If the duration of the marked value exceeds 24 h, then the marked value is simply discarded. If the inserted values for periods
t2 and
t3 in area A are
hA(
t2)′ and
hA(
t3)′, and the values within
t20 to
t40 are discarded, then the new H
A can be expressed as H
A′ = [
hA(
t1),
hA(
t2)′,
hA(
t3)′,
hA(
t4), …,
hA(
t19),
hA(
t41), …,
hA(
tn)].
After sorting out flood data for area A, we sort out the radar echo maps surrounding area A, which are usually obtained from the weather bureau. Assuming that the radar echo maps provided by the bureau are recorded at intervals of
k, we obtain radar echo map data of the surrounding
x ×
y grid with A as the center. Assuming that the time of the first radar echo map is
k1, and the interval between each image is
k, then we can represent
m continuous radar echo maps as P
A = [
pA(
k1),
pA(
k2), …,
pA(
km)], where
ki =
ki−1 +
k. The value of k usually ranges from 10 min to one hour. The
kith radar echo map
pA(
ki) in P
A can be expressed as
pA(
ki) = [
va,ki(1, 1),
va,ki(1, 2), …,
va,ki(1,
y),
va,ki(2, 1), …,
va,ki(2,
y), …,
va,ki(
x, 1), …,
va,ki(
x,
y)]. Note that A will not be in the center of the radar echo map when A is located at the edge of the map. In this situation, making
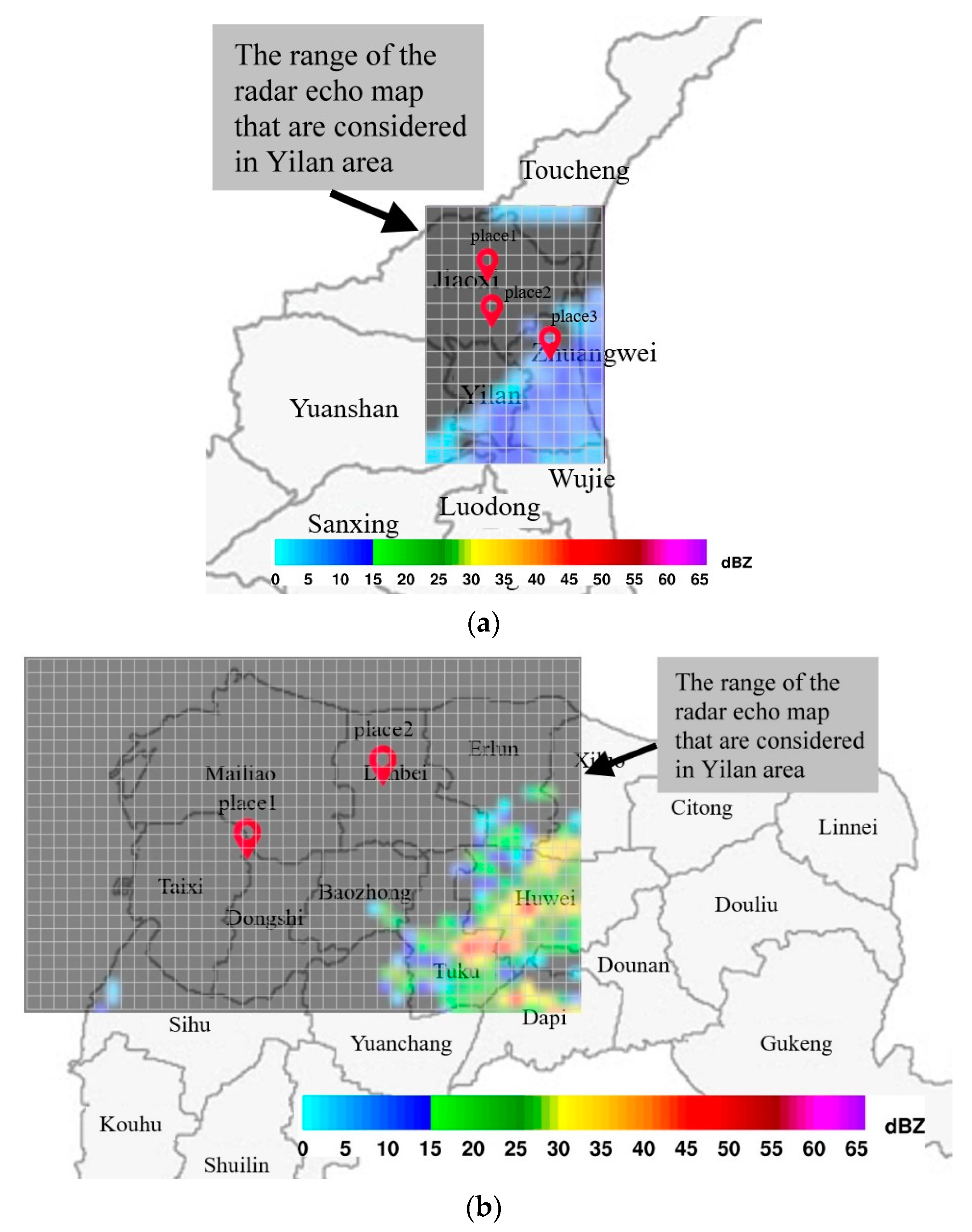
A the center would limit the range of the radar echo map, as shown in
Figure 4. Note also that the radar echo map grid is actually a rectangle, due to the limited the range of the radar echo map obtained from the government and limitations due to terrain and other factors. We must assume that the radar echo map obtained from the weather bureau is accurate and reasonable. The grid used for radar echo maps should be adjusted to the specifics of the intended application. The additional information provided by grids of high resolution can significantly increase CNN prediction accuracy, and our lightweight model based on the CNN architecture would also benefit from grid of higher resolution. Nonetheless, any improvement in accuracy would come at the cost of higher computational overhead. In other words, selecting the resolution of radar echo maps involves a trade-off between accuracy and computational capacity or efficiency. In fact, the computational demands of large-scale CNNs are likely to exceed the capacity of all but the most highly enabled computer systems.
Flood-related data and the radar echo map must be organized within a data set applicable to the CNN. This is achieved in two sub-steps: (1) Selection of flood and non-flood events, and (2) Combination of the event and the radar echo map. Sub-step (1) involves sorting through events one-by-one. Due to the rarity of flood events, most of the values in flood height data set HA′ are 0 (i.e., only rare flood events are greater than 0). Inputting HA′ directly into the CNN for training would result in data imbalance and corresponding inaccuracies. This situation can be avoided by balancing the ratio of non-flood events against flood events. We begin by recording the number of times the flood height value exceeded σ, where σ is the threshold value indicating a flood event, as defined by the government. We estimate the distribution of flood height levels, randomly select φ data points from the remaining non-flood events, and record when those data points occurred. For convenience, we assume that w pieces of data in HA′ are retrieved. Note that the newly retrieved data are expressed as HA″ = [hA(tr1)″, hA(tr2)″, …, hA(trw)″]. The times associated with these data points are TimeA = {tr1, tr2, …, trw}, where tr1, tr2, …, trw are sorted chronologically but may be discontinuous.
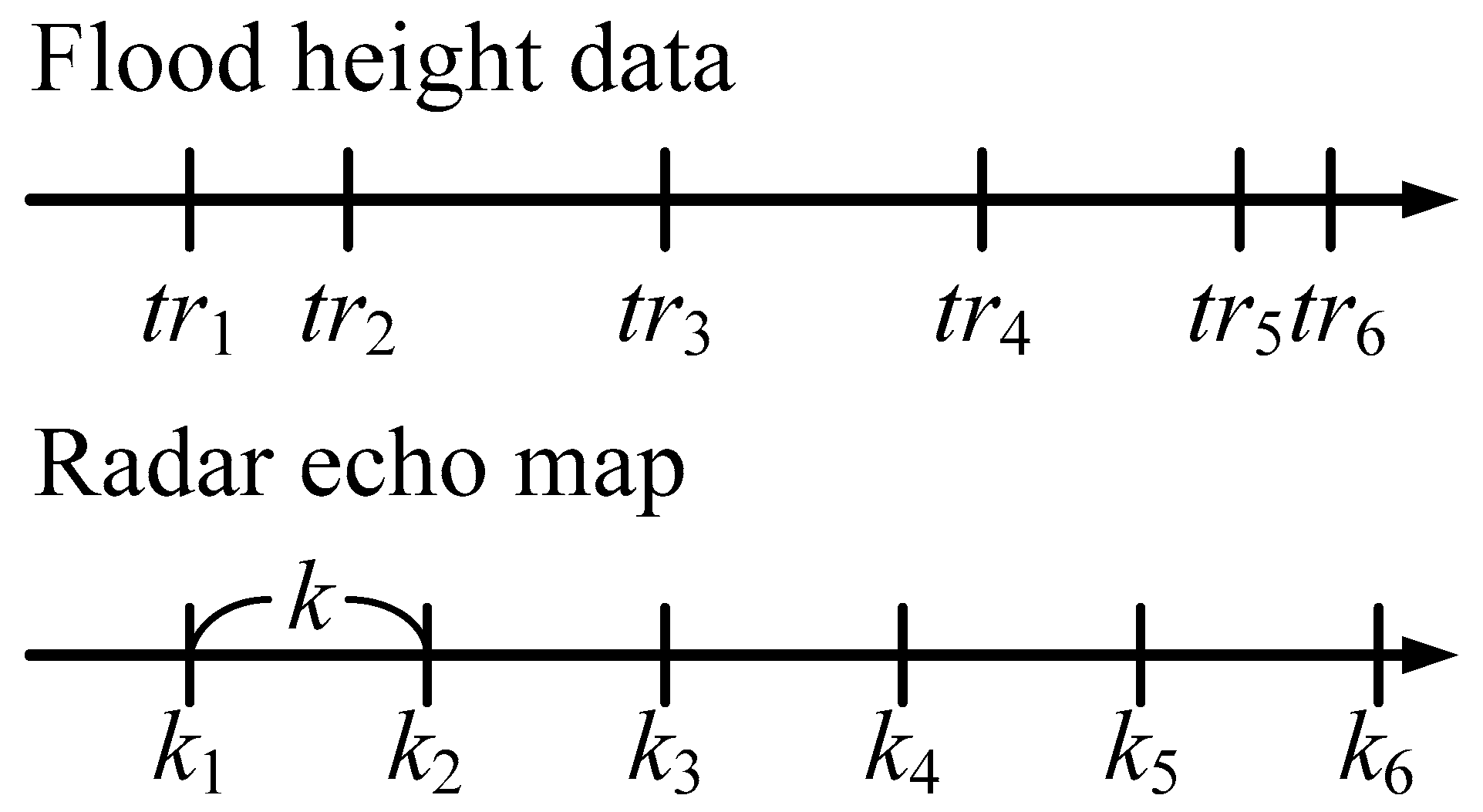
Sub-step (2) involves combining the data of flood height and the radar echo map. This sub-step is needed because the time intervals and time of the flood sensor and the radar echo map may be different. There is no direct correspondence, as shown in
Figure 5. The details of this sub-step are as follows. We assume that the radar echo map data set is P
A = [
pA(
k1),
pA(
k2), …,
pA(
km)], where
k1,
k2, …,
km are continuous points in time, and the intervals between each point in time are
k. We perform the following checks for the
ith time point
tri of Time
A.
Case 1: If there is a time point kj in k1, k2, …, km that precisely matches tri, then we combine the kjth radar echo map pA(kj) with flood height hA(tri)″ as a single set of inputs and outputs.
Case 2: If there is no time point in k1, k2, …, km that matches tri, and the time interval between tri and tri+1 is greater than k, then we find kj, the point in k1, k2, …, km closest to tri. We take the radar echo map pA(kj) of kj and flood height hA(tri)″ and combine them into a single set of inputs and outputs.
Case 3: If there is no time point in k1, k2, …, km that matches tri, and the time interval between tri and tri+1 is less than k, we find kj, the point in k1, k2, …, km closest to tri. We take the radar echo map pA(kj) of kj and flood height hA(tri)’’ and combine them into a single set of inputs and outputs. Note that tri+1 and hA(tri+1)’’ are not considered in subsequent calculations.
After checking all w time points in TimeA, we obtain a set that can be used as the input and output for the subsequent CNN [(pA(tcnn1), hA(tcnn1)″), (pA(tcnn2), hA(tcnn2)″), …, (pA(tcnnw′), hA(tcnnw′)″)], where tcnni represents the ith data in this set, and w′ is the total number of data points in the set (i.e., w′ < w).
3.2. CNN Architecture Used in Target Framework
In this section, we introduce the input, output, and network architecture of the proposed CNN. As described in the previous section, the ith input data of the CNN is pA(tcnni) in CNN_IO, which represents a radar echo map with a grid size of α × β × γ, where β and γ represent the size of the radar echo map, and α indicates the number of characteristics of the radar echo map. The ith output data of the CNN is hA(tcnni) in CNN_IO, which represents the flood height. As for the selection of CNN training, testing, and validation datasets, we recommend that the ratio should be set at 70%, 15%, 15% or 70%, 10%, 20% to meet most CNN training procedures. In addition, in order to maintain the independence of the three datasets, we suggest that the training, testing, and validation datasets be divided into different flooding events or into different flood years when the user has enough data.
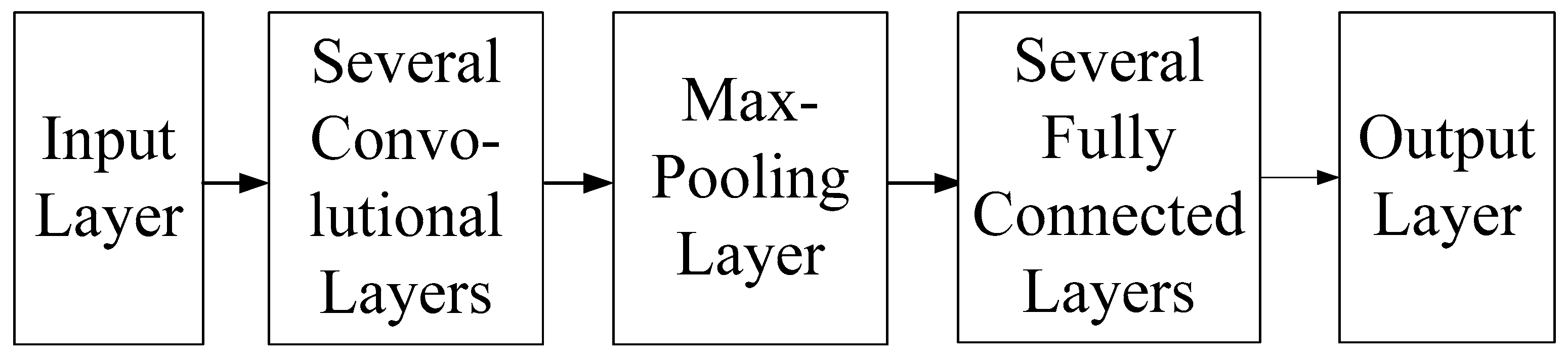
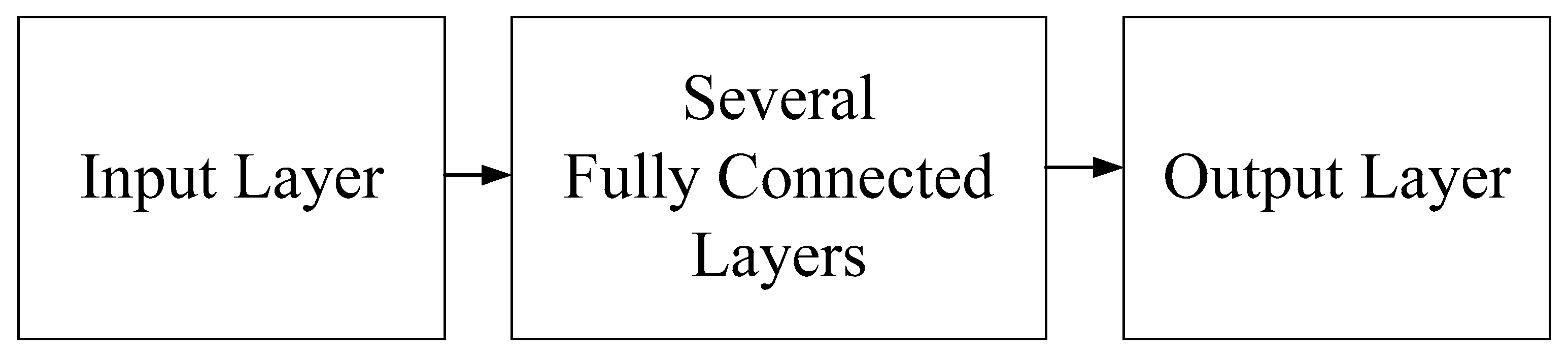
The internal architecture of the CNN used in this framework comprises an input layer, several convolutional layers, a max pooling layer, multiple fully connected layers, and an output layer, as shown in
Figure 6. The mathematical formula of each layer and its physical meaning in flood height prediction are described below. The input layer is used to transfer the radar echo map into the model. The mathematical formula of any neuron in this layer can be expressed as follows:
where
Oz,x,y is the output value of the neuron with the
zth feature located at (
x,
y). The multi-layer convolutional layer is used mainly to extract features from the radar echo map. Assuming that the size of the radar echo map received by the CNN is
x ×
y and the CNN uses a total of
n convolutional layers, we recommend setting the filter size of the first convolutional layer in accordance with the ratio of
x to
y. We do this because the rectangular data input of this CNN should be transformed into a square to facilitate subsequent processing. The filter size in the second convolutional layer is based on the output size of the previous layer. The number of convolutional layers depends on the size of the input radar echo map. Regardless of the convolutional layer in which a neuron is located, it can be expressed using the following mathematical formula:
where
oi(z,x,y) is the output value of the
ith neuron whose
zth feature is located at (
x,
y).
bik and
lik are, respectively, the corresponding bias vector and kernel in the layer.
I(•,•,•) is the input for this layer, and
act(•)is the Relu activation function.
After the convolutional layer processes the radar echo map, a max-pooling layer is used to reduce the model size and highlight the important characteristics in the feature space. If the input data of a neuron in this layer is (
Ci,
Ri,
Hi), then the output result is (
C0,
R0,
H0), the pool size of this layer is (
p,
p), and stride is
s, such that the mathematical formula of the neuron can be written as
After obtaining the results of the max-pooling layer, we use a multi-layer fully connected layer to model the connections between the important radar echo map features and the output flood height. The first layer of the fully connected layers begins by flattening the results of the max-pooling layer. Assuming that the result of the max-pooling layer is matrix (
Ci,
Ri,
Hi), then the input of the first fully connected layer will be a vector of length
Ci ×
Ri ×
Hi. Each neuron in these fully connected layers can be expressed using the following formula:
where
oi represents the output of the
ith node,
D represents the number of input features,
Ij represents the feature input value from the
jth node,
wij is the weight from the
jth node of the input to the
ith node of the output,
biasi is the the offset vector of the
ith node of the output, and
σ(•) is a sigmoid function.
Following completion of multi-layer fully connected layer calculations, the flood height prediction is output by the output layer, which uses only one neuron fully connected to the last neuron in the fully connected layer. The mathematical formula of the neuron in the output layer can be written as follows:
where
oj represents the output of a given node,
σ(•) is the sigmoid function, and
wij and
bj, respectively, indicate the corresponding weights and bias vectors.
3.3. Using Grad-Cam to Identify Key Grid Cells
This section explains the use of Grad-Cam to identify key grid cells to be marked by the CNN on the radar echo map for the prediction of flood height at the target location. We first introduce the operational concepts and formulas of Grad-Cam, and then introduce how Grad-Cam results can be used to identify key grid cells.
Generally speaking, after training a CNN and inputting data of the
ith grid, the CNN result is based on the
ith input. The Grad-Cam package uses gradient information of the previous convolutional layer in this CNN operation to infer the degree to which each cell of the
ith input influences the
ith output. A matrix is used to represent the degree of influence, and the size of the matrix is equal to the length and width of the input data. Scholars commonly represent this matrix using a heat map to make it easier to understand.
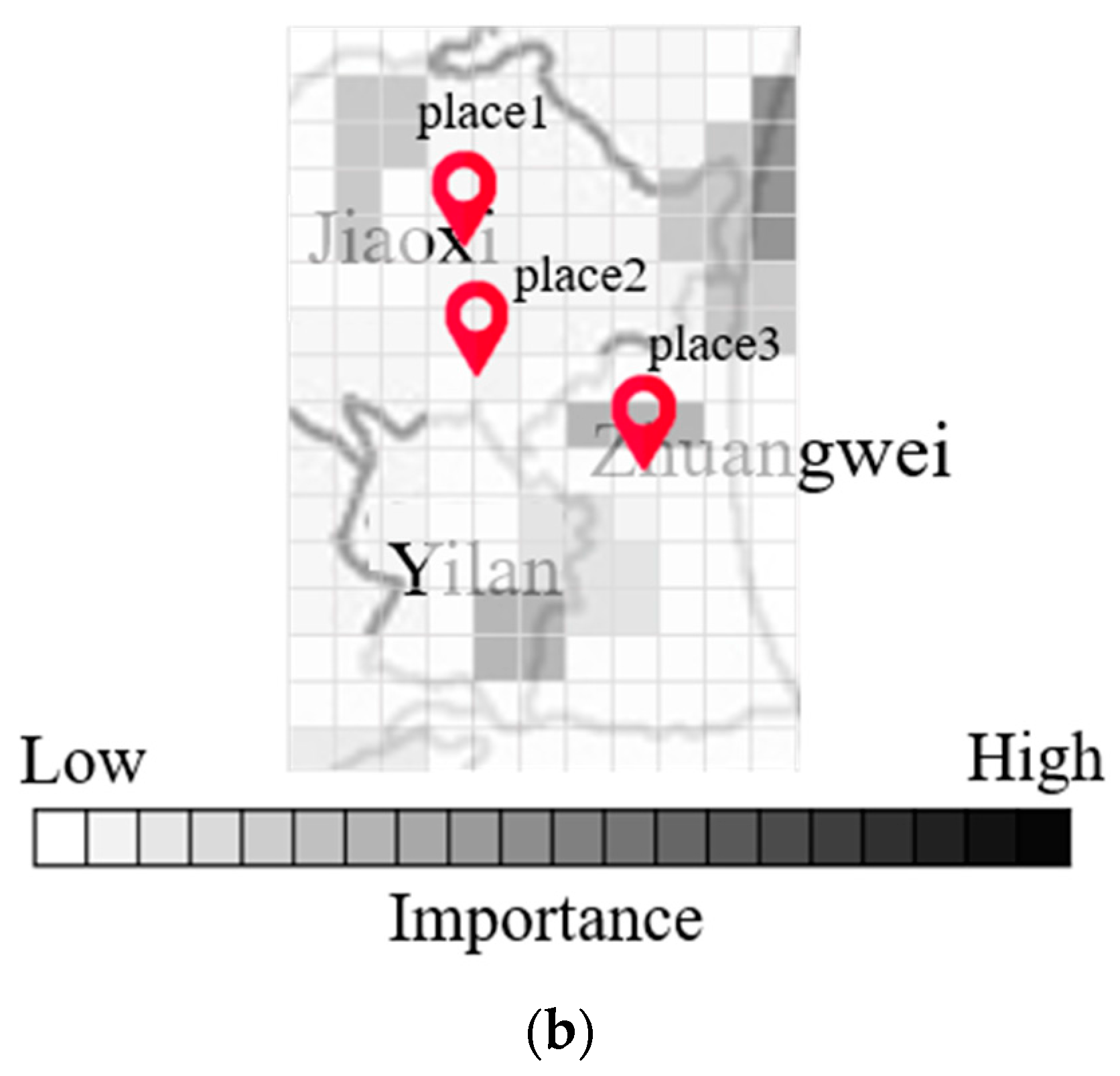
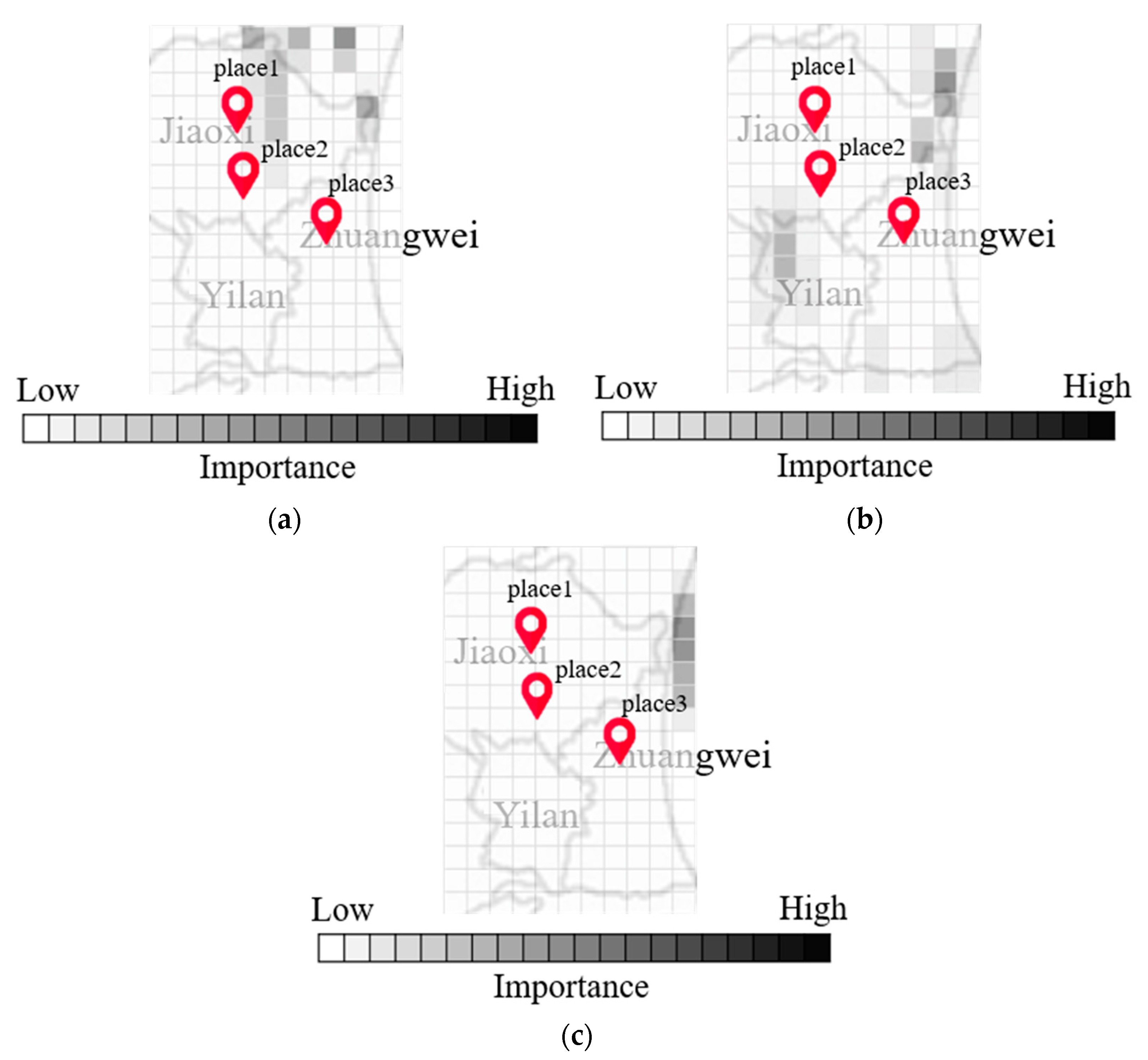
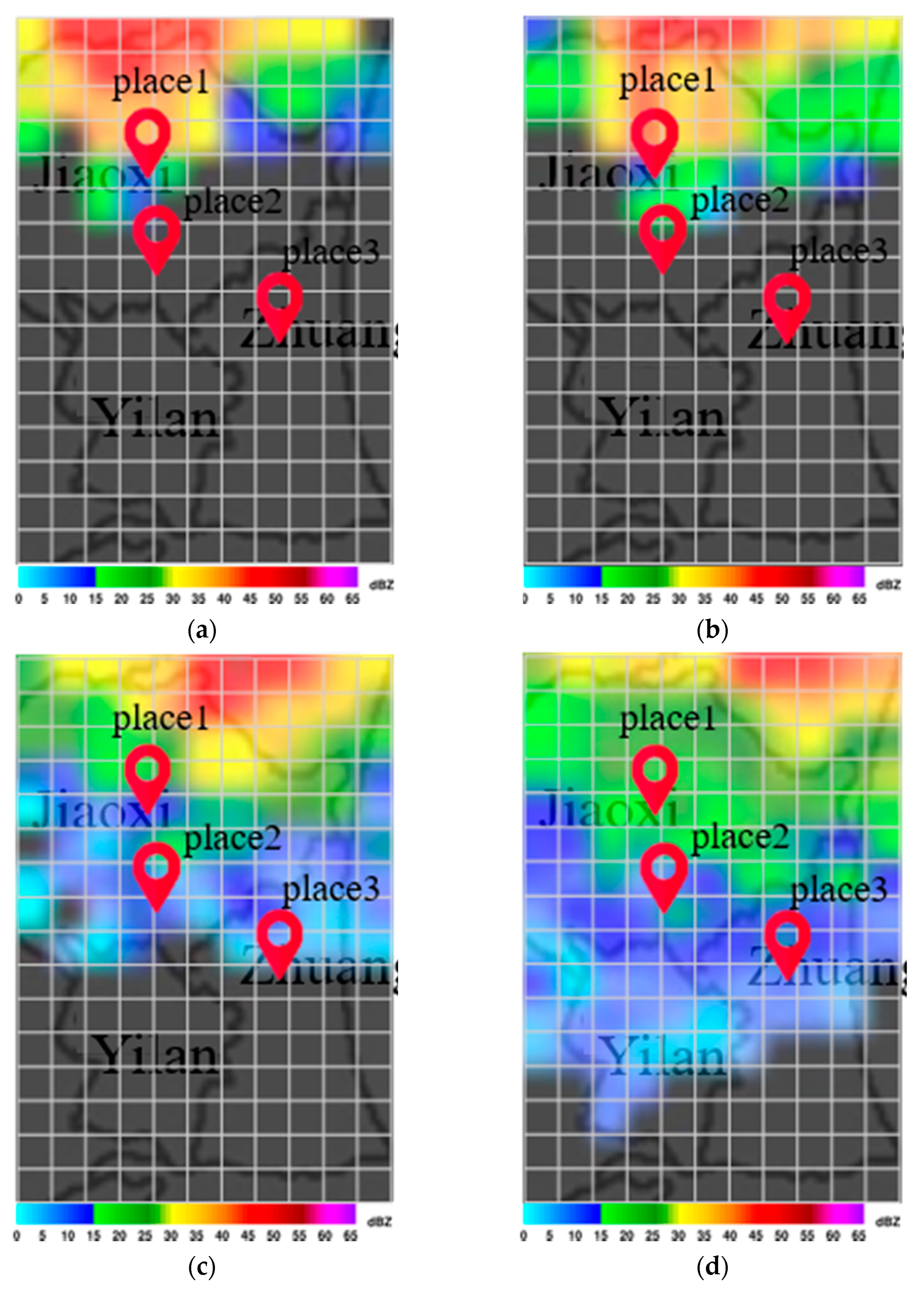
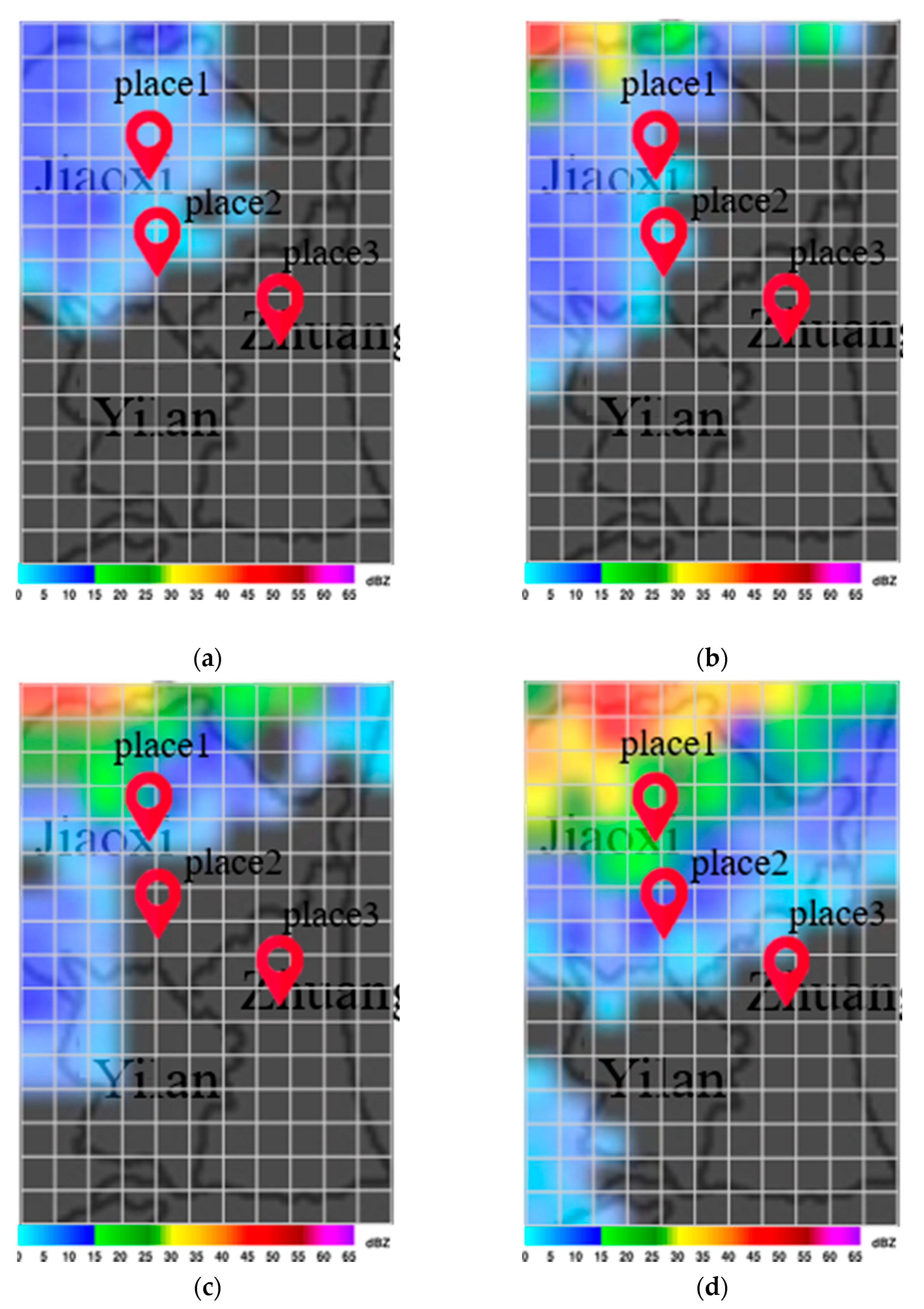
Figure 7a,b present maps indicating the degree of importance after inputting multiple radar echo maps into the CNN to derive the flood height. Note that the degree of blackening is proportional to the influence on the output value. Note also that the maps generated by Grad-Cam differ according to input, as shown in
Figure 7a,b. Differences in input data can have a profound influence on the output of each grid cell.
The formula used to calculate Grad-Cam is derived under the assumption that the length and width of the feature map set are
mf and
nf, the channel size is
sc, and the output result of the CNN is
ô. We can calculate the weight
wc of the
cth channel of the feature map
fc as follows:
where 1/(
mf ×
nf) is the term used to calculate global average pooling, and
∂ô/∂fc are gradients obtained via back propagation. We then combine the degree of importance of all feature maps to derive the degree to which each input grid cell influences the CNN output:
Note that the above formula also uses the Relu function to set all negative numbers to 0, and thereby complete the calculations.
Grad-Cam calculates the degree to which individual grid cells influence the output value corresponding to each input datum and generates a matrix representing the degree of influence. Thus, if we input
n pieces of data into the CNN, then we should obtain
n matrices; however (as mentioned previously), the grid cells representing a given location in different matrices may have different values. This makes it difficult to identify the key grid cells for modeling. Thus, we use following formula to calculate the importance of each grid cell.
where
n is the total number of input data,
impk(
i,
j) indicates the importance of grid cell (
i,
j) calculated by Grad-Cam for the
kth input data (1 ≤
k ≤
n),
Fimp(
i,
j) is the final importance calculation for grid cell (
i,
j),
wk is the weight value given by the user, indicating the degree of importance assigned by the user to each input. If the user believes that each piece of input data is of equal importance in prediction, then
wk is set to 1. Finally, Equation (11) can be used to rank the importance of all grid cells from large to small, whereupon the top-ranking cells are selected as key grid cells.
3.4. Lightweight Deep Neural Networks (LDNNs)
The key grid cells are treated as independent dimensions to be input into an LDNN for modeling. From a theoretical perspective, most of the regression models used in conventional machine learning, such as support vector regression [
32,
33],
k-nearest neighbors [
34,
35], and Random Forest [
36,
37,
38], could be used as an alternative to LDNN; however, we elected to use a deep neural network (DNN) in order to maximize prediction accuracy. Note that the number of key grid cells is far smaller than the number of cells in the entire radar echo map. Under these conditions, the computational cost of an LDNN is far lower than that of the CNN in the previous section.
The structure of the LDNN used in this paper is introduced in the following section, as shown in
Figure 8. The total number of layers and the number of neurons in each layer varied as a function of input (key grid cells). Note that the input layer is responsible only for transmitting input data. In the network, the number of neurons is equal to the number of key grid cells extracted in the previous step. The first fully connected layer is used to increase dimensionality. Assuming that the input layer has a total of
n neurons, there will be 2^ceiling(log
2n) neurons in this layer, where ceiling(•) represents the unconditional roundup function. The number of neurons after the second fully connected layer decreases by a multiple of 2 or 4 until reaching 1, and the last layer is the output layer. Without a loss of generality, the formula in each neuron of fully connected layers can be written as follows:
where
oj represent the output of a given node, tanh(•) is the tangent sigmoid function,
wij is the corresponding weight, and
bi is the bias vector corresponding to the
jth neuron.
Generally, the implementation of a neural network can be divided into offline model establishment procedures (training, testing, and verification) and online operational procedures. The time required to establish the model is dominated by the dimensionality of data input m and the number of data items in the dataset n. Note that m affects the calculation time after data is input into the model. Increasing m produces a corresponding increase in the numbers of layers, neurons, and weights between neurons, which increases the computational overhead. Note that n mainly affects the model training time. By reducing the value of m, an LDNN can reduce the time required to complete offline establishment procedures. Online calculation time generally refers to the time required to process an input after the model has been implemented online. This value depends largely on system capacity and the number of input dimensions m. In other words, LDNN reduces online calculation time by reducing the value of m.