Abstract
Flooding is one of the most prevalent types of natural catastrophes, and it can cause extensive damage to infrastructure and the natural environment. The primary method of flood risk management is flood susceptibility mapping (FSM), which provides a quantitative assessment of a region’s vulnerability to flooding. The objective of this study is to develop new ensemble models for FSM by integrating metaheuristic algorithms, such as genetic algorithms (GA), particle swarm optimization (PSO), and harmony search (HS), with the decision table classifier (DTB). The proposed algorithms were applied in the province of Sulaymaniyah, Iraq. Sentinel-1 synthetic aperture radar (SAR) data satellite images were used for flood monitoring (on 27 July 2019), and 160 flood occurrence locations were prepared for modeling. For the training and validation datasets, flood occurrence data were coupled to 1 flood-influencing parameters (slope, altitude, aspect, plan curvature, distance from rivers, land cover, geology, topographic wetness index (TWI), stream power index (SPI), rainfall, and normalized difference vegetation index (NDVI)). The certainty factor (CF) approach was used to determine the spatial association between the effective parameters and the occurrence of floods, and the resulting weights were employed as modeling inputs. According to the pairwise consistency technique, the NDVI and altitude are the most significant factors in flood modeling. The area under the receiver operating characteristic (AUROC) curve was used to evaluate the accuracy and effectiveness of ensemble models. The DTB-GA model was found to be the most accurate (AUC = 0.889), followed by the DTB-PSO model (AUC = 0.844) and the DTB-HS model (AUC = 0.812). This research’s hybrid models provide a reliable estimate of flood risk, and the risk maps are reliable for flood early-warning and control systems.
1. Introduction
Floods are one of the most catastrophic types of natural events around the globe, after excessive rainfall, persistent rainfall, and snowmelt combined with unfavorable conditions [1]. Floods are influenced by several factors, including climate, human activity, and physical situations [2]. Annual floods harm the lives of around 20 to 300 million people worldwide and cause approximately United States dollar (USD) 60 million in economic damage. The severity and frequency of floods will rise in the future due to global warming, economic and social development, and changes in land-use patterns [3,4]. The felling of forest trees and the degradation of pastures, as well as increases in population in the Middle East and North Africa, have increased the number of flood deaths, with these areas seeing an 11% increase in flood deaths compared to the previous century [5]. Floods cause environmental and economic harm in residential and agricultural areas, and one of the prevention strategies employed to limit these impacts is identifying flood-prone areas [6].
Determining flood-prone areas with high accuracy is critical to accurately predict this complex phenomenon [7] and is considered the first step in flood prevention and management [8]. Identifying places prone to flooding can be accomplished via flood susceptibility modeling in conjunction with a geographic information system (GIS) and remote sensing [5,9]. Flood susceptibility maps (FSM) are constructed using flood inventory maps as the primary data source [10]. Using in situ data to monitor the flood inventory and flood-related parameters may involve several obstacles, including a restricted number of measurement points, the insufficient distribution of those points across space, and a lack of up-to-date information [11]. Remote sensing images with high speed and comprehensive coverage have helped to overcome these limitations of field surveys in many regions of the world [12]. Therefore, to prepare a flood inventory map with high speed and accuracy, Sentinel-1 synthetic aperture radar (SAR) (Rome, Italy) images were used in this research.
Hydraulic, statistical, and machine learning models are typically employed for flood susceptibility modeling. Owing to the necessity for comprehensive and precise data, the findings of hydraulic models are subject to uncertainty [13]. Yang et al. [14] investigated the effects of the relationship between water level change and the adjustment of river channel geometry downstream of the Three Gorges dam on floods. Chai et al. [15] investigated the characteristics of water level evolution and drivers in a single discharge in Jingjiang near the Yangtze River. Due to the complex, dynamic structure of watersheds and the assumption that the interactions between phenomena are linear [8,16], statistical models presume that floods have a predefined relationship with the factors that cause them [17]. Machine learning models are based on nonlinear relationships and do not require an understanding of physical processes or statistical assumptions [5]. They also have lower computing cost and complexity, faster training, and higher accuracy than traditional models [18]. According to a literature review, various machine learning algorithms have been created and defined for flood modeling [5,8,18]. Despite these algorithms’ outstanding predictions, the various limitations of machine learning algorithms include over-fitting, the presence of complex mathematical functions [19], and prediction weaknesses due to the range of data [20]. Metaheuristic algorithms can solve problems with prediction errors, hyperparameter determination, and feature selection in machine learning algorithms [21]. The optimization of different machine learning algorithms by metaheuristic algorithms has been used to prepare flood susceptibility maps. In the Haraz watershed, Iran, Bui et al. [22] employed an adaptive neuro-fuzzy inference system (ANFIS) with culture (CA), bee (BA), and invasive weed optimization (IWO) algorithms for FSM. Termeh et al. [8] used the combination of ANFIS and the genetic algorithm (GA), ant colony optimization (ACO), and particle swarm optimization (PSO) to prepare a flood susceptibility map in Jahrom township, Iran. Wang et al. [23] performed ANFIS optimization with biogeography-based optimization (BBO) and the imperialistic competitive algorithm (ICA). Arora et al. [24] used differential evolution (DE), GA, and PSO, integrated with ANFIS, to prepare a flood susceptibility map in the Ganga plain, India. Rahmati et al. [25] used a combination of support vector regression (SVR) and the gray wolf optimizer (GWO) and bat optimizer (Bat) algorithms to prepare a flood susceptibility map. Rezaei et al. [26] used GWO and the whale optimization algorithm (WOA) to optimize SVR to create a flood susceptibility map in Ardabil Province, Iran. Panahi et al. [27] used the combination of SVR and PSO and a grasshopper optimization algorithm (GOA) to develop a flood susceptibility map. Dodangeh et al. [5] used the group method of data handling (GMDH) and DE and GA algorithms to prepare a flood susceptibility map in the Haraz-Neka watershed, Iran. Rezaei et al. [28] developed GMDH optimization with the GWO algorithm in flood modeling. Bui et al. [22] used a combination of an extreme learning machine (ELM) and a PSO algorithm to prepare a flood susceptibility map in north Vietnam. One of the problems of the decision table (DTB) algorithm is the inability to determine the desired parameters for modeling. In this algorithm, parameters are determined by trial and error. Therefore, in this research, metaheuristic algorithms were used to determine the optimal parameters of this algorithm. To the best of the authors’ knowledge, the DTB algorithm has not been used in combination with metaheuristic algorithms to prepare the flood susceptibility map. To optimize the DTB algorithm for modeling and building flood susceptibility maps, this work used the GA, PSO, and HS algorithms, which is a novel approach. Furthermore, images captured by Sentinel-1 were utilized to monitor flood zones in a broader and more precise manner. The purpose of this research was to monitor flood zones and prepare flood inventory maps using Sentinel-1 images and then undertake flood modeling with three combined algorithms (DTB-GA, DTB-PSO, and DTB-HS).
2. Methodology
The research method is shown in Figure 1. This research was carried out in four steps as follows:
Step 1: At this stage, independent and dependent variables were processed and prepared with the help of remote sensing and GIS. For this purpose, Sentinel-1 satellite images were used to monitor past floods.
Step 2: The certainty factor (CF) bivariate statistical approach was used to estimate the weight of the sub-criteria, while the consistency ratio method was employed to establish the significance of the criteria.
Step 3: At this stage, modeling was undertaken by optimizing the DTB algorithm with metaheuristic algorithms (GA, PSO, and HS).
Step 4: The flood susceptibility map was created using hybrid algorithms (DTB-GA, DTB-PSO, and DTB-HS) and then evaluated.
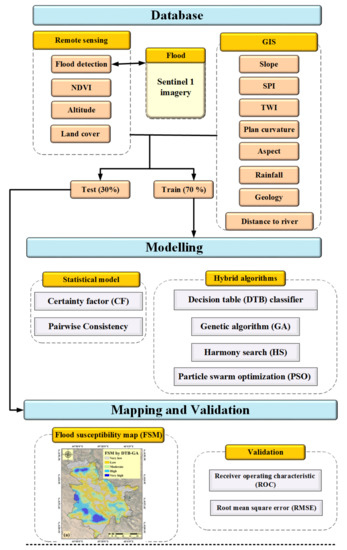
Figure 1.
General steps of research.
3. Material and Methods
3.1. Materials
3.1.1. Study Area
Sulaymaniyah is the largest governorate in the Kurdistan Region of Iraq and can be found in the northeastern part of the country, right on the border with Iran. Its geographical coordinates are 35°33′40′′ north and 45°26′14′′ east. The town of Sulaymaniyah sits at an elevation of around 830 m above mean sea level. Approximately 723,170 people live in the city of Sulaymaniyah. During June, July, and August, the Sulaymaniyah Governorate experienced a dry and warm summer with an average temperature of 31.5 °C. On the other hand, the average temperature during the winter months is approximately 7.6 °C. In Sulaymaniyah, the rainy season begins in October and lasts through May, with the heaviest rains occurring in November. In this region, floods are caused by heavy rainfall and climate change. Figure 2 shows the study region and the locations where flooding has occurred.
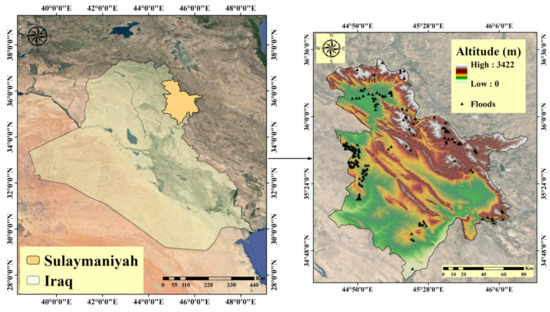
Figure 2.
Location of Sulaymaniyah province in Iraq with flood points.
3.1.2. Flood Detection and Inventory
A comparison of two images obtained before and after the examined events can identify the places that have historically been affected by flash floods. Unprecedented rainfall in 2019 triggered devastating flooding throughout broad swaths of Iraq. According to Iraqi civil defense officials, the peak of the flash floods happened on the 27–28 January 2019. Both the pre-flood inundation mapping (December 2018) and the post-flood inundation mapping (February 2019) made use of Sentinel-1 level 1 ground range-detected (GRD) products. Table 1 describes the Sentinel-1 data requirements in detail.

Table 1.
Description of Sentinel-1 data.
Flood monitoring using Sentinel-1 data was undertaken in the Google Earth Engine (GEE) platform (https://earthengine.google.com (accessed on 20 January 2022)). After the mosaicking of the images taken before and after the flood, the speckle filter was applied to the images. After generating the change detection map from images taken before and after the flood, thresholds were applied, and the binary map of the flood was created. In the next step, using a digital elevation model (DEM) (prepared from shuttle radar topography mission (SRTM) images), areas with a slope greater than 5% and permanent water areas (prepared using Global Surface Water Explorer) were excluded. Finally, pixels with fewer than four neighbors were excluded, and the final flood map is generated. The flood monitoring map is shown in Figure 3. The monitored flood map was used to identify 160 flood occurrence points (Figure 2) in the region, of which 70% (112 points) were used for modeling and 30% (48 points) for evaluation. An additional 160 non-flood areas were randomly generated for use in training and testing the strategy.
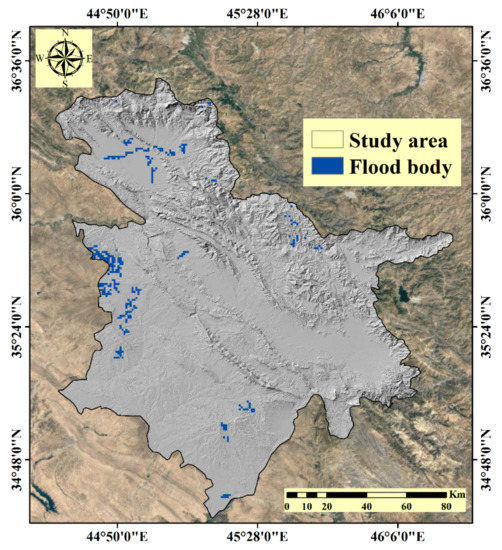
Figure 3.
Flood monitoring using Sentinel-1 images.
3.1.3. Conditioning Factors
We chose 11 flood conditioning parameters for this analysis based on previous research [8,29,30]. GEE was utilized to create remote sensing criteria. On this platform, a DEM, the normalized difference vegetation index (NDVI), and land cover were created with pixel sizes of 30 × 30 m. The DEM was created using images from the SRTM. Slope, slope aspect, altitude, topographic wetness index (TWI), stream power index (SPI), and plan curvature were prepared from the DEM. All criteria were prepared and processed in ArcGIS 10.3 (Environmental Systems Research Institute (ESRI), Redlands, California, USA) and SAGA GIS 8.2.1 (University of Göttingen, Göttingen, Germany) software with a pixel size of 30 × 30 m.
- Altitude
According to Termeh et al. [8], distinct climate characteristics at various altitudes lead to variations in soil and vegetation conditions, and high-altitude regions are less prone to floods [31] (Figure 4a).
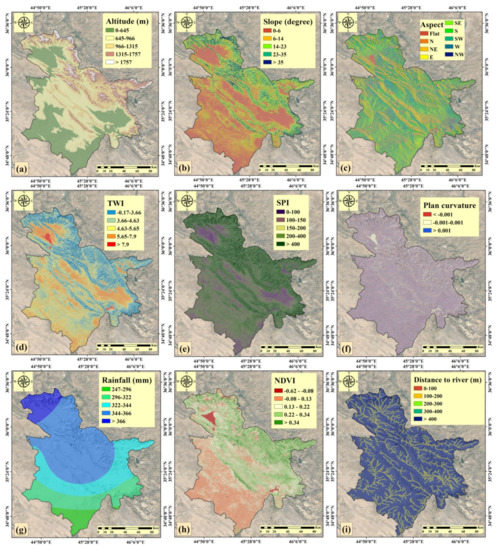
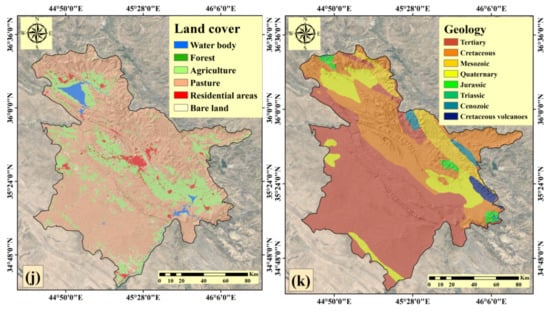
Figure 4.
Influential flood factors: (a) altitude, (b) slope, (c) slope aspect, (d) TWI, (e) SPI, (f) plan curvature, (g) rainfall, (h) NDVI, (i) distance to river, (j) land cover, and (k) geology.
- Slope
Water speed, infiltration, and runoff are all determined by the slope gradient, which is an essential factor in flood susceptibility [32,33]. Slopes can also help to accelerate soil erosion [10] (Figure 4b).
- Slope aspect
The slope aspect influences soil moisture patterns, local meteorological conditions, hydrological processes, and physiographic trends [20]. Waterlogging is less likely in shady areas than in sunny areas due to the influence of the slope aspect on local weather conditions [5] (Figure 4c).
- Topographic wetness index (TWI)
The TWI index measures the amount of flow accumulation in each site of the drainage basin and relates to the effect of gravity on the descent of water on a low slope [34] (Equation (1)):
where specifies the catchment area and β denotes the slope angle (Figure 4d).
- Stream power index (SPI)
The SPI is an index that can estimate the amount of erosive power a discharge has over a specific watershed area [35]. The flow’s power increases directly with the SPI value. The SPI index was calculated based on Equation (2) [8]:
where specifies the catchment area and β denotes the slope angle (Figure 4e).
- Plan curvature
Curvature, which represents the morphology of the topography in a particular place, can be used to define the degree to which the slope surface is distorted [23] (Figure 4f).
- Rainfall
There is a clear association between rainfall and flooding [20], and the likelihood of flooding increases as rainfall increases [36]. The rainfall map for the study area was generated using the dataset collected from 18 rain gauges across Iraq over 30 years (1991–2021) (https://climateknowledgeportal.worldbank.org accessed on 20 January 2022). The rainfall map was created using the kriging interpolation method (Figure 4g).
- Normalized difference vegetation index (NDVI)
One of the most widely used factors in determining flood susceptibility is the NDVI [37]. Dense vegetation helps prevent or lessen flooding, whereas places with no vegetation or weak vegetation are more susceptible to flooding [38].
where band 5 (NIR) represents near-infrared and band 4 (R) represents red. The GEE platform was used to process Landsat 8 images to produce the NDVI map (Figure 4h).
- Distance from the river
The main factor in the spread and intensity of floods, and the identification of flood-prone areas, is the distance from the river [39]. When a river’s storage capacity is low, the likelihood of flooding in areas near the river increases [40]. River networks were obtained from the DEM and the ArcHydro tool in ArcGIS 10.3 was used to prepare the distance from the river map (Figure 4i).
- Land cover
Land cover types have effects on hydrological processes, such as runoff generation, evaporation, transpiration, and infiltration [6]. Increased surface runoff is caused by impermeable surfaces and arid regions [39]. The GEE platform was used to build a 2020 land cover map by analyzing Sentinel-2 images [41] (Figure 4j).
- Geology
Many lithological units can be used in studying hydrological processes and can help develop a flood susceptibility map [7]. The geological map was created using 1:100,000 scale geological maps of Iraq (Figure 4k).
3.2. Methods
3.2.1. Certainty Factor (CF) Method
The CF method is among the most effective models for addressing inconsistency in input parameters [42]. The CF method can handle the difficulty of effectively merging diverse data for modeling purposes. The principal distinction between this method and other bivariate statistical methods is how the parameters are weighted. The weight of the criteria classes is calculated in the CF method using Equation (4) [43]:
where refers to the proportion of the number of floods in a class to the total number of pixels in that class, and refers to the ratio of the whole flood to the total number of pixels.
3.2.2. Pairwise Consistency Method
Pairwise consistency is a strategy developed by Liu and Setiono [44] based on the consistency measure for attribute subsets. The purpose of a consistency measure is to find features that divide the dataset into parts dominated by a single class. After that, the inconsistency rate is used to calculate the consistency measurement [45]. The consistency of an attribute subset is more significant the less inconsistent the subset is. Using Equations (5) and (6), the pairwise consistency assesses an attribute i ϵ {1, 2, …, n} [46]:
where is the consistency rate of the attributes i and j, and n is the number of attributes.
3.2.3. Decision Table (DTB) Classifier
The DTB is a rule-based system that illustrates the process of creating decisions for prediction [47]. The best-first search and cross-validation methods are used to evaluate feature subsets. A basic DTB consists of four components. In the upper left corner of a DTB is a list of all conditions. A decision table’s condition space, a Cartesian product of all condition-state sets, is located in the upper right corner. A DTB’s lower left section contains all the action topics needed to express decisions. The action space of a decision table is located in the lower right corner and is also a Cartesian product of all action sets [48]. The DTB algorithm is used to summarize the dataset using a decision table with the same amount of attributes as the original dataset. A category is allocated to a new data item by searching the decision table for the line that corresponds to the values in the data item’s non-class. The selection of highly discriminative qualities, given the class variable, is the critical method for learning in a decision table, and it is generally carried out by maximizing cross-validated performance [49].
3.2.4. Genetic Algorithm (GA)
The Darwinian theory of evolution served as an inspiration for the GA algorithm [50]. This algorithm simulates the survival of the fittest creatures and their genes. The GA is an algorithm based on populations [51]. The creation of new populations is accomplished through the repeated application of genetic operators to individuals already present in the population. The essential components of the GA include chromosome representation, selection, crossover, and mutation processes, as well as the computation of the objective function [52]. The GA continues as before: an actual population of chromosomes is produced either heuristically or arbitrarily. Each individual is evaluated by adding the required parameters and storing the population based on their fitness value, which is subsequently ranked. Hereditary processes known as crossover and mutation are responsible for introducing novel chromosomes into a population. The crossover procedure involves two select individuals (the parents) exchanging portions of their genomes to generate two new chromosomes. Meanwhile, by randomly evaluating new focuses in the search space, the mutation process avoids premature union to nearby optima. The stopping condition can be determined by a maximum number of generations or a pre-set fitness value [53].
3.2.5. Particle Swarm Optimization (PSO) Algorithm
Particle swarm optimization (PSO) refers to population-based algorithms that create and use random variables [54]. The social behavior of birds flying in flocks is the inspiration for the PSO algorithm. Particles are the individuals that participate in the PSO algorithm. These particles look around the community for the ideal location to serve as a target variable for predictive purposes. Every particle moves at its velocity and each one conducts a search, which is repeated to locate the optimal location [55]. During the process of each particle searching for a new place, the process is influenced by two different factors. The first element represents the particle’s best experience up to that iteration, and the second is the best experience that all of the particles have had collectively. The updating of the speed and position in this algorithm is calculated based on Equations (7) and (8) [56]:
where W is the inertia weight, C1 and C2 are the velocity constants, rand () is a random function ([0, 1]), is the particle’s current location, pbest is the ideal site for a particle, and gbest is the best position found by the entire particle.
3.2.6. Harmony Search (HS) Algorithm
The HS algorithm was initially developed as an attempt by musicians to achieve better harmonies by adjusting the pitches of their respective instruments [57]. The fundamental HS algorithm consists of three primary stages: (1) initialization, (2) harmony vector improvisation, and (3) harmony memory (HM) updating. In the first step of the process, the HS algorithm creates harmony memory size (HMS) randomized harmony vectors and puts them in the HM. Following that, a prospective candidate harmony is constructed by executing memory contraction and pitch adjustment procedures and random re-initialization on all individuals in the HM. The final step in the process involves determining whether or not the new candidate harmony is an improvement over the category with the lowest score in the HM. This process of searching is continued until the ending condition is satisfied [58].
3.2.7. Hybrid Algorithms
A flowchart for hybrid algorithms is shown in Figure 5. The DTB algorithm was optimized using metaheuristic algorithms (GA, PSO, and HS algorithms) in this study. The optimal parameters in the DTB algorithm were determined using metaheuristic algorithms. The parameters were then evaluated using the leave-one-out cross-validation (LOOCV) approach. In the next step, parameters were selected using an objective function (Equation (9)):
where N is the total number of data points, y(i) represents the ith measurement, and represents the prediction. In the last step, the nearest neighbor was used to determine the output of the DTB-GA, DTB-PSO, and DTB-HS algorithms.
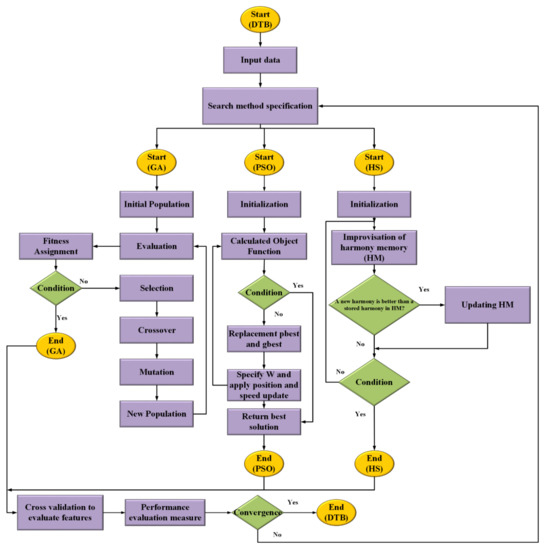
Figure 5.
Flowchart of DTB algorithm optimization.
3.2.8. Validation Methods
In this study, the root mean square error (RMSE) index (Equation (9)) was employed to evaluate the accuracy of the predictions made by the algorithms, and the receiver operating characteristic (ROC) curve was utilized to validate the FSM [59]. For this specific curve, “sensitivity” was plotted along the y-axis, and “1-Specificity” was located along the x-axis [60]. A value for the area under the curve (AUC) can also indicate the prediction ability. An AUC score of 1 indicates that the observed and simulated data are fully spatially consistent. For example, AUC values of 0.5 represent the level of agreement that can be explained by random chance alone, whereas values of 0 are regarded as meaningless [40].
4. Results
4.1. Results of Pairwise Consistency
An analysis of the association between 11 influential factors and the occurrence of flooding was carried out with the help of the pairwise consistency method. The importance of the criteria affecting floods according to the pairwise consistency method is shown in Figure 6. These findings indicate that NDVI (5.98) is the most influential factor in determining flood, followed by altitude (2.534), distance to the river (5.09), geology (4.7), SPI (4.36), plan curvature (4.28), TWI (3.9), rainfall (3.28), aspect (3.02), slope (2.65), and land cover (2.09).
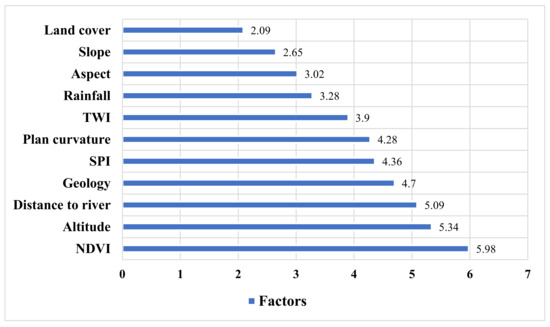
Figure 6.
Importance of factors using pairwise consistency.
4.2. Results of CF Method
The results of the association between independent and dependent variables, as determined using the CF method, are presented in Table 2. According to the altitude criterion, the class that ranges from 645–966 m has the maximum weight (CF = 0.25). According to the findings for the slope criterion, the class with an angle range of 0 to 6 degrees carries the most weight (CF = 0.24). The highest influence on flood occurrence was associated with high TWI (5.65–7.9). For the distance from the river factor, the highest significance was assigned to the 100–200 m class range (CF = 0.334). For the SPI factor, the maximum weight was assigned to the 100–150 range by the CF method (CF = 0.46). According to the findings for the NDVI factor, low levels of this factor (−0.08–0.13) have the highest weight (CF = 0.24). For land cover, the water body class was assigned the highest weight (CF = 0.5). For the aspect factor, the north class had the highest importance (CF= 0.24). According to the findings for the plan curvature factor, there is an increased risk of flooding when higher values of this parameter (more than 0.001) are present. The spatial association between flood occurrence and rainfall indicated that floods are more likely to occur in the 322–344 mm range for this factor (CF= 0.36). The geology criterion findings indicated the highest weight for the Quaternary class (CF = 0.63).

Table 2.
Weights obtained with the CF method.
4.3. Results of Hybrid Modeling
New hybrid algorithms, including DTB-GA, DTB-PSO, and DTB-HS, were conceived and developed by us using the Waikato Environment for Knowledge Analysis (WEKA 3.9.5) and ArcGIS 10.3 software. The training data consisted of 112 selected items of sample data, and the test data consisted of 48 selected items of sample data. Both the training and testing datasets consisted of 160 randomly selected non-flood samples. Then, these datasets were integrated to obtain the training and testing datasets. We chose seventy percent of the available data for training (the modeling process), and the remaining thirty percent were used for validation. The optimal parameters utilized in the metaheuristic algorithms are shown in Table 3.

Table 3.
Parameters of metaheuristic algorithms.
The metaheuristic algorithms obtained the best features for the input of the DTB algorithm in 30 different iterations. Figure 7 shows a convergence diagram for the metaheuristic algorithms in the optimization of the DTB algorithm. Since the objective function in the DTB algorithm optimization minimizes the RMSE index, the GA, PSO, and HS algorithms had the best objective function values, with values of 0.138, 0.158, and 0.183, respectively. The GA, PSO, and HS algorithms achieved the best accuracy in optimizing the DTB algorithm by selecting 7, 6, and 4 features, respectively (Table 4). Based on the results, geology, land cover, and rainfall parameters were the common choices among the three metaheuristic algorithms.
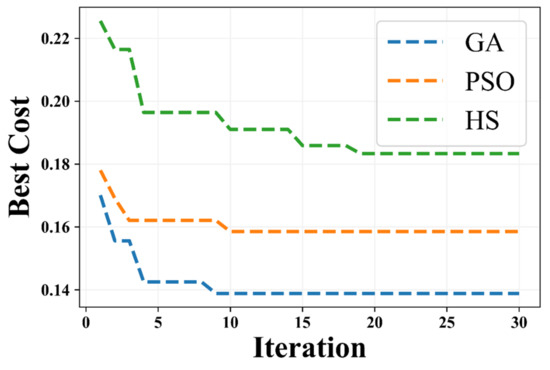
Figure 7.
DTB algorithm optimization convergence diagram.

Table 4.
Results of hybrid DTB with metaheuristic algorithms.
The RMSE metric was used to assess the goodness of fit and performance of the proposed algorithm (Table 5). According to Table 5, the RMSE value produced by the DTB algorithm after it was optimized with the GA algorithm was 0.2029 during the training phase and 0.4524 during the validation phase. The DTB-PSO had an RMSE of 0.2507 during the training phase and a value of 0.4571 during the validation phase. Furthermore, during training and validation, the HS-DTB algorithm computed RMSE values of 0.3232 and 0.459, respectively. Based on the results, the GA, PSO, and HS algorithms had the highest accuracy in DTB algorithm optimization, respectively. The abilities of these three hybrid algorithms to make accurate predictions using the training and test datasets are illustrated in Figure 8. In this figure, the closeness of the prediction values to the target values indicates the higher accuracy of the algorithm. Based on the outcomes of the training and test data, the DTB-HS algorithm predicts values that are distant from the target values, indicating this algorithm’s low accuracy. In the DTB-PSO and DTB-GA algorithms, the prediction values are closer to the target value, indicating their low error rate and high accuracy.

Table 5.
Results for metric index in hybrid algorithms.
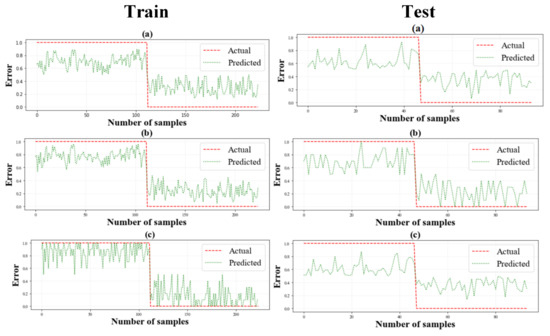
Figure 8.
Diagrams of modeling error with: (a) DTB-HS, (b) STB-PSO, and (c) DTB-GA algorithms.
4.4. Flood Susceptibility Mapping (FSM) and Validation
The hybrid algorithms learned and performed well using the training and testing datasets; hence, they were considered for the generation of flood susceptibility maps. After this step, the study region was converted into a comma-separated value (CSV) file, and the subsequent step involved calculating the flood probability for each pixel location in the study area. The next step involved classifying the flood susceptibility map into five groups, ranging from very low to very high risk, using the natural breaks approach [8]. The flood susceptibility maps obtained with the three hybrid algorithms are shown in Figure 9. Based on the flood susceptibility maps from the three algorithms, the north, southeast, and southwest regions of the study area are more vulnerable.
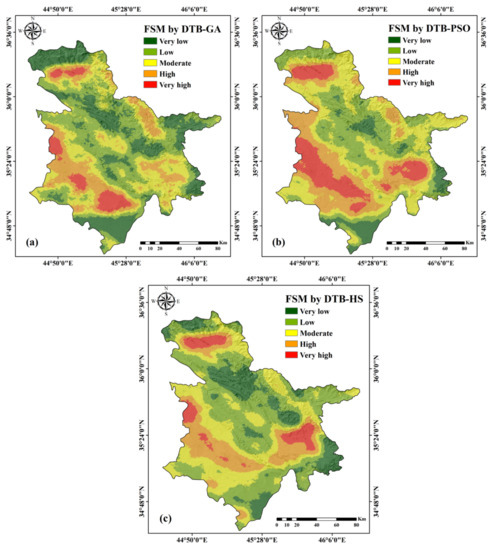
Figure 9.
Flood susceptibility mapping with: (a) DTB-GA, (b) DTB-PSO, and (c) DTB-HS.
The ROC curves for the testing (prediction accuracy) datasets are shown in Figure 10 and Table 6. The investigation revealed that the DTB-GA algorithm provides a high degree of prediction accuracy (AUC = 0.889). The AUC values for the DTB-PSO and DTB-HS in the testing datasets were 0.844 and 0.812, respectively.
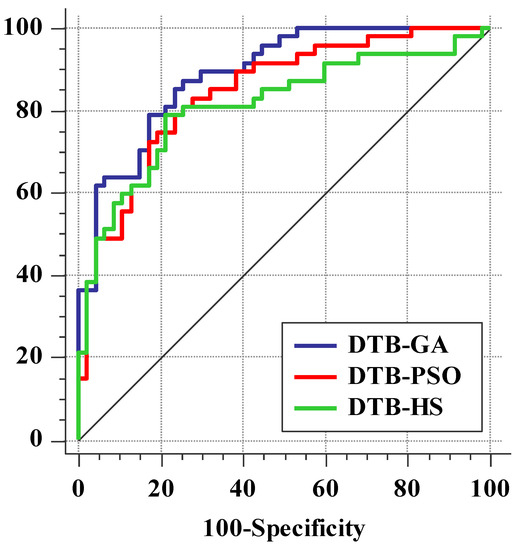
Figure 10.
Evaluation of hybrid models with ROC curves.

Table 6.
AUC results of hybrid models.
Figure 11 demonstrates the observed and predicted flood susceptibility using the DTB-GA, DTB-PSO, and DTB-HS with a Taylor diagram. The ability of all the hybrid algorithms to predict flooding was similar, but the DTB-GA produced the highest correlation. As a result, based on multiple evaluation indicators, the DTB-GA algorithm had the highest accuracy for flood prediction.
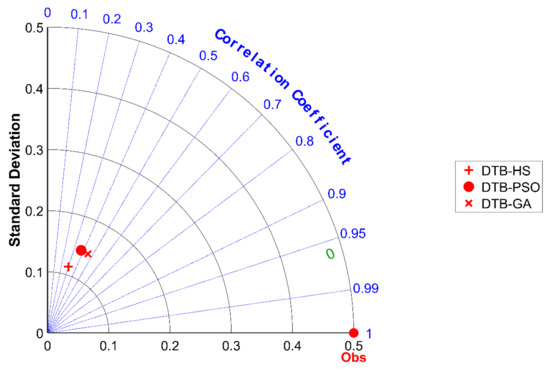
Figure 11.
Taylor diagram of hybrid models.
5. Discussion
5.1. Examining the Role of Factors in Flood Prediction
In this research, pairwise consistency and CF methods were used to determine the importance of parameters and investigate the spatial relationship between independent and dependent parameters. The pairwise consistency method determined that the parameters altitude, NDVI, and distance from the river were the most important in flood modeling. The results of this research regarding the effect of parameters on flood forecasting are consistent with the work by Bui et al. [61], Shafizadeh-Moghadam et al. [62], and Rahmati and Pourghasemi [63]. Altitude influences meteorological features, resulting in variances in vegetation and soil [64]. With changes from higher to lower altitudes, the terrain tends to flatten out, and the volume of water transported by rivers increases [31]. The NDVI can be used to show the relationship between flooding and vegetation within a watershed by reflecting changes in vegetation and surface water cover over time [65]. In the region, lower flood probabilities are correlated with higher vegetation densities [30]. In general, the existing streams in the watershed discharge surface currents, and moving away from the streams reduces the probability of flooding [33].
Based on the results of the CF method, the probability of flooding is higher at low altitudes. At lower elevations, there is potential for a more concentrated water flow [34]. This factor’s outcome is consistent with the findings provided by Hong et al. [20]. The slope result revealed that the likelihood of flooding increases with the decreasing value of the slope angle. When the ground is steeper, there is less time for water to permeate the ground, and when there is a higher concentration of water on lower slopes, there is high potential for flooding [66]. The finding confirms the research of Rahmati and Pourghasemi [63]. The results of the CF method showed that the probability of flooding is higher in north-facing aspects. As soils on north-facing slopes are saturated, the flow of surface waters is accelerated, which increases the likelihood of floods [67]. The CF technique demonstrated that an increase in the TWI value leads to an increase in the probability of flooding. As infiltration is minimal in pixels with a high TWI, runoff from rainfall selectively pools in these places when it rains [68]. The results of this criterion are consistent with the research by Shahabi et al. [65]. Based on the results of the CF method, with lower values for the SPI factor, the probability of flooding is higher. Lower SPI values are assigned to regions that have the potential to accumulate flow because of their topography [69]. The results of this criterion are consistent with the research by Shafizadeh-Moghadam et al. [62]. The results of the plan curvature factor showed that the highest number of floods occur in the flat class. Therefore, flat slope forms are more likely to accept and collect overbank flows and runoff as they are often lower in elevation [65]. The findings of this criterion are in line with the findings in the research conducted by Khosravi et al. [29]. The results of this study revealed that a distance to rivers of 100–200 m is the most relevant to flood occurrence. Flooding is more likely to occur near rivers because they react quickly to rainfall [8]. The results of the NDVI criterion indicated that regions with less vegetation are more susceptible to flooding. Water flow is reduced and slowed in areas with higher NDVI and high vegetation, while areas with low vegetation undergo flooding [69]. The results of the rainfall criterion showed that the probability of flooding is higher in the 300–400 mm class. The results of this criterion are consistent with the findings of the research that Shahabi et al. [65] carried out. According to the land cover criterion, water body and agriculture classes had the highest impact on the occurrence of floods. The reason for this is the location of the water bodies and agricultural zones in lower altitude areas in the study area. According to the geology criterion, the Quaternary class has a significant effect on the frequency of flooding in the study area. Since these formations are less permeable than other lithological formations, they quickly become saturated after heavy rain and direct runoff into nearby rivers [65].
5.2. Evaluation and Comparison of Algorithms
In this study, the creation of the flood susceptibility map was accomplished through the optimization of the DTB algorithm with the use of metaheuristic algorithms (GA, PSO, and HS). The results indicated good accuracy for the three metaheuristic algorithms in combination with the DTB algorithm. Pham et al. [70] confirmed the effectiveness of the DTB algorithm in generating flood susceptibility maps. Hybrid approaches take advantage of the benefits of two or more methods to achieve superior performance. Therefore, it may be concluded that hybrid techniques combine various individual methods to create a method with greater flexibility and capability. This can aid in enhancing performance and explain the abilities of models, hence promoting their widespread adoption [71]. Hybrid methods have so far been highly accurate in modeling natural hazards [72]. In optimizing the DTB algorithm, the results demonstrated that the GA algorithm is more accurate than the PSO and HS algorithms. In contrast to PSO and HS, the GA algorithm uses operators like crossover and mutation. This is the primary distinction between the three algorithms [73]. The GA algorithm provides several benefits, such as parallelism, the ability to discover global optima efficiently, and the capacity to manage vast and poorly understood search fields easily [74]. The benefits of the PSO algorithm include high convergence speed and control parameter robustness [75]. However, the PSO algorithm has disadvantages, such as early convergence and a tendency to get stuck in local optima [76], and in this research it was less accurate than the GA algorithm in optimizing the DTB algorithm. The primary issue of the HS algorithm is that it cannot find an acceptable balance between global and local searches [77]. Therefore, in this research, the HS algorithm was less accurate than the other two algorithms in optimizing the DTB algorithm. Various studies on the spatial modeling of natural hazards showed higher accuracy for the GA algorithm than the PSO algorithm in optimizing machine-learning algorithms. Moayedi et al. [78] showed that the GA algorithm was more accurate than PSO in optimizing the ANFIS algorithm for the preparation of a forest fire susceptibility map. Mehrabi et al. [79] showed that the GA-ANFIS algorithm had higher accuracy than the PSO-ANFIS algorithm in preparing a landslide susceptibility map. The GA algorithm was demonstrated by Arora et al. [24] to be more accurate than PSO when optimizing the ANFIS algorithm for the generation of a flood susceptibility map.
5.3. Strengths of the Research
The public, private, and non-profit sectors all rely on flood risk maps for a variety of purposes, including establishing and enforcing zoning, land use, and building standards; planning and constructing infrastructure and transportation networks; providing early warnings of floods; and managing and preparing for emergencies. Participatory or collaborative flood risk mapping projects can yield valuable insights, such as the location of safe evacuation routes, potential sites for emergency shelters, and the identities of those in the community who are at a higher risk of harm from flooding.
6. Conclusions and Remarks
The primary purpose of this study was to develop flood susceptibility maps for Iraq’s Sulaymaniyah province, utilizing DTB algorithm optimization via metaheuristic algorithms. The absence of appropriate field data for use in machine learning algorithms is one of the primary obstacles in the development of FSM. In this study, Sentinel-1 images were used to identify 150 flood occurrence points. Based on the results of the CF method, lower altitude, low slope, high TWI, low SPI, low NDVI, lower distances to the river, flat curvature, north slope aspects, water bodies and agricultural areas, Quaternary geological formations, and moderate rainfall had greater impacts on floods in the study area. The results showed that the NDVI and altitude criteria were more important than other factors in the study area. According to flood hazard maps and the significance of the criteria, it can be concluded that topography and land-cover factors have significant influences on the occurrence of floods in Iraq’s Sulaymaniyah region. The modeling results showed that the optimization of machine learning algorithms with metaheuristic algorithms resulted in acceptable accuracy in preparing flood susceptibility maps. The results can aid in detecting flood-susceptible areas in the province of Sulaymaniyah, and this strategy can be extended realistically to other parts of the globe, particularly data-scarce regions. In conclusion, developing a flood susceptibility map with an optimization method yields findings that are both accurate and practically applicable for the prevention and mitigation of future flooding. It is suggested that future studies compare different satellite images for flood monitoring. Furthermore, deep learning algorithms can be used in combination with metaheuristic algorithms for flood modeling.
Author Contributions
Conceptualization, S.A. and M.M.Y.; methodology, S.Z.P.; software, S.A. and S.Z.P.; validation, N.A.P., J.H. and I.M.; formal analysis, S.A. and S.Z.P.; investigation, M.M.Y. and M.E.; resources, M.E. and J.H.; data curation, S.A. and S.Z.P.; writing—original draft preparation, S.A., S.Z.P. and M.M.Y.; writing—review and editing, N.A.P., I.M. and M.E.; visualization, S.A. and M.M.Y.; supervision, N.A.P.; project administration, I.M. and J.H.; funding acquisition, J.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been supported by the RUDN University Scientific Projects Grant System, project no 202235-2-000.
Data Availability Statement
Data during the current study are not publicly available due to integrity and legal reasons but are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nachappa, T.G.; Piralilou, S.T.; Gholamnia, K.; Ghorbanzadeh, O.; Rahmati, O.; Blaschke, T. Flood susceptibility mapping with machine learning, multi-criteria decision analysis and ensemble using dempster shafer theory. J. Hydrol. 2020, 590, 125275. [Google Scholar] [CrossRef]
- Bui, D.T.; Ngo, P.-T.T.; Pham, T.D.; Jaafari, A.; Minh, N.Q.; Hoa, P.V.; Samui, P. A novel hybrid approach based on a swarm intelligence optimized extreme learning machine for flash flood susceptibility mapping. Catena 2019, 179, 184–196. [Google Scholar] [CrossRef]
- Costache, R.; Pham, Q.B.; Sharifi, E.; Linh, N.T.T.; Abba, S.I.; Vojtek, M.; Vojteková, J.; Nhi, P.T.T.; Khoi, D.N. Flash-flood susceptibility assessment using multi-criteria decision making and machine learning supported by remote sensing and gis techniques. Remote Sens. 2019, 12, 106. [Google Scholar] [CrossRef]
- Islam, A.; Sarkar, B. Analysing flood history and simulating the nature of future floods using gumbel method and log-pearson type iii: The case of the mayurakshi river basin, india. Bull. Geogr. Phys. Geogr. Ser. 2020, 19, 43–69. [Google Scholar] [CrossRef]
- Dodangeh, E.; Panahi, M.; Rezaie, F.; Lee, S.; Bui, D.T.; Lee, C.-W.; Pradhan, B. Novel hybrid intelligence models for flood-susceptibility prediction: Meta optimization of the gmdh and svr models with the genetic algorithm and harmony search. J. Hydrol. 2020, 590, 125423. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Jones, S.; Shabani, F. Identifying the essential flood conditioning factors for flood prone area mapping using machine learning techniques. Catena 2019, 175, 174–192. [Google Scholar] [CrossRef]
- Al-Abadi, A.M. Mapping flood susceptibility in an arid region of southern iraq using ensemble machine learning classifiers: A comparative study. Arab. J. Geosci. 2018, 11, 218. [Google Scholar] [CrossRef]
- Termeh, S.V.R.; Kornejady, A.; Pourghasemi, H.R.; Keesstra, S. Flood susceptibility mapping using novel ensembles of adaptive neuro fuzzy inference system and metaheuristic algorithms. Sci. Total Environ. 2018, 615, 438–451. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, H.; Chen, W.; Li, S.; Panahi, M.; Khosravi, K.; Shirzadi, A.; Shahabi, H.; Panahi, S.; Costache, R. Flood susceptibility mapping in dingnan county (China) using adaptive neuro-fuzzy inference system with biogeography based optimization and imperialistic competitive algorithm. J. Environ. Manag. 2019, 247, 712–729. [Google Scholar] [CrossRef]
- Samanta, R.K.; Bhunia, G.S.; Shit, P.K.; Pourghasemi, H.R. Flood susceptibility mapping using geospatial frequency ratio technique: A case study of subarnarekha river basin, india. Model. Earth Syst. Environ. 2018, 4, 395–408. [Google Scholar] [CrossRef]
- Kumar, P.; Debele, S.E.; Sahani, J.; Rawat, N.; Marti-Cardona, B.; Alfieri, S.M.; Basu, B.; Basu, A.S.; Bowyer, P.; Charizopoulos, N. An overview of monitoring methods for assessing the performance of nature-based solutions against natural hazards. Earth Sci. Rev. 2021, 217, 103603. [Google Scholar] [CrossRef]
- Watts, A.C.; Ambrosia, V.G.; Hinkley, E.A. Unmanned aircraft systems in remote sensing and scientific research: Classification and considerations of use. Remote Sens. 2012, 4, 1671–1692. [Google Scholar] [CrossRef]
- Mojaddadi Rizeei, H. Flood Risk Assessment Using Multi-Sensor Remote Sensing, Geographic Information System, 2D Hydraulic and Machine Learning Based Models. Ph.D. Thesis, University of Technology Sydney (UTS), Sydney, NSW, Australia, 2018. [Google Scholar]
- Yang, Y.; Zhang, M.; Sun, Z.; Han, J.; Wang, J. The relationship between water level change and river channel geometry adjustment in the downstream of the three gorges dam. J. Geogr. Sci. 2018, 28, 1975–1993. [Google Scholar]
- Chai, Y.; Yang, Y.; Deng, J.; Sun, Z.; Li, Y.; Zhu, L. Evolution characteristics and drivers of the water level at an identical discharge in the jingjiang reaches of the yangtze river. J. Geogr. Sci. 2020, 30, 1633–1648. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Razavi-Termeh, S.V.; Kariminejad, N.; Hong, H.; Chen, W. An assessment of metaheuristic approaches for flood assessment. J. Hydrol. 2020, 582, 124536. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Nampak, H.; Bui, Q.-T.; Tran, Q.-A.; Nguyen, Q.-P. Hybrid artificial intelligence approach based on neural fuzzy inference model and metaheuristic optimization for flood susceptibilitgy modeling in a high-frequency tropical cyclone area using gis. J. Hydrol. 2016, 540, 317–330. [Google Scholar]
- Mousavi, S.M.; Ataie-Ashtiani, B.; Hosseini, S.M. Comparison of statistical and mcdm approaches for flood susceptibility mapping in northern iran. J. Hydrol. 2022, 612, 128072. [Google Scholar] [CrossRef]
- Wang, Z.; Lai, C.; Chen, X.; Yang, B.; Zhao, S.; Bai, X. Flood hazard risk assessment model based on random forest. J. Hydrol. 2015, 527, 1130–1141. [Google Scholar] [CrossRef]
- Hong, H.; Tsangaratos, P.; Ilia, I.; Liu, J.; Zhu, A.-X.; Chen, W. Application of fuzzy weight of evidence and data mining techniques in construction of flood susceptibility map of poyang county, china. Sci. Total Environ. 2018, 625, 575–588. [Google Scholar] [CrossRef]
- Hoang, N.-D.; Tran, X.-L. Remote sensing–based urban green space detection using marine predators algorithm optimized machine learning approach. Math. Probl. Eng. 2021, 2021, 5586913. [Google Scholar] [CrossRef]
- Bui, D.T.; Panahi, M.; Shahabi, H.; Singh, V.P.; Shirzadi, A.; Chapi, K.; Khosravi, K.; Chen, W.; Panahi, S.; Li, S. Novel hybrid evolutionary algorithms for spatial prediction of floods. Sci. Rep. 2018, 8, 15364. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Hong, H.; Peng, L. Flood susceptibility mapping using convolutional neural network frameworks. J. Hydrol. 2020, 582, 124482. [Google Scholar] [CrossRef]
- Arora, A.; Arabameri, A.; Pandey, M.; Siddiqui, M.A.; Shukla, U.; Bui, D.T.; Mishra, V.N.; Bhardwaj, A. Optimization of state-of-the-art fuzzy-metaheuristic anfis-based machine learning models for flood susceptibility prediction mapping in the middle ganga plain, india. Sci. Total Environ. 2021, 750, 141565. [Google Scholar] [CrossRef]
- Rahmati, O.; Darabi, H.; Panahi, M.; Kalantari, Z.; Naghibi, S.A.; Ferreira, C.S.S.; Kornejady, A.; Karimidastenaei, Z.; Mohammadi, F.; Stefanidis, S. Development of novel hybridized models for urban flood susceptibility mapping. Sci. Rep. 2020, 10, 12937. [Google Scholar] [CrossRef]
- Rezaie, F.; Panahi, M.; Bateni, S.M.; Jun, C.; Neale, C.M.; Lee, S. Novel hybrid models by coupling support vector regression (svr) with meta-heuristic algorithms (woa and gwo) for flood susceptibility mapping. Nat. Hazards 2022, 1–37. [Google Scholar] [CrossRef]
- Panahi, M.; Dodangeh, E.; Rezaie, F.; Khosravi, K.; Van Le, H.; Lee, M.-J.; Lee, S.; Pham, B.T. Flood spatial prediction modeling using a hybrid of meta-optimization and support vector regression modeling. Catena 2021, 199, 105114. [Google Scholar] [CrossRef]
- Rezaie, F.; Bateni, S.M.; Heggy, E.; Lee, S. Utilizing the sar, gis, and novel hybrid metaheuristic-gmdh algorithm for flood susceptibility mapping. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 8612–8615. [Google Scholar]
- Khosravi, K.; Nohani, E.; Maroufinia, E.; Pourghasemi, H.R. A gis-based flood susceptibility assessment and its mapping in iran: A comparison between frequency ratio and weights-of-evidence bivariate statistical models with multi-criteria decision-making technique. Nat. Hazards 2016, 83, 947–987. [Google Scholar] [CrossRef]
- Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Bui, D.T.; Pham, B.T.; Khosravi, K. A novel hybrid artificial intelligence approach for flood susceptibility assessment. Environ. Model. Softw. 2017, 95, 229–245. [Google Scholar] [CrossRef]
- Cao, C.; Xu, P.; Wang, Y.; Chen, J.; Zheng, L.; Niu, C. Flash flood hazard susceptibility mapping using frequency ratio and statistical index methods in coalmine subsidence areas. Sustainability 2016, 8, 948. [Google Scholar] [CrossRef]
- Fernández, D.; Lutz, M.A. Urban flood hazard zoning in tucumán province, argentina, using gis and multicriteria decision analysis. Eng. Geol. 2010, 111, 90–98. [Google Scholar] [CrossRef]
- Al-Juaidi, A.E.; Nassar, A.M.; Al-Juaidi, O.E. Evaluation of flood susceptibility mapping using logistic regression and gis conditioning factors. Arab. J. Geosci. 2018, 11, 765. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Mansor, S.; Ahmad, N. Flood susceptibility assessment using gis-based support vector machine model with different kernel types. Catena 2015, 125, 91–101. [Google Scholar] [CrossRef]
- Abdel Hamid, H.; Wenlong, W.; Qiaomin, L. Environmental sensitivity of flash flood hazard using geospatial techniques. Glob. J. Environ. Sci. Manag. 2020, 6, 31–46. [Google Scholar]
- Segond, M.-L.; Wheater, H.S.; Onof, C. The significance of spatial rainfall representation for flood runoff estimation: A numerical evaluation based on the lee catchment, UK. J. Hydrol. 2007, 347, 116–131. [Google Scholar] [CrossRef]
- Ali, S.A.; Parvin, F.; Pham, Q.B.; Vojtek, M.; Vojteková, J.; Costache, R.; Linh, N.T.T.; Nguyen, H.Q.; Ahmad, A.; Ghorbani, M.A. Gis-based comparative assessment of flood susceptibility mapping using hybrid multi-criteria decision-making approach, naïve bayes tree, bivariate statistics and logistic regression: A case of topľa basin, slovakia. Ecol. Indic. 2020, 117, 106620. [Google Scholar] [CrossRef]
- Shrestha, R.; Di, L.; Eugene, G.Y.; Kang, L.; Shao, Y.-Z.; Bai, Y.-Q. Regression model to estimate flood impact on corn yield using modis ndvi and usda cropland data layer. J. Integr. Agric. 2017, 16, 398–407. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Lee, M.-J.; Pradhan, B.; Jebur, M.N.; Lee, S. Flood susceptibility mapping using integrated bivariate and multivariate statistical models. Environ. Earth Sci. 2014, 72, 4001–4015. [Google Scholar] [CrossRef]
- Shahabi, H.; Shirzadi, A.; Ghaderi, K.; Omidvar, E.; Al-Ansari, N.; Clague, J.J.; Geertsema, M.; Khosravi, K.; Amini, A.; Bahrami, S. Flood detection and susceptibility mapping using sentinel-1 remote sensing data and a machine learning approach: Hybrid intelligence of bagging ensemble based on k-nearest neighbor classifier. Remote Sens. 2020, 12, 266. [Google Scholar] [CrossRef]
- Karra, K.; Kontgis, C.; Statman-Weil, Z.; Mazzariello, J.C.; Mathis, M.; Brumby, S.P. Global land use/land cover with sentinel 2 and deep learning. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 4704–4707. [Google Scholar]
- Razavi-Termeh, S.V.; Sadeghi-Niaraki, A.; Choi, S.-M. Spatio-temporal modelling of asthma-prone areas using a machine learning optimized with metaheuristic algorithms. Geocarto Int. 2022, 1–26. [Google Scholar] [CrossRef]
- Cao, Y.; Jia, H.; Xiong, J.; Cheng, W.; Li, K.; Pang, Q.; Yong, Z. Flash flood susceptibility assessment based on geodetector, certainty factor, and logistic regression analyses in fujian province, China. ISPRS Int. J. Geo Inf. 2020, 9, 748. [Google Scholar] [CrossRef]
- Liu, H.; Setiono, R. A probabilistic approach to feature selection-a filter solution. In ICML; Citeseer: Princeton, NJ, USA; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1996; pp. 319–327. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.294.9980&rep=rep1&type=pdf (accessed on 20 January 2022).
- Jiménez, F.; Palma, G.S.J.; Miralles-Pechuán, L.; Botía, J. Multivariate feature ranking of gene expression data. arXiv 2021, arXiv:2111.02357. [Google Scholar]
- Jiménez, F.; Sánchez, G.; Palma, J.; Miralles-Pechuán, L.; Botía, J.A. Multivariate feature ranking with high-dimensional data for classification tasks. IEEE Access 2022, 10, 60421–60437. [Google Scholar] [CrossRef]
- Nilsen, P. Making sense of implementation theories, models, and frameworks. In Implementation Science 3.0; Springer: Cham, Switzerland, 2020; pp. 53–79. [Google Scholar]
- Chen, C.; Zhang, G.; Yang, J.; Milton, J.C. An explanatory analysis of driver injury severity in rear-end crashes using a decision table/naïve bayes (dtnb) hybrid classifier. Accid. Anal. Prev. 2016, 90, 95–107. [Google Scholar] [CrossRef]
- Kalmegh, S.R. Comparative analysis of the weka classifiers rules conjunctiverule & decisiontable on indian news dataset by using different test mode. Int. J. Eng. Sci. Invent. (IJESI) 2018, 7, 2319–6734. [Google Scholar]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Mirjalili, S. Evolutionary algorithms and neural networks. In Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2019; Volume 780. [Google Scholar]
- Maleki, N.; Zeinali, Y.; Niaki, S.T.A. A k-nn method for lung cancer prognosis with the use of a genetic algorithm for feature selection. Expert Syst. Appl. 2021, 164, 113981. [Google Scholar] [CrossRef]
- Reddy, G.T.; Reddy, M.; Lakshmanna, K.; Rajput, D.S.; Kaluri, R.; Srivastava, G. Hybrid genetic algorithm and a fuzzy logic classifier for heart disease diagnosis. Evol. Intell. 2020, 13, 185–196. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 1942–1948. [Google Scholar]
- Roy, C.; Das, D.K. A hybrid genetic algorithm (ga)–particle swarm optimization (pso) algorithm for demand side management in smart grid considering wind power for cost optimization. Sādhanā 2021, 46, 101. [Google Scholar] [CrossRef]
- Ramdania, D.; Irfan, M.; Alfarisi, F.; Nuraiman, D. Comparison of genetic algorithms and particle swarm optimization (pso) algorithms in course scheduling. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; p. 022079. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Gholami, J.; Pourpanah, F.; Wang, X. Feature selection based on improved binary global harmony search for data classification. Appl. Soft Comput. 2020, 93, 106402. [Google Scholar] [CrossRef]
- Razavi-Termeh, S.V.; Sadeghi-Niaraki, A.; Choi, S.-M. Effects of air pollution in spatio-temporal modeling of asthma-prone areas using a machine learning model. Environ. Res. 2021, 200, 111344. [Google Scholar] [CrossRef] [PubMed]
- Razavi-Termeh, S.V.; Khosravi, K.; Sadeghi-Niaraki, A.; Choi, S.-M.; Singh, V.P. Improving groundwater potential mapping using metaheuristic approaches. Hydrol. Sci. J. 2020, 65, 2729–2749. [Google Scholar] [CrossRef]
- Bui, Q.-T.; Nguyen, Q.-H.; Nguyen, X.L.; Pham, V.D.; Nguyen, H.D.; Pham, V.-M. Verification of novel integrations of swarm intelligence algorithms into deep learning neural network for flood susceptibility mapping. J. Hydrol. 2020, 581, 124379. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Valavi, R.; Shahabi, H.; Chapi, K.; Shirzadi, A. Novel forecasting approaches using combination of machine learning and statistical models for flood susceptibility mapping. J. Environ. Manag. 2018, 217, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Rahmati, O.; Pourghasemi, H.R. Identification of critical flood prone areas in data-scarce and ungauged regions: A comparison of three data mining models. Water Resour. Manag. 2017, 31, 1473–1487. [Google Scholar] [CrossRef]
- Lookingbill, T.; Urban, D. An empirical approach towards improved spatial estimates of soil moisture for vegetation analysis. Landsc. Ecol. 2004, 19, 417–433. [Google Scholar] [CrossRef]
- Shahabi, H.; Shirzadi, A.; Ronoud, S.; Asadi, S.; Pham, B.T.; Mansouripour, F.; Geertsema, M.; Clague, J.J.; Bui, D.T. Flash flood susceptibility mapping using a novel deep learning model based on deep belief network, back propagation and genetic algorithm. Geosci. Front. 2021, 12, 101100. [Google Scholar] [CrossRef]
- Yariyan, P.; Avand, M.; Abbaspour, R.A.; Torabi Haghighi, A.; Costache, R.; Ghorbanzadeh, O.; Janizadeh, S.; Blaschke, T. Flood susceptibility mapping using an improved analytic network process with statistical models. Geomat. Nat. Hazards Risk 2020, 11, 2282–2314. [Google Scholar] [CrossRef]
- Yıldız, N.; Şişman, A. Investigation of flood risk areas in ünye district with best-worst method using geographic information systems. Adv. Land Manag. 2022, 2, 21–28. [Google Scholar]
- Tien Bui, D.; Khosravi, K.; Li, S.; Shahabi, H.; Panahi, M.; Singh, V.P.; Chapi, K.; Shirzadi, A.; Panahi, S.; Chen, W. New hybrids of anfis with several optimization algorithms for flood susceptibility modeling. Water 2018, 10, 1210. [Google Scholar] [CrossRef]
- Turoğlu, H.; Dölek, İ. Floods and their likely impacts on ecological environment in Bolaman River basin (Ordu, Turkey). Res. J. Agric. Sci. 2011, 43, 167–173. [Google Scholar]
- Pham, B.T.; Luu, C.; Van Phong, T.; Nguyen, H.D.; Van Le, H.; Tran, T.Q.; Ta, H.T.; Prakash, I. Flood risk assessment using hybrid artificial intelligence models integrated with multi-criteria decision analysis in quang nam province, vietnam. J. Hydrol. 2021, 592, 125815. [Google Scholar] [CrossRef]
- Mahdi, J.M.; Lohrasbi, S.; Nsofor, E.C. Hybrid heat transfer enhancement for latent-heat thermal energy storage systems: A review. Int. J. Heat Mass Transf. 2019, 137, 630–649. [Google Scholar] [CrossRef]
- Nguyen, H.; Mehrabi, M.; Kalantar, B.; Moayedi, H.; Abdullahi, M.a.M. Potential of hybrid evolutionary approaches for assessment of geo-hazard landslide susceptibility mapping. Geomat. Nat. Hazards Risk 2019, 10, 1667–1693. [Google Scholar] [CrossRef]
- Harifi, S.; Mohammadzadeh, J.; Khalilian, M.; Ebrahimnejad, S. Hybrid-epc: An emperor penguins colony algorithm with crossover and mutation operators and its application in community detection. Prog. Artif. Intell. 2021, 10, 181–193. [Google Scholar] [CrossRef]
- Martinez, C.M.; Hu, X.; Cao, D.; Velenis, E.; Gao, B.; Wellers, M. Energy management in plug-in hybrid electric vehicles: Recent progress and a connected vehicles perspective. IEEE Trans. Veh. Technol. 2016, 66, 4534–4549. [Google Scholar] [CrossRef]
- Janiga, D.; Czarnota, R.; Stopa, J.; Wojnarowski, P. Self-adapt reservoir clusterization method to enhance robustness of well placement optimization. J. Pet. Sci. Eng. 2019, 173, 37–52. [Google Scholar] [CrossRef]
- Chen, F.; Sun, X.; Wei, D.; Tang, Y. Tradeoff strategy between exploration and exploitation for pso. In Proceedings of the 2011 Seventh International Conference on Natural Computation, Shanghai, China, 26–28 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1216–1222. [Google Scholar]
- Yang, X.-S. Harmony search as a metaheuristic algorithm. In Music-Inspired Harmony Search Algorithm; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–14. [Google Scholar]
- Moayedi, H.; Mehrabi, M.; Bui, D.T.; Pradhan, B.; Foong, L.K. Fuzzy-metaheuristic ensembles for spatial assessment of forest fire susceptibility. J. Environ. Manag. 2020, 260, 109867. [Google Scholar] [CrossRef]
- Mehrabi, M.; Pradhan, B.; Moayedi, H.; Alamri, A. Optimizing an adaptive neuro-fuzzy inference system for spatial prediction of landslide susceptibility using four state-of-the-art metaheuristic techniques. Sensors 2020, 20, 1723. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).