Experimental and Theoretical Explanations for the Initial Difference in the Hydraulic Head in Aquitards
Abstract
:1. Introduction
2. Materials and Methods
2.1. Tests
- (1)
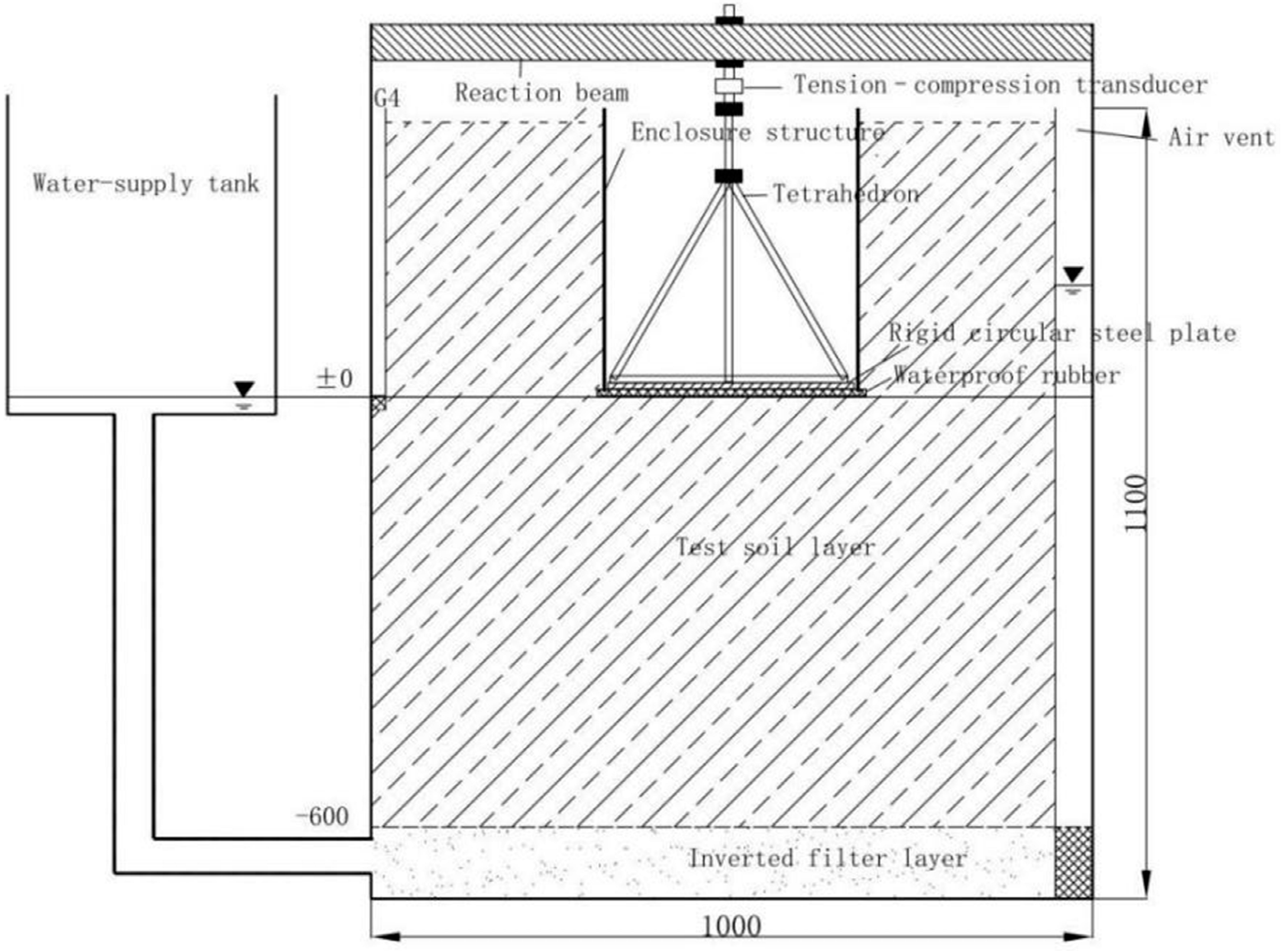
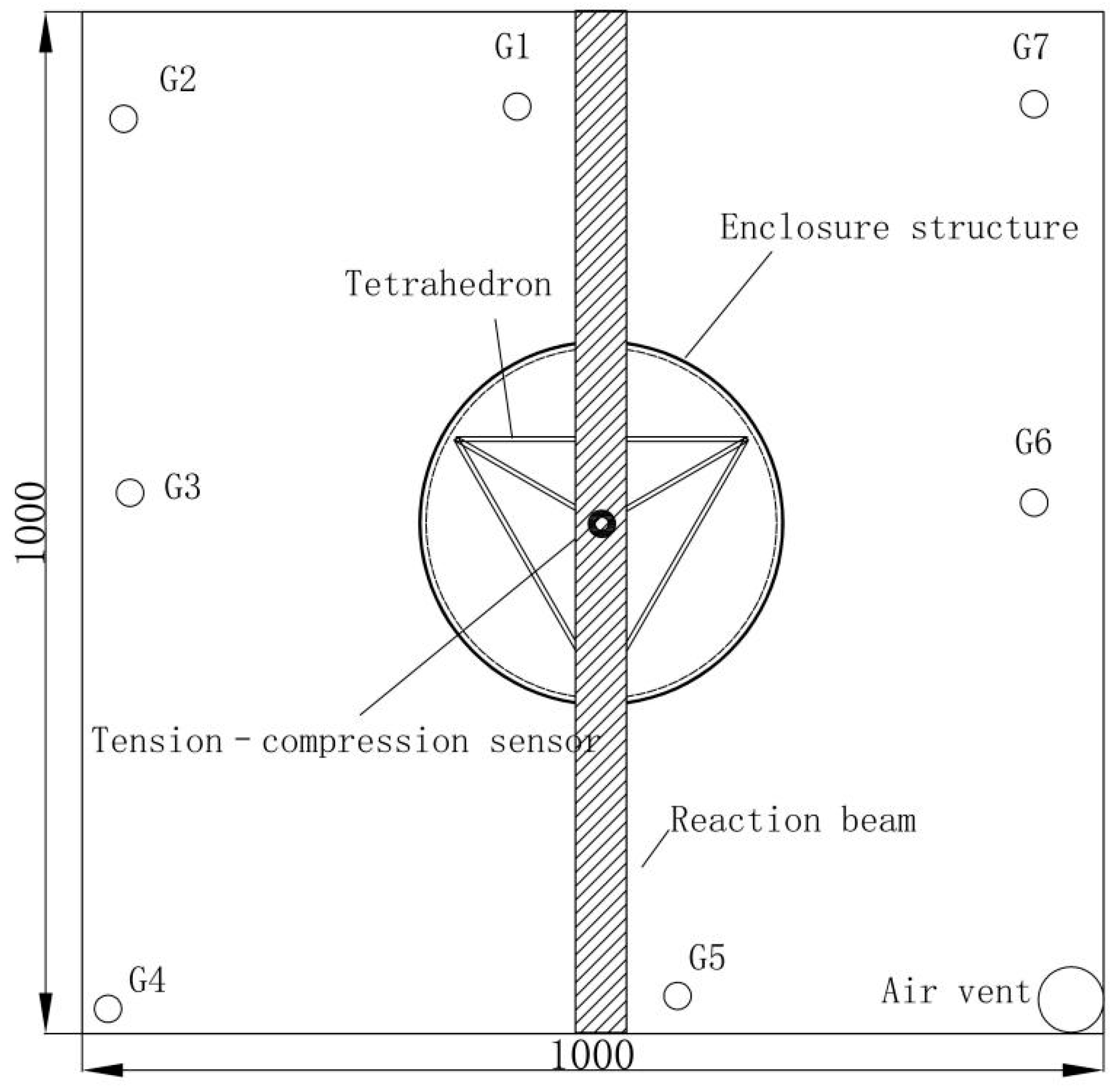
- Test design
- (2)
- Composition of the test setup
- (3)
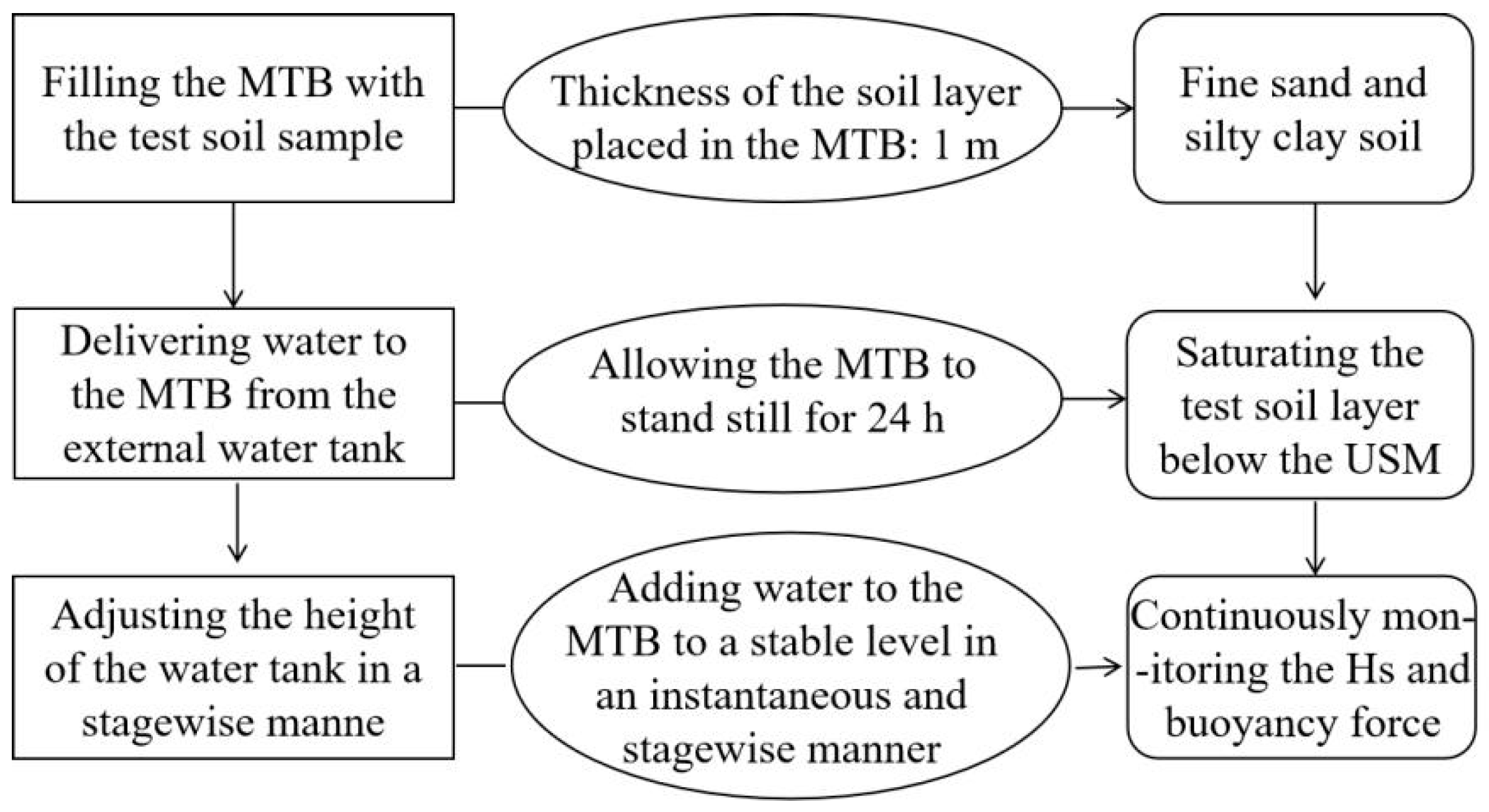
- Test procedure
- (1)
- Soil-sample preparation and filling. The fine sand and silty clay used in the tests were both retrieved from construction sites in Changchun. In this study, the effects of structured soils on test results were not considered. Therefore, remolded soils were used instead of undisturbed soils. The retrieved soil samples were manually crushed in the laboratory. Each soil sample was sprayed sparingly with water while being placed in the MTB layer by layer. Each layer was no thicker than 20 cm and was manually compacted before the subsequent layer was placed on top of it. The same procedure was followed to fill the MTB with each of the two test soil samples (i.e., fine sand and silty clay). Table 2 and Table 3 summarize the physical property metrics of the test soil samples placed in the MTB. The fine sand layer was first tested to examine test reliability. Subsequently, a continuous F2 monitoring test was performed with the silty clay layer;
- (2)
- Delivery of water from the external water tank. The external water tank was used to provide a continuous water supply to the MTB. hd was kept at the same level as the bottom of the rigid circular steel plate in the MTB. The Hs in the MTB was monitored continuously. After Hs stabilized, the MTB was allowed to stand still for 24 h to allow the test soil layer beneath the USM to be completely saturated;
- (3)
- F2 monitoring test. The height of the water-supply tank was adjusted to increase hd in a stagewise manner. The extent to which hd was increased at each stage depended on the Hs and F2 response speed inside the MTB. At the start of each stage, water was added to the water tank to maintain a stable hd for a certain period of time, after which the addition of water was terminated. After Hs stabilized, hd was increased again to commence the subsequent stage of the test. Throughout the test, Hs and F2 were monitored automatically and in real time.
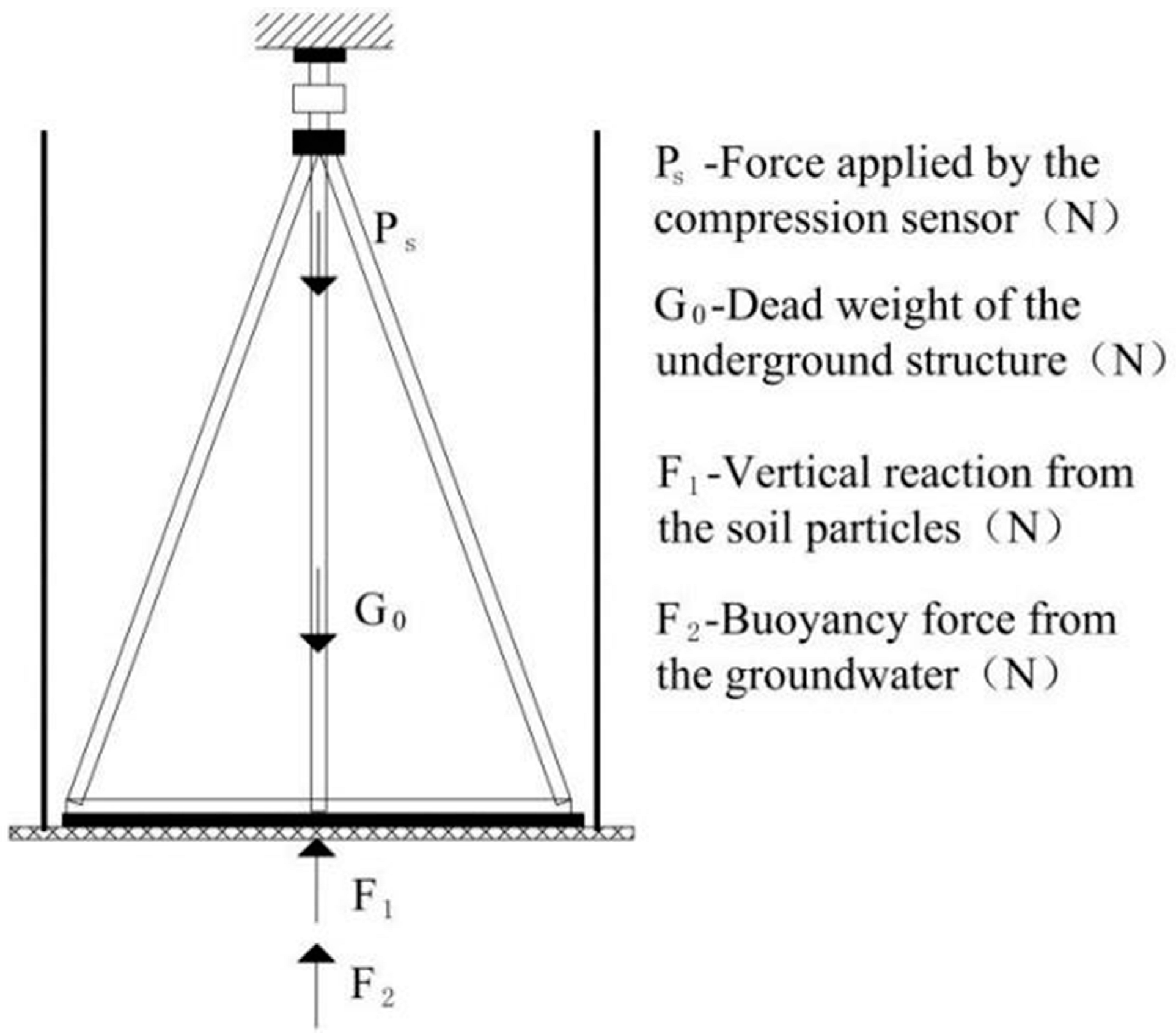
2.2. Force Analysis
3. Results and Discussion
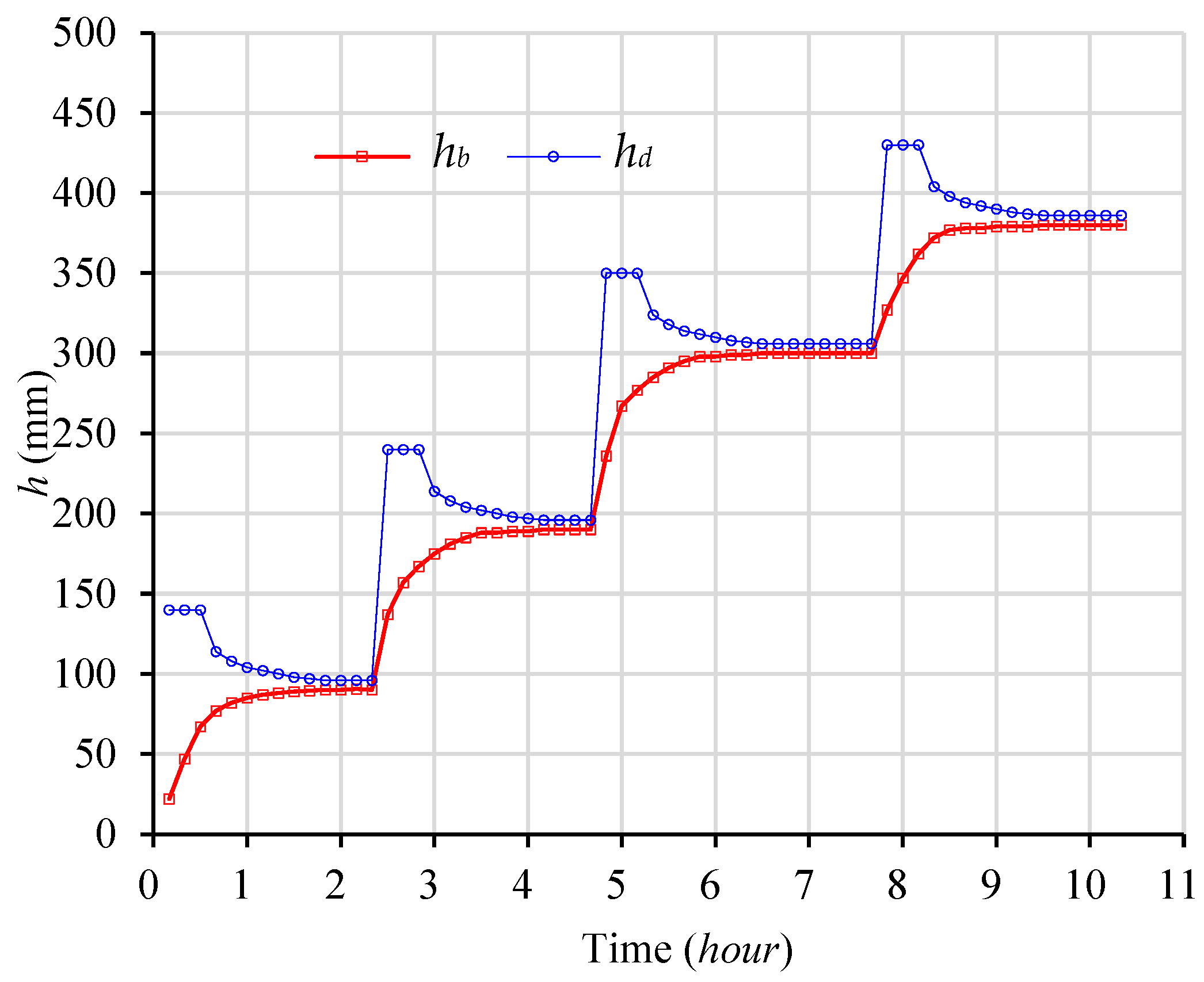
3.1. Presence of Δh0
3.1.1. Presence of Δh0 in the Tests
- (1)
- Dynamic variation in F2 under instantaneous water-supply conditions.
- (2)
- Comparison of the stable hd and hb.
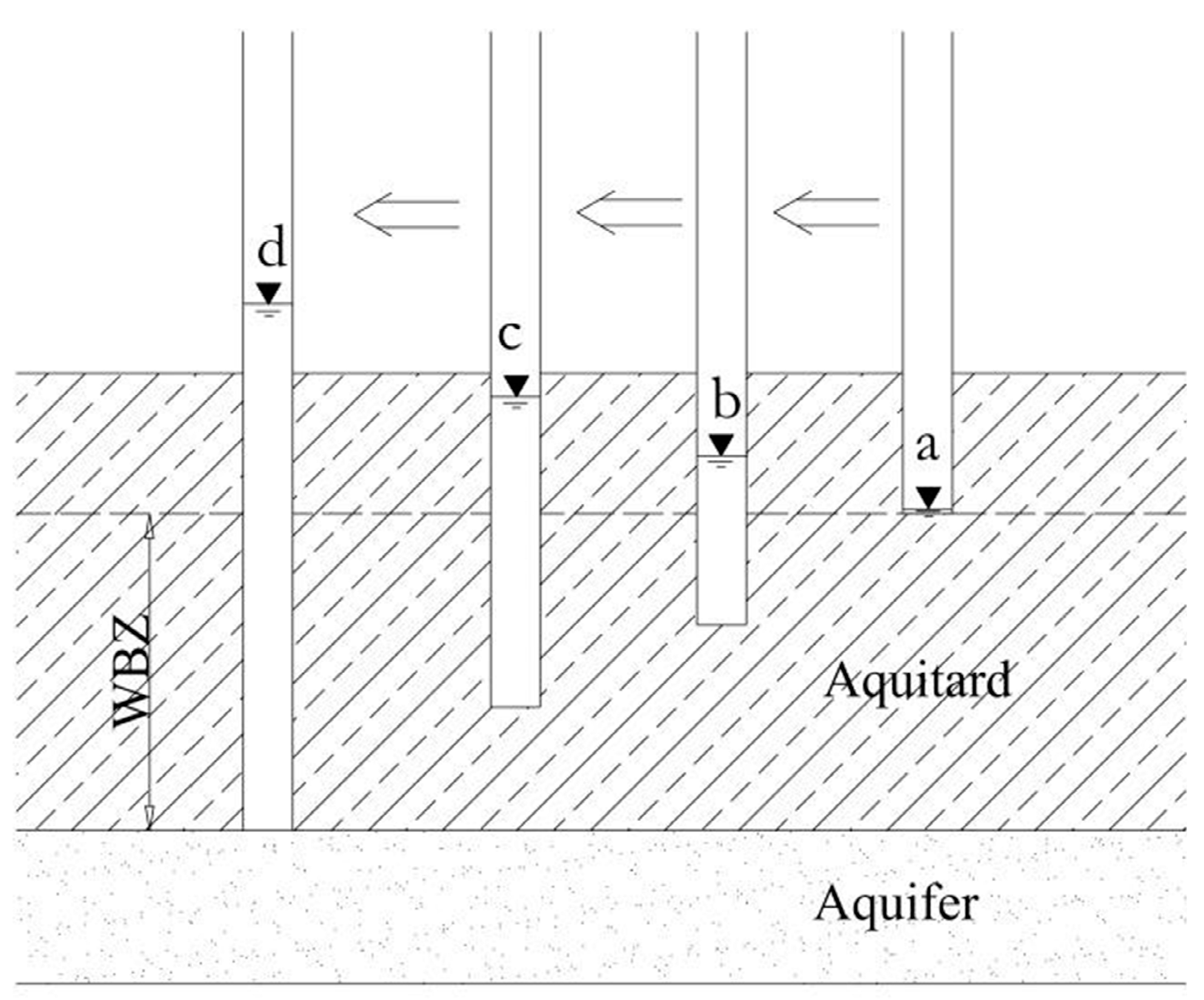
3.1.2. Presence of Δh0 in Real-World Engineering Settings
3.2. Theoretical Explanation for Δh0
3.3. Validation of Δh0
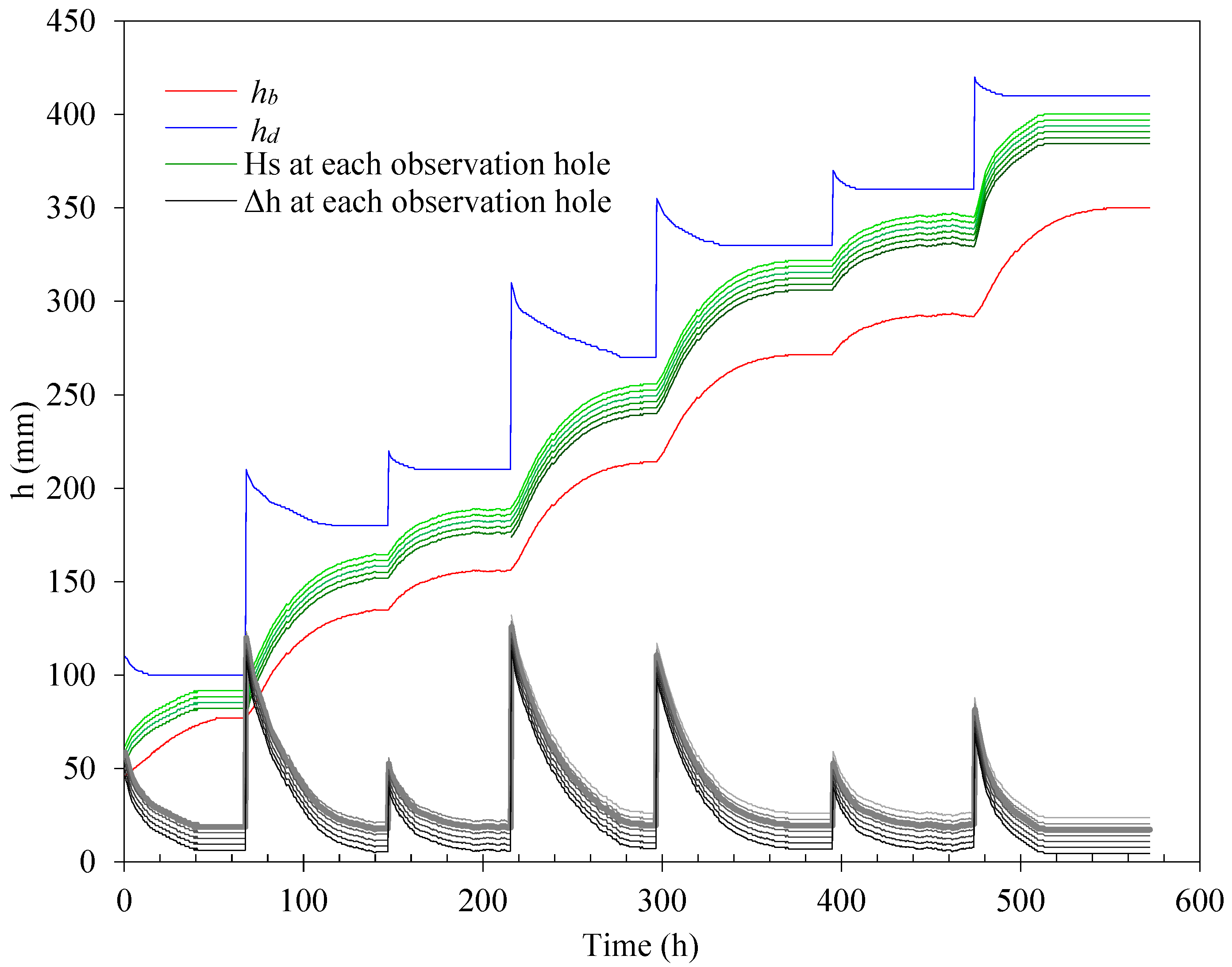
3.3.1. Variation in Hs and Δh
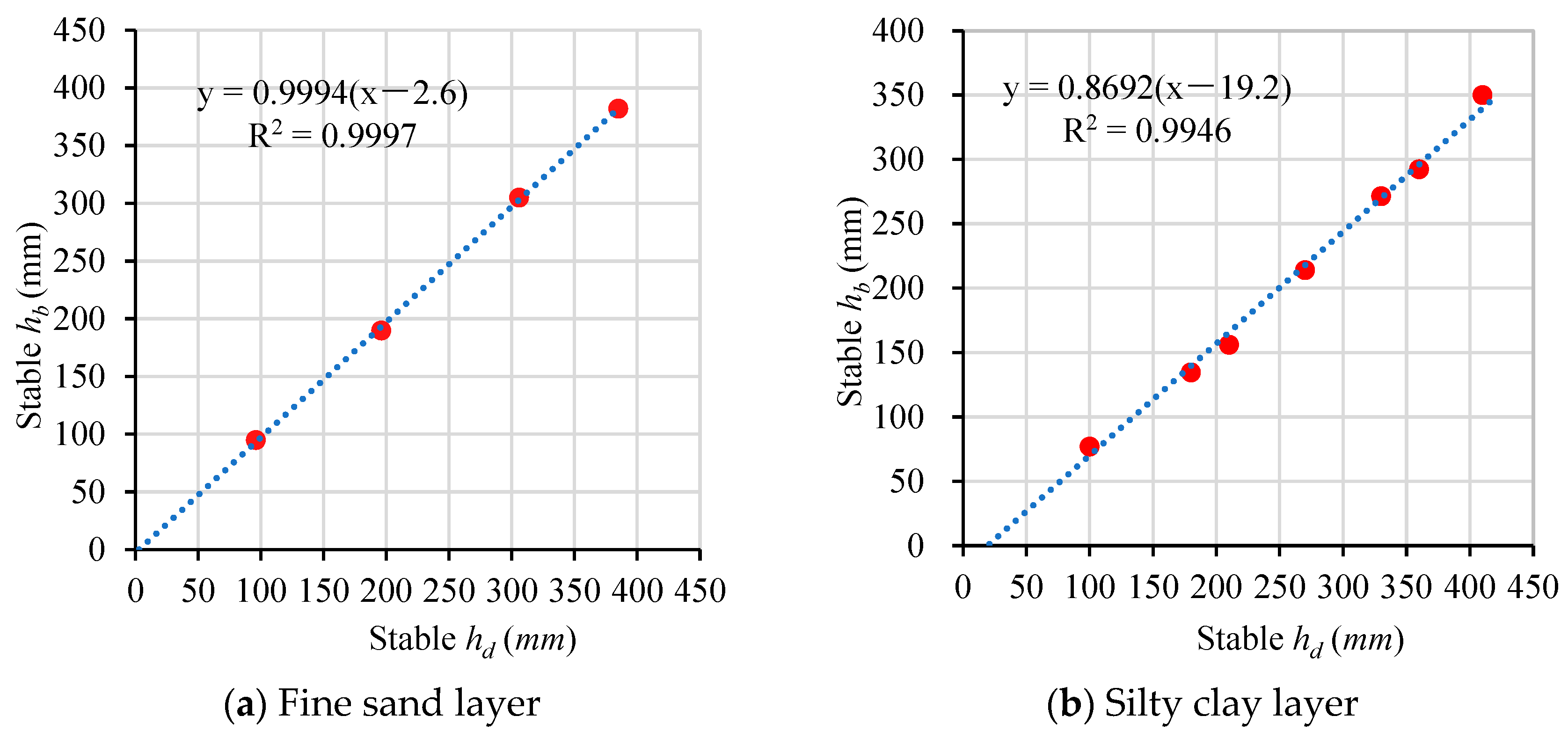
3.3.2. Variation in the Stable hd and H0
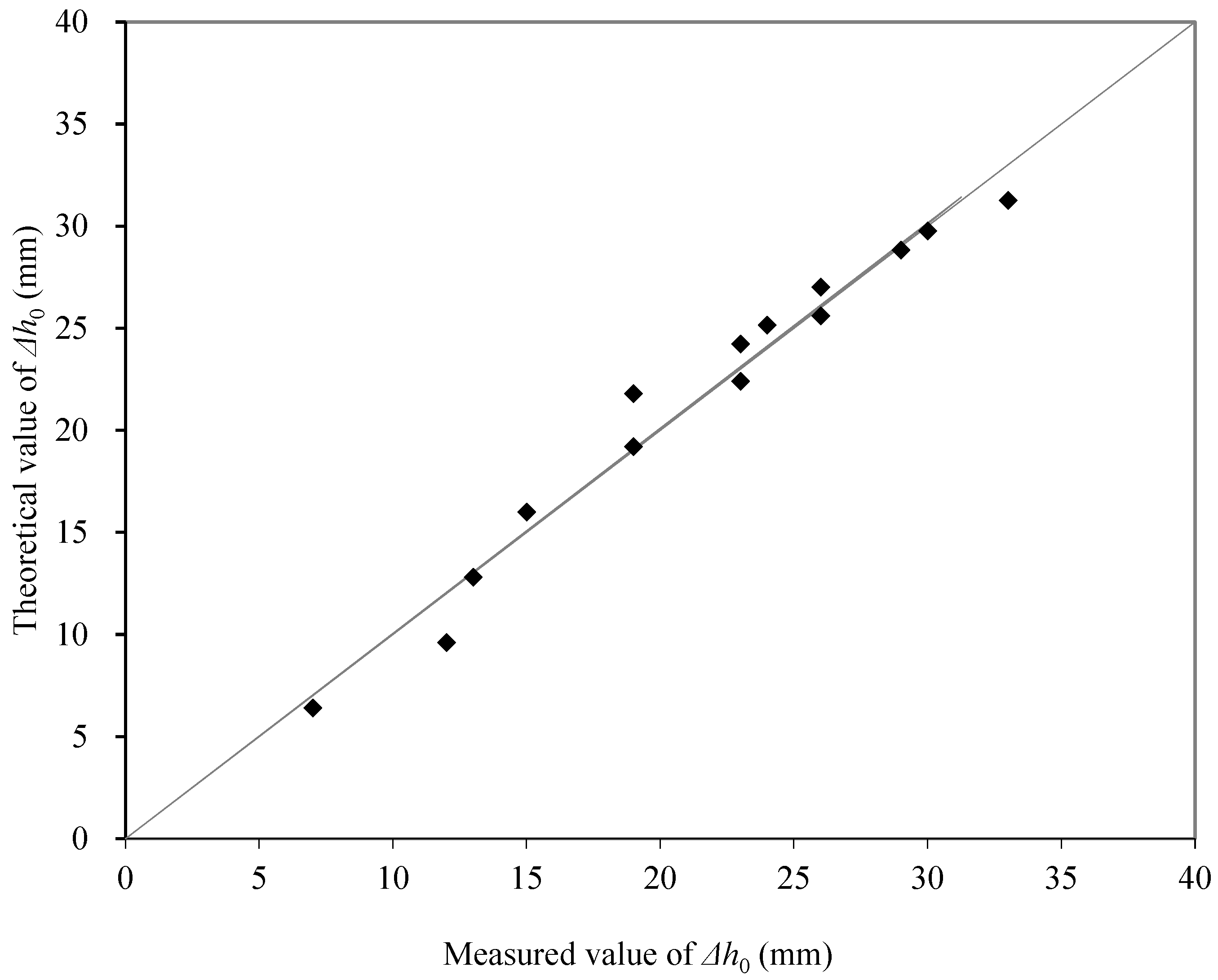
3.3.3. Comparison of the Theoretically Calculated and Measured Values of Δh0
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| PWP | Pore-water pressure |
| USM | Underground structure module |
| MTB | Model test box |
| ESM | Enclosure structure module |
| Symbols | |
| Δh | Hydraulic head difference |
| Δh0 | Initial hydraulic head difference |
| I | Hydraulic gradient |
| I0 | Initial I |
| L0 | Length of the corresponding seepage path |
| Hs | Head of the test soil layer |
| H0 | Stable initial head |
| Hc | Confined head in the aquifer |
| G0 | Dead weight of the USM |
| F1 | Vertical reaction of soil particles |
| F2 | Buoyancy force exerted by groundwater |
| Ps | Pressure detected by the tension–compression sensor |
| Ps0 | The force on the soil sample the when the buoyancy from the groundwater is zero |
| A | Area of the bottom of a rigid circular steel plate |
| G | Gravitational acceleration |
| hb | Buoyancy head from groundwater |
| hd | Delivery head |
References
- Bikçe, M.; Örnek, M.; Cansız, Ö.F. The effect of buoyancy force on structural damage: A case study. Eng. Fail. Anal. 2018, 92, 553–565. [Google Scholar] [CrossRef]
- Tang, H.Y.; Yang, D.; Wang, C.J.; Guo, H.X.; Dong, Q.P. Anti-floating problem and retrofit measures for a damaged basement. Mater. Res. Innov. 2015, 19, S8-219–S8-222. [Google Scholar] [CrossRef]
- Zhou, J.K.; Lin, C.H.; Chen, C.; Zhao, X.Y. Reduction of groundwater buoyancy on the basement in weak-permeable/impervious foundations. Adv. Civil. Eng. 2019, 2019, 7826513. [Google Scholar] [CrossRef]
- Huerta, D.A.; Sosa, V.; Vargas, M.C.; Ruiz-Suárez, J.C. Archimedes’ principle in fluidized granular systems. Phys. Rev. E 2005, 72, 031307. [Google Scholar] [CrossRef] [PubMed]
- dos Santos, F.C.; Santos, W.M.S.; Berbat, S.D. An analysis of floating bodies and the principle of archimedes. Rev. Bras. Ensino Fis. 2007, 29, 295–298. [Google Scholar]
- Barbot, A.; Lopes, J.B.; Soares, A.A. Relating water and energy by experimenting with urban water cycle, desalination of sea water and archimedes’ law. In Proceedings of the 6th International Technology, Education and Development Conference, Valencia, Spain, 5–7 March 2012; pp. 2534–2544. [Google Scholar]
- Kang, W.T.; Feng, Y.J.; Liu, C.S.; Blumenfeld, R. Archimedes’ law explains penetration of solids into granular media. Nat. Commun. 2018, 9, 1101. [Google Scholar] [CrossRef]
- Hisatake, M. A Proposed methodology for analysis of ground settlements caused by tunneling, with particular reference to the “buoyancy” effect. Tunn. Undergr. Space Technol. 2011, 26, 130–138. [Google Scholar] [CrossRef]
- Liu, X.Y.; Yuan, D.J. Mechanical analysis of anti-buoyancy safety for a shield tunnel under water in sands. Tunn. Undergr. Space Technol. 2015, 47, 153–161. [Google Scholar] [CrossRef]
- Xu, Z.J.; Yu, H.H. Non-contact experiment investigation of the interaction between the soil and underground granary subjected to water buoyancy. Appl. Sci. 2021, 11, 8988. [Google Scholar] [CrossRef]
- Zhang, J.W.; Cao, J.; Mu, L.; Wang, L.; Li, J. Buoyancy force acting on underground structures considering seepage of confined water. Complexity 2019, 2019, 7672930. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, L. Experiment on the computing method of anti-floating in underground structures. Sichuan Build. Sci. 2008, 34, 105–108. (In Chinese) [Google Scholar]
- Li, X.L.; Wang, B.L.; Li, X.; Ji, C. Analysis of anti-floating measures and construction parameters of shield tunnel through river under ultra-shallow covering. In Proceedings of the International Conference on Civil Engineering, Architecture and Building Materials, Jinan, China, 24–26 May 2013; pp. 628–634. [Google Scholar]
- Zhang, S.Q.; Yuan, W.J.; Zhang, H.H.; Huang, L.; Zhong, Y.F. Analytical and numerical anti-floating study concerning the shield tunnel across the river. In Proceedings of the International Conference on Structures and Building Materials, Guiyang, China, 9–10 March 2013; pp. 1087–1092. [Google Scholar]
- Tang, M.X.; Hu, H.S.; Zhang, C.L.; Hou, M.X.; Chen, H. Determination of anti-floating water level in guangzhou based on the distribution of the underground aquifers. In Proceedings of the GeoShanghai International Conference on Geoenvironment and Geohazard, Shanghai, China, 27–30 May 2018; pp. 468–480. [Google Scholar]
- Cui, Y.; Cui, J.; Wu, S. A model test of shallow underground structure buoyancy. Spec. Struct. 1999, 16, 32–36. (In Chinese) [Google Scholar]
- Xiang, K.; Zhou, S.; Zhan, C. Model test study of buoyance on shallow underground structure. J. Tongji Univ. (Nat. Sci.) 2010, 38, 346–352. (In Chinese) [Google Scholar]
- Zhou, P. Groundwater Uplift Mechanism Study under Complex Urban Environment. Master’s Thesis, China University of Geosciences (Beijing), Beijing, China, 2006. [Google Scholar]
- Song, L.; Kang, X.; Mei, G. Buoyancy force on shallow foundations in clayey soil: An experimental investigation based on the “Half Interval Search”. Ocean. Eng. 2017, 129, 637–641. [Google Scholar] [CrossRef]
- Song, L.; Huang, Q.; Yan, D.; Mei, G. Experimental study on effect of hydraulic gradient on permeability of clay. Chin. J. Geotech. Eng. 2018, 40, 1635–1641. (In Chinese) [Google Scholar]
- Zhang, Q.; Ouyang, L.; Wang, Z.; Liu, H.; Zhang, Y. Buoyancy reduction coefficients for underground silos in sand and clay. Indian Geotech. J. 2019, 49, 216–223. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, P.; Jia, M. Centrifugal model test of pore water pressure in soft clay. In Proceedings of the GeoShanghai 2018 International Conference: Fundamentals of Soil Behaviours, Shanghai, China, 28–30 May 2018. [Google Scholar]
- Zhang, Z. The Bond Water Dynamics Theory; Geology Press: Beijing, China, 1980; pp. 80–83. [Google Scholar]
- Kutiĺek, M. Non-darcian flow of water in soils—Laminar region: A review. Dev. Soil Sci. 1972, 2, 327–340. [Google Scholar]
- Mesri, G.; Rokhsar, A. Theory of consolidation for clays. J. Geotech. Geoenviron. Eng. 1974, 100, 889–904. [Google Scholar]
- Deng, Y.; Xie, H.; Huang, R.; Liu, C. Law of nonlinear flow in saturated clays and radial consolidation. Appl. Math. Mech. 2007, 28, 1427–1436. [Google Scholar] [CrossRef]
- Law, K.T.; Lee, C.F. Initial gradient in a dense glacial till. In Proceedings of the 10th International Conference on Soil Mechanics and Foundation Engineering, Stockholm, Sweden, 15–19 June 1981; Volume 1, pp. 441–446. [Google Scholar]




| Name | Type | Measuring Range | Composite Error (%F·S) | Diameter × Thickness (mm) | Material | Impedance (Ω) |
|---|---|---|---|---|---|---|
| Micro-PWP sensor | YSV3201 | 0–30 kPa | ≤0.05 | Φ15 × 20 | Stainless steel | 350 |
| Tension–compression sensor | H-2 | 0–100 kg | ≤0.05 | Φ40 × 30 | Stainless steel | 400 ± 10 |
| Test Soil Sample | Moisture Content W/% | Wet Density ρ/(g·cm–3) | Porosity e | Saturation Sr/% | Dry Density ρd/(g·cm–3) | Permeability Coefficient k (cm·s–1) |
|---|---|---|---|---|---|---|
| Sand | 26.7 | 1.96 | 0.64 | 96.1 | 1.63 | 5.59 × 10–3 |
| Test Soil Sample | W/% | ρ/(g·cm–3) | Porosity n/% | Sr/% | ρd/(g·cm–3) | Plasticity Index Ip | Liquidity Index IL | Permeability Coefficient k (cm·s–1) |
|---|---|---|---|---|---|---|---|---|
| Silty clay | 21.1 | 1.71 | 44.6 | 95.9 | 1.35 | 13.4 | 0.46 | 1.45 × 10–5 |
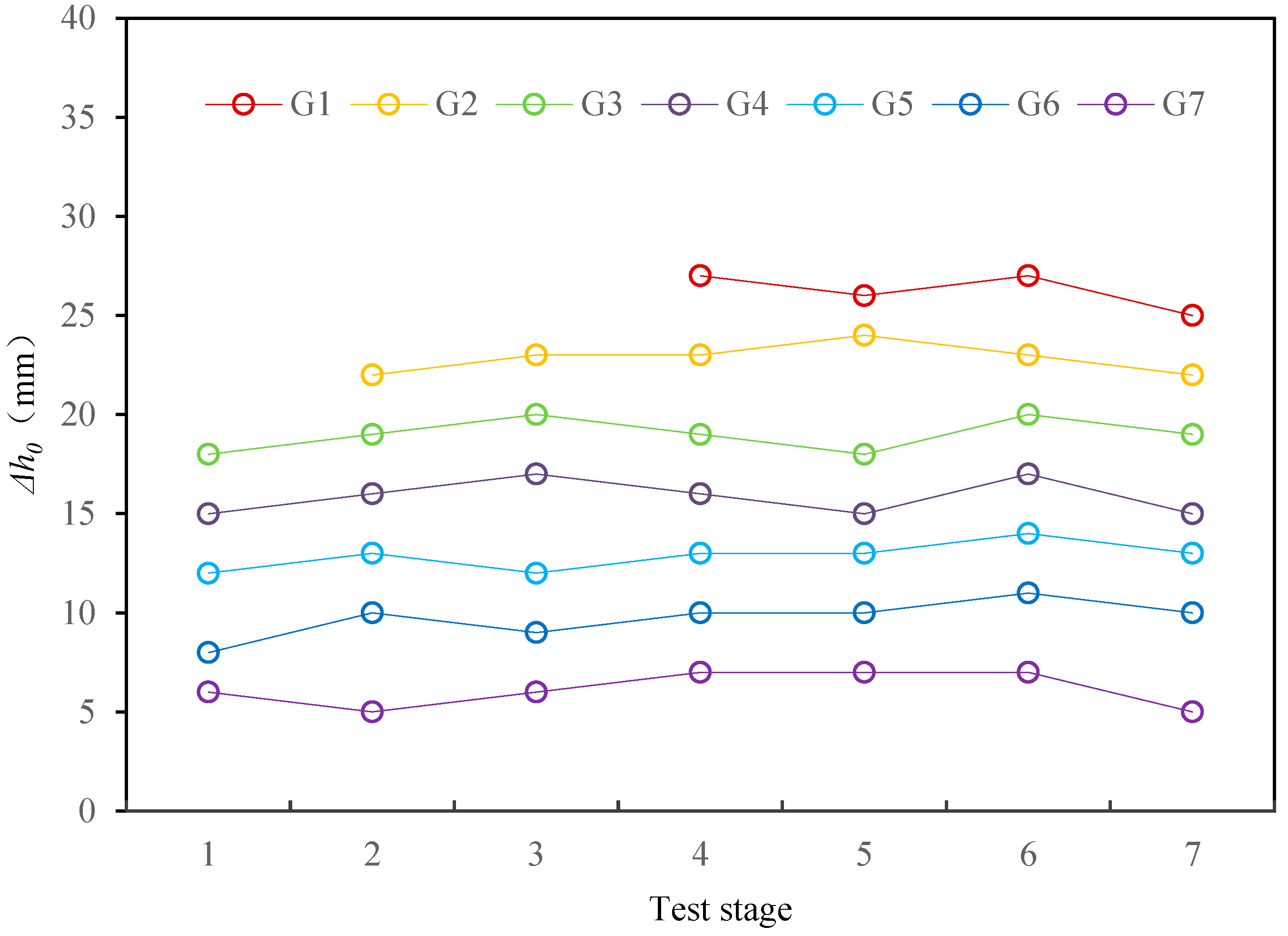
| Observation Hole | Depth (mm) | L0 (mm) | Δh0 (mm) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Stage 1 | Stage 2 | Stage 3 | Stage 4 | Stage 5 | Stage 6 | Stage 7 | Average | |||
| G1 | 200 | 800 | 27 | 26 | 27 | 25 | 26 | |||
| G2 | 300 | 700 | 22 | 23 | 23 | 20 | 23 | 22 | 23 | |
| G3 | 400 | 600 | 18 | 19 | 20 | 19 | 18 | 20 | 19 | 19 |
| G4 | 500 | 500 | 15 | 16 | 17 | 16 | 15 | 17 | 15 | 16 |
| G5 | 600 | 400 | 12 | 13 | 12 | 13 | 13 | 14 | 13 | 13 |
| G6 | 700 | 300 | 8 | 10 | 9 | 10 | 10 | 11 | 10 | 10 |
| G7 | 800 | 200 | 6 | 5 | 6 | 7 | 7 | 7 | 5 | 6 |
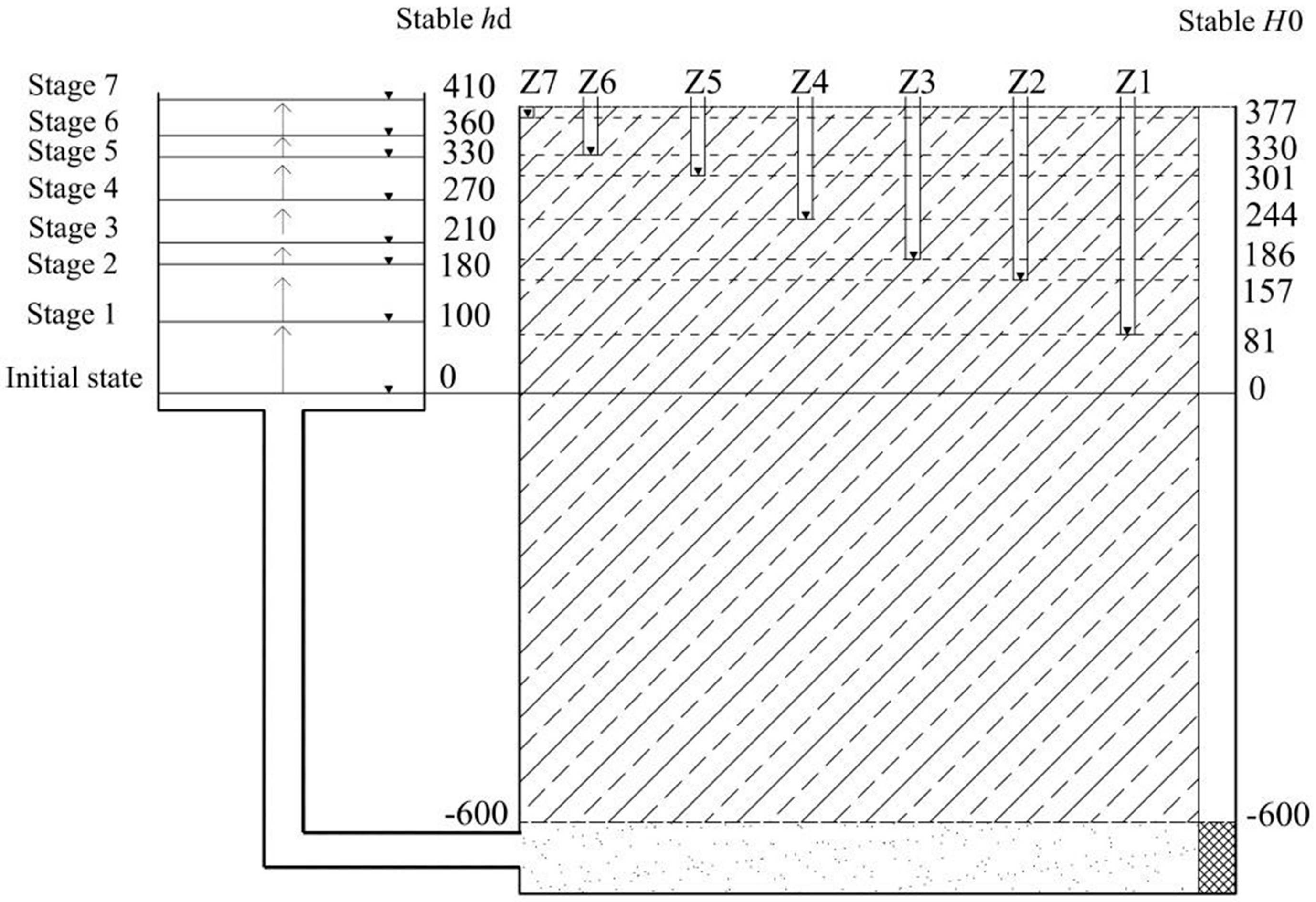
| Test Stage | Borehole | Stable hd (mm) | Stable H0 (mm) | Δh0 (mm) | L0 (mm) |
|---|---|---|---|---|---|
| 1 | Z1 | 100 | 81 | 19 | 681 |
| 2 | Z2 | 180 | 157 | 23 | 757 |
| 3 | Z3 | 210 | 186 | 24 | 786 |
| 4 | Z4 | 270 | 244 | 26 | 844 |
| 5 | Z5 | 330 | 301 | 29 | 901 |
| 6 | Z6 | 360 | 330 | 30 | 930 |
| 7 | Z7 | 410 | 377 | 33 | 977 |
| Test Sample | 1 | 2 | 3 | 4 | 5 | 6 | Average |
|---|---|---|---|---|---|---|---|
| I0 (dimensionless) | 0.031 | 0.033 | 0.035 | 0.033 | 0.029 | 0.032 | 0.032 |
| Observation Hole/Borehole | Depth (mm) | L0 (mm) | Theoretically Calculated Value of Δh0 (mm) |
|---|---|---|---|
| G1 | 200 | 800 | 26 |
| G2 | 300 | 700 | 22 |
| G3 | 400 | 600 | 19 |
| G4 | 500 | 500 | 16 |
| G5 | 600 | 400 | 13 |
| G6 | 700 | 300 | 10 |
| G7 | 800 | 200 | 6 |
| Z1 | 319 | 681 | 22 |
| Z2 | 243 | 757 | 24 |
| Z3 | 214 | 786 | 25 |
| Z4 | 156 | 844 | 27 |
| Z5 | 99 | 901 | 29 |
| Z6 | 70 | 930 | 30 |
| Z7 | 23 | 977 | 31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Du, C.; Ma, H.; Pang, W.; Huang, S.; Li, S. Experimental and Theoretical Explanations for the Initial Difference in the Hydraulic Head in Aquitards. Water 2022, 14, 3042. https://doi.org/10.3390/w14193042
Xu Y, Du C, Ma H, Pang W, Huang S, Li S. Experimental and Theoretical Explanations for the Initial Difference in the Hydraulic Head in Aquitards. Water. 2022; 14(19):3042. https://doi.org/10.3390/w14193042
Chicago/Turabian StyleXu, Yongliang, Chaoyang Du, Haizhi Ma, Wei Pang, Suhang Huang, and Shimin Li. 2022. "Experimental and Theoretical Explanations for the Initial Difference in the Hydraulic Head in Aquitards" Water 14, no. 19: 3042. https://doi.org/10.3390/w14193042
APA StyleXu, Y., Du, C., Ma, H., Pang, W., Huang, S., & Li, S. (2022). Experimental and Theoretical Explanations for the Initial Difference in the Hydraulic Head in Aquitards. Water, 14(19), 3042. https://doi.org/10.3390/w14193042







