Two-Step Simulation of Underwater Terrain in River Channel
Abstract
:1. Introduction
2. Methods
2.1. Data Preprocessing
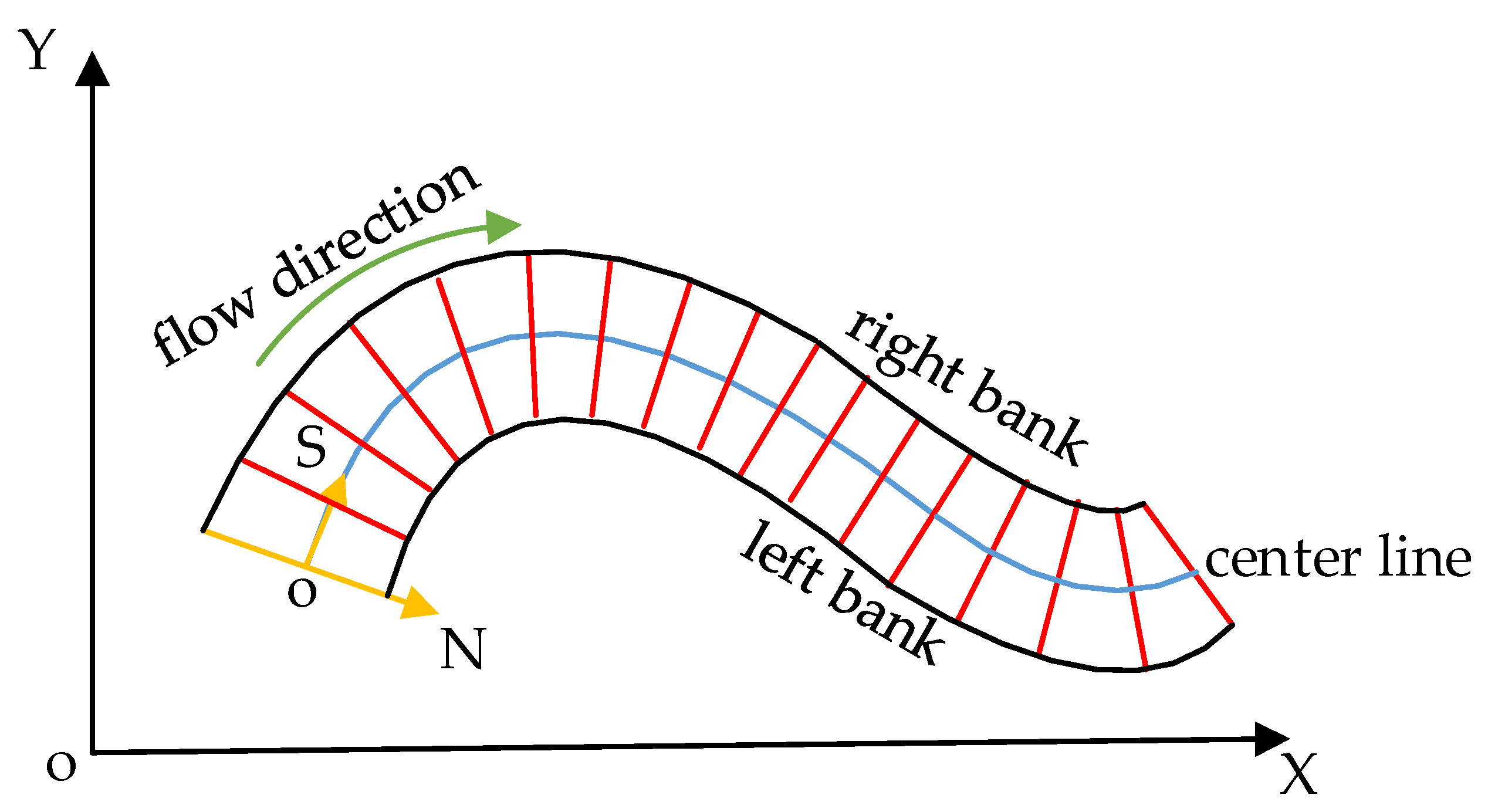
2.1.1. Spatial Reference Positioning
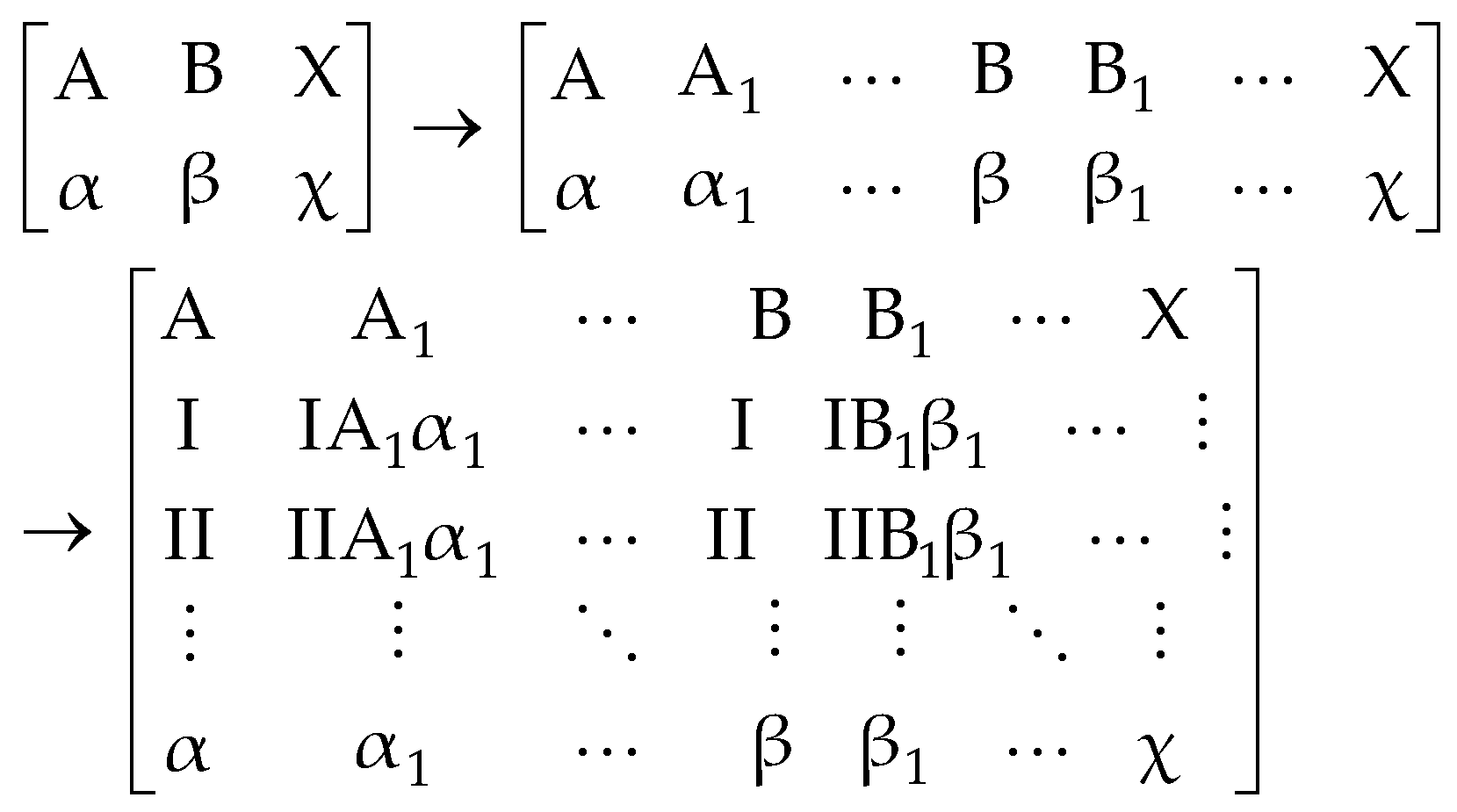
2.1.2. Spatial Element Coding
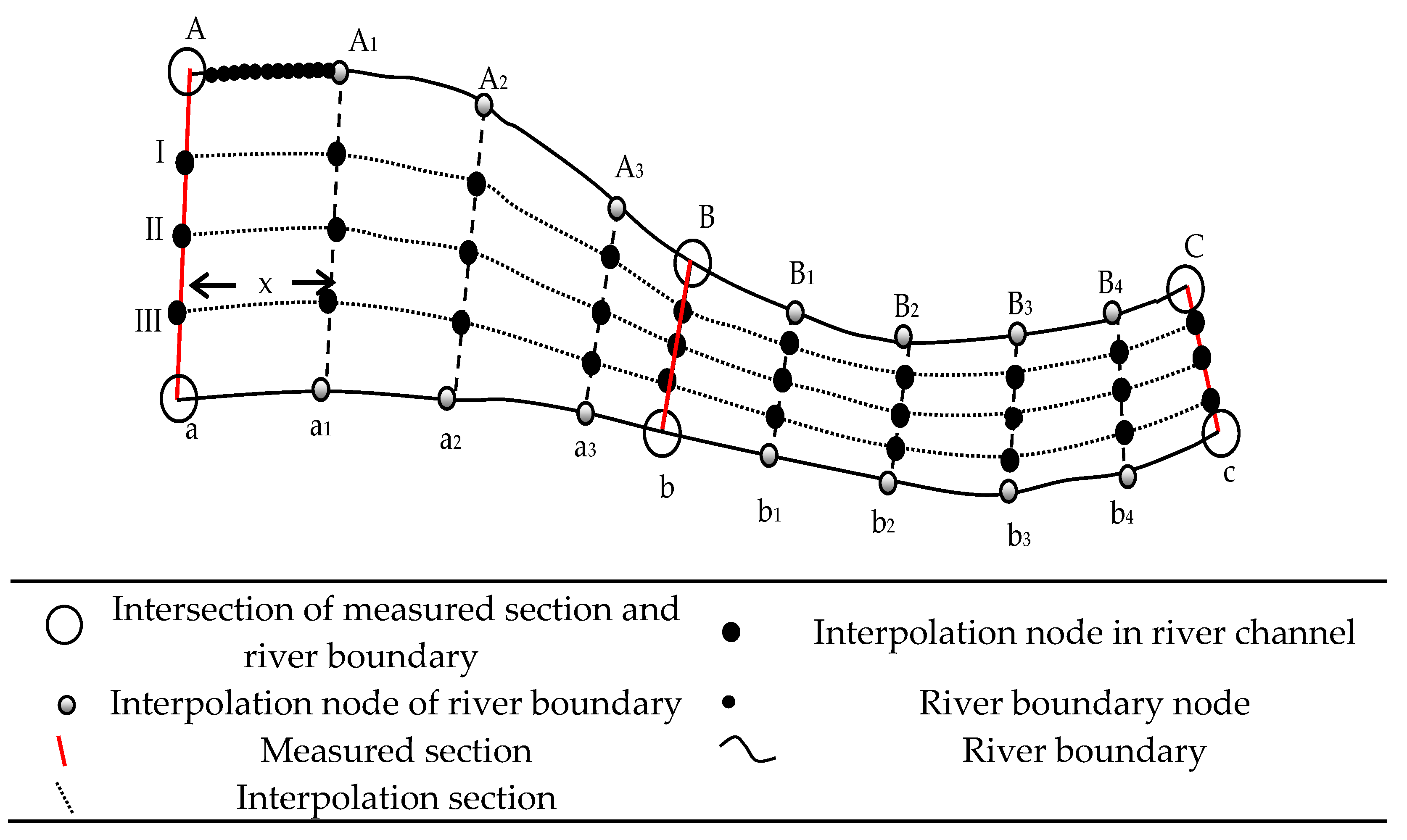
2.2. Global Linear Control
- (1)
- Calculation of horizontal positions of interpolation nodes
- (2)
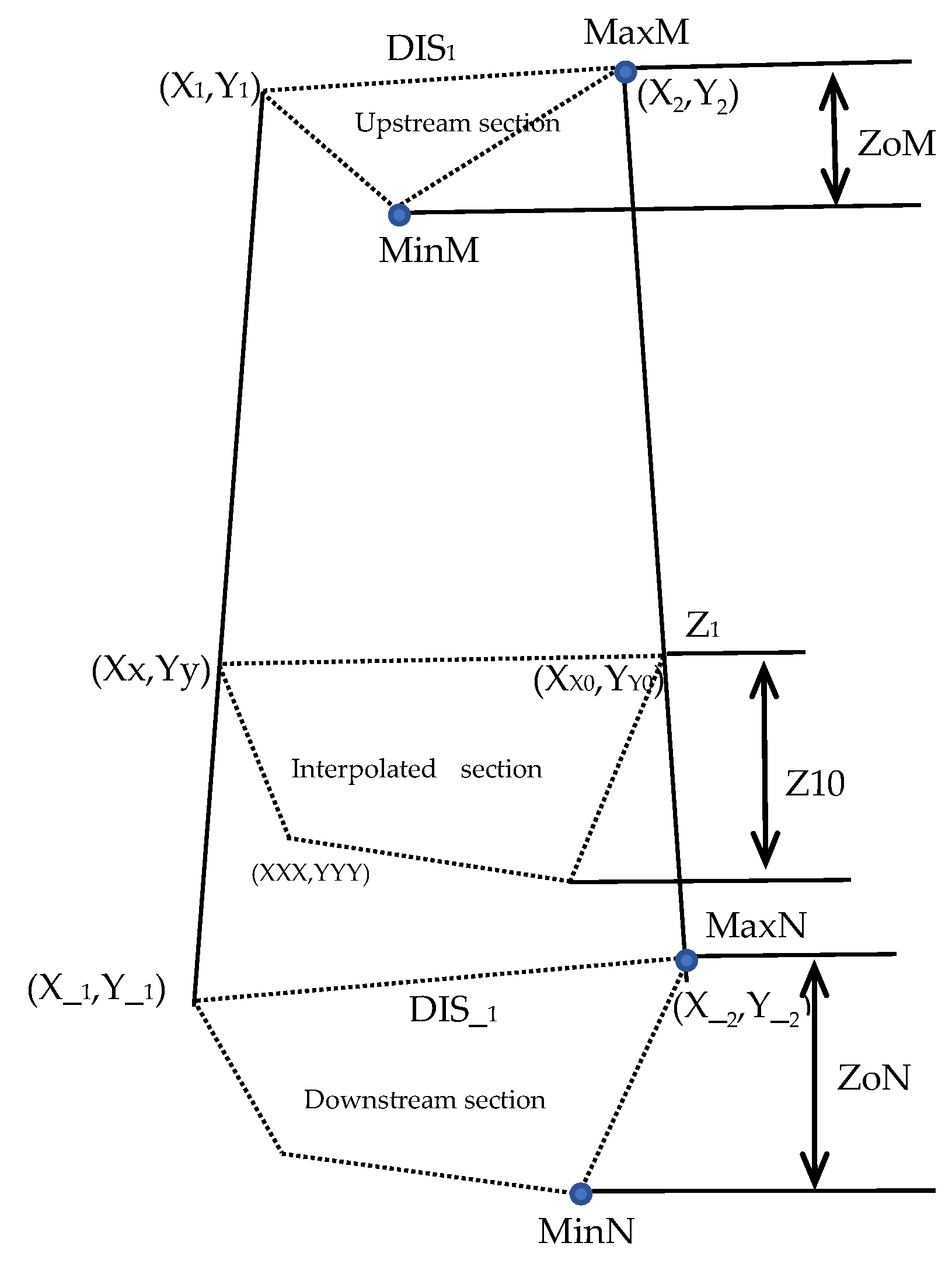
- Calculation of elevation of interpolation node
- (a)
- Maximal upstream elevation difference:
- (b)
- Maximal downstream elevation difference:
- (c)
- Interpolation section height difference:
- (d)
- Elevation of the highest point of interpolation section:
- (e)
- Elevation of the interpolation node:
2.3. Local Quadratic Interpolation
2.4. Verification of Simulated Terrain
3. Results and Discussion
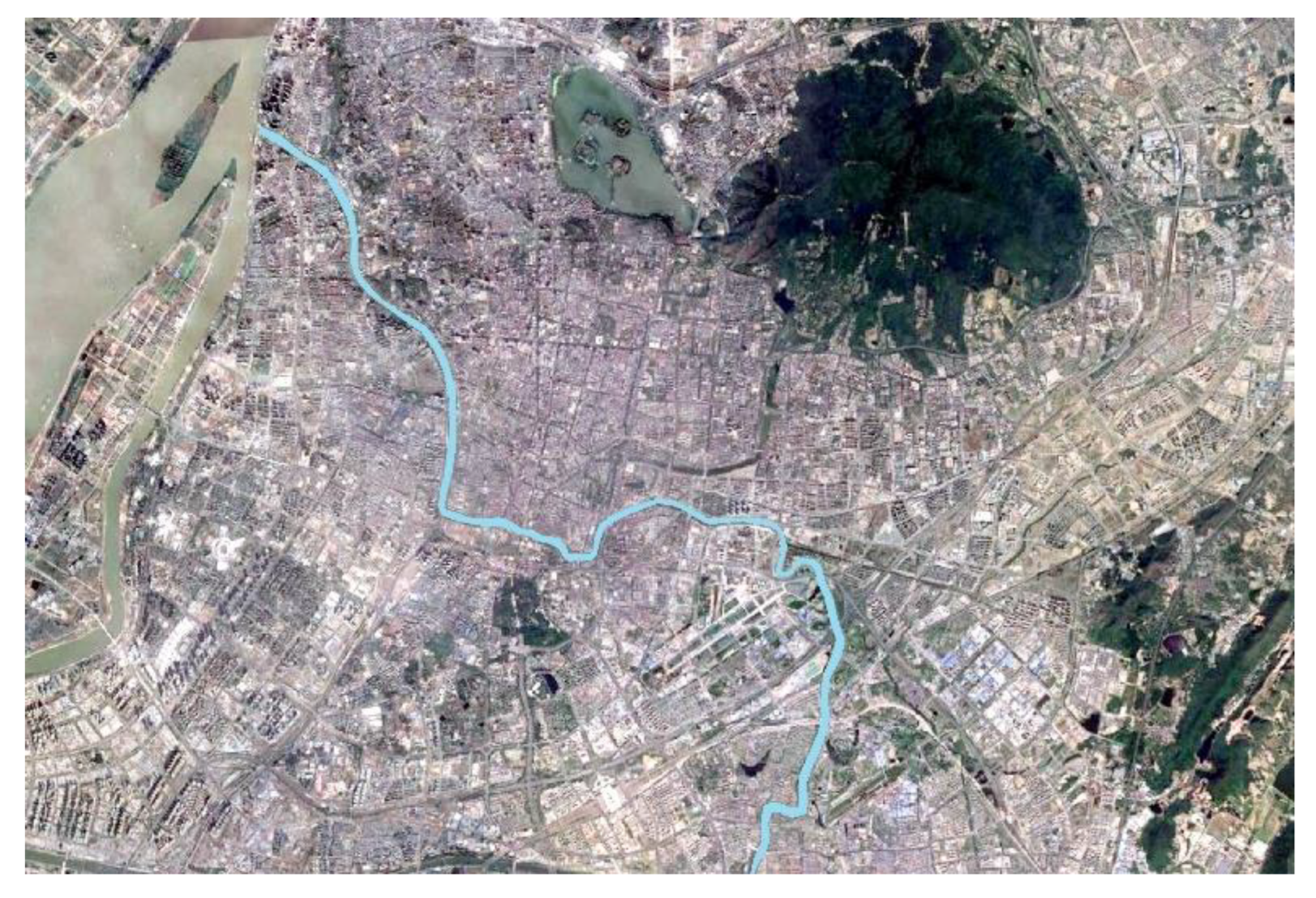
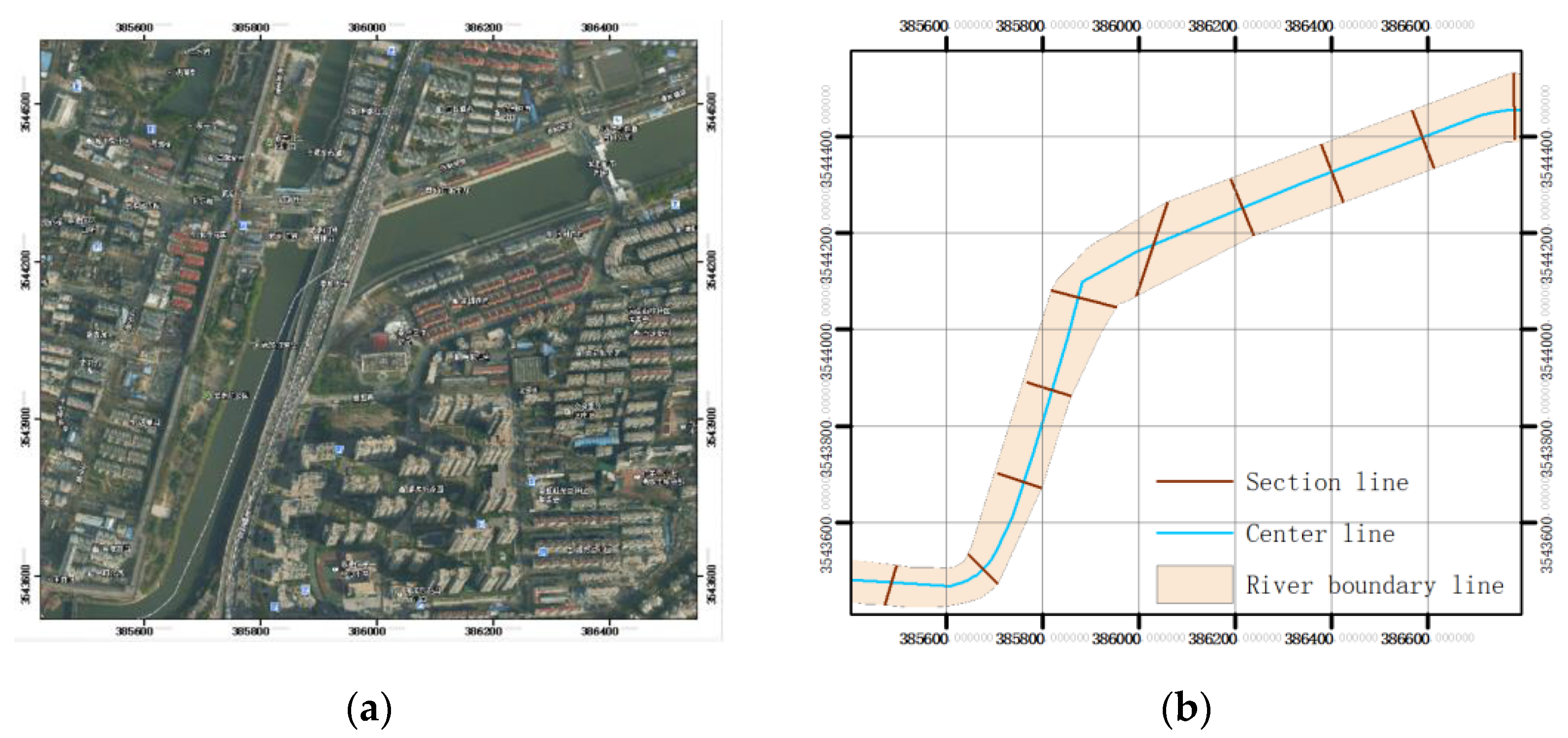
3.1. Study Data
3.2. Steps for 3D Surface Generation of River Terrain
3.3. Validation Analysis
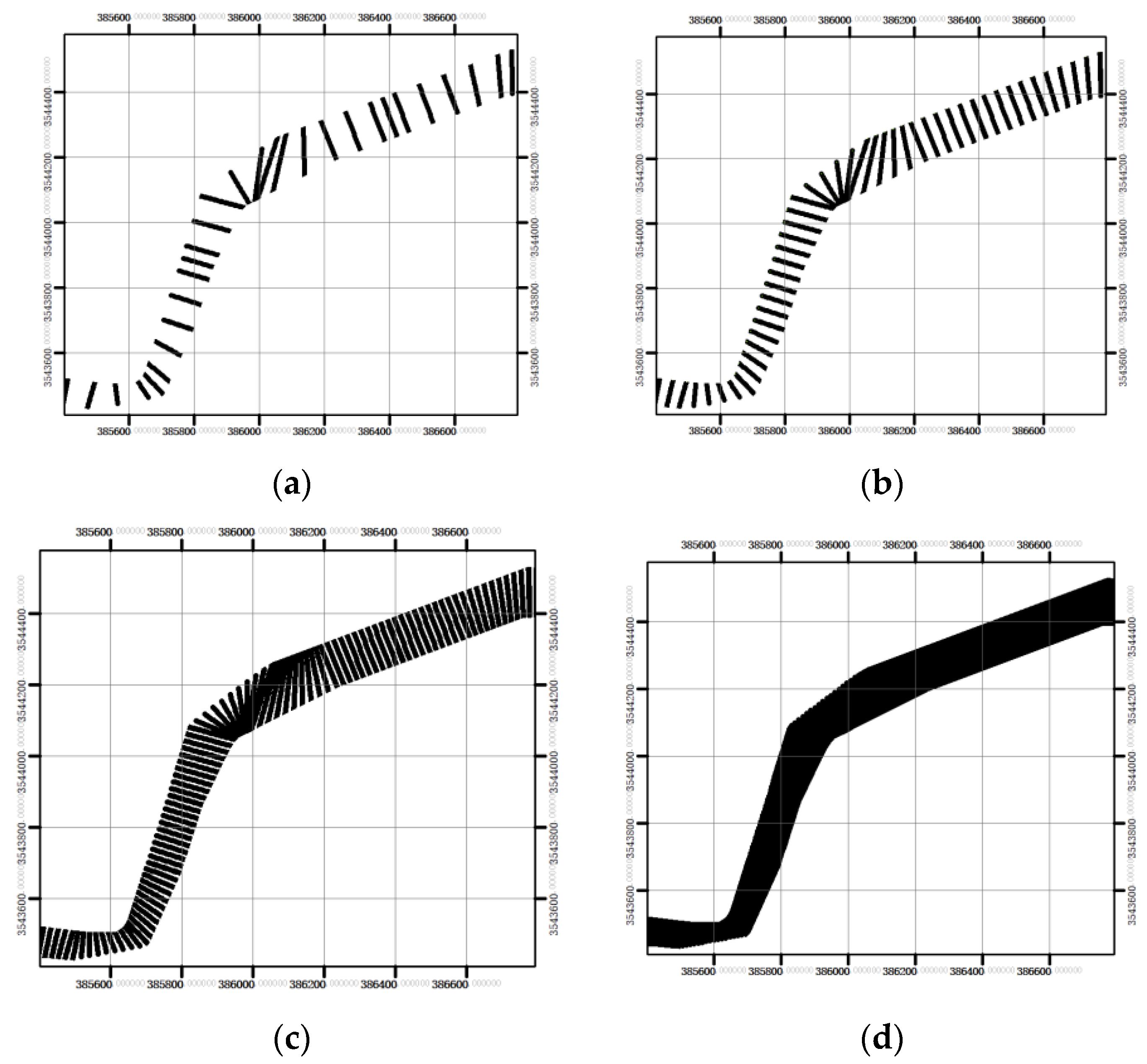
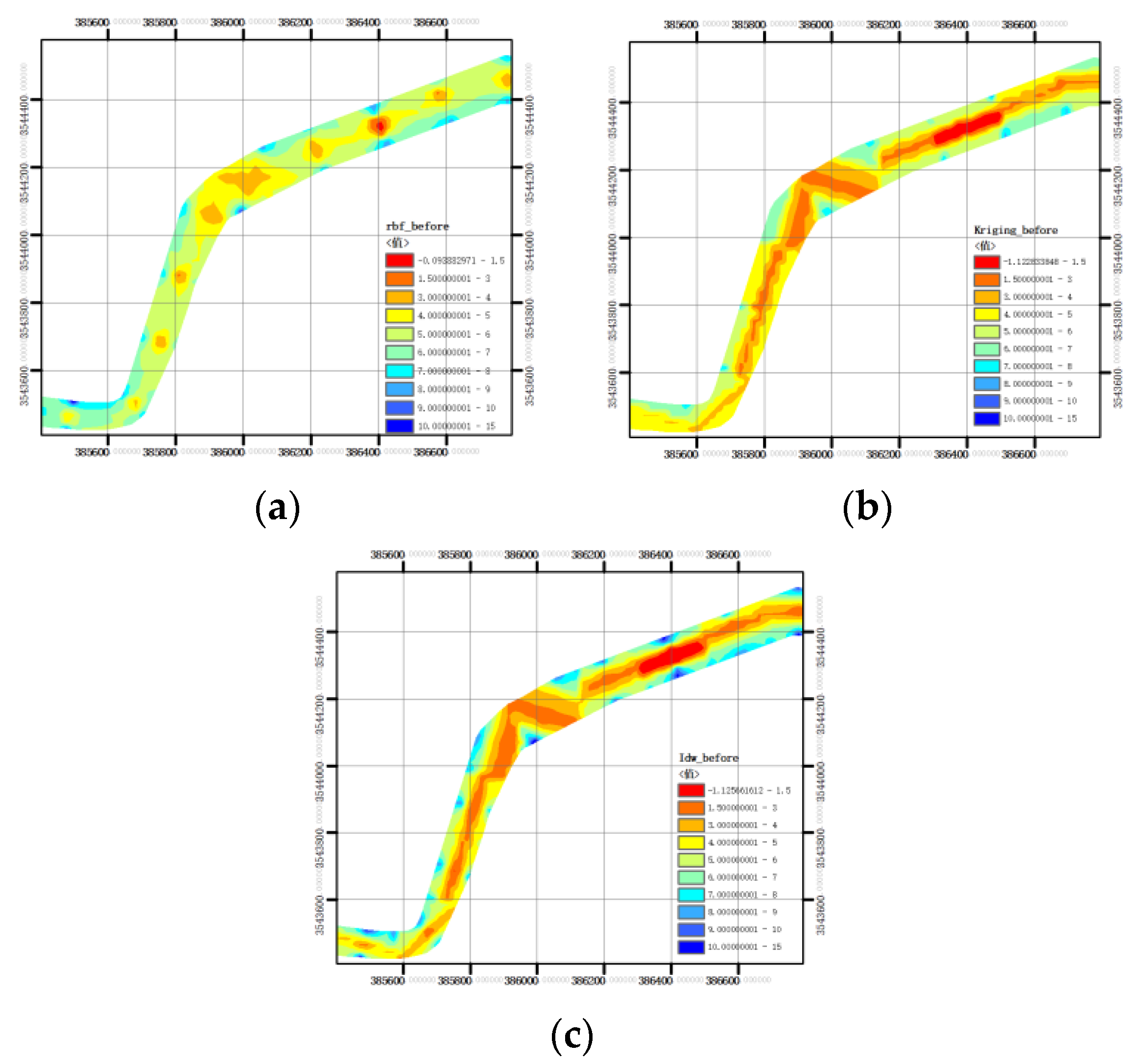
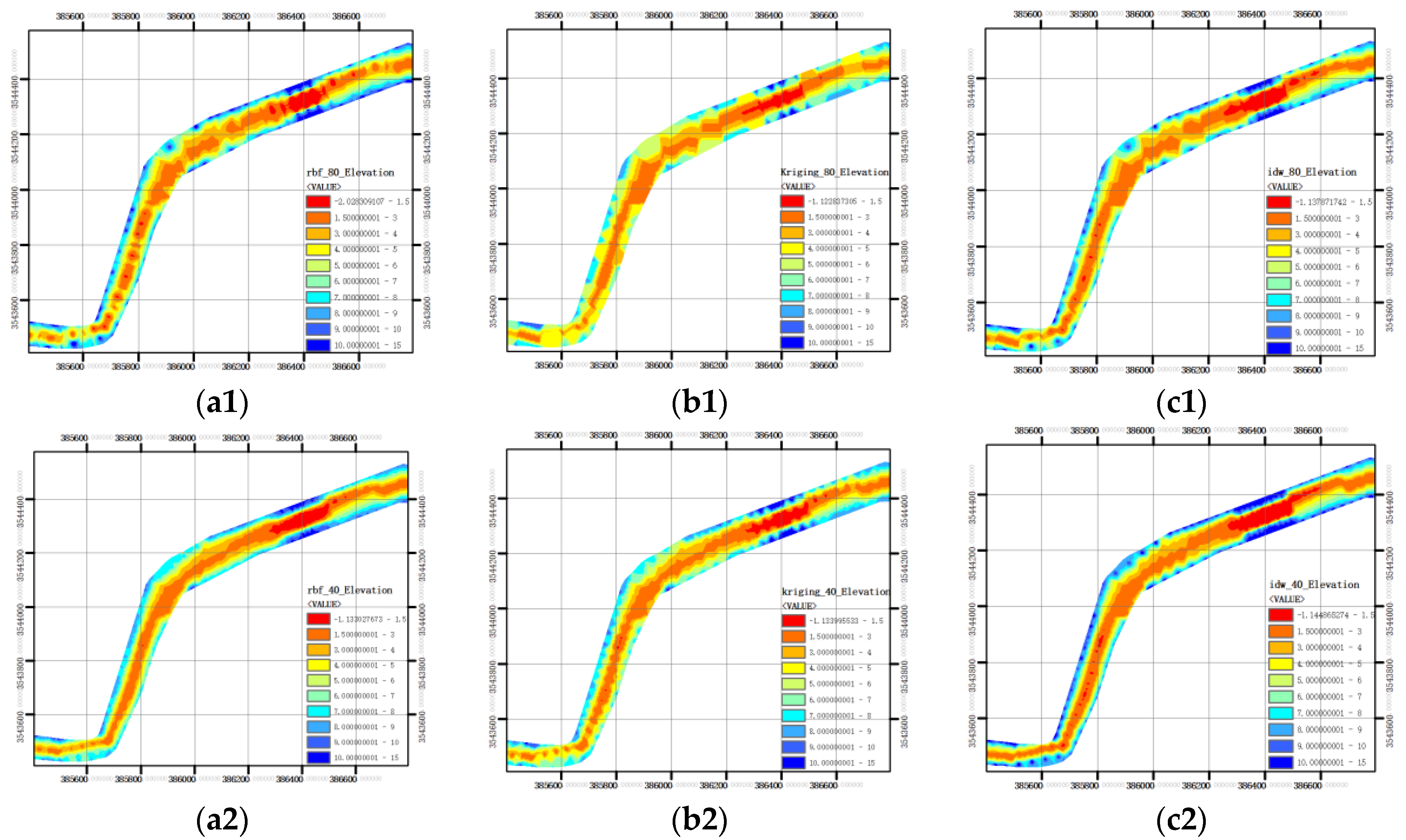
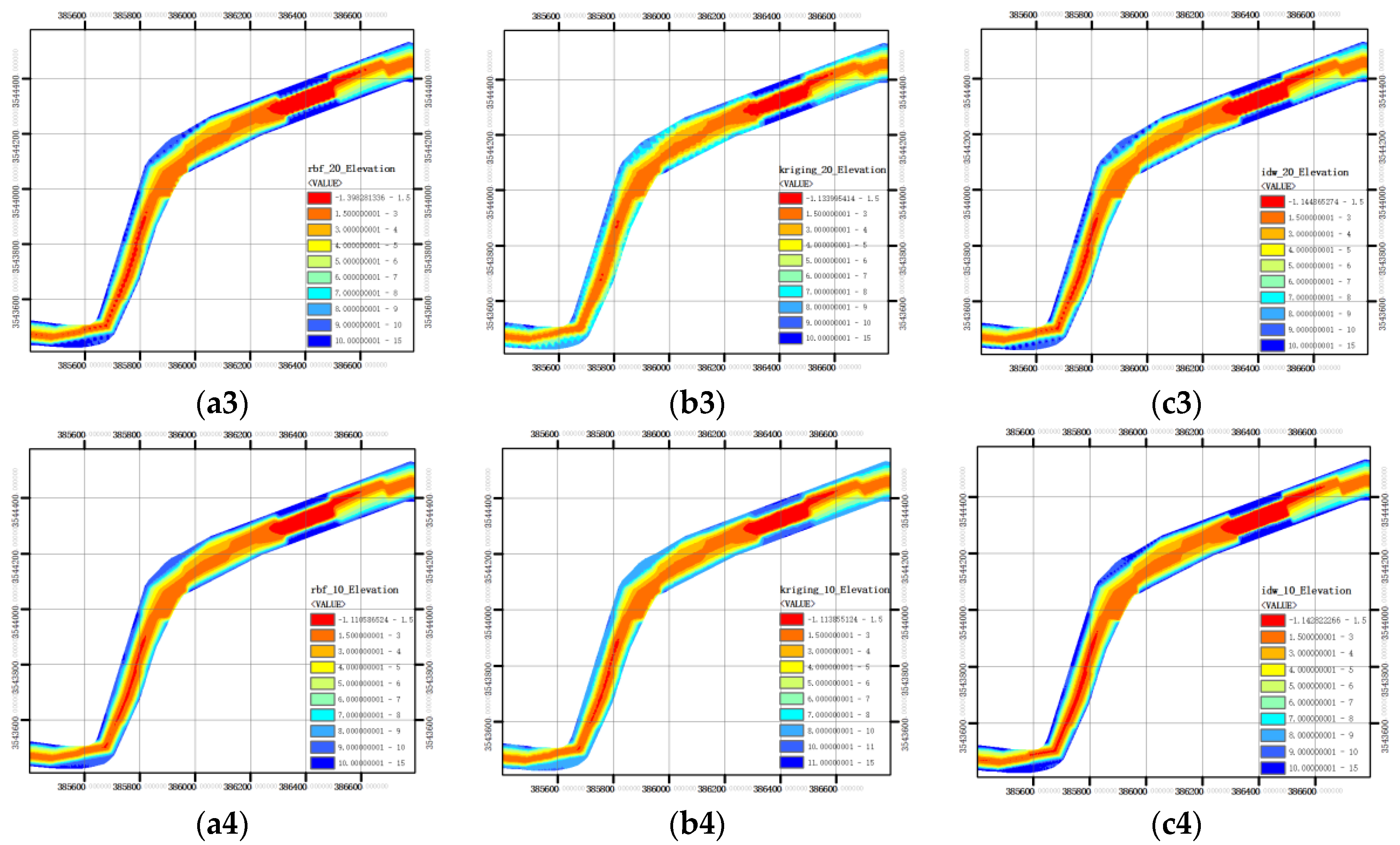
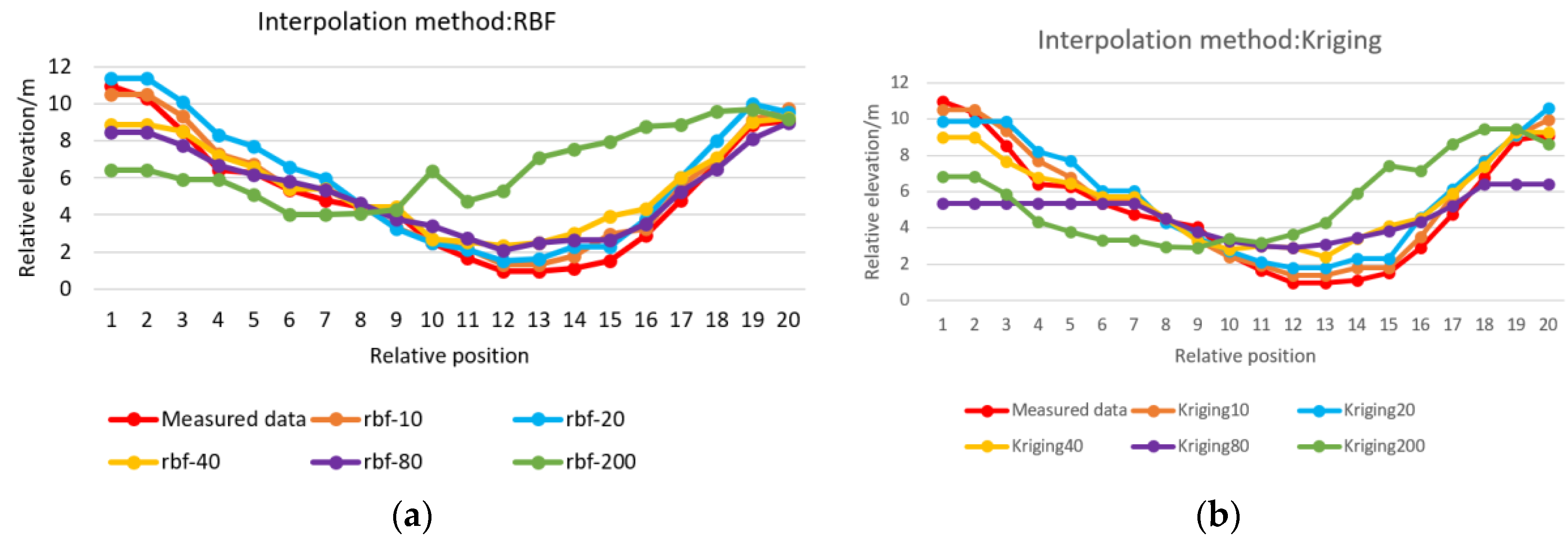
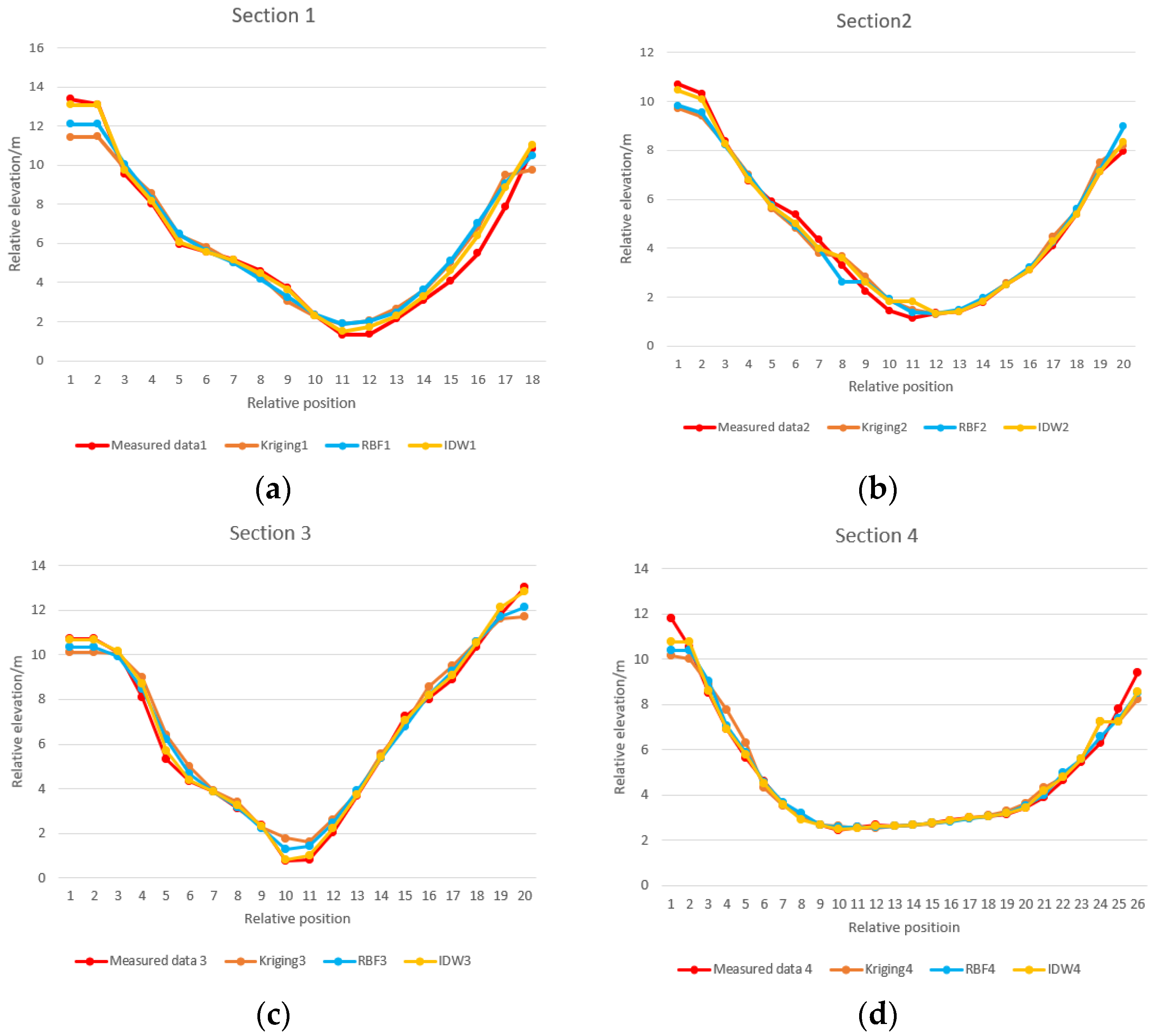
3.3.1. Influence of Section Densification on Spatial Modeling Results of Underwater Terrain
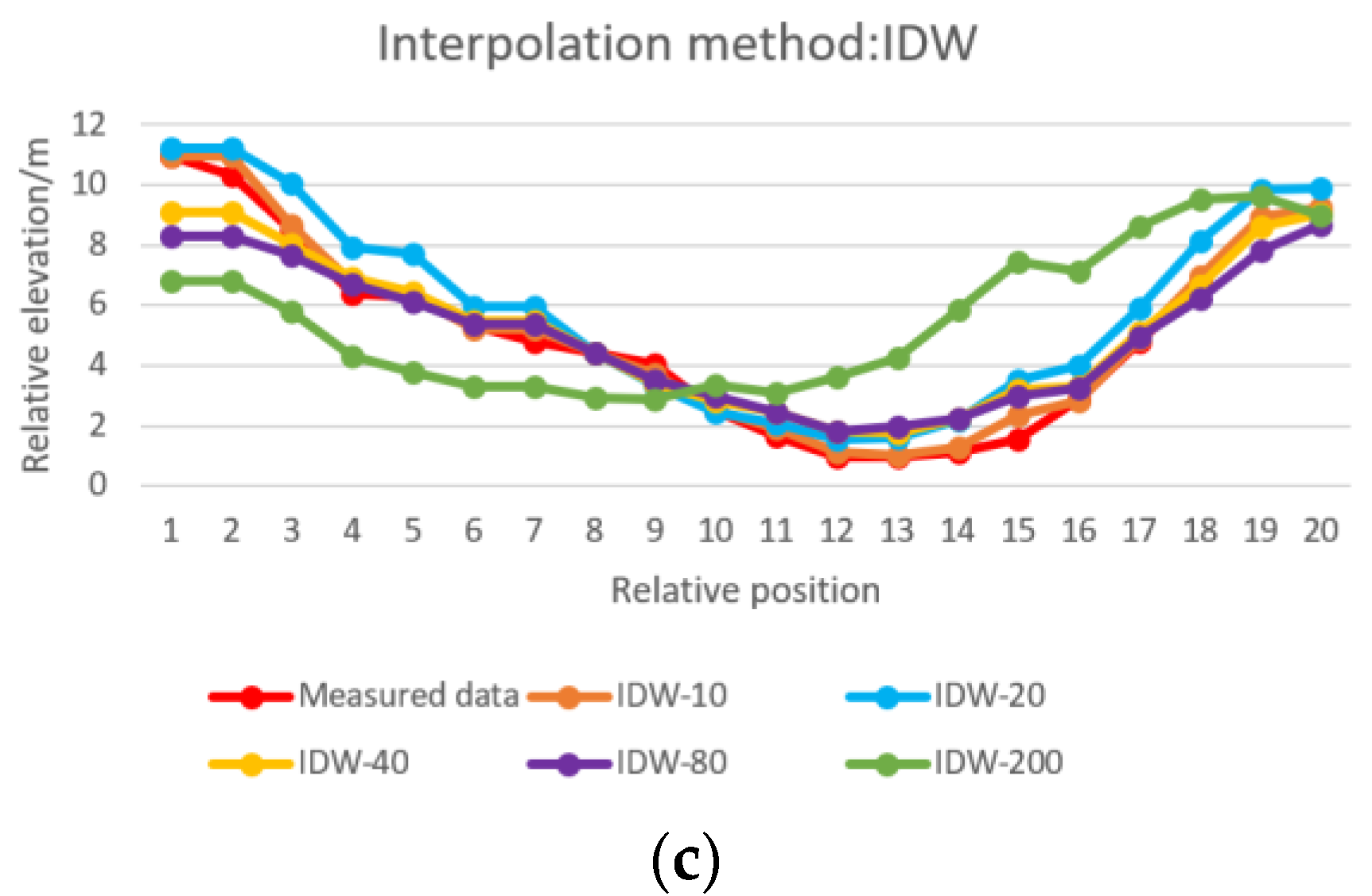
3.3.2. Influence of Section Spacing on Spatial Modeling Results of Underwater Terrain
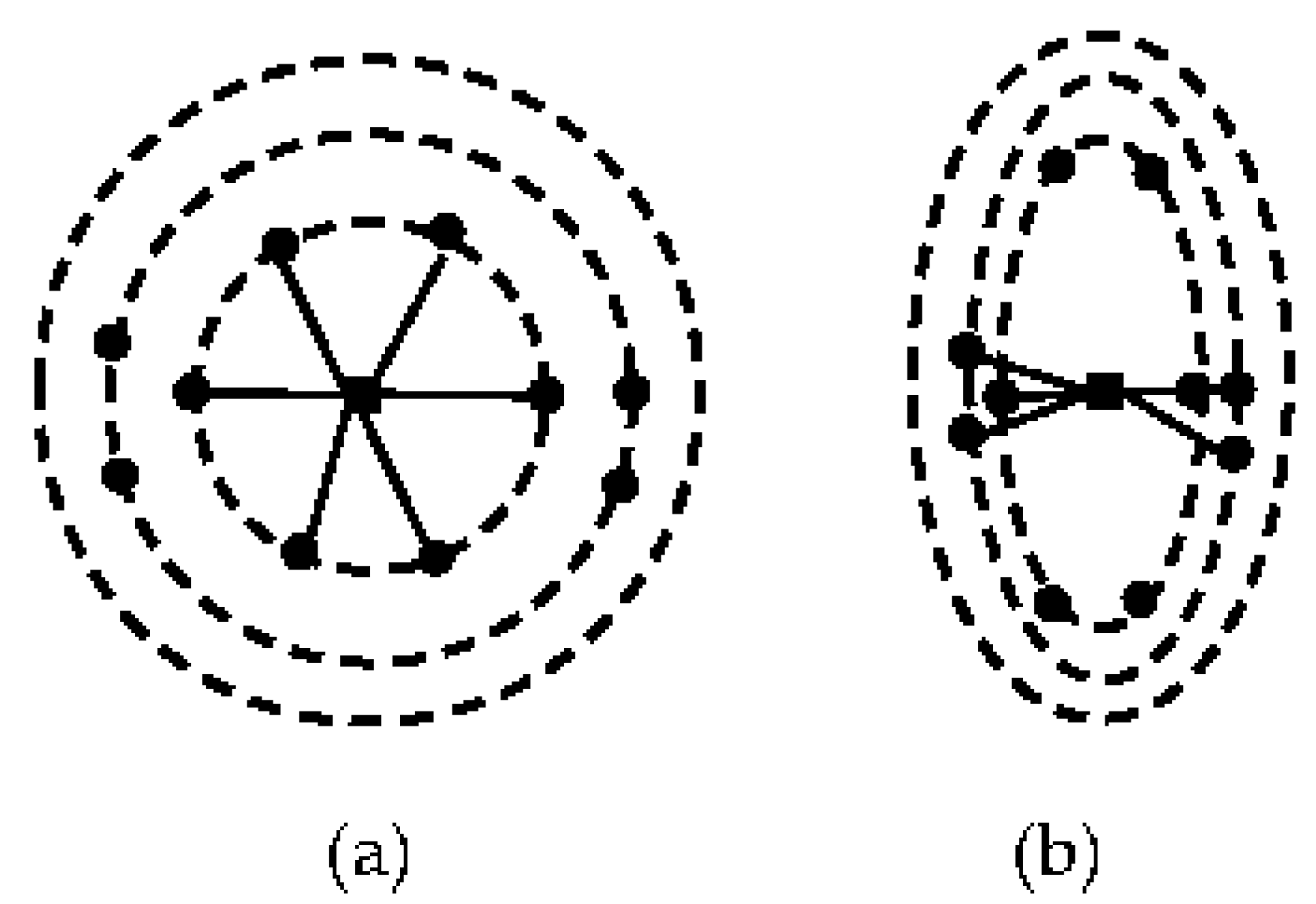
3.3.3. Influence of Anisotropy on Spatial Modeling Results of Underwater Terrain
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, K.; Jiang, C. Numerical Simulation Method and Application of Surface Water Environmental Impact Assessment; China Environment Publishing Group: Beijing, China, 2018; pp. 1–5. [Google Scholar]
- Clunies, G.J.; Mulligan, R.P.; Mallinson, D.J.; Walsh, J.P. Modeling hydrodynamics of large lagoons: Insights from the Albemarle-Pamlico Estuarine System. Estuar. Coast. Shelf Sci. 2017, 189, 90–103. [Google Scholar] [CrossRef]
- Shen, Y.; Diplas, P. Application of two- and three-dimensional computational fluid dynamics models to complex ecological stream flows. J. Hydrol. 2008, 348, 195–214. [Google Scholar] [CrossRef]
- Conner, J.T.; Tonina, D.; Company, I.P. Effect of cross-section interpolated bathymetry on 2D hydrodynamic model results in a large river. Earth Surf. Process. Landforms 2013, 475, 463–475. [Google Scholar] [CrossRef]
- Bonasia, R.; Ceragene, M. Hydraulic Numerical Simulations of La Sabana River Response Analysis. Water 2021, 13, 3516. [Google Scholar] [CrossRef]
- Eregno, F.E.; Tryland, I.; Tjomsland, T.; Kempa, M.; Heistad, A. Hydrodynamic modelling of recreational water quality using Escherichia colias an indicator of microbial contamination. J. Hydrol. 2018, 561, 179–186. [Google Scholar] [CrossRef]
- Li, Y.; Luo, Y. Research and Prospect of Numerical Simulation of River Water Environment Research and Prospect of Numerical Simulation of River Water Environment. IOP Conf. Ser. Earth Environ. Sci. 2021, 692, 2. [Google Scholar] [CrossRef]
- Ren, Y.; Sun, Z.; Zhou, W.; Zou, M. Construction and optimization of Irregular Triangulation Network for Canyon channel topographic data. Geospatial Inf. 2016, 14, 5–8. [Google Scholar] [CrossRef]
- Hou, M. River Terrain Reconstruction Based on Cellular Automata Method. Master’s Thesis, North China University of Water Resources and Electric Power, Zhengzhou, China, 2016. [Google Scholar]
- Chen, Z.; Xia, Y.; Wen, Y. A topographic interpolation method suitable for numerical simulation of river flow. In Proceedings of the 14th China Ocean (Shore) Engineering Symposium, Hohhot, China, 20 August 2009. [Google Scholar]
- Curtarelli, M.; Leão, J.; Ogashawara, I.; Lorenzzetti, J.; Stech, J. Assessment of Spatial Interpolation Methods to Map the Bathymetry of an Amazonian Hydroelectric Reservoir. ISPRS Int. J. Geo-Inf. 2015, 4, 220–235. [Google Scholar] [CrossRef]
- Amante, C.J.; Eakins, B.W.; Amante, C.J.; Eakins, B.W. Accuracy of Interpolated Bathymetry in Digital Elevation Models Accuracy of Interpolated Bathymetry in Digital Elevation Models. J. Coast. Res. 2016, 76, 123–133. [Google Scholar] [CrossRef]
- Kang, Y.; Ding, X.; Xu, F.; Zhang, C.; Ge, X. Topographic mapping on large-scale tidal flats with an iterative approach on the waterline method. Estuar. Coast. Shelf Sci. 2017, 190, 11–22. [Google Scholar] [CrossRef]
- Zhang, Y.; Xian, C.; Chen, H.; Grieneisen, M.L.; Liu, J.; Zhang, M. Spatial interpolation of river channel topography using the shortest temporal distance. J. Hydrol. 2016, 542, 450–462. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Kyriakidis, P.C. Spatial prediction of river channel topography by kriging. Earth Surf. Process. Landforms 2008, 867, 841–867. [Google Scholar] [CrossRef]
- Wu, C.; Mossa, J.; Mao, L.; Almulla, M.; Wu, C.; Mossa, J. Comparison of different spatial interpolation methods for historical hydrographic data of the lowermost Mississippi River. Ann. GIS. 2019, 25, 133–151. [Google Scholar] [CrossRef]
- Cai, S.; Xiao, G. Spatial variability analysis of precipitation anomaly point removal in Ningde City. J. China Hydrol. 2019, 39, 40–45. [Google Scholar] [CrossRef]
- Pu, Y.; Wang, R.; Luo, M.; Xu, Y.; Lin, Y. Comparison of Spatical Interpolation between Different Rainfall Levels: A Case Study of Rainfall in Nanchong City, Sichuan Province. J. China Hydrol. 2018, 38, 73–77. [Google Scholar]
- Bergonse, R.; Reis, E. Reconstructing pre-erosion topography using spatial interpolation techniques: A validation-based approach. J. Geogr. Sci. 2015, 25, 196–210. [Google Scholar] [CrossRef]
- Das, S. Extreme rainfall estimation at ungauged sites: Comparison between region-of-influence approach of regional analysis and spatial interpolation technique. Int. J. Climatol. 2018, 39, 407–423. [Google Scholar] [CrossRef]
- Zhao, K.; Cao, H.; Luo, P. Refined Pre-processing of Topography Data for 2D Numerical Simulation of River Channel. Yangtze River Sci. Res. Instig. 2021, 38, 16–19. [Google Scholar] [CrossRef]
- Jia, S.; Chen, Q.; Tang, L.; Dai, Z.; Zhang, L. A Method for Interpolating Digital Depth Model Based on Semiparametric Regression and Uncertainty Weighting. IOP Conf. Ser. Earth Environ. Sci. 2019, 237, 032001. [Google Scholar] [CrossRef]
- Duan, P. Anisotropy Radial Basis Function Spatial Interpolation Model Research for 3D Spatial Field. Acta Geod. Cartogr. Sin. 2018, 47, 1696. [Google Scholar] [CrossRef]
- Eriksson, M.; Siska, P.P. Understanding Anisotropy Computations 1. Math. Geol. 2000, 32, 683–700. [Google Scholar] [CrossRef]
- Zhu, S. Urban River Underwater Terrain Modeling and Research. Master’s Thesis, Hefie University of Technology, Hefei, China, 2016. [Google Scholar]
- Merwade, V.M.; Maidment, D.R.; Goff, J.A. Anisotropic considerations while interpolating river channel bathymetry. J. Hydrol. 2006, 331, 731–741. [Google Scholar] [CrossRef]
- Zhang, Y.; Hidalgo, J.; Parker, D. Impact of variability and anisotropy in the correlation decay distance for precipitation spatial interpolation in China. Clim. Res. 2017, 74, 81–93. [Google Scholar] [CrossRef]
- Yan, J.; Duan, X.; Zheng, W.; Liu, Y.; Deng, Y.; Hu, Z. An Adaptive IDW Algorithm Involving Spatial Heterogeneity. Geomatics Inf. Sci. Wuhan Univ. 2020, 45, 97–104. [Google Scholar] [CrossRef]
- Li, X.; Cao, C. The First Law of Geography and Spatial-Temporal Proximity. Chin. J. Nat. 2006, 29, 2969–2971. [Google Scholar] [CrossRef]
- Waseem, M.; Ajmal, M.; Kim, U.; Kim, T.-W. Development and evaluation of an extended inverse distance weighting method for stream flow estimation at an ungauged site. Hydrol. Res. 2016, 47, 333–343. [Google Scholar] [CrossRef]
- Duan, P.; Sheng, Y.; Li, J.; Lv, H.; Zhang, S. Adaptive IDW interpolation method and its application in the temperature field. Geogr. Res. 2014, 33, 1417–1426. [Google Scholar] [CrossRef]
- Yan, J.; Wu, B.; He, Q. An anisotropic IDW interpolation method with multiple parameters cooperative optimization. Acta Geod. Cartogr. Sin. 2021, 50, 675–684. [Google Scholar] [CrossRef]
| Spatial Interpolation Method | 200 m | 80 m | 40 m | 20 m | 10 m | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE (m) | RMSE (m) | MAE (m) | RMSE (m) | MAE (m) | RMSE (m) | MAE (m) | RMSE (m) | MAE (m) | RMSE (m) | |
| IDW | 2.46 | 2.87 | 0.77 | 1.01 | 0.62 | 0.80 | 0.91 | 1.05 | 0.21 | 0.30 |
| RBF | 3.00 | 3.70 | 0.82 | 1.03 | 0.86 | 1.12 | 0.90 | 1.12 | 0.50 | 0.38 |
| Kriging | 2.60 | 2.97 | 1.67 | 2.24 | 1.05 | 1.28 | 0.94 | 1.06 | 0.53 | 0.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.; Wang, B.; Sheng, Y.; Liu, C. Two-Step Simulation of Underwater Terrain in River Channel. Water 2022, 14, 3041. https://doi.org/10.3390/w14193041
Liang Y, Wang B, Sheng Y, Liu C. Two-Step Simulation of Underwater Terrain in River Channel. Water. 2022; 14(19):3041. https://doi.org/10.3390/w14193041
Chicago/Turabian StyleLiang, Yan, Bo Wang, Yehua Sheng, and Changqing Liu. 2022. "Two-Step Simulation of Underwater Terrain in River Channel" Water 14, no. 19: 3041. https://doi.org/10.3390/w14193041
APA StyleLiang, Y., Wang, B., Sheng, Y., & Liu, C. (2022). Two-Step Simulation of Underwater Terrain in River Channel. Water, 14(19), 3041. https://doi.org/10.3390/w14193041





