Influence of Data Length on the Determination of Data Adjustment Parameters in Conceptual Hydrological Modeling: A Case Study Using the Xinanjiang Model
Abstract
1. Introduction
1.1. Objectives
1.1.1. General Objective
1.1.2. Specific Objectives
- To introduce the parameter estimation method for model calibration considering the aridity index;
- To identify the variation of the model outputs over different data lengths and to decide the acceptable minimum data length using hypothesis analysis;
- To analyze the effectiveness of parameter estimation by removing the outliers in observed datasets with regression analysis.
2. Materials and Methods
2.1. Selection of Study Basins
2.2. Data Description
2.2.1. Doki River Basin
2.2.2. Data of U.S. Basins
2.3. Assessment of Performance of Model and Parameter Estimation for Data Analysis
2.3.1. The Functional Form of Aridity Index
2.3.2. Assessment of the Performance of the Model
2.4. XAJ Model Description
2.4.1. XAJ Model
2.4.2. Parameters of XAJ Model
2.4.3. Calibration of the XAJ Model
2.5. Evaluation of Model Performance by Efficiency Criteria
2.6. Application of Statistical Analysis
2.6.1. Hypothesis Analysis
2.6.2. Regression Analysis Approach
3. Results and Discussion
3.1. Estimation of Adjustment Parameter (Cep) Using Aridity Index
3.1.1. Annual Nash Results for the 28-Year Dataset
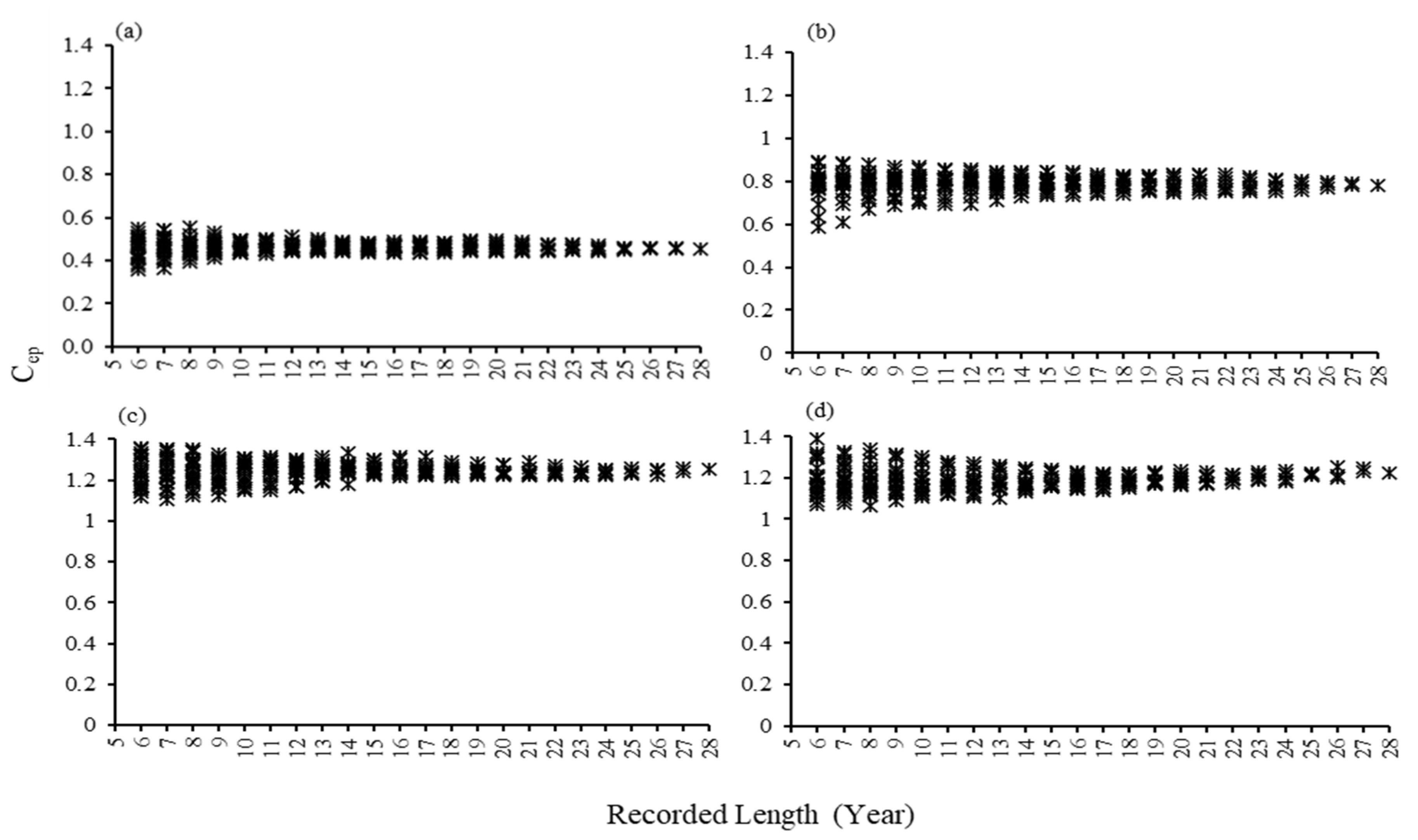
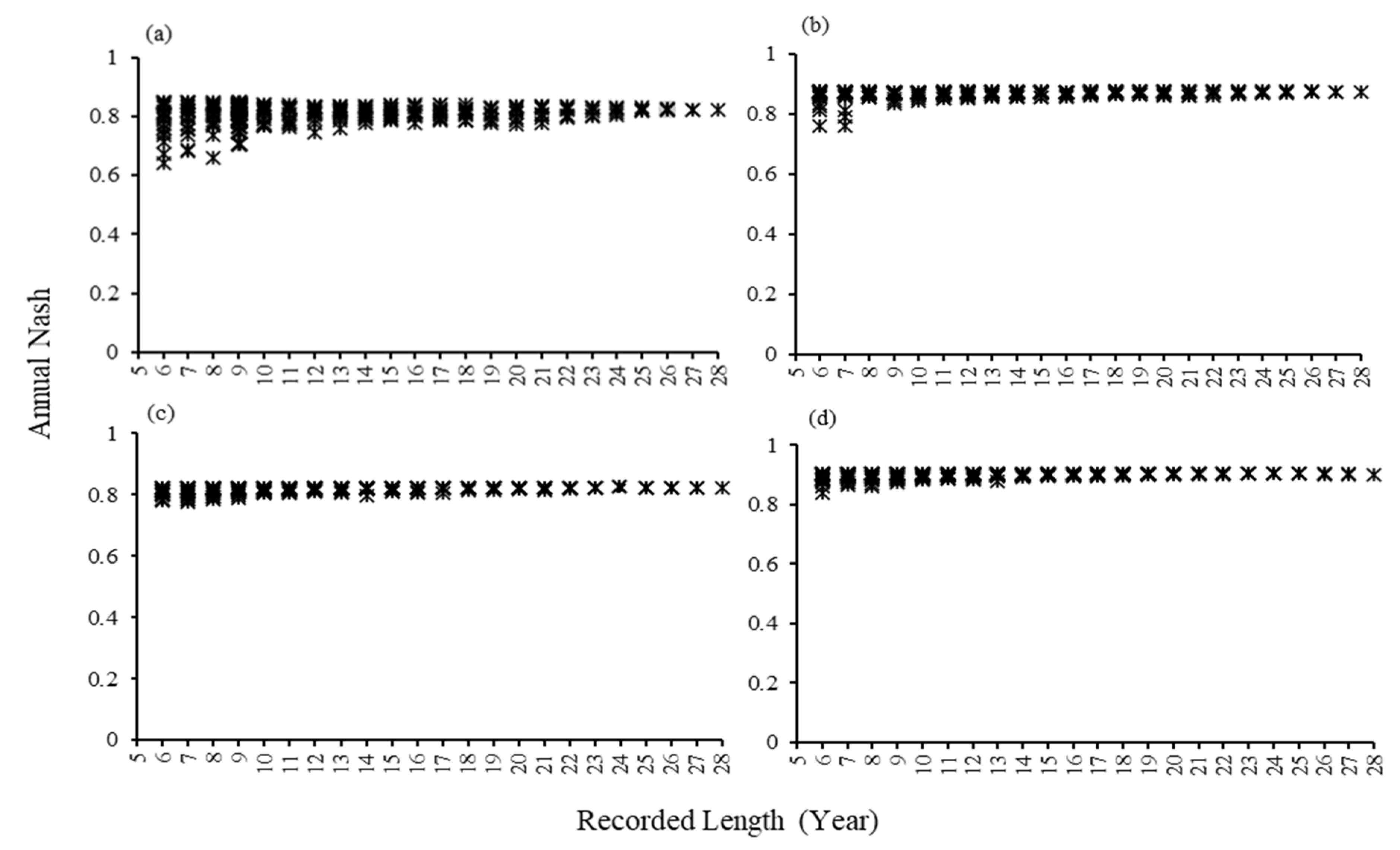
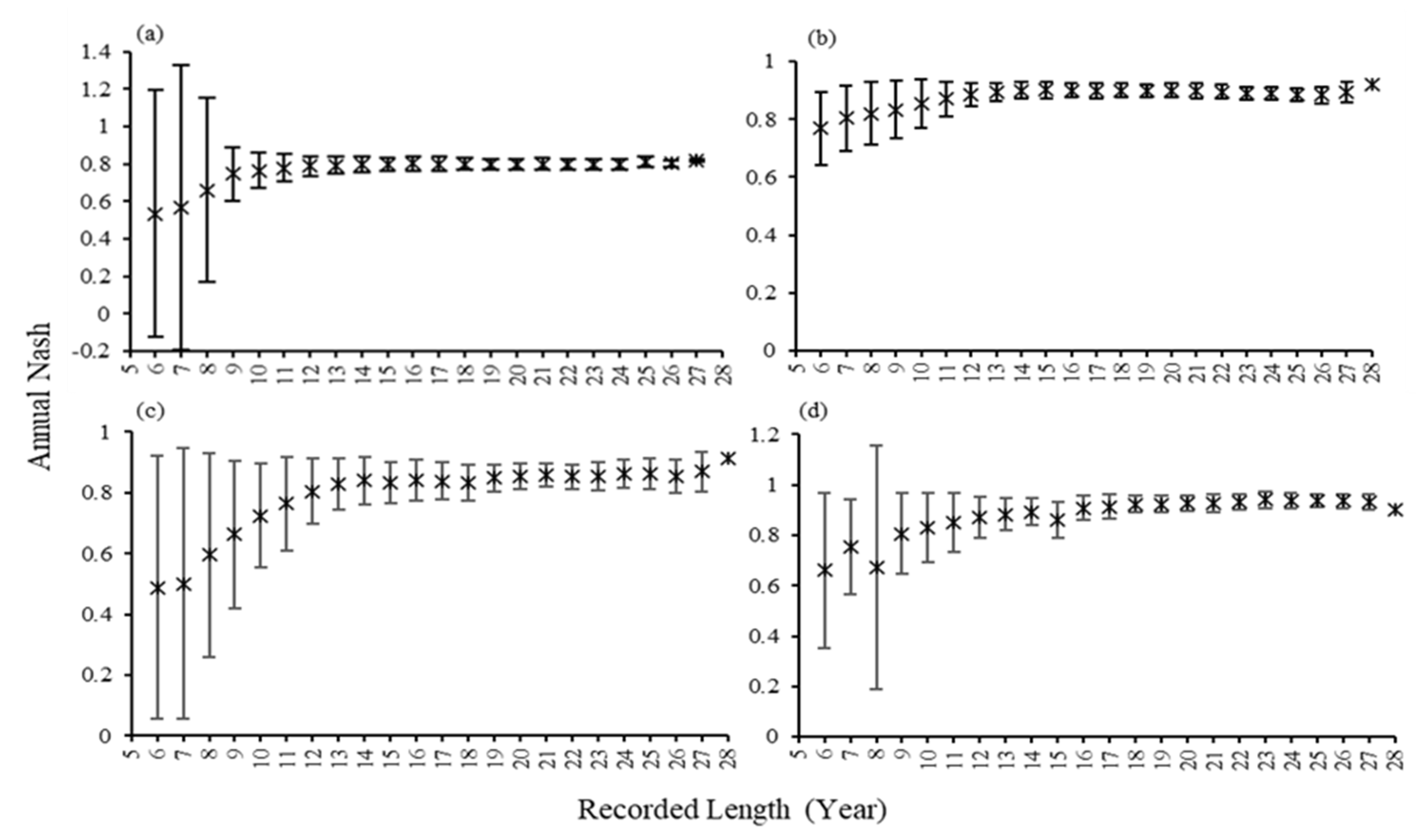
3.1.2. Annual Nash Results for Subsets
3.1.3. Comparative Evaluation of Nash Results between 28-Year Datasets and Subsets
3.1.4. Hypothesis Analysis over Subsets
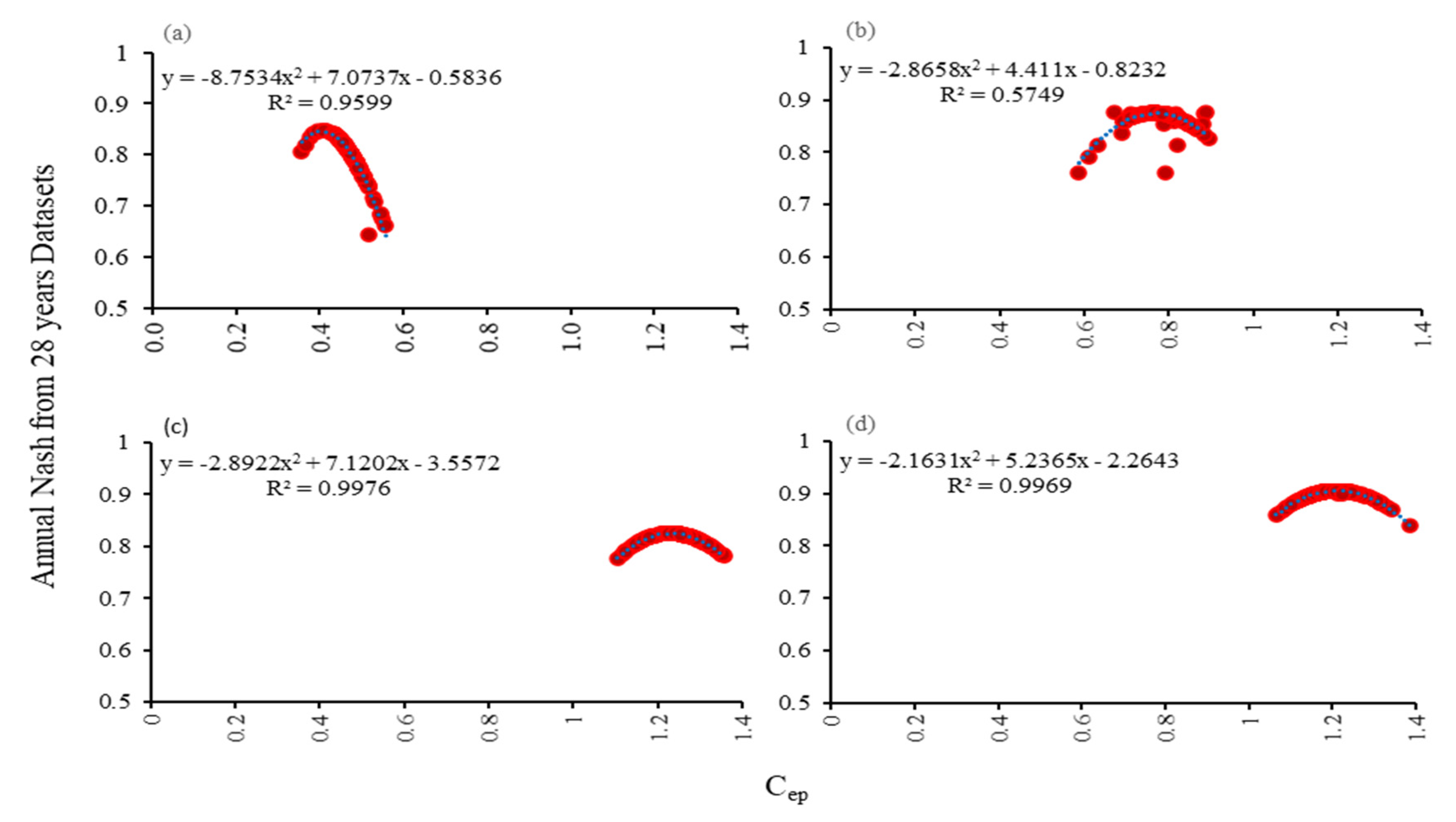
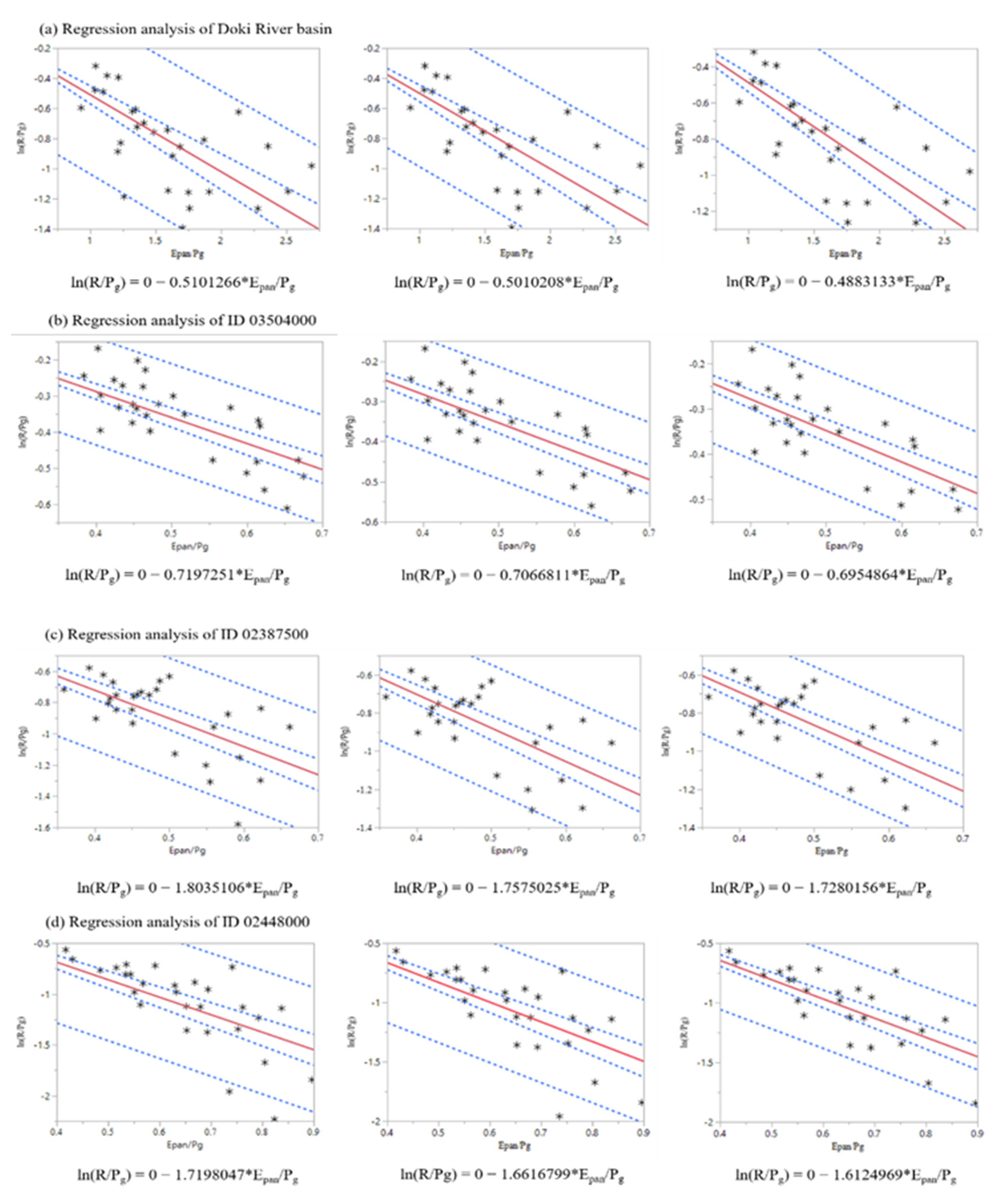
3.2. Analysis of the Impacts of Datasets Using Regression Analysis
3.2.1. Calculation of Simulated (Optimized Cep) in Four River Basins
3.2.2. Regression Analysis in the 28-year Dataset
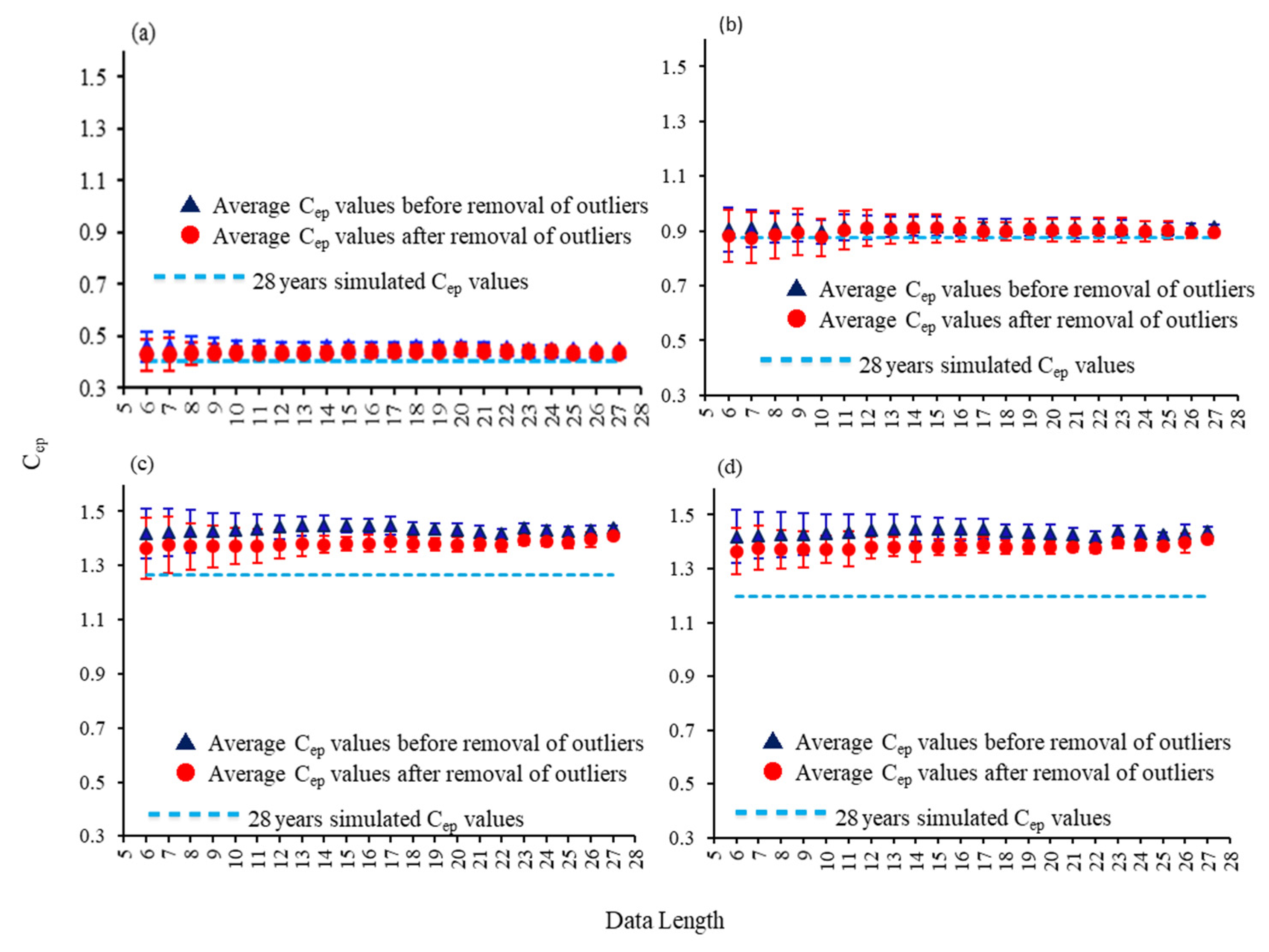
3.2.3. Regression Analysis in Subsets
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Perry, L.K. Water Resources Research Institute. Wyo. Univ. Water Resour. Res. Inst. Water Resour. Ser. 1974, 44, 4823–4839. [Google Scholar]
- Lidén, R.; Harlin, J. Analysis of conceptual rainfall–runoff modelling performance in different climates. J. Hydrol. 2000, 238, 231–247. [Google Scholar] [CrossRef]
- Jain, S.K.; Mani, P.; Jain, S.K.; Prakash, P.; Singh, V.P.; Tullos, D.; Kumar, S.; Agarwal, S.P.; Dimri, A.P. A Brief review of flood forecasting techniques and their applications. Int. J. River Basin Manag. 2018, 16, 329–344. [Google Scholar] [CrossRef]
- Ronco, P.; Gallina, V.; Torresan, S.; Zabeo, A.; Semenzin, E.; Critto, A.; Marcomini, A. The KULTURisk Regional Risk Assessment methodology for water-related natural hazards—Part 1: Physical–environmental assessment. Hydrol. Earth Syst. Sci. 2014, 18, 5399–5414. [Google Scholar] [CrossRef]
- Tingsanchali, T. Urban flood disaster management. Procedia Eng. 2012, 32, 25–37. [Google Scholar] [CrossRef]
- Cvetkovic, V.M.; Martinović, J. Innovative Solutions for Flood Risk Management. Int. J. Disaster Risk Manag. 2020, 2, 71–99. [Google Scholar] [CrossRef]
- Ming, X.; Liang, Q.; Xia, X.; Li, D.; Fowler, H.J. Real-Time Flood Forecasting Based on a High-Performance 2-D Hydrodynamic Model and Numerical Weather Predictions. Water Resour. Res. 2020, 56, e2019WR025583. [Google Scholar] [CrossRef]
- Dibike, Y.; Solomatine, D. River flow forecasting using artificial neural networks. Phys. Chem. Earth Part B Hydrol. Ocean. Atmos. 2001, 26, 1–7. [Google Scholar] [CrossRef]
- Todini, E. Hydrological catchment modelling: Past, present and future. Hydrol. Earth Syst. Sci. 2007, 11, 468–482. [Google Scholar] [CrossRef]
- Nayak, P.; Venkatesh, B.; Krishna, B.; Jain, S.K. Rainfall-runoff modeling using conceptual, data driven, and wavelet based computing approach. J. Hydrol. 2013, 493, 57–67. [Google Scholar] [CrossRef]
- Chen, H.; Xu, C.-Y.; Guo, S. Comparison and evaluation of multiple GCMs, statistical downscaling and hydrological models in the study of climate change impacts on runoff. J. Hydrol. 2012, 434–435, 36–45. [Google Scholar] [CrossRef]
- Hapuarachchi, H.A.P.; Li, Z.; Wang, S. Application of SCE-UA Method for Calibrating the Xinanjiang Watershed Model. J. Lake Sci. 2001, 13, 304–314. [Google Scholar] [CrossRef][Green Version]
- Perrin, C.; Oudin, L.; Andréassian, V.; Serna, C.R.; Michel, C.; Mathevet, T. Impact of limited streamflow data on the efficiency and the parameters of rainfall—Runoff models. Hydrol. Sci. J. 2007, 52, 131–151. [Google Scholar] [CrossRef]
- Li, X.; Lu, M. Multi-step Optimization of Parameters in the Xinanjiang Model Taking into Account Their Time Scale Dependency. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2012, 68, I_145–I_150. [Google Scholar] [CrossRef]
- Bloschl, G.; Reszler, C.; Komma, J. A spatially distributed flash flood forecasting model. Environ. Model. Softw. 2008, 23, 464–478. [Google Scholar] [CrossRef]
- Niemczynowicz, J. Urban hydrology and water management—Present and future challenges. Urban Water 1999, 1, 1–14. [Google Scholar] [CrossRef]
- Krajewski, W.; Smith, J. Radar hydrology: Rainfall estimation. Adv. Water Resour. 2002, 25, 1387–1394. [Google Scholar] [CrossRef]
- Yan, K.; Di Baldassarre, G.; Solomatine, D.P.; Schumann, G.J. A review of low-cost space-borne data for flood modelling: Topography, flood extent and water level. Hydrol. Process. 2015, 29, 3368–3387. [Google Scholar] [CrossRef]
- Al-Sabhan, W.; Mulligan, M.; Blackburn, G. A real-time hydrological model for flood prediction using GIS and the WWW. Comput. Environ. Urban Syst. 2003, 27, 9–32. [Google Scholar] [CrossRef]
- Brath, A.; Montanari, A.; Toth, E. Analysis of the effects of different scenarios of historical data availability on the calibration of a spatially-distributed hydrological model. J. Hydrol. 2004, 291, 232–253. [Google Scholar] [CrossRef]
- Pappenberger, F.; Thielen, J.; Del Medico, M. The impact of weather forecast improvements on large scale hydrology: Analysing a decade of forecasts of the European Flood Alert System. Hydrol. Process. 2011, 25, 1091–1113. [Google Scholar] [CrossRef]
- Sorooshian, S.; Gupta, V.K.; Fulton, J.L. Evaluation of Maximum Likelihood Parameter estimation techniques for conceptual rainfall-runoff models: Influence of calibration data variability and length on model credibility. Water Resour. Res. 1983, 19, 251–259. [Google Scholar] [CrossRef]
- Li, C.Z.; Wang, H.; Liu, J.; Yan, D.H.; Yu, F.L.; Zhang, L. Effect of calibration data series length on performance and optimal parameters of hydrological model. Water Sci. Eng. 2010, 3, 378–393. [Google Scholar] [CrossRef]
- Finger, D.; Vis, M.; Huss, M.; Seibert, J. The value of multiple data set calibration versus model complexity for improving the performance of hydrological models in mountain catchments. Water Resour. Res. 2015, 51, 1939–1958. [Google Scholar] [CrossRef]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2019, 236, 111402. [Google Scholar] [CrossRef]
- Hughes, D.; Kapangaziwiri, E.; Sawunyama, T. Hydrological model uncertainty assessment in southern Africa. J. Hydrol. 2010, 387, 221–232. [Google Scholar] [CrossRef]
- Chen, L.; Xu, J.; Wang, G.; Shen, Z. Comparison of the multiple imputation approaches for imputing rainfall data series and their applications to watershed models. J. Hydrol. 2019, 572, 449–460. [Google Scholar] [CrossRef]
- Güntner, A. Improvement of Global Hydrological Models Using GRACE Data. Surv. Geophys. 2008, 29, 375–397. [Google Scholar] [CrossRef]
- Hattermann, F.F.; Krysanova, V.; Gosling, S.N.; Dankers, R.; Daggupati, P.; Donnelly, C.; Flörke, M.; Huang, S.; Motovilov, Y.; Buda, S.; et al. Cross-scale intercomparison of climate change impacts simulated by regional and global hydrological models in eleven large river basins. Clim. Chang. 2017, 141, 561–576. [Google Scholar] [CrossRef]
- Winsemius, H.C.; Schaefli, B.; Montanari, A.; Savenije, H.H.G. On the calibration of hydrological models in ungauged basins: A framework for integrating hard and soft hydrological information. Water Resour. Res. 2009, 45, e2009wr007706. [Google Scholar] [CrossRef]
- Pellicciotti, F.; Buergi, C.; Immerzeel, W.W.; Konz, M.; Shrestha, A.B. Challenges and Uncertainties in Hydrological Modeling of Remote Hindu Kush–Karakoram–Himalayan (HKH) Basins: Suggestions for Calibration Strategies. Mt. Res. Dev. 2012, 32, 39–50. [Google Scholar] [CrossRef]
- Harlin, J. Development of a Process Oriented Calibration Scheme for the HBV Hydrological Model. Hydrol. Res. 1991, 22, 15–36. [Google Scholar] [CrossRef]
- Yapo, P.O.; Gupta, H.V.; Sorooshian, S. Automatic calibration of conceptual rainfall-runoff models: Sensitivity to calibration data. J. Hydrol. 1996, 181, 23–48. [Google Scholar] [CrossRef]
- Gan, T.Y.; Biftu, G.F. Automatic Calibration of Conceptual Rainfall-Runoff Models: Optimization Algorithms, Catchment Conditions, and Model Structure. Water Resour. Res. 1996, 32, 3513–3524. [Google Scholar] [CrossRef]
- Huang, Q.; Qin, G.; Zhang, Y.; Tang, Q.; Liu, C.; Xia, J.; Chiew, F.H.S.; Post, D. Using Remote Sensing Data-Based Hydrological Model Calibrations for Predicting Runoff in Ungauged or Poorly Gauged Catchments. Water Resour. Res. 2020, 56, e2020WR028205. [Google Scholar] [CrossRef]
- Anctil, F.; Perrin, C.; Andréassian, V. Impact of the length of observed records on the performance of ANN and of conceptual parsimonious rainfall-runoff forecasting models. Environ. Model. Softw. 2004, 19, 357–368. [Google Scholar] [CrossRef]
- Boughton, W. Large sample basin experiments for hydrological model parameterization: Results of the model parameter experiment—MOPEX. Aust. J. Water Resour. 2007, 11, 119–120. [Google Scholar]
- Beven, K. Rainfall-Runoff Modelling: The Primer; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Lu, M. Recent and future studies of the Xinanjiang Model. J. Hydraul. Eng. 2021, 52, 432–441. [Google Scholar] [CrossRef]
- Azida, A.; Bakar, A.B.U.; Lu, M. Effects of temporal resolution on river flow forecasting with simple interception model within a distributed hydrological model. Int. J. Res. Rev. Appl. Sci. 2011, 8, 5–13. [Google Scholar]
- Duan, Q.; Schaake, J.; Andréassian, V.; Franks, S.; Goteti, G.; Gupta, H.; Gusev, Y.; Habets, F.; Hall, A.; Hay, L.; et al. Model Parameter Estimation Experiment (MOPEX): An overview of science strategy and major results from the second and third workshops. J. Hydrol. 2006, 320, 3–17. [Google Scholar] [CrossRef]
- Arora, V.K. The use of the aridity index to assess climate change effect on annual runoff. J. Hydrol. 2002, 265, 164–177. [Google Scholar] [CrossRef]
- Quan, C.; Han, S.; Utescher, T.; Zhang, C.; Liu, Y.-S. Validation of temperature–precipitation based aridity index: Paleoclimatic implications. Palaeogeogr. Palaeoclim. Palaeoecol. 2013, 386, 86–95. [Google Scholar] [CrossRef]
- Li, X.; Lu, M. Application of Aridity Index in Estimation of Data Adjustment Parameters in the Xinanjiang Model, Jstage.Jst.Go.Jp. 58. 2014. Available online: https://www.jstage.jst.go.jp/article/jscejhe/70/4/70_28/_article/-char/ja/ (accessed on 25 June 2022).
- Schreiber, P. About the relationship between precipitation and the flow of water in rivers in Central Europe. Z. Meteorol. 1904, 21, 441–452. (In German) [Google Scholar]
- Budyko, M.I. Evaporation under Natural Conditions, Gidrometeorizdat, Leningrad; IPST: Jerusalem, Israel, 1948; Volume 635. [Google Scholar]
- Zhao, R.-J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Kyi, K.H.; Lu, M.; Li, X. Development of a user-friendly web-based rainfall-runoff model. Hydrol. Res. Lett. 2016, 10, 8–14. [Google Scholar] [CrossRef]
- Zhao, R.J.; Liu, X.R. The Xinanjiang Model. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Highlands Ranch, CO, USA, 1995; pp. 215–232. [Google Scholar]
- Rahman, M.M.; Lu, M.; Kyi, K.H. Variability of soil moisture memory for wet and dry basins. J. Hydrol. 2015, 523, 107–118. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Schaefli, B.; Gupta, H.V. Do Nash values have value? Hydrol. Process. 2007, 21, 2075–2080. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Pfister, L.; Kirchner, J.W. Debates-Hypothesis testing in hydrology: Theory and practice. Water Resour. Res. 2017, 53, 1792–1798. [Google Scholar] [CrossRef]
- Naghettini, M. (Ed.) Fundamentals of Statistical Hydrology; Springer: Berlin, Germany, 2017. [Google Scholar] [CrossRef]
- Stevens, J.P. Outliers and influential data points in regression analysis. Psychol. Bull. 1984, 95, 334–344. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Knudsen, J. Operational Validation and Intercomparison of Different Types of Hydrological Models. Water Resour. Res. 1996, 32, 2189–2202. [Google Scholar] [CrossRef]
- Lu, M.; Li, X. Time scale dependent sensitivities of the XinAnJiang model parameters. Hydrol. Res. Lett. 2014, 8, 51–56. [Google Scholar] [CrossRef]
- Colla, V.; Vannucci, M. Outlier Detection Methods for Industrial Applications. In Advances in Robotics, Automation and Control; BoD-Books on Demand: Norderstedt, Germany, 2008. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.K.-V. Computing Surveys (CSUR), Undefined 2009, Anomaly Detection: A Survey, Dl.Acm.Org. 2009. Available online: https://dl.acm.org/doi/abs/10.1145/1541880.1541882 (accessed on 25 June 2022).



| MOPEX ID | Location | Drainage Area (km2) | Data Length (Year) | Mean Precipitation (mm/Year) | Mean Potential Evaporation (mm/Year) | ||
|---|---|---|---|---|---|---|---|
| Long. | Lat. | State | |||||
| Doki | 34.29 | 133.81 | Kagawa, Japan | 106.8 | 28 | 1200 | 1700 |
| 03504000 | −83.62 | 35.13 | NC | 135 | 28 | 1893 | 762 |
| 02387500 | −84.94 | 34.58 | GA | 4144 | 28 | 1480 | 901 |
| 02448000 | −88.56 | 33.10 | MS | 1989 | 28 | 1421 | 1057 |
| MOPEX ID | Mean Precipitation (mm/Year) | Median Precipitation (mm/Year) | Minimum Precipitation (mm/Year) | Maximum Precipitation (mm/Year) | Standard Deviation |
|---|---|---|---|---|---|
| Doki | 1200 | 1344 | 821 | 2290 | 358 |
| 03504000 | 1893 | 2052 | 1427 | 4425 | 571 |
| 02387500 | 1480 | 1481 | 1047 | 1931 | 228 |
| 02448000 | 1421 | 1345 | 979 | 2102 | 290 |
| Parameter | Physical Meaning | Range | Pre-Optimized Values | |||
|---|---|---|---|---|---|---|
| Group I | Doki River Basin | MOPEX ID: 3504000 | MOPEX ID: 2387500 | MOPEX ID: 2448000 | ||
| Cp | The ratio of measured precipitation to actual precipitation | 0.8–1.2 | 1 | 1 | 1 | 1 |
| Cep | The ratio of potential evapotranspiration to pan evaporation | 0.8–1.2 | 0.4436 | 0.7908 | 1.25 | 1.2016 |
| Group II | ||||||
| S.M. | Areal mean free water capacity of the surface soil layer (mm) | 1–50 | 20 | 40 | 30 | 50 |
| EX | The areal mean of the free water capacity of the surface soil layer (mm) | 0.5–2.5 | 1.5 | 1.2 | 0.5 | 0.5 |
| KI | Outflow coefficients of the free water storage to interflow | 0–0.7; KI + KG = 0.7 | 0.4 | 0.1 | 0.3 | 0.55 |
| KG | Outflow coefficients of the free water storage to groundwater | 0–0.7; KI + KG = 0.7 | 0.3 | 0.6 | 0.4 | 0.15 |
| Cs | Recession constant of the lower interflow storage | 0.5–0.9 | 0.0098 | 0.6 | 0.85 | 0.758 |
| Ci | Recession constant for the lower interflow storage | 0.5–0.9 | 0.5 | 0.9 | 0.75 | 0.8 |
| Cg | Daily recession constant of groundwater storage | 0.9835–0.998 | 0.99 | 0.982 | 0.989 | 0.984 |
| Group III | ||||||
| b | Exponent of the tension water capacity curve | 0.1–0.3 | 0.25 | 0.3 | 0.15 | 0.15 |
| imp | Ratio of the impervious to the total area of the basin | 0–0.005 | 0.02 | 0.02 | 0.01 | 0.01 |
| WUM | Water capacity in the upper soil layer (mm) | 5–20 | 20 | 20 | 20 | 20 |
| WLM | Water capacity in the lower soil layer (mm) | 60–90 | 90 | 80 | 80 | 80 |
| WDM | Water capacity in the deeper soil layer (mm) | 10–100 | 80 | 60 | 160 | 160 |
| C | Coefficient of deep evapotranspiration | 0.1–0.3 | 0.1 | 0.15 | 0.15 | 0.15 |
| Recorded Year (n) | (i = 1, 2, 3, …, 28) | Numbers of Subsets [(28 − n) + 1] | |
|---|---|---|---|
| Year Start | Year End | ||
| 6 | 23 | ||
| 7 | 22 | ||
| 8 | 21 | ||
| ⋮ | ⋮ | ||
| 26 | 3 | ||
| 27 | 2 | ||
| 28 | 1 | ||
| Cep | ||||
|---|---|---|---|---|
| Regression Analysis | Doki River Basin | Basin ID 3504000 | Basin ID 2387500 | Basin ID 2448000 |
| Cep in First Stage | 0.444 | 0.828 | 2.074 | 1.978 |
| Cep in Second Stage | 0.436 | 0.813 | 2.018 | 1.911 |
| Cep in Third Stage | 0.425 | 0.800 | 1.987 | 1.854 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zin, T.T.; Lu, M. Influence of Data Length on the Determination of Data Adjustment Parameters in Conceptual Hydrological Modeling: A Case Study Using the Xinanjiang Model. Water 2022, 14, 3012. https://doi.org/10.3390/w14193012
Zin TT, Lu M. Influence of Data Length on the Determination of Data Adjustment Parameters in Conceptual Hydrological Modeling: A Case Study Using the Xinanjiang Model. Water. 2022; 14(19):3012. https://doi.org/10.3390/w14193012
Chicago/Turabian StyleZin, Thandar Tun, and Minjiao Lu. 2022. "Influence of Data Length on the Determination of Data Adjustment Parameters in Conceptual Hydrological Modeling: A Case Study Using the Xinanjiang Model" Water 14, no. 19: 3012. https://doi.org/10.3390/w14193012
APA StyleZin, T. T., & Lu, M. (2022). Influence of Data Length on the Determination of Data Adjustment Parameters in Conceptual Hydrological Modeling: A Case Study Using the Xinanjiang Model. Water, 14(19), 3012. https://doi.org/10.3390/w14193012






