Risk Propagation Evolution Analysis of Oil and Gas Leakage in FPSO Oil and Gas Processing System by Mapping Bow-Tie into Directed Weighted Complex Network
Abstract
:1. Introduction
1.1. Literature Review
- Compared with traditional methods such as FTA, ETA, and BN, adjacency matrices in CN can more effectively represent and analyze complex correlations between hazardous events, which is beneficial for risk mitigation.
- The method under CN theory is highly scalable. Most of the risk scenarios studied by traditional methods are limited by existing accident reports. However, in this study, CN can be combined with a path-planning algorithm to simulate the risk propagation paths in various scenarios and solve the shortest propagation paths with different consequences under various initial trigger factors.
- There are more quantitative analysis perspectives under CN theory that can be used to evaluate hazardous events, such as degree distribution, degree correlation coefficient, betweenness, average path length, eigenvector, clustering coefficient, etc., which are not available in traditional risk analysis methods.
1.2. Innovative Contribution
- A model based on a BT model mapped to CN is explored to deal with the evolution method of fire and explosion accidents caused by oil and gas leakage in FPSO oil and gas processing systems.
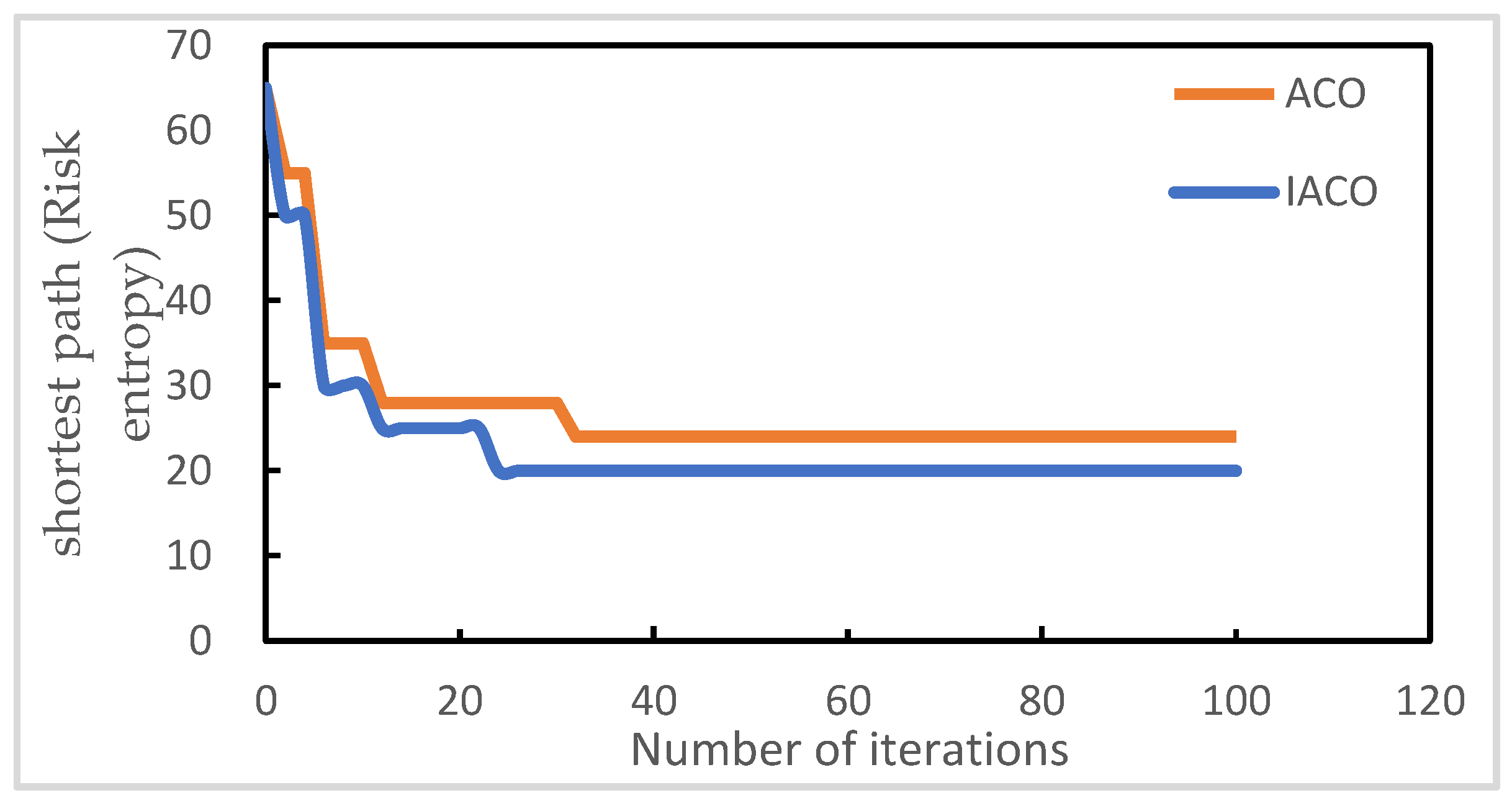
- A shortest path planning algorithm based on risk graph theory is proposed, i.e., an IACO algorithm, which is extended to solve the shortest path problem with uncertainty.
1.3. Organization
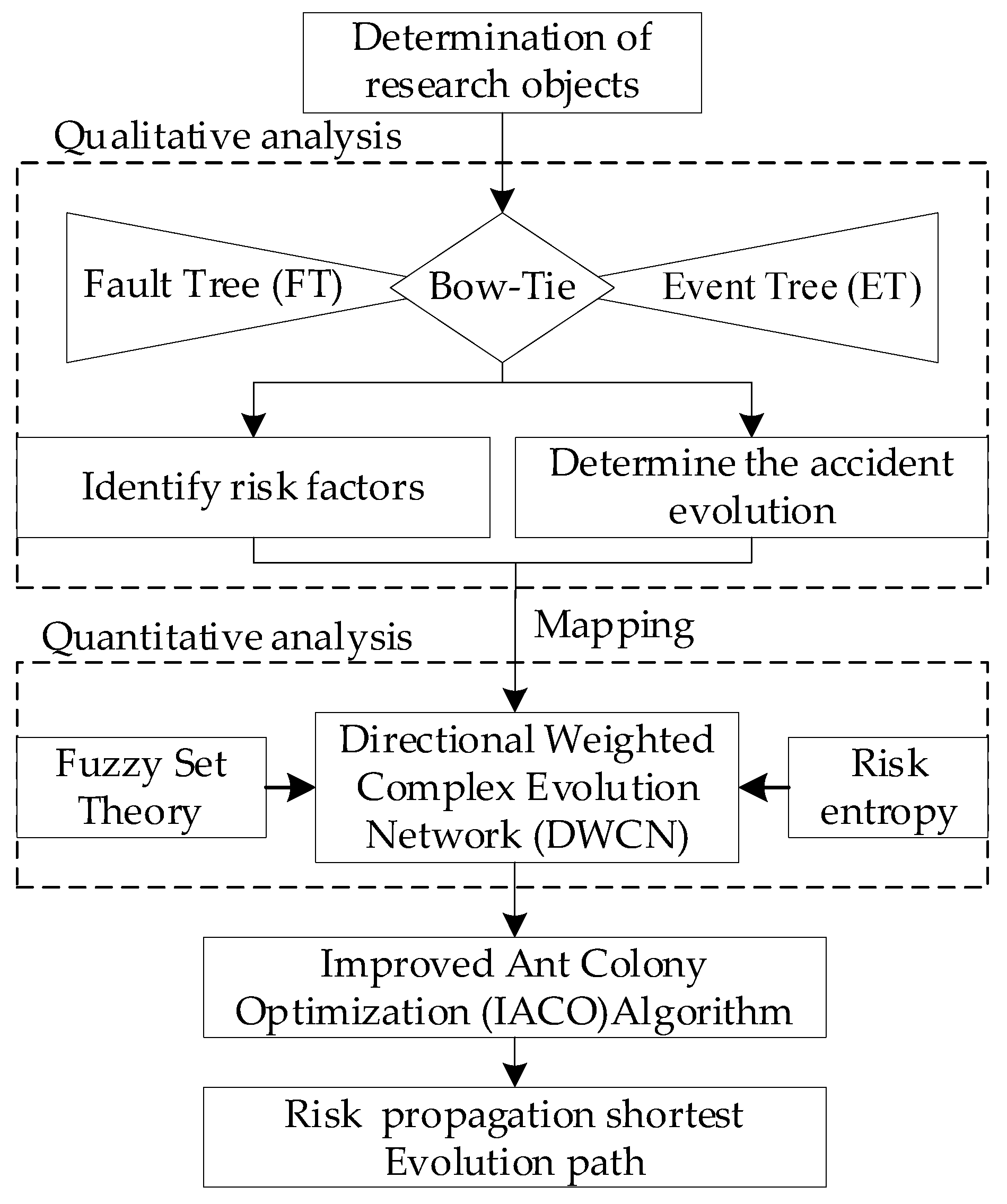
2. Proposed Methodology
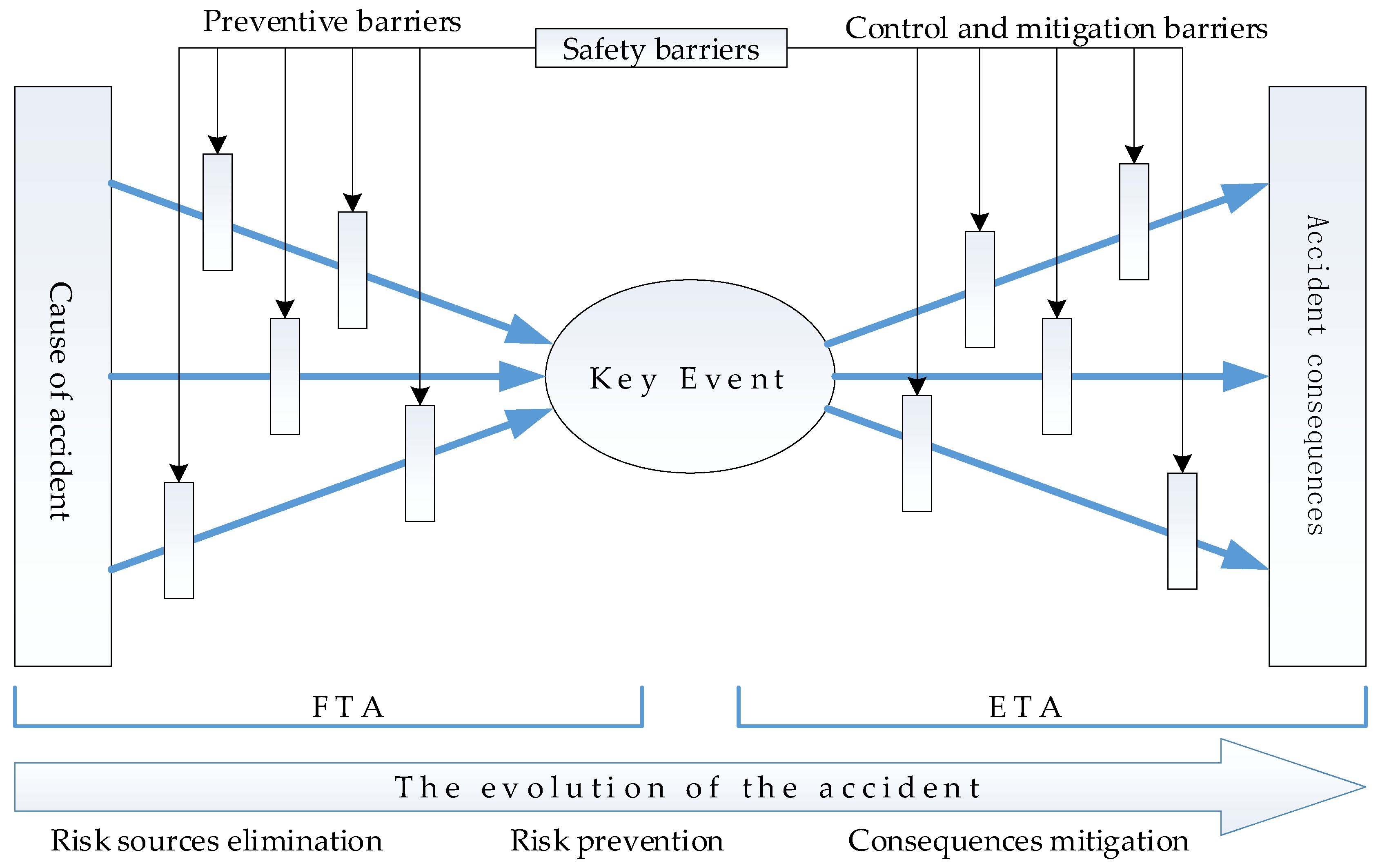
2.1. The Establishment of BT Model
2.1.1. Bow-Tie Analysis Method
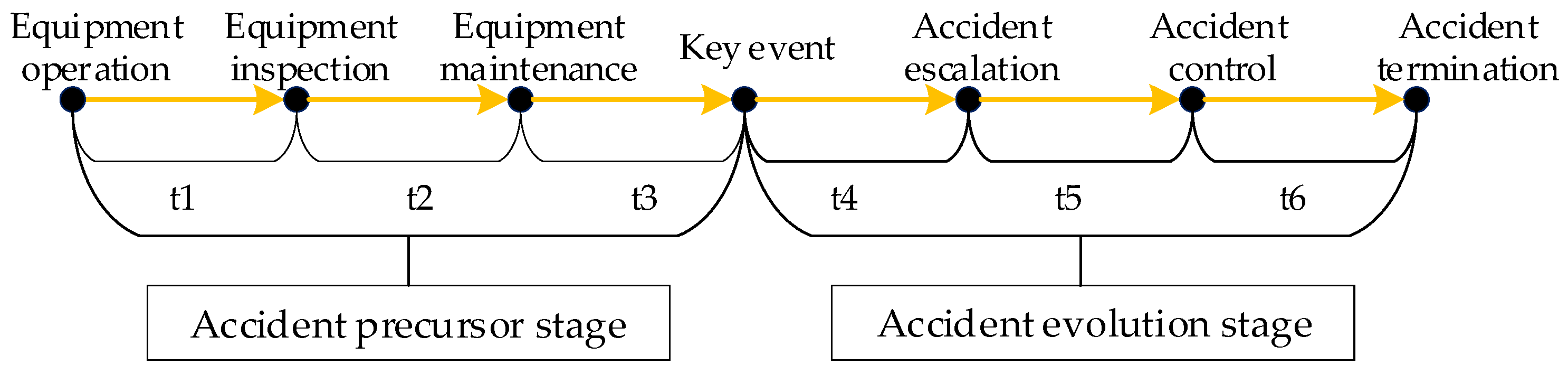
2.1.2. Window of Opportunity during Accident Evolution
2.2. BT Mapping into CN
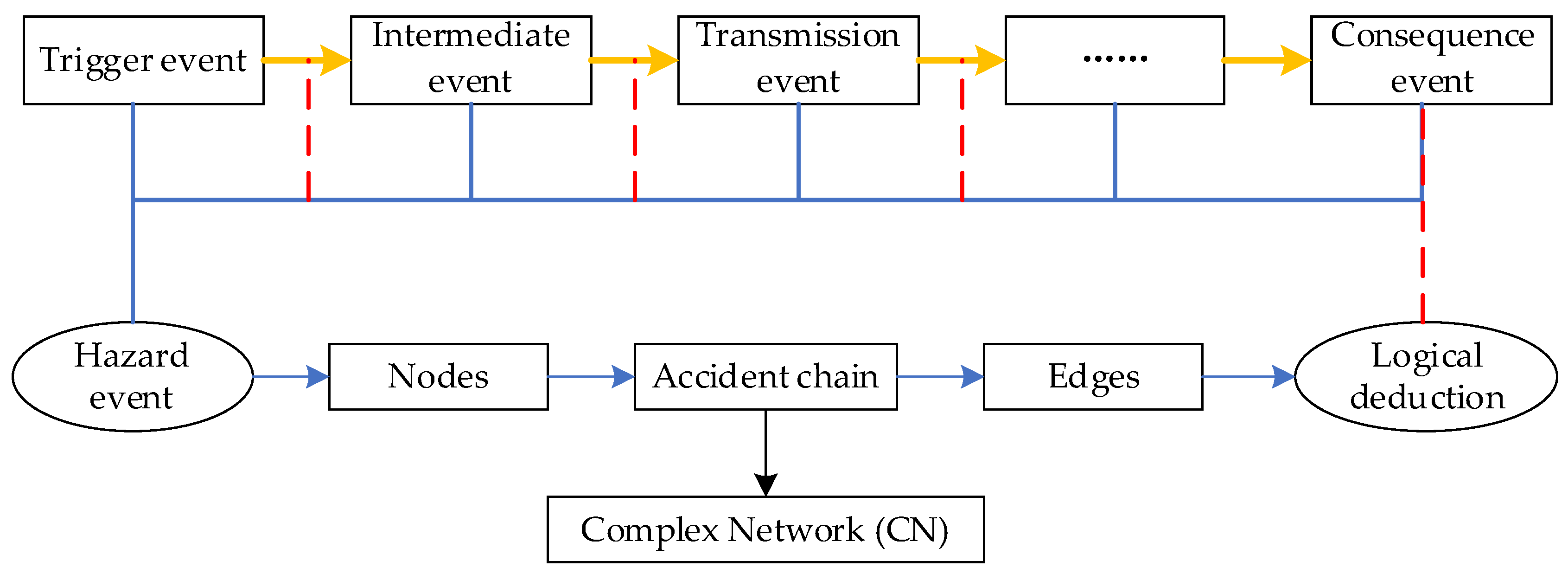
2.2.1. Mapping Principles
- Initial trigger event: Also known as risk source, this is the source event, which is the weakest event that triggers the accident, and the occurrence of this event will lead to the possibility of subsequent events.
- Transmission event: The occurrence of this event will most likely trigger the occurrence of a top-level event. During the risk evolution process, the occurrence of transmission events should be avoided.
- Consequence event: This is the final consequence event of network evolution, which is the end of risk propagation.
- Intermediate event: Between the risk source and the transmission event, this is the key factor that triggers the transmission event, and it is also the follow-up event of the risk source.
- Mapped nodes
- 2.
- Mapped edges
2.2.2. CN Model
2.3. Risk Entropy of CN
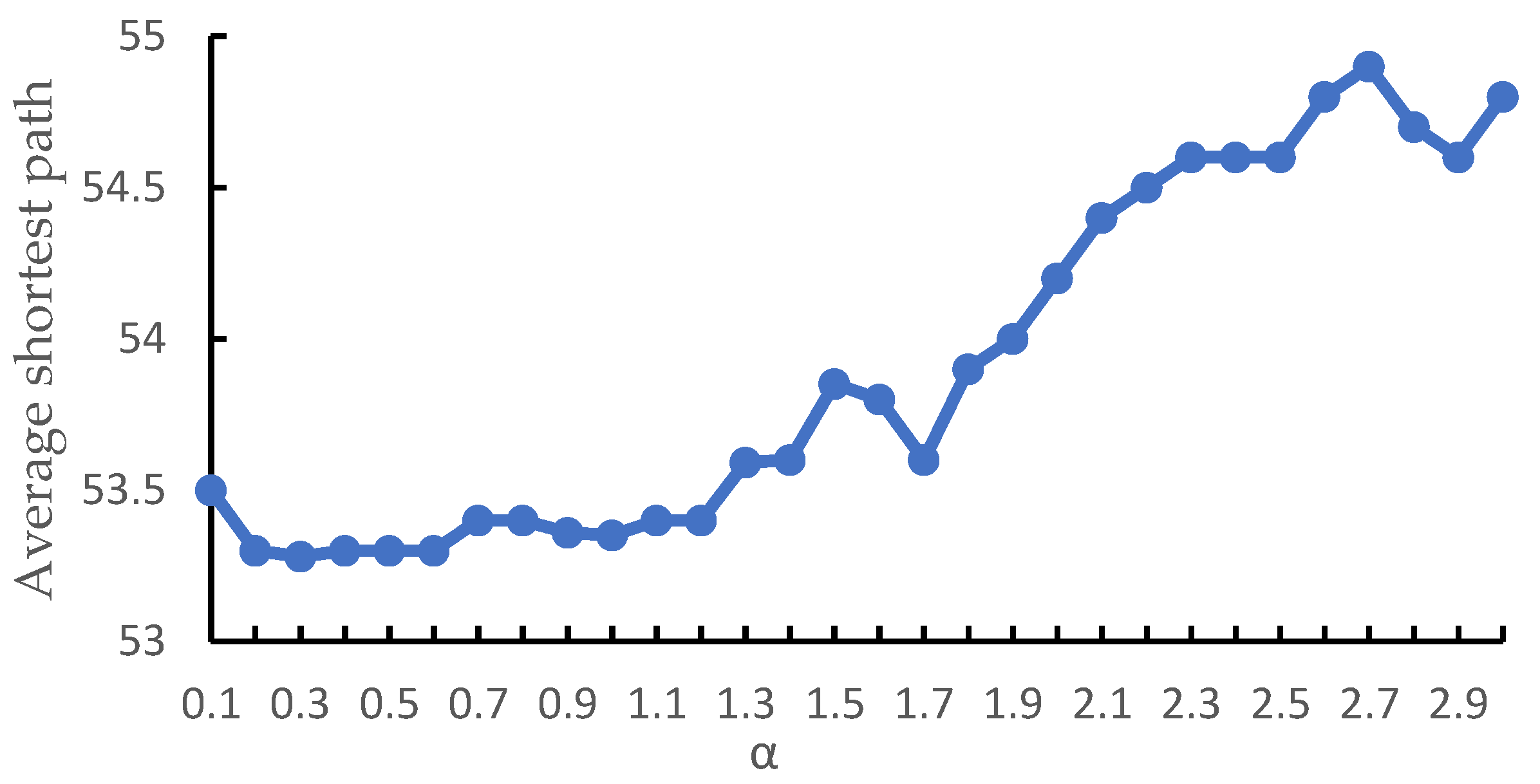
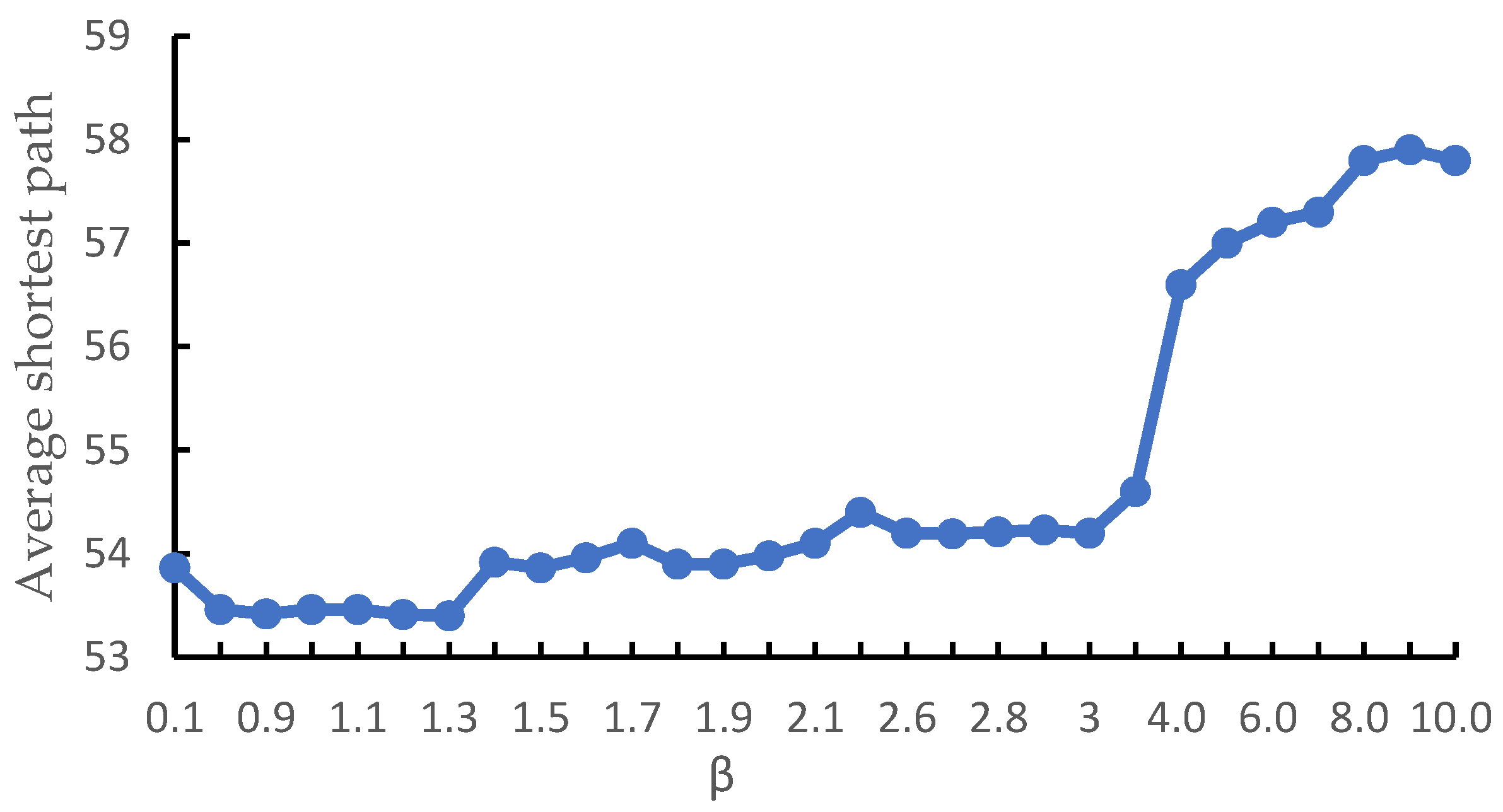
2.4. Risk Evolution Shortest Path Calculation Based on IACO Algorithm
- The heuristic function is improved
- 2.
- Update rules of pheromone concentration be improved
3. Case Study
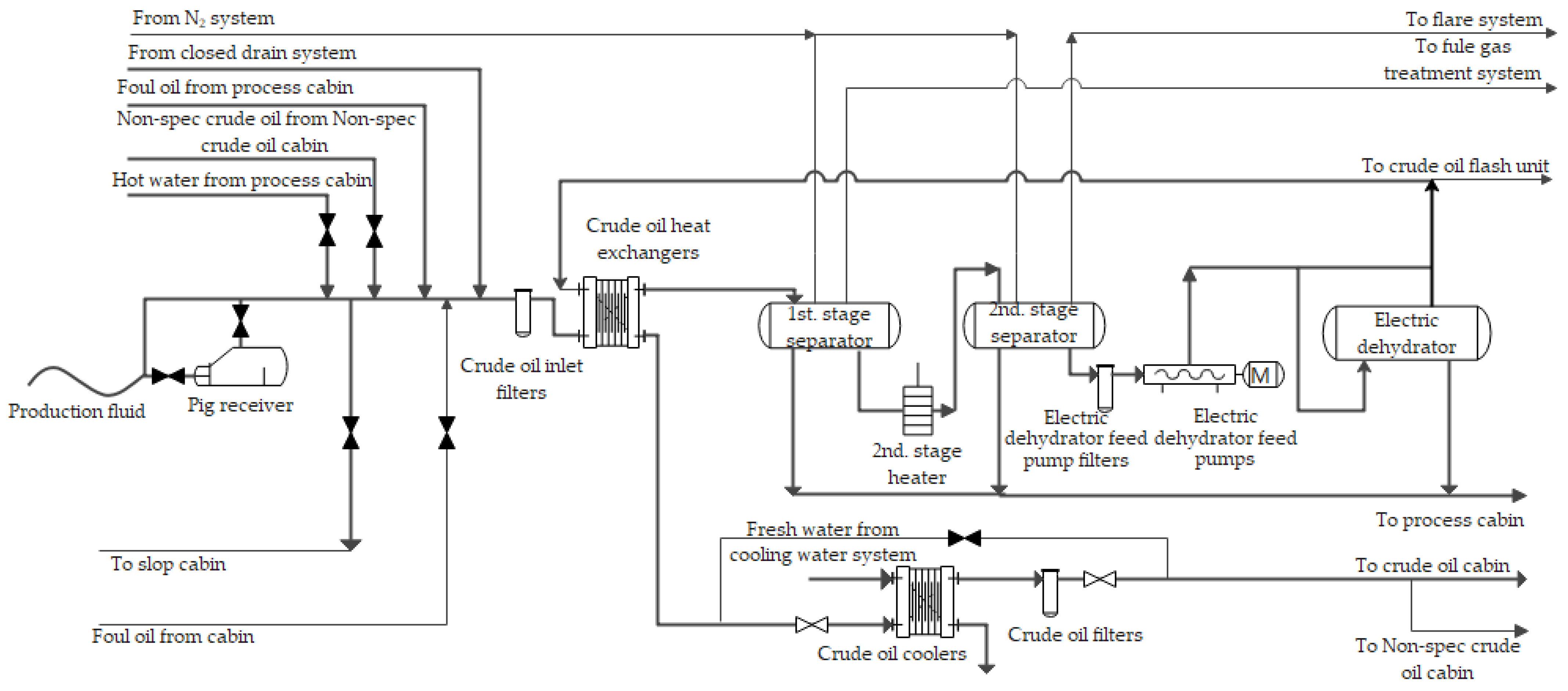
3.1. FPSO Oil and Gas Processing System
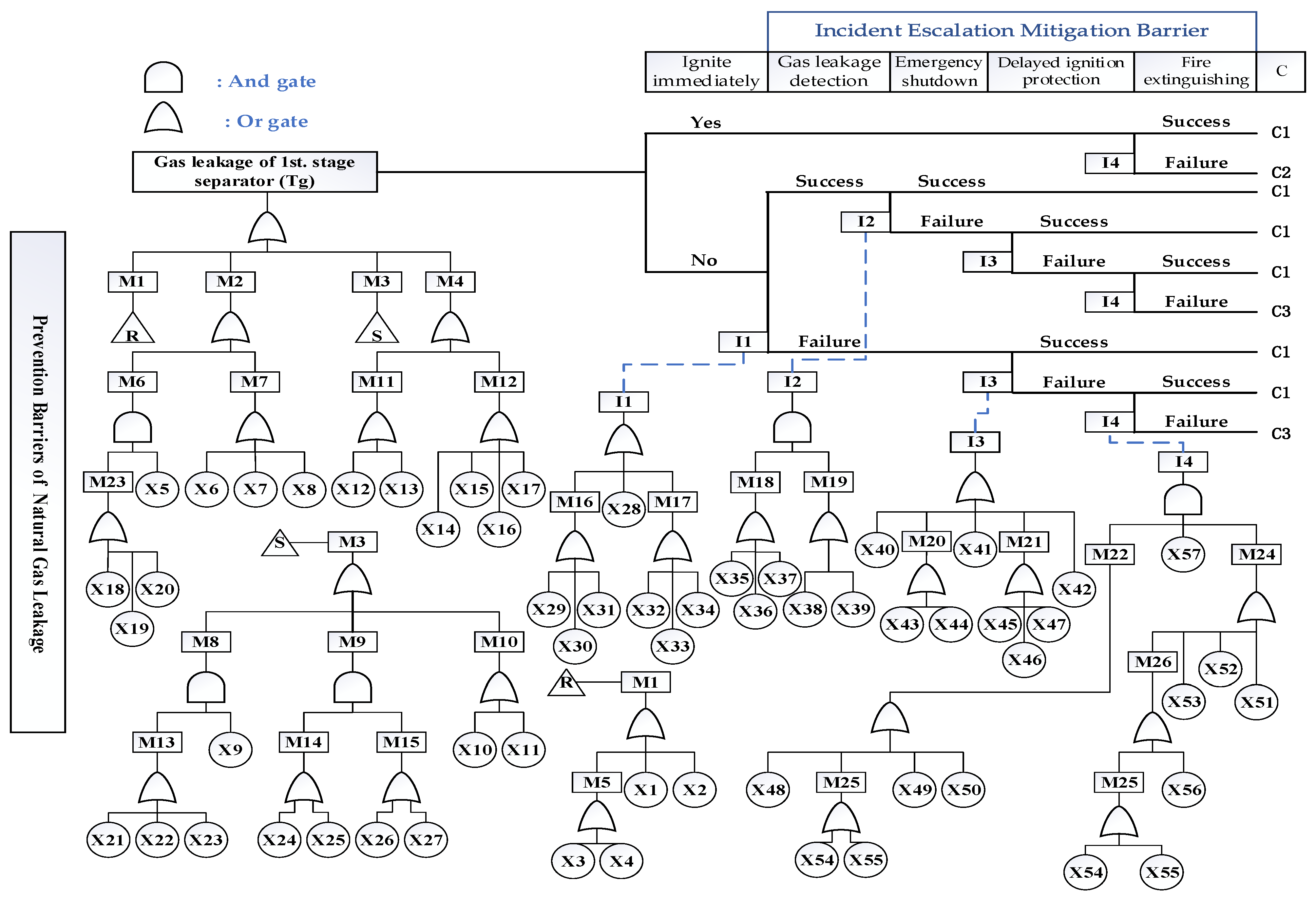
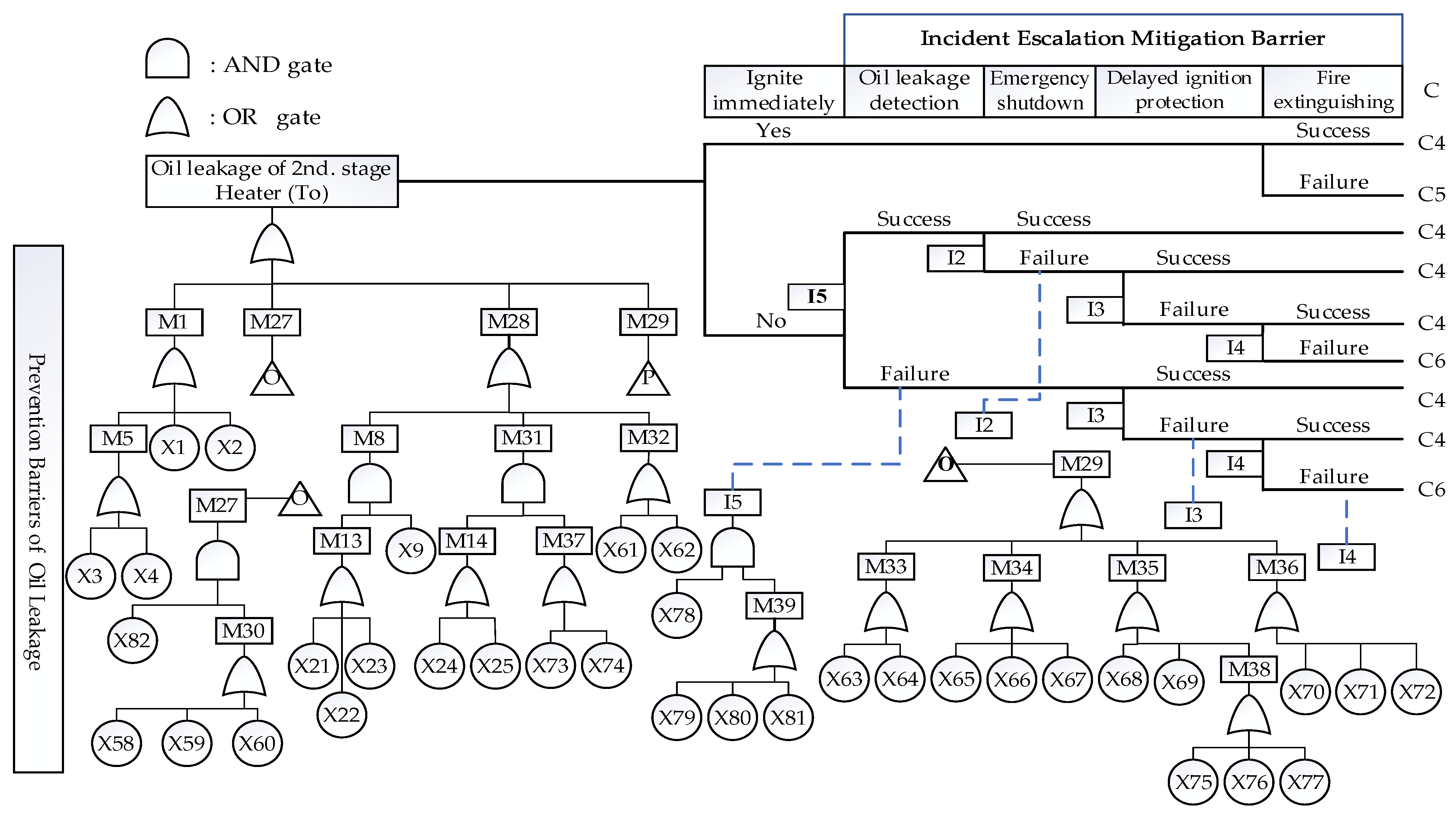
3.2. Qualitative Analysis Based on BT Model
- Gas leakage diffusion (C1): when the natural gas is in a state of high concentration, the oxygen in the air will not be sufficient to sustain life, resulting in the death of people by suffocation. Additionally, when natural gas diffuses in the air, there will always be a danger of explosion, which may eventually evolve into a VCE accident.
- JF (C2/C5): the persistence of the flame depends on the continuation of the leakage, and the burning speed of the flame depends on the amount of gas leakage. The impact of fire is mainly transmitted through thermal radiation. Thermal radiation is the main factor that affects surrounding equipment and personnel.
- VCE (C3): when the combustible gas leaks and accumulates to form a certain concentration field of combustibles, after encountering the ignition source, a VCE will occur. The overpressure wave generated by the explosion will have a serious impact on human survival and equipment, buildings, etc.
- Crude oil pollution (C4): after an oil spill spreads, it will cause pollution and corrosion threats to the devices, and accelerate the aging and damage of the devices. Simultaneously, there will always be a fire hazard after oil pollution. Additionally, it may evolve into a PF when it encounters ignition sources.
- PF (C6): this refers to the fire caused by the leakage of flammable liquid on the ground, and the main damage to the surrounding environment is thermal radiation. PFs not only occur more frequently than other fire forms, but last a long time and are difficult to extinguish.
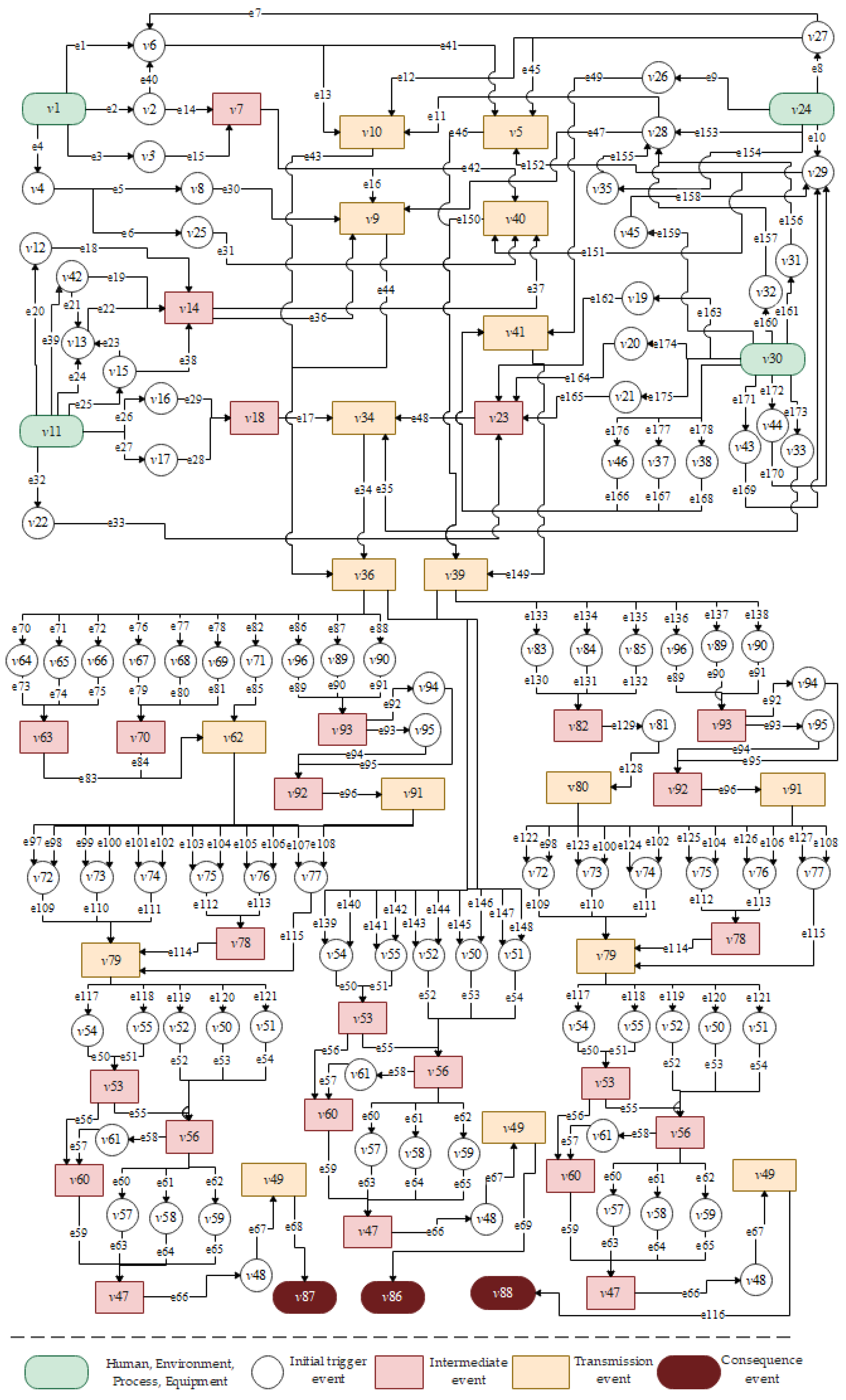
3.3. CN Model of Oil and Gas Leakage Risk Evolution
3.4. The Shortest Path of Risk Evolution
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Edge | Direction | Probability | Risk Entropy | Edge | Direction | Probability | Risk Entropy |
|---|---|---|---|---|---|---|---|
| e1 | v1~v6 | 2.502 × 10−05 | 10.596 | e90 | v89~v93 | 9.930 × 10−01 | 0.007 |
| e2 | v1~v2 | 3.226 × 10−04 | 8.039 | e91 | v90~v93 | 9.910 × 10−01 | 0.009 |
| e3 | v1~v3 | 8.467 × 10−04 | 7.074 | e92 | v93~v94 | 1.208 × 10−03 | 6.719 |
| e4 | v1~v4 | 1.368 × 10−03 | 6.594 | e93 | v93~v95 | 8.467 × 10−04 | 7.074 |
| e5 | v4~v8 | 7.328 × 10−05 | 9.521 | e94 | v95~v92 | 8.890 × 10−01 | 0.118 |
| e6 | v4~v25 | 7.328 × 10−05 | 9.521 | e95 | v94~v92 | 9.940 × 10−01 | 0.006 |
| e7 | v27~v6 | 3.878 × 10−05 | 10.158 | e96 | v92~v91 | 9.910 × 10−01 | 0.009 |
| e8 | v24~v27 | 3.750 × 10−03 | 5.586 | e97 | v62~v72 | 3.577 × 10−03 | 5.633 |
| e9 | v24~v26 | 7.328 × 10−05 | 9.521 | e98 | v91~v72 | 3.577 × 10−03 | 5.633 |
| e10 | v24~v29 | 1.287 × 10−03 | 6.656 | e99 | v62~v73 | 1.258 × 10−02 | 4.375 |
| e11 | v28~v10 | 3.441 × 10−04 | 7.974 | e100 | v91~v73 | 1.258 × 10−02 | 4.375 |
| e12 | v27~v10 | 5.663 × 10−06 | 12.082 | e101 | v62~v74 | 7.882 × 10−04 | 7.146 |
| e13 | v6~v10 | 2.128 × 10−03 | 6.153 | e102 | v91~v74 | 7.882 × 10−04 | 7.146 |
| e14 | v2~v7 | 1.001 × 10−04 | 9.209 | e103 | v62~v75 | 1.927 × 10−04 | 8.554 |
| e15 | v3~v7 | 1.927 × 10−04 | 8.554 | e104 | v91~v75 | 1.927 × 10−04 | 8.554 |
| e16 | v7~v9 | 2.493 × 10−03 | 5.994 | e105 | v62~v76 | 4.802 × 10−04 | 7.641 |
| e17 | v18~v34 | 9.632 × 10−03 | 4.643 | e106 | v91~v76 | 4.802 × 10−04 | 7.641 |
| e18 | v12~v14 | 1.733 × 10−03 | 6.358 | e107 | v62~v77 | 8.531 × 10−03 | 4.764 |
| e19 | v42~v14 | 9.054 × 10−05 | 9.310 | e108 | v91~v77 | 8.531 × 10−03 | 4.764 |
| e20 | v11~v12 | 1.309 × 10−02 | 4.336 | e109 | v72~v79 | 5.944 × 10−04 | 7.428 |
| e21 | v42~v13 | 9.910 × 10−01 | 0.009 | e110 | v73~v79 | 7.882 × 10−04 | 7.146 |
| e22 | v13~v14 | 1.946 × 10−02 | 3.939 | e111 | v74~v79 | 1.967 × 10−02 | 3.928 |
| e23 | v15~v13 | 9.850 × 10−01 | 0.015 | e112 | v75~v78 | 9.200 × 10−01 | 0.083 |
| e24 | v11~v13 | 6.851 × 10−03 | 4.983 | e113 | v76~v78 | 9.300 × 10−01 | 0.073 |
| e25 | v11~v15 | 8.467 × 10−04 | 7.074 | e114 | v78~v79 | 9.660 × 10−01 | 0.035 |
| e26 | v11~v16 | 2.502 × 10−05 | 10.596 | e115 | v77~v79 | 1.780 × 10−04 | 8.634 |
| e27 | v11~v17 | 1.001 × 10−04 | 9.209 | e116 | v49~v88 | 8.620 × 10−01 | 0.149 |
| e28 | v17~v18 | 8.860 × 10−01 | 0.121 | e117 | v79~v54 | 1.208 × 10−03 | 6.719 |
| e29 | v16~v18 | 8.960 × 10−01 | 0.110 | e118 | v79~v55 | 9.054 × 10−05 | 9.310 |
| e30 | v8~v9 | 6.387 × 10−03 | 5.053 | e119 | v79~v52 | 2.624 × 10−03 | 5.943 |
| e31 | v25~v40 | 5.865 × 10−03 | 5.139 | e120 | v79~v50 | 7.882 × 10−04 | 7.146 |
| e32 | v11~v22 | 7.882 × 10−04 | 7.146 | e121 | v79~v51 | 1.636 × 10−03 | 6.416 |
| e33 | v22~v23 | 1.044 × 10−02 | 4.562 | e122 | v80~v72 | 3.577 × 10−03 | 5.633 |
| e34 | v34~v36 | 9.960 × 10−01 | 0.004 | e123 | v80~v73 | 1.258 × 10−02 | 4.375 |
| e35 | v33~v34 | 8.650 × 10−01 | 0.145 | e124 | v80~v74 | 7.882 × 10−04 | 7.146 |
| e36 | v14~v9 | 1.733 × 10−03 | 6.358 | e125 | v80~v75 | 1.927 × 10−04 | 8.554 |
| e37 | v14~v40 | 2.624 × 10−03 | 5.943 | e126 | v80~v76 | 4.802 × 10−04 | 7.641 |
| e38 | v15~v14 | 2.254 × 10−02 | 3.792 | e127 | v80~v77 | 8.531 × 10−03 | 4.764 |
| e39 | v11~v42 | 1.927 × 10−04 | 8.554 | e128 | v81~v80 | 1.679 × 10−02 | 4.087 |
| e40 | v2~v6 | 5.426 × 10−02 | 2.914 | e129 | v82~v81 | 8.467 × 10−04 | 7.074 |
| e41 | v6~v5 | 8.531 × 10−03 | 4.764 | e130 | v83~v82 | 8.840 × 10−01 | 0.123 |
| e42 | v7~v40 | 5.944 × 10−04 | 7.428 | e131 | v84~v82 | 9.120 × 10−01 | 0.092 |
| e43 | v10~v36 | 9.960 × 10−01 | 0.004 | e132 | v85~v82 | 8.100 × 10−01 | 0.211 |
| e44 | v9~v36 | 9.970 × 10−01 | 0.003 | e133 | v39~v83 | 3.226 × 10−04 | 8.039 |
| e45 | v27~v5 | 3.878 × 10−05 | 10.158 | e134 | v39~v84 | 7.882 × 10−04 | 7.146 |
| e46 | v5~v39 | 9.793 × 10−02 | 2.323 | e135 | v39~v85 | 5.782 × 10−04 | 7.456 |
| e47 | v28~v9 | 9.220 × 10−01 | 0.081 | e136 | v39~v96 | 8.467 × 10−04 | 7.074 |
| e48 | v23~v34 | 4.247 × 10−02 | 3.159 | e137 | v39~v89 | 1.287 × 10−03 | 6.656 |
| e49 | v26~v41 | 4.745 × 10−02 | 3.048 | e138 | v39~v90 | 1.733 × 10−03 | 6.358 |
| e50 | v54~v53 | 9.910 × 10−01 | 0.009 | e139 | v36~v54 | 3.577 × 10−03 | 5.633 |
| e51 | v55~v53 | 9.650 × 10−01 | 0.036 | e140 | v39~v54 | 3.577 × 10−03 | 5.633 |
| e52 | v52~v56 | 8.960 × 10−01 | 0.110 | e141 | v36~v55 | 6.570 × 10−03 | 5.025 |
| e53 | v50~v56 | 8.890 × 10−01 | 0.118 | e142 | v39~v55 | 6.570 × 10−03 | 5.025 |
| e54 | v51~v56 | 9.110 × 10−01 | 0.093 | e143 | v36~v52 | 2.493 × 10−03 | 5.994 |
| e55 | v53~v56 | 5.617 × 10−02 | 2.879 | e144 | v39~v52 | 2.493 × 10−03 | 5.994 |
| e56 | v53~v60 | 6.307 × 10−02 | 2.764 | e145 | v36~v50 | 8.531 × 10−03 | 4.764 |
| e57 | v61~v60 | 8.980 × 10−01 | 0.108 | e146 | v39~v50 | 8.531 × 10−03 | 4.764 |
| e58 | v56~v61 | 9.120 × 10−01 | 0.092 | e147 | v36~v51 | 3.750 × 10−03 | 5.586 |
| e59 | v60~v47 | 9.500 × 10−01 | 0.051 | e148 | v39~v51 | 3.750 × 10−03 | 5.586 |
| e60 | v56~v57 | 1.780 × 10−04 | 8.634 | e149 | v41~v39 | 8.900 × 10−01 | 0.117 |
| e61 | v56~v58 | 1.383 × 10−04 | 8.886 | e150 | v40~v39 | 9.440 × 10−01 | 0.058 |
| e62 | v56~v59 | 4.802 × 10−04 | 7.641 | e151 | v29~v40 | 9.793 × 10−02 | 2.323 |
| e63 | v57~v47 | 8.960 × 10−01 | 0.110 | e152 | v29~v5 | 4.383 × 10−02 | 3.127 |
| e64 | v58~v47 | 8.550 × 10−01 | 0.157 | e153 | v24~v28 | 1.733 × 10−03 | 6.358 |
| e65 | v59~v47 | 9.120 × 10−01 | 0.092 | e154 | v24~v35 | 3.226 × 10−04 | 8.039 |
| e66 | v47~v48 | 3.226 × 10−04 | 8.039 | e155 | v35~v28 | 4.907 × 10−04 | 7.620 |
| e67 | v48~v49 | 9.220 × 10−01 | 0.081 | e156 | v31~v28 | 1.733 × 10−03 | 6.358 |
| e68 | v49~v87 | 9.330 × 10−01 | 0.069 | e157 | v32~v28 | 1.733 × 10−03 | 6.358 |
| e69 | v49~v86 | 9.440 × 10−01 | 0.058 | e158 | v45~v29 | 2.760 × 10−03 | 5.892 |
| e70 | v36~v64 | 2.015 × 10−03 | 6.207 | e159 | v30~v45 | 2.760 × 10−03 | 5.892 |
| e71 | v36~v65 | 1.927 × 10−04 | 8.554 | e160 | v30~v32 | 8.467 × 10−04 | 7.074 |
| e72 | v36~v66 | 2.453 × 10−04 | 8.313 | e161 | v30~v31 | 3.750 × 10−03 | 5.586 |
| e73 | v64~v63 | 9.330 × 10−01 | 0.069 | e162 | v19~v23 | 8.531 × 10−03 | 4.764 |
| e74 | v65~v63 | 9.410 × 10−01 | 0.062 | e163 | v30~v19 | 2.129 × 10−05 | 10.757 |
| e75 | v66~v63 | 9.330 × 10−01 | 0.069 | e164 | v20~v23 | 4.783 × 10−03 | 5.343 |
| e76 | v36~v67 | 2.760 × 10−03 | 5.892 | e165 | v21~v23 | 6.552 × 10−05 | 9.633 |
| e77 | v36~v68 | 3.878 × 10−05 | 10.158 | e166 | v46~v41 | 9.793 × 10−02 | 2.323 |
| e78 | v36~v69 | 5.225 × 10−03 | 5.254 | e167 | v37~v41 | 5.617 × 10−02 | 2.879 |
| e79 | v67~v70 | 7.070 × 10−02 | 2.649 | e168 | v38~v41 | 5.426 × 10−02 | 2.914 |
| e80 | v68~v70 | 9.920 × 10−01 | 0.008 | e169 | v43~v29 | 2.760 × 10−03 | 5.892 |
| e81 | v69~v70 | 5.426 × 10−02 | 2.914 | e170 | v44~v29 | 2.760 × 10−03 | 5.892 |
| e82 | v36~v71 | 1.780 × 10−04 | 8.634 | e171 | v30~v43 | 3.020 × 10−04 | 8.105 |
| e83 | v63~v62 | 8.660 × 10−01 | 0.144 | e172 | v30~v44 | 2.493 × 10−03 | 5.994 |
| e84 | v70~v62 | 9.330 × 10−01 | 0.069 | e173 | v30~v33 | 8.161 × 10−05 | 9.414 |
| e85 | v71~v62 | 9.660 × 10−01 | 0.035 | e174 | v30~v20 | 1.640 × 10−04 | 8.715 |
| e86 | v36~v96 | 1.780 × 10−04 | 8.634 | e175 | v30~v21 | 1.001 × 10−04 | 9.209 |
| e87 | v36~v89 | 6.552 × 10−05 | 9.633 | e176 | v30~v46 | 1.003 × 10−03 | 6.904 |
| e88 | v36~v90 | 6.428 × 10−04 | 7.350 | e177 | v30~v37 | 3.692 × 10−03 | 5.602 |
| e89 | v96~v93 | 9.940 × 10−01 | 0.006 | e178 | v30~v38 | 1.287 × 10−03 | 6.656 |
References
- Khan, S.A.R.; Zhang, Y.; Anees, M.; Golpîra, H.; Lahmar, A.; Qianli, D. Green supply chain management, economic growth and environment: A GMM based evidence. J. Clean. Prod. 2018, 185, 588–599. [Google Scholar] [CrossRef]
- Bucelli, M.; Landucci, G.; Haugen, S.; Paltrinieri, N.; Cozzani, V. Assessment of safety barriers for the prevention of cascading events in oil and gas offshore installations operating in harsh environment. Ocean Eng. 2018, 158, 171–185. [Google Scholar] [CrossRef]
- Shimamura, Y. FPSO/FSO: State of the art. J. Mar. Sci. Technol. 2002, 7, 59–70. [Google Scholar] [CrossRef]
- Meng, H.; Kloul, L.; Rauzy, A. Production availability analysis of Floating Production Storage and Offloading (FPSO) systems. Appl. Ocean Res. 2018, 74, 117–126. [Google Scholar] [CrossRef]
- Vinnem, J.E. FPSO Cidade de São Mateus gas explosion–Lessons learned. Saf. Sci. 2018, 101, 295–304. [Google Scholar] [CrossRef]
- Gupta, S.; Chan, S. A CFD based explosion risk analysis methodology using time varying release rates in dispersion simulations. J. Loss Prev. Process. Ind. 2016, 39, 59–67. [Google Scholar] [CrossRef]
- Heinrich, H.W.; Superintendent, A. Relation of accident statistics to industrial accident prevention. Proc. Casuallity Act. Soc. 1930, 16, 170–174. [Google Scholar]
- Suraji, A.; Duff, A.R.; Peckitt, S.J. Development of causal model of construction accident causation. J. Constr. Eng. Manag. 2001, 127, 337–344. [Google Scholar] [CrossRef]
- Reason, J. Human error: Models and management. BMJ 2000, 320, 768–770. [Google Scholar] [CrossRef]
- Rasmussen, J. Risk management in a dynamic society: A modelling problem. Saf. Sci. 1997, 27, 183–213. [Google Scholar] [CrossRef]
- Leveson, N. A new accident model for engineering safer systems. Saf. Sci. 2004, 42, 237–270. [Google Scholar] [CrossRef] [Green Version]
- Shahriar, A.; Sadiq, R.; Tesfamariam, S. Risk analysis for oil & gas pipelines: A sustainability assessment approach using fuzzy based bow-tie analysis. J. Loss Prev. Process Ind. 2012, 25, 505–523. [Google Scholar]
- Khakzad, N.; Khan, F.; Amyotte, P. Dynamic risk analysis using bow-tie approach. Reliab. Eng. Syst. Saf. 2012, 104, 36–44. [Google Scholar] [CrossRef]
- Papazoglou, I.A.; Aneziris, O.N. Master Logic Diagram: Method for hazard and initiating event identification in process plants. J. Hazard. Mater. 2003, 97, 11–30. [Google Scholar] [CrossRef]
- Liu, Z.K.; Ma, Q.; Cai, B.P.; Liu, Y.H.; Zheng, C. Risk assessment on deepwater drilling well control based on dynamic Bayesian network. Process Saf. Environ. 2021, 149, 643–654. [Google Scholar] [CrossRef]
- Liao, P.C.; Guo, Z.; Wang, T.; Wen, J.; Tsai, C.H. Interdependency of construction safety hazards from a network perspective: A mechanical installation case. Int. J. Occup. Saf. Ergon. 2020, 26, 245–255. [Google Scholar] [CrossRef]
- Hu, X.B.; Gheorghe, A.V.; Leeson, M.S.; Leng, S.; Bourgeois, J.; Qu, X. Risk and safety of complex network systems. Math. Probl. Eng. 2016, 2016, 8983915. [Google Scholar] [CrossRef]
- Lam, C.Y.; Tai, K. Network topological approach to modeling accident causations and characteristics: Analysis of railway incidents in Japan. Reliab. Eng. Syst. Saf. 2020, 193, 106626. [Google Scholar] [CrossRef]
- Liu, Z.K.; Ma, Q.; Cai, B.P.; Shi, X.W.; Zheng, C.; Liu, Y.H. Risk coupling analysis of subsea blowout accidents based on dynamic bayesian network and NK model. Reliab. Eng. Syst. Saf. 2021, 218, 108160. [Google Scholar] [CrossRef]
- Mi, J.H.; Lu, N.; Li, Y.F.; Huang, H.Z.; Bai, L.B. An evidential network-based hierarchical method for system reliability analysis with common cause failures and mixed uncertainties. Reliab. Eng. Syst. Saf. 2022, 2022, 108295. [Google Scholar] [CrossRef]
- Singh, K.; Maiti, J. A novel data mining approach for analysis of accident paths and performance assessment of risk control systems. Reliab. Eng. Syst. Saf. 2020, 202, 107041. [Google Scholar] [CrossRef]
- Zarei, E.; Gholamizadeh, K.; Khan, F.; Khakzad, N. A dynamic domino effect risk analysis model for rail transport of hazardous material. J. Loss Prev. Process Ind. 2022, 74, 104666. [Google Scholar] [CrossRef]
- Wu, Y.P.; Chen, Z.L.; Zhao, X.D.; Gong, H.D.; Su, X.C.; Chen, Y.C. Propagation model of cascading failure based on discrete dynamical system. Reliab. Eng. Syst. Saf. 2021, 209, 107424. [Google Scholar] [CrossRef]
- Wang, Q.; Jia, G.Z.; Jia, Y.N.; Song, W.Y. A new approach for risk assessment of failure modes considering risk interaction and propagation effects. Reliab. Eng. Syst. Saf. 2021, 216, 108044. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, C.; Ding, L.; Sekula, P.; Love, P.E.; Zhou, C. Combining association rules mining with complex networks to monitor coupled risks. Reliab. Eng. Syst. Saf. 2019, 186, 194–208. [Google Scholar] [CrossRef]
- Fang, C.; Marle, F.; Zio, E.; Bocquet, J.C. Network theory-based analysis of risk interactions in large engineering projects. Reliab. Eng. Syst. Saf. 2012, 106, 1–10. [Google Scholar] [CrossRef]
- Granovetter, M.S. The strength of weak ties. Am. J. Sociol. 1973, 78, 1360–1380. [Google Scholar] [CrossRef]
- Serrano, M.A.; Boguna, M. Clustering in complex networks. I. General formalism. Phys. Rev. E 2006, 74, 056114. [Google Scholar] [CrossRef]
- McAuley, J.J.; Costa, L.; Caetano, T.S. Rich-club phenomenon across complex network hierarchies. Appl. Phys. Lett. 2007, 91, 084103. [Google Scholar] [CrossRef]
- Xue, L.N.; Fan, J.C.; Zhang, L.B. Bow-tie model for offshore drilling blowout accident. J. Saf. Sci. Technol. 2013, 9, 79–83. [Google Scholar]
- Ismail, F.Y.; Fatemi, A.; Johnston, M.V. Cerebral plasticity: Window of opportunity in the developing brain. Eur. J. Paediatr. Neurol. 2017, 21, 23–48. [Google Scholar] [CrossRef]
- Langer, M.; Brandt, C.; Zellinger, C.; Loscher, W. Therapeutic window of opportunity for the neuroprotective effect of valproate versus the competitive AMPA receptor antagonist NS1209 following status epilepticus in rats. Neuropharmacology 2011, 61, 1033–1047. [Google Scholar] [CrossRef]
- Kwak, K.; Yoon, H. Unpacking transnational industry legitimacy dynamics, windows of opportunity, and latecomers’ catch-up in complex product systems. Res. Policy 2020, 49, 103954. [Google Scholar] [CrossRef]
- Yap, X.S.; Truffer, B. Shaping selection environments for industrial catch-up and sustainability transitions: A systemic perspective on endogenizing windows of opportunity. Res. Policy 2019, 48, 1030–1047. [Google Scholar] [CrossRef]
- Luo, Q.S.; Yang, G.S. Research on Complex Network Model of Collapse Accident Risk Evolution and Risk Mitigation Countermeasures. J. Eng. Manag. 2020, 34, 28–33. [Google Scholar]
- Koromila, I.; Aneziris, O.; Nivolianitou, Z.; Deligianni, A.; Bellos, E. Stakeholder analysis for safe LNG handling at ports. Saf. Sci. 2022, 146, 105565. [Google Scholar] [CrossRef]
- Meng, X.K.; Chen, G.M.; Zhu, H.W. Complex network analysis on risk evolution of submarine pipeline leakage. J. Saf. Sci. Technol. 2017, 13, 26–31. [Google Scholar]
- Hu, R.M.; Lü, H.T.; Chen, J. Risk evaluation model of security and protection network based on risk entropy and Neyman-Pearson criterion. Acta Autom. Sin. 2014, 40, 2737–2746. [Google Scholar]
- Clausius, R. The Mechanical Theory of Heat: With Its Applications to the SteamEngine and to the Physical Properties of Bodies; John van Voorst: London, UK, 1867. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Gao, X.F.; Xianzang, Y.Y.; You, X.T.; Dang, Y.R.; Chen, G.H.; Wang, X.L. Reachability for airline networks: Fast algorithm for shortest path problem with time windows. Theor. Comput. Sci. 2018, 749, 66–79. [Google Scholar] [CrossRef]
- Dragan, F.F.; Leitert, A. On the minimum eccentricity shortest path problem. Theor. Comput. Sci. 2017, 694, 66–78. [Google Scholar] [CrossRef]
- Mozes, S.; Nussbaum, Y.; Weimann, O. Faster shortest paths in dense distance graphs with applications. Theor. Comput. Sci. 2018, 711, 11–35. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Lavalle, S.M.; Kuffner, J.J. Randomized kinodynamic planning. In Proceedings of the IEEE International Conference on Robotics and Automation, Detroit, MI, USA, 10–15 May 1999. [Google Scholar]
- Mohiuddin, M.A.; Khan, S.A.; Engelbrecht, A.P. Fuzzy particle swarm optimization algorithms for the open shortest path first weight setting problem. Appl. Intell. 2016, 45, 598–621. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, M. Exploring genetic algorithm for shortest path optimization in data networks. Glob. J. Comput. Sci. Technol. 2010, 10, 8–12. [Google Scholar]
- Rares, M. Adaptive mutation in genetic algorithms for shortest path routing problem. In Proceedings of the 7th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Bucharest, Romania, 25–27 June 2015. [Google Scholar]
- Wang, Y.; Chen, J.D.; Ning, W.; Yu, H.; Lin, S.M.; Wang, Z.D.; Pang, G.S.; Chen, C. A time-sensitive network scheduling algorithm based on improved ant colony optimization. Alex. Eng. J. 2021, 60, 107–114. [Google Scholar] [CrossRef]
- Changdar, C.; Pal, R.K.; Mahapatra, G.S. A genetic ant colony optimization based algorithm for solid multiple travelling salesmen problem in fuzzy rough environment. Soft Comput. 2017, 21, 4661–4675. [Google Scholar] [CrossRef]
- Ashour, W.; Muqat, R.; Al-Talli, H. Optimization of Traveling Salesman Problem based on Adaptive Affinity Propagation and Ant Colony Algorithms. Int. J. Comput. 2018, 181, 25–31. [Google Scholar] [CrossRef]
- Calle, J.; Rivero, J.; Cuadra, D.; Isasi, P. Extending ACO for fast path search in huge graphs and social networks. Expert Syst. Appl. 2017, 86, 292–306. [Google Scholar] [CrossRef]
- Baeza, D.; Ihle, C.F.; Ortiz, J.M. A comparison between ACO and Dijkstra algorithms for optimal ore concentrate pipeline routing. J. Clean Prod. 2017, 144, 149–160. [Google Scholar] [CrossRef]
- Fang, Z.X.; Zong, X.L.; Li, Q.Q.; Li, Q.P.; Xiong, S.W. Hierarchical multi-objective evacuation routing in stadium using ant colony optimization approach. J. Transp. Geogr. 2011, 19, 443–451. [Google Scholar] [CrossRef]
- Ajeil, F.H.; Ibraheem, I.K.; Azar, A.T.; Humaidi, A.J. Grid-based mobile robot path planning using aging-based ant colony optimization algorithm in static and dynamic environments. Sensors 2020, 20, 1880. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.Y.; Yang, L.; Zhang, Y.; Meng, S. Robot path planning based on improved ant colony algorithm with potential field heuristic. Control. Decis. 2018, 33, 1775–1781. [Google Scholar]
- Chang, Y.J.; Wu, X.F.; Zhang, C.S. Dynamic Bayesian networks based approach for risk analysis of subsea wellhead fatigue failure during service life. Reliab. Eng. Syst. Saf. 2019, 188, 454–462. [Google Scholar] [CrossRef]
- Zarei, E.; Khakzad, N.; Cozzani, V.; Reniers, G. Safety analysis of process systems using Fuzzy Bayesian Network (FBN). J. Loss Prev. Process. Ind. 2019, 57, 7–16. [Google Scholar] [CrossRef]
- Zhu, H.D.; Sun, Z.; Wu, D. Path planning for mobile robot in 3D space based on improved ant colony algorithm. J. Cent. Chin. Norm. Univ. Nat. Sci. 2016, 50, 812–817. [Google Scholar]
| Linguistic Variables | Trapezoidal Fuzzy Number | Qualitative Description | Probabilistic Representation |
|---|---|---|---|
| Very Low (VL) | (0,0,0.1,0.2) | Almost impossible to happen | (0, 10−6) |
| Low (L) | (0.1,0.25,0.25,0.4) | May happen | (10−6, 10−3) |
| Medium (M) | (0.3,0.5,0.5,0.7) | Sometimes happen | (10−3, 10−2) |
| High (H) | (0.6,0.8,0.8,1) | Happen several times | (10−2, 10−1) |
| Very High (VH) | (0.9,0.95,1,1) | Happen frequently | (10−1, 1) |
| Item | Event | Item | Event |
|---|---|---|---|
| X1 | Rainstorm | X42 | Hitting sparks |
| X2 | Hurricane | X43 | Smoking |
| X3 | Crane falling hitting | X44 | Thermal processing |
| X4 | Touch by mistake while repairing | X45 | Heat generation from pumps |
| X5 | Missing detection of separator defects | X46 | Heat generation from Pipe |
| X6 | Joints not tightly sealed | X47 | Heat generation from HT electrical equipment |
| X7 | Valves not tightly closed | X48 | Smoke detector failure |
| X8 | Flanges not tightly closed | X49 | Sprinkler valve failure |
| X9 | Corrosion of internal substance | X50 | Sprinkler head clogged |
| X10 | Stress concentration of separator | X51 | Foam production unit failure |
| X11 | Residual stress of separator | X52 | Foam gun clogged |
| X12 | N2 input line failure | X53 | Pipeline broken |
| X13 | N2 system failure | X54 | Fire pump failure |
| X14 | Gas pipe blockage | X55 | Damaged fire pipe network |
| X15 | Valve clogged | X56 | Not enough foam |
| X16 | Pressure regulating valve failure | X57 | Dry powder fire extinguishing equipment failure |
| X17 | Liquid volume too large | X58 | Improper selection of heater shell |
| X18 | Improper selection of separator body | X59 | Material defection of heater shell |
| X19 | Material defection of separator | X60 | Weld defection of heater shell |
| X20 | Weld defection of separator | X61 | Residual stress of heater shell |
| X21 | Not enough preservatives | X62 | Stress concentration of heater shell |
| X22 | Corrosion inhibitor injection line failure | X63 | Heater bolt material defect |
| X23 | Corrosion inhibitor injection pump failure | X64 | Heater bolt corrosion failure |
| X24 | Wear corrosion | X65 | Gasket material defect |
| X25 | Electrochemical corrosion | X66 | Gasket crush rupture |
| X26 | Separator anti-corrosion coating failure | X67 | Gasket corrosion failure |
| X27 | Separator cathodic protection failure | X68 | Flange material defect |
| X28 | Power failure of detector system | X69 | Flange corrosion failure |
| X29 | Gas detector malfunction | X70 | Relatively low preload. |
| X30 | Logic controller failure | X71 | Uneven preload |
| X31 | Actuator failure | X72 | Shim deviation |
| X32 | Incorrect installation of gas detector | X73 | anti-corrosion coating failure of heater shell |
| X33 | Not removed of gas detector cover | X74 | Cathodic protection failure of heater shell |
| X34 | Incorrect installation height of gas detector | X75 | Flange surface rough |
| X35 | Emergency shut-off valve failure | X76 | Flange surface impurity |
| X36 | Control program failure | X77 | Flange surface be scratched |
| X37 | Executive power failure | X78 | Oil leakage undiscovered |
| X38 | Manual valve failure | X79 | Pressure sensor failure |
| X39 | Operation error | X80 | Pressure transmission signal failure |
| X40 | Lightning | X81 | Pressure alarm failure |
| X41 | Static electricity | X82 | Missed detection of defects in heater |
| Item | Event | Item | Event | Item | Event |
|---|---|---|---|---|---|
| M1 | Third damaged | M14 | Exposed to corrosive environments | M27 | Heater defect |
| M2 | Separator defect | M15 | Separator exterior corrosion protection failure | M28 | Heater corrosion perforation |
| M3 | Separator corrosion perforation | M16 | Gas detection system failure | M29 | Leakage at heater flange connection |
| M4 | Leakage at seals | M17 | Inability to effectively detect gas leakage | M30 | Defect of heater design and manufacturing |
| M5 | External hitting | M18 | Emergency shutdown failure | M31 | Heater external corrosion |
| M6 | Separator body defect | M19 | Manual shutdown failure | M32 | Heater stress corrosion |
| M7 | Separator not tightly sealed | M20 | Open flame | M33 | Heater bolt failure |
| M8 | Internal corrosion | M21 | Equipment hot surface | M34 | Heater Gasket Failure |
| M9 | Separator external corrosion | M22 | Fire water system failure | M35 | Heater flange failure |
| M10 | Separator stress corrosion | M23 | Defect of separator design and manufacturing | M36 | Incorrect heater flange installation |
| M11 | N2 supply failure | M24 | Foam fire extinguishing system failure | M37 | External anti-corrosion failure of heater |
| M12 | Separator overpressure | M25 | Insufficient water pressure | M38 | Flange surface defect |
| M13 | Internal anti-corrosion measures failure | M26 | Insufficient foam mix | M39 | Pressure monitoring failure |
| Item | Description |
|---|---|
| I1 | Gas leakage detection failure |
| I2 | Emergency shutdown failure |
| I3 | Ignition protection failure |
| I4 | Fire extinguishing failure |
| I5 | Oil leakage detection failure |
| Item | Consequence |
|---|---|
| C1 | Gas leakage pollution |
| C2 | Gas jet fire |
| C3 | vapor cloud explosion |
| C4 | Oil leakage pollution |
| C5 | liquid jet fire |
| C6 | Pool fire |
| No. | Risk Events | No. | Risk Events |
|---|---|---|---|
| v1 | Environmental factors | v49 | Fire extinguishing failure |
| v2 | Hurricane | v50 | Smoke detector failure |
| v3 | Rainstorm | v51 | Sprinkler valve failure |
| v4 | Environmental corrosion | v52 | Sprinkler head clogged |
| v5 | Heater rupture | v53 | Insufficient water pressure |
| v6 | Crane falling | v54 | Fire pump failure |
| v7 | Equipment wear | v55 | Damaged fire pipe network |
| v8 | Separator exterior corrosion protection failure | v56 | Fire water system failure |
| v9 | Separator corrosion perforation | v57 | Foam production unit failure |
| v10 | Separator rupture | v58 | Foam gun clogged |
| v11 | Process flow factors | v59 | Pipeline broken |
| v12 | Corrosion of internal substance | v60 | Insufficient foam mix |
| v13 | Not enough preservatives | v61 | Not enough foam |
| v14 | Internal corrosion | v62 | Gas leakage detection failure |
| v15 | Corrosion inhibitor injection pump failure | v63 | Gas detection system failure |
| v16 | N2 system failure | v64 | Gas detector malfunction |
| v17 | N2 input pipe failure | v65 | Logic controller failure |
| v18 | N2 supply failure | v66 | Actuator failure |
| v19 | Pressure regulating valve failure | v67 | Incorrect installation of gas detector |
| v20 | Valve clogged | v68 | Not removed of gas detector cover |
| v21 | Gas pipe blockage | v69 | Incorrect installation height of gas detector |
| v22 | Liquid volume too large | v70 | Inability to effectively detect gas leakage |
| v23 | Overpressure | v71 | Power failure of detector system |
| v24 | Human factors | v72 | Lightning |
| v25 | External anti-corrosion failure of heater | v73 | Static electricity |
| v26 | Incorrect heater flange installation | v74 | Hitting sparks |
| v27 | Touch by mistake while repairing | v75 | Smoking |
| v28 | Missing detection of separator defects | v76 | Thermal processing |
| v29 | Missed detection of heater defects | v77 | Equipment hot surface |
| v30 | Equipment factors | v78 | Open flame |
| v31 | Weld defection of separator | v79 | Ignition protection failure |
| v32 | Material defection of separator | v80 | Oil leakage detection failure |
| v33 | Separator not tightly sealed | v81 | Leakage undiscovered |
| v34 | Separator seal leakage | v82 | Pressure monitoring failure |
| v35 | Improper selection of separator body | v83 | Pressure sensor failure |
| v36 | Separator gas leakage | v84 | Pressure transmission signal failure |
| v37 | Heater gasket failure | v85 | Pressure alarm failure |
| v38 | Heater flange failure | v86 | JF |
| v39 | Heater oil leakage | v87 | VCE |
| v40 | Heater corrosion perforation | v88 | PF |
| v41 | Heater flange connection failure | v89 | Control program failure |
| v42 | Corrosion inhibitor injection pipe failure | v90 | Executive power failure |
| v43 | Weld defection of heater shell | v91 | Emergency shutdown failure |
| v44 | Material defection of heater shell | v92 | Manual shutdown failure |
| v45 | Improper selection of heater shell | v93 | Automatic shutdown failure |
| v46 | Heater bolt failure | v94 | Manual valve failure |
| v47 | Foam fire extinguishing system failure | v95 | Operation error |
| v48 | Dry powder fire extinguishing equipment failure | v96 | Emergency shut-off valve failure |
| Initial Events | Shortest Path to Leakage | Shortest Path to Escalate | Risk Entropy | Total Probability | |
|---|---|---|---|---|---|
| JF | v1 | v1→v2→v6→v10→v36 | v36→v52→v56→v61→v60 →v47→v48→v49→v86 | 30.4 | 6.15 × 10−14 |
| v11 | v11→v13→v14→v40→v39 | v39→v52→v56→v61→v60 →v47→v48→v49→v86 | 29.0 | 2.47 × 10−13 | |
| v24 | v24→v28→v9→v36 | v36→v52→v56→v61→v60 →v47→v48→v49→v86 | 19.8 | 2.64 × 10−9 | |
| v30 | v30→v37→v41→v39 | v39→v52→v56→v61→v60 →v47→v48→v49→v86 | 21.9 | 3.06 × 10−10 | |
| PF | v1 | v1→v2→v6→v5→v39 | v39→v96→v93→v94→v92 →v91→v73→v79→v52→v56 →v61→v60→v47→v48 →v49→v88 | 57.9 | 6.82 × 10−26 |
| v11 | v11→v12→v14→v40→v39 | 53.8 | 4.52 × 10−24 | ||
| v24 | v24→v29→v40→v39 | 50.8 | 8.49 × 10−23 | ||
| v30 | v30→v37→v41→v39 | 48.3 | 1.1 × 10−21 | ||
| VCE | v1 | v1→v2→v6→v10→v36 | v36→v64→v63→v62→v73 →v79→v52→v56→v61→v60 →v47→v48→v49→v87 | 51.4 | 4.94 × 10−23 |
| v11 | v11→v12→v14→v9→v36 | 49.5 | 3.2 × 10−22 | ||
| v24 | v24→v28→v9→v36 | 40.7 | 2.12 × 10−18 | ||
| v30 | v30→v33→v34→v36 | 44.2 | 6.4 × 10−20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Sun, L.; Sun, H.; Meng, X.; Kang, J. Risk Propagation Evolution Analysis of Oil and Gas Leakage in FPSO Oil and Gas Processing System by Mapping Bow-Tie into Directed Weighted Complex Network. Water 2022, 14, 2857. https://doi.org/10.3390/w14182857
Wang L, Sun L, Sun H, Meng X, Kang J. Risk Propagation Evolution Analysis of Oil and Gas Leakage in FPSO Oil and Gas Processing System by Mapping Bow-Tie into Directed Weighted Complex Network. Water. 2022; 14(18):2857. https://doi.org/10.3390/w14182857
Chicago/Turabian StyleWang, Longting, Liping Sun, Hai Sun, Xiangkun Meng, and Jichuan Kang. 2022. "Risk Propagation Evolution Analysis of Oil and Gas Leakage in FPSO Oil and Gas Processing System by Mapping Bow-Tie into Directed Weighted Complex Network" Water 14, no. 18: 2857. https://doi.org/10.3390/w14182857







