Hydrological Response to Meteorological Droughts in the Guadalquivir River Basin, Southern Iberian Peninsula
Abstract
:1. Introduction
2. Data and Methodology
3. Results and Discussion
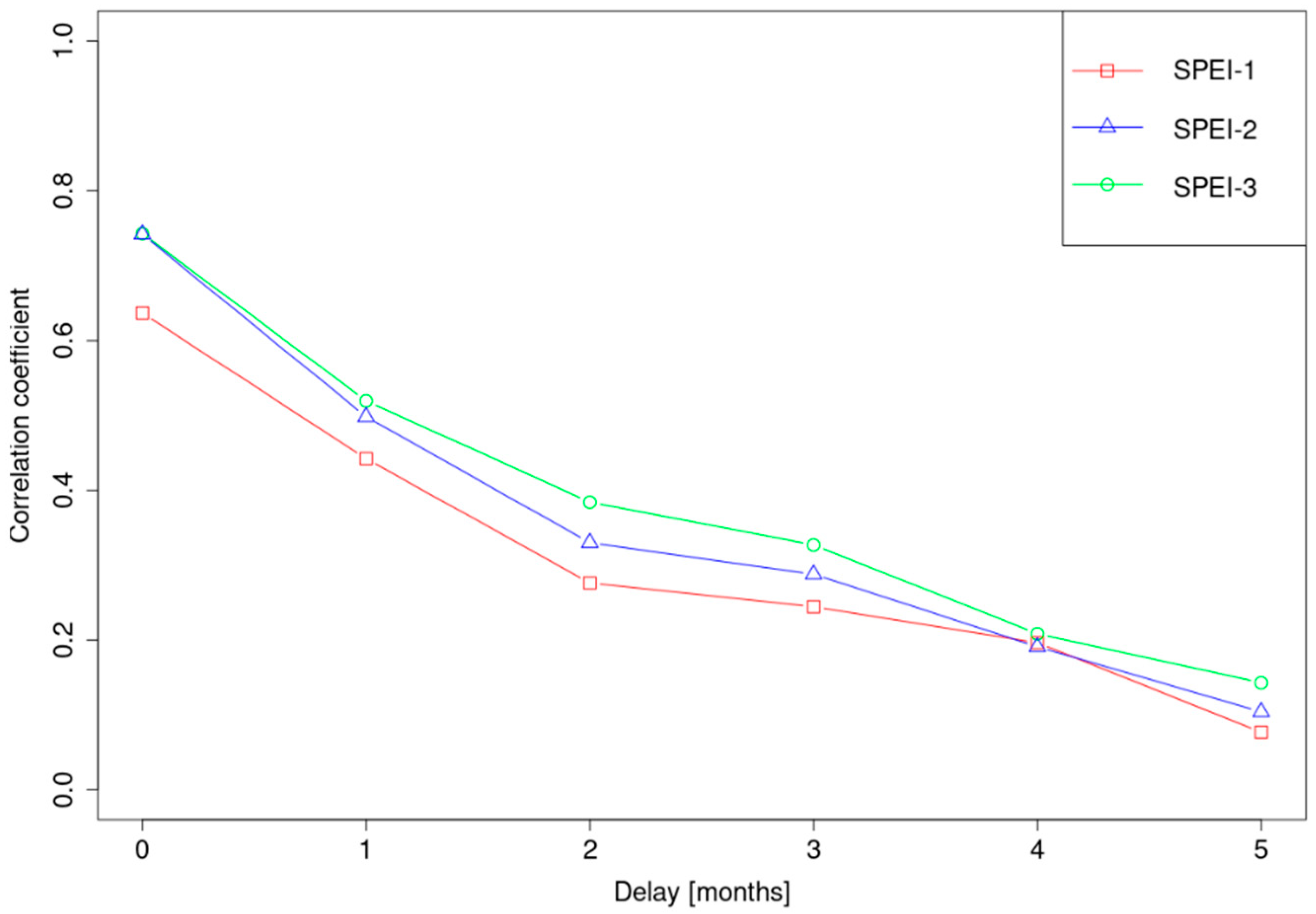
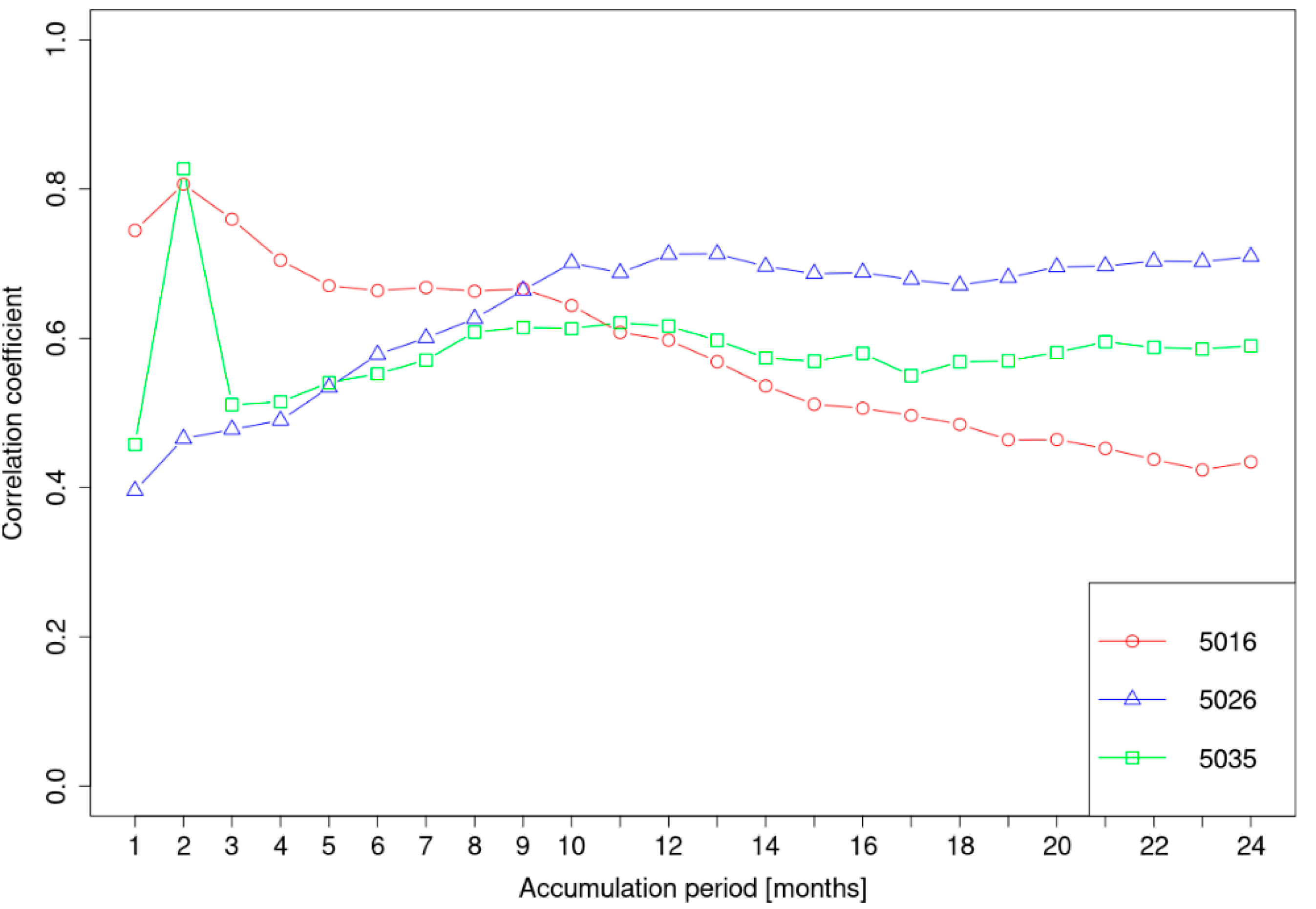
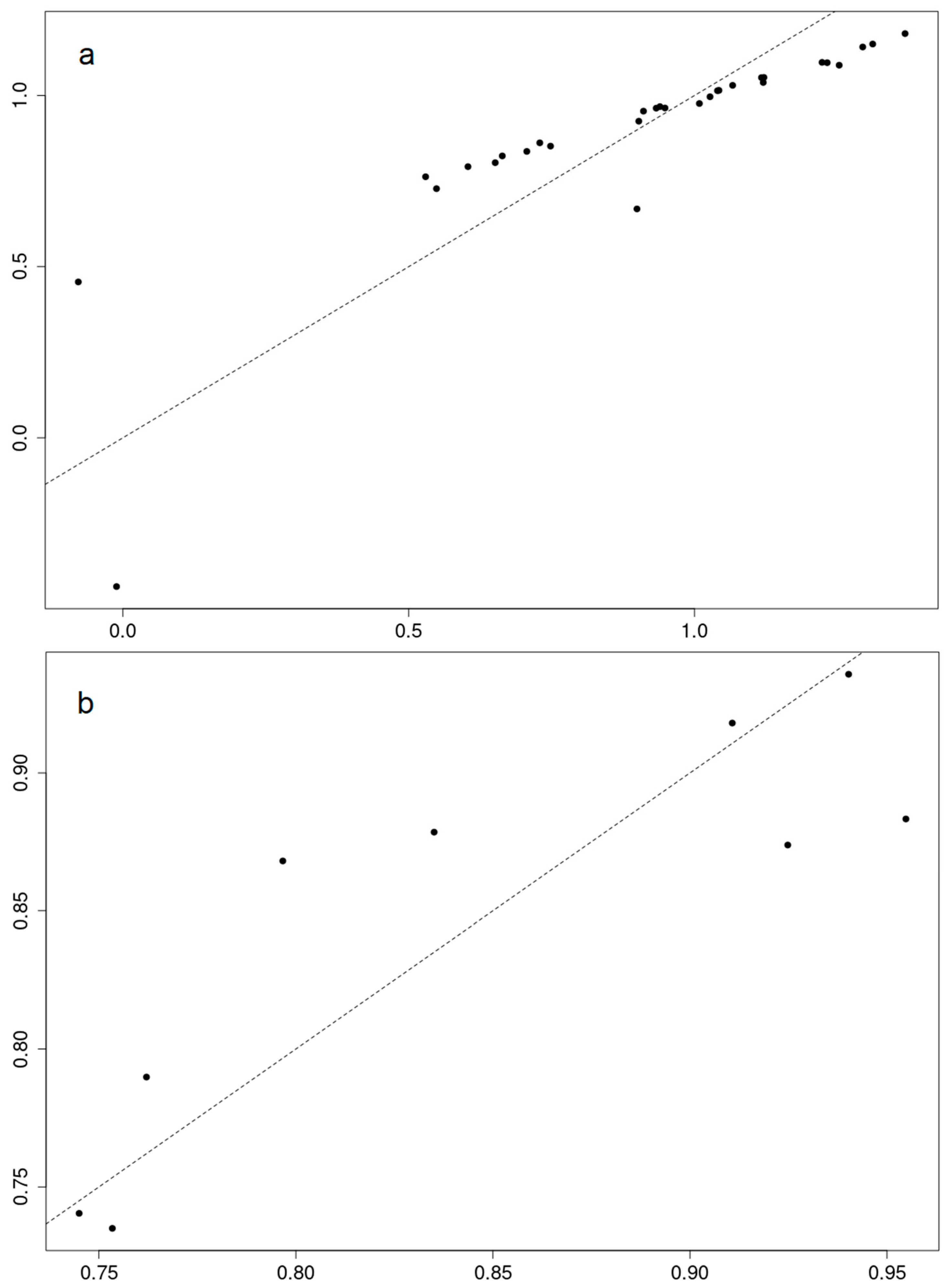
3.1. Correlations between SSI and SPEI
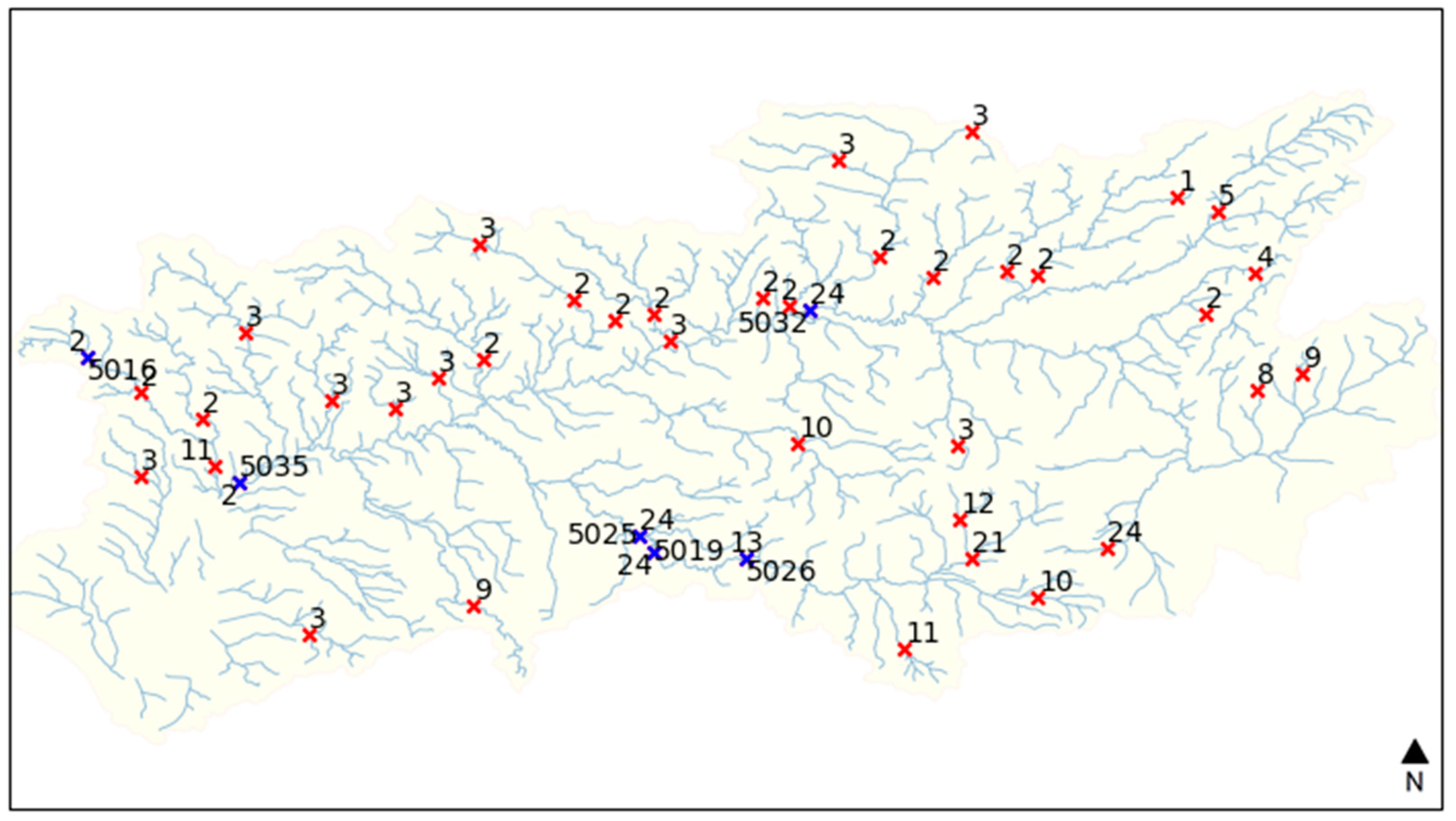
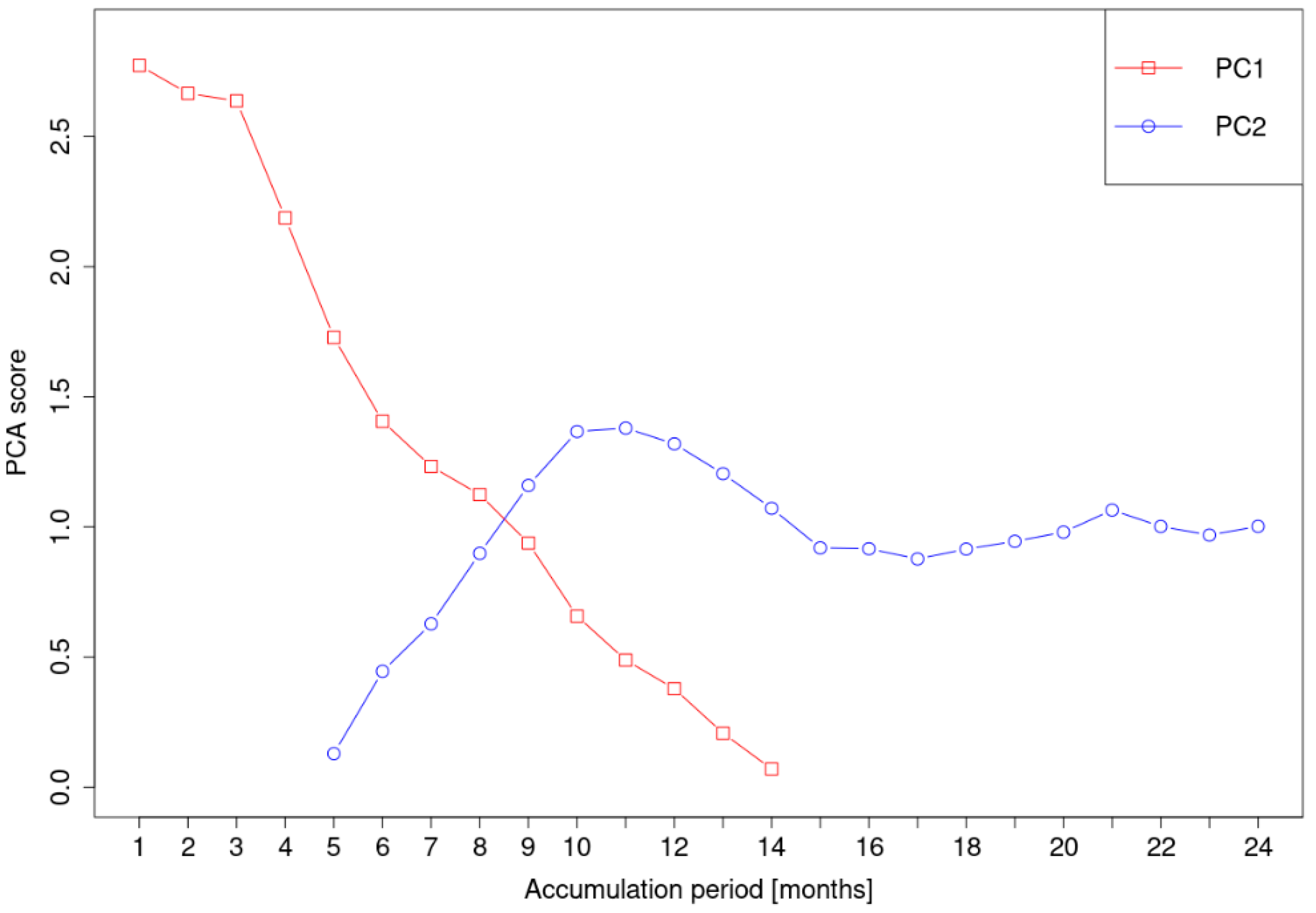
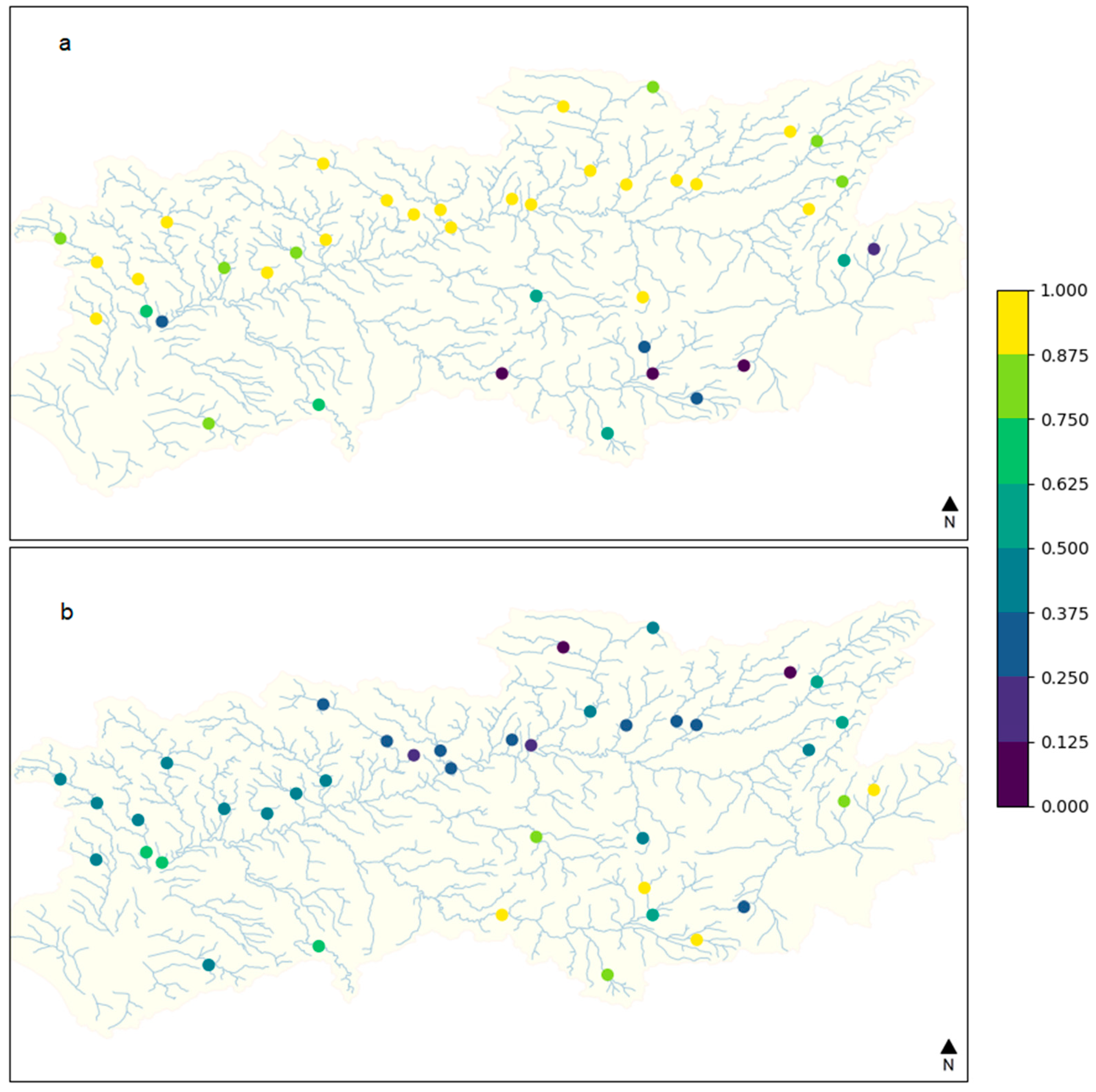
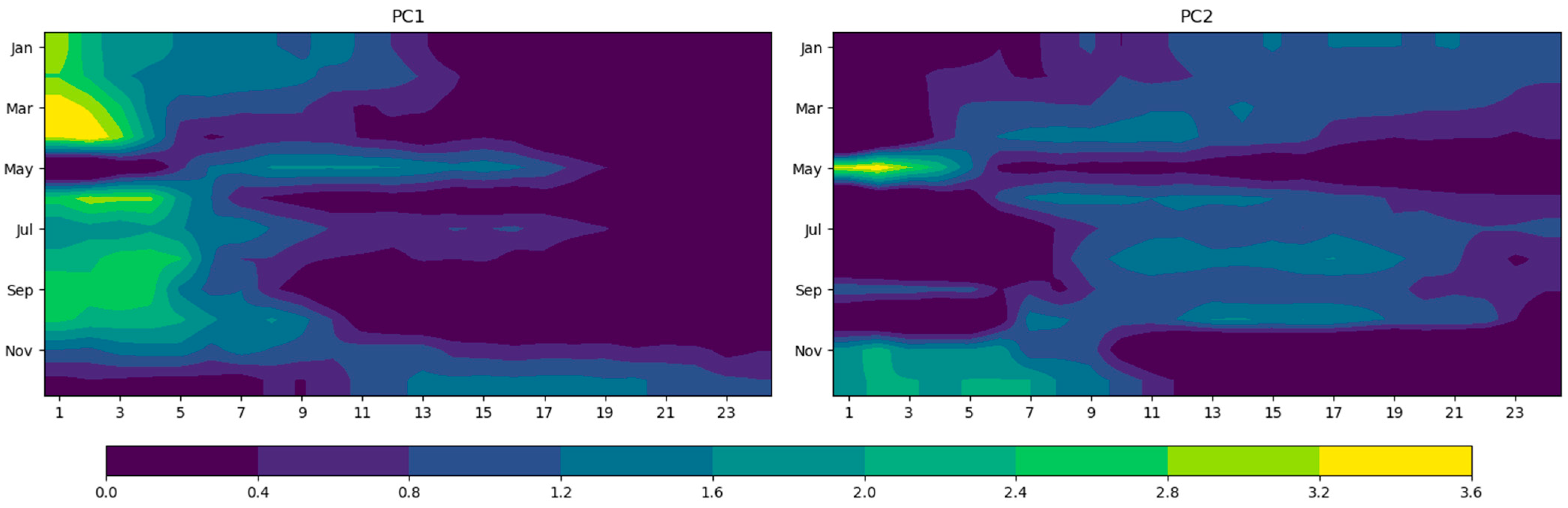
3.2. PCA Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Birkmann, J.; Jamshed, A.; McMillan, J.M.; Feldmeyer, D.; Totin, E.; Solecki, W.; Ibrahim, Z.Z.; Roberts, D.; Kerr, R.B.; Poertner, H.-O.; et al. Understanding human vulnerability to climate change: A global perspective on index validation for adaptation planning. Sci. Total Environ. 2021, 803, 150065. [Google Scholar] [CrossRef] [PubMed]
- García-Ruiz, J.M.; López-Moreno, I.; Vicente-Serrano, S.M.; Lasanta-Martínez, T.; Beguería, S. Mediterranean water resources in a global change scenario. Earth-Sci. Rev. 2011, 105, 121–139. [Google Scholar] [CrossRef]
- García-Valdecasas Ojeda, M.; Gámiz-Fortis, S.R.; Romero-Jiménez, E.; Rosa-Cánovas, J.J.; Yeste, P.; Castro-Díez, Y.; Esteban-Parra, M.J. Projected changes in the Iberian Peninsula drought characteristics. Sci. Total Environ. 2021, 757, 143702. [Google Scholar] [CrossRef] [PubMed]
- Peña-Gallardo, M.; Vicente-Serrano, S.M.; Hannaford, J.; Lorenzo-Lacruz, J.; Svoboda, M.; Domínguez-Castro, F.; Maneta, M.; Tomas-Burguera, M.; El Kenawy, A. Complex influences of meteorological drought time-scales on hydrological droughts in natural basins of the contiguous Unites States. J. Hydrol. 2019, 568, 611–625. [Google Scholar] [CrossRef]
- López-Moreno, J.; Vicente-Serrano, S.; Zabalza, J.; Beguería, S.; Lorenzo-Lacruz, J.; Azorín-Molina, C.; Morán-Tejeda, E. Hydrological response to climate variability at different time scales: A study in the Ebro basin. J. Hydrol. 2013, 477, 175–188. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Domínguez-Castro, F.; McVicar, T.R.; Tomas-Burguera, M.; Peña-Gallardo, M.; Noguera, I.; López-Moreno, J.I.; Peña, D.; El Kenawy, A. Global characterization of hydrological and meteorological droughts under future climate change: The importance of timescales, vegetation-CO2 feedbacks and changes to distribution functions. Int. J. Climatol. 2020, 40, 2557–2567. [Google Scholar] [CrossRef]
- Yongxiao, C.; Jianping, Y.; Huaibin, W. Relationship between meteorological and hydrological drought in the mountain areas: A study in the upper reaches of Ying River, China. Desalination Water Treat. 2021, 220, 22–35. [Google Scholar] [CrossRef]
- Álvarez-Garreton, C.; Boisier, J.; Garreaud, R.; Seibert, J.; Vis, M. Progressive water deficits during multiyear droughts in basins with long hydrological memory in Chile. Hydrol. Earth Syst. Sci. 2021, 25, 429–446. [Google Scholar] [CrossRef]
- Yang, Y.; McVicar, T.R.; Donohue, R.J.; Zhang, Y.; Roderick, M.L.; Chiew, F.H.; Zhang, L.; Zhang, J. Lags in hydrologic recovery following an extreme drought: Assessing the roles of climate and catchment characteristics. Water Resour. Res. 2017, 53, 4821–4837. [Google Scholar] [CrossRef]
- Koster, R.D.; Suarez, M.J. Soil Moisture Memory in Climate Models. J. Hydrometeorol. 2001, 2, 558–570. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Vicente-Serrano, S.; Beguería, S.; López-Moreno, J.I. A Multi-scalar drought index sensitive to global warming: The Standardized Precipitation Evapotranspiration Index—SPEI. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; López-Moreno, J.I.; Beguería, S.; Lorenzo-Lacruz, J.; Azorín-Molina, C.; Morán-Tejeda, E. Accurate Computation of a Streamflow Drought Index. J. Hydrol. Eng. 2012, 17, 318–332. [Google Scholar] [CrossRef]
- Tomas-Burguera, M.; Vicente-Serrano, S.M.; Peña-Angulo, D.; Domínguez-Castro, F.; Noguera, I.; El Kenawy, A. Global Characterization of the Varying Responses of the Standardized Precipitation Evapotranspiration Index to Atmospheric Evaporative Demand. J. Geophys. Res. Atmos. 2020, 125, 17. [Google Scholar] [CrossRef]
- Mehr, A.D.; Sorman, A.U.; Kahya, E.; Afshar, M.H. Climate change impacts on meteorological drought using SPI and SPEI: Case study of Ankara, Turkey. Hydrol. Sci. J. 2020, 65, 254–268. [Google Scholar] [CrossRef]
- Zare Abyaneh, H.; Ghabaei Sough, M.; Mosaedi, A. Drought monitoring based on Standardized Precipitation Evaoptranspiration Index (SPEI) under the effect of climate change. J. Water Soil Agric. Sci. Technol. 2015, 29, 374–392. [Google Scholar] [CrossRef]
- Stahl, K. Hydrological Drought: A Study Across Europe. Ph.D. Thesis, Albert-Ludwigs-University of Freiburg, Freiburg, Germany, 2001. [Google Scholar]
- Yeste, D.J.; Martin-Rosales, W.; Molero, E.; Esteban-Parra, M.J.; Rueda, F. Climate-driven trends in the streamflow records of a reference hydrologic network in Southern Spain. J. Hydrol. 2018, 556, 55–72. [Google Scholar] [CrossRef]
- Zhang, X.; Zengchao, H.; Singh, V.; Zhang, Y.; Feng, S.; Xu, Y.; Hao, F. Drought propagation under global warming: Characteristics, approaches, processes, and controlling factors. Sci. Total Environ. 2022, 838, 6021. [Google Scholar] [CrossRef]
- Yılmaz, M.; Alp, H.; Tosunoğlu, F.; Aşıkoğlu, Ö.L.; Eriş, E. Impact of climate change on meteorological and hydrological droughts for Upper Coruh Basin, Turkey. Nat. Hazards 2022, 112, 1039–1063. [Google Scholar] [CrossRef]
- Dikici, M. Drought analysis with different indices for the Asi Basin (Turkey). Sci. Rep. 2020, 10, 20739. [Google Scholar] [CrossRef]
- Chanyang, S.; Park, S.-Y.; Kim, J.-S.; Lee, J.-H. Prognostic and diagnostic assessment of hydrological drought using water and energy budget-based indices. J. Hydrol. 2020, 591, 125549. [Google Scholar] [CrossRef]
- Salimi, H.; Asadi, E.; Darbandi, S. Meteorological and hydrological drought monitoring using several drought indices. Appl. Water Sci. 2021, 11, 11. [Google Scholar] [CrossRef]
- Calvache, M.L.; Duque, C.; Pulido-Velázquez, D. Summary Editorial: Impacts of global change on groundwater in Western Mediterranean countries. Environ. Earth Sci. 2020, 79, 531. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Yao, H.; Gao, L.; Chen, Y.; Liu, M. Non-linear relationship of hydrological drought responding to meteorological drought and impact of a large reservoir. J. Hydrol. 2017, 551, 495–507. [Google Scholar] [CrossRef]
- Edossa, D.C.; Babel, M.S.; Gupta, A.D. Drought analysis in the Awash River Basin, Ethiopia. Water Resour. Manag. 2010, 24, 1441–1460. [Google Scholar] [CrossRef]
- Morán-Tejeda, E.; López-Moreno, J.I.; Ceballos-Barbancho, A.; Vicente-Serrano, S.M. River regimes and recent hydrological changes in the Duero basin (Spain). J. Hydrol. 2011, 404, 241–258. [Google Scholar] [CrossRef]
- Serrano Notivoli, R.; De Luis, M.; Beguería, S.; Saz, M.Á. SPREAD (Spanish PREcipitation At Daily scale). ESSD 2017, 9, 721–738. [Google Scholar]
- Tomás-Burguera, M.; Beguería, S.; Vicente Serrano, S.M.; Reig-Gracia, F.; Latorre Garcés, B. SPETo (Spanish reference evapotranspiration). Copernic. Publ. 2019, 11, 1917–1930. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO Irrigation and drainage paper 56; FAO—Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Confederación Hidrográfica del Guadalquivir, “S.A.I.H. del Guadalquivir”. 2021. Available online: https://www.chguadalquivir.es/saih/ (accessed on 5 July 2021).
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1964.
- Lorenzo-Lacruz, J.; Vicente-Serrano, S.; González-Hidalgo, J.; López-Moreno, J.; Cortesi, N. Hydrological drought response to meteorological drought in the Iberian Peninsula. Clim. Res. 2013, 58, 117–131. [Google Scholar] [CrossRef]
- Likens, G.E.; Bormann, F.H. Biogeochemistry of a Forested Ecosystem; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kazemzadeh, M.; Malekian, A. Spatial characteristics and temporal trends of meteorological and hydrological droughts in northwestern Iran. Nat. Hazards 2016, 80, 191–210. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Smith, C.; Wallace, J.M. An Intercomparison of Methods for finding Coupled Patterns in Climate Data. J. Clim. 1992, 5, 541–560. [Google Scholar] [CrossRef]
- Demšar, U.; Harris, P.; Brunsdon, C.; Fotheringham, A.S.; McLoone, S. Principal Component Analysis on Spatial Data: An Overview. Ann. Assoc. Am. Geogr. 2012, 103, 106–128. [Google Scholar] [CrossRef]
- Barreira, S. Differences between Temporal (S-Mode) and Spatial (T-Mode) Principal Component Analysis of Antarctic Sea Ice Monthly Concentration Anomalies: Relationship with Climate Variables. Geophys. Res. Abstr. 2011, 13, EGU2011-146. [Google Scholar]
- Hannachi, A.; Unkel, S.; Trendafilov, N.; Jolliffe, I. Independent Component Analysis of Climate Data: A New Look at EOF Rotation. J. Clim. 2009, 22, 2797–2812. [Google Scholar] [CrossRef]
- Vejmelka, M.; Pokorná, L.; Hlinka, J.; Hartman, D.; Jajcay, N.; Paluš, M. Non-random correlation structures and dimensionality reduction in multivariate climate data. Clim. Dyn. 2015, 44, 2663–2682. [Google Scholar] [CrossRef]
- Khodayar, S.; Sehlinger, A.; Feldmann, H.; Kottmeier, C. Sensitivity of soil moisture initialization for decadal predictions under different regional climatic conditions in Europe. Int. J. Climatol. 2014, 35, 1899–1915. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.; Huang, Q.; Huang, G.; Wang, H.; Leng, G.; Wang, L. Identifying drought propagation by simultaneously considering linear and nonlinear dependence in the Wei River basin of the Loess Plateau, China. J. Hydrol. 2020, 591, 125287. [Google Scholar] [CrossRef]
- Fang, X.; Pomeroy, J.W. Snowmelt runoff sensitivity analysis to drought on the Canadian prairies. Hydrol. Processes 2007, 21, 2594–2609. [Google Scholar] [CrossRef]
- Oertel, M.; Meza, F.J.; Gironás, J.; Scott, C.A.; Rojas, F.; Pineda-Pablos, N. Drought Propagation in Semi-Arid River Basins in Latin America: Lessons from Mexico to the Southern Cone. Water 2018, 10, 1564. [Google Scholar] [CrossRef]
- Heudorfer, B.; Stahl, K. Comparison of different threshold level methods for drought propagation analysis in Germany. Hydrol. Res. 2017, 5, 1311–1326. [Google Scholar] [CrossRef]
- van Langen, S.C.H.; Costa, A.C.; Ribeiro Neto, G.G.; van Oel, R. Effect of a reservoir network on drought propagation in a semi-arid catchment in Brazil. Hydrol. Sci. J. 2021, 66, 1567–1583. [Google Scholar] [CrossRef]
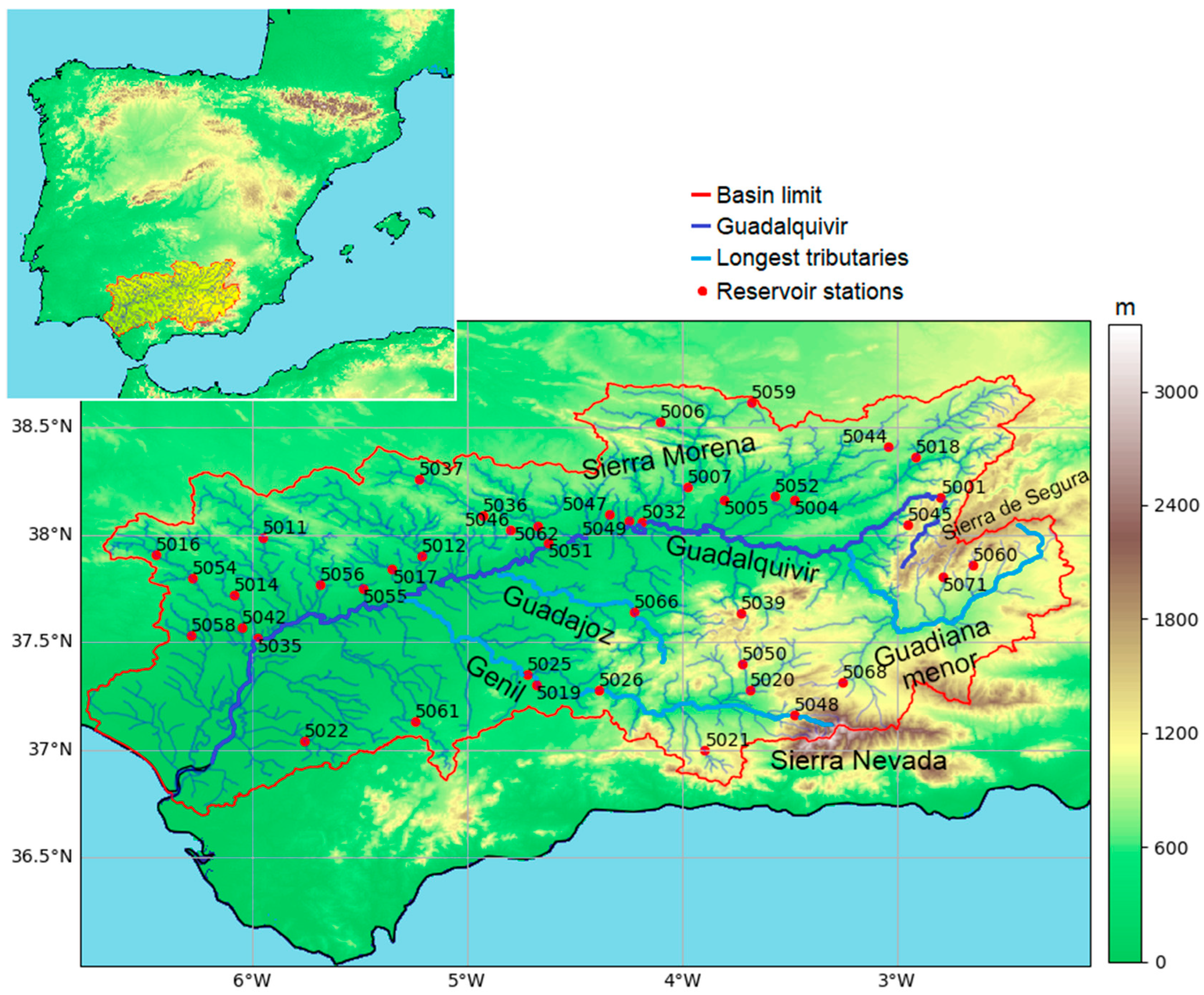
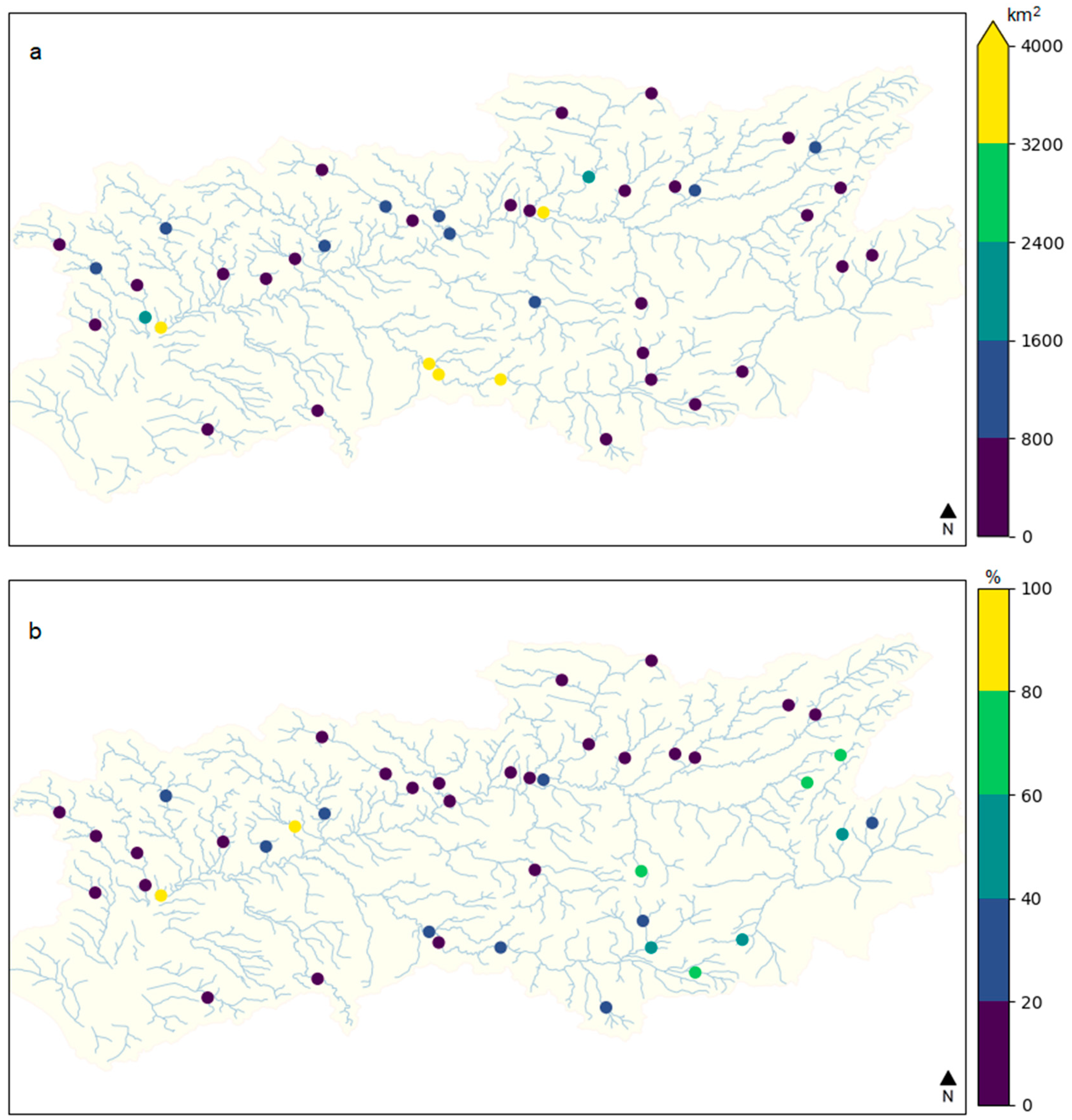

| Reference | Longitude [o] | Latitude [o] | Mean Monthly Streamflow (m3/s) | Altitude [m] | Area [km2] | Permeability [%] |
|---|---|---|---|---|---|---|
| 5001 | −2.795 | 38.175 | 13.08 | 550 | 550 | 78.13 |
| 5004 | −3.476 | 38.164 | 11.07 | 296 | 1330 | 1.07 |
| 5005 | −3.804 | 38.161 | 7.18 | 276 | 550 | 0 |
| 5006 | −4.099 | 38.526 | 5.65 | 511 | 557.48 | 10.01 |
| 5007 | −3.973 | 38.227 | 16.35 | 276 | 2300 | 2.31 |
| 5011 | −5.952 | 37.985 | 13.57 | 256 | 1100 | 32.26 |
| 5012 | −5.209 | 37.903 | 22.43 | 86.2 | 1078.5 | 23.87 |
| 5014 | −6.087 | 37.72 | 10.48 | 228.92 | 525 | 0 |
| 5016 | −6.45 | 37.909 | 7.71 | 286 | 408 | 4.02 |
| 5017 | −5.348 | 37.843 | 6.13 | 136 | 311 | 85.11 |
| 5018 | −2.913 | 38.365 | 11.31 | 506 | 1323 | 5.38 |
| 5019 | −4.676 | 37.301 | 28.84 | 214 | 5219 | 16.73 |
| 5020 | −3.681 | 37.277 | 3.39 | 605.4 | 626 | 55.49 |
| 5021 | −3.892 | 36.997 | 3.85 | 769 | 307 | 24.61 |
| 5022 | −5.757 | 37.043 | 6.45 | 13 | 460 | 18.10 |
| 5025 | −4.72 | 37.351 | 31.87 | 173 | 5830 | 29.49 |
| 5026 | −4.386 | 37.278 | 31.59 | 304 | 5000 | 20.13 |
| 5032 | −4.185 | 38.06 | 73.65 | 174 | 20,137 | 36.18 |
| 5035 | −5.975 | 37.52 | 186.46 | 8 | 46,860 | 91.94 |
| 5036 | −4.924 | 38.088 | 12.60 | 391.5 | 980 | 0 |
| 5037 | −5.222 | 38.26 | 4.34 | 470 | 439 | 5.24 |
| 5039 | −3.727 | 37.635 | 1.17 | 705 | 99 | 63.44 |
| 5042 | −6.049 | 37.569 | 18.67 | 6.5 | 1755 | 1.42 |
| 5044 | −3.038 | 38.409 | 0.63 | 681.3 | 62.59 | 9.91 |
| 5045 | −2.951 | 38.047 | 1.03 | 960.3 | 18 | 77.30 |
| 5046 | −4.798 | 38.022 | 0.58 | 487.5 | 28 | 0 |
| 5047 | −4.339 | 38.094 | 1.22 | 231 | 48.26 | 0 |
| 5048 | −3.475 | 37.161 | 5.35 | 808 | 176 | 76.51 |
| 5049 | −4.249 | 38.069 | 14.61 | 167.75 | 790 | 0 |
| 5050 | −3.72 | 37.402 | 2.06 | 755 | 245 | 32.16 |
| 5051 | −4.624 | 37.961 | 17.51 | 105 | 1287 | 1.05 |
| 5052 | −3.569 | 38.181 | 9.94 | 356 | 663 | 0 |
| 5054 | −6.279 | 37.798 | 15.76 | 190 | 850 | 4.49 |
| 5055 | −5.484 | 37.749 | 6.01 | 73.65 | 243 | 28.35 |
| 5056 | −5.684 | 37.772 | 11.18 | 207 | 459 | 9.96 |
| 5058 | −6.283 | 37.534 | 6.70 | 63.8 | 228 | 3.82 |
| 5059 | −3.68 | 38.618 | 2.27 | 681 | 135.12 | 0 |
| 5060 | −2.647 | 37.859 | 2.09 | 972.5 | 152 | 38.04 |
| 5061 | −5.242 | 37.131 | 3.77 | 207 | 297.6 | 1.72 |
| 5062 | −4.673 | 38.043 | 17.47 | 151.5 | 1209 | 0 |
| 5066 | −4.225 | 37.64 | 10.23 | 294 | 1185 | 3.44 |
| 5068 | −3.254 | 37.314 | 1.40 | 870 | 184.4 | 47.24 |
| 5071 | −2.786 | 37.807 | 5.70 | 837.5 | 110 | 51.29 |
| Variable | PC1 | PC2 |
|---|---|---|
| Altitude | 0.38 | 7.34 × 10−3 |
| Permeability | 0.28 | 0.70 |
| Catchment area | 5.05 × 10−9 | 3.2 × 10−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romero-Jiménez, E.; García-Valdecasas Ojeda, M.; Rosa-Cánovas, J.J.; Yeste, P.; Castro-Díez, Y.; Esteban-Parra, M.J.; Gámiz-Fortis, S.R. Hydrological Response to Meteorological Droughts in the Guadalquivir River Basin, Southern Iberian Peninsula. Water 2022, 14, 2849. https://doi.org/10.3390/w14182849
Romero-Jiménez E, García-Valdecasas Ojeda M, Rosa-Cánovas JJ, Yeste P, Castro-Díez Y, Esteban-Parra MJ, Gámiz-Fortis SR. Hydrological Response to Meteorological Droughts in the Guadalquivir River Basin, Southern Iberian Peninsula. Water. 2022; 14(18):2849. https://doi.org/10.3390/w14182849
Chicago/Turabian StyleRomero-Jiménez, Emilio, Matilde García-Valdecasas Ojeda, Juan José Rosa-Cánovas, Patricio Yeste, Yolanda Castro-Díez, María Jesús Esteban-Parra, and Sonia R. Gámiz-Fortis. 2022. "Hydrological Response to Meteorological Droughts in the Guadalquivir River Basin, Southern Iberian Peninsula" Water 14, no. 18: 2849. https://doi.org/10.3390/w14182849







