Optimal Sprinkler Application Rate of Water–Fertilizer Integration Machines Based on Radial Basis Function Neural Network
Abstract
:1. Introduction
2. Neural Network Training Set Data Acquisition
2.1. RBF Neural Network Basic Theory
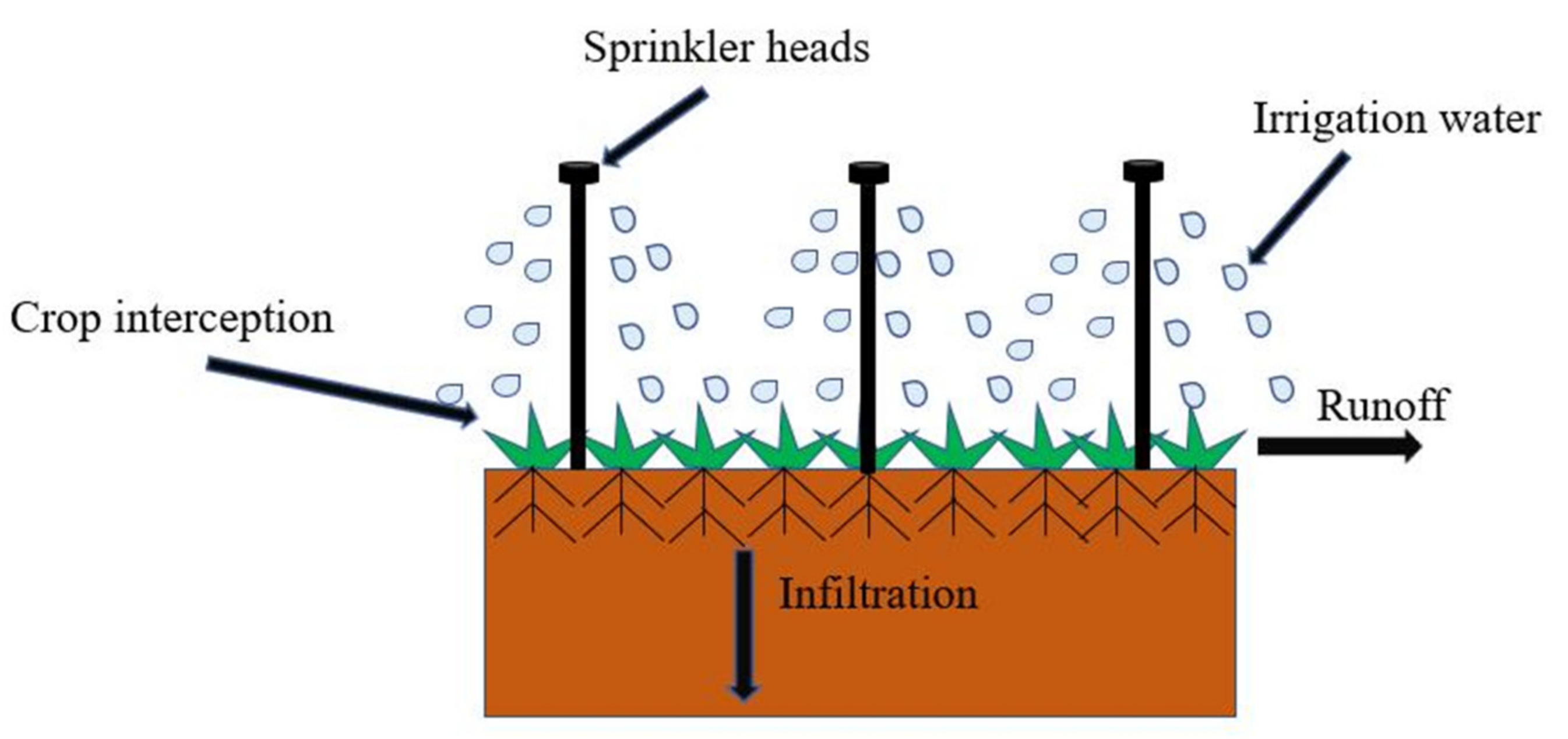
2.2. Spray Irrigation Soil Hydrology Model
2.2.1. Soil Water Infiltration Process Equation
2.2.2. Unsaturated Soil Hydraulic Properties Function
2.2.3. Irrigation Water Interception Equation
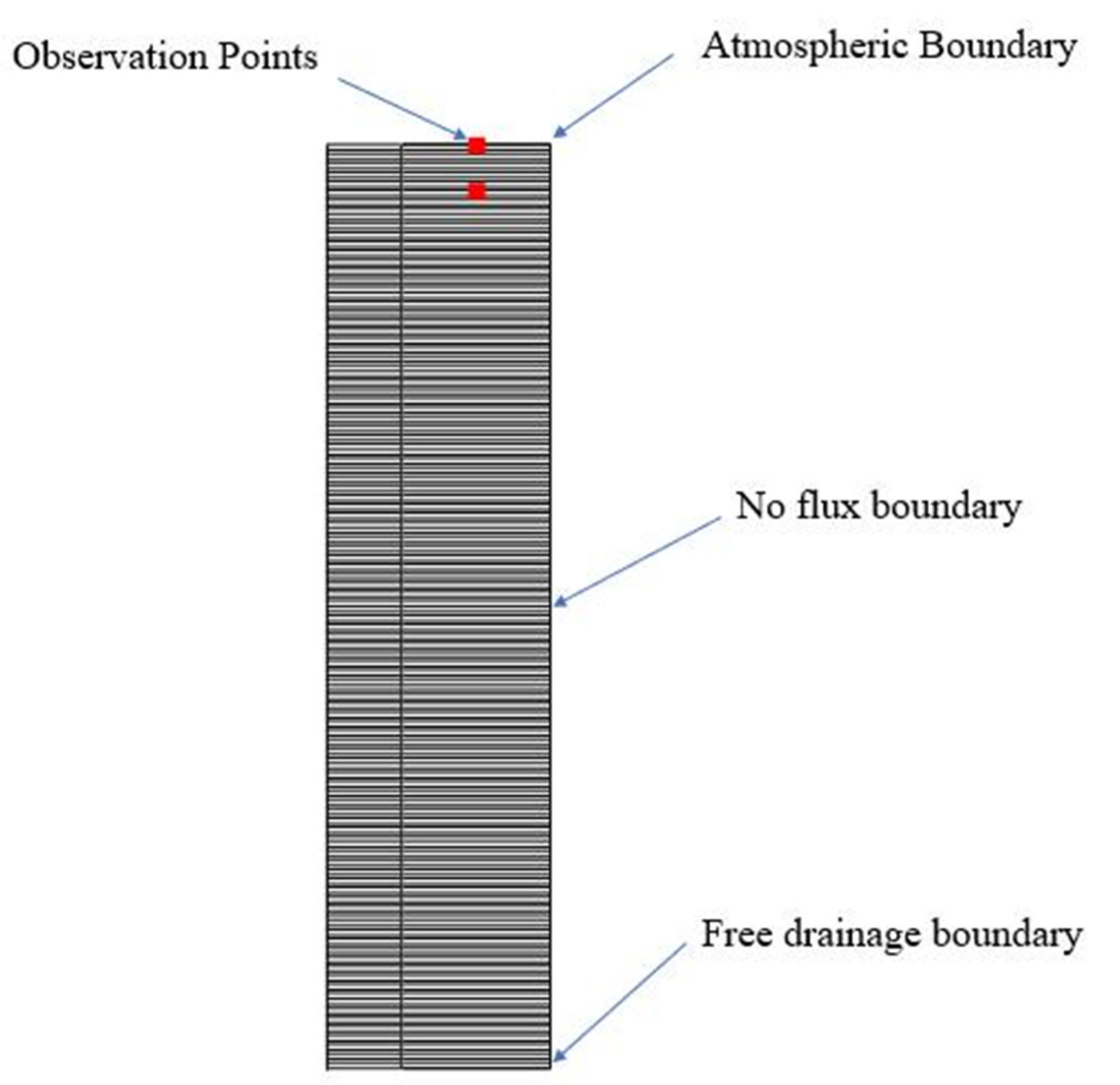
2.2.4. Soil Profile Parameter Setting
2.3. Determination of Simulation Parameters
2.4. Acquire and Analyze Data
2.4.1. Simulation Data
2.4.2. Data Analysis
3. Determination of Neural Network Input and Output Layers
4. Training Data Pre-Processing
5. Basic Theory of Neural Networks
5.1. BP Neural Network Basic Theory
5.2. Generalized Regression Neural Network Theory
6. Evaluation Criteria for Neural Networks
7. Training and Comparison
7.1. Neural Network Parameter Determination
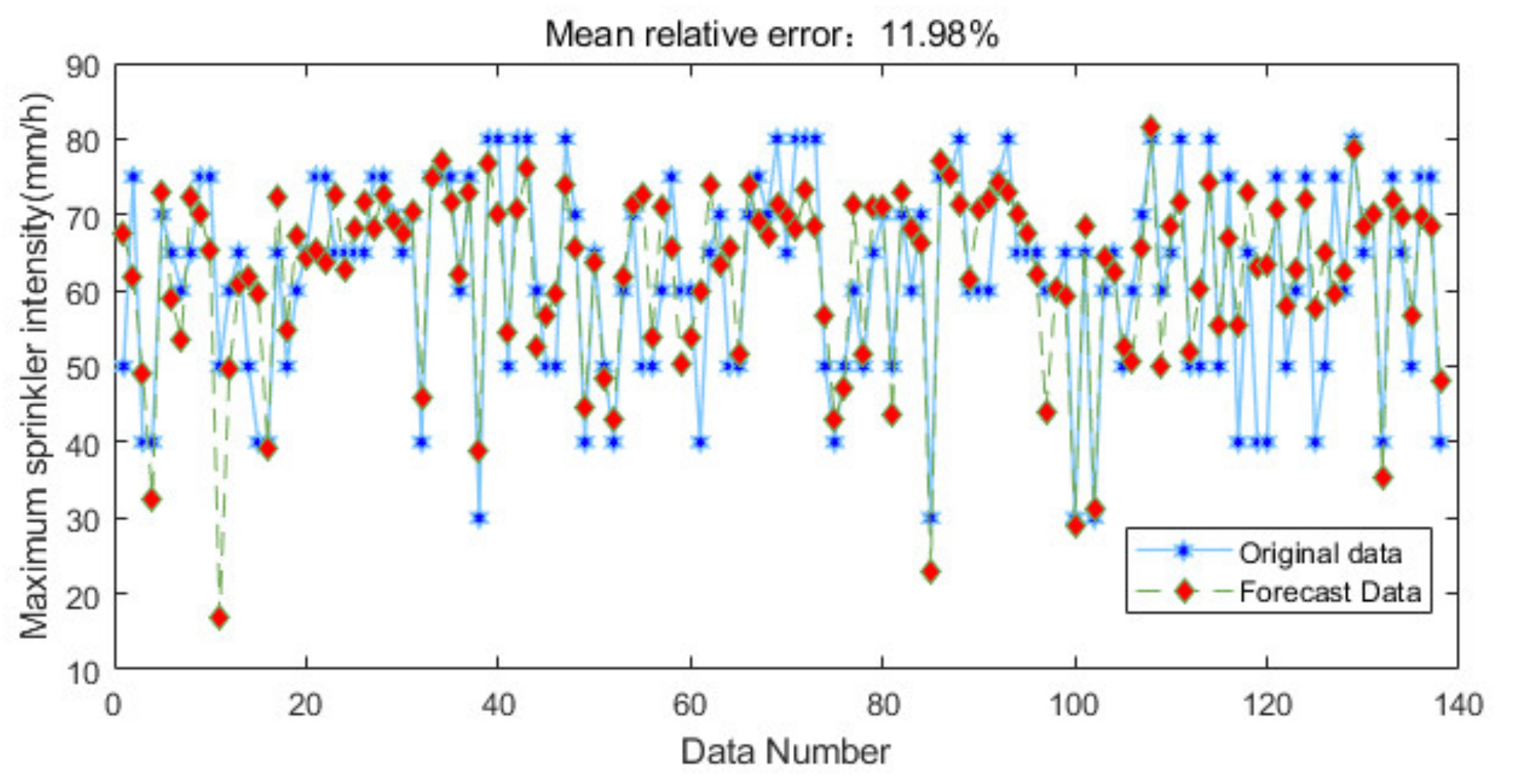
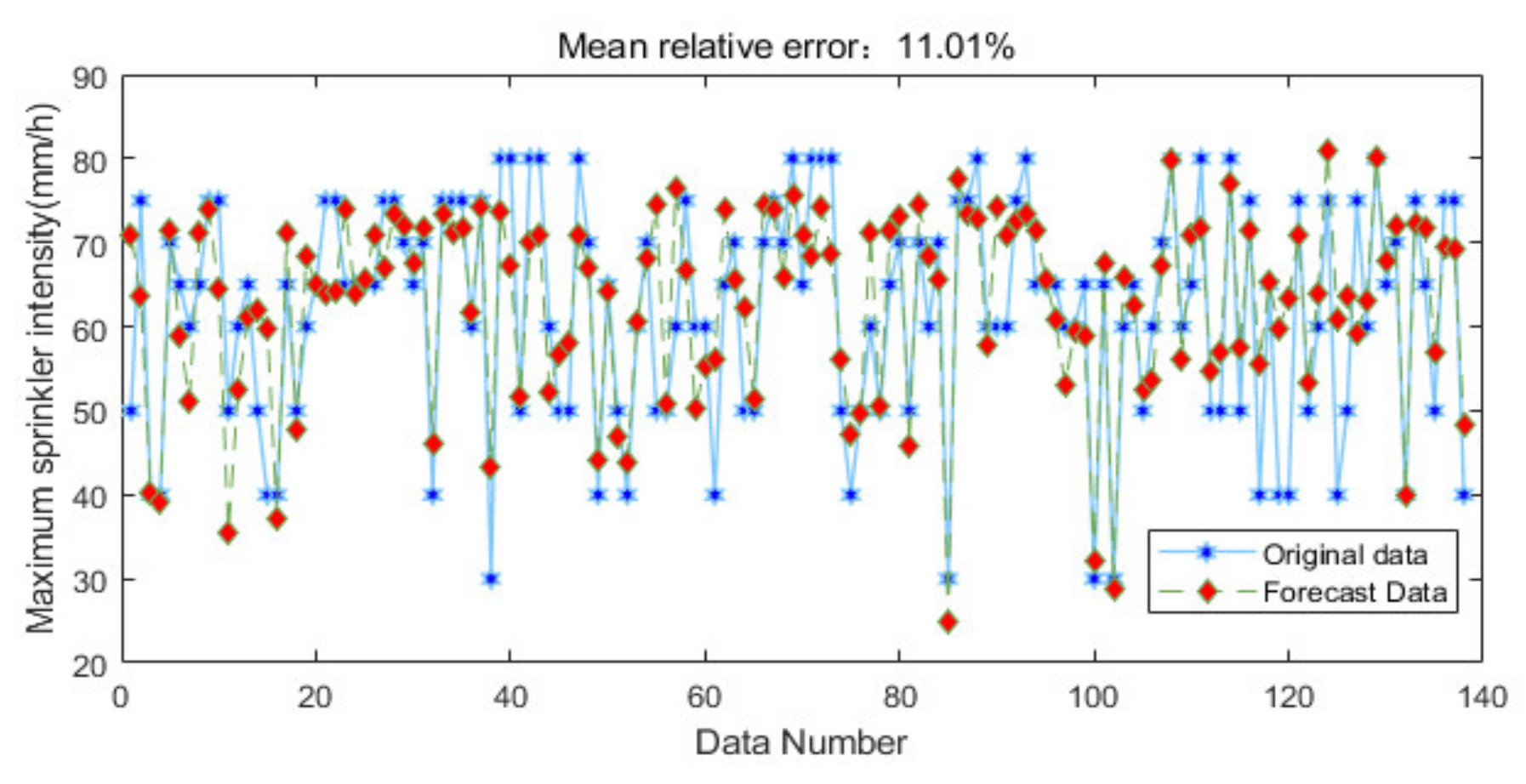
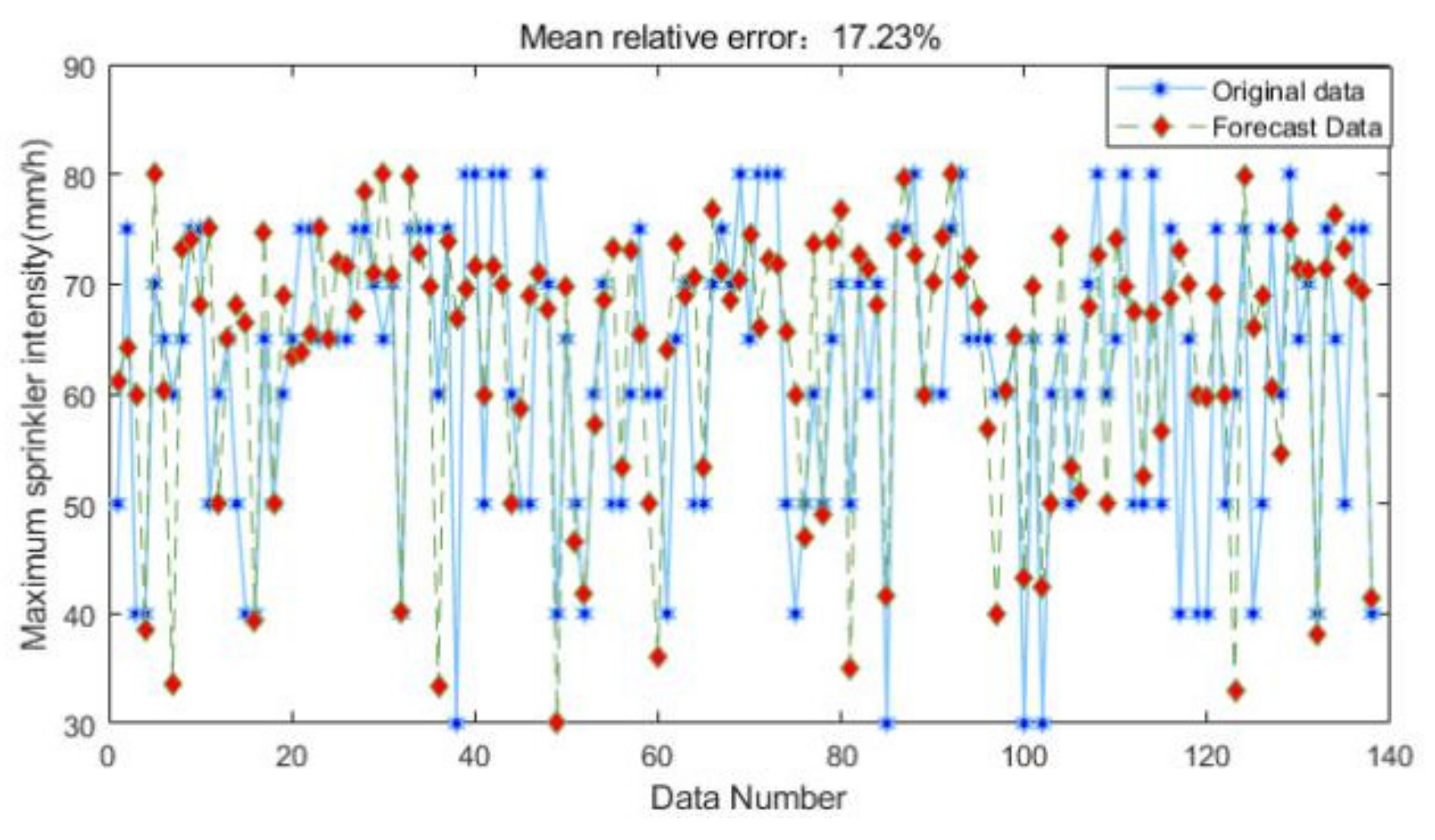
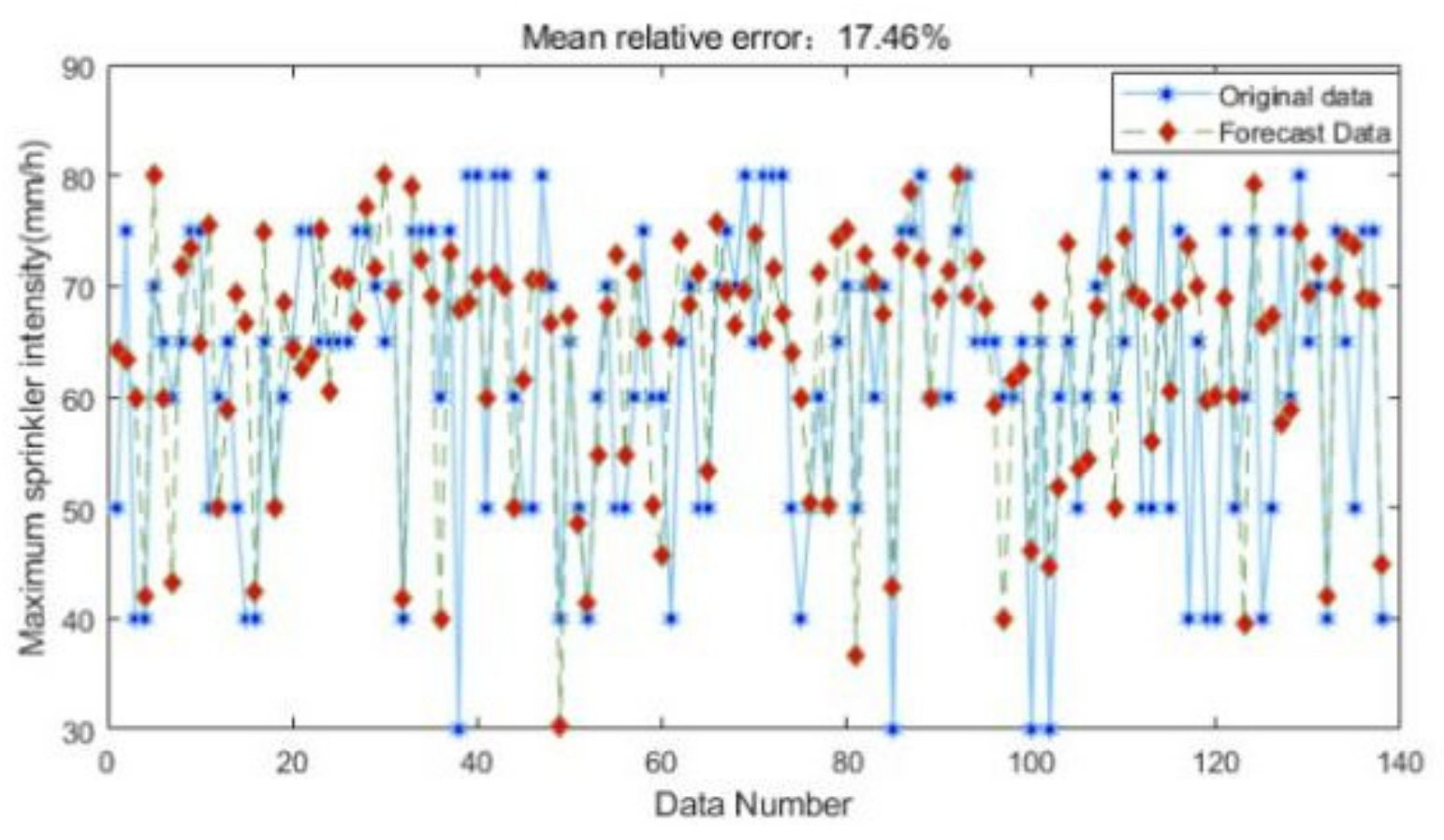
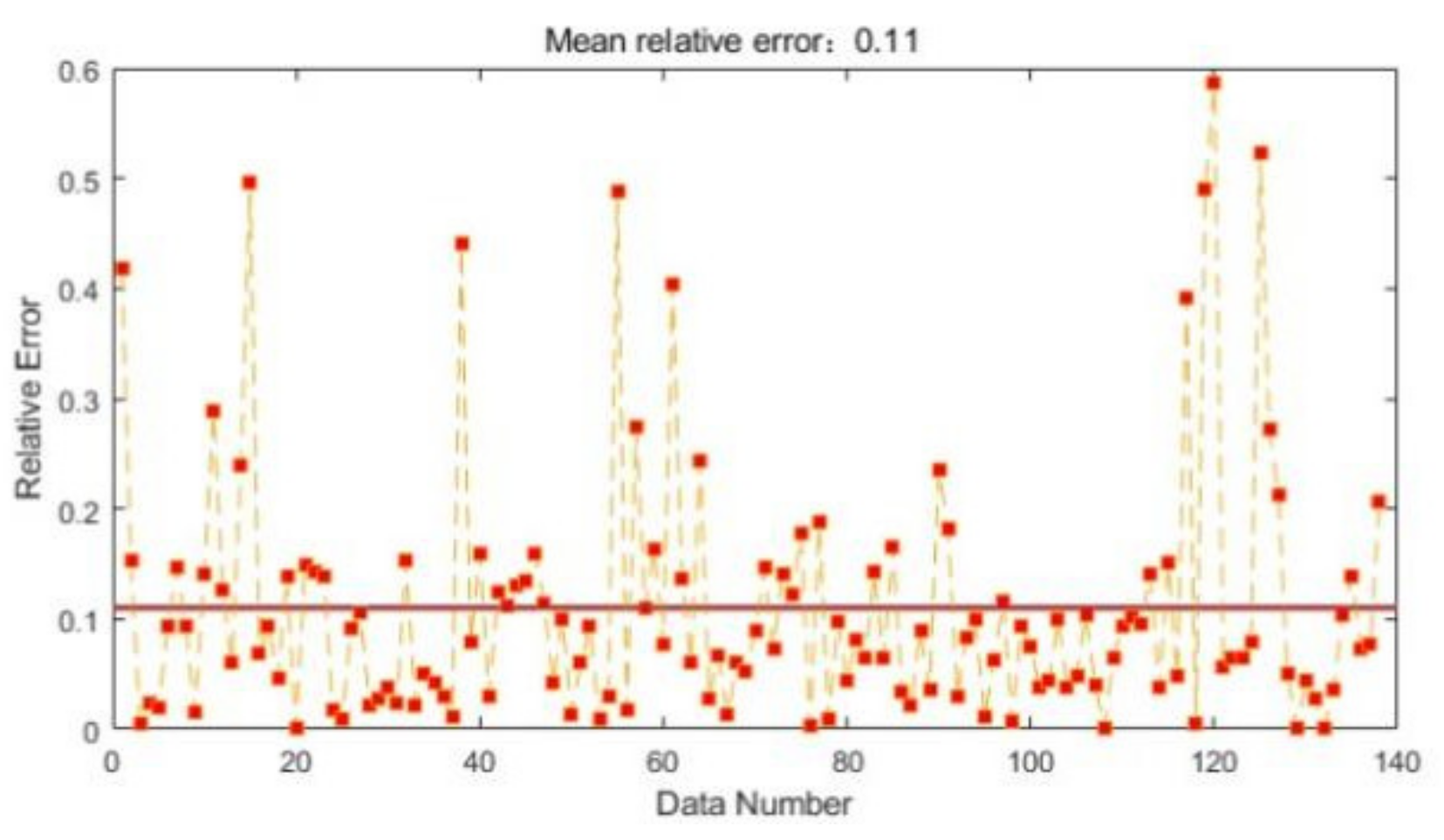
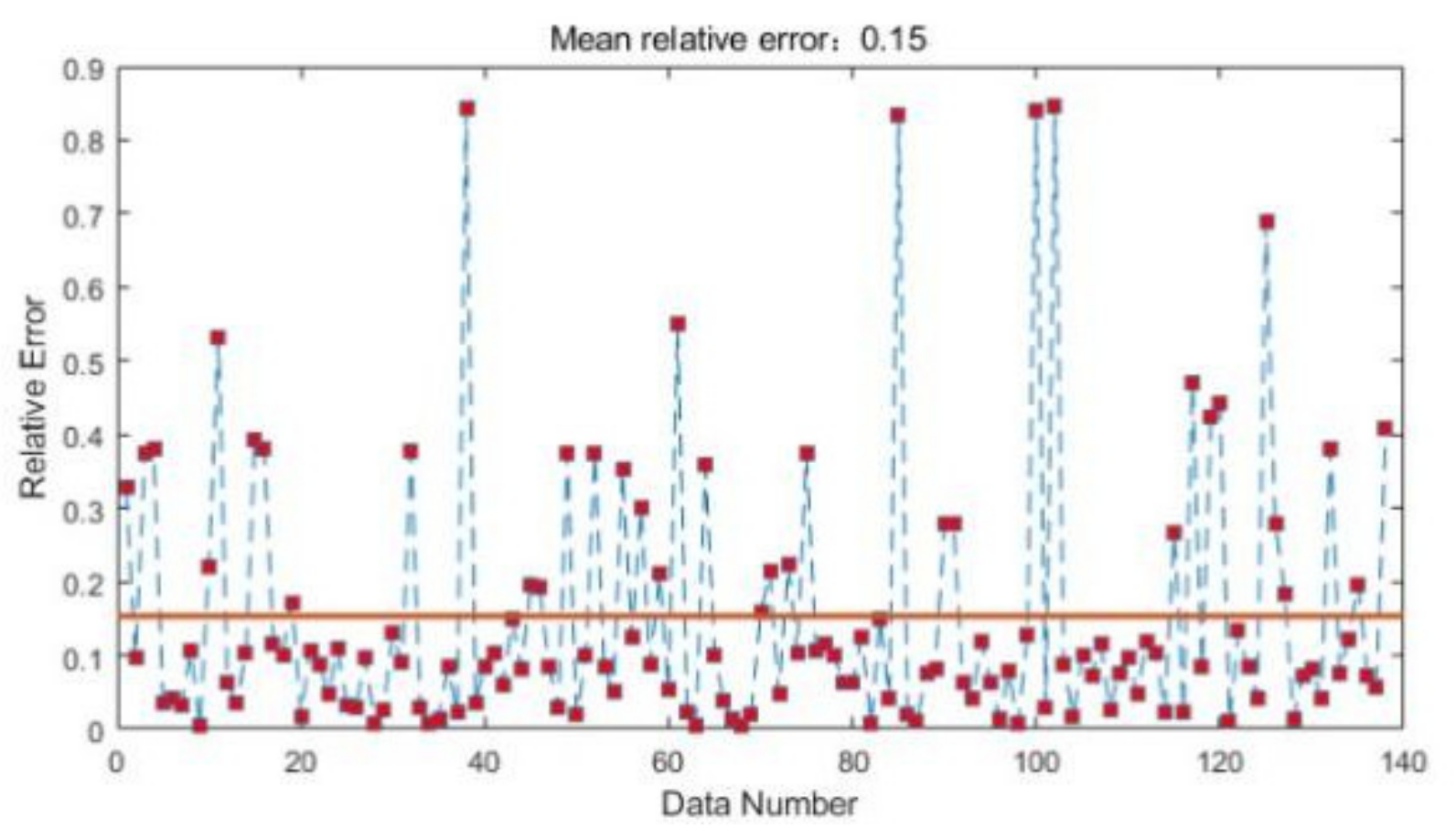
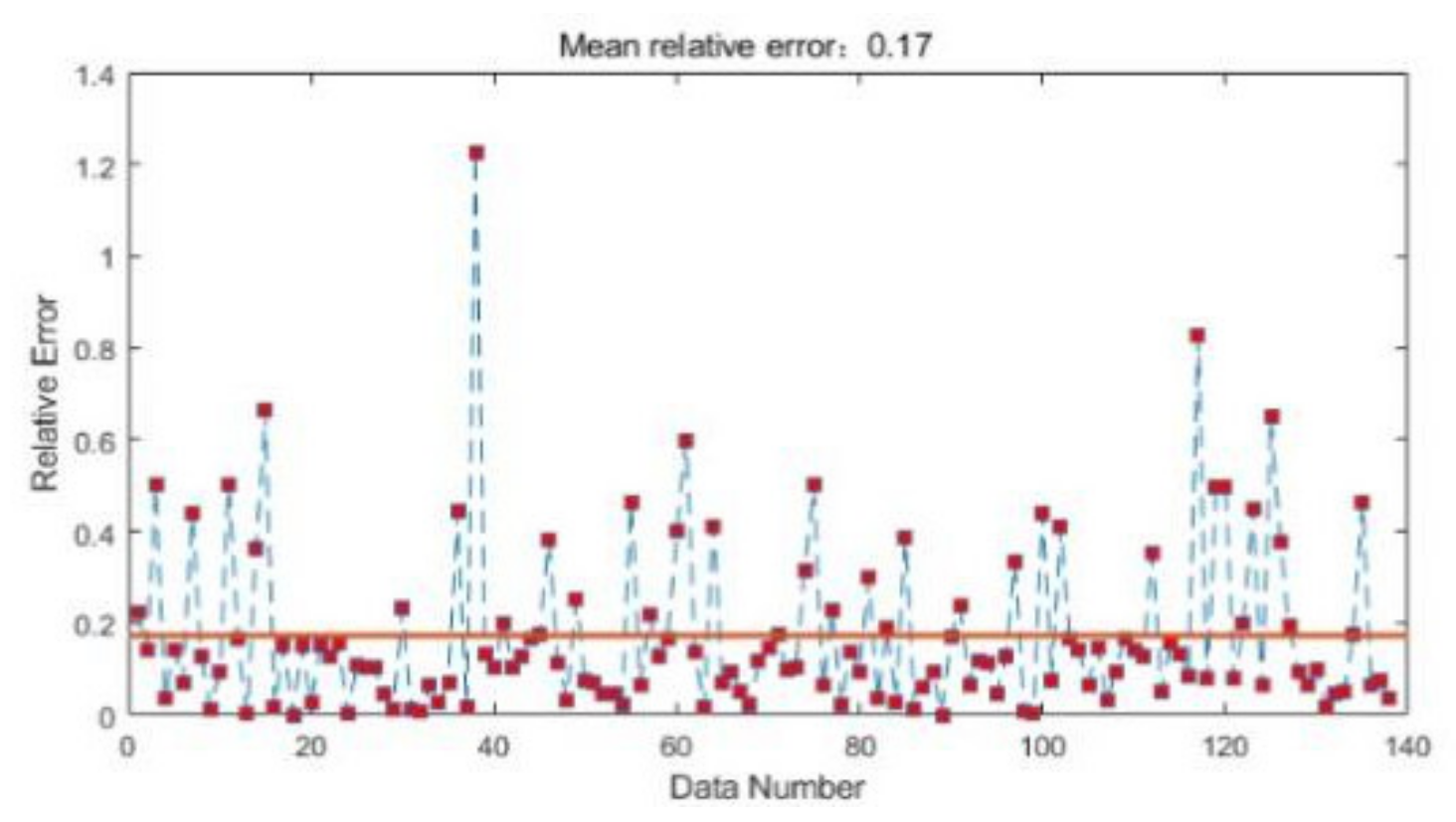
7.2. Comparison of Neural Network Errors
8. Empirical Formula for Total Irrigation Water
9. Experimental Verification
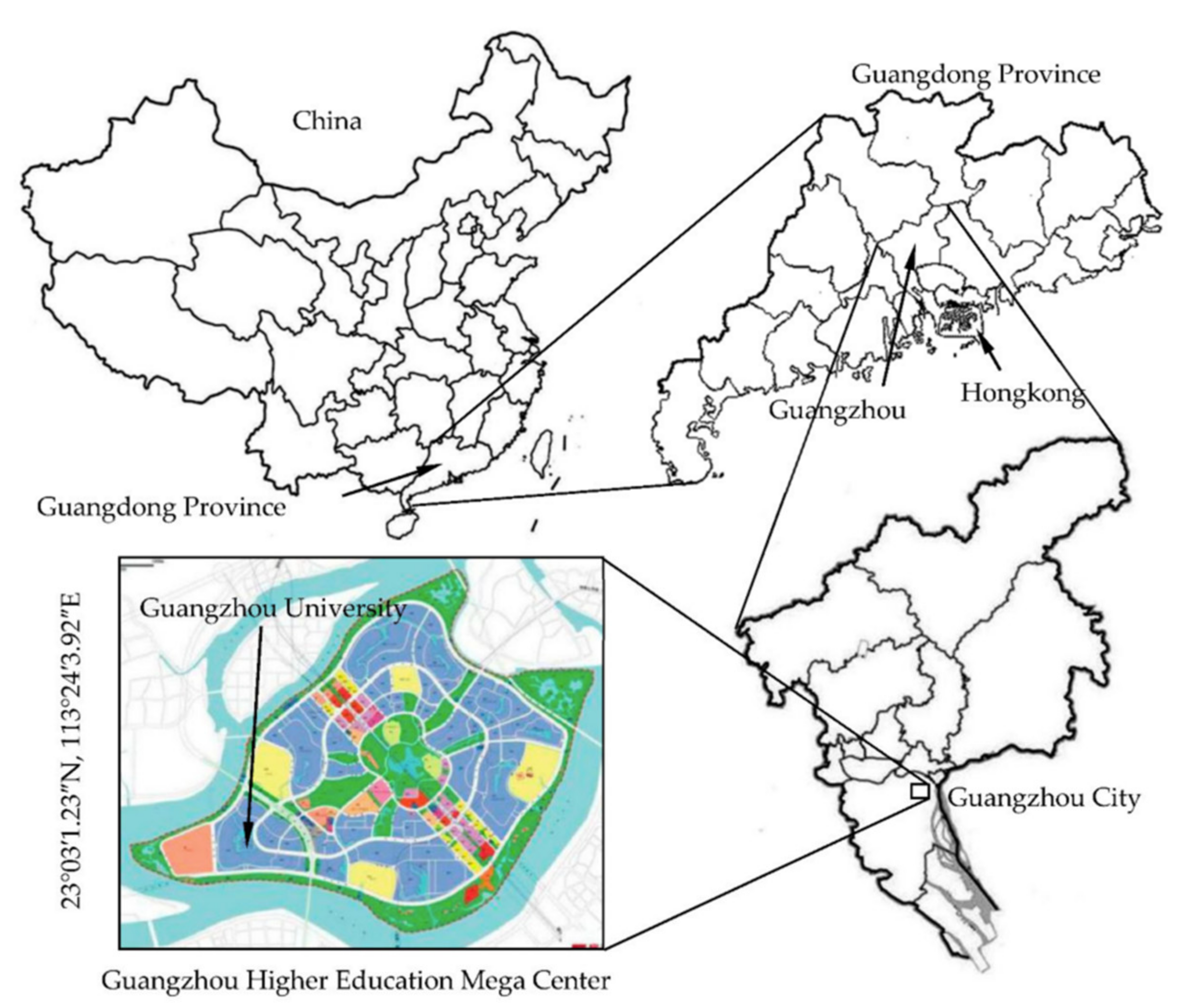
9.1. Spray Irrigation Soil Infiltration Experiment Site
9.2. Experimental Soil Samples
9.3. Construction of Experimental Platform
9.3.1. Soil Infiltration Device
9.3.2. Sprinkler Irrigation Equipment
9.3.3. Soil Moisture Data Measurement and Transmission System
9.4. Experimental Steps
- (1)
- As shown in Figure 23, the amount of water required to dry the soil to the moisture content in the table was calculated based on the initial soil moisture content listed in Table 5. The soil is then spread out and the water is sprayed evenly on top of the soil to ensure uniformity of soil moisture content.
- (2)
- The soil with the required initial moisture content was left to stand for 24 h and then filled into the soil sample bottles at 2 cm intervals according to the soil bulk density given in Table 5.
- (3)
- As shown in Figure 24, at the top end of the soil sample bottle, the soil surface is covered with another layer of grass to simulate crop interception.
- (4)
- (5)
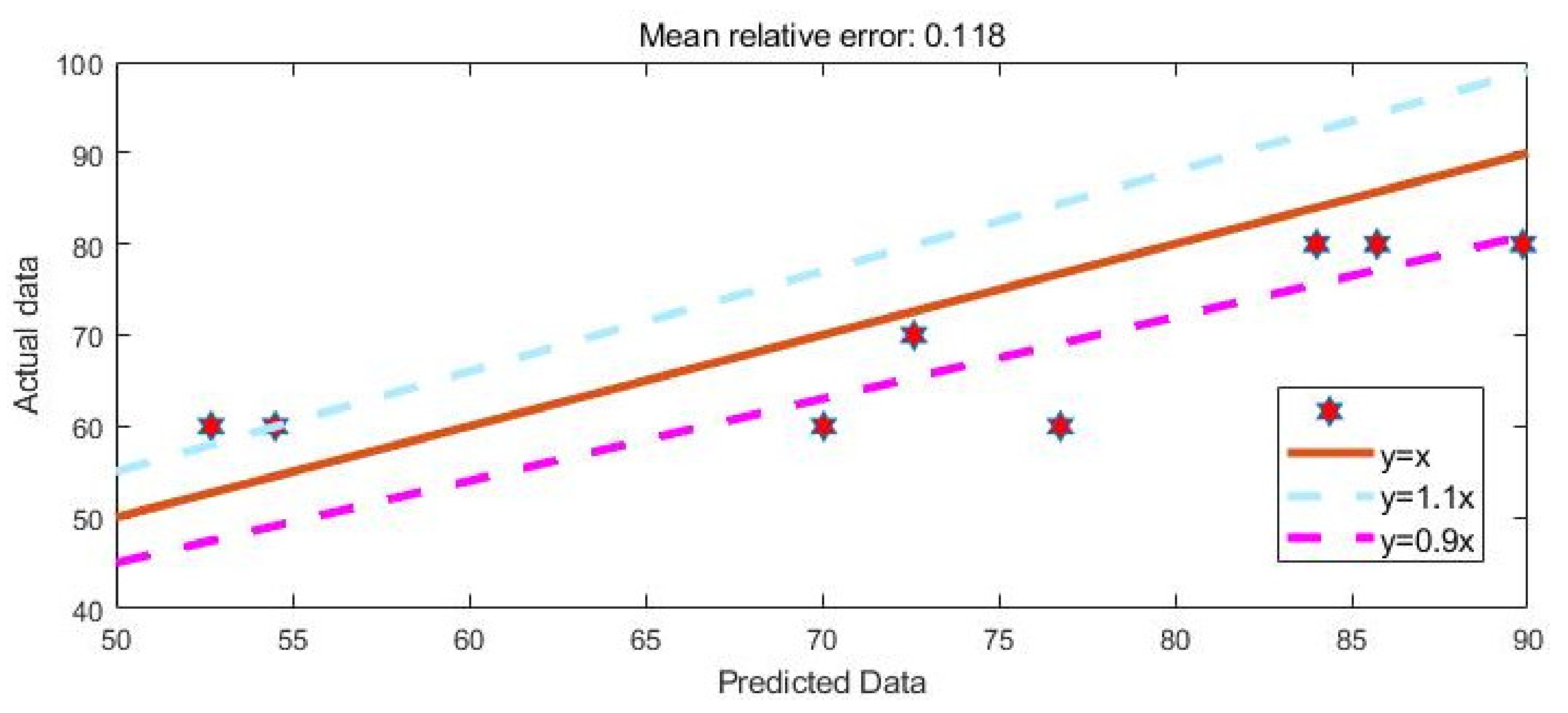
9.5. Comparison of Neural Network Prediction Results with the Actual Situation
10. Value Evaluation Using Optimal Spray Intensity
11. Conclusions
- (1)
- In this paper, the highest accuracy of the optimal sprinkler application rate predicted by RBF neural network is obtained by trial and error method when the smoothing parameter is 1.14. The average relative error of its prediction is 0.11 and the RBF neural network is compared with BP neural network and generalized regression neural network. It can be found that the RBF neural network has the highest prediction accuracy. This indicates that RBF neural network is more suitable for the prediction of sprinkler application rate than other neural networks.
- (2)
- Comparing the experimental data with the prediction results, the relative error of RBF neural network prediction is around 10%. This indicates that the RBF neural network has some practical value in the prediction of sprinkler application rate.
- (3)
- The RBF neural network not only predicts the best sprinkler application rate with high accuracy, but also its fast computing speed makes it ideal for placement into embedded devices.
- (4)
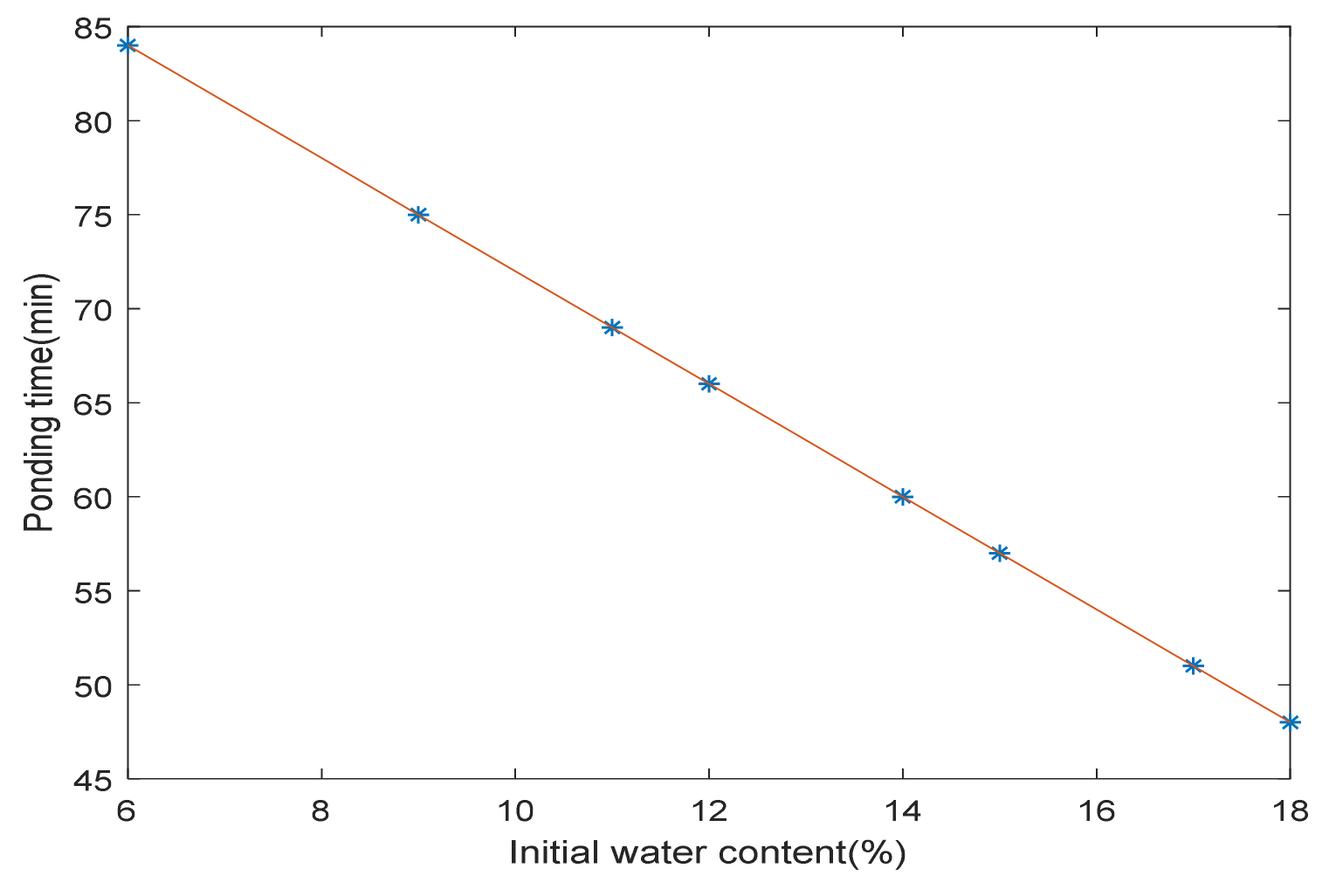
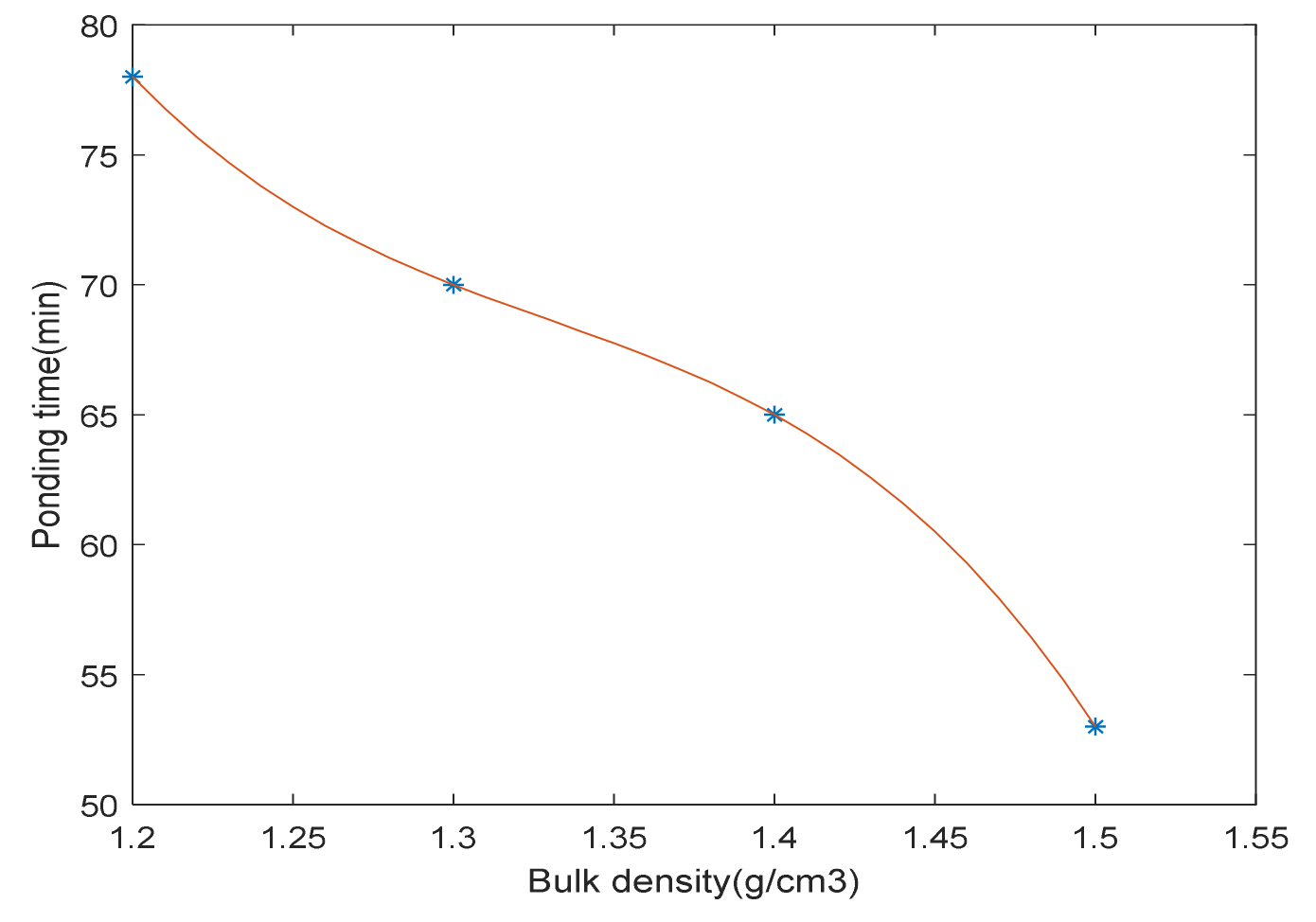
- Among the initial soil water content, bulk density and sprinkler application rate, the most complex effect on soil water accumulation time is the sprinkler application rate.
- (5)
- The finite element values simulated by the soil infiltration model established by the partial differential equation do not differ much from the actual values. Therefore, applying the finite element method to soil infiltration can greatly reduce the complexity of soil infiltration experiments.
- (6)
- The maximum application rate of sprinkler irrigation predicted by combining the RBF neural network with the total irrigation volume formula was compared with the conventional recommended application rate of sprinkler irrigation in actual sprinkler irrigation using the lawn as an example. When the optimal application rate of sprinkler irrigation proposed in this paper was used, the sprinkler time was greatly reduced. For an irrigation volume of 58 mm, for example, the optimal application rate of sprinkler irrigation saves 3.4 h and improves the overall efficiency by about 70%, which greatly reduces irrigation losses due to long sprinkler time and also reduces the operation and maintenance costs of the equipment.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, K.; Song, B.; Zhu, D.L. The Influence of Sinusoidal Oscillating Water Flow on Sprinkler and Impact Kinetic Energy Intensities of Laterally-Moving Sprinkler Irrigation Systems. Water 2019, 11, 1325. [Google Scholar] [CrossRef]
- Maraseni, T.N.; Mushtaq, S.; Reardon-Smith, K. Re-evaluating the rationale for irrigation technology adoption through an integrated trade-off analysis: Case study of a cotton farming system in Australia. J. Water Clim. Chang. 2014, 5, 328–340. [Google Scholar] [CrossRef]
- Zhang, L.; Fu, B.Y.; Ren, N.W.; Huang, Y. Effect of Pulsating Pressure on Water Distribution and Application Uniformity for Sprinkler Irrigation on Sloping Land. Water 2019, 11, 13. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Griensven, A.V.; Liew, M.W.V. MT3DMS: Model Use, Calibration, and Validation. Trans. Asabe 2012, 55, 1549–1559. [Google Scholar] [CrossRef]
- Gencoglan, C.; Gencoglan, S.; Merdun, H.; Ucan, K. Determination of ponding time and number of on-off cycles for sprinkler irrigation applications. Agric. Water Manag. 2005, 72, 47–58. [Google Scholar] [CrossRef]
- Espinosa, F.E.C.; Torres, P.; Feyen, J. Experimental assessment of the sprinkler application rate for steep sloping fields. J. Irrig. Drain. Eng. ASCE 2007, 133, 276–278. [Google Scholar] [CrossRef]
- Dadhich, S.M.; Singh, R.P.; Mahar, P.S. Saving time in sprinkler irrigation application through cyclic operation: A theoretical approach. Irrig. Drain. 2012, 61, 631–635. [Google Scholar] [CrossRef]
- DeBoer, D.W.; Chu, S.T. Sprinkler technologies, soil infiltration, and runoff. J. Irrig. Drain. Eng. ASCE 2001, 127, 234–239. [Google Scholar] [CrossRef]
- Trejo-Alonso, J.; Fuentes, C.; Chavez, C.; Quevedo, A.; Gutierrez-Lopez, A.; Gonzalez-Correa, B. Saturated Hydraulic Conductivity Estimation Using Artificial Neural Networks. Water 2021, 13, 705. [Google Scholar] [CrossRef]
- D’Emilio, A.; Aiello, R.; Consoli, S.; Vanella, D.; Iovino, M. Artificial Neural Networks for Predicting the Water Retention Curve of Sicilian Agricultural Soils. Water 2018, 10, 1413. [Google Scholar] [CrossRef] [Green Version]
- Dehghanisanij, H.; Emami, S.; Achite, M.; Linh, N.T.T.; Pham, Q.B. Estimating Yield and Water Productivity of Tomato Using a Novel Hybrid Approach. Water 2021, 13, 3615. [Google Scholar] [CrossRef]
- Gu, J.; Yin, G.H.; Huang, P.F.; Guo, J.L.; Chen, L.J. An improved back propagation neural network prediction model for subsurface drip irrigation system. Comput. Electr. Eng. 2017, 60, 58–65. [Google Scholar] [CrossRef]
- Chen, Z.L.; Zhao, C.J.; Wu, H.R.; Miao, Y.S. A Water-saving Irrigation Decision-making Model for Greenhouse Tomatoes based on Genetic Optimization T-S Fuzzy Neural Network. KSII Trans. Internet Inf. Syst. 2019, 13, 2925–2948. [Google Scholar]
- Al-Naji, A.; Fakhri, A.B.; Gharghan, S.K.; Chahl, J. Soil color analysis based on a RGB camera and an artificial neural network towards smart irrigation: A pilot study. Heliyon 2021, 7, 9. [Google Scholar] [CrossRef]
- Perea, G.; Poyato, C.; Montesinos, P.; Diaz, J.A.R. Prediction of applied irrigation depths at farm level using artificial intelligence techniques. Agric. Water Manag. 2018, 206, 229–240. [Google Scholar] [CrossRef]
- Cao, C.; Song, S.Y.; Chen, J.P.; Zheng, L.J.; Kong, Y.Y. An Approach to Predict Debris Flow Average Velocity. Water 2017, 9, 205. [Google Scholar] [CrossRef]
- Wei, D.F. Network traffic prediction based on RBF neural network optimized by improved gravitation search algorithm. Neural Comput. Appl. 2017, 28, 2303–2312. [Google Scholar] [CrossRef]
- Arbat, G.; Puig-Bargues, J.; Barragan, J.; Bonany, J.; de Cartagena, F.R. Monitoring soil water status for micro-irrigation management versus modelling approach. Biosyst. Eng. 2008, 100, 286–296. [Google Scholar] [CrossRef]
- Aster, R.C.; Thurber, C.H.; Borchers, B. Parameter Estimation and Inverse Problems; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Mi, L.; Luo, W. An Approximate Analytical Solution of Van Genuchten Model. In Proceedings of the 2017 2nd International Symposium on Advances in Electrical, Electronics and Computer Engineering (ISAEECE 2017), Guangzhou, China, 25–26 March 2017. [Google Scholar]
- Mao, Y.W.; Liu, S.; Nahar, J.; Liu, J.F.; Ding, F. Soil moisture regulation of agro-hydrological systems using zone model predictive control. Comput. Electron. Agric. 2018, 154, 239–247. [Google Scholar] [CrossRef]
- Lei, W.K.; Dong, H.Y.; Chen, P.; Lv, H.B.; Fan, L.Y.; Mei, G.X. Study on Runoff and Infiltration for Expansive Soil Slopes in Simulated Rainfall. Water 2020, 12, 19. [Google Scholar]
- Yang, G.; Wu, X.P.; Song, Y.X.; Chen, Y.C. Fault diagnosis of complicated machinery system based on genetic algorithm and fuzzy RBF neural network. In Advances in Natural Computation; Jiao, L., Wang, L., Gao, X., Liu, J., Wu, F., Eds.; Lecture Notes in Computer Science; Springer-Verlag: Berlin, Germany, 2006; Volume 4222, Pt 2, pp. 908–917. [Google Scholar]
- Chen, S.Y.; Fang, G.H.; Huang, X.F.; Zhang, Y.H. Water Quality Prediction Model of a Water Diversion Project Based on the Improved Artificial Bee Colony-Backpropagation Neural Network. Water 2018, 10, 806. [Google Scholar] [CrossRef]
- Wang, Z.; Jia, L.M.; Qin, Y.; Wang, Y. Railway passenger traffic volume prediction based on neural network. Appl. Artif. Intell. 2007, 21, 1–10. [Google Scholar]
- Cai, H.H.; Wu, Z.H.; Huang, C.; Huang, D.Z. Wind Power Forecasting Based on Ensemble Empirical Mode Decomposition with Generalized Regression Neural Network Based on Cross-Validated Method. J. Electr. Eng. Technol. 2019, 14, 1823–1829. [Google Scholar] [CrossRef]
- Firat, M.; Gungor, M. Generalized Regression Neural Networks and Feed Forward Neural Networks for prediction of scour depth around bridge piers. Adv. Eng. Softw. 2009, 40, 731–737. [Google Scholar] [CrossRef]
- Zhang, F.Q.; Wu, S.Y.; Wang, Y.O.; Xiong, R.; Ding, G.Y.; Mei, P.; Liu, L.Y. Application of Quantum Genetic Optimization of LVQ Neural Network in Smart City Traffic Network Prediction. IEEE Access 2020, 8, 104555–104564. [Google Scholar] [CrossRef]
- Deng, D.; Zhao, W.W.; Wan, D.C. Vortex-induced vibration prediction of a flexible cylinder by three-dimensional strip model. Ocean Eng. 2020, 205, 17. [Google Scholar] [CrossRef]
- Liang, Z.W.; Liu, X.C.; Zou, T.; Xiao, J.R. Adaptive Prediction of Water Droplet Infiltration Effectiveness of Sprinkler Irrigation Using Regularized Sparse Autoencoder-Adaptive Network-Based Fuzzy Inference System (RSAE-ANFIS). Water 2021, 13, 791. [Google Scholar] [CrossRef]
- Zobeck, T.M. Rapid soil particle size analyses using laser diffraction. Appl. Eng. Agric. 2004, 20, 633–639. [Google Scholar] [CrossRef]
- Li, J.T.; Wa, S.; Song, G.J.; Qiao, X.Y.; Wang, J.H. Modification of Zhengzhou Groundwater Balance Test Site-General Idea and Application Outlook. Hydrogeol. Eng. Geol. 2019, 7. [Google Scholar]
- Chu, C.W.; Zhu, Z.C.; Bian, H.T.; Jiang, J.C. Design of self-heating test platform for sulfide corrosion and oxidation based on Fuzzy PID temperature control system. Meas. Control 2021, 54, 1082–1096. [Google Scholar] [CrossRef]





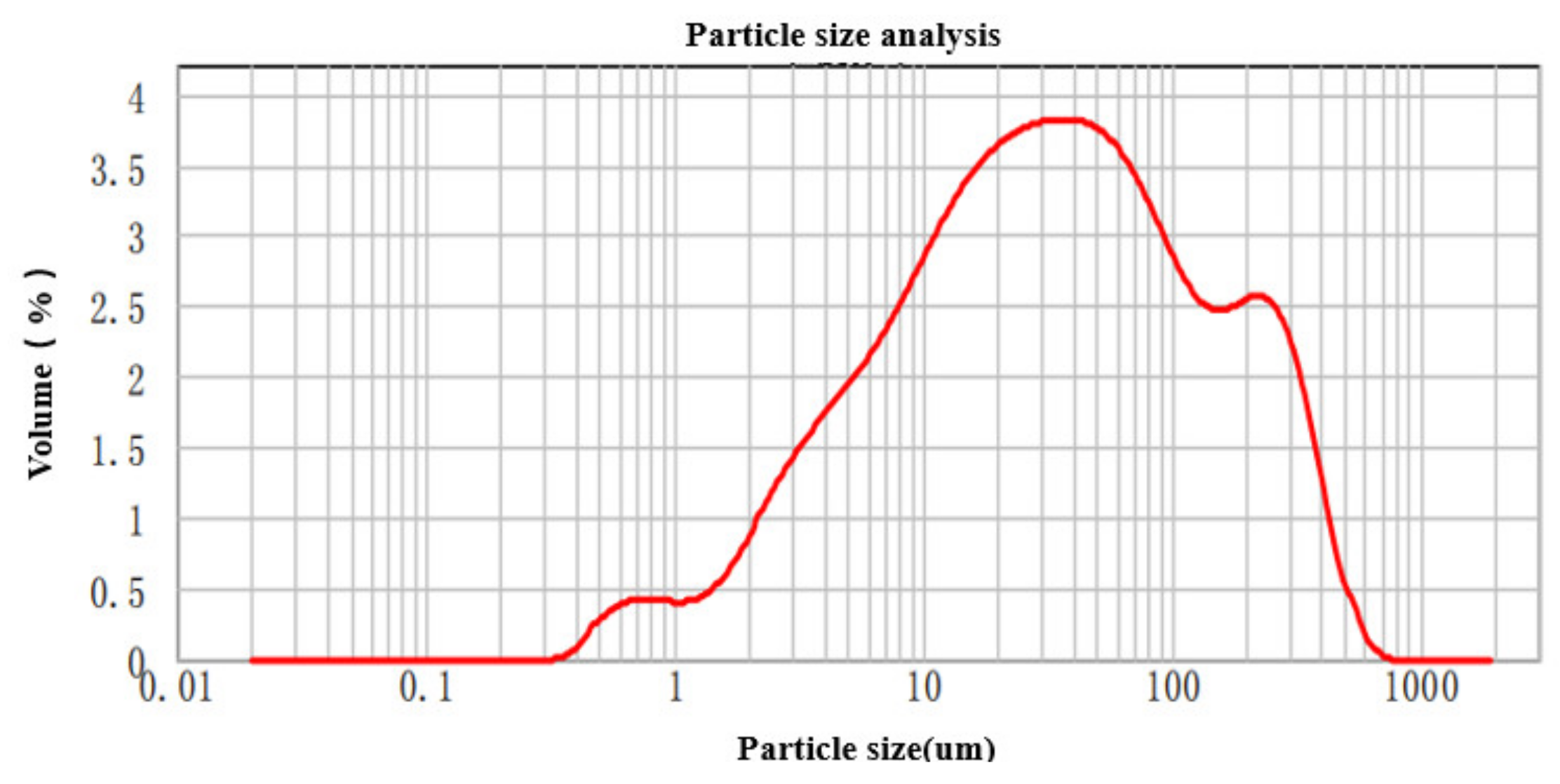

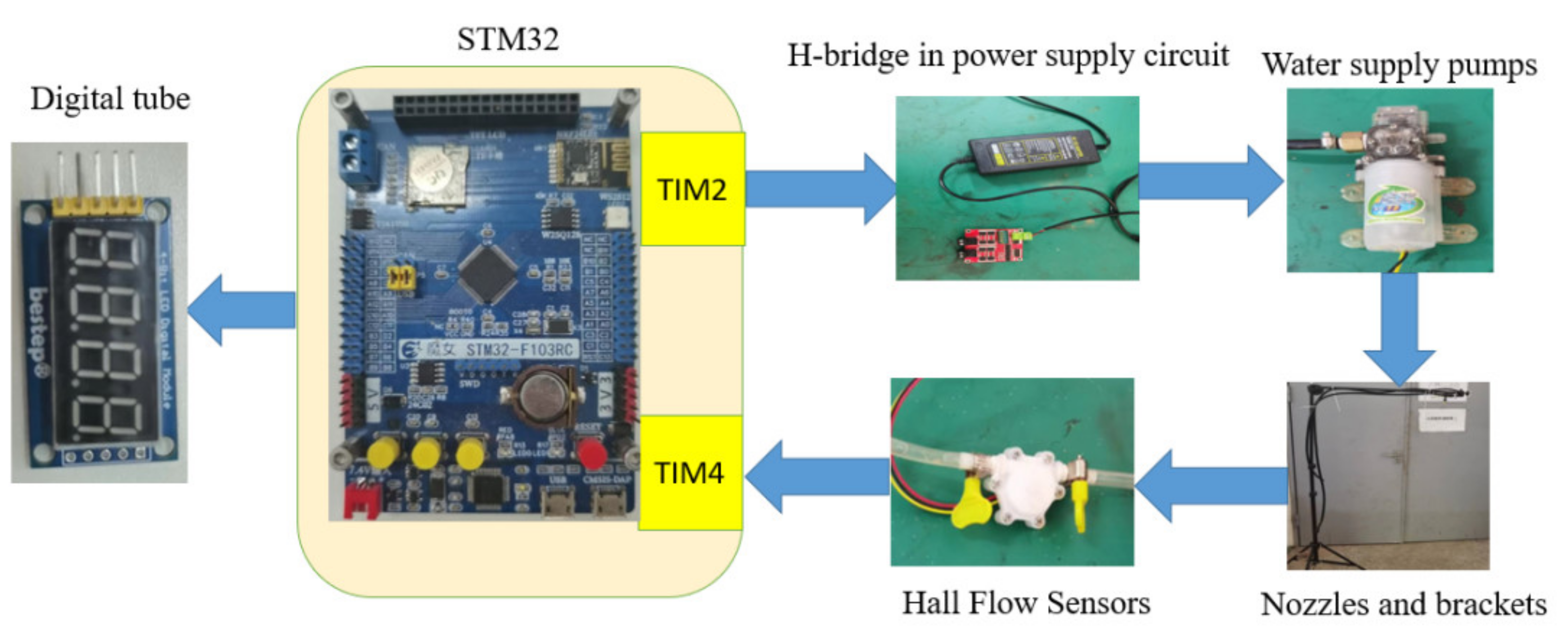
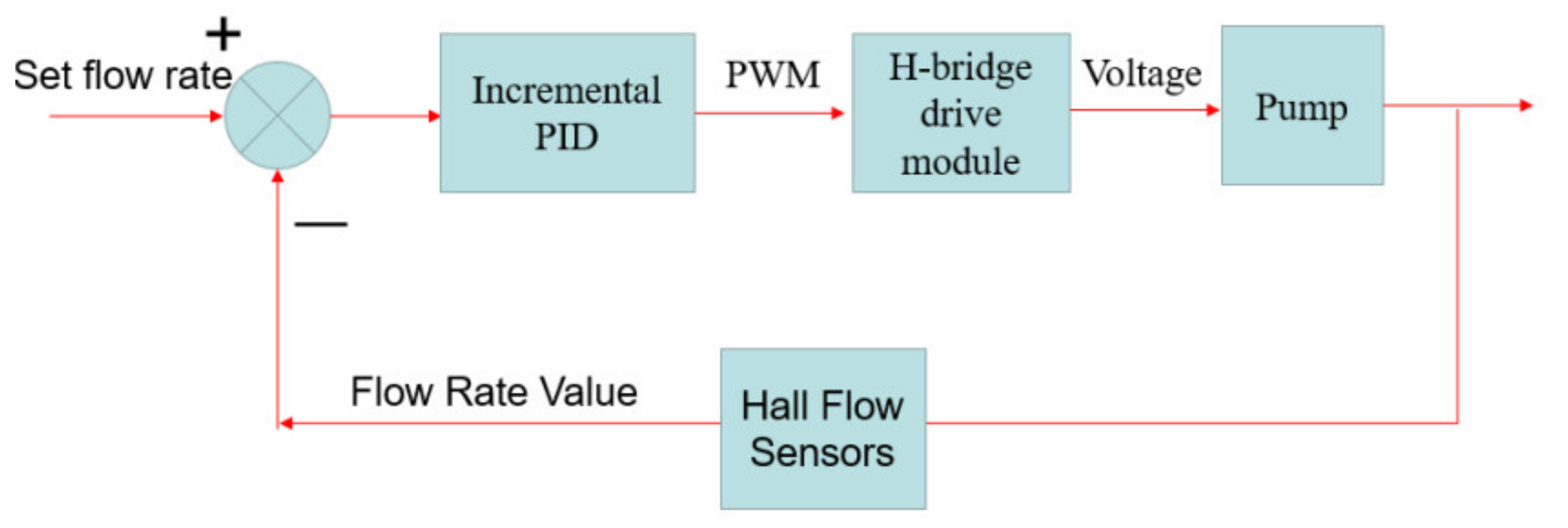
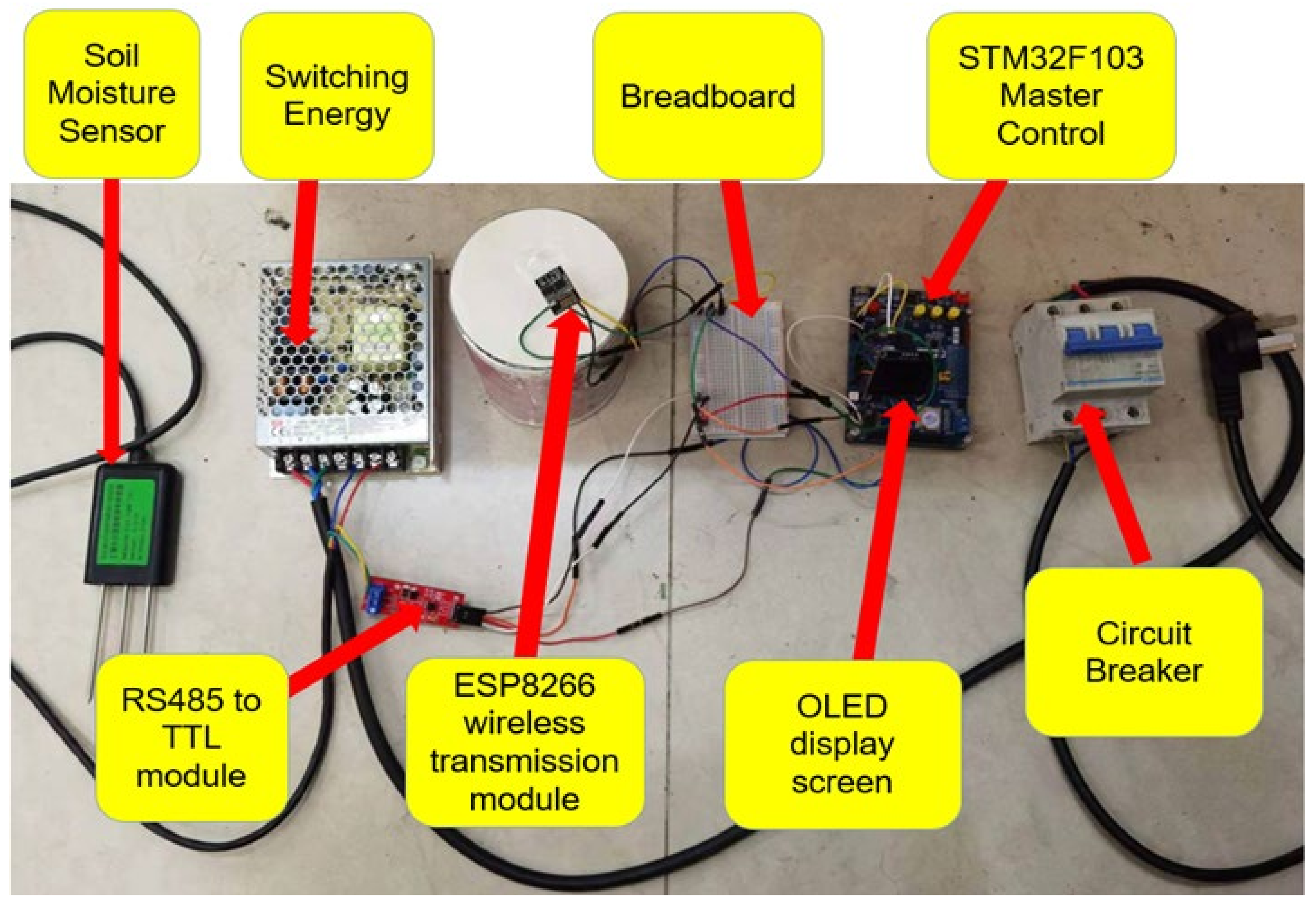


| Condition | Sand (%) | Silt (%) | Clay (%) | Soil Texture |
|---|---|---|---|---|
| 1 | 55 | 45 | 0 | Sandy loamy soil |
| 2 | 60 | 30 | 10 | Sandy loamy soil |
| 3 | 64 | 30 | 6 | Sandy loamy soil |
| 4 | 68 | 27 | 5 | Sandy loamy soil |
| 5 | 70 | 15 | 15 | Sandy loamy soil |
| 6 | 75 | 13 | 12 | Sandy loamy soil |
| 7 | 80 | 11 | 9 | Sandy loamy soil |
| Initial Moisture Content (%) | 6 | 9 | 11 | 12 | 14 | 15 | 17 | 18 |
| Application rate of sprinkler irrigation(mm/h) | 30 | 40 | 50 | 60 | 65 | 70 | 75 | 80 |
| Soil Texture | Initial Moisture Content (%) | Bulk Density (g/cm3) | Application Rate of Sprinkler Irrigation (mm/h) | Time of Ponding (min) |
|---|---|---|---|---|
| Condition1 | 6 | 1.5 | 30 | 84 |
| Condition1 | 9 | 1.5 | 30 | 75 |
| Condition1 | 11 | 1.5 | 30 | 69 |
| Condition1 | 12 | 1.5 | 30 | 66 |
| Condition1 | 14 | 1.5 | 30 | 60 |
| Condition2 | 6 | 1.3 | 30 | 169 |
| Condition2 | 6 | 1.4 | 30 | 134 |
| Condition2 | 6 | 1.5 | 30 | 113 |
| Condition2 | 9 | 1.3 | 30 | 156 |
| Condition2 | 9 | 1.4 | 30 | 122 |
| Condition3 | 6 | 1.3 | 40 | 93 |
| Condition3 | 6 | 1.4 | 40 | 83 |
| Condition3 | 6 | 1.5 | 40 | 74 |
| Condition3 | 9 | 1.3 | 40 | 87 |
| Condition3 | 9 | 1.4 | 40 | 76 |
| Condition3 | 9 | 1.5 | 40 | 67 |
| Condition3 | 11 | 1.3 | 40 | 90 |
| Condition4 | 11 | 1.3 | 50 | 62 |
| Condition4 | 11 | 1.4 | 50 | 55 |
| Condition4 | 11 | 1.5 | 50 | 51 |
| Condition4 | 12 | 1.3 | 50 | 69 |
| Condition4 | 12 | 1.4 | 50 | 53 |
| Condition4 | 12 | 1.5 | 50 | 49 |
| Condition4 | 14 | 1.3 | 50 | 62 |
| Condition4 | 14 | 1.4 | 50 | 49 |
| Original data (mm) | 85 | 35 | 76.5 | 24 | 53 | 42 | 60 | 62 | 34.67 |
| Post-processing data (mm) | 1 | −0.64 | 0.72 | −1 | −0.05 | −0.41 | 0.18 | 0.25 | −0.65 |
| Initial Moisture Content (%) | Bulk Density (g/cm3) | Application Rate of Sprinkler Irrigation (mm/h) |
|---|---|---|
| 15 | 1.3 | 60 |
| 15 | 1.4 | 60 |
| 16 | 1.3 | 60 |
| 18 | 1.3 | 70 |
| 18 | 1.4 | 60 |
| 18 | 1.5 | 80 |
| 18 | 1.4 | 80 |
| 16 | 1.5 | 80 |
| Condition | Time of Ponding (min) | Total Irrigation Volume (mm) |
|---|---|---|
| 1 | 56 | 56 |
| 2 | 50 | 50 |
| 3 | 55 | 55 |
| 4 | 40 | 47 |
| 5 | 44 | 44 |
| 6 | 30 | 40 |
| 7 | 32 | 43 |
| 8 | 31 | 41 |
| Condition | Predicted Application Rate of Sprinkler Irrigation (mm/h) |
|---|---|
| 1 | 55 |
| 2 | 77 |
| 3 | 53 |
| 4 | 73 |
| 5 | 70 |
| 6 | 84 |
| 7 | 90 |
| 8 | 86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhu, X.; Liang, Z.; Zou, T. Optimal Sprinkler Application Rate of Water–Fertilizer Integration Machines Based on Radial Basis Function Neural Network. Water 2022, 14, 2838. https://doi.org/10.3390/w14182838
Liu X, Zhu X, Liang Z, Zou T. Optimal Sprinkler Application Rate of Water–Fertilizer Integration Machines Based on Radial Basis Function Neural Network. Water. 2022; 14(18):2838. https://doi.org/10.3390/w14182838
Chicago/Turabian StyleLiu, Xiaochu, Xiangjin Zhu, Zhongwei Liang, and Tao Zou. 2022. "Optimal Sprinkler Application Rate of Water–Fertilizer Integration Machines Based on Radial Basis Function Neural Network" Water 14, no. 18: 2838. https://doi.org/10.3390/w14182838
APA StyleLiu, X., Zhu, X., Liang, Z., & Zou, T. (2022). Optimal Sprinkler Application Rate of Water–Fertilizer Integration Machines Based on Radial Basis Function Neural Network. Water, 14(18), 2838. https://doi.org/10.3390/w14182838








