CFD Simulation of a Submersible Passive Rotor at a Pipe Outlet under Time-Varying Water Jet Flux
Abstract
:1. Introduction
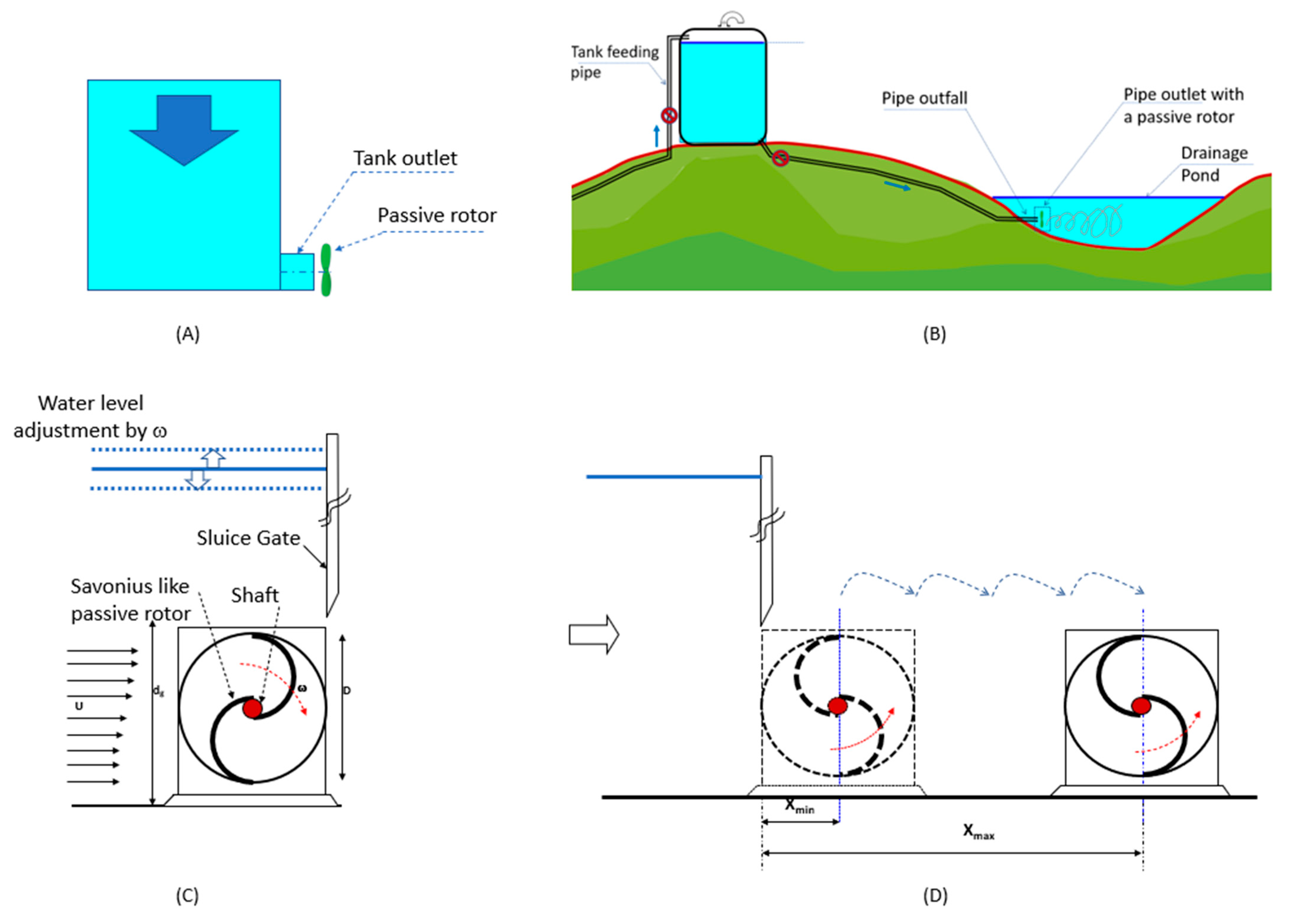
- Use of a passive rotor at the water tank pipe outlet to increase the effluent drainage rate from the effluent tanks in water treatment facilities [5];
- Use of a passive rotor at the outlet of pipe outfall to improve mixing;
- Using a passive rotor upstream of a water level control gate to adjust the upstream water afflux by controlling the rotation of the passive rotor without the need to change the gate opening [3].
- Using passive rotors downstream of a sluice gate for energy dissipation
2. Method Statement
2.1. Study Objectives
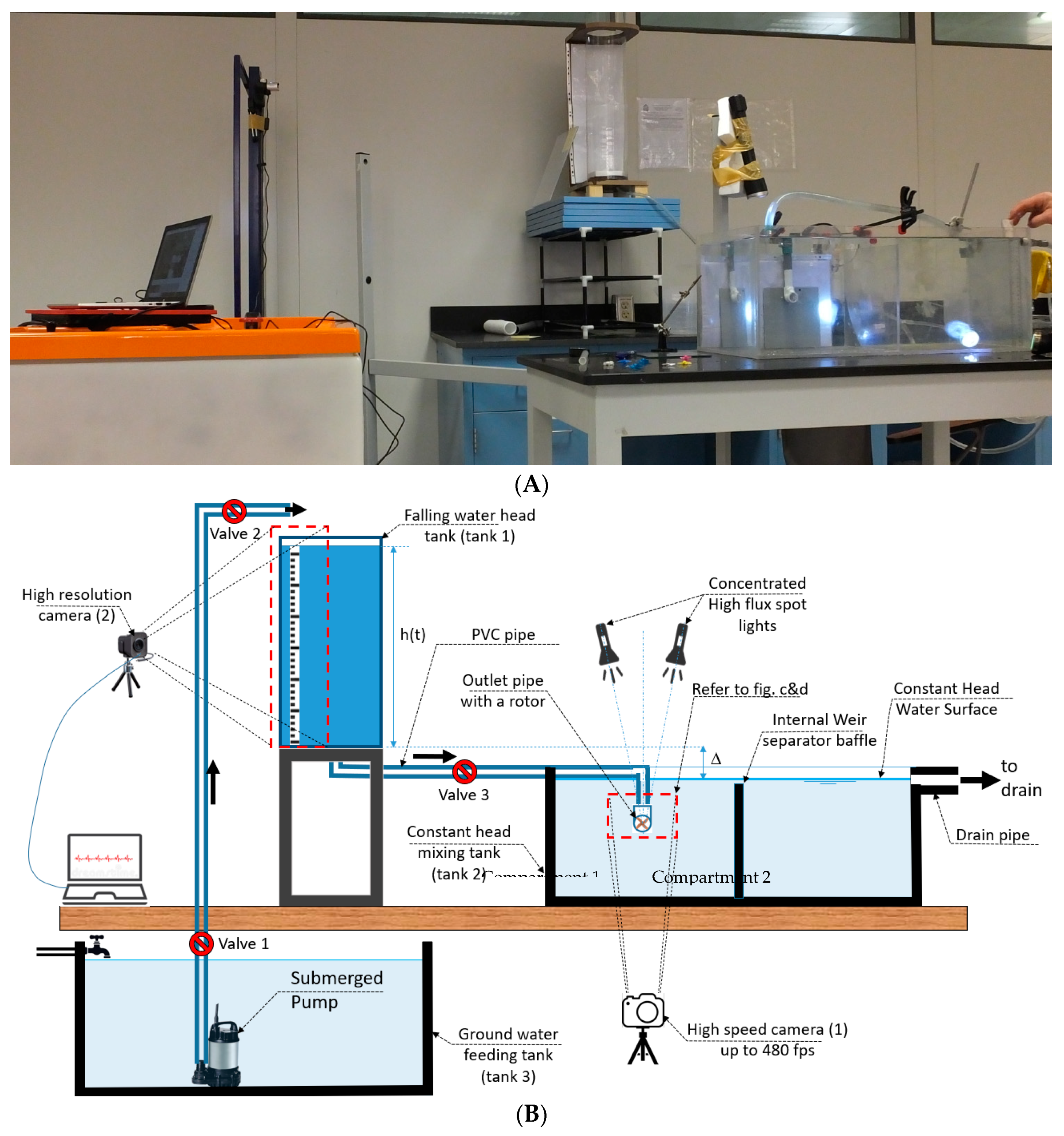
2.2. Physical Experiment
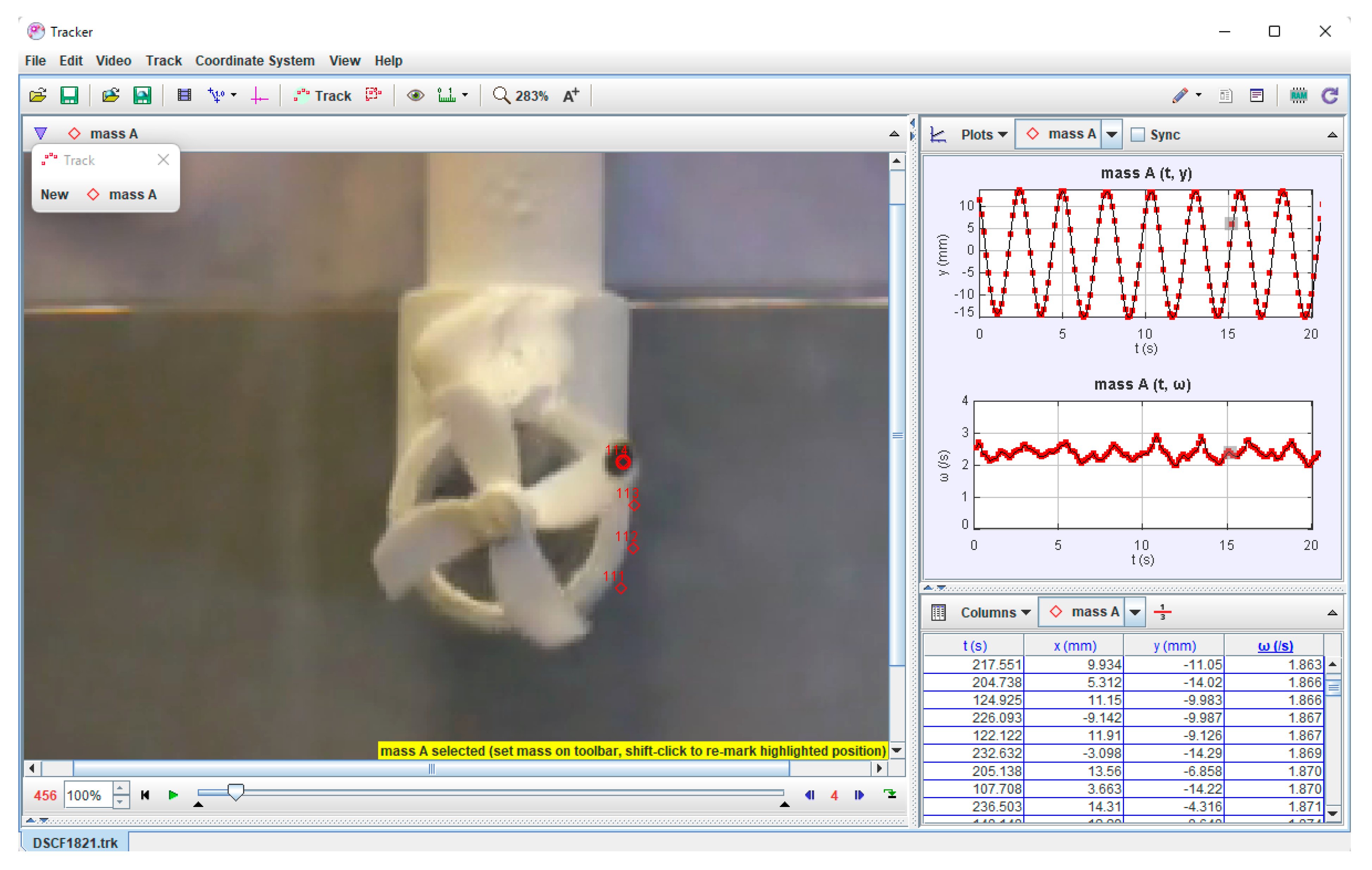
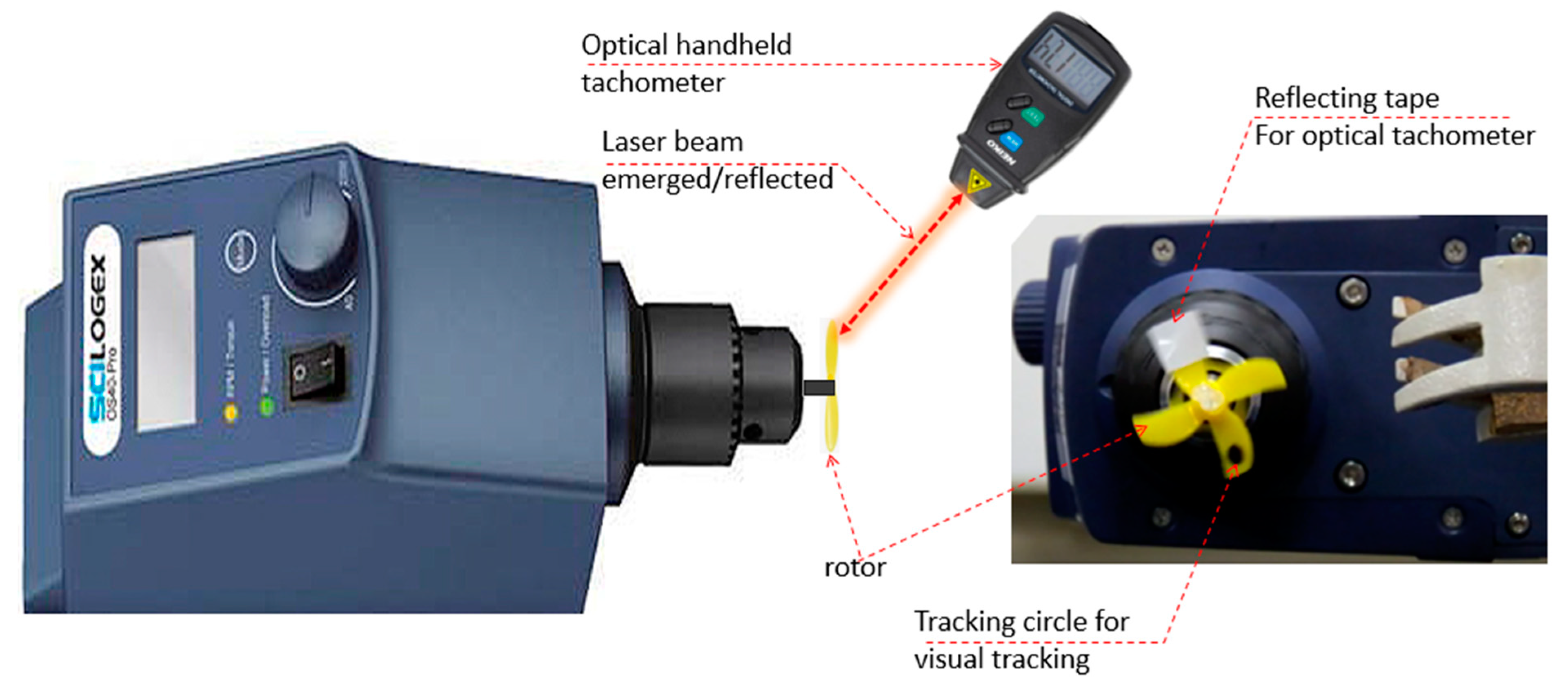
2.3. Measurements via Video Tracking
2.4. Accuracy of Measuring the Angular Speed Using Video Auto-tracking Tracking
2.5. Numerical Techniques for Rotating Elements in FLUENT
2.6. Assumptions and Simplifications
- There is no eccentricity for the shaft of the rotor to the center of the pipe outlet;
- The shaft of the rotor revolves smoothly around its pivot without resistance;
- The shaft and its rotor have the same angular speed (i.e., no slipping took place);
- No deformation is allowed regarding the blades of the rotor during the simulation;
- The rotor blade is assumed rigid enough, and its deformation is neglected;
- The direction of the water flux from the pipe outlet (before impinging on the rotor) is mainly horizontal, with no inclination;
- For practical reasons, the main focus of the simulation is directed on capturing the decelerated period for the rotor (refer to the calibration section) since this period is the dominating stage, and the accelerating zone lasts less than 1.5% of the whole simulation time.
3. Numerical Model Development
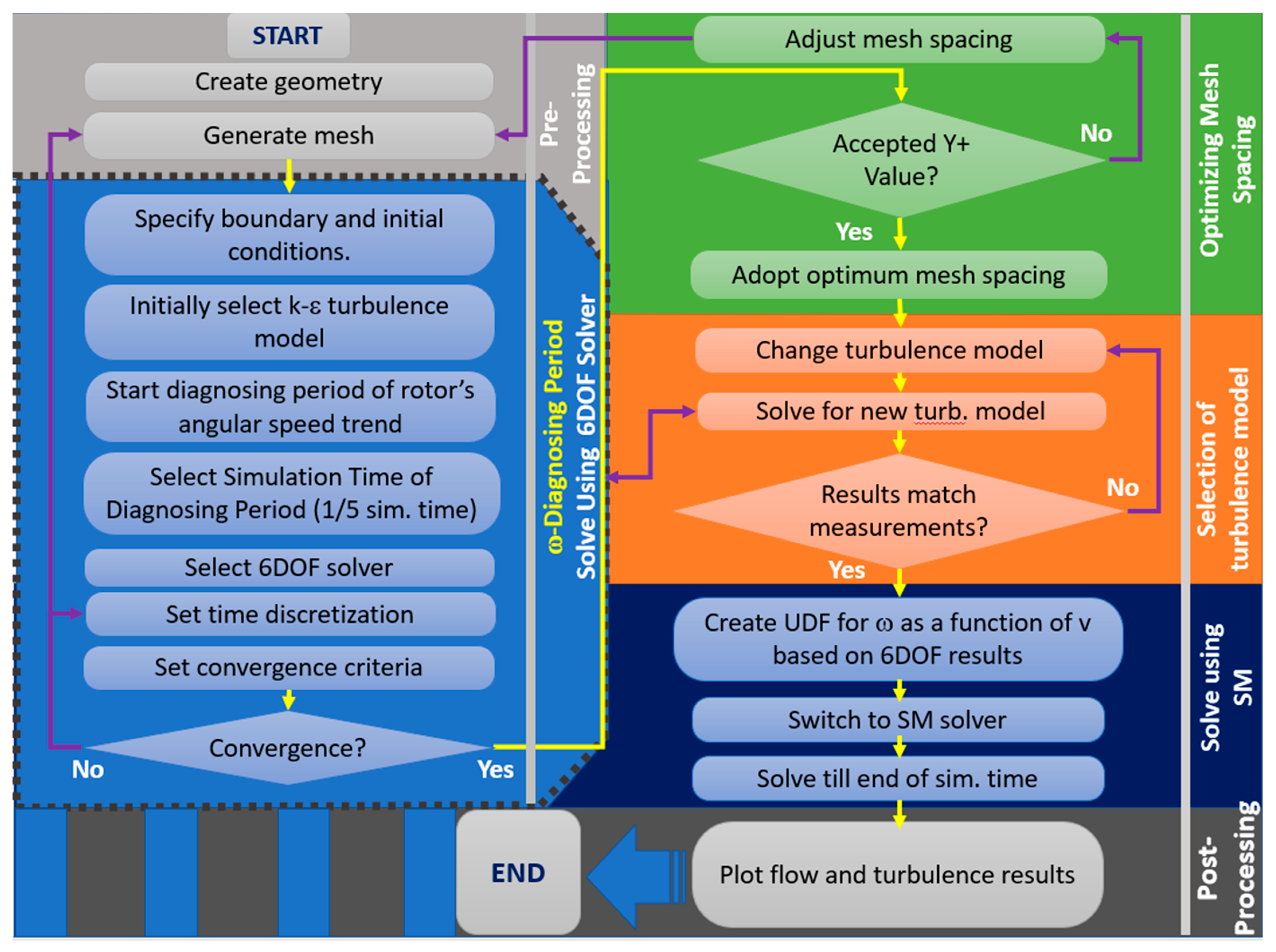
3.1. Workflow Development
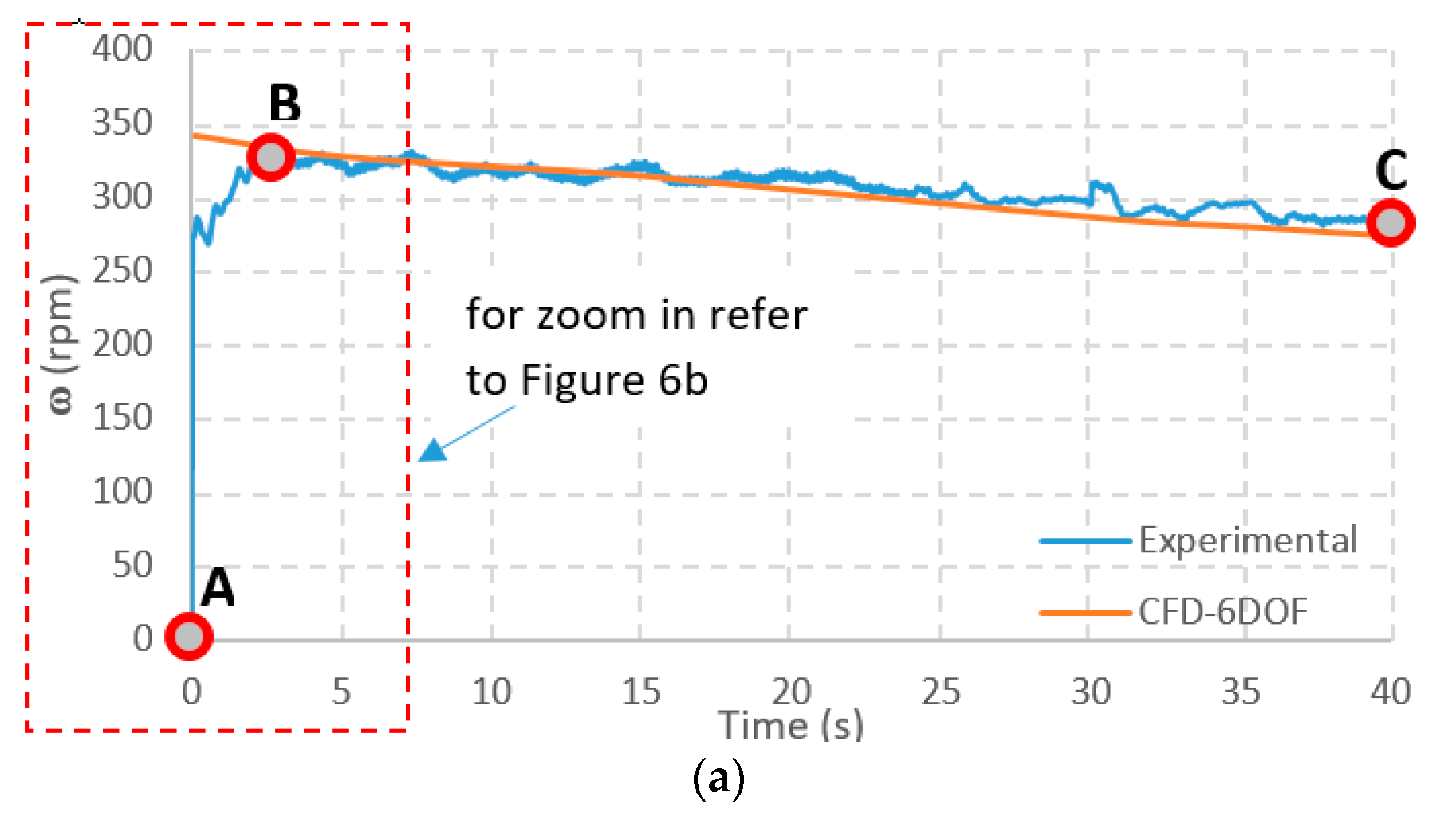
- Start the simulation using the dynamic mesh method using the 6DOF solver for about 21% of the required total simulation time (for the study on hand, for the first 40 s);
- The k-e turbulence model will be initially selected, and the accuracy of the generated mesh will be checked near the boundaries by assessing the y+ plot;
- The simulation will be repeated many times, and each time, a different turbulence model will be tried, and the rotor’s angular speed results will be compared with the measurements;
- Identify the most relevant turbulence model that gives the best match with the measurements;
- Based on the obtained results of the optimal turbulence model, identify the relation between the rotor’s angular speed (ω) and the pipe outlet velocity (υ) and create a user-defined function (UDF) for it;
- Switch the model to the sliding mesh (SM) technique while adopting the optimal turbulence model, and start the simulation until the end of the simulation time.
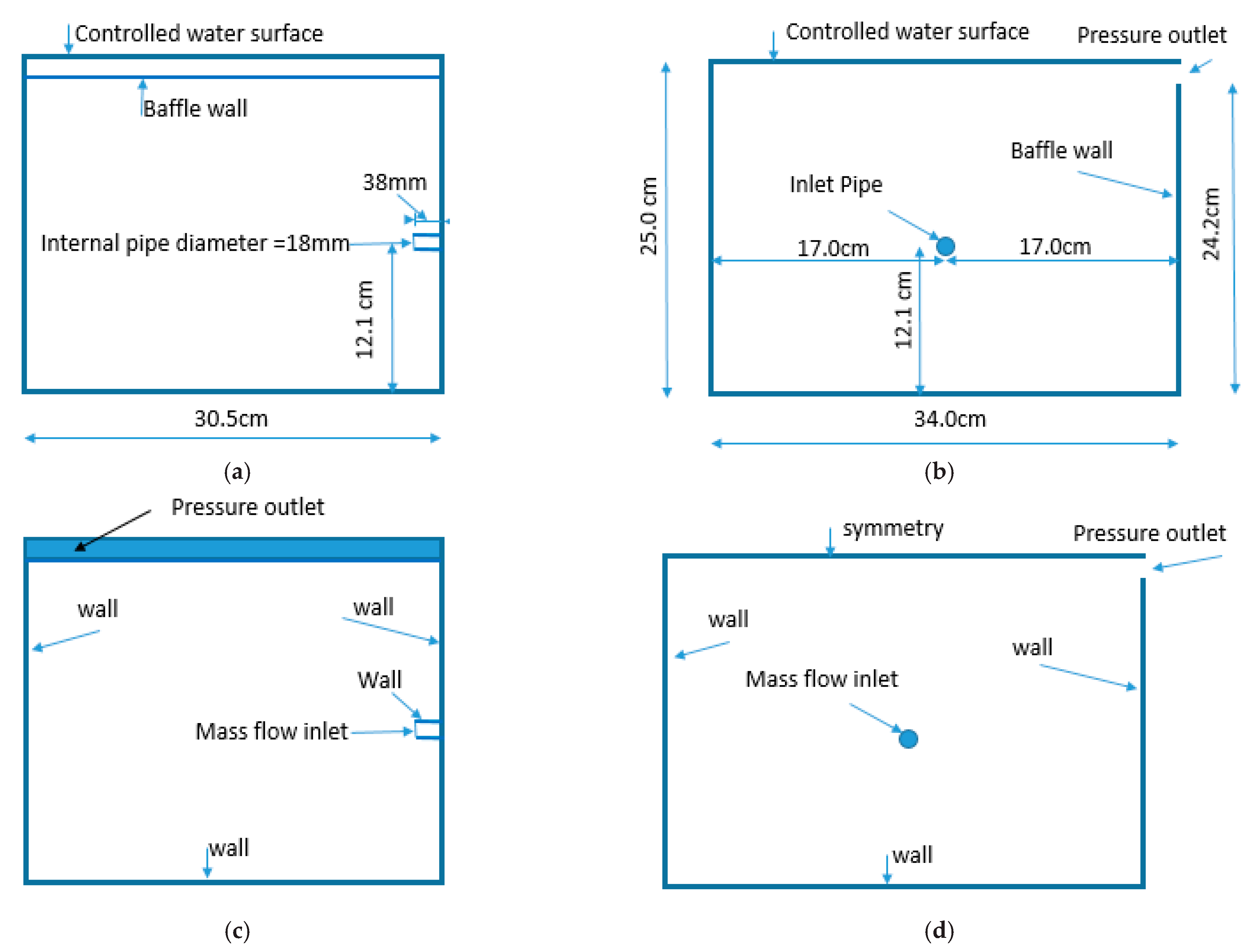
3.2. The Geometry of the CFD Model
3.2.1. The Boundary Conditions
The Inlet Boundary
The Outlet Boundary
The Top of the Model and the Other Boundaries
3.2.2. Solver Parameters
4. Calibration and Accuracy Assessment of the Numerical Model
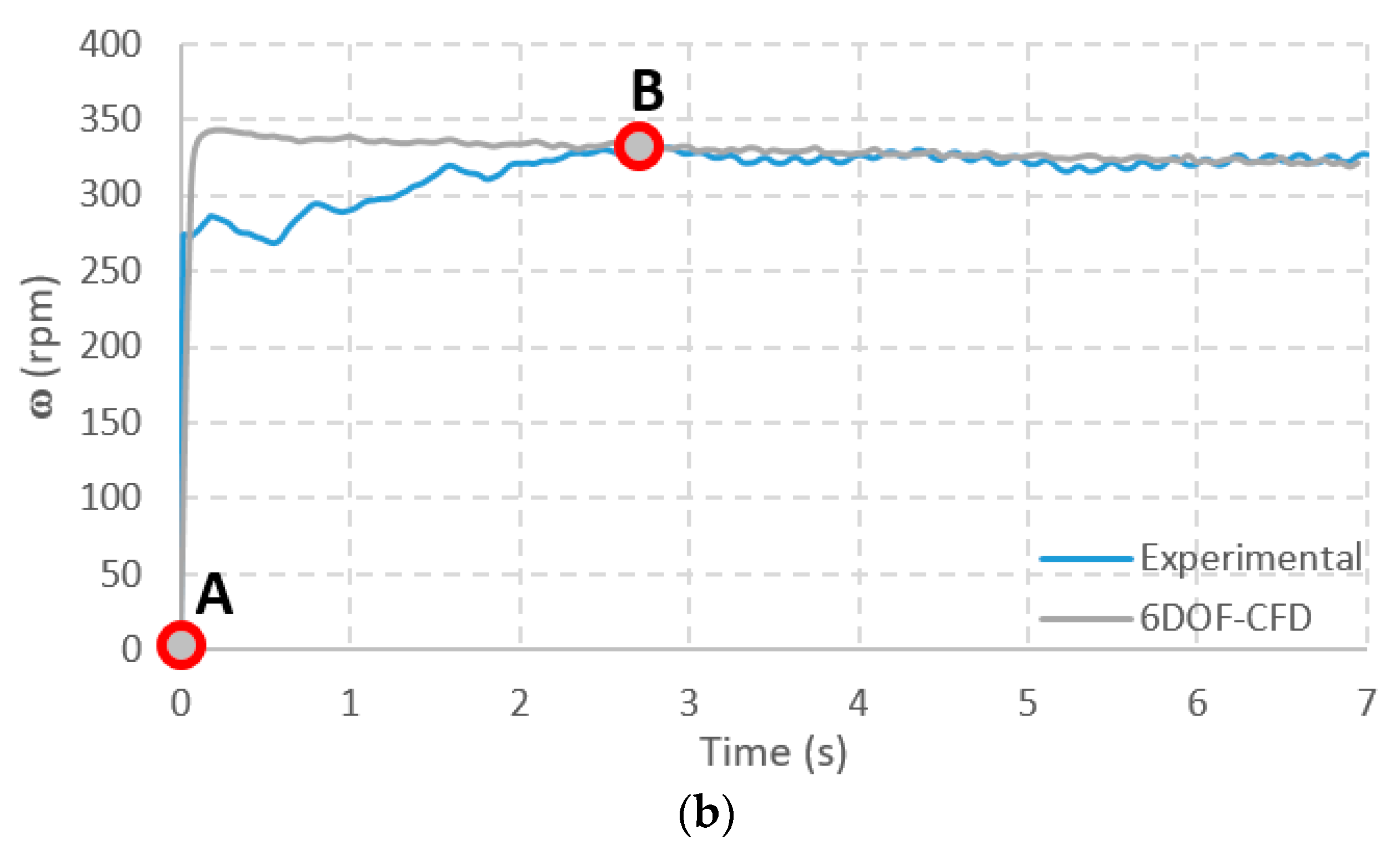
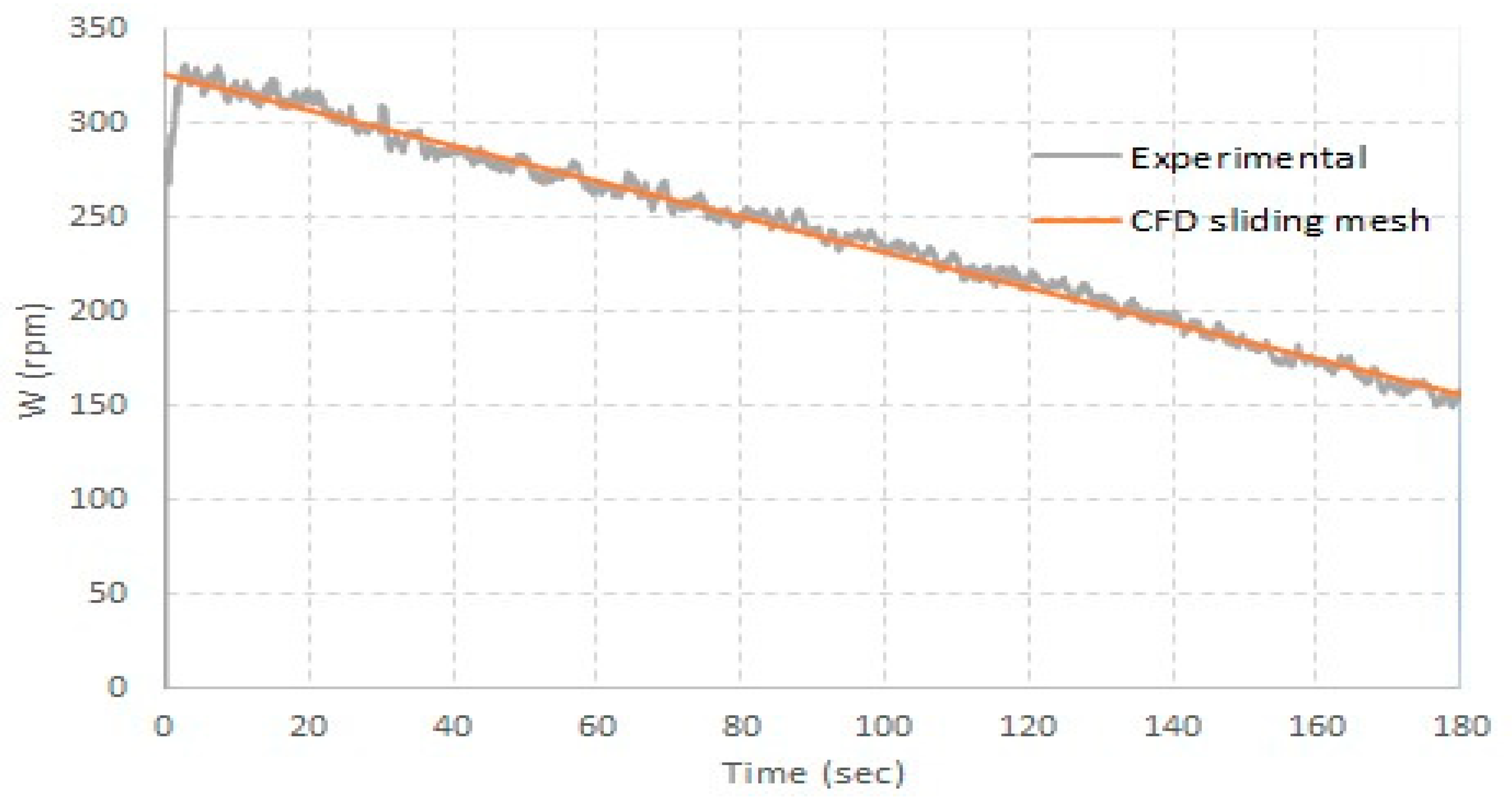
4.1. Measurements of the Rotor’s Angular Speed
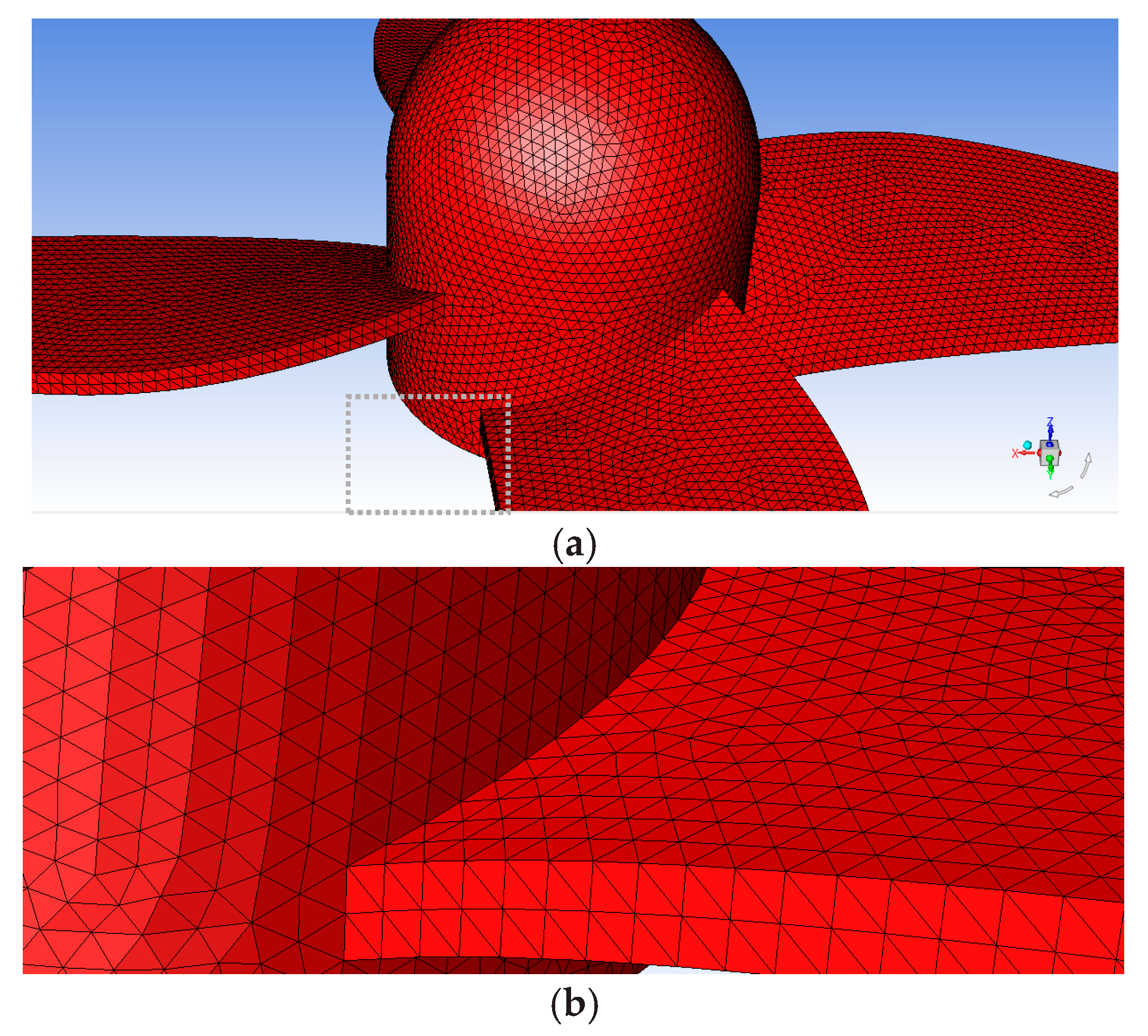
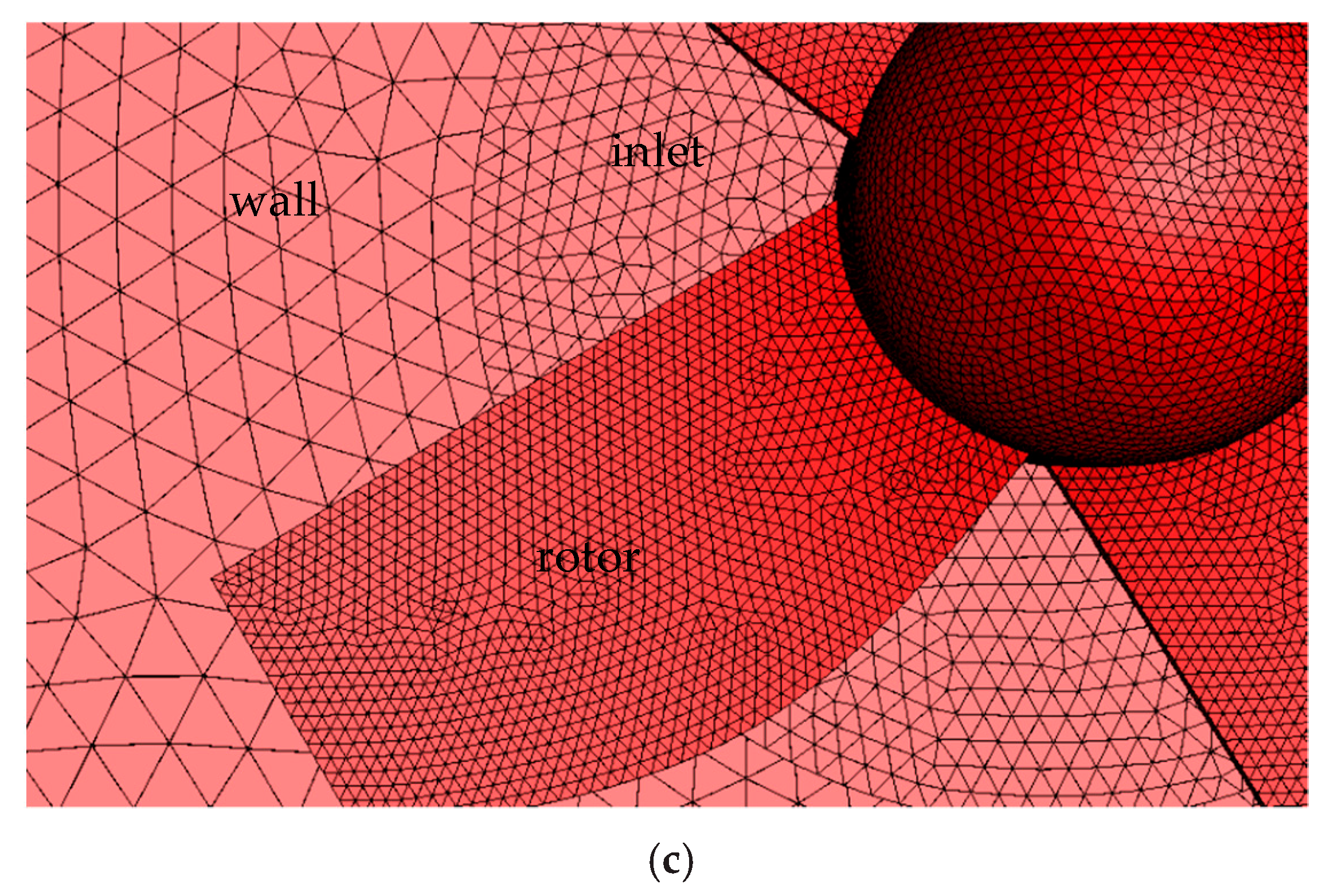
4.2. Model Discretization and GCI Analysis
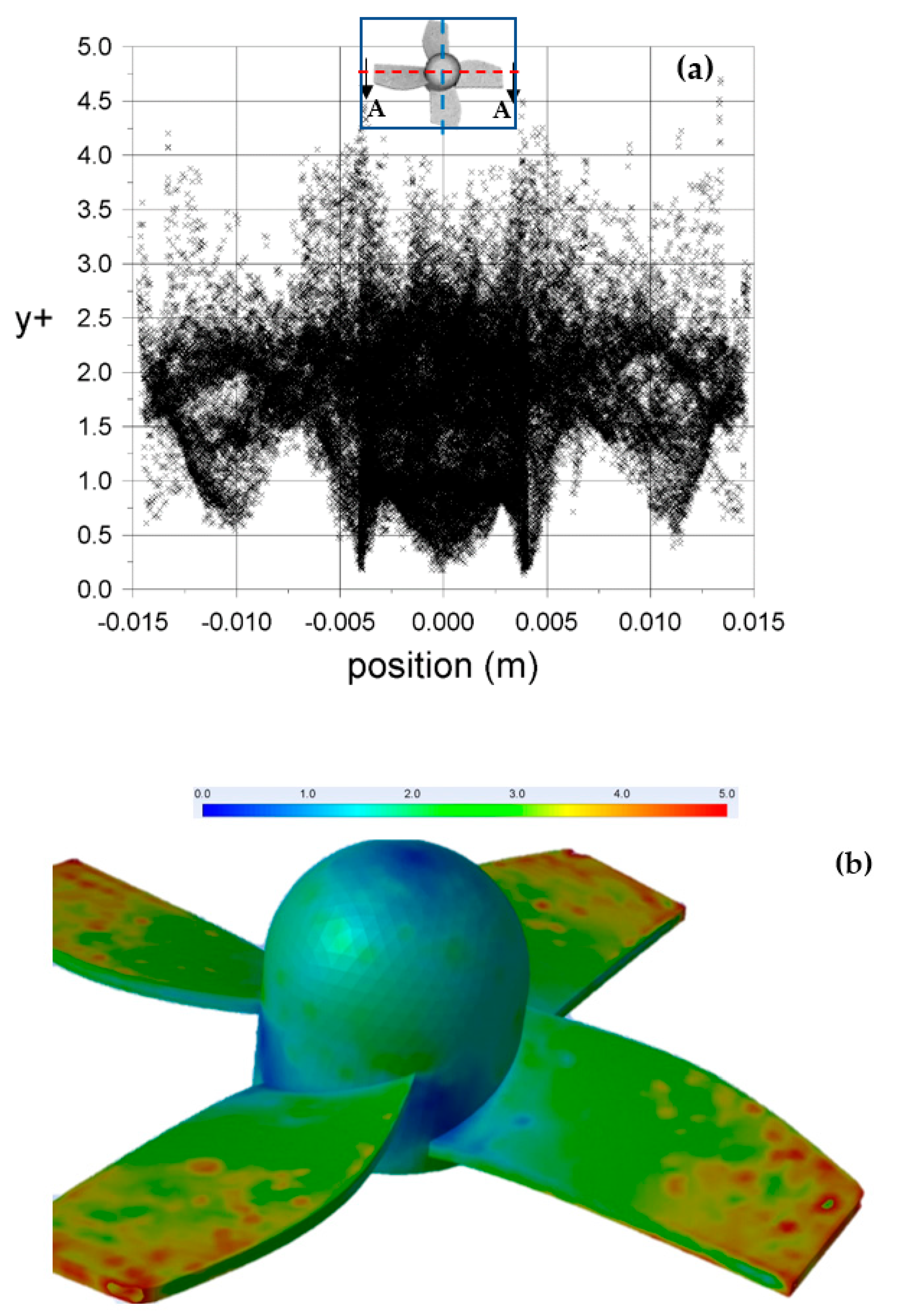
4.3. Checking Model Discretization near the Boundary
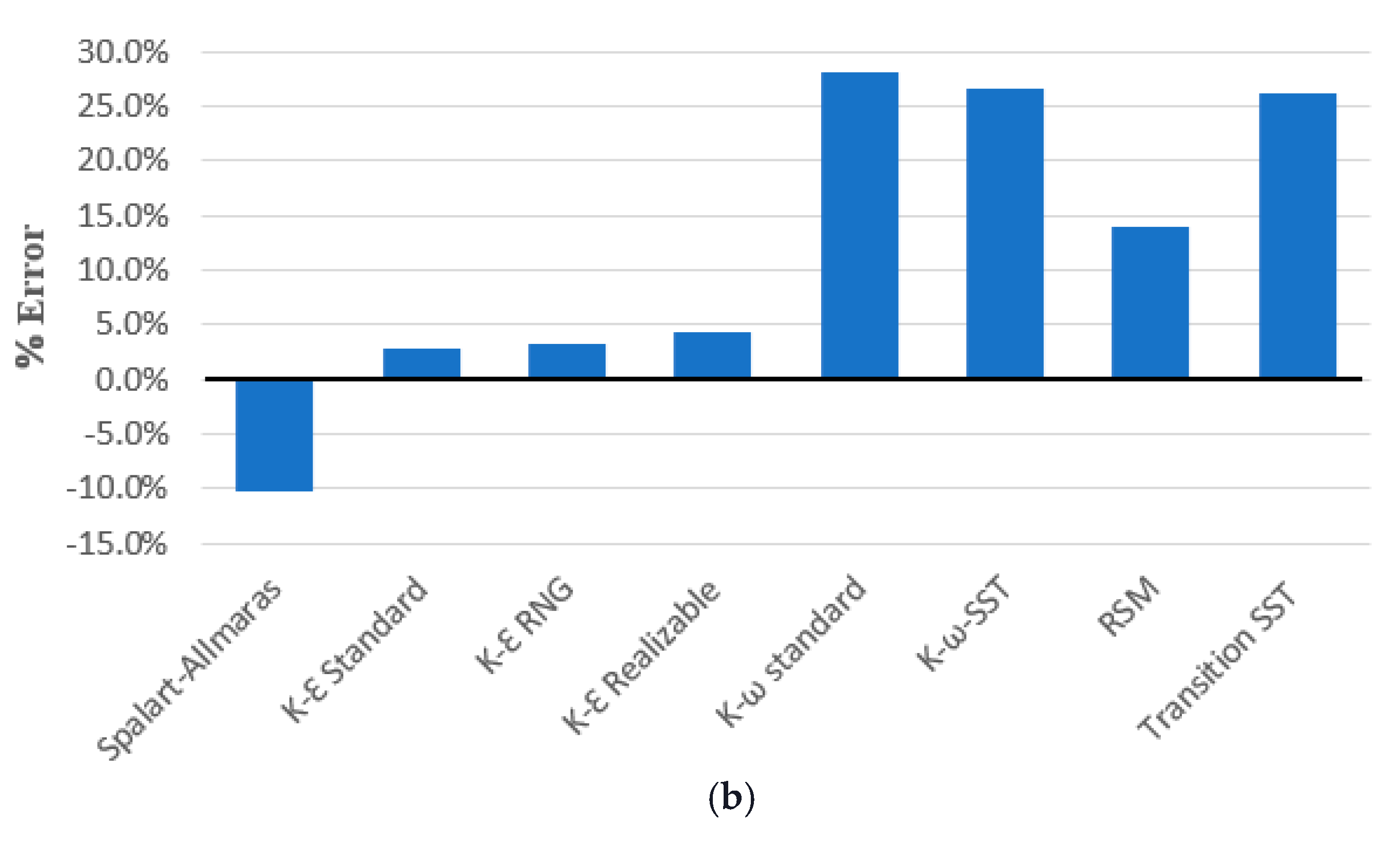
4.4. The Sensitivity of the Turbulence Model
4.4.1. The Maximum Angular Speed
4.4.2. Comparison of the Temporal Variation in the Rotor’s Angular Speed
4.5. Computational Resources
4.6. The Relation between the Angular Speed and the Pipe Outlet Water Velocity
5. Results and Discussion
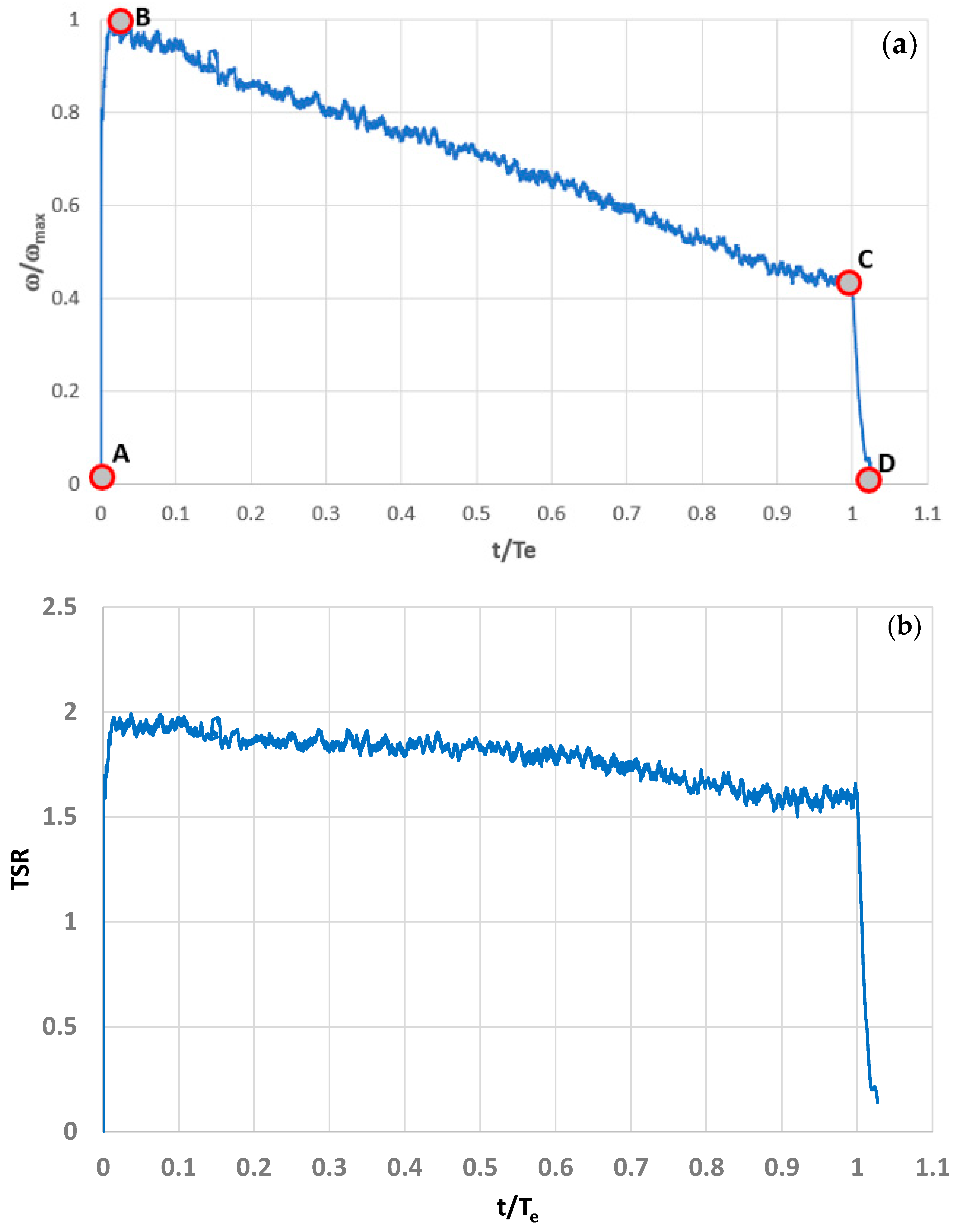
5.1. Perturbation of Angular Speed
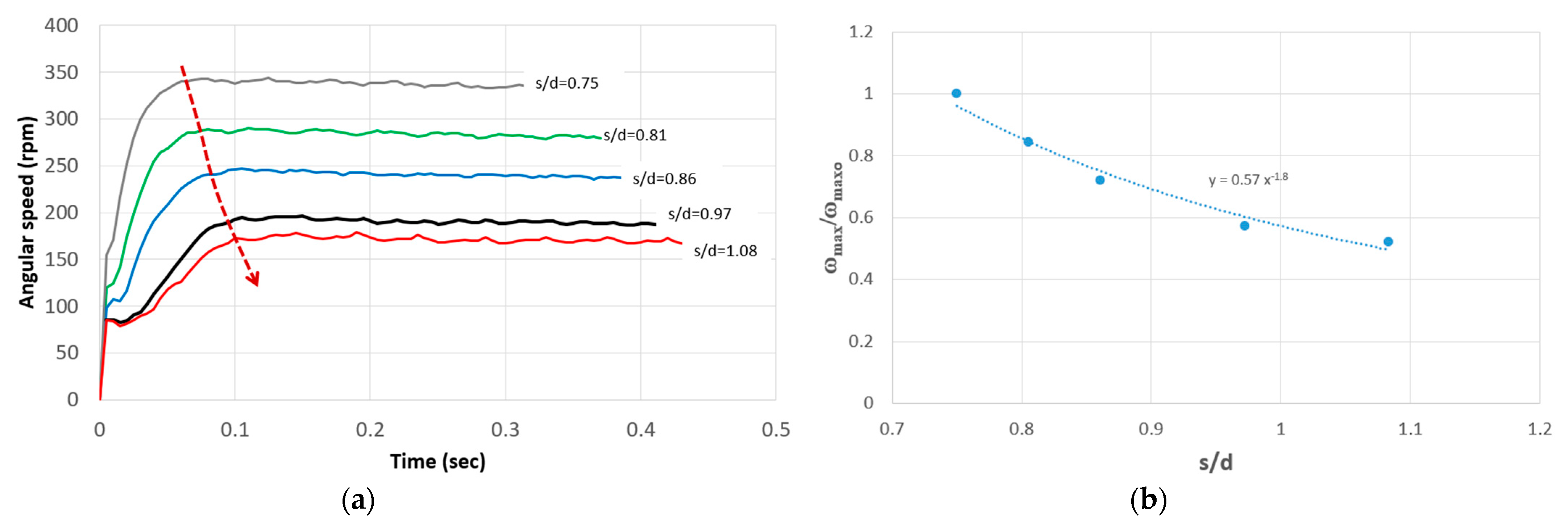
5.2. Effect of the Outlet–Rotor Gap Distance
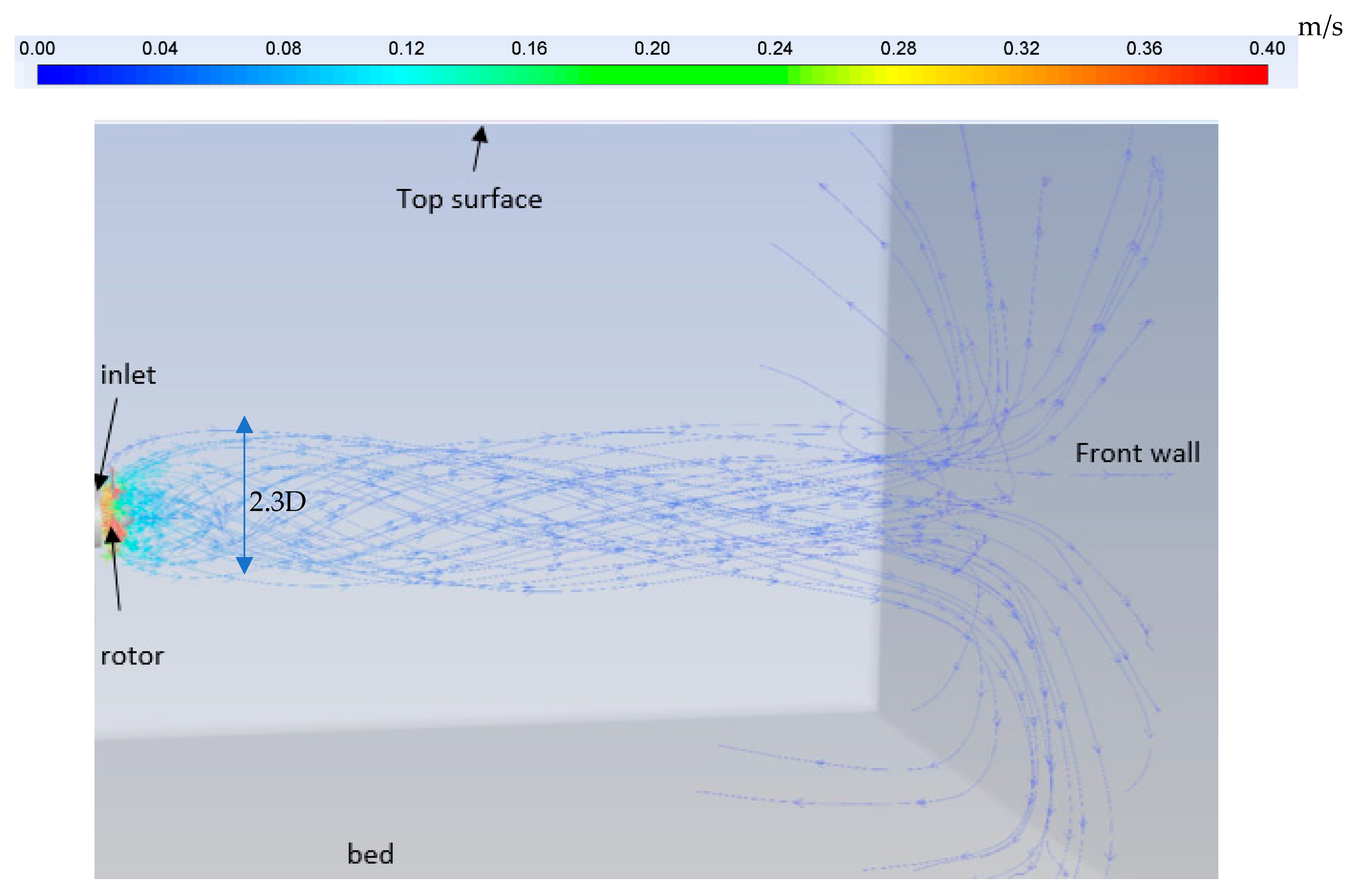
5.3. Effect of the Passive Rotor on the near Downstream Flow Field
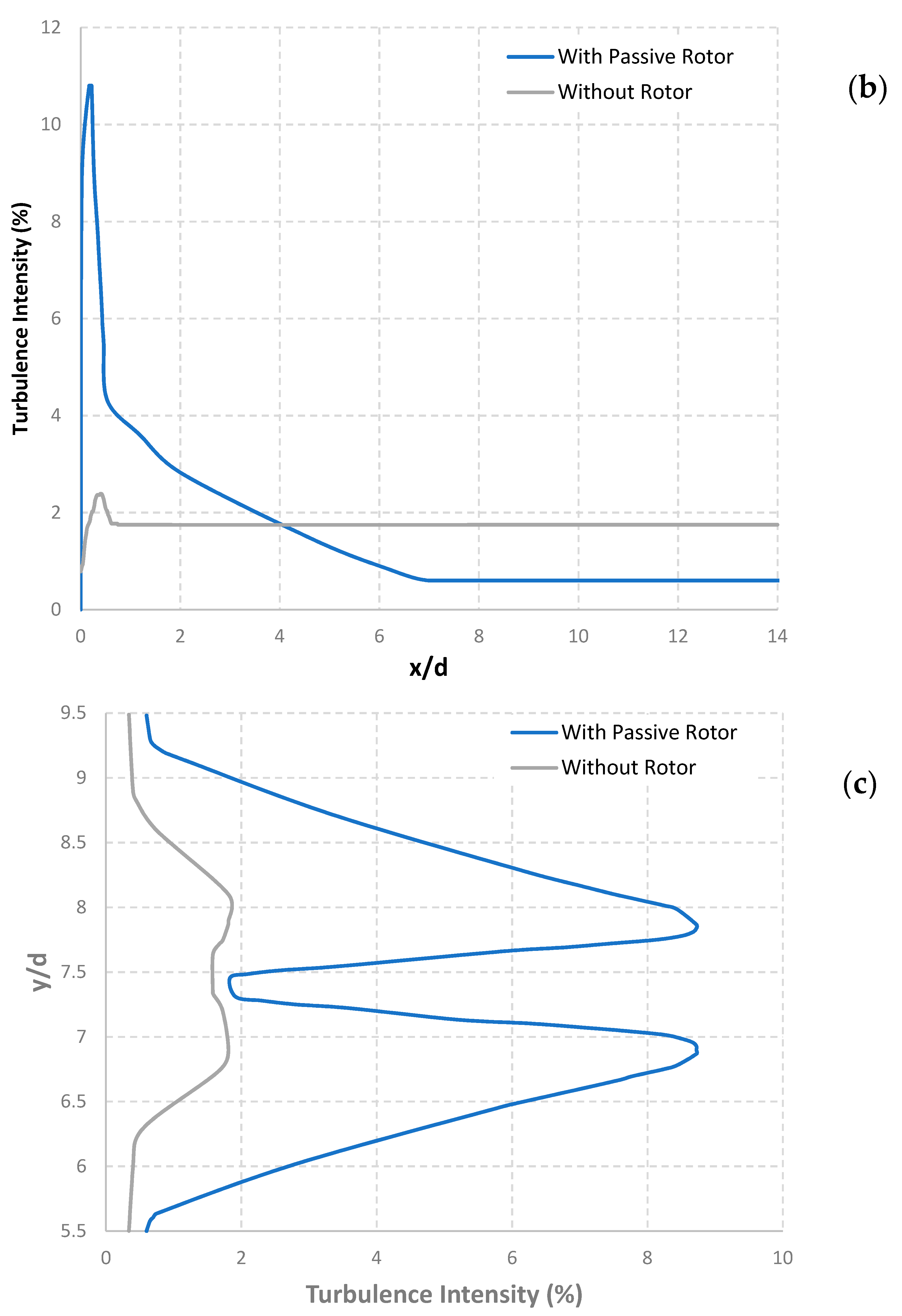
5.4. Effect of the Passive Rotor on the Turbulence Intensity
6. Conclusions and Challenges
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Bank. The Role of Desalination in an Increasingly Water-Scarce World; World Bank: Washington, DC, USA, 2019. [Google Scholar]
- Available online: https://ussaudi.org/water-in-saudi-arabia-desalination-wastewater-and-privatization/ (accessed on 19 June 2022).
- Lim, J. Consideration of structural constraints in passive rotor blade design for improved performance. Aeronaut. J. 2016, 120, 1604–1631. [Google Scholar] [CrossRef]
- Elgamal, M.; Abdel-Mageed, N.; Helmi, A.; Ghanem, A. Hydraulic performance of sluice gate with unloaded upstream rotor. Water SA 2017, 43, 563. [Google Scholar] [CrossRef]
- Elgamal, M.; Kriaa, K.; Farouk, M. Drainage of a Water Tank with pipe outlet loaded by a passive rotor. Water 2021, 13, 1872. [Google Scholar] [CrossRef]
- ANSYS. ANSYS FLUENT User’s Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Patil, H.; Patel, A.K.; Pant, H.J.; Vinod, A.V. CFD simulation model for mixing tank using multiple reference frame (MRF) impeller rotation. ISH J. Hydraul. Eng. 2018, 27, 200–209. [Google Scholar] [CrossRef]
- Durkacz, J.; Islam, S.; Chan, R.; Fong, E.; Gillies, H.; Karnik, A.; Mullan, T. CFD modelling and prototype testing of a Vertical Axis Wind Turbines in planetary cluster formation. Energy Rep. 2021, 7, 119–126. [Google Scholar] [CrossRef]
- Lanzafame, R.; Mauro, S.; Messina, M. Wind turbine CFD modeling using a correlation-based transitional model. Renew. Energy 2013, 52, 31–39. [Google Scholar] [CrossRef]
- Carcangiu, C.E. CFD-RANS Study of Horizontal Axis Wind Turbines. Ph.D. Thesis, Dipartimento di Ingegneria Meccanica, DIMeCa, Cagliari, Italy, January 2008. [Google Scholar]
- Wang, J.-F.; Piechna, J.; Müller, N. A Novel Design Of Composite Water Turbine Using CFD. J. Hydrodyn. 2012, 24, 11–16. [Google Scholar] [CrossRef]
- McNaughton, J.; Afgan, I.; Apsley, D.D.; Rolfo, S.; Stallard, T.; Stansby, P.K. A Simple Sliding-Mesh Interface Procedure and Its Application to the CFD Simulation of a Tidal-Stream Turbine. Int. J. Numer. Methods Fluids 2013, 74, 250–269. [Google Scholar] [CrossRef]
- Laín, S.; Cortés, P.; López, O.D. Numerical Simulation of the Flow Around a Straight Blade Darrieus Water Turbine. Energies 2020, 13, 1137. [Google Scholar] [CrossRef]
- Mao, X.; Chen, D.; Wang, Y.; Mao, G.; Zheng, Y. Investigation on Optimization of Self-Adaptive Closure Law for Load Rejection to a Reversible Pump Turbine Based on CFD. J. Clean. Prod. 2020, 283, 124739. [Google Scholar] [CrossRef]
- Dick, E.; Vierendeels, J.; Serbruyns, S.; Voorde, J.V. Performance prediction of centrifugal pumps with CFD-tools. Task Q. 2001, 5, 579–594. [Google Scholar]
- Mejia, O.D.L.; Mejia, O.E.; Escorcia, K.M.; Suarez, F.; Laín, S. Comparison of Sliding and Overset Mesh Techniques in the Simulation of a Vertical Axis Turbine for Hydrokinetic Applications. Processes 2021, 9, 1933. [Google Scholar] [CrossRef]
- Bouvant, M.; Betancour, J.; Velásquez, L.; Rubio-Clemente, A.; Chica, E. Design optimization of an Archimedes screw turbine for hydrokinetic applications using the response surface methodology. Renew. Energy 2021, 172, 941–954. [Google Scholar] [CrossRef]
- Warjito; Prakoso, A.P.; Budiarso; Adanta, D. CFD simulation methodology of cross-flow turbine with six degree of freedom feature. AIP Conf. Proc. 2020, 2255, 020033. [Google Scholar] [CrossRef]
- Khanjanpour, M.H.; Javadi, A.A. Experimental and CFD Analysis of Impact of Surface Roughness on Hydrodynamic Performance of a Darrieus Hydro (DH) Turbine. Energies 2020, 13, 928. [Google Scholar] [CrossRef]
- Prakoso, A.P.; Warjito, W.; Siswantara, A.I.; Budiarso, B.; Adanta, D. Comparison Between 6-DOF UDF and Moving Mesh Approaches in CFD Methods for Predicting Cross-Flow PicoHydro Turbine Performance. CFD Lett. 2019, 11, 86–96. [Google Scholar]
- Lopez, O.D.; Meneses, D.P.; Lain, S. Computational Study of the Interaction Between Hydrodynamics and Rigid Body Dynamics of a Darrieus Type H Turbine. In CFD for Wind and Tidal Offshore Turbines; Springer: Cham, Switzerland, 2015; pp. 59–68. [Google Scholar]
- Chen, F.; Zhu, G.; Jing, L.; Zheng, W.; Pan, R. Effects of diameter and suction pipe opening position on excavation and suction rescue vehicle for gas-liquid two-phase position. Eng. Appl. Comput. Fluid Mech. 2020, 14, 1128–1155. [Google Scholar] [CrossRef]
- Benavides-Morán, A.; Rodríguez-Jaime, L.; Laín, S. Numerical Investigation of the Performance, Hydrodynamics, and Free-Surface Effects in Unsteady Flow of a Horizontal Axis Hydrokinetic Turbine. Processes 2021, 10, 69. [Google Scholar] [CrossRef]
- Hu, J.; Xu, G.; Shi, Y.; Huang, S. The influence of the blade tip shape on brownout by an approach based on computational fluid dynamics. Eng. Appl. Comput. Fluid Mech. 2021, 15, 692–711. [Google Scholar] [CrossRef]
- Li, Y.-B.; Fan, Z.-J.; Guo, D.-S.; Li, X.-B. Dynamic flow behavior and performance of a reactor coolant pump with distorted inflow. Eng. Appl. Comput. Fluid Mech. 2020, 14, 683–699. [Google Scholar] [CrossRef]
- Hsu, C.-H.; Chen, J.-L.; Yuan, S.-C.; Kung, K.-Y. CFD Simulations on the Rotor Dynamics of a Horizontal Axis Wind Turbine Activated from Stationary. Appl. Mech. 2021, 2, 147–158. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. Trans. ASME 2008, 130. [Google Scholar] [CrossRef] [Green Version]
- Balduzzi, F.; Bianchini, A.; Maleci, R.; Ferrara, G.; Ferrari, L. Critical issues in the CFD simulation of Darrieus wind turbines. Renew. Energy 2016, 85, 419–435. [Google Scholar] [CrossRef]
- Maître, T.; Amet, E.; Pellone, C. Modeling of the flow in a Darrieus water turbine: Wall grid refinement analysis and comparison with experiments. Renew. Energy 2013, 51, 497–512. [Google Scholar] [CrossRef]
- Borkowski, D.; Węgiel, M.; Ocłoń, P.; Węgiel, T. CFD model and experimental verification of water turbine integrated with electrical generator. Energy 2019, 185, 875–883. [Google Scholar] [CrossRef]
- Kaniecki, M.; Krzemianowski, Z.; Banaszek, M. Computational fluid dynamics simulations of small capacity Kaplan turbines. Trans. Inst. Fluid-Flow Mach. 2011, 71–84. Available online: https://yadda.icm.edu.pl/baztech/element/bwmeta1.element.baztech-article-BWM8-0039-0004 (accessed on 12 August 2022).
- Adanta, D.; Nasution, S.B.; Budiarso; Warjito; Siswantara, A.I.; Trahasdani, H. Open flume turbine simulation method using six-degrees of freedom feature. AIP Conf. Proc 2020, 2227, 020017. [Google Scholar] [CrossRef]
- Mohamed, A.; Ridha, A.; Boualem, C.; Tayeb, K. Two-Dimensional CFD Simulation Coupled with 6DOF Solver for analyzing Operating Process of Free Piston Stirling Engine. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 55, 29–38. [Google Scholar]
- Prakash, S.; Nath, D.R. A computational method for determination of open water performance of a marine propeller. Int. J. Comput. Appl. 2012, 58, 0975–8887. [Google Scholar]
- Wu, J.; Shimmei, K.; Tani, K.; Niikura, K.; Sato, J. CFD-based design optimization for hydro turbines. J. Fluids Eng. 2007, 129, 159–168. [Google Scholar] [CrossRef]
- Khunthongjan, P.; Janyalertadun, A. A study of diffuser angle effect on ducted water current turbine performance using CFD. Songklanakarin J. Sci. Technol. 2012, 34, 61–67. [Google Scholar]
- Liu, Y. Development and computational validation of an improved analytic performance model of the hydroelectric paddle wheel. Distrib. Gener. Altern. Energy J. 2015, 30, 58–80. [Google Scholar]
- Kutty, H.A.; Rajendran, P. 3D CFD Simulation and Experimental Validation of Small APC Slow Flyer Propeller Blade. Aerospace 2017, 4, 10. [Google Scholar] [CrossRef]
- Krasilnikov, V.; Sun, J.; Halse, K.H. CFD investigation in scale effect on propellers with different magnitude of skew in turbulent flow. In Proceedings of the First International Symposium on Marine Propulsors, Trondheim, Norway, 22–24 June 2009; pp. 25–40. [Google Scholar]
- Thakur, N.; Biswas, A.; Kumar, Y.; Basumatary, M. CFD analysis of performance improvement of the Savonius water turbine by using an impinging jet duct design. Chin. J. Chem. Eng. 2018, 27, 794–801. [Google Scholar] [CrossRef]
- Tog, R.A.; Tousi, A.; Tourani, A. Comparison of turbulence methods in CFD analysis of compressible flows in radial turbomachines. Aircr. Eng. Aerosp. Technol. 2008, 80, 657–665. [Google Scholar] [CrossRef]
- Cao, H.; He, D.; Xi, S.; Chen, X. Vibration signal correction of unbalanced rotor due to angular speed fluctuation. Mech. Syst. Signal Process. 2018, 107, 202–220. [Google Scholar] [CrossRef]
- Sang, L.Q.; Murata, J.; Morimoto, M.; Kamada, Y.; Maeda, T.; Li, Q. Experimental investigation of load fluctuation on horizontal axis wind turbine for extreme wind direction change. J. Fluid Sci. Technol. 2017, 12, JFST0005. [Google Scholar] [CrossRef] [Green Version]
- Basse, N.T. Turbulence Intensity Scaling: A Fugue. Fluids 2019, 4, 180. [Google Scholar] [CrossRef] [Green Version]



| Parameters | Settings |
|---|---|
| Solver | Pressure-based, transient |
| Velocity formulation | Absolute |
| Turbulence model | Standard k-ε |
| Water density | 998.2 kg/m3 |
| Water viscosity | 0.001003 kg/m·s |
| Pressure discretization | Body Force Weighted |
| Gravity | 9.81 m/s2 |
| The inlet | Unsteady mass flow inlet |
| The outlet | Pressure outlet |
| The top of the tank | Symmetry |
| All other boundaries | Wall |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farouk, M.; Kriaa, K.; Elgamal, M. CFD Simulation of a Submersible Passive Rotor at a Pipe Outlet under Time-Varying Water Jet Flux. Water 2022, 14, 2822. https://doi.org/10.3390/w14182822
Farouk M, Kriaa K, Elgamal M. CFD Simulation of a Submersible Passive Rotor at a Pipe Outlet under Time-Varying Water Jet Flux. Water. 2022; 14(18):2822. https://doi.org/10.3390/w14182822
Chicago/Turabian StyleFarouk, Mohamed, Karim Kriaa, and Mohamed Elgamal. 2022. "CFD Simulation of a Submersible Passive Rotor at a Pipe Outlet under Time-Varying Water Jet Flux" Water 14, no. 18: 2822. https://doi.org/10.3390/w14182822





