A Novel Method to Identify Radial Drainage Based on Morphological Features
Abstract
:1. Introduction
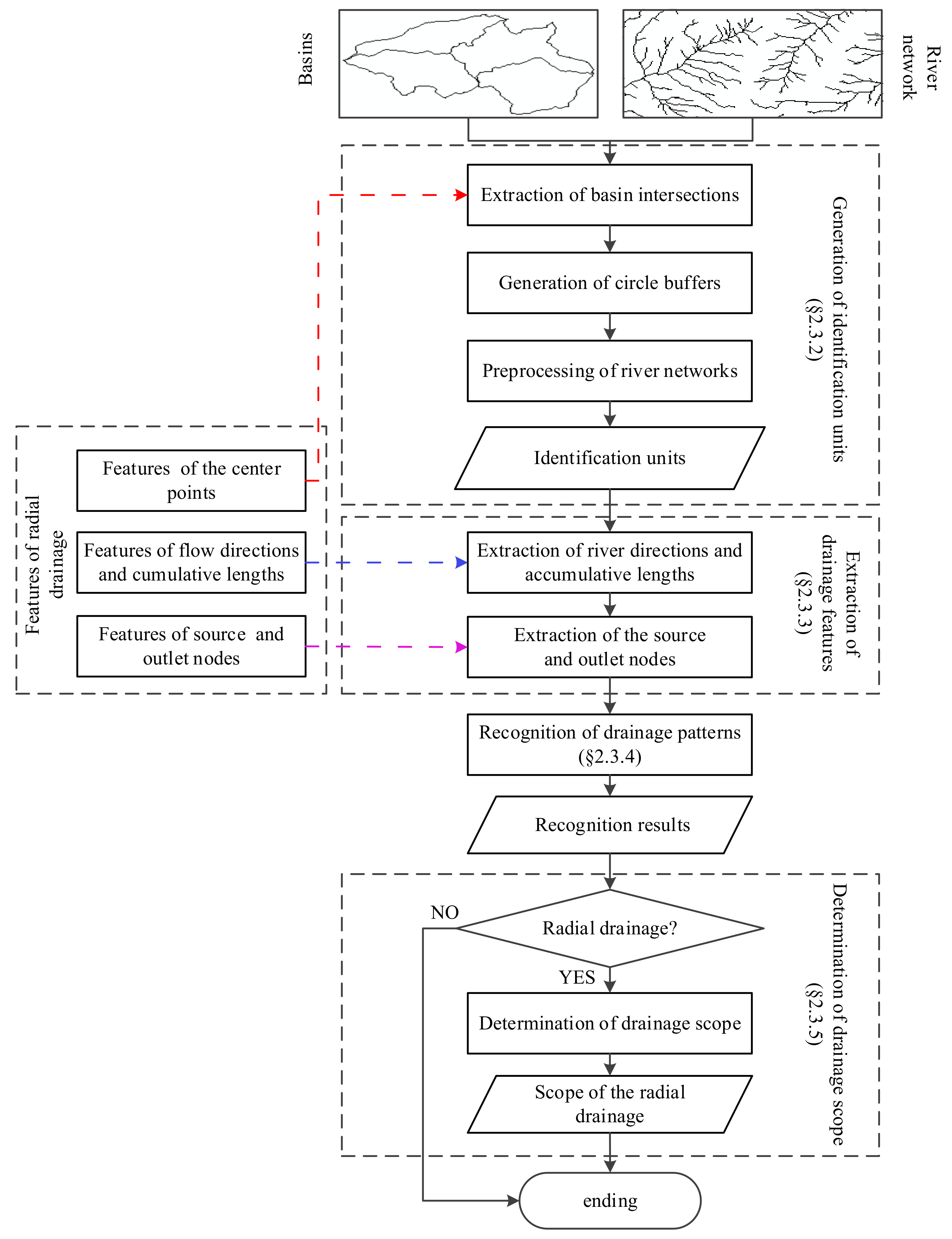
2. Materials and Methods
2.1. Study Area
2.2. Experiment Data
2.3. Methods
2.3.1. Morphological Features of RD
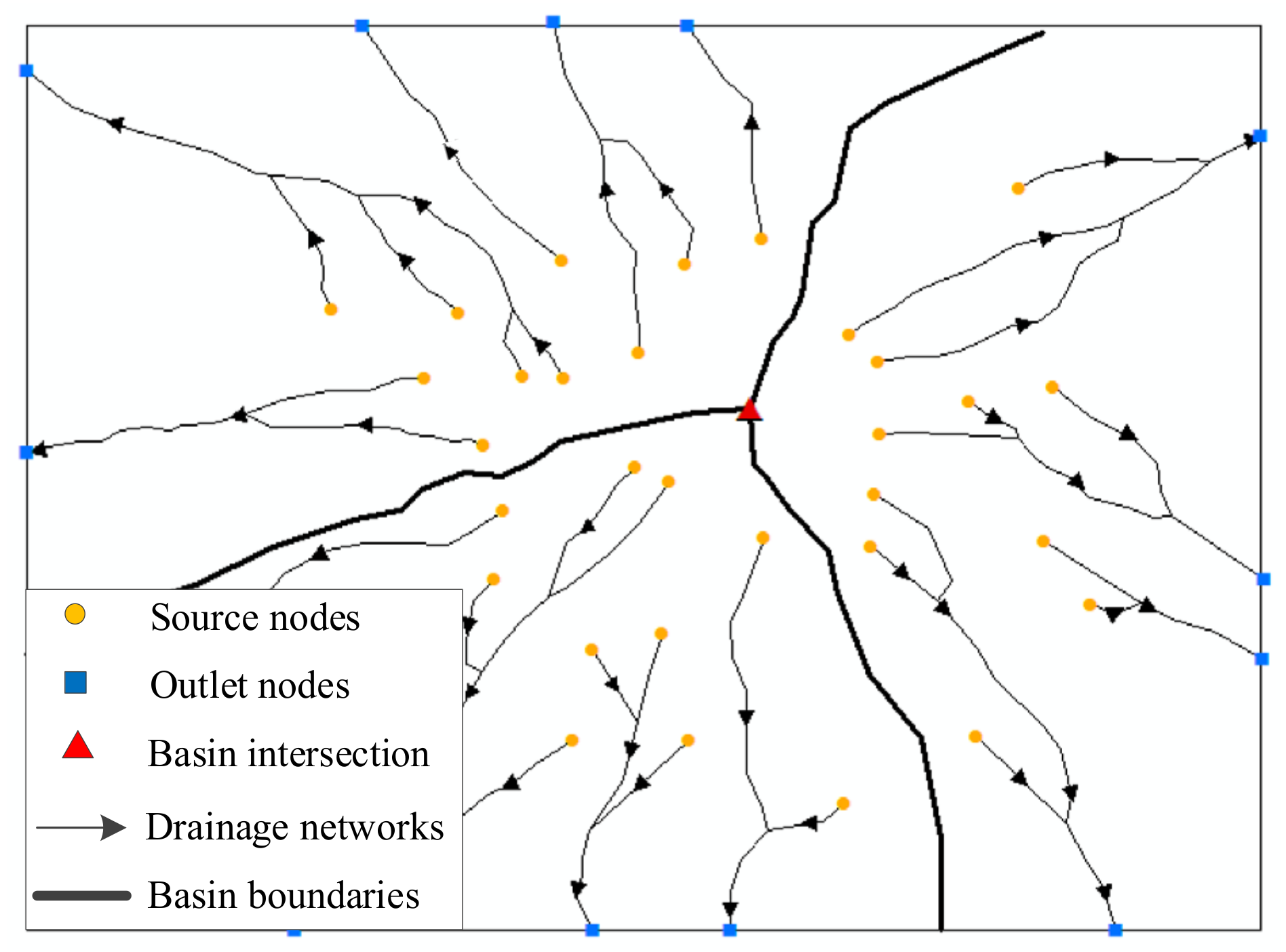
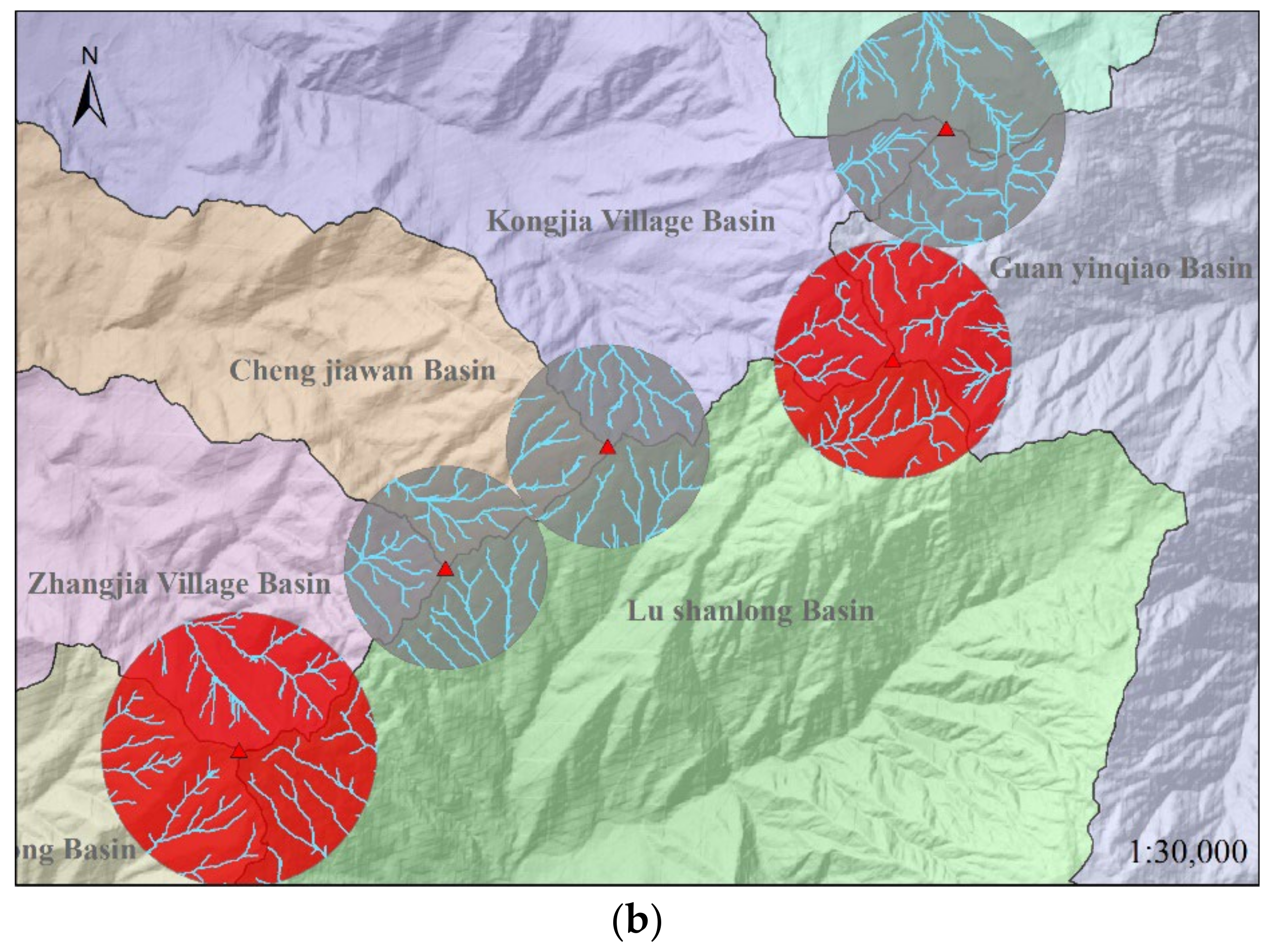
- It develops in the adjacent parts of multiple basins. RD is a pattern that uniformly diverges from the center to the surrounding area (Figure 5), so the shape of identification units can be abstracted into a circle. In most cases, the river networks of a region are always divided into multiple basins, and RD often exists where the multiple basins intersect. Therefore, the basins’ intersections could be the RD pattern’s central points.
- Its rivers always uniformly diverge from the center to the surrounding area, so the shape of identification units can be abstracted into a circle. The distribution characteristics of rivers in all directions can be acquired by calculating the flow directions and accumulative lengths in the identification units.
- The number of the source nodes is not less than the outlet nodes, and the average distance from all the source nodes to the center point is less than that between all the outlet nodes and the center point.
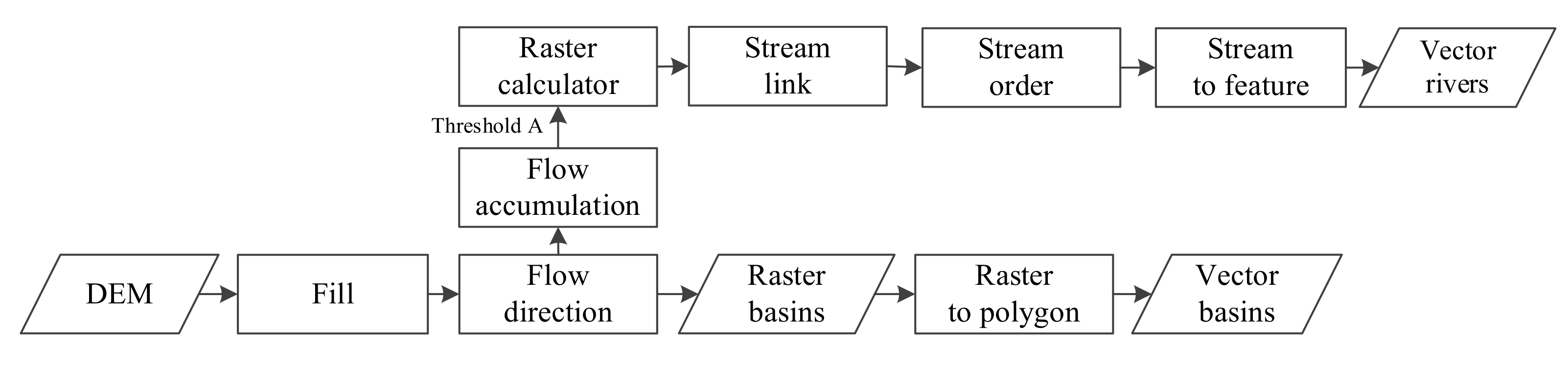
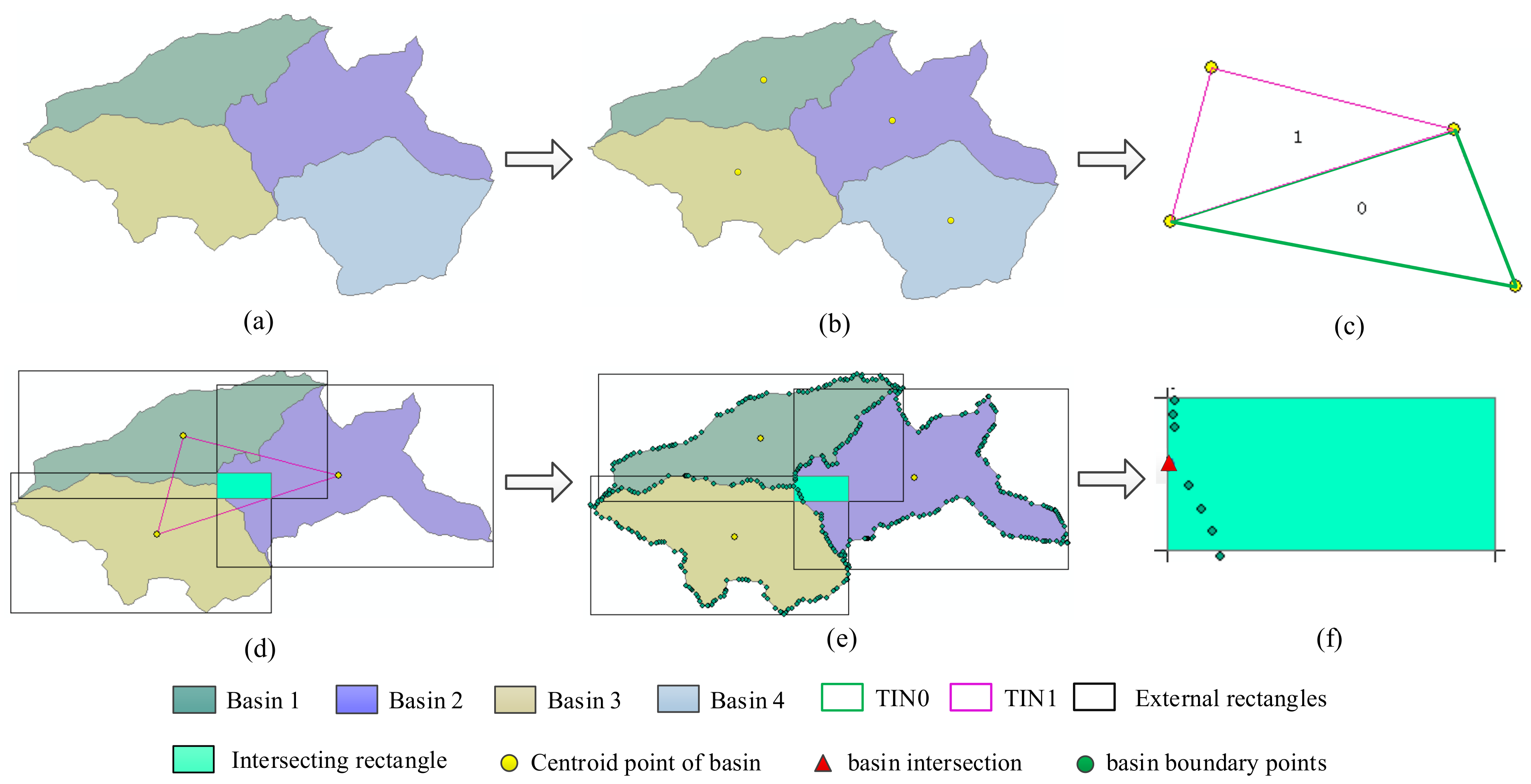
2.3.2. Generation of Identification Units
- Generating external rectangles of the three adjacent basins by reading one triangle in the D-TIN;
- Obtaining the intersecting area of the three external rectangles;
- Taking the point belonging to three adjacent basins as the basin intersection and putting it into the set ;
- Repeating steps (2)–(4) until all the triangles are formed.
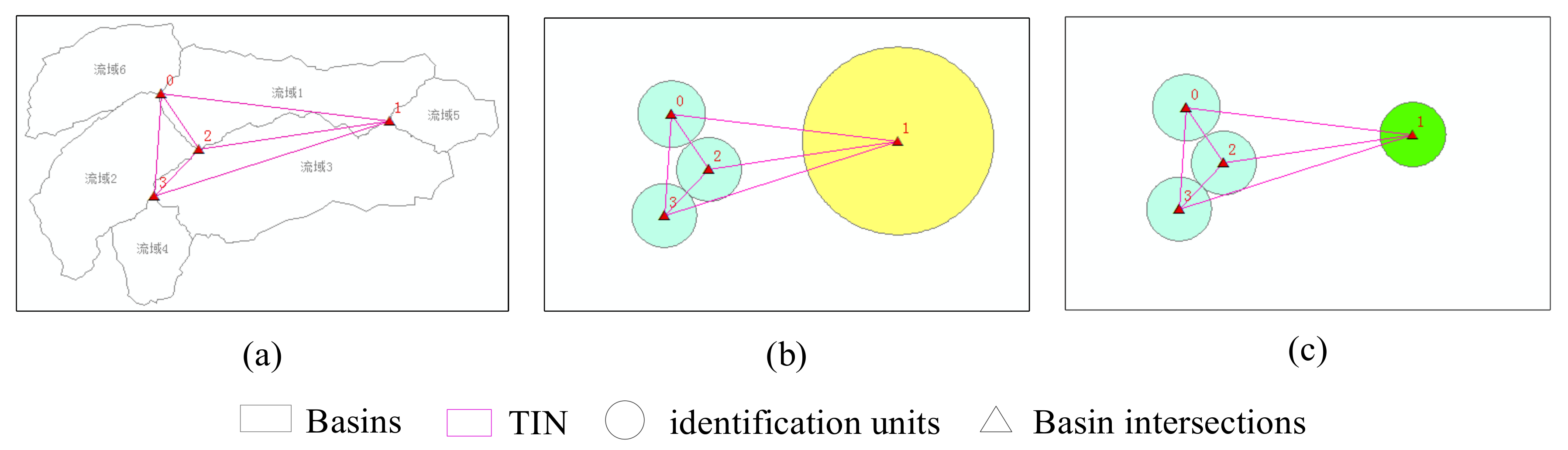
- Reading the D-TINs constructed above, calculating the length of all TIN edges, and then putting them into the array Ldis[i][k], i ∈ [0, m−1], k ∈ [0, n−1], where m is the number of D-TINs, and n is the number of the edges of a TIN, n ∈ [0, 3);
- Searching the minimum TIN edge distance that does not equal zero in each TIN and saving half of it to the array R[i];
- Calculating the average distance ad in accordance with Formula (1):where Min and Max are the minimum and maximum threshold of the buffer radius set by the user, respectively;
- In accordance with Formula (1), calculating the optimized radius array R’[m]:
- Deleting the river segments whose stream order is greater than 2;
- In each identification unit, calculating the distance between the last point (or the first point) of each river segment and the center of the unit (the distance is marked as dl (or df)). If Formula (3) is satisfied, then the stream is a radial river segment. Conversely, the stream is a non-radial river segment.
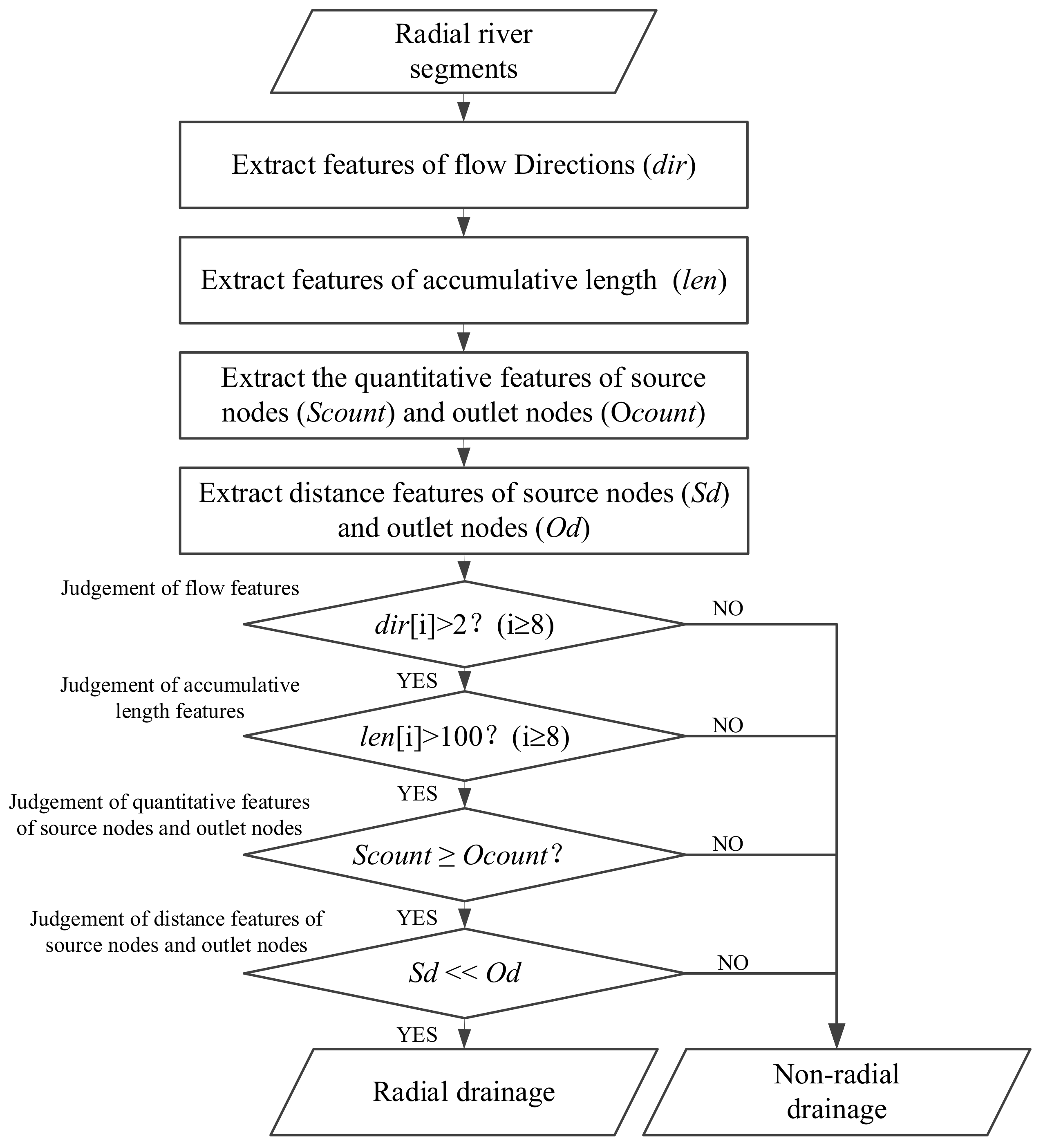
2.3.3. Extraction of Drainage Features
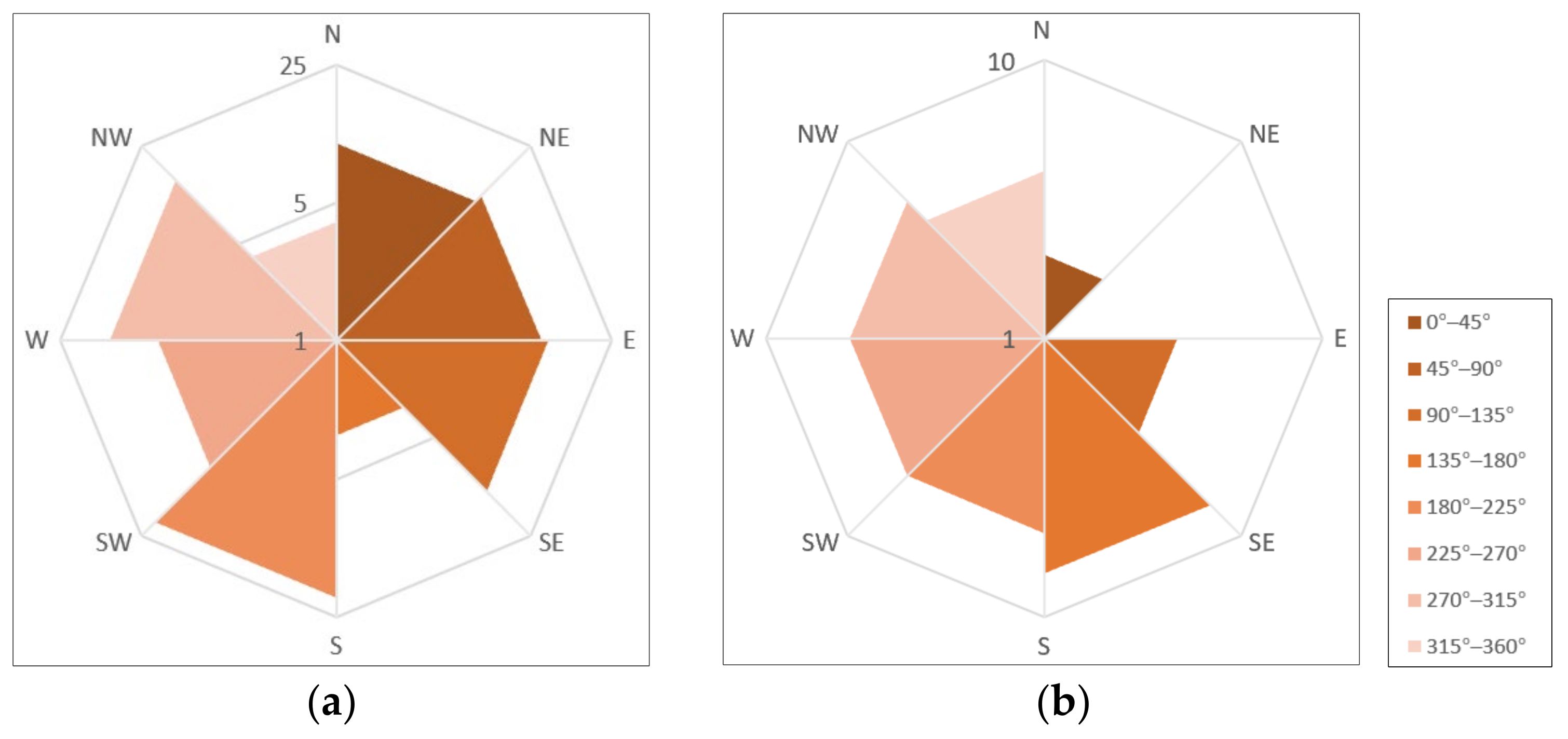
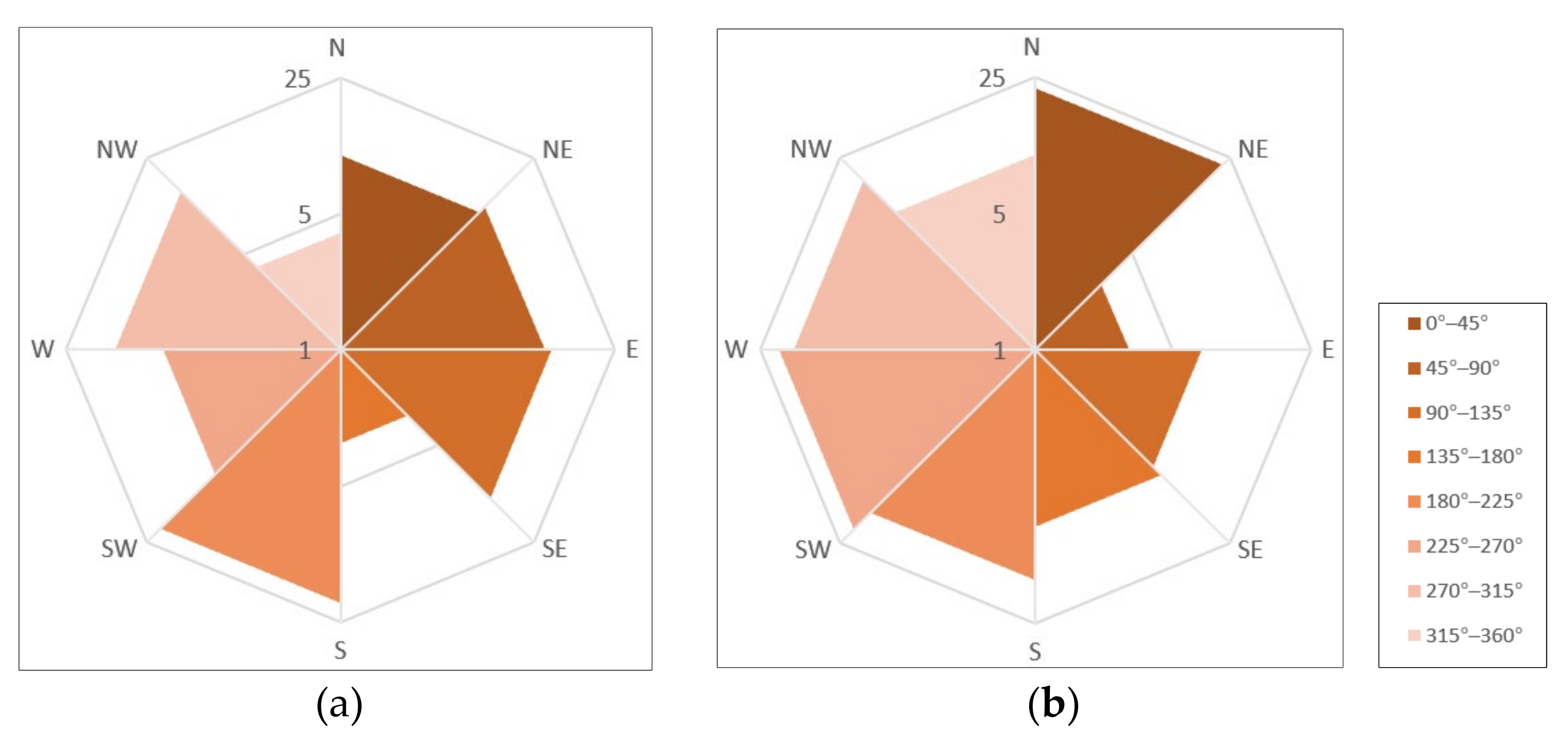
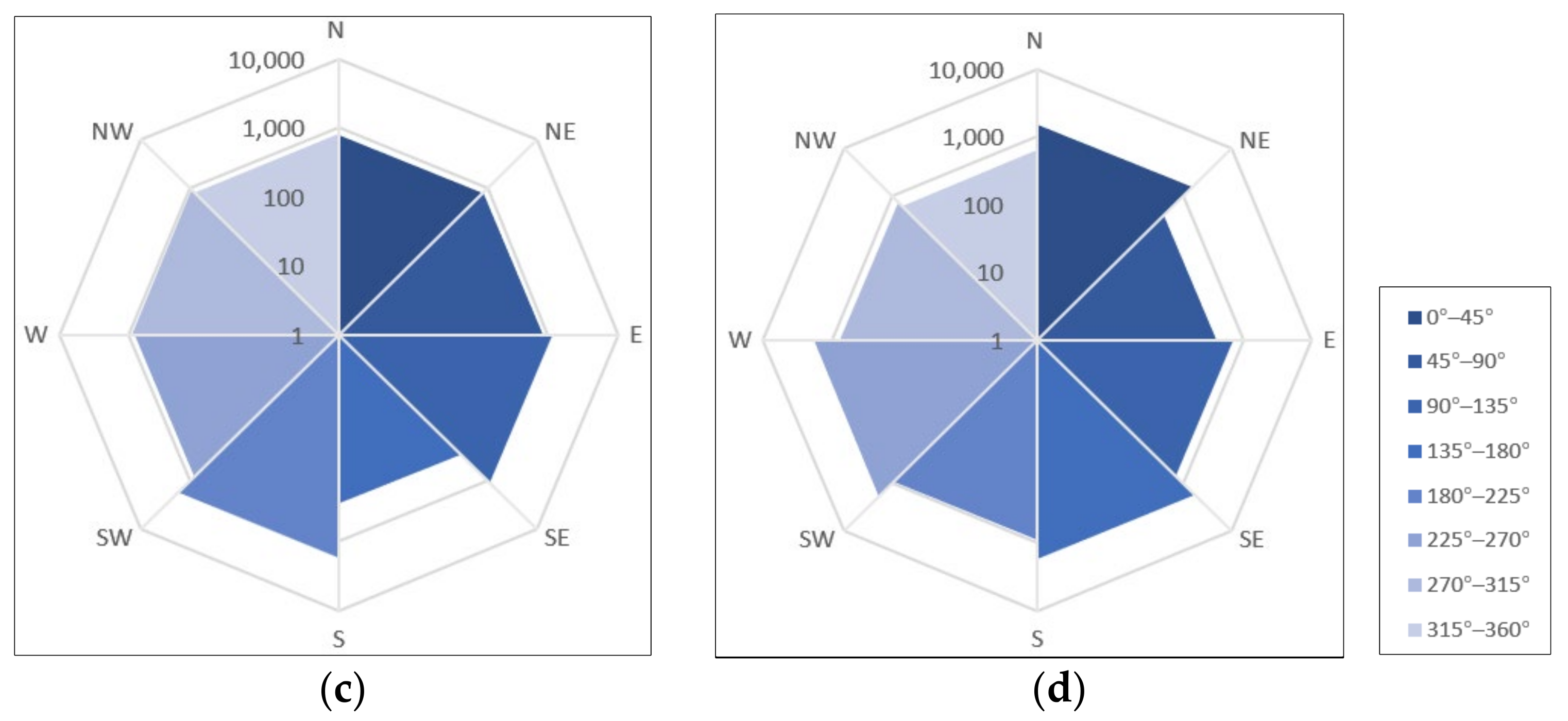
- Calculating the angle range according to Formula (4):where N is the number of flow directions for a rose chart. Generally, N is an integer and a multiple of 8;t = 360°/N
- Calculating the flow frequency and accumulative length in each interval and saving them to the array dir[N] and len[N], respectively.
- Obtaining the first and last point of each river segment;
- Obtaining the points whose in-degree is 0 and putting them into SnodeList. Similarly, obtaining the points whose out-degree is 0 and putting them into OnodeList;
- Marking the number of elements in SnodeList and OnodeList as Scount and Ocount, respectively;
- Calculating the average distance from all the points in SnodeList (or OnodeList) to the center point and marked as Sd (or Od).
2.3.4. Recognition of Drainage Patterns
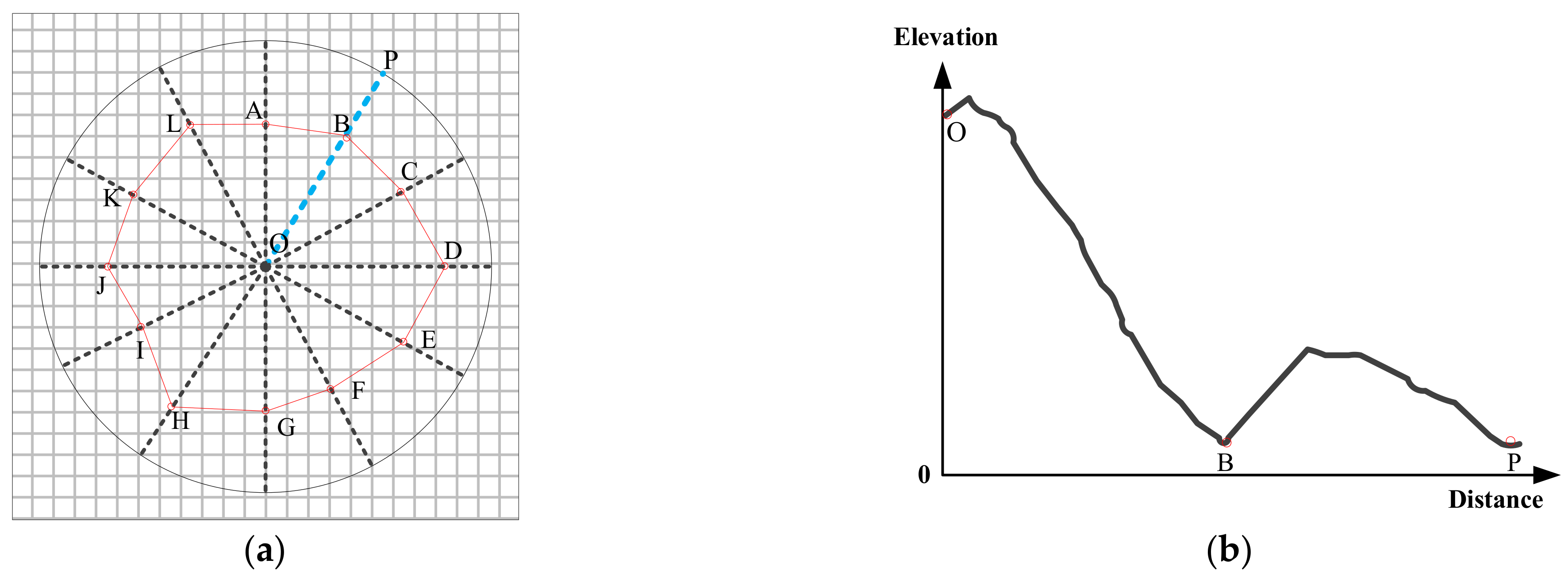
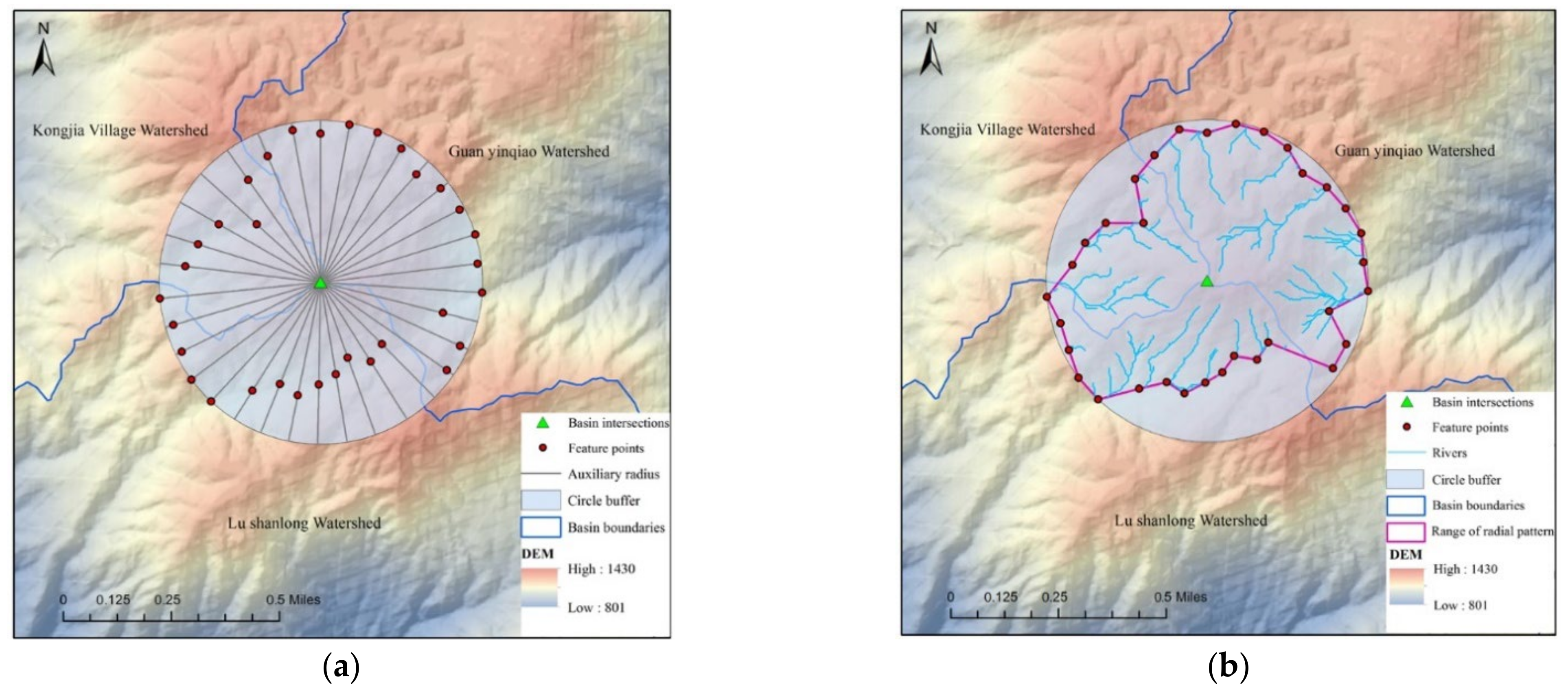
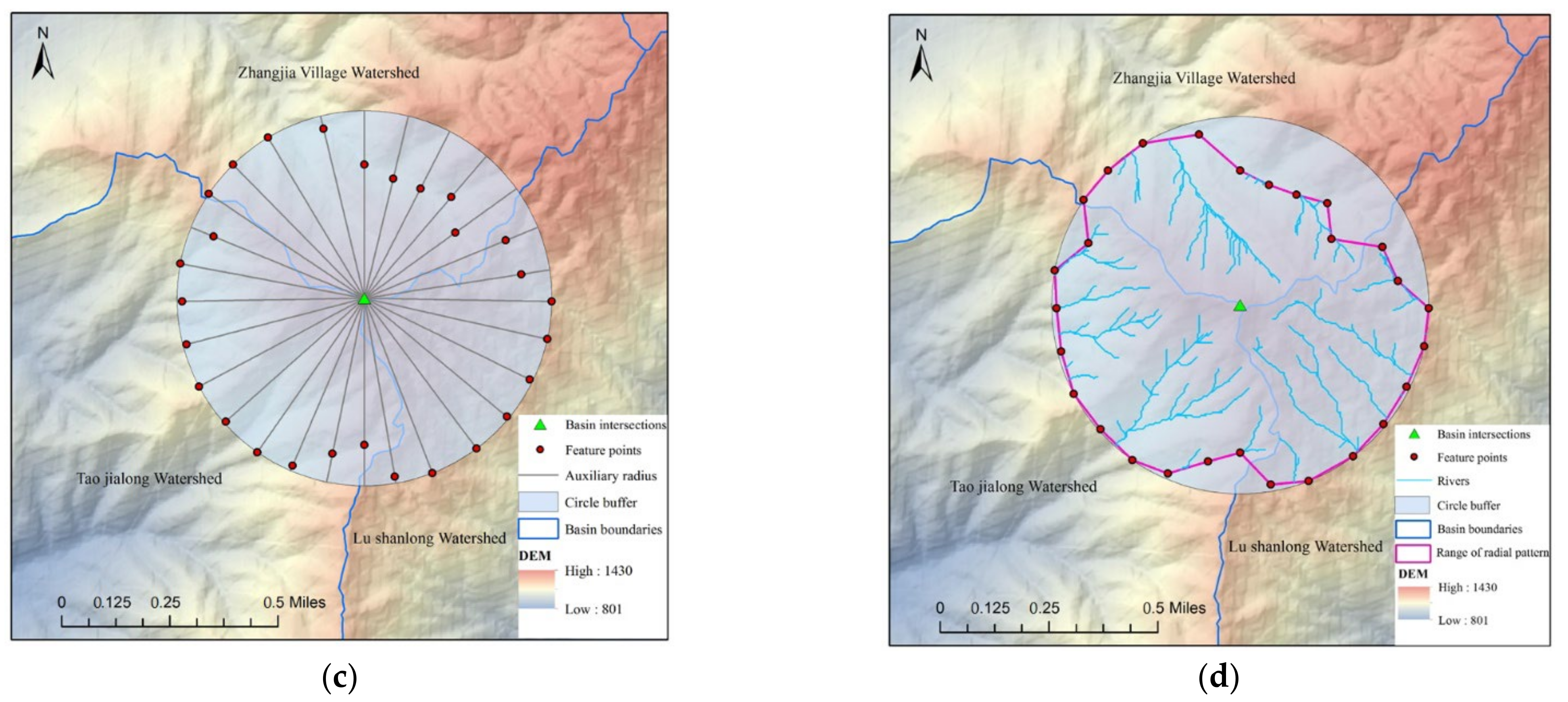
2.3.5. Determination of Drainage Scope
- Generating N auxiliary radii uniformly in each identification unit (N is a positive integer) and discretizing these radii into the points;
- Obtaining the elevations of the points with DEM;
- Among the points of an auxiliary radius, searching for the point with the lowest elevation, and finding all the other points that have approximate elevation with the minimum point, then taking the closest point to the center point from the minimum point and all the other points as the feature point, finally adding the feature point to the set SP;
- Repeating steps (3) until all the auxiliary radii are finished;
- Connecting all points in SP orderly as the scope line of RD.
3. Results
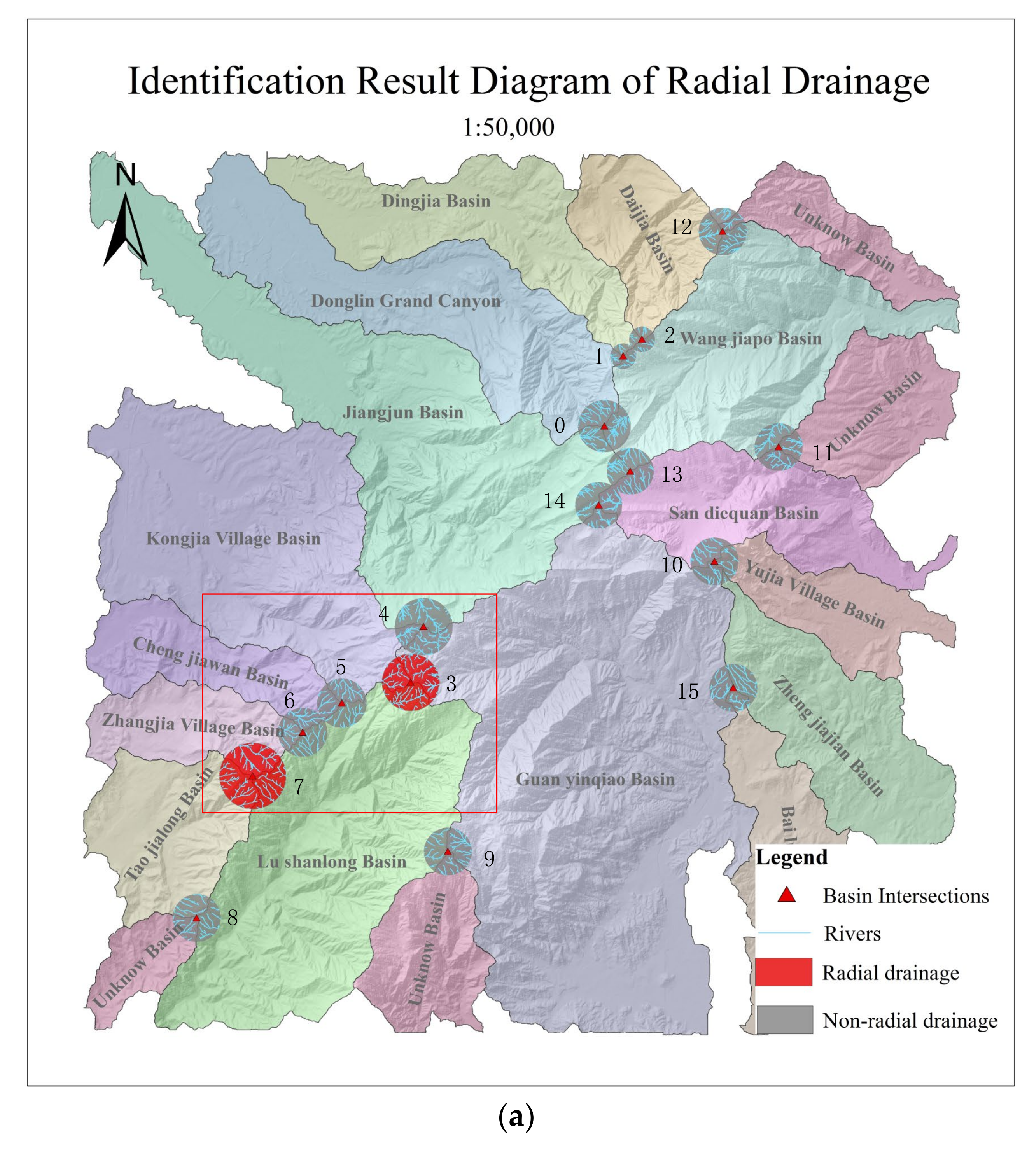
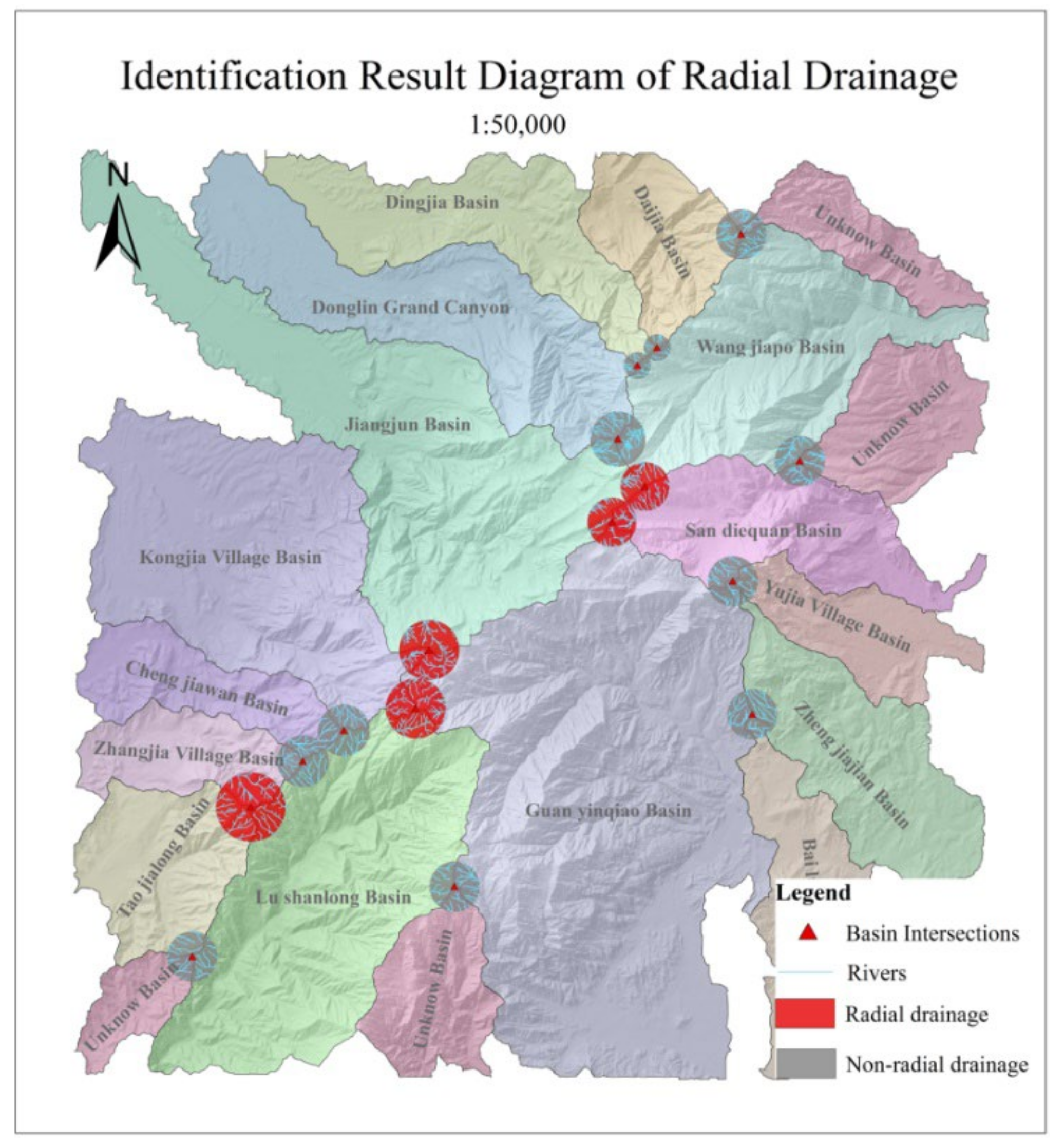
3.1. Identification Results of RD
3.2. Result of RD Scope
4. Discussion
4.1. Validation of Identification Results
4.2. Several Aspects That Affect the Recognition Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zernitz; Emilie, R. Drainage patterns and their significance. J. Geol. 1932, 40, 498–521. [Google Scholar] [CrossRef]
- Morisawa, M.E. Rivers: Form and Process; Geomophology Texts 7; Longman: London, UK, 1988. [Google Scholar]
- Argialas, D.P.; Lyon, J.G.; Mintzer, O.W. Quantitative description and classification of drainage pattern. Photogramm. Eng. Remote Sens. 1988, 54, 505–509. [Google Scholar]
- Charlton, R. Fundamentals of Fluvial Geomorphology. In Sedimentation Engineering; Routledge: London, UK, 2007. [Google Scholar]
- Yang, J.C.; Li, Y.L. Principles of Geomorphology; Peking University Press: Beijing, China, 2001. [Google Scholar]
- Twidale, C.R. River patterns and their meaning. Earth-Sci. Rev. 2004, 67, 159–218. [Google Scholar] [CrossRef]
- Ai, T.H.; Liu, Y.L.; Huang, Y.F. The Hierarchical Watershed Partitioning and Generalization of River Network. J. Surv. Mapp. 2007, 2, 231–236; 243. [Google Scholar]
- Lubowe, J.K. Stream junction angles in the dendritic drainage pattern. Am. J. Sci. 1964, 262, 325–339. [Google Scholar] [CrossRef]
- Soykan, A.; Cürebal, I.; Efe, R.; Sönmez, S. Geomorphological features and seismicity of Bigadi? Plain and its immediate vicinity. Procedia—Soc. Behav. Sci. 2014, 120, 524–531. [Google Scholar] [CrossRef]
- Bamousa, A.O.; Matar, S.S.; Mohamed, D. Structural and geomorphic features accommodating groundwater of al-madinah city, Saudi Arabia. Arab. J. Geosci. 2013, 6, 3127–3132. [Google Scholar] [CrossRef]
- Haakon, F. Structural Geology; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Roger, M. Geological Methodsin Mineral Exploration and Mining, 2nd ed.; Springer: Berlin/Heidelberg, Germany; London, UK; New York, NY, USA, 2010; 13p. [Google Scholar]
- Alfonso, I.M.; Niemann, J.D. Identification and characterization of dendritic, parallel, pinnate, rectangular, and trellis networks based on deviations from planform self-similarity. J. Geophys. Res. Earth Surf. 2008, 113(F2), F02015.1–F02015.21. [Google Scholar]
- Vimal, S.; Nagesh Kumar, D.; Jaya, I. Extraction of drainage pattern from ASTER and SRTM data for a river basin using GIS tools. In Proceedings of 2012 International Conference on Environment, Energy and Biotechnology, Jeju Island, South Korea, 28 November 2012; Volume 33, pp. 126–130. [Google Scholar]
- Zhang, L.; Guilbert, E. Automatic Drainage Pattern Recognition in River Networks; Taylor and Francis, Inc.: Philadelphia, PA, USA, 2013; Volume 27, pp. 2319–2342. [Google Scholar]
- Zhang, L.; Guilbert, E. A study of variables characterizing drainage patterns in river networks. Remote Sens. Spat. Inf. Sci. 2012, 39, 29–34. [Google Scholar] [CrossRef]
- Jung, K.; Marpu, P.R.; Ouarda, T.B.M.J. Improved classification of drainage networks using junction angles and secondary tributary lengths. Geomorphology 2015, 239, 41–47. [Google Scholar] [CrossRef]
- Jung, K.; Ouarda, T.B.M.J. Classification of drainage network types in the arid and semi-arid regions of Arizona and California. J. Arid. Environ. 2017, 144, 60–73. [Google Scholar] [CrossRef]
- Xie, G.G.; Deng, B.R. Establishment of Lushan ridge group of Lushan area in the Neoproterozoic, Jiangxi province. Geol. Sci. Technol. Jiangxi 1996, 4, 167–171. [Google Scholar]
- Huang, C.G.; Zhong, C.G. Neoproterozoic marine volcanic activity and petrographic features in the Lushan area. Jiangxi Geol. 2000, 14, 99–104. [Google Scholar]
- Shi, Z.G. Neoproterozoic Strata and Tectonic Evolution in Lushan Area, JIANGXI Province. Ph.D. Thesis, Chinese Academy of Geological Science, Beijing, China, 2014. [Google Scholar]
- Zhang, Z.G.; Wang, L.C. Guide to Field Practice of Geography in Lushan Area; Science Press: Beijing, China, 2011. [Google Scholar]
- Jackson, J.; Norris, R.; Youngson, J. The structural evolution of active fault and fold systems in central Otago, New Nealand: Evidence revealed by drainage patterns. J. Struct. Geol. 1996, 18, 217–234. [Google Scholar] [CrossRef]
- Yang, C.C.B.; Chen, W.S.; Wu, L.C.; Lin, C.W. Active deformation front delineated by drainage pattern analysis and vertical movement rates, southwestern coastal plain of Taiwan. J. Asian Earth Sci. 2008, 31, 251–264. [Google Scholar] [CrossRef]
- Pérez-Peña, J.V.; Azor, A.; Azañón, J.M.; Keller, E.A. Active tectonics in the Sierra Nevada (Betic Cordillera, SE Spain): Insights from geomorphic indexes and drainage pattern analysis. Geomorphology 2010, 119, 74–87. [Google Scholar] [CrossRef]
- Guang, Y.H.; Zheng, F.L.; Wang, B. DEM Based Extraction of River Networks in Binzhou River Basin of Heilongjiang Province. Bull. Soil Water Conserv. 2012, 32, 127–131. [Google Scholar]
- LI, J.; Tang, G.A.; Zhang, T. Conflux Threshold of Extracting Stream Networks from DEMs in North Shanxi Province of Loess Plateau. Bull. Soil Water Conserv. 2007, 2, 75–78. [Google Scholar]
- Xiong, L.H.; Guo, S.L. Method for extracting digital channel network from digital elevation model of watershed. J. Yangtze River Sci. Res. Inst. 2003, 4, 14–17. [Google Scholar]
- Lanyan, M.A. Research on drainage network extraction in LiaoHe basin based on SRTM DEM and aster GDEM. J. Anhui Agric. Sci. 2010, 39, 2692–2695. [Google Scholar]
- Turcotte, R.; Fortin, J.P.; Rousseau, A.N.; Massicotte, S.; Villeneuve, J.P. Determination of the drainage structure of a watershed using a digital elevation model and a digital river and lake network. J. Hydrol. 2001, 240, 225–242. [Google Scholar] [CrossRef]
- Strahler, A.N. Quantitative analysis of watershed geomorphology. Eos Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef]
- Strahler, A.N. Dynamic basis of geomorphology. Geol. Soc. Am. Bull. 1952, 63, 923–938. [Google Scholar] [CrossRef]
- Shreve, R.L. Statistical law of stream numbers. J. Geol. 1966, 74, 17–37. [Google Scholar] [CrossRef]
- O’Callaghan, J.F.; Mark, D.M. The extraction of drainage networks from digital elevation data. Comput. Vis. Graph. Image Processing 1984, 28, 323–344. [Google Scholar] [CrossRef]
- Zhang, G.S. Contemporary Geomorphology; Science Press: Beijing, China, 2005. [Google Scholar]
- Chew, L.P. Constrained Delaunay triangulations. Algorithmica 1989, 4, 97–108. [Google Scholar] [CrossRef]
- Anglada, M.V. An improved incremental algorithm for constructing restricted Delaunay triangulations. Comput. Graph. 1997, 21, 215–223. [Google Scholar] [CrossRef]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H. The quickhull algorithm for convex hulls. ACM Trans. Math. Softw. 1996, 22, 469–483. [Google Scholar] [CrossRef]
- Yu, G.F.; Yan, B.Z. Drawing of ancient flow rose chart based on VB. West-China Explor. Eng. 2005, 9, 71–72. [Google Scholar]
- Bharani, R.; Sivaprakasam, A. Meteorosoft: A excel function for wind data processing and rose diagram. Earth Sci. Inform. 2020, 13, 965–971. [Google Scholar] [CrossRef]
- David, J.S.; David, C.P.P. Making rose diagrams fit-for-purpose. Earth-Sci. Rev. 2020, 201, 103055. [Google Scholar]


| Method Name | Meaning of Flow Direction | Advantage | Disadvantage |
|---|---|---|---|
| The first and last point connection method | Overall flow | Considers the whole conditions and is simple | Difficult to describe local conditions |
| Minimum bounding rectangle method | Overall flow | Considers the whole conditions | Difficult to describe local conditions and more complex |
| Interval division method | Advantage flow | Considers the whole and local conditions | Threshold limit and more complex |
| ID | NAR | NRR | WSCRF | WSALCR | TNSP | TNOP | ADSC | ADOC | IRDP |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 168 | 66 | No | No | 41 | 9 | 320.82 | 400.19 | No |
| 1 | 37 | 20 | No | No | 12 | 5 | 152.53 | 209.64 | No |
| 2 | 31 | 20 | No | No | 12 | 11 | 174.51 | 240.21 | No |
| 3 | 199 | 82 | Yes | Yes | 50 | 6 | 346.25 | 417.78 | Yes |
| 4 | 233 | 71 | No | Yes | 41 | 9 | 341.97 | 402.02 | No |
| 5 | 117 | 50 | No | No | 31 | 4 | 282.50 | 358.26 | No |
| 6 | 110 | 31 | No | No | 17 | 4 | 258.07 | 344.25 | No |
| 7 | 239 | 102 | Yes | Yes | 66 | 6 | 379.01 | 446.77 | Yes |
| 8 | 107 | 53 | No | No | 31 | 7 | 291.91 | 368.42 | No |
| 9 | 110 | 54 | No | No | 31 | 13 | 280.86 | 358.80 | No |
| 10 | 120 | 64 | No | No | 32 | 7 | 328.57 | 391.13 | No |
| 11 | 163 | 53 | No | No | 30 | 5 | 286.97 | 346.80 | No |
| 12 | 121 | 58 | No | No | 37 | 9 | 269.47 | 338.36 | No |
| 13 | 119 | 57 | No | No | 38 | 12 | 294.21 | 381.19 | No |
| 14 | 152 | 75 | No | No | 44 | 12 | 293.46 | 345.21 | No |
| 15 | 127 | 31 | No | No | 17 | 5 | 253.02 | 303.25 | No |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, X.; Li, A.-B.; Wang, K.-L.; Chen, H. A Novel Method to Identify Radial Drainage Based on Morphological Features. Water 2022, 14, 2820. https://doi.org/10.3390/w14182820
Wan X, Li A-B, Wang K-L, Chen H. A Novel Method to Identify Radial Drainage Based on Morphological Features. Water. 2022; 14(18):2820. https://doi.org/10.3390/w14182820
Chicago/Turabian StyleWan, Xia, An-Bo Li, Kai-Liang Wang, and Hao Chen. 2022. "A Novel Method to Identify Radial Drainage Based on Morphological Features" Water 14, no. 18: 2820. https://doi.org/10.3390/w14182820





