Application of Particle Swarm Optimization for Auto-Tuning of the Urban Flood Model
Abstract
:1. Introduction
2. Materials and Methods
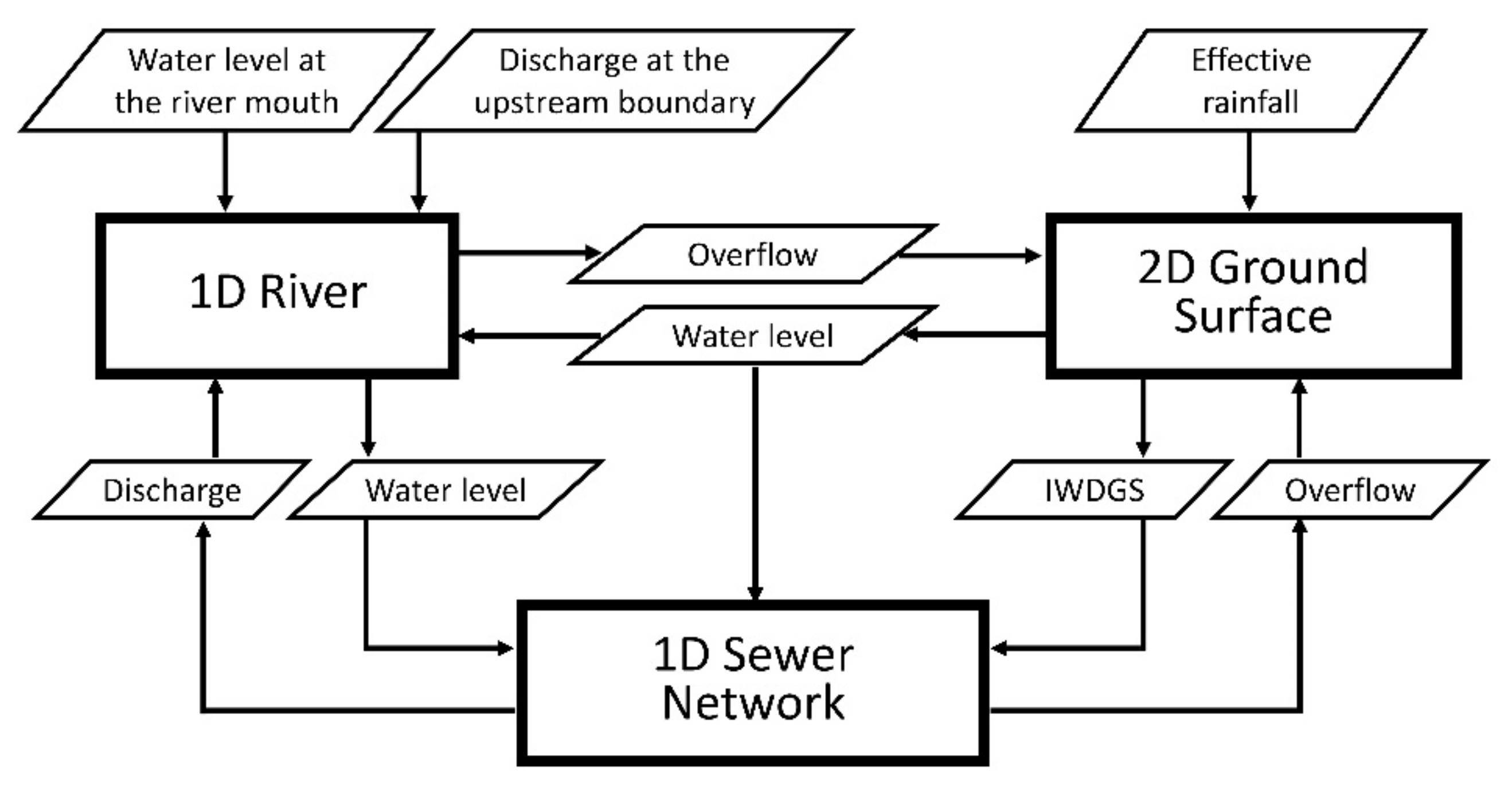
2.1. Outline of the Urban Flood Model
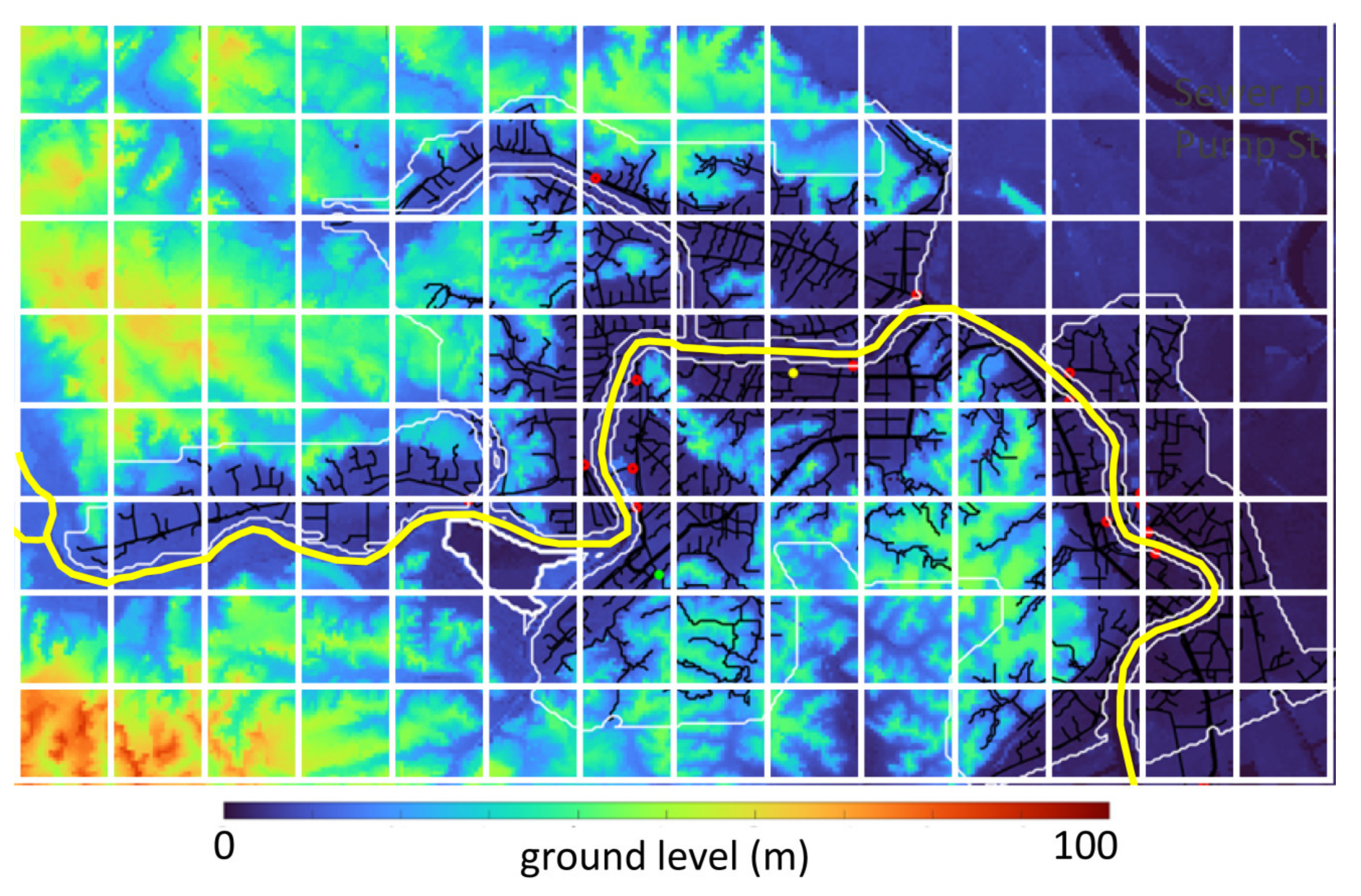
2.2. Description of the Case Study
2.3. Sensitivity Analysis
2.4. Setup of PSO for Auto-Tuning of the Urban Flood Model
2.5. Application of PSO to the Case Study Site
3. Results and Discussions
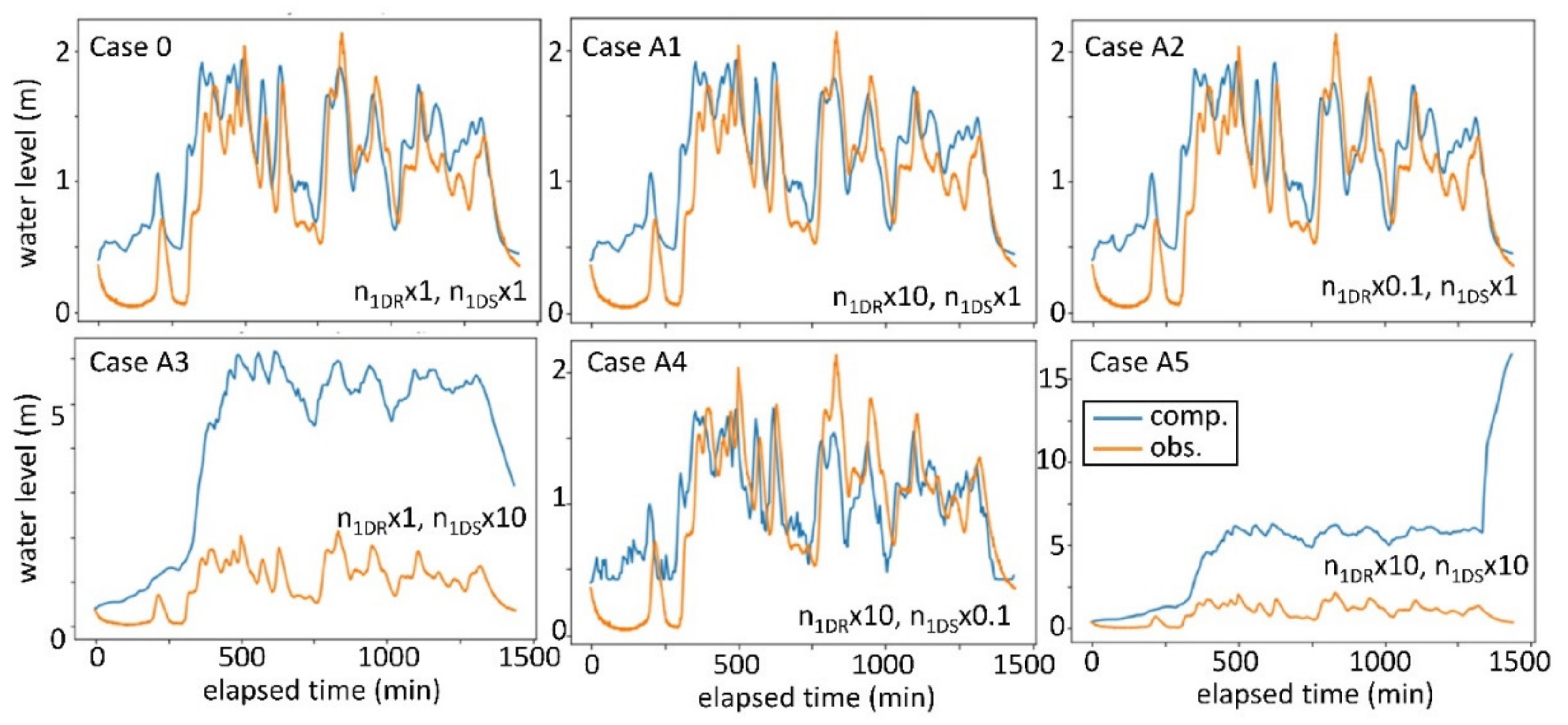
3.1. Model Sensitivity to Manning’s Roughness
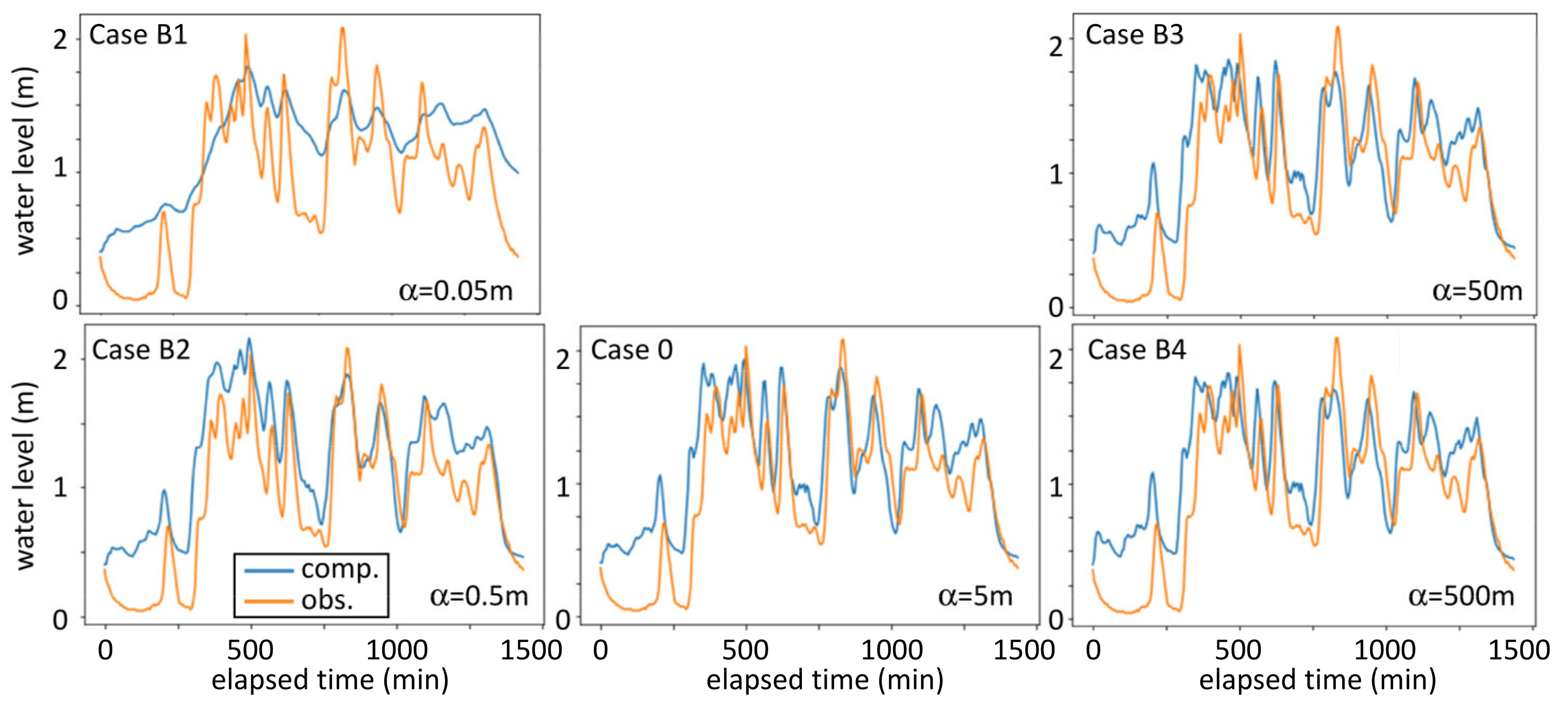
3.2. Model Sensitivity to the Coefficient, α
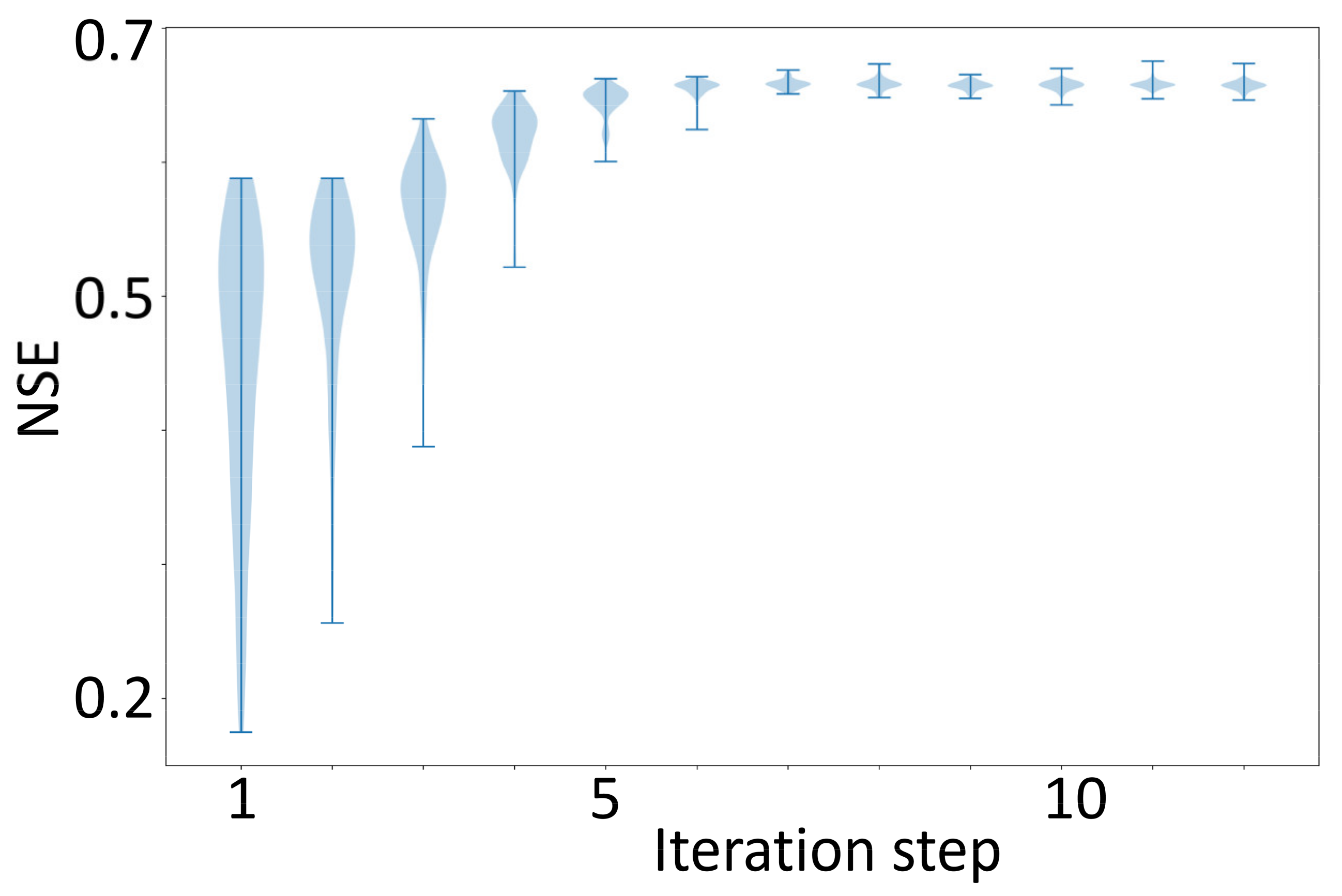
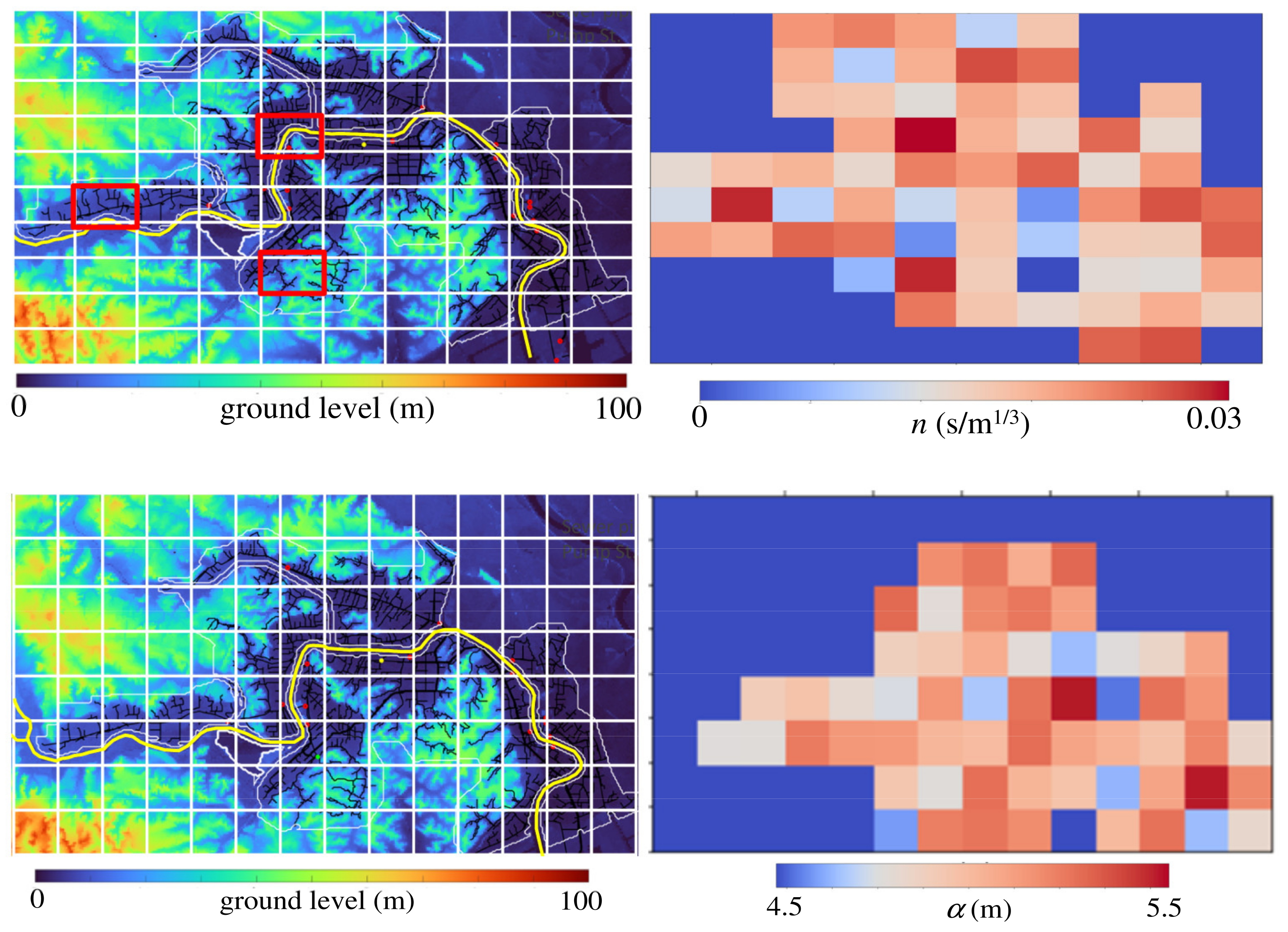
3.3. Application of the Present PSO-Based Auto-Tuning System
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- O’Donnell, E.C.; Thorne, C.R. Drivers of future urban flood risk. Philos. Trans. R. Soc. A 2020, 378, 23. [Google Scholar] [CrossRef] [PubMed]
- Ashley, R.; Garvin, S.; Pasche, E.; Vassilopoulos, A.; Zevenbergen, C. Advances in Urban Flood Management; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K.; et al. Flood risk and climate change: Global and regional perspectives. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef]
- Miller, J.D.; Hutchins, M. The impacts of urbanisation and climate change on urban flooding and urban water quality: A review of the evidence concerning the United Kingdom. J. Hydrol.-Reg. Stud. 2017, 12, 345–362. [Google Scholar] [CrossRef]
- Shaw, R.; Surjan, A.; Parvin, G.A. Urban Disasters and Resilience in Asia; Butterworth-Heinemann: Oxford, UK, 2016. [Google Scholar]
- Adnan, M.S.G.; Abdullah, A.M.; Dewan, A.; Hall, J.W. The effects of changing land use and flood hazard on poverty in coastal Bangladesh. Land Use Policy 2020, 99, 104868. [Google Scholar] [CrossRef]
- Yin, J.; Yu, D.P.; Yin, Z.; Liu, M.; He, Q. Evaluating the impact and risk of pluvial flash flood on intra-urban road network: A case study in the city center of Shanghai, China. J. Hydrol. 2016, 537, 138–145. [Google Scholar] [CrossRef]
- Huong, H.T.L.; Pathirana, A. Urbanization and climate change impacts on future urban flooding in Can Tho city, Vietnam. Hydrol. Earth Syst. Sci. 2013, 17, 379–394. [Google Scholar] [CrossRef]
- Hallegatte, S.; Green, C.; Nicholls, R.J.; Corfee-Morlot, J. Future flood losses in major coastal cities. Nat. Clim. Chang. 2013, 3, 802–806. [Google Scholar] [CrossRef]
- Hammond, M.J.; Chen, A.S.; Djordjevic, S.; Butler, D.; Mark, O. Urban flood impact assessment: A state-of-the-art review. Urban Water J. 2015, 12, 14–29. [Google Scholar] [CrossRef]
- Henonin, J.; Russo, B.; Mark, O.; Gourbesville, P. Real-time urban flood forecasting and modelling–a state of the art. J. Hydroinform. 2013, 15, 717–736. [Google Scholar] [CrossRef]
- DHI. MIKE-Flood User Manual. Available online: https://manuals.mikepoweredbydhi.help/2021/Water_Resources/MIKE_FLOOD_UserManual.pdf (accessed on 29 July 2022).
- Xpswmm Reference Manual. Available online: https://dokumen.tips/documents/xpswmm-reference-manual.html?page=37 (accessed on 29 July 2022).
- Innovyze. InfoWorks ICM Help Documentation. Available online: https://help.innovyze.com/display/infoworksicm/Table+of+Contents (accessed on 29 July 2022).
- Qi, W.C.; Ma, C.; Xu, H.S.; Chen, Z.F.; Zhao, K.; Han, H. A review on applications of urban flood models in flood mitigation strategies. Nat. Hazards 2021, 108, 31–62. [Google Scholar] [CrossRef]
- Piadeh, F.; Behzadian, K.; Alani, A.M. A critical review of real-time modelling of flood forecasting in urban drainage systems. J. Hydrol. 2022, 607, 16. [Google Scholar] [CrossRef]
- Ravazzani, G.; Amengual, A.; Ceppi, A.; Homar, V.; Romero, R.; Lombardi, G.; Mancini, M. Potentialities of ensemble strategies for flood forecasting over the Milano urban area. J. Hydrol. 2016, 539, 237–253. [Google Scholar] [CrossRef]
- Shrestha, A.; Mascaro, G.; Garcia, M. Effects of stormwater infrastructure data completeness and model resolution on urban flood modeling. J. Hydrol. 2022, 607, 18. [Google Scholar] [CrossRef]
- Paquier, A.; Bazin, P.H. Estimating uncertainties for urban floods modelling. Houille Blanche-Revue Internationale De L Eau. La Houille Blanche 2014, 6, 13–18. [Google Scholar] [CrossRef]
- Yu, D.P.; Coulthard, T.J. Evaluating the importance of catchment hydrological parameters for urban surface water flood modelling using a simple hydro-inundation model. J. Hydrol. 2015, 524, 385–400. [Google Scholar] [CrossRef]
- Bellos, V.; Kourtis, I.M.; Moreno-Rodenas, A.; Tsihrintzis, V.A. Quantifying Roughness Coefficient Uncertainty in Urban Flooding Simulations through a Simplified Methodology. Water 2017, 9, 944. [Google Scholar] [CrossRef]
- Ehteram, M.; Othman, F.B.; Yaseen, Z.M.; Afan, H.A.; Allawi, M.F.; Malek, M.B.A.; Ahmed, A.N.; Shahid, S.; Singh, V.P.; El-Shafie, A. Improving the Muskingum Flood Routing Method Using a Hybrid of Particle Swarm Optimization and Bat Algorithm. Water 2018, 10, 807. [Google Scholar] [CrossRef]
- He, Y.Y.; Wan, J.H. Flood hazard assessment based on fuzzy clustering iterative model and chaotic particle swarm optimization. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 933–942. [Google Scholar] [CrossRef]
- He, Y.Y.; Xu, Q.F.; Yang, S.L.; Liao, L. Reservoir flood control operation based on chaotic particle swarm optimization algorithm. Appl. Math. Model. 2014, 38, 4480–4492. [Google Scholar] [CrossRef]
- Peng, Y.; Ye, S.G.; Zhou, H.C.; Kang, H.G.; IEEE. Model of Flood Control Operation of Reservoir Based on Particle Swarm Optimization Algorithm and Its Application. Proc. Int. Conf. Comput. Sci. Netw. Tech. 2011, 1, 368–371. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Yazdani, M.; Jolai, F. Lion Optimization Algorith, (LOA): A nature-inspired metaheuristic algorithm. J. Comput. Des. Eng. 2016, 3, 24–36. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Hajiaghaei-Keshteli, M.; Tavakkoli-Moghaddam, R. Red deer algorithm (RDA): A new nature-inspired meta-heuristic. Soft Comput. 2020, 24, 14637–14665. [Google Scholar] [CrossRef]
- Kuok, K.K.; Harun, S.; Shamsuddin, S.M. Particle swarm optimization feedforward neural network for modeling runoff. Int. J. Envir. Sci. Tech. 2010, 7, 67–78. [Google Scholar] [CrossRef]
- Niu, W.J.; Feng, Z.K.; Cheng, C.T.; Zhou, J.Z. Forecasting Daily Runoff by Extreme Learning Machine Based on Quantum-Behaved Particle Swarm Optimization. J. Hydrol. Eng. 2018, 23, 04018002. [Google Scholar] [CrossRef]
- Romlay, M.R.M.; Rashid, M.M.; Toha, S.F. Development of Particle Swarm Optimization Based Rainfall-Runoff Prediction Model for Pahang River, Pekan. In Proceedings of the 2016 International Conference on Computer and Communication Engineering, Kuala Lumpur, Malaysia, 26–27 July 2016; pp. 306–310. [Google Scholar]
- Taormina, R.; Chau, K.W. Data-driven input variable selection for rainfall-runoff modeling using binary-coded particle swarm optimization and Extreme Learning Machines. J. Hydrol. 2015, 529, 1617–1632. [Google Scholar] [CrossRef]
- Tada, T. Parameter Optimization of Hydrological Model Using the PSO Algorithm. J. Jpn. Soci. Hydro. Water Res. 2007, 20, 450–461. [Google Scholar] [CrossRef]
- Wu, L.H.; Tajima, Y.; Sanuki, H.; Shibuo, Y.; Furumai, H. A novel approach for determining integrated water discharge from the ground surface to trunk sewer networks for fast prediction of urban floods. J. Flood Risk Manag. 2022, 15, 17. [Google Scholar] [CrossRef]
- Chaudhry, M.H. Applied Hydraulic Transients; Springer: New York, NY, USA, 1979. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. Proc. Int. Conf. Neural Netw. 1995, 1, 1942–1948. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Cavanaugh, J.E.; Shumway, R.H. A bootstrap variant of AIC for state-space model selection. Stat. Sin. 1997, 7, 473–496. [Google Scholar]

| Case | α (m) | ||
|---|---|---|---|
| 0 | 0.025 | 0.013 | 5 |
| A1 | 0.25 | 0.013 | 5 |
| A2 | 0.0025 | 0.013 | 5 |
| A3 | 0.025 | 0.13 | 5 |
| A4 | 0.25 | 0.0013 | 5 |
| A5 | 0.25 | 0.13 | 5 |
| B1 | 0.025 | 0.013 | 0.05 |
| B2 | 0.025 | 0.013 | 0.5 |
| B3 | 0.025 | 0.013 | 50 |
| B4 | 0.025 | 0.013 | 500 |
| Case | NSE | KGE | RMSE (m) | NRMSE |
|---|---|---|---|---|
| case 0 | 0.55 | −0.70 | 0.36 | 0.23 |
| after tuning | 0.69 | 0.65 | 0.29 | 0.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Tajima, Y.; Wu, L. Application of Particle Swarm Optimization for Auto-Tuning of the Urban Flood Model. Water 2022, 14, 2819. https://doi.org/10.3390/w14182819
Jiang L, Tajima Y, Wu L. Application of Particle Swarm Optimization for Auto-Tuning of the Urban Flood Model. Water. 2022; 14(18):2819. https://doi.org/10.3390/w14182819
Chicago/Turabian StyleJiang, Lechuan, Yoshimitsu Tajima, and Lianhui Wu. 2022. "Application of Particle Swarm Optimization for Auto-Tuning of the Urban Flood Model" Water 14, no. 18: 2819. https://doi.org/10.3390/w14182819






