Effect of Mo.S.E. Closures on Wind Waves in the Venetian Lagoon: In Situ and Numerical Analyses
Abstract
:1. Introduction
2. Materials and Methods
2.1. Investigated Area
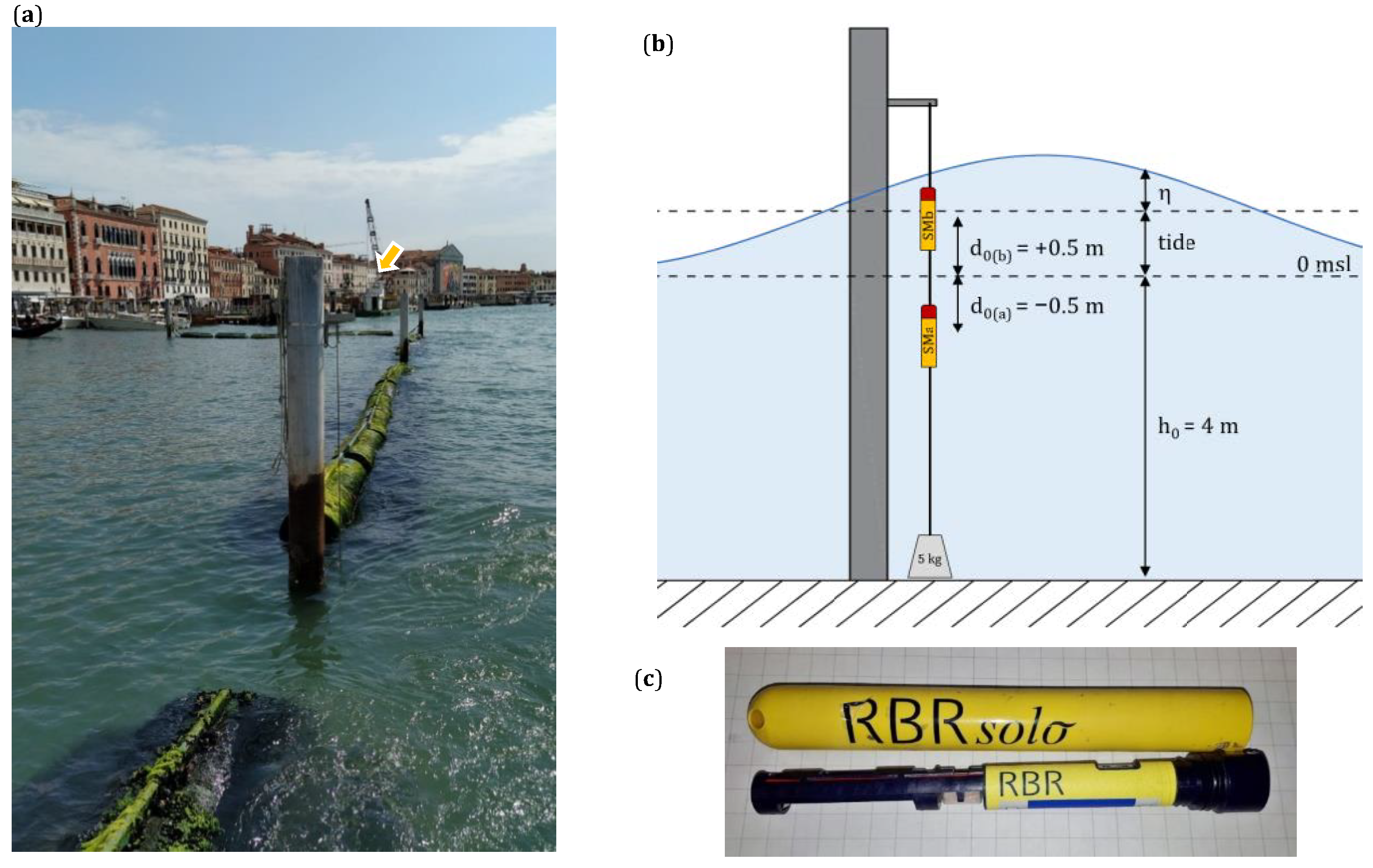
2.2. In Situ Wave Measurements
2.3. Numerical Wave Modelling
3. Results
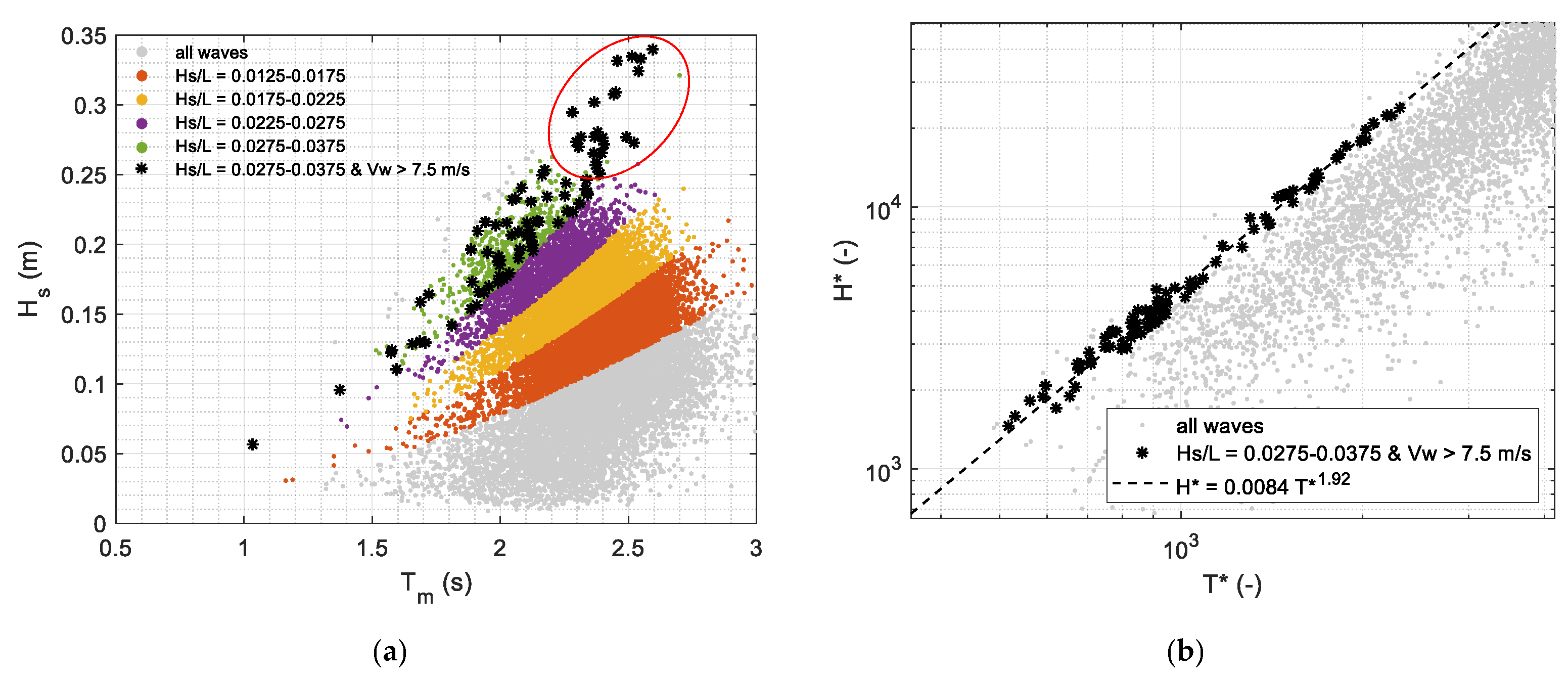
3.1. Measured and Computed Wind Waves
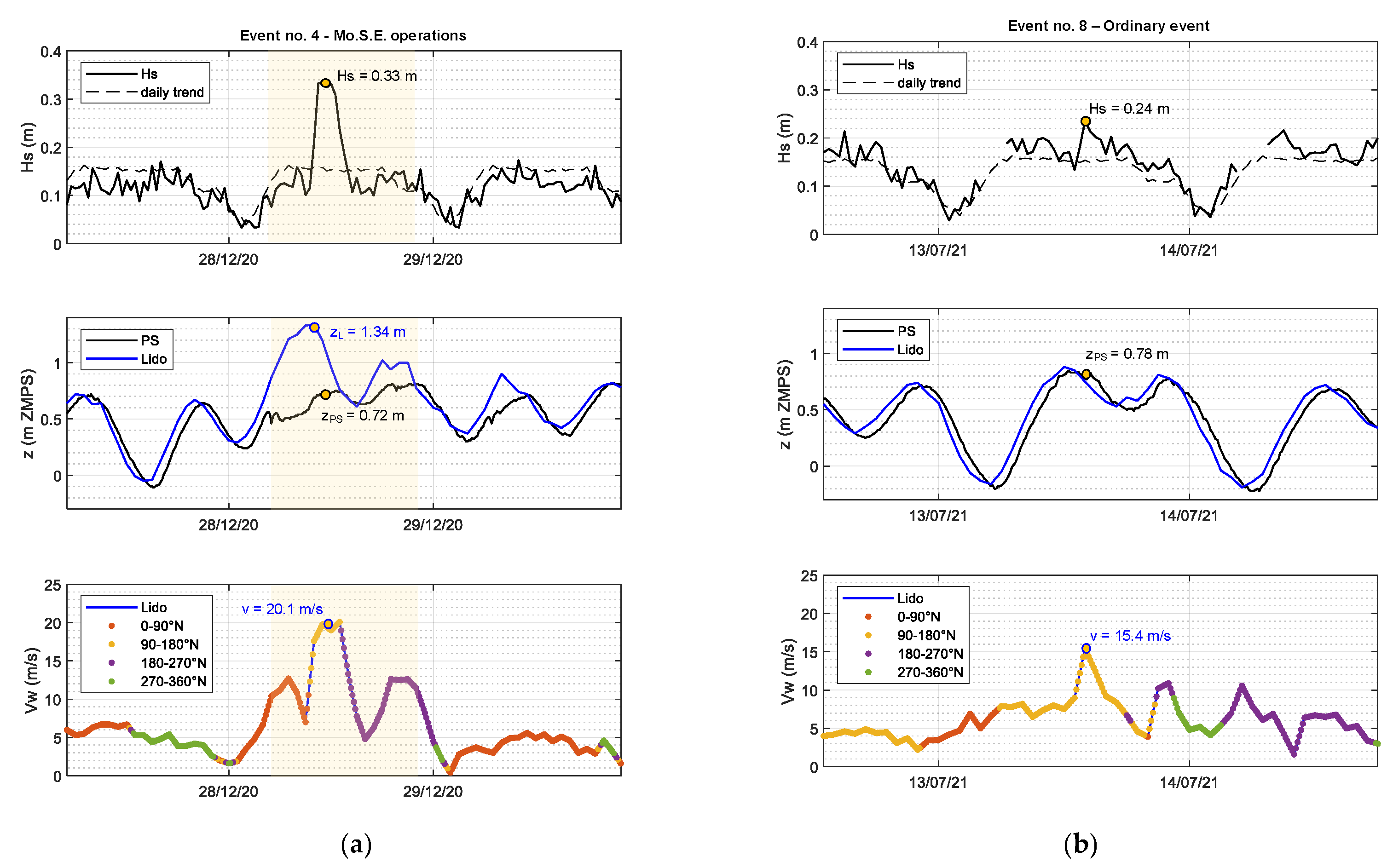
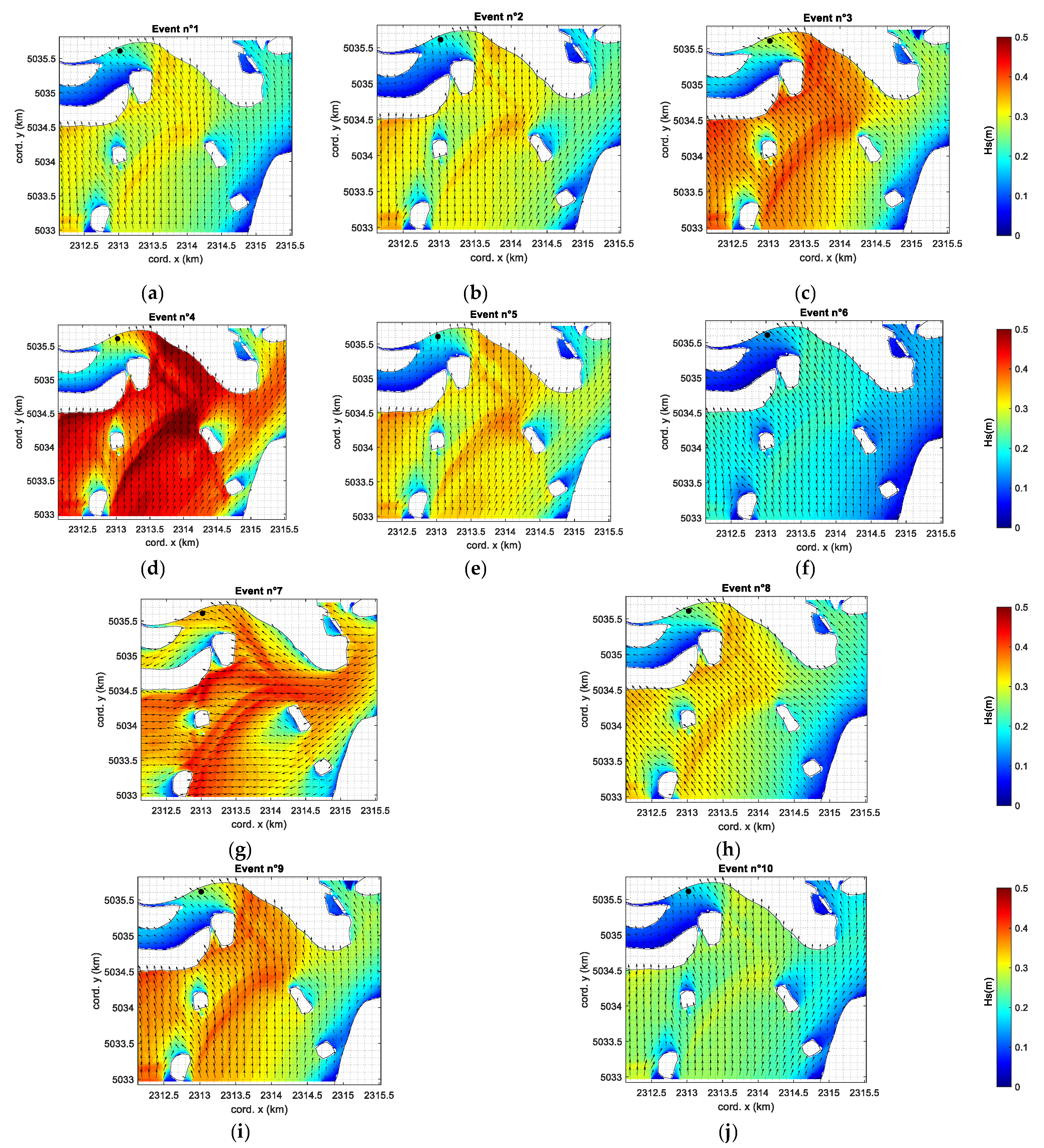
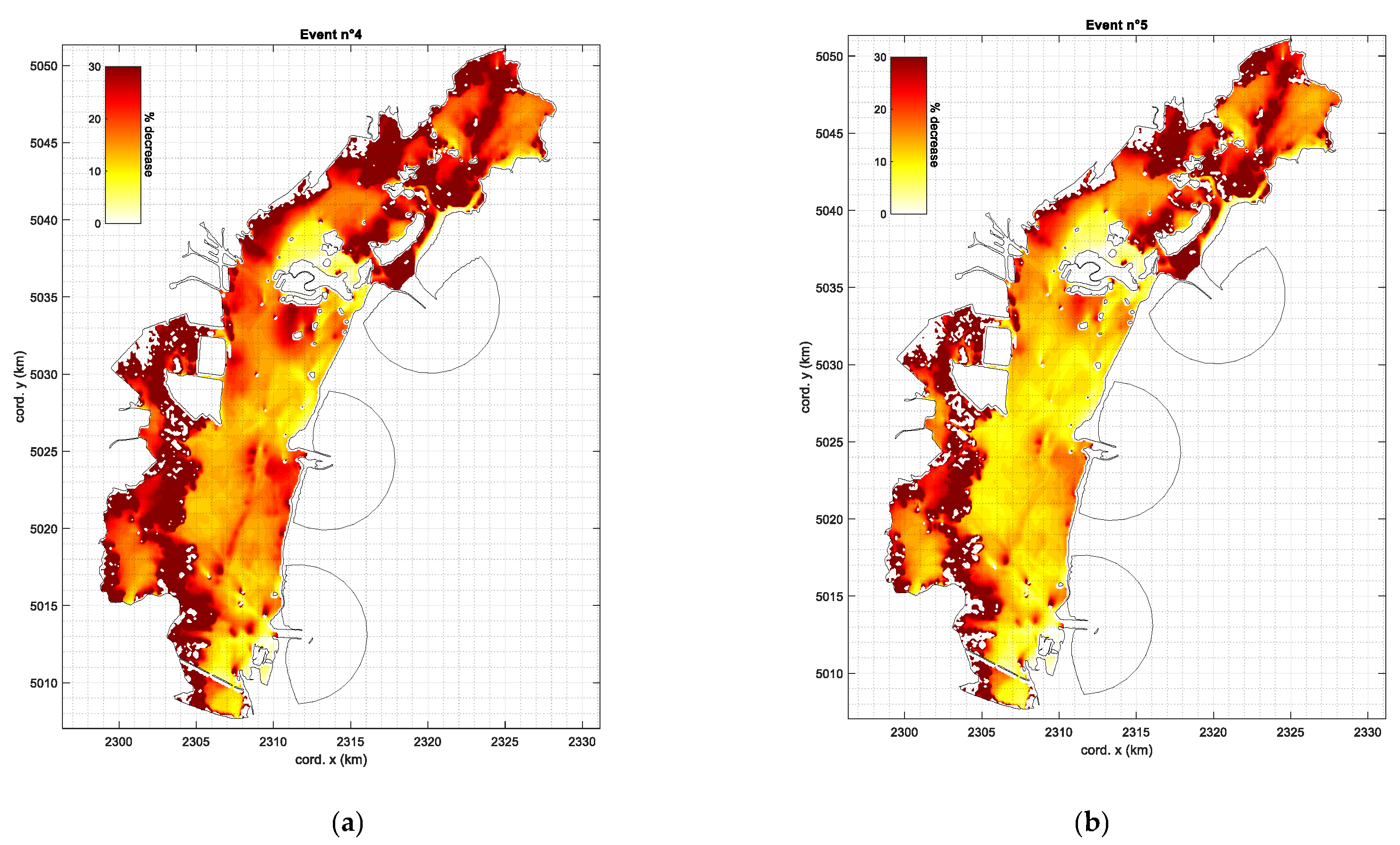
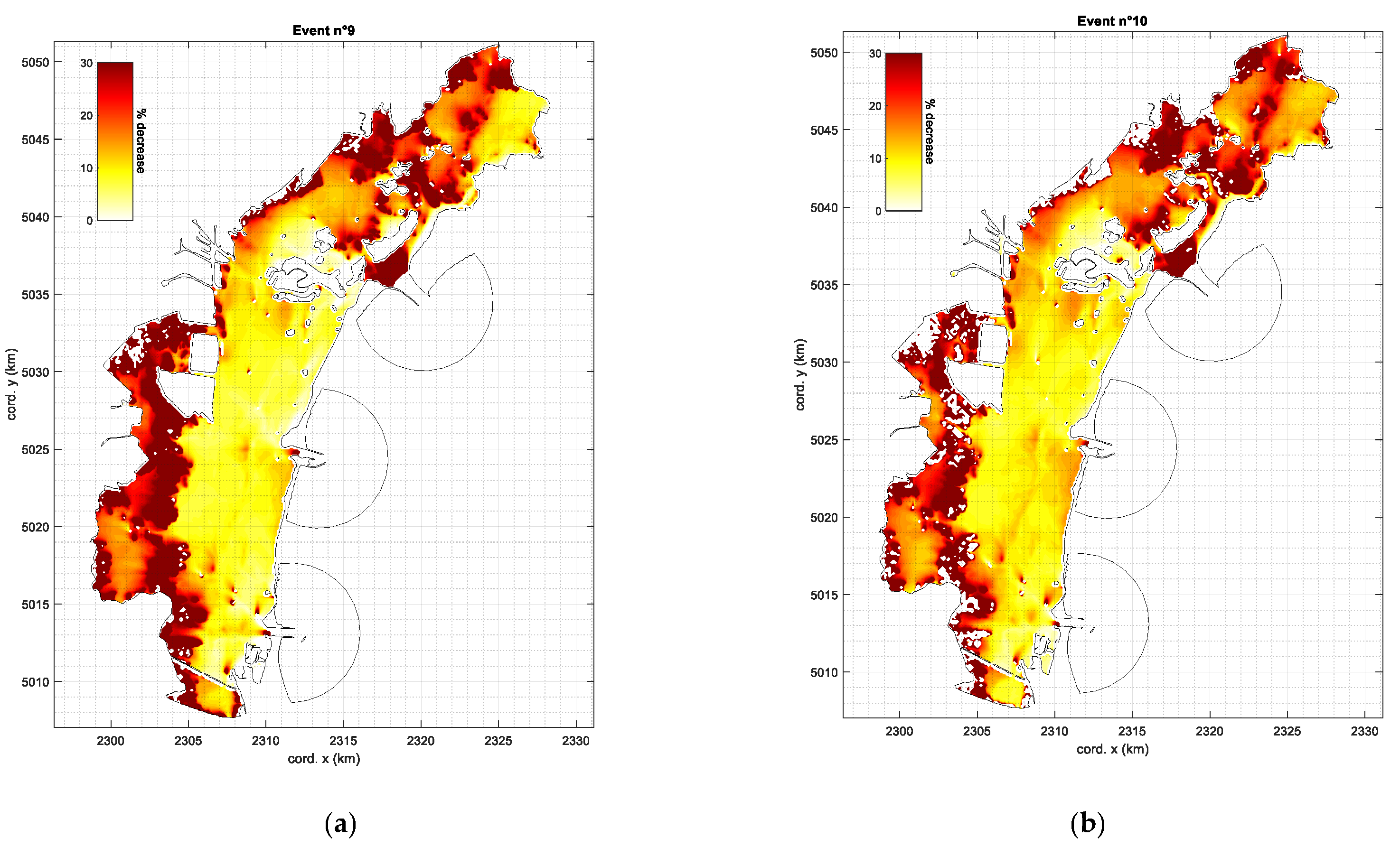
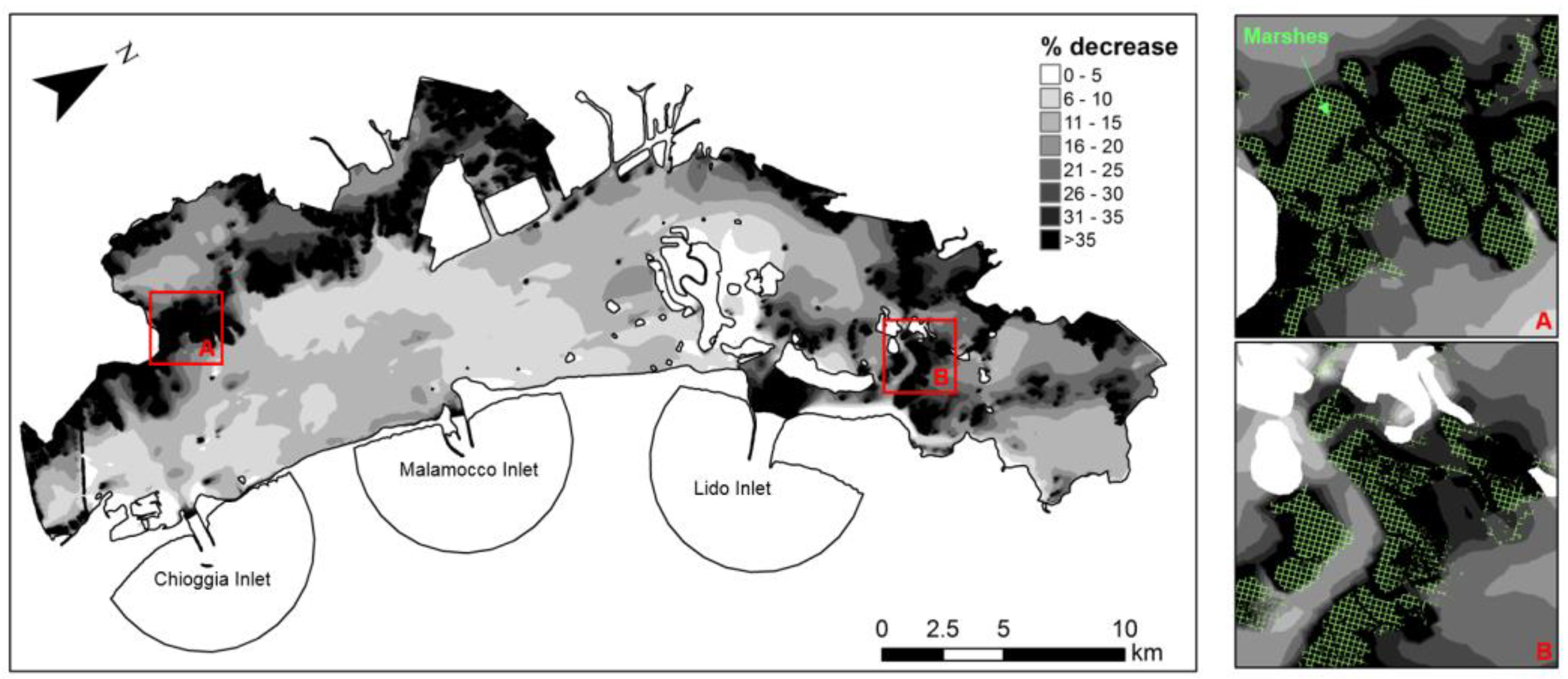
3.2. Effect of Mo.S.E. Closures on Wind Waves
- Event no. 1 closed scenario z = 0.69 m, open scenario z = 1.19 m (z decrease ~ 42%);
- Event no. 3, closed scenario z = 0.83 m, open scenario z = 1.28 m (z decrease ~ 35%);
- Event no. 4, closed scenario z = 0.72 m, open scenario z = 1.34 m (z decrease ~ 46%);
- Event no. 5, closed scenario z = 0.56 m, open scenario z = 1.07 m (z decrease ~ 47%);
- Event no. 9, closed scenario z = 0.81 m, open scenario z = 1.38 m (z decrease ~ 41%);
- Event no. 10, closed scenario z = 0.58 m, open scenario z = 1.05 m (z decrease ~ 45%).
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fletcher, C.A.; Spencer, T. Flooding and Environmental Challenges for Venice and Its Lagoon: State of Knowledge; Cambridge University Press: Cambridge, UK, 2005; ISBN 978-0-521-84046-0. [Google Scholar]
- Defendi, V.; Kovačević, V.; Arena, F.; Zaggia, L. Estimating sediment transport from acoustic measurements in the Venice Lagoon inlets. Cont. Shelf Res. 2010, 30, 883–893. [Google Scholar] [CrossRef]
- Ghinassi, M.; Brivio, L.; D'Alpaos, A.; Finotello, A.; Carniello, L.; Marani, M.; Cantelli, A. Morphodynamic evolution and sedimentology of a microtidal meander bend of the Venice Lagoon (Italy). Mar. Pet. Geol. 2018, 96, 391–404. [Google Scholar] [CrossRef]
- Scarpa, G.M.; Zaggia, L.; Manfè, G.; Lorenzetti, G.; Parnell, K.; Soomere, T.; Rapaglia, J.; Molinaroli, E. The effects of ship wakes in the Venice Lagoon and implications for the sustainability of shipping in coastal waters. Sci. Rep. 2019, 9, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trincardi, F.; Barbanti, A.; Bastianini, M.; Benetazzo, A.; Cavaleri, L.; Chiggiato, J.; Papa, A.; Pomaro, A.; Sclavo, M.; Tosi, L.; et al. The 1966 flooding of Venice: What time taught us for the future. Oceanography 2016, 29, 178–186. [Google Scholar] [CrossRef] [Green Version]
- Trigo, I.F.; Davies, T.D. Meteorological conditions associated with sea surges in Venice: A 40 year climatology. Int. J. Climatol. J. R. Meteorol. Soc. 2002, 22, 787–803. [Google Scholar] [CrossRef]
- Lionello, P.; Nicholls, R.J.; Umgiesser, G.; Zanchettin, D. Venice Flooding and Sea Level: Past Evolution, Present Issues, and Future Projections (Introduction to the Special Issue). Nat. Hazards Earth Syst. Sci. 2021, 21, 2633–2641. [Google Scholar] [CrossRef]
- Zanchettin, D.; Bruni, S.; Raicich, F.; Lionello, P.; Adloff, F.; Androsov, A.; Antonioli, F.; Artale, V.; Carminati, E.; Ferrarin, C.; et al. Sea-level rise in Venice: Historic and future trends. Nat. Hazards Earth Syst. Sci. 2021, 21, 2643–2678. [Google Scholar] [CrossRef]
- Umgiesser, G. The impact of operating the mobile barriers in Venice (MOSE) under climate change. J. Nat. Conserv. 2020, 54, 125783. [Google Scholar] [CrossRef]
- Mel, R.; Carniello, L.; D'Alpaos, L. Addressing the effect of the Mo. SE barriers closure on wind setup within the Venice lagoon. Estuar. Coast. Shelf Sci. 2019, 225, 106249. [Google Scholar] [CrossRef]
- Tognin, D.; Finotello, A.; D’Alpaos, A.; Viero, D.P.; Pivato, M.; Mel, R.A.; Defina, A.; Bertuzzo, E.; Marani, M.; Carniello, L. Loss of geomorphic diversity in shallow tidal embayments promoted by storm-surge barriers. Sci. Adv. 2022, 8, eabm8446. [Google Scholar] [CrossRef]
- Tommasini, L.; Carniello, L.; Ghinassi, M.; Roner, M.; D'Alpaos, A. Changes in the wind-wave field and related salt-marsh lateral erosion: Inferences from the evolution of the Venice Lagoon in the last four centuries. Earth Surf. Process. Landf. 2019, 44, 1633–1646. [Google Scholar] [CrossRef]
- Carniello, L.; D’Alpaos, A.; Defina, A. Modeling wind waves and tidal flows in shallow micro-tidal basins. Estuar. Coast. Shelf Sci. 2011, 92, 263–276. [Google Scholar] [CrossRef]
- Christakos, K.; Björkqvist, J.V.; Tuomi, L.; Furevik, B.R.; Breivik, Ø. Modelling wave growth in narrow fetch geometries: The white-capping and wind input formulations. Ocean. Model. 2021, 157, 101730. [Google Scholar] [CrossRef]
- Moeini, M.H.; Etemad-Shahidi, A. Application of two numerical models for wave hindcasting in Lake Erie. Appl. Ocean. Res. 2007, 29, 137–145. [Google Scholar] [CrossRef]
- Aydoğan, B.; Ayat, B. Performance evaluation of SWAN ST6 physics forced by ERA5 wind fields for wave prediction in an enclosed basin. Ocean. Eng. 2021, 240, 109936. [Google Scholar] [CrossRef]
- Scarton, F. Long-term trend of the waterbird community breeding in a heavily man-modified coastal lagoon: The case of the Important Bird Area “Lagoon of Venice”. J. Coast. Conserv. 2017, 21, 35–45. [Google Scholar] [CrossRef]
- Molinaroli, E.; Guerzoni, S.; Sarretta, A.; Masiol, M.; Pistolato, M. Thirty-year changes (1970 to 2000) in bathymetry and sediment texture recorded in the Lagoon of Venice sub-basins, Italy. Mar. Geol. 2009, 258, 115–125. [Google Scholar] [CrossRef] [Green Version]
- Sarretta, A.; Pillon, S.; Molinaroli, E.; Guerzoni, S.; Fontolan, G. Sediment budget in the Lagoon of Venice, Italy. Cont. Shelf Res. 2010, 30, 934–949. [Google Scholar] [CrossRef] [Green Version]
- Ferrarin, C.; Cucco, A.; Umgiesser, G.; Bellafiore, D.; Amos, C.L. Modelling fluxes of water and sediment between Venice Lagoon and the sea. Cont. Shelf Res. 2010, 30, 904–914. [Google Scholar] [CrossRef] [Green Version]
- Bellafiore, D.; Umgiesser, G.; Cucco, A. Modeling the water exchanges between the Venice Lagoon and the Adriatic Sea. Ocean. Dyn. 2008, 58, 397–413. [Google Scholar] [CrossRef]
- Tambroni, N.; Seminara, G. Are inlets responsible for the morphological degradation of Venice Lagoon? J. Geophys. Res. Earth Surf. 2006, F03013, 111. [Google Scholar] [CrossRef] [Green Version]
- Scarpa, G.M.; Braga, F.; Manfè, G.; Lorenzetti, G.; Zaggia, L. Towards an Integrated Observational System to Investigate Sediment Transport in the Tidal Inlets of the Lagoon of Venice. Remote Sens. 2022, 14, 3371. [Google Scholar] [CrossRef]
- Ackroyd, P. Venice: Pure City; Nan, A.T., Ed.; Doubleday: New York, NY, USA, 2009. [Google Scholar]
- Ivajnšič, D.; Kaligarič, M.; Fantinato, E.; Del Vecchio, S.; Buffa, G. The fate of coastal habitats in the Venice Lagoon from the sea level rise perspective. Appl. Geogr. 2018, 98, 34–42. [Google Scholar] [CrossRef] [Green Version]
- Umgiesser, G.; Bajo, M.; Ferrarin, C.; Cucco, A.; Lionello, P.; Zanchettin, D.; Papa, A.; Tosoni, A.; Ferla, M.; Coraci, E.; et al. The prediction of floods in Venice: Methods, models and uncertainty. Nat. Hazards Earth Syst. Sci. 2021, 21, 2679–2704. [Google Scholar] [CrossRef]
- Helsby, R. Sand Transport in Northern Venice Lagoon through the Tidal Inlet of Lido; University of Southampton: Southhampton, UK, 2008. [Google Scholar]
- Ruol, P.; Martinelli, L.; Favaretto, C. Vulnerability Analysis of the Venetian Littoral and Adopted Mitigation Strategy. Water 2018, 10, 984. [Google Scholar] [CrossRef] [Green Version]
- Canestrelli, P.; Mandich, M.; Pirazzoli, P.A.; Tomasin, A. Wind, Depression and Seiches: Tidal Perturbations in Venice (1951–2000); Centro Previsioni e Segnalazioni Maree: Venice, Italy, 2001; pp. 1–104. [Google Scholar]
- Cavaleri, L.; Bajo, M.; Barbariol, F.; Bastianini, M.; Benetazzo, A.; Bertotti, L.; Chiggiato, J.; Ferrarin, C.; Trincardi, F.; Umgiesser, G. The 2019 flooding of Venice and its implications for future predictions. Oceanography 2020, 33, 42–49. [Google Scholar] [CrossRef] [Green Version]
- Magistrato Alle Acque. Interventi alle Bocche Lagunari per la Regolazione dei Flussi di Marea–Studio di Impatto Am-bientale del Progetto di Massima, Allegato 6, Tema 5; Magistrato Alle Acque: Venice, Italy, 1997; p. 163. (In Italian) [Google Scholar]
- Favaretto, C.; Volpato, M.; Martinelli, L.; Ruol, P. Numerical investigation on wind set-up and wind waves in front of Piazza San Marco, Venice (IT). In Proceedings of the 30th International Ocean and Polar Engineering Conference, Virtual, 11–16 October 2020. [Google Scholar]
- Ruol, P.; Favaretto, C.; Volpato, M.; Martinelli, L. Flooding of Piazza San Marco (Venice): Physical model tests to evaluate the overtopping discharge. Water 2020, 12, 427. [Google Scholar] [CrossRef] [Green Version]
- Mel, R.A.; Viero, D.P.; Carniello, L.; Defina, A.; D'Alpaos, L. The first operations of Mo. SE system to prevent the flooding of Venice: Insights on the hydrodynamics of a regulated lagoon. Estuar. Coast. Shelf Sci. 2021, 261, 107547. [Google Scholar] [CrossRef]
- Karimpour, A.; Chen, Q. Wind wave analysis in depth limited water using OCEANLYZ, A MATLAB toolbox. Comput. Geosci. 2017, 106, 181–189. [Google Scholar] [CrossRef]
- Cavaleri, L.; Ewing, J.A.; Smith, N.D. Measurement of the pressure and velocity field below surface waves. In Turbulent Fluxes through the Sea Surface, Wave Dynamics, and Prediction; Springer: Boston, MA, USA, 1978; pp. 257–272. [Google Scholar]
- Booij, N.; Holthuijsen, L.H.; Ris, R.C. The "SWAN" wave model for shallow water. In Coastal Engineering Proceedings, 1; Elsevier: Orlando, FL, USA, 1996; pp. 668–676. [Google Scholar]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef] [Green Version]
- Favaretto, C.; Martinelli, L.; Vigneron, E.M.P.; Ruol, P. Wave Hindcast in Enclosed Basins: Comparison among SWAN, STWAVE and CMS-Wave Models. Water 2022, 14, 1087. [Google Scholar] [CrossRef]
- Sartini, L.; Mentaschi, L.; Besio, G. Evaluating third generation wave spectral models performances in coastal areas. An application to Eastern Liguria. In Proceedings of the OCEANS 2015-Genova, Genova, Italy, 18–21 May 2015; pp. 1–10. [Google Scholar]
- Battjes, J.A.; Janssen, J.P.F.M. Energy loss and set-up due to breaking of random waves. In Proceedings of the 16th International Conference on Coastal Engineering, ASCE, Hamburg, Germany, 27 August–3 September 1978; pp. 569–587. [Google Scholar]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, A.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Ergaenzungsheft Zur Dtsch. Hydrogr. Z. Reihe A 1973, 93. Available online: https://www.researchgate.net/publication/256197895_Measurements_of_wind-wave_growth_and_swell_decay_during_the_Joint_North_Sea_Wave_Project_JONSWAP (accessed on 17 July 2022).
- Komen, J.G.; Hasselmann, S.; Hasselmann, K. On the existence of a fully developed wind-sea spectrum. J. Phys. Oceanogr. 1984, 14, 1271–1285. [Google Scholar] [CrossRef]
- Zijlema, M.; Van Vledder, G.P.; Holthuijsen, L.H. Bottom friction and wind drag for wave models. Coast. Eng. 2012, 65, 19–26. [Google Scholar] [CrossRef]
- Bottema, M.; van Vledder, G. Effective fetch and non-linear four-wave interactions during wave growth in slanting fetch conditions. Coast. Eng. 2008, 55, 261–275. [Google Scholar] [CrossRef]
- Coronavirus, le Misure Adottate dal Governo nel Periodo Febbraio 2021–Maggio 2022. Available online: https://www.governo.it/it/coronavirus-misure-del-governo (accessed on 17 May 2022).
- Coronavirus, le Misure Adottate dal Governo nel Periodo Febbraio 2020–Febbario 2021. Available online: https://www.sitiarcheologici.palazzochigi.it/www.governo.it/febbraio%202021/it/coronavirus-misure-del-governo.html (accessed on 17 May 2022).
- Braga, F.; Scarpa, G.M.; Brando, V.E.; Manfè, G.; Zaggia, L. COVID-19 lockdown measures reveal human impact on water transparency in the Venice Lagoon. Sci. Total Environ. 2020, 736, 139612. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, H.; Lorke, A.; Peeters, F. The relative importance of wind and ship waves in the littoral zone of a large lake. Limnol. Oceanogr. 2008, 53, 368–380. [Google Scholar] [CrossRef] [Green Version]
- Toba, Y. Local balance in the air-sea boundary processes. I. On the growth process of wind waves. J. Oceanogr. Soc. Jpn. 1972, 28, 109–120. [Google Scholar] [CrossRef]
- Badulin, S.I.; Grigorieva, V.G. On discriminating swell and wind-driven seas in Voluntary Observing Ship data. J. Geophys. Res. Ocean. 2012, 117, C00J29. [Google Scholar] [CrossRef] [Green Version]
- Gagnaire-Renou, E.; Benoit, M.; Badulin, S.I. On weakly turbulent scaling of wind sea in simulations of fetch-limited growth. J. Fluid Mech. 2011, 669, 178–213. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow forecasting through conceptual models-Part I: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; LeGates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. Space Phys. 1985, 90, 8995. [Google Scholar] [CrossRef] [Green Version]
- Vieira, F.; Cavalcante, G.; Campos, E. Analysis of wave climate and trends in a semi-enclosed basin (Persian Gulf) using a validated SWAN model. Ocean. Eng. 2020, 196, 106821. [Google Scholar] [CrossRef]
- Tognin, D.; D’Alpaos, A.; Marani, M.; Carniello, L. Marsh resilience to sea-level rise reduced by storm-surge barriers in the Venice Lagoon. Nat. Geosci. 2021, 14, 906–911. [Google Scholar] [CrossRef]




| n | t | Mo.S.E. Closures | HS (m) Max | Tm (s) | z (m ZMPS) at Punta Della Salute | z (m ZMPS) Max at Lido Inlet | Vw (m/s) at Lido Inlet | Dw (°N) at Lido Inlet |
|---|---|---|---|---|---|---|---|---|
| 1 | 03/10/2020 08:00 | yes | 0.23 | 2.25 | 0.69 | 1.19 | 14.6 | 145 |
| 2 | 26/10/2020 16:30 | no | 0.22 | 2.15 | 0.70 | 0.87 | 14.1 | 161 |
| 3 | 05/12/2020 19:00 | yes | 0.34 | 2.59 | 0.83 | 1.28 | 17.4 | 137 |
| 4 | 28/12/2020 11:00 | yes | 0.33 | 2.51 | 0.72 | 1.34 | 20.1 | 168 |
| 5 | 22/01/2021 21:30 | yes | 0.21 | 2.07 | 0.56 | 1.07 | 15.0 | 171 |
| 6 | 18/03/2021 00:30 | no | 0.17 | 1.89 | 0.40 | 0.40 | 10.6 | 144 |
| 7 | 06/04/2021 10:00 | no | 0.29 | 2.28 | 0.41 | 0.44 | 22.2 | 92 |
| 8 | 13/07/2021 14:00 | no | 0.24 | 2.34 | 0.78 | 0.85 | 15.4 | 130 |
| 9 | 01/11/2021 18:00 | yes | 0.30 | 2.37 | 0.81 | 1.38 | 16.5 | 145 |
| 10 | 04/11/2021 00:00 | yes | 0.19 | 2.07 | 0.58 | 1.05 | 12.5 | 159 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Favaretto, C.; Manfè, G.; Volpato, M.; Scarpa, G.M. Effect of Mo.S.E. Closures on Wind Waves in the Venetian Lagoon: In Situ and Numerical Analyses. Water 2022, 14, 2579. https://doi.org/10.3390/w14162579
Favaretto C, Manfè G, Volpato M, Scarpa GM. Effect of Mo.S.E. Closures on Wind Waves in the Venetian Lagoon: In Situ and Numerical Analyses. Water. 2022; 14(16):2579. https://doi.org/10.3390/w14162579
Chicago/Turabian StyleFavaretto, Chiara, Giorgia Manfè, Matteo Volpato, and Gian Marco Scarpa. 2022. "Effect of Mo.S.E. Closures on Wind Waves in the Venetian Lagoon: In Situ and Numerical Analyses" Water 14, no. 16: 2579. https://doi.org/10.3390/w14162579
APA StyleFavaretto, C., Manfè, G., Volpato, M., & Scarpa, G. M. (2022). Effect of Mo.S.E. Closures on Wind Waves in the Venetian Lagoon: In Situ and Numerical Analyses. Water, 14(16), 2579. https://doi.org/10.3390/w14162579







