Analysis of the Flow Energy Loss and Q-H Stability in Reversible Pump Turbine as Pump with Different Guide Vane Opening Angles
Abstract
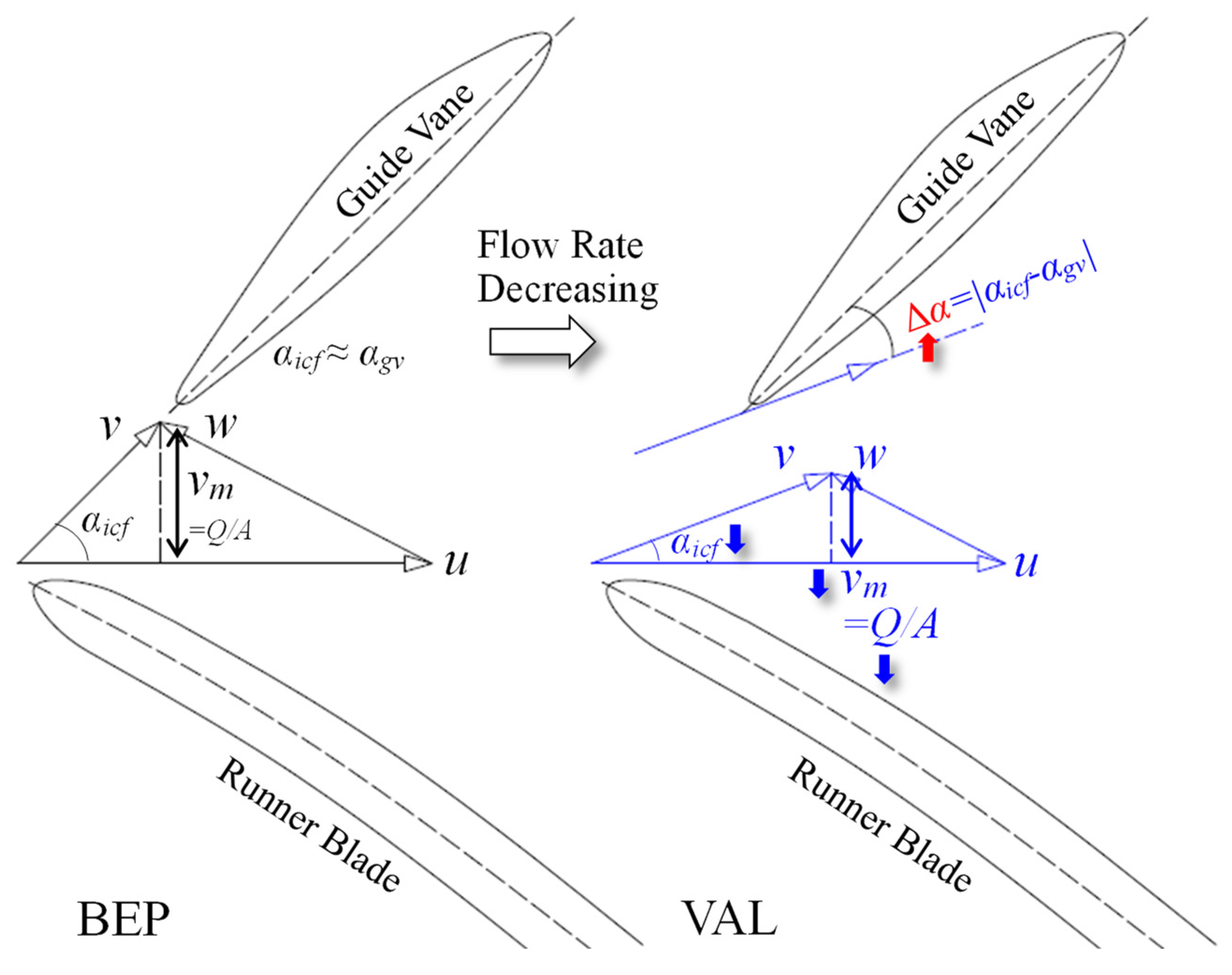
:1. Introduction
2. Research Objective
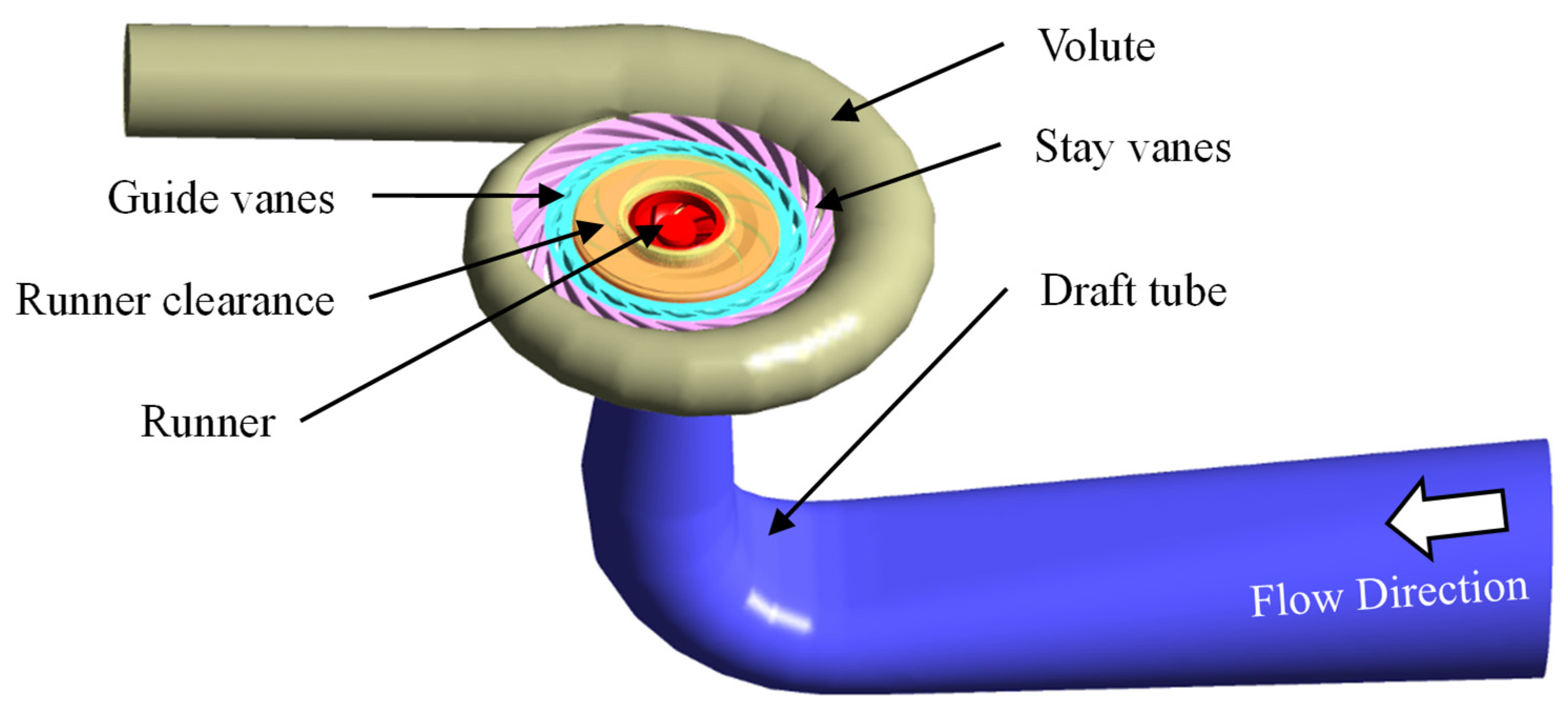
| Parameter | Symbol | Value |
|---|---|---|
| Runner blade number | Zr | 9 |
| Guide vane blade number | Zg | 22 |
| Stay vane blade number | Zs | 22 |
| Runner diameter | D1 | 554 [mm] |
| Design head | Hd | 52.9 [m] |
| Maximum head | Hmax | 58.0 [m] |
| Minimum head | Hmin | 50.8 [m] |
| Rated rotational speed | nd | 1100 [rpm] |
| Specific speed | nq | 34.6 |
3. Methodology
3.1. Governing Equations
3.2. Computational Fluid Dynamics Setup
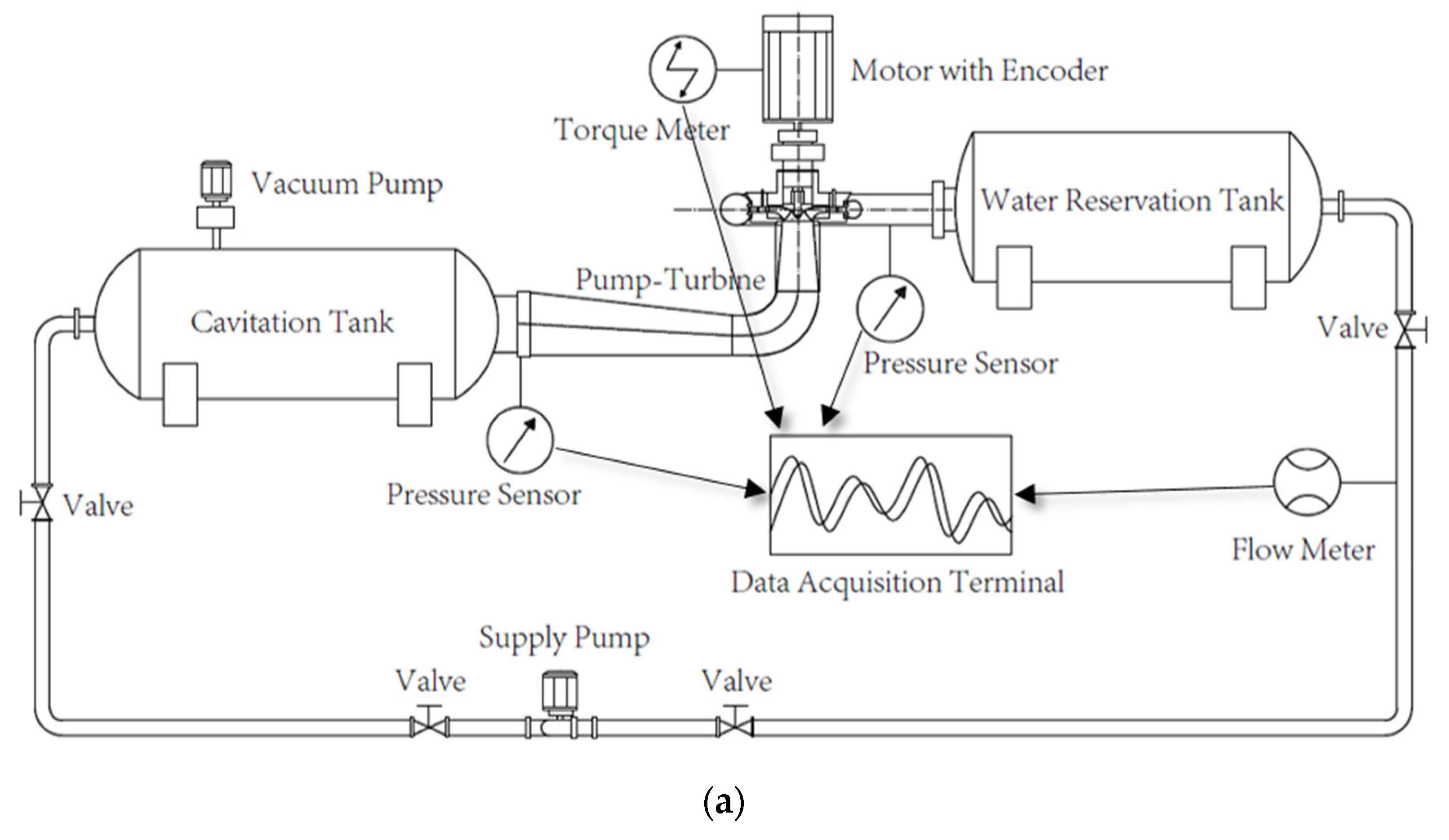
3.3. Model Test
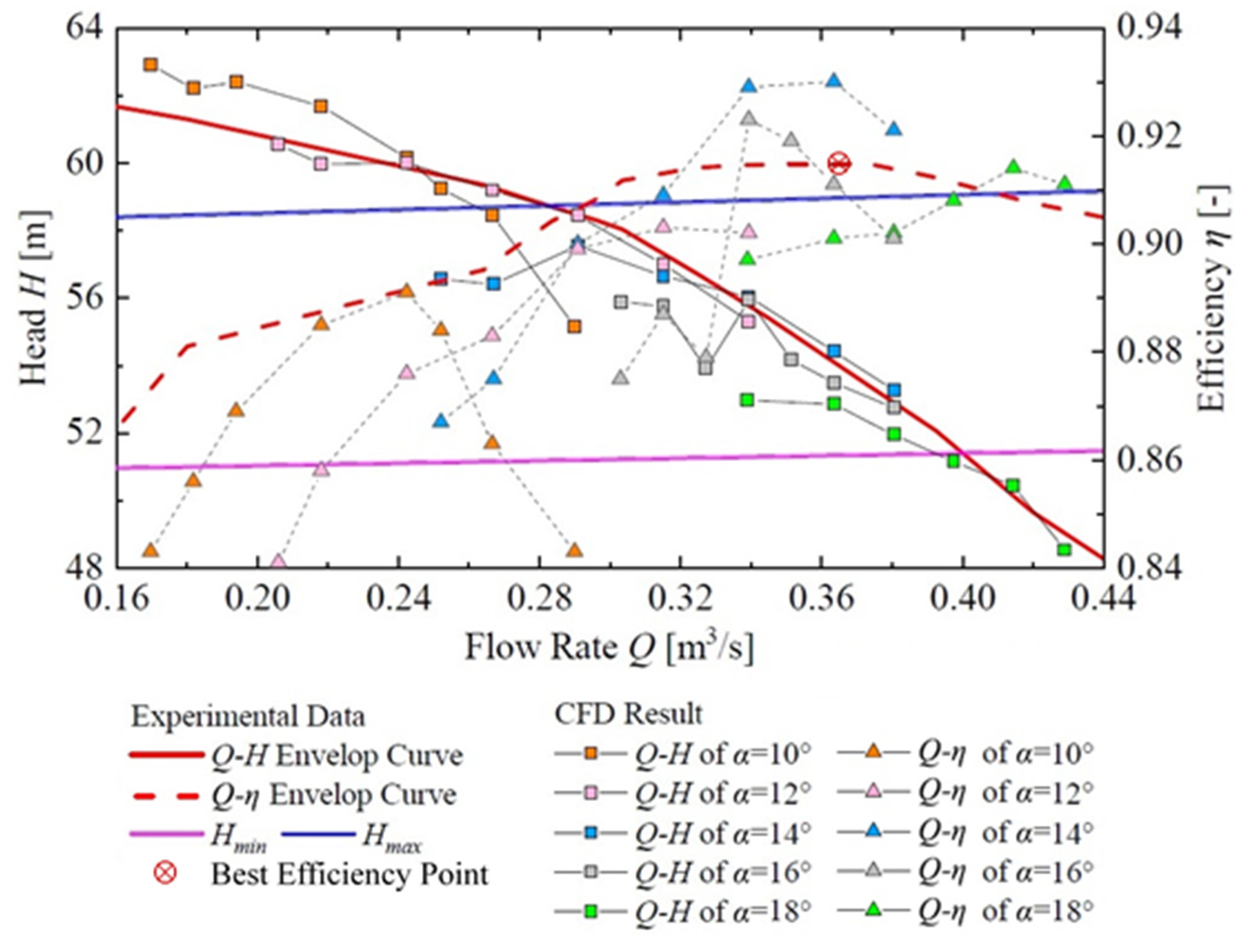
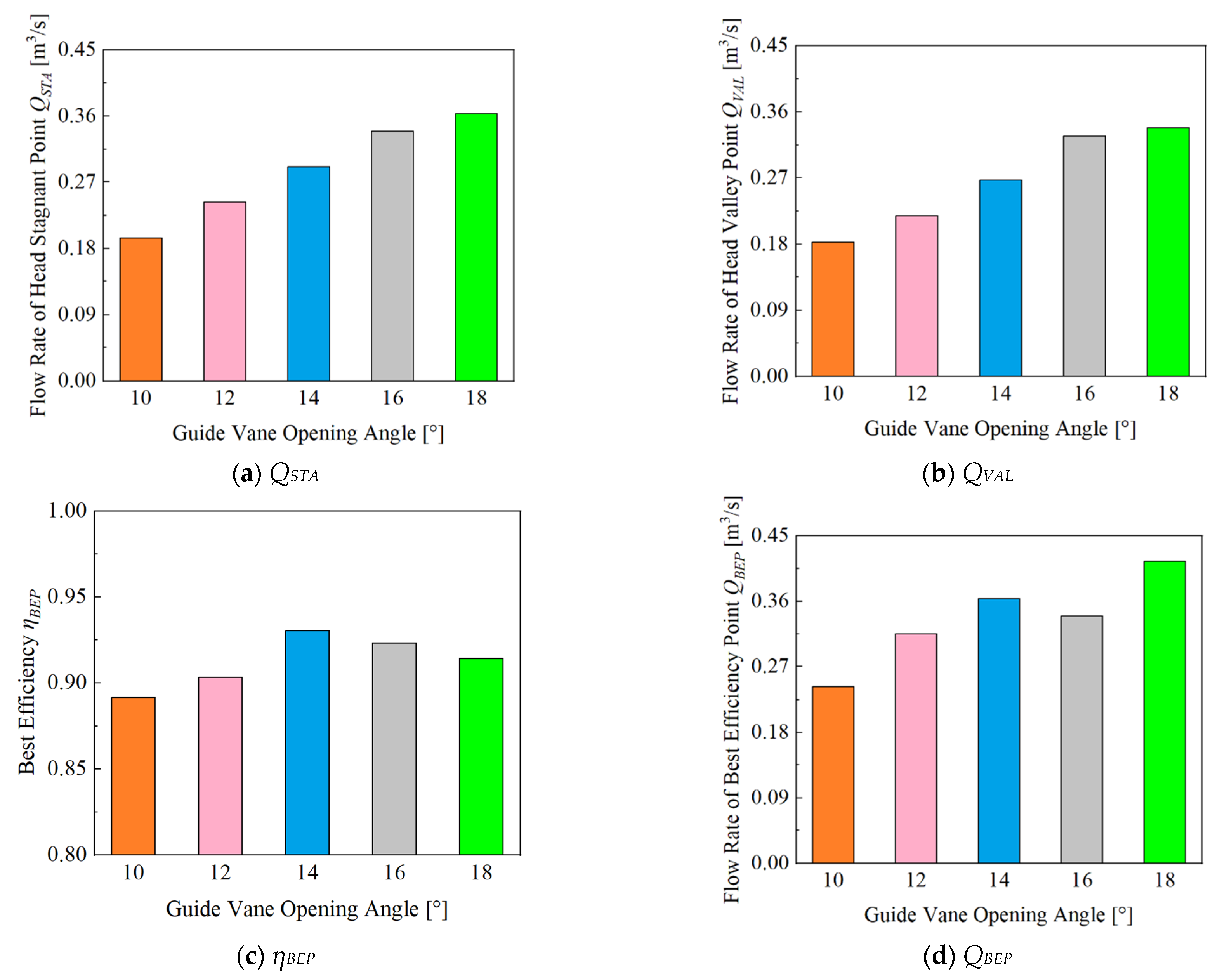
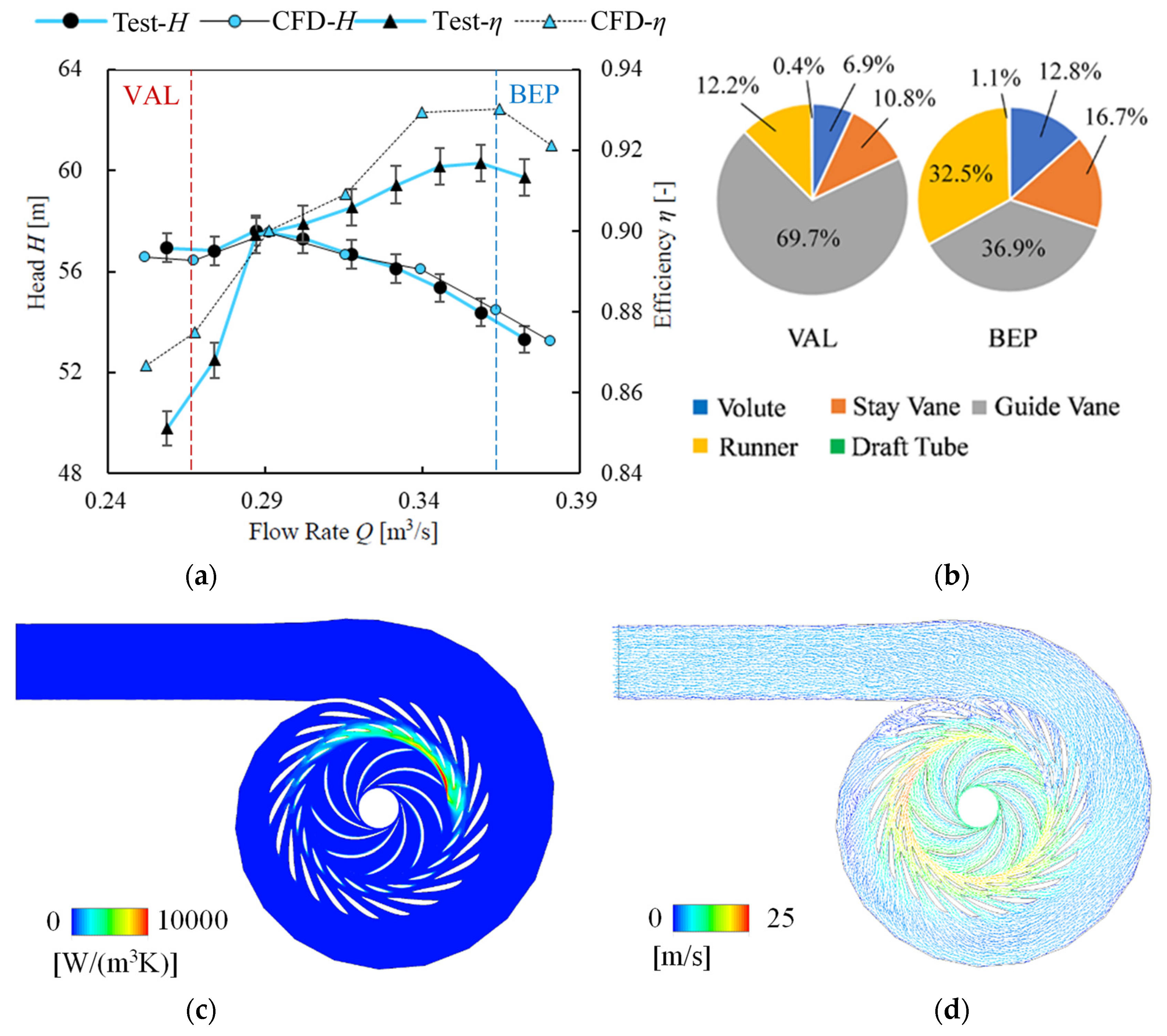
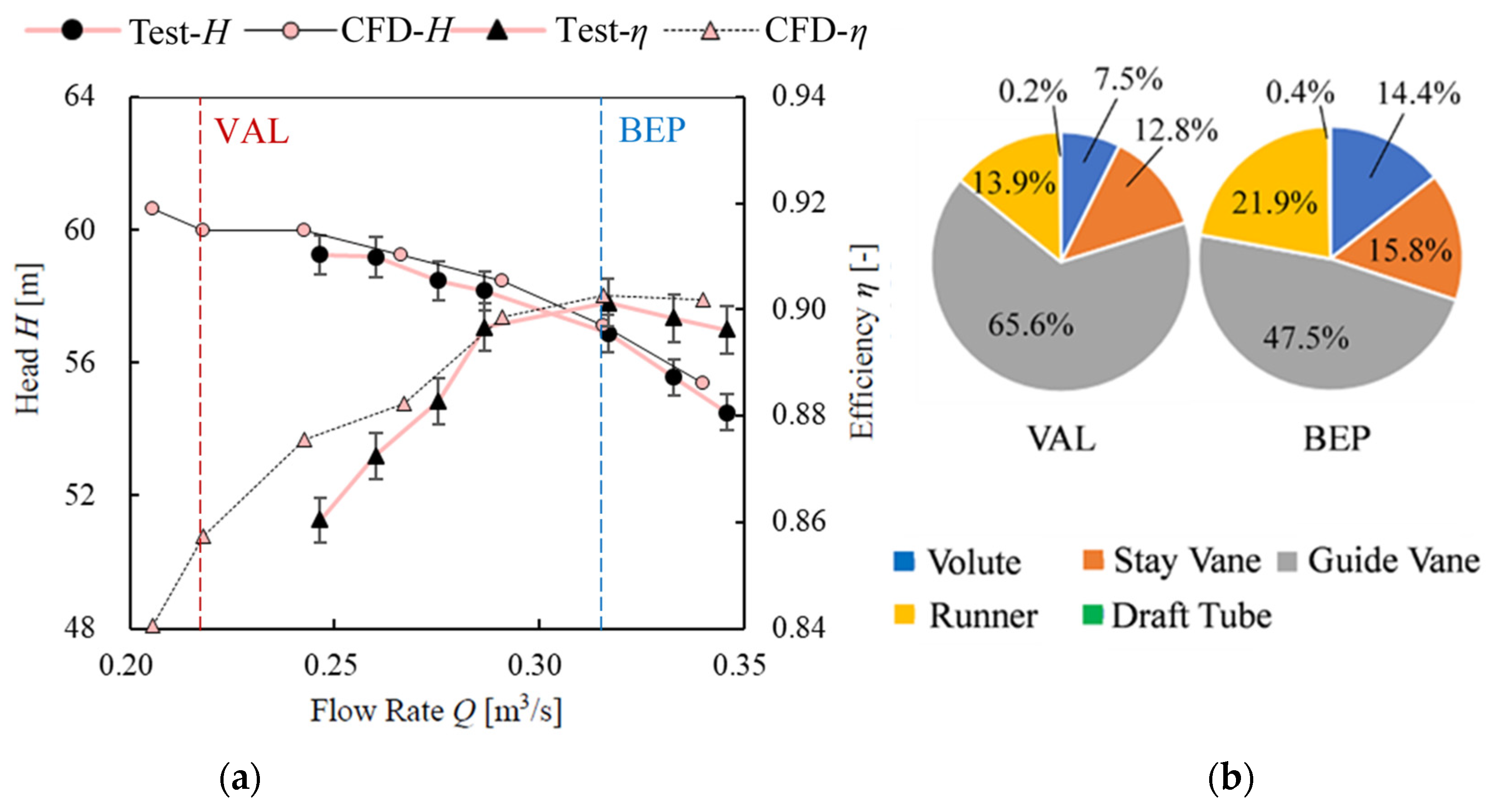
4. Comparison of Energy Performance
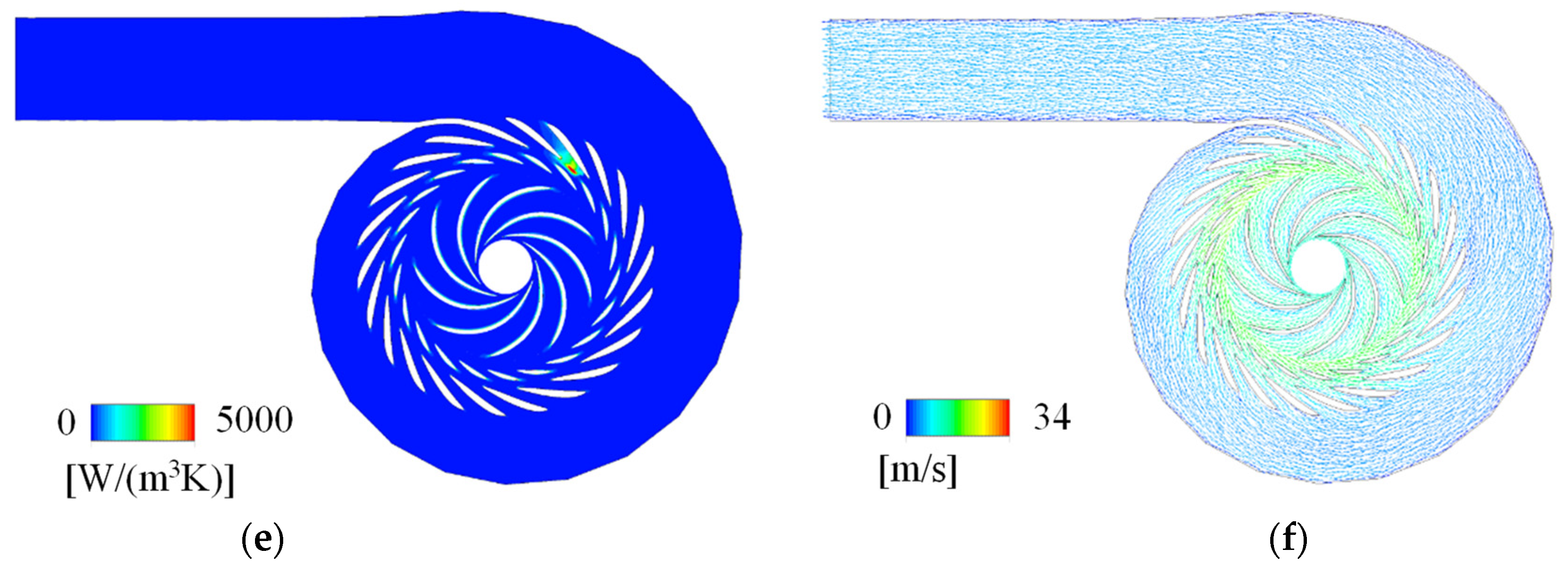
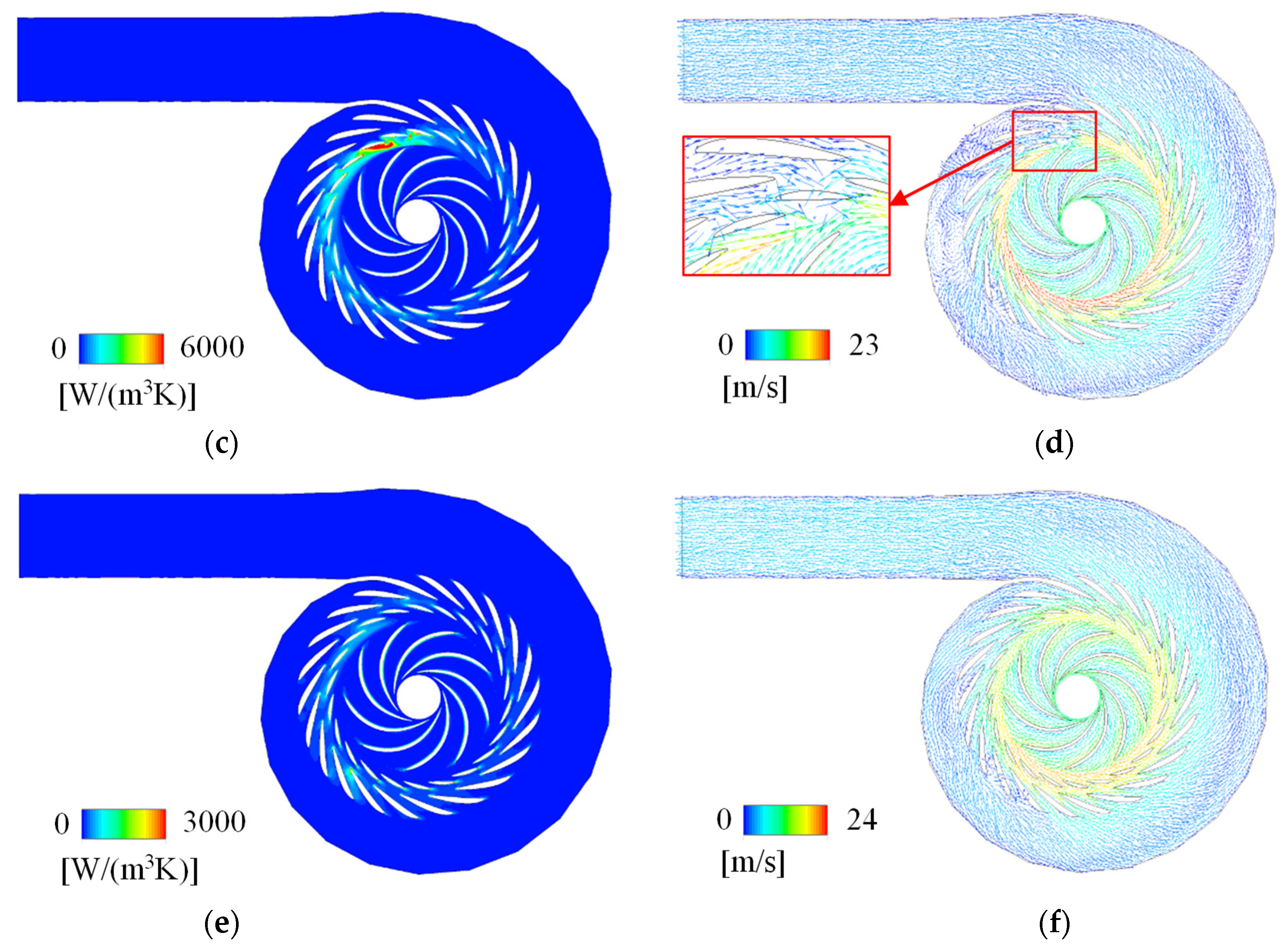
5. Analysis of Internal Flow
5.1. Large Guide Vane Opening Angle (18 Degrees)
5.2. Medium-Large Guide Vane Opening Angle (16 Degrees)
5.3. Medium Guide Vane Opening Angle (14 Degrees)
5.4. Medium-Small Guide Vane Opening Angle (12 Degrees)
5.5. Small Guide Vane Opening Angle (10 Degrees)
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jin, B. Research on performance evaluation of green supply chain of automobile enterprises under the background of carbon peak and carbon neutralization. Energy Rep. 2021, 7, 594–604. [Google Scholar] [CrossRef]
- Tan, X.; Liu, J.; Xu, Z.; Yao, L.; Ji, G.; Shan, B. Power supply and demand balance during the 14th five-year plan period under the goal of carbon emission peak and carbon neutrality. Electr. Power 2021, 54, 1–6. [Google Scholar]
- Kong, Y.; Kong, Z.; Liu, Z.; Wei, C.; Zhang, J.; An, G. Pumped storage power stations in China: The past, the present, and the future. Renew. Sustain. Energy Rev. 2017, 71, 720–731. [Google Scholar] [CrossRef]
- He, Y.; Guan, L.; Cai, Q.; Liu, X.; Li, C. Analysis of securing function and economic benefit of pumped storage station in power grid. Power Syst. Technol. 2004, 28, 54–57+67. [Google Scholar]
- Xu, F.; Chen, L.; Jin, H.; Liu, Z. Modeling and application analysis of optimal joint operation of pumped storage power station and wind power. Autom. Electr. Power Syst. 2013, 37, 149–154. [Google Scholar]
- Anagnostopoulos, J.S.; Papantonis, D.E. Pumping station design for a pumped-storage wind-hydro power plant. Energy Convers. Manag. 2007, 48, 3009–3017. [Google Scholar] [CrossRef]
- Yan, J.; Koutnik, J.; Seidel, U.; Hubner, B. Compressible simulation of rotor-stator interaction in pump-turbines. IOP Conf. Ser.-Earth Environ. Sci. 2010, 12, 012008. [Google Scholar] [CrossRef]
- Li, D.; Gong, R.; Wang, H.; Wei, X.; Liu, Z.; Qin, D. Unstable head-flow characteristics of pump-turbine under different guide vane openings in pump mode. J. Drain. Irrig. Mach. Eng. 2016, 34, 1–8. [Google Scholar]
- Zhu, D.; Xiao, R.; Tao, R.; Liu, W. Impact of guide vane opening angle on the flow stability in a pump-turbine in pump mode. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2017, 231, 2484–2492. [Google Scholar] [CrossRef]
- Yao, Y.; Xiao, Y.; Zhu, W.; Zhai, L.; An, S.; Wang, Z. Numerical analysis of a model pump-turbine internal flow behavior in pump hump district. IOP Conf. Ser.-Earth Environ. Sci. 2014, 22, 032040. [Google Scholar]
- Li, D.; Wang, H.; Xiang, G.; Gong, R.; Wei, X.; Liu, Z. Unsteady simulation and analysis for hump characteristics of a pump turbine model. Renew. Energy 2015, 77, 32–42. [Google Scholar]
- Li, D.; Wang, H.; Qin, Y.; Wei, X.; Qin, D. Numerical simulation of hysteresis characteristic in the hump region of a pump-turbine model. Renew. Energy 2018, 115, 433–447. [Google Scholar] [CrossRef]
- Xiao, Y.; Yao, Y.; Wang, Z.; Zhang, J.; Luo, Y.; Zeng, C.; Zhu, W. Hydrodynamic mechanism analysis of the pump hump district for a pump-turbine. Eng. Comput. 2016, 33, 957–976. [Google Scholar] [CrossRef]
- Lu, Z.; Xiao, R.; Tao, R.; Li, P.; Liu, W. Influence of guide vane profile on the flow energy dissipation in a reversible pump-turbine at pump mode. J. Energy Storage 2022, 49, 104161. [Google Scholar] [CrossRef]
- Song, H.; Zhang, J.; Huang, P.; Cai, H.; Cao, P.; Hu, B. Analysis of rotor-stator interaction of a pump-turbine with splitter blades in a pump mode. Mathematics 2020, 8, 1465. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, T.; Li, J.; Yu, J. Experimental study of load variations on pressure fluctuations in a prototype reversible pump turbine in generating mode. J. Fluids Eng. 2017, 139, 074501. [Google Scholar] [CrossRef]
- Zhang, C.; Xia, L.; Diao, W. Influence of flow structures evolution on hump characteristics of a model pump-turbine in pump mode. J. Zhejiang Univ. Eng. Sci. 2017, 51, 2249–2258. [Google Scholar]
- Yang, J.; Pavesi, G.; Liu, X.; Xie, T.; Liu, J. Unsteady flow characteristics regarding hump instability in the first stage of a multistage pump-turbine in pump mode. Renew. Energy 2018, 127, 377–385. [Google Scholar] [CrossRef]
- Wang, H.; Wu, G.; Wu, W.; Wei, X.; Chen, Y.; Li, H. Numerical simulation and analysis of the hump district of Francis pump-turbine. J. Hydroelectr. Eng. 2012, 31, 253–258. [Google Scholar]
- Yang, J.; Yuan, S.; Pavesi, G.; Li, C.; Ye, Z. Study of hump instability phenomena in pump turbine at large partial flow conditions on pump mode. J. Mech. Eng. 2016, 52, 170–178. [Google Scholar] [CrossRef]
- Zhao, W.; Wu, B.; Xu, J. Aerodynamic design and analysis of a multistage vaneless counter-rotating turbine. J. Turbomach. 2014, 137, 061008. [Google Scholar] [CrossRef]
- Vanzante, D.E.; To, W.M.; Chen, J.P. Blade row interaction effects on the performance of a moderately loaded NASA transonic compressor stage. Am. Soc. Mech. Eng. 2003, 1, 969–980. [Google Scholar]
- Sun, Y.; Ren, Y. Unsteady loss analyses of the flow in single-stage transonic compressor. J. Tsinghua Univ. Sci. Technol. 2009, 49, 759–762. [Google Scholar]
- Esfahani, J.A.; Modirkhazeni, M.S. Accuracy analysis of predicted velocity profiles of laminar duct flow with entropy generation method. Appl. Math. Mech. 2013, 34, 971–984. [Google Scholar] [CrossRef]
- Kluxen, R.; Behre, S.; Jeschke, P.; Guendogdu, Y. Loss mechanisms of interplatform steps in a 1.5-stage axial flow turbine. J. Turbomach. 2017, 139, 031007. [Google Scholar] [CrossRef]
- Soltanmohamadi, R.; Lakzian, E. Improved design of Wells turbine for wave energy conversion using entropy generation. Meccanica 2016, 51, 1713–1722. [Google Scholar] [CrossRef]
- Zeinalpour, M.; Mazaheri, K. Entropy minimization in turbine cascade using continuous adjoint formulation. Eng. Optim. 2015, 48, 213–230. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Herwig, H.; Kock, F. Direct and indirect methods of calculating entropy generation rates in turbulent convective heat transfer problems. Heat Mass Transf. 2007, 43, 207–215. [Google Scholar] [CrossRef]
- Tao, R.; Zhao, X.; Wang, Z. Evaluating the transient energy dissipation in a centrifugal impeller under rotor-stator interaction. Entropy 2019, 21, 271. [Google Scholar] [CrossRef]
- Zhou, Q.; Xia, L.; Zhang, C. Internal mechanism and improvement criteria for the runaway oscillation stability of a pump-turbine. Appl. Sci. 2018, 8, 2193. [Google Scholar] [CrossRef]
- Guan, X. Modern Pumps Theory and Design; China Astronautic Publishing House: Beijing, China, 2011; pp. 32–37. [Google Scholar]
- Capurso, T.; Stefanizzi, M.; Pascazio, G.; Camporeale, S.M.; Torresi, M. Dependency of the slip phenomenon on the inertial forces inside radial runners. AIP Conf. Proc. 2019, 2191, 020034. [Google Scholar]
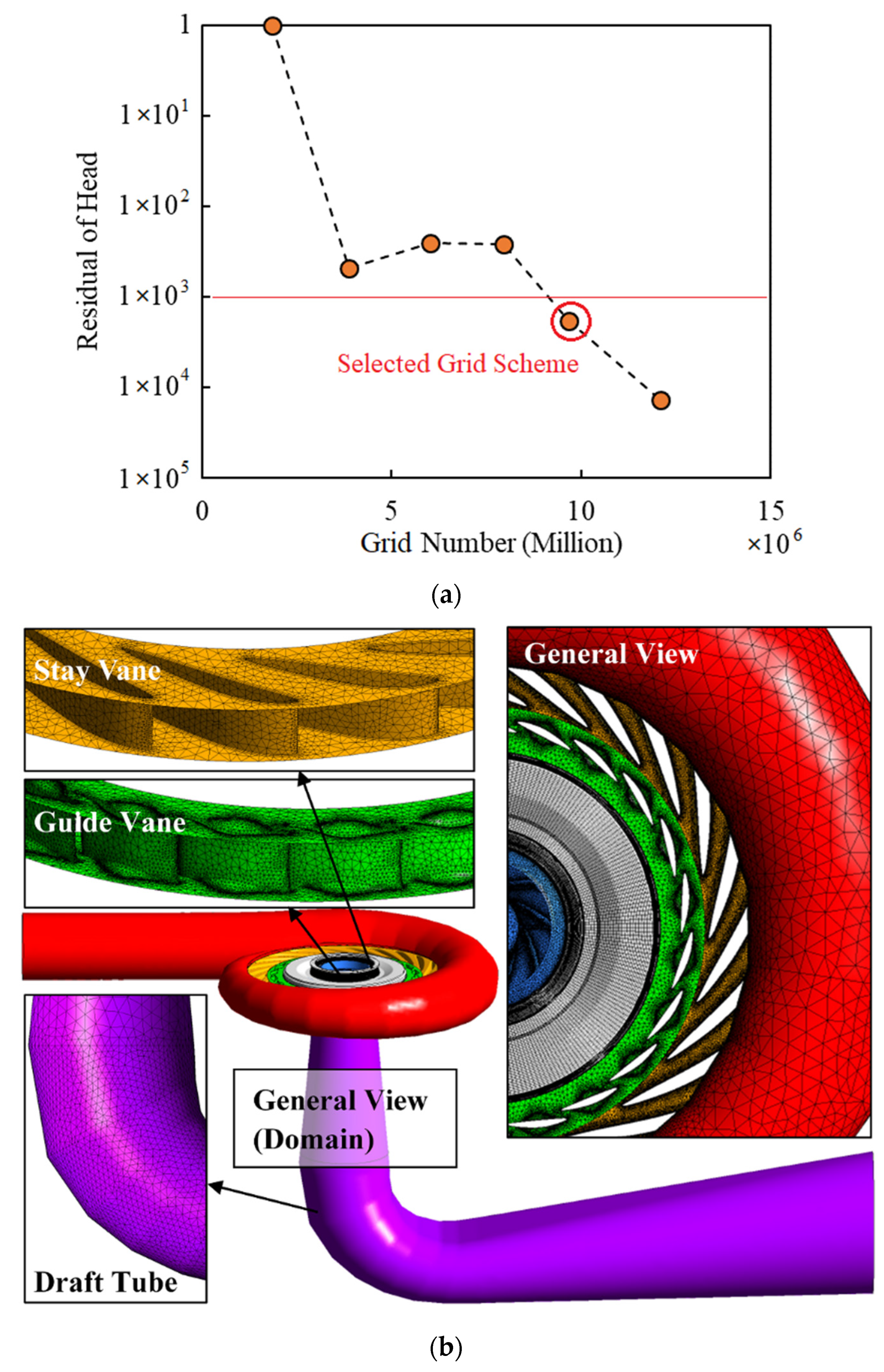

| Component | Grid Number |
|---|---|
| Draft tube | 388,445 |
| Runner (including clearance) | 3,368,717 |
| Guide vane | 1,462,120 |
| Stay vane | 2,669,804 |
| Volute | 1,779,870 |
| Total | 9,668,956 |
| Quantity | Apparatus | Type | Uncertainty |
|---|---|---|---|
| Flow rate | Electromagnetic flowmeter | Rosemount 8705TSE | ±0.1% |
| Rotation speed | Rotary encoder | E6B2-CWZ1X | ±0.02% |
| Head | Differential pressure sensor | SHAE 1151HP6E | ±0.1% |
| Torque | Load sensor | GWT MP47/22C3 | ±0.015% |
| Tail-water pressure | Absolute pressure sensor | Rosemount 1151AP | ±0.1% |
| Guide vane angle | Angular displacement sensor | BGJ 60 | ±0.10° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, W.; Zhu, D.; Tao, R.; Wang, Z. Analysis of the Flow Energy Loss and Q-H Stability in Reversible Pump Turbine as Pump with Different Guide Vane Opening Angles. Water 2022, 14, 2526. https://doi.org/10.3390/w14162526
Yan W, Zhu D, Tao R, Wang Z. Analysis of the Flow Energy Loss and Q-H Stability in Reversible Pump Turbine as Pump with Different Guide Vane Opening Angles. Water. 2022; 14(16):2526. https://doi.org/10.3390/w14162526
Chicago/Turabian StyleYan, Wei, Di Zhu, Ran Tao, and Zhengwei Wang. 2022. "Analysis of the Flow Energy Loss and Q-H Stability in Reversible Pump Turbine as Pump with Different Guide Vane Opening Angles" Water 14, no. 16: 2526. https://doi.org/10.3390/w14162526






