1. Introduction
Bed shear stress is one of the most important parameters in fluvial and marine hydraulics which relates the flow hydraulic conditions to sediment transport [
1,
2] and is used to estimate flow resistance [
3]. An inaccurate measurement of this parameter leads to a significant error in the estimation of the sediment transport rate, especially under the incipient motion of sediment particles [
4]. On the other hand, an accurate measurement of this parameter is often a problematic and challenging issue [
5]. The selection of the most efficient and reliable method for estimating bed shear stress is one of the main challenges that researchers face in their research. Bed shear stress is an indicator of the ability of the flow to entrain and transport sediment particles [
6], which affects sediment erosion and deposition as well as particle diffusion [
7]. Considering the scale of the bed shear stress estimation, the methods for estimating bed shear stress can be divided into two groups including the small-scale and reach-averaged approaches. In the small-scale method, bed shear stress is estimated at a specific local situation, which is characterized by direct and indirect methods. In recent decades, one can accurately measure velocity fluctuations in three dimensions by applying advanced devices such as acoustic doppler velocimeter (ADV) and laser doppler velocimeter (LDV). As a consequence, the estimation of bed shear stress based on turbulence measurements has become popular [
2]. Using devices such as ADV, it is possible to obtain vertical distribution profiles of velocity and turbulence at a specific location and determine the local bed shear stress using indirect methods. By assessing both advantages and disadvantages of different indirect approaches, Kim et al. [
7] suggested that all possible methods should be applied simultaneously to achieve a reliable bed shear stress estimation.
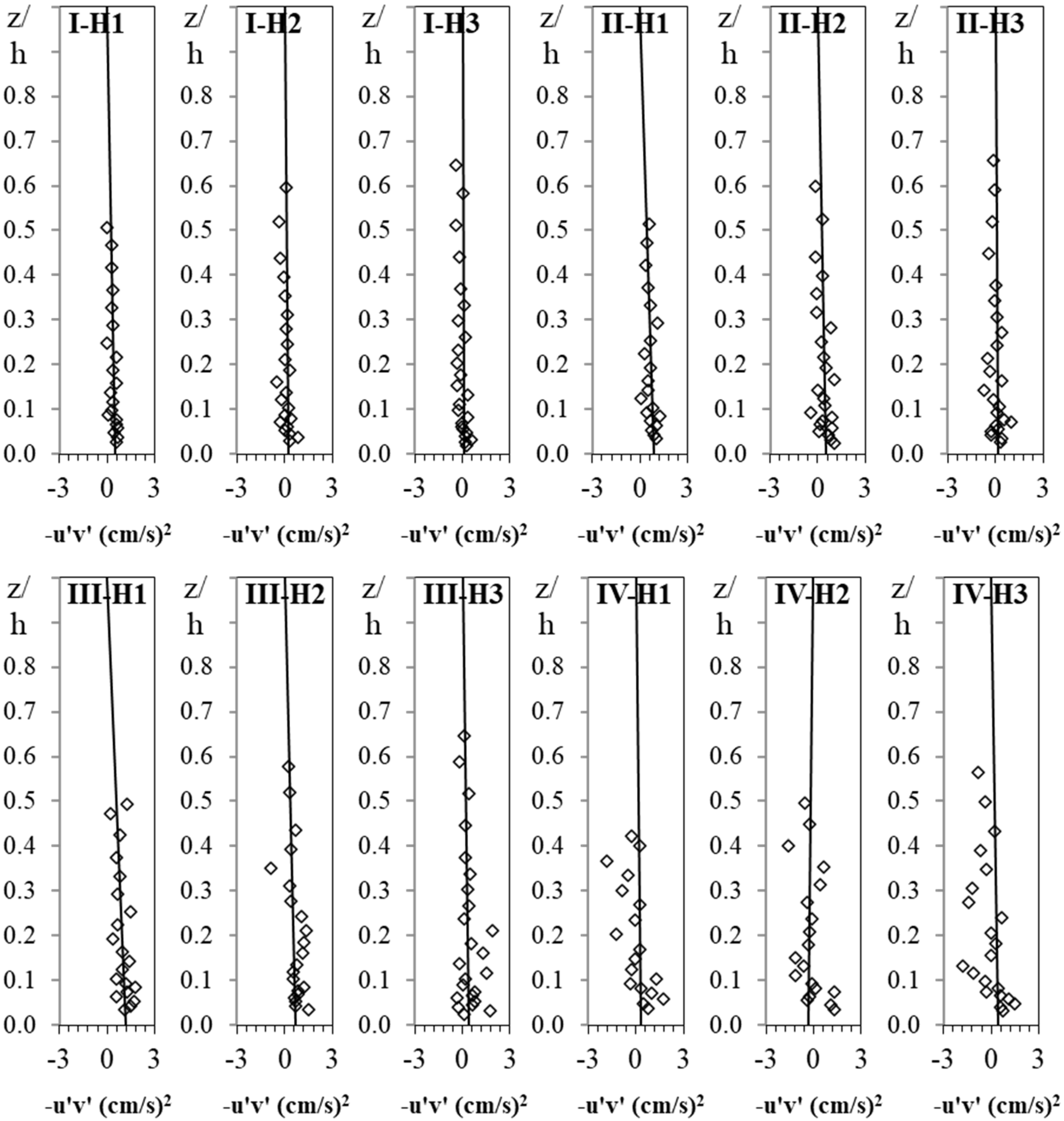
Turbulent stresses or Reynold stresses for an incompressible flow include Reynolds shear stresses (τ
xz = −
ρu′w′, τ
xy = −
ρu′v′, and τ
yz = −
ρv′w′) and Reynolds normal stresses (σ
x = −
ρu′
2, σ
y = −
ρv′
2, and σ
z = −
ρw′
2), where u′, v′, and w′ are the velocity fluctuations in the streamwise, spanwise, and vertical directions, respectively [
5]. For simplification, the Reynolds stress is often divided by the mass density
ρ with the dimension of [L
2/T
2]. These terms are called either the second moments or second-order correlations which are not never zero. They are used to describe characteristics of turbulent flow in the Cartesian coordinate system, which are investigated in this study to estimate bed shear stress, along with TKE.
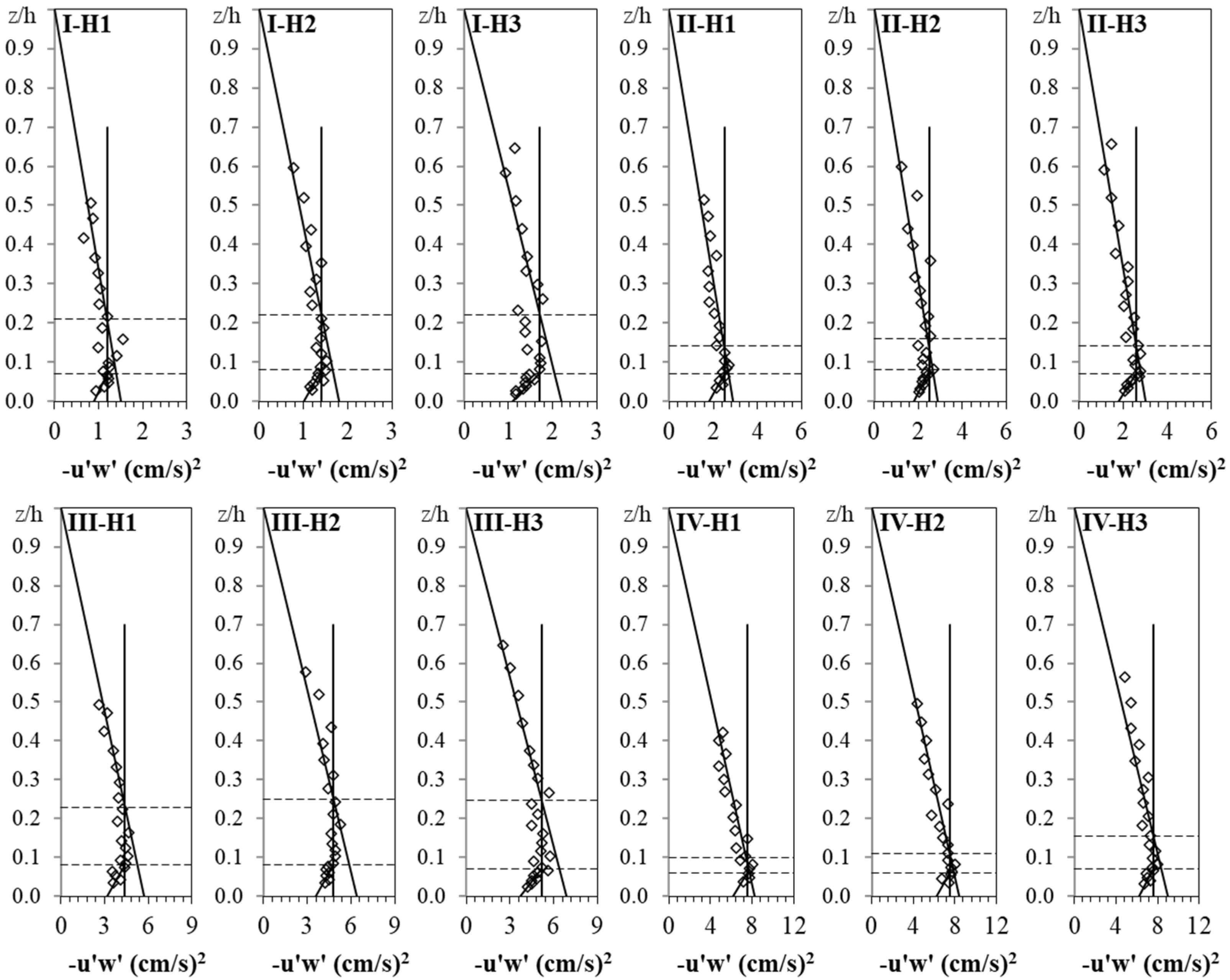
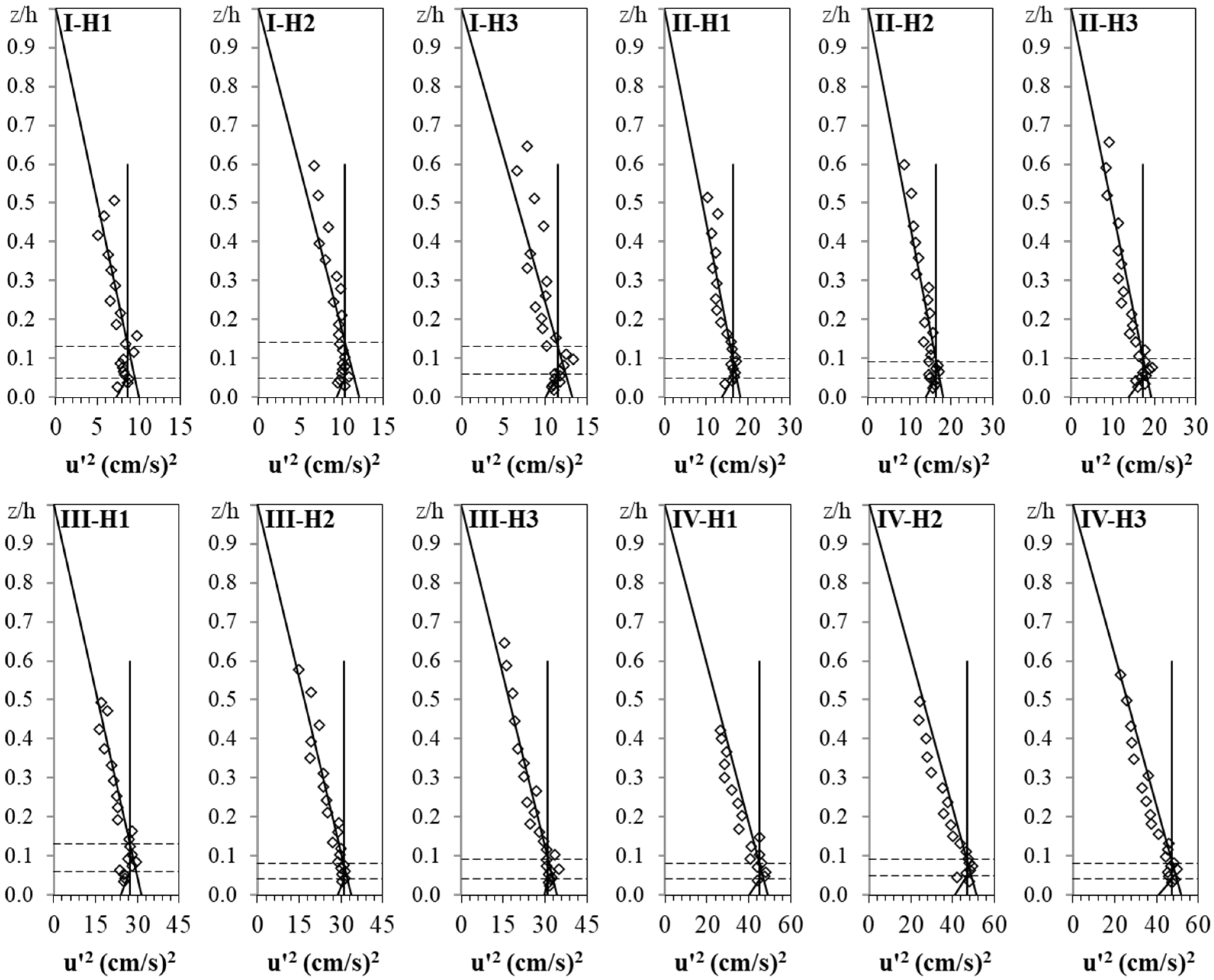
Extending the linear portion of the vertical distribution of −u′w′ (above the damping zone near the bed) towards the bed is one of the most reliable approaches to estimate bed shear stress in steady-uniform flows [
5,
8,
9,
10]. This approach is also called the direct covariance method [
7] and can be used effectively in presence of sediment movement [
9] as efficiently as under the fixed bed condition. This method can be used to determine bed shear stress directly, but the access to advanced equipment with high frequency for acquiring velocity fluctuations is a major challenge in a natural river condition [
11]. Sarkar and Dey [
12] claimed that the damping zone of the −u′w′ profile is related to a reduction in the turbulence intensity in both streamwise and vertical directions in the zone near a channel bed. They argued that this phenomenon may be due to the effect of flow non-uniformity in the vicinity of the channel bed, which changes the linear distribution of −u′w′ in the zone near the bed. This damping zone is also reported by Dey et al. [
13] under conditions of the incipient motion of sediment particles, and by Dey et al. [
8] under conditions of bed load movement, both at a higher distance from the bed compared to the immobile bed conditions. Dey et al. [
8] reported that, in the presence of sediment transport, the vertical distribution of Reynolds shear stress over the entire flow depth showed a reduction. It was claimed that the reason for this reduction is related to the extra momentum that the main flow provides to maintain the motion of sediment particles and overcome the bed resistance. Additionally, the excessive damping of Reynolds shear stress near the bed, in mobile bed, can be related to decrease in the velocity fluctuations as a result of the reduction of the difference between the flow velocity and the movement speed of the sand particles [
8]. Cossu and Wells [
14] pointed out that the maximum value in the Reynolds shear stress verticals occurs at a point inside of the boundary layer where the velocity gradient is the maximum, but below this zone, the Reynolds shear stress decreases, and the viscous stresses increases.
It should be noted that in the presence of vegetation patches in the channel bed, the vertical distribution profile of Reynolds shear stress changes [
15], and the method of the linear extension of the profile towards the channel bed is not practical. In non-uniform flows, Afzalimehr [
16] and Emadzadeh et al. [
17] took attention to the distribution of −u′w′ at the depth below the damping zone and derived a non-linear regression line across the entire water depth to estimate the bed shear stress. In general, the approach by means of −u′w′ is not only sensitive to the possible misalignment of the ADV probe from the flow streamwise direction but also affected by the non-uniformity of the flows [
2,
18,
19]. It can also be affected by the presence of secondary currents [
7]. To solve these problems, especially in oceanography, some researchers applied vector addition of −u′w′ and −v′w′ equal to (u′w′
2 + v′w′
2)
0.5, to estimate the bed shear stress [
14,
20,
21,
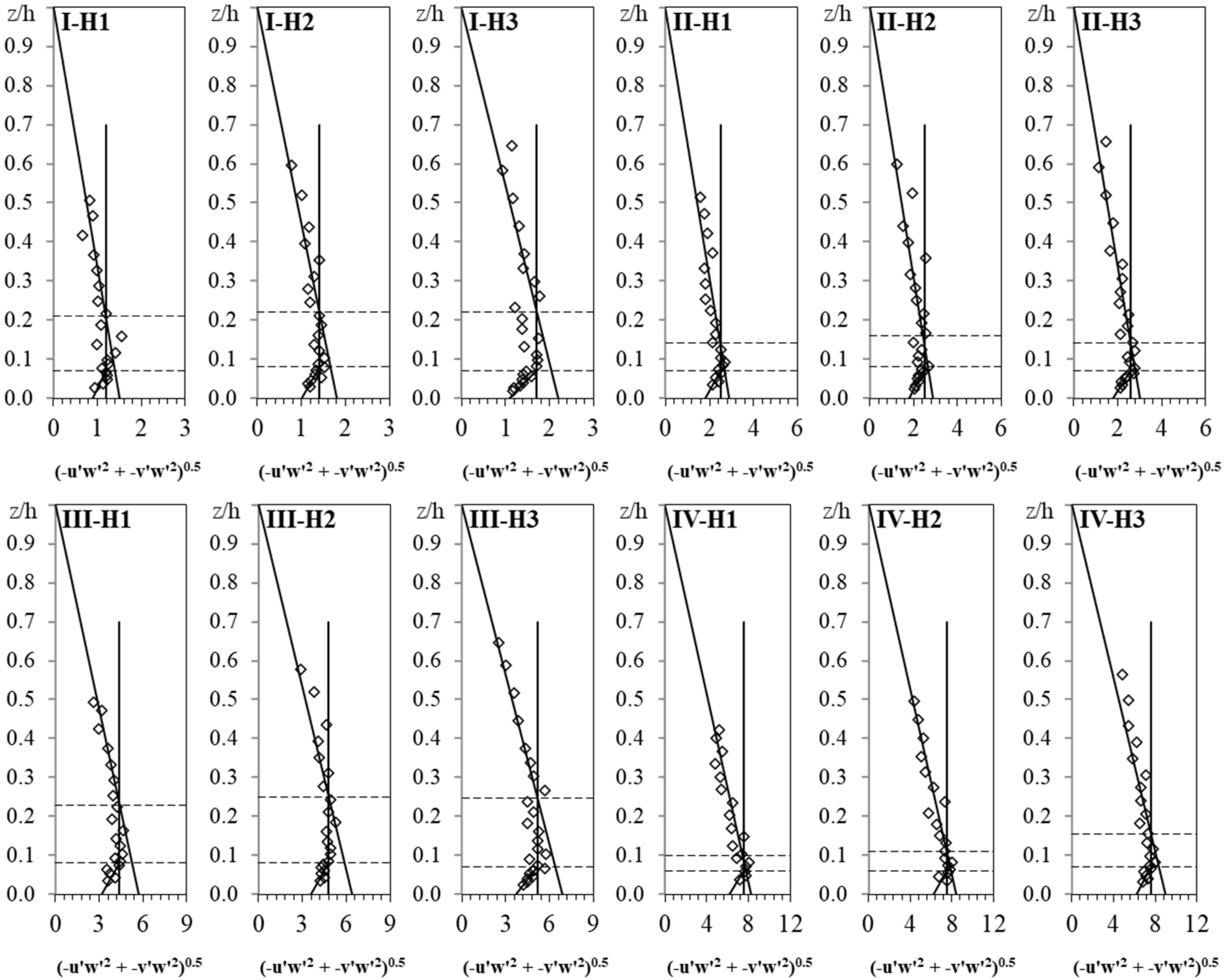
22]. This approach can be especially useful in the field study of rivers and seas, where correct aligning the ADV probe with the flow streamwise direction is prone to error. However, the necessity of applying this approach in laboratory conditions needs to be investigated, especially when the flow is uniform, the secondary current is negligible and the ADV probe is well-aligned with the flow streamwise direction.
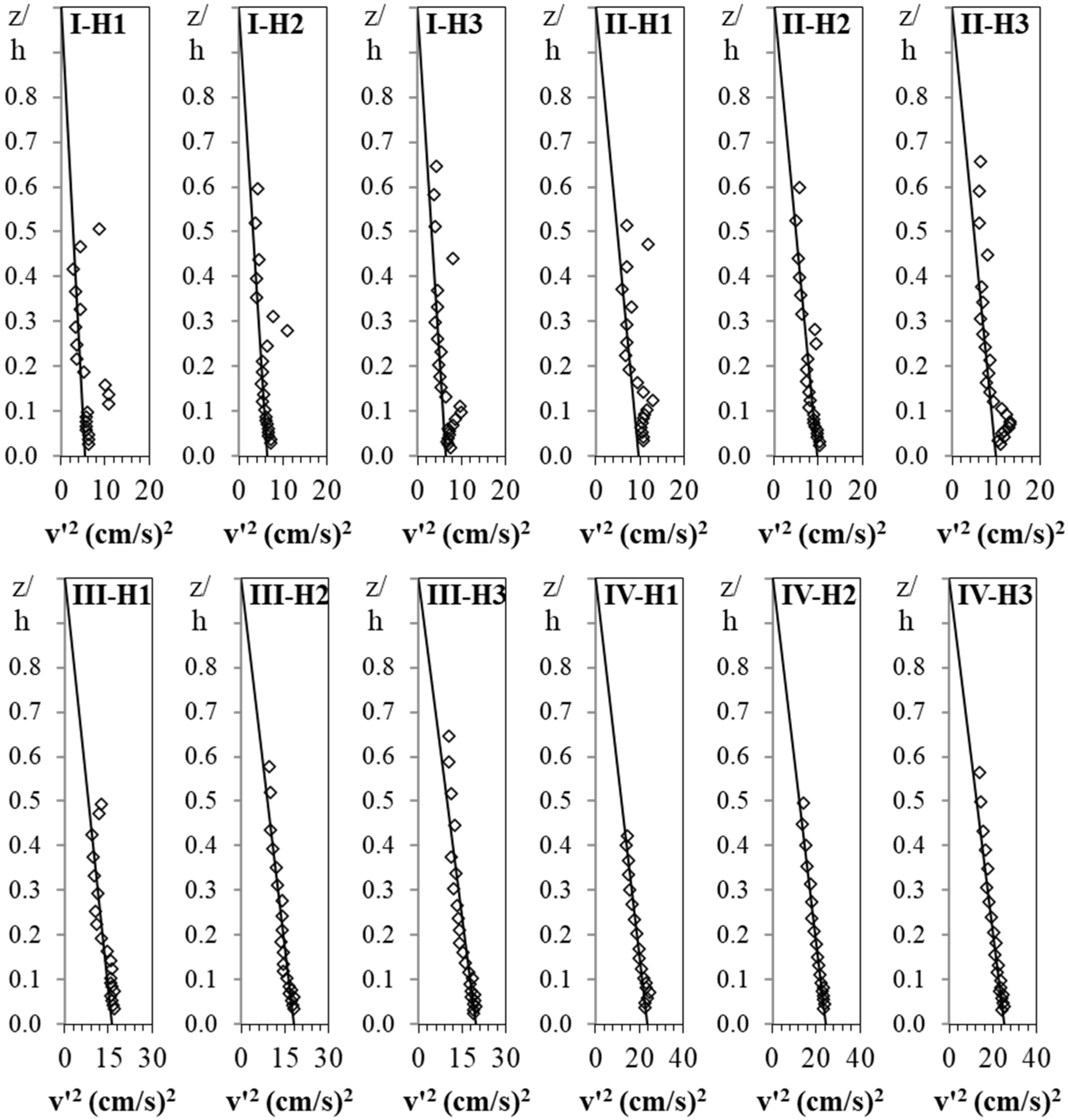
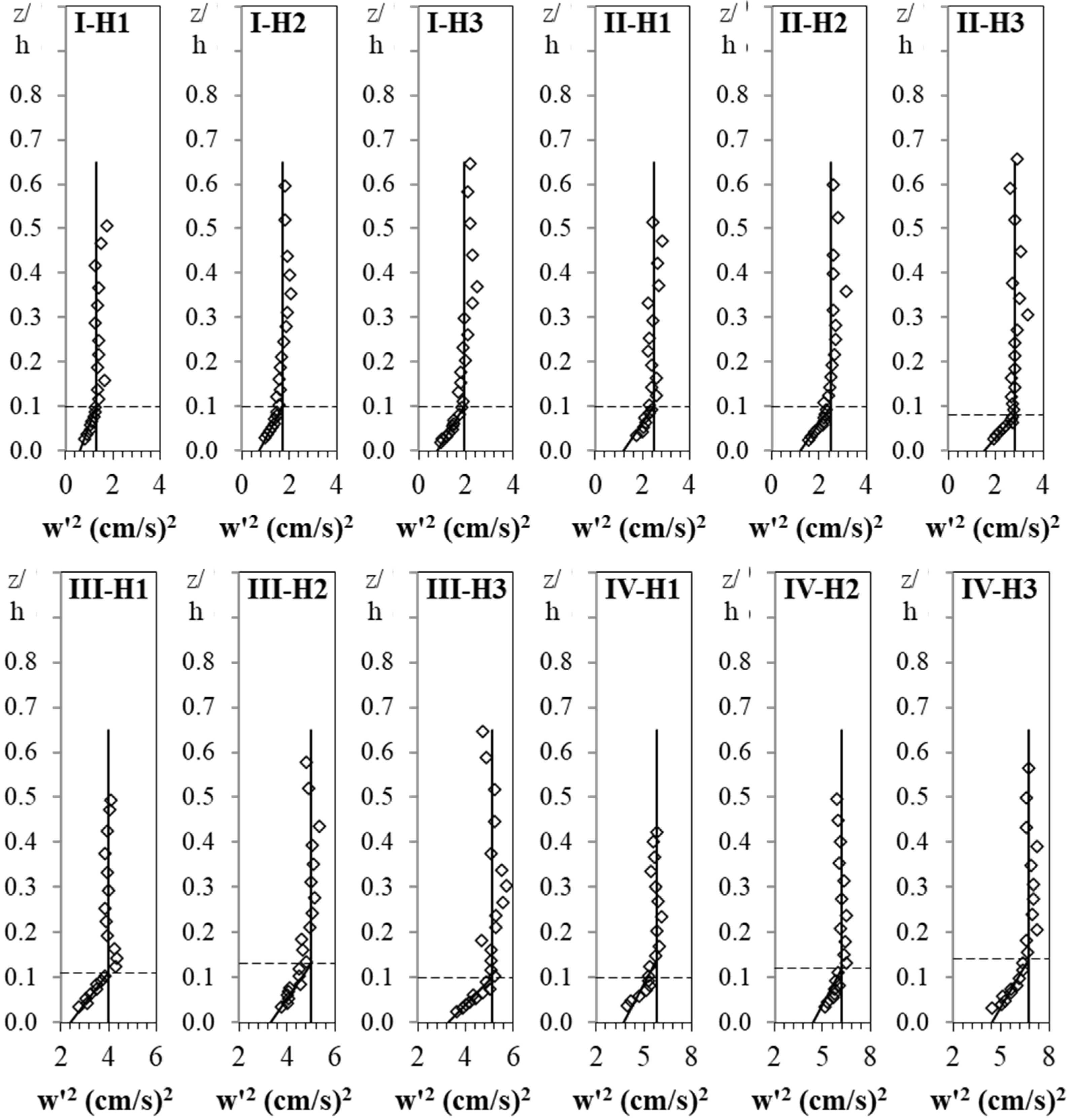
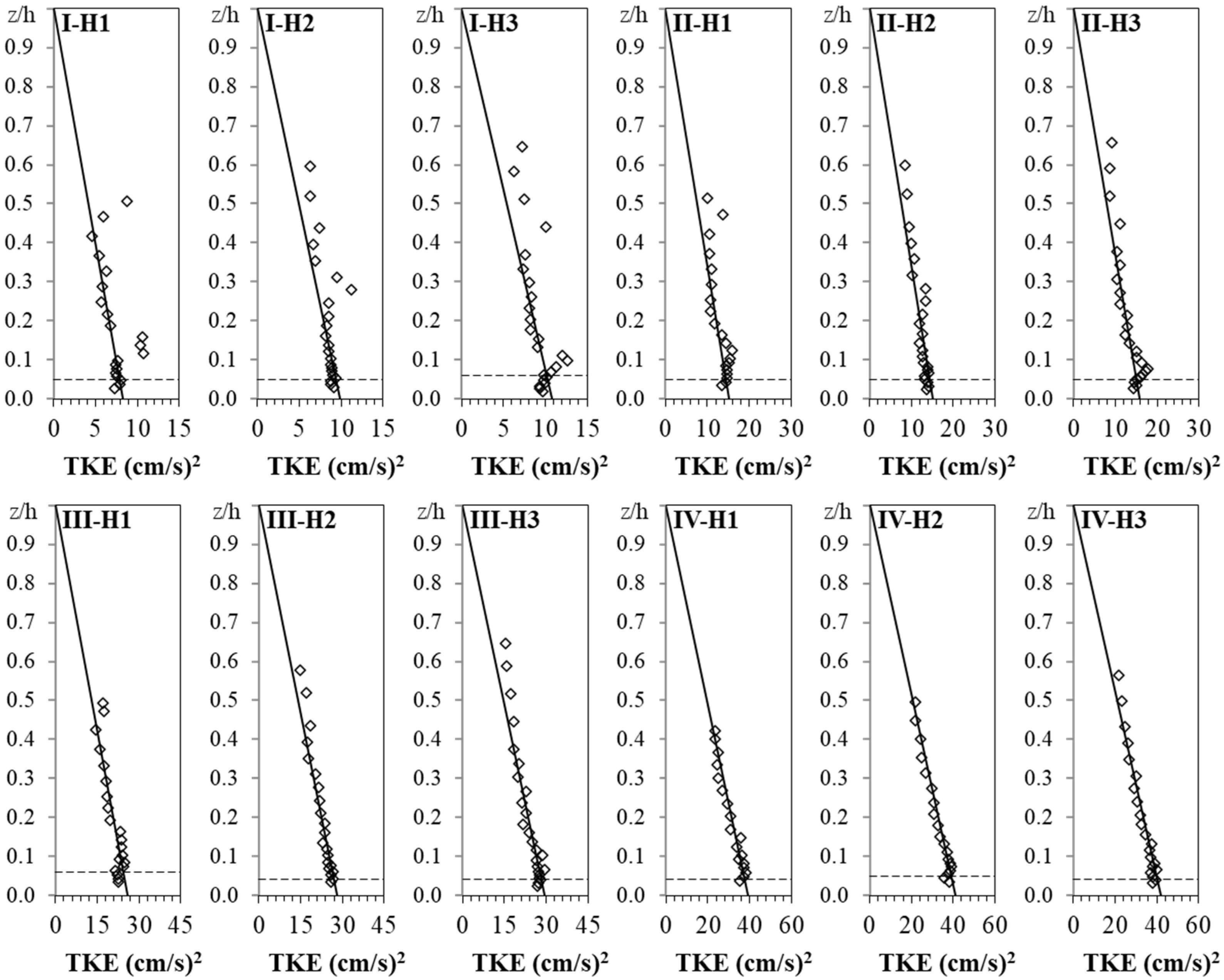
The turbulent kinetic energy TKE is the result of the absolute intensity of velocity fluctuations from the mean velocity in a cartesian coordinate system [
23] and is equal to the sum of u′
2, v′
2, and w′
2 divided by 2 multiplied by the mass density of water. Some researchers claimed that TKE is proportional to the bed shear stress with a simple linear relationship which can be used to determine the bed shear stress [
7,
19]. Obviously, applying all three components of the u′
2, v′
2, and w′
2 in three directions [
18], makes the TKE approach less sensitive to the misalignment of the ADV probe from the correct flow streamwise direction [
19]. To estimate the bed shear stress, TKE should be multiplied by a specified coefficient of 0.19 [
19,
21,
23,
24,
25,
26,
27], or 0.20 [
28,
29] or 0.21 [
7], generally related to oceanography studies. Kim et al. [
7] claimed that the TKE method is the most reliable approach, but more research work is required in the case of the coefficient that relates TKE to bed shear stress. This approach is widely accepted in oceanography studies, but surprisingly was rarely used in fluvial studies [
2,
26]. Biron et al. [
2] successfully used this method with a coefficient of 0.19 in river studies. Pope et al. [
23] claimed that the TKE approach could be used effectively in situations such as the presence of vegetation patches and bedforms in river beds where the application of some other well-known methods is almost impossible.
Voulgaris and Trowbridge [
30] revealed that an ADV can acquire w′
2 more accurately than u′
2 and claimed that u′
2 is more affected by noise errors. In this way, Kim et al. [
7] tried to modify the TKE method and proposed that w′
20 could be multiplied by a coefficient of 0.9 to estimate the bed shear stress. Results of experimental studies by Zhang et al. [
26] showed that the w′
2 method for measuring bed shear stress in rivers could be more handful than the TKE method, but the value of the coefficient needs to be modified. However, it seems that this approach needs to be further studied for clarifying to what extent the estimation of the bed shear stress can only rely on w′
2.
Some researchers indicated that the above-mentioned methods for determining bed shear stress by means of −u′w′, TKE, and w′
2 can be applied using the one-point measurement approach, especially in oceanography [
2,
7,
23,
31]. Biron et al. [
2] and Pope et al. [
23] satisfactorily applied the one-point measurement approach to estimate the bed shear stress by using both −u′w′ and TKE, respectively. Kim et al. [
7] reported that the one-point measurement approach for determining the bed shear stress by using −u′w′ was a reliable method under a tidal condition. They recommended that the ADV sampling volume should be sufficiently close to the bed, located inside the constant shear stress layer. They also suggested that the ADV sampling volume should be at certain distance from the bed to avoid the influence of the bed materials on the sampling volume. Rashid [
31] argued that the depth for the one-point measurement approach should be as close as possible to the bed, and thus recommended a depth of 4 mm above the sand bed for the one-point measurement method to estimate the bed shear stress using −u′w′, TKE, and w′
2.
Despite the important role of the bed shear stress in studies of fluvial hydraulics, there is a lack of knowledge regarding the performance of different methods based on turbulence characteristics, especially under the critical condition of transitional flow over a sandy bed. The methods based on both TKE and w′2 are well-known methods used by oceanographers but have not received enough attention in river studies by river engineers. It is necessary to examine the applicability of these approaches in river studies and determine the appropriate coefficients in order to estimate the bed shear stress, especially under the conditions mentioned above. Additionally, the possibility of using other Reynolds normal stresses including u′2 and v′2 to estimate the bed shear stress should be examined. The necessity of the approach of the vector addition of −u′w′ and −v′w′ for different conditions in the laboratory needs to be investigated. By analyzing and simplifying all vertical distribution of Reynolds shear and normal stresses as well as TKE, the main purpose of this study is to investigate all possible ways for estimating bed shear stress under the mentioned specific conditions and answer some questions such as: is it sufficient to estimate bed shear stress by multiplying the values of Reynolds normal shear stresses including u′2, v′2, and w′2 as well as TKE at the bed by a specified constant coefficient? Are the determined coefficients dependent on the values of shear Reynolds number within the range of transitional flow conditions?
2. Materials and Methods
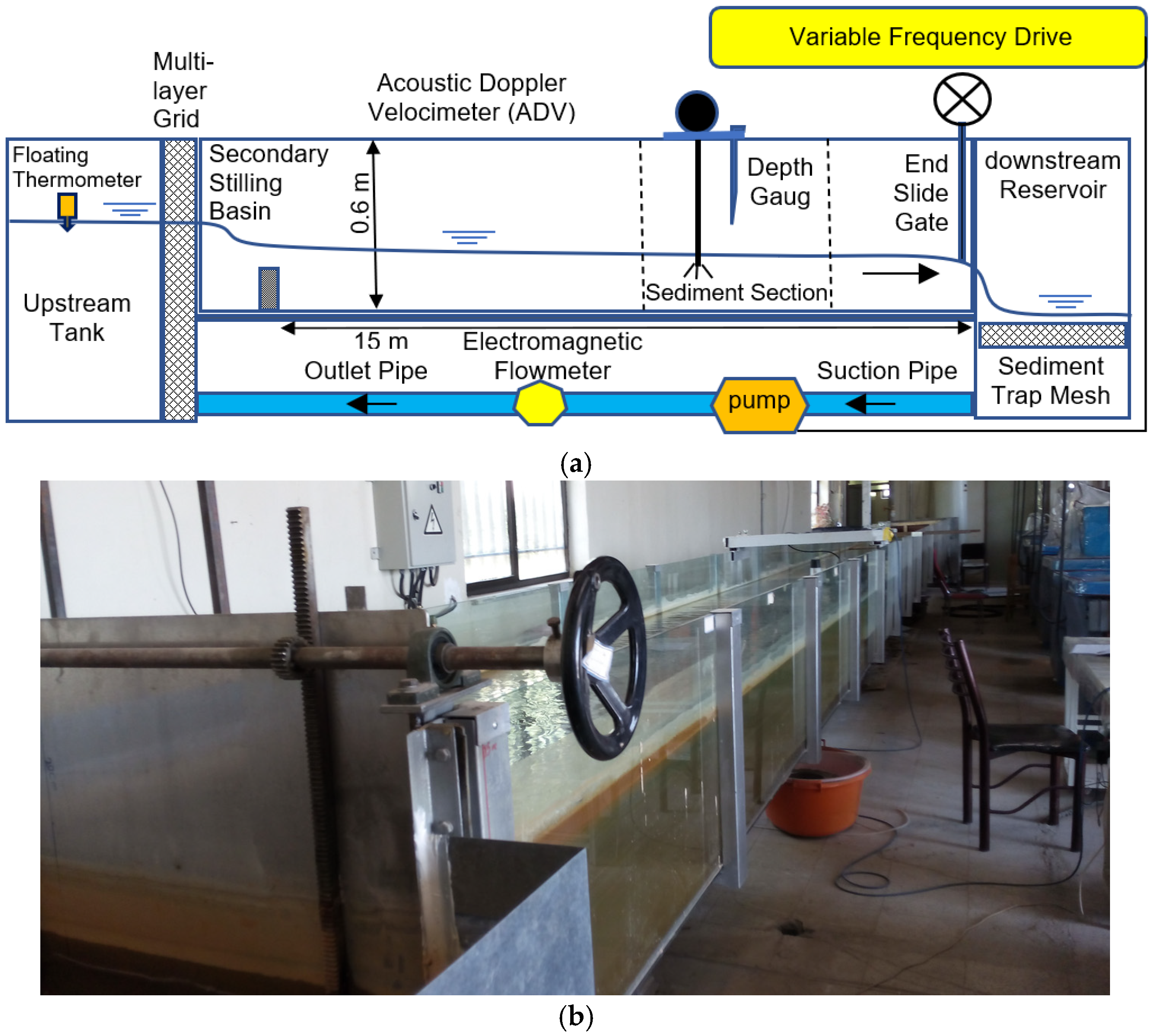
A rectangular long and wide flume was used for doing experiments (
Figure 1). The flume is 15 m long, 0.6 m deep, and 0.9 m wide. This wide and long flume enables the flow to achieve a fully developed flow with a minimal side-walls effect. The flume side walls are transparent to facilitate observations of the movement of sediment particles during each experimental run. Water was recirculated between the upstream storage tank and the downstream reservoir using a pipeline with a centrifugal pump (
Figure 2a) with a discharge capacity of 50 lit/s. Water was spilled over a slide-gate located at the end of the flume (
Figure 2b) into a downstream reservoir (equipped with a sediment trap mesh). The water temperature was continuously recorded using a floating electrical thermometer located in the upstream water tank. In order to reduce the flow oscillations and dissipate additional disturbances, a multi-layer grid was placed in the upstream tank and a secondary stilling basin at the flume entrance. The flow discharge was measured using a high-precision electromagnetic flowmeter (
Figure 2c) with a maximum relative percentage error of 0.5%, installed on the pump outlet pipe. The flow rate was regulated by adjusting the frequency rate applied to the pump electromotor, using a variable frequency drive (
Figure 2d). A simple depth point gauge with a resolution of 0.5 mm was used to measure the water depth during each experimental run.
An acoustic doppler velocimeter (ADV) including a four-beam down-looking probe was applied to record velocity fluctuations in three directions in a cartesian coordinate system including the streamwise u (to the downstream), spanwise v (to the left side), and vertical w (from the bed towards the water surface) directions. All measurements of flow velocities were taken under conditions of incipient motion of sediment particles in the sandy bed. According to the ADV user instructions available at
www.nortek-as.com, accessed on 26 October 2015, the ADV acoustic frequency was 10 MHz able up to 200 Hz sampling frequency made by the Nortek Corporation with a maximum relative percentage error equal to 0.5%. The last version (version 1.22) of Nortek’s specific interface software named Vectrino Plus was used to collect data. At each point, the ADV measurement lasted 2 min for collecting 24,000 data. The first point for velocity measurement should be at least 60 mm below the water surface considering the approximate distance of 50 mm between the ADV transducer and focal point of the sampling volume, together with a required probe-head submergence of at least 10 mm underwater to avoid bubble exposure. On the other hand, to avoid interference of the sampling volume with the channel bed, it was inevitable to ignore data collection at a distance of 3–4 mm to the bed. Therefore, because of the inherent limitation of the ADV device, data sampling along each profile was limited to a range of 3–4 mm above the bed to 60 mm below the water surface.
Because data collected using an ADV can be affected by the doppler signal noise [
32], the data should be refined using software called WinADV32 (version 2.024, Water Resources Research Laboratory, U.S. Bureau of Reclamation, Denver, Colorado, downloaded from
http://www.usbr.gov/wrrl). In this case, a filter called the phase–space threshold despiking developed by Goring and Nikora [
32] and modified by Wahl [
33] was applied. Additionally, the minimum acceptable correlation coefficient and signal-to-noise ratio were determined equal to 70 and 15, respectively. Finally, after removing about 18% of the damaged sample data, the profiles for flow velocity, TKE, and Reynolds normal and shear stresses were obtained. In this way, by using the “Data Conversion” command and selecting the NDV option in the Vectrino Plus software (version 1.22, Nortek AS, Vangkroken 2, NO-1351 RUD, Norway, downloaded from
www.nortek-as.com), the extension of the files acquired by ADV was converted from “vno” to the “adv” in order to be available for the WinADV32. Then, in the WinADV32 software, after determining the desired filters by running the “Process Many” commands, the summary statistics of the filtered data were computed for all points of a profile and merged into a file with the extension of “sum”. This file could be opened in the MS-Excel software to draw the vertical distribution of velocity and turbulence characteristics.
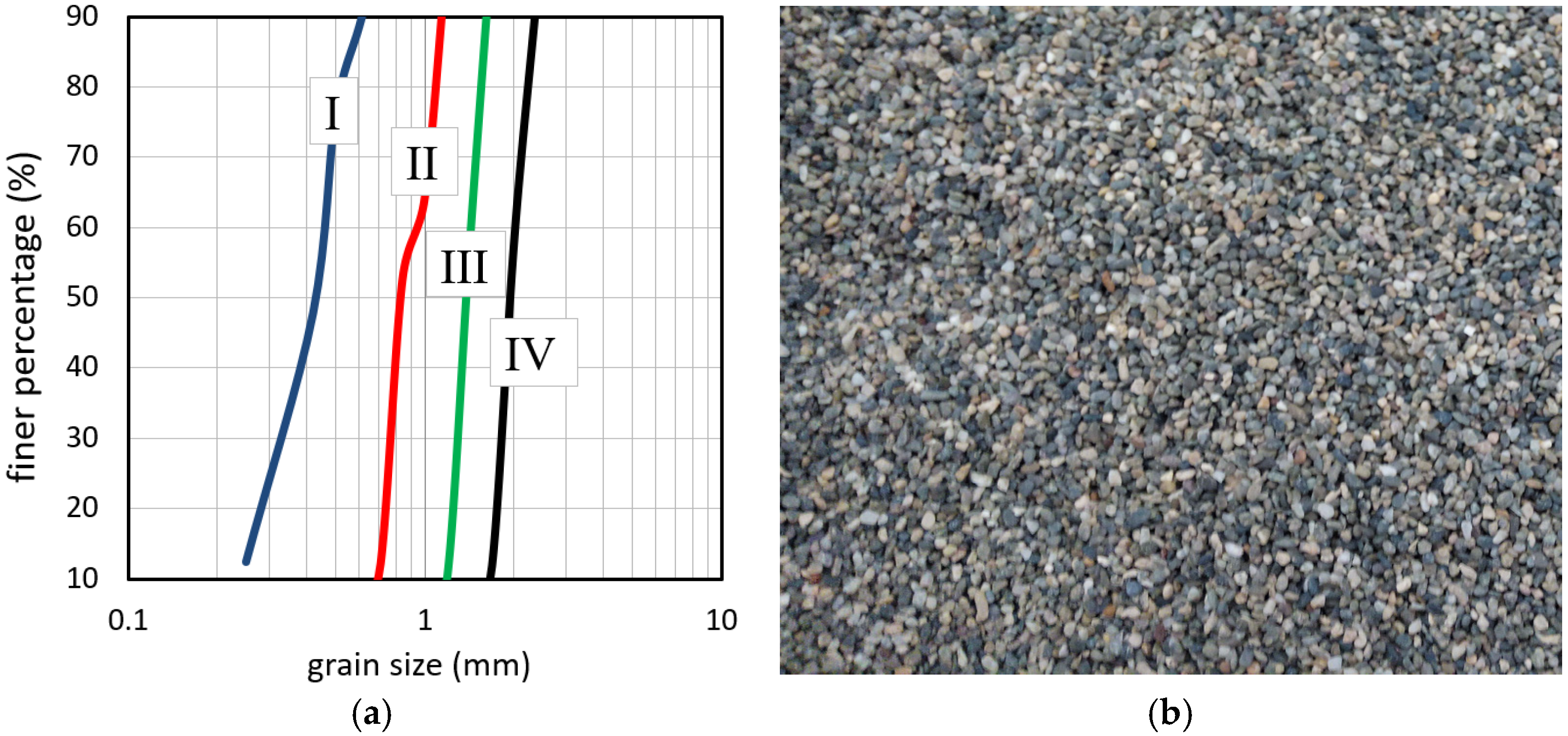
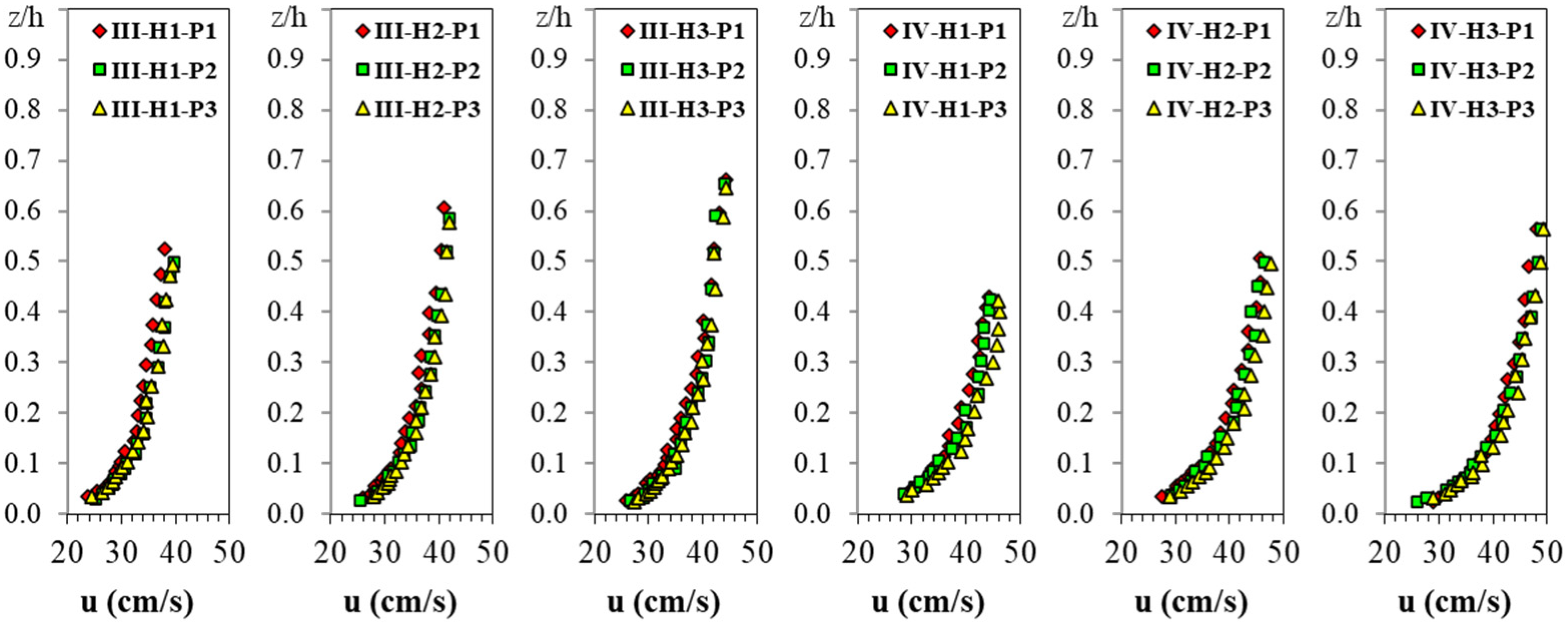
Four groups of uniform sand particles numbered I, II, III, and IV with median grain sizes of 0.43, 0.83, 1.38, and 1.94 mm, with a mass density of 2.65 g/cm
3 were used in this experimental study. The median grain size of all four groups is less than 2 mm in the range of sand grain size [
34]. According to the well-known grain size classification [
5], group “I” was classified as medium sand, group II as coarse sand, and both groups III and IV as very coarse sand. The geometric standard deviation of particle size distribution is between 1.16 to 1.45, indicating an acceptable uniform distribution of sediment particles. The grain size distribution curves of four sediment groups were presented in
Figure 3a together with a picture of a sample of sediment used in this experiment (
Figure 3b). Three flow depths H1, H2, and H3 equal to 100, 120, and 140 mm, respectively, were used for experiments using sediment groups “I”, “II”, and “III”. For sediment group “IV”, three flow depths of 91, 104, and 120 mm, respectively, were used. The bed of a flume section which is 4 m long was covered with a sand layer with a thickness of 3 cm. It should be noticed that this homogeneous sandy bed is different from the real situation in natural rivers, but this assumption is necessary for this study to evaluate the flow characteristics under the condition of incipient motion of different sizes of sediment particles. The flume section between this sand bed and flume entrance was 8 m long and can provide suitable conditions for a fully developed flow. To reduce the effect of the end slide-gate, the flume section with the sand bed was located 3 m upstream from the end slide-gate of the flume. The flume bed of both the upstream and downstream sections from the sand bed section was covered with coarse material that was unable to move during the experiments.
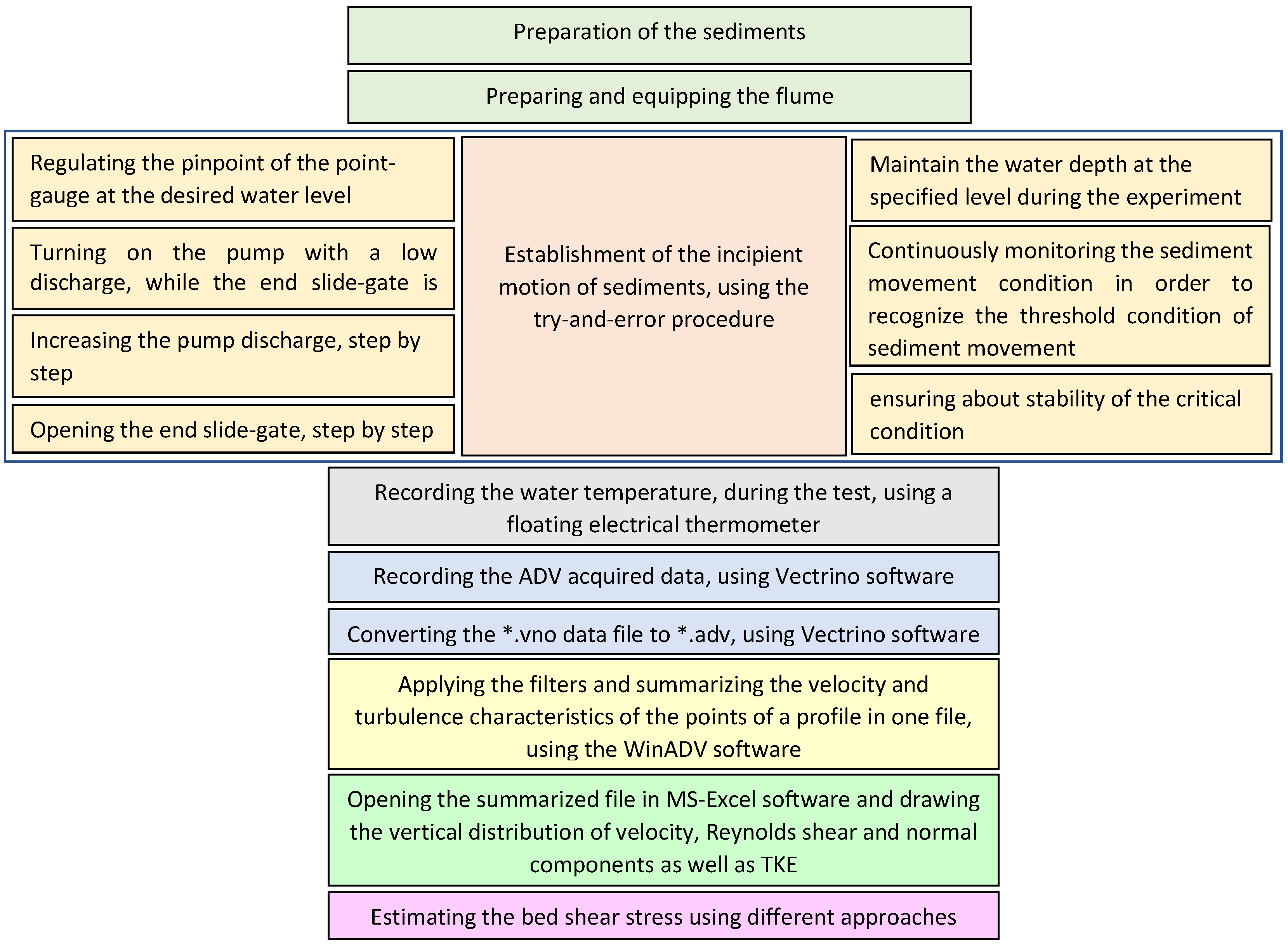
The medium transport of the Kramer visual observation method was considered as the criterion for determining the threshold condition which indicated the movement of a large number of particles with median grain size, without changing the bed-surface configuration [
9]. By changing the pump discharge and adjusting the end slide-gate at the end of the flume, the specified flow velocity can be created at the desired water depth. Firstly, the pinpoint of the point gauge was fixed at the level of desired water surface. To prevent sediment particles from washing away, the pump was turned on with a low flow rate of about 5 lit/s, using the variable frequency drive, while the end slide-gate was closed. Once touching the pre-regulated pinpoint of the point gauge with water, by slightly opening of the end slide-gate a uniform low-velocity flow was established at the desired water depth. To increase the flow velocity to achieve the incipient motion of bed materials at the pre-determined water depth, using the try-and-error procedure, the pump discharge and the opening of the end slide-gate were increased gradually. This time-consuming procedure continued until achieving the threshold condition. It should be noted that the mobility of sediment particles was monitored for about 10 min to ensure about stability of the critical condition. The experimental process for all experiments was summarized in
Figure 4.
4. Conclusions
Twelve experiments have been conducted to investigate the relationship between the turbulence characteristics and the bed shear stress under conditions of incipient motion of sand particles in the shallow transitional flows. The vertical distribution of −u′w′ showed a linearly increasing trend from the zero value at the water surface to the depth of z/h = 0.18; then followed by a damping zone with relatively unchanged −u′w′ at the depth of 0.07 < z/h < 0.18, and finally a decreasing zone with a decrease in −u′w′ towards the bed. By extending a regression line in the increasing zone, the value of the −u′w′0 was determined, which was considered as the bed shear stress and used to evaluate results using other methods. Results showed that, under such a laboratory condition with uniform flow and well-aligned ADV probe, the vector addition of the −u′w′ and −v′w′ is not necessary. The vertical distribution of u′2 has the same distribution profile as that of −u′w′, and can be simplified into three zones, but with a less height of the damping zone, and less recognizable the decreasing zone. The values of v′2 decreased linearly towards the bed without any detectable turning points. With respect of w′2, the values in the main flow were almost constant and started to decrease at the depth of z/h = 0.11 without any obvious damping zone. Along TKE verticals, a dominated increasing zone and a small decreasing zone were observed with a turning point near the bed at a depth of z/h = 0.05. The bed shear stress can be effectively estimated by multiplying the values of u′20, v′20, w′20, and TKE0 by 0.17, 0.33, 1.24, and 0.20, respectively. The estimated coefficient for TKE is in agreement with those in the literature. Since the TKE method applies all three components of Reynolds normal stresses in three directions, the TKE method seems to be preferred to comparing to the u′2, v′2, and w′2 methods. By classifying the laboratory experiments into two groups of A and B with a range of shear Reynolds number, respectively, from 5 to 14 and from 34 to 61, the bed shear stress for group A was estimated by multiplying the values of u′20, v′20, w′20, and TKE0 by 0.16, 0.30, 1.13, and 0.19, respectively, and for group B 0.18, 0.35, 1.36 and 0.22, respectively. This means under a transitional flow condition, to estimate −u′w′0, the coefficients for multiplying by u′20, v′20, w′20, and TKE0 are slightly increased from the hydraulically smooth to hydraulically rough flow conditions. For the one-point measurement approach, the middle point of the damping zone (at a depth of z/h = 0.13 for −u′w′ and z/h = 0.08 for u′2) was recommended to be used for estimating −u′w′0 and u′20 by multiplying the related values by 1.22 for −u′w′ and 1.12 for u′2, respectively. Given the linear distribution of v′2 and TKE from the zero value at the water surface to the bed, the value at the bed could be estimated which is equal to the one-point measured value divided by the difference between one and its relative depth at that point, considering z/h > 0.05 for TKE. In the case of w′2, it is recommended the depth for estimating w′20 using the one-point measurement approach should be selected in the unchanged zone with the depth of z/h > 0.11. It was estimated that the values of u′20, v′20, and w′20 are, respectively, about 60.5%, 31.3%, and 8.2% of their summation. The results of this study could be applied in such conditions similar to the current experiments. However, further studies should be carried out for other situations such as different particle sizes of bed material, bed load conditions, different water depths, and flow regimes.