Numerical Modeling of Flash Flood Risk Mitigation and Operational Warning in Urban Areas
Abstract
:1. Introduction
2. Methodology
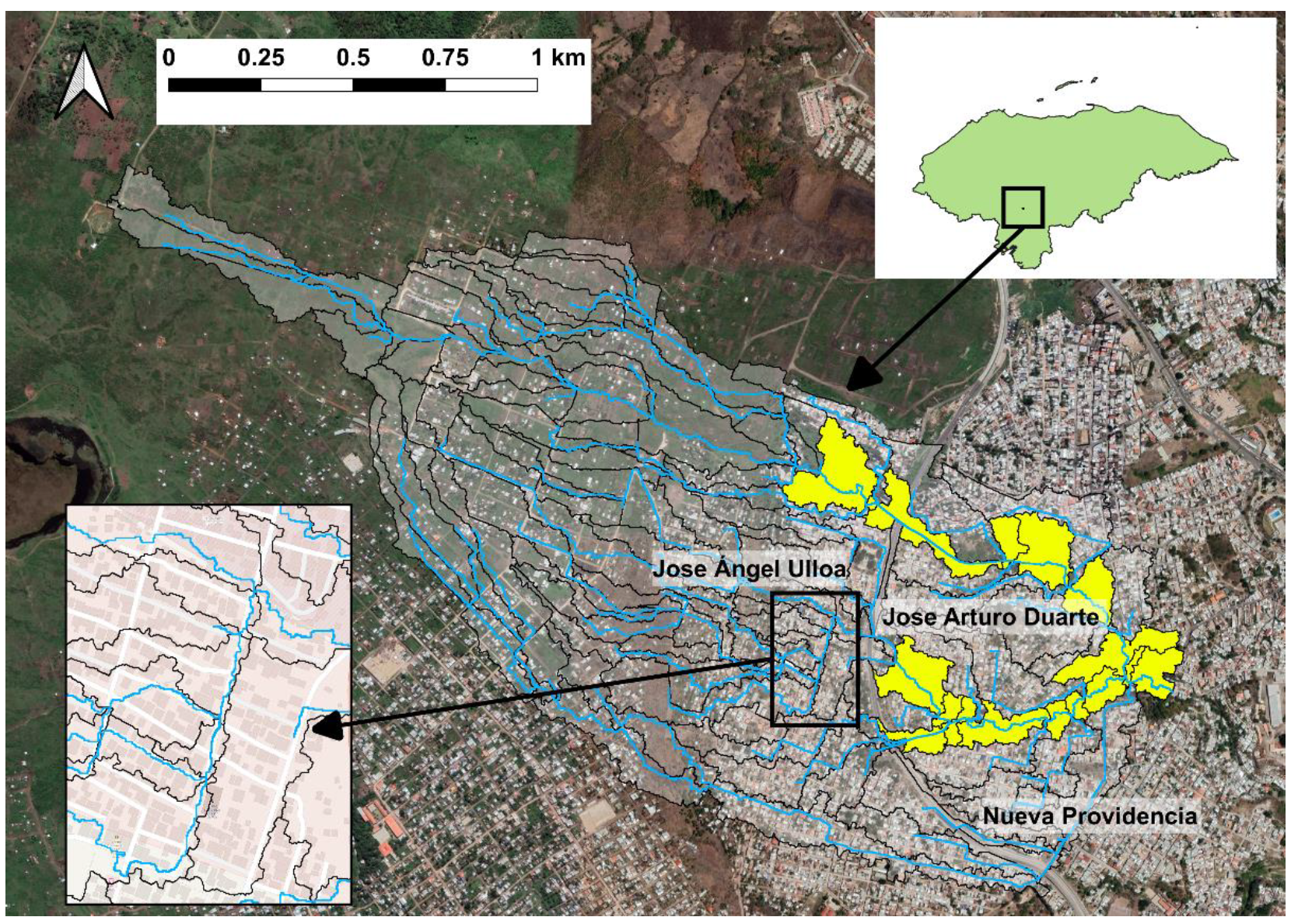
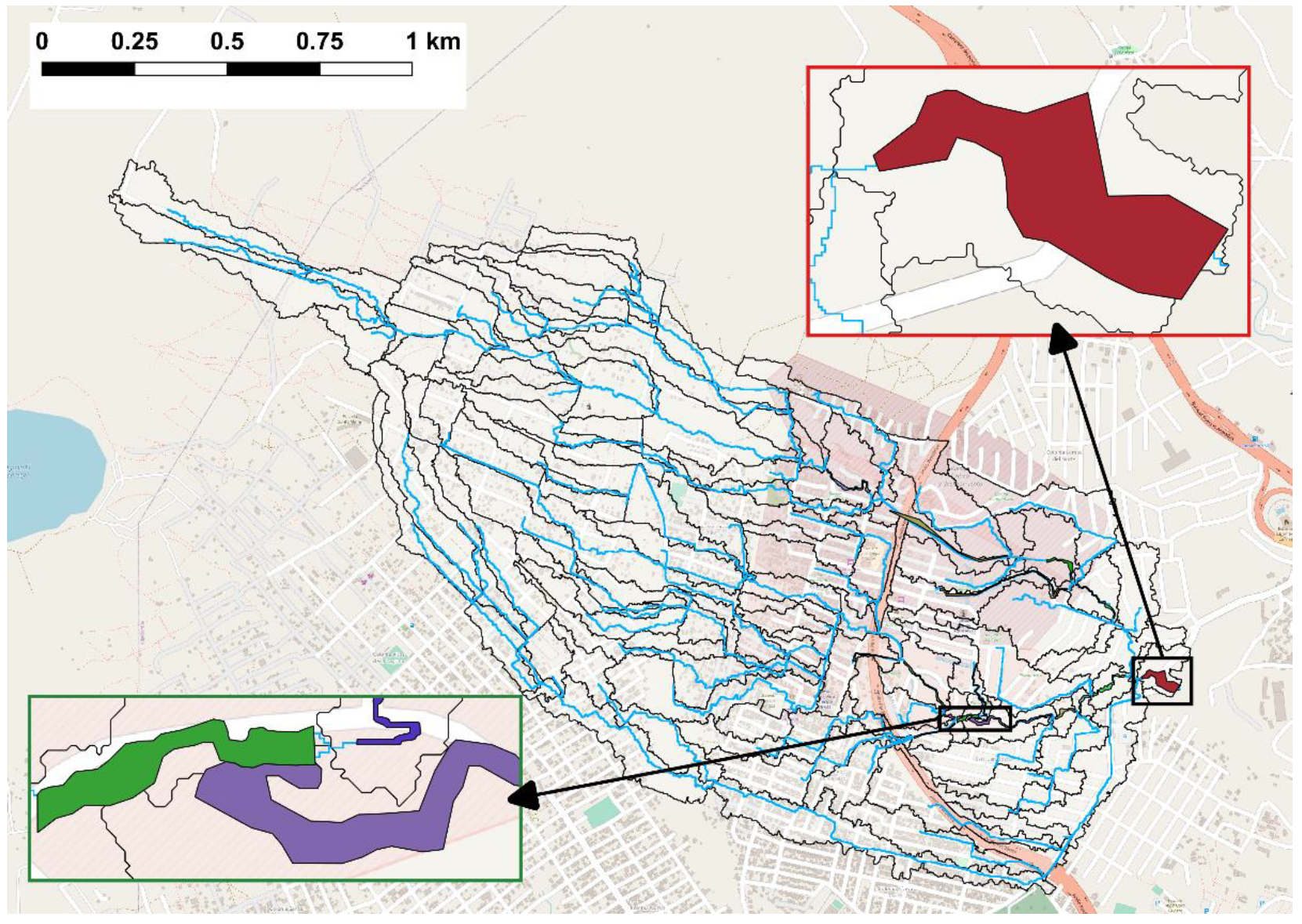
2.1. Site Description and Basin Delineation
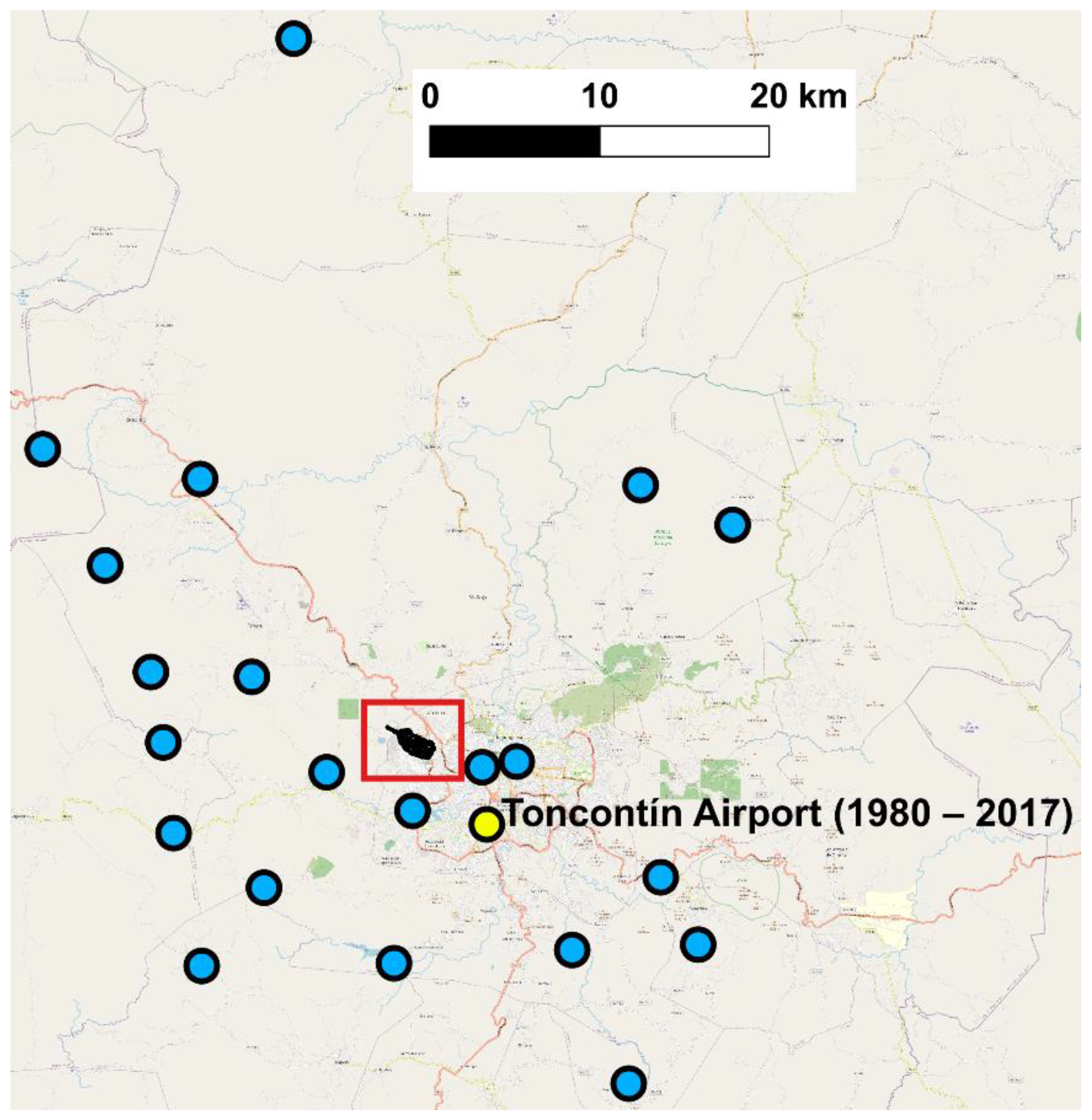
2.2. Extreme Storm Precipitation Analysis and Design
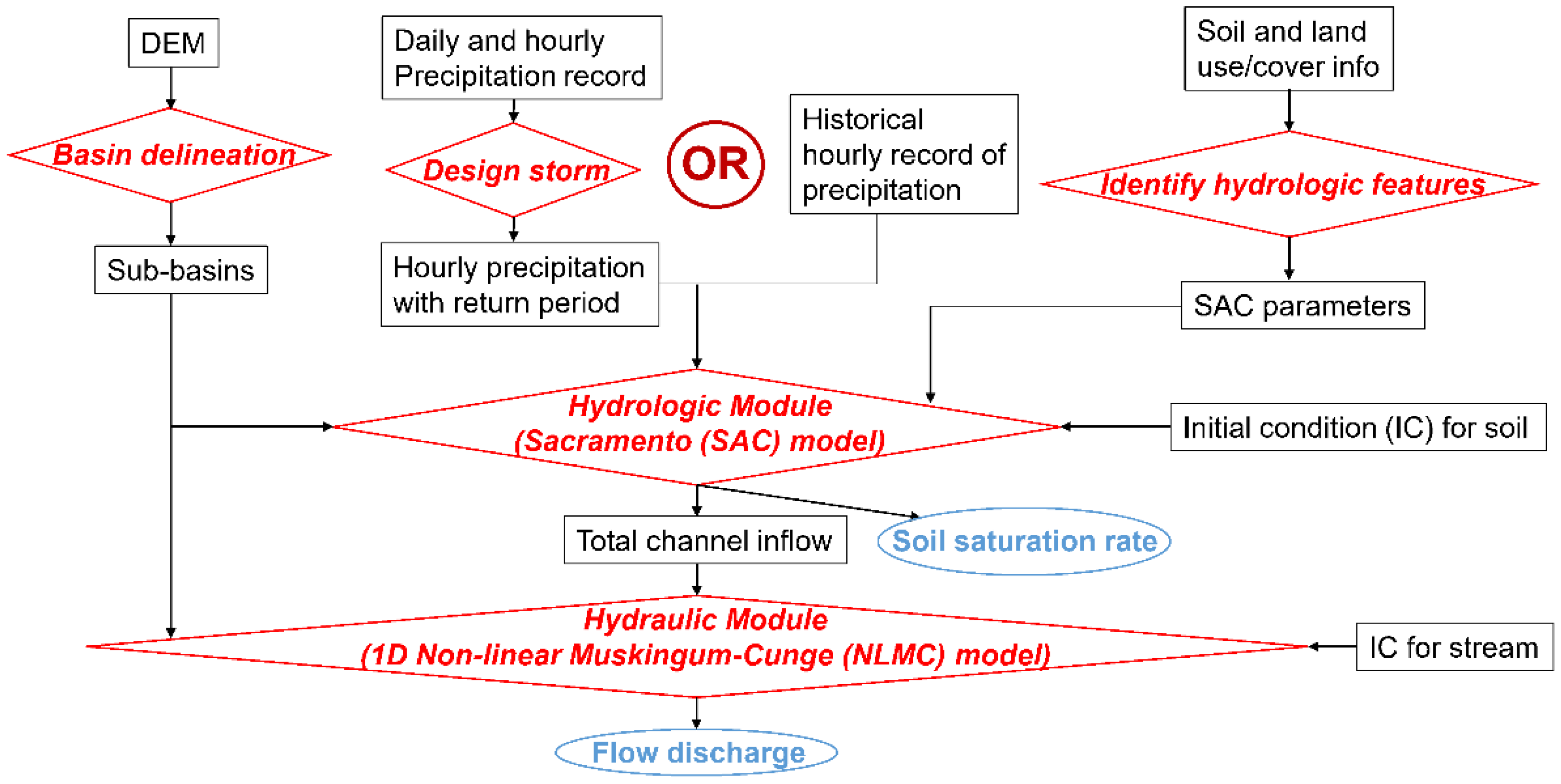
2.3. Hydrologic and Hydraulic Modeling
2.3.1. Spatially Distributed Hydrologic Modeling
2.3.2. Distributed Hydraulic Routing Model
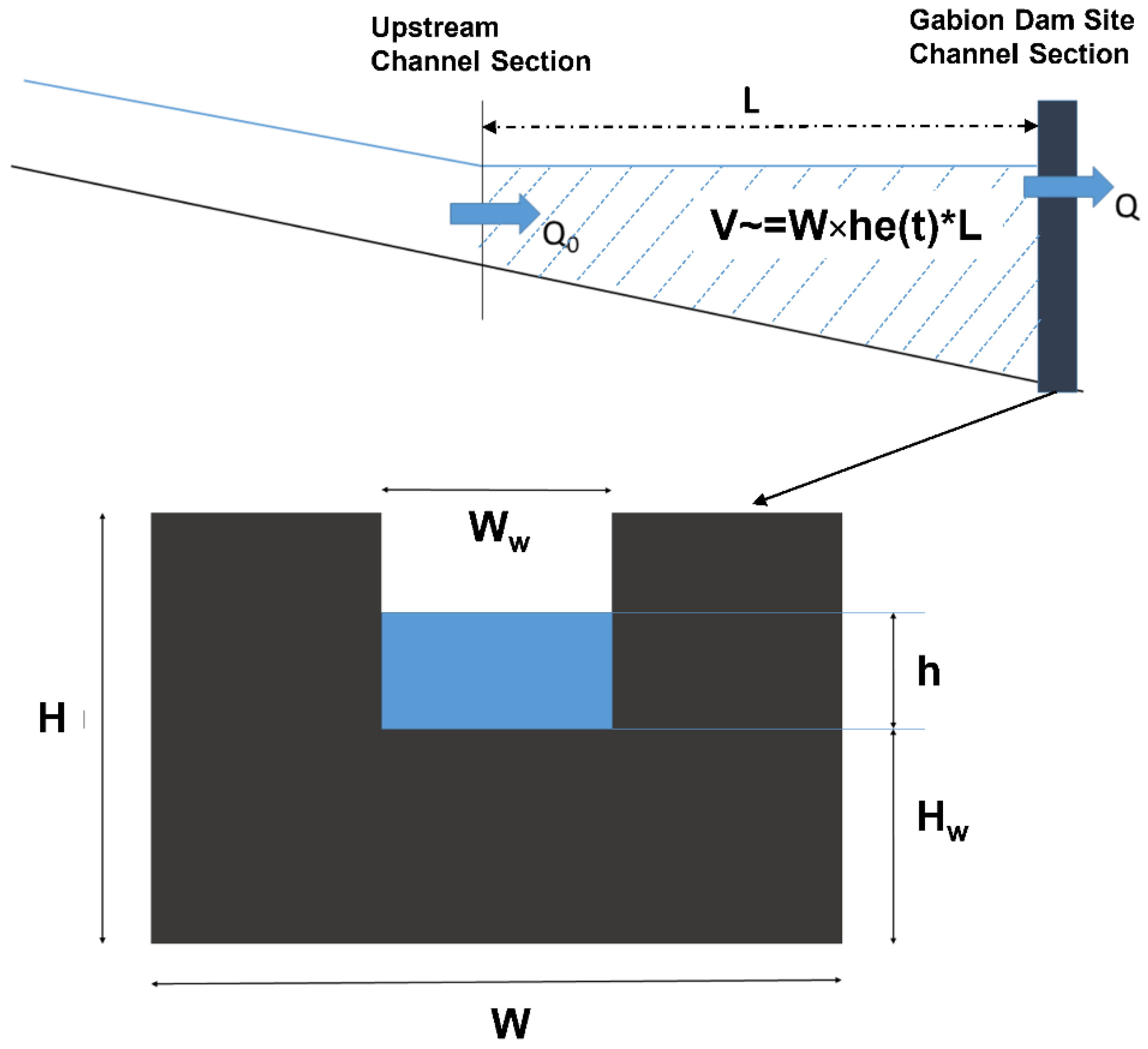
2.4. Mitigation Measures
3. Results and Discussion
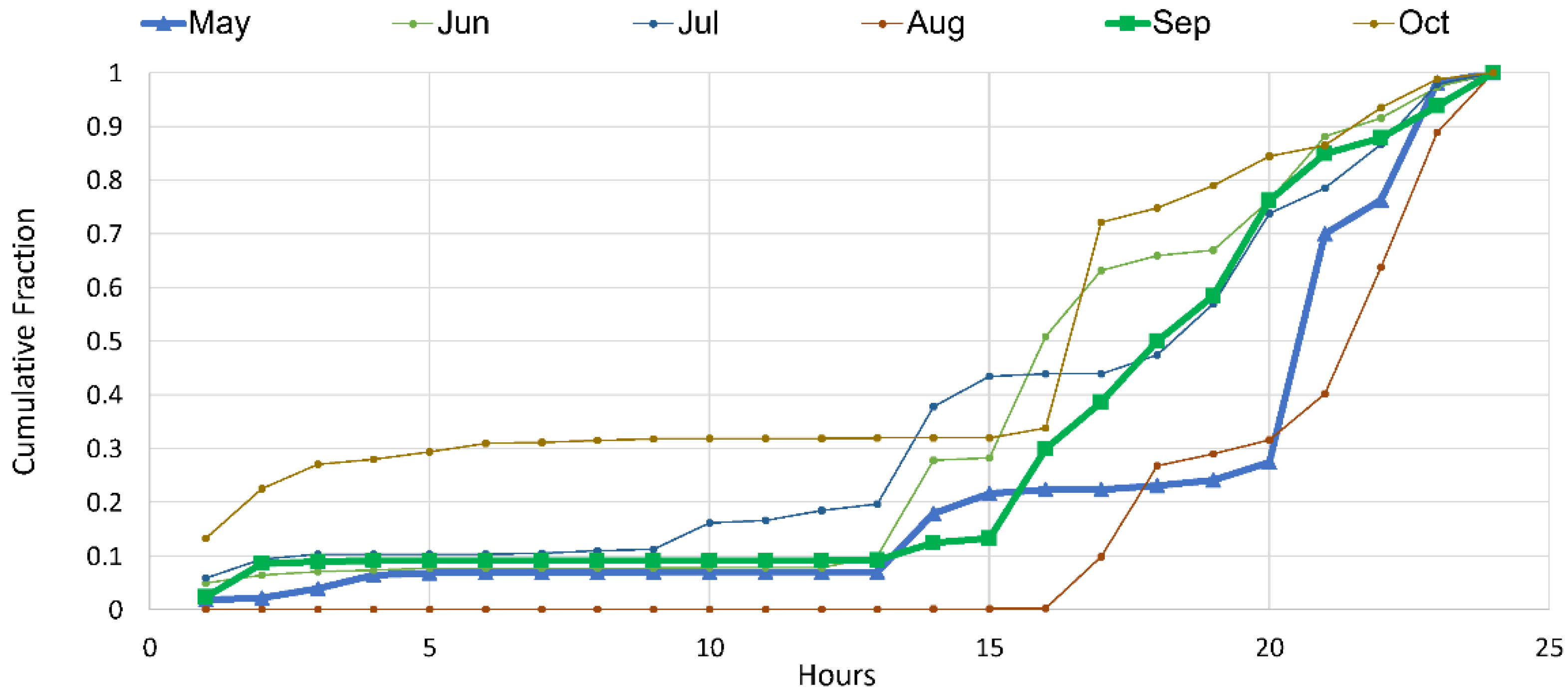
3.1. Estimation of Storm Precipitation of a Given Return Period
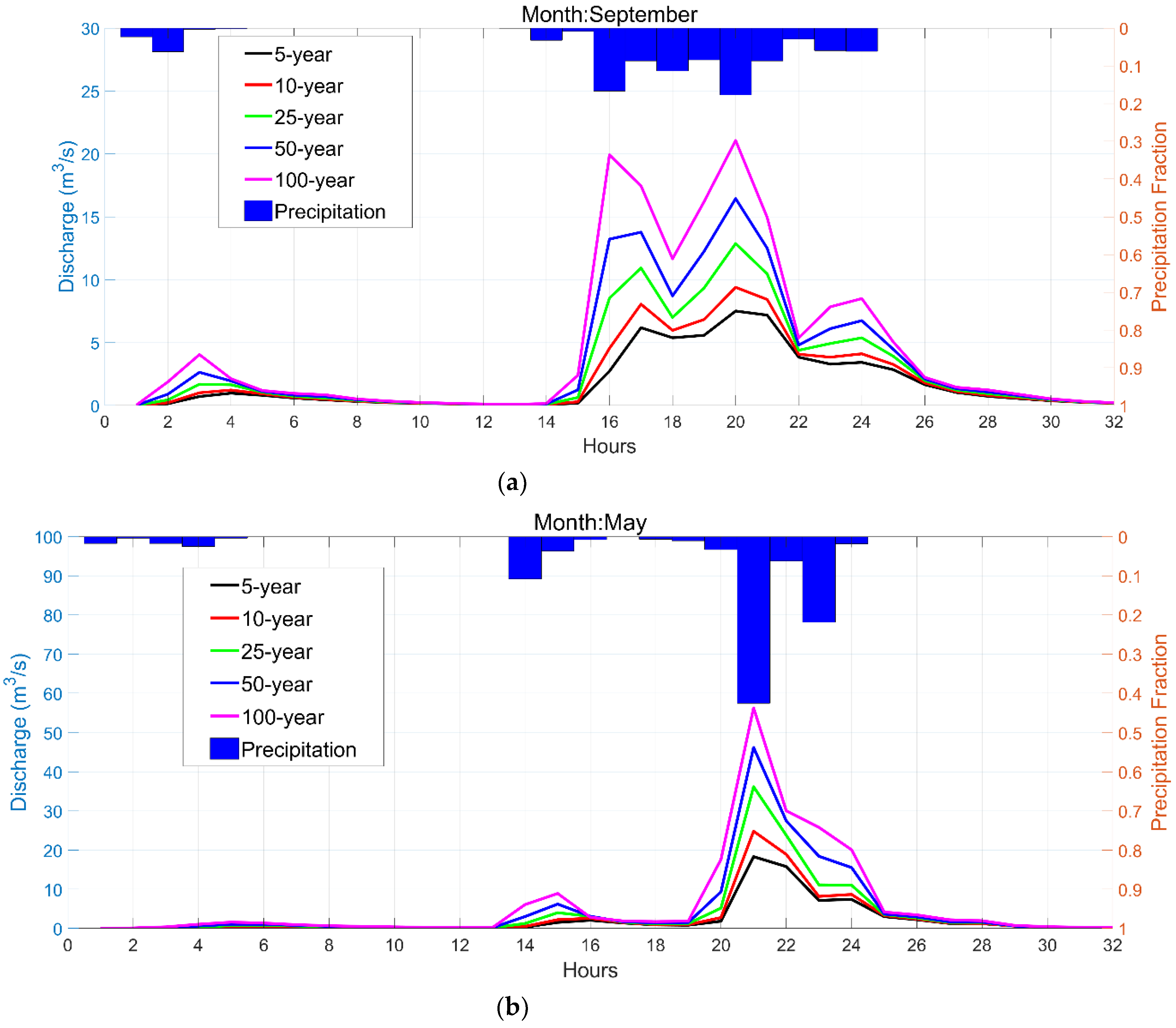
3.2. Flow Discharge Analysis
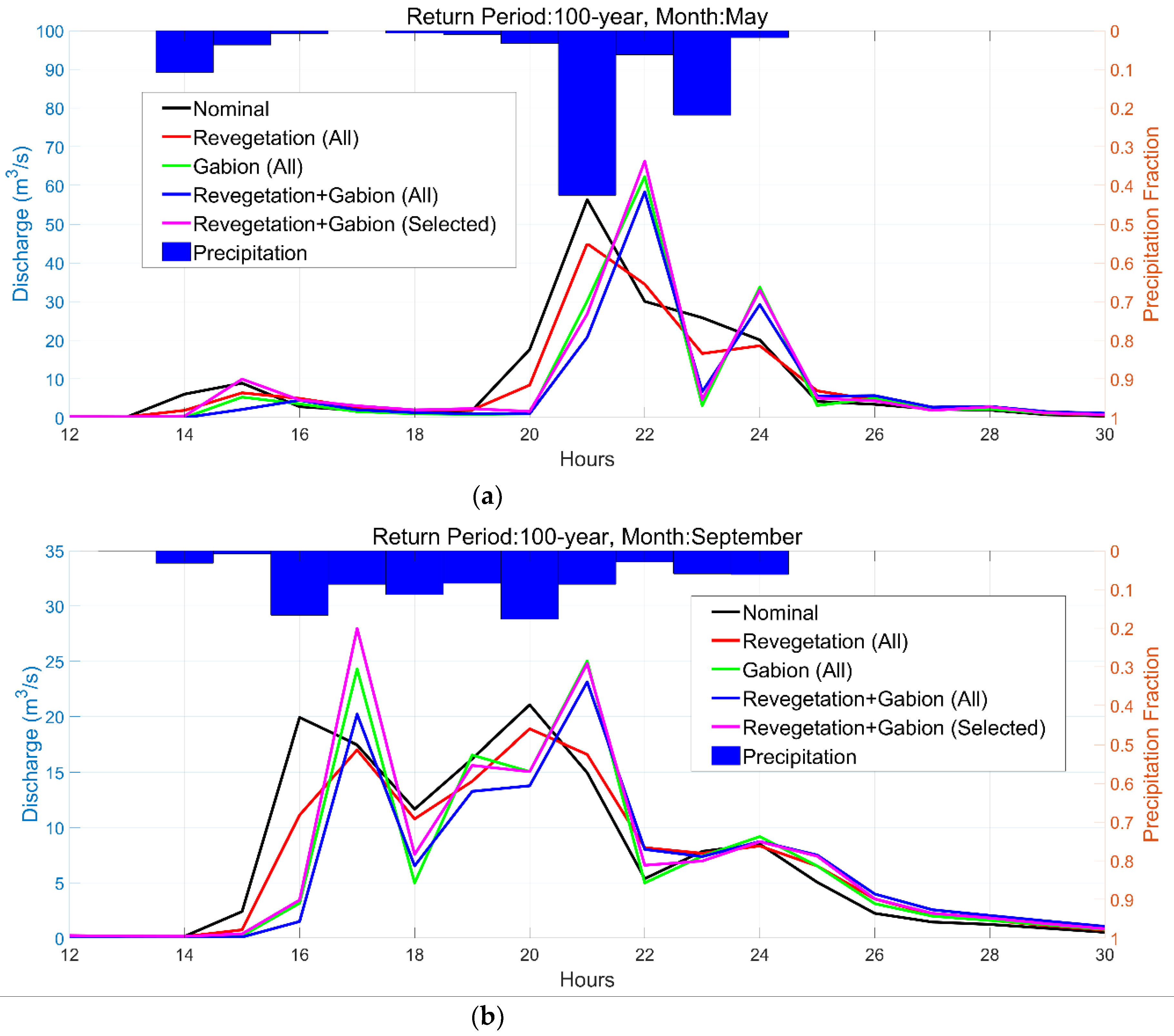
3.3. Impact of the Mitigation Plans for Flood Control
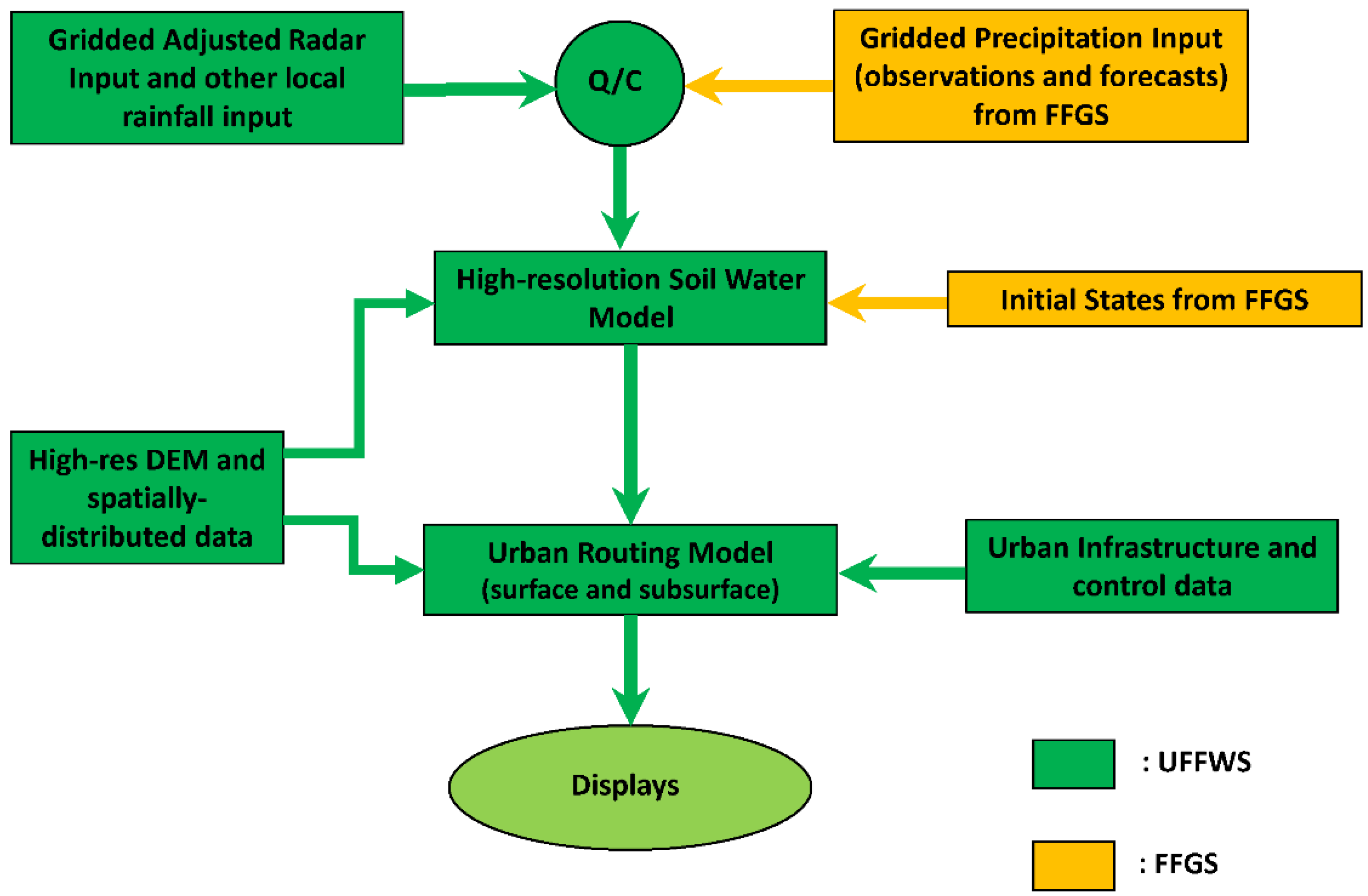
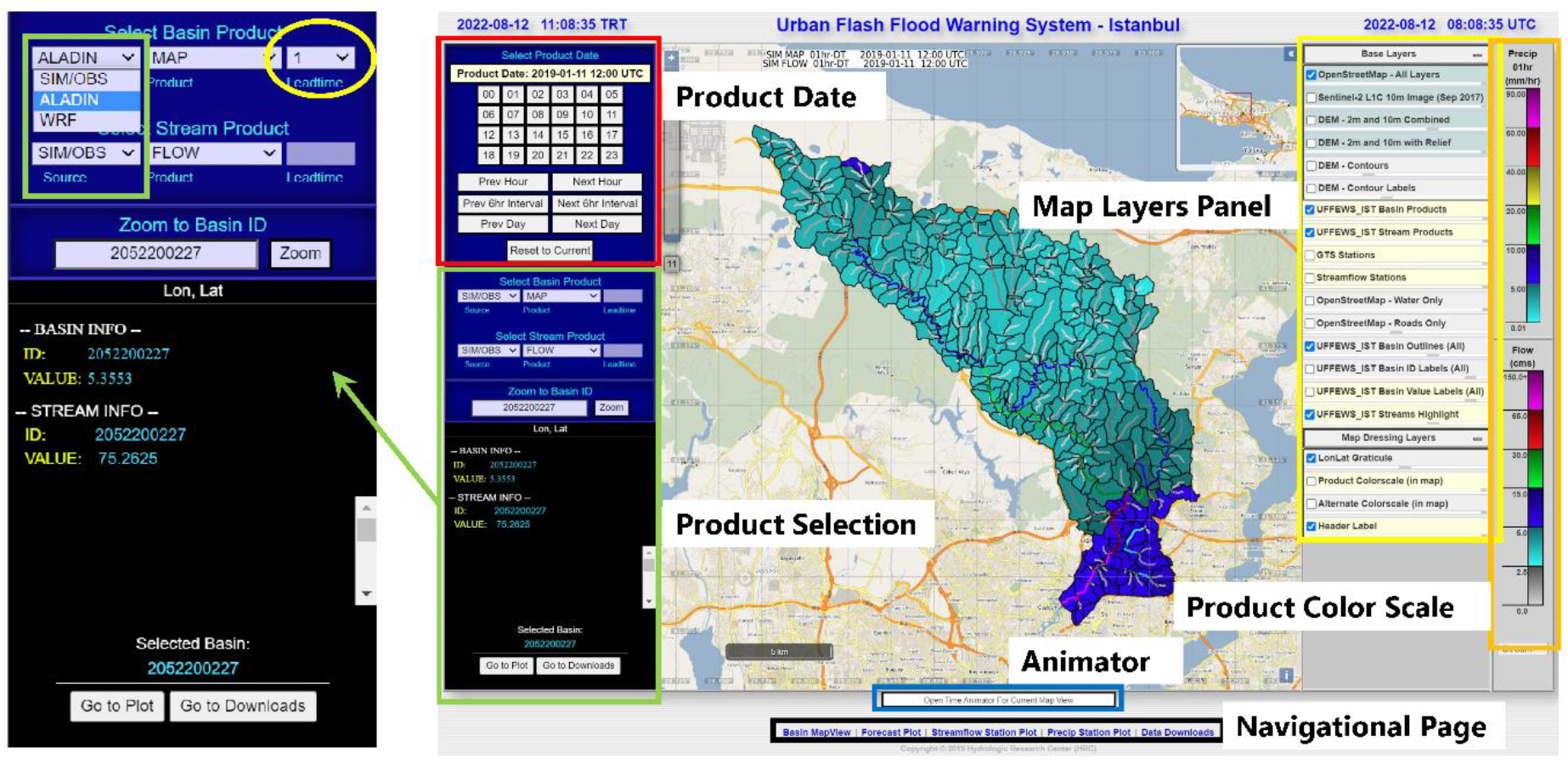
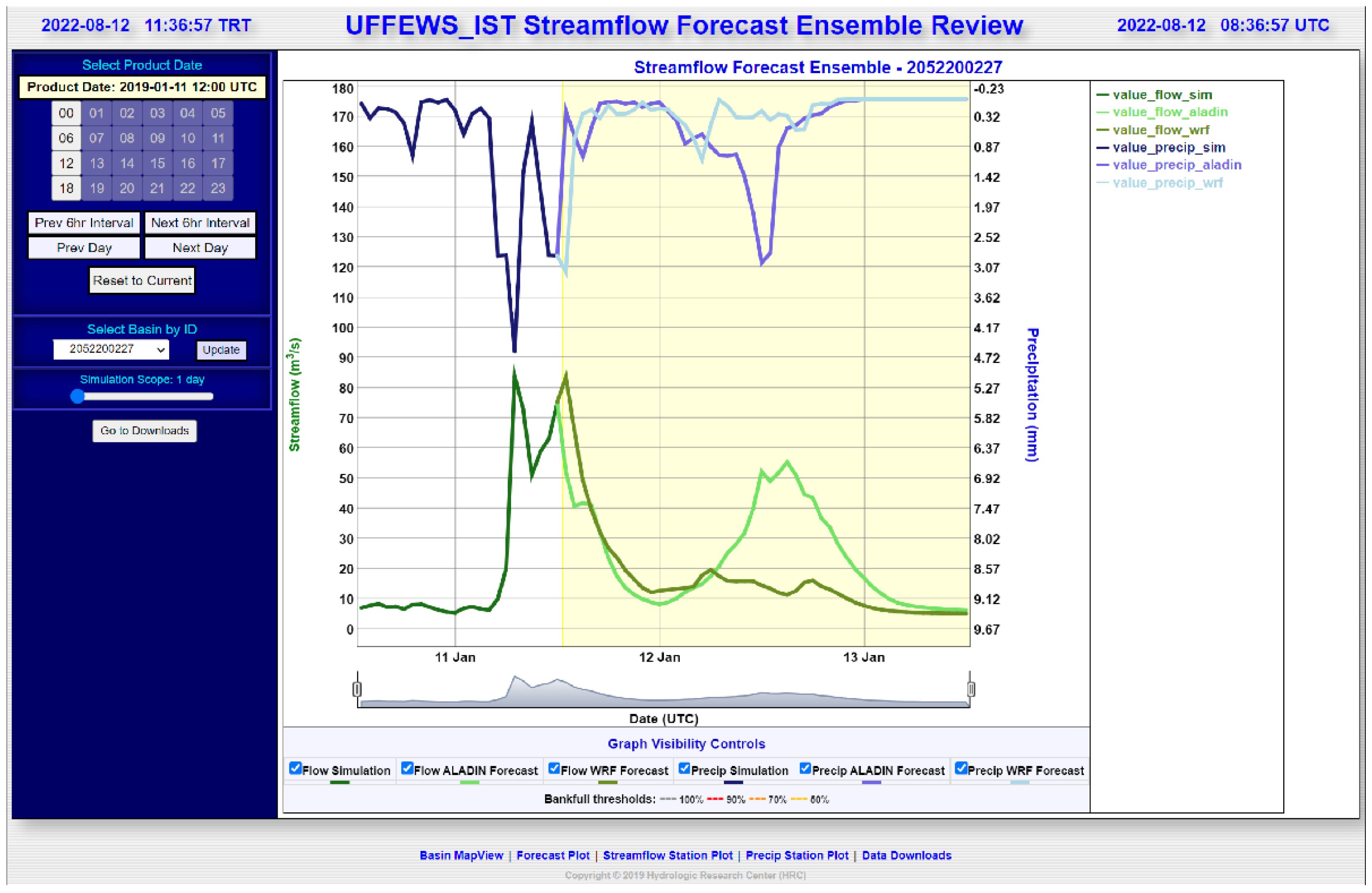
4. Operational Urban Flash Flood Warning System (UFFWS)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bennet, G.; Carroll, N. Gaining Depth: State of Watershed Investment. 2014. Available online: www.ecosystemmarketplace.com/reports/sowi2014 (accessed on 9 August 2022).
- Johnson, N.; Ravnborg, H.M.; Westermann, O.; Probst, K. User participation in watershed management and research. Water Policy 2002, 3, 507–520. [Google Scholar] [CrossRef]
- Hooke, J.M. Geomorphological impacts of an extreme flood in SE Spain. Geomorphology 2016, 263, 19–38. [Google Scholar] [CrossRef]
- Diakakis, M.; Andreadakis, E.; Nikolopoulos, E.; Spyrou, N.; Gogou, M.; Deligiannakis, G.; Katsetsiadou, N.; Antoniadis, Z.; Melaki, M.; Georgakopoulos, A.; et al. An integrated approach of ground and aerial observations in flash flood disaster investigations. The case of the 2017 Mandra flash flood in Greece. Int. J. Disaster Risk Reduct. 2019, 33, 290–309. [Google Scholar] [CrossRef]
- Khajehei, S.; Ahmadalipour, A.; Shao, W.; Moradkhani, H. A Place-based Assessment of Flash Flood Hazard and Vulnerability in the Contiguous United States. Sci. Rep. 2020, 10, 448. [Google Scholar] [CrossRef]
- NWS. NWS Preliminary US Flood Fatality Statistics. 2022. Available online: http://www.weather.gov/arx/usflood (accessed on 9 August 2022).
- Colombo, A.G.; Hervas, J.; Arellano, A.L.V. Guidelines on Flash Floods Prevention and Mitigation; NEDIES: Ispra, Italy, 2002; Available online: https://reliefweb.int/sites/reliefweb.int/files/resources/6617C1258AB7B300C1256CA700556650-ec-flash-2002.pdf (accessed on 9 August 2022). [CrossRef]
- Lee, J.G.; Selvakumar, A.; Alvi, K.; Riverson, J.; Zhen, J.X.; Shoemaker, L.; Lai, F. A watershed-scale design optimization model for stormwater best management practices. Environ. Model. Softw. 2012, 37, 6–18. [Google Scholar] [CrossRef]
- Yazdi, J.; Moghaddam, M.S.; Saghafian, B. Optimal Design of Check Dams in Mountainous Watersheds for Flood Mitigation. Water Resour. Manag. 2018, 32, 4793–4811. [Google Scholar] [CrossRef]
- Abdel-Fattah, M.; Kantoush, S.A.; Saber, M.; Sumi, T. Evaluation of Structural Measures for Flash Flood Mitigation in Wadi Abadi Region of Egypt. J. Hydrol. Eng. 2021, 26, 04020062. [Google Scholar] [CrossRef]
- Julien, P.; Ab Ghani, A.; Zakaria, N.; Abdulla, R.; Chang, C.K. Case study: Flood mitigation of the Muda river, Malaysia. J. Hydraul. Eng. 2010, 36, 251–261. [Google Scholar] [CrossRef]
- Kantoush, S.A.; Saber, M.; Abdel-Fattah, M.; Sumi, T. Integrated Strategies for the Management of Wadi Flash Floods in the Middle East and North Africa (MENA) Arid Zones: The ISFF Project. In Wadi Flash Floods; Natural Disaster Science and Mitigation Engineering: DPRI, reports; Sumi, T., Kantoush, S.A., Saber, M., Eds.; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Vinet, F.; Lumbroso, D.; Defossez, S.; Boissier, L. A comparative analysis of the loss of life during two recent floods in France: The sea surge caused by the storm Xynthia and the flash flood in Var. Nat. Hazards 2012, 61, 1179–1201. [Google Scholar] [CrossRef]
- Yin, J.; Yu, D.; Yin, Z.; Liu, M.; He, Q. Evaluating the impact and risk of pluvial flash flood on intra-urban road network: A case study in the city center of Shanghai, China. J. Hydrol. 2016, 537, 138–145. [Google Scholar] [CrossRef]
- NWS, Flash Flooding Definition. 2016. Available online: https://www.weather.gov/phi/FlashFloodingDefinition (accessed on 9 August 2022).
- Costa, J.E. Multiple flow processes accompanying a dam-break flood in a small upland watershed, Centralia, Washington. USGS Water-Resour. Investig. Rep. 1994, 94, 4026. [Google Scholar]
- Yang, Q.; Guan, M.; Peng, Y.; Chen, H. Numerical investigation of flash flood dynamics due to cascading failures of natural landslide dams. Eng. Geol. 2020, 276, 105765. [Google Scholar] [CrossRef]
- Chen, J.; Liu, W.; Zhao, W.; Jiang, T.; Zhu, Z.; Chen, X. Magnitude amplification of flash floods caused by large woody in Keze gully in Jiuzhaigou National Park, China. Geomat. Nat. Hazards Risk 2021, 12, 2277–2299. [Google Scholar] [CrossRef]
- Zhong, M.; Jiang, T.; Li, K.; Lu, Q.; Wang, J.; Zhu, J. Multiple environmental factors analysis of flash flood risk in Upper Hanjiang River, southern China. Environ. Sci. Pollut. Res. 2020, 27, 37218–37228. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Huang, Y. Why Flash Floods Occur Differently across Regions? A Spatial Analysis of China. Water 2020, 12, 3344. [Google Scholar] [CrossRef]
- Ma, B.; Wu, Z.; Wang, H.; Guo, Y. Study on the Classification of Urban Waterlogging Rainstorms and Rainfall Thresholds in Cities Lacking Actual Data. Water 2020, 12, 3328. [Google Scholar] [CrossRef]
- Saber, M.; Abdrabo, K.I.; Habiba, O.M.; Kantosh, S.A.; Sumi, T. Impacts of Triple Factors on Flash Flood Vulnerability in Egypt: Urban Growth, Extreme Climate, and Mismanagement. Geosciences 2020, 10, 24. [Google Scholar] [CrossRef]
- Li, G.-F.; Xiang, X.-Y.; Tong, Y.-Y.; Wang, H.-M. Impact assessment of urbanization on flood risk in the Yangtze River Delta. Stoch. Environ. Res. Risk Assess. 2013, 27, 1683–1693. [Google Scholar] [CrossRef]
- Miller, J.D.; Hess, T. Urbanisation impacts on storm runoff along a rural-urban gradient. J. Hydrol. 2017, 552, 474–489. [Google Scholar] [CrossRef]
- Abebe, Y.; Kabir, G.; Tesfamariam, S. Assessing urban areas vulnerability to pluvial flooding using GIS applications and Bayesian Belief Network model. J. Clean. Prod. 2017, 174, 1629–1641. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate, Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar]
- Gippel, C.J. Edward River: Hydraulic Effect of Snags and Management Options; to NSW Department of Land and Water Conservation, Albury, NSW; Fluvial Systems Pty Ltd, Vic.: Melbourne, Australia, 1999. [Google Scholar]
- Wolff, C.G.; Burges, S.J. An analysis of the influence of river channel properties on flood frequency. J. Hydrol. 1994, 153, 317–337. [Google Scholar] [CrossRef]
- Woltemade, C.J.; Potter, K.W. A watershed modeling analysis of fluvial geomorphologic influences on flood peak attenuation. Water Resour. Res. 1994, 30, 1933–1942. [Google Scholar]
- Rutherfurd, I.D.; Hoang, T.; Prosser, I.; Abernethy, B.; Jayasuriya, N. The impact of gully networks on the time-to-peak and size of flood hydrographs. In 23rd Hydrology and Water Resources Symposium; Institution of Engineers: Hobart, Australia, 1996. [Google Scholar]
- Tzioutzios, C.; Kastridis, A. Multi-Criteria Evaluation (MCE) Method for the Management of Woodland Plantations in Floodplain Areas. ISPRS Int. J. Geo-Inf. 2020, 9, 725. [Google Scholar] [CrossRef]
- Riis, T.; Kelly-Quinn, M.; Aguiar, F.; Manolaki, M.; Bruno, D.; Bejarano, M.; Clerici, N.; Rosário Fernandes, M.; Franco, J.; Pettit, N.; et al. Global Overview of Ecosystem Services Provided by Riparian Vegetation. BioScience 2020, 70, 501–514. [Google Scholar] [CrossRef]
- Anderson, B.G.; Rutherford, I.D.; Western, A.W. An analysis of the influence of riparian vegetation on the propagation of flood waves. Env. Model. Softw. 2006, 21, 1290–1296. [Google Scholar] [CrossRef]
- Marsh, W.M. Landscape Planning: Environmental Applications, 5th ed.; John Wiley & Sons, Inc.: Danvers, MA, USA, 2010; pp. 267–268. [Google Scholar]
- Posner, A.J.; Georgakakos, K.P. Community Scale Flash Flood Mitigation, Reference Guide to Optimizing Project Design. In HRC Reference Guide; Hydrologic Research Center: San Diego, CA, USA, 2016; p. 29. [Google Scholar]
- Posner, A.J.; Georgakakos, K.P. Quantifying the impact of community-scale flood mitigation. Int. J. Disaster Risk Reduct. 2017, 24, 189–208. [Google Scholar] [CrossRef]
- USGS. Flood-Hazard Mapping in Honduras in Response to Hurricane Mitch; Water-Resources Investigations Report 01-4277; USGS: Tacoma, WA, USA, 2002. [Google Scholar]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- Murphy, M.J.; Georgakakos, K.P.; Shamir, E. Climatological analysis of December rainfall in the Panama Canal Watershed. Int. J. Climatol. 2014, 34, 403–415. [Google Scholar] [CrossRef]
- Shamir, E.; Georgakakos, K.P.; Murphy, M.J. Frequency analysis of the 7–8 December 2010 extreme precipitation in the Panama Canal Watershed. J. Hydrol. 2013, 480, 136–148. [Google Scholar] [CrossRef]
- Carpenter, T.M.; Georgakakos, K.P. Continuous streamflow simulation with the HRCDHM distributed hydrologic model. J. Hydrol. 2004, 298, 61–79. [Google Scholar] [CrossRef]
- Reed, S.; Koren, V.; Smith, M.; Zhang, Z.; Moreda, F.; Seo, D.-J.; Participants, A.D. Overall distributed model intercomparison project results. J. Hydrol. 2004, 298, 27–60. [Google Scholar] [CrossRef]
- Georgakakos, K. A Generalized Stochastic Hydrometeorological Model for Flood and Flash-Flood Forecasting: 1. Formulation. Water Resour. Res. 1986, 22, 2083–2095. [Google Scholar] [CrossRef]
- Kitanidis, P.K.; Bras, R.L. Real-time forecasting with a conceptual hydrologic model, 1, Analysis of uncertainty. Water Resour. Res. 1980, 6, 1025–1033. [Google Scholar] [CrossRef]
- FAO. Harmonized World Soils Database, Version 1.2. Food and Agriculture Organization of the United Nations, Rome, Italy, and International Institute for Applied Systems Analysis, Laxenburg, Austria. 2008. Available online: http://www.fao.org/soils-portal/soil-survey/soil-maps-and-databases/harmonized-world-soil-database-v12/en (accessed on 9 August 2022).
- Georgakakos, K.P. Overview of the Global Flash Flood Guidance system and its application worldwide. WMO Bull. 2018, 67, 41–46. [Google Scholar]
- Borivoj, T.; Gibbon, M.I.T. Operational regional flash flood guidance systems. WMO Bull. 2018, 67, 47–50. [Google Scholar]
- Shamir, E.; Georgakakos, K.P.; Spencer, C.; Modrick, T.M.; Murphy, M.J.; Jubach, R. Evaluation of real time flash flood forecasts for Haiti during the passage of Hurricane Tomas, November 4–6, 2010. Nat. Hazards 2013, 67, 459–482. [Google Scholar] [CrossRef]
- Georgakakos, K.P.; Modrick, T.M.; Shamir, E.; Campbell, R.; Cheng, Z.; Jubach, R.; Sperfslage, J.A.; Spencer, C.R.; Banks, R. The Flash Flood Guidance System Implementation Worldwide: A Successful Multidecadal Research-to-Operations Effort. Bull. Am. Meteorol. Soc. 2022, 103, E665–E679. [Google Scholar] [CrossRef]
- Fread, D.L. Channel Routing, in Hydrological Forecasting; Anderson, M.G., Burt, T.P., Eds.; John Wiley: New York, NY, USA, 1985; pp. 437–503. [Google Scholar]
- Georgakakos, A.P.; Georgakakos, K.P.; Baltas, E.A. A state-space model for hydrologic river routing. Water Resour. Res. 1990, 26, 827–838. [Google Scholar]
- Brunner, G.W.; Gorbrecht, J. A Muskingum-Cunge Channel Flow Routing Method for Drainage Networks. ASCE J. Hydraul. 1991, 117, 30. [Google Scholar]
- Yoo, C.; Lee, J.; Lee, M. Parameter Estimation of the Muskingum Channel Flood-Routing Model in Ungauged Channel Reaches. J. Hydrol. Eng. 2017, 22, 05017005. [Google Scholar] [CrossRef]
- Barati, R.; Badfar, M.; Azizyan, G.; Akbari, G.H. Discussion of “Parameter Estimation of Extended Nonlinear Muskingum Models with the Weed Optimization Algorithm” by Farzan Hamedi, Omid Bozorg-Haddad, Maryam Pazoki, Hamid-Reza Asgari, Mehran Parsa and Hugo A. Loáiciga. J. Irrig. Drain. Eng. 2018, 144, 07017021. [Google Scholar] [CrossRef]
- Ehteram, M.; Binti Othman, F.; Mundher Yaseen, Z.; Abdulmohsin Afan, H.; Falah Allawi, M.; Abdul Malek, M.B.; Najah Ahmed, A.; Shahid, S.; Singh, V.P.; El-Shafie, A. Improving the Muskingum Flood Routing Method Using a Hybrid of Particle Swarm Optimization and Bat Algorithm. Water 2018, 10, 807. [Google Scholar] [CrossRef]
- Modrick, T.M.; Georgakakos, K.P. Regional bankfull geometry application for southern California mountain streams and hydrologic applications. Geomorphology 2014, 221, 242–260. [Google Scholar] [CrossRef]
- Cheng, Z.; Georgakakos, K.P. Trip report for HRC travel to Tegucigalpa with a list of pending data (3–7 July 2017); HRC Technical Note No. 93; Hydrologic Research Center: San Diego, California, USA, 2017; p. 35. [Google Scholar]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- US Department of Transportation. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; USDoT Report No FHWA-T8-84-204; US Department of Transportation: McLean, VA, USA, 1984; p. 62. [Google Scholar]
- Phillips, J.V.; Tadayon, S. Selection of Manning’s Roughness Coefficient for Natural and Constructed Vegetated and Non-Vegetated Channels, and Vegetation Maintenance Plan Guidelines for Vegetated Channels in Central Arizona; US Geological Survey Scientific Investigations Report 2006-5108; USGS: Reston, Virginia, USA, 2006; p. 41. [Google Scholar]
- Mishra, A.; Froebrich, J.; Gassman, P.W. Gassman, Evaluation of the SWAT model for assessing sediment control structures in a small watershed in India. Trans. Am. Soc. Agric. Biol. Eng. 2007, 50, 469–477. [Google Scholar]
- Tague, C.L.; Band, L.E. Evaluating explicit and implicit routing for watershed hydro-ecological models of forest hydrology at the small catchment scale. Hydrol. Process. 2001, 15, 1415–1439. [Google Scholar] [CrossRef]
- Gaume, E.; Bain, V.; Bernardara, P.; Newinger, O.; Barbuc, M.; Bateman, A.; Blaškovičová, L.; Blöschl, G.; Borga, M.; Dumitrescu, A.; et al. A compilation of data on European flash floods. J. Hydrol. 2009, 367, 70–78. [Google Scholar] [CrossRef]
- Kastridis, A.; Theodosiou, G.; Fotiadis, G. Investigation of Flood Management and Mitigation Measures in Ungauged NATURA Protected Watersheds. Hydrology 2021, 8, 170. [Google Scholar] [CrossRef]
- Marchi, L.; Borga, M.; Preciso, E.; Gaume, E. Characterisation of selected extreme flash floods in Europe and implications for flood risk management. J. Hydrol. 2010, 394, 118–133. [Google Scholar] [CrossRef]
- Paola, B.L. When streams collide. Nature 1997, 387, 232–233. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsoe, J. The Mechanics of Scour in the Marine Environment; World Scientific: Singapore, 2002. [Google Scholar]
- Yu, D.; Lane, S.N. Urban fluvial flood modelling using a two-dimensional diffusion wave treatment, part 1: Mesh resolution effects. Hydrol. Process. 2006, 20, 1541–1565. [Google Scholar] [CrossRef]
- Yu, D.; Lane, S.N. Urban fluvial flood modelling using a two-dimensional diffusion wave treatment, part 2: Development of a sub grid-scale treatment. Hydrol. Process. 2006, 20, 1567–1583. [Google Scholar] [CrossRef]
- Brown, I. Modelling future landscape change on coastal floodplains using a rule-based GIS. Environ. Modell. Softw. 2006, 21, 1479–1490. [Google Scholar] [CrossRef]






| UZTWM (mm) | UZFWM (mm) | LZTWM (mm) | LZFPM (mm) | LZFSM (mm) | UZK (Fraction) | LZPK (Fraction) | LZSK (Fraction) | ZPERC | REXP | PFREE (Fraction) | SIDE (Fraction) | ADIMP (Fraction) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9 | 5.4 | 36 | 15.22 | 6.38 | 0.145 | 0.000651 | 0.0453 | 85 | 2.5 | 0.295 | 0 | 0.05 |
| Length of Reservoir (L) | Width of Reservoir (W) | Width of Weir (Ww) | Height of Weir (Hw) | Total Height (H) |
|---|---|---|---|---|
| 50 | 10 | 1 | 2 | 3 |
| Month | α (1/d) | β (mm/d) |
|---|---|---|
| JAN | 0.002029 | −2.041 |
| FEB | 0.001084 | −1.122 |
| MAR | 0.001389 | −0.9467 |
| APR | 0.0008147 | −0.9621 |
| MAY | 0.003453 | 1.013 |
| JUN | 0.007451 | −3.268 |
| JUL | 0.003383 | −2.179 |
| AUG | 0.002351 | 2.348 |
| SEP | 0.005956 | −0.5184 |
| OCT | 0.007418 | −2.796 |
| NOV | 0.002696 | −1.995 |
| DEC | 0.001937 | −1.505 |
| 5-Year | 10-Year | 25-Year | 50-Year | 100-Year |
|---|---|---|---|---|
| 83.64 | 99.98 | 129.46 | 160.21 | 201.08 |
| Nominal | Revegetation (All) | Gabion (All) | Revegetation + Gabion (All) | Revegetation + Gabion (Selected) |
|---|---|---|---|---|
| 27.27 | 26.25 | 27.75 | 27.43 | 28.18 |
| 5-Year | 10-Year | 25-Year | 50-Year | 100-Year | |
|---|---|---|---|---|---|
| May | 18.3 | 24.8 | 36.2 | 46.2 | 56.3 |
| September | 6.19 | 8.05 | 10.9 | 13.2 | 19.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Z.; Georgakakos, K.P.; Spencer, C.R.; Banks, R. Numerical Modeling of Flash Flood Risk Mitigation and Operational Warning in Urban Areas. Water 2022, 14, 2494. https://doi.org/10.3390/w14162494
Cheng Z, Georgakakos KP, Spencer CR, Banks R. Numerical Modeling of Flash Flood Risk Mitigation and Operational Warning in Urban Areas. Water. 2022; 14(16):2494. https://doi.org/10.3390/w14162494
Chicago/Turabian StyleCheng, Zhengyang, Konstantine P. Georgakakos, Cristopher R. Spencer, and Randall Banks. 2022. "Numerical Modeling of Flash Flood Risk Mitigation and Operational Warning in Urban Areas" Water 14, no. 16: 2494. https://doi.org/10.3390/w14162494






