Reservoir Operation Management with New Multi-Objective (MOEPO) and Metaheuristic (EPO) Algorithms
Abstract
:1. Introduction
- Investigating the reservoir Performance Indexes through the change of operation policies (HR, SOP, and multi-objective optimization)
- Comparing operation policies generated by GEP logical and arithmetic operators
- Developing appropriate policies for the future period.
2. Materials and Methods
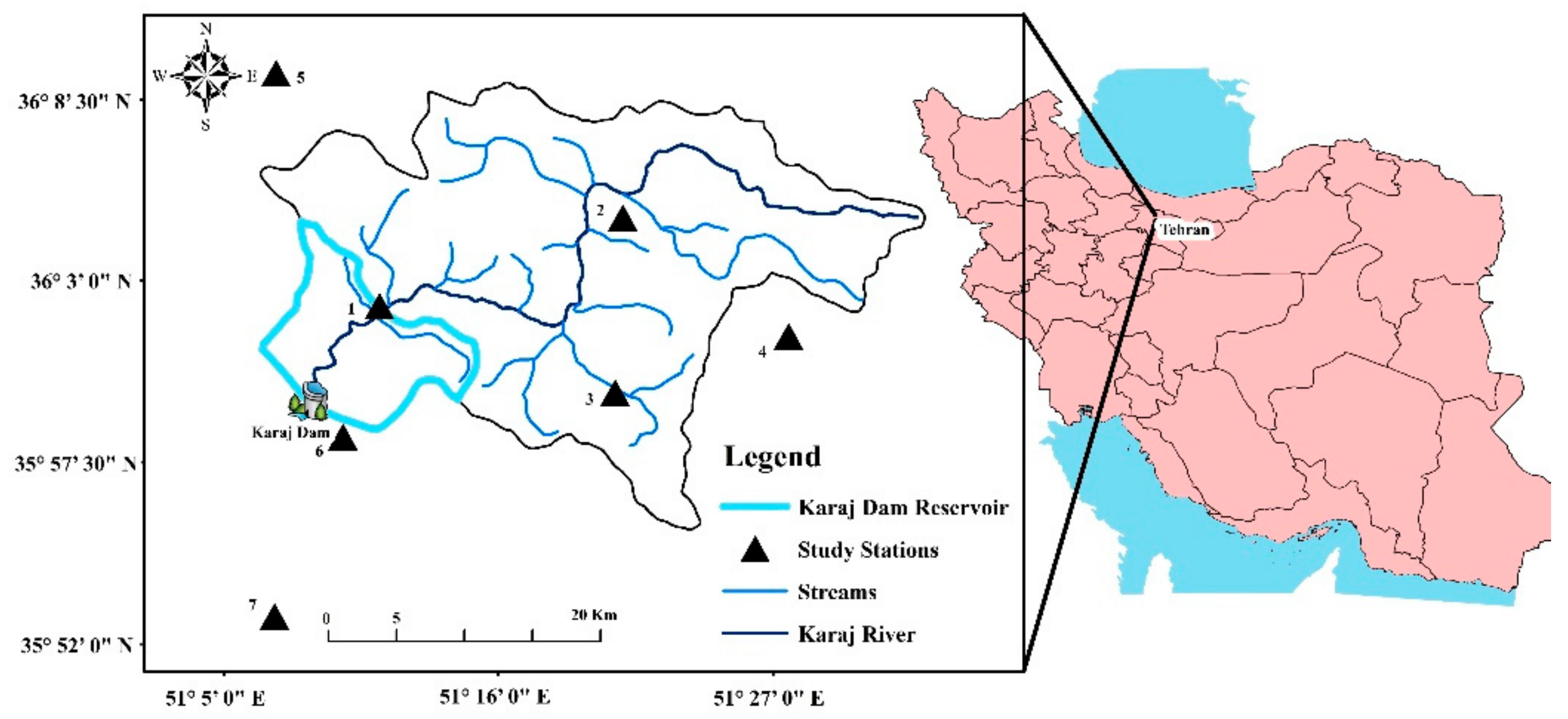
2.1. Study Area and Input Data
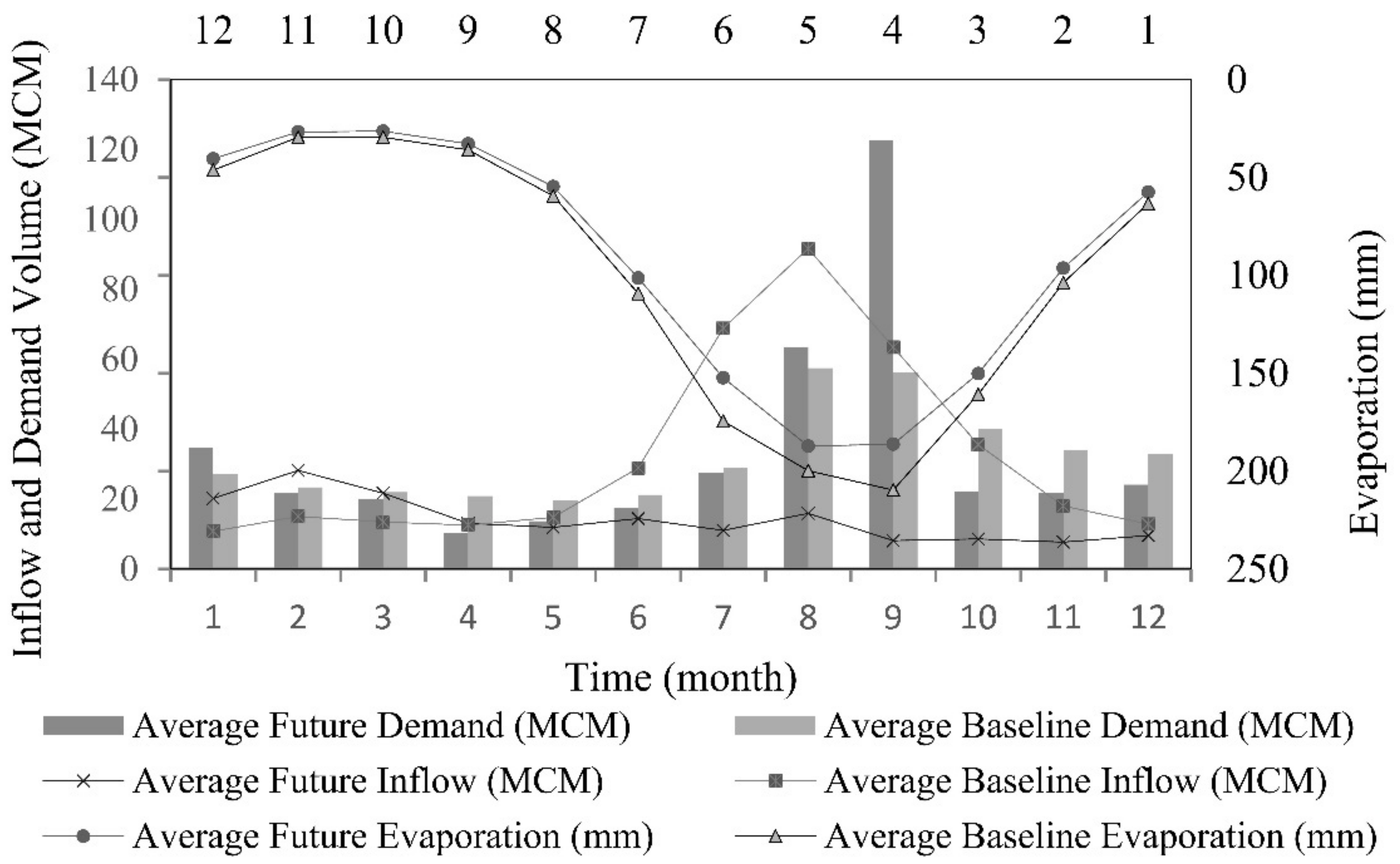
2.1.1. Baseline and Future Temperature and Precipitation
2.1.2. Simulate Inflow to Dam Reservoir
2.1.3. Future Agriculture and Domestic Demands
2.2. Research Models
2.2.1. Reservoir Operation Using Standard Operation Policy (SOP)
- MAE: mean absolute errors as objective function
- RSPt: total demand per month
- rspt: total output based on SOP (observational) in t period.
2.2.2. Reservoir Operation Using Hedging Rule (HR)
2.2.3. Multi-Objective Optimization
2.2.4. Gene Expression Programming
2.2.5. Emperor Penguin Optimization (EPO) and Multi-Objective Emperor Penguin Optimization (MOEPO)
2.2.6. Reservoir Operation Rule Generation Using EPO, MOEPO Algorithms and GEP
- The first scenario, development of baseline rules based on the volume of available water in the reservoir using EPOba in the baseline condition.
- The second scenario, development of baseline rules based on the volume of available water in the reservoir using the EPOad in the baseline condition.
- The third scenario, development of future rules based on the volume of available water in the reservoir using the EPOba under future condition.
- The fourth scenario, development of future rules based on the volume of available water in the reservoir using the EPOad under future condition.
2.3. Vulnerability and Reliability Indexes
- Dt: Demand volume in the t period
- Dmax: Maximum demand in the under-review period.
- Ret: the released volume from the reservoir in the t period.
3. Results
3.1. Integrate SOP and HR Using EPOad and EPOba
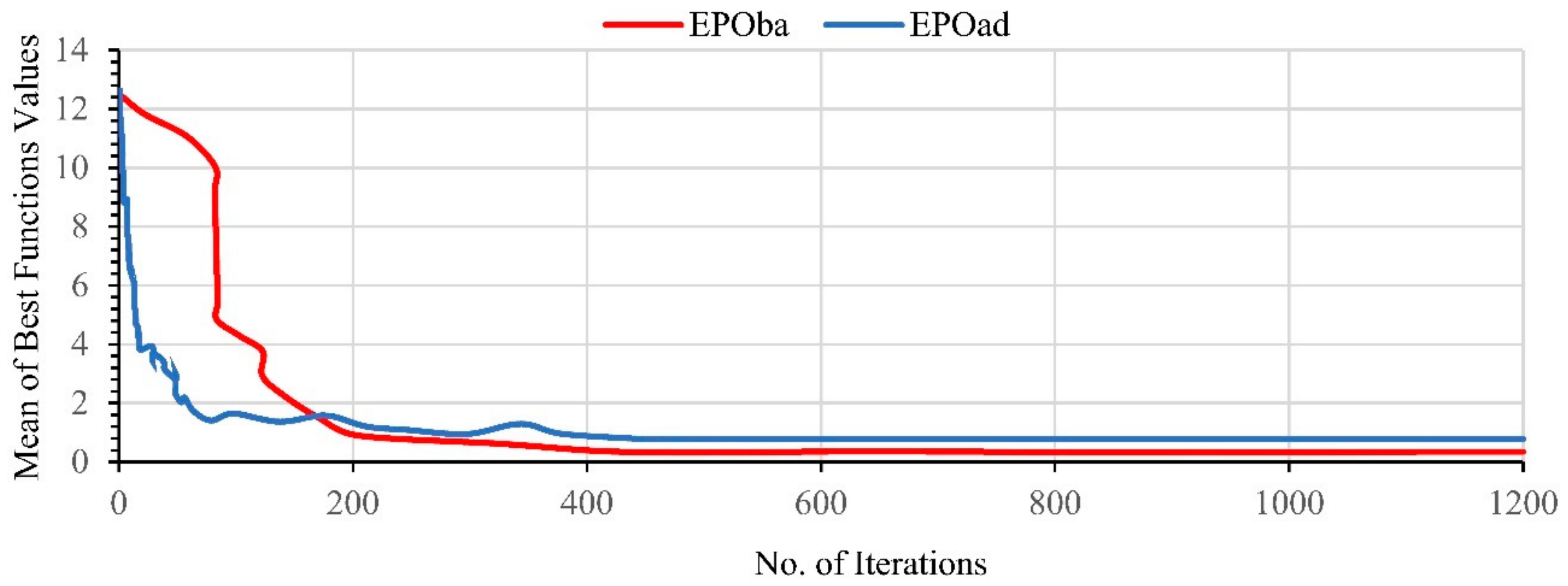
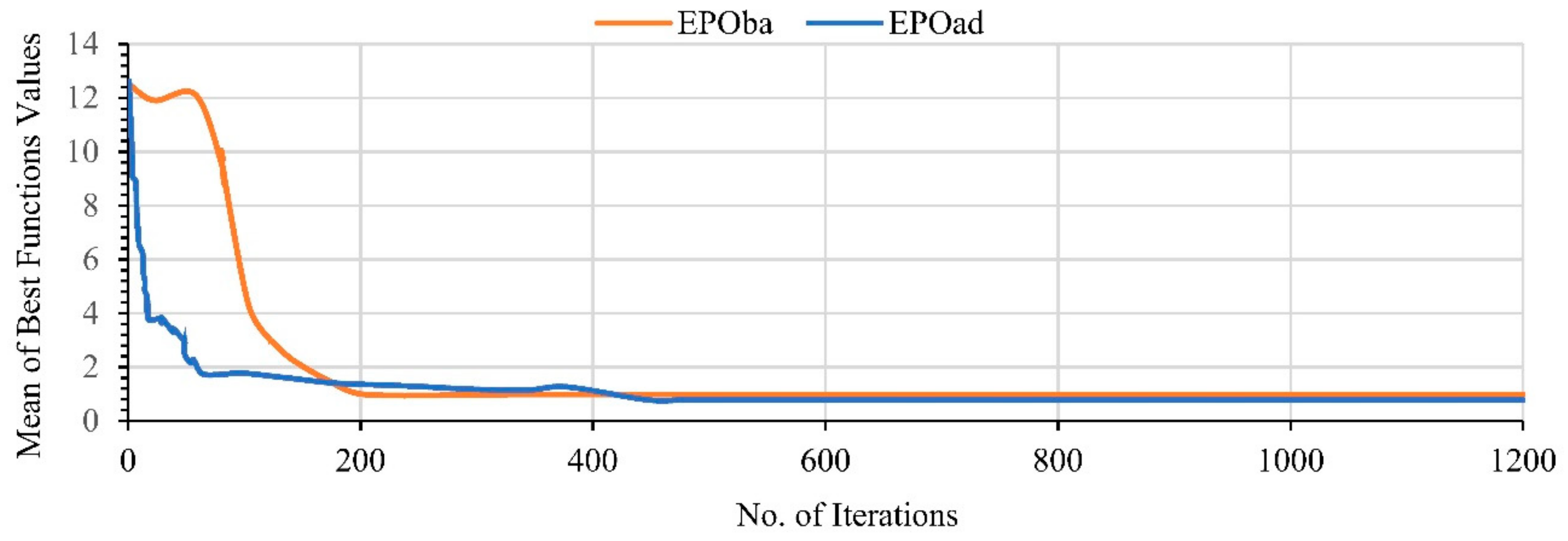
3.1.1. Validation of the SOP Simulation with EPO
- RSPt: Total released water based on Reservoir System Policy in the t period
- AWt: Available water in the dam reservoir (in the t period).
3.1.2. Validation of the HR Simulation with EPO
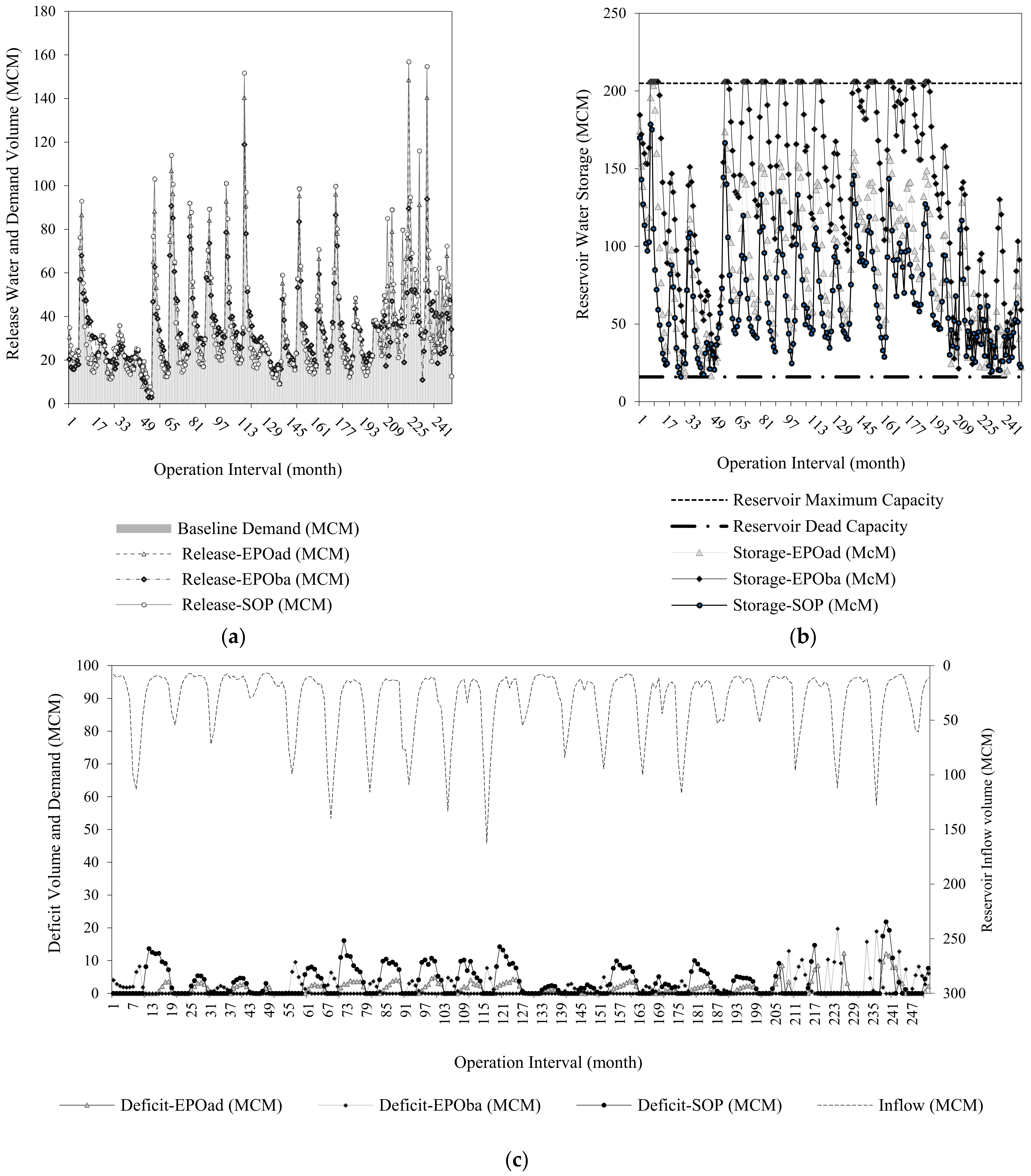
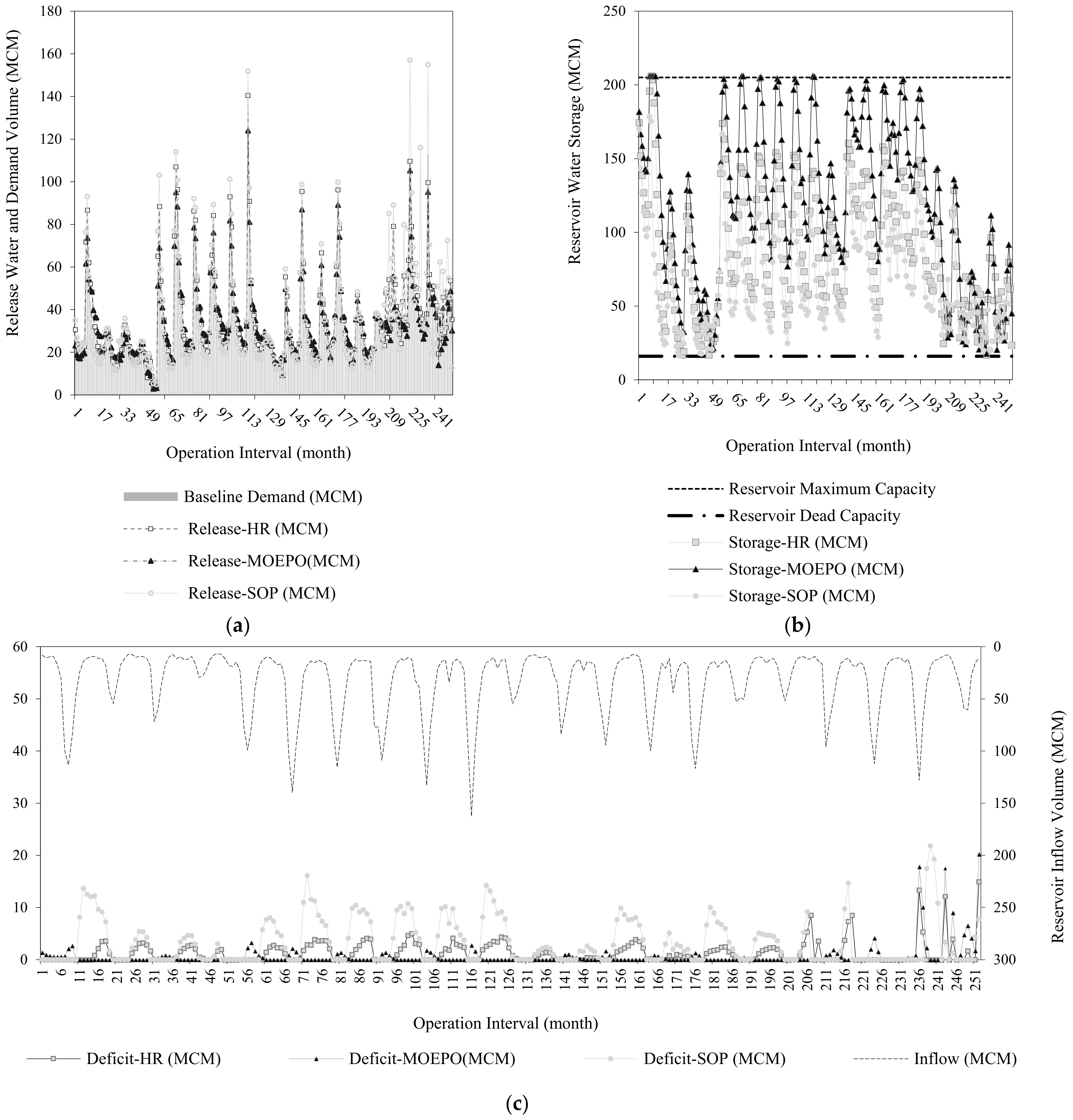
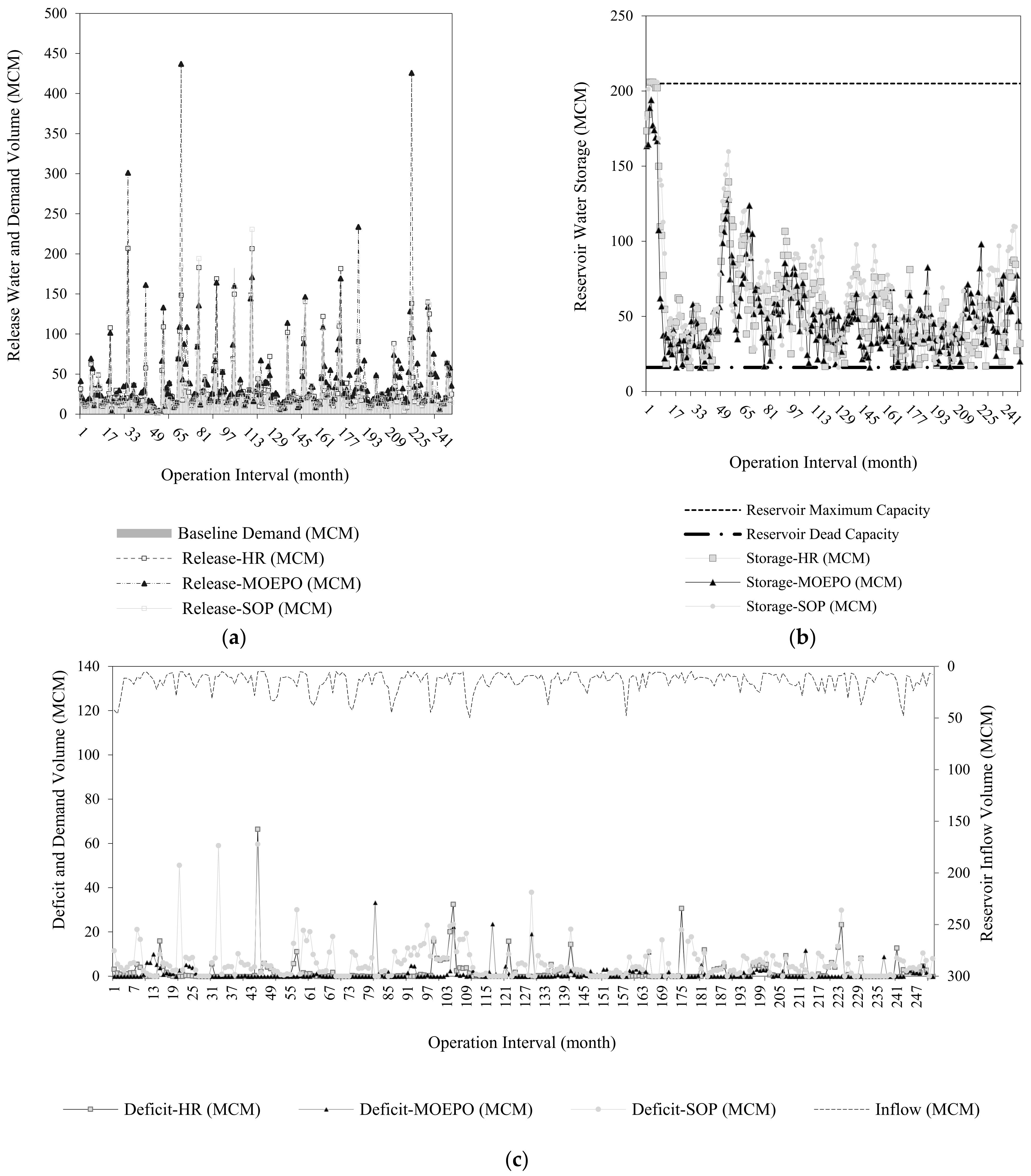
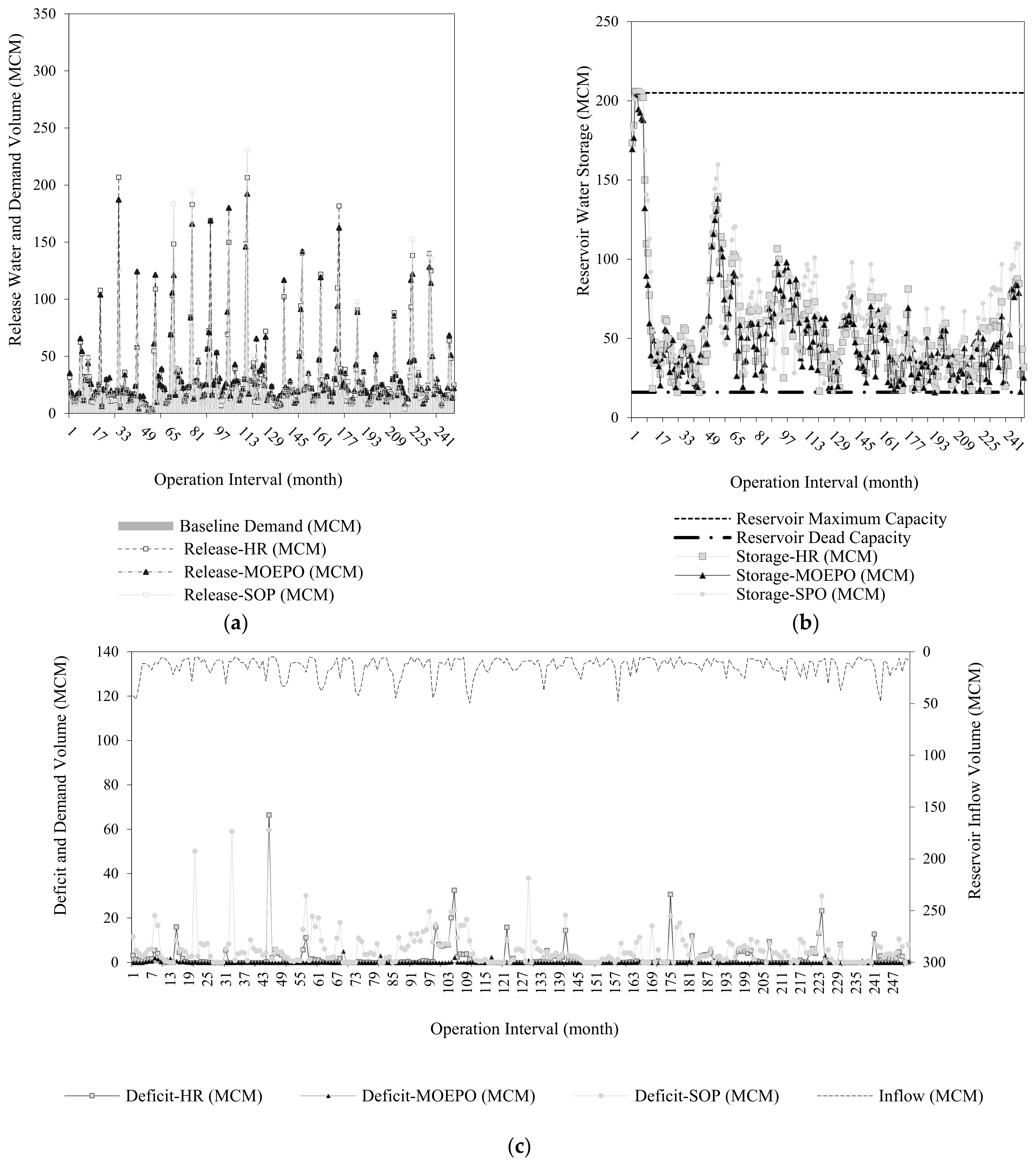
3.1.3. Comparison of the Results of HR and SOP in Extracting Allocation Rules in Four Scenarios
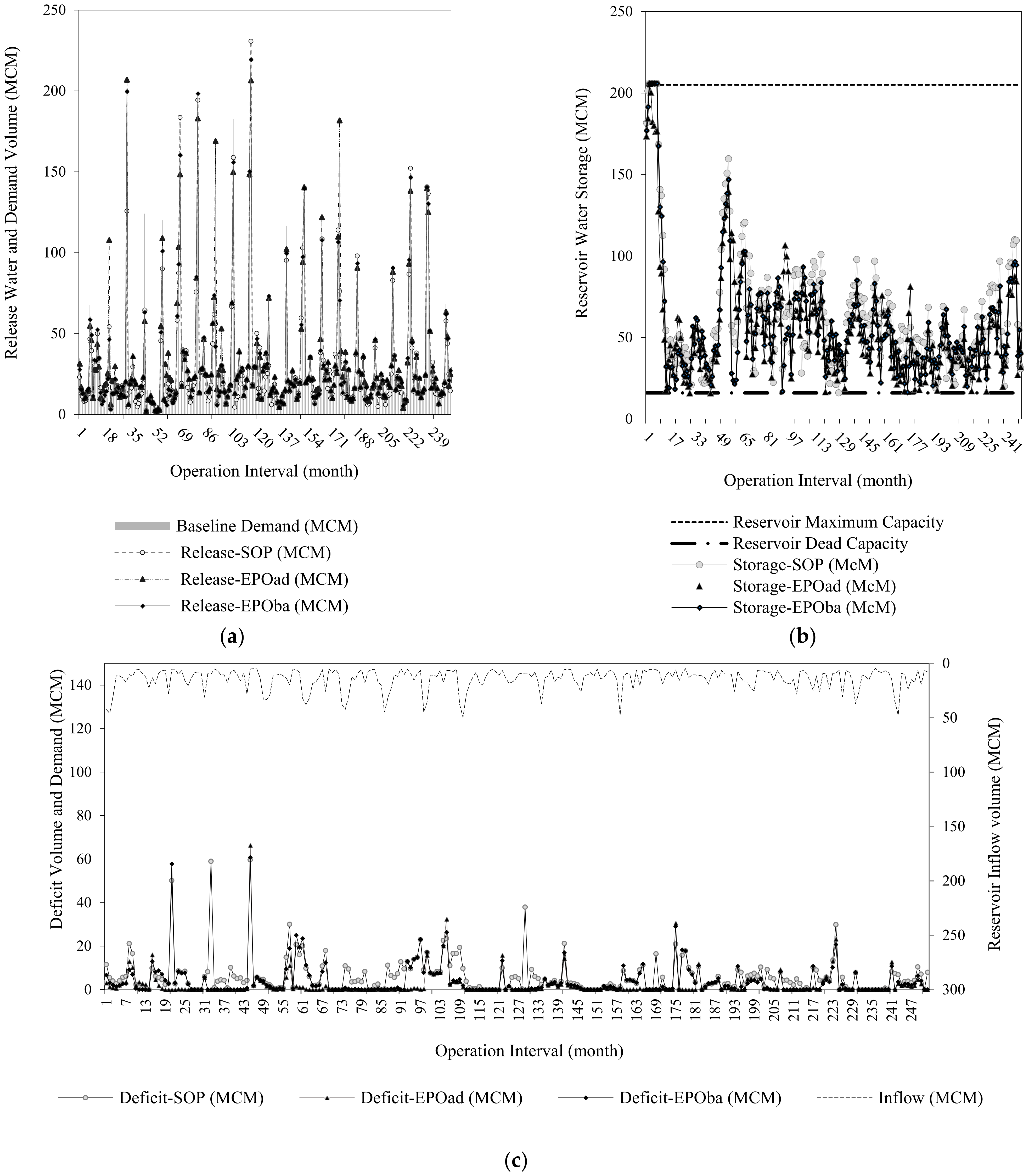
3.2. Comparison of the Results of Multi-Objective Optimization (MOEPO) and SOP in Extracting Allocation Rules in Four Scenarios
Operation Rules and Three Considered Scenarios
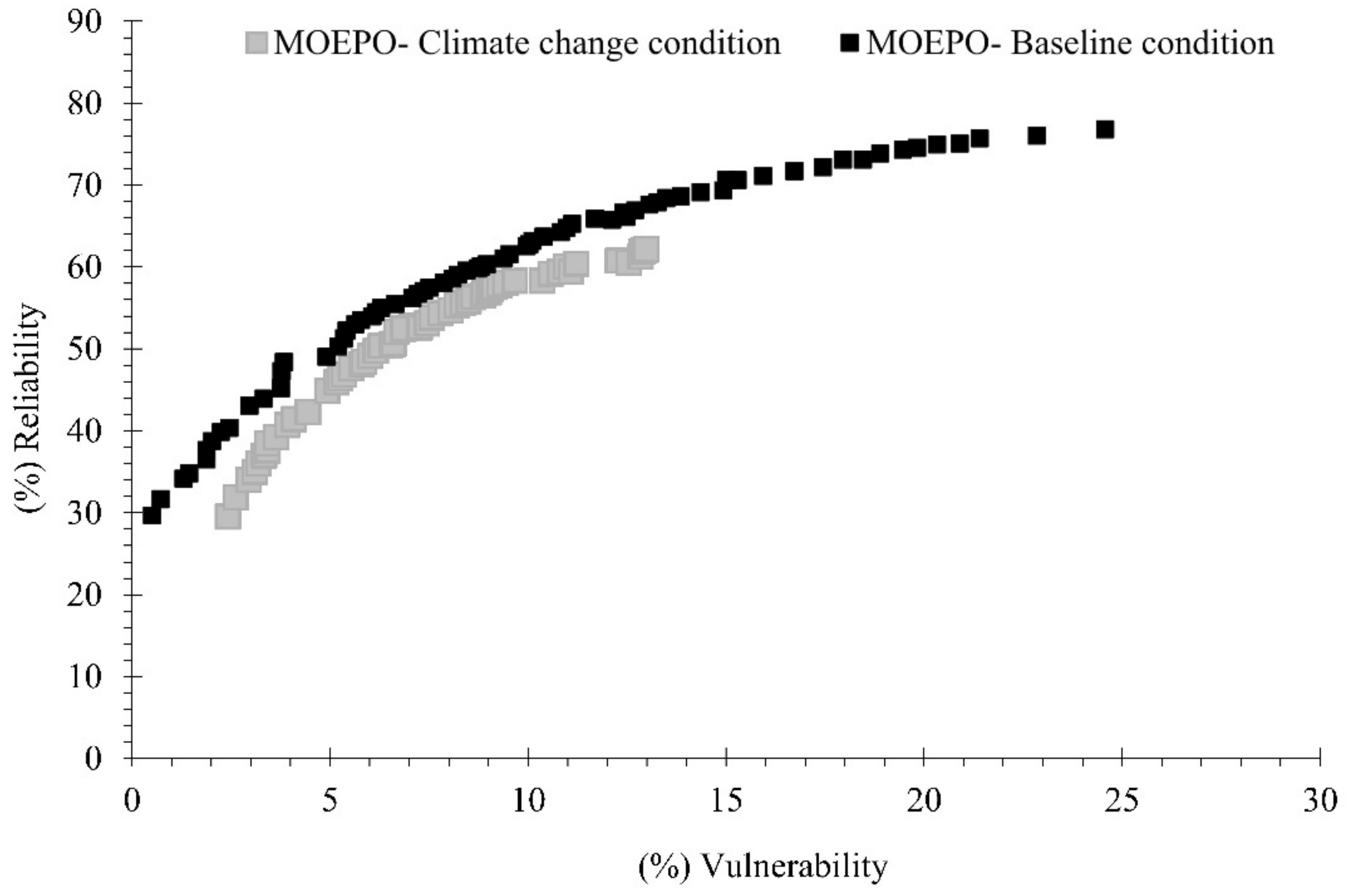
4. Discussion
5. Conclusions
- The boolean function increased the accuracy and performance of the generated allocation rules.
- The multi-objective optimization policy, SOP, and HR were classified from the most to the least based on improving the Performance Indexes.
- To increase the performance of the dam reservoir, it is necessary to generate particular management policies for each interval.
- The suggestions for future study are:
- Comparing this Metaheaustric algorithm with other well-known in terms of solving time consumption, convergence, etc.
- Investigating the Agriculture adaptation strategies (Deficit Irrigation, Changing cultivation date, etc.) in improving the system performance.
- Investigating other decision variables in Performance Indexes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Standard Operation Policy
- AWt: Available water volume during period t
- St: Reservoir storage volume in the t period
- Qt: Inflow volume during the period t
- Et: Evaporation depth from the surface of the reservoir during the t period
- At and At+1: the reservoir surface areas at the beginning and end of the t th period, which use Equations (A3) and (A4), respectively.where a0 and a1 are constant coefficients of the surface-volume curve of the reservoir.
- rspt: total output based on SOP (observational) in t period
- D: the average volume of demand over the entire period of operation.
- Smax: the maximum volume or reservoir capacity (constant number).
Appendix A.2. Hedging Rule

Appendix A.2.1. Objective Function
- LSR: Long-term Shortage Ratio (as objective function)
- RSPHt: total output (sum of release and overflow) based on the HR in t period.
- Dt: the demand in t.
- Dmax: the highest demand during t.
Appendix A.2.2. Constraint
- St: the reservoir storage in t.
- Smin: reservoir dead volume.
Appendix A.3. Multi Objective Optimization of Dam Reservoir Operation
- F(u1): Objective function related to the vulnerability index
- F(u2): Objective function related to the reliability index
- Dt: Demand volume in the t period
- Dmax: Maximum demand in the under-review period.
- : the released volume from the reservoir in t period.
References
- Raje, D.; Mujumdar, P.P. Reservoir Performance under Uncertainty in Hydrologic Impacts of Climate Change. Adv. Water Resour. 2010, 33, 312–326. [Google Scholar] [CrossRef]
- Neelakantan, T.; Sasireka, K. Hydropower Reservoir Operation Using Standard Operating and Standard Hedging Policies. Citeseer 2013, 5, 1191–1196. [Google Scholar]
- Men, B.; Wu, Z.; Li, Y.; Liu, H. Reservoir Operation Policy Based on Joint Hedging Rules. Water 2019, 11, 419. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Cai, X.; Wang, Z. Optimality Conditions for a Two-stage Reservoir Operation Problem. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Alimohammadi, H.; Massah Bavani, A.R.; Roozbahani, A. Mitigating the Impacts of Climate Change on the Performance of Multi-Purpose Reservoirs by Changing the Operation Policy from SOP to MLDR. Water Resour. Manag. 2020, 34, 1495–1516. [Google Scholar] [CrossRef]
- Sattari, M.T.; Apaydin, H.; Ozturk, F. Operation Analysis of Eleviyan Irrigation Reservoir Dam by Optimization and Stochastic Simulation. Stoch. Environ. Res. Risk Assess. 2009, 23, 1187–1201. [Google Scholar] [CrossRef]
- Allawi, M.F.; Jaafar, O.; Hamzah, F.M.; El-Shafie, A. Novel Reservoir System Simulation Procedure for Gap Minimization between Water Supply and Demand. J. Clean. Prod. 2019, 206, 928–943. [Google Scholar] [CrossRef]
- Mansouri, S.; Fathian, H.; Shahbazi, A.N.; Lour, M.A.; Asareh, A. Multi Objective Simulation-Optimization Operation of Dam Reservoir in Low Water Regions Based on Hedging Principles. Res. Sq. 2022. [Google Scholar] [CrossRef]
- Allawi, M.F.; Jaafar, O.; Mohamad Hamzah, F.; Abdullah, S.M.S.; El-Shafie, A. Review on Applications of Artificial Intelligence Methods for Dam and Reservoir-Hydro-Environment Models. Environ. Sci. Pollut. Res. 2018, 25, 13446–13469. [Google Scholar] [CrossRef]
- Hue, C.; Boullé, M.; Lemaire, V. Online Learning of Aweighted Selective Naive Bayes Classifier with Non-Convex Optimization. Stud. Comput. Intell. 2017, 665, 3–17. [Google Scholar] [CrossRef]
- Cruz-Duarte, J.M.; Amaya, I.; Ortiz-Bayliss, J.C.; Pillay, N. Naïve Hyper-Heuristic Online Learning to Generate Unfolded Population-Based Metaheuristics to Solve Continuous Optimization Problems. In Proceedings of the 2021 IEEE Symposium Series on Computational Intelligence, SSCI 2021, Orlando, FL, USA, 5–7 December 2021. [Google Scholar] [CrossRef]
- Goodarzian, F.; Kumar, V.; Abraham, A. Hybrid Meta-Heuristic Algorithms for a Supply Chain Network Considering Different Carbon Emission Regulations Using Big Data Characteristics. Soft Comput. 2021, 25, 7527–7557. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Dulebenets, M.A.; Hajiaghaei-Keshteli, M.; Tavakkoli-Moghaddam, R.; Safaeian, M.; Mirzahosseinian, H. Two Hybrid Meta-Heuristic Algorithms for a Dual-Channel Closed-Loop Supply Chain Network Design Problem in the Tire Industry under Uncertainty. Adv. Eng. Inform. 2021, 50, 101418. [Google Scholar] [CrossRef]
- Rabbani, M.; Oladzad-Abbasabady, N.; Akbarian-Saravi, N. Ambulance Routing in Disaster Response Considering Variable Patient Condition: NSGA-II and MOPSO Algorithms. J. Ind. Manag. Optim. 2022, 18, 1035–1062. [Google Scholar] [CrossRef]
- Dulebenets, M.A. An Adaptive Polyploid Memetic Algorithm for Scheduling Trucks at a Cross-Docking Terminal. Inf. Sci. 2021, 565, 390–421. [Google Scholar] [CrossRef]
- Pasha, J.; Nwodu, A.L.; Fathollahi-Fard, A.M.; Tian, G.; Li, Z.; Wang, H.; Dulebenets, M.A. Exact and Metaheuristic Algorithms for the Vehicle Routing Problem with a Factory-in-a-Box in Multi-Objective Settings. Adv. Eng. Inform. 2022, 52, 101623. [Google Scholar] [CrossRef]
- Nawi, N.M.; Khan, A.; Rehman, M.Z.; Chiroma, H.; Herawan, T. Weight Optimization in Recurrent Neural Networks with Hybrid Metaheuristic Cuckoo Search Techniques for Data Classification. Math. Probl. Eng. 2015, 2015, 868375. [Google Scholar] [CrossRef] [Green Version]
- Panda, N.; Majhi, S.K. Effectiveness of Swarm-Based Metaheuristic Algorithm in Data Classification Using Pi-Sigma Higher Order Neural Network. Adv. Intell. Syst. Comput. 2021, 1199, 77–88. [Google Scholar] [CrossRef]
- Tu, L.-T.; Bradai, A. On the Performance of Physical Layer Security of RIS-Aided Communications. In Proceedings of the 2021 IEEE Conference on Antenna Measurements & Applications (CAMA); IEEE: Piscataway, NJ, USA, 2021; pp. 570–574. [Google Scholar]
- Gomes, L.S.; Maia, A.G.; de Medeiros, J.D.F. Fuzzified Hedging Rules for a Reservoir in the Brazilian Semiarid Region. Environ. Chall. 2021, 4, 100125. [Google Scholar] [CrossRef]
- Djebedjian, B.; Abdel-Gawad, H.A.A.; Ezzeldin, R.M. Global Performance of Metaheuristic Optimization Tools for Water Distribution Networks. Ain Shams Eng. J. 2021, 12, 223–239. [Google Scholar] [CrossRef]
- Lee, H.M.; Jung, D.; Sadollah, A.; Lee, E.H.; Kim, J.H. Performance Comparison of Metaheuristic Optimization Algorithms Using Water Distribution System Design Benchmarks. In Harmony Search and Nature Inspired Optimization Algorithms; Springer: New York, NY, USA, 2019; pp. 97–104. [Google Scholar]
- Bilal; Pant, M. Parameter Optimization of Water Distribution Network–A Hybrid Metaheuristic Approach. Mater. Manuf. Processes 2020, 35, 737–749. [Google Scholar] [CrossRef]
- NA, S. Groundwater Vulnerability Mapping Using the Modified DRASTIC Model: The Metaheuristic Algorithm Approach. Environ. Monit. Assess. 2021, 193, 1–19. [Google Scholar]
- Karimi-Rizvandi, S.; Goodarzi, H.V.; Afkoueieh, J.H.; Chung, I.-M.; Kisi, O.; Kim, S.; Linh, N.T.T. Groundwater-Potential Mapping Using a Self-Learning Bayesian Network Model: A Comparison among Metaheuristic Algorithms. Water 2021, 13, 658. [Google Scholar] [CrossRef]
- Al-Fugara, A.; Ahmadlou, M.; Shatnawi, R.; AlAyyash, S.; Al-Adamat, R.; Al-Shabeeb, A.A.-R.; Soni, S. Novel Hybrid Models Combining Meta-Heuristic Algorithms with Support Vector Regression (SVR) for Groundwater Potential Mapping. Geocarto Int. 2022, 37, 2627–2646. [Google Scholar] [CrossRef]
- Samantaray, S.; Das, S.S.; Sahoo, A.; Satapathy, D.P. Evaluating the Application of Metaheuristic Approaches for Flood Simulation Using GIS: A Case Study of Baitarani River Basin, India. Mater. Today Proc. 2022, 61, 452–465. [Google Scholar] [CrossRef]
- Yin, J.; Guo, S.; Wu, X.; Yang, G.; Xiong, F.; Zhou, Y. A Meta-Heuristic Approach for Multivariate Design Flood Quantile Estimation Incorporating Historical Information. Hydrol. Res. 2019, 50, 526–544. [Google Scholar] [CrossRef]
- Song, C.; Yao, L.; Hua, C.; Ni, Q. Comprehensive Water Quality Evaluation Based on Kernel Extreme Learning Machine Optimized with the Sparrow Search Algorithm in Luoyang River Basin, China. Environ. Earth Sci. 2021, 80, 1–10. [Google Scholar] [CrossRef]
- Almubaidin, M.A.A.; Ahmed, A.N.; Sidek, L.B.M.; Elshafie, A. Using Metaheuristics Algorithms (MHAs) to Optimize Water Supply Operation in Reservoirs: A Review. Arch. Comput. Methods Eng. 2022, 2022, 1–35. [Google Scholar] [CrossRef]
- Dogani, A.; Dourandish, A.; Ghorbani, M.; Shahbazbegian, M.R. A Hybrid Meta-Heuristic for a Bi-Objective Stochastic Optimization of Urban Water Supply System. IEEE Access 2020, 8, 135829–135843. [Google Scholar] [CrossRef]
- Chong, K.L.; Lai, S.H.; Ahmed, A.N.; Zaafar, W.Z.W.; Rao, R.V.; Sherif, M.; Sefelnasr, A.; El-Shafie, A. Review on Dam and Reservoir Optimal Operation for Irrigation and Hydropower Energy Generation Utilizing Meta-Heuristic Algorithms. IEEE Access 2021, 9, 19488–19505. [Google Scholar] [CrossRef]
- Sharifi, M.R.; Akbarifard, S.; Madadi, M.R.; Qaderi, K.; Akbarifard, H. Application of MOMSA Algorithm for Optimal Operation of Karun Multi Objective Multi Reservoir Dams with the Aim of Increasing the Energy Generation. Energy Strategy Rev. 2022, 42, 100883. [Google Scholar] [CrossRef]
- Donyaii, A.; Sarraf, A.; Ahmadi, H. Application of a New Approach in Optimizing the Operation of the Multi-Objective Reservoir. J. Hydraul. Struct. 2020, 6, 1–20. [Google Scholar]
- Donyaii, A.; Sarraf, A.; Ahmadi, H. Evaluation of Whale, Fruit Fly and Cuckoo Search Algorithms in Optimizing Multi-Objective Operation of Golestan Dam Reservoir Based on Multi-Criteria Decision-Making Method. Water Resour. Eng. 2020, 13, 85–100. [Google Scholar]
- Babamiri, O.; Marofi, S. A Multi-Objective Simulation–Optimization Approach for Water Resource Planning of Reservoir–River Systems Based on a Coupled Quantity–Quality Model. Environ. Earth Sci. 2021, 80, 1–19. [Google Scholar] [CrossRef]
- Azari, A.; Hamzeh, S.; Naderi, S. Multi-Objective Optimization of the Reservoir System Operation by Using the Hedging Policy. Water Resour. Manag. 2018, 32, 2061–2078. [Google Scholar] [CrossRef]
- Zhao, S.Z.; Suganthan, P.N. Two-Lbests Based Multi-Objective Particle Swarm Optimizer. Eng. Optim. 2011, 43, 1–17. [Google Scholar] [CrossRef]
- Sun, Y.; Guan, Y.; Wang, H.; Wu, G. Autotrophic Nitrogen Removal in Combined Nitritation and Anammox Systems through Intermittent Aeration and Possible Microbial Interactions by Quorum Sensing Analysis. Bioresour. Technol. 2019, 272, 146–155. [Google Scholar] [CrossRef]
- Ravi, V.; Pradeepkumar, D.; Deb, K. Financial Time Series Prediction Using Hybrids of Chaos Theory, Multi-Layer Perceptron and Multi-Objective Evolutionary Algorithms. Swarm Evol. Comput. 2017, 36, 136–149. [Google Scholar] [CrossRef]
- Qi, R.; Qian, F.; Li, S.; Wang, Z. Chaos-Genetic Algorithm for Multiobjective Optimization. In Proceedings of the World Congress on Intelligent Control and Automation (WCICA), Dalian, China, 21–23 June 2006; Volume 1, pp. 1563–1566. [Google Scholar]
- Marichelvam, M.K.; Prabaharan, T.; Yang, X.S. A Discrete Firefly Algorithm for the Multi-Objective Hybrid Flowshop Scheduling Problems. IEEE Trans. Evol. Comput. 2014, 18, 301–305. [Google Scholar] [CrossRef]
- Patel, V.K.; Savsani, V.J. A Multi-Objective Improved Teaching-Learning Based Optimization Algorithm (MO-ITLBO). Inf. Sci. 2016, 357, 182–200. [Google Scholar] [CrossRef]
- Rashedi, E.; Rashedi, E.; Nezamabadi-pour, H. A Comprehensive Survey on Gravitational Search Algorithm. Swarm Evol. Comput. 2018, 41, 141–158. [Google Scholar] [CrossRef]
- Cheng, J.; Yen, G.G.; Zhang, G. A Grid-Based Adaptive Multi-Objective Differential Evolution Algorithm. Inf. Sci. 2016, 367–368, 890–908. [Google Scholar] [CrossRef]
- Yosefipoor, P.; Saadatpour, M.; Solis, S.S.; Afshar, A. An Adaptive Surrogate-Based, Multi-Pollutant, and Multi-Objective Optimization for River-Reservoir System Management. Ecol. Eng. 2022, 175, 106487. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, J.; Xu, Y.-P.; Guo, Y.; Wang, Y. Scenario-Based Multi-Objective Optimization of Reservoirs in Silt-Laden Rivers: A Case Study in the Lower Yellow River. Sci. Total Environ. 2022, 829, 154565. [Google Scholar] [CrossRef] [PubMed]
- Talatahari, S.; Aalami, M.T.; Parsiavash, R. Multi-Objective Optimization of Double Curvature Arch Dams Subjected to Seismic Loading Using Charged System Search. arXiv 2022, arXiv:arXiv.2207.04366. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Solgi, M.; Bozorg-Haddad, O.; Loáiciga, H.A. A Multi-Objective Optimization Model for Operation of Intermittent Water Distribution Networks. Water Supply 2020, 20, 2630–2647. [Google Scholar] [CrossRef]
- Kumar, V.; Yadav, S.M. Multi-Objective Reservoir Operation of the Ukai Reservoir System Using an Improved Jaya Algorithm. Water Supply 2022, 22, 2287–2310. [Google Scholar] [CrossRef]
- Yoosefdoost, I.; Khashei-Siuki, A.; Tabari, H.; Mohammadrezapour, O. Runoff Simulation under Future Climate Change Conditions: Performance Comparison of Data-Mining Algorithms and Conceptual Models. Water Resour. Manag. 2022, 2022, 1–25. [Google Scholar] [CrossRef]
- Viertel, K. The Development of the Concept of Uniform Convergence in Karl Weierstrass’s Lectures and Publications between 1861 and 1886. Arch. Hist. Exact Sci. 2021, 75, 455–490. [Google Scholar] [CrossRef]
- Stefánsson, A.; Končar, N.; Jones, A.J. A Note on the Gamma Test. Neural Comput. Appl. 1997, 5, 131–133. [Google Scholar] [CrossRef]
- Doorenbos, J.; Pruitt, W.O. Guidelines for Predicting Crop Water Requirements. FAO Irrig. Drain. Pap. 1977, 24, 144. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56. Fao Rome 1998, 300, D05109. [Google Scholar]
- Mohammadrezapour, O.; Yoosefdoost, I.; Ebrahimi, M. Cuckoo Optimization Algorithm in Optimal Water Allocation and Crop Planning under Various Weather Conditions (Case Study: Qazvin Plain, Iran). Neural Comput. Appl. 2017, 31, 1879–1892. [Google Scholar] [CrossRef]
- Ferreira, C. undefined Gene Expression Programming: A New Adaptive Algorithm for Solving Problems. Complex Syst. 2001, 13, 87–129. [Google Scholar]
- Dhiman, G.; Kumar, V. Emperor Penguin Optimizer: A Bio-Inspired Algorithm for Engineering Problems. Knowl. -Based Syst. 2018, 159, 20–50. [Google Scholar] [CrossRef]
- Kaur, H.; Rai, A.; Bhatia, S.S.; Dhiman, G. MOEPO: A Novel Multi-Objective Emperor Penguin Optimizer for Global Optimization: Special Application in Ranking of Cloud Service Providers. Eng. Appl. Artif. Intell. 2020, 96, 104008. [Google Scholar] [CrossRef]
- Zhou, M.; Chen, J.; Huang, H.; Zhang, D.; Zhao, S.; Shadabfar, M. Multi-Source Data Driven Method for Assessing the Rock Mass Quality of a NATM Tunnel Face via Hybrid Ensemble Learning Models. Int. J. Rock Mech. Min. Sci. 2021, 147, 104914. [Google Scholar] [CrossRef]
- Ghorbani, H.; Wood, D.A.; Mohamadian, N.; Rashidi, S.; Davoodi, S.; Soleimanian, A.; Shahvand, A.K.; Mehrad, M. Adaptive Neuro-Fuzzy Algorithm Applied to Predict and Control Multi-Phase Flow Rates through Wellhead Chokes. Flow Meas. Instrum. 2020, 76, 101849. [Google Scholar] [CrossRef]
- Hashimoto, T.; Stedinger, J.R.; Loucks, D.P. Reliability, Resiliency, and Vulnerability Criteria for Water Resource System Performance Evaluation. Water Resour. Res. 1982, 18, 14–20. [Google Scholar] [CrossRef] [Green Version]
- Zou, H.; Liu, D.; Guo, S.; Xiong, L.; Liu, P.; Yin, J.; Zeng, Y.; Zhang, J.; Shen, Y. Quantitative Assessment of Adaptive Measures on Optimal Water Resources Allocation by Using Reliability, Resilience, Vulnerability Indicators. Stoch. Environ. Res. Risk Assess. 2019, 34, 103–119. [Google Scholar] [CrossRef]
- Wang, Z.; Zhen, H.-L.; Deng, J.; Zhang, Q.; Li, X.; Yuan, M.; Zeng, J. Multiobjective Optimization-Aided Decision-Making System for Large-Scale Manufacturing Planning. IEEE Trans. Cybern. 2021, 52, 8326–8339. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Kang, J.; Kwong, S.; Wang, X.; Zhang, Q. An Evolutionary Multi-Objective Optimization Framework of Discretization-Based Feature Selection for Classification. Swarm Evol. Comput. 2021, 60, 100770. [Google Scholar] [CrossRef]
- Ashofteh, P.-S.; Haddad, O.B.; Akbari-Alashti, H.; Mariño, M.A. Determination of Irrigation Allocation Policy under Climate Change by Genetic Programming. J. Irrig. Drain. Eng. 2014, 141, 04014059. [Google Scholar] [CrossRef] [Green Version]

| Algorithm | MAD 1 | MSE 2 | RMSE 3 | MAPE 4 | R(XY) 5 | NS 6 | MAE 7 | R2 | SSE 8 |
|---|---|---|---|---|---|---|---|---|---|
| EPOad | 0.774 | 1.513 | 1.230 | 4.487 | 0.999 | 0.995 | −0.774 | 0.997 | 381.386 |
| EPOba | 0.511 | 12.276 | 3.504 | 2.124 | 0.98 | 0.961 | −0.24 | 0.961 | 3093.48 |
| Scenarios | Reliability (%) | Vulnerability (%) |
|---|---|---|
| First | 43.56 | 9.44 |
| Second | 55.88 | 6.73 |
| Third | 29.74 | 23.45 |
| Fourth | 36.65 | 14.65 |
| Algorithm | MAD | MSE | RMSE | MAPE | R(XY) | NS | MAE | R2 | SSE |
|---|---|---|---|---|---|---|---|---|---|
| EPOad | 1.734 | 22.838 | 4.779 | 10.245 | 0.97 | 0.927 | −0.98 | 0.93 | 5755.17 |
| EPOba | 1.113 | 9.656 | 3.107 | 5.308 | 0.99 | 0.966 | −0.98 | 0.95 | 2433.26 |
| Sc. | Reliability % | Vulnerability % | Parameter Changes in Scenarios | Reliability Change % | Vulnerability Change % |
|---|---|---|---|---|---|
| First | 48.41 | 8.15 | Comparison of the first and second | 11.60 | −40.03 |
| Second | 54.76 | 5.82 | Comparison of the third and fourth | 12.44 | −5.51 |
| Third | 33.49 | 11.11 | Comparison of the first and third | −44.55 | 26.64 |
| Fourth | 38.25 | 10.53 | Comparison of the second and fourth | −43.16 | 44.73 |
| Method | Sc. | Vulnerability % | Reliability % | Parameter Changes in Scenarios | Vulnerability Change % | Reliability Change % |
|---|---|---|---|---|---|---|
| MOEPO | First Scenario | 4.33 | 48 | Comparison of the first and third | 0 | −4.3478 |
| Second Scenario | 5.98 | 46 | Comparison of the Second and third | −38.106 | 0 | |
| Third Scenario | 4.33 | 46 | Comparison of the first and second | 27.592 | −4.3478 | |
| SOP | Baseline Condition | 14 | 48 | Comparison of the first scenario and Baseline condition | −35.714 | 25 |
| Future Condition | 16 | 46 | Comparison of the Second scenario and Baseline condition | −31.25 | 26.087 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoosefdoost, I.; Basirifard, M.; Álvarez-García, J. Reservoir Operation Management with New Multi-Objective (MOEPO) and Metaheuristic (EPO) Algorithms. Water 2022, 14, 2329. https://doi.org/10.3390/w14152329
Yoosefdoost I, Basirifard M, Álvarez-García J. Reservoir Operation Management with New Multi-Objective (MOEPO) and Metaheuristic (EPO) Algorithms. Water. 2022; 14(15):2329. https://doi.org/10.3390/w14152329
Chicago/Turabian StyleYoosefdoost, Icen, Milad Basirifard, and José Álvarez-García. 2022. "Reservoir Operation Management with New Multi-Objective (MOEPO) and Metaheuristic (EPO) Algorithms" Water 14, no. 15: 2329. https://doi.org/10.3390/w14152329








