Vertical Dense Effluent Discharge Modelling in Shallow Waters
Abstract
:1. Literature Review and Research Needs
2. Dimensional Analysis
3. Numerical Model
3.1. Governing Equations
3.2. Numerical Solver and Schemes
3.3. Boundary Conditions
3.4. Turbulence Model
3.5. Numerical Cases
4. Results and Discussion
4.1. Discharge Evolution
4.2. Discharge Dilution
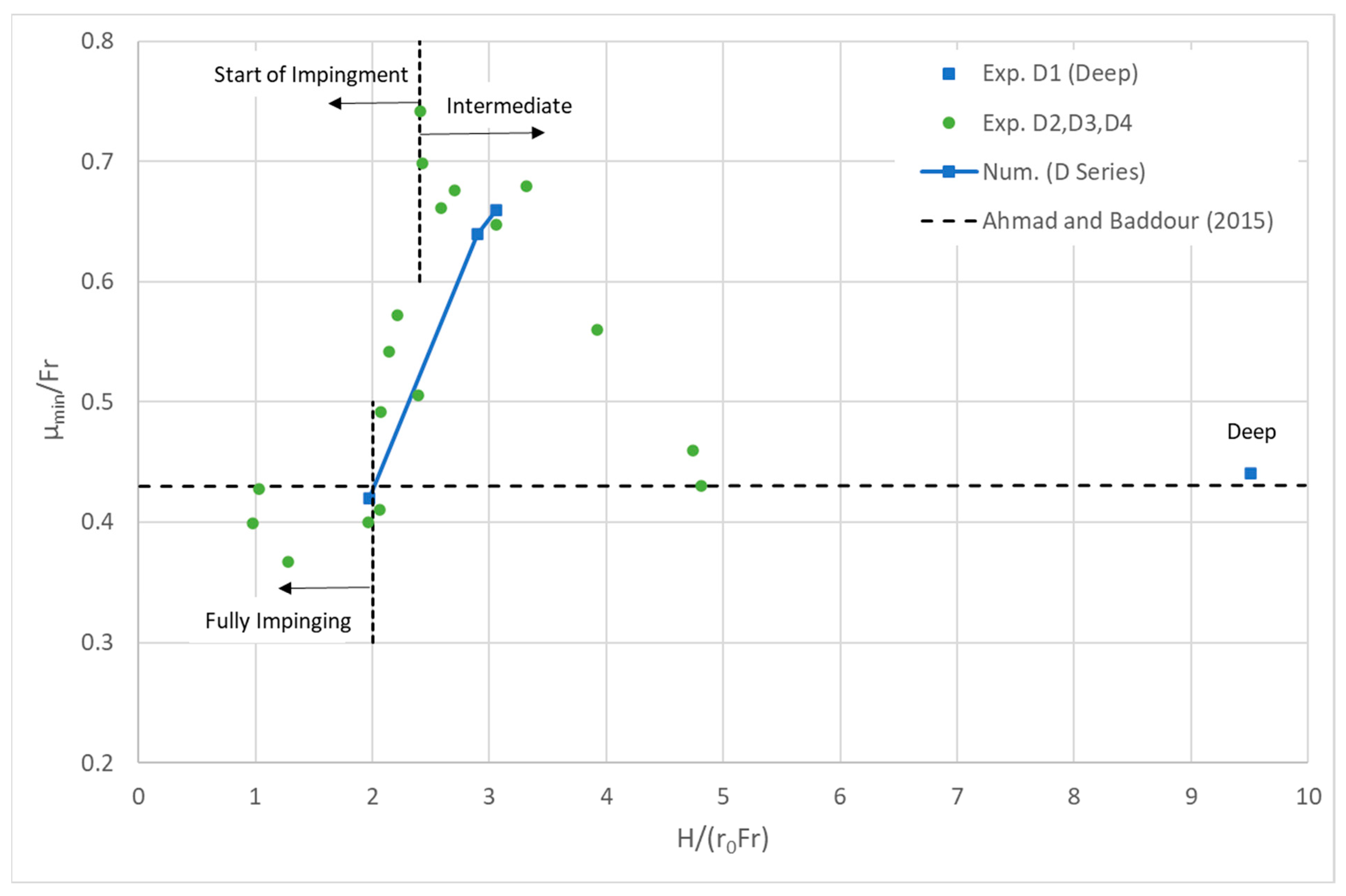
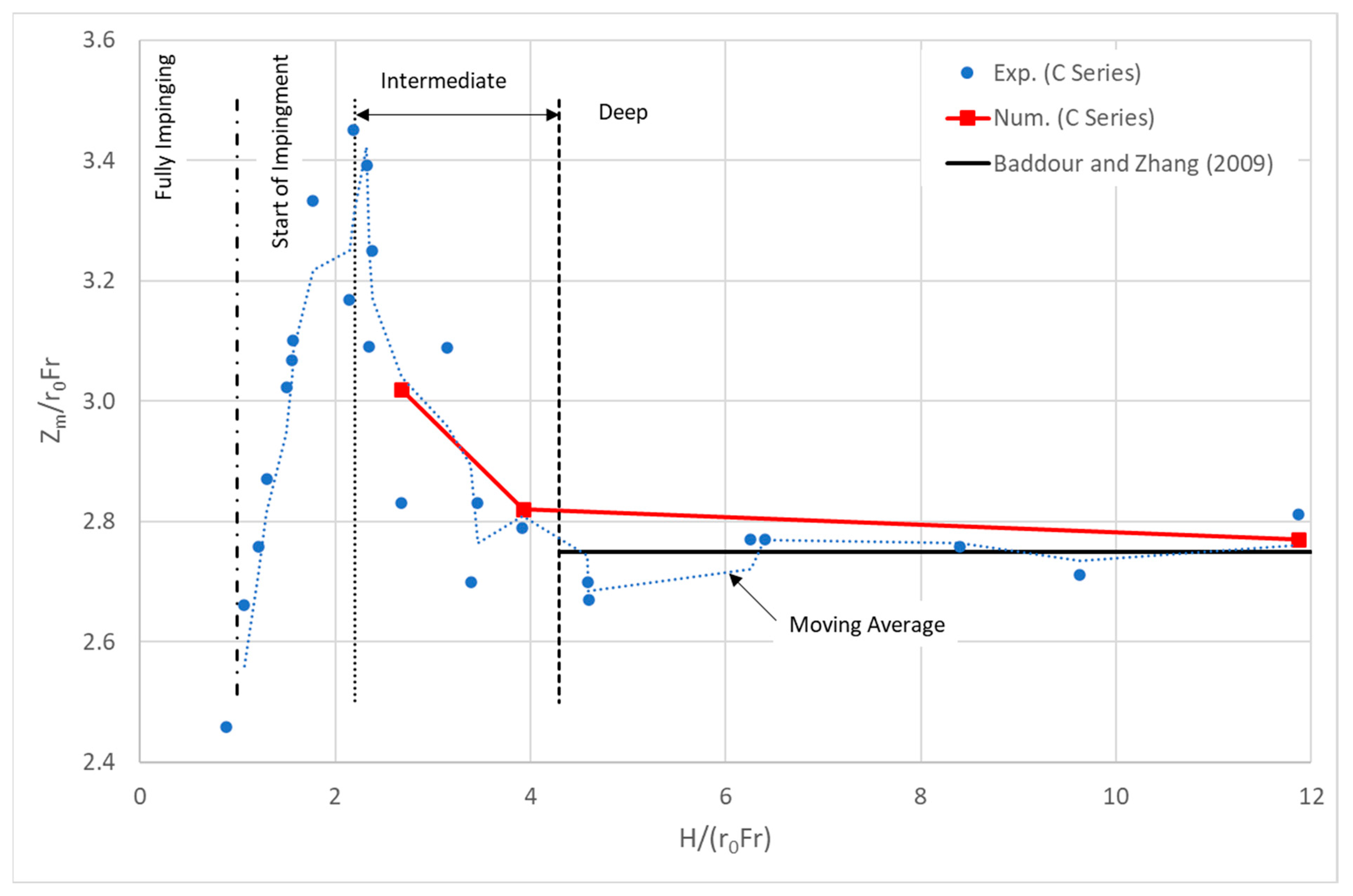
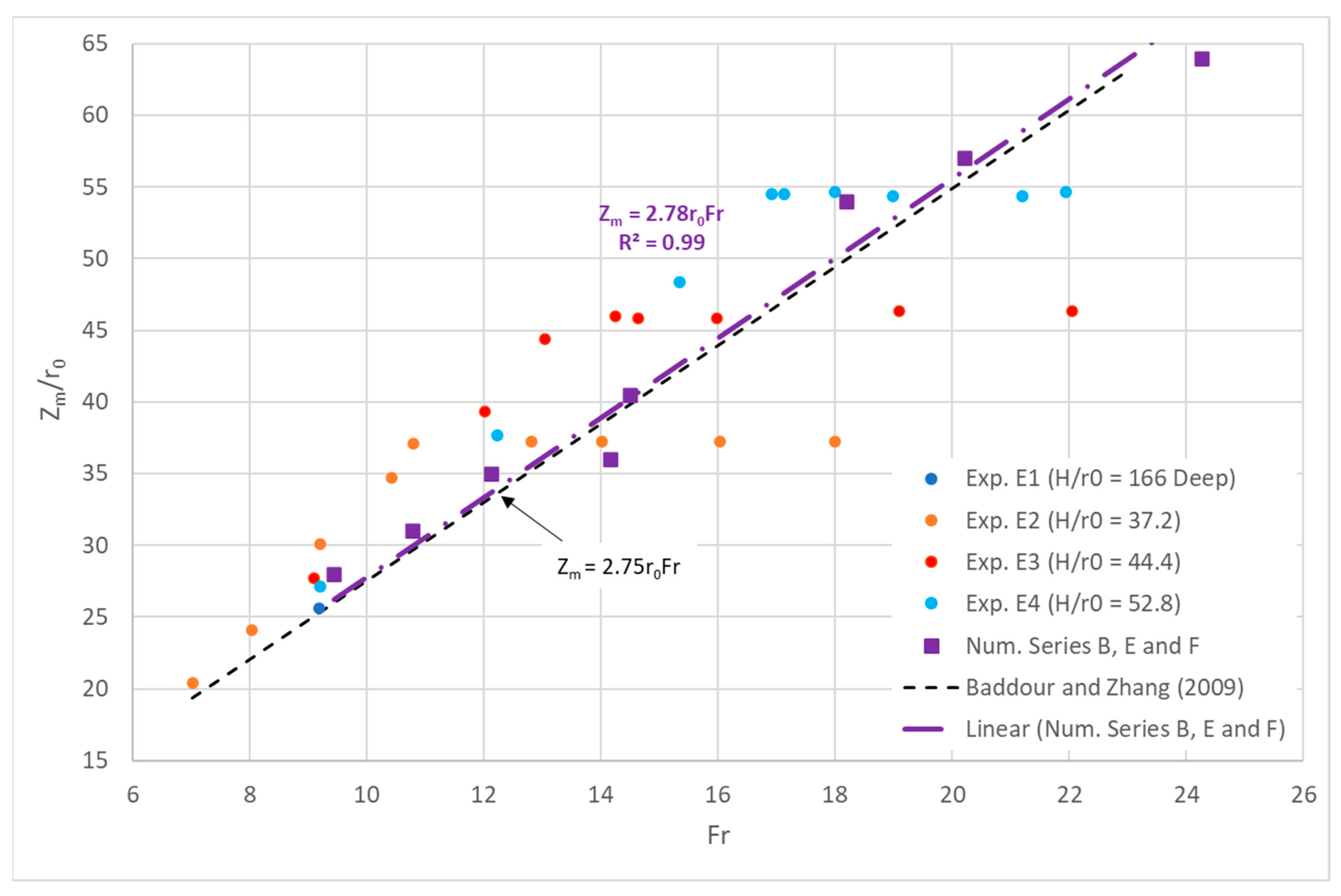
4.3. Discharge Maximum Rise
4.4. Spreading Radius
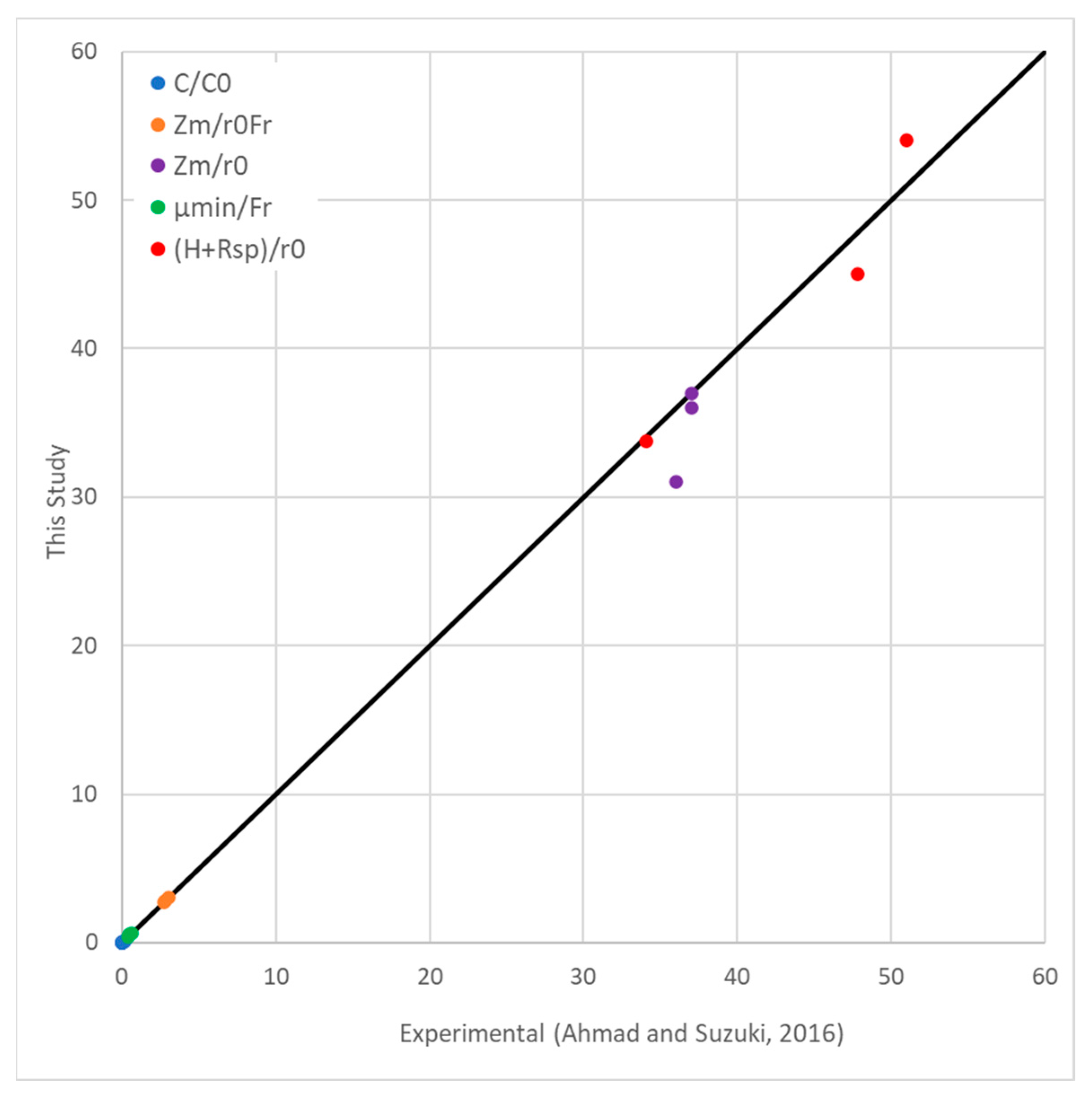
4.5. Quantitative Comparison
5. Conclusions and Recommendations
- The vertical discharge under an intermediate regime results in higher discharge maximum rise compared with that observed in a deep regime. This is because there is less pressure of the water column above the discharge in the intermediate regime. Another contributing factor may be the stress conditions between two boundaries (i.e., discharge front boundary and water surface boundary) and viscous forces between two fluids with different densities.
- The return point minimum dilution is higher for the vertical jet in an intermediate regime when compared with a deep flow regime. The return point minimum dilution significantly reduces in the fully impinging regime. The surface attachment will make the overall trajectory of the jet longer, but the mixing reduces the area of surface attachment, due to the reduced water entrainment (e.g., from atmosphere).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| B0 | buoyancy flux [m4/s3] |
| C | concentration at each cell [ppm/ppt] |
| C0 | discharge concentration [ppm/ppt] |
| Ca | ambient concentration [ppm/ppt] |
| C1 | return point concentration [ppm/ppt] |
| Fr | densimetric Froude number [-] |
| G | gravitational acceleration [m/s2] |
| g0′ | reduced gravitational acceleration [m/s2] |
| gs′ | effective gravity scale [m/s2] |
| H | water depth above nozzle level [m] |
| K | turbulent kinetic energy [m2/s2] |
| Ls | length scale to normalize jet height [m] |
| M0 | momentum flux [m4/s2] |
| Prt | turbulent Prandtl number [-] |
| Q0 | discharge volume flux [m3/s] |
| turbulent scalar flux [-] | |
| r | radial distance [m] |
| r0 | nozzle radius [m] |
| Rsp | jet lateral spread [m] |
| u | fluid velocity [m/s] |
| U0 | discharge initial velocity [m/s] |
| Zm | discharge maximum rise [m] |
| calar diffusivity [kg/ms] | |
| turbulent dispersity | |
| Kronecker delta [-] | |
| fluid viscosity [Ns/m2] | |
| minimum return point dilution [-] | |
| turbulent eddy viscosity [m2/s] | |
| fluid density at each cell [kg/m3] | |
| discharge density [kg/m3] | |
| ambient density [kg/m3] | |
| Reynolds stresses [-] |
References
- Bleninger, T.; Niepelt, A.; Jirka, G.H. Desalination Plant Discharge Calculator; Paper BD 180 for EDS Congress; Institute for Hydrodynamics, University of Karlsruhe: Baden, Germany, 2009. [Google Scholar]
- Purnama, A.; Al-Barwani, H.H.; Al-Lawatia, M. Modeling dispersion of brine waste discharge from a coastal desalination plant. Desalination 2003, 155, 41–47. [Google Scholar] [CrossRef]
- Ahmad, N.; Baddour, R.E. Minimum return dilution method to regulate the discharge of brine from desalination plants. Can. J. Civ. Eng. 2014, 41, 389–395. [Google Scholar] [CrossRef]
- Yannopoulos, P.; Noutsopoulos, G. The plane vertical turbulent buoyant jet. J. Hydraul. Res. 1990, 28, 565–580. [Google Scholar] [CrossRef]
- Zhang, H.; Baddour, R.E. Maximum penetration of vertical round dense jets at small and large Froude numbers. J. Hydraul. Eng. 1998, 124, 550–553. [Google Scholar] [CrossRef]
- Baddour, R.E.; Zhang, H. Density effect on round turbulent hypersaline fountains. J. Hydraul. Eng. 2009, 135, 57–59. [Google Scholar] [CrossRef]
- Elhaggag, M.E.; Elgamal, M.; Farouk, M.I. Experimental and Numerical Investigation of Desalination Plant Outfalls in Limited Disposal Areas. J. Environ. Prot. 2011, 2, 828–839. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, N.; Baddour, R.E. Dilution and penetration of vertical negatively buoyant thermal jets. J. Hydraul. Eng. 2012, 138, 850–857. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A. Numerical Modeling of Vertical Buoyant Jets Subjected to Lateral Confinement. J. Hydraul. Eng. 2017, 143, 04017016. [Google Scholar] [CrossRef] [Green Version]
- Lemckert, C.J. Spreading radius of fountains after impinging a free surface. In Proceedings of the 15th Australian Fluid Mechanics Conference, Sydney, NSW, Australia, 13–17 December 2004. [Google Scholar]
- Ahmad, N.; Suzuki, T. Study of dilution, height, and lateral spread of vertical dense jets in marine shallow water. Water Sci. Technol. 2016, 73, 2986–2997. [Google Scholar] [CrossRef] [PubMed]
- Cooper, P.; Hunt, G.R. Impinging axisymmetric turbulent fountains. Phys. Fluids 2007, 19, 117101–117109. [Google Scholar] [CrossRef] [Green Version]
- Baum, M.J.; Gibbes, B. Field-scale numerical modeling of dense multiport diffuser outfall in crossflow. J. Hydraul. Eng. 2019, 146, 05019006. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Leschziner, M. Statistical Turbulence Modelling for Fluid Dynamics—Demystified: An Introductory Text for Graduate Engineering Students; Imperial College Press: London, UK, 2016. [Google Scholar]
- Gildeh, H.K.; Mohammadian, A.; Nistor, I.; Qiblawey, H. Numerical Modeling of Turbulent Buoyant Wall Jets in Stationary Ambient Water. J. Hydraul. Eng. 2014, 140, 04014012. [Google Scholar] [CrossRef] [Green Version]
- Gildeh, H.K.; Mohammadian, A.; Nistor, I.; Qiblawey, H. Numerical modeling of 30° and 45° inclined dense turbulent jets in stationary ambient. Environ. Fluid Mech. 2015, 15, 537–562. [Google Scholar] [CrossRef]
- Gildeh, H.K.; Mohammadian, A.; Nistor, I.; Qiblawey, H.; Yan, X. CFD modeling and analysis of the behavior of 30° and 45° inclined dense jets—new numerical insights. J. Appl. Water Eng. Res. 2016, 4, 112–127. [Google Scholar] [CrossRef]
- Gildeh, H.K.; Mohammadian, A.; Nistor, I. Inclined Dense Effluent Discharge Modelling in Shallow Waters. Environ. Fluid Mech. 2021, 21, 955–987. [Google Scholar] [CrossRef]
- Mohammadian, A.; Gildeh, H.K.; Nistor, I. CFD Modeling of Effluent Discharges: A Review of Past Numerical Studies. J. Water 2020, 12, 856. [Google Scholar] [CrossRef] [Green Version]
- Launder, B.E.; Reece, G.J.; Rodi, W. Progress in the Development of a Reynolds-Stress Turbulence Closure. J. Fluid Mech. 1975, 68, 537–566. [Google Scholar] [CrossRef] [Green Version]
- Holstein, D.M.; Lemckert, C.J. Spreading of energetic submerged fountains impinging on a rigid surface. In Proceedings of the 14th Australian Fluid Mechanics Conference, Adelaide University, Adelaide, SA, Australia, 10–14 December 2001. [Google Scholar]
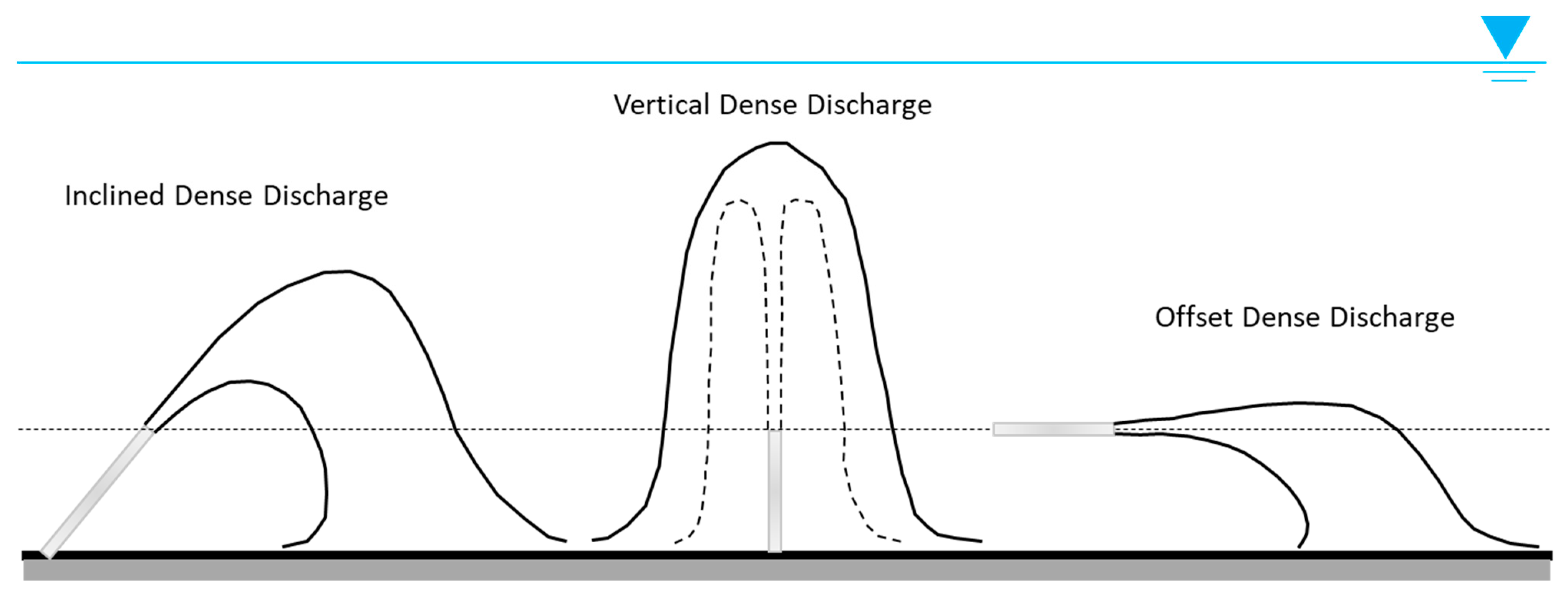
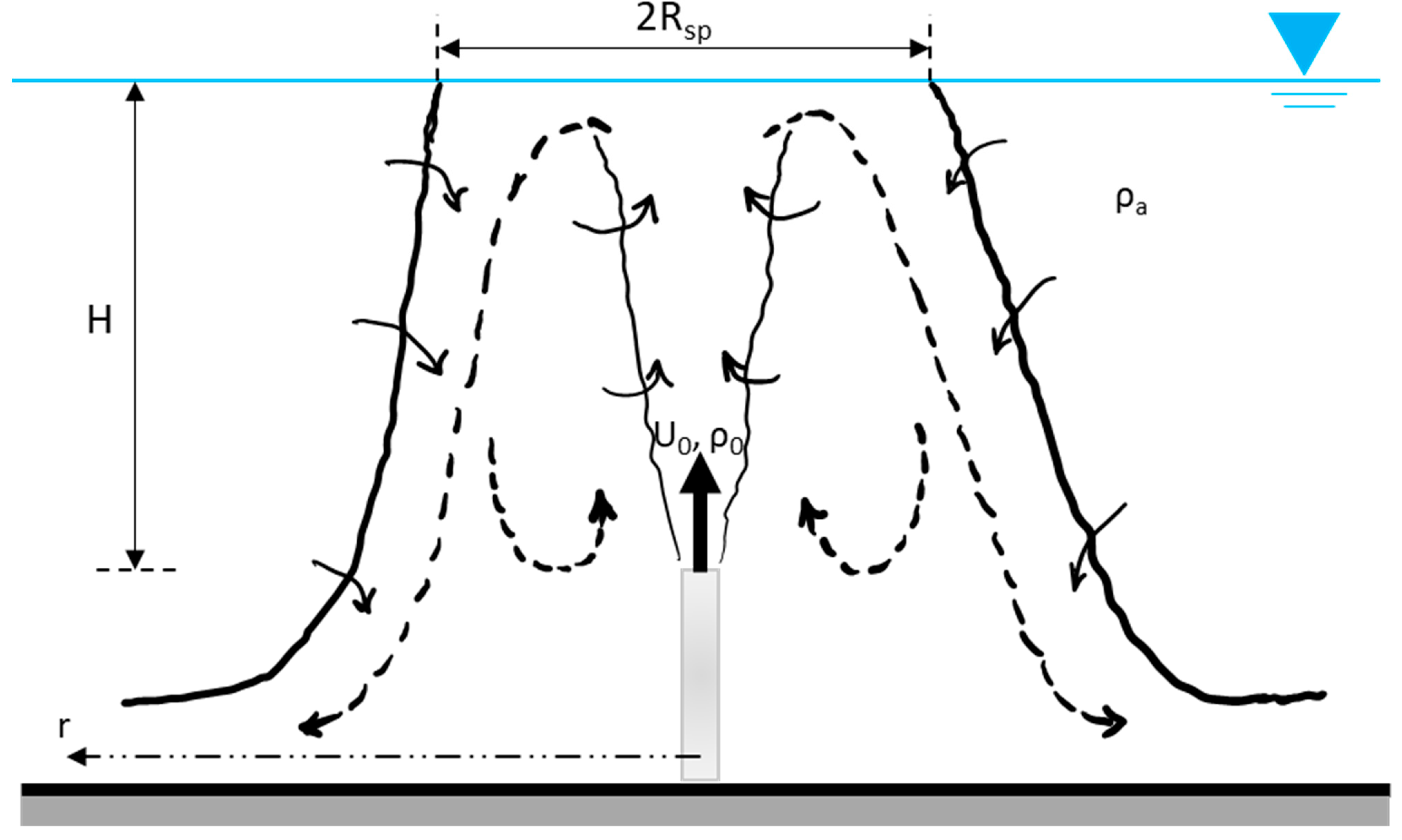

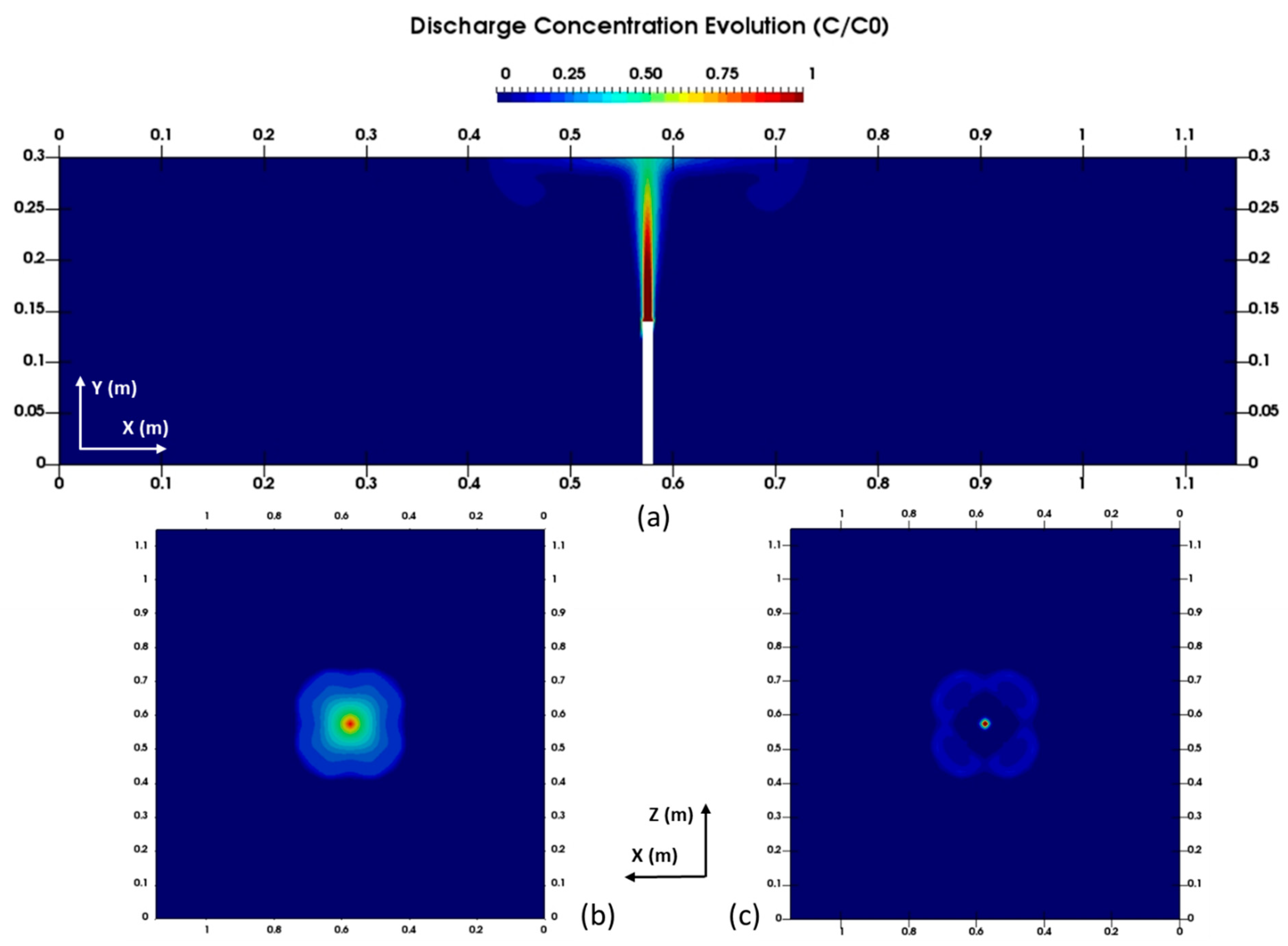

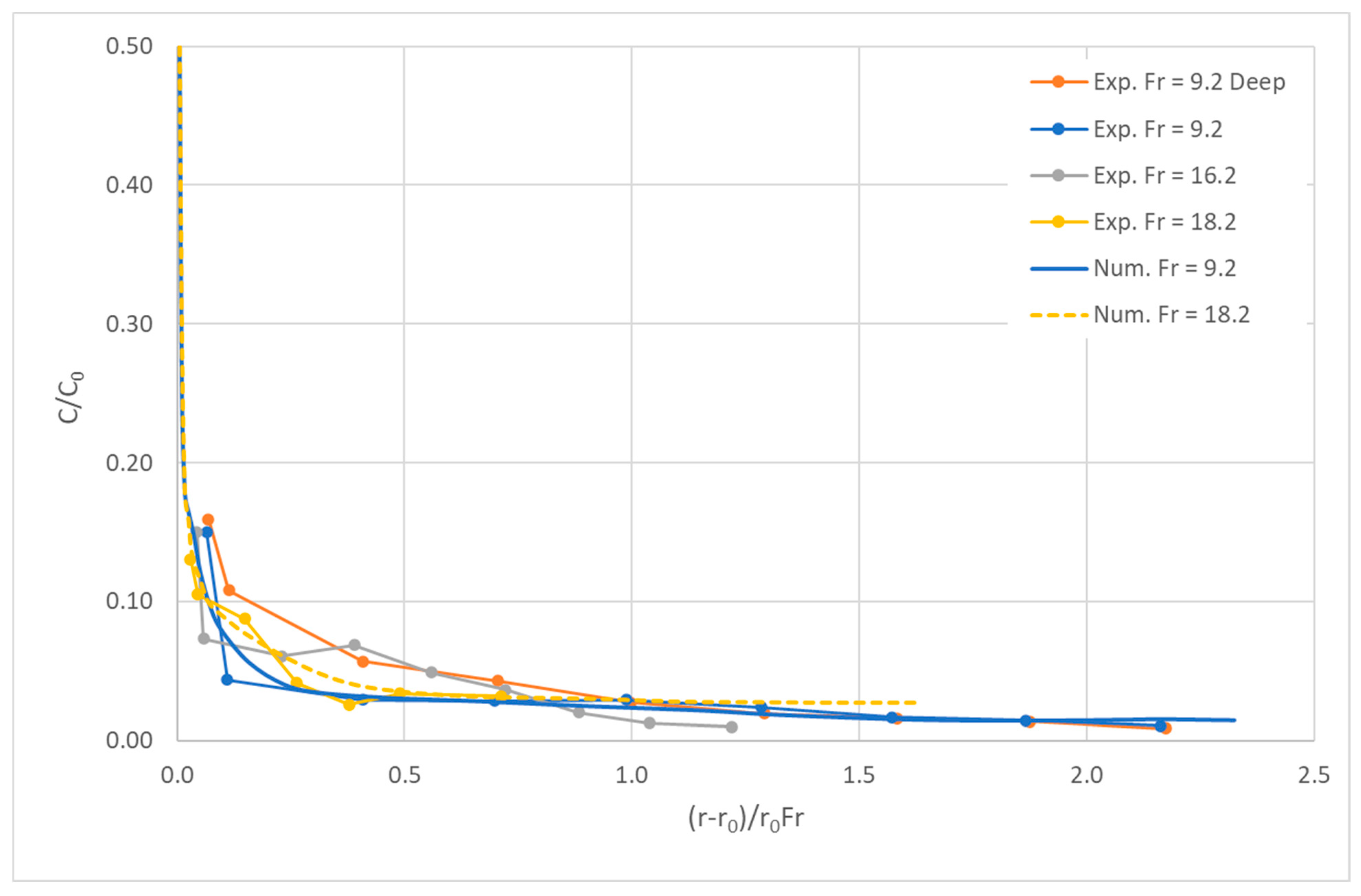

| Study | Findings |
|---|---|
| Yannopoulos and Noutsopoulos [4] | Studied the plane vertical turbulent buoyant jets to find the discharge flow spreading coefficients (Kc and Kw for velocity and concentration, respectively). They included a large range of discharge Froude numbers and showed that γ (spreading parameter) is constant (γ = 0.6). |
| Zhang and Baddour [5] | Investigated the maximum height of vertical dense fountains with a large range of Froude numbers from small to large. They found out that Zm/Lm reaches an asymptotic value for high Froude numbers (i.e., Fr > 7) and argued that the mass flux at discharge point has a negligible influence on the maximum discharge penetration. |
| Baddour and Zhang [6] | Conducted an experimental investigation to find out the effect of density on round turbulent fountains. Their results revealed that the maximum penetration height of the discharge (Zm/Lm) was a function of relative density difference (Δρ/ρa). They concluded that the Zm/Lm decreases from 3.06 to 2.59 at Δρ/ρa = 0.001 and Δρ/ρa = 0.1, respectively. |
| Elhaggag et al. [7] | Studied the vertical dense discharges numerically using a computational fluid dynamics (CFD) model. They used FLUENT to model the vertical jets, however, this study did not verify the model using experimental data. |
| Ahmad and Baddour [8] | Performed an experimental study of the terminal rise height and dilution of vertical dense jets. They quantified vertical and horizontal penetrations of the jet using thermometers and comparing with findings of previous studies. They concluded that the vertical jet penetration matched those from previous studies but the horizontal spread was smaller with a value of δm = 1.4r0Fr, where r0 is the radius of nozzle and Fr is the discharge densimetric Froude number. |
| Yan and Mohammadian [9] | Studied the lateral confinement impact on the vertical buoyant jets numerically using the OpenFOAM CFD model. They stated that the buoyancy-modified k-ɛ turbulence model was able to produce reasonable results for such jets. They also varied the Prandtl number (Pr) and turbulent Prandtl number (Prt) for various Froude numbers and claimed this affects the jet predictions. |
| Deep | Intermediate | Impinging |
|---|---|---|
| H/r0 > 1.5 Zm/r0 | Zm/r0 < H/r0 < 1.5 Zm/r0 | H < Zm |
| Experiment Series | Experiment # | D (2r0) (mm) | U0 (m/s) | Δρ/ρa | ρ0 (kg/m3) | Fr | H/r0 | Fr/(H/r0) |
|---|---|---|---|---|---|---|---|---|
| A (Initial run) | 1 | 9.45 | 0.54 | 0.018 | 1011.89 | 18.69 | 34.0 | 0.55 |
| B (Fixed H and variable Fr) | 2 | 9.45 | 0.28 | 0.019 | 1012.89 | 9.44 | 37.2 | 0.25 |
| 3 | 9.45 | 0.54 | 0.019 | 1012.89 | 18.20 | 37.2 | 0.49 | |
| C (Fixed Fr and variable H) | 4 | 9.45 | 0.25 | 0.015 | 1008.91 | 9.48 | 25.4 | 0.37 |
| 5 | 9.45 | 0.25 | 0.015 | 1008.91 | 9.48 | 37.2 | 0.25 | |
| 6 | 9.45 | 0.25 | 0.015 | 1008.91 | 9.48 | 166.0 | 0.06 | |
| D (Variable Fr and variable H) | 7 | 9.45 | 0.56 | 0.019 | 1012.89 | 18.87 | 37.2 | 0.51 |
| 8 | 9.45 | 0.45 | 0.019 | 1012.89 | 15.16 | 44.4 | 0.34 | |
| 9 | 9.45 | 0.54 | 0.019 | 1012.89 | 18.20 | 52.8 | 0.34 | |
| E (Fixed H and variable Fr, intermediate Fr range) | 10 | 9.45 | 0.32 | 0.019 | 1012.89 | 10.80 | 37.2 | 0.29 |
| 11 | 9.45 | 0.36 | 0.019 | 1012.89 | 12.13 | 37.2 | 0.33 | |
| 12 | 9.45 | 0.42 | 0.019 | 1012.89 | 14.15 | 37.2 | 0.38 | |
| F (Fixed H and variable Fr, high Fr range) | 13 | 9.45 | 0.43 | 0.019 | 1012.89 | 14.50 | 37.2 | 0.39 |
| 14 | 9.45 | 0.60 | 0.019 | 1012.89 | 20.22 | 37.2 | 0.54 | |
| 15 | 9.45 | 0.72 | 0.019 | 1012.89 | 24.26 | 37.2 | 0.65 |
| Parameter/Error | C/C0 | Zm/r0Fr | Zm/r0 | μmin/Fr | (H + Rsp)/r0 |
|---|---|---|---|---|---|
| RMSE | 0.02 | 0.02 | 2.94 | 0.01 | 2.38 |
| ME | 0.00 | 0.01 | −2.00 | 0.01 | −0.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gildeh, H.K.; Mohammadian, A.; Nistor, I. Vertical Dense Effluent Discharge Modelling in Shallow Waters. Water 2022, 14, 2312. https://doi.org/10.3390/w14152312
Gildeh HK, Mohammadian A, Nistor I. Vertical Dense Effluent Discharge Modelling in Shallow Waters. Water. 2022; 14(15):2312. https://doi.org/10.3390/w14152312
Chicago/Turabian StyleGildeh, Hossein Kheirkhah, Abdolmajid Mohammadian, and Ioan Nistor. 2022. "Vertical Dense Effluent Discharge Modelling in Shallow Waters" Water 14, no. 15: 2312. https://doi.org/10.3390/w14152312








