Improving Results of Existing Groundwater Numerical Models Using Machine Learning Techniques: A Review
Abstract
:1. Introduction
1.1. Physically Based Models in Groundwater Management
1.2. Uncertainty and Error Types of Physically-Based Models
1.3. Machine Learning Models
1.4. Machine Learning for Groundwater Level Forecasting: Current State of the Research
1.5. Aim of This Work
2. Modelling Techniques Explored in This Review
2.1. Physically Based Numerical Groundwater Flow Models
2.2. Machine Learning Models
2.2.1. Artificial Neural Networks (ANNs)
2.2.2. Radial Basis Function Network (RBF)
2.2.3. Adaptive Neuro-Fuzzy Inference System (ANFIS)
2.2.4. Time Lagged Recurrent Neural Networks (TLRNs)
2.2.5. Extreme Learning Machine (ELM)
2.2.6. Bayesian Network (BN)
2.2.7. Instance-Based Weighting (IBW)
2.2.8. Support Vector Machine (SVM)
2.2.9. Decision Trees (DT)
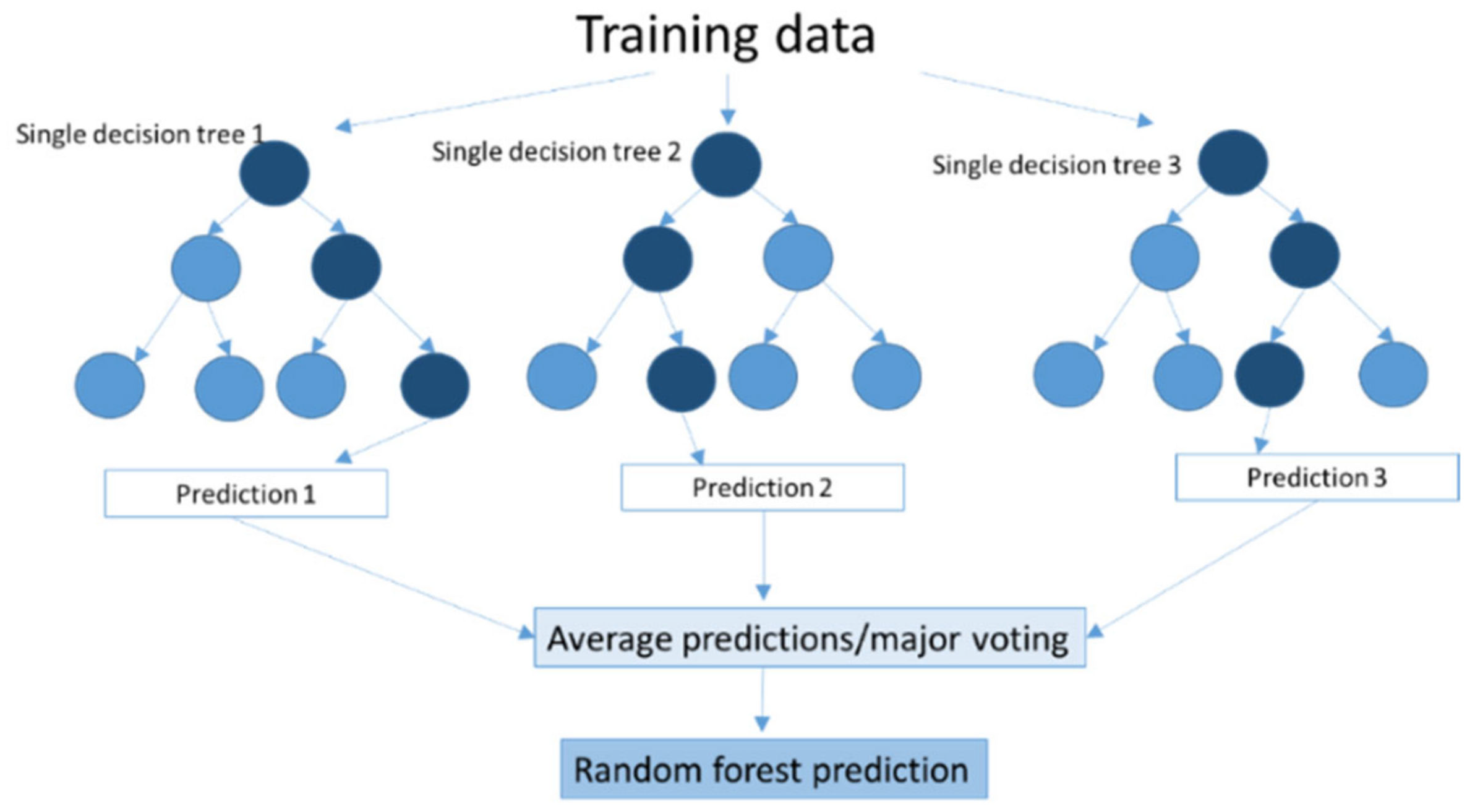
2.2.10. Random Forest (RF)
2.2.11. Gradient-Boosted Regression Trees (GBRT)
3. Bibliographic Review
3.1. Comparing Results of a Physically-Based Model and a Surrogate Machine Learning Model
- (1)
- The sensitivity of ANN performance to data availability was assessed by using different sizes of training sets. The results showed that, during validation, acceptable prediction accuracy was achieved with a relatively small number of training sets.
- (2)
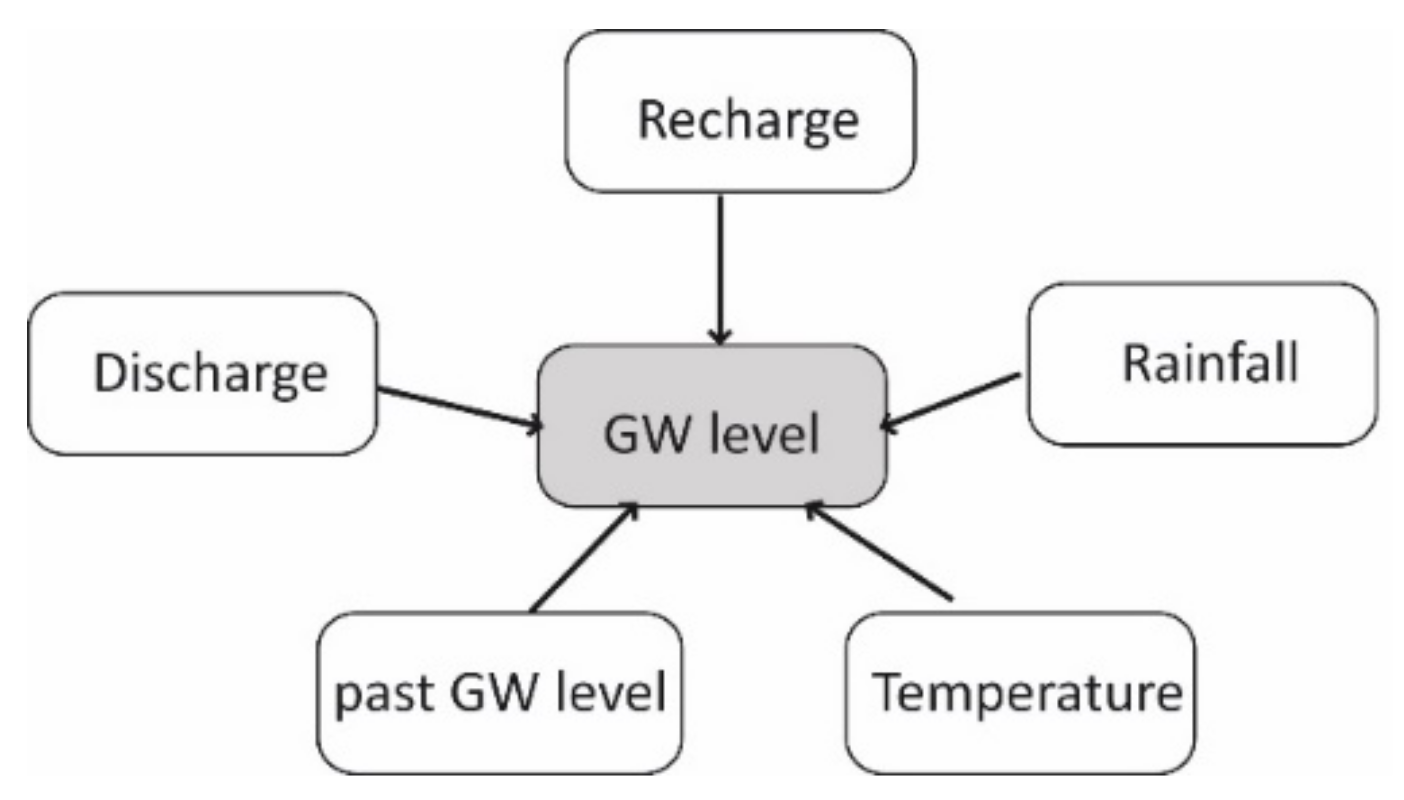
- Input parameters groundwater withdrawals and rainfall were included in the sensitivity analysis. Results showed that, in the unconfined aquifer, short-term oscillations were correlated most strongly to rainfall, while in the underlying semiconfined aquifer the water level was mostly influenced by withdrawals. Since these results are in accordance with the hydrological conditions, the authors concluded that the physical dynamics of the system must be sufficiently understood by the modeller in order to identify the important predictor input variables.
- (3)
- The effect of measurement error and data noise (inherently present in most hydrologic data set) on ANN performance was assessed by introducing normally distributed random noise into the input variables of the training set. The results demonstrated that the ANN can filter out noise in the training data and effectively learn groundwater system behaviour.
3.2. Comparing Results of a Physically-Based Model and Different Machine Learning Models
3.3. Testing Hybrid or Ensemble Models
3.4. Reducing and Correcting Model Errors by Means of Machine Learning Approaches
4. General Results
4.1. Key Area of Groundwater Model Use
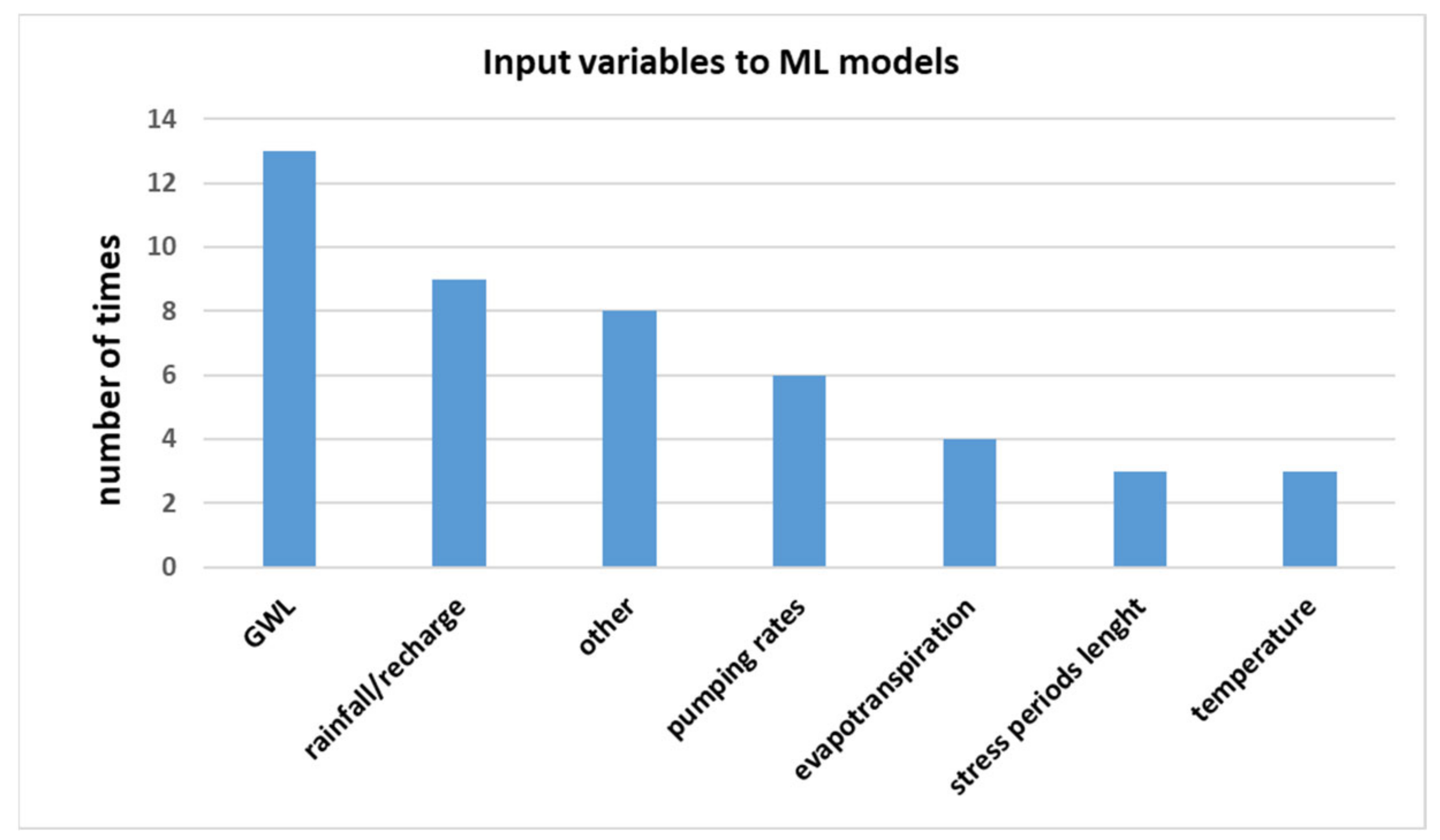
4.2. Input Variables Employed for Machine Learning Modelling
4.3. Simulation Period of Physically-Based Models
4.4. Time Step
4.5. Data Set Size
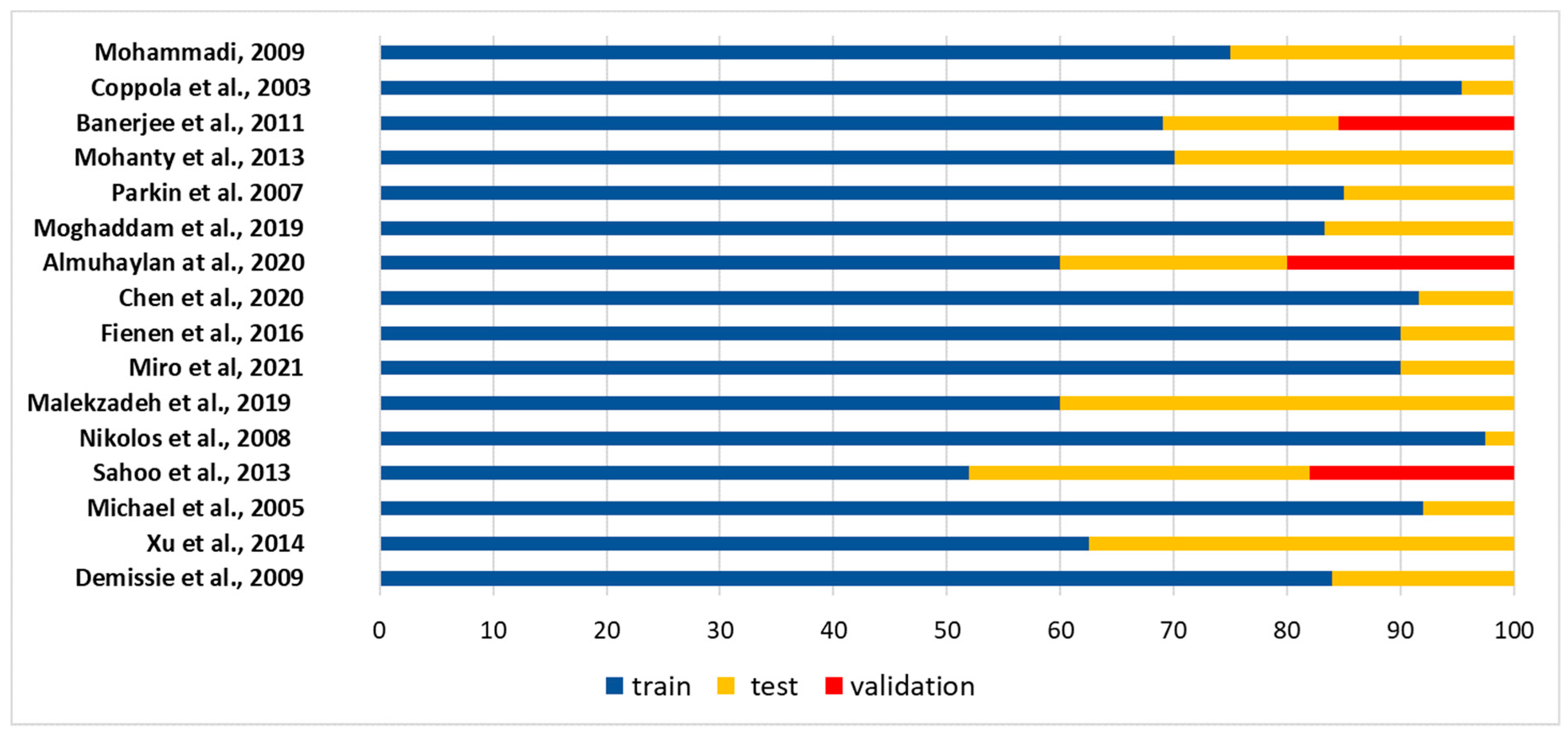
4.6. Subset for Machine Learning Model Training, Validation and Testing
4.7. Used Software
5. Specific Results
5.1. Properties of the Machine Learning Techniques Used in the Reviewed Papers
- -
- Feed-forward multilayer perceptron with a backpropagation learning algorithm was the most used ANN technique in the reviewed papers.
- -
- The training algorithms used in the reviewed papers were Levenberg Marquardt, Bayesian regularisation, scaled conjugate gradient, quick propagation algorithm, backpropagation algorithm, and resilient backpropagation. The most used were Levenberg Marquardt [60,117], which integrates the advantages of two training algorithms, namely the steepest descent, and Gaussian–Newton methods, and searches for the global minima function to optimise the solution [68]; some authors point out that this is the less time-consuming algorithm.
- -
- The transfer functions used for the hidden layer are: sigmoid, sine, hardlim, triangle basis, radial basis, hyperbolic tangent, linear, and logistic.
- -
- The most common structure of ANN in the reviewed papers is a feed-forward ANN with a single hidden layer, with sigmoid transfer function in the hidden layer and linear transfer function in output layer. The best structure and number of hidden neurons are chosen by trial-and-error or cross-validation.
- -
- The final structure of multilayer perceptron is usually chosen as the one resulting in minimum error and maximum efficiency during training.
- -
- ANNs are capable of achieving substantially higher predictive accuracy at observation wells than the physically-based numerical model, with fewer inputs and lower developmental effort and cost. The choice of the appropriate training data size is a key issue; it should be evaluated considering many aspects, such as the required model accuracy, the number of connection weights, the complexity, and the level of noise in the system [3]. Moreover, it is important to find the optimal ANN topology ensuring satisfactory generalisation capability for any given problem. This is generally achieved by testing different topologies and transfer functions.
5.2. Comparison between Machine Learning Techniques
- -
- The performance of ANN with RBF as the activation function performed the best in simulating groundwater dynamics in arid basins, compared with ANN multilayer perceptron and SVM [63]. In detail, SVM performed the best in the training stage, while RBF in the verification stage; ANN’s performance was lower than these two.
- -
- Regarding ANFIS, no improvements are remarked with respect to ANNs, although greater performance with respect to the MODFLOW numerical model is documented [68].
- -
- With respect to multilayer perceptron ANN, TLRNs can provide an appropriate tool for processing time-varying information. The main advantage is that TLRNs require a lower memory compared to multilayer perceptron, due to their lower network size. Furthermore, TLRNs have a low sensitivity to noise.
- -
- Compared to simple ANN, ELM showed better performance, much less modelling time, less modelling error, and less weights norm [100].
- -
- With respect to ANN, BN models provided easier implementation, higher prediction accuracy, and a greater ability to deal with missing or incomplete data [46]. It allows an uncertainty estimation more accurate than other machine learning models because the variables are modelled by means of probability distributions. When used as a metamodel, replacing a regional groundwater model to simulate the source of water-to-well [95], BN showed lower cross validation predictive skill compared with ANN and GBRT. However, the BN includes estimates of the uncertainty of predictions as part of the technique. GBRT required the least time with respect to BN and ANN. Thus, in this case, the choice between a statistical learning approach such as ANN or GBRT and the BN approach depends upon the preference of the modeller and the aims of the problem.
- -
- When used to predict the annual change in GWL as effect of managed recharge, RF produced the most accurate average basin GWL representation respect to observations, compared with SVM and ANN [99].
5.3. Results of Testing Hybrid or Ensemble Models
- -
- ELM and WA-ELM were both used to simulate GWL in an arid basin [100]. However, the ELM model with the db2 mother wavelet for data pre-processing showed a better performance with a significant accuracy improvement compared with the physically-based models.
- -
- The hybrid approach of Nikolos et al. [101] provides a fast way to integrate the physically-based models within an evolution-based optimisation procedure (DE algorithm) by replacing the calls of the PTC model with an ANN. The ANN provides a tool to perform an optimisation run with the DE algorithm with very short time, serving as a fast and accurate surrogate model.
- -
- The hybrid modelling approach HANN [102] showed a high model structure strength since it integrated a robust data pre-processing and input variable selection techniques.
- -
- Using machine learning models in hierarchical approach can significantly improve the results of physics-based models [82]; moreover, by that way, advantages and disadvantages of different machine learning models are identified and insights are provided into which data are most valuable to long-term monitoring objectives and which are not. In particular, Michael et al. [82] found that DT consistently provided the most accurate predictions of hydraulic head compared with IDW and ANN. However, when using all of the data across time, IDW showed substantial improvements. Given that IDW is simple to use and is widely accepted among practitioners, it could be considered as an optimum choice.
- -
- The computational time of regional physically-based models can be substantially reduced by introducing an empirical (or statistical) representation of numerical models; this consists of machine learning models trained using numerical models inputs and outputs, which can be used to make predictions of variable of interest [95,99].
5.4. Results of Machine Learning Models Used to Reduce or Correct Errors in Physically-Based Models
6. Discussion
- -
- The numerical models are comparatively more reliable. While showing a lower prediction error than the physical models, machine learning models cannot return many of the outputs of a physical model, such as flux estimates or total water balance.
- -
- Xu et al. [79] found that data-driven models are difficult to interpret physically. The updated head no longer conserved mass for the given model inputs, which can confound the physical interpretation of the results and prevent understanding errors in the conceptualisation of the groundwater system.
- -
- Numerical models exhibit a higher generalisation ability than machine learning methods because they are based on the physics of the system [63]. Conversely, machine learning models are applicable to problems that require a high number of model runs without considering the physical system (e.g., optimisations, real-time models, sensitivity/uncertainty analysis).
- -
- Usually, while the machine learning models may be more efficacious for predicting short-term GWL and reproducing highly localised flow impacts, numerical modelling is more appropriate for long-term projections, or in areas where field data are insufficient for the given problem. However, it should be remarked that Almuhaylan et al. [68] were able to use machine learning models to perform long-term prediction (up to 50 years), by training the ANN/ANFIS model for the prediction of changes in groundwater levels instead of the direct simulation of water levels.
- -
- when few field data exist, the results of numerical models can be improved by training machine learning models, which allow to obtain accurate groundwater level forecasting at specific observation wells;
- -
- machine learning models cannot substitute a numerical model as one single model, but can be used to simulate water table fluctuation at every individual observation well with reduced computational time;
- -
- accurate results of machine learning models in specific test sites can be used to obtain the best GWL data required by the numerical model as input;
- -
- the physical dynamics of the system must be sufficiently understood by the modeller in order to identify the important predictor input variables of machine learning models. Results of numerical models help to understand the physical system; this can help, in turn, choosing the input parameters for machine learning models. Coppola et al. [3] suggested using ANNs to perform a sensitivity analysis on the interrelationships between input and output variables;
- -
- Numerical models can simulate different scenarios, allowing for detection areas requiring particular management strategies, thereby supporting the design of an effective monitoring network, which, in turn, may improve both machine learning predictive capability and performance.
- -
- The aim of the work, for example: improvement of prediction at some well location, numerical model error correction, numerical model updating;
- -
- the need to produce a probability distribution of the results and obtain uncertainty estimation within the model, (i.e., in areas with few data);
- -
- the availability of data for training and testing (number and spatial-temporal distribution);
- -
- the need to speed up decision making processes and reduce the computational time;
- -
- the degree of expertise of the modeller, which should drive the searching for a good compromise between model complexity and prediction performance.
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Daliakopoulos, I.N.; Tsanis, I.K. Comparison of an artificial neural network and a conceptual rainfall–runoff model in the simulation of ephemeral streamflow. Hydrol. Sci. J. 2016, 61, 2763–2774. [Google Scholar] [CrossRef]
- Besaw, L.E.; Rizzo, D.M.; Bierman, P.R.; Hackett, W.R. Advances in ungauged streamflow prediction using artificial neural networks. J. Hydrol. 2010, 386, 27–37. [Google Scholar] [CrossRef]
- Coppola, E., Jr.; Szidarovszky, F.; Poulton, M.; Charles, E. Artificial neural network approach for predicting transient water levels in a multilayered groundwater system under variable state, pumping, and climate conditions. J. Hydrol. Eng. 2003, 8, 348–360. [Google Scholar] [CrossRef]
- Neuman, S.P.; Wierenga, P.J. A Comprehensive Strategy of Hydrogeologic Modeling and Uncertainty Analysis for Nuclear Facilities and Sites (NUREG/CR-6805); Report prepared for US Nuclear Regulatory Commission: Washington, DC, USA, 2003; p. 309. [Google Scholar]
- Cooley, R.L. A theory for modeling ground-water flow in heterogeneous media. In US Geological Survey Professional Paper 1679; U.S. Geological Survey: Reston, VA, USA, 2004; p. 220. [Google Scholar]
- Doherty, J.; Christensen, S. Use of paired simple and complex models to reduce predictive bias and quantify uncertainty. Water Resour. Res. 2011, 47, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Refsgaard, J.C.; van der Sluijs, J.P.; Brown, J.; van der Keur, P. A framework for dealing with uncertainty due to model structure error. Adv. Water Resour. 2006, 29, 1586–1597. [Google Scholar] [CrossRef] [Green Version]
- Hunt, R.J.; Welter, D.E. Taking account of “unknown unknowns”. GroundWater 2010, 48, 477. [Google Scholar] [CrossRef]
- Tiedeman, C.R.; Hill, M.C. Model calibration and issues related to validation, sensitivity analysis, post-audit, uncertainty evaluation and assessment of prediction data needs. In Groundwater: Resource Evaluation, Augmentation, Contamination, Restoration, Modeling and Management; Thangarajian, M., Ed.; Springer: New York, NY, USA, 2007; pp. 237–282. [Google Scholar]
- Liu, Y.; Gupta, H.V. Uncertainty in hydrologic modeling: Toward an integrated data assimilation framework. Water Resour. Res. 2007, 43, 1–18. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Stauffer, P.H.; Wohling, T.; Robinson, B.A.; Vesselinov, V.V. Inverse modeling of subsurface flow and transport properties: A review with new developments. Vadose Zone J. 2008, 7, 843–864. [Google Scholar] [CrossRef]
- Bierkens, M.F. Modeling water table fluctuations by means of a stochastic differential equation. Water Resour. Res. 1998, 34, 2485–2499. [Google Scholar] [CrossRef]
- Bidwell, V.J. Realistic forecasting of groundwater level, based on the Eigenstructure of aquifer dynamics. Math. Comput. Simul. 2005, 69, 12–20. [Google Scholar] [CrossRef] [Green Version]
- Maier, H.R.; Dandy, G.C. The use of artificial neural networks for the prediction of water quality parameters. Water Resour. Res. 1996, 32, 1013–1022. [Google Scholar] [CrossRef]
- Maity, R.; Nagesh Kumar, D. Probabilistic prediction of hydroclimatic variables with nonparametric quantification of uncertainty. J. Geophys. Res. Atmos. 2008, 113, 1–12. [Google Scholar] [CrossRef]
- Vellido, A.; Martín-Guerrero, J.D.; Lisboa, P.J. Making machine learning models interpretable. In Proceedings of the European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Bruges, Belgium, 25–27 April 2012; pp. 163–172. [Google Scholar]
- Abraham, A.; Pedregosa, F.; Eickenberg, M.; Gervais, P.; Mueller, A.; Kossaifi, J.; Gramfort, A.; Thirion, B.; Varoquaux, G. Machine learning for neuroimaging with scikit-learn. Front. Neuroinform. 2014, 14, 1–10. [Google Scholar]
- Park, C.; Took, C.C.; Seong, J.K. Machine learning in biomedical engineering. Biomed. Eng. Lett. 2018, 8, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Reich, Y. Machine learning techniques for civil engineering problems. Comput.-Aided Civ. Infrastruct. Eng. 1997, 12, 295–310. [Google Scholar] [CrossRef]
- Reich, Y.; Barai, S.V. Evaluating machine learning models for engineering problems. Artif. Intell. Eng. 1999, 13, 257–272. [Google Scholar] [CrossRef]
- Vadyala, S.R.; Betgeri, S.N.; Matthews, J.C.; Matthews, E. A review of physics-based machine learning in civil engineering. Results Eng. 2021, 13, 100316. [Google Scholar] [CrossRef]
- Zander, S.; Nguyen, T.; Armitage, G. Automated traffic classification and application identification using machine learning. In Proceedings of the IEEE Conference on Local Computer Networks 30th Anniversary, Sydney, Australia, 15–17 November 2005; (LCN’05) l. pp. 250–257. [Google Scholar]
- Yu, H.; Wu, Z.; Wang, S.; Wang, Y.; Ma, X. Spatiotemporal recurrent convolutional networks for traffic prediction in transportation networks. Sensors 2017, 17, 1501. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.; Kieu, L.M.; Wen, T.; Cai, C. Deep learning methods in transportation domain: A review. IET Intell. Transp. Syst. 2018, 12, 998–1004. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Kamrava, S.; Bai, T.; Sahimi, M. Machine learning in geo-and environmental sciences: From small to large scale. Adv. Water Resour. 2020, 142, 103619. [Google Scholar] [CrossRef]
- Sun, A.Y.; Scanlon, B.R. How can Big Data and machine learning benefit environment and water management: A survey of methods, applications, and future directions. Environ. Res. Lett. 2019, 14, 073001. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef] [Green Version]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef] [Green Version]
- Choubin, B.; Mosavi, A.; Alamdarloo, E.H.; Hosseini, F.S.; Shamshirband, S.; Dashtekian, K.; Ghamisi, P. Earth fissure hazard prediction using machine learning models. Environ. Res. 2019, 179, 108770. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Jeong, J.H.; Resop, J.P.; Mueller, N.D.; Fleisher, D.H.; Yun, K.; Butler, E.E.; Timlin, D.J.; Shim, K.-M.; Gerber, J.S.; Reddy, V.R.; et al. Random forests for global and regional crop yield predictions. PLoS ONE 2016, 11, e0156571. [Google Scholar] [CrossRef]
- Lamorski, K.; Šimůnek, J.; Sławiński, C.; Lamorska, J. An estimation of the main wetting branch of the soil water retention curve based on its main drying branch using the machine learning method. Water Resour. Res. 2017, 53, 1539–1552. [Google Scholar] [CrossRef] [Green Version]
- Povak, N.A.; Hessburg, P.F.; McDonnell, T.C.; Reynolds, K.M.; Sullivan, T.J.; Salter, R.B.; Cosby, B.J. Machine learning and linear regression models to predict catchment-level base cation weathering rates across the southern Appalachian Mountain region, USA. Water Resour. Res. 2014, 50, 2798–2814. [Google Scholar] [CrossRef]
- Singh, N.; Chakrapani, G. ANN modelling of sediment concentration in the dynamic glacial environment of Gangotri in Himalaya. Env. Monit Assess 2015, 187, 1–14. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, J.J. A comparison of methods to avoid overfitting in neural networks training in the case of catchment runoff modelling. J. Hydrol. 2013, 476, 97–111. [Google Scholar] [CrossRef]
- Kingston, G.B.; Maier, H.R.; Lambert, M.F. Calibration and validation of neural networks to ensure physically plausible hydrological modeling. J. Hydrol. 2005, 314, 158–176. [Google Scholar] [CrossRef]
- Solomatine, D.P. Data-driven modeling and computational intelligence methods in hydrology. In Encyclopedia of Hydrological Sciences; Anderson, M., Ed.; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Deka, P.C. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar]
- Lange, H.; Sippel, S. Machine learning applications in hydrology. In Forest-Water Interactions; Levia, D.F., Carlyle-Moses, D.E., Lida, S., Michalzik, B., Nanko, K., Tischer, A., Eds.; Ecological Studies; Springer Nature: Cham, Switzerland, 2020; Volume 240, pp. 233–257. [Google Scholar] [CrossRef]
- Rasouli, K.; Hsieh, W.W.; Cannon, A.J. Daily streamflow forecasting by machine learning methods with weather and climate inputs. J. Hydrol. 2012, 414, 284–293. [Google Scholar] [CrossRef]
- Xu, T.; Liang, F. Machine learning for hydrologic sciences: An introductory overview. Wiley Interdiscip. Rev. Water 2021, 8, e1533. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.W. An enhanced extreme learning machine model for river flow forecasting: State-of-the-art, practical applications in water resource engineering area and future research direction. J. Hydrol. 2019, 569, 387–408. [Google Scholar] [CrossRef]
- Wu, W.; Dandy, G.C.; Maier, H.R. Protocol for developing ANN models and its application to the assessment of the quality of the ANN model development process in drinking water quality modelling. Environ. Model. Softw. 2014, 54, 108–127. [Google Scholar] [CrossRef]
- Fienen, M.N.; Nolan, B.T.; Kauffman, L.J.; Feinstein, D.T. Metamodeling for groundwater age forecasting in the Lake Michigan Basin. Water Resour. Res. 2018, 54, 4750–4766. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Solomatine, D.P. Applications of data-driven modelling and machine learning in control of water resources. In Computational Intelligence in Control; Mohammadian, M., Sarker, R.A., Yao, X., Eds.; Idea Group Publishing: Hershey, PA, USA, 2002; pp. 197–217. [Google Scholar]
- Yan, J.; Jia, S.; Lv, A.; Zhu, W. Water resources assessment of China’s transboundary river basins using a machine learning approach. Water Resour. Res. 2019, 55, 632–655. [Google Scholar] [CrossRef]
- Nourani, V.; Baghanam, A.H.; Adamowski, J.; Kisi, O. Applications of hybrid wavelet–artificial intelligence models in hydrology: A review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]
- Rajaee, T.; Ebrahimi, H.; Nourani, V. A review of the artificial intelligence methods in groundwater level modeling. J. Hydrol. 2019, 572, 336–351. [Google Scholar] [CrossRef]
- McDonald, M.G.; Harbaugh, A.W. A modular three-dimensional finite-difference ground-water flow model. In US Geological Survey Report 06-A1; US Geological Survey: Reston, VA, USA, 1988; p. 586. [Google Scholar]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; Mcdonald, M.G. MODFLOW-2000, the US geological survey modular ground-water model—User guide to modularization concepts and the ground-water flow process. In US Geological Survey Open-File Report 00-92; US Geological Survey: Reston, VA, USA, 2000; p. 121. [Google Scholar]
- Winston, R.B. MODFLOW-related freeware and shareware resources on the internet. Comput. Geosci. 1999, 25, 377–382. [Google Scholar] [CrossRef]
- Voss, C.I. A Finite-Element Simulation Model for Saturated–Unsaturated, Fluid-Density-dependent Ground-Water Flow with Energy Transport or Chemically Reactive Single-species. In Water-Resources Investigations Report 84-4369; US Geological Survey: Reston, VA, USA, 1984. [Google Scholar] [CrossRef]
- Babu, D.K.; Pinder, G.F. A finite element–finite difference alternating direction algorithm for 3- dimensional groundwater transport. Adv. Water Resour. 1984, 7, 116–119. [Google Scholar] [CrossRef]
- Bentley, L.R.; Kieper, G.M. Verification of the Princeton Transport Code (PTC). In Engineering Hydrology, Proceedings of the Symposium Sponsored by the Hydraulics Division of the American Society of Civil Engineers, San Francisco, CA, USA, 25–30 July 1993; American Society of Civil Engineers: New York, NY, USA, 1993; pp. 1037–1042. [Google Scholar]
- Ewen, J.; Parkin, G.; O’Connell, P.E. SHETRAN: A coupled surface/subsurface modelling system for 3D water flow and sediment and solute transport in river basins. ASCE J. Hydrol. Eng. 2000, 5, 250–258. [Google Scholar] [CrossRef] [Green Version]
- Hsu, K.L.; Gupta, H.V.; Sorooshian, S. Artificial neural network modeling of the rainfall-runoff process. Water Resour. Res. 1995, 31, 2517–2530. [Google Scholar] [CrossRef]
- Schalkoff, R.J. Artificial Neural Networks; McGraw-Hill Higher Education: New York, NY, USA, 1997; p. 448. [Google Scholar]
- Mohammadi, K. Groundwater Table Estimation Using MODFLOW and Artificial Neural Networks. In Practical Hydroinformatics; Abrahart, R.J., See, L.M., Solomatine, D.P., Eds.; Water Science and Technology Library: Springer: Berlin/Heidelberg, Germany, 2009; Volume 68. [Google Scholar] [CrossRef]
- Samarasinghe, S. Neural Networks for Applied Sciences and Engineering: From Fundamentals to Complex Pattern Recognition; Auerbach Publications: New York, NY, USA, 2016; ISBN 0429115784. [Google Scholar]
- Taormina, R.; Chau, K.-W.; Sethi, R. Artificial neural network simulation of hourly groundwater levels in a coastal aquifer system of the Venice lagoon. Eng. Appl. Artifi. Intellig. 2012, 25, 1670–1676. [Google Scholar] [CrossRef] [Green Version]
- Wunsch, A.; Liesch, T.; Broda, S. Forecasting groundwater levels using nonlinear autoregressive networks with exogenous input (NARX). J. Hydrol. 2018, 567, 743–758. [Google Scholar] [CrossRef]
- Chen, C.; He, W.; Zhou, H.; Xue, Y.; Zhu, M. A comparative study among machine learning and numerical models for simulating groundwater dynamics in the Heihe River Basin, northwestern China. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Schwenker, F.; Kestler, H.A.; Palm, G. Three learning phases for radial-basis-function networks. Neural Netw. 2001, 14, 439–458. [Google Scholar] [CrossRef]
- Buhmann, M.D. Radial Basis Functions: Theory and Implementations; Cambridge University Press: Cambridge, UK, 2003; p. 258. [Google Scholar]
- Jang, J.S.R. ANFIS adaptive-network-based fuzzy inference systems. IEEE Trans. Syst. Man. Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Kurtulus, B.; Razack, M. Modeling daily discharge responses of a large karstic aquifer using soft computing methods: Artificial neural network and neuro-fuzzy. J. Hydrol. 2010, 381, 101–111. [Google Scholar] [CrossRef]
- Almuhaylan, M.R.; Ghumman, A.R.; Al-Salamah, I.S.; Ahmad, A.; Ghazaw, Y.M.; Haider, H.; Shafiquzzaman, M. Evaluating the Impacts of Pumping on Aquifer Depletion in Arid Regions Using MODFLOW, ANFIS and ANN. Water 2020, 12, 2297. [Google Scholar] [CrossRef]
- Chen, S.H.; Lin, Y.H.; Chang, L.C.; Chang, F.J. The strategy of building a flood forecast model by neuro fuzzy network. Hydr. Proc. 2006, 20, 1525–1540. [Google Scholar] [CrossRef]
- Haykin, S. Communication Systems, 2nd ed.; Wiley: New York, NY, USA, 1994; pp. 45–90. [Google Scholar]
- Saharia, M.; Bhattacharjya, R.K. Geomorphology-based time-lagged recurrent neural networks for runoff forecasting. KSCE J. Civ. Eng. 2012, 16, 862–869. [Google Scholar] [CrossRef]
- Sattari, M.; Taghi, K.Y.; Pal, M. Performance evaluation of artificial neural network approaches in forecasting reservoir inflow. Appl. Math. Model. 2012, 36, 2649–2657. [Google Scholar] [CrossRef]
- Huang, G.B.; Chen, L.; Siew, C.K. Universal approximation using incremental constructive feedforward networks with random hidden nodes. IEEE Trans. Neural Netw. 2006, 17, 879–892. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.B.; Chen, L. Convex incremental extreme learning machine. Neurocomputing 2007, 70, 3056–3062. [Google Scholar] [CrossRef]
- Huang, G.B.; Chen, L. Enhanced random search based incremental extreme learning machine. Neurocomputing 2008, 71, 3460–3468. [Google Scholar] [CrossRef]
- Moghaddam, H.K.; Moghaddam, H.K.; Rahimzadeh Kivi, Z.; Bahreinimotlagh, M.; Javad Alizadeh, M. Developing comparative mathematic models, BN and ANN for forecasting of groundwater levels. Groundw. Sustain. Dev. 2019, 9, 100237. [Google Scholar] [CrossRef]
- Cleary, J.G.; Trigg, L.E. K*: An instance-based learner using an entropic distance measure. In Machine Learning, Proceedings of the Twelfth International Conference, San Francisco, CA, USA, 9–12 July 1995; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1995; pp. 108–114. [Google Scholar]
- Smith, E.E.; Medin, D.L. Categories and Concepts; Harvard University Press: Cambridge, MA, USA, 1981; p. 203. [Google Scholar]
- Xu, T.; Valocchi, A.J.; Choi, J.; Amir, E. Use of machine learning methods to reduce predictive error of groundwater models. Groundwater 2014, 52, 448–460. [Google Scholar] [CrossRef]
- Aha, D.W. Feature Weighting for Lazy Learning algorithms. In Feature Extraction, Construction and Selection: A Data Mining Perspective; The American Statistical Association: Boston, MA, USA, 1998; Volume 1, p. 410. [Google Scholar]
- Aha, D.W.; Kibler, D.; Albert, M.C. Instance-Based Learning Algorithms. Mach. Learn. 1991, 6, 37–66. [Google Scholar] [CrossRef] [Green Version]
- Michael, W.J.; Minsker, B.S.; Tcheng, D.; Valocchi, A.J.; Quinn, J.J. Integrating data sources to improve hydraulic head predictions: A hierarchical machine learning approach. Water Resour. Res. 2005, 41, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; p. 314. [Google Scholar]
- Gunn, S.R. Support vector machines for classification and regression. In ISIS Technical Report; University of Southampton: Southampton, UK, 1998; p. 66. [Google Scholar]
- Demissie, Y.K.; Valocchi, A.J.; Minsker, B.S.; Bailey, B.A. Integrating a calibrated groundwater flow model with error-correcting data-driven models to improve predictions. J. Hydrol. 2009, 364, 257–271. [Google Scholar] [CrossRef]
- Yoon, H.; Jun, S.-C.; Hyun, Y.; Bae, G.-O.; Lee, K.-K. A comparative study of artificial neural networks and support vector machines for predicting groundwater levels in a coastal aquifer. J. Hydrol. 2011, 396, 128–138. [Google Scholar] [CrossRef]
- Cao, L.J.; Chua, K.S.; Chong, W.K.; Lee, H.P.; Gu, Q.M. A comparison of PCA, KPCA and ICA for dimensionality reduction in support vector machine. Neurocomputing 2003, 55, 321–336. [Google Scholar] [CrossRef]
- Vapnik, V.N. Statistical Learning Theory; John Wiley & Sons: New York, NY, USA, 1998; p. 768. [Google Scholar]
- Smola, A.J.; Sch¨olkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routhledge: New York, NY, USA, 1984; p. 368. [Google Scholar]
- Anderton, S.P.; White, S.M.; Alvera, B. Evaluation of spatial variability of snow water equivalent in a high mountain catchment. Hydrol. Processes 2004, 18, 435–453. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Aertsen, W.; Kint, V.; Van Orshoven, J.; Muys, B. Evaluation of Modelling Techniques for Forest Site Productivity Prediction in Contrasting Ecoregions Using Stochastic Multicriteria Acceptability Analysis (SMAA). Environ. Model. Softw. 2011, 26, 929–937. [Google Scholar] [CrossRef] [Green Version]
- Fienen, M.N.; Nolan, B.T.; Feinstein, D.T. Evaluating the sources of water to wells: Three techniques for metamodeling of a groundwater flow model. Environ. Model. Softw. 2016, 77, 95–107. [Google Scholar] [CrossRef]
- Banerjee, P.; Singh, V.S.; Chatttopadhyay, K.; Chandra, P.C.; Singh, B. Artificial neural network model as a potential alternative for groundwater salinity forecasting. J. Hydrol. 2011, 398, 212–220. [Google Scholar] [CrossRef]
- Mohanty, S.; Jha, M.K.; Kumar, A.; Sudheer, K.P. Artificial neural network modeling for groundwater level forecasting in a river island of eastern India. Water Resour. Manag. 2010, 24, 1845–1865. [Google Scholar] [CrossRef]
- Parkin, G.; Birkinshaw, S.J.; Younger, P.L.; Rao, Z.; Kirk, S. A numerical modelling and neural network approach to estimate the impact of groundwater abstractions on river flows. J. Hydrol. 2007, 339, 15–28. [Google Scholar] [CrossRef]
- Aghlmand, R.; Abbasi, A. Application of MODFLOW with boundary conditions analyses based on limited available observations: A case study of Birjand plain in East Iran. Water 2019, 11, 1904. [Google Scholar] [CrossRef] [Green Version]
- Feinstein, D.T.; Eaton, T.T.; Hart, D.J.; Krohelski, J.T.; Bradbury, K.R. Regional aquifer model for southeastern Wisconsin; Report 1: Data collection, conceptual model development, numerical model construction, and model calibration. In US Geological Survey Techniques Report; US Geological Survey: Reston, VA, USA, 2005. [Google Scholar]
- Miro, M.E.; Groves, D.; Tincher, B.; Syme, J.; Tanverakul, S.; Catt, D. Adaptive water management in the face of uncertainty: Integrating machine learning, groundwater modeling and robust decision making. Clim. Risk Manag. 2021, 34, 100383. [Google Scholar] [CrossRef]
- Malekzadeh, M.; Kardar, S.; Shabanlou, S. Simulation of groundwater level using MODFLOW, extreme learning machine and Wavelet-Extreme Learning Machine models. Groundw. Sustain. Dev. 2019, 9, 100279. [Google Scholar] [CrossRef]
- Nikolos, I.K.; Stergiadi, M.; Papadopoulou, M.P.; Karatzas, G.P. Artificial neural networks as an alternative approach to groundwater numerical modelling and environmental design. Hydrol. Processes Int. J. 2008, 22, 3337–3348. [Google Scholar] [CrossRef]
- Sahoo, S.; Jha, M.K. Groundwater-level prediction using multiple linear regression and artificial neural network techniques: A comparative assessment. Hydrogeol. J. 2013, 21, 1865–1887. [Google Scholar] [CrossRef]
- Clark, B.R.; Hart, R.M.; Gurdak, J.J. Groundwater availability of the Mississippi Embayment. In US Geological Survey Professional Paper 2011; US Geological Survey: Reston, VA, USA, 1785; p. 62. [Google Scholar]
- Luckey, R.R.; Becker, M.F. Hydrogeology, water use, and simulation of flow in the High Plains aquifer in northwestern Oklahoma, southeastern Colorado, southwestern Kansas, northeastern New Mexico, and northwestern Texas. In US Geological Survey Water Resources Investment Report 99-4104; US Geological Survey: Reston, VA, USA, 1999; p. 73. [Google Scholar]
- Quinn, J.J.; Negri, M.C.; Hinchman, R.R.; Moos, L.P.; Wozniak, J.B.; Gatliff, E.G. Predicting the effect of deep-rooted hybrid poplars on the groundwater flow system at a large-scale phytoremediation site. Int. J. Phytoremediation 2001, 3, 41–60. [Google Scholar] [CrossRef]
- Lefebvre, C.; Principe, J. NeuroSolutions User’s Guide; Neurodimension Inc.: Gainesville, FL, USA, 1998; p. 786. [Google Scholar]
- Uusitalo, L. Advantages and challenges of Bayesian networks in environmental modelling. Ecol. Model. 2007, 203, 312–318. [Google Scholar] [CrossRef]
- Liu, Z.; Malone, B.; Yuan, C. Empirical evaluation of scoring functions for Bayesian network model selection. BMC Bioinform. 2012, 13, 1–16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Misiti, M.; Misiti, Y.; Oppenheim, G.; Poggi, J.M. Wavelet Toolbox for Use with Matlab; The Mathworks, Inc.: Natick, MA, USA, 1996; p. 1030. [Google Scholar]
- Nikolos, I.K. Inverse design of aerodynamic shapes using differential evolution coupled with artificial neural network. In Proceedings of the ERCOFTAC Conference in Design Optimization: Methods and Applications, Athens, Greece, 31 March–2 April 2004. [Google Scholar]
- Feinstein, D.T.; Hunt, R.; Reeves, H. Regional groundwater-flow model of the Lake Michigan Basin in support of Great Lakes Basin water availability and use studies. In Scientific Investigations Report 2010–5109; United States Geological Survey: Reston, VA, USA, 2010. [Google Scholar]
- Fienen, M.N.; Nolan, B.T.; Feinstein, D.T.; Starn, J.J. Metamodels to Bridge the Gap between Modeling and Decision Support; United States Geological Survey: Reston, VA, USA, 2015; p. 860. [Google Scholar]
- Republican River Compact Administration (RRCA). Appendix A: Groundwater Model for 1918–2000 (June 30, 2003). Available online: https://www.republicanrivercompact.org/v12p/html/ch01.html (accessed on 4 April 2022).
- Welge, M.; Auvil, L.; Shirk, A.; Bushell, C.; Bajcsy, P.; Cai, D.; Redman, T.; Clutter, D.; Aydt, R.; Tcheng, D. Data to Knowledge, Technical Report; Automated Learning Group, National Center for Supercomputing Applications: Urbana, IL, USA, 2003. [Google Scholar]
- Djurovic, N.; Domazet, M.; Stricevic, R.; Pocuca, V.; Spalevic, V.; Pivic, R.; Gregoric, E.; Domazet, U. Comparison of Groundwater Level Models Based on Artificial Neural Networks and ANFIS. Sci. World J. 2015, 13, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| n | Reference | Region of Study (Country) | Key Area of Model Use | Used ML Models | Input Variables to ML Model | ML Model Time Step | Range of Total Data (Number of Data or Observation Wells) | PB Simulation Time (Time Step) | Size of the PB Model Domain | Field of Application of the ML Technique | Journal (202+C:L0 IF) | Aquifer or Basin Hydrostratigraphy |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Mohammadi, 2009 [59] | Chamchamal plain (Iran) | Farming and agricoltural systems | ANN | MODFLOW output | monthly | 1986–1998 (144 sets) | 1 year (monthly) | 145.7 Km2 | using the results of PB models to train a single ML model | Pratical hydroinformatics (book) | Alluvial (karst bedrock) |
| 2 | Coppola et al., 2003 [3] | Northwest Hillsborough Wellfield (USA) | Planning and supply | ANN | GWL, pumping rates, P, T, dew point, wind speed conditions, stress period lenghts | weekly | January 1995–August 2000, (212 sets) | 20 years (monthly) | 10,359.9 Km2 | using the results of PB models to train a single ML model | Journal of hydrologic engineering (2.064) | Highly permeable limestone overlain by low permeability clay and, above, sand with interbedded clay |
| 3 | Banajeree et al., 2011 [96] | Kavaratti, island of the Lakshadweep archipelago (India) | Coastal water management | ANN | not mentioned in the paper | monthly | 2005–2007 (23 sets) | 5 years (monthly) | 2D model, with section lenght = 2650 m and depth 1000 m | using the results of PB models to train a single ML model | Journal of hydrology (5.722) | Coastal |
| 4 | Mohanty et al., 2013 [97] | Kathajodi-Surua Inter-basin of Odisha (India) | Coastal water management | ANN, TLRNs | GWL, P, E, river stage, SWL, pumping rates | weekly | February 2004–May 2007 (174 sets) | 3 years, (weekly) | 114.5 m2 | using the results of PB models to train a single ML model | Journal of hydrology (5.722) | Alluvial |
| 5 | Parkin et al., 2007 [98] | Winterbourne stream, Thames Basin, Berkshire (UK) | aquifer-river interaction | ANN | GWL, river flow depletion | daily | Not specified (1 well) | 25 years (daily) | Regional aquifer: 200 Km2. Valley aquifer: 2 Km2 | using the results of PB models to train a single ML model | Journal of hydrology (5.722) | Alluvial |
| 6 | Moghaddam et al., 2019 [76] | BirjandAquifer, South Khorasan (Iran) | Drought-prone regions | ANN, BN | GWL, E, T, EP, Discharge | monthly | 2002–2014 (1872 sets) | 12 years | 277.8 Km2 ([99]) | using the results of PB models to train and compare different ML models | Groundwater for sustainable development (no IF) | Alluvial |
| 7 | Almuhaylan at al., 2020 [68] | Saq Aquifer in Quassim (Saudi Arabia) | Drought-prone regions | ANN, ANFIS | GWL, pumping rates | not specified | 1980–2018 (55 wells) | not specified | 600 Km2 | using the results of PB models to train and compare different ML models | Water (3.103) | Sandstone |
| 8 | Chen et al., 2020 [63] | Heihe River Basin (China) | Drought-prone regions | ANN, RBF, SVM | pumping rates, recharge, streamflow rates | monthly | 1986–2008 (11,088 sets) | 22 years (monthly) | 21,120 Km2 | using the results of PB models to train and compare different ML models | Scientific reports (4.380 | Alluvial |
| 9 | Fienen et al., 2016 [95] | Lake Michigan Basin (USA) | Planning and supply | ANN, GBRT, BN | parameters expected to have predictive power to the source of water to wells | not specified | 1864–2005, (4911 sets) | 141 years (variable, [100]) | 204,764.4 Km2 | using the results of PB models to train and compare different ML models | Environmental modelling and software (5.288) | Glacial deposits |
| 10 | Miro et al., 2021 [101] | San Bernardino and Rialto-Colton basins, San Bernardino Valley Municipal Water District - Valley District (USA) | Drought-prone regions | RF, SVM, ANN | Recharge, pumping rates | not specified | 2015–2050 (not specified) | 35 years (monthly) | 3000 Km2 | using the results of PB models to train and compare different ML models | Climate risk management (4.090) | Basin comprising ancient metamorphic bedrock, eolic sands, ancient fans, recent alluvium |
| 11 | Malekzadeh et al., 2019 [102] | Kabodarahang Plain, Hamadan (Iran) | Farming and agricoltural systems | ELM, WA-ELM | decomposed sub-series of observed GWL | monthly | August 1990–September 2015 (301 sets) | 10 years (monthly) | not specified | using the results of PB models to train a single ML model | Groundwater for sustainable development (no IF) | Alluvial (limestone bedrock) |
| 12 | Nikolos et al., 2008 [103] | Northern Rhodes Island (Greece) | Coastal water management | ANN combined with DE algorithm | GWL, pumping rates | daily | 1997–1998 (3125 sets) | 1 year (2 seasonal stress periods) | 217 Km2 | using the results of PB models to test hybrid or ensamble modelling approaches | Hydrological processes (3.565) | Coastal |
| 13 | Sahoo et al., 2017 [104] | High Plains aquifer and Mississippi River Valley aquifer (USA) | Farming and agricoltural systems | Automated hybrid artificial neural network (HANN) | GWL, P, T, streamflow, climate indexes, irrigation demand, NAO index | monthly | 1980–2012, (HPA: 263,808 sets. MRVA: 115,368 sets) | 33 years (monthly) | MRVA: 405,720 Km2 ([105]). HPA: 3.34 Km2 ([106]) | using the results of PB models to test hybrid or ensamble modelling approaches | Water resource research (5.240) | High Plain Aquifer: ancient alluvial fans and quaternary deposits. Mississippi River Valley Alluvial Aquifer: Tertiary and Quaternary clay, silt, sand and gravel deposits. |
| 14 | Michael et al., 2005 [82] | Argonne National Laboratory, Illinois (USA) | Contaminant/phytoremediation | DT, IDW, ANN | GWL, P | quartely | November 1999–March 2001 (22 wells with quarterly data); May 2001 (7 wells with hourly data) | 6 years, (monthly) | 4.8 Km2 ([107]) | using the results of PB models to test hybrid or ensamble modelling approaches | Water resource research (5.240) | Glacial deposits |
| 15 | Xu et al., 2014 [79] | Republican River Basin and Spokane Valley-Rathdrum Prairie aquifer (USA) | Planning and supply | Cluster analysis, IBW, SVM | GWL, well location, observation time | monthly | RRCA: 1918–2007 (300,000 sets). SVRP: 1990–2005 (2191 sets) | RRCA: 89 years. SVRP: 15 years, (monthly) | RRCA: 79,396 Km2. SVRP: 844.3 Km2 | using ML techniques for PB models errors reduction/correction | Groundwater (2.671) | Alluvial |
| 16 | Demissie et al., 2009 [85] | Argonne National Laboratory, Illinois (USA) | Contaminant/phytoremediation | ANN, DT, SVM, IBW | GWL, EVP, stress periods | monthly | 2000–2005, (3600 sets) [107] | 6 year (monthly) | 0.75 Km2 | using ML techniques for PB models errors reduction/correction | Journal of hydrology (5.722) | Glacial deposits |
| Machine Learning Model | Software | Commercial/Free | n of Times |
|---|---|---|---|
| ANN | Matlab | c | 3 |
| R-neuralnet package | f | 1 | |
| LINGO | c | 1 | |
| not specified | 7 | ||
| RBF | Matlab | c | 1 |
| ANFIS | Matlab | c | 1 |
| TLRN | NeuroSolution | c | 1 |
| ELM, WA-ELM | Matlab, Matlab wavelet toolbox | c | 1 |
| BN | Hugin Lite 8.3; | c | 1 |
| netica Software, CVNetica (for cv) | c | 1 | |
| IBW | Matlab Statistic Toolbox TM | c | 1 |
| not specified | 1 | ||
| SVM | Matlab Statistic Toolbox TM | c | 2 |
| not specified | 2 | ||
| DT | not specified | 1 | |
| RF | R (randomForest package) | f | 1 |
| not specified | 1 | ||
| GBRT | Phyton (scikit-learn library) | f | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Salvo, C. Improving Results of Existing Groundwater Numerical Models Using Machine Learning Techniques: A Review. Water 2022, 14, 2307. https://doi.org/10.3390/w14152307
Di Salvo C. Improving Results of Existing Groundwater Numerical Models Using Machine Learning Techniques: A Review. Water. 2022; 14(15):2307. https://doi.org/10.3390/w14152307
Chicago/Turabian StyleDi Salvo, Cristina. 2022. "Improving Results of Existing Groundwater Numerical Models Using Machine Learning Techniques: A Review" Water 14, no. 15: 2307. https://doi.org/10.3390/w14152307
APA StyleDi Salvo, C. (2022). Improving Results of Existing Groundwater Numerical Models Using Machine Learning Techniques: A Review. Water, 14(15), 2307. https://doi.org/10.3390/w14152307






