Grid-Point Rainfall Trends, Teleconnection Patterns, and Regionalised Droughts in Portugal (1919–2019)
Abstract
:1. Introduction
2. Material and Models
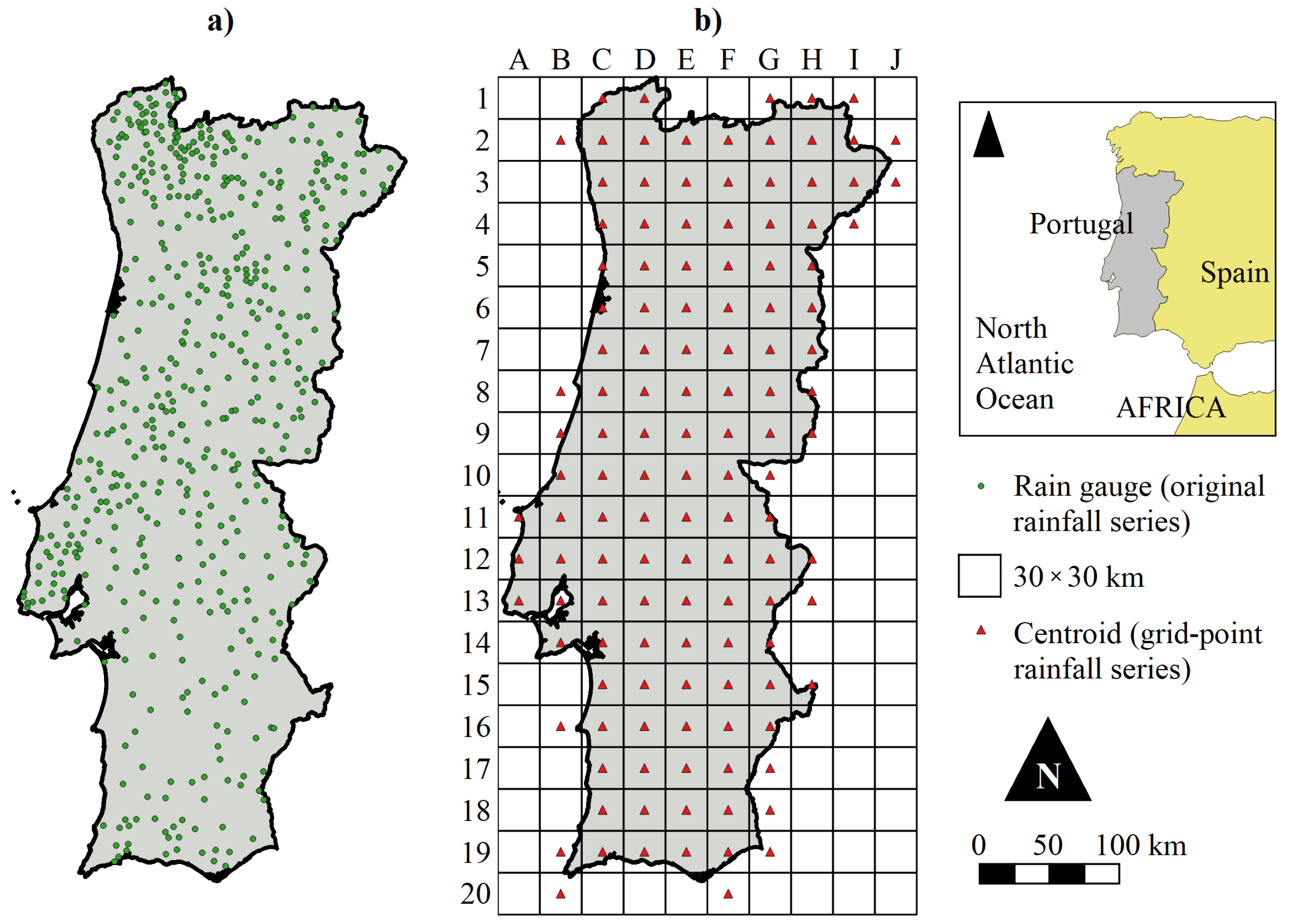
2.1. Grid-Point Rainfall and North Atlantic Oscillation Index Data Set
2.2. Monotonic and Sequential Trend Models
- The values of the original series were replaced by their ranks , arranged in ascending order.
- The magnitudes of , , were compared with , , and at each of the comparisons, the number of cases were counted and denoted by .
- A statistic was defined as follows:
- The mean and variance of the test statistic were computed as:
- The sequential values of the statistic u() were then calculated as:
3. Results
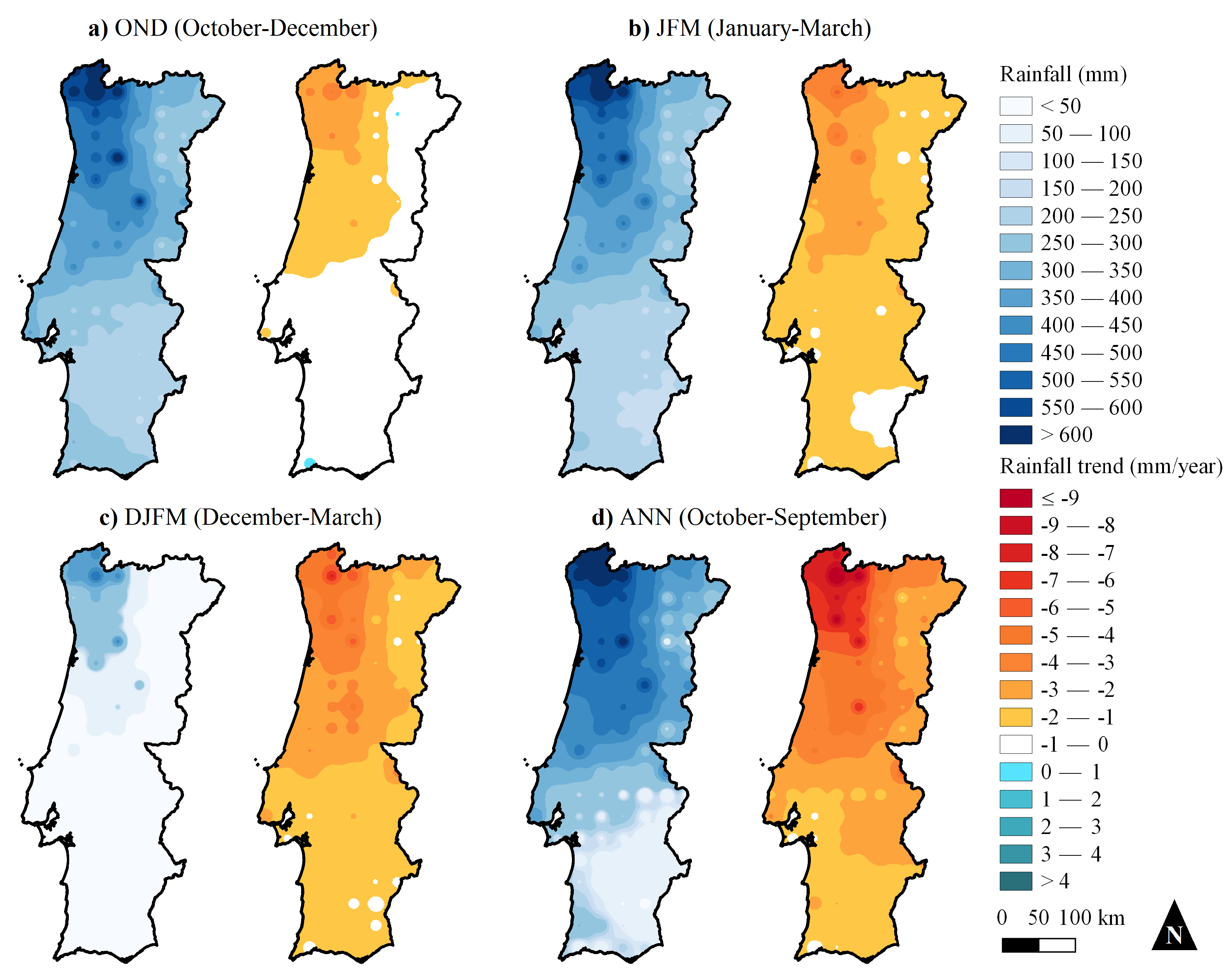
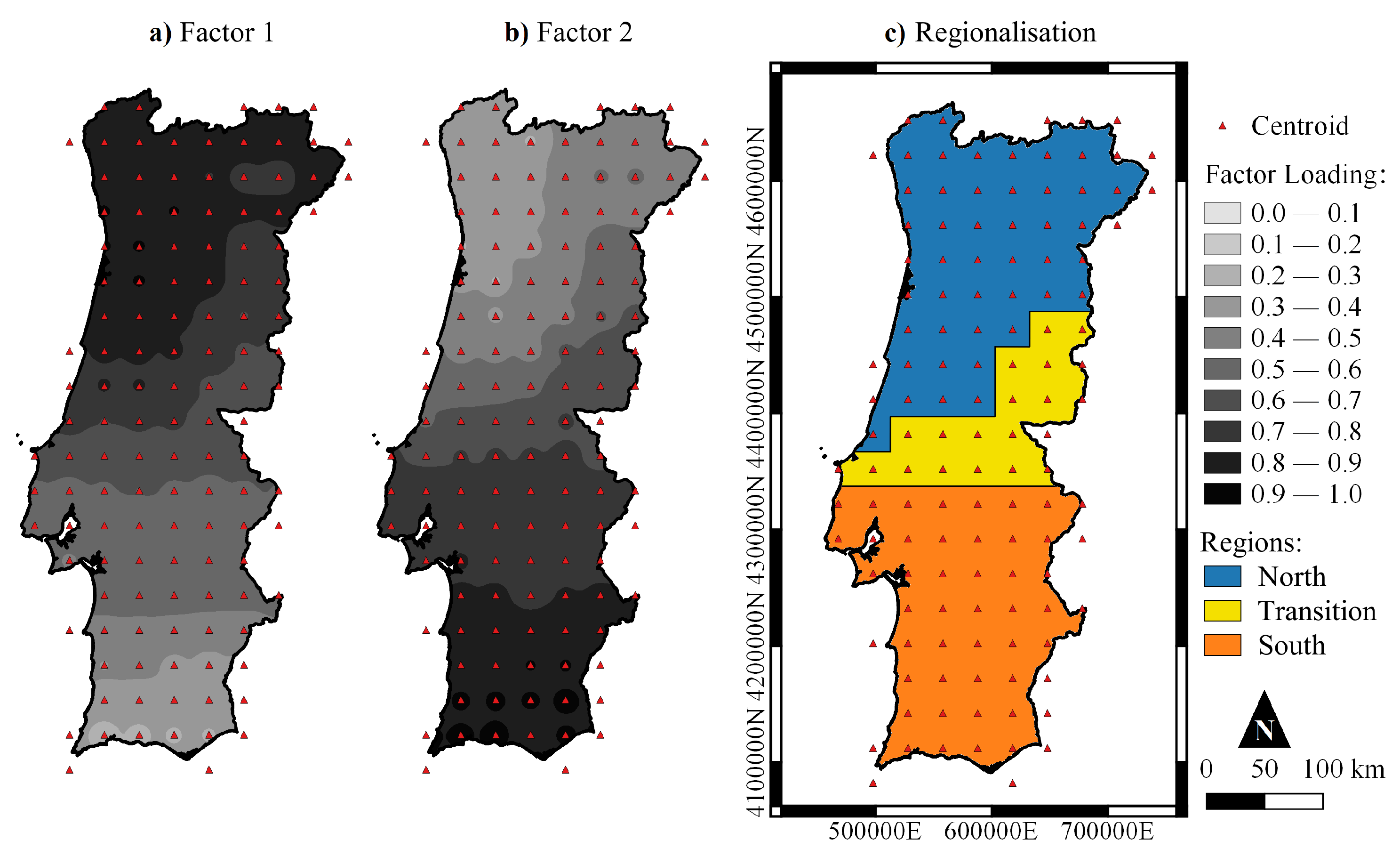
3.1. Spatial Distribution of the Grid-Point Rainfall and Their Trends
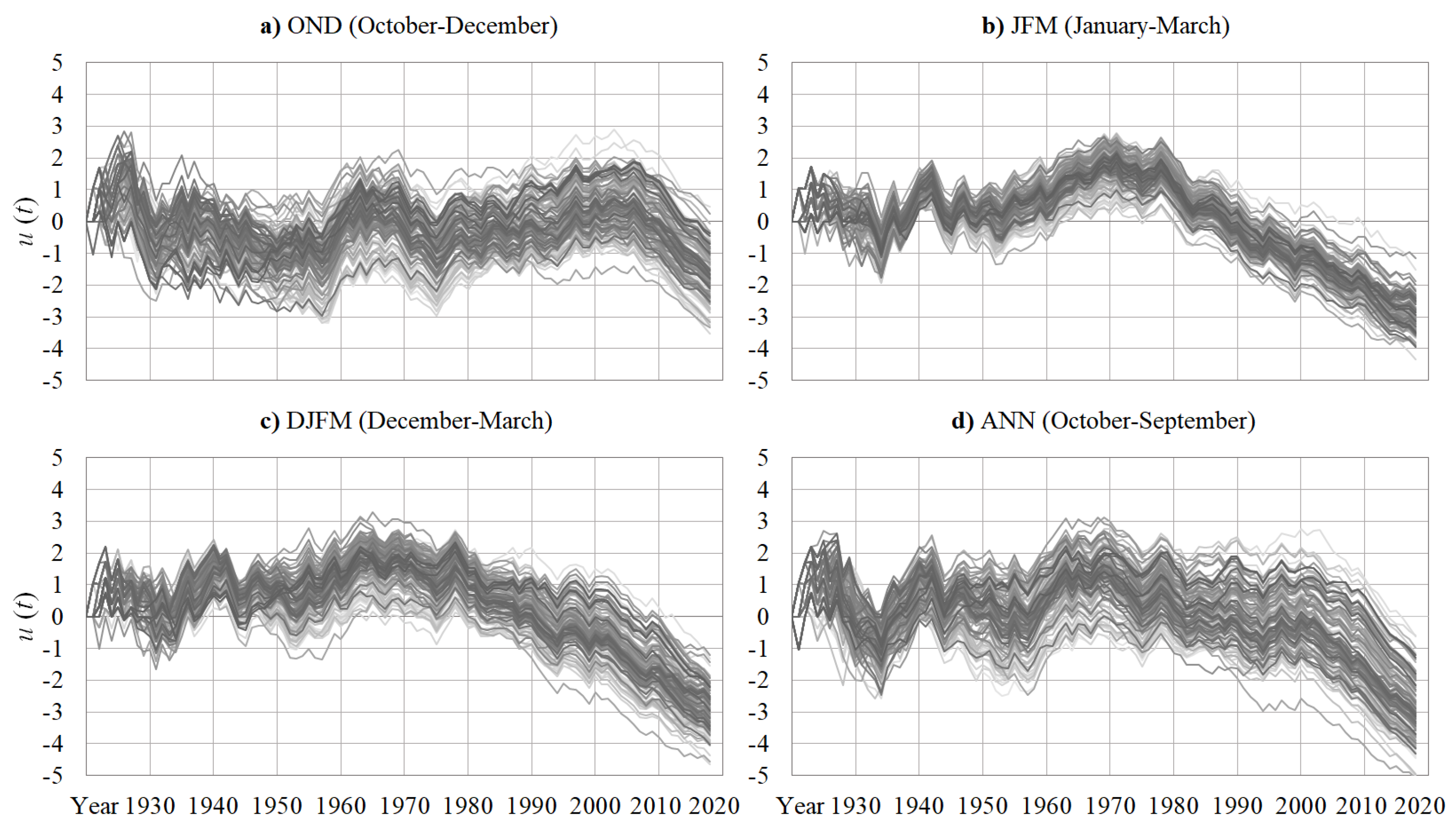
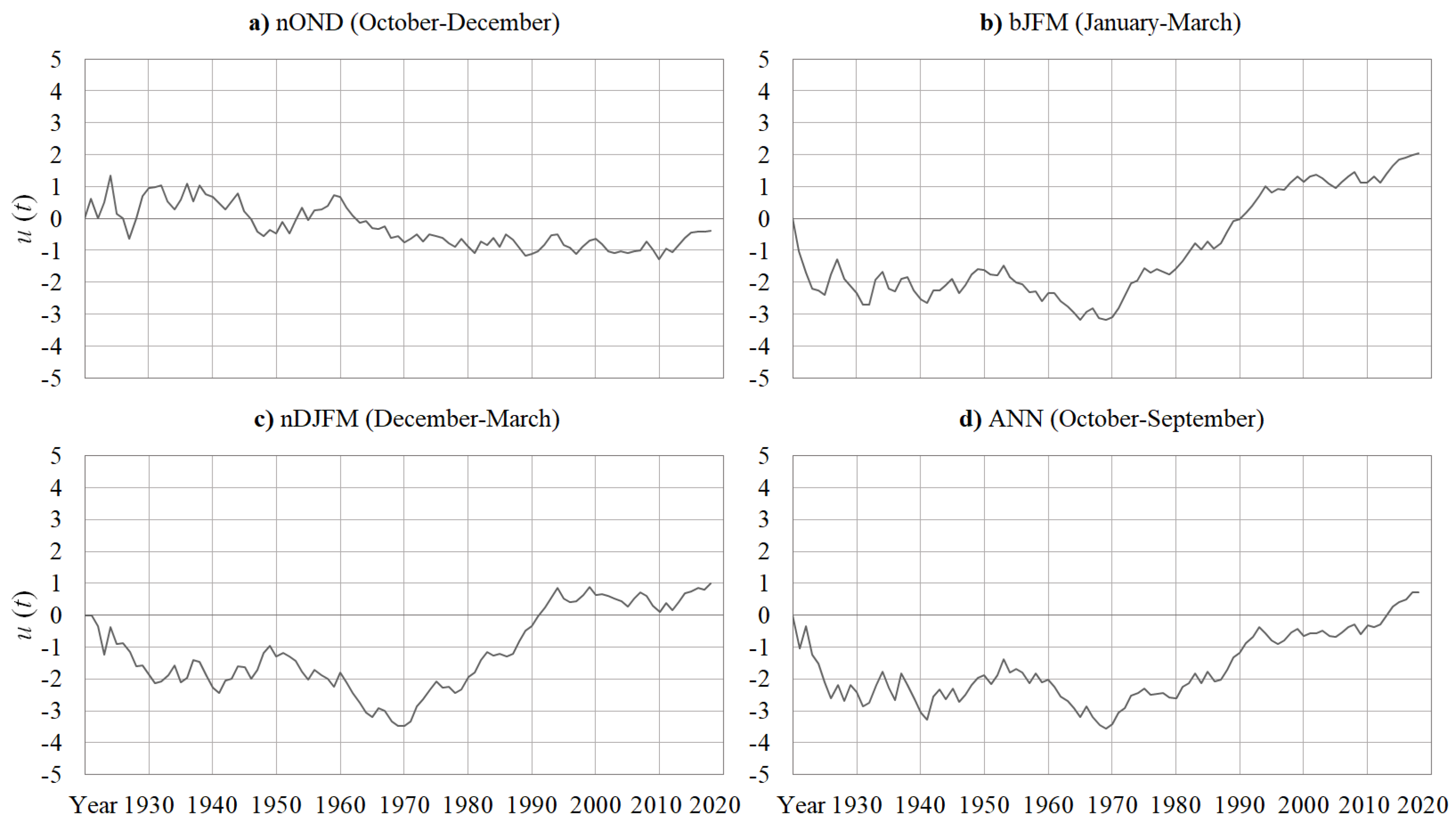
3.2. Sequential Observed Trends in Rainfall and in the North Atlantic Oscillation
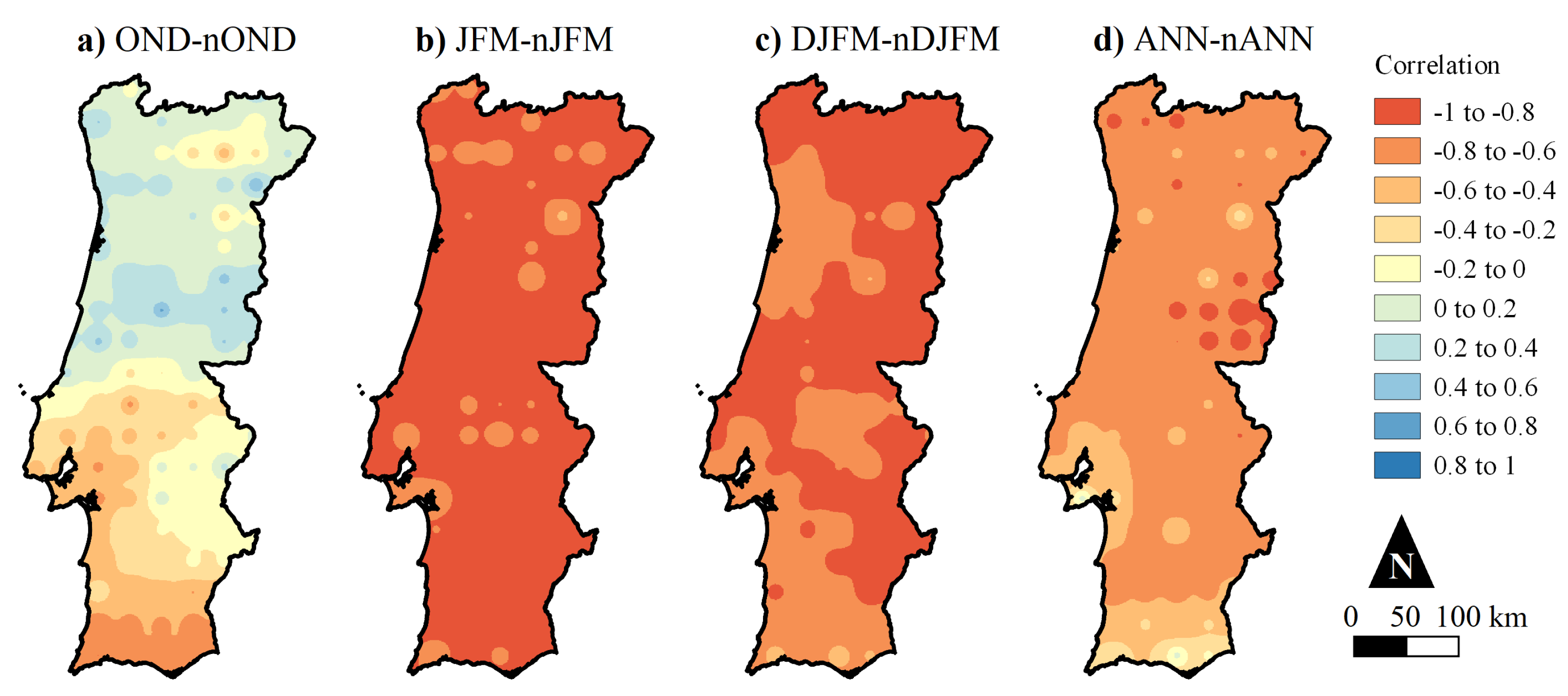
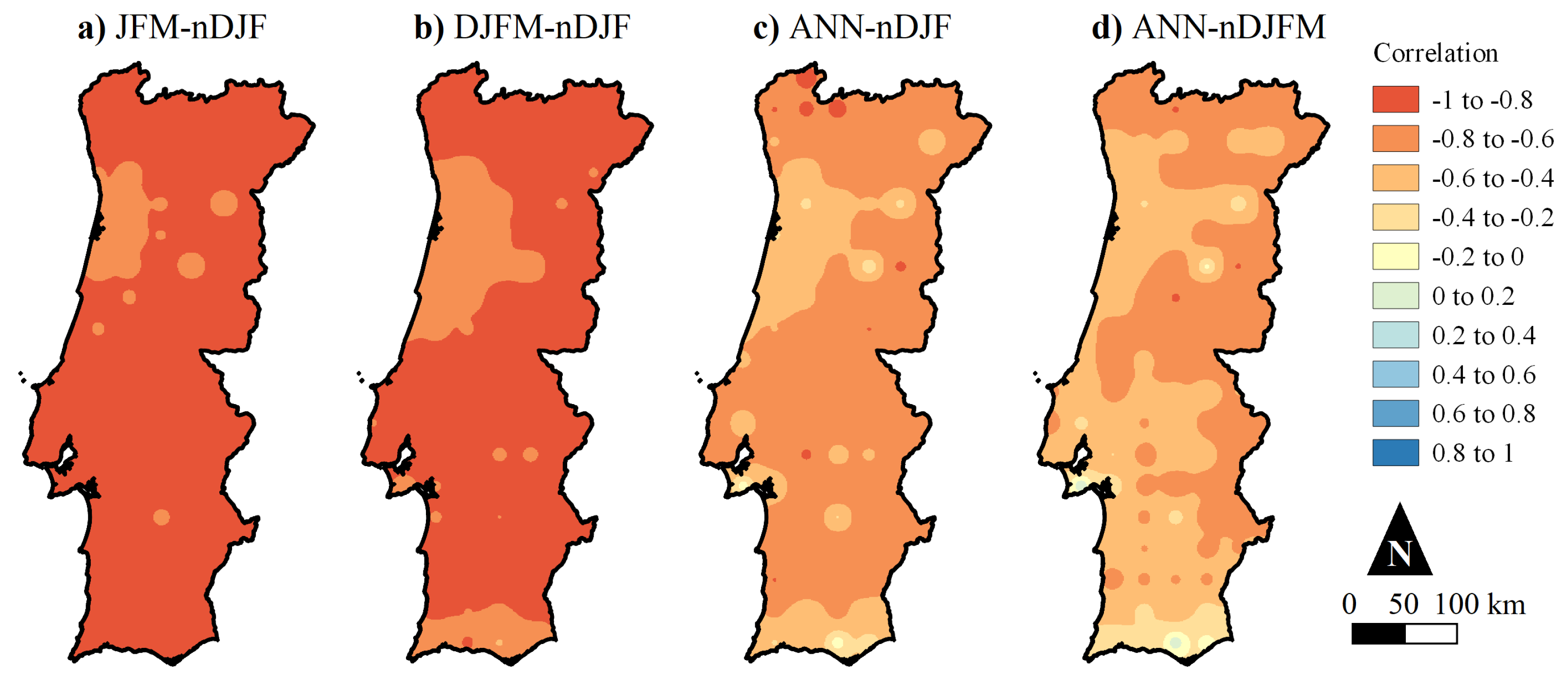
3.3. Teleconnection between the Grid-Point Rainfall Trends and the NAOI Trends
4. Discussion
4.1. Persistent Influence of the North Atlantic Oscillation on Rainfall Trends
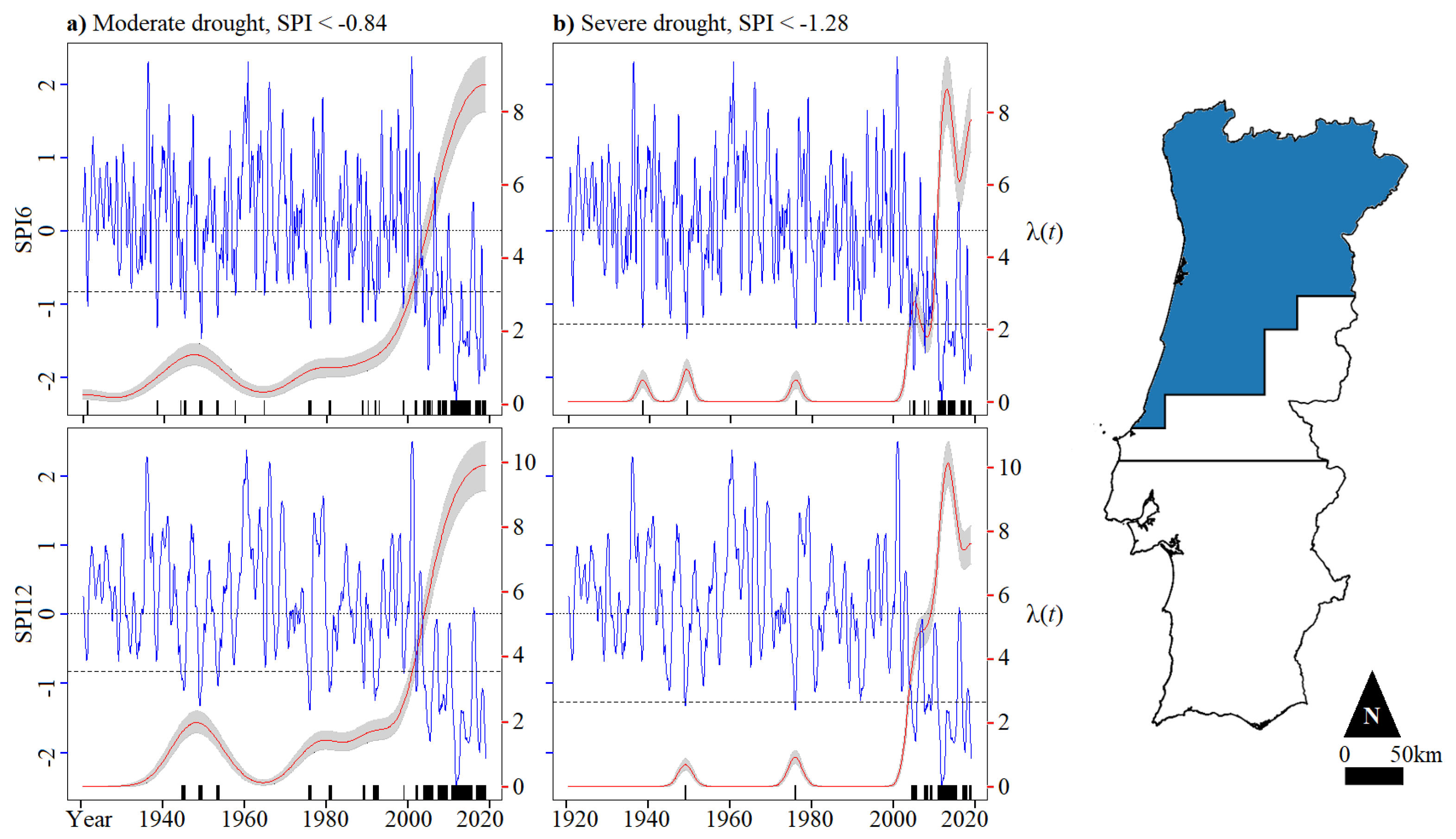
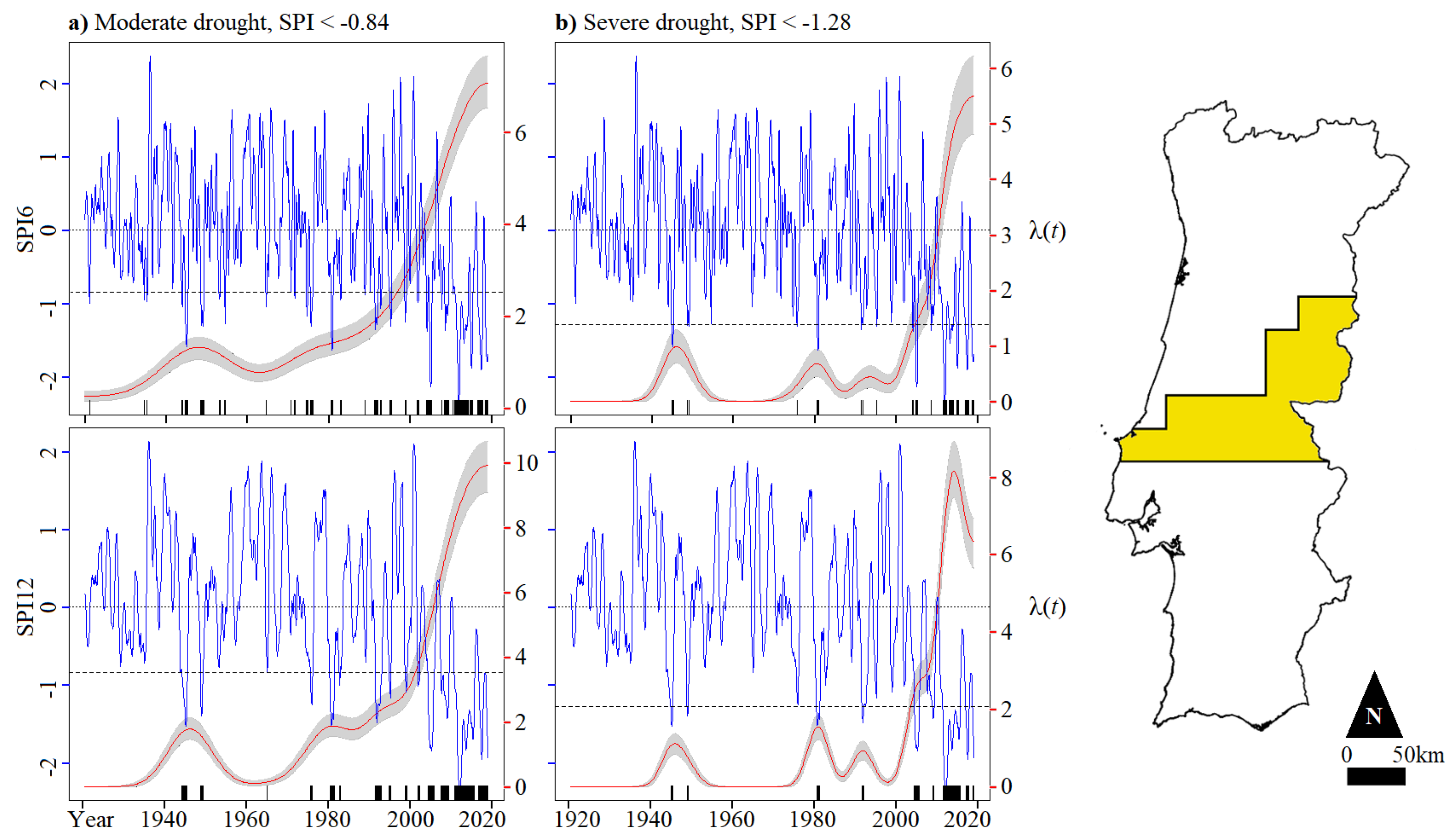
4.2. Regionalised Droughts in Portugal during 1919–2019
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zeleňáková, M.; Purcz, P.; Blišt’an, P.; Alkhalaf, I.; Hlavatá, H.; Portela, M.M.; Silva, A.T. Precipitation trends detection as a tool for integrated water resources management in Slovakia. Management 2017, 13, 17. [Google Scholar] [CrossRef]
- Harvey, L.D. Global Warming; Taylor & Francis Group: Abingdon, UK, 1999. [Google Scholar]
- Koutsoyiannis, D. Revisiting the global hydrological cycle: Is it intensifying? Hydrol. Earth Syst. Sci. 2020, 24, 3899–3932. [Google Scholar] [CrossRef]
- Rahmstorf, S.; Foster, G.; Cahill, N. Global temperature evolution: Recent trends and some pitfalls. Environ. Res. Lett. 2017, 12, 054001. [Google Scholar] [CrossRef]
- Change, C. IPCC fourth assessment report. Phys. Sci. Basis 2007, 2, 580–595. [Google Scholar]
- Pereira, S.C.; Carvalho, D.; Rocha, A. Temperature and Precipitation Extremes over the Iberian Peninsula under Climate Change Scenarios: A Review. Climate 2021, 9, 139. [Google Scholar] [CrossRef]
- Abrantes, F.; Rodrigues, T.; Rufino, M.; Salgueiro, E.; Oliveira, D.; Gomes, S.; Oliveira, P.; Costa, A.; Mil-Homens, M.; Drago, T. The climate of the Common Era off the Iberian Peninsula. Clim. Past 2017, 13, 1901–1918. [Google Scholar] [CrossRef] [Green Version]
- Costa, A.C.; Soares, A. Trends in extreme precipitation indices derived from a daily rainfall database for the South of Portugal. Int. J. Climatol. A J. R. Meteorol. Soc. 2009, 29, 1956–1975. [Google Scholar] [CrossRef]
- Santos, M.; Fragoso, M. Precipitation variability in Northern Portugal: Data homogeneity assessment and trends in extreme precipitation indices. Atmos. Res. 2013, 131, 34–45. [Google Scholar] [CrossRef]
- Da Silva, R.M.; Santos, C.A.; Moreira, M.; Corte-Real, J.; Silva, V.C.; Medeiros, I.C. Rainfall and river flow trends using Mann–Kendall and Sen’s slope estimator statistical tests in the Cobres River basin. Nat. Hazards 2015, 77, 1205–1221. [Google Scholar] [CrossRef]
- Nunes, A.; Lourenço, L. Precipitation variability in Portugal from 1960 to 2011. J. Geogr. Sci. 2015, 25, 784–800. [Google Scholar] [CrossRef]
- Santos, M.; Fonseca, A.; Fragoso, M.; Santos, J.A. Recent and future changes of precipitation extremes in mainland Portugal. Theor. Appl. Climatol. 2019, 137, 1305–1319. [Google Scholar] [CrossRef]
- Portela, M.M.; Espinosa, L.A.; Zelenakova, M. Long-term rainfall trends and their variability in mainland Portugal in the last 106 years. Climate 2020, 8, 146. [Google Scholar] [CrossRef]
- Portela, M.M.; Espinosa, L.A.; Zelenakova, M. Updated Rainfall Series and Their Trends for Mainland Portugal (1913–2019). WIT Trans. Ecol. Environ. 2021, 250, 3–12. [Google Scholar]
- Hurrell, J.W. Influence of variations in extratropical wintertime teleconnections on Northern Hemisphere temperature. Geophys. Res. Lett. 1996, 23, 665–668. [Google Scholar] [CrossRef]
- Rousi, E.; Rust, H.W.; Ulbrich, U.; Anagnostopoulou, C. Implications of winter NAO flavors on present and future European climate. Climate 2020, 8, 13. [Google Scholar] [CrossRef] [Green Version]
- Santos, J.; Corte-Real, J.; Leite, S. Weather regimes and their connection to the winter rainfall in Portugal. Int. J. Climatol. A J. R. Meteorol. Soc. 2005, 25, 33–50. [Google Scholar] [CrossRef]
- Trigo, R.M.; Zêzere, J.L.; Rodrigues, M.L.; Trigo, I.F. The influence of the North Atlantic Oscillation on rainfall triggering of landslides near Lisbon. Nat. Hazards 2005, 36, 331–354. [Google Scholar] [CrossRef]
- North, G.R.; Pyle, J.A.; Zhang, F. General Circulation of the Atmosphere | Teleconnections. Encyclopedia of Atmospheric Sciences; Elsevier: Amsterdam, The Netherlands, 2014; Volume 1. [Google Scholar]
- Espinosa, L.A.; Portela, M.M. Rainfall trends over a small island teleconnected to the North Atlantic oscillation-the case of Madeira Island, Portugal. Water Resour. Manag. 2020, 34, 4449–4467. [Google Scholar] [CrossRef]
- Espinosa, L.A.; Portela, M.M.; Rodrigues, R. Rainfall trends over a North Atlantic small island in the period 1937/1938–2016/2017 and an early climate teleconnection. Theor. Appl. Climatol. 2021, 144, 469–491. [Google Scholar] [CrossRef]
- Hurrell, J.; Ncar, S. The Climate Data Guide: Hurrell North Atlantic Oscillation (NAO) Index (Station-Based). 2020. Available online: https://climatedataguide.ucar.edu/climate-data/hurrell-north-atlantic-oscillation-nao-index-station-based (accessed on 10 December 2021).
- Hofstra, N.; Haylock, M.; New, M.; Jones, P.; Frei, C. Comparison of six methods for the interpolation of daily, European climate data. J. Geophys. Res. Atmos. 2008, 113, 3–9. [Google Scholar] [CrossRef] [Green Version]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Prasanna, V.; Subere, J.; Das, D.K.; Govindarajan, S.; Yasunari, T. Development of daily gridded rainfall dataset over the Ganga, Brahmaputra and Meghna river basins. Meteorol. Appl. 2014, 21, 278–293. [Google Scholar] [CrossRef]
- Bartier, P.M.; Keller, C.P. Multivariate interpolation to incorporate thematic surface data using inverse distance weighting (IDW). Comput. Geosci. 1996, 22, 795–799. [Google Scholar] [CrossRef]
- Stahl, K.; Moore, R.; Floyer, J.; Asplin, M.; McKendry, I. Comparison of approaches for spatial interpolation of daily air temperature in a large region with complex topography and highly variable station density. Agric. For. Meteorol. 2006, 139, 224–236. [Google Scholar] [CrossRef]
- Tveito, O.; Wegehenkel, M.; van der Wel, F.; Dobesch, H. Spatialisation of climatological and meteorological information with the support of GIS (Working Group 2). In The Use of Geographic Information Systems in Climatology and Meteorology, Final Report; COST (European Cooperation in Science and Technology): Amsterdam, The Netherlands, 2006; pp. 37–172. [Google Scholar]
- WMO. Guidelines on Ensemble Prediction Systems and Forecasting; World Meteorological Organisation: Geneva, Switzerland, 2012. [Google Scholar]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Griffin: London, UK, 1948. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Sneyres, R. Technical Note No. 143 on the Statistical Analysis of Time Series of Observation; World Meteorological Organisation: Geneva, Switzerland, 1990. [Google Scholar]
- Pearson, K. Notes on the history of correlation. Biometrika 1920, 13, 25–45. [Google Scholar] [CrossRef]
- Baines, P.G.; Folland, C.K. Evidence for a rapid global climate shift across the late 1960s. J. Clim. 2007, 20, 2721–2744. [Google Scholar] [CrossRef] [Green Version]
- Kosaka, Y.; Xie, S.P. Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature 2013, 501, 403–407. [Google Scholar] [CrossRef] [Green Version]
- Yevjevich, V.M. Probability and Statistics in Hydrology; Water Resources Publication: Fort Collins, CO, USA, 1972; pp. 237–241. [Google Scholar]
- Choi, Y.W.; Ahn, J.B.; Kryjov, V.N. November seesaw in northern extratropical sea level pressure and its linkage to the preceding wintertime Arctic Oscillation. Int. J. Climatol. 2016, 36, 1375–1386. [Google Scholar] [CrossRef]
- Knmi, I. Trends in annual and summer precipitation across Europe between 1960 and 2015. Royal Netherlands Meteorological Institute (KNMI). 2017. Available online: http://www.knmi.nl (accessed on 7 June 2022).
- Chen, X.; Wang, S.; Hu, Z.; Zhou, Q.; Hu, Q. Spatiotemporal characteristics of seasonal precipitation and their relationships with ENSO in Central Asia during 1901–2013. J. Geogr. Sci. 2018, 28, 1341–1368. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhang, K.; Gu, P.; Feng, H.; Yin, Y.; Chen, W.; Cheng, B. Changes in precipitation extremes in the Yangtze River Basin during 1960–2019 and the association with global warming, ENSO, and local effects. Sci. Total Environ. 2021, 760, 144244. [Google Scholar] [CrossRef] [PubMed]
- Emmanuel, I. Linkages between El Niño-Southern Oscillation (ENSO) and precipitation in West Africa regions. Arab. J. Geosci. 2022, 15, 1–11. [Google Scholar] [CrossRef]
- Sánchez-López, G.; Hernández, A.; Pla-Rabès, S.; Trigo, R.M.; Toro, M.; Granados, I.; Sáez, A.; Masqué, P.; Pueyo, J.J.; Rubio-Inglés, M.; et al. Climate reconstruction for the last two millennia in central Iberia: The role of East Atlantic (EA), North Atlantic Oscillation (NAO) and their interplay over the Iberian Peninsula. Quat. Sci. Rev. 2016, 149, 135–150. [Google Scholar] [CrossRef] [Green Version]
- Luppichini, M.; Barsanti, M.; Giannecchini, R.; Bini, M. Statistical relationships between large-scale circulation patterns and local-scale effects: NAO and rainfall regime in a key area of the Mediterranean basin. Atmos. Res. 2021, 248, 105270. [Google Scholar] [CrossRef]
- De Lima, M.I.P.; Santo, F.E.; Ramos, A.M.; Trigo, R.M. Trends and correlations in annual extreme precipitation indices for mainland Portugal, 1941–2007. Theor. Appl. Climatol. 2015, 119, 55–75. [Google Scholar] [CrossRef]
- Brandimarte, L.; Di Baldassarre, G.; Bruni, G.; D’Odorico, P.; Montanari, A. Relation between the North-Atlantic Oscillation and hydroclimatic conditions in Mediterranean areas. Water Resour. Manag. 2011, 25, 1269–1279. [Google Scholar] [CrossRef]
- Bevacqua, E.; Zappa, G.; Lehner, F.; Zscheischler, J. Precipitation trends determine future occurrences of compound hot–dry events. Nat. Clim. Chang. 2022, 12, 350–355. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Van Lanen, H.A. Hydrological Drought: Processes and Estimation Methods for Streamflow and Groundwater; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- White, D.; Richman, M.; Yarnal, B. Climate regionalization and rotation of principal components. Int. J. Climatol. 1991, 11, 1–25. [Google Scholar] [CrossRef]
- Lyra, G.B.; Oliveira-Júnior, J.F.; Zeri, M. Cluster analysis applied to the spatial and temporal variability of monthly rainfall in Alagoas state, Northeast of Brazil. Int. J. Climatol. 2014, 34, 3546–3558. [Google Scholar] [CrossRef]
- Cattell, R.B. The scree test for the number of factors. Multivar. Behav. Res. 1966, 1, 245–276. [Google Scholar] [CrossRef]
- Yarnal, B. Synoptic Climatology in Environmental Analysis: A Primer; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Jennrich, R.I. Rotation methods, algorithms, and standard errors. In Factor Analysis at 100; Routledge: London, UK, 2007; pp. 329–350. [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Espinosa, L.A.; Portela, M.M.; Pontes Filho, J.D.; Studart, T.M.D.C.; Santos, J.F.; Rodrigues, R. Jointly modeling drought characteristics with smoothed regionalized SPI series for a small island. Water 2019, 11, 2489. [Google Scholar] [CrossRef] [Green Version]
- Agnew, C. Using the SPI to Identify Drought. In Drought Network News (1994–2001); University College London: London, UK, 2000; Available online: https://digitalcommons.unl.edu/droughtnetnews/ (accessed on 10 December 2021).
- Liu, D.; You, J.; Xie, Q.; Huang, Y.; Tong, H. Spatial and temporal characteristics of drought and flood in Quanzhou based on standardized precipitation index (SPI) in recent 55 years. J. Geosci. Environ. Prot. 2018, 6, 25–37. [Google Scholar] [CrossRef] [Green Version]
- Silva, A.T.; Portela, M.; Naghettini, M. Nonstationarities in the occurrence rates of flood events in Portuguese watersheds. Hydrol. Earth Syst. Sci. 2012, 16, 241–254. [Google Scholar] [CrossRef] [Green Version]
- Silva, A. Nonstationarity and Uncertainty of Extreme Hydrological Events. Ph.D. Dissertation, IST/UTL, Lisbon, Portugal, 2017. [Google Scholar]
- Cowling, A.; Hall, P.; Phillips, M.J. Bootstrap confidence regions for the intensity of a Poisson point process. J. Am. Stat. Assoc. 1996, 91, 1516–1524. [Google Scholar] [CrossRef]
- Mudelsee, M. The bootstrap in climate risk analysis. In In Extremis; Springer: Berlin/Heidelberg, Germany, 2011; pp. 44–58. [Google Scholar]
- Eade, R.; Stephenson, D.; Scaife, A.; Smith, D. Quantifying the rarity of extreme multi-decadal trends: How unusual was the late twentieth century trend in the North Atlantic Oscillation? Clim. Dyn. 2022, 58, 1555–1568. [Google Scholar] [CrossRef]
- Barnston, A.G.; Livezey, R.E. Classification, seasonality and persistence of low-frequency atmospheric circulation patterns. Mon. Weather Rev. 1987, 115, 1083–1126. [Google Scholar] [CrossRef]
- Tošić, I.; Putniković, S. Influence of the East Atlantic/West Russia pattern on precipitation over Serbia. Theor. Appl. Climatol. 2021, 146, 997–1006. [Google Scholar] [CrossRef]
- Greve, P.; Orlowsky, B.; Mueller, B.; Sheffield, J.; Reichstein, M.; Seneviratne, S.I. Global assessment of trends in wetting and drying over land. Nat. Geosci. 2014, 7, 716–721. [Google Scholar] [CrossRef]
- Nunes, A.N.; Lopes, P. Streamflow Response to Climate Variability and Land-Cover Changes in the River Beça Watershed, Northern Portugal. In River Basin Management; IntechOpen: London, UK, 2016; pp. 61–80. [Google Scholar]
- Allan, R.P.; Hawkins, E.; Bellouin, N.; Collins, B. Summary for Policymakers; IPCC: Geneva, Switzerland, 2021. [Google Scholar]
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The concept of Essential Climate Variables in support of climate research, applications, and policy. Bull. Am. Meteorol. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef]
- Hébert, R.; Lovejoy, S.; Tremblay, B. An observation-based scaling model for climate sensitivity estimates and global projections to 2100. Clim. Dyn. 2021, 56, 1105–1129. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espinosa, L.A.; Portela, M.M. Grid-Point Rainfall Trends, Teleconnection Patterns, and Regionalised Droughts in Portugal (1919–2019). Water 2022, 14, 1863. https://doi.org/10.3390/w14121863
Espinosa LA, Portela MM. Grid-Point Rainfall Trends, Teleconnection Patterns, and Regionalised Droughts in Portugal (1919–2019). Water. 2022; 14(12):1863. https://doi.org/10.3390/w14121863
Chicago/Turabian StyleEspinosa, Luis Angel, and Maria Manuela Portela. 2022. "Grid-Point Rainfall Trends, Teleconnection Patterns, and Regionalised Droughts in Portugal (1919–2019)" Water 14, no. 12: 1863. https://doi.org/10.3390/w14121863
APA StyleEspinosa, L. A., & Portela, M. M. (2022). Grid-Point Rainfall Trends, Teleconnection Patterns, and Regionalised Droughts in Portugal (1919–2019). Water, 14(12), 1863. https://doi.org/10.3390/w14121863






