Parametric Study on Abutment Scour under Unsteady Flow
Abstract
:1. Introduction
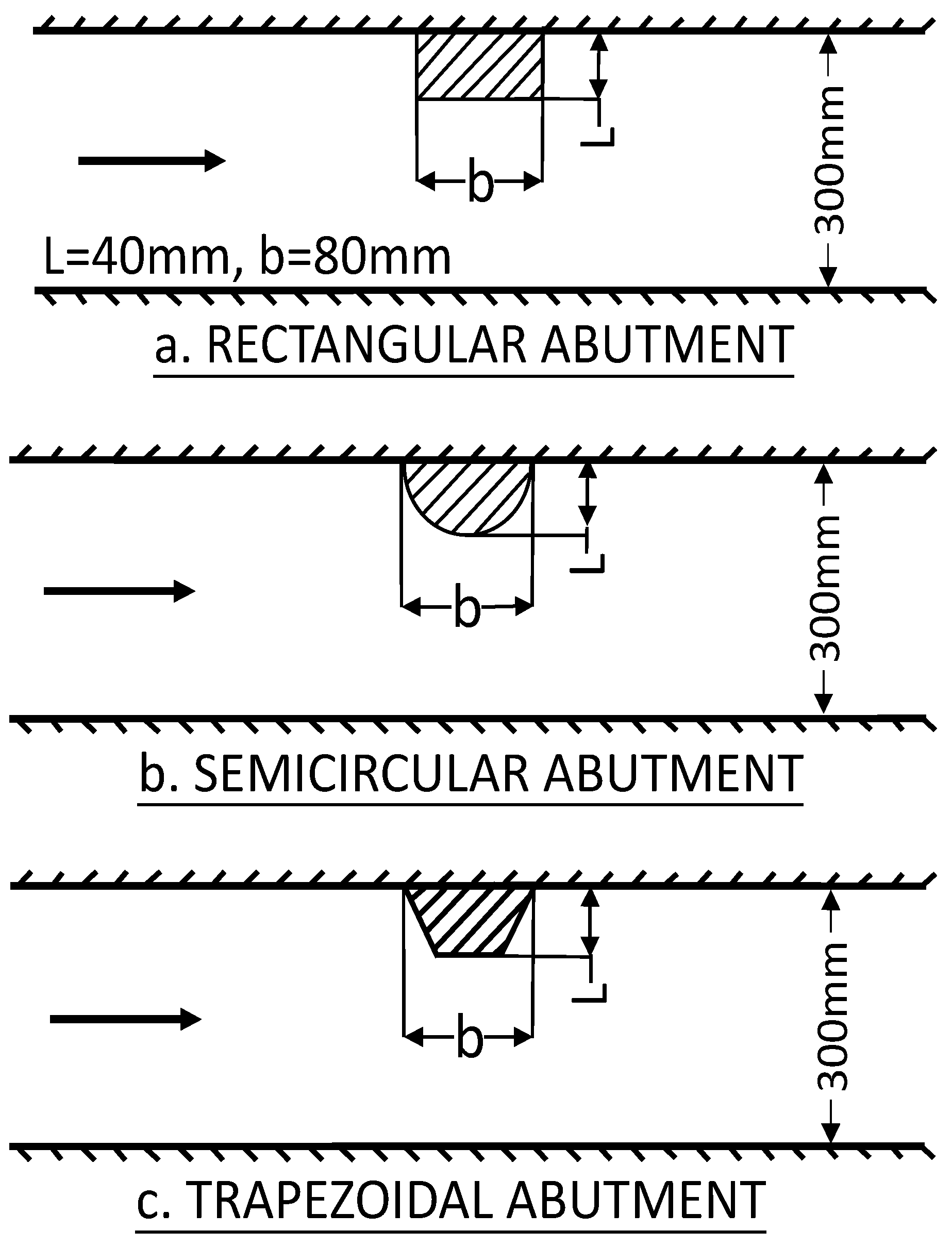
2. Experimental Setup and Procedure
3. Influence of Various Parameters on Scour Depth
4. Computational Model for Evolution of Abutment Scour
- (1)
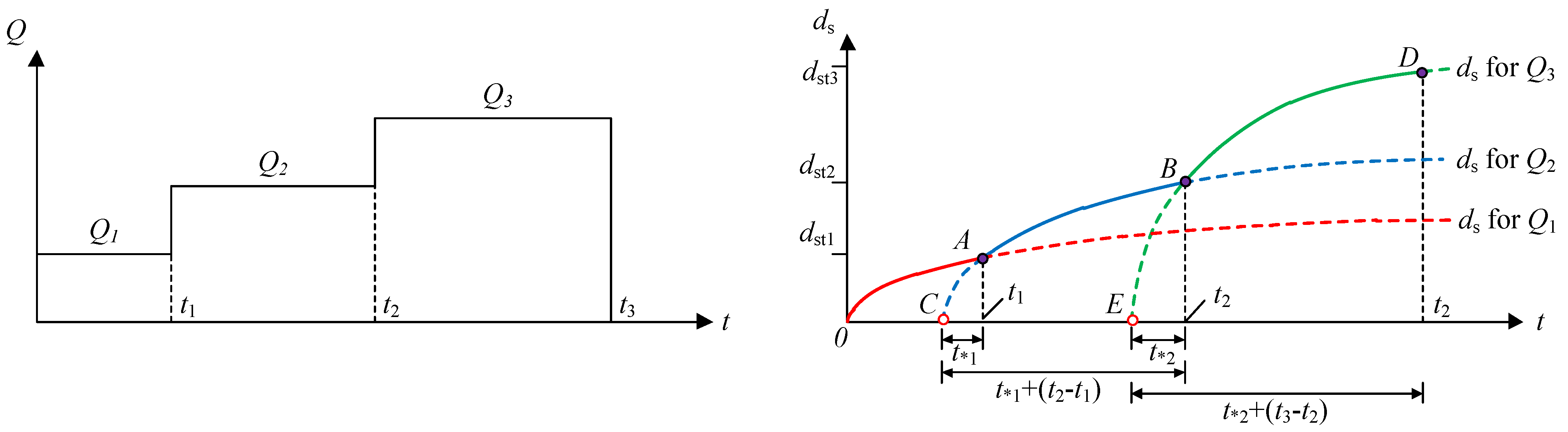
- For the first flow discharge Q1 of duration t1, scour depth evolution follows the red line (OA curve) under the steady flow condition. The final scour depth at t1 is denoted as ds1.
- (2)
- When the flow discharge increases from Q1 to Q2, scour depth evolution changes to follow the blue line (AB curve) under the steady flow condition, and point C is the virtual origin for the scouring process. As the scouring process can memorize the previous scour depth and because Q2 > Q1, the time (t*,1) required for the scour depth to reach ds1 is less than t1. The corresponding scour depth evolution from t1 to t2 is represented by the AB curve. To solve t*,1, one can use the intersection point A of OA curve and CB curve, and if we let , then t*,1 can be obtained as .
- (3)
- Similar to the computing procedure mentioned in step 2, when the flow rate increases from Q2 to Q3 (>Q2), scour depth evolution follows the green line under the steady flow condition, and point E is the virtual origin for the scouring process. As Q3 > Q2, the time (t*,2) required for the scour depth to reach dst2 is less than t*,1 + (t2 − t1). The corresponding scour depth evolution from t2 to t3 is shown by the BD curve. Time t*,2 can be solved by using the same method as mentioned in step 2, .
- (4)
- Repeat the procedure until all of the subdivisions are completed.
- (5)
- Obtain the temporal variation of scour depth under unsteady flow conditions.
- (6)
- Coleman et al. [18] reported that flow shallowness (y/L) has a significant effect on the evolution of abutment scour depth. Hence, for obtaining the best regression result, the data shown in Table 2 were classified into three groups as (1) y/L < 1; (2) 1 ≤ y/L < 2; and (3) 2 ≤ y/L. The coefficients of Equation (1) based on the range of flow shallowness are listed in Table 3. In general, the R2-values for all ranges of flow shallowness are very good.
5. Results of Computational Model
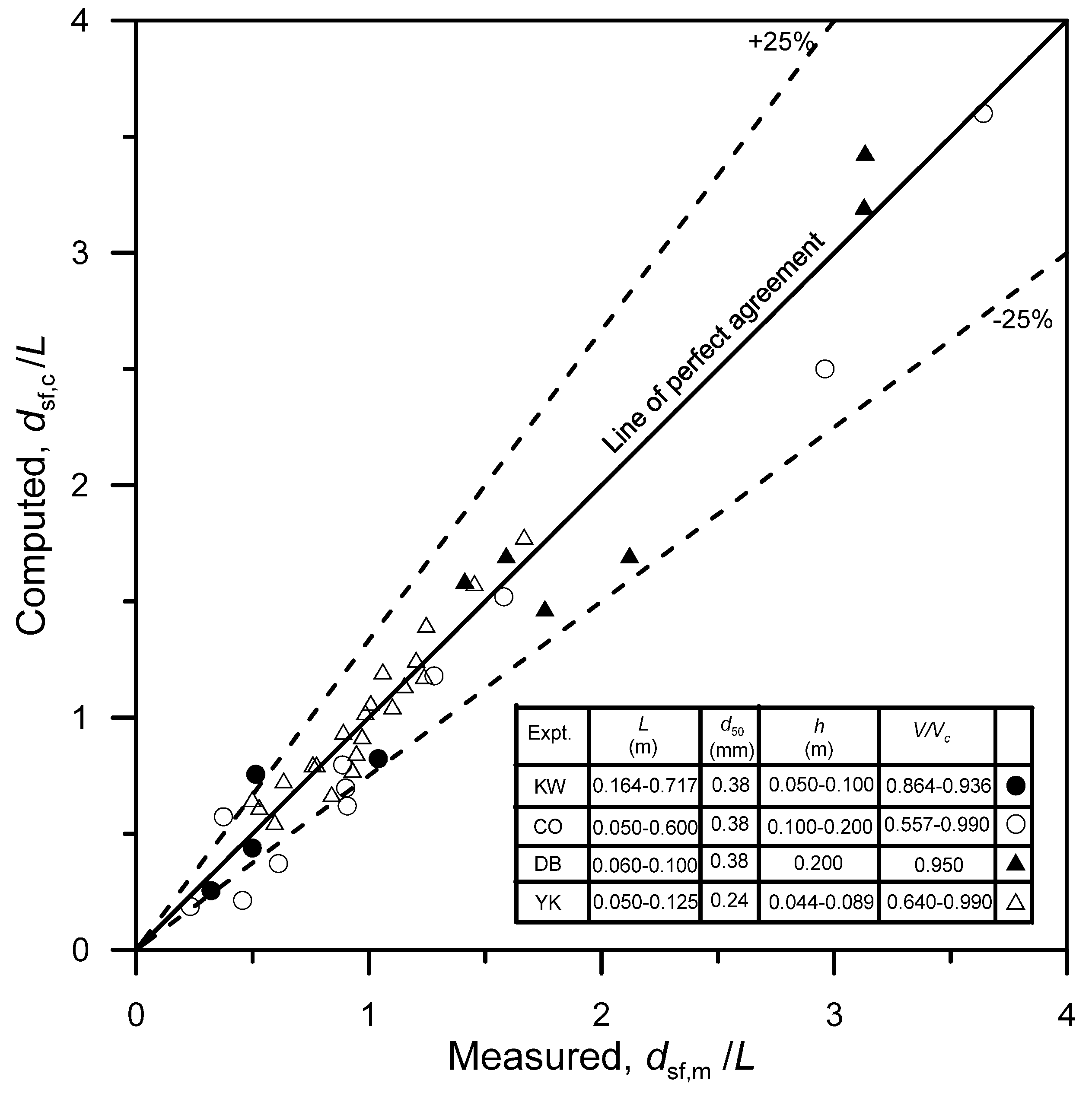
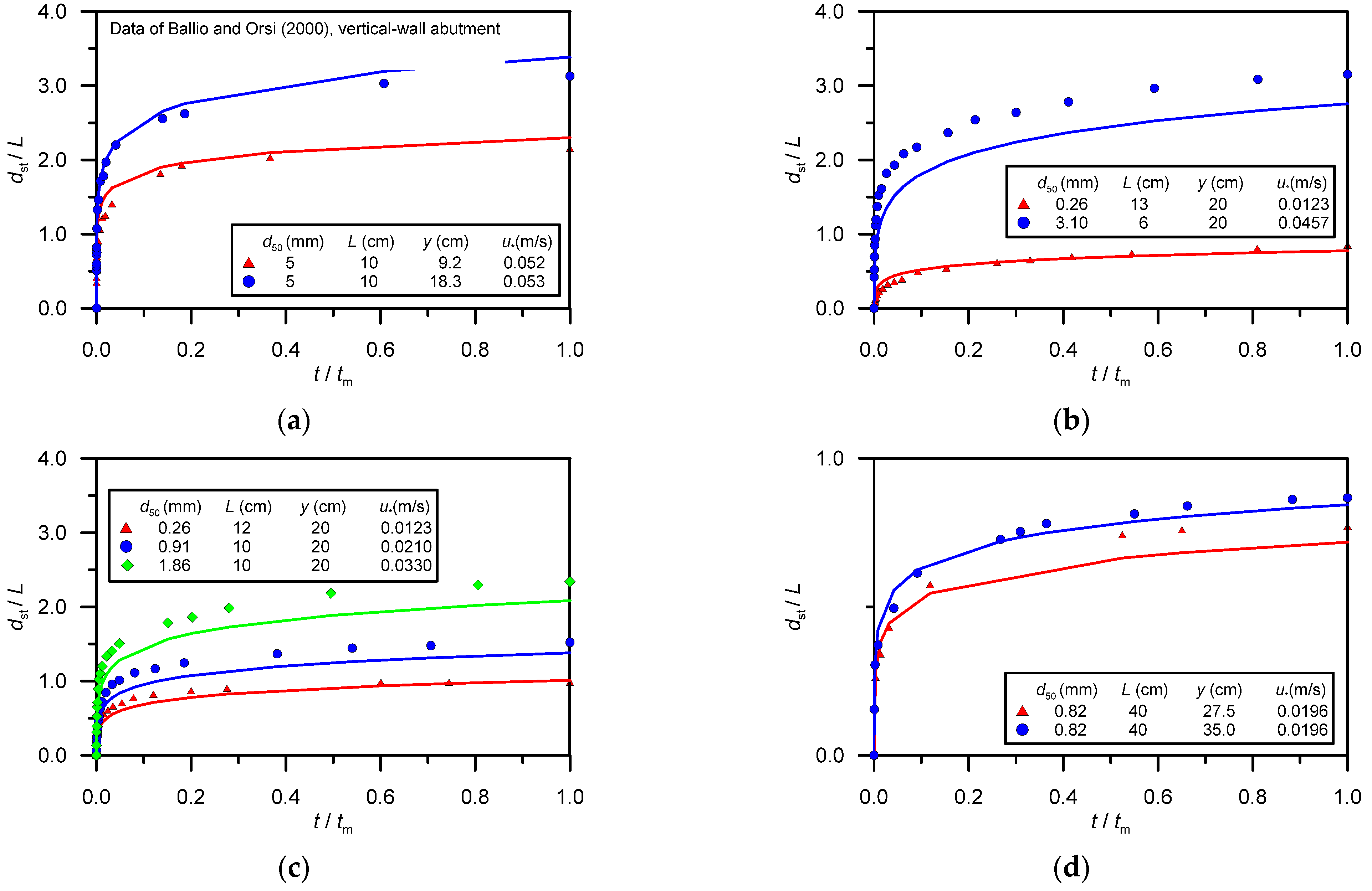
5.1. Comparison Using Steady Flow Data
5.2. Comparison Using Unsteady Flow Data
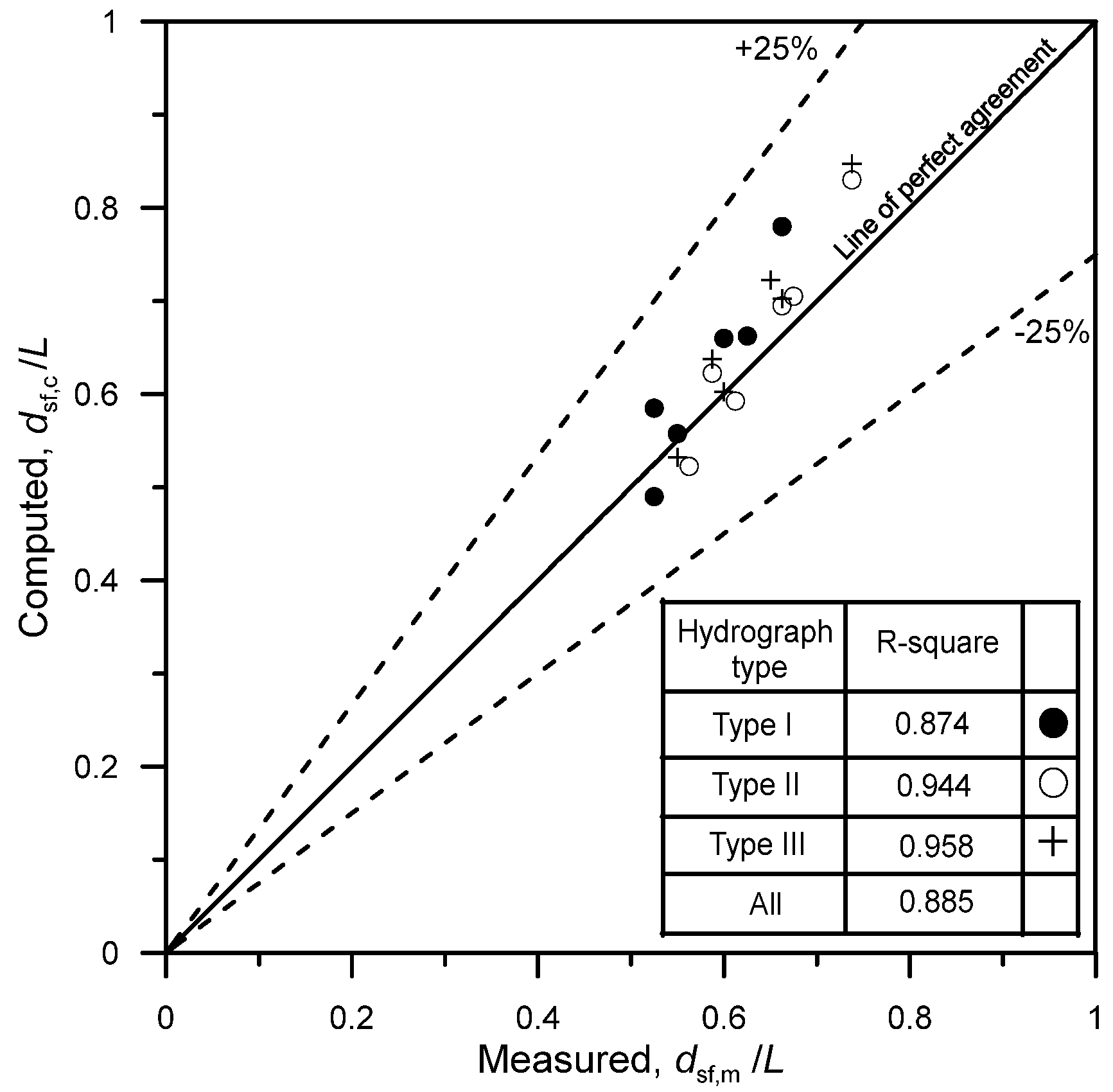
6. Statistical Results
7. Discussions
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Notations
| a0–a4 | regression constants [M0L0T0]; |
| b | longitudinal length of an abutment [M0L1T0]; |
| dsf,c | calculated final scour depth after a hydrograph [M0L1T0]; |
| dsf,m | measured final scour depth after a hydrograph [M0L1T0]; |
| dst | temporal variation of abutment scour depth [M0L1T0]; |
| d50 | median grain size [M0L1T0]; |
| Fd | densimetric particle Froude number, V/(g′d50)0.5 [M0L0T0]; |
| g | gravitational acceleration [M0L1T−2]; |
| g′ | relative gravitational acceleration, [(ρs-ρ)/ρ]g [M0L1T−2]; |
| k1–k2 | constants [M0L0T0]; |
| L | transverse length of an abutment [M0L1T0]; |
| LR | length scale, L(2/3)y(1/3) [M0L1T0]; |
| m | measured quantity (scour depth) |
| mean values of measured quantity (scour depth) | |
| N | number of data points [M0L1T0]; |
| p | predicted quantity (scour depth) |
| mean values of predicted quantity (scour depth) | |
| Q | flow discharge [M0L3T−1]; |
| T | time [M0L0T1]; |
| TR | relative time, t/tR [M0L0T0]; |
| td | base period for hydrograph [M0L0T−1]; |
| tm | final time of scour experiment corresponding to peak discharge [M0L0T1]; |
| tR | reference time scale, LR/[( g′d50)0.5], [M0L0T1]; |
| V | average approach flow velocity [M0L1T−1]; |
| Vc | critical velocity [M0L1T−1]; |
| y | approach flow depth [M0L1T0]; |
| ρ | density of fluid [M1L−3T−1]; and |
| ρs | density of sediment particle [M1L−3T−1]. |
References
- Gill, M.A. Erosion of sand beds around spur dikes. J. Hydraul. Div. ASCE 1972, 98, 1587–1602. [Google Scholar] [CrossRef]
- Laursen, E.M. Analysis of relief bridge scour. J. Hydraul. Div. ASCE 1963, 89, 93–118. [Google Scholar] [CrossRef]
- Melville, B.W. Pier and Abutment scour—An integrated approach. J. Hydraul. Eng. ASCE 1997, 123, 125–136. [Google Scholar] [CrossRef]
- Sturm, T.W.; Janjua, N.S. Bridge abutment scour in a floodplain. In Proceedings of the 1993 National Conference on Hydraulic Engineering ASCE, San Francisco, CA, USA, 25–30 July 1993; pp. 767–772. [Google Scholar]
- Breusers, H.N.C.; Nicollet, G.; Shen, H.W. Local scour around cylindrical piers. J. Hydraul. Res. 1977, 15, 211–252. [Google Scholar] [CrossRef]
- Dargahi, B. Local Scouring around Bridge Piers—A Review of Practice and Theory; Hydraulic Laboratory, Royal Institute of Technology: Stockholm, Sweden, 1982. [Google Scholar]
- Breusers, H.N.C.; Raudkivi, A.J. Scouring. IAHR Hydraulic Design Manual 2; A.A. Balkema: Rotterdam, The Netherlands, 1991. [Google Scholar]
- Dey, S. Local scour at piers, part 1: A review of development of research. Int. J. Sediment Res. 1997, 12, 23–44. [Google Scholar]
- Dey, S. Local scour at piers, part II: Bibliography. Int. J. Sediment Res. 1997, 12, 47–57. [Google Scholar]
- Hoffmans, G.J.C.M.; Verheij, H.C. Scour Manual; A.A. Balkema: Rotterdam, The Netherlands, 1997. [Google Scholar]
- Melville, B.W.; Coleman, S.E. Bridge Scour; Water Resources Publication, LLC.: Highlands Ranch, CO, USA, 2000; p. 550. [Google Scholar]
- Richardson, E.V.; Davis, S.R. Evaluating Scour at Bridges, 4th ed.; Hydraulic Engineering Circular (HEC) 18, Report FHWA NHI 01-001; US Department of Transportation, Federal Highway Administration: Washington, DC, USA, 2001. [Google Scholar]
- Barbhuiya, A.K.; Dey, S. Local scour at abutments: A review. Sadhana 2004, 29, 449–476. [Google Scholar] [CrossRef]
- Tey, C.B. Local Scour at Bridge Abutments; School of Engineering, The University of Auckland: Auckland, New Zealand, 1984. [Google Scholar]
- Cardoso, A.H.; Bettess, R. Effects of time and channel geometry on scour at bridge abutments. J. Hydraul. Eng. ASCE 1999, 125, 388–399. [Google Scholar] [CrossRef]
- Ballio, F.; Oris, E. Time evolution of scour around bridge abutments. Water Eng. Res. 2000, 2, 243–259. [Google Scholar]
- Oliveto, G.; Hager, W.H. Temporal evolution of clear water pier and abutment scour. J. Hydraul. Eng. ASCE 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Coleman, S.E.; Lauchlan, C.S.; Melville, B.W. Clear-water scour development at bridge abutments. J. Hydraul. Res. 2003, 41, 521–531. [Google Scholar] [CrossRef]
- Dey, S.; Barbhuiya, A.K. Time variation of scour at abutments. J. Hydraul. Eng. ASCE 2005, 131, 11–23. [Google Scholar] [CrossRef]
- Yanmaz, A.M.; Kose, O. A semi-empirical model for clear-water scour evolution at bridge abutments. J. Hydraul. Res. 2009, 47, 110–118. [Google Scholar]
- Kothyari, U.C.; Garde, R.J.; Ranga Raju, K.G. Temporal variation of scour around circular bridge piers. J. Hydraul. Eng. 1992, 118, 1091–1106. [Google Scholar] [CrossRef]
- Briaud, J.L.; Chen, H.C.; Kwak, K.W.; Han, S.W.; Ting, F.C.K. Multiflood and multilayer method for scour rate prediction at bridge piers. J. Geotech. Geoenviron. Eng. 2001, 127, 114–125. [Google Scholar] [CrossRef]
- Chang, W.Y.; Lai, J.S.; Yen, C.L. Evolution of scour depth at circular bridge piers. J. Hydraul. Eng. ASCE 2004, 130, 905–913. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Further results to time-dependent local scour at bridge elements. J. Hydraul. Eng. ASCE 2005, 131, 97–105. [Google Scholar] [CrossRef]
- Hong, J.H.; Chiew, Y.M.; Yeh, P.H. Comparisons of time-dependent pier-scour models under unsteady flow conditions. In Proceedings of the 7th International Conference on Scour and Erosion, Perth, Australia, 2–4 December 2014; pp. 473–481. [Google Scholar]
- Kwan, T.F. Study of Abutment Scour; School of Engineering, The University of Auckland: Auckland, New Zealand, 1984. [Google Scholar]
- Laursen, E.M.; Toch, A. Scour around Bridge Piers and Abutments; Iowa Highways Research Board: Ames, Iowa, 1956. [Google Scholar]
- Liu, S.Y.; Chang, F.M.; Skinner, M.M. Effect of Bridge Construction on Scour and Backwater; CER 60 HKL 22; Civil Engineering Section, Colorado State University: Fort Collins, CO, USA, 1961. [Google Scholar]
- Garde, R.J.; Subramanya, K.; Nambudripad, K.D. Closure of Study of scour around spur-dikes. J. Hydraul. Div. ASCE 1963, 89, 167–175. [Google Scholar] [CrossRef]
- Wong, W.H. Scour at Bridge Abutments; School of Engineering, University of Auckland: Auckland, New Zealand, 1982. [Google Scholar]
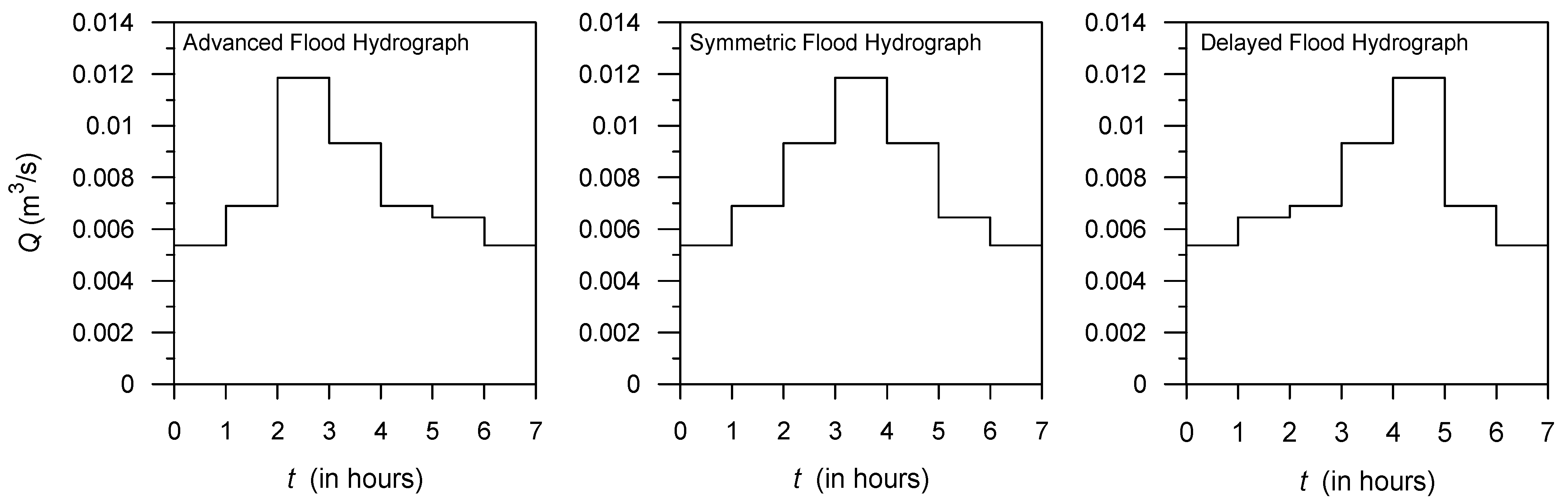

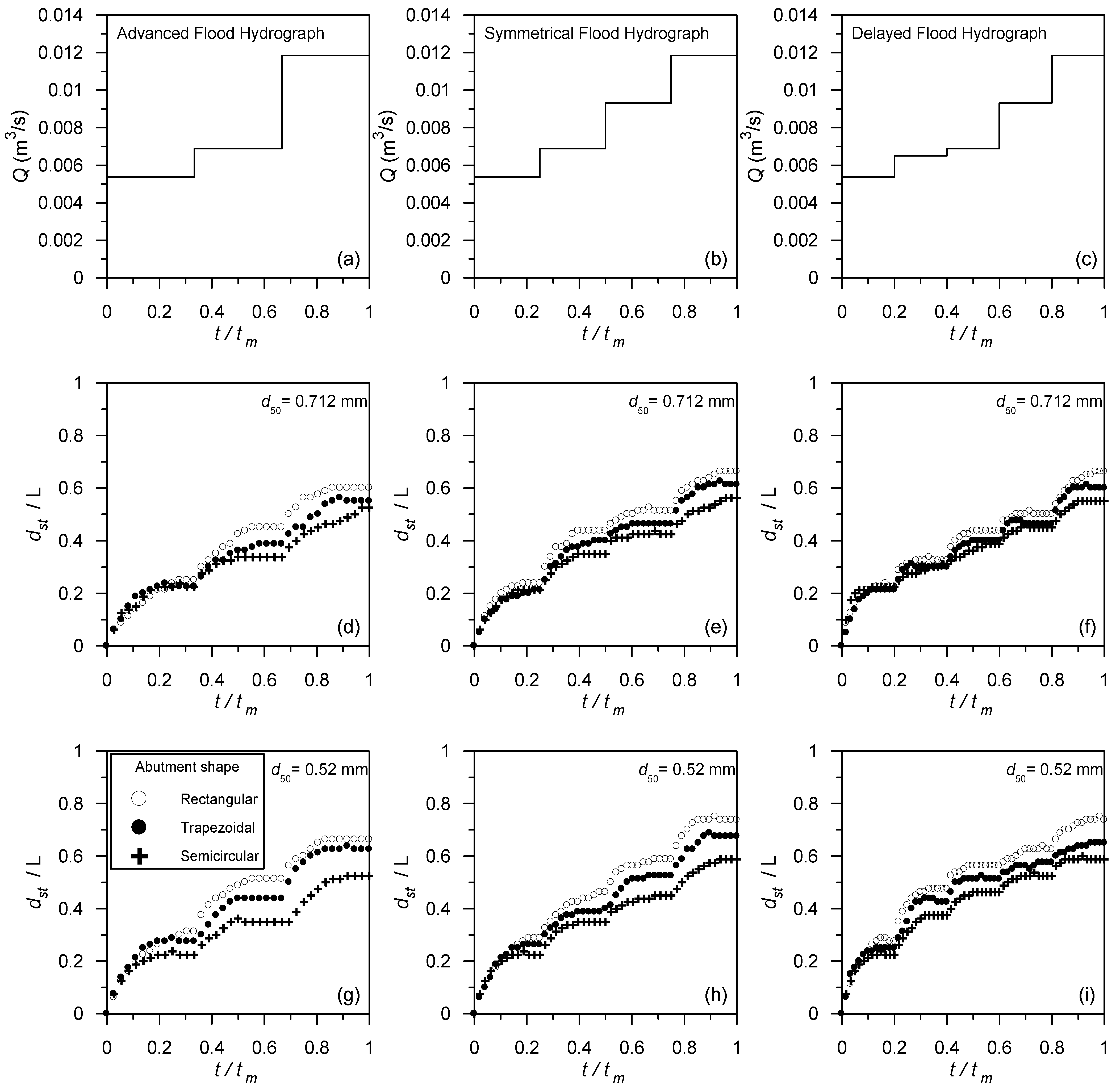

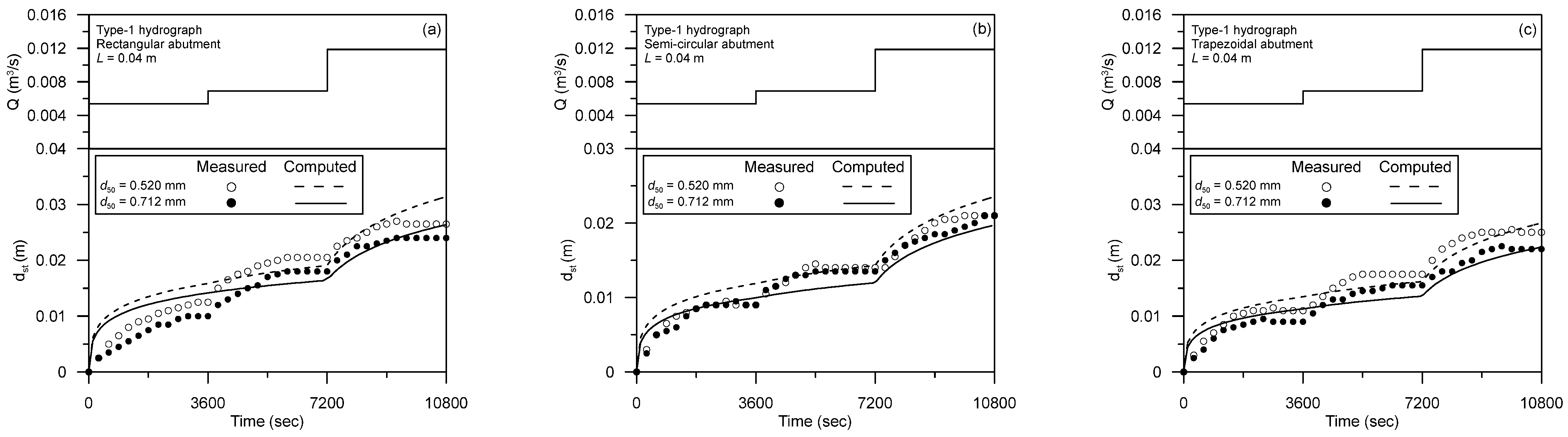
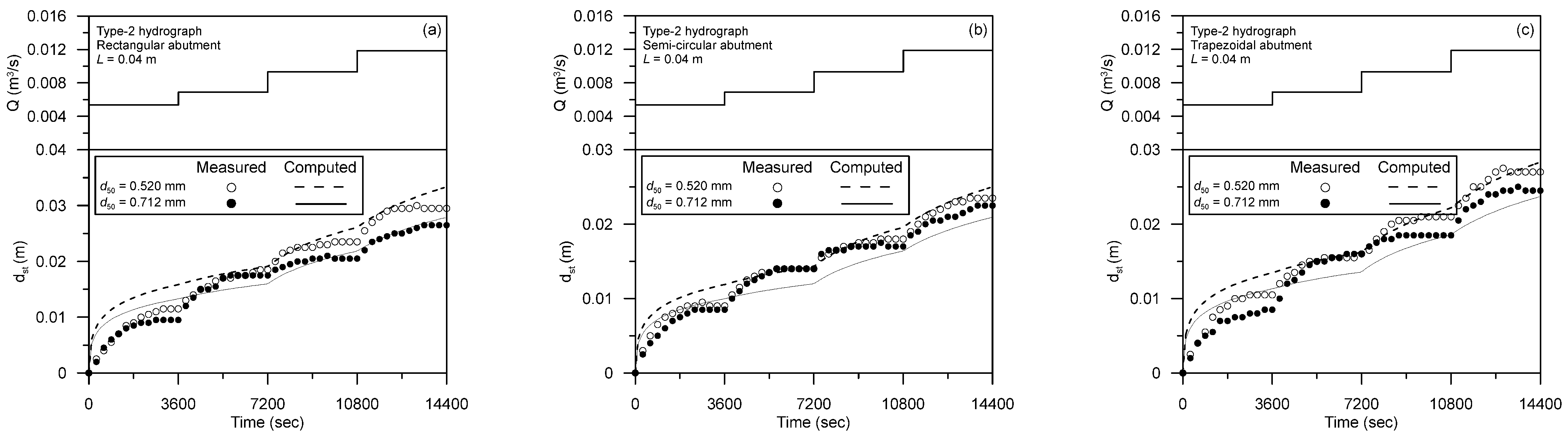
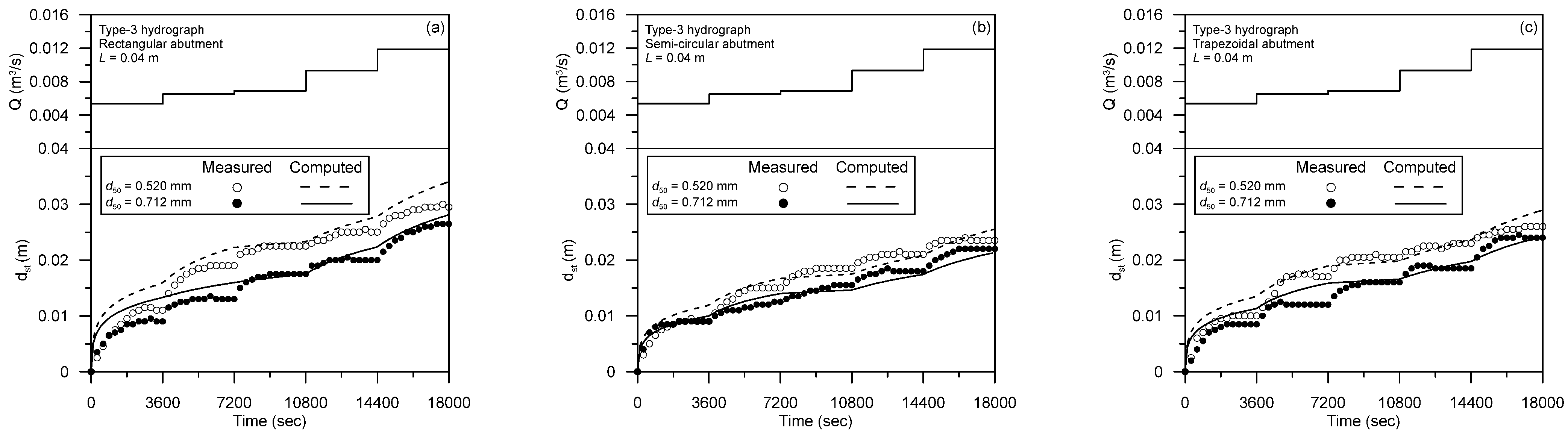
| Hydrograph Type | Abutment Type | d50 (mm) | V (m/s) | y (m) | Observed dsf,m (m) |
|---|---|---|---|---|---|
| Type I | Rectangular | 0.520 | 0.20, 0.19, 0.22 | 0.09, 0.12, 0.18 | 0.0265 |
| 0.712 | 0.0240 | ||||
| Semi-circular | 0.520 | 0.0210 | |||
| 0.712 | 0.0210 | ||||
| Trapezoidal | 0.520 | 0.0250 | |||
| 0.712 | 0.0220 | ||||
| Type II | Rectangular | 0.520 | 0.20, 0.19, 0.21, 0.22 | 0.09, 0.12, 0.15, 0.18 | 0.0295 |
| 0.712 | 0.0265 | ||||
| Semi-circular | 0.520 | 0.0235 | |||
| 0.712 | 0.0225 | ||||
| Trapezoidal | 0.520 | 0.0270 | |||
| 0.712 | 0.0245 | ||||
| Type III | Rectangular | 0.520 | 0.20, 0.22, 0.19, 0.21, 0.22 | 0.09, 0.10, 0.12, 0.15, 0.18 | 0.0295 |
| 0.712 | 0.0265 | ||||
| Semi-circular | 0.520 | 0.0235 | |||
| 0.712 | 0.0220 | ||||
| Trapezoidal | 0.520 | 0.0260 | |||
| 0.712 | 0.0240 |
| Expt. Number | L (cm) | d50 (mm) | V/Vc | y (cm) | dsf,m (m) | dsf,c (m) | tm (min) |
|---|---|---|---|---|---|---|---|
| KW-1 | 71.7 | 0.85 | 0.936 | 5 | 0.231 | 0.183 | 6944 |
| KW-2 | 31.4 | 0.85 | 0.936 | 5 | 0.157 | 0.138 | 3095 |
| KW-3 | 16.4 | 0.85 | 0.936 | 5 | 0.084 | 0.124 | 4904 |
| KW-4 | 16.4 | 0.85 | 0.864 | 10 | 0.171 | 0.135 | 1430 |
| CO-1 | 30 | 0.82 | 0.742 | 20 | 0.272 | 0.186 | 4740 |
| CO-3 | 30 | 0.82 | 0.742 | 20 | 0.112 | 0.172 | 2277 |
| CO-8 | 60 | 0.82 | 0.599 | 12 | 0.140 | 0.112 | 3711 |
| CO-14 | 60 | 0.82 | 0.557 | 20 | 0.274 | 0.128 | 4760 |
| CO-17 | 60 | 0.82 | 0.742 | 20 | 0.367 | 0.223 | 5571 |
| CO-23 | 30 | 0.82 | 0.848 | 20 | 0.266 | 0.239 | 4868 |
| CO-25 | 5 | 1.02 | 0.588 | 20 | 0.064 | 0.059 | 3698 |
| CO-30 | 5 | 1.02 | 0.731 | 10 | 0.079 | 0.076 | 4096 |
| CO-34 | 30 | 0.8 | 0.949 | 10 | 0.270 | 0.209 | 5285 |
| CO-37 | 5 | 0.85 | 0.989 | 20 | 0.182 | 0.180 | 5429 |
| CO-40 | 5 | 0.85 | 0.980 | 10 | 0.148 | 0.125 | 3713 |
| DB-1 | 8 | 0.26 | 0.950 | 20 | 0.127 | 0.136 | 6795 |
| DB-2 | 10 | 0.26 | 0.950 | 20 | 0.141 | 0.159 | 4164 |
| DB-3 | 10 | 0.52 | 0.950 | 20 | 0.176 | 0.147 | 3542 |
| DB-4 | 8 | 0.91 | 0.950 | 20 | 0.170 | 0.136 | 4205 |
| DB-5 | 6 | 1.86 | 0.950 | 20 | 0.188 | 0.206 | 3083 |
| DB-6 | 8 | 3.1 | 0.950 | 20 | 0.250 | 0.256 | 3976 |
| YK-1 | 12.5 | 1.8 | 0.777 | 8.9 | 0.126 | 0.133 | 360 |
| YK-2 | 12.5 | 1.8 | 0.777 | 8.3 | 0.123 | 0.128 | 360 |
| YK-3 | 12.5 | 1.8 | 0.741 | 7.5 | 0.118 | 0.106 | 360 |
| YK-4 | 12.5 | 1.8 | 0.713 | 6.8 | 0.116 | 0.097 | 360 |
| YK-5 | 12.5 | 1.8 | 0.682 | 6.1 | 0.105 | 0.084 | 360 |
| YK-6 | 12.5 | 1.8 | 0.640 | 5.3 | 0.074 | 0.069 | 360 |
| YK-7 | 10 | 1.8 | 0.777 | 8.9 | 0.120 | 0.125 | 360 |
| YK-8 | 10 | 1.8 | 0.751 | 8.3 | 0.115 | 0.114 | 360 |
| YK-9 | 10 | 1.8 | 0.741 | 7.5 | 0.110 | 0.105 | 360 |
| YK-10 | 10 | 1.8 | 0.713 | 6.8 | 0.097 | 0.092 | 360 |
| YK-11 | 10 | 1.8 | 0.682 | 6.1 | 0.078 | 0.080 | 360 |
| YK-12 | 10 | 1.8 | 0.640 | 5.3 | 0.050 | 0.065 | 360 |
| YK-13 | 5 | 1.8 | 0.777 | 8.9 | 0.083 | 0.089 | 360 |
| YK-14 | 5 | 1.8 | 0.751 | 8.3 | 0.073 | 0.079 | 360 |
| YK-15 | 5 | 1.8 | 0.741 | 7.5 | 0.062 | 0.070 | 360 |
| YK-16 | 5 | 1.8 | 0.713 | 6.8 | 0.053 | 0.060 | 360 |
| YK-17 | 12.5 | 0.9 | 0.985 | 5.2 | 0.095 | 0.100 | 360 |
| YK-18 | 12.5 | 0.9 | 0.899 | 4.4 | 0.066 | 0.077 | 360 |
| YK-19 | 10 | 0.9 | 0.985 | 5.2 | 0.089 | 0.094 | 360 |
| YK-20 | 10 | 0.9 | 0.899 | 4.4 | 0.063 | 0.073 | 360 |
| YK-21 | 5 | 0.9 | 0.985 | 5.2 | 0.062 | 0.059 | 360 |
| Coefficients | |||
|---|---|---|---|
| 0.209 | 0.100 | 0.022 | |
| 0.263 | 0.424 | 0.700 | |
| −0.427 | −0.523 | −0.469 | |
| 1.857 | 2.168 | 2.274 | |
| 1.269 | 1.594 | 1.938 | |
| R2-value | 0.892 | 0.916 | 0.935 |
| Hydrograph Type | Abutment Type | d50 (mm) | Observed dsf,m (m) | Computed dsf,c (m) |
|---|---|---|---|---|
| Type I | Rectangular | 0.520 | 0.0265 | 0.0312 |
| 0.712 | 0.0240 | 0.0264 | ||
| Semi-circular | 0.520 | 0.0210 | 0.0234 | |
| 0.712 | 0.0210 | 0.0196 | ||
| Trapezoidal | 0.520 | 0.0250 | 0.0265 | |
| 0.712 | 0.0220 | 0.0223 | ||
| Type II | Rectangular | 0.520 | 0.0295 | 0.0332 |
| 0.712 | 0.0265 | 0.0278 | ||
| Semi-circular | 0.520 | 0.0235 | 0.0249 | |
| 0.712 | 0.0225 | 0.0209 | ||
| Trapezoidal | 0.520 | 0.0270 | 0.0282 | |
| 0.712 | 0.0245 | 0.0237 | ||
| Type III | Rectangular | 0.520 | 0.0295 | 0.0339 |
| 0.712 | 0.0265 | 0.0281 | ||
| Semi-circular | 0.520 | 0.0235 | 0.0255 | |
| 0.712 | 0.0220 | 0.0213 | ||
| Trapezoidal | 0.520 | 0.0260 | 0.0289 | |
| 0.712 | 0.0240 | 0.0241 |
| Hydrograph Type | Abutment Shape | d50 (mm) | RMSE (m) | MAPE (%) | Correlation Coefficient R |
|---|---|---|---|---|---|
| Type-I | Rectangular | 0.520 | 0.00289 | 24.79 | 0.95 |
| 0.712 | 0.00293 | 31.63 | 0.94 | ||
| Semi-circular | 0.520 | 0.00160 | 14.53 | 0.98 | |
| 0.712 | 0.00145 | 13.09 | 0.98 | ||
| Trapezoidal | 0.520 | 0.00181 | 14.94 | 0.97 | |
| 0.712 | 0.00171 | 16.99 | 0.97 | ||
| Type-II | Rectangular | 0.520 | 0.00272 | 22.41 | 0.98 |
| 0.712 | 0.00197 | 17.95 | 0.97 | ||
| Semi-circular | 0.520 | 0.00126 | 10.62 | 0.99 | |
| 0.712 | 0.00189 | 15.36 | 0.97 | ||
| Trapezoidal | 0.520 | 0.00158 | 13.98 | 0.99 | |
| 0.712 | 0.00220 | 20.63 | 0.97 | ||
| Type-III | Rectangular | 0.520 | 0.00265 | 19.43 | 0.98 |
| 0.712 | 0.00200 | 15.33 | 0.98 | ||
| Semi-circular | 0.520 | 0.00143 | 11.04 | 0.98 | |
| 0.712 | 0.00120 | 7.46 | 0.98 | ||
| Trapezoidal | 0.520 | 0.00168 | 12.14 | 0.97 | |
| 0.712 | 0.00180 | 16.13 | 0.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raikar, R.V.; Hong, J.-H.; Deshmukh, A.R.; Guo, W.-D. Parametric Study on Abutment Scour under Unsteady Flow. Water 2022, 14, 1820. https://doi.org/10.3390/w14111820
Raikar RV, Hong J-H, Deshmukh AR, Guo W-D. Parametric Study on Abutment Scour under Unsteady Flow. Water. 2022; 14(11):1820. https://doi.org/10.3390/w14111820
Chicago/Turabian StyleRaikar, Rajkumar V., Jian-Hao Hong, Anandrao R. Deshmukh, and Wen-Dar Guo. 2022. "Parametric Study on Abutment Scour under Unsteady Flow" Water 14, no. 11: 1820. https://doi.org/10.3390/w14111820
APA StyleRaikar, R. V., Hong, J.-H., Deshmukh, A. R., & Guo, W.-D. (2022). Parametric Study on Abutment Scour under Unsteady Flow. Water, 14(11), 1820. https://doi.org/10.3390/w14111820







