Abstract
Due to the complexity of calculating the minimum required volume of water tanks and the associated regime of pumping water into the tank depending on the consumption pattern in the water supply systems, finding the functional dependence of these variables is a complex process. The main idea of this paper was to provide a methodology for the calculation of the minimum water tank volume considering all input variables, which could be used in a simple and applicable way in everyday water supply management and engineering. As a final product, a desktop application TankOPT was developed that is easy to run and use on a PC with a user-friendly interface for data entry (data on maximum daily consumption and the pattern of daily water consumption). A software solution was created based on a numerical model that simplifies the usual manual calculations using known spreadsheet software and solves this problem. The solution was determined with combinations of the start and duration of water pumping in the water tank, for which the minimum required volume of the tank is obtained. JavaScript programming language was used to create the app. The use and operation of the application are shown through two hypothetical examples.
1. Introduction
Water tank volume is one of the most important decision variables in water supply systems [1,2]. Water tank quantities have a role in balancing inequities between inflow and outflow, as well as in securing the required pressure conditions in the water supply systems. Municipal water tanks have three main functions: to balance user demand (balancing storage), provide water for firefighting (fire storage), and maintain the water supply if source interruptions occur (emergency storage) [3,4]. Water consumption and the pumping regime are also related variables in ensuring these requirements. The sizing of the water tank is based on the calculations of the biggest deficit and/or the surplus between the inflow and outflow of the tank applying the Ripple rule [5,6].
Population growth, energy consumption, and water consumption are the basic decision variables when designing a water supply system. It must be emphasized that any extension of the volume of water tanks is limited due to the space and financial constraints, but also with any possible reflections on the pressure conditions in the water supply systems. This is directly linked to extensions in financial costs regarding the building of new water chambers, control valves, and/or pressure-reducing equipment. Analysis and management of the inflow into the water tank are among the possible solutions. The inflow of the water can be controlled, while output depends on the water consumption by the end-users (residents, tourism, industry), which is very hard to predict or even calculate exactly. For such a purpose, the impact of the input and output (pumping regime and consumption patterns) on the changes in the water tank is of crucial importance, concerning the maximum daily consumption, which is the main input parameter for the sizing of not only the water tanks but also the entire components of the water supply system.
Given that the functional dependencies of all the mentioned parameters are not clearly defined and that their relationships are not directly proportional, finding the optimal solution in the process of designing water tanks as components of the water supply system is an extremely complex problem. The water tank and associated pumping station, which delivers water to the tank when energy is used, are usually designed according to deterministic guidelines that specify minimal water tank volume and optimal pump capacity. Such guidelines must accommodate a large range of possible conditions, meaning that systems are potentially overdesigned, but reliable.
The idea of the presented research was to investigate how the pumping regime and the maximum daily water consumption with a predefined consumption pattern in the settlement affect required storage (water tank) volume. The aim was also to build a mathematical model that will use this relationship and simplify the calculation of the minimum required volume of the tank, specifically by finding the optimal start and duration of the water pumping that leads to satisfying all requirements, without increasing the size of the water tank since it needs to be economically acceptable for construction, maintenance, and operation. This directly points to an imperative for the minimization of the water tank volume due to economic reasons. The main goal of the project, as part of which this research was conducted, was to develop a program/application for optimizing the calculation of the required volume of the water tank in relation to the relevant consumption and pumping regimes into the tank to minimize both water tank investment costs and operating pumping station costs. The program would be applicable when designing new tanks, as well as for optimizing existing systems with already built tanks. The main emphasis was on the simplification of existing “manual” calculations and adaptation to the daily needs of scientists as well as experts who deal with operational activities related to adjustments to changes in the mode of operation of pumping stations and tanks. In other words, an approach for the simulation of water tanks as decision variables for water distribution system design optimization was developed.
In water supply, the optimal schedule of water pumping is often determined in relation to electricity prices during the day [7] because pumping systems represent major operational expenditure and account for the greatest use of energy [8,9]. This is exactly why pump scheduling is one of the most important tasks in the operation of a water distribution system [10]. Speaking strictly in terms of costs, tanks represent quite a small portion of the whole network costs, as opposed to the pipe’s considerable construction and/or replacement costs, or the pump’s operational costs, yet their impact on the overall network performance is significant and disproportionate to their costs; an ill-placed tank may significantly increase pipe design costs for the network as a system, or cause exceedingly high operational costs, affecting pump design, while at the same time reducing quality performance indices, such as reliability and resilience [11]. Tanks must be filled at off-peak periods using pumps, thus adding pump decision variables alongside tank variables.
It is necessary to point out that any shifting of the pumping regime (e.g., during the day and night, due to the cheaper electric energy) also affects the size of the required water tank volume. Specific working hours and whether renewable energy sources (RESs) are used as the energy source could also influence the required water tank volume, especially in the case of the intermittent dynamics of a particular RES.
Given the specified norms and legislation requirements that most often define the requirements for fire and emergency storage, their impact on the calculation of operational (balancing) storage, i.e., water tank volume, can be neglected [2,12,13]. Therefore, since the emergency and fire storage can be considered as constant volumes, and for the remainder of this paper, only balancing tank volume will be analyzed.
2. Background with Literature Review
Although an extensive literature review has been conducted, it should be noted that there are not many literature sources that address this issue. Early research on this issue was focused on the analysis of how a change in the capacity of pumping (filling the water tank) affects the water tank volume during 24 h of continuous pumping [2]. In this case, water tank volume was not affected. Plantak et al. [12] have shown that decreasing the pumping time, and shifting the start of the pumping to different hourly periods during the day, has an impact on the water tank volume. These authors showed that with a constant value of maximum daily consumption and a constant consumption pattern, the required volume of operational storage (volume of the water tank) changes depending on the mode of water abstraction, i.e., the beginning and duration of the tank filling. Together with the conclusions of other authors [14] that the issue of optimizing the operation of water tanks and associated pumping stations is not a straightforward problem, this was the motivation for further research with a detailed elaboration of the analyzed problem.
Although the principle is the same, the application of the open reservoir’s optimization models (with the impact of the precipitation, infiltration, and evaporation) does not come into account, because the time unit for their modeling is averaged monthly [15], despite the quality and refined methodology. The application of models with short- and long-period risk analysis [16] is a very promising solution. Targeted volumes of the water storage, as an important part of the water supply system, were calculated regarding the duration of the input data time series. However, the method lacks the calculation of the values with a certain probability of occurrence. Changes in the water tank volumes should be calculated exactly. As a part of that, the reliability of the calculated water tank volume is directly related to the continuity and availability of the water supply. The methodology given in [17] presents a multi-objective, mixed-integer, linear programming model, which incorporates reliability, resilience, and vulnerability as objectives to investigate the release policy of a water tank used for a single purpose in terms of water supply. Specifically, the authors elaborated on and solved four usual problems in water tank management: the probability of occurrence of a specified undesirable outcome, the number of occurrences over a specified length of time, the expected number of occurrences during a specified period, and the investment required to prevent occurrence (reduced probability) of risk. An elegant solution with the valve control and changes in the pumping regime, with respect to the water tank filling, was given by Khatavkar and Mays [18]. As in [17], the demerit of this method is also a lack of the functionally defined dependence between input- and output-relevant parameters, with water tank volume as a key parameter.
Neelakantan and Pundarikanthan [19] aimed at improving the tank operation performance through the simulation–optimization procedure with the application of the hedging rule, which is a more appropriate rule for reservoir operation under deficit conditions. The hedging rule distributes deficits over a longer period by rationing the water supply, and it makes the system sustainable with a marginal reduction in supply. A methodology was demonstrated in a case study with a water supply system which was a water shortage system requiring the efficient use of water. The solution was presented using the unconstrained nonlinear programming model for optimizing the management decision variables (input and output parameters). In addition, to speed up the optimization process, a neural network model was developed for the simulation of the tank system operation and was used instead of a conventional simulation model. The combined neural network simulation–optimization model was used for screening the operation policies. The main shortcomings are reflected in the fact that the model uses average monthly values. This is not accurate enough for water supply systems, where changes occur in much shorter time intervals, and the calculation is based on balancing the inflow and consumption on an hourly basis, not daily.
Fuzzy logic was found to be a very efficient and practical tool for solving the problem of the optimal sizing of the water tank [20]. The idea was to transform crisp inputs such as the inflow, tank storage, and outflow (consumption) into fuzzy variables. Even though fuzzy logic was applied on an open reservoir with more inputs, compared to the municipal water supply tanks, the methodology could be applied as previously described. Shortcomings include the fact that fuzzy logic is based on a linguistic (subjective) description of input and output parameters (“high”, “very high”, etc.), with categorization into the levels/ranges based on such classification.
Shifting the water pumping and consumption regime impacts the expenses for the used electric energy. Matching the consumption pattern with a cheap tariff entails not only changing the water tank volume and the water level directly influencing available water quantities, but also pressure in the system [21]. Moreover, consumption peaks and electricity tariff peaks most often coincide. Pumping cost optimization was the main goal of the research, but this led to a change in the pressure conditions in the system, which was identified as a problem.
Case studies in Palestine [22] and Korea [23] analyzed the proposal to change the occasional pumping regime to a continuous (permanent) one, which implies an analysis of the pumping regime regarding the duration and start of pumping. These studies confirmed that the pumping regime does not only affect the cost of pumping, but also the duration and reliability of the water supply system. Meguid [24] and Giustolisi et al. [25] concluded that pumping with increased capacity outside the peak periods (of both water consumption and electric tariffs) is optimal due to a more even distribution of energy consumption regarding both a hydraulic and economic requirement.
The methodology presented in [10] is an approach for modeling explicit pump scheduling that considers the pump start/end run times and pump status (on/off) at the beginning of the scheduling period as decision variables. The drawback of this research is that uncertainties exist, as water demands may not be fulfilled due to switching the pumping regime from one to another. A novel management approach for the optimal design and operation of water pumping systems, which uses Genetic Algorithm Optimization [26] for the optimal design and operation of water pumping systems, reduces power consumption by about 15–20%. Genetic Algorithm Optimization was also successfully applied in [27], where using different tank trigger levels for the peak and off-peak tariff periods allowed the pumps to operate more effectively in the off-peak tariff period. This also guarantees that the pumps are switched on when the tank level reaches the lower trigger. Electric energy and demand costs were taken into account in [28], together with modeling of the pumping regime and water tank volume. It is a solution that satisfies water supply system constraints, water demands, and hydraulic requirements, but with the preconditions of availability of all types of sensors (i.e., power, pressure, water level, etc.), automatic control valves, switches, and supervisory control and data acquisition, which means that there are limitations that may mean that demand or pressure conditions will not be completely satisfied.
In general, all models and methodologies for solving the problem of modeling the water tank volumes are divided into linear programming (LP), dynamic programming (DP), nonlinear programming (NLP), and simulations [29]. The algorithm demonstrated in [11], which uses Genetic Algorithm Optimization, provides optimization of the water tank volume, where four conditions are fulfilled. These are operational volume capacities to meet hourly demand variations for 24 h with “normal day” demand, for each tank separately (per tank); filling capacity for 24 h with “normal day” demand, for each tank separately (per tank); operational volume capacity for the network as a whole; and filling capacity for the network as a whole. The presented research is a base idea for overlapping all ‘’day’’ demands in the new algorithm, which was one of the main drivers for the development of the solution presented in this paper.
As pumping stations are the largest consumers of energy and cause the largest operating costs in water supply systems [8,9,30], modeling or analysis of water abstraction and consumption regimes are surely necessary steps for techno-economic analysis of water supply systems. Based on the literature review, it can be concluded that the relationship between the change in the pumping regime and its impact on the pumping capacity, as well as on the size of the water tank, has not been sufficiently analyzed [7,12].
Although many new methods have been presented through the development and acceleration of computational programs with an interdisciplinary approach, and some complex and often expensive software solutions already exist, there are still some issues that are not completely solved. These are, in most cases, averaging the input and output parameters, while the “black box” is not transparently and strictly described. Many methods are based on a statistical calculation of reliability, which is not 100 percent fulfilled. This drives the need for a new algorithm that would solve the described problems in a simple and applicable way, as presented in the remainder of this paper.
3. Methodology and Description of the Created Application
3.1. Water Tank Sizing Procedure
Calculation of the required water tank volume is usually carried out by using spreadsheet software as this is appropriate due to the use of the Ripple formula, which is presented by Equation (1) [2,5]. The calculation and methodology presented below only apply to operational storage (water tank volume).
The water tank volume V is determined by a graphical or numerical procedure over integral curve methodology [5]. It is a simple procedure based on the assumption that in the period of exchange (usually 1 day, up to 7 days), all water that flowed into the tank, QPS, flows out of it, as represented by QWS:
where t is usually from 1 to 24 h. The value QWS depends on the water consumption regime as influenced by the habits of end consumers, and QPS depends on the pumping station operation regime.
V = max[∑365(QPS,t − QWS,t)], 1 ≤ t ≤ 24,
The usual constraint related to the volume of the tank V(t) at the observed moment t is defined by Equation (2) [31]:
where Vmin (t) is the minimum required volume of water in the tank, and VMAX (t) is the maximum allowable volume of water in the tank. It is clear that during the 24 h when the inflow QPS,t into the water tank is constant for each hour, the water tank volume does not change, despite the outflow, i.e., water consumption QWS,t [2].
Vmin (t) ≤ V (t) ≤ VMAX(t), ∀ t,
Boundary conditions must also be defined by Equation (3) [31]:
where Vstart is the volume of water in the tank at the beginning of pumping, and Vend is the volume of water in the tank at the end of pumping.
Vi(1) = Vstart, Vi(t + 1) = Vend,
Following the intention of this paper, and the main goal of the minimization of the water tank volume, i.e., the optimal sizing, the optimization algorithm can be described as: the minimization of f (V), which is subject to limitations and conditions in Equations (4)–(8).
tstart,t 1 ≤ t ≤ 24
tduration,t 1 ≤ t ≤ 24
QPS,t = f (Qmax,daily, QWS,t)
QWS,t = f (Qmax,daily)
V = f (Qmax,daily)
The idea is to see how the start of the water pumping, tstart,t, and duration of the pumping, tduration,t, impact water tank volume considering maximum daily water consumption, Qmax,daily. It was found that the calculation for each specific water tank volume requires the opening of a separate spreadsheet or some kind of automatic calculation to speed it up.
In any case, the pump should deliver the entire Qmax,daily to the water tank on the day of the maximum consumption. In relation to how many hours a day pumping is carried out (Tp), the pumping capacity (flow of pumping in one hour—Qi) will vary according to Equation (9).
Equation (1) clearly states that different input water pumping profiles, as well as different water consumption profiles, require a different water tank volume, V, all with the respect to the maximum daily water consumption Qmax,daily. Due to the requirements (5)–(9), it is obvious that the classical procedure for the minimization of the water tank volume consists of the three steps:
1. Calculation of the water tank volume considering all different daily pumping regime profiles and only one defined daily water consumption profile.
Further expansion of the calculation includes the calculation of the water tank volumes for all other combinations of the water consumption profiles. For one water consumption profile, there are 576 variants of filling the water tank, all with respect to the start and duration of the pumping. As mentioned, for each hour of the day the start of pumping with different durations (1–24 h) is taken into the account. According to Equations (1) and (9), if the pumping duration is longer, the water tank volume is smaller, and vice versa.
2. Graphical representation of the calculated water tank volumes, all regarding the start tstart,t and duration tduration,t of the water pumping into the tank.
An Excel spreadsheet is appropriate for both the calculation procedure (based on Equation (1)) and the representation of the obtained water tank volumes. Different pumping durations and starting hours define different water tank volumes.
3. Selection of the minimum calculated water tank on the basis of the obtained diagram.
Graphical representation of the obtained water tank volumes facilitates selection while checking should be always carried out in more detail in the Excel tables, where the calculation was performed. Obviously, the most common task in the sizing process, as well as in the process of monitoring the operational work of the water tank, is the determination/calculation of the minimum possible water tank volume. This task is necessary as it ensures the existing volume is reserved, and/or new water tank volume if the extension of the water consumption is going to happen, or when changing the water pumping regime (for example, when the water pumping regime is changed due to application of renewable energy sources, etc.).
3.2. Software Solution for Sizing the Water Tank
The algorithm used for the calculation procedure in this paper is shown in Figure 1, as well as in more detail in the enclosed pseudocodes (Figure 2 and Figure 3).
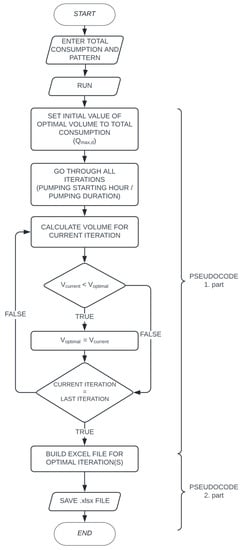
Figure 1.
The flowchart of the calculation procedure within the developed application.

Figure 2.
Pseudocode 1—calculation of the minimum required tank volume.

Figure 3.
Pseudocode 2—creating an Excel file.
The TankOPT application created using the described algorithm is an upgrade and further simplification of a previously created program within the same research that required the use of a terminal (Command Prompt) to run. A desktop application is easy to run and has a user-friendly interface, where the required inputs are entered in predefined fields.
The created application assumes for each hour of the day the start of pumping water into the water tank with different durations (1–24 h). Eventually, this results in a total of 576 different options. The application returns and indicates the optimal solution (or solutions in the case of the existence of multiple solutions with the same minimum required volume of water tank).
The application was built using the JavaScript programming language (JS), one of the most popular and widely used programming languages that allows you to implement complex features on web pages as well as create programs and run them locally on your computer.
For input parameters, the application accepts the maximum daily water consumption in [m3] and the percentage values of consumption for each of the time intervals (hours) during the day (24 h—24 intervals—24 values), the total sum of which must be 100%.
The second part of the generated code refers to the creation of a graphical interface and desktop application. The programming language used was also JavaScript with the use of Electron.js to create a desktop application and React.js to create and design a user interface. Electron.js could be described as a runtime used to build desktop applications with JavaScript. It uses the main file of the application and builds a desktop application with the native GUI (Graphical User Interface). The MaterialUI and Styled components were used as program tools to design the interface, while the previously mentioned Electron.js was used to create the desktop application.
The process to run this application is the same as any other desktop application. A setup file is provided, which is used as an installer for the given application. Once this is complete, the resulting .exe file is used to open the application itself.
After launching, the application directly asks you to enter the maximum daily consumption and percentage values in the appropriate fields, and, as a result, provides an .xlsx document that contains information on optimal iterations—solutions with minimum water tank volume required.
If the application runs successfully, without any errors, it returns optimal iteration(s) data, in the form of an .xlsx file. This file’s format corresponds to the content of the usual manual (MS Excel) calculations of the required volume of a water tank for the start time and duration of pumping that the program previously recognized as optimal, i.e., for which the minimum required volume of water tank is obtained. The resulting file consists of one or more sheets, depending on the number of possible solutions with a minimum volume of water storage (each sheet represents one solution). Each sheet represents one “manual” calculation (with different combinations of pumping start hour and duration) of the required volume of the water tank and contains data on water consumption for each hour within the day with the maximum water consumption for which the tank is designed. Furthermore, for each hour, the data on the inflow into the water tank are given. The difference between the inflow of water in the water tank and the water consumption per hour for a particular hour further represents the surplus or deficit of water in the tank for that hour. The volume of the tank is obtained in the last column by summing the surpluses/deficits in the tank through all hours during the day. Eventually, each solution (sheet) is defined by the data on the starting hour and duration of pumping time and the corresponding minimum required volume of the water tank. The resulting volume in all solutions (sheets), if more than one, is the same.
The application also has some error handling implemented (it envisages the possibility of the incorrect entry of some of the required inputs). If the value entered for total daily consumption is not entered in digits, the error message appears under the input indicating that the entered value should be a number. If no required percentage values are entered before starting the calculation, an error message appears saying that all 24 percentage values are required and should be entered correctly. If the sum of values in percentage inputs is not equal to 100% when executing the program, an error message appears saying that the total sum of all hourly percentage values must be 100%.
All above-mentioned errors prevent calculations from running and require the user to correct the errors before submitting the values for the calculation.
4. Case Study—Results and Discussion
The methodology and application used were presented in a hypothetical example which has been previously discussed [2,12] for a settlement of 8970 inhabitants (with the assumed specific water consumption of 160 l per person per day and a coefficient of daily unevenness of consumption of Kd = 1.70), with regard to two variants of the water consumption profiles. The maximum daily water consumption was Qmax,daily = 2440 m3/day. Although the presented analysis could be performed with absolutely any combination of the maximum daily consumption and the corresponding consumption patterns, for practical reasons, an example was chosen that was previously analyzed as part of already published research. The size of the settlement, as well as the specific water consumption, could therefore be chosen arbitrarily, and regardless of the choice, the functioning of the application has been unquestionably proven by multiple tests. The mentioned required water volumes and water consumption quantities for both variants are shown in Figure 4 and Figure 5 and are defined in accordance with the rules of the profession. Two different patterns of water consumption were defined with the same total maximum daily water consumption to show the influence of the water consumption regime on the required volume of water storage. The first consumption regime (Figure 4) represents the usual water consumption during the working day in settlements with three peaks of consumption: morning, noon, and evening, of which the most pronounced is the one in the middle of the day (usual lunchtime). The second consumption regime (Figure 5) shows the usual water consumption in settlements with two consumption peaks (noon and evening) characteristic of weekends in settlements of the selected size. Notwithstanding the above, the presented procedure is the same for any regime of daily water consumption, where it is only necessary to take into account that the total sum of hourly values of water consumption within one day ultimately gives the sum of Qmax,daily.
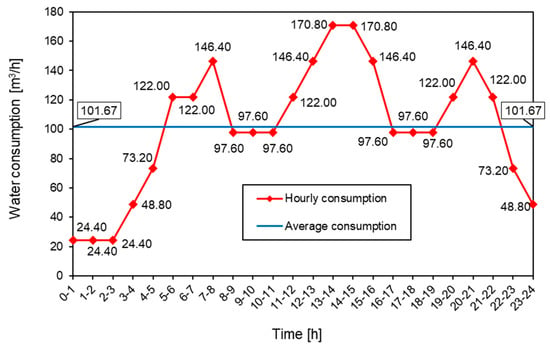
Figure 4.
Daily water consumption regime for Qdaily =2440 m3/day—Variant I [12].
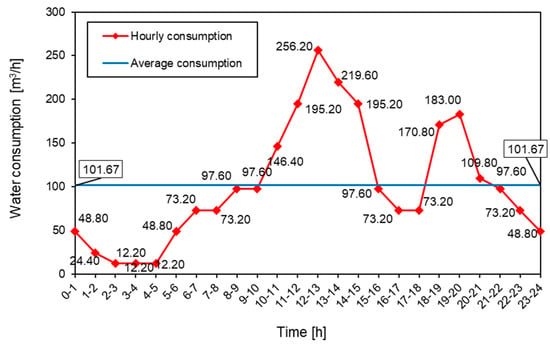
Figure 5.
Daily water consumption regime for Qdaily = 2440 m3/day—Variant II [12].
In the case of occasional water abstraction and pumping into the tank, that is, at different starts and durations of pumping, water tank volumes were calculated for the maximum daily water consumption of Qmax,daily = 2440 m3/day for Variant I and Variant II using Equation (1) to determine their impact on the tank volume. It should be noted that the water tank volumes calculated for the Qmax,daily also satisfy all requirements for the water consumption during the year, since consumption on all other days is accordingly lower.
The primary tasks are finding minimum and maximum volumes for particular starts and durations of the water pumping. Furthermore, the intention is to determine the impact on the water tank volume. The mentioned calculations, concerning the different beginnings and durations of pumping for Variants I and II, are shown in Figure 6 and Figure 7. The legend in these figures shows the pumping start time, where 0 starts at 00:00, 1 starts at 01:00, etc.
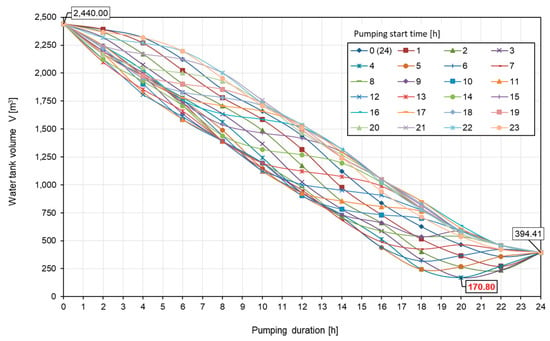
Figure 6.
Changes in water tank volume V with respect to the different hours of pumping starts and different pumping durations for Variant I.
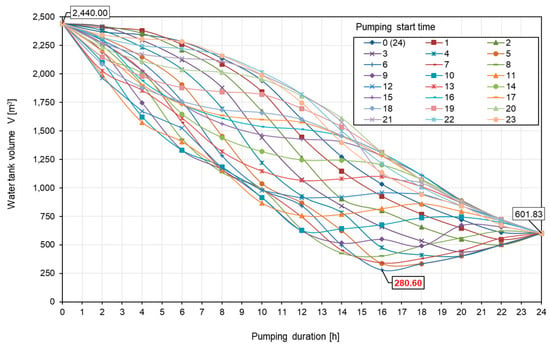
Figure 7.
Changes in water tank volume V with respect to the different hours of pumping starts and different pumping durations for Variant II.
The water tank volume was equal to 2440 m3, as shown in both Figure 6 and Figure 7, which corresponds to the maximum daily water consumption Qmax,daily, while values of 394.41 m3 (Figure 6) and 601.83 m3 (Figure 7) correspond related to the continuous pumping throughout the day, i.e., over a duration of 24 h, with constant hourly pumping capacity Qi (Equation (9)).
Based on the graphs shown, the relationship between the start and duration of pumping, maximum daily consumption, and the minimum required volume of the water tank is not linear; moreover, this relationship is very complex. The optimal solution (with the minimum required volume of water tank) was the one for which the minimum of all curves shown in the graphs above was recorded, and, for both variants, this value is indicated by a red data label in the figures. Such a solution may be unique, as in the case of Variant II (minimum required water tank volume of 280.60 m3 was obtained for pumping starting at 6 am and lasting 16 h), or might be obtained for several different combinations of starts and durations of pumping, as in the case of Variant I (minimum water tank volume was obtained when pumping starting started at 3 am and lasted 20 h, or if pumping started at 4 am and lasted 19 or 20 h). The following will show the use of the created application and the simplified procedure for reaching the same solution. The presented results, obtained as the output of the created application, completely coincide with the results of the “manual” calculation for the considered hypothetical examples within the previously published research [2,12]. A closer look at the presented results for the analyzed examples shows the expected trend that more pronounced fluctuations in daily consumption (as in the case of Variant II compared to Variant I) resulted in a higher required minimum volume of water storage. On the other hand, the consumption regime, although it has an impact on the duration of pumping, is not expected to have a direct impact on operating costs due to different water pumping duration. This is because a longer pumping duration means less pumping capacity is needed compared to pumping with a shorter duration (or it is possible to apply frequency regulation of pumps if the same pump is selected in both cases), which will ultimately result in mostly equal total electricity consumption since in both cases the pump must deliver the same total amount of water to the tank within one day, i.e., Qmax,daily. The difference in operating costs will of course be due to the period of operation of the pumps within the day if there is the usual division into cheap and expensive tariffs, as already stated by other authors [8,9,23]. There is also a possibility of using the previously mentioned alternative energy sources (for example, solar energy in the light part of the day) [3], where the upgraded application would play a role in analyzing various alternative solutions for the start and duration of water pumping. This is an additional case demonstrating the applicability of the planned upgrades of the TankOPT application in optimizing the functioning of the planned, as well as existing, water supply systems.
The created application is a software solution of a mathematical model that accepts input data on the maximum daily consumption and its distribution by hours within the day. The interface that opens after starting the desktop application with the entered data for the previously described Variant I is shown in Figure 8. In the second step, a new window opens after running the application by simply clicking the “Run” button. Within the opened window, one needs to enter the desired name of the Excel file and select the location on the computer where one wants to save it, with the mandatory addition of the .xlsx extension. In this way, a file with outputs is created, i.e., with the optimal solution(s). The program works by analyzing all possible 576 variants of filling the water tank (regarding the start and duration of the pumping—the program assumes, for each hour of the day, the start of pumping with different durations (1–24 h)) and selects the solution(s) with the minimum required volume of the tank saved in the created Excel file.
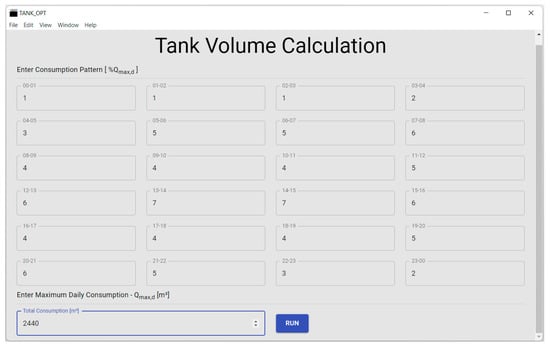
Figure 8.
Screenshot of startup and input fields of the created application with entered values for Variant I.
Figure 9 shows screenshots of the windows after opening the created file for Variant I. Three combinations are shown that give the optimal solution with the minimum required volume of the water tank, which are contained within a single Excel file, each in a separate sheet. Each sheet is named in the format of pumping start_pumping duration, i.e., sheet 3_20 means the combination (solution) for which pumping starts at 3 am and lasts 20 h.
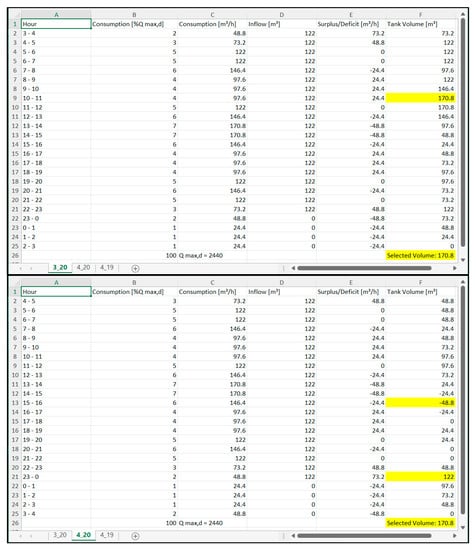
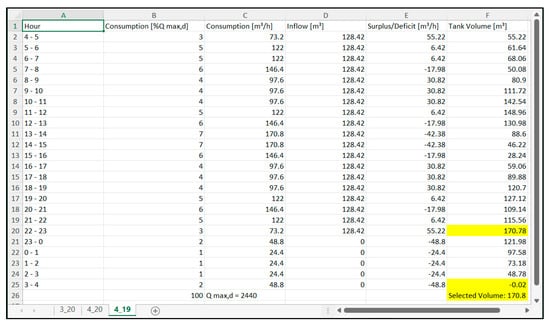
Figure 9.
Screenshot of the obtained results (created MS excel file) for Variant I—multiple (3×) solutions (sheets) with minimum water tank volume.
Figure 10 shows the same thing for Variant II where a unique solution is obtained, i.e., an Excel file with only one sheet, named 6_16, which means that the minimum required volume of the water tank is obtained for the start of pumping at 6 am and duration of 16 h. This is in accordance with the previously presented optimums for both variants defined on the basis of graphical representations in Figure 6 and Figure 7, each of which was obtained by manual calculation, i.e., by creating 576 different sheets in Excel and summarizing all the obtained results.
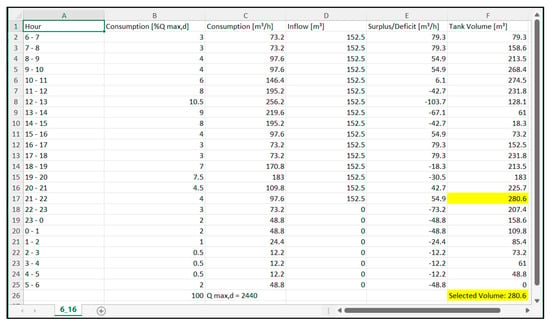
Figure 10.
Screenshot of the obtained results (created MS excel file) for Variant II—single solution with minimum water tank volume.
Calculation of the single point on diagrams in Figure 6 and Figure 7, in the usual way, using Equation (1) and spreadsheet software (MS Excel, for example), requires a long-term separate manual calculation procedure for each point (each point is one sheet). This is a long-lasting and exhausting procedure to obtain the final diagram, i.e., to find the required minimum, as well as all other values of the water tank volume, V. The TankOPT program application drastically decreases the time for the calculation through the algorithm shown in Figure 1. This greatly facilitates finding the optimal solution(s) in everyday engineering practices and also offers the possibility for further upgrades of the program, allowing for the implementation of measures to optimize water supply systems, specifically water tanks and related pumping regimes, as one of the most complex variables in decision-making processes in water supply systems.
Of course, all of the above applies under the condition that all water demands are satisfied, just as in the case of standard hydraulic network solvers that are not able to represent water distribution networks affected by pressure deficit conditions [32]. This is an area to consider in the future through further upgrades of this or similar applications and their possible linking to other software solutions to cover additional conditions, especially in the case of water scarcity and/or pressure deficits, where dynamic unsteady flow and pressure-driven analysis come into consideration (for example, as presented in [33].
The application created and described through this research, TankOPT, was conceived as a widely available and open-source application, and the authors are ready to share it, along with installation and startup instructions, with anyone interested.
5. Conclusions
Due to the complexity of functional relationships of decision variables in the process of defining the required volume of the water tank in relation to the water consumption and pumping regime, finding the optimal solution with the minimum required volume of the tank by conventional calculations using simple spreadsheet software is a demanding and time-consuming process. The JavaScript programming language was used to create a numerical model in the form of a software solution to this problem. The final product is a desktop application (TankOPT) that is easy to install and run on the Windows operating system, with a unique user-friendly interface designed to make the application easier to use. The application accepts as input data the maximum daily water consumption (as the basic parameter on the basis of which the sizing of the water tank is usually performed) and the distribution of water consumption within the day (24 percentage values, one for each hour of the day). The output is a solution in the form of an .xlsx file containing one or more sheets for which the minimum required volume of the tank is obtained, where each sheet is defined by the beginning and duration of pumping water into the tank. In this way, an applicable solution was created for everyday engineering needs, as well as for further research development in defining the functional relationships of decision variables in the design of water supply systems and their functional units. The selection of two hypothetical examples showed that the presented methodology and a software application could be used for sizing the water tanks and adjusting the water pumping regimes when consumption patterns are known, with the additional assumption that all water demands are satisfied, i.e., the water distribution network is able to deliver all water demands.
As part of the further development of the application, efforts will be made to upgrade it with the possibility of discontinuous filling of the water tank during the day, which will require significantly greater use of computer memory. The idea is also to develop a solution to the opposite problem if there is a built system and water tank, and the goal is to define the optimal regime of water pumping in relation to the known consumption pattern. With the method described above, we plan to consider the cost effectiveness of filling the tank at different times of the day (e.g., during the night period, which has cheaper electricity tariffs, or using solar energy during the day to run pumping stations, as well as solutions with other RESs), all with the aim of minimizing total investment and operating costs.
Author Contributions
Conceptualization, D.N. and B.D.; methodology, D.N. and B.D.; software, D.N.; validation, D.N., B.D. and S.D.; resources, D.N. and B.D.; writing—original draft preparation, D.N. and B.D.; writing—review and editing, J.H.; visualization, D.N.; supervision, J.H.; project administration, D.N.; funding acquisition, D.N. and B.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the University North program for scientific and artistic research support in 2021 under the grant Soldo_Nakić_Đurin, “Development of a program/application for optimizing the calculation of the minimum required volume of water tank”.
Data Availability Statement
All data available upon the reasonable request to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Fu, G.; Ni, G.; Zhang, C. Recent Advances in Adaptive Catchment Management and Reservoir Operation. Water 2019, 11, 427. [Google Scholar] [CrossRef] [Green Version]
- Đurin, B. Some Aspects of the Operation Work of Pump Station and Water Reservoir. Period. Polytech. Civ. Eng. 2016, 60, 345–353. [Google Scholar] [CrossRef] [Green Version]
- Đurin, B.; Margeta, J. Analysis of the Possible Use of Solar Photovoltaic Energy in Urban Water Supply Systems. Water 2014, 6, 1546–1561. [Google Scholar] [CrossRef] [Green Version]
- Van Zyl, J.E.; Le Gat, Y.; Piller, O.; Walski, T.M. Impact of Water Demand Parameters on the Reliability of Municipal Storage Tanks. J. Water Resour. Plan. Manag. 2012, 138, 553–561. [Google Scholar] [CrossRef]
- Rippl, W. The Capacity of Storage-Reservoirs for Water-Supply. Proc. Inst. Civ. Eng. 2012, 71, 270–278. [Google Scholar]
- Đurin, B.; Margeta, J.; Bojanic, D. The Impact of the Water Consumption Regime on the Work of Reservoirs. E-Water 2015, 1, 1–21. [Google Scholar]
- Đurin, B.; Baic, L.; Kovac, S. New aspects of the connection between the pumping and the consumption regime of drinking water in human settlements. In Proceedings of the 7th International Scientific and Professional Conference Water for All, Osijek, Croatia, 9–10 March 2017; pp. 76–86. [Google Scholar]
- Scarpa, F.; Lobba, A.; Becciu, G. Expeditious Pump Rescheduling in Multisource Water Distribution Networks. Proc. Eng. 2015, 119, 1078–1087. [Google Scholar] [CrossRef] [Green Version]
- Yu, G.; Powell, R.S.; Sterling, M.J.H. Optimized pump scheduling in water distribution systems. J. Optim. Theory Appl. 1994, 83, 463–488. [Google Scholar] [CrossRef]
- Bagirov, A.M.; Barton, A.F.; Mala-Jetmarova, H.; Al Nuaimat, A.; Ahmed, S.T.; Sultanova, N.; Yearwood, J. An algorithm for minimization of pumping costs in water distribution systems using a novel approach to pump scheduling. Math. Comp. Mod. 2013, 57, 873–886. [Google Scholar] [CrossRef]
- Vamvakeridou-Lyroudia, L.S.; Savic, D.A.; Walters, G.A. Tank Simulation for the Optimization of Water Distribution Networks. J. Hyd. Eng. 2007, 133, 625–636. [Google Scholar] [CrossRef] [Green Version]
- Plantak, L.; Đurin, B.; Dzeba, T.; Dadar, S. Optimization of water reservoir volume in an urban water supply system. Rev. Fac. Ing. Univ. Ant. 2021, 103, 1–17. [Google Scholar] [CrossRef]
- Bhargava, D.S.; Gupta, P.K. Variation effect on the economical design of service reservoirs. Indian J. Eng. Mater. Sci. 2004, 11, 107–112. [Google Scholar]
- Bessler, F.T.; Savic, D.A.; Walters, G.A. Water Reservoir Control with Data Mining. J. Water Resour. Plan. Manag. 2003, 129, 26–34. [Google Scholar] [CrossRef]
- Stephenson, D.; Petersen, M.S. Chapter 7: Reservoir sizing. In Developments in Water Science; Elsevier: Amsterdam, The Netherlands, 1991; Volume 41, pp. 130–160. [Google Scholar]
- Bonaccorso, B.; Cancelliere, A.; Nicolosi, V.; Rossi, G.; Cristaudo, G. Chapter 9. Methods for risk assessment in water supply systems. In Drought Management Guidelines Technical Annex; Iglesias, A., Moneo, M., López-Francos, A., Eds.; CIHEAM/EC MEDA Water: Zaragoza, Spain, 2007; pp. 343–372. [Google Scholar]
- Moy, W.-S.; Cohon, J.L.; ReVelle, C.S. A Programming Model for Analysis of the Reliability, Resilience, and Vulnerability of a Water Supply Reservoir. Water Resour. Res. 1986, 22, 489–498. [Google Scholar] [CrossRef]
- Khatavkar, P.N.; Mays, L.W. Testing an optimization–simulation model for optimal pump and valve operations with required storage tank turnovers. J. Water Manag. Model. 2019, 27, C464. [Google Scholar] [CrossRef]
- Neelakantan, T.R.; Pundarikanthan, N.V. Hedging Rule Optimisation for Water Supply Reservoirs System. Water Resour. Manag. 1999, 13, 409–426. [Google Scholar] [CrossRef]
- Panigraphi, D.P.; Mujumdar, P.P. Reservoir Operation Modelling with Fuzzy Logic. Water Resour. Manag. 2000, 14, 89–109. [Google Scholar] [CrossRef]
- Bohórquez, J.; Saldarriaga, J.; Vallejo, D. Pumping pattern optimization in order to reduce WDS operation costs. Proc. Eng. 2015, 119, 1069–1077. [Google Scholar] [CrossRef] [Green Version]
- Abu-Madi, M.; Trifunović, N. Impacts of supply duration on the design and performance of intermittent water distribution systems in the West Bank. Water Int. 2013, 38, 263–282. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.; Choi, T.; Kim, M.; Han, S.; Koo, J. Optimal operation efficiency and control of water pumps in multiple water reservoir system: Case study in Korea. Water Sci. Technol. Water Supply 2015, 15, 59–65. [Google Scholar] [CrossRef]
- Meguid, H.S.S.A. Pressure, Leakage and Energy Management in Water Distribution Systems. Ph.D. Thesis, De Montfort University, Leicester, UK, March 2011. [Google Scholar]
- Giustolisi, O.; Laucelli, D.; Berardi, L. Operational Optimization: Water Losses versus Energy Costs. J. Hyd. Eng. 2013, 139, 410–423. [Google Scholar] [CrossRef]
- Dadar, S.; Ðurin, B.; Alamatian, E.; Plantak, L. Impact of the pumping regime on electricity cost savings in urban water supply system. Water 2021, 13, 1141. [Google Scholar] [CrossRef]
- Marchi, A.; Simpson, A.R.; Lambert, M.F. Pump Operation Optimization Using Rule-based Controls. Proc. Eng. 2017, 186, 210–217. [Google Scholar] [CrossRef]
- Al-Ani, D.; Habibi, S. Optimal operation of water pumping stations. Trans. Ecol. Environ. 2014, 178, 1743–3541. [Google Scholar]
- Yeh, W.W.-G. Reservoir Management and Operations Models: A State-of-the-Art Review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Margeta, J. Water Supply of Settlements: Planning, Design, Management, Water Treatment—Published Lectures; Faculty of Civil Engineering and Architecture: Split, Croatia, 2011. [Google Scholar]
- Ming, B.; Liu, P.; Bai, T.; Tang, R.; Feng, M. Improving Optimization Efficiency for Reservoir Operation Using a Search Space Reduction Method. Water Resour. Manag. 2017, 31, 1173–1190. [Google Scholar] [CrossRef]
- Menapace, A.; Avesani, D. Global Gradient Algorithm Extension to Distributed Pressure Driven Pipe Demand Model. Water Resour. Manag. 2019, 33, 1717–1736. [Google Scholar] [CrossRef] [Green Version]
- Menapace, A.; Avesani, D.; Righetti, M.; Bellin, A.; Pisaturo, G. Uniformly Distributed Demand EPANET Extension. Water Resour. Manag. 2018, 32, 2165–2180. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).