Flood Risk Modeling under Uncertainties: The Case Study of Croatia
Abstract
:1. Introduction
2. Materials and Methods
2.1. Case Study Description
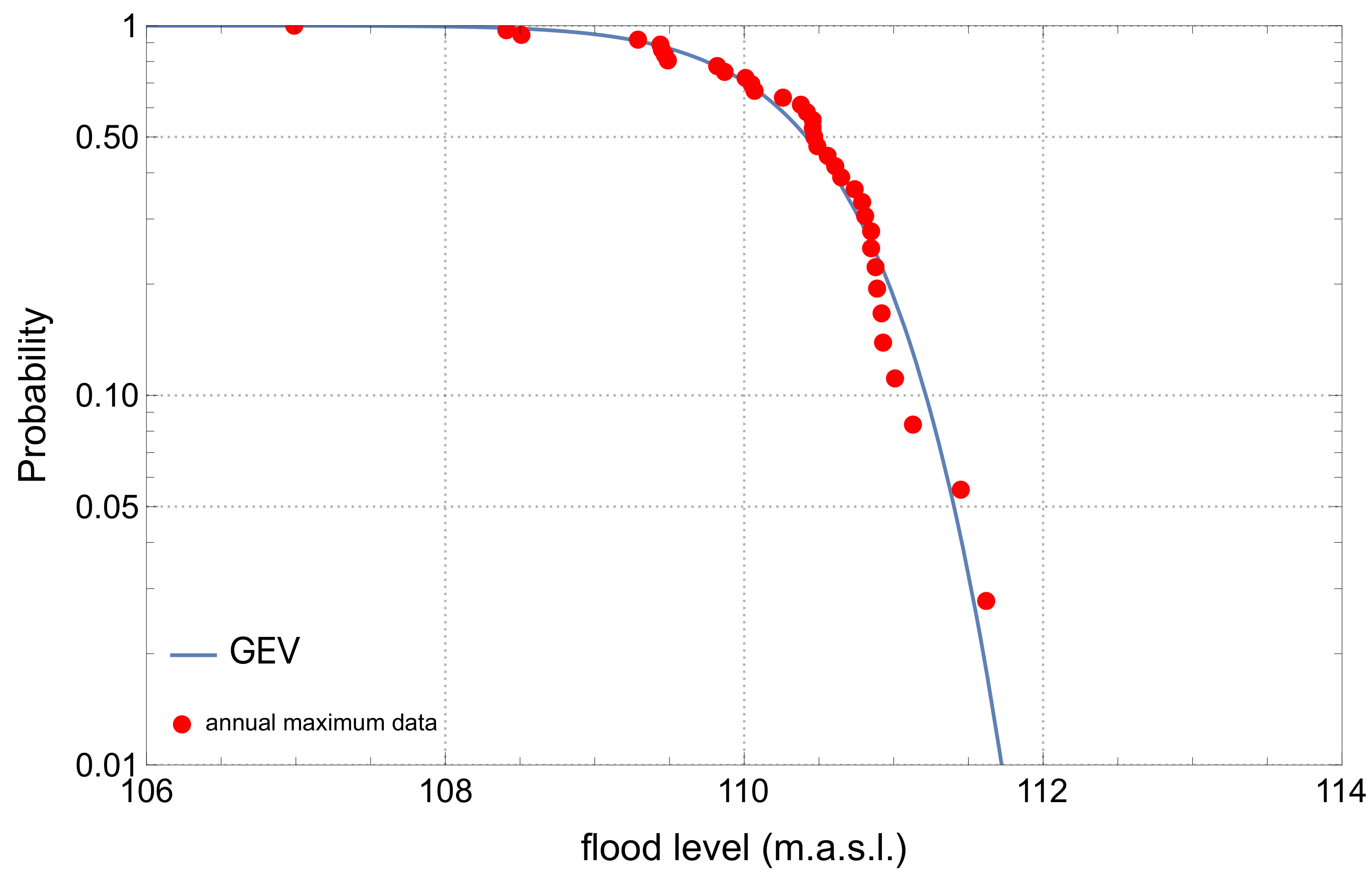
2.2. Flood Frequency Analysis
3. Results
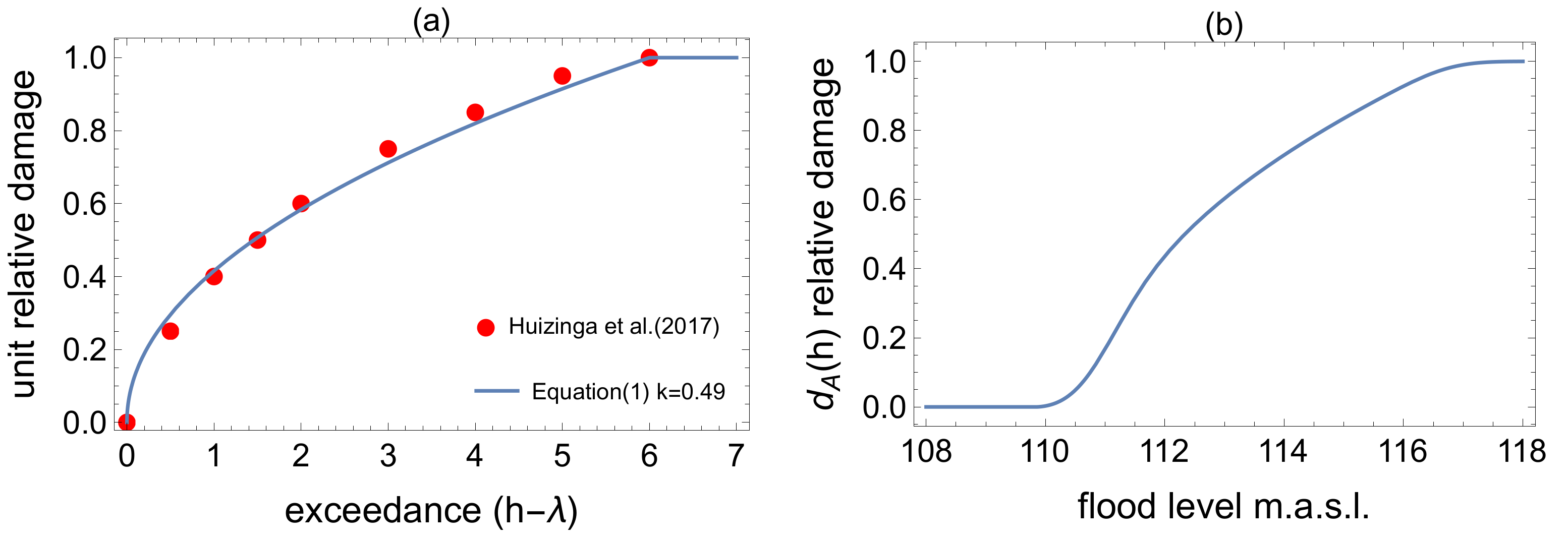
3.1. Flood Damage Estimates for Risk Characterization
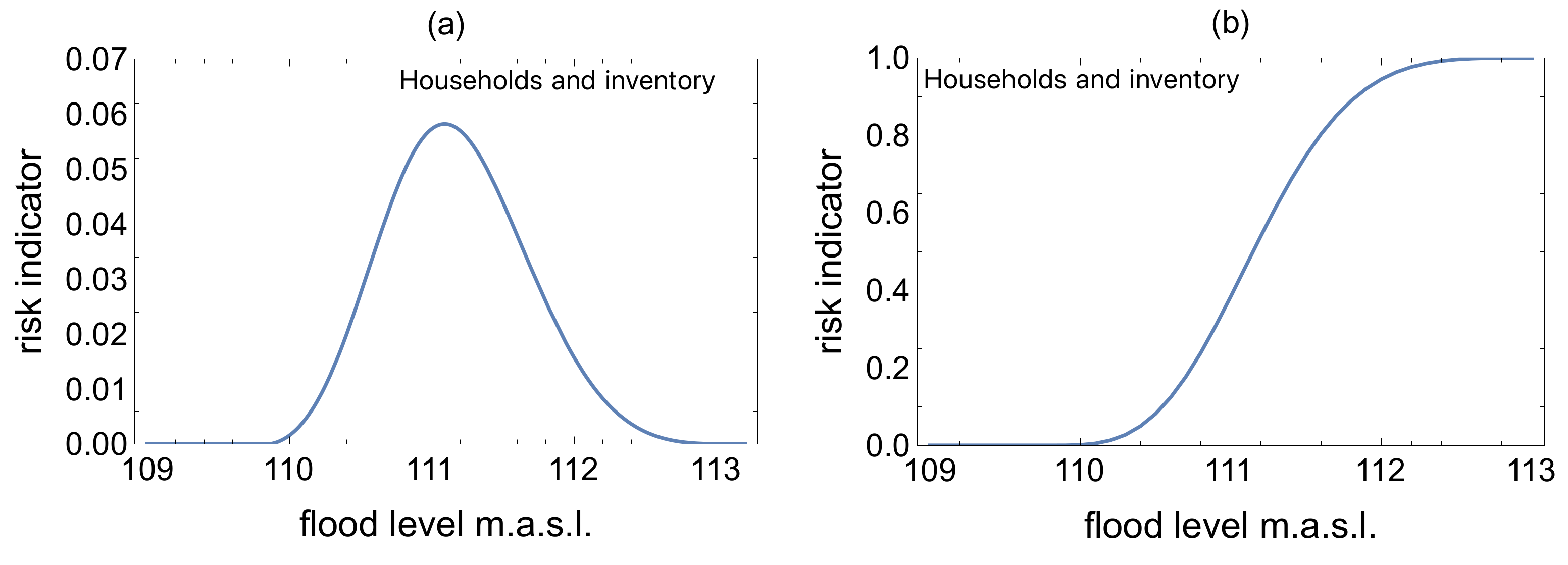
3.2. Flood Risk Indicators
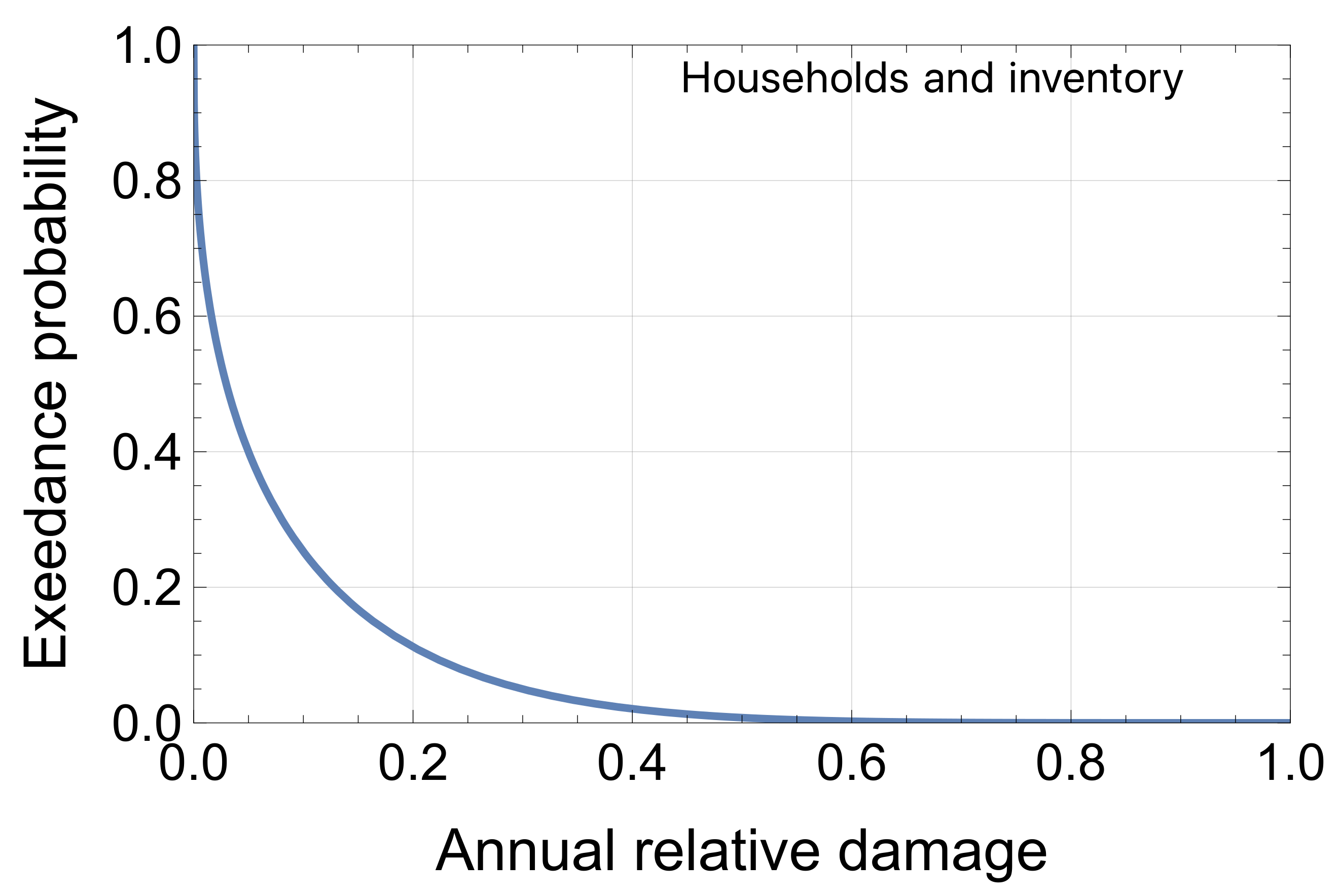
3.3. Annual Damage Distribution
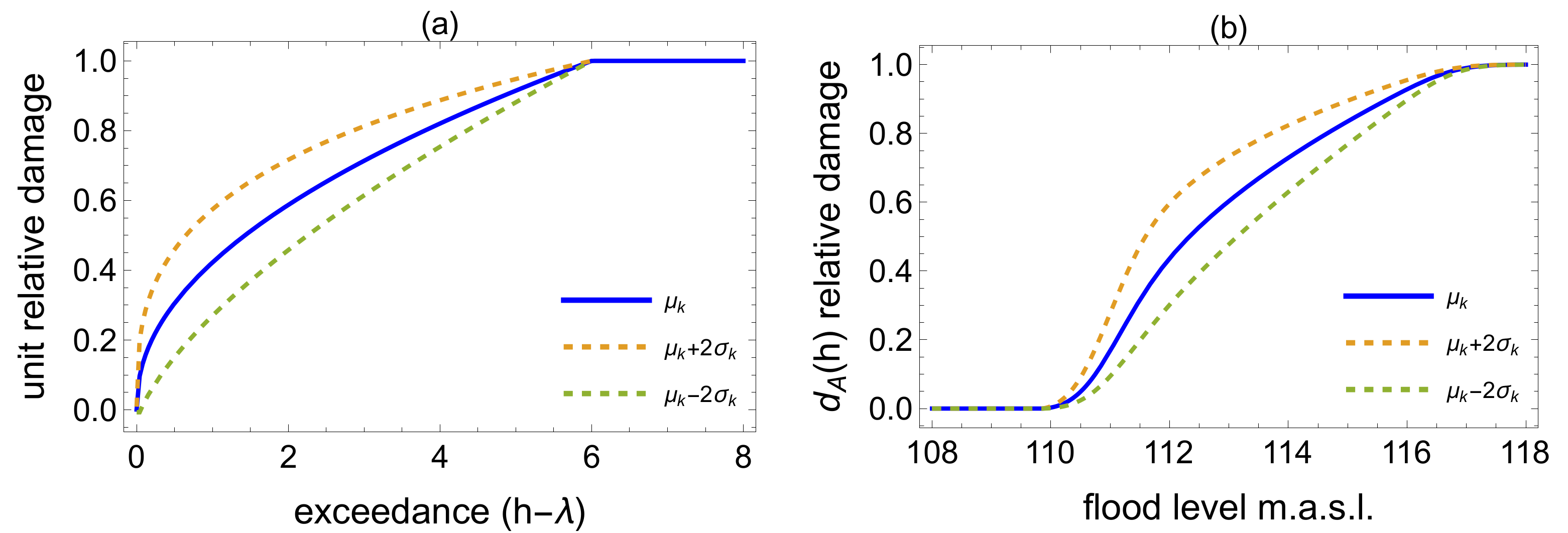
3.4. Uncertainty in the Damage Function
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leopold, L.B.; Langbein, L.B. The Concept of Entropy in Landscape Evolution. Geology 1962, 500, A1–A20. [Google Scholar] [CrossRef]
- Wagenaar, D.J.; Dahm, R.J.; Diermanse, F.L.M.; Dias, W.P.S.; Dissanayake, D.M.S.S.; Vajja, H.P.; Gehrels, J.C.; Bouwer, L.M. Evaluating adaptation measures for reducing flood risk: A case study in the city of Colombo, Sri Lanka. Int. J. Disaster Risk Reduct. 2019, 37, 101162. [Google Scholar] [CrossRef]
- European Commission. Directive 2007/60/EC on the Assessment and Management of Flood Risks; European Palament: Brussels, Belgium, 2007; Available online: https://eur-lex.europa.eu/eli/dir/2007/60/oj (accessed on 15 January 2022).
- Boso, F.; de Barros, F.P.J.; Fiori, A.; Bellin, A. Performance analysis of statistical spatial measures for contaminant plume characterization toward risk-based decision making. Water Resour. Res. 2013, 49, 3119–3132. [Google Scholar] [CrossRef]
- De Barros, F.P.J.; Bellin, A.; Cvetkovic, V.; Dagan, G.; Fiori, A. Aquifer heterogeneity controls on adverse human health effects and the concept of the hazard attenuation factor. Water Resour. Res. 2016, 52, 5911–5922. [Google Scholar] [CrossRef] [Green Version]
- Enzenhoefer, R.; Nowak, W.; Helmig, R. Probabilistic exposure risk assessment with advective–dispersive well vulnerability criteria. Adv. Water Resour. 2012, 36, 121–132. [Google Scholar] [CrossRef]
- Tartakovsky, D.M.; Dentz, M.; Lichtner, P. Probability density functions for advective-reactive transport with uncertain reaction rates. Water Resour. Res. 2009, 45, W07414. [Google Scholar] [CrossRef]
- Andričević, R.; Galešić, M. Contaminant dilution measure for the solute transport in an estuary. Adv. Water Resour. 2018, 117, 65–74. [Google Scholar] [CrossRef]
- Andričević, R.; Srzić, V.; Gotovac, H. Risk characterization for toxic chemicals transported in aquifers. Adv. Water Resour. 2012, 36, 86–97. [Google Scholar] [CrossRef]
- Di Dato, M.; Galešić, M.; Šimundić, P.; Andričević, R. A novel screening tool for the health risk in recreational waters near estuary: The Carrying Capacity indicator. Sci. Total Environ. 2019, 694, 133584. [Google Scholar] [CrossRef]
- Merz, B.; Kreibich, H.; Schwarze, R.; Thieken, A. Review article assessment of economic flood damage. Nat. Hazards Earth Syst. Sci. 2010, 10, 1697–1724. [Google Scholar] [CrossRef]
- Wagenaar, D.; de Jong, J.; Bouwer, L.M. Multi-variable flood damage modeling with limited data using supervised learning approaches. Nat. Hazards Earth Syst. Sci. 2017, 17, 1683–1696. [Google Scholar] [CrossRef] [Green Version]
- Wagenaar, D.; Lüdtke, S.; Schröter, K.; Bouwer, L.M.; Kreibich, H. Regional and temporal transferability of multivariable flood damage models. Water Resour. Res. 2018, 54, 3688–3703. [Google Scholar] [CrossRef] [Green Version]
- Jonkman, S.N.; Vrijling, J.K.; Vrouwenvelder, A.C.W.M. Methods for the estimation of loss of life due to floods: A literature review and a proposal for a new method. Nat. Hazards 2008, 46, 353–389. [Google Scholar] [CrossRef] [Green Version]
- Olsen, A.; Zhou, Q.; Linde, J.; Arnbjerg-Nielsen, K. Comparing Methods of Calculating Expected Annual Damage in Urban Pluvial Flood Risk Assessments. Water 2015, 7, 255–270. [Google Scholar] [CrossRef] [Green Version]
- Ward, P.J.; van Pelt, S.; de Keizer, O.; Aerts, J.C.J.H.; Beersma, J.; van den Hurk, B.; te Linde, A. Including climate change projections in probabilistic flood risk assessment. J. Flood Risk Manag. 2014, 7, 141–151. [Google Scholar] [CrossRef]
- Dottori, F.; Figueiredo, R.; Martina, M.L.V.; Molinari, D.; Scorzini, A.R. INSYDE: A synthetic, probabilistic flood damage model based on explicit cost analysis. Nat. Hazards Earth Syst. Sci. 2016, 16, 2577–2591. [Google Scholar] [CrossRef] [Green Version]
- Foudi, S.; Osés-Eraso, N.; Tamayo, I. Integrated spatial flood risk assessment: The case of Zaragoza. Land Use Policy 2015, 42, 278–292. [Google Scholar] [CrossRef]
- Wing, O.E.J.; Pinter, N.; Bates, P.D.; Kousky, C. New insights into US flood vulnerability revealed from flood insurance big data. Nat. Commun. 2020, 11, 1444. [Google Scholar] [CrossRef] [Green Version]
- Prahl, B.F.; Rybski, D.; Boettle, M.; Kropp, J.P. Damage functions for climate-related hazards: Unification and uncertainty analysis. Nat. Hazards Earth Syst. Sci. 2016, 16, 1189–1203. [Google Scholar] [CrossRef] [Green Version]
- Boettle, M.; Rybski, D.; Kropp, J.P. How changing sea level extremes and protection measures alter coastal flood damages. Water Resour. Res. 2013, 49, 1199–1210. [Google Scholar] [CrossRef]
- Merz, B.; Hall, J.; Disse, M.; Schumann, A. Fluvial flood risk management in a changing world. Nat. Hazards Earth Syst. Sci. 2010, 10, 509–527. [Google Scholar] [CrossRef] [Green Version]
- Boettle, M.; Kropp, J.P.; Reiber, L.; Roithmeier, O.; Rybski, D.; Walther, C. About the influence of elevation model quality and small-scale damage functions on flood damage estimation. Nat. Hazards Earth Syst. Sci. 2011, 11, 3327–3334. [Google Scholar] [CrossRef]
- Morita, M.; Tung, Y.-K. Uncertainty quantification of flood damage estimation for urban drainage risk management. Water Sci. Technol. 2019, 80, 478–486. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hall, J.; Solomatine, D. A framework for uncertainty analysis in flood risk management decisions. Int. J. River Basin Manag. 2008, 2, 85–98. [Google Scholar] [CrossRef] [Green Version]
- De Moel, H.; Aerts, J.C.C.H. Effect of uncertainty in land use, damage models and inundation depth on flood damage estimates. Nat. Hazards 2011, 58, 407–425. [Google Scholar] [CrossRef] [Green Version]
- Azarnivand, A.; Malekian, A. Analysis of flood risk management strategies based on a group decision making process via Interval-valued intuitionistic fuzzy numbers. Water Resour. Manag. 2016, 30, 1903–1921. [Google Scholar] [CrossRef]
- Rojas, R.; Feyen, L.; Watkiss, P. Climate change and river loods in the European Union: Socio-economic consequences and the costs and benefits of adaptation. Glob. Environ. Chang. 2013, 23, 1737–1751. [Google Scholar] [CrossRef]
- Ward, P.J.; de Moel, H.; Aerts, J.C.J.H. How are flood risk estimates affected by the choice of return-periods? Nat. Hazards Earth Syst. Sci. 2011, 11, 3181–3195. [Google Scholar] [CrossRef] [Green Version]
- Merz, B.; Elmer, F.; Thieken, A.H. Significance of high probability/low damage versus low probability/high damage flood events. Nat. Hazards Earth Syst. Sci. 2009, 9, 1033–1046. [Google Scholar] [CrossRef]
- Croatian Meteorological and Hydrological Service. Climate Monitoring. 2019. Available online: https://meteo.hr/ (accessed on 25 October 2020).
- Jurković, R.S. Water balance components during recent floods in Croatia. Croat. Meteorol. J. 2016, 51, 61–70. [Google Scholar]
- Huizinga, J.; de Moel, H.; Szewczyk, W. Global Flood Depth-Damage Functions. Methodology and the Database with Guidelines; EUR 28552 EN; Publications Office of the European Union: Luxembourg, 2017. [Google Scholar]
- Zhou, Q.; Mikkelsen, P.S.; Halsnæs, K.; Arnbjerg-Nielsen, K. Framework for economic pluvial flood risk assessment considering climate change effects and adaptation benefits. J. Hydrol. 2012, 414, 539–549. [Google Scholar] [CrossRef]
- Kekez, T.; Knezić, S.; Andričević, R. Incorporating Uncertainty of the System Behavior in Flood Risk Assessment—Sava River Case Study. Water 2020, 12, 2676. [Google Scholar] [CrossRef]
- Athanasios Papoulis, S. Probability, Random Variables, and Stochastic Processes, 2nd ed.; McGrow-Hill: New York, NY, USA, 1984. [Google Scholar]
- Humphreys, N. Exceedance probability in catastrophic modeling. Casualty Actuar. Soc. E-Forum 2021, 1–61. [Google Scholar]
- Hammond, M.J.; Chen, A.S.; Djordjević, S.; Butler, D.; Mark, O. Urban flood impact assessment: A state-of-the-art review. Urban Water J. 2015, 12, 14–29. [Google Scholar] [CrossRef] [Green Version]



| Type of Asset | Quantity at Risk | Unit Value | Total Damage |
|---|---|---|---|
| Households and inventory | households footprint area 34,000 m | 507 €/m | 17.238 € |
| EAD | Standard Deviation | Skewness | Kurtosis |
|---|---|---|---|
| 0.074 | 0.1 | 1.75 | 5.55 |
| Flood Event (Years) | Annual Probability of Occurrence [] | Annual Relative Damage | Monetary Loss () € | Expected Monetary Loss [] | Exceedance Probability % |
|---|---|---|---|---|---|
| 10 | 0.1 | 0.23 | 3.96 | 0.396 | 8.7 |
| 25 | 0.04 | 0.33 | 5.7 | 0.22 | 4 |
| 50 | 0.02 | 0.39 | 6.7 | 0.13 | 2.8 |
| 100 | 0.01 | 0.43 | 7.4 | 0.074 | 2 |
| 500 | 0.002 | 0.49 | 8.4 | 0.017 | 1.4 |
| 1000 | 0.001 | 0.51 | 7.24 | 0.00724 | 0.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kekez, T.; Andricevic, R.; Knezic, S. Flood Risk Modeling under Uncertainties: The Case Study of Croatia. Water 2022, 14, 1585. https://doi.org/10.3390/w14101585
Kekez T, Andricevic R, Knezic S. Flood Risk Modeling under Uncertainties: The Case Study of Croatia. Water. 2022; 14(10):1585. https://doi.org/10.3390/w14101585
Chicago/Turabian StyleKekez, Toni, Roko Andricevic, and Snjezana Knezic. 2022. "Flood Risk Modeling under Uncertainties: The Case Study of Croatia" Water 14, no. 10: 1585. https://doi.org/10.3390/w14101585






