Hunting for Information in Streamflow Signatures to Improve Modelled Drainage
Abstract
:1. Introduction
- Test the hypothesis that hydrological signatures hold information on the contribution of drain flow to total streamflow.
- Test the degree to which model calibration can be guided and drain flow simulation improved by including selected hydrological signatures in the objective functions.
2. Data and Methods
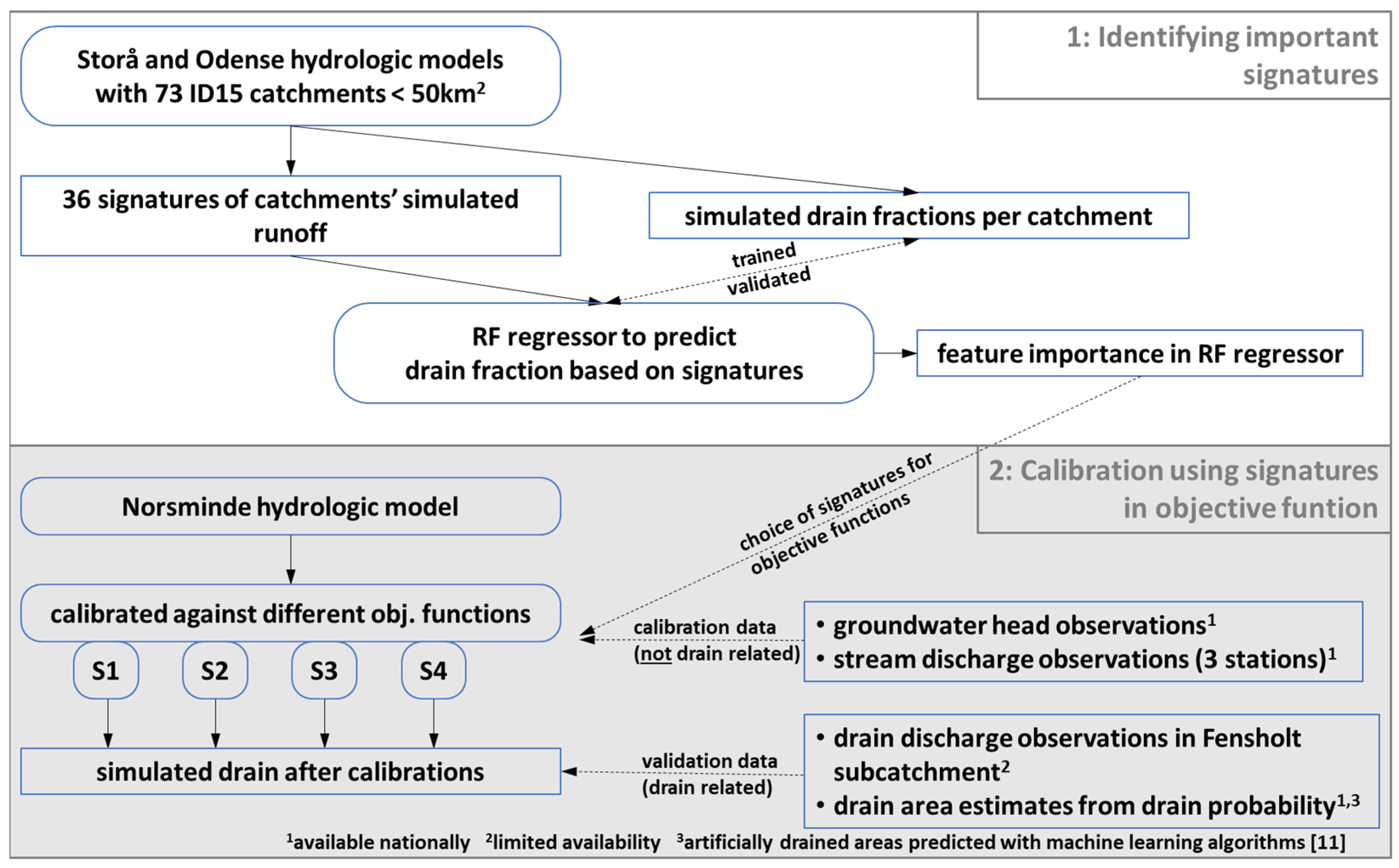
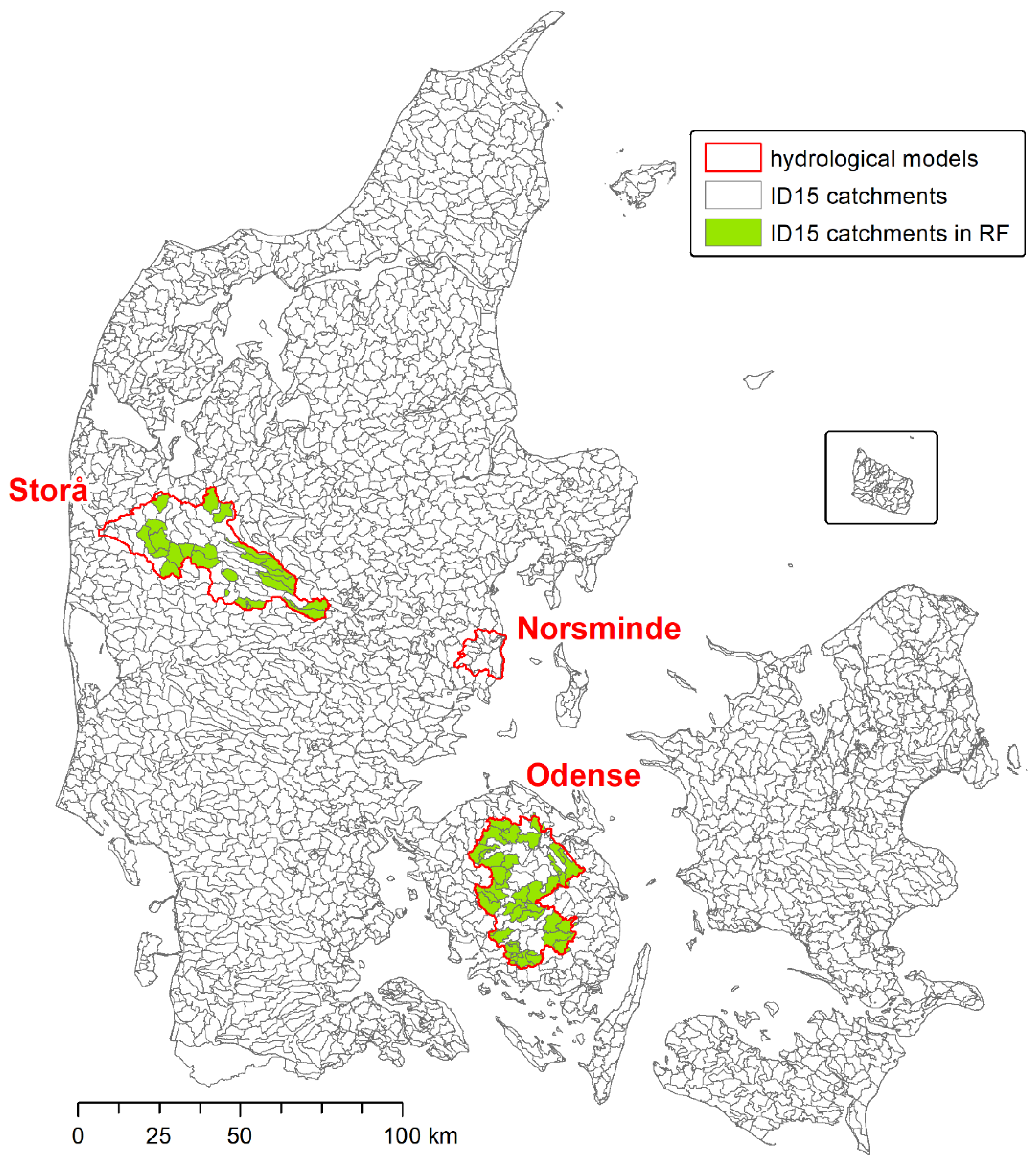
2.1. Hydrological Modelling
2.2. Machine Learning Regressors to Predict Drain Fraction
2.2.1. Simulated Discharge Used in Machine Learning Regression
2.2.2. Hydrological Signatures
| Signature | Unit | Explanation | |
|---|---|---|---|
| BFI5 | Baseflow index, 5-day period | - | For entire time series, and separate for each season |
| BFI5 w/s | BFI5 winter/summer ratio | - | Summer: Jun, Jul, Aug. Winter: Jan, Feb, Mar |
| BFI20 | Baseflow index, 20-day period | - | |
| SFDC | Slope of the middle third of the flow duration curve | - | |
| rcoeff | Runoff coefficient | - | Precipitation taken from model forcing |
| CV | Coefficient of variation | - | For entire time series, and separate for each season |
| CV w/s | Coefficient of variation winter/summer | - | |
| RBFI | Richards–Baker–Flashiness index | - | [51] |
| skew | skewness: mean (q)/median (q) | - | |
| mriser | Mean change in q while hydrograph is rising | mm/d | |
| mfallr | Mean change in q while hydrograph is falling | mm/d | |
| qm | Mean specific runoff | mm | For entire time series, and separate for each season |
| qm w/s | Mean specific runoff winter/summer ratio | - | |
| f2ms | first peak after Aug 1st > 2 × mean (q summer) | doy | As indication for start of flow from tile drains |
| fp3ms | first peak after Aug 1st > 3 × mean (q summer) | doy | As indication for start of flow from tile drains |
| fp2m | first peak after Aug 1st > 2 × median (q) | doy | As indication for start of flow from tile drains |
| fp3m | first peak after Aug 1st > 3 × median (q) | doy | As indication for start of flow from tile drains |
| Qq99 | 0.99 flow quantile | mm/d | |
| Qq95 | 0.95 flow quantile | mm/d | |
| Qq90 | 0.90 flow quantile | mm/d | |
| Qq10 | 0.10 flow quantile | mm/d | |
| Qq5 | 0.05 flow quantile | mm/d | |
| Qq1 | 0.01 flow quantile | mm/d | |
| hQv | High flow variability | - | Mean of annual maximum q/median q |
| lQv | Low flow variability | - | Mean of annual minimum q/median q |
| lfD | Low flow duration | d/y | Average number of days per year where q < 0.5 × mean (q) |
| lfED | Low flow event duration | d | Average length of events of q < 0.5 × mean (q) |
| lfEF | Low flow event frequency | y−1 | Occurrences of q < 0.5 × mean (q) |
| hfD | High flow duration | d/y | Average number of days per year where q > 3 × median (q) |
| hfED | High flow event duration | d | Average length of events of q > 3 × median (q) |
| hfEF | High flow event frequency | y−1 | Occurrences of q > 3 × median (q) |
| minq7d | Mean minimum discharge measured over 7 consecutive days | mm/d | |
| minq30d | Mean minimum discharge measured over 30 consecutive days | mm/d | |
| maxq7d | Mean maximum discharge measured over 7 consecutive days | mm/d | |
| maxq30d | Mean maximum discharge measured over 30 consecutive days | mm/d | |
| catcharea | Catchment area | km2 | (only physical catchment characteristic used in analysis) |
2.3. Norsminde Hydrological Model
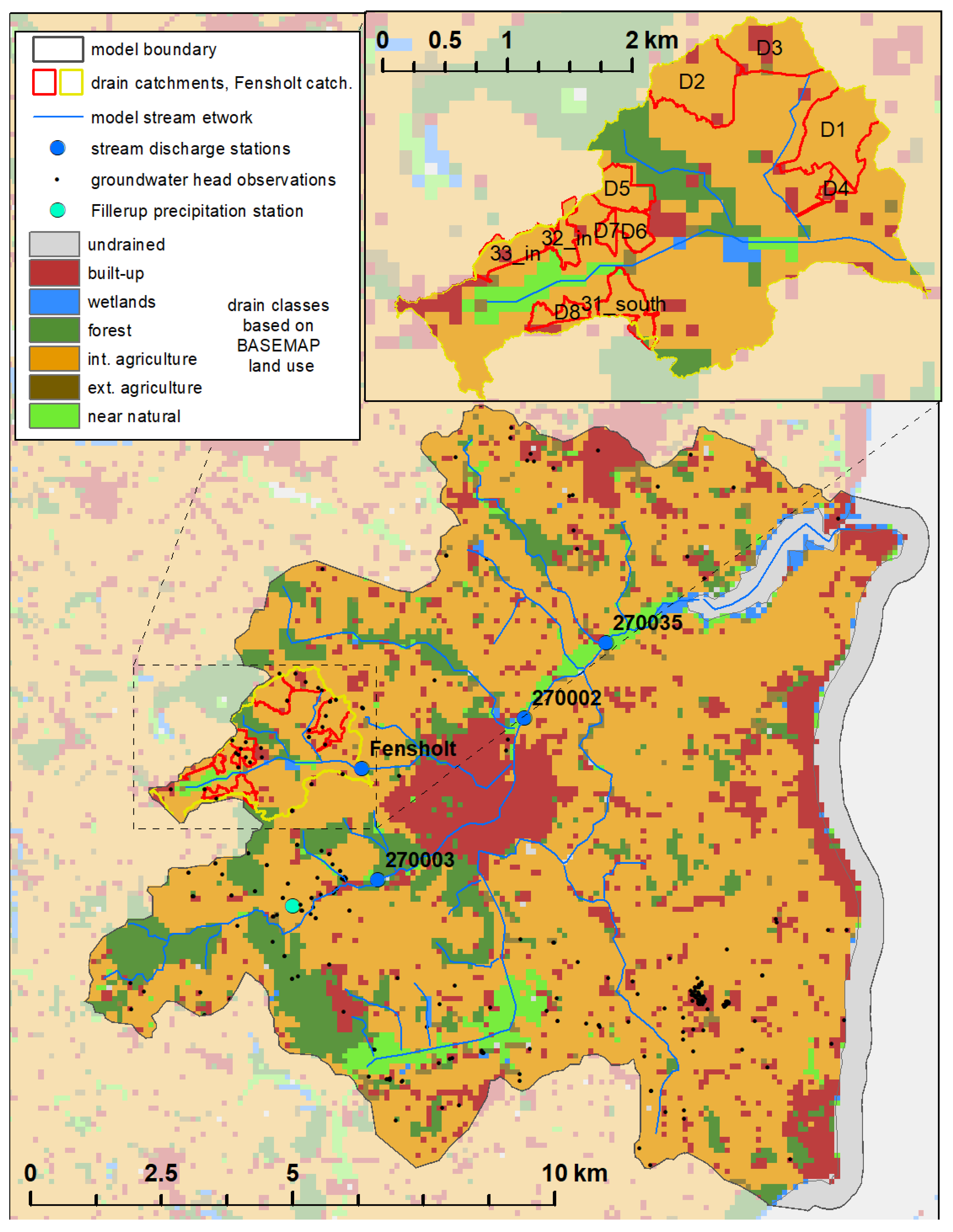
2.3.1. Hydrological Model—Drain Setup
2.3.2. Hydrological Model—Calibration Data
2.3.3. Hydrological Model—Drain Validation Data
2.3.4. Hydrological Model—Calibration Setup
3. Results
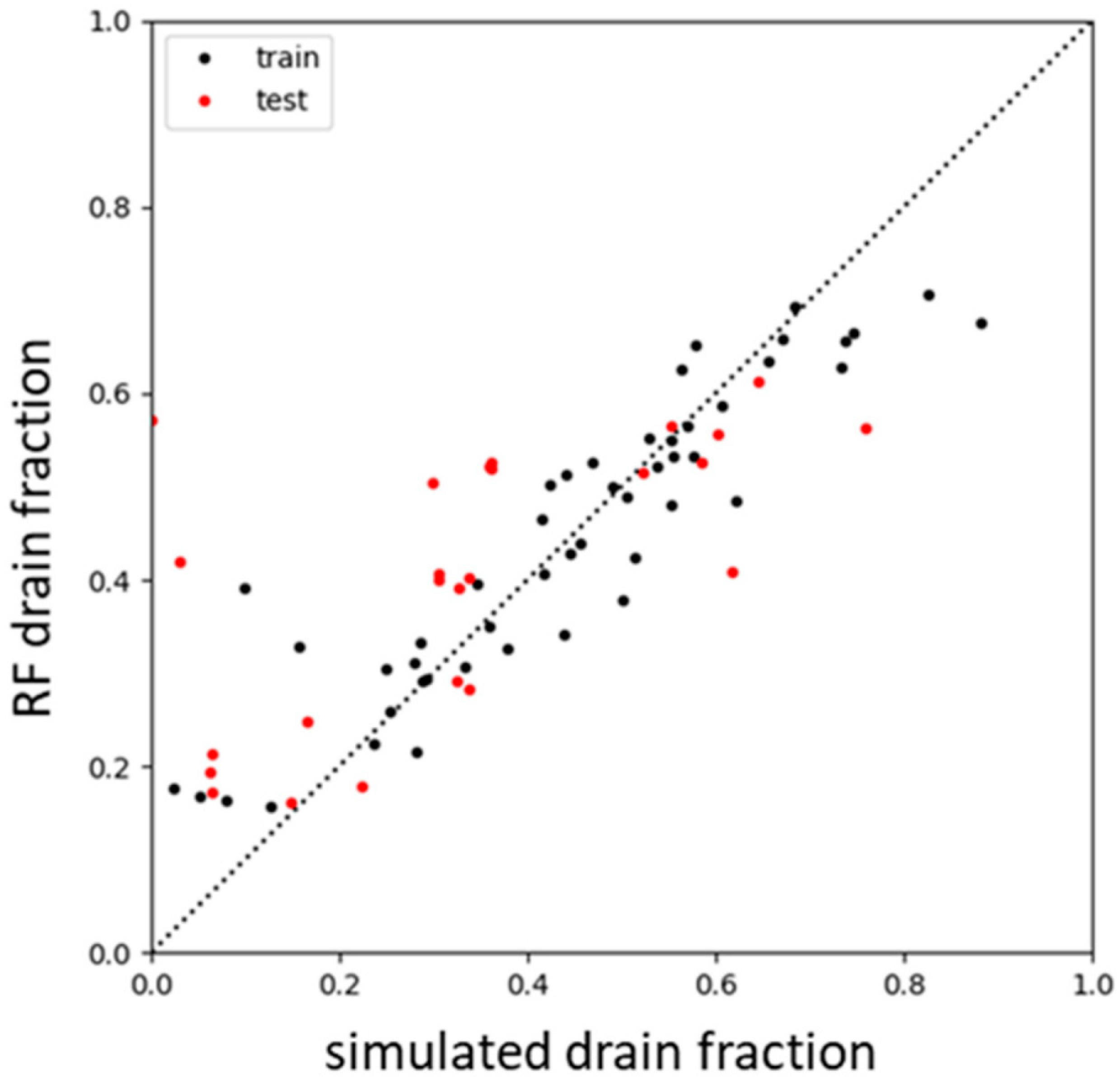
3.1. RF Regressors Predicting Drain Fraction
3.2. Evaluation of the Hydrological Model Calibration Scenarios
3.2.1. Evaluation against Calibration Data
3.2.2. Evaluation against Drain-Related Validation Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Olesen, S.E. Kortlægning Af Potentielt Dræningsbehov På Landbrugsarealer Opdelt Efter Landskabselement, Geologi, Jordklasse, Geologisk Region Samt Høj/Lavbund; DJF Intern Rapport Markbrug Nr. 21; Det Jordbrugsvidenskabelige Fakultet, Aarhus Universitet: Tejle, Denmark, 2009. [Google Scholar]
- De Lange, W.J.; Prinsen, G.F.; Hoogewoud, J.C.; Veldhuizen, A.A.; Verkaik, J.; Oude Essink, G.H.P.; Van Walsum, P.E.V.; Delsman, J.R.; Hunink, J.C.; Massop, H.T.L.; et al. An Operational, Multi-Scale, Multi-Model System for Consensus-Based, Integrated Water Management and Policy Analysis: The Netherlands Hydrological Instrument. Environ. Model. Softw. 2014, 59, 98–108. [Google Scholar] [CrossRef] [Green Version]
- Kiesel, J.; Fohrer, N.; Schmalz, B.; White, M.J. Incorporating Landscape Depressions and Tile Drainages of a Northern German Lowland Catchment into a Semi-Distributed Model. Hydrol. Processes 2010, 24, 1472–1486. [Google Scholar] [CrossRef]
- Sandin, M.; Piikki, K.; Jarvis, N.; Larsbo, M.; Bishop, K.; Kreuger, J. Spatial and Temporal Patterns of Pesticide Concentrations in Streamflow, Drainage and Runoff in a Small Swedish Agricultural Catchment. Sci. Total Environ. 2018, 610, 623–634. [Google Scholar] [CrossRef]
- Thomas, N.W.; Arenas, A.A.; Schilling, K.E.; Weber, L.J. Numerical Investigation of the Spatial Scale and Time Dependency of Tile Drainage Contribution to Stream Flow. J. Hydrol. 2016, 538, 651–666. [Google Scholar] [CrossRef]
- Williams, M.R.; King, K.W.; Fausey, N.R. Contribution of Tile Drains to Basin Discharge and Nitrogen Export in a Headwater Agricultural Watershed. Agric. Water Manag. 2015, 158, 42–50. [Google Scholar] [CrossRef]
- Arenas Amado, A.; Schilling, K.E.; Jones, C.S.; Thomas, N.; Weber, L.J. Estimation of Tile Drainage Contribution to Streamflow and Nutrient Loads at the Watershed Scale Based on Continuously Monitored Data. Environ. Monit. Assess. 2017, 189, 426. [Google Scholar] [CrossRef]
- Hansen, A.L.; Storgaard, A.; He, X.; Højberg, A.L.; Refsgaard, J.C.; Iversen, B.V.; Kjaergaard, C. Importance of Geological Information for Assessing Drain Flow in a Danish till Landscape. Hydrol. Processes 2019, 33, 450–462. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Auken, E.; Bamberg, C.A.; Christensen, B.S.B.; Clausen, T.; Dalgaard, E.; Effersø, F.; Ernstsen, V.; Gertz, F.; Hansen, A.L.; et al. Nitrate Reduction in Geologically Heterogeneous Catchments—A Framework for Assessing the Scale of Predictive Capability of Hydrological Models. Sci. Total Environ. 2014, 468, 1278–1288. [Google Scholar] [CrossRef] [PubMed]
- Koganti, T.; Van De Vijver, E.; Allred, B.J.; Greve, M.H.; Ringgaard, J.; Iversen, B.V. Mapping of Agricultural Subsurface Drainage Systems Using a Frequency-Domain Ground Penetrating Radar and Evaluating Its Performance Using a Single-Frequency Multi-Receiver Electromagnetic Induction Instrument. Sensors 2020, 20, 3922. [Google Scholar] [CrossRef] [PubMed]
- Møller, A.B.; Beucher, A.; Iversen, B.V.; Greve, M.H. Predicting Artificially Drained Areas by Means of a Selective Model Ensemble. Geoderma 2018, 320, 30–42. [Google Scholar] [CrossRef]
- De Schepper, G.; Therrien, R.; Refsgaard, J.C.; Hansen, A.L. Simulating Coupled Surface and Subsurface Water Flow in a Tile-Drained Agricultural Catchment. J. Hydrol. 2015, 521, 374–388. [Google Scholar] [CrossRef]
- Højberg, A.L.; Troldborg, L.; Stisen, S.; Christensen, B.B.S.; Henriksen, H.J. Stakeholder Driven Update and Improvement of a National Water Resources Model. Environ. Model. Softw. 2013, 40, 202–213. [Google Scholar] [CrossRef]
- Stisen, S.; Ondracek, M.; Troldborg, L.; Schneider, R.J.M.; van Til, M.J. National Vandressource Model—Modelopstilling Og Kalibrering Af DK-Model 2019; Danmarks og Grønlands Geologiske Undersøgelse Rapport 2019/31; GEUS: Copenhagen, Denmark, 2019. [Google Scholar]
- Hansen, A.L.; Refsgaard, J.C.; Baun Christensen, B.S.; Jensen, K.H. Importance of Including Small-Scale Tile Drain Discharge in the Calibration of a Coupled Groundwater-Surface Water Catchment Model. Water Resour. Res. 2013, 49, 585–603. [Google Scholar] [CrossRef] [Green Version]
- Turunen, M.; Warsta, L.; Paasonen-Kivekäs, M.; Nurminen, J.; Myllys, M.; Alakukku, L.; Äijö, H.; Puustinen, M.; Koivusalo, H. Modeling Water Balance and Effects of Different Subsurface Drainage Methods on Water Outflow Components in a Clayey Agricultural Field in Boreal Conditions. Agric. Water Manag. 2013, 121, 135–148. [Google Scholar] [CrossRef]
- Olden, J.D.; Poff, N.L. Redundancy and the Choice of Hydrologic Indices for Characterizing Streamflow Regimes. River Res. Appl. 2003, 19, 101–121. [Google Scholar] [CrossRef]
- Yadav, M.; Wagener, T.; Gupta, H. Regionalization of Constraints on Expected Watershed Response Behavior for Improved Predictions in Ungauged Basins. Adv. Water Resour. 2007, 30, 1756–1774. [Google Scholar] [CrossRef]
- McMillan, H.; Westerberg, I.; Branger, F. Five Guidelines for Selecting Hydrological Signatures. Hydrol. Processes 2017, 31, 4757–4761. [Google Scholar] [CrossRef] [Green Version]
- McMillan, H. Linking Hydrologic Signatures to Hydrologic Processes: A Review. Hydrol. Processes 2020, 34, 1393–1409. [Google Scholar] [CrossRef]
- McMillan, H.; Gueguen, M.; Grimon, E.; Woods, R.; Clark, M.; Rupp, D.E. Spatial Variability of Hydrological Processes and Model Structure Diagnostics in a 50km2 Catchment. Hydrol. Processes 2014, 28, 4896–4913. [Google Scholar] [CrossRef]
- Sawicz, K.; Wagener, T.; Sivapalan, M.; Troch, P.A.; Carrillo, G. Catchment Classification: Empirical Analysis of Hydrologic Similarity Based on Catchment Function in the Eastern USA. Hydrol. Earth Syst. Sci. 2011, 15, 2895–2911. [Google Scholar] [CrossRef] [Green Version]
- Carrillo, G.; Troch, P.A.; Sivapalan, M.; Wagener, T.; Harman, C.; Sawicz, K. Catchment Classification: Hydrological Analysis of Catchment Behavior through Process-Based Modeling along a Climate Gradient. Hydrol. Earth Syst. Sci. 2011, 15, 3411–3430. [Google Scholar] [CrossRef] [Green Version]
- Kuentz, A.; Arheimer, B.; Hundecha, Y.; Wagener, T. Understanding Hydrologic Variability across Europe through Catchment Classification. Hydrol. Earth Syst. Sci. 2017, 21, 2863–2879. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Vaze, J.; Chiew, F.H.S.; Teng, J.; Li, M. Predicting Hydrological Signatures in Ungauged Catchments Using Spatial Interpolation, Index Model, and Rainfall-Runoff Modelling. J. Hydrol. 2014, 517, 936–948. [Google Scholar] [CrossRef]
- Donnelly, C.; Andersson, J.C.M.; Arheimer, B. Using Flow Signatures and Catchment Similarities to Evaluate the E-HYPE Multi-Basin Model across Europe. Hydrol. Sci. J. 2016, 61, 255–273. [Google Scholar] [CrossRef]
- Fenicia, F.; Kavetski, D.; Savenije, H.H.G.; Clark, M.P.; Schoups, G.; Pfister, L.; Freer, J. Catchment Properties, Function, and Conceptual Model Representation: Is There a Correspondence? Hydrol. Processes 2014, 28, 2451–2467. [Google Scholar] [CrossRef]
- Euser, T.; Winsemius, H.C.; Hrachowitz, M.; Fenicia, F.; Uhlenbrook, S.; Savenije, H.H.G. A Framework to Assess the Realism of Model Structures Using Hydrological Signatures. Hydrol. Earth Syst. Sci. 2013, 17, 1893–1912. [Google Scholar] [CrossRef] [Green Version]
- Jehn, F.U.; Chamorro, A.; Houska, T.; Breuer, L. Trade-Offs between Parameter Constraints and Model Realism: A Case Study. Sci. Rep. 2019, 9, 10729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nijzink, R.C.; Almeida, S.; Pechlivanidis, I.G.; Capell, R.; Gustafssons, D.; Arheimer, B.; Parajka, J.; Freer, J.; Han, D.; Wagener, T.; et al. Constraining Conceptual Hydrological Models With Multiple Information Sources. Water Resour. Res. 2018, 54, 8332–8362. [Google Scholar] [CrossRef] [Green Version]
- Fenicia, F.; Kavetski, D.; Reichert, P.; Albert, C. Signature-Domain Calibration of Hydrological Models Using Approximate Bayesian Computation: Empirical Analysis of Fundamental Properties. Water Resour. Res. 2018, 54, 3958–3987. [Google Scholar] [CrossRef]
- Pfannerstill, M.; Guse, B.; Fohrer, N. Smart Low Flow Signature Metrics for an Improved Overall Performance Evaluation of Hydrological Models. J. Hydrol. 2014, 510, 447–458. [Google Scholar] [CrossRef]
- Shafii, M.; Tolson, B.A. Optimizing Hydrological Consistency by Incorporating Hydrological Signatures into Model Calibration Objectives. Water Resour. Res. 2015, 51, 3796–3814. [Google Scholar] [CrossRef] [Green Version]
- Winsemius, H.C.; Schaefli, B.; Montanari, A.; Savenije, H.H.G. On the Calibration of Hydrological Models in Ungauged Basins: A Framework for Integrating Hard and Soft Hydrological Information. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef] [Green Version]
- King, K.W.; Fausey, N.R.; Williams, M.R. Effect of Subsurface Drainage on Streamflow in an Agricultural Headwater Watershed. J. Hydrol. 2014, 519, 438–445. [Google Scholar] [CrossRef]
- Macrae, M.L.; English, M.C.; Schiff, S.L.; Stone, M. Intra-Annual Variability in the Contribution of Tile Drains to Basin Discharge and Phosphorus Export in a First-Order Agricultural Catchment. Agric. Water Manag. 2007, 92, 171–182. [Google Scholar] [CrossRef]
- Boland-Brien, S.J.; Basu, N.B.; Schilling, K.E. Homogenization of Spatial Patterns of Hydrologic Response in Artificially Drained Agricultural Catchments. Hydrol. Processes 2014, 28, 5010–5020. [Google Scholar] [CrossRef]
- Shafii, M.; Craig, J.R.; Macrae, M.L.; English, M.C.; Schiff, S.L.; Van Cappellen, P.; Basu, N.B. Can Improved Flow Partitioning in Hydrologic Models Increase Biogeochemical Predictability? Water Resour. Res. 2019, 55, 2939–2960. [Google Scholar] [CrossRef]
- Hansen, A.L.; Gunderman, D.; He, X.; Refsgaard, J.C. Uncertainty Assessment of Spatially Distributed Nitrate Reduction Potential in Groundwater Using Multiple Geological Realizations. J. Hydrol. 2014, 519, 225–237. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An Introduction to the European Hydrological System—Systeme Hydrologique Europeen, “SHE”, 1: History and Philosophy of a Physically-Based, Distributed Modelling System. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- DHI. MIKE SHE, Volume 2: Reference Guide; DHI: Hørsholm, Denmark, 2019; p. 374. [Google Scholar]
- Henriksen, H.J.; Troldborg, L.; Nyegaard, P.; Sonnenborg, T.O.; Refsgaard, J.C.; Madsen, B. Methodology for Construction, Calibration and Validation of a National Hydrological Model for Denmark. J. Hydrol. 2003, 280, 52–71. [Google Scholar] [CrossRef]
- Jakobsen, P.R.; Hermansen, B.; Tougaard, L. Danmarks Digitale Jordartskort 1:25000—Version 4.0; Danmarks og Grønlands Geologiske Undersøgelse Rapport 2015/30; GEUS: Copenhagen, Denmark, 2015. [Google Scholar]
- Scharling, M. Klimagrid Danmark Nedbør 10x10 Km (Ver. 2)—Metodebeskrivelse; Technical Report 99-15; Danish Meteorological Institute: Copenhagen, Denmark, 1999.
- Scharling, M. Klimagrid Danmark—Nedbør, Lufttemperatur og Potentiel Fordampning 20X20 & 40x40 Km—Metodebeskrivelse; Technical Report 99-12; Danish Meteorological Institute: Copenhagen, Denmark, 1999.
- Stisen, S.; Sonnenborg, T.O.; Højberg, A.L.; Troldborg, L.; Refsgaard, J.C. Evaluation of Climate Input Biases and Water Balance Issues Using a Coupled Surface-Subsurface Model. Vadose Zone J. 2011, 10, 37–53. [Google Scholar] [CrossRef]
- Stisen, S.; Schneider, R.; Ondracek, M.; Henriksen, H.J. Modellering Af Terrænnært Grundvand, Vandstand i Vandløb Og Vand På Terræn for Storå Og Odense Å. Slutrapport (FODS 6.1 Fasttrack Metodeudvikling); Danmarks og Grønlands Geologiske Undersøgelse Rapport 2018/36; GEUS: Copenhagen, Denmark, 2018. [Google Scholar]
- Zhang, Y.; Chiew, F.H.S.; Li, M.; Post, D. Predicting Runoff Signatures Using Regression and Hydrological Modeling Approaches. Water Resour. Res. 2018, 54, 7859–7878. [Google Scholar] [CrossRef]
- Houska, T.; Kraft, P.; Chamorro-Chavez, A.; Breuer, L. SPOTting Model Parameters Using a Ready-Made Python Package. PLoS ONE 2015, 10, e0145180. [Google Scholar] [CrossRef]
- Karlsson, I.B.; Højberg, A.L.; He, X.; Iversen, B.V. Testing the Use of Drain Flow Measurements to Guide Calibration and Improving Local Scale Model Performance in a Distributed Hydrological Catchment Model for a Danish Glacial Till Area. Presented at the AGU Fall Meeting 2018, Washington, DC, USA, 10–14 December 2018. [Google Scholar]
- Baker, D.B.; Richards, R.P.; Loftus, T.T.; Kramer, J.W. A New Flashiness Index: Characteristics and Applications to Midwestern Rivers and Streams. J. Am. Water Resour. Assoc. 2004, 40, 503–522. [Google Scholar] [CrossRef]
- He, X.; Højberg, A.L.; Jørgensen, F.; Refsgaard, J.C. Assessing Hydrological Model Predictive Uncertainty Using Stochastically Generated Geological Models. Hydrol. Processes 2015, 29, 4293–4311. [Google Scholar] [CrossRef]
- Danish EPA. FOHM—Fælles Offentlig Hydrologisk Model. Available online: https://mst.dk/natur-vand/vand-i-hverdagen/grundvand/grundvandskortlaegning/kortlaegning-2016-2020/fohm-faelles-offentlig-hydrologisk-model/ (accessed on 11 March 2020).
- Thompson, J.R.; Sørenson, H.R.; Gavin, H.; Refsgaard, A. Application of the Coupled MIKE SHE / MIKE 11 Modelling System to a Lowland Wet Grassland in Southeast England. J. Hydrol. 2004, 293, 151–179. [Google Scholar] [CrossRef]
- Levin, G.; Jepsen, M.R.; Blemmer, M. Basemap, Technical Documentation of a Model for Elaboration of a Land-Use and Land-Cover Map for Denmark; Techincal Report from DCE-Danish Centre for Environment and Energy; Aarhus University, DCE: Silkeborg, Denmark, 2012. [Google Scholar]
- DHI. MIKE SHE, Volume 1: User Guide; DHI: Hørsholm, Denmark, 2019; p. 448. [Google Scholar]
- Jørgensen, L.F.; Stockmarr, J. Groundwater Monitoring in Denmark: Characteristics, Perspectives and Comparison with Other Countries. Hydrogeol. J. 2009, 17, 827–842. [Google Scholar] [CrossRef]
- Petersen, R.J.; Prinds, C.; Iversen, B.V.; Engesgaard, P.; Jessen, S.; Kjaergaard, C. Riparian Lowlands in Clay Till Landscapes: Part I—Heterogeneity of Flow Paths and Water Balances. Water Resour. Res. 2020, 56, e2019WR025808. [Google Scholar] [CrossRef]
- Doherty, J. Calibration and Uncertainty Analysis for Complex Environmental Models; Watermark Numerical Computing: Brisbane, Australia, 2015. [Google Scholar]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Schneider, R.; Henriksen, H.J.; Stisen, S. A Robust Objective Function for Calibration of Groundwater Models in Light of Deficiencies of Model Structure and Observations. Hydrol. Earth Syst. Sci. Discuss. 2020, 1–26. [Google Scholar] [CrossRef] [Green Version]
- De Schepper, G. Simulating Surface Water and Groundwater Flow Dynamics in Tile-Drained Catchments; Université Laval: Québec, QC, Canada, 2015. [Google Scholar]
- Pool, S.; Vis, M.J.P.; Knight, R.R.; Seibert, J. Streamflow Characteristics from Modeled Runoff Time Series-Importance of Calibration Criteria Selection. Hydrol. Earth Syst. Sci. 2017, 21, 5443–5457. [Google Scholar] [CrossRef] [Green Version]
- Hallouin, T.; Bruen, M.; O’Loughlin, F.E. Calibration of Hydrological Models for Ecologically Relevant Streamflow Predictions: A Trade-off between Fitting Well to Data and Estimating Consistent Parameter Sets? Hydrol. Earth Syst. Sci. 2020, 24, 1031–1054. [Google Scholar] [CrossRef] [Green Version]
- Motarjemi, S.K.; Møller, A.B.; Plauborg, F.; Iversen, B.V. Predicting National-Scale Tile Drainage Discharge in Denmark Using Machine Learning Algorithms. J. Hydrol. Reg. Stud. 2021, 36, 100839. [Google Scholar] [CrossRef]
| Drain Class—MIKE SHE | Drain Time Constant (s−1) | Drain Depth (m) | BASEMAP Land Use Classes |
|---|---|---|---|
| undrained | 0 | 0.0 | harbour, basin, stream, sea, lake |
| near-natural | 1 × 10−9 | 0.1 | undefined, building, track, tank_track, fire_line, |
| wetlands | 1 × 10−9 | 0.1 | wetland, coast, bog, wet_meadow |
| forest | 1 × 10−8 | 1.0 | Forest |
| built-up | 1 × 10−8 | 1.0 | road, rail, runway, city_centre, high_buildings, low_buildings, parking_lot, technical_areas, recreation, sport_facility, cemetary, resource_extraction |
| extensive agriculture | 1 × 10−8 | 1.0 | agriculture_extensive |
| intensive agriculture | 1 × 10−7 | 1.0 | agriculture_undefined, agriculture_intensive |
| S1 | S2 | S3 | S4 | ||
|---|---|---|---|---|---|
| gw heads | 0.333 | 0.333 | 0.333 | 0.333 | |
| KGE | 0.667 | 0.333 | 0.333 | 0.333 | |
| signature residuals | hfED | - | 0.333 | 0.167 | 0.056 |
| skew | - | - | 0.167 | 0.056 | |
| CV | - | - | - | 0.056 | |
| qm w/s | - | - | - | 0.056 | |
| lfED | - | - | - | 0.056 | |
| SFDC | - | - | - | 0.056 | |
| S1 | S2 | S3 | S4 | ||
|---|---|---|---|---|---|
| weighted MAE, groundwater heads | 3.00 | 3.08 | 3.07 | 3.12 | |
| weighted ME, groundwater heads | 1.31 | 1.54 | 1.30 | 1.40 | |
| mean KGE | 0.63 | 0.62 | 0.61 | 0.63 | |
| mean absolute water balance error | 0.20 | 0.21 | 0.21 | 0.20 | |
| mean absolute residuals, signatures | hfED | 7.79 | 6.40 | 7.24 | 7.20 |
| skew | 0.38 | 0.22 | 0.18 | 0.26 | |
| CV | 0.08 | 0.06 | 0.06 | 0.05 | |
| qm w/s | 0.90 | 0.74 | 0.55 | 0.47 | |
| lfED | 22.2 | 18.1 | 18.5 | 18.0 | |
| SFDC | 0.73 | 0.41 | 0.61 | 0.41 | |
| S1 | S2 | S3 | S4 | ||
|---|---|---|---|---|---|
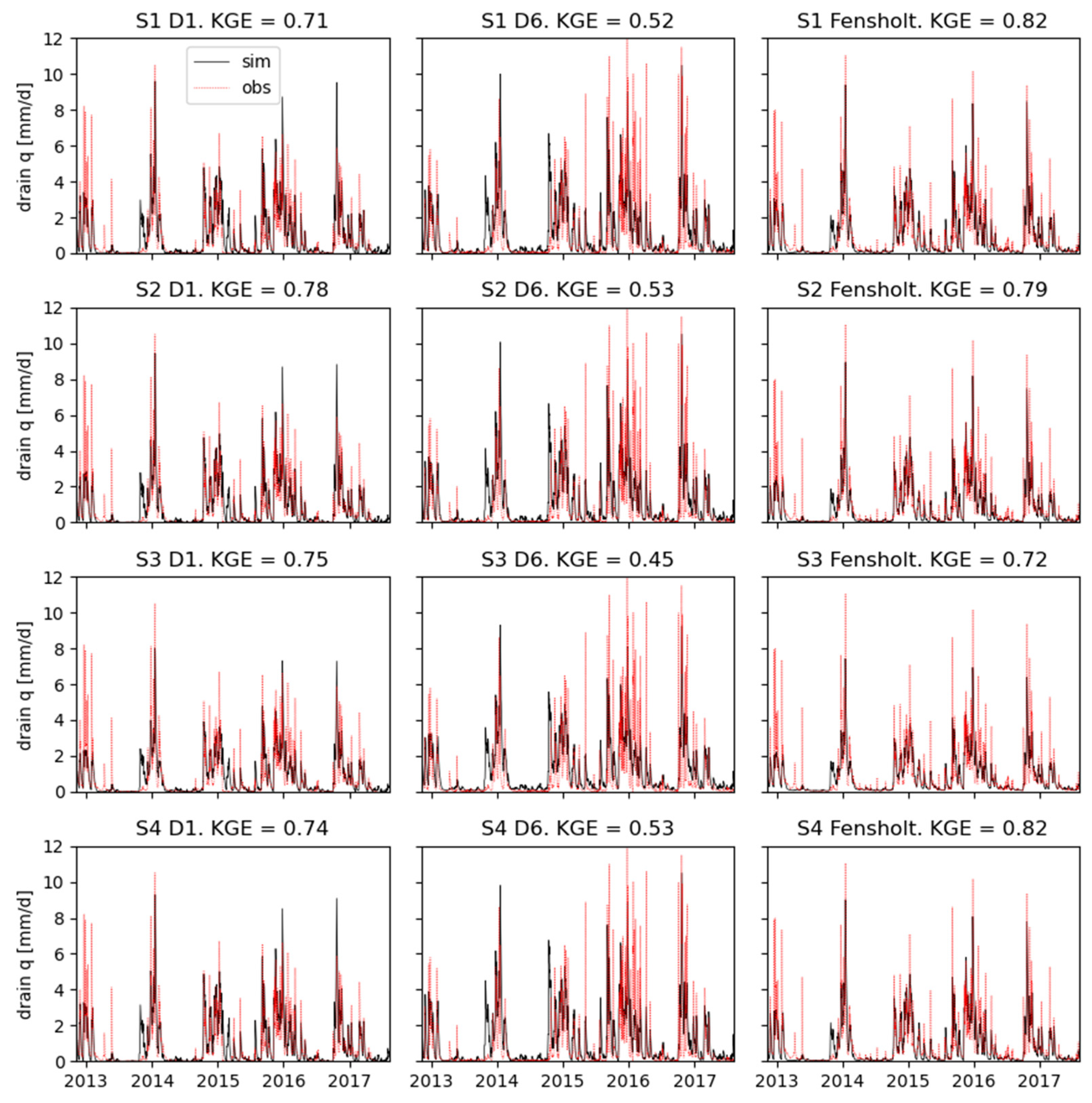
| drain flow time series | mean KGE, D1 to D8 | 0.52 | 0.45 | 0.36 | 0.49 |
| KGE, Fensholt | 0.82 | 0.79 | 0.72 | 0.82 | |
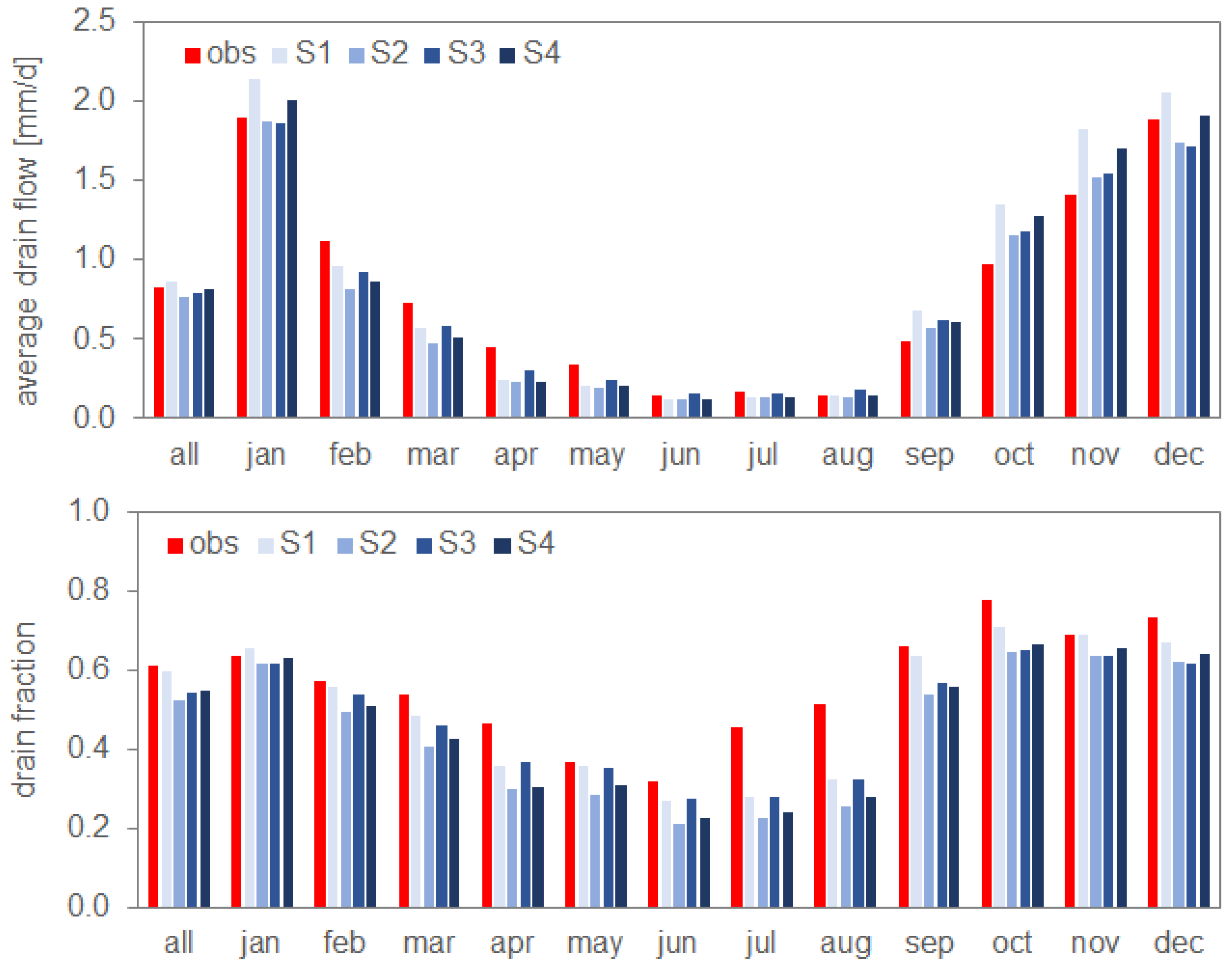
| average monthly and yearly drain flow for Fensholt | ME drain fraction, yearly | 0.02 | 0.09 | 0.07 | 0.06 |
| MAE drain fractions, monthly | 0.06 | 0.12 | 0.09 | 0.11 | |
| ME drain flow, yearly (mm/d) | −0.05 | 0.05 | 0.03 | 0.01 | |
| MAE drain flow, monthly (mm/d) | 0.18 | 0.13 | 0.11 | 0.15 | |
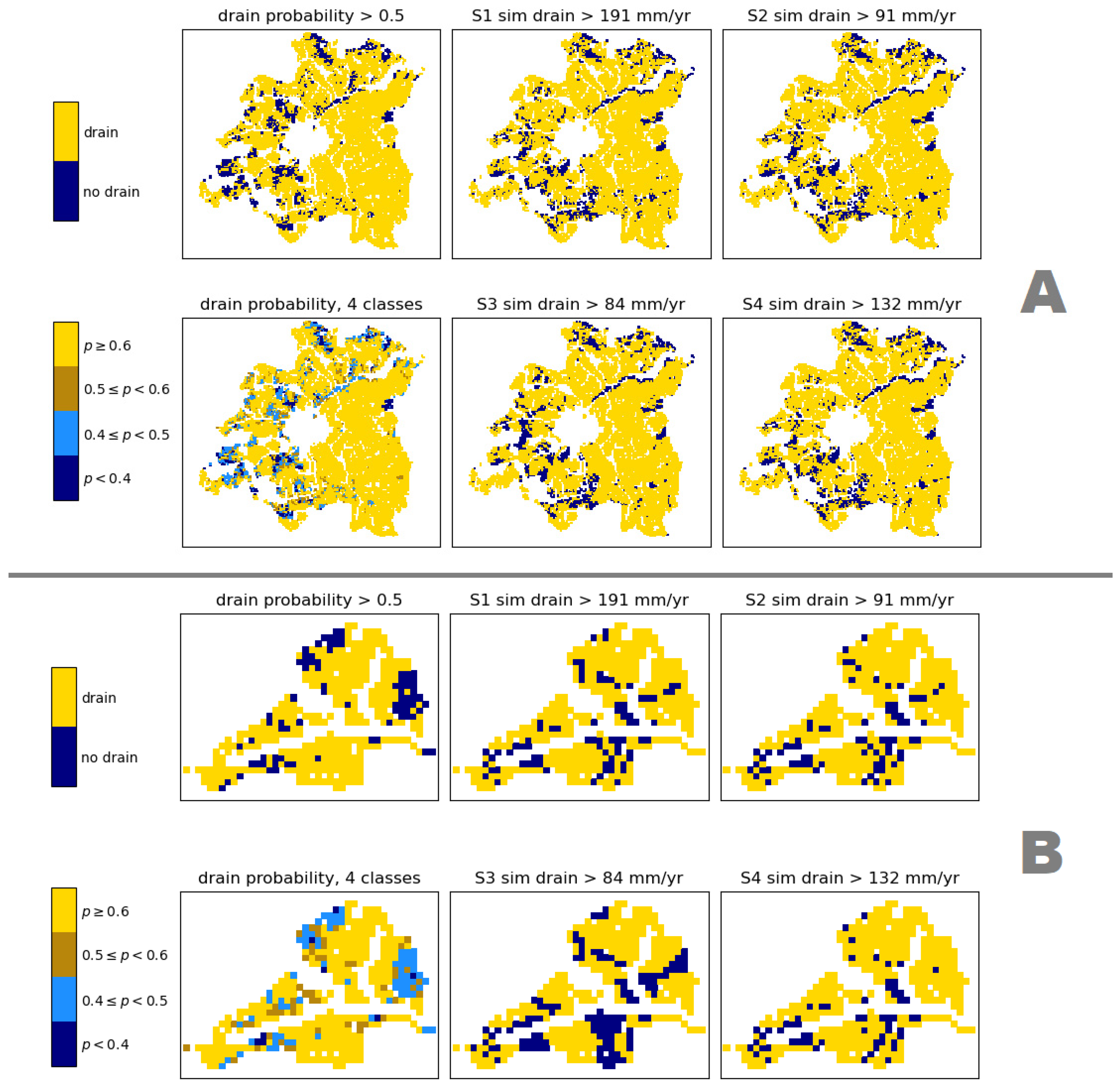
| spatial distribution of drain/no drain | R2 drain prob. vs. sim. drain, Norsminde | 0.30 | 0.34 | 0.29 | 0.35 |
| R2 drain prob. vs. sim. drain, Fensholt | 0.08 | 0.07 | 0.08 | 0.04 | |
| streamflow Fensholt | KGE | 0.82 | 0.78 | 0.74 | 0.81 |
| water balance error | 0.01 | 0.01 | 0.02 | −0.01 | |
| summer water balance error | −0.10 | −0.40 | −0.37 | −0.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schneider, R.; Stisen, S.; Højberg, A.L. Hunting for Information in Streamflow Signatures to Improve Modelled Drainage. Water 2022, 14, 110. https://doi.org/10.3390/w14010110
Schneider R, Stisen S, Højberg AL. Hunting for Information in Streamflow Signatures to Improve Modelled Drainage. Water. 2022; 14(1):110. https://doi.org/10.3390/w14010110
Chicago/Turabian StyleSchneider, Raphael, Simon Stisen, and Anker Lajer Højberg. 2022. "Hunting for Information in Streamflow Signatures to Improve Modelled Drainage" Water 14, no. 1: 110. https://doi.org/10.3390/w14010110
APA StyleSchneider, R., Stisen, S., & Højberg, A. L. (2022). Hunting for Information in Streamflow Signatures to Improve Modelled Drainage. Water, 14(1), 110. https://doi.org/10.3390/w14010110







