Abstract
Present and prospective climate change will likely affect the hydrological cycle in sensitive areas, such as the Alps, thus impacting water-based activities. A most representative example is hydropower production, i.e., exploitation of water to produce energy. In the Italian Alps hydropower is strictly dependent upon water from snow and ice melt, and both are decreasing in response to global warming. Here, we study the effects of potential climate change scenarios at 2100 upon hydropower production from the Chavonne plant, in Valle d’Aosta region of Italy, a run-of-the-river (ROR) plant taking water from two high altitude glacierized catchments of Val di Cogne, and Valsavarenche. We use Poli-Hydro, a state-of-the-art hydrological model to mimic the hydrological budget of the area, including ice and snow melt share. Projections of the hydrological budget were built until 2100 by means of selected climate change scenarios, under proper downscaling. We used runs of three General Circulation Models (GCMs), EC-Earth, CCSM4, and ECHAM6.0 under three Representative Concentration Pathways RCP 2.6, RCP 4.5, and RCP 8.5 from AR5 of IPCC, and of their updated version under four Shared Socio-Economic Pathways SSP1 2.6, SSP2 4.5, SSP3 7.0, and SSP5 8.5 from AR6. We then assessed hydropower production changes against a recent control run CR period (2005–2015). Mean annual flow is estimated at 14.33 m3 s−1 during CR, with ice melt contribution ca. 2%, and snow melt contribution ca. 44%. Ice cover in 2005 was estimated as 19.2 km2, reaching in 2015, 9.93 km2. Mean hydropower production was estimated at 153.72 GWh during the CR. Temperature would largely increase throughout the century (+0.93 °C on average at the half century, +2.45 °C at the end of the century). The ice covered area would be largely depleted (ca. −86%, −94% respectively), with reduced contribution of ice melt (0.23%, <0.1%, respectively) and snow melt (ca. 37%, 33%, respectively). Precipitation would show uncertain patterns, and hence incoming discharge at the plant would erratically vary (−29% to +24% half century, −27% to +59% end of century). Hydropower production displays a large dependence upon monthly discharge patterns, with mostly positive variations (+2.90% on average at half century, +6.95% on average at end of century), with its change driven by exceedance of plant’s capacity.
1. Introduction
Ongoing climate change is modifying the hydrological cycle, and water availability thereby. Particularly ice caps, glaciers, and seasonal snow will suffer most in this sense. In turn, hydropower plants in mountain areas largely depend upon ice/snow melt. The expected trends of increasing temperature henceforth will impact the hydrological cycle of these regions, solid precipitation will decrease, and snow melt will occur earlier, and be smaller [1], eventually shifting the hydrological regime. The Alps of Italy are paradigmatic of the effects of climate change on the cryosphere [2,3,4,5]. There is much evidence of glacier retreat in the Alps [6,7,8]. According to Diolaiuti et al. [8], glaciers in the Valle d’Aosta region lost 44.3 km2 of area during 1975–2005, i.e., −27% of their initial area. Area reduction rate increased more recently, from −1.1 km2 year−1 during 1975–1999 to 2.8 km2 year−1 during 1999–2005. The authors therein displayed that (i) air temperatures increased during spring and summer, (ii) total precipitation did not change significantly, and iii) solid precipitation reduced visibly, also driving ice loss. In the authors focused upon glaciers in the Lombardia region of Italy (ca. 200 km east of Val D’Aosta), and found a reduction of ca. −25 km2 of ice cover during 1991–2003, again linked to increasing temperatures [7]. In the Ortes-Cevedale glacier group [7], ice cover reduced by −40% during 1954–2007.
Ice cover reduction, and modified seasonal snow-cover dynamics may provide impact upon hydropower production within the Alps. Accordingly, assessment of future hydropower potential is of paramount importance [5].
Here, we assessed the effects of potential climate change scenarios upon the energy production of the Chavonne plant, which collects water from the Val di Cogne and the Valsavarenche, in the Valle d’Aosta region of Italy, and particularly in the Gran Paradiso National Park area, an area of tremendous ecological value, and also displaying very large hydropower potential.
The manuscript is organized as follows. In the section “Literature review” we provide some scientific background from recent studies tackling hydropower assessment in the Italian Alps under prospective climate change. In the section “Data and methods”, we discuss the area of interest, and the plant, we report the data used here for the model setup, and we describe the main traits of the model. In the section “Results” we report about the performance of the model, the projected hydrological cycle, and energy production thereby. The section “Discussion” benchmarks our findings against others from recent literature, and reports uncertainties in the simulation, its limitations and outlooks. The “Conclusions” section provides final remarks.
2. Literature Review
Recent studies explored potentially modified hydropower potential in the Italian Alps. Among others, Ravazzani et al. [9] assessed climate change impact (A1B story line of IPCC) upon hydropower production in the Toce river basin in the Italian Alps, ca. 100 km NE of Chavonne, projecting a general increase in production, with reduction in summer, possibly given by reduced snow melt therein. They did not consider ice cover dynamics under climate change.
Bombelli et al. [10] used Poli-Hydro to assess the potential impact of climate change (using GCMs from CMIP5, and RCPs as here) upon hydropower production in the cryospheric area of the upper Valtellina valley in the Italian Alps. They reported that mean flows for hydropower production may decrease along the century. At the end of the century they projected potential for increase of energy production, except for the warmest scenarios.
Patro et al. [11] evaluated the effects of climate change on hydropower production in forty-two alpine catchments, with existing run-of-the-river plants, during 2016–2065, however under simplified assumptions about glaciers’ cover evolution. They projected decrease in summer discharge, and reduced energy production.
To assess potential variations in hydropower production, especially in high altitude areas, one needs to accurately depict the cryospheric processes, and the components of the hydrological flow locally, and to evaluate potential hydrological variations under prospective climate change scenarios.
Here, we focused upon the Chavonne plant, which collects water from the Val di Cogne and the Valsavarenche, in the Valle d’Aosta region of Italy.
We used here the Poli-Hydro model, developed to provide a most possible realistic simulation of the hydrological cycle in cryospheric areas, to perform hydrological modelling during the calibration period 2005–2018, and therefore we projected hydrological variables until 2100, by means of climate outputs from six general circulation models under three RCP, and four SSPs. We then used the so-simulated discharges to calculate the plant’s energy production, and benchmark it against the control run period.
Our work here provides results that are original in the field, and proper, because:
- (i)
- We used Poli-Hydro, a semi-distributed model, fully accounting for changes in cryospheric process under climate change, including glaciers’ flow/melting, and snow cover accumulation/depletion, so gathering scenarios that were largely significant from the hydrological point of view;
- (ii)
- We originally provided climate, and hydrological scenarios in this part of Italy, using the latest, most recently released climate scenarios of the AR6 of the IPCC, unexploited hitherto as far as we know;
- (iii)
- We studied for the first time to our knowledge, present and future hydro-power productivity in the Val d’Aosta valley, and particularly in the Gran Paradiso National Park area, an area of tremendous ecological value, and displaying a very large hydropower potential, to be properly exploited henceforward.
3. Data and Methods
3.1. Case Study
The Val di Cogne valley takes its name from the homonymous town. It is located in the south of Valle d’Aosta region, and is nestled within the Dora Baltea catchment, a tributary of the Po river. The streams therein mainly receive water from snow melt, and from high altitude lakes, and they merge into the Grand-Eyvia, the main stream.
The Valsavarenche is located right next to Val di Cogne, and it takes its name from the Savara creek. Like Val di Cogne, Valsavarenche is included in the Dora Baltea catchment, with its southernmost part belonging to the Gran Paradiso massif (4061 m above the sea level m ASL), where the National Gran Paradiso Park of Italy, an area of tremendous ecological value is nestled.
The Chavonne plant, located in the town of Villeneuve, draws water from three intakes, located on the three streams Grand-Eyvia, Savara, and Nomenon. The overall drainage is 358 km2, with ca. 21 km2 (ca. 6%) covered in ice (as of December 2012), and the altitude range is 4056–1295 m ASL. The plant is located at 675 m ASL. It has five Pelton turbines, and an installed power of 27 MW. The water collected from the three intakes moves through diversion channels, and a gallery connecting the two valleys, delivering water down to a tank at 1251 m ASL, in the Poignon municipality, with a total vertical jump (hydropower head) of ca. 584 m.
3.2. Hydro-Meteorological Data (2005–2018)
Poli-Hydro requires inputs, such as a digital terrain model (DTM), land use information, and meteorological data. In this study, a DTM (Figure 1) available from the geo-portal of the Valle d’Aosta region was used, with a resolution of 100 × 100 m2 (LIDAR campaigns in 2005, 2008), compatible with simulation of scenarios using Poli-Hydro. Land use was made available by ISPRA (Istituto Superiore per la Protezione e la Ricerca Ambientale) of Italy, under the project Corine Land Cover (CLC) 2012. Sixteen automatic weather stations (AWS)s, made available on the web portal of the Centro Funzionale Regione Autonoma Valle D’Aosta, CFVDA, within and outside the plant’s catchment provided temperature data (Table 1). Data from these stations were used to estimate a monthly vertical lapse rate. Furthermore, thirteen of such AWSs provided (total) precipitation data, both via heating, and via combined measurements of rainfall, and snow depth, the latter converted into snow water equivalent (SWE) by means of estimates of snow density from daily minimum temperature [12,13]. The vertical gradient of total precipitation was also assessed.
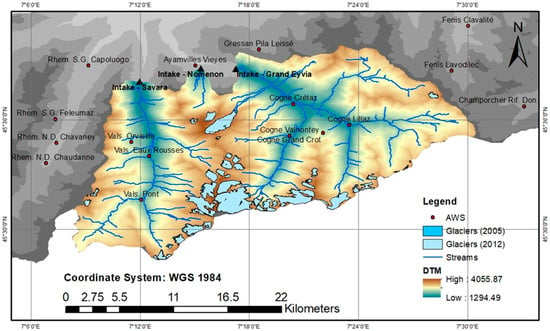
Figure 1.
Chavonne plant’s catchment, streams, and glaciers’ outline (2005 and 2012). Automated weather stations (AWS)s used to retrieve meteorological records for Poli-Hydro. Figure prepared by the authors using ArcMap.

Table 1.
Val di Cogne and Valsavarenche, coordinates of the AWS stations for temperature, precipitation, radiation and discharge. The data were made available by the Centro Funzionale Regione Autonoma Valle D’Aosta, CFVDA. T is temperature, Pl is liquid rainfall, H is heated gauge, S is snow depth, R is solar radiation, W is water level (streamflow).
Three of the considered AWSs provided radiation data, that we used here to assess snow melting [3] through a mixed degree day model. We calculated a clear sky index CSI, i.e., the ratio between observed and theoretical radiation.
For future scenarios, on those days when it rained or snowed, we were able to assess CSI as a function of precipitation. For dry days, we took CSI as the average of values under clear sky conditions.
3.3. Glacier’s Cover Dynamics, Climate and Hydropower Projections (2019–2100)
The Poli-Ice module of Poli-Hydro can mimic the glaciers’ evolution in time [3]. No records of ice thickness were available to model the glacier evolution during the calibration period (2005–2018). We thus used the data of an ice-covered area ICA for the years 2005 and 2012, available from the glacier cadastre of the Valle d’Aosta region. We took an initial ICA as from 2005 observation, and we then compared the ICA simulated by Poli-Hydro at 2012 against the observed value. To set up the Poli-Ice module, we used ice flow parameters obtained from measurements from a well-monitored Alpine glacier [3].
No detailed data about plant production were made available from CVA SpA (Compagnia Valdostana delle Acque), operator of the plant, but information about the plant mean annual production was accessible on the web, i.e., 140 GWh. Pelton turbines operate in the plant, with a maximum full capacity of 7 m3 s−1.
To project future hydrology, and consequently hydropower until 2100, we relied on temperature and precipitation scenarios, given by CMIP5 and CMIP6 of the Intergovernmental Panel on Climate Change IPCC. We used outputs of three General Circulation Models, namely Ec-Earth (European Consortium Earth system model, version 2 for CMIP5 and version 3 for CMIP6), CCSM4 (Community System Model, version 4 for CMIP5), CESM2 (Community Earth System Model, version 2 for CMIP6), and ECHAM (European Center Hamburg Model, version 6.0 for CMIP5 and version 6.3 for CMIP6).
We considered three Representative Concentration pathways (RCPs, AR5), and four Shared Socio-Economic Pathways (SSP, AR6), [14,15]. We used RCP 2.6, RCP 4.5, and RCP 8.5, and SSP1 2.6, SSP2 4.5, SSP3 7.0, and SSP5 8.5, a combination of SSP1, SSP2, SSP3, and SSP5 with RCP 2.6, RCP 4.5, RCP 7.0, and RCP 8.5. The GCMs provide simulated meteorological data at a coarse spatial resolution (ca. 10–200 km grid side). Therefore, to apply these data at the local scale, it was necessary to perform statistical downscaling [16,17] against measures obtained at the AWSs during 2005–2018. We thus obtained twenty-one climate scenarios, serving as inputs for Poli-Hydro to project forward future hydrological variables.
3.4. Ice Flow Modelling and Mass Balance
Thanks to its module Poli-Ice, Poli-Hydro is able to model ice flow. By means of a simplified force-balance of the glacier, Poli-Ice estimates ice velocity as a function of a basal shear stress [Pa] of the glacier [3,18]. To work properly, the module requires an initial ice thickness [m]. Once is provided, one can determine the basal shear stress as [19]
where is the ice density (917 kg m−3), (m s−2) is acceleration due to gravity, [.] local slope of the bedrock (approximated from ice surface slope). Here data were not available. It was therefore necessary to first estimate . Haeberli and Holzle [20] provide an empirical formula linking glacier’s altitude jump [m] (i.e., the difference between the maximum and minimum altitude), with .
We derived based on observations in reference [21], focusing on the Gran Paradiso massif, and we therefore obtained , and . was 0.5 km, and = 50 KPa.
Poli-Ice calculates daily glacier’s mass balance using snow mass balance, and ice accumulation/melting. Snow/ice melting is calculated using a mixed degree day approach [3], accounting for temperature and radiation
[mm day−1] is the melting of either ice or snow, [°C] is the air temperature, . [mm day−1 °C−1] is the temperature melt factor for ice/snow, [mm day−1 W−1 m−2] is the radiation melt factor for ice/snow, [-] is the albedo of ice/snow, taken here respectively 0.3/0.7 as an average value from observations on alpine glaciers [3], [W m−2] is the incident radiation in each cell, and is an air temperature threshold, set at 0 °C.
We tuned the snowmelt module by means of snow depth, temperature, and radiation data, available at the AWSs. We used Martinec’s method [22] to account for compaction of snow, and we validated the module using the Nash-Sutcliffe coefficient as a goodness of fit index.
We then applied the so-tuned snow melt factors to simulate snow and ice melt during 2005–2018. The ice melt factors were tuned iteratively. Since was calculated from , coming in turn from the altitude range of the glacier, multiple checks needed to be made. The first check was on the percentage error between the observed and simulated ice area, not to be larger than 1%. Two other checks were carried out against mean annual ice flow melt, no greater than 5 m year−1, and mean annual ice velocity, below 10 m year−1 [3,4].
3.5. Hydrological Model
Poli-Hydro is a semi-distributed, physically based model, already used in several previous studies [3,23,24,25], so we report here the main traits of the model. Poli-Hydro divides the catchment into cells accordingly to the DEM raster, and within each cell it calculates soil water balance at a daily scale. To do so, the model requires inputs of precipitation, temperature, and snow/ice melt (from the Poli-Ice module) to produce outputs of evapotranspiration, surface, and sub-surface discharge. Potential evapotranspiration (ETP) is evaluated from the Hargreaves-Samani equation [26]. Sub-surface discharge is a function of soil water content, while the surface discharge comes after soil saturation. The discharge in each cell is routed to the outlet section by means of a Nash-like IUH (instantaneous unit hydrograph [3]).
3.6. Hydrological and Hydropower Projections
We fed Poli-Hydro with the twenty-one downscaled data given by the combination of GCMs with RCPs and SSPs from CMIP5 and CMIP6, in order to obtain future projections of the hydrological cycle, i.e., discharge and glacier evolution, up to 2100. The downscaled data regarding temperature and precipitation, the latter was necessary to obtain projected radiation data, by means of the CSI. With runoff data from the projections, it was possible to evaluate future hydropower production.
The Chavonne plant is a run-of-the-river plant, therefore its energy production is directly proportional to the amount of incoming discharge, as suggested by the following equations
and
Therein, [W] is the generated power, is the plant’s efficiency, [m3 s−1] is the discharge flowing into the turbines, and [m] the total head at the intake section of the turbine.
Here we had no information about the overall plant efficiency, and we therefore assumed it was constant over the operating range of the machine. We used the following formula, directly derived from the straightforward definition of the power produced by the plant
where is installed power, and is plant capacity. Data about minimum in-stream flow and allowance for irrigation purposes were available here [27]. Such flows were withdrawn from usable discharge the plant.
4. Results
4.1. Model Tuning, and Hydrological Projections
In Table 2 we report the tuned parameters of Poli-Hydro. Mean yearly discharge at the plant was estimated Qav = 14.33 m3 s−1 during CR (2005–2015). Contribution of snow melt was ca. 43.5%, whereas ice melt contributed for 1.6% only.

Table 2.
Tuning parameters for Poli-Hydro. Thermal melting factor and radiation melting factor are both reported for ice and snow, as well as the albedo. Parameters calculated by the authors, using the Poli-Hydro model.
Tuning of ice melt parameters brought a percentage error (ICA) of +0.65%, with a mean annual ice melt of 3 m year−1 at peak, and a mean annual ice velocity of 25 m year−1 at peak.
Energy production by the plant was estimated into E = 153.72 GWh in the control period. In Figure 2, we report changes of Qav, ΔQ, for P1 2040–2049, and P2 2090–2099, against CR, and changes in energy production ΔE. Visibly, ΔE seems not proportional to Q. In Figure 3, monthly Q is estimated for all models, and scenarios, for P1, P2, and CR. In most cases a significant reduction of Q occurs during summer JAS. Conversely, Q increases during fall OND, and in spring AMJ, and even during winter JFM in 2090–2099. Thus, one has earlier peaks, and summer decreases. Figure 4 reports monthly E, in CR, and P1/P2. Visibly, the significant decrease of Q in summer does not match the slight decrease of E, especially during 2040–2049.
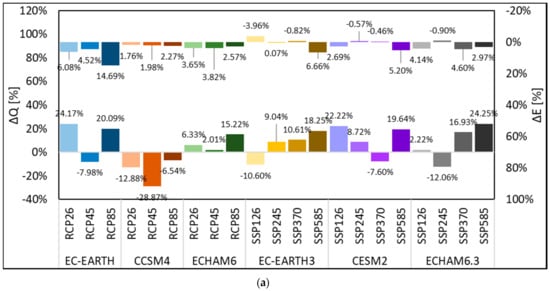
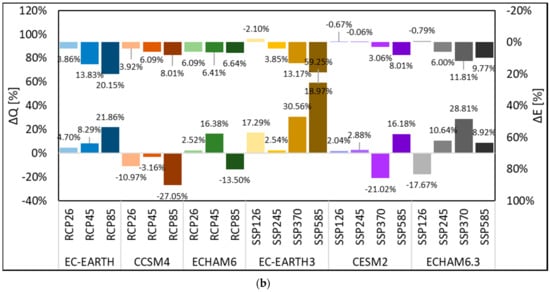
Figure 2.
Mean projected annual variations of incoming discharge ΔQ and energy production ΔE with respect to the control run (CR) (2005–2015). In the x axis, we report the General Circulation Models (GCM), and the corresponding Representative Concentration Pathways (RCP) (for CMIP5), and Shared Socio-Economic Pathways (SSP) (for CMIP6). In the left y axis, we reported the projected annual (percentage) variation of the incoming discharge ΔQ. In the right y axis, i.e., with the uppermost bars, with values to be read upside-down, we report the projected annual (percentage) variation of energy production, ΔE. (a) Period P1. (b) Period P2.
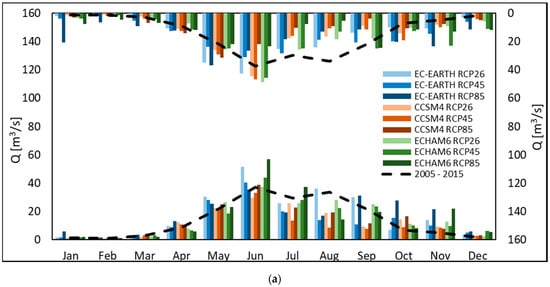
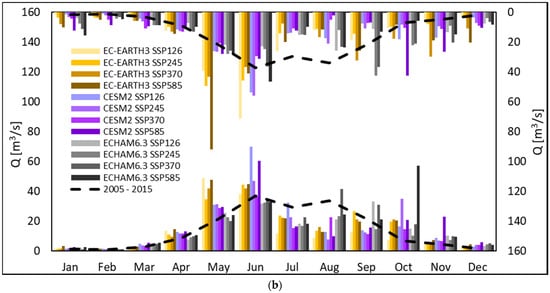
Figure 3.
Mean projected monthly incoming discharge Q (m3 s−1) at the Chavonne plant. In the left y axis, we reported the monthly incoming discharge during the period P1, 2040−2049. In the right y axis, i.e., with the uppermost bars, with values to be read upside-down, we reported the monthly incoming discharge during the period P2, 2090–2099. We also report control run (2005–2015, black dashed line). (a) GCMs: Ec-Earth, CCSM4, ECHAM6.0. Scenarios: RCP 2.6, RCP 4.5, RCP 8.5. (b) GCMs: Ec-Earth3, CESM2, ECHAM6.3. Scenarios: SSP1 2.6, SSP2 4.5, SSP3 7.0, SSP5 8.5.
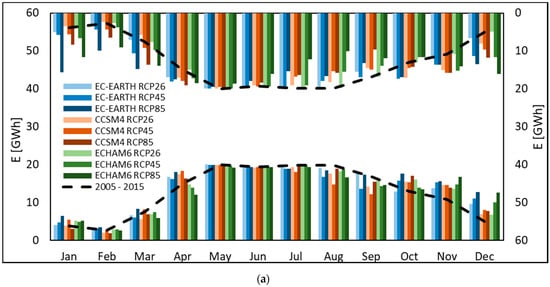
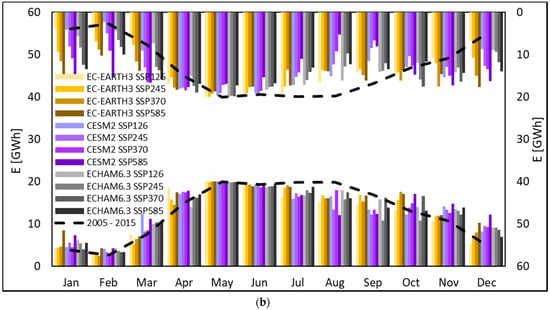
Figure 4.
Mean projected monthly incoming discharge E (GWh) at the Chavonne plant. In the left y axis, we reported monthly E during the period P1, 2040–2049. In the right y axis, i.e., with the uppermost bars, with values to be read upside-down, we reported monthly E during the period P2, 2090–2099. We also report control run (2005–2015, black dashed line). (a) GCMs: Ec-Earth, CCSM4, ECHAM6.0. Scenarios: RCP 2.6, RCP 4.5, RCP 8.5. (b) GCMs: Ec-Earth3, CESM2, ECHAM6.3. Scenarios: SSP1 2.6, SSP2 4.5, SSP3 7.0, SSP5 8.5.
This stems from the maximum capacity of the plant. Even if Q is smaller in summer, the capacity of the plant remains Qp = 7 m3 s−1. Therefore, until Q > Qp, energy production E is not affected much (however, some decrease occurs during JAS in P2). On the other hand, in P1/P2 Q would increase above Qp during months where previously (CR), this would not happen, so E visibly increases, typically in winter.
4.2. Mean Hydrological and Hydropower Scenarios
Here we report for reference averaged results among different GCMs, under different RCPs and SSPs in Figure 5 (E, Q, and snow melt Ms). During P1, a visible reduction of summer discharge does not affect E largely. On the contrary, increased Q in fall brings much greater E than now. The slight increase of E in winter is clearly due to increased temperatures, with less solid precipitation, and more rainfall. In decade P2 this behavior is all the more evident. Production in winter largely increases, when Q > Qp, 7 m3 s−1. This is because the contribution from snow melt is bigger. In some scenarios, typically RCP 8.5, and SSP5 8.5, snow melt peak is anticipated in April (however, with much lower values than now in P2, i.e., end of century). Summer flows, despite being half of the CR values, lead to energy production decreased by only a third or so, because Q is still above Qp.
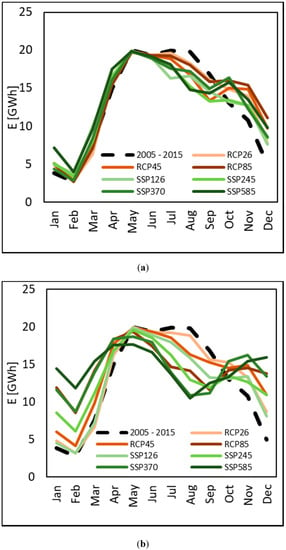
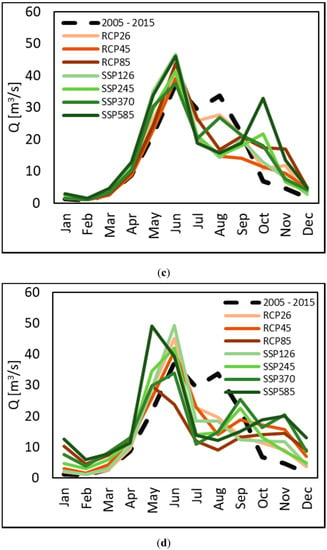
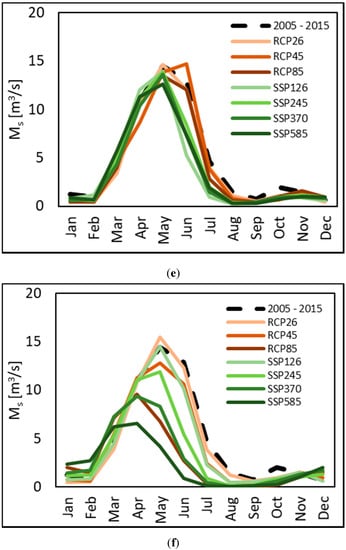
Figure 5.
Projected mean monthly values of energy production E (GWh), discharge Q (m3 s−1) and snow melt Ms (m3 s−1). Each line displays the value for a given RCP/SSP, averaged for all GCMs (CMIP5/CMIP6). (a) E period P1. (b) E period P2. (c) Q period P1. (d) Q period P2. (e) Ms period P1. (f) Ms period P2.
5. Discussion
5.1. Cryospheric Water under Future Climate Change
Cryospheric water is very sensitive to climate change [16,28], and the contribution of ice/snow melt would be drastically reduced after glaciers’ down wasting, as largely conjectured in the Alps.
Grossi et al. [29] projected until 2100 the evolution of Mandrone glacier (12 km2) in the Adamello group, ca. 200 km east of our case study area. They used scenarios from a regional climate model called COSMO-CLM. They report temperature increases of +1.0 °C and +2.6 °C, respectively, for 2050 and 2100. Mass balance therein projected a loss of 1.97 m of water equivalent per year m w.e. year−1, in 2050, and 3.97 m w.e. year−1 in 2100, against 1.44 m w.e. year−1 in their CR (1995–2009).
Garavaglia et al. [30] simulated (1927–2007), and then projected dynamics of the Forni glacier (ca. 11 km2 between 2500 and 3200 m ASL, ca. 50 km North of Adamello). They used a 1D ice flow model, calibrated with a large dataset from field surveys, and two GCMs (Ec-Earth, ECHAM6), under RCP 2.6, 4.5, and 8.5. They projected ice volume in 2030 to decrease largely (−52% for ECHAM6 RCP4.5 to −35% for Ec-Earth RCP2.6). Ice cover would decrease from −95% (ECHAM6 RCP8.5) to −83% (Ec-Earth RCP2.6).
Aili et al. [4] studied the glaciers (321 km2, mean altitude 2192 m ASL) within the Mallero river in Northern Italy (Sondrio town), projecting mass balance until 2100. From their calculations ICA would decrease to 10.9 km 2 (average on all scenarios), and IWE (ice water equivalent) to 0.52 × 109 m3, with a decrease of −59% and −52%, respectively, from their last estimates in 2007 (ICA = 26.3 km2, IWE = 1.1 × 109 m3).
Stucchi et al. [31] analyzed the Sabbione glacier (ca. 100 km northeast of Chavonne), and from ICA = 2.9 km2, IWE = 53.7 × 107 m3 in 2018, they projected in 2045–2059 ICA = 1.0 km2 (−66%), and IWE = 10.7 × 107 m3 (−80%) under the best case scenario, ECHAM RCP 2.6.
Under their worst scenario, CCSM RCP 8.5, they had ICA = 0.1 km2 (−98%) and IWE = 4 × 105 m3 (−99%). At the end of century 2086–2100, they estimated an ICA = 0.37 km2 (−87%) and IWE = 2.8 × 106 m3 (−95%) under ECHAM RCP 2.6.
In our study here, ICA would change from 19.15 km2 in 2005 to 5.91–1.24 km2 (Ec-Earth RCP 2.6, −69%, and CESM2 SSP5 8.5, −94%) in 2050, whereas total ice volume would change to 491.9 × 106 m3 in 2005 to 216.8−56.1 × 106 m3 (Ec-Earth RCP 2.6, −56%, Ec-Earth3 SSP5 8.5, −86%). In 2100, ICA would reach 1.31 km2 (−93.2%, average among all models and scenarios), and IWE would reach 54.24 × 106 m3 (−89%, average among all models and scenarios). During our tuning period, the rate of change of ICA is −1.41% year−1 (2005–2010), and −6.43% year−1 in 2011–2018, suggesting rapid acceleration of glacier shrinkage even in present days.
5.2. Hydropower Production under Climate Change
Our results provide potential modification in hydropower production, provide hints for further discussion, and benchmarks against recent literature.
Ravazzani et al. [9] assessed the climate change impact (A1B story line of IPCC) upon hydropower production in the Toce river basin in the Italian Alps, nestling also in the Sabbione catchment. They simulated future hydrology by means of outputs from two regional climate models until 2050. They projected an increase in production during fall, winter, and spring (vs. 2001–2010), and a reduction in June and July, with an average yearly increase of +11% to +19% (2031–2050).
Bombelli et al. [10] assessed the potential impact of climate change (using GCMs from CMIP5, and RCPs as here) upon hydropower production in the cryospheric area of the upper Valtellina valley (810–3800 m ASL, 899 km2, 26 km2 ICA) in the Italian Alps. They reported that mean flow for hydropower production may decrease along the course of the century under all scenarios (−21% to +7%, average −5% at half century, −17% to −2%, average −8% at the end of the century). At the end of the century they projected an increase on average energy production (−7% to +6%, +1% on average, with a decrease however under the warmest scenario RCP 8.5, −4% on average).
Patro et al. [11] evaluated the effects of climate change on hydropower production in forty-two alpine catchments with existing run-of-the-river plants, during 2016–2065. They depict an average decrease in summer discharge of ca. −30%, with energy production reducing by −3% in 2065, as discharge may still be greater than the plants’ capacity.
In our study, the mean annual flow discharge would display an uncertain direction of change (−29% for CCSM4 RCP 4.5, to +24% for ECHAM6.3 SSP5 8.5 at half century, −27% for CCSM4 RCP 8.5 to +59% for Ec-Earth3 SSP5 8.5, at the end of the century). Hydropower production shows mostly positive variation (−4% for Ec-Earth3 SSP1 2.6 to +15% for Ec-Earth RCP 8.5, +2.90% on average at half century, −2% for Ec-Earth3 SSP1 2.6 to + 20% for Ec-Earth RCP 8.5, +6.95% on average at the end of the century).
Supposedly, increase in production would result from increased precipitation under some scenarios, larger water availability than now in fall because of trading snowfall for rainfall (driven by temperature), and anticipated melt in spring. A combination of all such factors would result in more homogeneous energy production monthly (Figure 4), in most cases with larger energy production than now.
To explore the link between projected production, and the hydro-meteorological drivers, we analyzed here changes in hydropower production E against the corresponding changes in climate and hydrologic variables. Particularly, we assessed the (linear) correlation coefficient ρxy between changes of energy production (vs. CR 2005–2015) against the corresponding variations of discharge , temperature , snow melt , precipitation . The projected changes of the ice covered area do not play a major role in the variation of E, since ice melt contribution is relatively low (<2%). Therefore, we did not report here. In Figure 6 we report only those variables (and periods, P1, P2) with correlation ρxy (in absolute value, positive or negative) so that |ρxy| > 0.5. These are, for P1, ΔP (ρxy = 0.65), and for P2, ΔT, ΔQ, ΔMs (ρxy = 0.62, 0.60, −0.52, respectively).
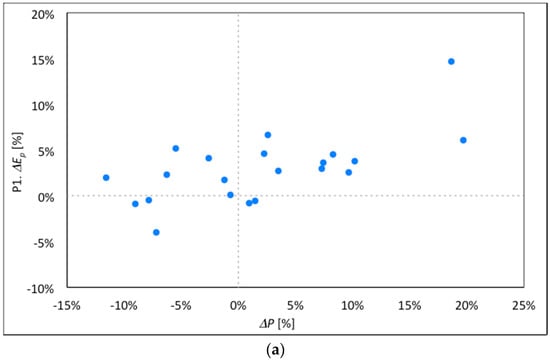
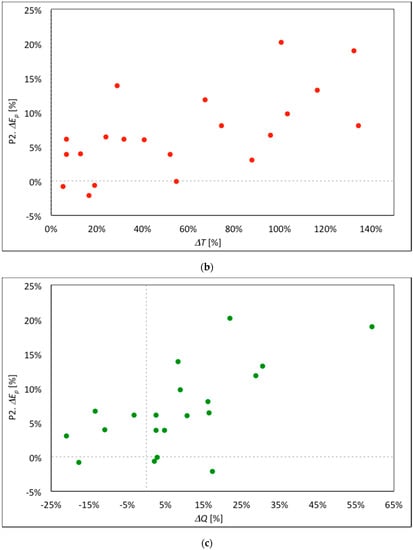
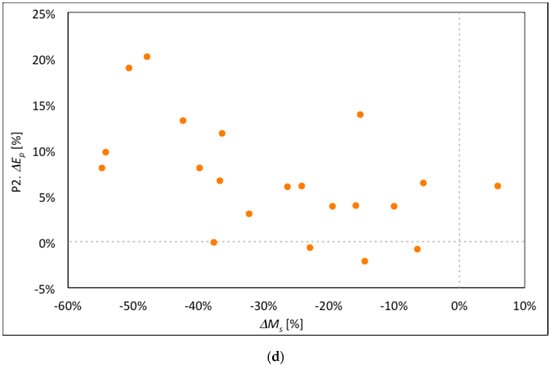
Figure 6.
Chavonne plant. Percentage energy production variations , against discharge variations , temperature variations , snow melt variations , and precipitation variations . We report variables (and periods, P1, P2) with correlation |ρxy| > 0.5, explained in the text. (a) Period P1. against . (b) Period P2. against . (c) Period P2. against . (d) Period P2. against .
During P1 2040–2049, is weakly linked to , and in some cases (Ec-Earth RCP 4.5, CCSM4 RCP 2.6, 4.5, 8.5, Ec-Earth3 SSP3 7.0, CESM2 SSP2 4.5) an increase in temperature results in a decrease in energy production (not shown for shortness). The link between and is slightly better defined (and the more water, the larger production), but six out of twenty-one scenarios (Ec-Earth RCP 4.5, CCSM4 RCP 2.6, 4.5, 8.5, Ec-Earth3 SSP3 7.0, CESM2 SSP2 4.5) show a decrease in incoming discharge, with an increase of energy production or vice versa (not shown). Generally in P1 seems weakly (negatively) linked to , although five cases (ECHAM6 RCP 4.5, Ec-Earth3 SSP1 2.6, Ec-Earth SSP3 7.0, CESM2 SSP2 4.5, SSP3 7.0, ECHAM6.3 SSP2 4.5) display a positive link (decreasing snow melt leads to decreased production, not shown). In P1, seems the most (positively) linked to (reported in Figure 6a), albeit there are cases (CCSM4 RCP 2.6, 4.5, 8.5, Ec-Earth3 SSP2 4.5, SSP3 7.0, CESM2 SSP2 4.5, SSP5 8.5, ECHAM6.3 SSP1 2.6) where positive changes of energy occur under negative changes in precipitation, and vice versa.
In P2 2090–2099, a clear positive link emerges between and (Figure 6b), with only four cases (Ec-Earth3 SSP1 2.6, CESM2 SSP1 2.6, SSP2 4.5, ECHAM6.3 SSP1 2.6) of negative relation. The positive link between and is also clear in P2 (Figure 6c). In Figure 6d, negative usually brings positive , except in five cases (ECHAM6 RCP2.6, Ec-Earth3 SSP1 2.6, CESM2 SSP1 2.6, SSP1 4.5, ECHAM6.3 SSP1 2.6), which seemingly suggest that more production would occur with less solid precipitation in the future. and seem sparsely linked in P2 (not shown).
Accordingly, the direction and magnitude of changes in energy production against modified climate and hydrology in the area will depend upon the nonlinear, complex interaction between climate and hydrological regime in time (e.g., at the monthly, or even daily scale), and the plant’s operation, at partial or full capacity Qp. Daily scale hydrological simulation as here seems a proper tool to assess prospectively modified production.
5.3. Limitations and Outlooks
Our study was aimed at producing an array of scenarios for the present and future expected hydrological dynamics and of hydropower production in an Alpine valley using the Chavonne plant as a case study. We believe that our hydrological model likely provides a credible depiction of the hydrological processes in the area.
No observations about ice thickness in the area were available. However, ice thickness was estimated through simplifying assumptions. Given the little expected share of melt water from ice in energy production, such noise seems negligible.
The introduction of lapse rates of precipitation and temperature with altitude implies some approximation, possibly affecting the outputs, however necessary to depict vertical variability in high mountain areas as here. Model tuning was also peculiar here.
No discharge data were available at the plant intake, so tuning was pursued using stations (Cogne Crétaz and Eaux Rousses) in different locations. Despite these two stations being within the plant’s catchment, the difference between was simulated, and real flows may not negligible, and may be with uncertainties in the findings.
The GCMs poor resolution required downscaling in order to reproduce local meteorological phenomena, introducing further noise.
While all GCMs and RCPs and SSPs consistently project (positive) temperature variations along the century, precipitation projections are more erratic, within a range of ca. ± 20%. This issue is widely known for precipitation in the Alps [4,28,32] and generally in mountains worldwide [18,25,33]. Accordingly, one needs to investigate a large as possible array of conditions, and more GCMs/RCPs/SSPs, to evaluate potential effects of different precipitation regimes.
Regarding RCPs and SSPs, in principle all of them can be taken as equally likely until the end of the century, so they represent equally possible evolutions of climate, and of hydropower systems in cascade. Nevertheless, recent analysis [34] labelled recent climate evolution to be somewhat closer to RCP 8.5 than to others. Under such a scenario (RCP 8.5, and SSP5 8.5), our findings show the largest increase of hydropower production.
More simplifications were introduced in the energy production assessment. No energy production data for the plant were available, therefore we could not directly verify our findings. Our calculated changes in energy production , albeit affected by uncertainties, should however depict a credible picture in terms of potential, relative gain/loss of energy production, under given climate scenarios.
6. Conclusions
Our what if analysis showed the link between cryospheric dynamics, hydrology, and hydropower production under present, and possibly future climate change in the Chavonne plant’s catchment, paradigmatic of ROR systems in the Alps.
The complexity of local hydrology made it necessary to accurately model the link between climate and discharge, using Poli-Hydro, normally performing well [3] after proper tuning.
We demonstrated that hydropower potential until the end of the century would increase under most CGMs and scenarios, except under five scenarios (Ec-Earth3 SSP1 2.6, SSP3 7.0, CESM2 SSP2 4.5, SSP3 7.0, ECHAM6.3 SSP2 4.5) at half century, and under four scenarios (Ec-Earth3 SSP1 2.6, CESM2 SSP1 2.6, SSP2 4.5, ECHAM6.3 SSP1 2.6) at the end of the century. Energy production would depend upon changes on a monthly scale, rather than upon yearly flows, because of the threshold effect given by plant capacity Qp. Changes on a monthly scale respond to global warming effects, mainly with increases in winter, spring, and autumn, and decreases in summer. This results in a decrease of solid precipitation, in favor of the liquid kind, giving readily available water in otherwise dry periods.
The Chavonne plant is currently working as a ROR plant. It would be of interest to analyze changes in hydropower production when introducing an operation from a reservoir, and optimal management thereby. This would allow storage during the low demand period (winter), and production during summer, when hydropower demand will be the largest under climate change, possibly with increasing revenues [10,31].
Large uncertainty is of course expected when it comes to projection of future hydrology, and hydropower potential. However, our work here provides results that may be viewed as credible for preliminary brainstorming, given that we accounted for complex hydrological, and cryospheric processes in the area, their changes under global warming, and we used the most recently released climate scenarios of the AR6 of the IPCC, unexploited hitherto in the area, and as expected, provided realistic scenarios under their RCPs/SSPs assumptions.
Our work may be of use for other scientists, and for water managers, interested in future hydro-power productivity in the Val d’Aosta valley, an area of tremendous ecological value, and further displaying a large hydropower potential, to be properly exploited henceforward.
Author Contributions
Conceptualization, T.D. and G.M.B.; methodology, T.D.; software, G.M.B., D.B.; validation, T.D.; formal analysis, T.D., G.M.B.; investigation, D.B., G.M.; resources, D.B., G.M.; data curation, T.D., G.M.B.; writing—original draft preparation, T.D.; writing—review and editing, D.B.; visualization, T.D.; supervision, D.B., G.M.; project administration, D.B., G.M.; funding acquisition, D.B., G.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no specific external funding.
Acknowledgments
Support to the present work was provided in fulfilment of the activity of the Climate-Lab laboratory of Politecnico di Milano (https://www.climatelab.polimi.it/en/), an interdepartmental laboratory on climate change at Politecnico, which is kindly acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 9. [Google Scholar] [CrossRef]
- Viganò, G.; Confortola, G.; Fornaroli, R.; Cabrini, R.; Canobbio, S.; Mezzanotte, V. Effects of future climate change on a river habitat in an italian alpine catchment. J. Hydrol. Eng. 2016, 21, 1–14. [Google Scholar] [CrossRef]
- Soncini, A.; Bocchiola, D.; Azzoni, R.S.; Diolaiuti, G. A methodology for monitoring and modeling of high altitude Alpine catchments. Prog. Phys. Geogr. 2017, 41, 393–420. [Google Scholar] [CrossRef]
- Aili, T.; Soncini, A.; Bianchi, A.; Diolaiuti, G.; D’Agata, C.; Bocchiola, D. Assessing water resources under climate change in high-altitude catchments: A methodology and an application in the Italian Alps. Theor. Appl. Climatol. 2019, 135, 56–135. [Google Scholar] [CrossRef]
- D’Agata, C.; Bocchiola, D.; Soncini, A.; Maragno, D.; Smiraglia, C.; Diolaiuti, G.A. Recent area and volume loss of Alpine glaciers in the Adda River of Italy and their contribution to hydropower production. Cold Reg. Sci. Technol. 2018, 148, 84–172. [Google Scholar] [CrossRef]
- D’Agata, C.; Bocchiola, D.; Maragno, D.; Smiraglia, C.; Diolaiuti, G. Glacier Shrinkage Driven by Climate Change during Half a Century (1954–2007) in the Ortles-Cevedale Group. Theor. Appl. Climatol. 2014, 116, 169–190. [Google Scholar] [CrossRef]
- Diolaiuti, G.; Bocchiola, D.; D’agata, C.; Smiraglia, C. Evidence of climate change impact upon glaciers’ recession within the Italian Alps: The case of Lombardy glaciers. Theor. Appl. Climatol. 2012, 109, 45–429. [Google Scholar] [CrossRef]
- Diolaiuti, G.A.; Bocchiola, D.; Vagliasindi, M.; D’Agata, C.; Smiraglia, C. The 1975-2005 glacier changes in Aosta Valley (Italy) and the relations with climate evolution. Prog. Phys. Geogr. 2012, 36, 85–764. [Google Scholar] [CrossRef]
- Ravazzani, G.; Valle, F.D.; Gaudard, L.; Mendlik, T.; Gobiet, A.; Mancini, M. Assessing climate impacts on hydropower production: The case of the Toce river basin. Climiate 2016, 4, 16. [Google Scholar] [CrossRef]
- Bombelli, G.M.; Soncini, A.; Bianchi, A.; Bocchiola, D. Potentially modified hydropower production under climate change in the Italian Alps. Hydrol. Process 2019, 33, 1–18. [Google Scholar] [CrossRef]
- Patro, E.R.; De Michele, C.; Avanzi, F. Future perspectives of run-of-the-river hydropower and the impact of glaciers’ shrinkage: The case of Italian Alps. Appl. Energy 2018, 231, 699–713. [Google Scholar] [CrossRef]
- Bocchiola, D.; Rosso, R. The distribution of daily Snow water Equivalent in the Central Italian Alps. Adv. Water Resour. 2007, 30, 47–135. [Google Scholar]
- Valt, M.; Chiambretti, I.; Dellavedova, P. Fresh snow density on the Italian Alps. Geophys. Res. 2014, 16, 9715. [Google Scholar]
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A.; Manning, M.R.; Rose, S.K.; Van Vuuren, D.P. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 56–747. [Google Scholar] [CrossRef]
- Riahi, K.; Van Vuuren, D.P.; Kriegler, E.; Edmonds, J.; Neill, B.C.O.; Fujimori, S. The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: An overview. Glob. Environ. Chang. 2017, 42, 68–153. [Google Scholar] [CrossRef]
- Groppelli, B.; Soncini, A.; Bocchiola, D.; Rosso, R. Evaluation of future hydrological cycle under climate change scenarios in a mesoscale Alpine watershed of Italy. Nat. Hazards Earth Syst. Sci. 2011, 11, 85–1769. [Google Scholar] [CrossRef]
- Groppelli, B.; Bocchiola, D.; Rosso, R. Spatial downscaling of precipitation from GCMs for climate change projections using random cascades: A case study in Italy. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Soncini, A.; Bocchiola, D.; Confortola, G.; Bianchi, A.; Rosso, R.; Mayer, C. Future hydrological regimes in the upper Indus basin: A case study from a high-altitude glacierized catchment. J. Hydrometeorol. 2015, 16, 26–306. [Google Scholar] [CrossRef]
- Cuffey, K.M.; Oerlemans, J. Glaciers and climate change: A meteorologist’s view. J. Glaciol. 2002, 48, 173. [Google Scholar] [CrossRef][Green Version]
- Haeberli, W. Application of inventory data for estimating characteristics of and regional climate-change effects on mountain glaciers: A pilot study with the European Alps. Ann. Glaciol. 1995, 21, 206–212. [Google Scholar] [CrossRef]
- Carturan, L.; Baroni, C.; Brunetti, M.; Carton, A.; Fontana, G.D.; Salvatore, M.C. Analysis of the mass balance time series of glaciers in the Italian Alps. Cryosphere 2016, 10, 695–712. [Google Scholar] [CrossRef]
- Martinec, J.; Rango, A. Parameter values for snowmelt runoff modelling. J. Hydrol. 1986, 84, 197–219. [Google Scholar] [CrossRef]
- Akbari-Alashti, H.; Soncini, A.; Dinpashoh, Y.; Fakheri-Fard, A.; Talatahari, S.; Bocchiola, D. Operation of two major reservoirs of Iran under IPCC scenarios during the XXI century. Hydrol. Process 2018, 32, 71–3254. [Google Scholar] [CrossRef]
- Bocchiola, D.; Soncini, A. Water Resources Modeling and Prospective Evaluation in the Indus River Under Present and Prospective Climate Change. In Indus River Basin: Water Security and Sustainability; Khan, S., Adams, T., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 17–56. [Google Scholar]
- Soncini, A.; Bocchiola, D.; Confortola, G.; Minora, U.; Vuillermoz, E.; Salerno, F. Future hydrological regimes and glacier cover in the Everest region: The case study of the upper Dudh Koshi basin. Sci. Total Environ. 2016, 565, 101–1084. [Google Scholar] [CrossRef] [PubMed]
- Hargreaves, G.H. Estimation of Potential and Crop Evapotranspiration. Trans. Am. Soc. Agric. Eng. 1974, 17, 4–701. [Google Scholar] [CrossRef]
- Ceriani, E.; Fiou, M. Impianto Idroelettrico di Chavonne—Studio di Impatto Ambientale. Regione Autonoma Valle D’Aosta, Ed.; 2010, p. 327. (In Italian). Available online: https://www.regione.vda.it/territorio/allegati/progetti_via_898_SINTESI.pdf (accessed on 14 July 2020).
- Confortola, G.; Soncini, A.; Bocchiola, D. Climate change will affect hydrological regimes in the Alps. Rev. géographie Alp 2014, 101-3. [Google Scholar] [CrossRef]
- Grossi, G.; Caronna, P.; Ranzi, R. Hydrologic vulnerability to climate change of the Mandrone glacier (Adamello-Presanella group, Italian Alps). Adv. Water Resour. 2013, 55, 190–203. [Google Scholar] [CrossRef]
- Garavaglia, R.; Marzorati, A.; Confortola, G.; Bocchiola, D.; Lombardo, S.; Senese, A. Evoluzione del ghiacciaio dei Forni. Neve. E Valanghe 2018, 8, 60–67. [Google Scholar]
- Stucchi, L.; Bombelli, G.M.; Bianchi, A.; Bocchiola, D. Hydropower from the alpine cryosphere in the era of climate change. The case of the Sabbione storage plant in Italy. Water 2019, 11, 1599. [Google Scholar] [CrossRef]
- Faggian, P.; Giorgi, F. An analysis of global model projections over Italy, with particular attention to the Italian Greater Alpine Region (GAR). Clim. Chang. 2009, 96, 58–239. [Google Scholar] [CrossRef]
- Bocchiola, D.; Soncini, A.; Senese, A.; Diolaiuti, G. Modelling Hydrological Components of the Rio Maipo of Chile, and Their Prospective Evolution under Climate Change. Climiate 2018, 6, 57. [Google Scholar] [CrossRef]
- Fuss, S.; Canadell, J.G.; Peters, G.P.; Tavoni, M.; Andrew, R.M.; Ciais, P. COMMENTARY: Betting on negative emissions. Nat. Clim. Chang. 2014, 4, 3–850. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).