Generalised Linear Models for Prediction of Dissolved Oxygen in a Waste Stabilisation Pond
Abstract
1. Introduction
2. Materials and Methods
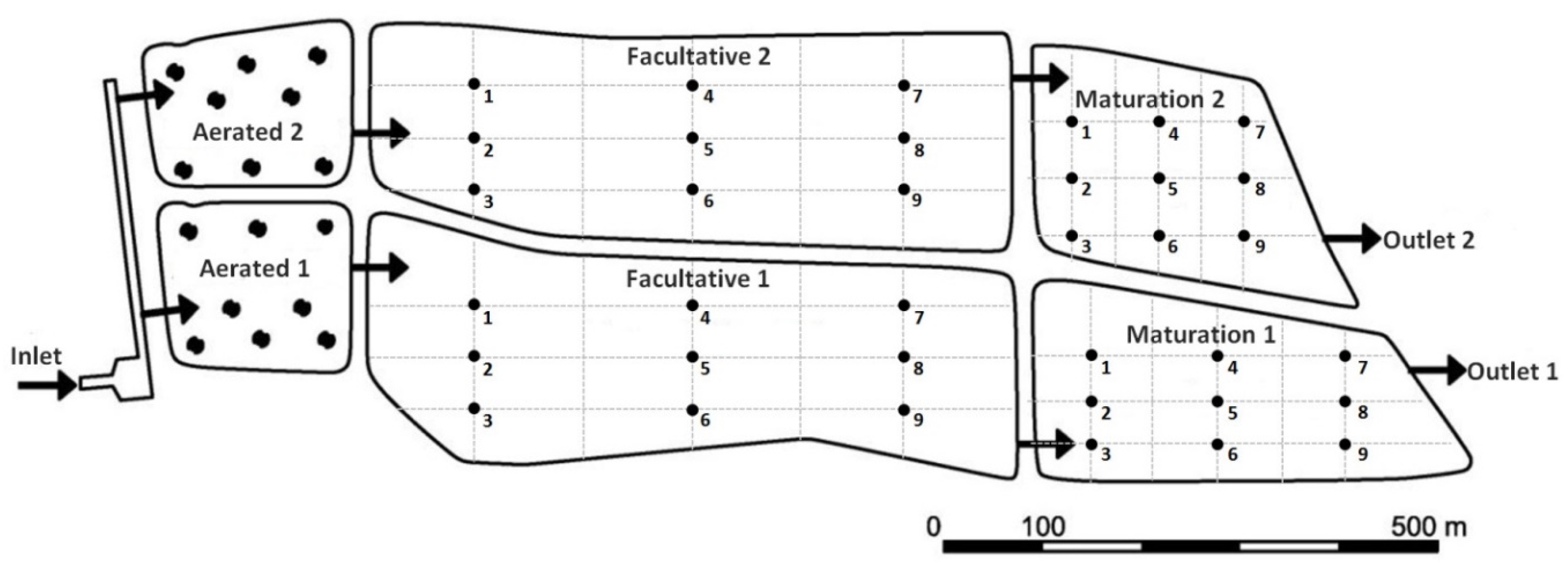
2.1. Study Area
2.2. Sampling Scheme
2.3. Model Construction and Diagnostics
2.3.1. Variables Used to Develop Models
2.3.2. Model Development
2.3.3. Model Diagnostics and Assessment
2.4. Model Comparison
2.5. Model Parameters and Their Importance
3. Results
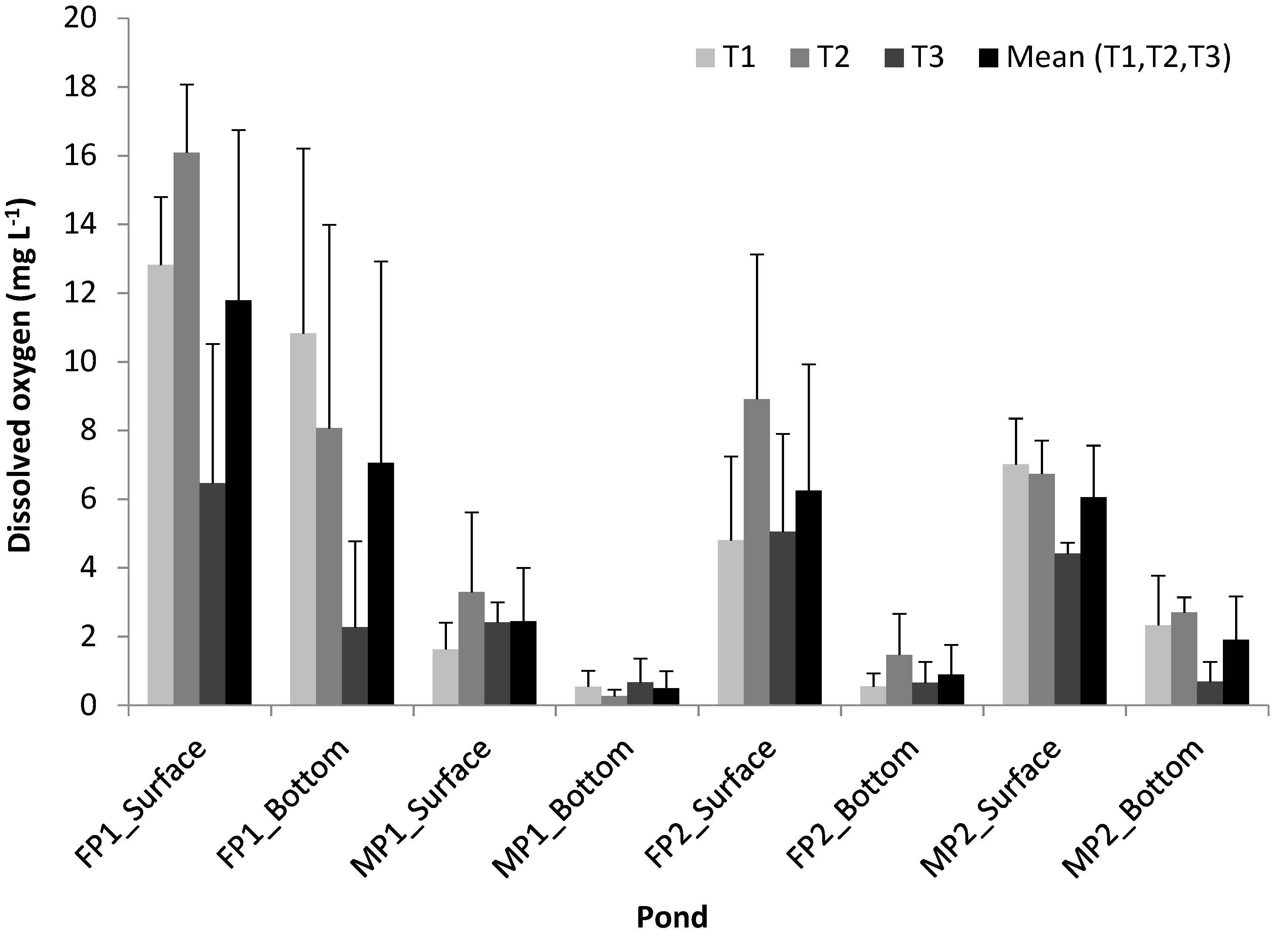
3.1. Variability of Physicochemical and Biological Parameters and Climatic Conditions in the Ponds
3.2. Optimal Models for Prediction of Dissolved Oxygen in the Ponds
3.3. Importance of the Predictor Variables
4. Discussion
4.1. Variability of the Physicochemical and Biological Parameters and Climatic Conditions in the Ponds
4.2. Model Comparison
4.3. Predictive Accuracy of the Optimal Models
4.4. Importance of the Predictor Variables in the Optimal Models
4.5. Application and Limitations of the Models
5. Conclusions
- There was a large variability of chlorophyll a, DO, and climatic conditions across the three sampling times. Within a pond, higher concentration of chlorophyll a and DO were observed near the surface than near the bottom. Between the two pond types, chlorophyll a and DO in the FPs were higher than those in the MPs. No large variability of BOD within a pond was observed across the three sampling times but there was a decrease of BOD from FPs to MPs.
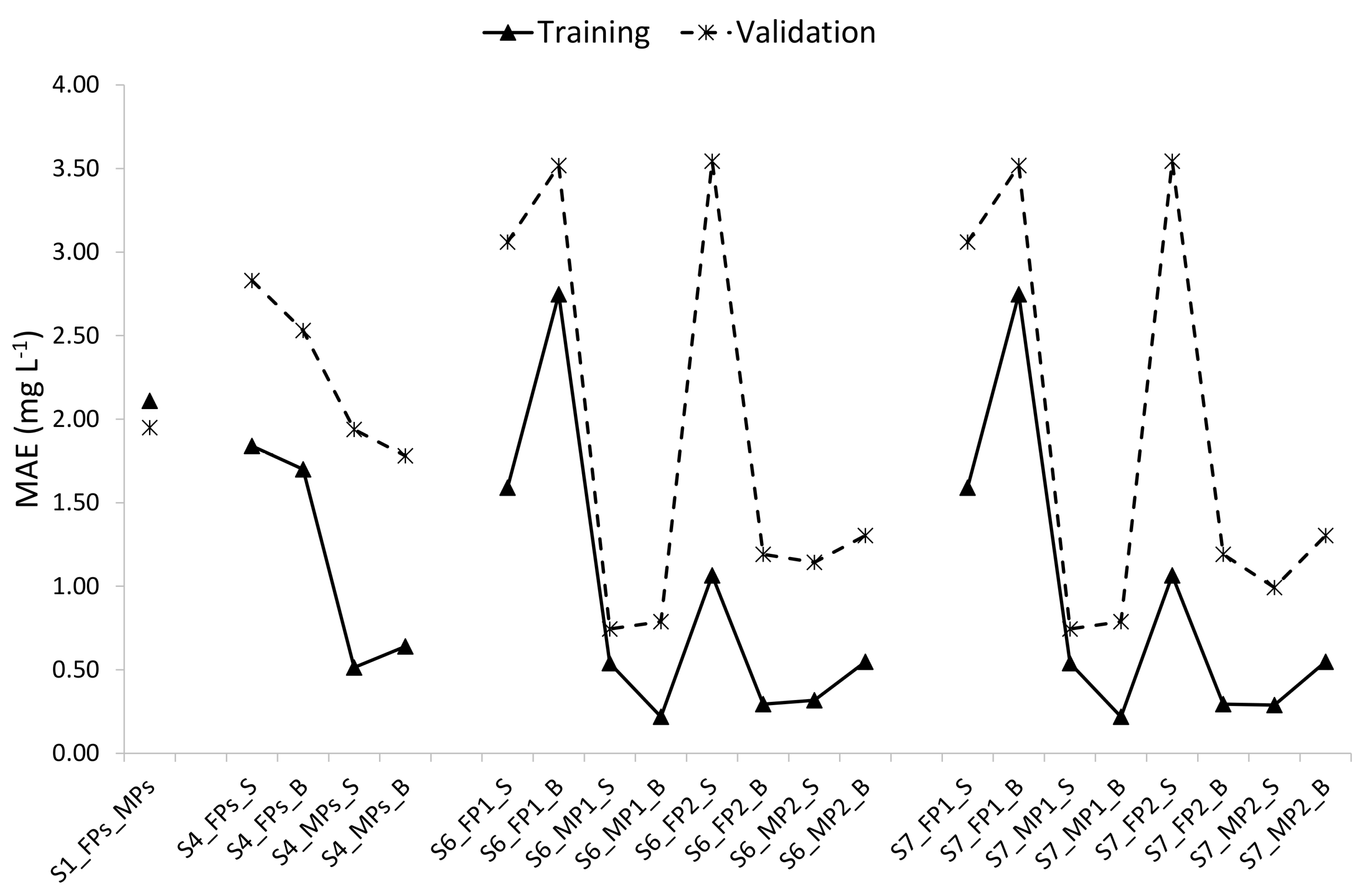
- Among the 83 models developed based on different data partitioning and cross-validation strategies, the 8 models developed specifically for each pond and each depth were the optimal ones. These optimal models depict varying MAEs of DO in the range of 0.21–2.75 mg L−1, in the training period and 0.54–3.54 mg L−1 in the validation period, and SMAPEs of dissolved oxygen were in the range of 3.18–38.70% in the training period and 7.54–89.24% in the validation period. Among the 8 optimal models, the optimal models of MPs performed better than those of FPs and within a pond, the optimal models for the surface seemed to perform better than those for the bottom.
- Among the variables used to predict dissolved oxygen, chlorophyll a and BOD appeared to be representative predictor variables. Additionally, water temperature and climatic conditions also highly influenced DO.
- The effect of the timing variable (expressed at the time points the samples were taken) did not show a strong effect on the prediction of DO.
- The results of this study are valuable in the management of WSP and provide basic insights into oxygen-related processes, which could help in further development of advanced models for WSPs.
- Despite the limitation of the data-driven approach for global extrapolation, it is expected that the data partitioning and cross-validation strategies developed in this study, could be widely applied to identify the optimal models for prediction purposes.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mara, D.D. Domestic Wastewater Treatment in Developing Countries; Earthscan Publications: London, UK, 2004. [Google Scholar]
- Ho, L.; Goethals, P.L.M. Municipal wastewater treatment with pond technology: Historical review and future outlook. Ecol. Eng. 2020, 148, 105791. [Google Scholar] [CrossRef]
- Ho, L.T.; Van Echelpoel, W.; Goethals, P.L.M. Design of waste stabilization pond systems: A review. Water Res. 2017, 123, 236–248. [Google Scholar] [CrossRef]
- Ho, L.; Goethals, P. Research hotspots and current challenges of lakes and reservoirs: A bibliometric analysis. Scientometrics 2020. [Google Scholar] [CrossRef]
- Motulsky, H.; Christopoulos, A. Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2013. [Google Scholar]
- McDonald, J.H. Handbook of Biological Statistics; Sparky House Publishing, University of Delaware: Newark, DE, USA, 2009. [Google Scholar]
- Sah, L.; Rousseau, D.P.; Hooijmans, C.M. Numerical modelling of waste stabilization ponds: Where do we stand? Water Air Soil Pollut. 2012, 223, 3155–3171. [Google Scholar] [CrossRef]
- Wood, M.G.; Greenfield, P.F.; Howes, T.; Johns, M.R.; Keller, J. Computational fluid dynamic modelling of wastewater ponds to improve design. Water Sci. Technol. 1995, 31, 111–118. [Google Scholar] [CrossRef]
- Shilton, A.; Mara, D.D. CFD (computational fluid dynamics) modelling of baffles for optimizing tropical waste stabilization pond systems. Water Sci. Technol. 2005, 51, 103–106. [Google Scholar] [CrossRef]
- Alvarado, A.; Vesvikar, M.; Cisneros, J.F.; Maere, T.; Goethals, P.; Nopens, I. CFD study to determine the optimal configuration of aerators in a full-scale waste stabilization pond. Water Res. 2013, 47, 4528–4537. [Google Scholar] [CrossRef]
- Dochain, D.; Gregoire, S.; Pauss, A.; Schaegger, M. Dynamical modelling of a waste stabilisation pond. Bioproc. Biosyst. Eng. 2003, 26, 19–26. [Google Scholar] [CrossRef]
- Kayombo, S.; Mbwette, T.S.A.; Mayo, A.W.; Katima, J.H.Y.; Jorgensen, S.E. Modelling diurnal variation of dissolved oxygen in waste stabilization ponds. Ecol. Model. 2000, 127, 21–31. [Google Scholar] [CrossRef]
- Ho, L.T.; Alvarado, A.; Larriva, J.; Pompeu, C.; Goethals, P. An integrated mechanistic modeling of a facultative pond: Parameter estimation and uncertainty analysis. Water Res. 2019, 151, 170–182. [Google Scholar] [CrossRef]
- Ho, L.; Pompeu, C.; Van Echelpoel, W.; Thas, O.; Goethals, P. Model-based analysis of increased loads on the performance of activated sludge and waste stabilization ponds. Water 2018, 10, 1410. [Google Scholar] [CrossRef]
- Sah, L.; Rousseau, D.P.L.; Hooijmans, C.M.; Lens, P.N.L. 3D model for a secondary facultative pond. Ecol. Model. 2011, 222, 1592–1603. [Google Scholar] [CrossRef]
- Munoz, R.; Kollner, C.; Guieysse, B.; Mattiasson, B. Photosynthetically oxygenated salicylate biodegradation in a continuous stirred tank photobioreactor. Biotechnol. Bioeng. 2004, 87, 797–803. [Google Scholar] [CrossRef] [PubMed]
- Mara, D.D.; Pearson, H.W. Waste Stabilization Ponds: Design Manual for Mediterranean Europe; World Health Organization. Regional Office for Europe: Geneva, Switzerland, 1998. [Google Scholar]
- Pearson, H.W.; Mara, D.D.; Mills, S.W.; Smallman, D.J. Factors determining algal populations in waste stabilization ponds and the influence of algae on pond performance. Water Sci. Technol. 1987, 19, 131–140. [Google Scholar] [CrossRef]
- Banks, C.J.; Koloskov, G.B.; Lock, A.C.; Heaven, S. A computer simulation of the oxygen balance in a cold climate winter storage WSP during the critical spring warm-up period. Water Sci. Technol. 2003, 48, 189–196. [Google Scholar] [CrossRef]
- Alvarado, A.; Sanchez, E.; Durazno, G.; Vesvikar, M.; Nopens, I. CFD analysis of sludge accumulation and hydraulic performance of a waste stabilization pond. Water Sci. Technol. 2012, 66, 2370–2377. [Google Scholar] [CrossRef]
- Verbyla, M.E.; Iriarte, M.M.; Guzman, A.M.; Coronado, O.; Almanza, M.; Mihelcic, J.R. Pathogens and fecal indicators in waste stabilization pond systems with direct reuse for irrigation: Fate and transport in water, soil and crops. Sci. Total Environ. 2016, 551, 429–437. [Google Scholar] [CrossRef]
- APHA. Standard Methods for the Examination of Water and Wastewater; American Public Health Association (APHA): Washington, DC, USA, 2005. [Google Scholar]
- SPSS Inc. SPSS-X User’s Guide; McGraw-Hill, Inc.: New York, USA, 1985. [Google Scholar]
- Ellis, K.V. Stabilization ponds—Design and operation. Crit. Rev. Environ. Sci. Technol. 1983, 13, 69–102. [Google Scholar] [CrossRef]
- Zuur, A.F.; Leno, E.N.; Elphick, C.S. A protocol for data exploration to avoid common statistical problems. Methods Ecol. Evol. 2010, 1, 3–14. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Goodwin, P.; Lawton, R. On the asymmetry of the symmetric MAPE. Int. J. Forecast. 1999, 15, 405–408. [Google Scholar] [CrossRef]
- Rosner, B. Fundamentals of Biostatistics; Cengage Learning: Boston, MA, USA, 2010. [Google Scholar]
- Zuur, A.F.; Ieno, E.N. A protocol for conducting and presenting results of regression-type analyses. Methods Ecol. Evol. 2016, 7, 636–645. [Google Scholar] [CrossRef]
- Pearson, H. Microbiology of waste stabilization ponds. In Pond Treatment Technology; IWA publishing: London, UK, 2005; pp. 14–43. [Google Scholar]
- Montemezzani, V.; Duggan, I.C.; Hogg, I.D.; Craggs, R.J. Control of zooplankton populations in a wastewater treatment High Rate Algal Pond using overnight CO2 asphyxiation. Algal Res. 2017, 26, 250–264. [Google Scholar] [CrossRef]
- Ho, L.; Pham, D.; Van Echelpoel, W.; Muchene, L.; Shkedy, Z.; Alvarado, A.; Espinoza-Palacios, J.; Arevalo-Durazno, M.; Thas, O.; Goethals, P. A closer look on spatiotemporal variations of dissolved oxygen in waste stabilization ponds using mixed models. Water 2018, 10, 201. [Google Scholar] [CrossRef]
- Pearson, H.W.; Mara, D.D.; Thompson, W.; Maber, S.P. Studies on high-altitude waste stabilization ponds in peru. Water Sci. Technol. 1987, 19, 349–353. [Google Scholar] [CrossRef]
- Juanico, M.; Weinberg, H.; Soto, N. Process design of waste stabilization ponds at high altitude in Bolivia. Water Sci. Technol. 2000, 42, 307–313. [Google Scholar] [CrossRef]
- Lloyd, B.J.; Leitner, A.R.; Vorkas, C.A.; Guganesharajah, R.K. Under-performance evaluation and rehabilitation strategy for waste stabilization ponds in Mexico. Water Sci. Technol. 2002, 48, 35–43. [Google Scholar] [CrossRef]
- Recio-Garrido, D.; Kleiner, Y.; Colombo, A.; Tartakovsky, B. Dynamic model of a municipal wastewater stabilization pond in the arctic. Water Res. 2018, 144, 444–453. [Google Scholar] [CrossRef]
- Ho, L.T.; Pham, D.T.; Van Echelpoel, W.; Alvarado, A.; Espinoza-Palacios, J.E.; Arevalo-Durazno, M.B.; Goethals, P.L.M. Exploring the influence of meteorological conditions on the performance of a waste stabilization pond at high altitude with structural equation modeling. Water Sci. Technol. 2018, 78, 37–48. [Google Scholar] [CrossRef]
- Gerardi, M.H. The Biology and Troubleshooting of Facultative Lagoons; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Pham, D.T.; Everaert, G.; Janssens, N.; Alvarado, A.; Nopens, I.; Goethals, P.L.M. Algal community analysis in a waste stabilisation pond. Ecol. Eng. 2014, 73, 302–306. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model. Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Shmueli, G. To explain or to predict? Statist. Sci. 2010, 25, 289–310. [Google Scholar] [CrossRef]
- Von Sperling, M. Waste Stabilisation Ponds; IWA publishing: London, UK, 2007. [Google Scholar]
- Butler, E.; Hung, Y.T.; Al Ahmad, M.S.; Yeh, R.Y.L.; Liu, R.L.H.; Fu, Y.P. Oxidation pond for municipal wastewater treatment. Appl. Water Sci. 2017, 7, 31–51. [Google Scholar] [CrossRef]
- Shilton, A. Pond Treatment Technology; IWA publishing: London, UK, 2005. [Google Scholar]
- Krzywinski, M.; Altman, N. Points of significance: Power and sample size. Nat. Methods 2013, 10, 1139–1140. [Google Scholar] [CrossRef]
- Muller, S.; Scealy, J.L.; Welsh, A.H. Model selection in linear mixed models. Stat. Sci. 2013, 28, 135–167. [Google Scholar] [CrossRef]
- Field, A. Discovering Statistics Using SPSS; SAGE Publications: Thousand Oaks, CA, USA, 2009. [Google Scholar]
- Abdi, H. Part (semi partial) and partial regression coefficients. In Encyclopedia of Measurement and Statistics; Sage Publications: Thousand Oaks, CA, USA, 2007; pp. 736–740. [Google Scholar]
- Beaujean, A.A. Sample size determination for regression models using Monte Carlo methods in R. Pract. Assess. Res. Eval. 2014, 19, 2. [Google Scholar]


| Pond | Training Dataset | Validation Dataset | Full Optimal Model | MAE ± sd (mg L−1) | SMAPE ± sd (%) | R2 | ||
|---|---|---|---|---|---|---|---|---|
| Training | Validation | Training | Validation | |||||
| FP1_Surface | T2T3 FP1_Surface | T1 FP1_Surface | DO = −43.718 + 0.039Chl + 0.204BOD + 1.772AT | 1.59 ± 0.73 | 3.06 ± 2.74 | 11.75 ± 14.17 | 11.01 ± 10.03 | 0.909 |
| FP1_Bottom | T2T3 FP1_Bottom | T1 FP1_Bottom | DO = −9.550 + 0.447BOD | 2.75 ± 2.20 | 3.52 ± 3.00 | 38.70 ± 31.49 | 20.08 ± 24.08 | 0.540 |
| MP1_Surface | T1T2 MP1_Surface | T3 MP1_Surface | DO = −2.024 + 0.012Chl + 0.007SR | 0.54 ± 0.46 | 0.74 ± 0.43 | 17.50 ± 21.64 | 17.64 ± 10.07 | 0.854 |
| MP1_Bottom | T1T2 MP1_Bottom | T3 MP1_Bottom | DO = 7.470 − 0.445WT + 0.095AT | 0.22 ± 0.18 | 0.79 ± 0.46 | 30.61 ± 17.28 | 49.19 ± 30.84 | 0.391 |
| FP2_Surface | T1T3 FP2_Surface | T2 FP2_Surface | DO = −40.463 + 0.014Chl + 0.201BOD + 1.448WT + 0.496AT | 1.07 ± 0.67 | 3.54 ± 2.62 | 12.66 ± 9.47 | 20.91 ± 10.35 | 0.752 |
| FP2_Bottom | T1T3 FP2_Bottom | T2 FP2_Bottom | DO = −2.494 + 0.119BOD | 0.29 ± 0.22 | 1.19 ± 1.10 | 25.29 ± 13.71 | 51.89 ± 25.79 | 0.424 |
| MP2_Surface | T1T2 MP2_Surface | T3 MP2_Surface | DO = −15.016 + 0.016Chl + 1.952WT+ 0.004SR − 0.947WS − 0.969AT | 0.32 ± 0.27 | 1.14 ± 0.77 | 2.35 ± 2.00 | 10.88 ± 6.42 | 0.885 |
| MP2_Bottom | T1T2 MP2_Bottom | T3 MP2_Bottom | DO = −5.773 + 0.018Chl + 0.407BOD | 0.55 ± 0.32 | 1.30 ± 1.35 | 13.51 ± 12.82 | 71.62 ± 33.56 | 0.624 |
| Model | Model Parameter | Mean | Standard Deviation | Unstandardised Coefficient | Standardised Coefficient | 95% Confidence Interval for Coefficient | Change of DO by Change of Each Variable † | ||
|---|---|---|---|---|---|---|---|---|---|
| Coefficient | Standard Error | Lower Bound | Upper Bound | ||||||
| FP1 Surface | DO | 11.28 | 5.90 | ||||||
| Constant | −43.718 | 5.975 | −56.533 | −30.904 | |||||
| Chlorophyll a | 430.22 | 109.10 | 0.039 | 0.005 | 0.713* | 0.028 | 0.049 | 4.21 | |
| BOD | 41.67 | 7.74 | 0.204 | 0.068 | 0.268* | 0.058 | 0.351 | 1.58 | |
| Air temperature | 16.87 | 2.09 | 1.772 | 0.238 | 0.626* | 1.263 | 2.282 | 3.69 | |
| FP1 Bottom | DO | 5.17 | 5.31 | ||||||
| Constant | −9.550 | 4.050 | −18.375 | −0.725 | |||||
| BOD | 32.93 | 8.72 | 0.447 | 0.119 | 0.735* | 0.187 | 0.707 | 3.90 | |
| MP1 Surface | DO | 2.46 | 1.89 | ||||||
| Constant | −2.024 | 0.511 | −3.113 | −0.935 | |||||
| Chlorophyll a | 245.73 | 108.63 | 0.012 | 0.002 | 0.678* | 0.008 | 0.016 | 1.28 | |
| Solar radiation | 228.86 | 121.67 | 0.007 | 0.002 | 0.448* | 0.004 | 0.010 | 0.85 | |
| MP1 Bottom | DO | 0.402 | 0.369 | ||||||
| Constant | 7.470 | 2.299 | 2.571 | 12.370 | |||||
| Water temperature | 18.59 | 0.86 | −0.445 | 0.143 | −1.035* | −0.750 | −0.139 | −0.38 | |
| Air temperature | 12.60 | 3.25 | 0.095 | 0.038 | 0.833* | 0.014 | 0.176 | 0.31 | |
| FP2 Surface | DO | 4.92 | 2.58 | ||||||
| Constant | −40.463 | 10.646 | −63.462 | −17.463 | |||||
| Chlorophyll a | 343.74 | 128.96 | 0.014 | 0.003 | 0.691* | 0.006 | 0.021 | 1.78 | |
| BOD | 31.67 | 6.87 | 0.201 | 0.061 | 0.536* | 0.070 | 0.333 | 1.38 | |
| Water temperature | 18.21 | 0.66 | 1.448 | 0.659 | 0.371* | 0.025 | 2.871 | 0.96 | |
| Air temperature | 15.88 | 2.06 | 0.496 | 0.216 | 0.396* | 0.029 | 0.962 | 1.02 | |
| FP2 Bottom | DO | 0.60 | 0.49 | ||||||
| Constant | −2.494 | 1.046 | −4.773 | −0.215 | |||||
| BOD | 25.93 | 2.70 | 0.119 | 0.040 | 0.651* | 0.032 | 0.207 | 0.32 | |
| MP2 Surface | DO | 6.87 | 1.14 | ||||||
| Constant | −15.016 | 12.656 | −42.590 | 12.558 | |||||
| Chlorophyll a | 242.92 | 63.72 | 0.016 | 0.002 | 0.910* | 0.011 | 0.021 | 1.04 | |
| Water temperature | 19.32 | 0.23 | 1.952 | 0.688 | 0.387* | 0.453 | 3.451 | 0.44 | |
| Solar radiation | 568.57 | 193.24 | 0.004 | 0.001 | 0.604* | 0.001 | 0.006 | 0.69 | |
| Wind speed | 3.73 | 1.05 | −0.947 | 0.174 | −0.871* | −1.326 | −0.558 | −0.99 | |
| Air temperature | 18.89 | 0.46 | −0.969 | 0.376 | −0.386* | −1.787 | −0.151 | −0.44 | |
| MP2 Bottom | DO | 2.51 | 1.05 | ||||||
| Constant | −5.773 | 1.723 | −9.446 | −2.100 | |||||
| Chlorophyll a | 67.04 | 33.85 | 0.018 | 0.006 | 0.592* | 0.005 | 0.032 | 0.62 | |
| BOD | 17.33 | 2.63 | 0.407 | 0.082 | 1.016* | 0.233 | 0.581 | 1.07 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, D.T.; Ho, L.; Espinoza-Palacios, J.; Arevalo-Durazno, M.; Van Echelpoel, W.; Goethals, P. Generalised Linear Models for Prediction of Dissolved Oxygen in a Waste Stabilisation Pond. Water 2020, 12, 1930. https://doi.org/10.3390/w12071930
Pham DT, Ho L, Espinoza-Palacios J, Arevalo-Durazno M, Van Echelpoel W, Goethals P. Generalised Linear Models for Prediction of Dissolved Oxygen in a Waste Stabilisation Pond. Water. 2020; 12(7):1930. https://doi.org/10.3390/w12071930
Chicago/Turabian StylePham, Duy Tan, Long Ho, Juan Espinoza-Palacios, Maria Arevalo-Durazno, Wout Van Echelpoel, and Peter Goethals. 2020. "Generalised Linear Models for Prediction of Dissolved Oxygen in a Waste Stabilisation Pond" Water 12, no. 7: 1930. https://doi.org/10.3390/w12071930
APA StylePham, D. T., Ho, L., Espinoza-Palacios, J., Arevalo-Durazno, M., Van Echelpoel, W., & Goethals, P. (2020). Generalised Linear Models for Prediction of Dissolved Oxygen in a Waste Stabilisation Pond. Water, 12(7), 1930. https://doi.org/10.3390/w12071930








