Study on the Characteristic Point Location of Depth Average Velocity in Smooth Open Channels: Applied to Channels with Flat or Concave Boundaries
Abstract
1. Introduction
2. Methodology
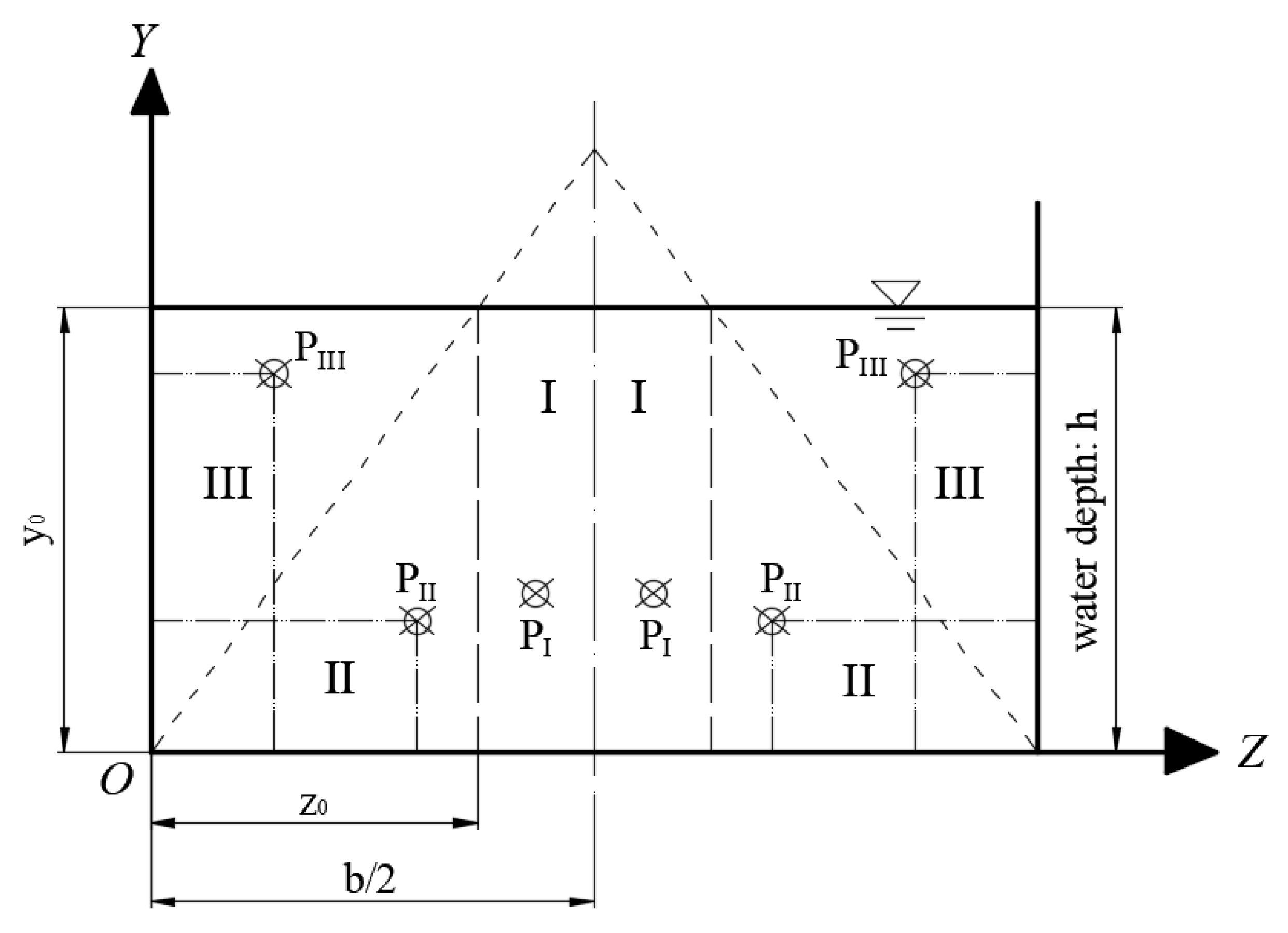
2.1. CPL in Rectangular Channels
2.1.1. Existing Form of the Division Line in Rectangular Channels
- (a)
- Determination of the location of division line in wide–shallow channel (b/h ≥ 2)
- (b)
- Determination of the location of division line in narrow–deep channel (b/h ≤ 2)
2.1.2. CPL of Lines in Rectangular Channel
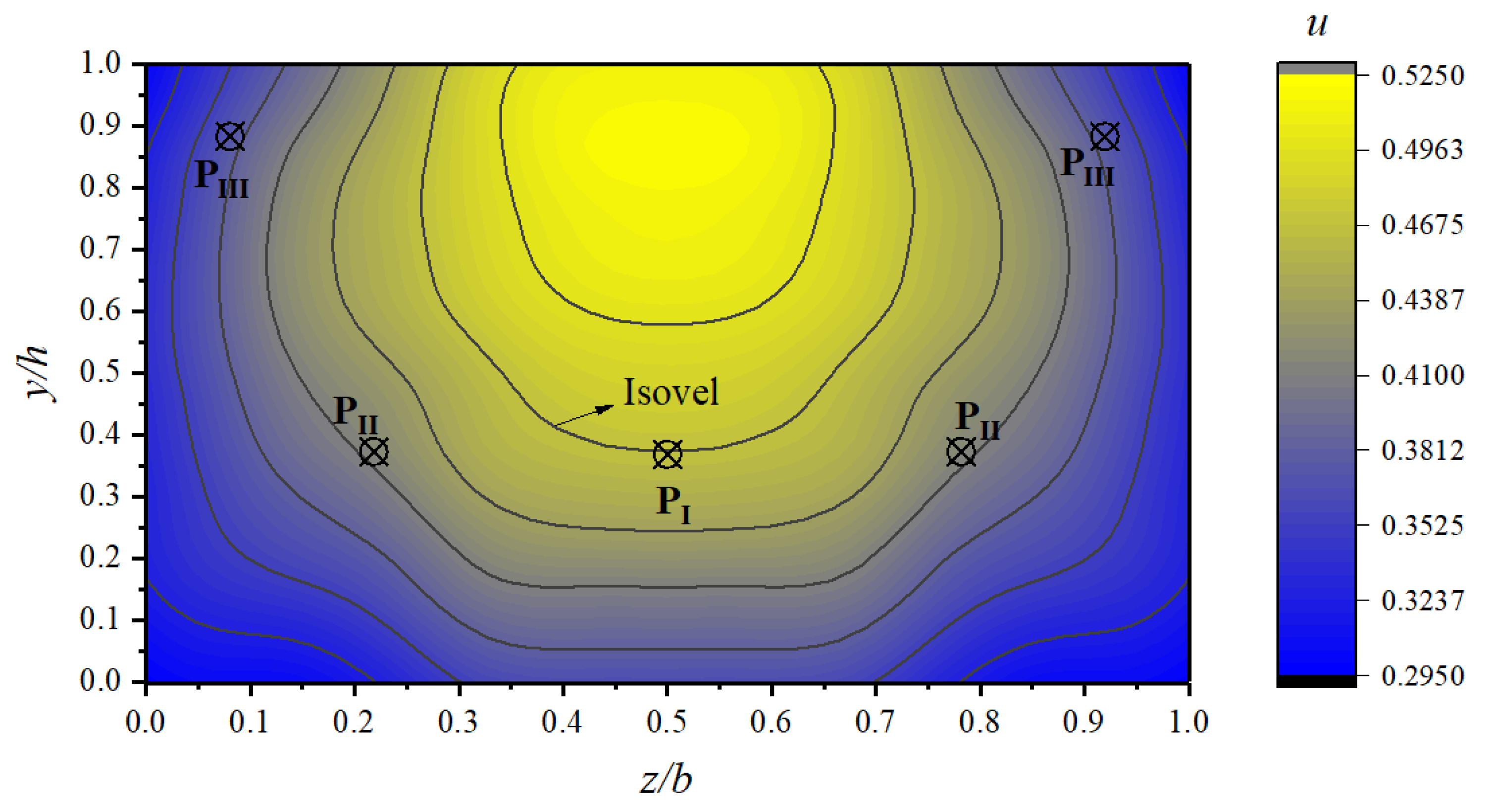
2.1.3. CPL of Regions in Rectangular Channel
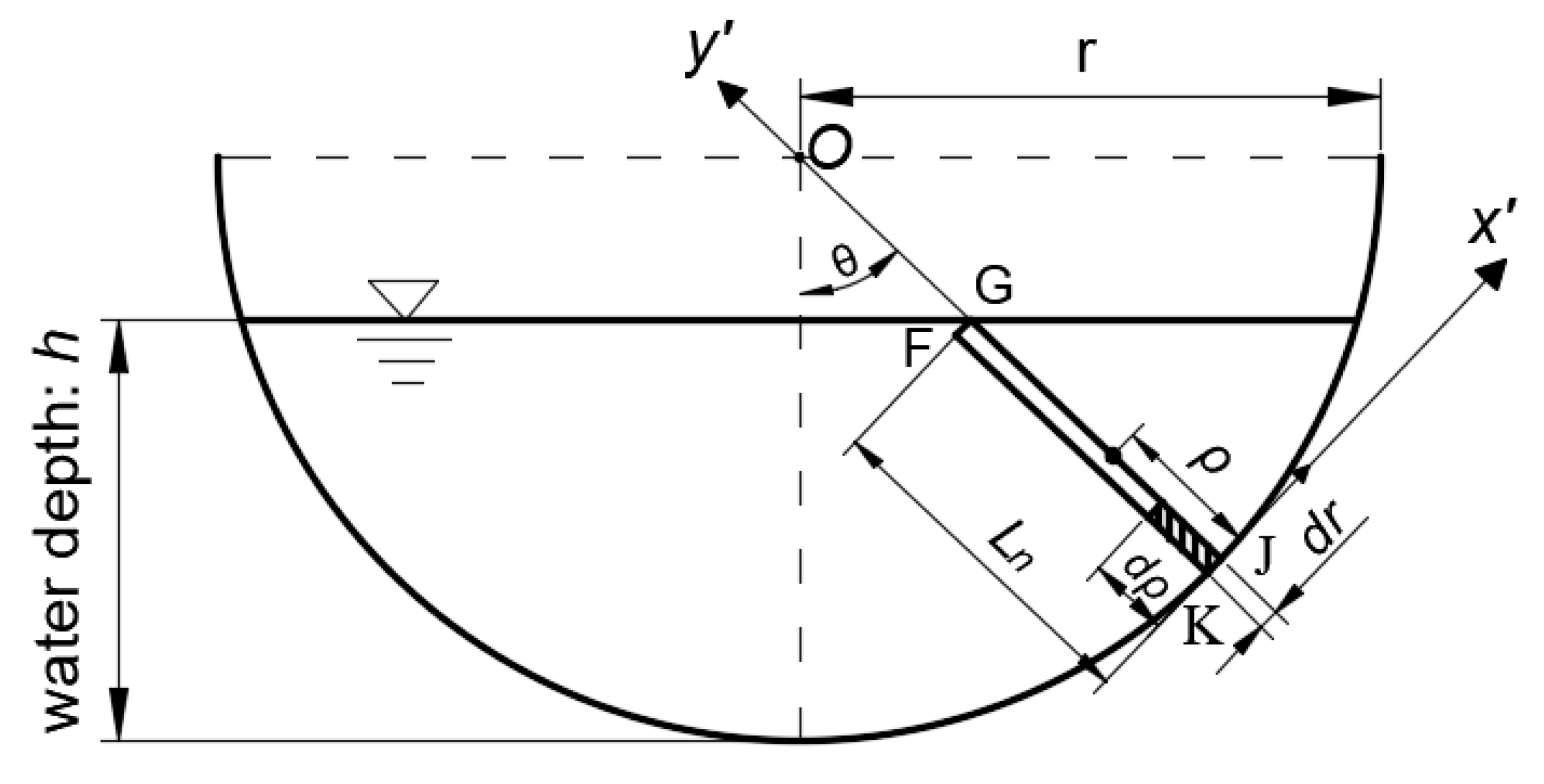
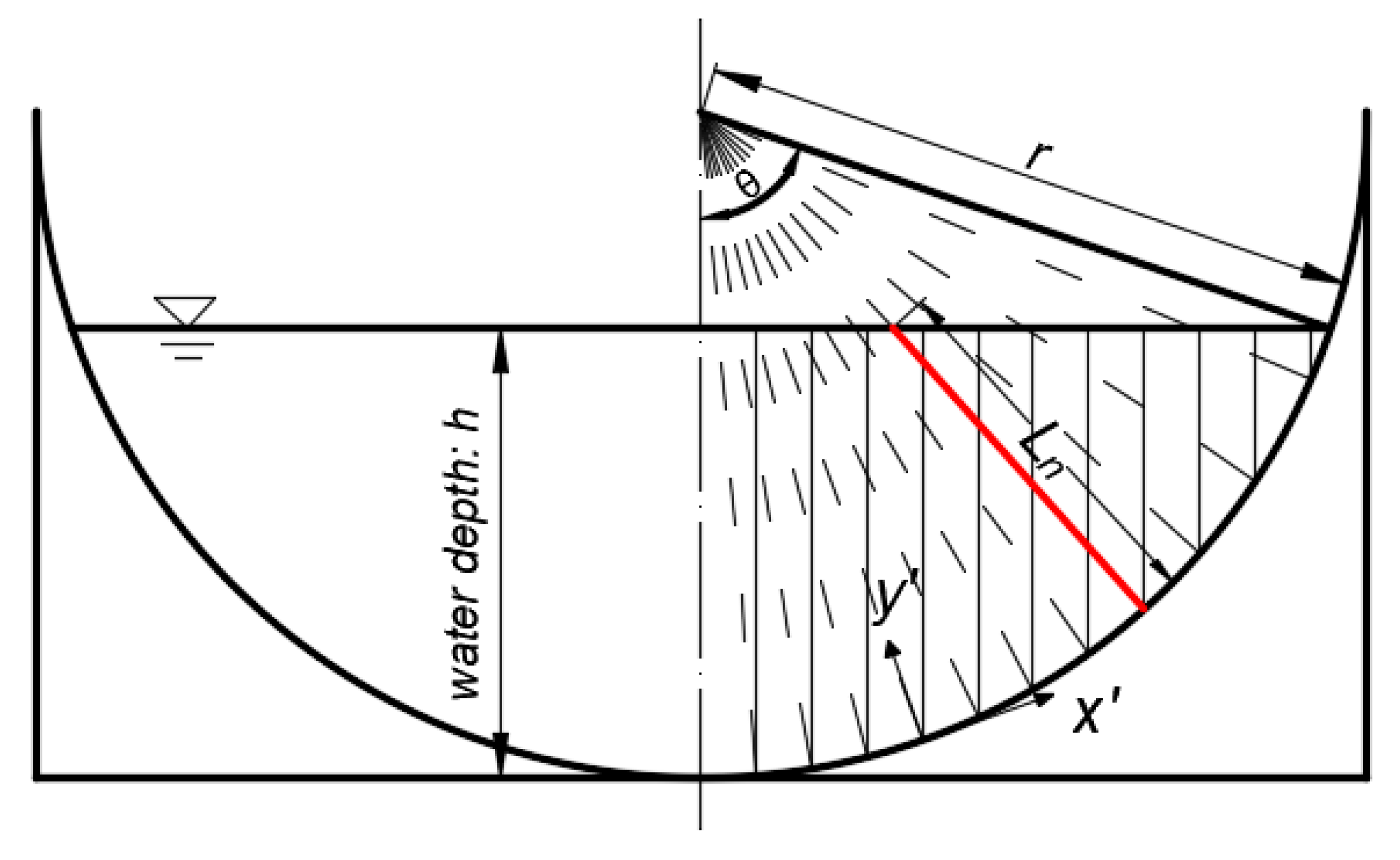
2.2. CPL in Semi-Circular Channel
2.3. Discharge of Rectangular and Semi-Circular Channel
2.3.1. Discharge in a Rectangular Channel
2.3.2. Discharge in a Semi-Circular Channel
3. Experimental Setup
4. Results and Discussion
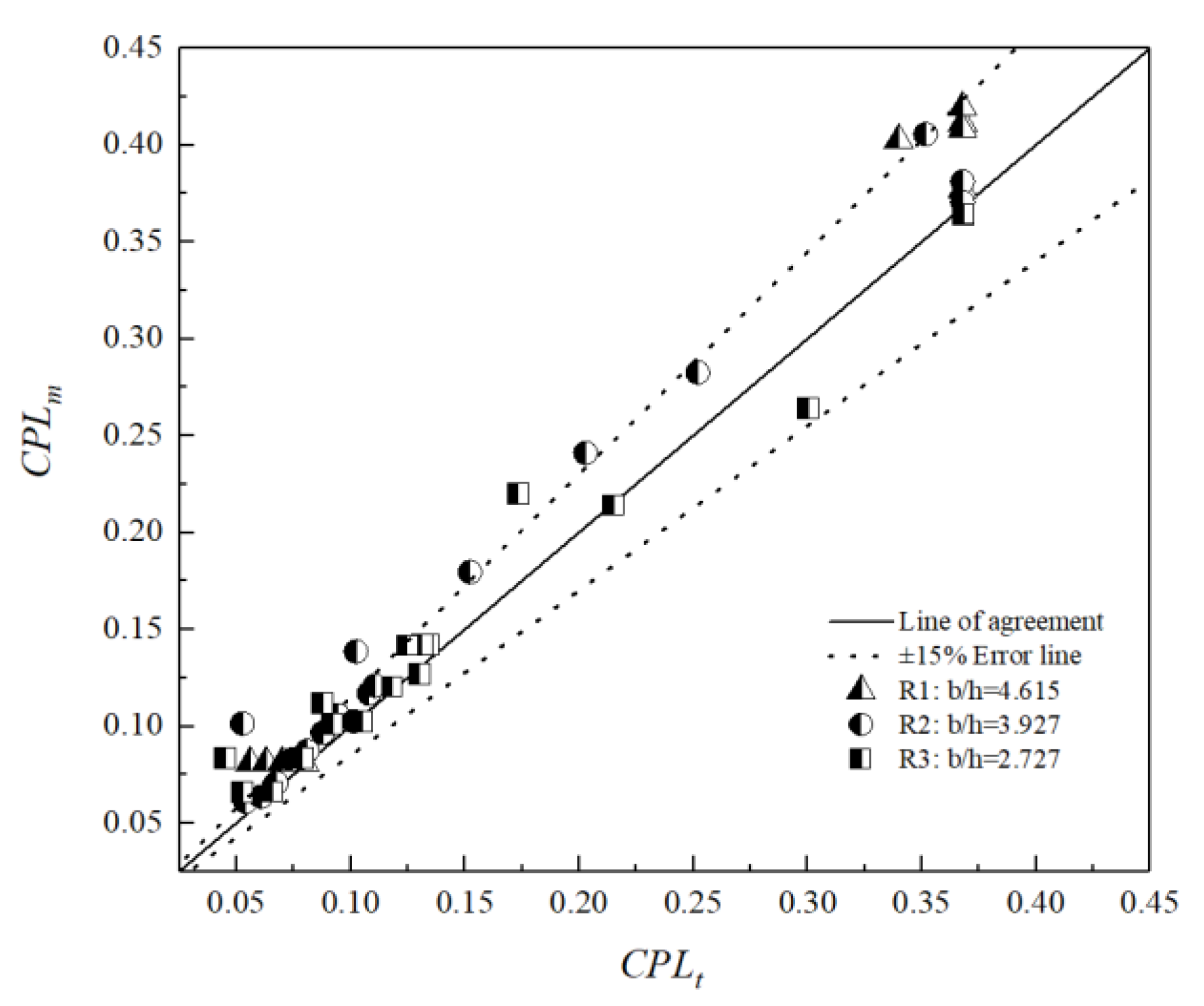
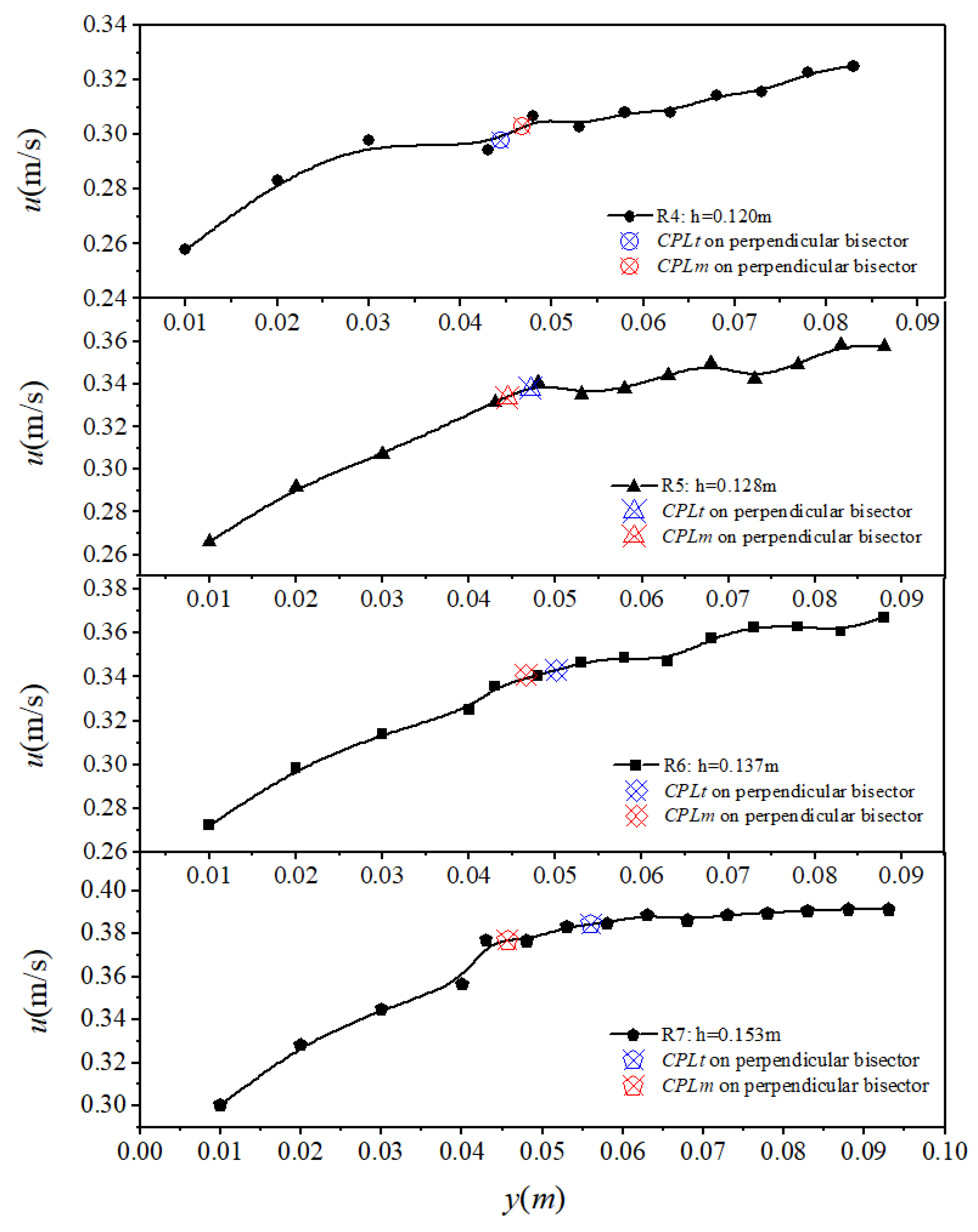
4.1. Analysis with Rectangular Channels
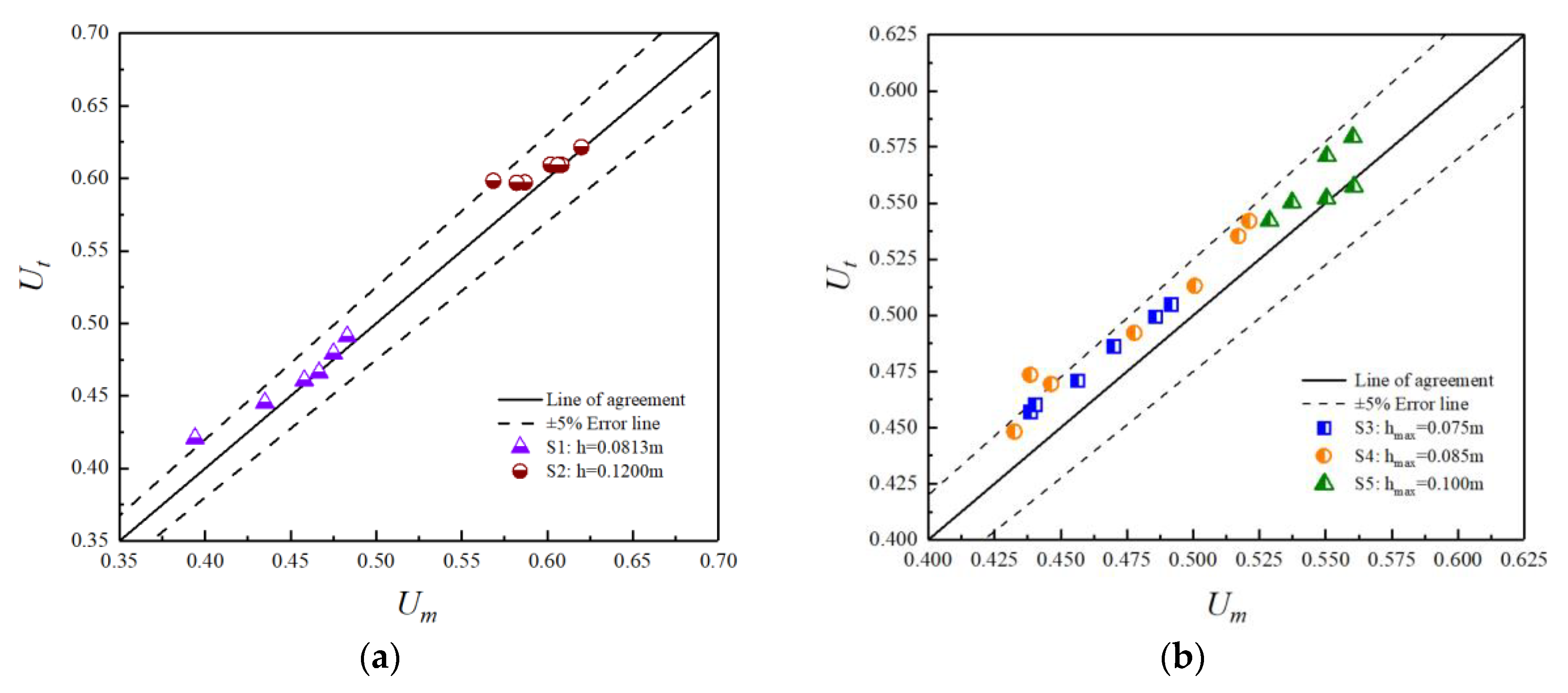
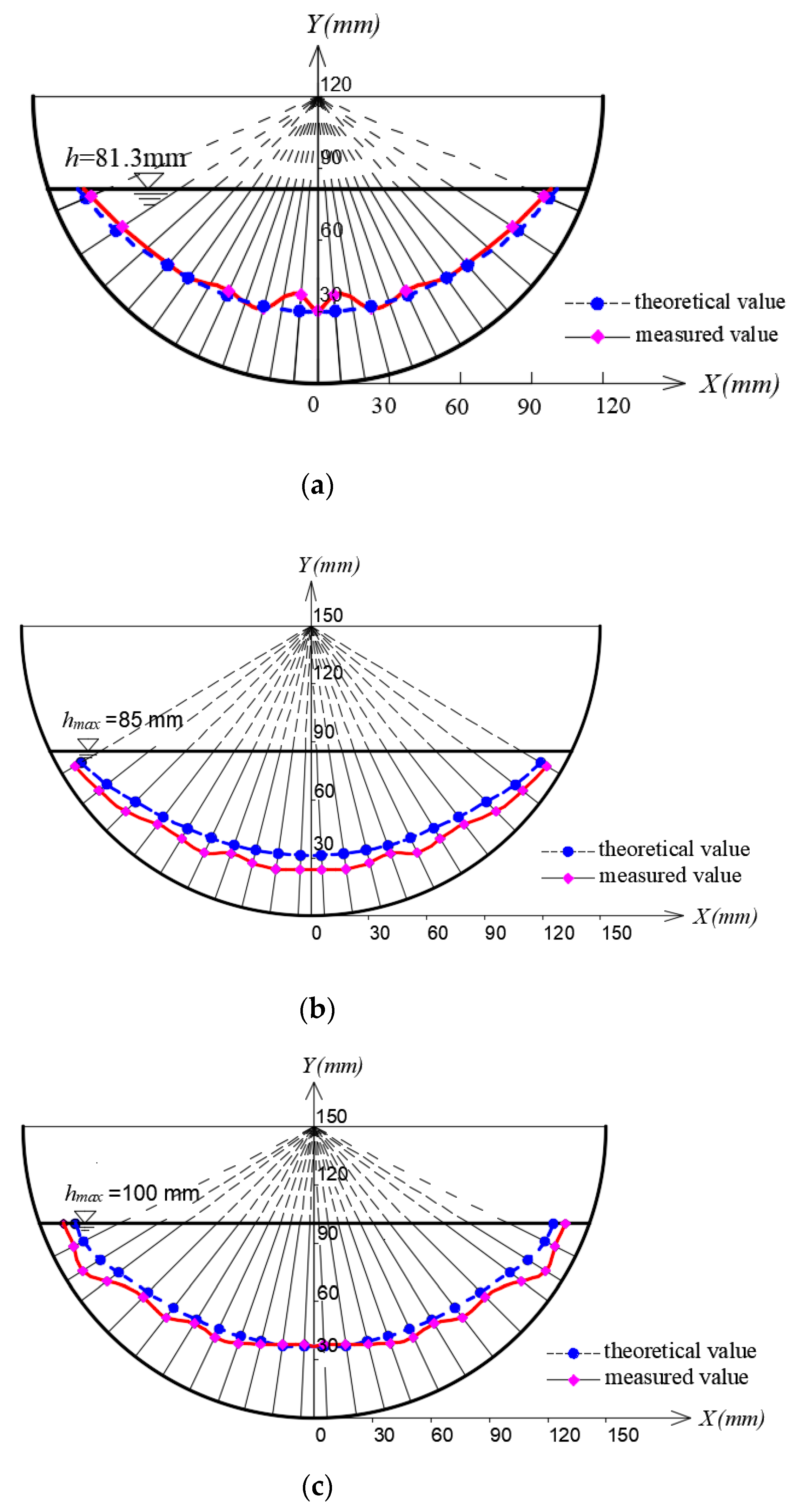
4.2. Analysis with Semi-Circular Channels
5. Summary
- (1)
- Based on Yang et al.’ s partitioning theory [21,22,27], this paper gives a re-description of the existing form of the division line of a rectangular cross-section channel. That is, whether the channel cross-section is wide–shallow or narrow–deep with the center line of the cross-section as the symmetrical axis, and whether the intersection points of the left and right division lines intersect on or above the water surface.
- (2)
- This paper analyzes characteristic points in flat channels (e.g., rectangular channel) and concave boundary channels (e.g., semi-circular channel). In the rectangular channel, the division line divides the section into three regions. In each region, the analysis is conducted in the direction perpendicular to the bottom or side wall of the channel. In the semi-circular channel, the analysis is conducted along the normal direction. Based on the log-law, the theoretical expressions for calculating the location of the average velocity characteristic points in flat and concave boundary channels are derived through the formula transformation.
- (3)
- The velocity data in different experimental sites are used to verify the validity of the CPL formulas applied to flat and concave boundary channels. Moreover, the discharge calculation formulas of channels are given through discussion with CPL.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mancosu, N.; Snyder, R.L.; Kyriakakis, G.; Spano, D. Water Scarcity and Future Challenges for Food Production. Water 2015, 7, 975–992. [Google Scholar] [CrossRef]
- Salehi, S.; Azimi, A.H. Discharge Characteristics of Weir-Orifice and Weir-Gate Structures. J. Irrig. Drain. Eng. 2019, 145. [Google Scholar] [CrossRef]
- Samani, Z. Three simple flumes for flow measurement in open channels. J. Irrig. Drain. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Samani, Z.; Magallanez, H. Simple flume for flow measurement in open channel. J. Irrig. Drain. Eng. 2000, 126, 127–129. [Google Scholar] [CrossRef]
- Keulegan, G.H. Laws of turbulent flow in open channels. J. Res. Natl. Bur. Stand. 1938, 21, 707–741. [Google Scholar] [CrossRef]
- Zanoun, E.-S.; Durst, F.; Bayoumy, O.; Al-Salaymehc, A. Wall skin friction and mean velocity profiles of fully developed turbulent pipe flows. Exp. Therm. Fluid. Sci. 2007, 32, 249–261. [Google Scholar] [CrossRef]
- Nikuradse, J. Laws of Flow in Rough Pipes (1950 translation); National Advisory Committee for Aeronautics: Washington, DC, USA, 1933; NACA-TM-1292. Available online: https://ntrs.nasa.gov/search.jsp?R=19930093938 (accessed on 15 January 2020).
- Cardoso, A.H.; Graf, W.H.; Gust, G. Uniform-Flow in a Smooth Open Channel. J. Hydraul. Res. 1989, 27, 606–616. [Google Scholar] [CrossRef]
- Steffler, P.M.; Rajaratnam, N.; Peterson, A.W. LDA Measurements in Open Channel. J. Hydraul. Eng.-ASCE 1985, 111. [Google Scholar] [CrossRef]
- Nezu, I.; Rodi, W. Open-Channel Flow Measurements with a Laser Doppler Anemometer. J. Hydraul. Eng. 1986, 112, 335–355. [Google Scholar] [CrossRef]
- Chiu, C.L. Entropy and 2-D velocity distribution in open channels. J. Hydraul. Eng. 1988, 114, 738–756. [Google Scholar] [CrossRef]
- Chiu, C.L. Application of entropy concept in open-channel flow study. J. Hydraul. Eng. 1991, 117, 615–628. [Google Scholar] [CrossRef]
- Chiu, C.L.; Murray, D.W. Variation of velocity distribution along non-uniform open-channel flow. J. Hydraul. Eng. 1992, 118, 989–1001. [Google Scholar]
- Maghrebi, M.F. Application of the single point measurement in discharge estimation. Adv. Water Resour. 2006, 29, 1504–1514. [Google Scholar] [CrossRef]
- Bretheim, J.U.; Meneveau, C.; Gayme, D.F. Standard logarithmic mean velocity distribution in a band-limited restricted nonlinear model of turbulent flow in a half-channel. Phys. Fluids 2015, 27. [Google Scholar] [CrossRef]
- Hong, J.H.; Guo, W.D.; Wang, H.W.; Yeh, P.H. Estimating discharge in gravel-bed river using non-contact ground-penetrating and surface-velocity radars. River Res. Appl. 2017, 33, 1177–1190. [Google Scholar] [CrossRef]
- Moramarco, T.; Barbetta, S.; Tarpanelli, A. From Surface Flow Velocity Measurements to Discharge Assessment by the Entropy Theory. Water 2017, 9, 120. [Google Scholar] [CrossRef]
- Johnson, E.D.; Cowen, E.A. Estimating bed shear stress from remotely measured surface turbulent dissipation fields in open channel flows. Water Resour. Res. 2017, 53, 1982–1996. [Google Scholar] [CrossRef]
- Johnson, E.D.; Cowen, E.A. Remote determination of the velocity index and mean streamwise velocity profiles. Water Resour. Res. 2017, 53, 7521–7535. [Google Scholar] [CrossRef]
- Khuntia, J.R.; Kamalini, D.; Khatua, K.K. Prediction of depth-averaged velocity in an open channel flow. Appl. Water Sci. 2018, 8, 172. [Google Scholar] [CrossRef]
- Han, Y.; Yang, S.Q.; Dharmasiri, N.; Sivakumar, M. Experimental study of smooth channel flow division based on velocity distribution. J. Hydraul. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Yang, S.Q.; Han, Y.; Lin, P.Z.; Jiang, C.B.; Walker, R. Experimental study on the validity of flow region division. J. Hydro-Environ. Res. 2014, 8, 421–427. [Google Scholar] [CrossRef]
- Melling, A.; Whitelaw, J.H. Turbulent flow in a rectangular duct. J. Fluid Mech. 1976, 78, 289–315. [Google Scholar] [CrossRef]
- Tracy, H.J. Turbulent flow in a three-dimensional channel. J. Hydraul. Div. 1965, 91, 9–35. [Google Scholar]
- Einstein, H.A. Formulas for the transportation of bed load. Trans. ASCE 1942, 107, 133–169. [Google Scholar]
- Chien, N.; Wang, Z. Mechanics of Sediment Transport; Science Press: Beijing, China, 1986. (In Chinese) [Google Scholar]
- Yang, S.Q.; Lim, S.Y. Mechanism of energy transportation and turbulent flow in a 3D channel. J. Hydraul. Eng.-ASCE 1997, 123, 684–692. [Google Scholar] [CrossRef]
- Luo, J. Study on the Hydraulic Characteristics of Pressure-Free Uniform Flow in Circular Section Pipeline. Master’s Thesis, Tsinghua University, Beijing, China, 2016. (In Chinese). [Google Scholar]
- Knight, D.W.; Sterling, M. Boundary shear in circular pipes running partially full. J. Hydraul. Eng.-ASCE 2000, 126, 263–275. [Google Scholar] [CrossRef]
- Chiu, C.L.; Chiou, J.D. Structure of 3-D flow in rectangular open channels. J. Hydraul. Eng.-ASCE 1986, 112, 1050–1068. [Google Scholar] [CrossRef]
- Stearns, F.P. A reason why the maximum velocity of water flowing in open channels is below the surface. Trans. Am. Soc. Civ. Eng. 1883, 7, 331–338. [Google Scholar]
- Murphy, C. Accuracy of stream measurements. Water Supply Irrig. 1904, 95, 111–112. [Google Scholar]
- Tominaga, A.; Nezu, I. Turbulent structure in compound open-channel flows. J. Hydraul. Eng.-ASCE 1991, 117, 21–41. [Google Scholar] [CrossRef]
- Mirauda, D.; Pannone, M.; De Vincenzo, A. An Entropic Model for the Assessment of Streamwise Velocity Dip in Wide Open Channels. Entropy. 2018, 20, 69. [Google Scholar] [CrossRef]
- Coles, D. The Law of the Wake in the Turbulent Boundary Layer. J. Fluid Mech. 1956, 1, 191–226. [Google Scholar] [CrossRef]
- Absi, R. An ordinary differential equation for velocity distribution and dip-phenomenon in open channel flows. J. Hydraul. Res. 2011, 49, 82–89. [Google Scholar] [CrossRef]



| Cross-Sectional Shape | Conditions | Channel Width: b (m) | Channel Radius: r (m) | Flow Discharge: Q (m3/s) | Water Depth: h (m) |
|---|---|---|---|---|---|
| Rectangle | R1 a | 0.3 | - | 0.004 | 0.065 |
| R2 a | 0.004 | 0.091 | |||
| R3 a | 0.004 | 0.110 | |||
| R4 b | 0.8 | - | 0.031 | 0.120 | |
| R5 b | 0.033 | 0.128 | |||
| R6 b | 0.039 | 0.137 | |||
| R7 b | 0.044 | 0.153 | |||
| Semi-circle | S1 c | - | 0.120 | 0.005 | 0.0813 |
| S2 c | 0.012 | 0.1200 | |||
| S3 a | - | 0.150 | 0.003 | 0.075 | |
| S4 a | 0.005 | 0.085 | |||
| S5 a | 0.008 | 0.100 |
| Average Error Value along Normal Direction | Average Error Value along Vertical Direction | ||
|---|---|---|---|
| Normal Slope kn | Average Error Value E (%) | The Distance from the Vertical Line to the Central Line z/b | Average Error Value E (%) |
| 11.9 | 2.156661 | 0.083 | 3.528655 |
| 5.91 | 3.117373 | 0.167 | 3.441878 |
| 3.87 | 2.578154 | 0.250 | 2.827718 |
| 2.82 | 3.073467 | 0.333 | 7.846099 |
| 2.18 | 3.217222 | 0.417 | 6.557529 |
| 1.73 | 2.584048 | 0.500 | 10.55338 |
| 1.39 | 2.047317 | 0.583 | 12.39980 |
| 1.11 | 2.207014 | 0.667 | 19.05022 |
| 0.88 | 2.758453 | 0.750 | 21.84237 |
| 0.66 | 4.707039 | 0.833 | 30.18244 |
| Degree of Angle with the Two-Line Method | Q Calculation (m3/s) | Q Measurement (m3/s) | Relative Error (%) | ||
|---|---|---|---|---|---|
| θ1 (°) | θ2 (°) | θ3 (°) | |||
| 71/3 | 71/3 | 71/3 | 0.00526 | 0.005 | 5.10 |
| 18 | 34 | 19 | 0.00565 | 12.90 | |
| 18 | 23 | 30 | 0.00531 | 6.27 | |
| 29 | 32 | 10 | 0.00551 | 10.09 | |
| 35 | 26 | 10 | 0.00542 | 8.48 | |
| 36 | 21 | 14 | 0.00533 | 6.61 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Chen, J.; Han, Y.; Ma, Z.; Wu, J. Study on the Characteristic Point Location of Depth Average Velocity in Smooth Open Channels: Applied to Channels with Flat or Concave Boundaries. Water 2020, 12, 430. https://doi.org/10.3390/w12020430
Li T, Chen J, Han Y, Ma Z, Wu J. Study on the Characteristic Point Location of Depth Average Velocity in Smooth Open Channels: Applied to Channels with Flat or Concave Boundaries. Water. 2020; 12(2):430. https://doi.org/10.3390/w12020430
Chicago/Turabian StyleLi, Tongshu, Jian Chen, Yu Han, Zhuangzhuang Ma, and Jingjing Wu. 2020. "Study on the Characteristic Point Location of Depth Average Velocity in Smooth Open Channels: Applied to Channels with Flat or Concave Boundaries" Water 12, no. 2: 430. https://doi.org/10.3390/w12020430
APA StyleLi, T., Chen, J., Han, Y., Ma, Z., & Wu, J. (2020). Study on the Characteristic Point Location of Depth Average Velocity in Smooth Open Channels: Applied to Channels with Flat or Concave Boundaries. Water, 12(2), 430. https://doi.org/10.3390/w12020430






