Modified Convergent Flow Tracing Method for Evaluating Advective Velocity and Effective Porosity in Fractured Rock Aquifers
Abstract
:1. Introduction
2. Field Study
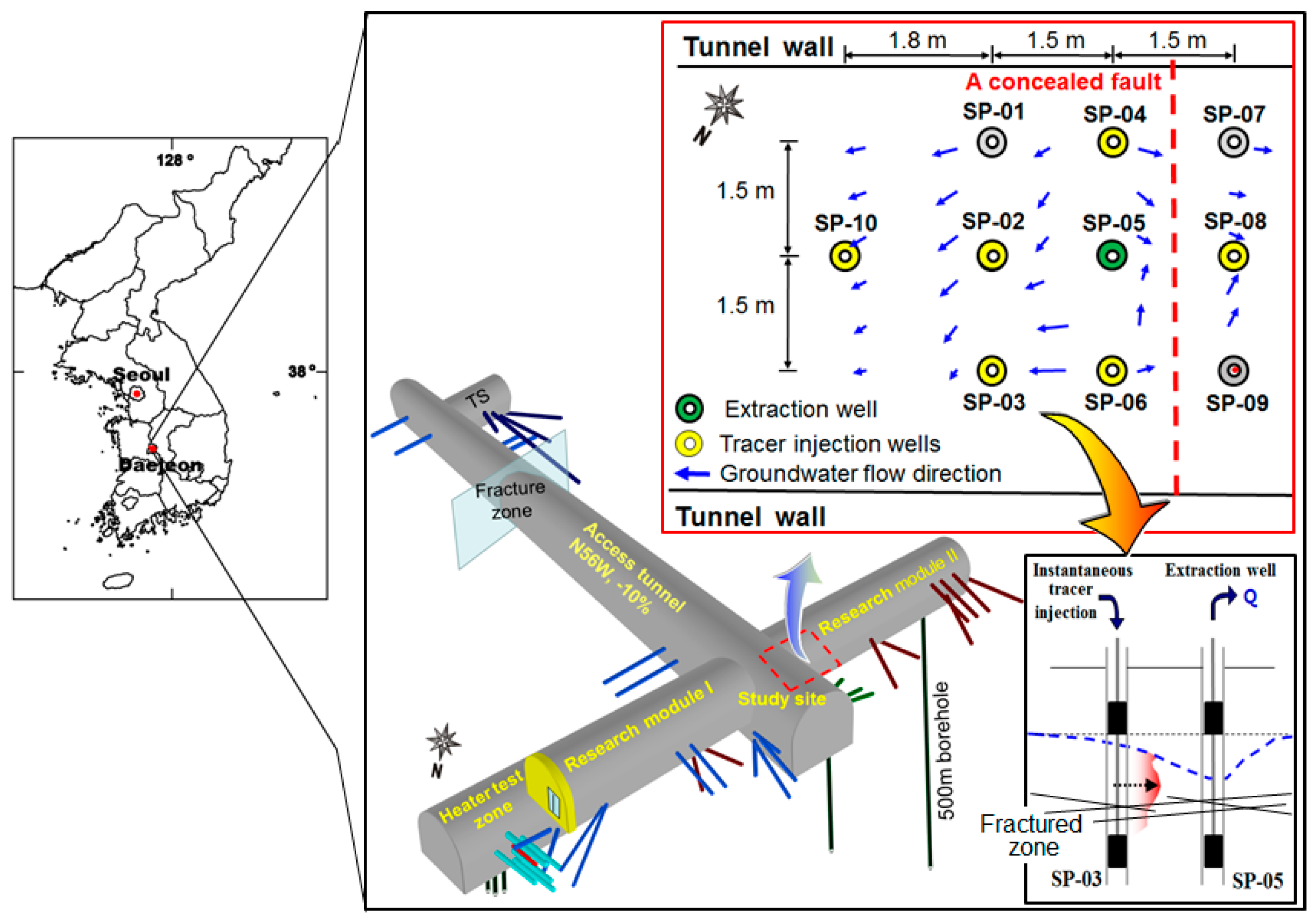
2.1. Field Site
2.2. Hydraulic Characteristics
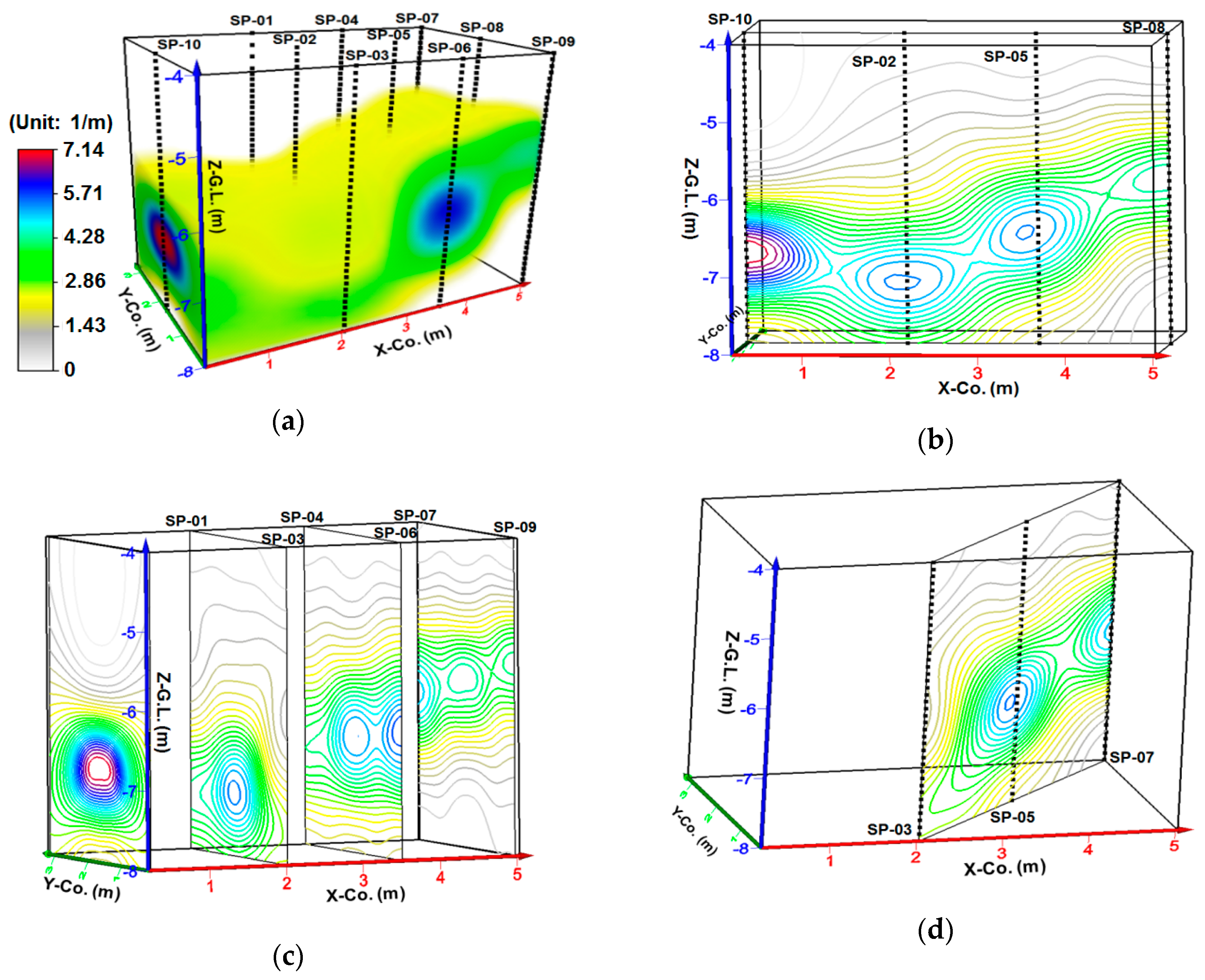
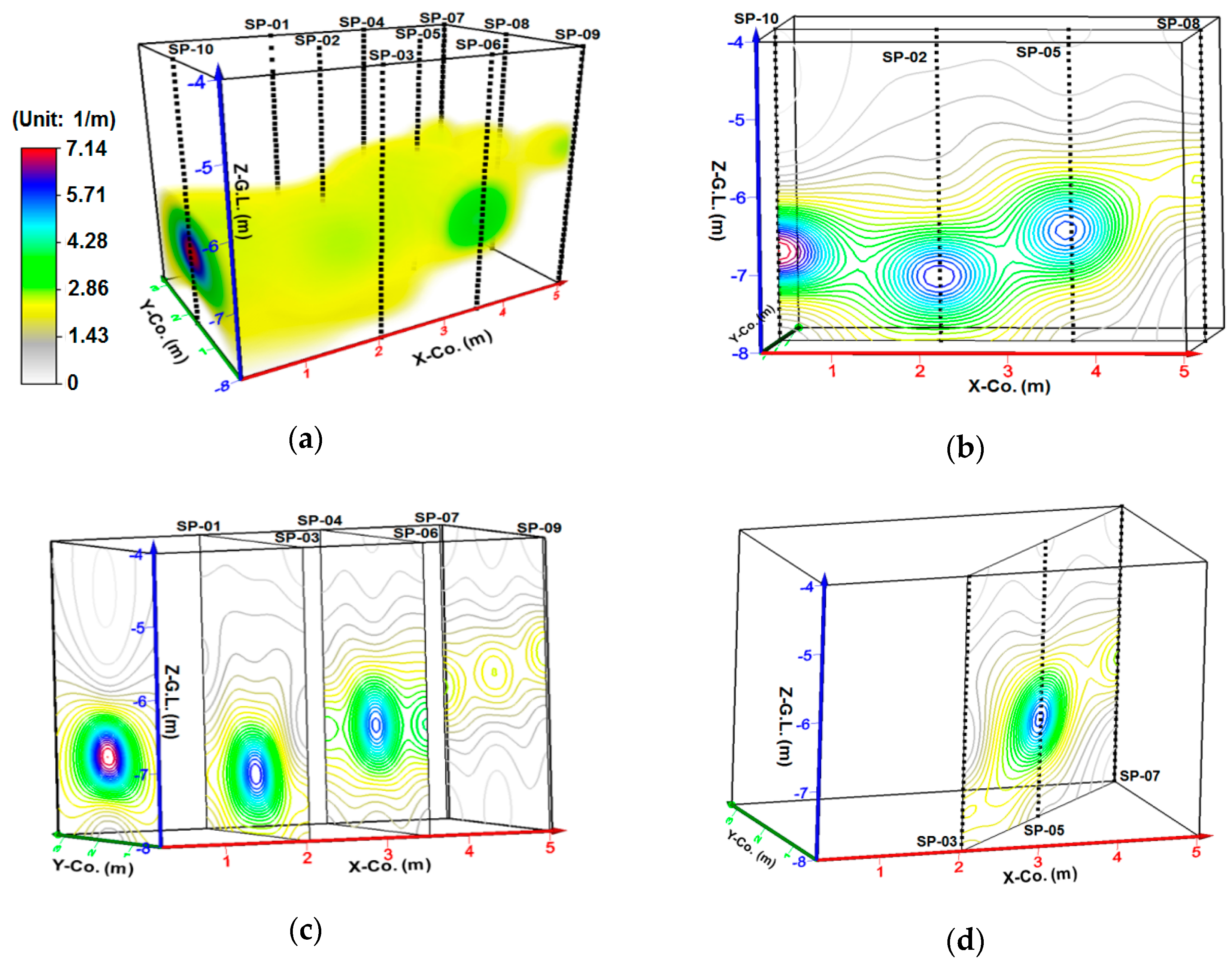
2.3. Aquifer Characteristics
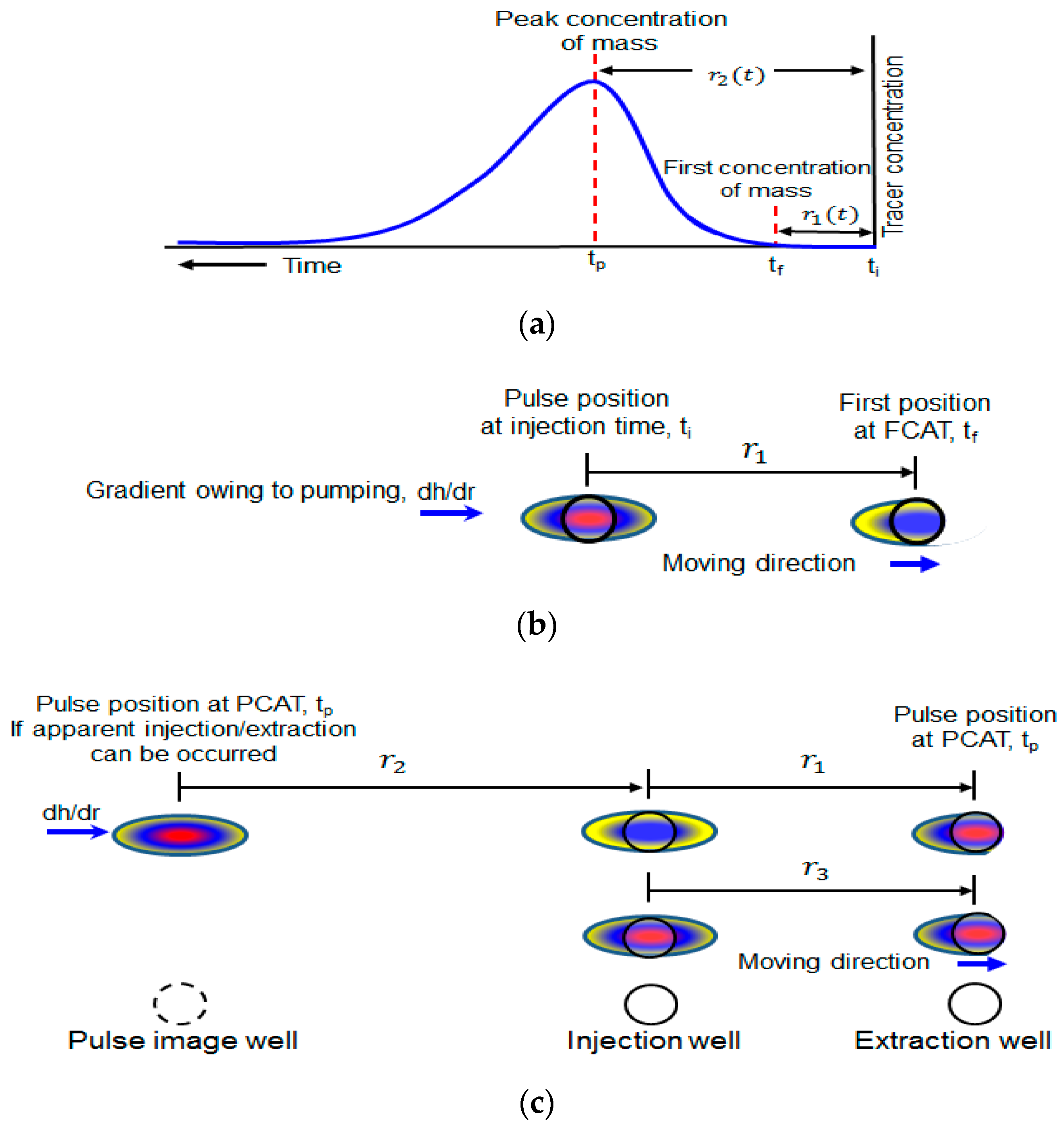
3. Theory and Experiment
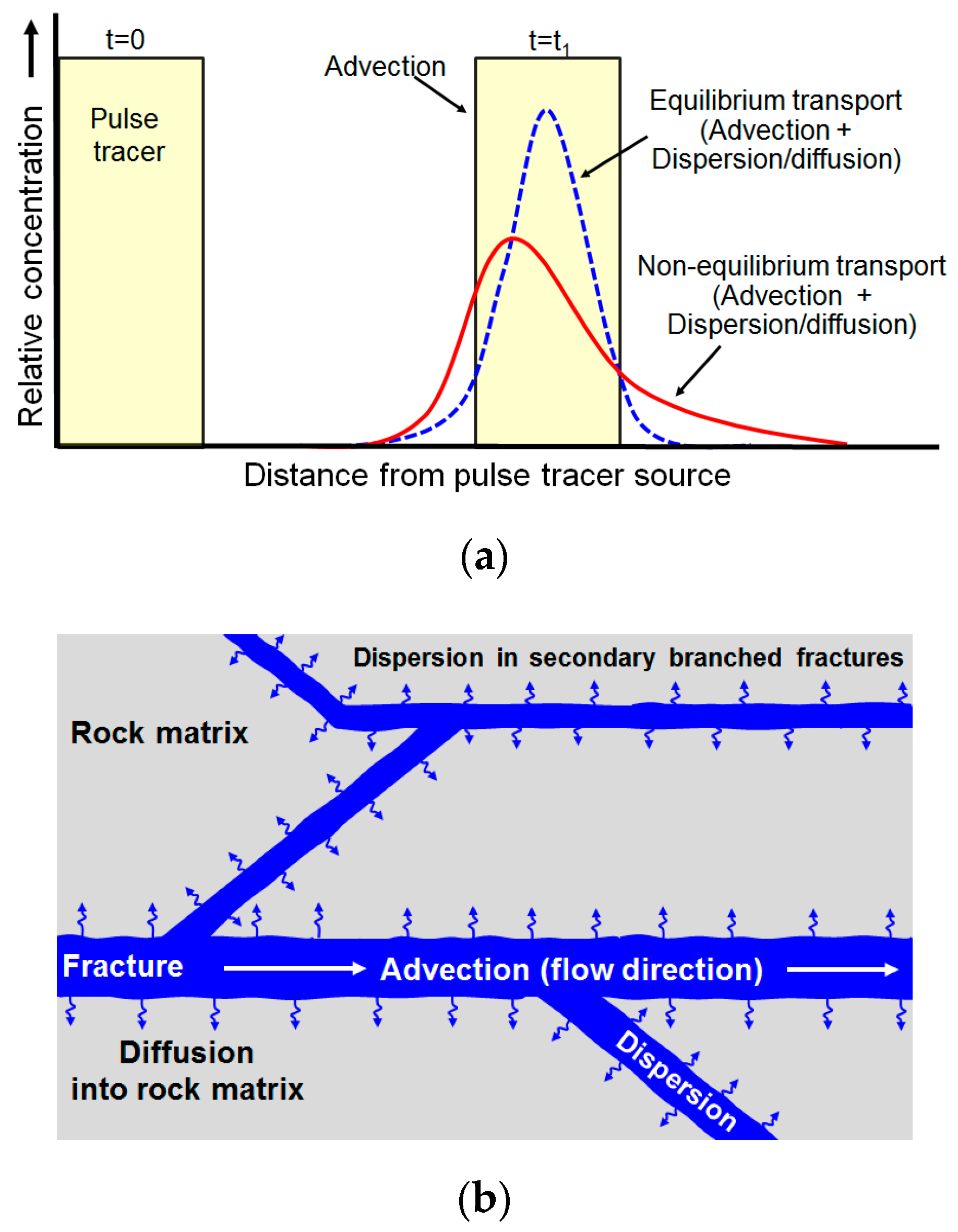
3.1. Overview
3.2. Modified Method
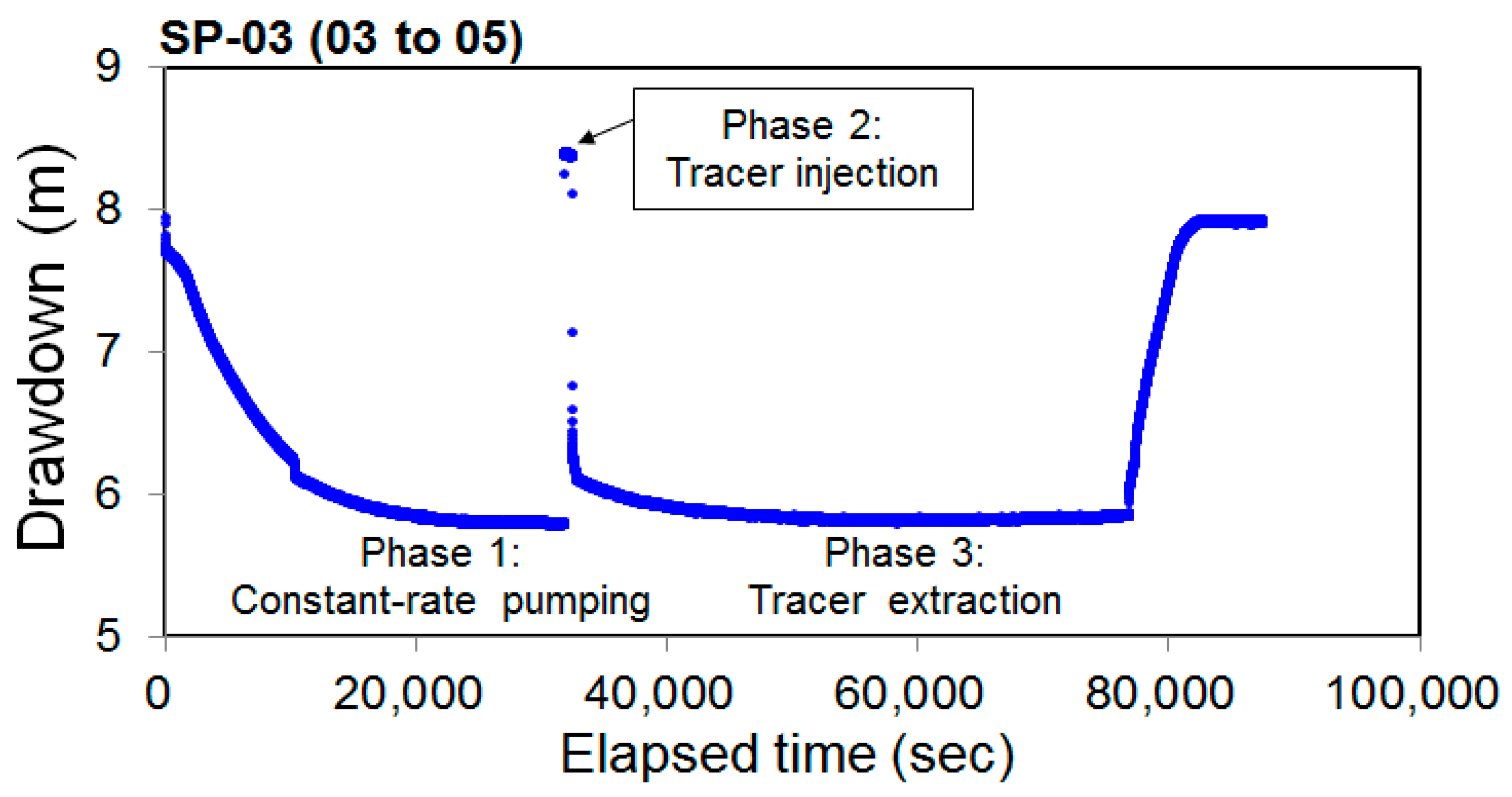
3.3. Experimental Methods
3.3.1. Convergent Flow Tracer Test
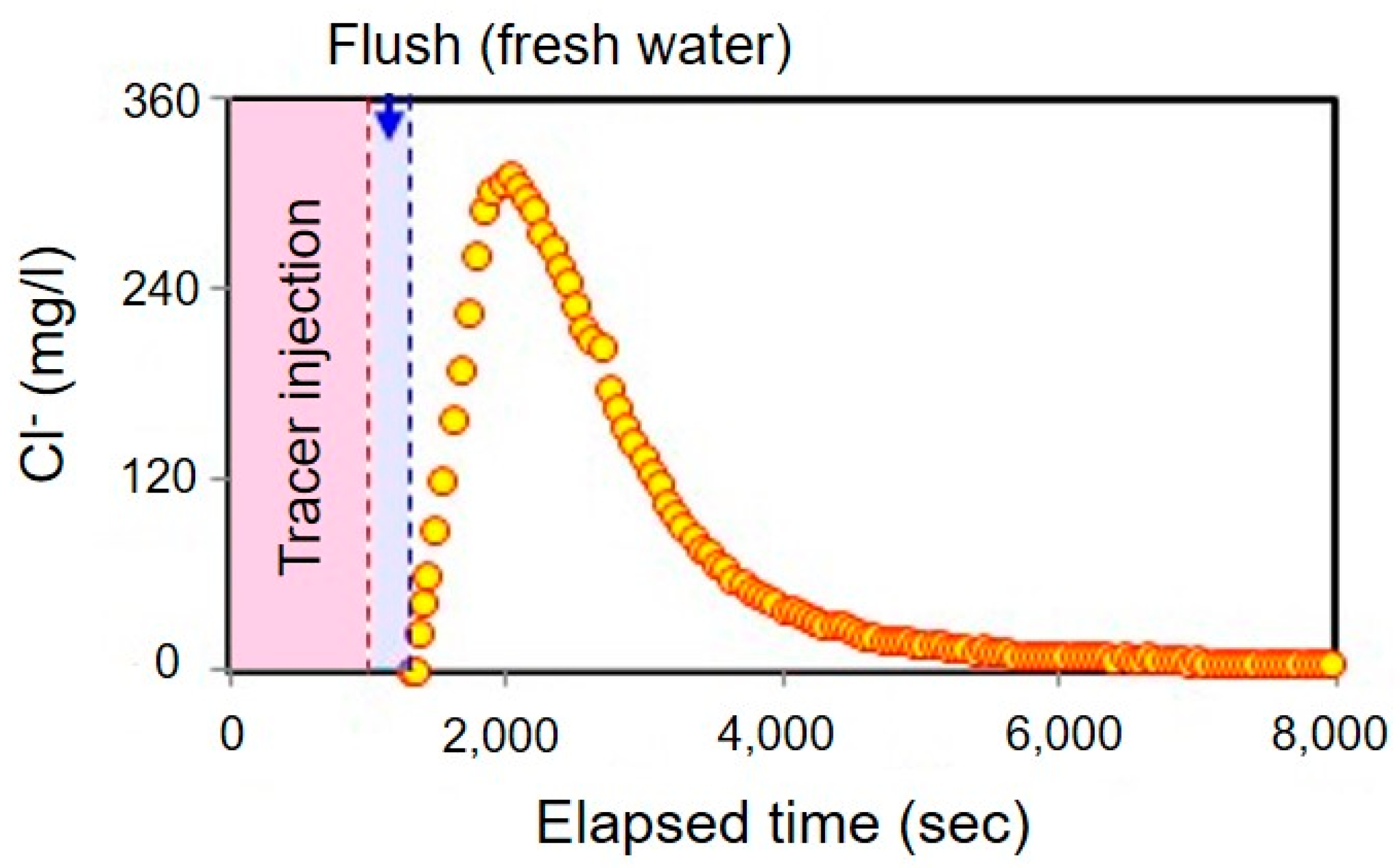
3.3.2. Push-Pull Test
4. Field Results and Interpretation
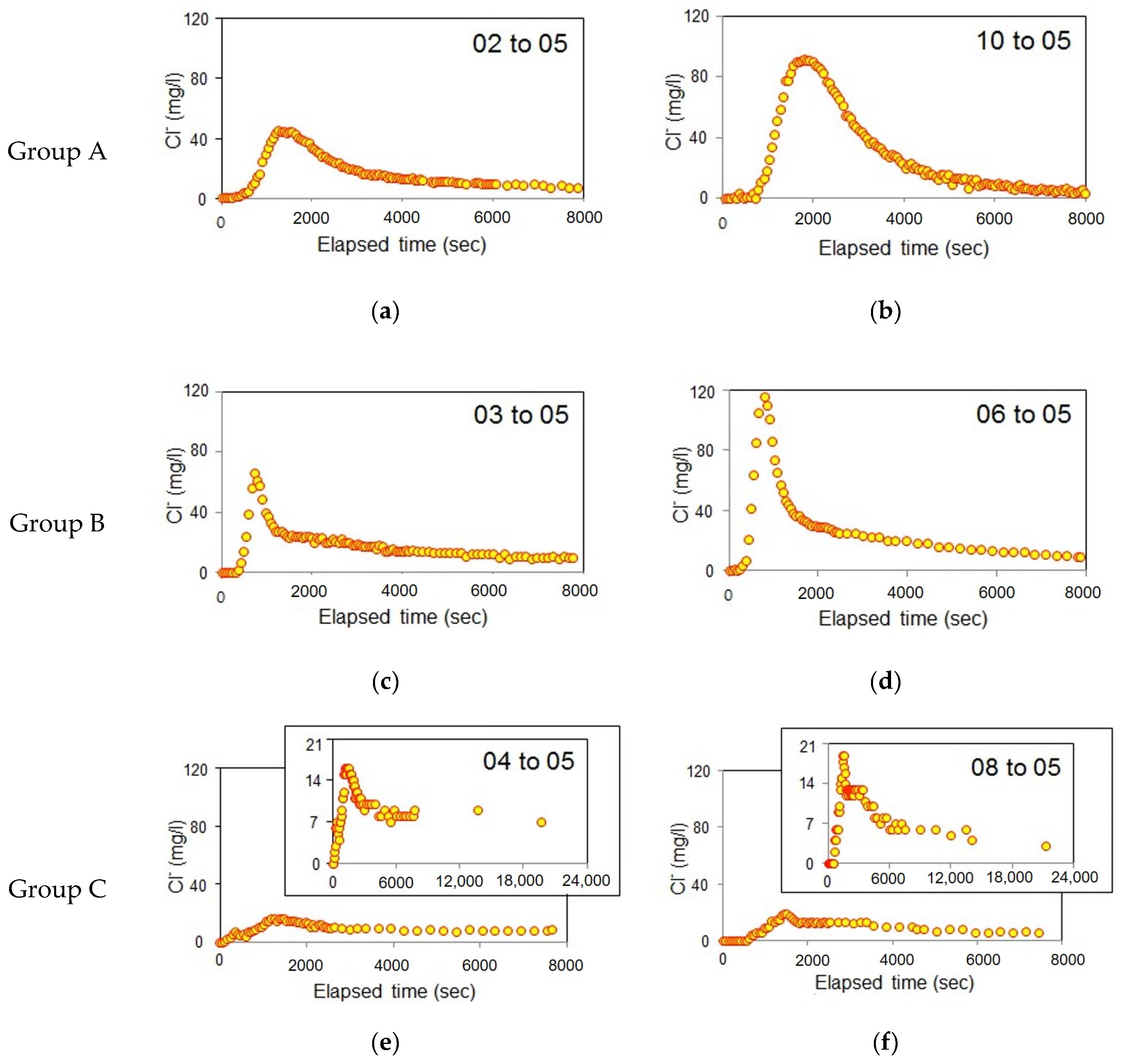
4.1. Analysis of Breakthrough Curves in CFTT and PPT
4.2. Advective and Effective Porosity
4.3. Comparative Analysis of Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Worthington, S.R.H. Diagnostic tests for conceptualizing transport in bedrock aquifers. J. Hydrol. 2015, 529, 365–372. [Google Scholar] [CrossRef]
- Brkić, Ž.; Mladen Kuhta, M.; Hunjak, T. Groundwater flow mechanism in the well-developed karst aquifer system in the western Croatia: Insights from spring discharge and water isotopes. CATENA 2018, 161, 14–26. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon; Saraswati Press: Paris, France, 1856; p. 647. [Google Scholar]
- Leap, D.I.; Kaplan, P.G.A. Single-well tracing method for estimating regional advective velocity in a confined aquifer: Theory and preliminary laboratory verification. Water Resour. Res. 1988, 24, 993–998. [Google Scholar] [CrossRef]
- Hall, S.H.; Luttrell, S.P.; Cronin, W.E. A method for Estimating Effective Porosity and Ground-Water Velocity. Ground Water 1991, 29, 171–174. [Google Scholar] [CrossRef]
- Stephens, D.B.; Hsu, K.-C.; Prieksat, M.A.; Ankeny, M.D.; Blandford, N.; Roth, T.L.; Kelsey, J.A.; Whitworth, J.R. A comparison of estimated and calculated effective porosity. Hydrogeol. J. 1998, 6, 156–165. [Google Scholar] [CrossRef]
- Fernàndez-Garcia, D.; Sànchez-Vila, X.; Illangasekare, T.H. Convergent-flow tracer tests in heterogeneous media: Combined experimental-numerical analysis for determination of equivalent transport parameters. J. Contam. Hydrol. 2002, 57, 129–145. [Google Scholar]
- Neuman, S.P. On the tensorial nature of advective porosity. Adv. Water Resour. 2005, 28, 149–159. [Google Scholar] [CrossRef]
- Lee, S.Y.; Bail, M.-H.; Cho, W.J.; Hahn, P.-S. Rock weathering and geochemical characteristics in the KURT. J. Korean Radioact. Waste Soc. 2006, 4, 321–328. [Google Scholar]
- Kim, G.Y.; Koh, Y.K.; Bae, D.S.; Kim, C.S. Mineralogical characteristics of fracture-filling minerals from the deep borehole in the Yuseong area for the radioactive waste disposal project. J. Miner. Soc. Korea 2004, 17, 99–114. [Google Scholar]
- Barker, J.A. A generalized radial flow model for hydraulic tests in fractured rock. Water Resour. Res. 1988, 24, 1796–1804. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Kitanidis, P.K. Applicability of the Dual-domain Model to Nonaggregated Porous Media. Ground Water 2012, 50, 927–934. [Google Scholar] [CrossRef] [PubMed]
- Hauns, M.; Jeannin, P.-Y.; Atteia, O. Dispersion, retardation and scale effect in tracer breakthrough curves in karst conduits. J. Hydrol. 2001, 241, 177–193. [Google Scholar] [CrossRef]
- Becker, M.W.; Shapiro, A.M. Tracer transport in fractured crystalline rock: Evidence of nondiffusive breakthrough tailing. Water Resour. Res. 2000, 36, 1677–1686. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, A.; Makita, H.; Niibori, Y.; Fomin, S.A.; Chugunov, V.A.; Hashida, T. Characterization of tracer responses using fractional derivative-based mathematical model and its application to prediction of mass transport in fractured reservoirs. GRC Trans. 2012, 36, 1391–1396. [Google Scholar]
- Zlotnik, V.A.; Logan, J.D. Boundary conditions for convergent radial tracer tests and effect of well bore mixing volume. Water Resour. Res. 1996, 32, 2323–2328. [Google Scholar] [CrossRef] [Green Version]
- Hoehn, E.; Roberts, P.V. Advection-Dispersion Interpretation of Tracer Observations in an Aquifer. Ground Water 1982, 20, 457–465. [Google Scholar] [CrossRef]
- Maloszewski, P.; Zuber, A. Tracer experiments in fractured rocks—Matrix diffusion and the validity of models. Water Resour. Res. 1993, 29, 2723–2735. [Google Scholar] [CrossRef]
- Taylor, G.I. Dispersion of soluble matter in solvent flowing slowly through a tube. P. Roy. Soc. A-Math. Phy. 1953, A219, 186–203. [Google Scholar]
- John, A.K.; Lake, L.W.; Bryant, S.L.; Jennings, J.W. Investigation of Field Scale Dispersion. Soc. Petrol. Eng. 2008, 1–19. [Google Scholar] [CrossRef]
- Rossier, Y.; Kiraly, L. Effect de la dilution sur la dé determination des dispervisites par interprétation des essais de tracage dans les aquifers. Bull. Du Centre D’hydrogéol. De Neuchâtel 1992, 11, 1–15. [Google Scholar]
- Liedtke, L.; Götschenberg, A.; Jobmann, M.; Siemering, W. Observations of Tracer Behaviour in Micro-Fissures and Fractures as well as Numerical Transport were Made in Grimsel Hard Rock Laboratory: BOHRLOCHKRANZVERSUCH Experimentelle und Numerische Untersuchungen zum Stoff Transport in Geklüftetem Fels; Technischer Bericht 94-02; Nationale Genossenschaft für die Lagerung Radioaktiver Abfälle, Bundesanstalt tür Geowissenschaften und Rohstoffe: Hannover, Germany, 1994; p. 197. [Google Scholar]
- Haggerty, R.; Fleming, S.W. Tracer tests in a fractured dolomite: 2. Analysis of mass transfer in single-well injection-withdrawal test. Water Resour. Res. 2001, 37, 1129–1142. [Google Scholar] [CrossRef] [Green Version]
- Callahan, T.J.; Reimus, P.W. Using multiple experimental methods to determine fracture/matrix interactions and dispersion of nonreactive solutes in saturated volcanic tuff. Water Resour. Res. 2000, 36, 3547–3558. [Google Scholar] [CrossRef] [Green Version]
- Rubin, Y.; Ezzedine, S. The travel times of solutes at the Cape Cod Tracer Experiment: Data analysis, modeling, and structural parameters inference. Water Resour. Res. 1997, 33, 1537–1547. [Google Scholar] [CrossRef]
- Niemann, W.L.; Rovey, C.W., II. Comparison of Hydraulic Conductivity Values Obtained from Aquifer Pumping Tests and Conservative Tracer Tests. Ground Water Monit. Remed. 2000, 20, 122–128. [Google Scholar] [CrossRef]
- Gaspar, E.; Oncescu, M. Radioactive Tracers in Hydrology; Elsevier: New York, NY, USA, 1972. [Google Scholar]
- Domenico, P.A.; Schwartz, F.W. Physical and Chemical Hydrogeology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1998; p. 506. [Google Scholar]
- Kang, D.H.; Chung, S.Y.; Kim, B.W. The characteristics of hydrodynamic dispersion in a horizontally heterogeneous fractured rock through single well injection withdrawal tracer tests. J. Soil Groundw. Environ. 2006, 11, 53–60. [Google Scholar]
- Kim, B.-W.; Koh, Y.-K.; Park, K.-W.; Ji, S.-H.; Ryu, J.-H.; Jeong, H.Y. A Modified Two-Well Tracing Method for Advective Velocity and Effective Porosity from Single-Well Tracing Method; KAERI Report No. KAERI/TR-6342/2016, Technical Report; KAERI: Daejeon, Korea, 2016; pp. 1–52. [Google Scholar]



| Well ID | Separation Distance (m) | Q (m3/s) | K (m/s) | b (m) | I | Note |
|---|---|---|---|---|---|---|
| 02 to 05 | 1.50 | 1.18 × 10−5 | 2.17 × 10−6 | 1.12 | 0.31 | Two-well test |
| 03 to 05 | 2.21 | 1.18 × 10−5 | 2.27 × 10−6 | 1.12 | 0.28 | Two-well test |
| 04 to 05 | 1.50 | 1.18 × 10−5 | 3.38 × 10−6 | 1.12 | 0.28 | Two-well test |
| 05 to 05 | 0 | 1.18 × 10−5 | 2.17 × 10−6 | 1.12 | 0.14 | Single well test |
| 06 to 05 | 1.50 | 1.17 × 10−5 | 3.08 × 10−6 | 1.12 | 0.30 | Two-well test |
| 08 to 05 | 1.50 | 1.18 × 10−5 | 3.67 × 10−6 | 1.12 | 0.31 | Two-well test |
| 10 to 05 | 3.33 | 1.18 × 10−5 | 2.24 × 10−6 | 1.12 | 0.16 | Two-well test |
| Well ID | Fractures (1) | Permeability Fractures | Well ID | Fractures (1) | Permeability Fractures |
|---|---|---|---|---|---|
| SP-01 | 2.68 | 0.89 | SP-06 | 5.36 | 2.68 |
| SP-02 | 4.46 | 4.46 | SP-07 | 4.46 | 1.79 |
| SP-03 | 2.68 | 1.79 | SP-08 | 4.46 | 1.79 |
| SP-04 | 2.68 | 1.79 | SP-09 | 3.57 | 1.79 |
| SP-05 | 4.46 | 4.46 | SP-10 | 7.14 | 5.36 |
| Well ID | Separation Distance (m) | Accumulative Recovery Rate of Tracer (%) | Note |
|---|---|---|---|
| 02 to 05 | 1.50 | 92.83 | CFTT |
| 03 to 05 | 2.21 | 77.01 | CFTT |
| 04 to 05 | 1.50 | 88.64 | CFTT |
| 06 to 05 | 1.50 | 90.98 | CFTT |
| 08 to 05 | 1.50 | 96.25 | CFTT |
| 10 to 05 | 3.33 | 91.06 | CFTT |
| Type of Tests | Convergent Flow Tracer Tests | Push-Pull Test | ||||||
|---|---|---|---|---|---|---|---|---|
| Trial Well (SP) | 02 to 05 | 03 to 05 | 04 to 05 | 06 to 05 | 08 to 05 | 10 to 05 | 05 | |
| Travel Time (s) | FCAT | 300 | 360 | 180 | 210 | 570 | 480 | 1535 |
| P | 1260 | 720 | 1200 | 720 | 1440 | 1800 | 1192 | |
| E (1) | 1560 | 1080 | 1380 | 930 | 2010 | 2280 | 2637 | |
| (m/s) | 2.6 × | 3.3 × | 2.2 × | 3.0 × | 1.0 × | 3.3 × | 2.4 × | |
| 2.6 × | 1.9 × | 4.3 × | 3.1 × | 1.1 × | 3.6 × | 1.3 × | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, B.-W.; Lee, H. Modified Convergent Flow Tracing Method for Evaluating Advective Velocity and Effective Porosity in Fractured Rock Aquifers. Water 2020, 12, 3565. https://doi.org/10.3390/w12123565
Kim B-W, Lee H. Modified Convergent Flow Tracing Method for Evaluating Advective Velocity and Effective Porosity in Fractured Rock Aquifers. Water. 2020; 12(12):3565. https://doi.org/10.3390/w12123565
Chicago/Turabian StyleKim, Byung-Woo, and Hangbok Lee. 2020. "Modified Convergent Flow Tracing Method for Evaluating Advective Velocity and Effective Porosity in Fractured Rock Aquifers" Water 12, no. 12: 3565. https://doi.org/10.3390/w12123565




