Sediment Bed Borehole Advection Method
Abstract
:1. Introduction
2. Materials and Methods
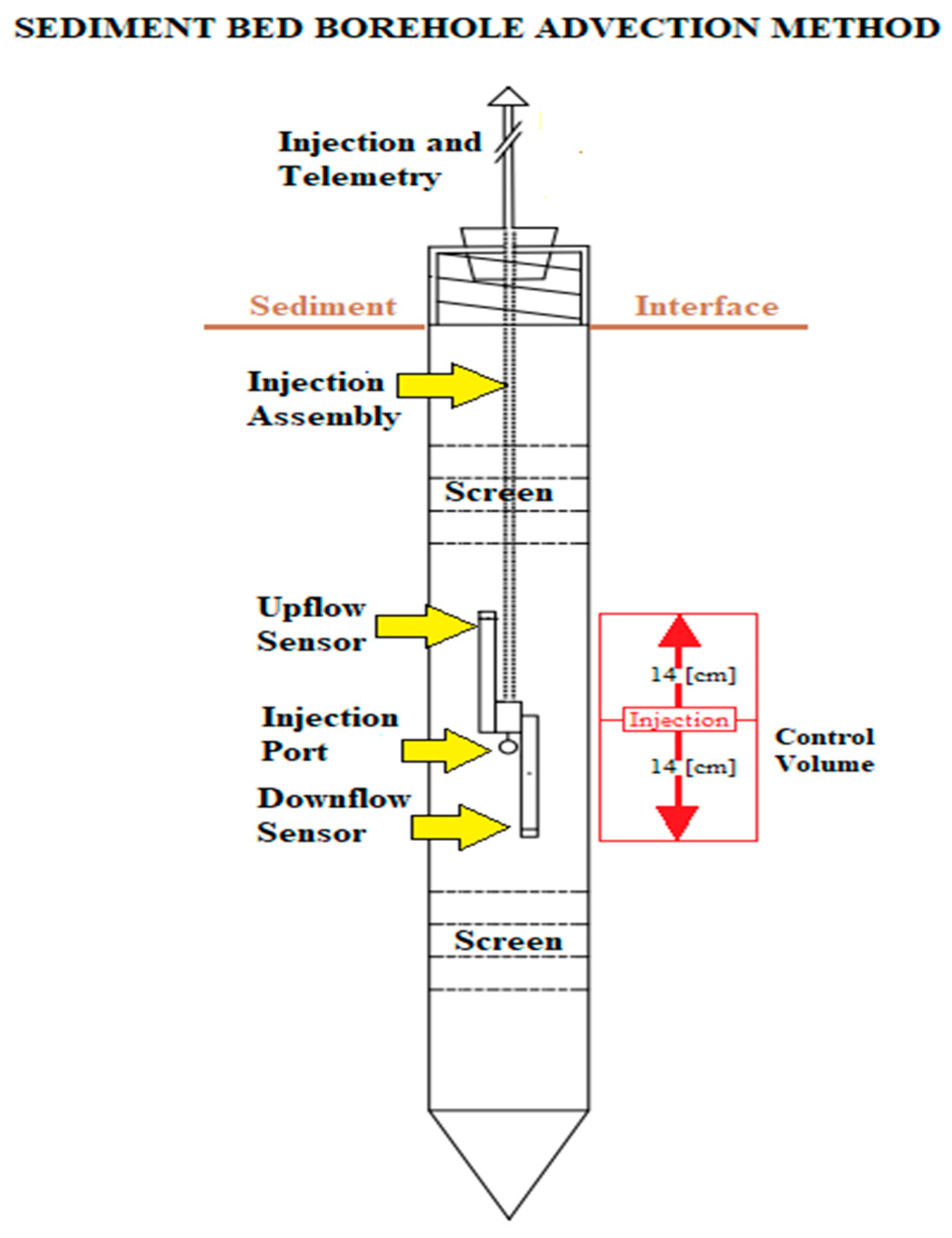
2.1. Design
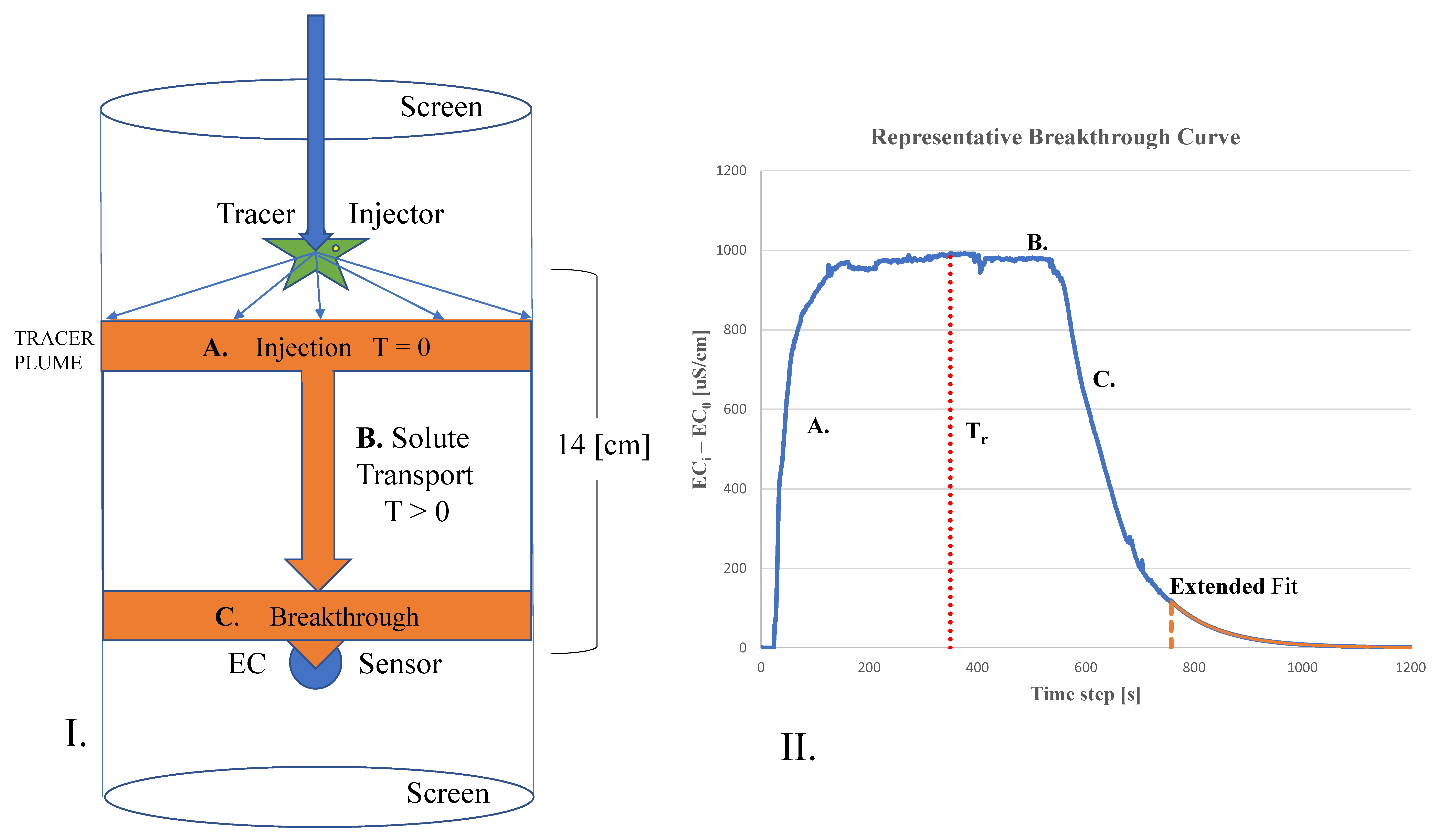
2.2. Theory and Operation
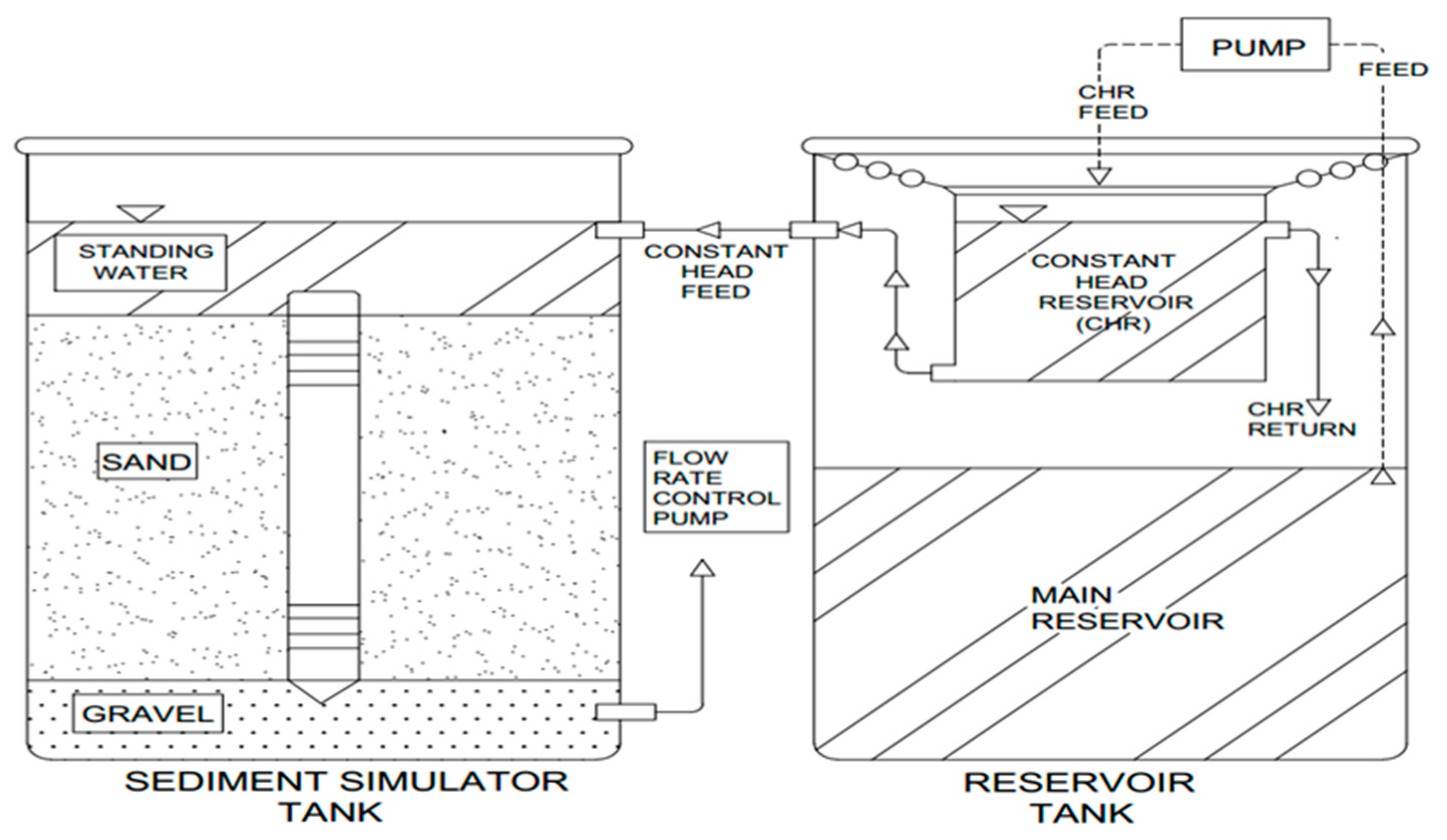
2.3. Sand Tank Experimental Design
2.4. Simulator Media
2.5. Test Protocol
2.6. Tracer Concentration and Volume
2.7. Data Collection
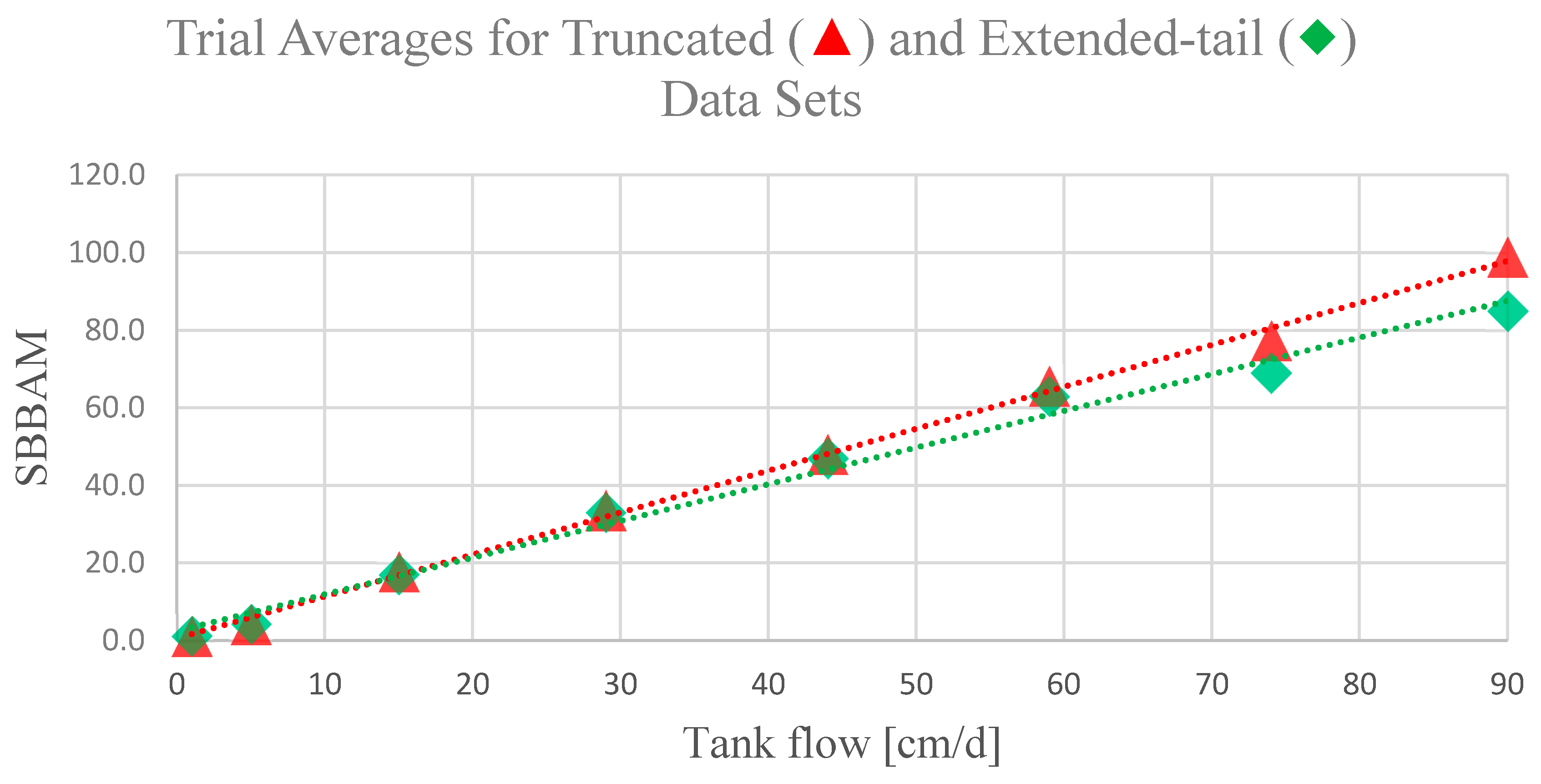
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Krause, S.; Hannah, D.M.; Fleckenstein, J.H.; Heppell, C.M.; Kaeser, D.; Pickup, R.W.; Pinay, G.; Robertson, A.L.; Wood, P.J. Inter-disciplinary perspectives on processes in the hyporheic zone. Ecohydrology 2011, 4, 481–499. [Google Scholar] [CrossRef] [Green Version]
- Winter, T.; Harvey, J.; Franke, O.; Alley, W. Groundwater and Surface Water: A Single Resource. In Circular; U.S. Geological Survey: Reston, VA, USA, 1999; p. 1139. [Google Scholar]
- Sophocleous, M. Interactions between groundwater and surface water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Layton, L.; Klammler, H.; Hatfield, K.; Cho, J.; Newman, M.; Annable, M.D. Development of a passive sensor for measuring vertical cumulative water and solute mass fluxes in lake sediments and streambeds. Adv. Water Resour. 2017, 105, 1–12. [Google Scholar] [CrossRef]
- Brodie, R.S.; Baskaran, S.; Ransley, T.; Spring, J. Seepage meter: Progressing a simple method of directly measuring water flow between surface water and groundwater systems. Aust. J. Earth Sci. 2009, 56, 3–11. [Google Scholar] [CrossRef]
- Belanger, T.V.; Montgomery, M.T. Seepage meter errors. Limnol. Oceanogr. 1992, 37, 1787–1795. [Google Scholar] [CrossRef]
- Kaleris, V. Quantifying the exchange rate between groundwater and small streams. J. Hydraul. Res. 1998, 36, 913–932. [Google Scholar] [CrossRef]
- Murdoch, L.C.; Kelly, S.E. Factors affecting the performance of conventional seepage meters. Water Resour. Res. 2003, 39, 1163. [Google Scholar] [CrossRef]
- Kennedy, C.D.; Murdoch, L.C.; Genereux, D.P.; Corbett, D.R.; Stone, K.; Pham, P.; Mitasova, H. Comparison of Darcian flux calculations and seepage meter measurements in a sandy streambed in North Carolina, United States. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Rau, G.C.; Andersen, M.S.; McCallum, A.M.; Roshan, H.; Acworth, R.I. Heat as a tracer to quantify water flow in near-surface sediments. Earth-Sci. Rev. 2014, 129, 40–58. [Google Scholar] [CrossRef] [Green Version]
- Silliman, S.E.; Booth, D.F. Analysis of time-series measurements of sediment temperature for identification of gaining vs. losing portions of Juday Creek, Indiana. J. Hydrol. 1993, 146, 131–148. [Google Scholar] [CrossRef]
- Rudnick, S.; Lewandowski, J.; Nutzmann, G. Estimation of lacustrine groundwater discharge using heat as a tracer and vertical hydraulic gradients—A comparison. Proc. Int. Assoc. Hydrol. Sci. 2015, 365, 79–84. [Google Scholar] [CrossRef] [Green Version]
- Healy, R.W.; Winter, T.C.; LaBaugh, J.W.; Franke, O.L. Water Budgets: Foundations for Effective Water-Resources and Environmental Management. In Circular; US Geological Survey: Reston, VA, USA, 2007. [Google Scholar]
- Kunz, J.V.; Annable, M.D.; Cho, J.; Von Tümpling, W.; Hatfield, K.; Rao, S.; Borchardt, D.; Rode, M. Quantifying nutrient fluxes with a new hyporheic passive flux meter (HPFM). Biogeosciences 2017, 14, 631–649. [Google Scholar] [CrossRef]
- Hatfield, K.; Annable, M.; Cho, J.; Rao, P.S.C.; Klammler, H. A direct passive method for measuring water and contaminant fluxes in porous media. J. Contam. Hydrol. 2004, 75, 155–181. [Google Scholar] [CrossRef]
- Annable, M.D.; Hatfield, K.; Cho, J.; Klammler, H.; Parker, B.L.; Cherry, J.A.; Rao, P.S.C. Field-Scale Evaluation of the Passive Flux Meter for Simultaneous Measurement of Groundwater and Contaminant Fluxes. Environ. Sci. Technol. 2005, 39, 7194–7201. [Google Scholar] [CrossRef]
- Freeze, R.; Cherry, J. Groundwater; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Shook, G. A systematic method for tracer test analysis: An example using Beowawe tracer data. In Proceedings of the Thirtieth Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 31 January–2 February 2005. [Google Scholar]
- Drost, W.; Klotz, D.; Koch, A.; Moser, H.; Neumaier, F.; Rauert, W. Point dilution methods of investigating ground water flow by means of radioisotopes. Water Resour. Res. 1968, 4, 125–146. [Google Scholar] [CrossRef]
- Klammler, H.; Hatfield, K.; Nemer, B.; Mathias, S.A. A trigonometric interpolation approach to mixed-type boundary problems associated with permeameter shape factors. Water Resour. Res. 2011, 47, 03510. [Google Scholar] [CrossRef] [Green Version]
- Danckwerts, P. Continuous flow systems. Distribution of residence times. Chem. Eng. Sci. 1953, 2, 1–13. [Google Scholar] [CrossRef]
| TANK | Units | |
|---|---|---|
| Volume | m3/d | 0.21 |
| Height | m | 0.9 |
| Diameter | m | 0.58 |
| Area | m2 | 0.264 |
| Gravel Layer | m | 0.1 |
| Sand Layer | m | 0.54 |
| Standing Water | m | 0.17 |
| SBBAM CASING | ||
| Total Length | cm | 69.5 |
| Outer Dia. (OD) (a) | cm | 6 |
| Inner Dia. (ID) (r) | cm | 5 |
| Screen Length (s) | cm | 5.4 |
| Distance b/w Screens (p) | cm | 36.5 |
| Nominal | Error ± 1-STD | Two-Tail 95% Confidence Interval | Extended-Tail Adj | % Diff | ||
|---|---|---|---|---|---|---|
| cm/day | cm/day | (%) | UB (+) | LB (−) | cm/day | (%) |
| 1 | 1.2 ± 0.4 | 20 ± 30 | 1.8 | 0.6 | * | - |
| 5 | 4.3 ± 1.3 | 14 ± 30 | 6.3 | 2.3 | * | - |
| 15 | 18 ± 3.0 | 19 ± 20 | 22.7 | 13.1 | 17 ± 3 | −5 |
| 29 | 34 ± 3.5 | 16 ± 12 | 39.2 | 28 | 33 ± 3.6 | −2 |
| 44 | 48 ± 2.3 | 9 ± 5 | 53.8 | 42.4 | 47 ± 3.6 | −2 |
| 59 | 66 ± 4.4 | 11 ± 7 | 76.5 | 54.7 | 63 ± 2.7 | −3 |
| 74 | 77 ± 5.4 | 4.6 ± 7 | 86 | 68.8 | 70 ± 3.9 | −11 |
| 90 | 99 ± 9.0 | 10 ± 10 | 113.3 | 84.7 | 85 ± 2.9 | −14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Augustine, S.; Cho, J.; Klammler, H.; Hatfield, K.; Annable, M.D. Sediment Bed Borehole Advection Method. Water 2020, 12, 3380. https://doi.org/10.3390/w12123380
Augustine S, Cho J, Klammler H, Hatfield K, Annable MD. Sediment Bed Borehole Advection Method. Water. 2020; 12(12):3380. https://doi.org/10.3390/w12123380
Chicago/Turabian StyleAugustine, Scott, Jaehyun Cho, Harald Klammler, Kirk Hatfield, and Michael D. Annable. 2020. "Sediment Bed Borehole Advection Method" Water 12, no. 12: 3380. https://doi.org/10.3390/w12123380





