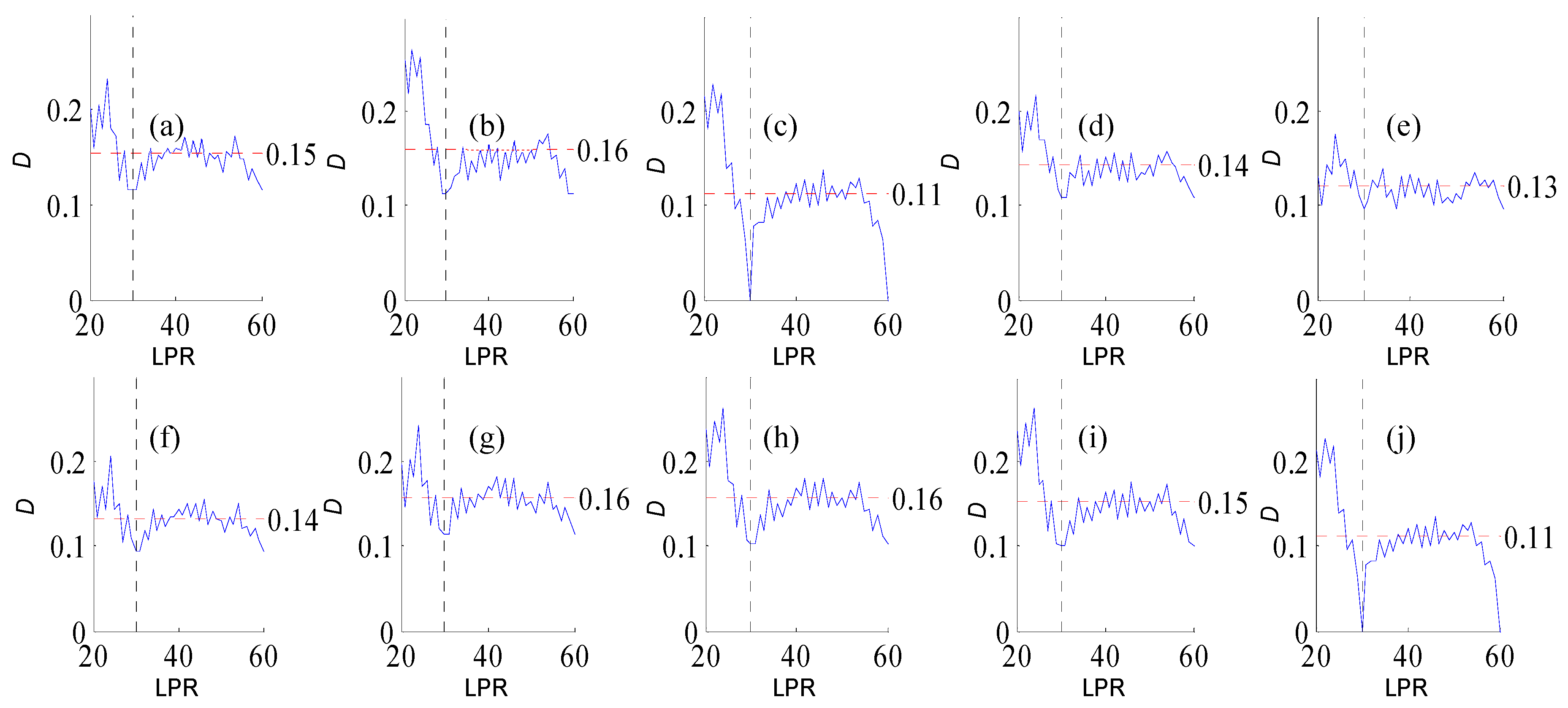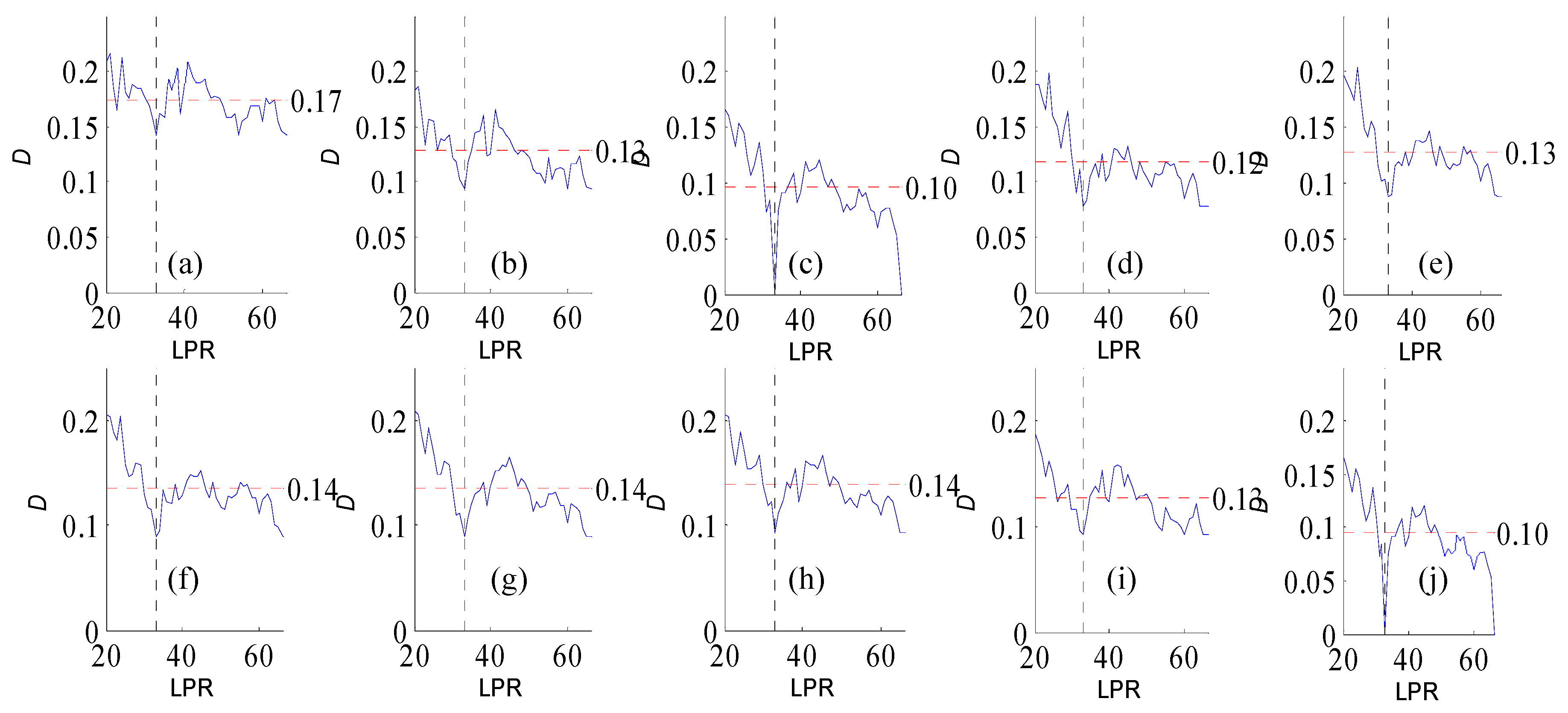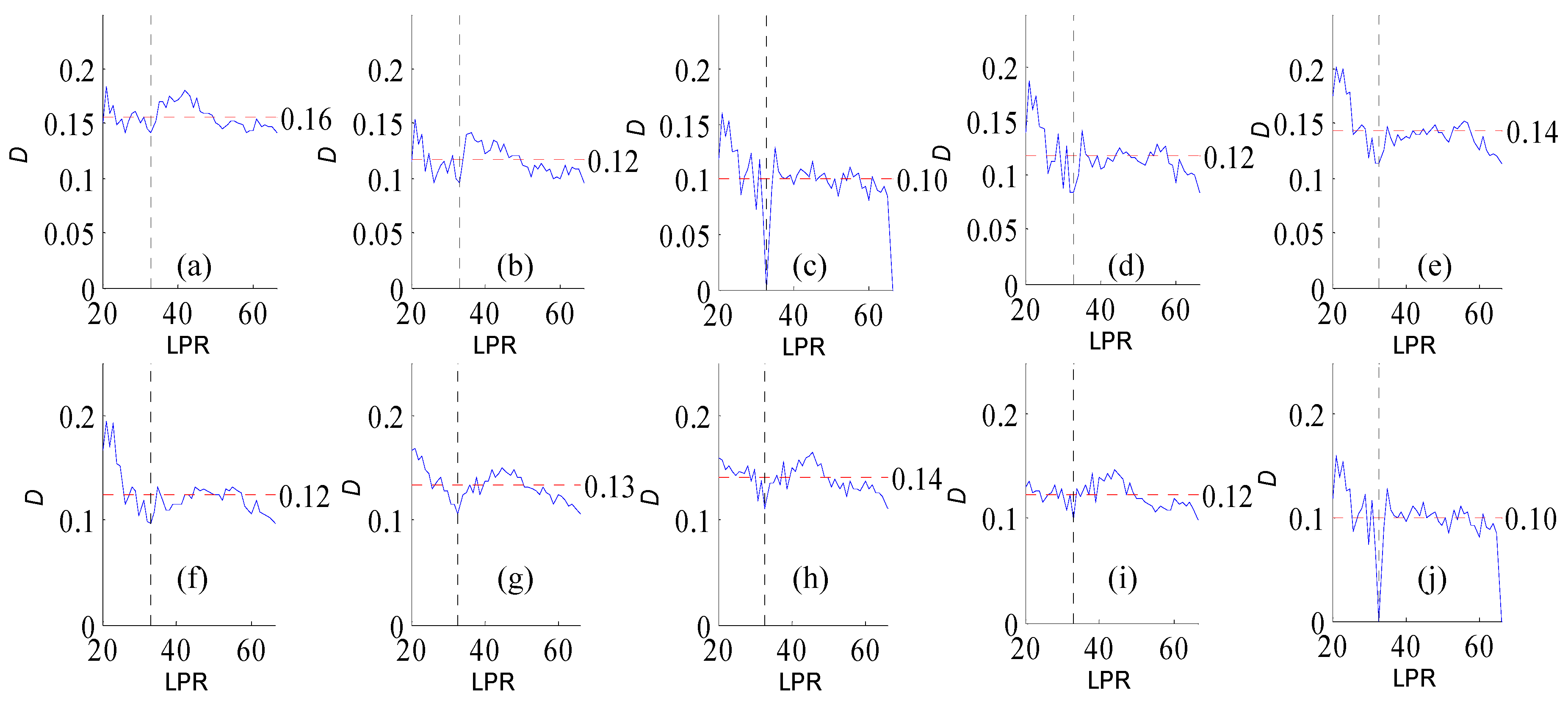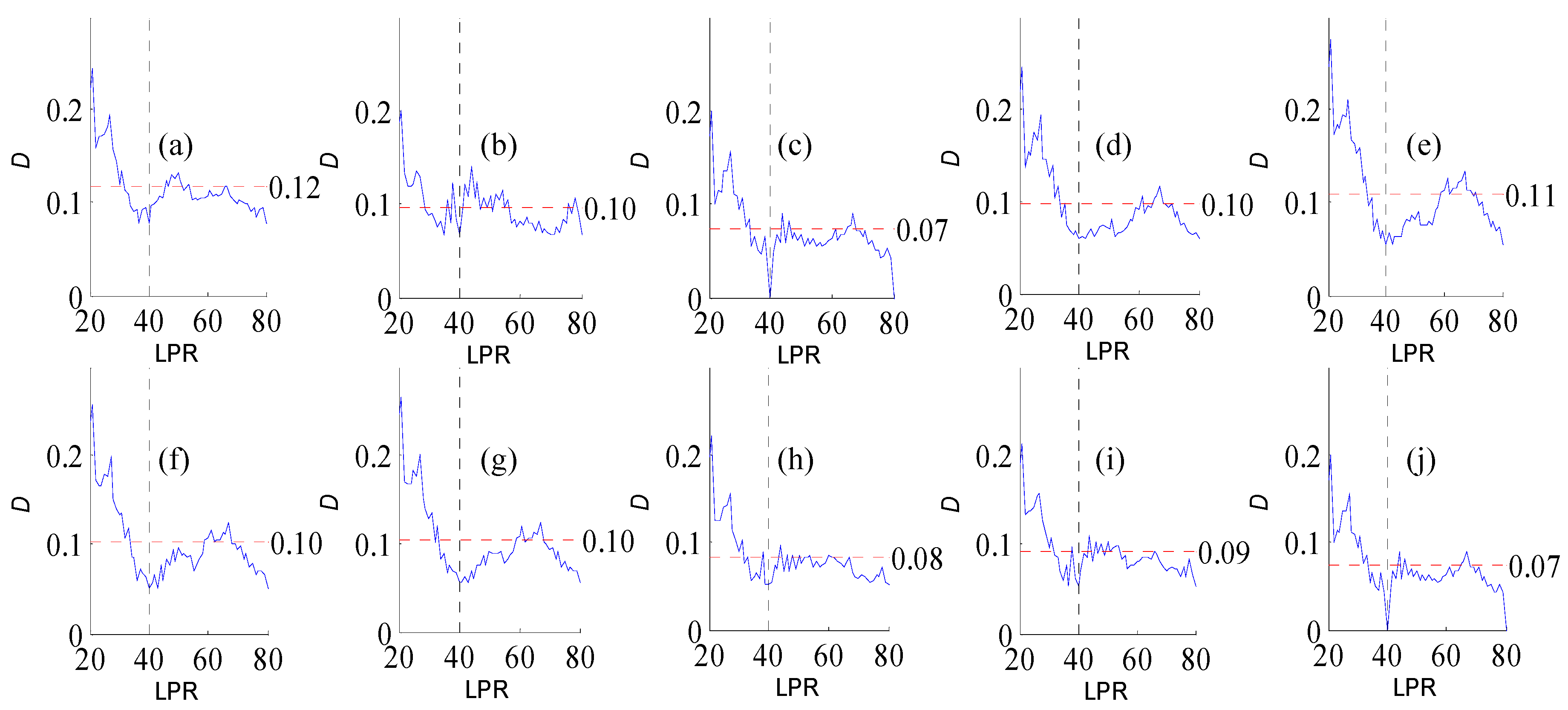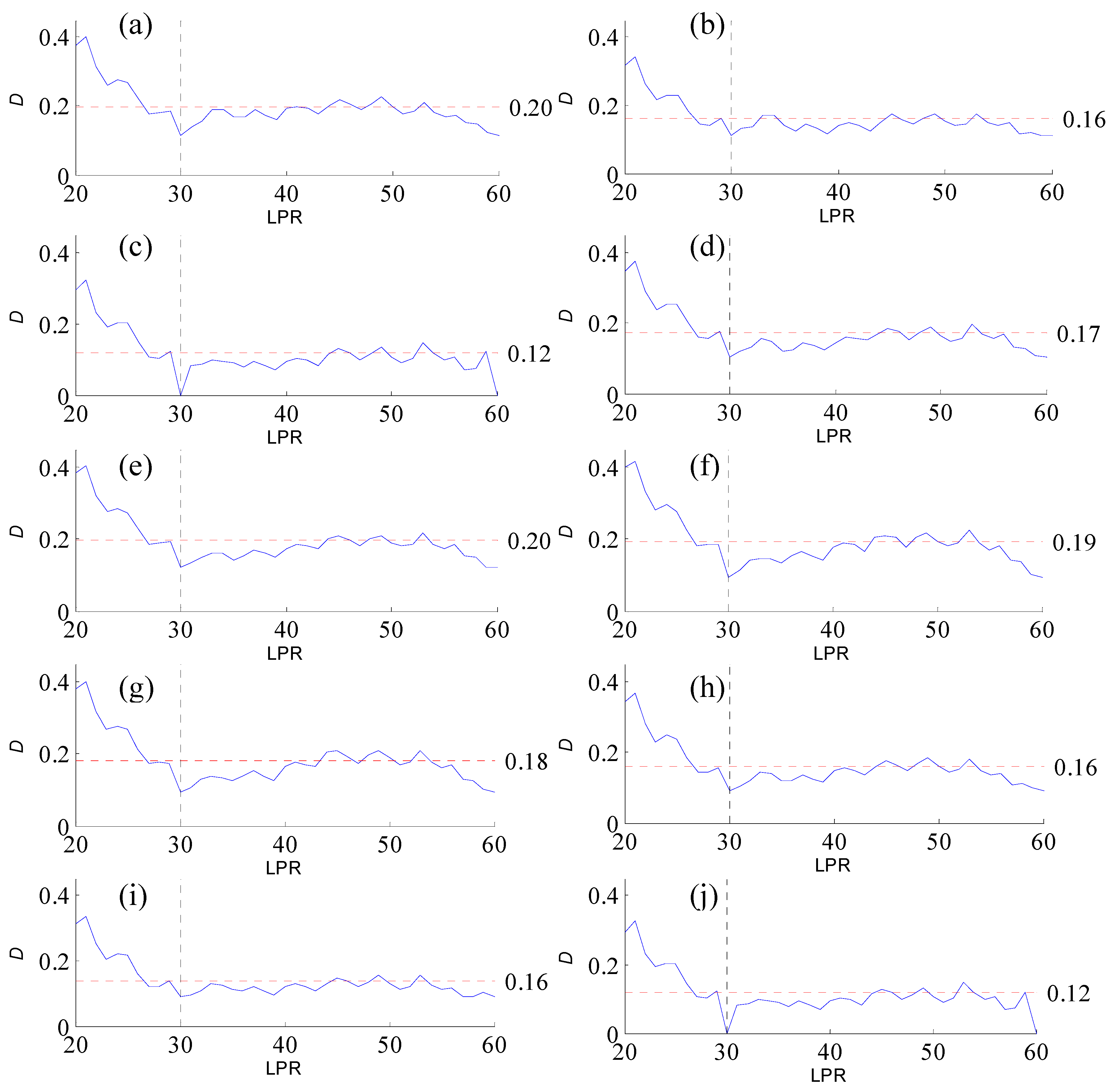Appendix A
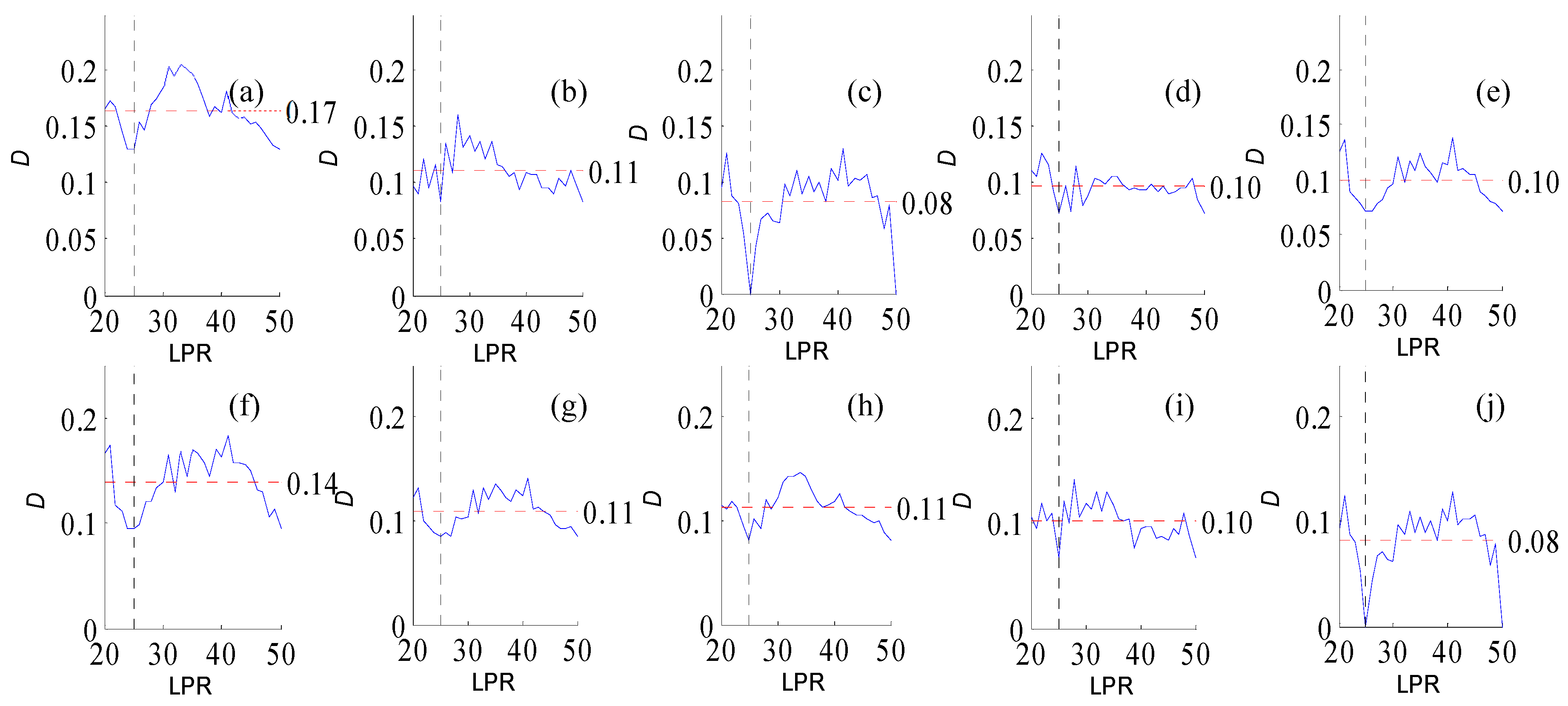
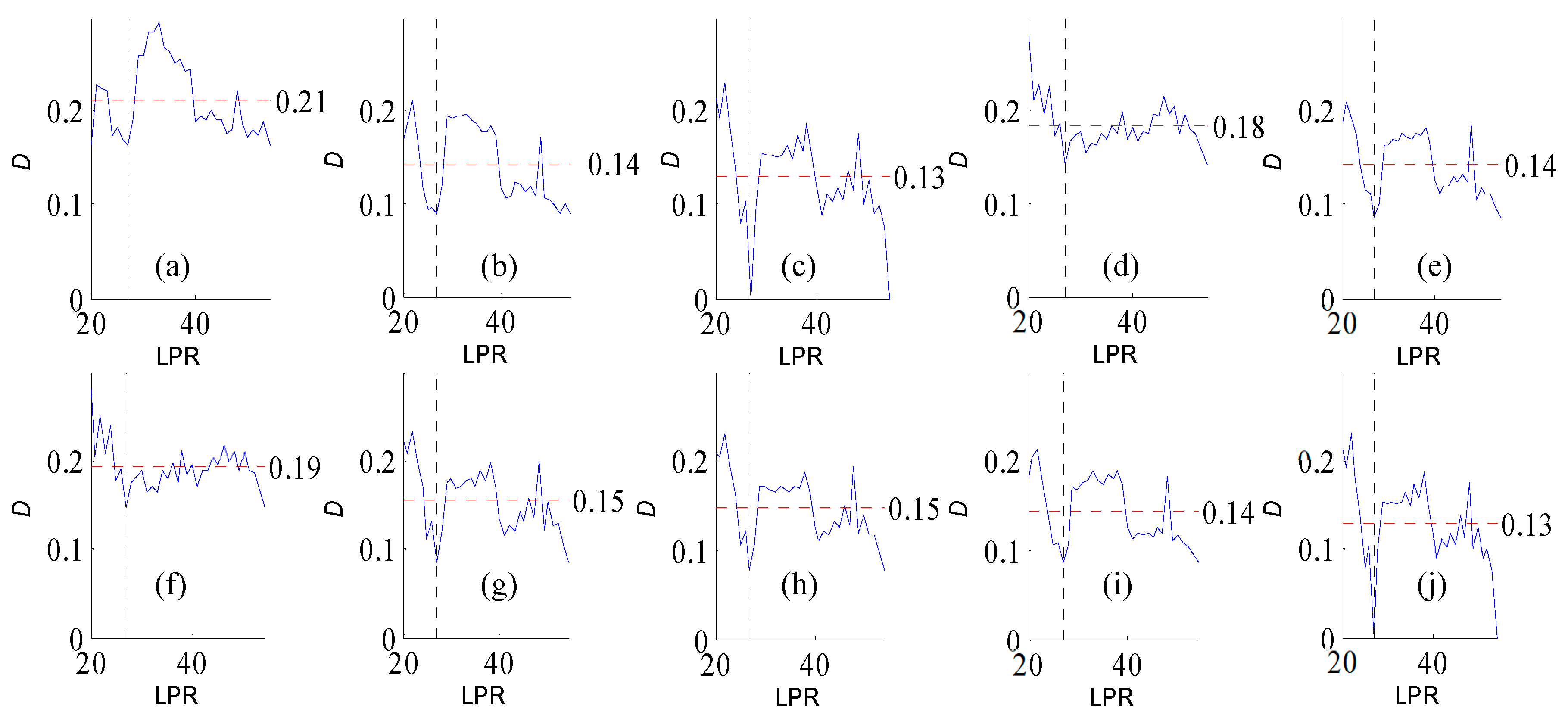
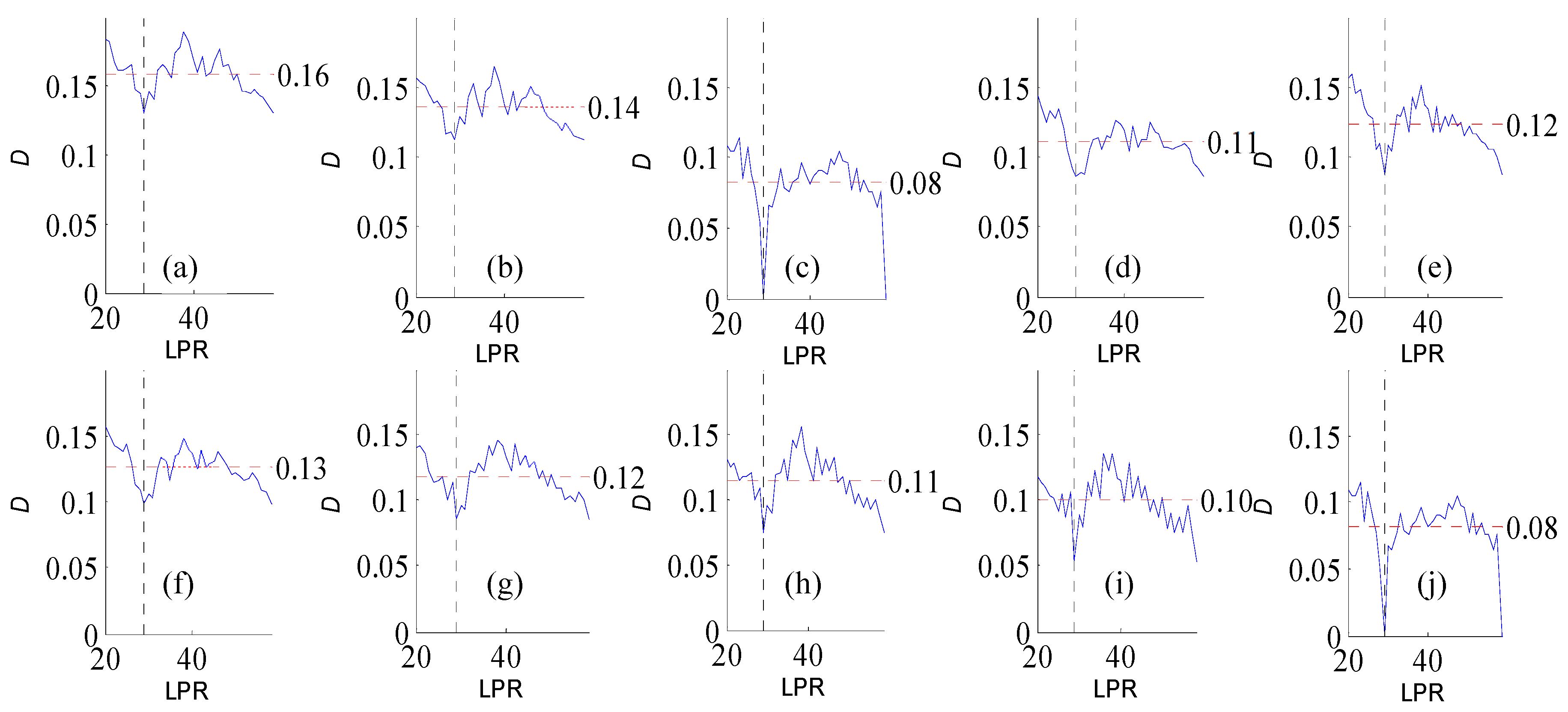
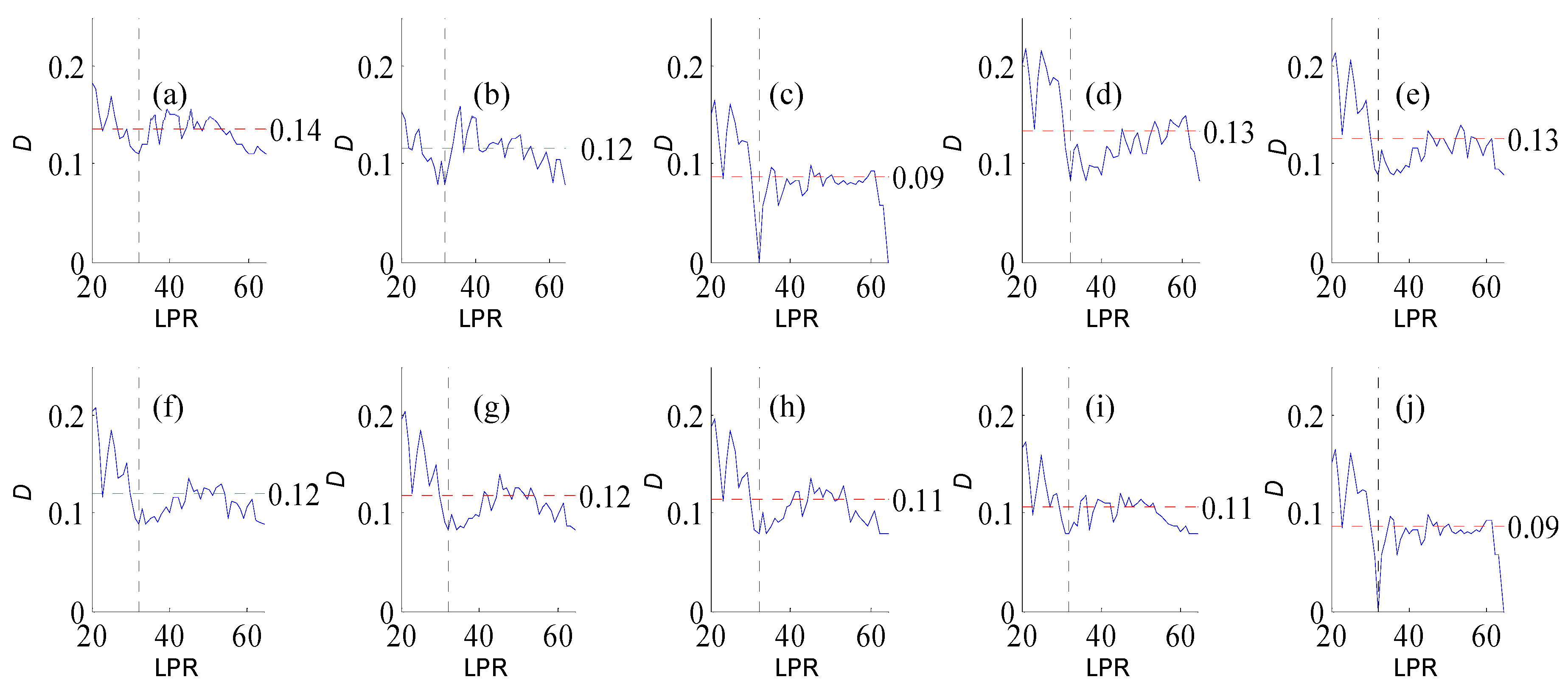
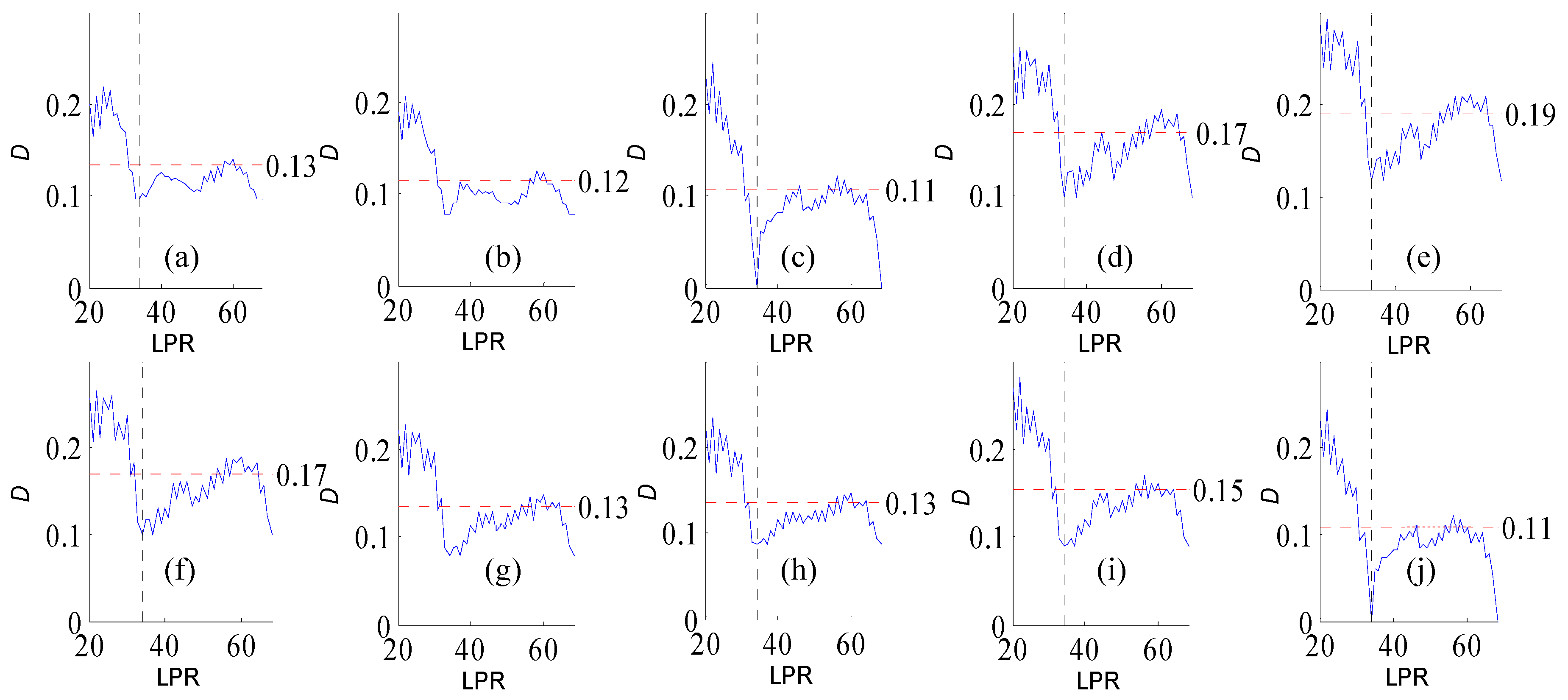
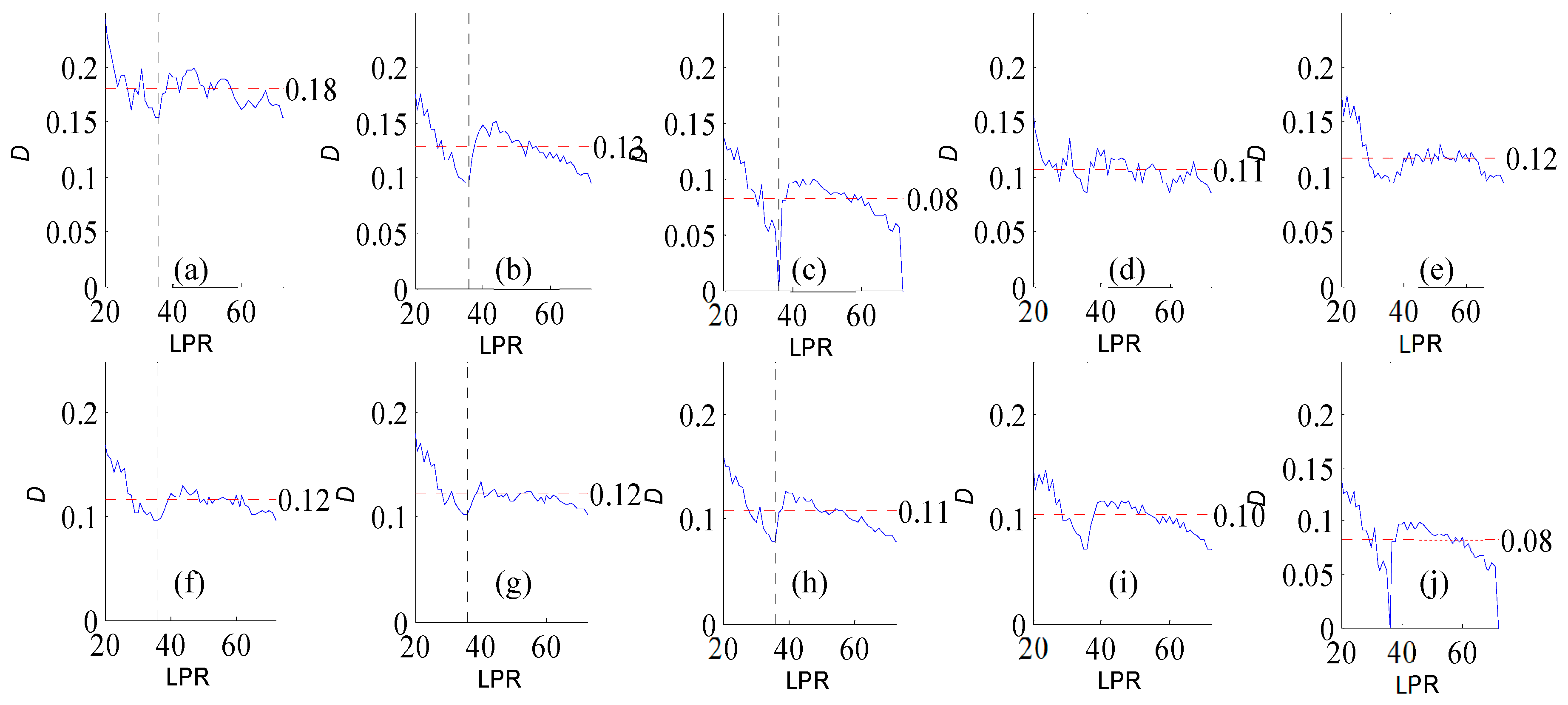
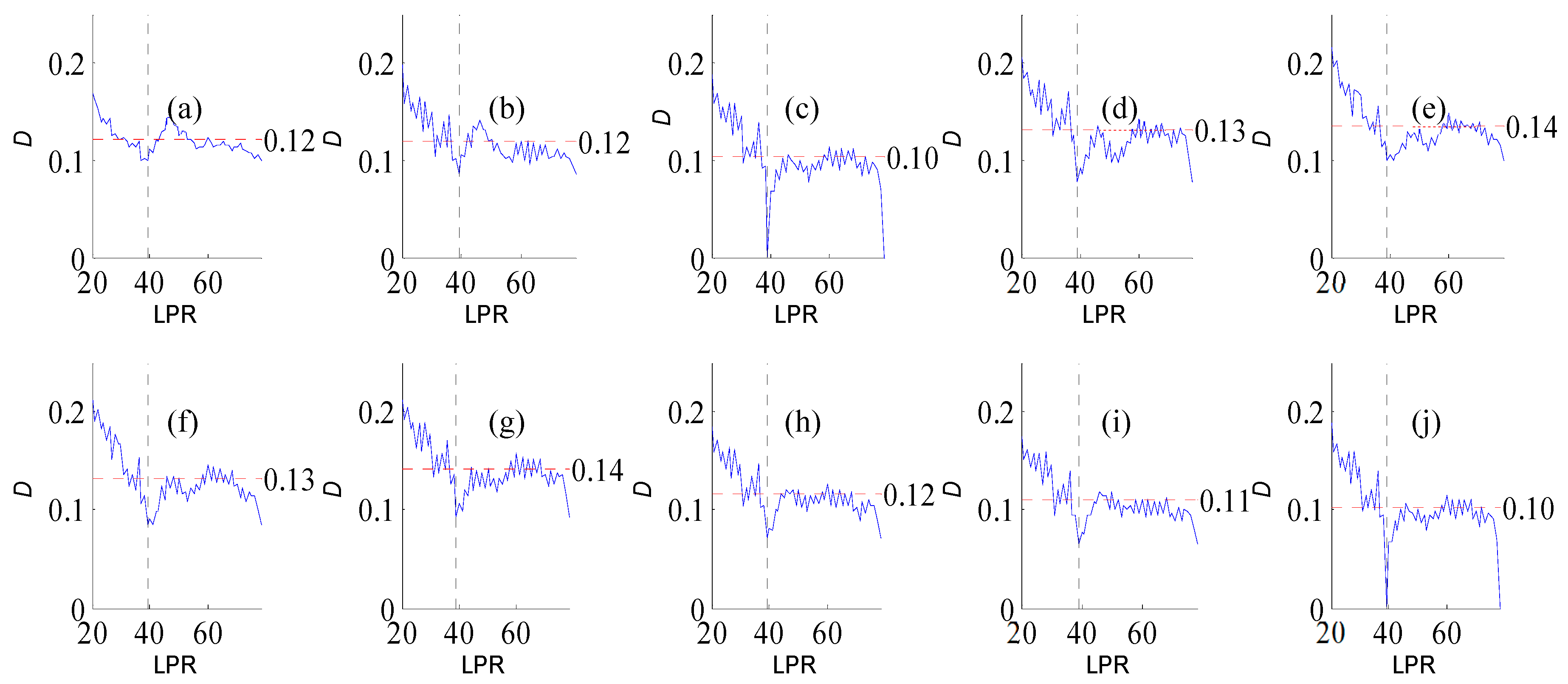
Figure A1.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 25 years. (a–j) correspond to post-impact flow time series length = 18, 21, 25, 29, 32, 36, 39, 43, 46, and 50 years, respectively. The abscissa value for the vertical dotted line is 25. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A1.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 25 years. (a–j) correspond to post-impact flow time series length = 18, 21, 25, 29, 32, 36, 39, 43, 46, and 50 years, respectively. The abscissa value for the vertical dotted line is 25. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
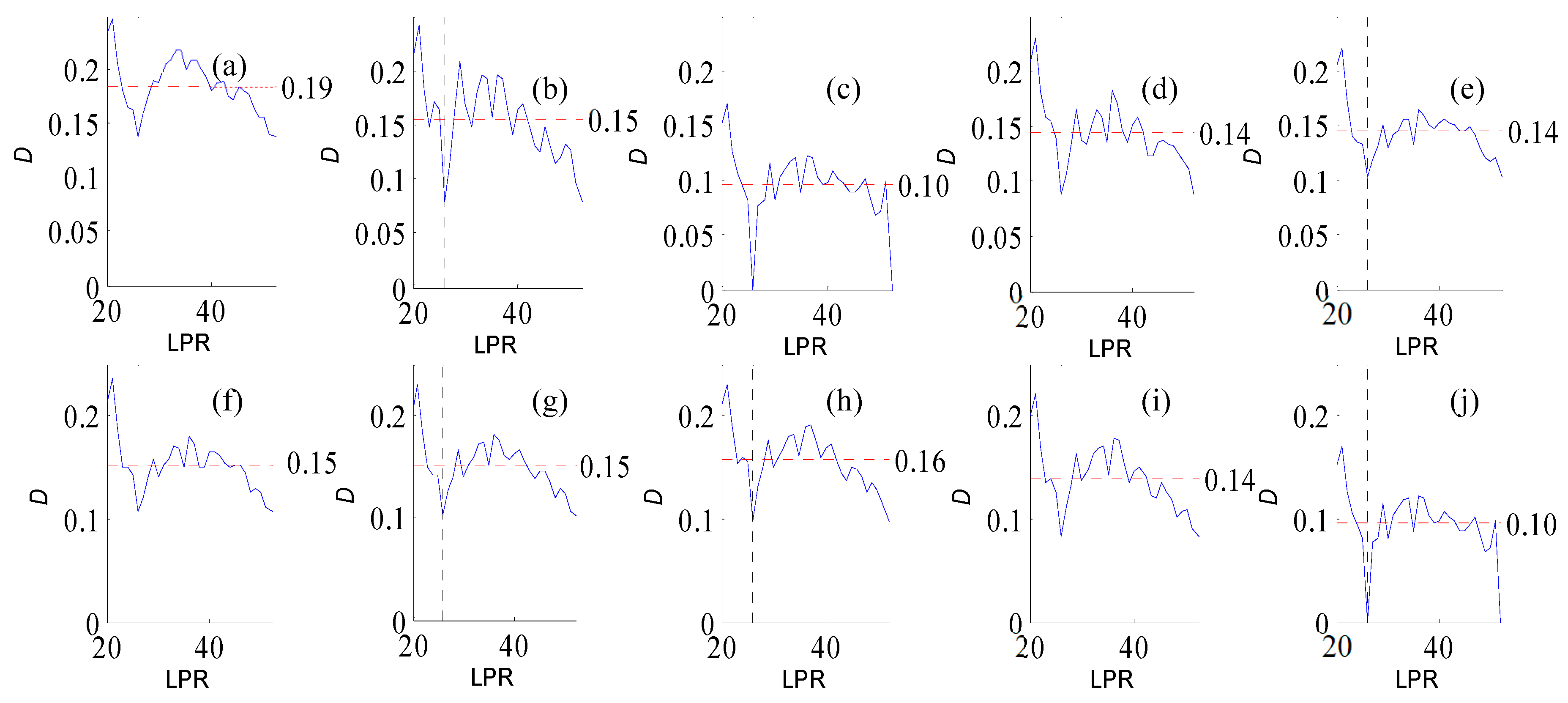
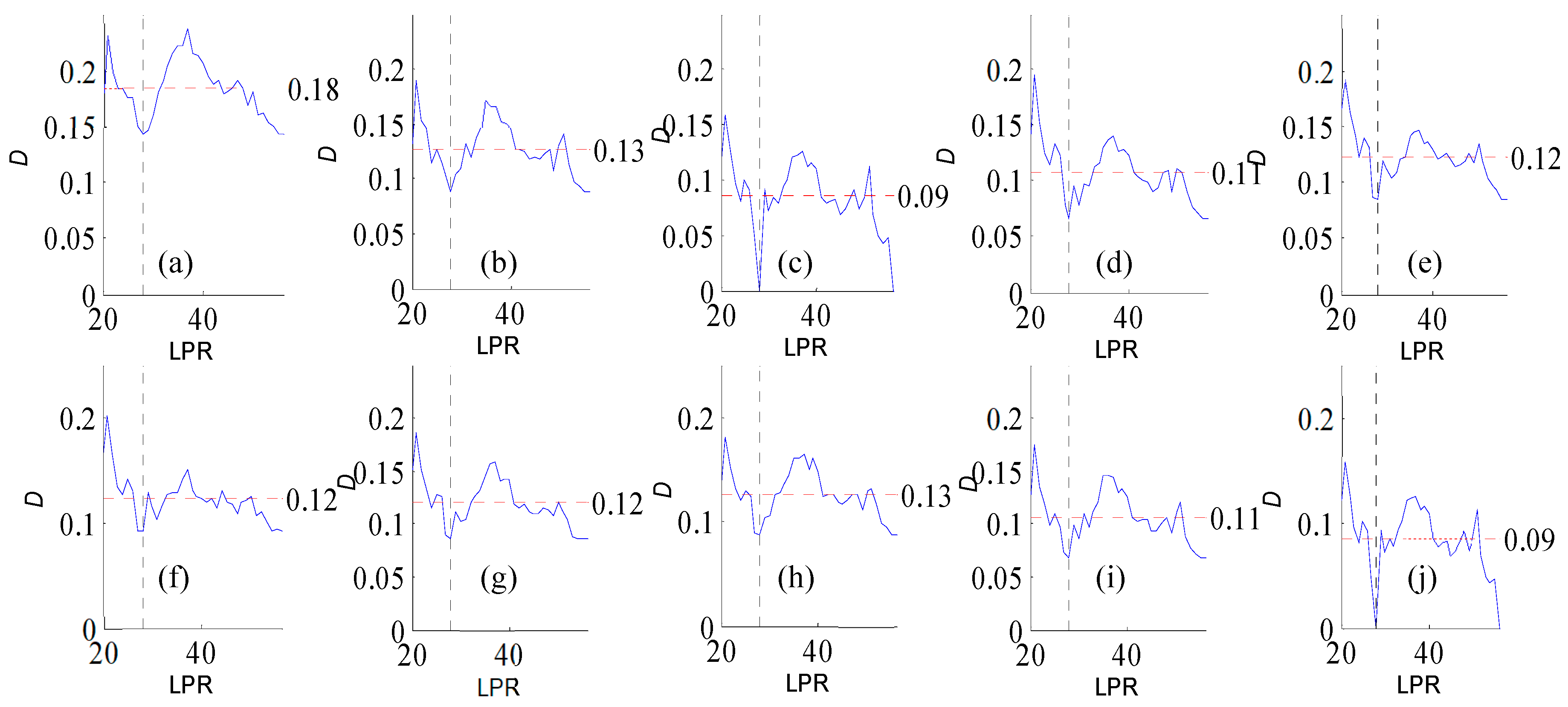
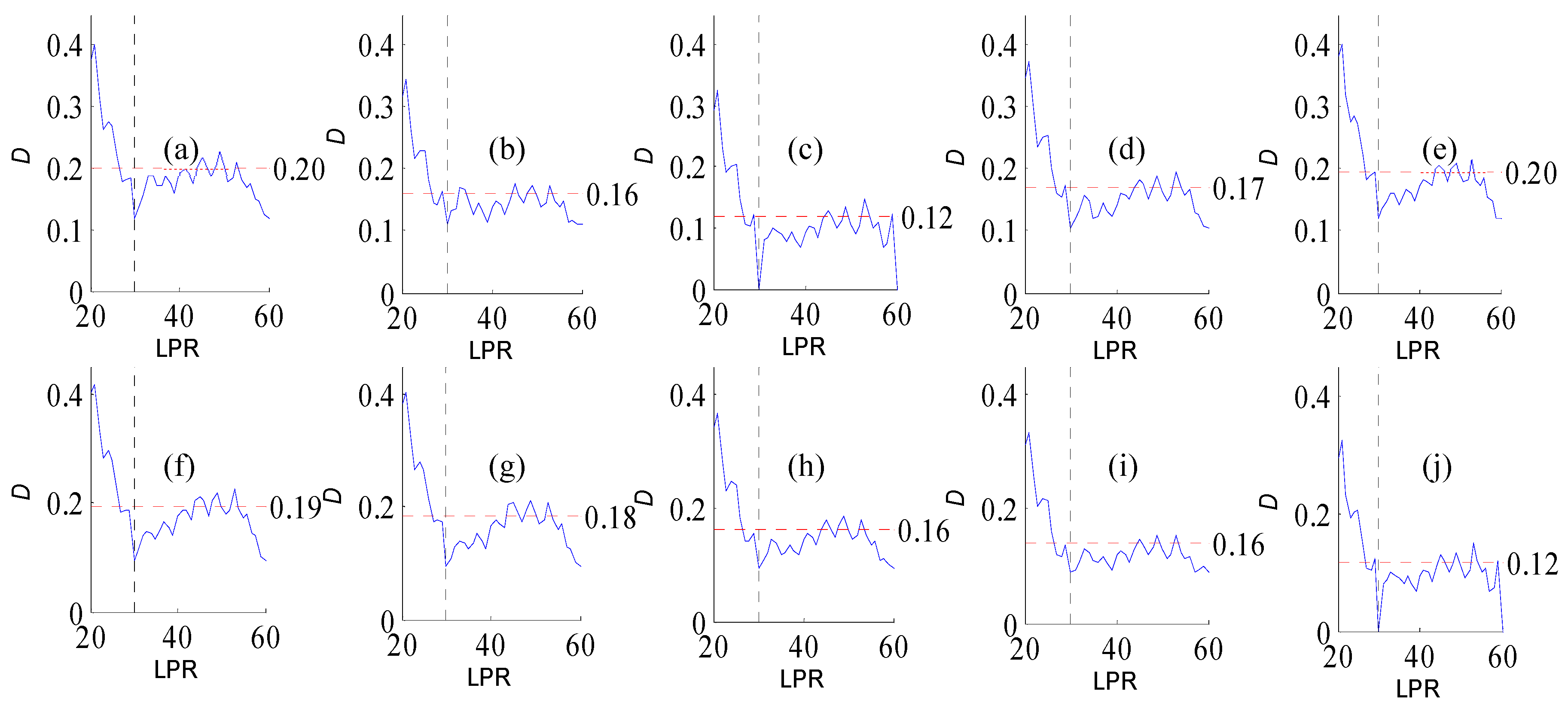
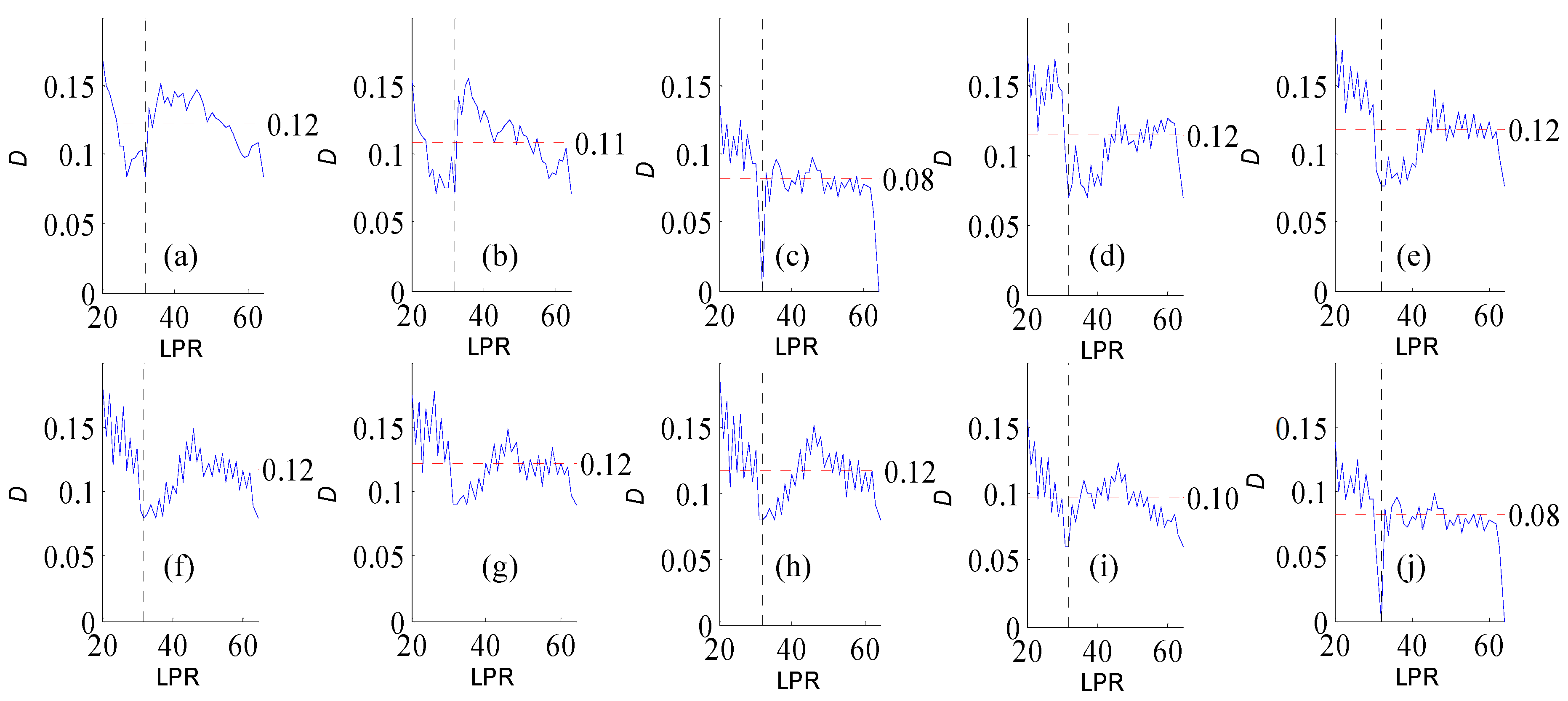
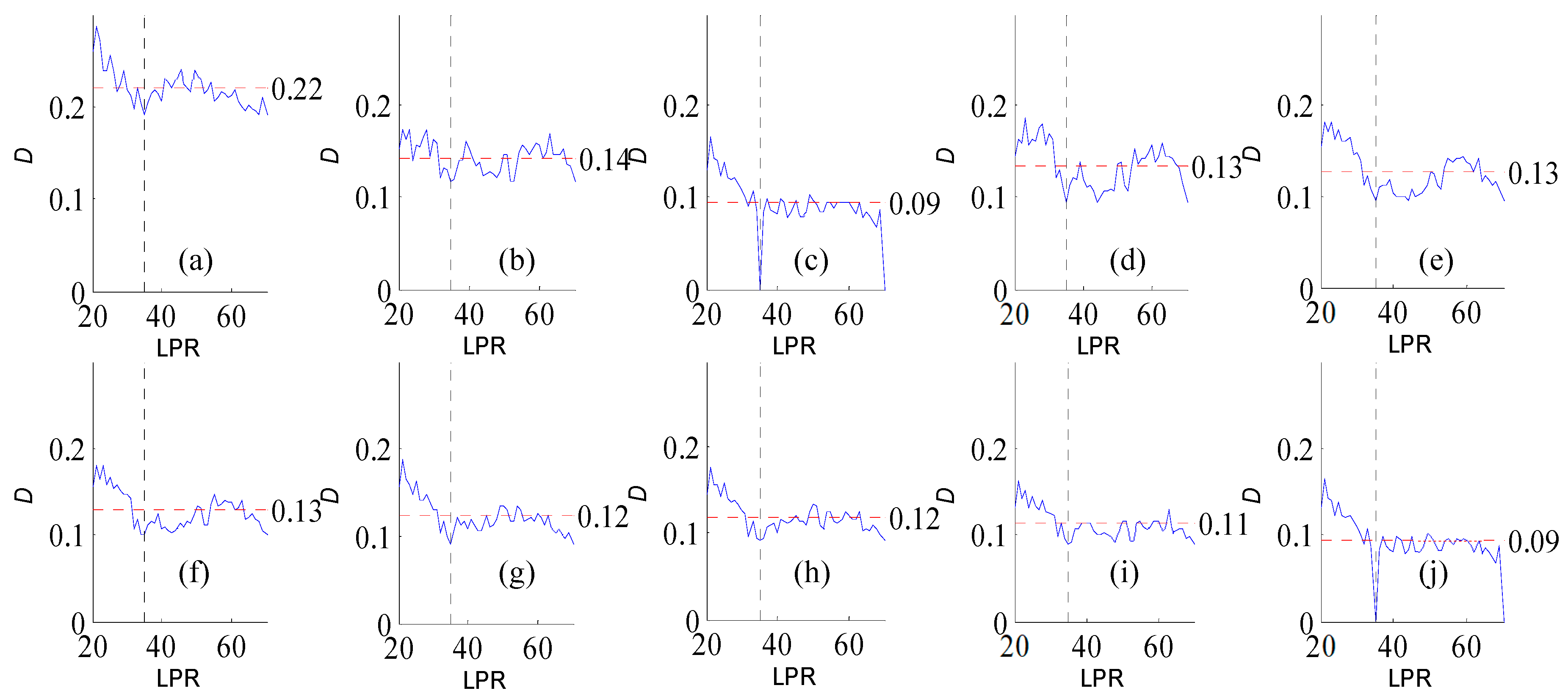
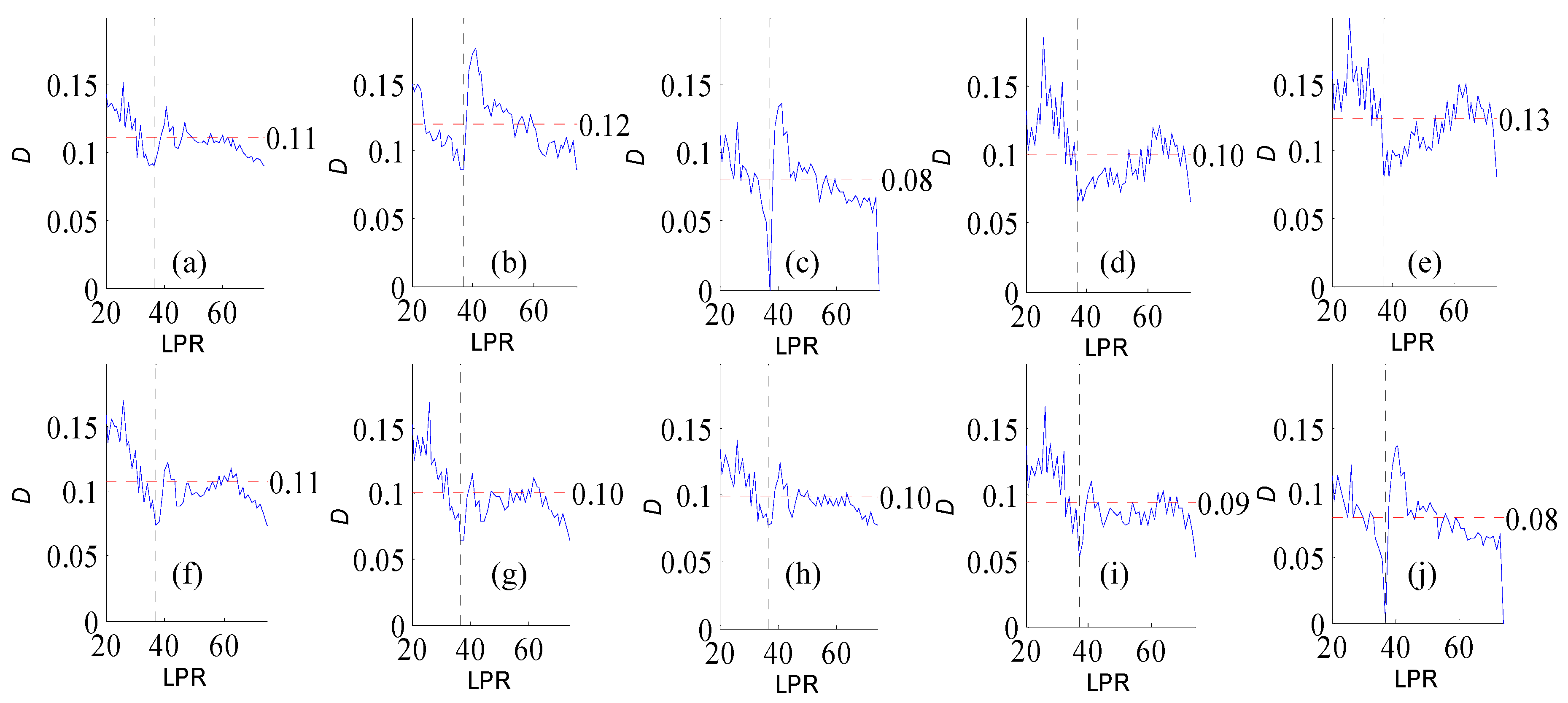
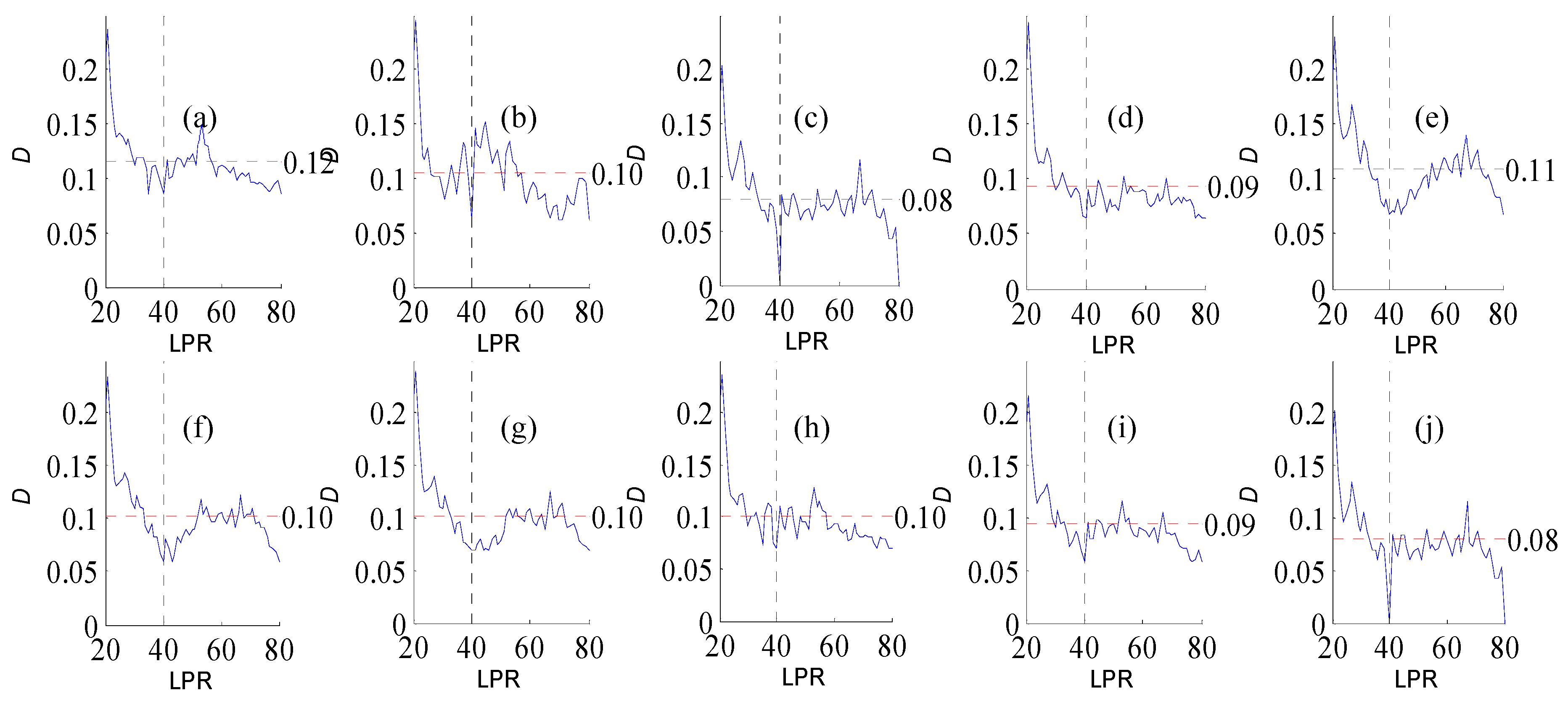
Figure A2.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 25 years. Figure (a–j) correspond to pre-impact flow time series length = 18, 21, 25, 29, 32, 36, 39, 43, 46, and 50 years, respectively. The abscissa value for the vertical dotted line is 25. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A2.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 25 years. Figure (a–j) correspond to pre-impact flow time series length = 18, 21, 25, 29, 32, 36, 39, 43, 46, and 50 years, respectively. The abscissa value for the vertical dotted line is 25. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
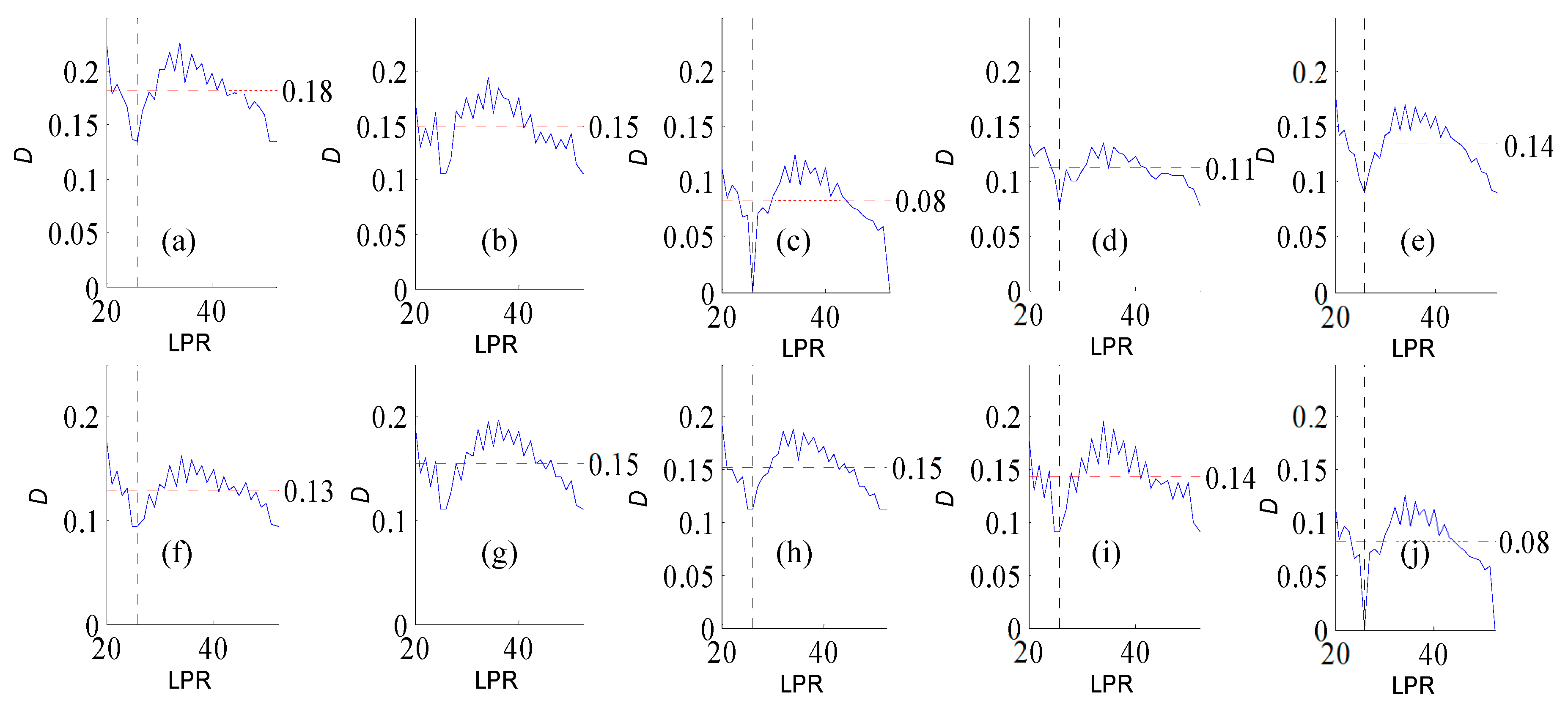
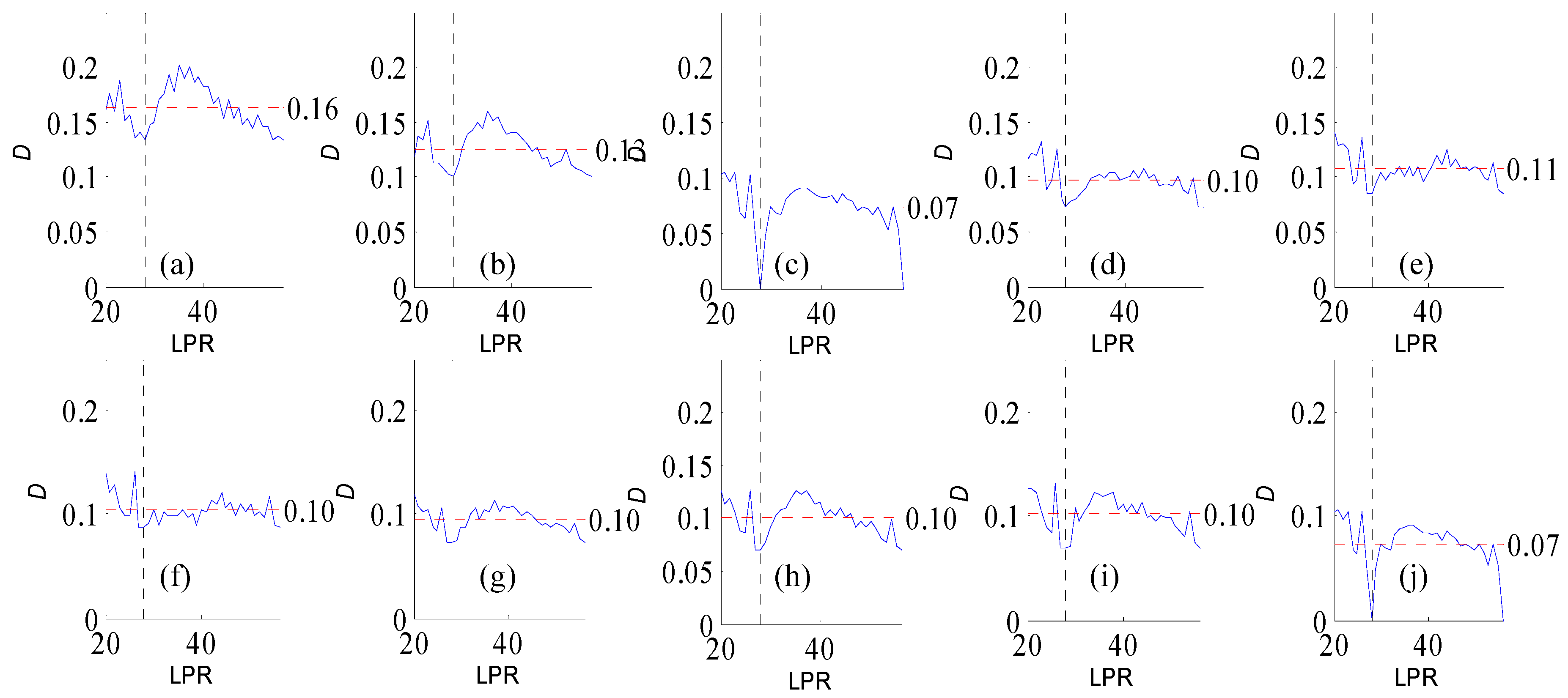
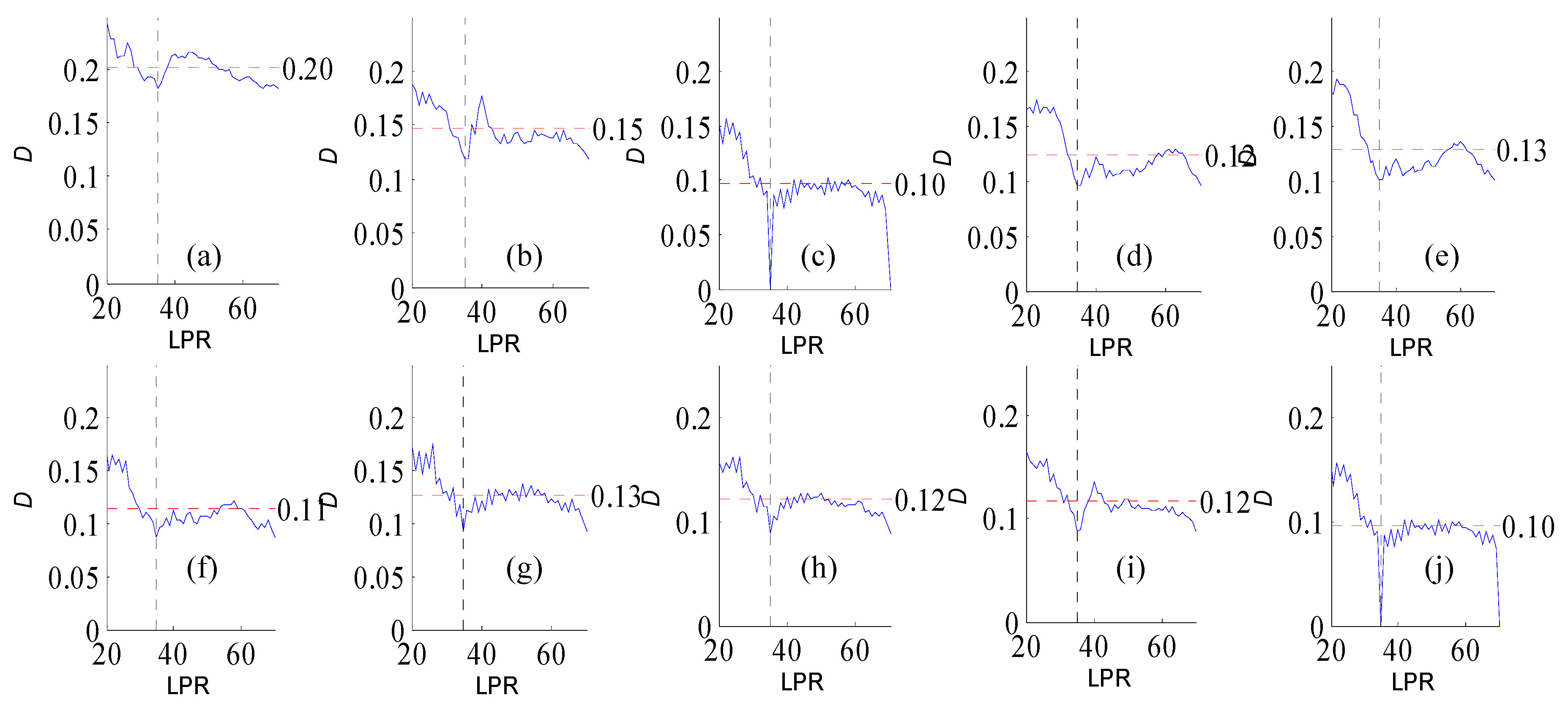
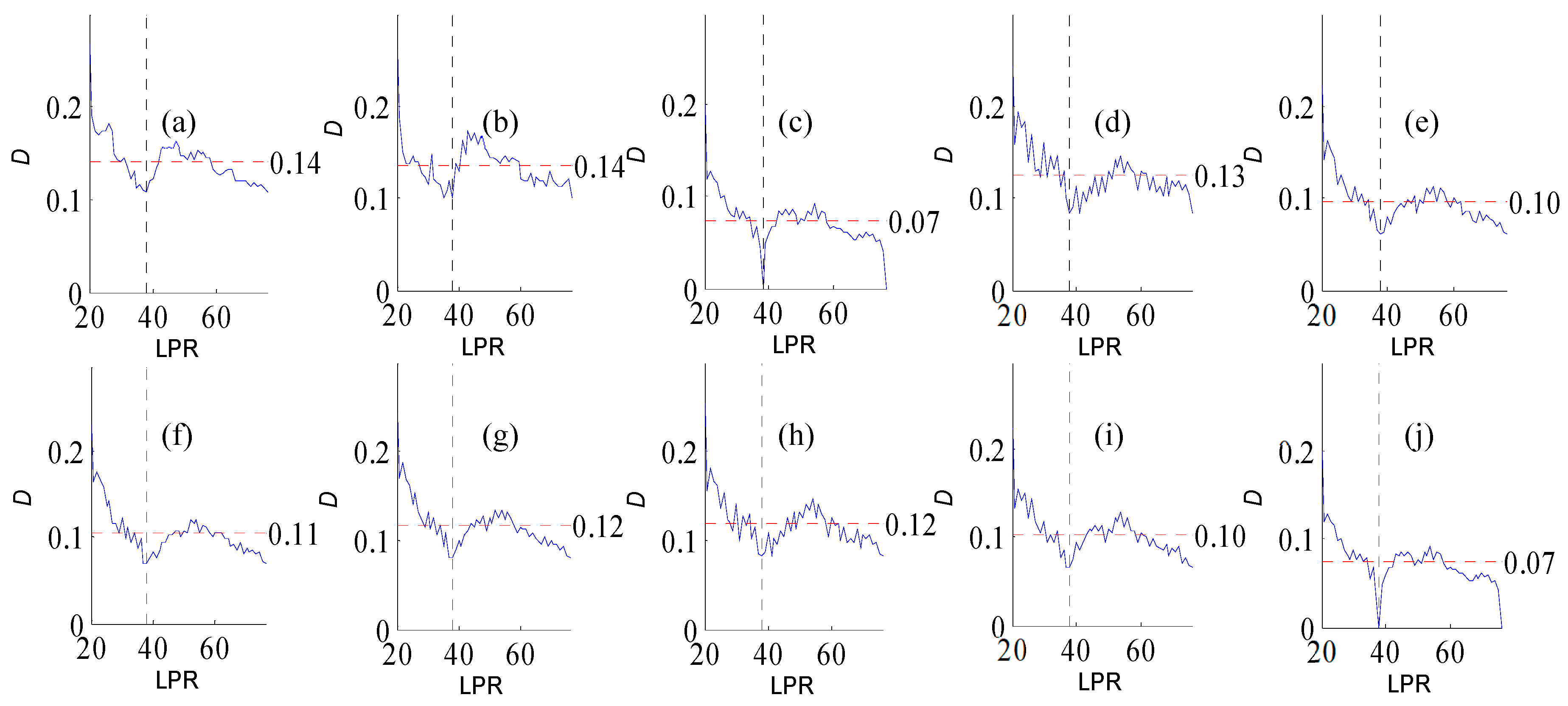
Figure A3.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 26 years. (a–j) correspond to post-impact flow time series length = 19, 22, 26, 30, 33, 37, 41, 45, 48, and 52 years, respectively. The abscissa value for the vertical dotted line is 26. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A3.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 26 years. (a–j) correspond to post-impact flow time series length = 19, 22, 26, 30, 33, 37, 41, 45, 48, and 52 years, respectively. The abscissa value for the vertical dotted line is 26. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
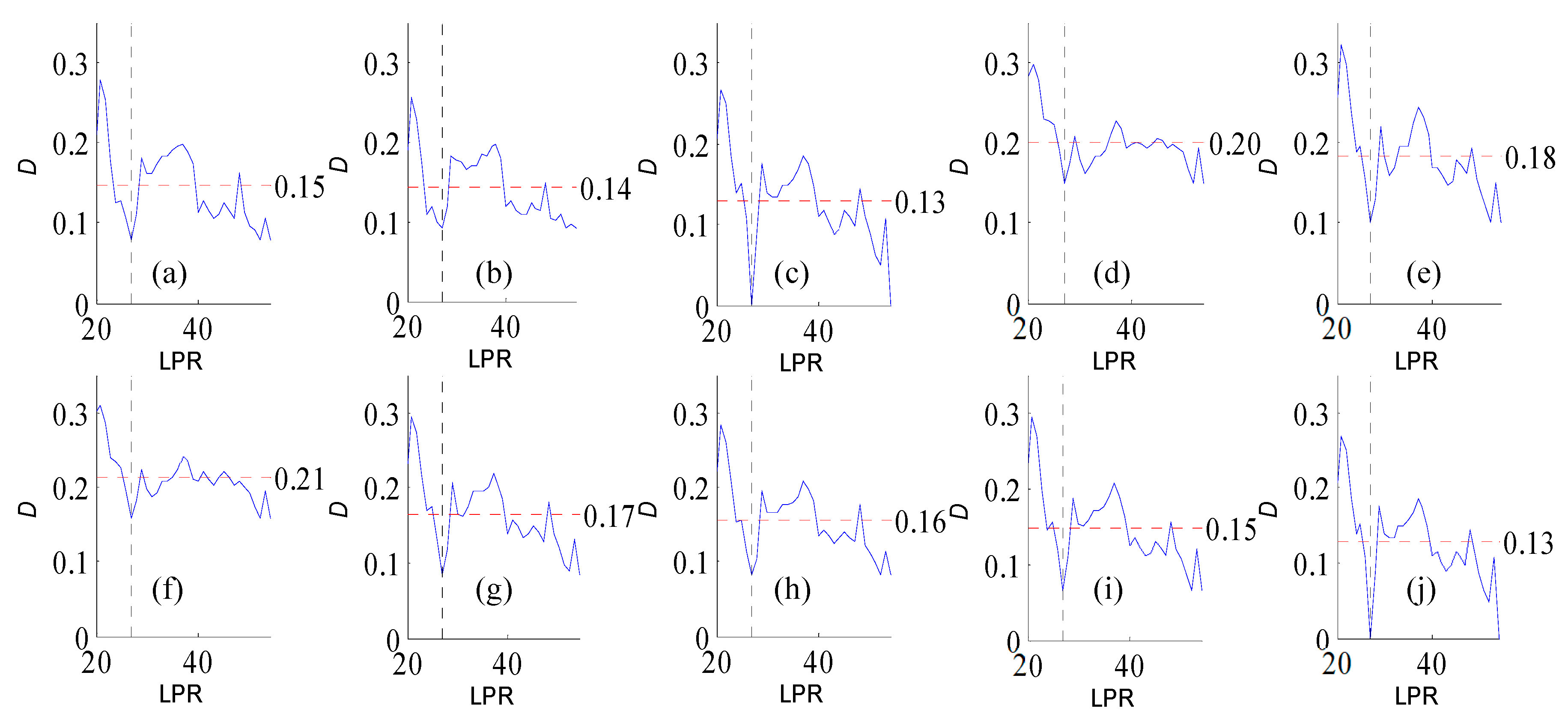
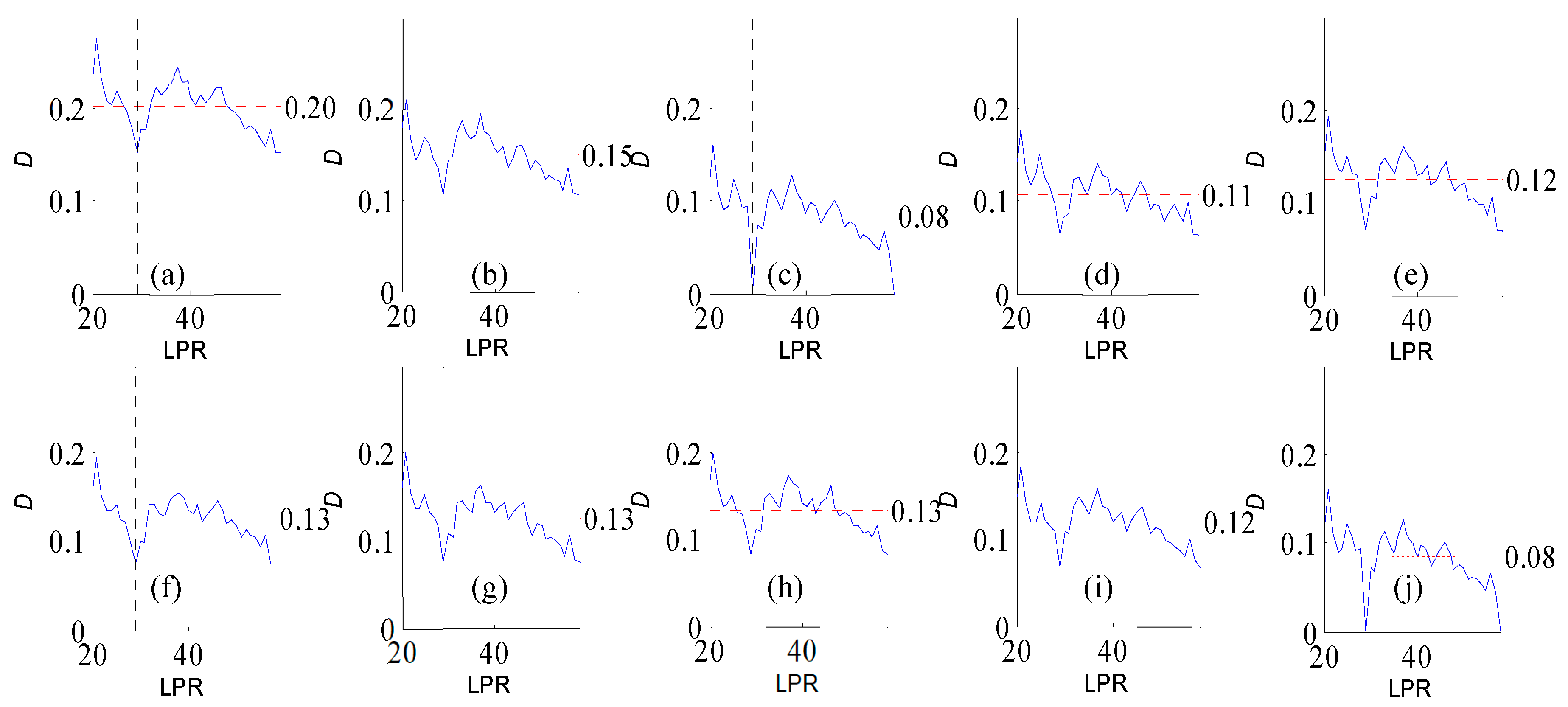
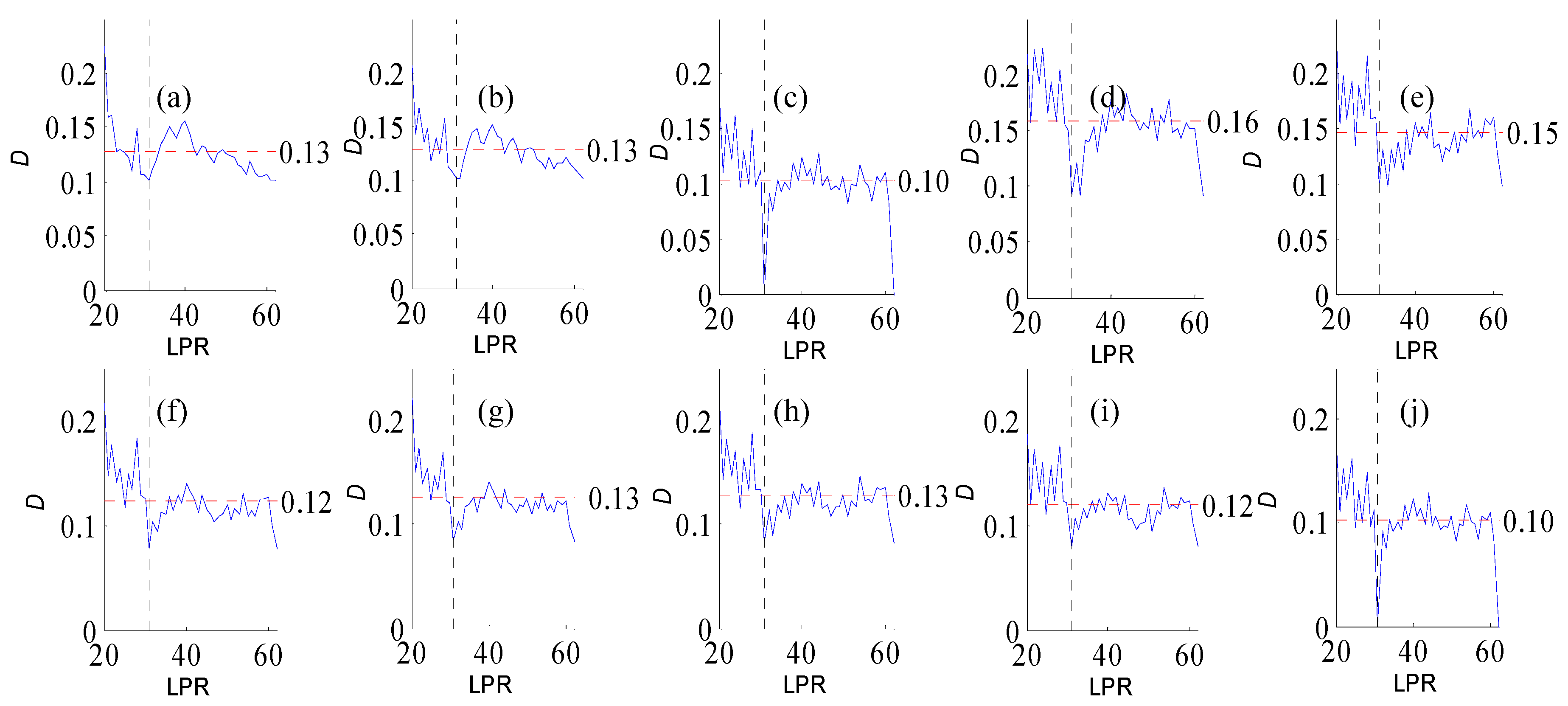
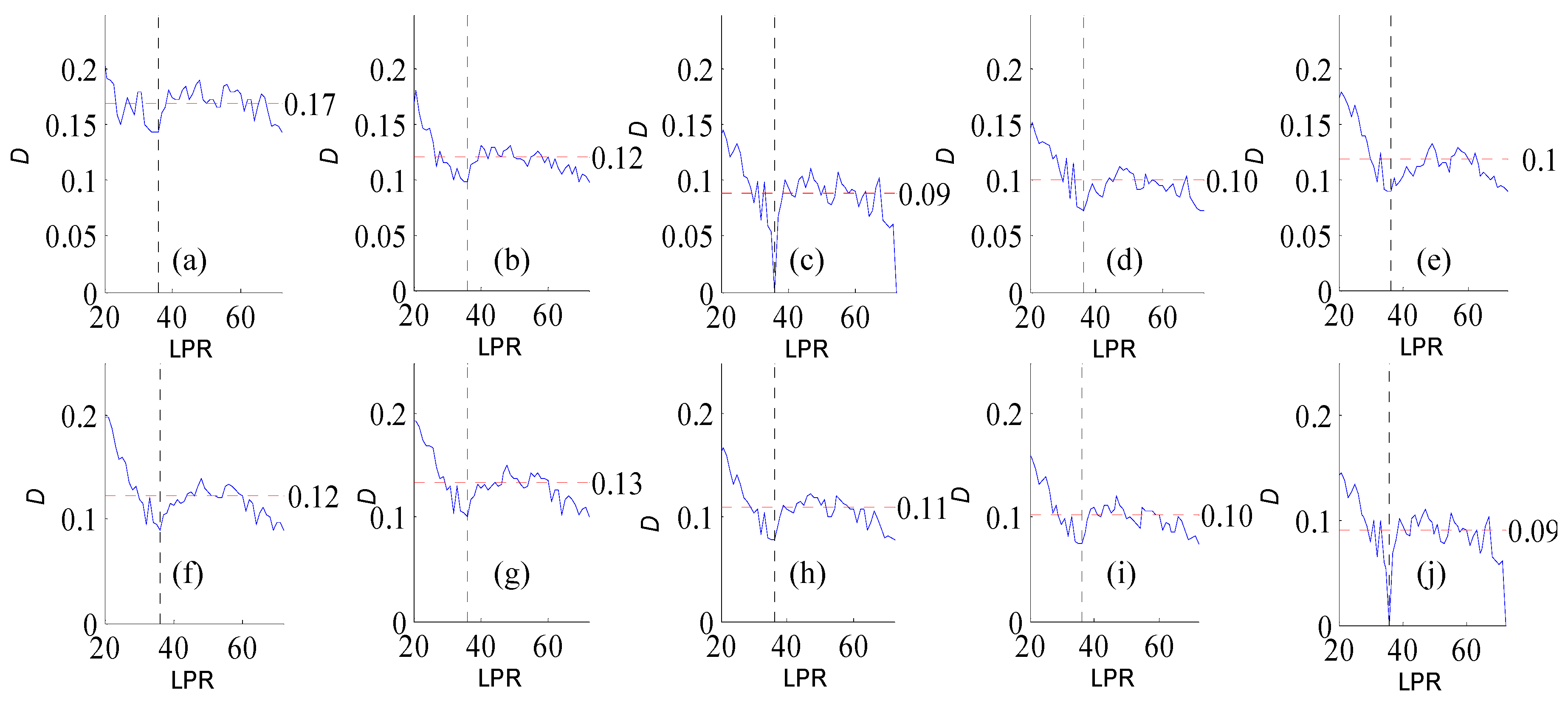
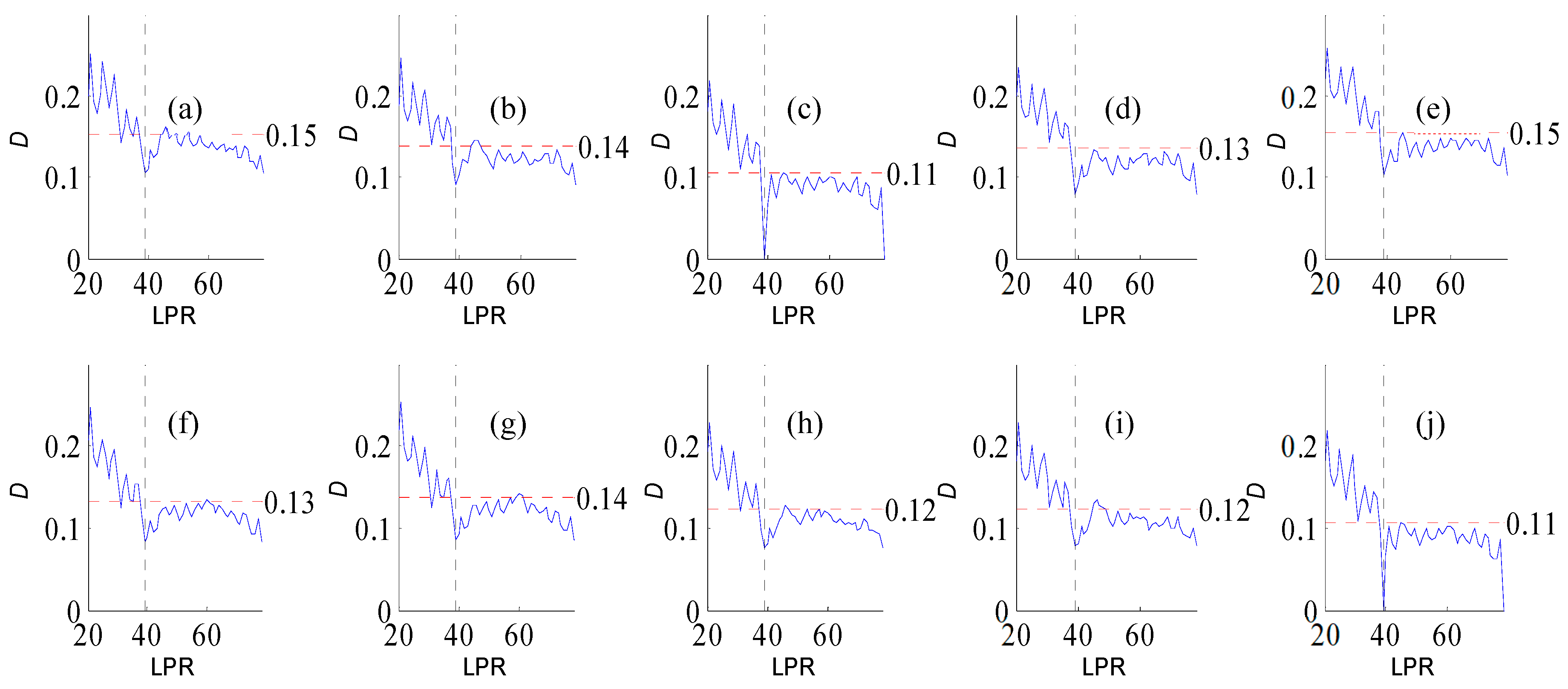
Figure A4.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 26 years. (a–j) correspond to pre-impact flow time series length = 19, 22, 26, 30, 33, 37, 41, 45, 48, 52 years, respectively. The abscissa value for the vertical dotted line is 26. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A4.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 26 years. (a–j) correspond to pre-impact flow time series length = 19, 22, 26, 30, 33, 37, 41, 45, 48, 52 years, respectively. The abscissa value for the vertical dotted line is 26. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A5.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 27 years. (a–j) correspond to pre-impact flow time series length = 19, 23, 27, 31, 35, 39, 42, 46, 50, and 54 years, respectively. The abscissa value for the vertical dotted line is 27. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A5.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 27 years. (a–j) correspond to pre-impact flow time series length = 19, 23, 27, 31, 35, 39, 42, 46, 50, and 54 years, respectively. The abscissa value for the vertical dotted line is 27. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A6.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 27 years. (a–j) correspond to pre-impact flow time series length = 19, 23, 27, 31, 35, 39, 42, 46, 50, and 54 years, respectively. The abscissa value for the vertical dotted line is 27. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A6.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 27 years. (a–j) correspond to pre-impact flow time series length = 19, 23, 27, 31, 35, 39, 42, 46, 50, and 54 years, respectively. The abscissa value for the vertical dotted line is 27. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A7.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 28 years. (a–j) correspond to pre-impact flow time series length = 20, 24, 28, 32, 36, 40, 44, 48, 52, and 56 years, respectively. The abscissa value for the vertical dotted line is 28. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A7.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 28 years. (a–j) correspond to pre-impact flow time series length = 20, 24, 28, 32, 36, 40, 44, 48, 52, and 56 years, respectively. The abscissa value for the vertical dotted line is 28. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A8.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 28 years. (a–j) correspond to pre-impact flow time series length = 20, 24, 28, 32, 36, 40, 44, 48, 52, and 56 years, respectively. The abscissa value for the vertical dotted line is 28. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A8.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 28 years. (a–j) correspond to pre-impact flow time series length = 20, 24, 28, 32, 36, 40, 44, 48, 52, and 56 years, respectively. The abscissa value for the vertical dotted line is 28. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A9.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 29 years. (a–j) correspond to pre-impact flow time series length = 21, 25, 29, 33, 37, 41, 46, 50, 54, and 58 years, respectively. The abscissa value for the vertical dotted line is 29. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A9.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 29 years. (a–j) correspond to pre-impact flow time series length = 21, 25, 29, 33, 37, 41, 46, 50, 54, and 58 years, respectively. The abscissa value for the vertical dotted line is 29. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A10.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 29 years. (a–j) correspond to pre-impact flow time series length = 21, 25, 29, 33, 37, 41, 46, 50, 54, and 58 years, respectively. The abscissa value for the vertical dotted line is 29. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A10.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 29 years. (a–j) correspond to pre-impact flow time series length = 21, 25, 29, 33, 37, 41, 46, 50, 54, and 58 years, respectively. The abscissa value for the vertical dotted line is 29. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A11.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 30 years. (a–j) correspond to pre-impact flow time series length = 21, 26, 30, 34, 39, 43, 47, 51, 56, and 60 years, respectively. The abscissa value for the vertical dotted line is 30. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A11.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 30 years. (a–j) correspond to pre-impact flow time series length = 21, 26, 30, 34, 39, 43, 47, 51, 56, and 60 years, respectively. The abscissa value for the vertical dotted line is 30. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A12.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 30 years. (a–j) correspond to pre-impact flow time series length = 21, 26, 30, 34, 39, 43, 47, 51, 56, and 60 years, respectively. The abscissa value for the vertical dotted line is 30. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A12.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 30 years. (a–j) correspond to pre-impact flow time series length = 21, 26, 30, 34, 39, 43, 47, 51, 56, and 60 years, respectively. The abscissa value for the vertical dotted line is 30. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A13.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 31 years. (a–j) correspond to pre-impact flow time series length = 22, 27, 31, 35, 40, 44, 49, 53, 58, and 62 years, respectively. The abscissa value for the vertical dotted line is 31. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A13.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 31 years. (a–j) correspond to pre-impact flow time series length = 22, 27, 31, 35, 40, 44, 49, 53, 58, and 62 years, respectively. The abscissa value for the vertical dotted line is 31. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A14.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 31 years. (a–j) correspond to pre-impact flow time series length = 22, 27, 31, 35, 40, 44, 49, 53, 58, and 62 years, respectively. The abscissa value for the vertical dotted line is 31. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A14.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 31 years. (a–j) correspond to pre-impact flow time series length = 22, 27, 31, 35, 40, 44, 49, 53, 58, and 62 years, respectively. The abscissa value for the vertical dotted line is 31. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A15.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 32 years. (a–j) correspond to pre-impact flow time series length = 23, 27, 32, 37, 41, 46, 50, 55, 59, and 64 years, respectively. The abscissa value for the vertical dotted line is 32. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A15.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 32 years. (a–j) correspond to pre-impact flow time series length = 23, 27, 32, 37, 41, 46, 50, 55, 59, and 64 years, respectively. The abscissa value for the vertical dotted line is 32. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A16.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 32 years. (a–j) correspond to pre-impact flow time series length = 23, 27, 32, 37, 41, 46, 50, 55, 59, and 64 years, respectively. The abscissa value for the vertical dotted line is 32. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A16.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 32 years. (a–j) correspond to pre-impact flow time series length = 23, 27, 32, 37, 41, 46, 50, 55, 59, and 64 years, respectively. The abscissa value for the vertical dotted line is 32. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A17.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 33 years. (a–j) correspond to pre-impact flow time series length = 24, 28, 33, 38, 42, 47, 52, 57, 61, and 66 years, respectively. The abscissa value for the vertical dotted line is 33. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A17.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 33 years. (a–j) correspond to pre-impact flow time series length = 24, 28, 33, 38, 42, 47, 52, 57, 61, and 66 years, respectively. The abscissa value for the vertical dotted line is 33. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A18.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 33 years. (a–j) correspond to pre-impact flow time series length = 24, 28, 33, 38, 42, 47, 52, 57, 61, and 66 years, respectively. The abscissa value for the vertical dotted line is 33. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A18.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 33 years. (a–j) correspond to pre-impact flow time series length = 24, 28, 33, 38, 42, 47, 52, 57, 61, and 66 years, respectively. The abscissa value for the vertical dotted line is 33. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A19.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 34 years. (a–j) correspond to pre-impact flow time series length = 24, 29, 34, 39, 44, 49, 53, 58, 63, and 68 years, respectively. The abscissa value for the vertical dotted line is 34. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A19.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 34 years. (a–j) correspond to pre-impact flow time series length = 24, 29, 34, 39, 44, 49, 53, 58, 63, and 68 years, respectively. The abscissa value for the vertical dotted line is 34. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A20.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 34 years. (a–j) correspond to pre-impact flow time series length = 24, 29, 34, 39, 44, 49, 53, 58, 63, and 68 years, respectively. The abscissa value for the vertical dotted line is 34. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A20.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 34 years. (a–j) correspond to pre-impact flow time series length = 24, 29, 34, 39, 44, 49, 53, 58, 63, and 68 years, respectively. The abscissa value for the vertical dotted line is 34. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A21.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 35 years. (a–j) correspond to pre-impact flow time series length = 25, 30, 35, 40, 45, 50, 55, 60, 65, and 70 years, respectively. The abscissa value for the vertical dotted line is 35. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A21.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 35 years. (a–j) correspond to pre-impact flow time series length = 25, 30, 35, 40, 45, 50, 55, 60, 65, and 70 years, respectively. The abscissa value for the vertical dotted line is 35. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A22.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 35 years. (a–j) correspond to pre-impact flow time series length = 25, 30, 35, 40, 45, 50, 55, 60, 65, and 70 years, respectively. The abscissa value for the vertical dotted line is 35. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A22.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 35 years. (a–j) correspond to pre-impact flow time series length = 25, 30, 35, 40, 45, 50, 55, 60, 65, and 70 years, respectively. The abscissa value for the vertical dotted line is 35. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A23.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under the periodicity of 36 years. (a–j) correspond to pre-impact flow time series length = 26, 31, 36, 41, 46, 51, 57, 62, 67, and 72 years, respectively. The abscissa value for the vertical dotted line is 36. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A23.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under the periodicity of 36 years. (a–j) correspond to pre-impact flow time series length = 26, 31, 36, 41, 46, 51, 57, 62, 67, and 72 years, respectively. The abscissa value for the vertical dotted line is 36. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A24.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 36 years. (a–j) correspond to pre-impact flow time series length = 26, 31, 36, 41, 46, 51, 57, 62, 67, and 72 years, respectively. The abscissa value for the vertical dotted line is 37. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A24.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 36 years. (a–j) correspond to pre-impact flow time series length = 26, 31, 36, 41, 46, 51, 57, 62, 67, and 72 years, respectively. The abscissa value for the vertical dotted line is 37. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A25.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 37 years. (a–j) correspond to pre-impact flow time series length = 26, 32, 37, 42, 48, 53, 58, 63, 69, and 74 years, respectively. The abscissa value for the vertical dotted line is 37. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A25.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 37 years. (a–j) correspond to pre-impact flow time series length = 26, 32, 37, 42, 48, 53, 58, 63, 69, and 74 years, respectively. The abscissa value for the vertical dotted line is 37. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A26.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 37 years. (a–j) correspond to pre-impact flow time series length = 26, 32, 37, 42, 48, 53, 58, 63, 69, and 74 years, respectively. The abscissa value for the vertical dotted line is 37. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A26.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 37 years. (a–j) correspond to pre-impact flow time series length = 26, 32, 37, 42, 48, 53, 58, 63, 69, and 74 years, respectively. The abscissa value for the vertical dotted line is 37. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A27.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 38 years. (a–j) correspond to pre-impact flow time series length = 27, 33, 38, 43, 49, 54, 60, 65, 71, and 76 years, respectively. The abscissa value for the vertical dotted line is 38. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A27.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 38 years. (a–j) correspond to pre-impact flow time series length = 27, 33, 38, 43, 49, 54, 60, 65, 71, and 76 years, respectively. The abscissa value for the vertical dotted line is 38. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A28.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 38 years. (a–j) correspond to pre-impact flow time series length = 27, 33, 38, 43, 49, 54, 60, 65, 71, and 76 years, respectively. The abscissa value for the vertical dotted line is 39. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A28.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 38 years. (a–j) correspond to pre-impact flow time series length = 27, 33, 38, 43, 49, 54, 60, 65, 71, and 76 years, respectively. The abscissa value for the vertical dotted line is 39. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A29.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 39 years. (a–j) correspond to pre-impact flow time series length = 28, 33, 39, 45, 50, 56, 61, 67, 72, and 78 years, respectively. The abscissa value for the vertical dotted line is 39. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A29.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 39 years. (a–j) correspond to pre-impact flow time series length = 28, 33, 39, 45, 50, 56, 61, 67, 72, and 78 years, respectively. The abscissa value for the vertical dotted line is 39. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A30.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 39 years. (a–j) correspond to pre-impact flow time series length = 28, 33, 39, 45, 50, 56, 61, 67, 72, and 78 years, respectively. The abscissa value for the vertical dotted line is 39. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A30.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 39 years. (a–j) correspond to pre-impact flow time series length = 28, 33, 39, 45, 50, 56, 61, 67, 72, and 78 years, respectively. The abscissa value for the vertical dotted line is 39. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A31.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 40 years. (a–j) correspond to pre-impact flow time series length = 29, 34, 40, 46, 51, 57, 63, 69, 74, and 80 years, respectively. The abscissa value for the vertical dotted line is 40. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A31.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of pre-impact flow time series (LPR) under a periodicity of 40 years. (a–j) correspond to pre-impact flow time series length = 29, 34, 40, 46, 51, 57, 63, 69, 74, and 80 years, respectively. The abscissa value for the vertical dotted line is 40. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A32.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 40 years. (a–j) correspond to pre-impact flow time series length = 29, 34, 40, 46, 51, 57, 63, 69, 74, and 80 years, respectively. The abscissa value for the vertical dotted line is 40. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.
Figure A32.
Variation of flow regime alteration degree (D) measured by the RVA with change in the length of post-impact flow time series (LPR) under a periodicity of 40 years. (a–j) correspond to pre-impact flow time series length = 29, 34, 40, 46, 51, 57, 63, 69, 74, and 80 years, respectively. The abscissa value for the vertical dotted line is 40. The ordinate value for the horizontal dotted line is the mean degree of flow regime alteration in each subfigure.