Hydrological Modelling in Data Sparse Environment: Inverse Modelling of a Historical Flood Event
Abstract
:1. Introduction
- check the flood-peak-magnitude plausibility from the hydrological perspective and
- understand and quantify the flood generating processes and
- differentiate between model output uncertainty caused by uncertain model parameters and inputs, especially in a data sparse environment.
2. Material and Methods
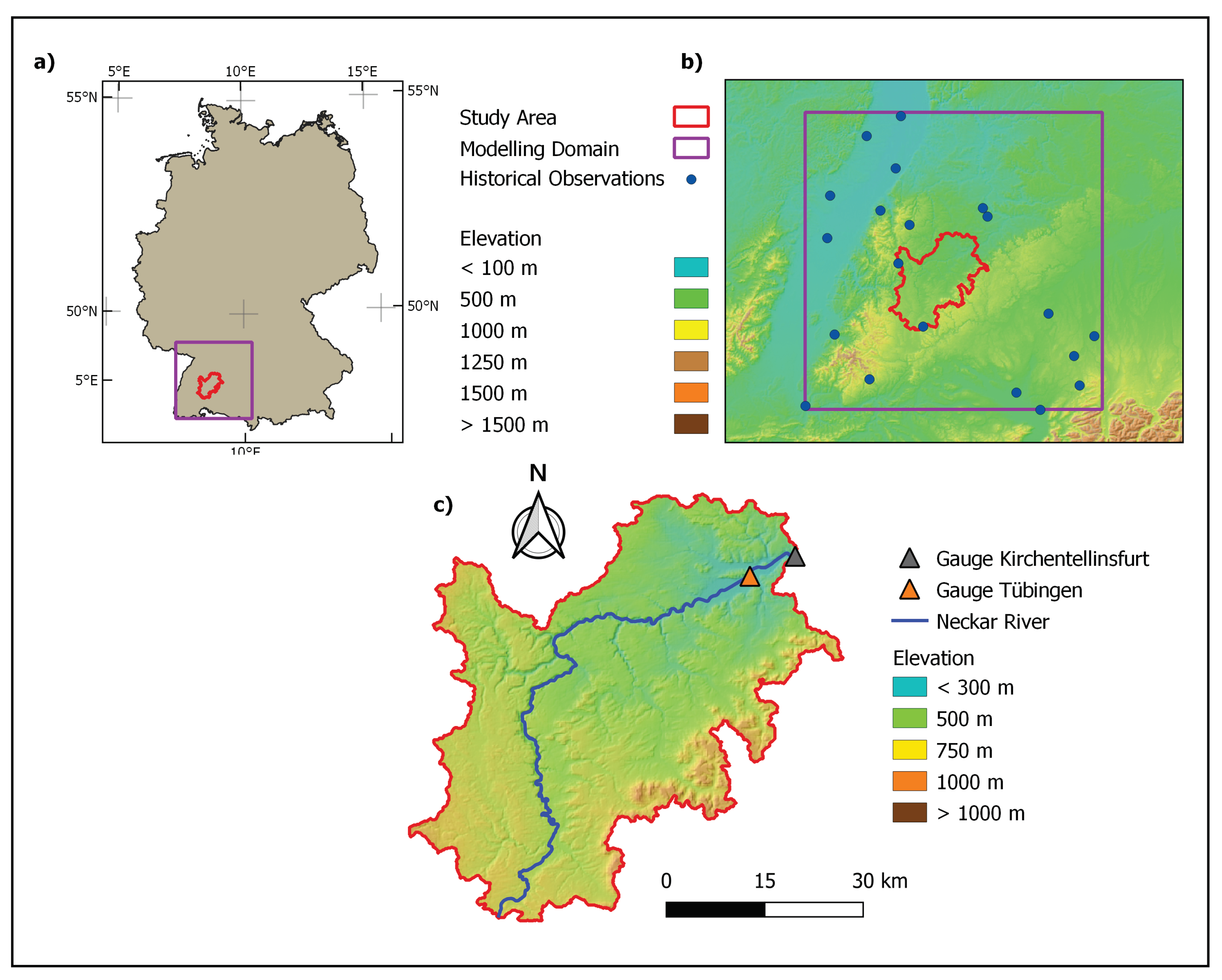
2.1. Study Area
2.2. Data
2.3. Hydrometeorological Conditions before and during the Flood Event
2.4. Hydrological Model Setup
2.5. Hydrological Model Calibration
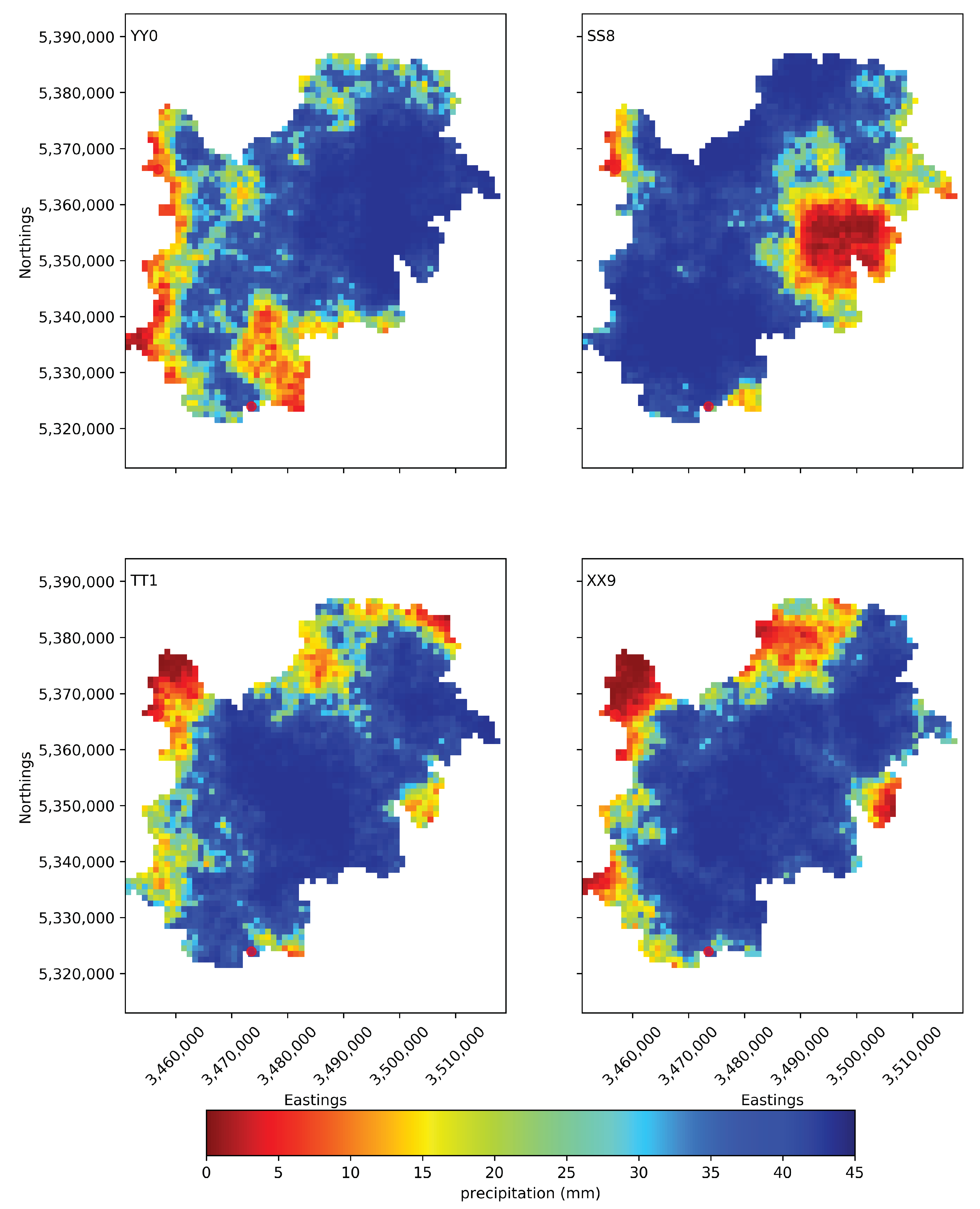
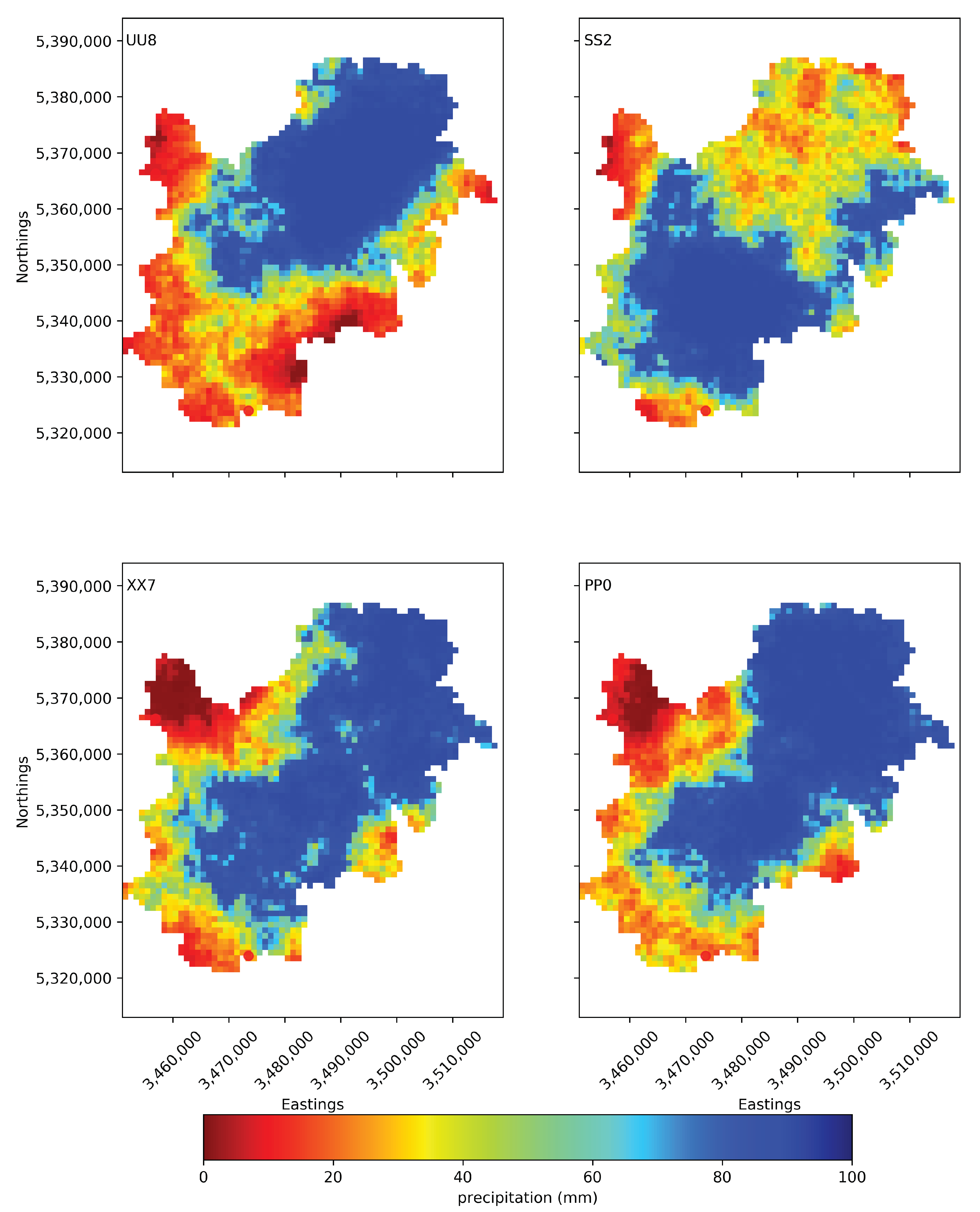
2.6. Historical Precipitation Simulation
- match the observed precipitation measured at the observation locations;
- have values which match the distribution of the observed values of the same day;
- have spatial variability which does not contradict the observations and have the variogram of a typical day of the season;
- and using them as input for the hydrological model, the resulting calculated discharge matches the observed discharge well.
3. Results
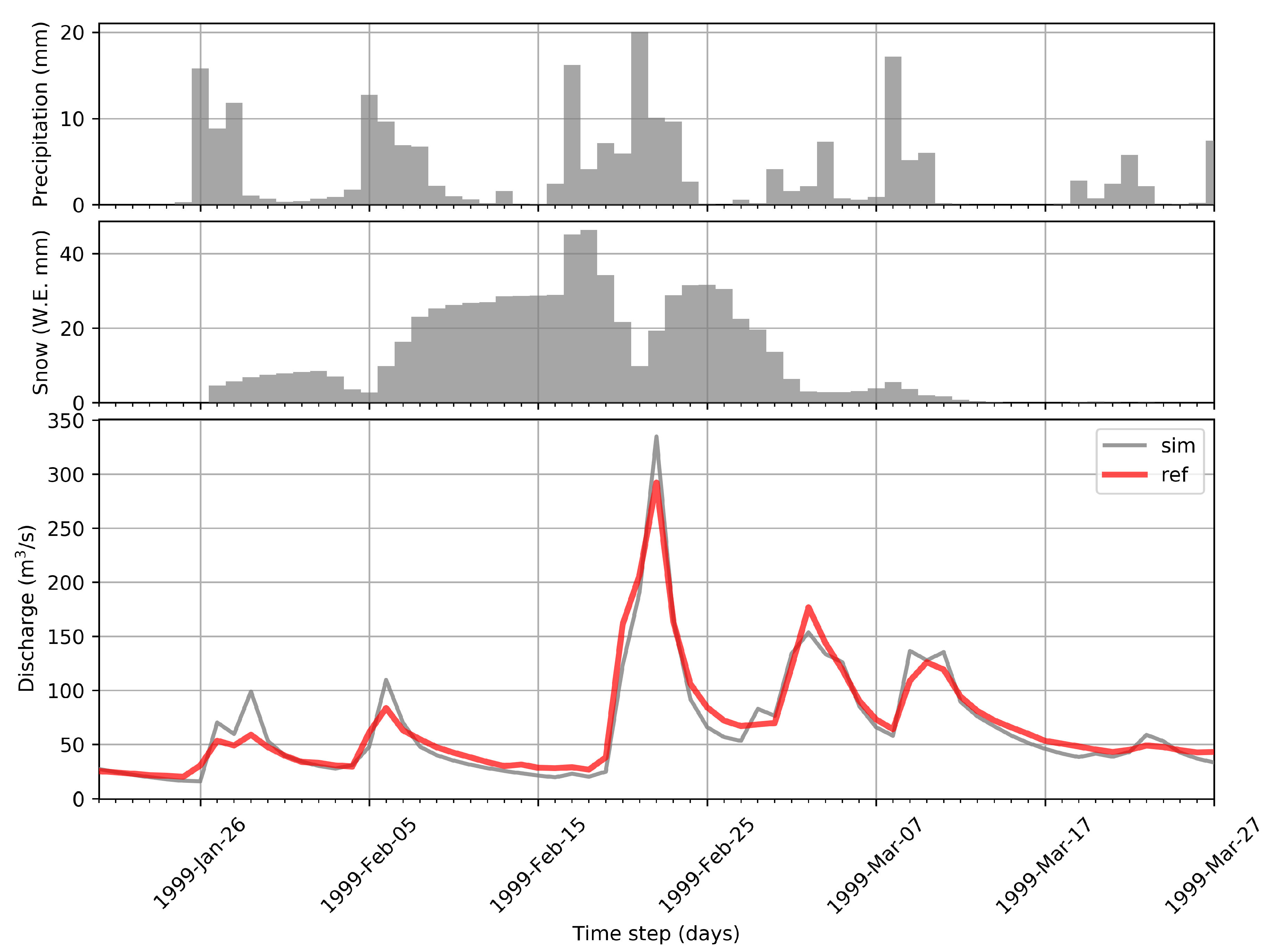
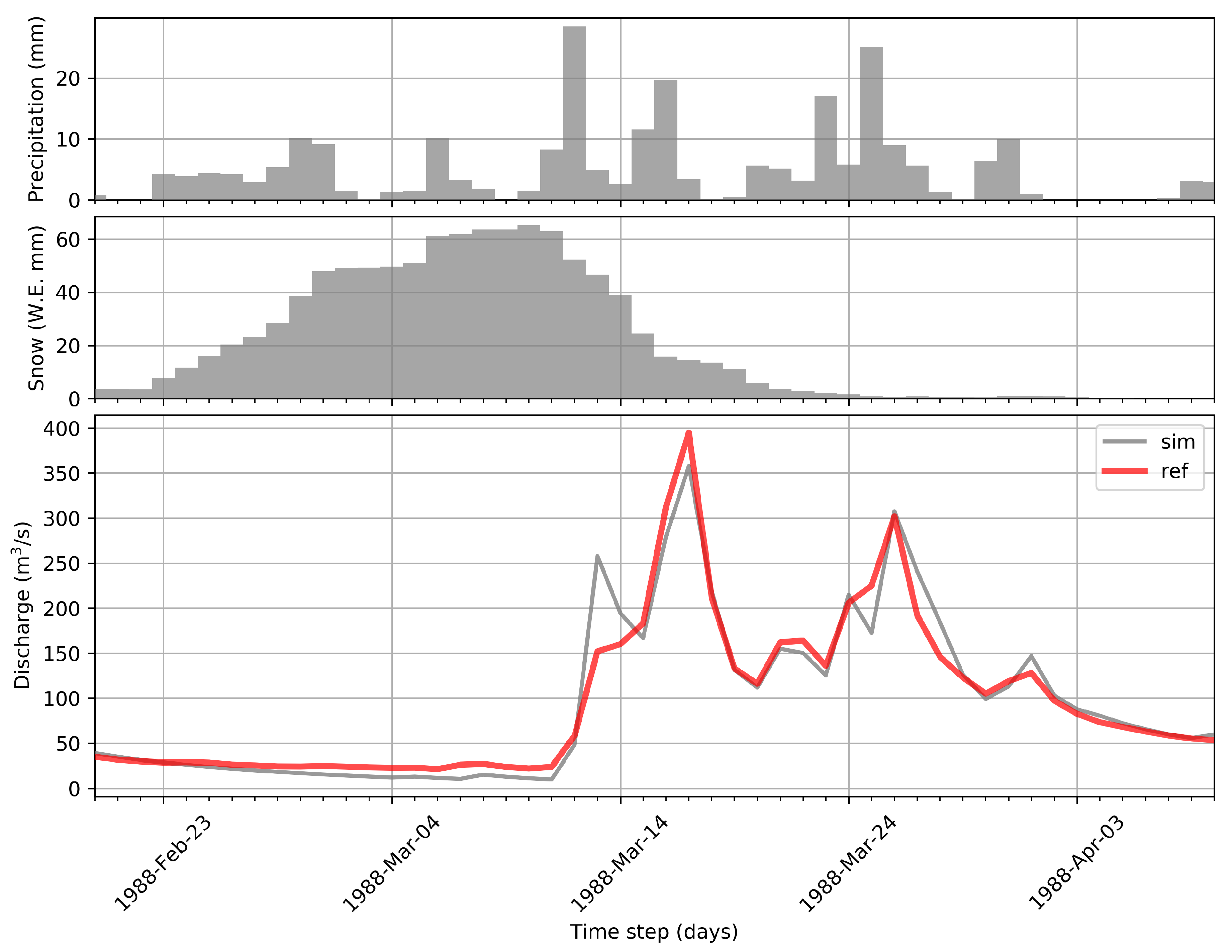
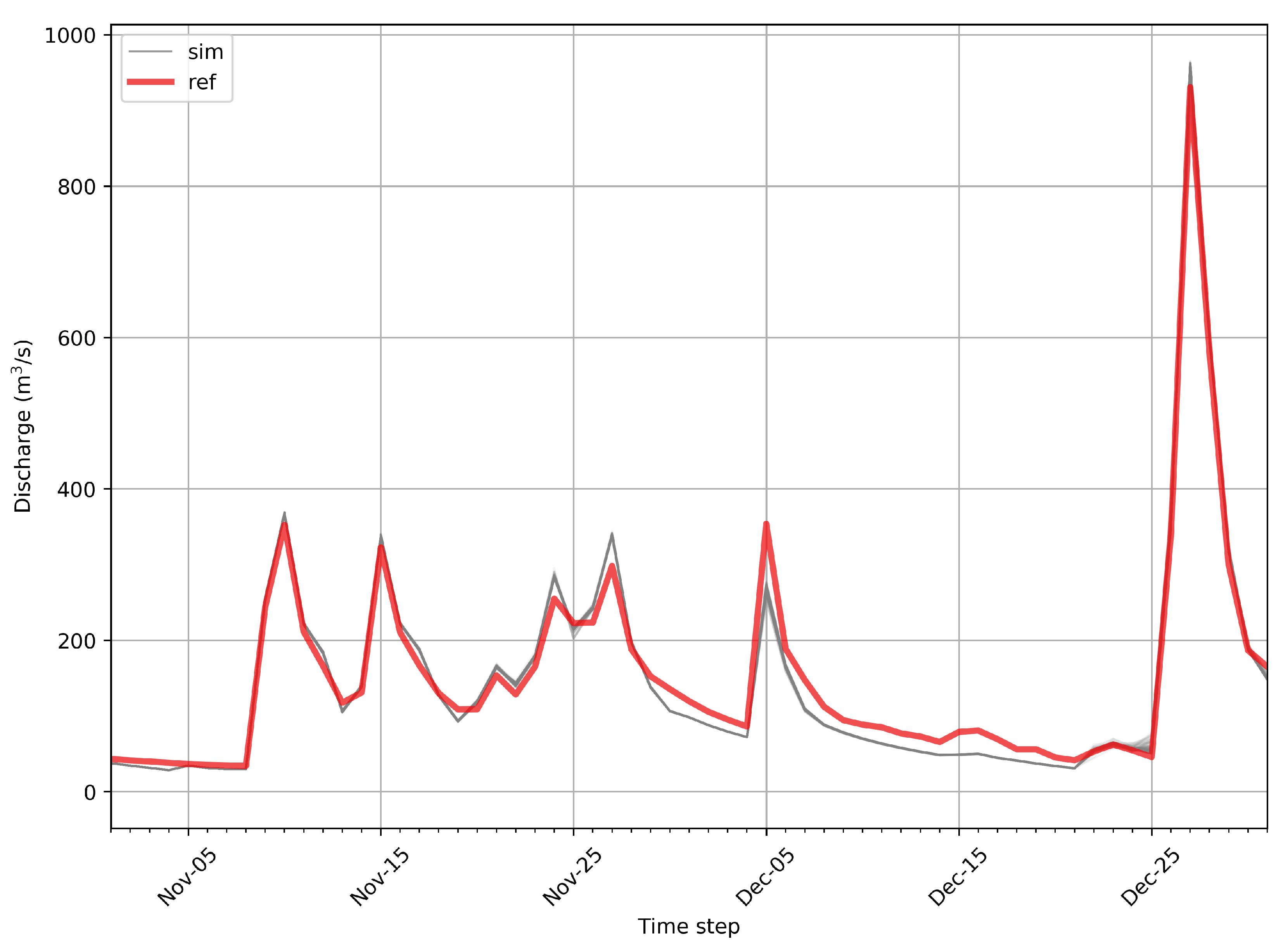
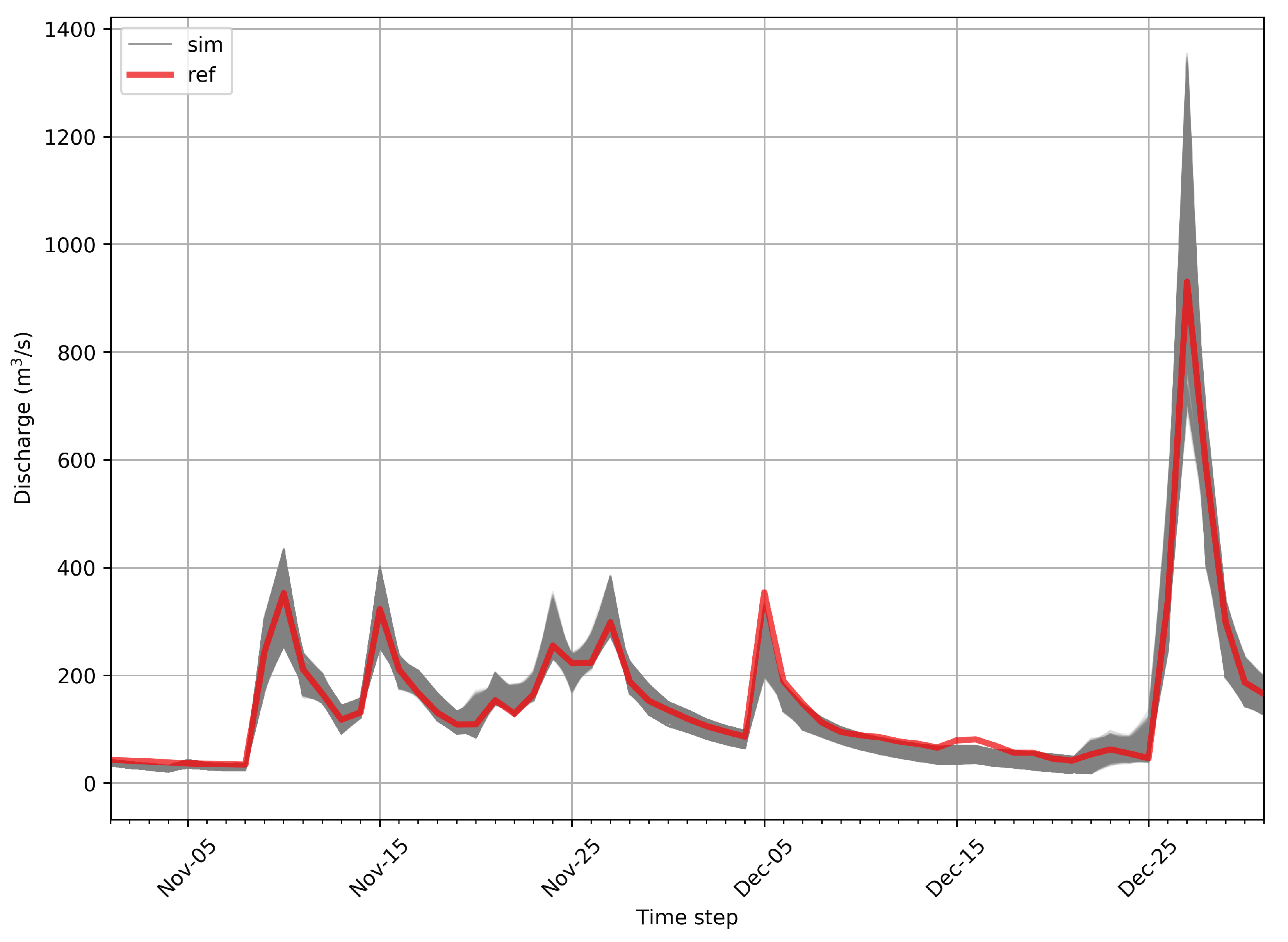
3.1. Calibration and Validation Performance
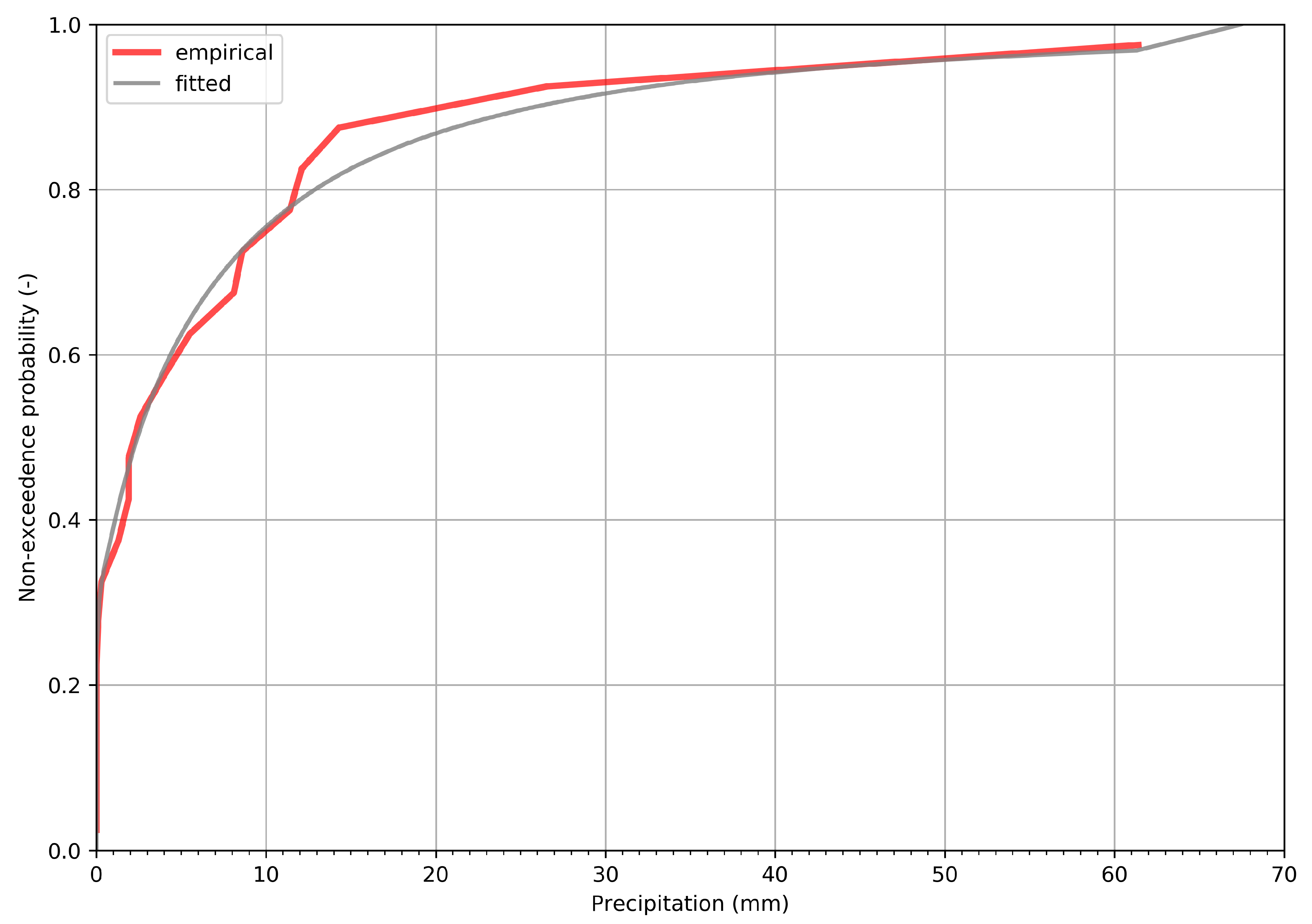
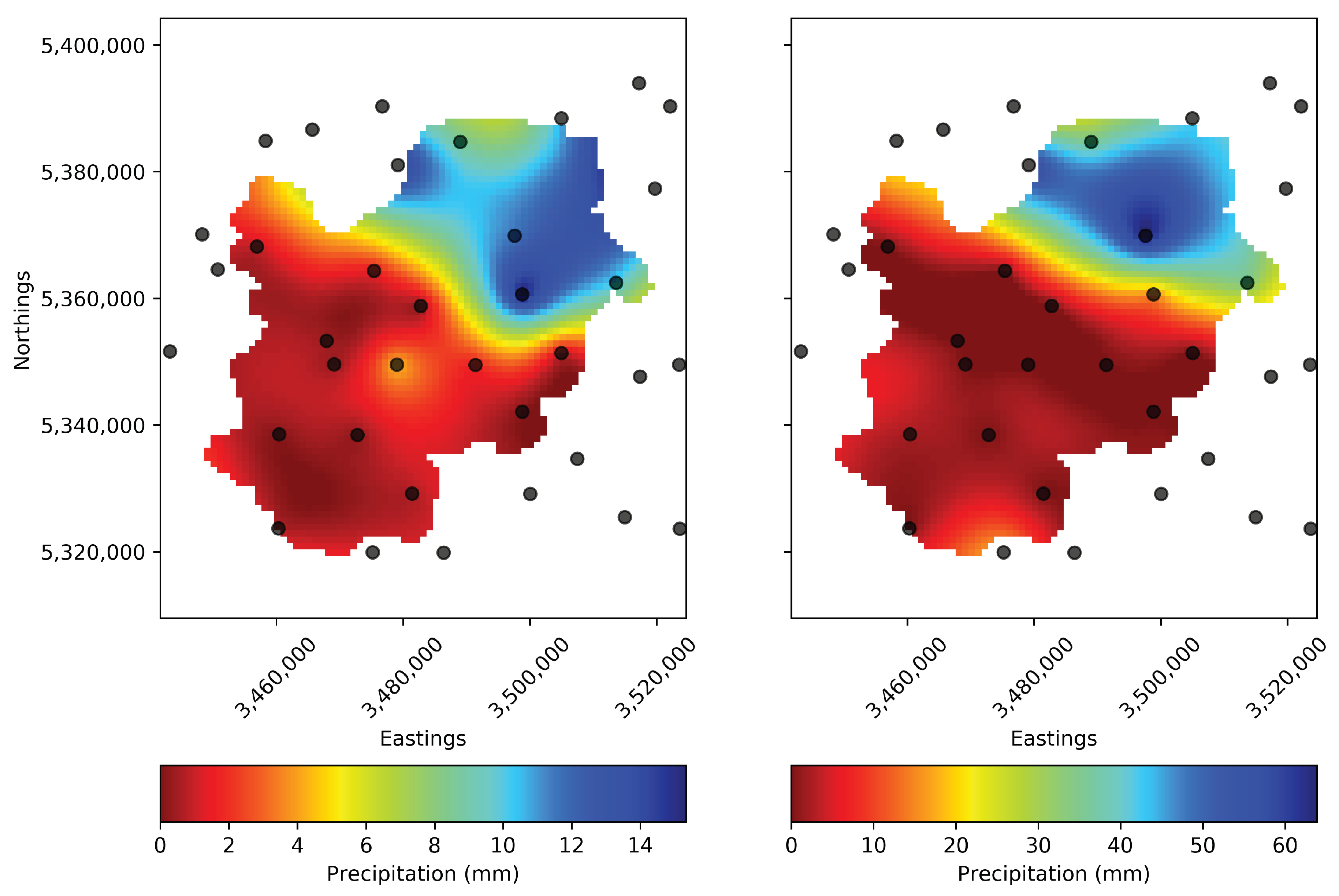
3.2. Inverted Precipitation Performance
3.3. Inverted Precipitation Plausibility
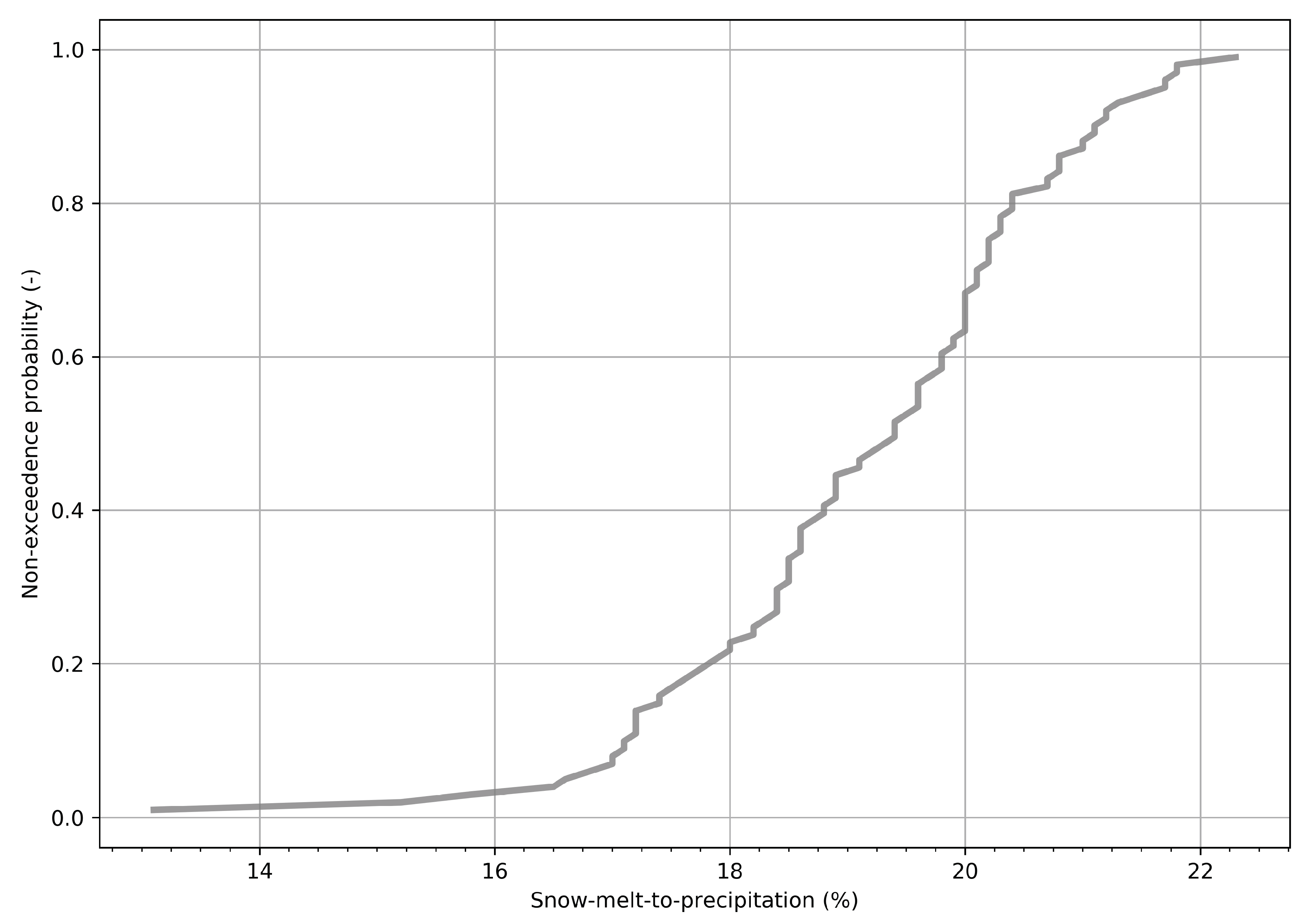
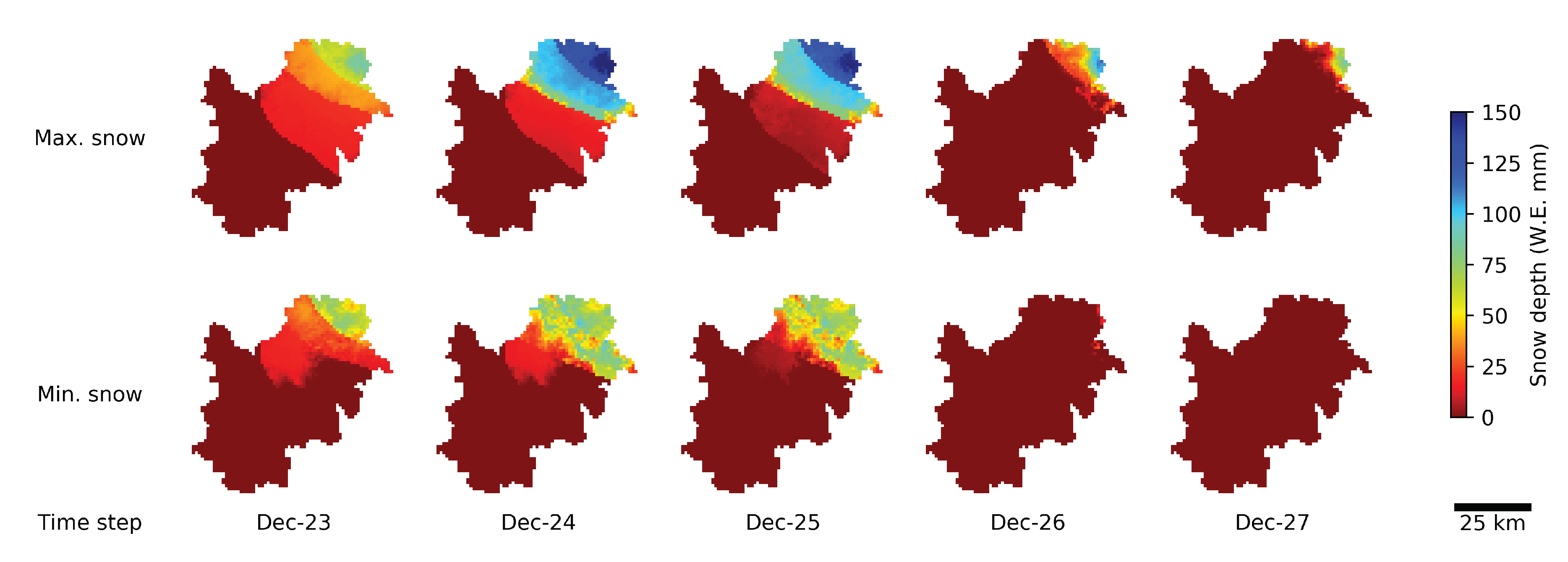
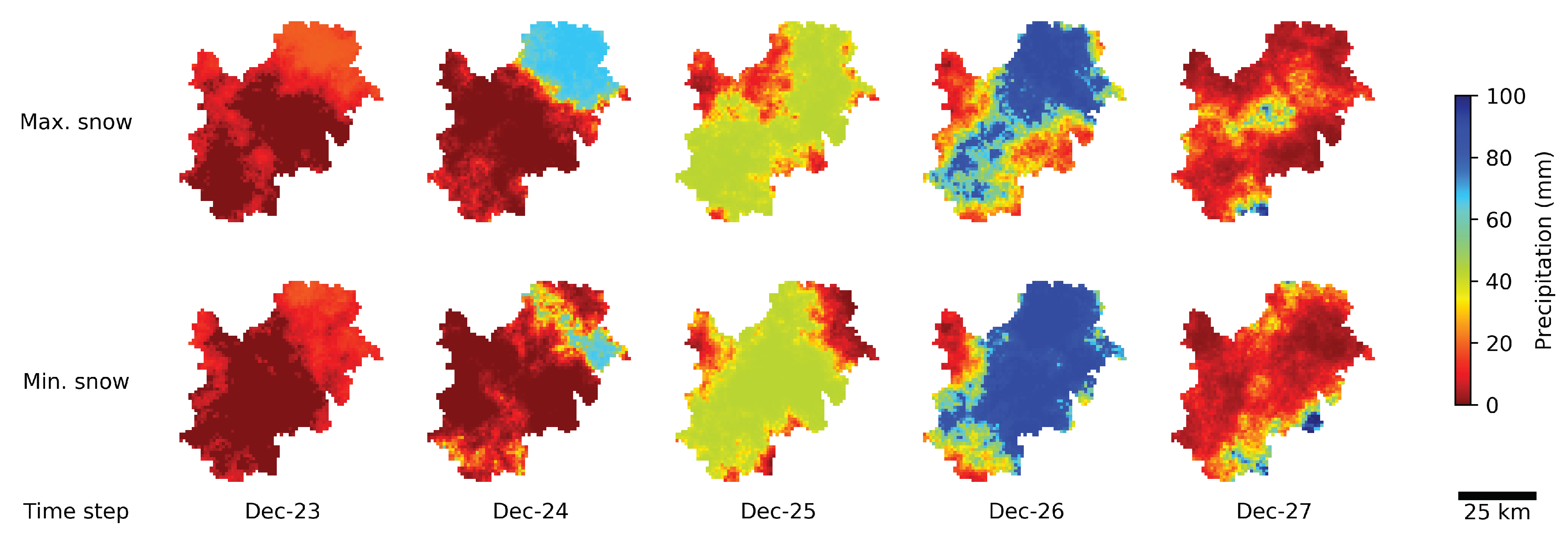
3.4. Snowmelt Contribution to the Peak
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DE | Differential Evolution |
| HBV | Hydrologiska Byråns Vattenbalansavdelning model |
| IDW | Inverse distance weighting |
| NSE | Nash-Sutcliffe efficiency |
| OK | Ordinary Kriging |
| PET | Potential evapotranspiration |
| ROPE | Robust Parameter Estimation |
| W.E. | Water Equivalent |
References
- Benito, G.; Lang, M.; Barriendos, M.; Llasat, M.C.; Francés, F.; Ouarda, T.; Thorndycraft, V.; Enzel, Y.; Bardossy, A.; Coeur, D.; et al. Use of Systematic, Palaeoflood and Historical Data for the Improvement of Flood Risk Estimation. Review of Scientific Methods. Nat. Hazards 2004, 31, 623–643. [Google Scholar] [CrossRef]
- Glaser, R.; Riemann, D.; Schönbein, J.; Barriendos, M.; Brázdil, R.; Bertolin, C.; Camuffo, D.; Deutsch, M.; Dobrovolný, P.; van Engelen, A.; et al. The variability of European floods since AD 1500. Clim. Chang. 2010, 101, 235–256. [Google Scholar] [CrossRef]
- Sudhaus, D.; Seidel, J.; Bürger, K.; Dostal, P.; Imbery, F.; Mayer, H.; Glaser, R.; Konold, W. Discharges of past flood events based on historical river profiles. Hydrol. Earth Syst. Sci. 2008, 12, 1201–1209. [Google Scholar] [CrossRef] [Green Version]
- Herget, J.; Roggenkamp, T.; Krell, M. Estimation of peak discharges of historical floods. Hydrol. Earth Syst. Sci. 2014, 18, 4029–4037. [Google Scholar] [CrossRef] [Green Version]
- Bürger, K.; Seidel, J.; Dostal, P.; Imbery, F.; Barriendos, M.; Mayer, H.; Glaser, R. Hydrometeorological reconstruction of the 1824 flood event in the Neckar River basin (southwest Germany). Hydrol. Sci. J. 2006, 51, 864–877. [Google Scholar] [CrossRef]
- Seidel, J.; Imbery, F.; Dostal, P.; Sudhaus, D.; Bürger, K. Potential of historical meteorological and hydrological data for the reconstruction of historical flood events—The example of the 1882 flood in southwest Germany. Nat. Hazards Earth Syst. Sci. 2009, 9, 175–183. [Google Scholar] [CrossRef]
- Bomers, A.; van der Meulen, B.; Schielen, R.M.J.; Hulscher, S.J.M.H. Historic Flood Reconstruction with the Use of an Artificial Neural Network. Water Resour. Res. 2019, 55, 9673–9688. [Google Scholar] [CrossRef] [Green Version]
- Fischer, S.; Schumann, A. Spatio-temporal consideration of the impact of flood event types on flood statistic. Stoch. Environ. Res. Risk Assess. 2020, 34, 1331–1351. [Google Scholar] [CrossRef]
- Kirchner, J.W. Catchments as simple dynamical systems: Catchment characterization, rainfall-runoff modeling, and doing hydrology backward. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef] [Green Version]
- Herrnegger, M.; Nachtnebel, H.P.; Schulz, K. From runoff to rainfall: Inverse rainfall–runoff modelling in a high temporal resolution. Hydrol. Earth Syst. Sci. 2015, 19, 4619–4639. [Google Scholar] [CrossRef] [Green Version]
- Wright, A.J.; Walker, J.P.; Pauwels, V.R.N. Estimating rainfall time series and model parameter distributions using model data reduction and inversion techniques. Water Resour. Res. 2017, 53, 6407–6424. [Google Scholar] [CrossRef]
- Boudhraâ, H.; Cudennec, C.; Andrieu, H.; Slimani, M. Net rainfall estimation by the inversion of a geomorphology-based transfer function and discharge deconvolution. Hydrol. Sci. J. 2018, 63, 285–301. [Google Scholar] [CrossRef]
- Wright, A.J.; Walker, J.P.; Pauwels, V.R.N. Identification of Hydrologic Models, Optimized Parameters, and Rainfall Inputs Consistent with In Situ Streamflow and Rainfall and Remotely Sensed Soil Moisture. J. Hydrometeorol. 2018, 19, 1305–1320. [Google Scholar] [CrossRef]
- Grundmann, J.; Hörning, S.; Bárdossy, A. Stochastic reconstruction of spatio-temporal rainfall patterns by inverse hydrologic modelling. Hydrol. Earth Syst. Sci. 2019, 23, 225–237. [Google Scholar] [CrossRef] [Green Version]
- Brázdil, R.; Kundzewicz, Z.W.; Benito, G. Historical hydrology for studying flood risk in Europe. Hydrol. Sci. J. 2006, 51, 739–764. [Google Scholar] [CrossRef]
- DWD. 2020. Available online: https://opendata.dwd.de/climate_environment/CDC/observations_germany/climate/daily/ (accessed on 18 November 2019).
- LUBW. 2020. Available online: https://udo.lubw.baden-wuerttemberg.de/public/ (accessed on 6 February 2020).
- Wackernagel, H. Ordinary Kriging. In Multivariate Geostatistics: An Introduction with Applications; Springer: New York, NY, USA, 2004; Chapter 11; pp. 74–81. [Google Scholar]
- Hargreaves, G.; Samani, Z. Estimating potential evapotranspiration. J. Irrig. Drain. Div. 1982, 108, 225–230. [Google Scholar]
- Shepard, D. A Two-Dimensional Interpolation Function for Irregularly-Spaced Data. In Proceedings of the 1968 23rd ACM National Conference, ACM ’68, New York, NY, USA, 27–29 August 1968; Association for Computing Machinery: New York, NY, USA, 1968; pp. 517–524. [Google Scholar] [CrossRef]
- Bergström, S. The HBV Model: Its Structure and Applications; SMHI Reports Hydrology; SMHI: Norrköping, Sweden, 1992. [Google Scholar]
- Das, T.; Bárdossy, A.; Zehe, E.; He, Y. Comparison of conceptual model performance using different representations of spatial variability. J. Hydrol. 2008, 356, 106–118. [Google Scholar] [CrossRef]
- Francés, F.; Vélez, J.I.; Vélez, J.J. Split-parameter structure for the automatic calibration of distributed hydrological models. J. Hydrol. 2007, 332, 226–240. [Google Scholar] [CrossRef]
- Anwar, F.; Bárdossy, A. HBV in C++ and Cython. 2020. Available online: https://github.com/faizan90/hydmodeling/tree/master/models/hbvs/ (accessed on 6 August 2020).
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models. 1. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Bárdossy, A.; Singh, S.K. Robust estimation of hydrological model parameters. Hydrol. Earth Syst. Sci. 2008, 12, 1273–1283. [Google Scholar] [CrossRef] [Green Version]
- Cullmann, J.; Krausse, T.; Saile, P. Parameterising hydrological models—Comparing optimisation and robust parameter estimation. J. Hydrol. 2011, 404, 323–331. [Google Scholar] [CrossRef]
- Scott, D. Multivariate Density Estimation: Theory, Practice, and Visualization; A Wiley-interscience publication; Wiley: Hoboken, NJ, USA, 1992. [Google Scholar]
- Hörning, S.; Sreekanth, J.; Bárdossy, A. Computational efficient inverse groundwater modeling using Random Mixing and Whittaker-Shannon interpolation. Adv. Water Resour. 2019, 123, 109–119. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. GLUE: 20 years on. Hydrol. Process. 2014, 28, 5897–5918. [Google Scholar] [CrossRef] [Green Version]
- Bárdossy, A.; Das, T. Influence of rainfall observation network on model calibration and application. Hydrol. Earth Syst. Sci. 2008, 12, 77–89. [Google Scholar] [CrossRef] [Green Version]
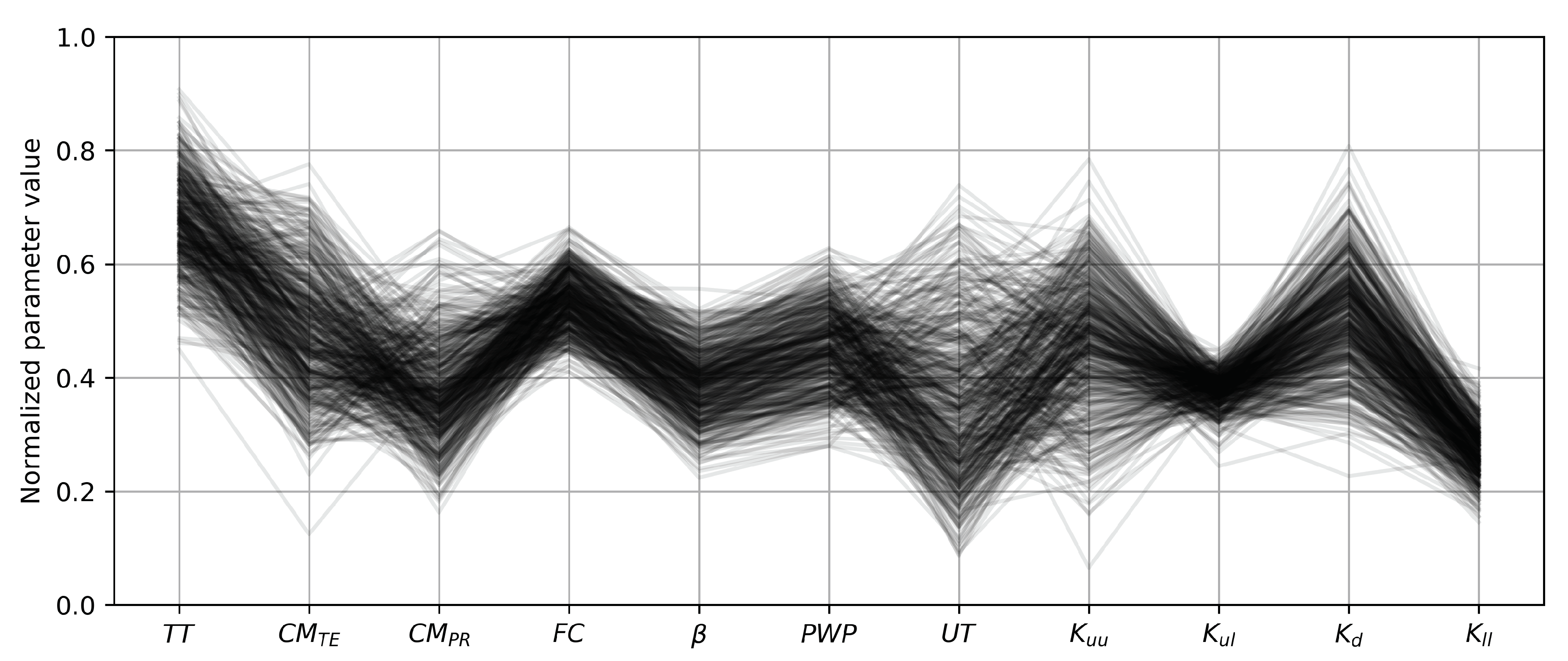
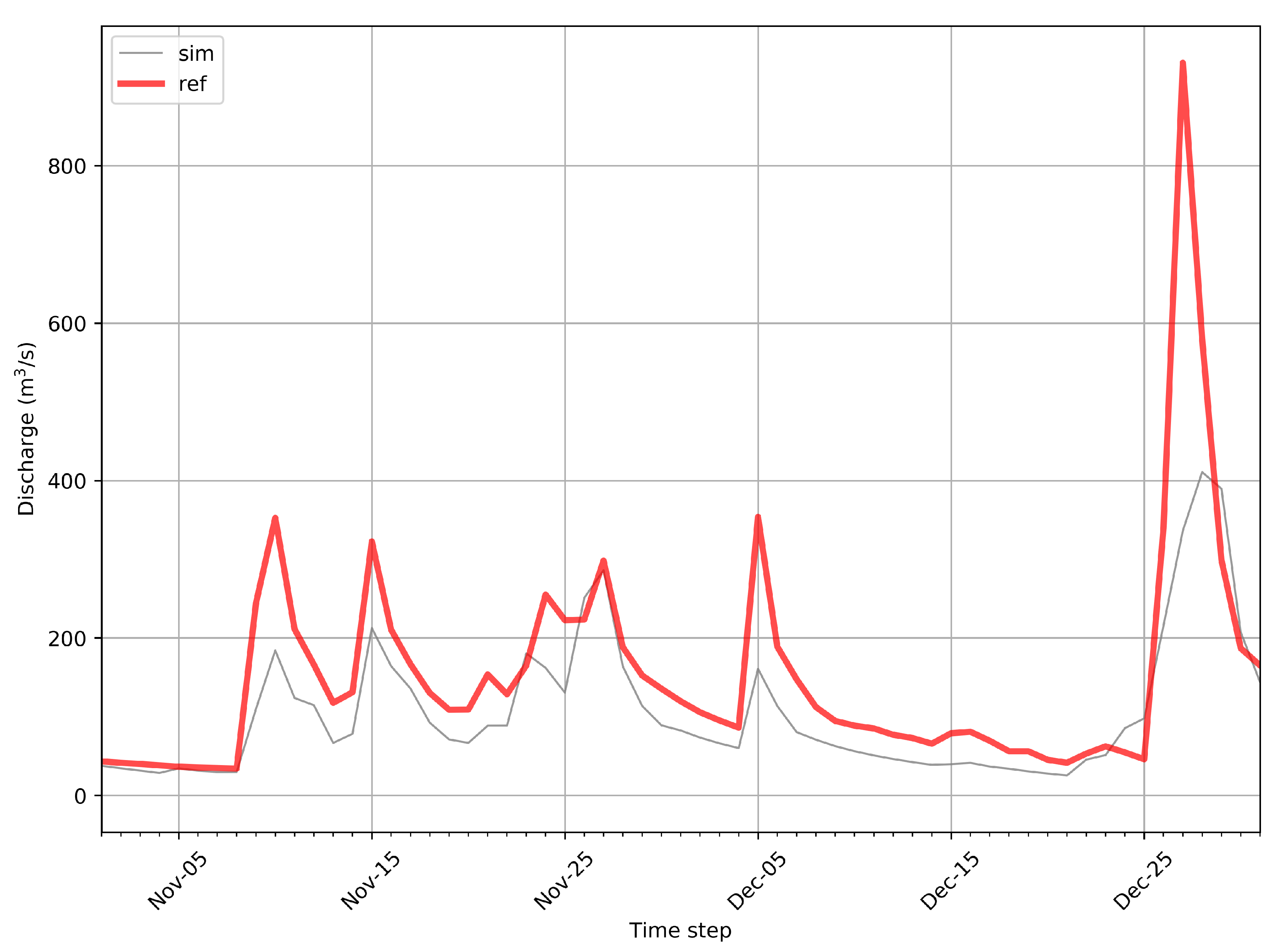
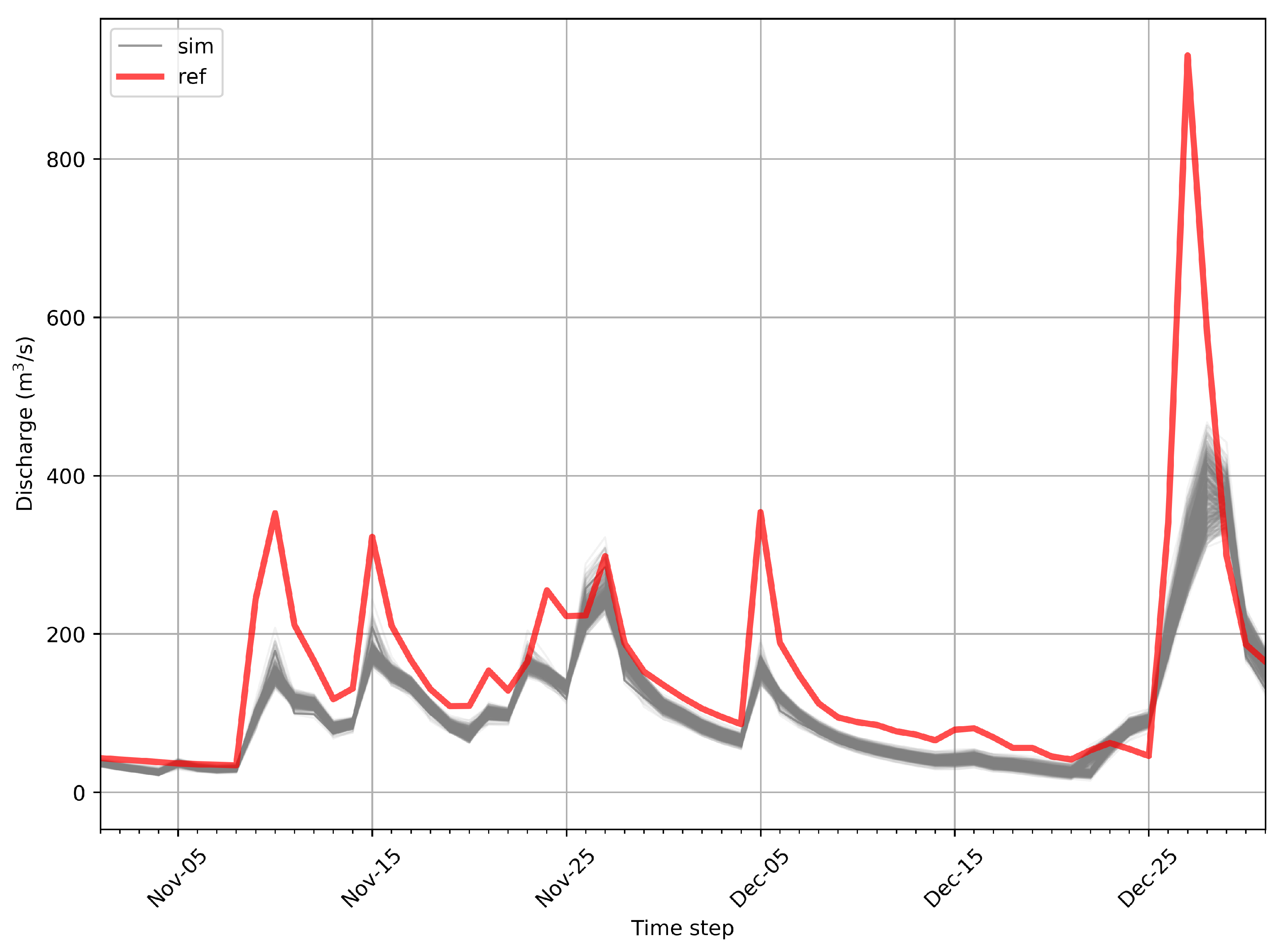
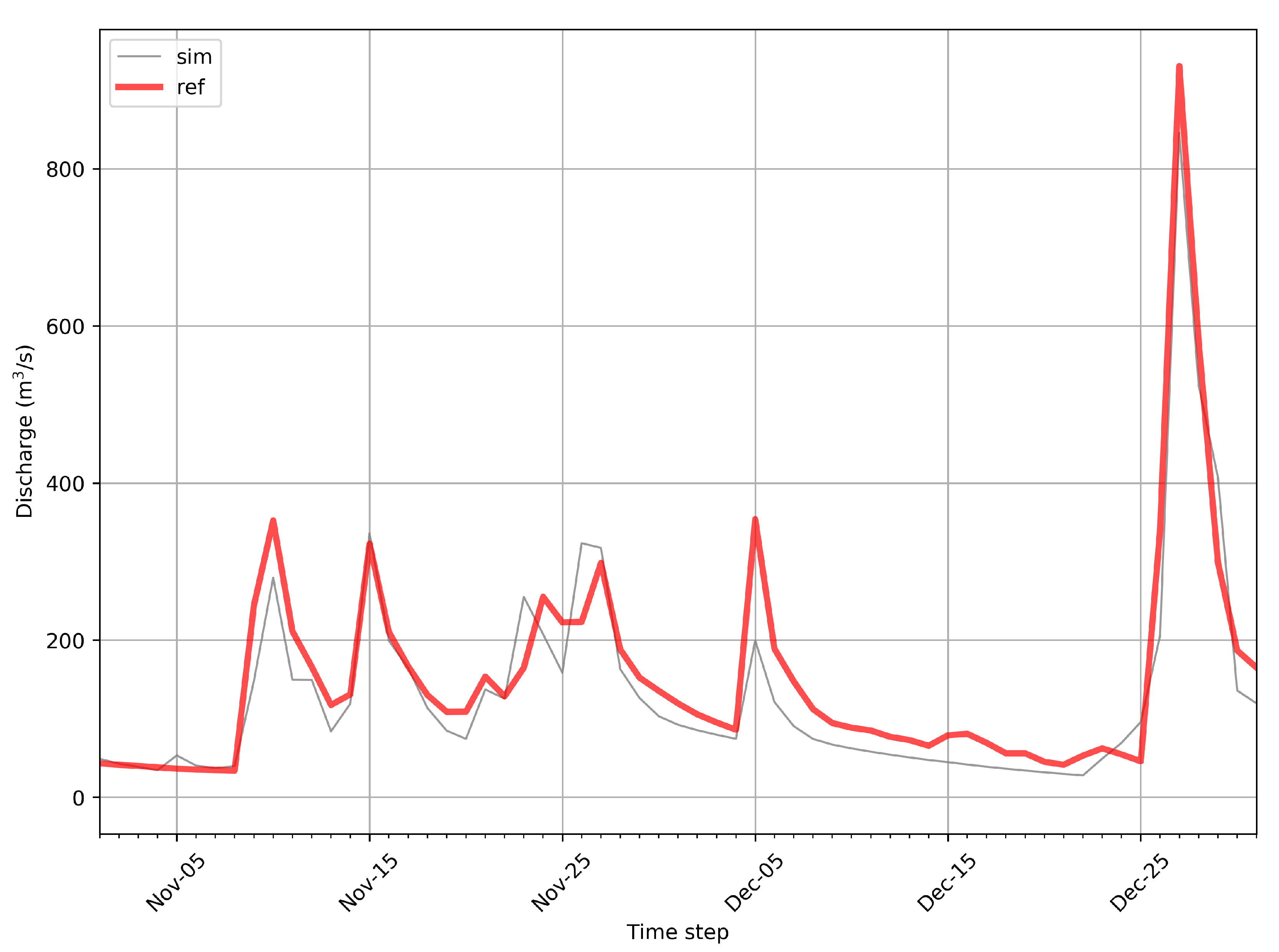
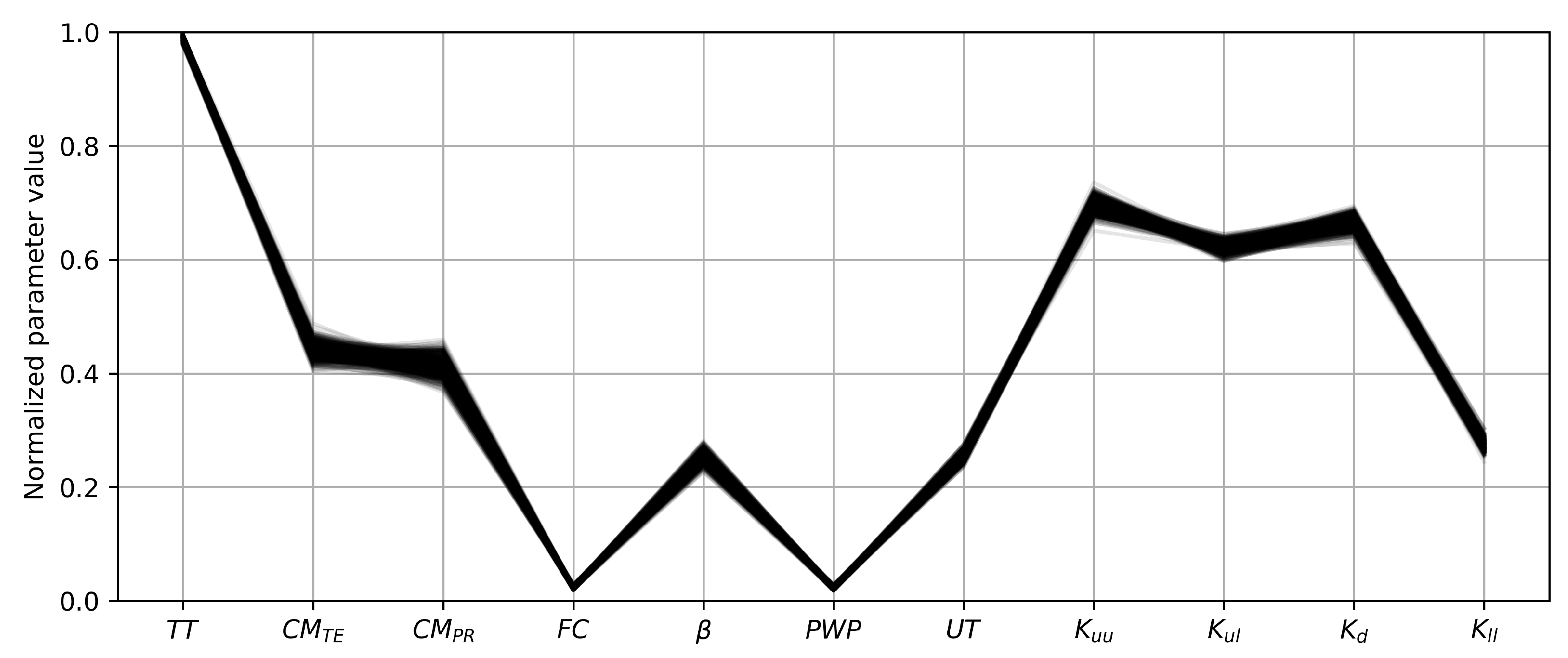
| Parameter | Units | Minimum | Maximum | 1991–2000 | 1882 |
|---|---|---|---|---|---|
| C | −1 | 1 | 0.21 | 0.84 | |
| mm/day/C | 0 | 4 | 2.94 | 0 | |
| mm/day/C/mm | 0 | 2 | 0.14 | 0.31 | |
| mm | 1 | 700 | 385 | 16 | |
| - | 0 | 7 | 2.44 | 1.62 | |
| mm | 1 | 700 | 323 | 16 | |
| mm | 0 | 100 | 7 | 26 | |
| 1/day | 0 | 0.7 | 0.27 | 0.70 | |
| 1/day | 0 | 0.6 | 0.14 | 0.35 | |
| 1/day | 0 | 0.7 | 0.30 | 0.65 | |
| 1/day | 0 | 0.3 | 0.08 | 0.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bárdossy, A.; Anwar, F.; Seidel, J. Hydrological Modelling in Data Sparse Environment: Inverse Modelling of a Historical Flood Event. Water 2020, 12, 3242. https://doi.org/10.3390/w12113242
Bárdossy A, Anwar F, Seidel J. Hydrological Modelling in Data Sparse Environment: Inverse Modelling of a Historical Flood Event. Water. 2020; 12(11):3242. https://doi.org/10.3390/w12113242
Chicago/Turabian StyleBárdossy, András, Faizan Anwar, and Jochen Seidel. 2020. "Hydrological Modelling in Data Sparse Environment: Inverse Modelling of a Historical Flood Event" Water 12, no. 11: 3242. https://doi.org/10.3390/w12113242
APA StyleBárdossy, A., Anwar, F., & Seidel, J. (2020). Hydrological Modelling in Data Sparse Environment: Inverse Modelling of a Historical Flood Event. Water, 12(11), 3242. https://doi.org/10.3390/w12113242





