Numerical Investigation of Multiple-Impact Behavior of Granular Flow on a Rigid Barrier
Abstract
1. Introduction
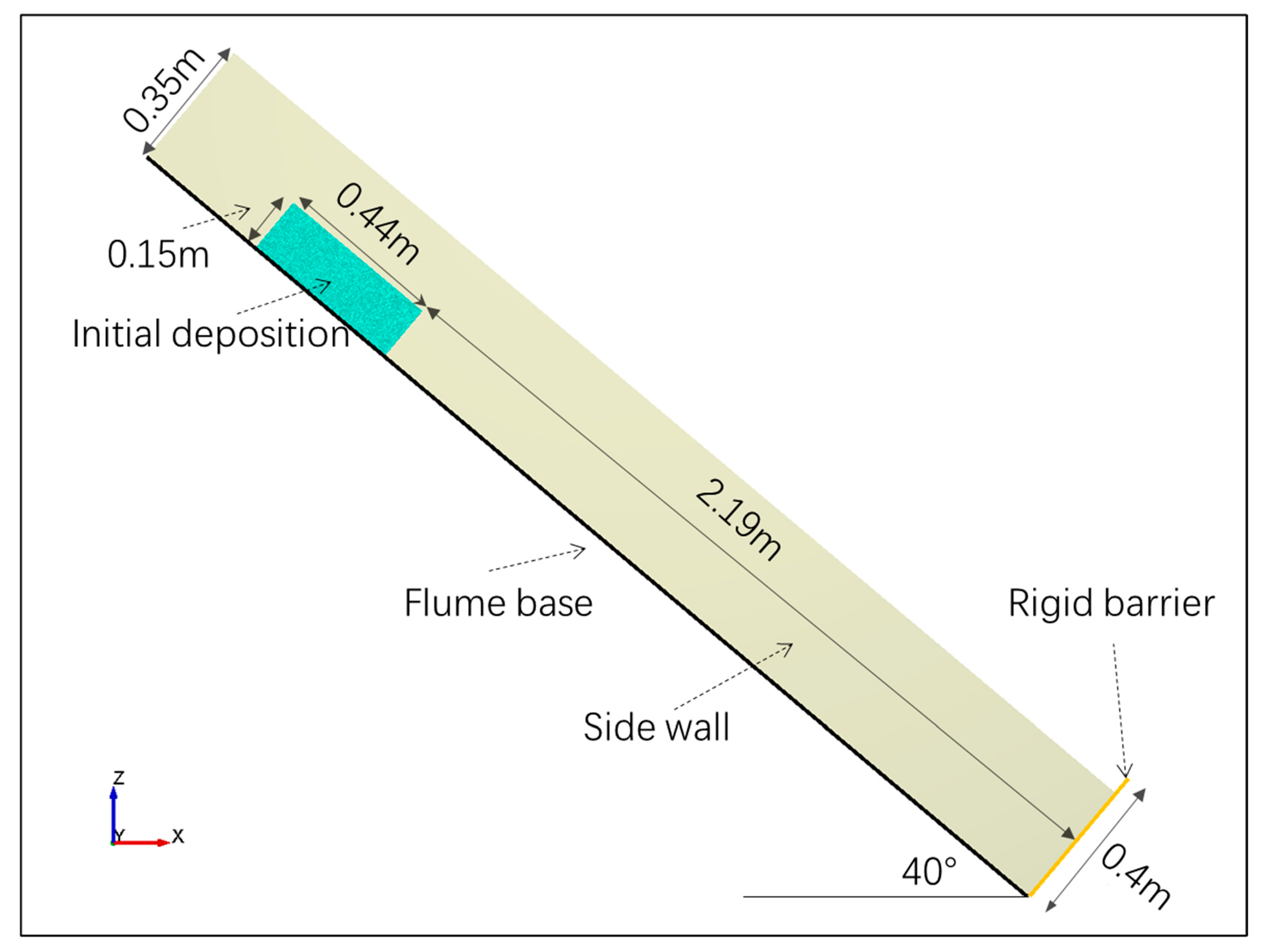
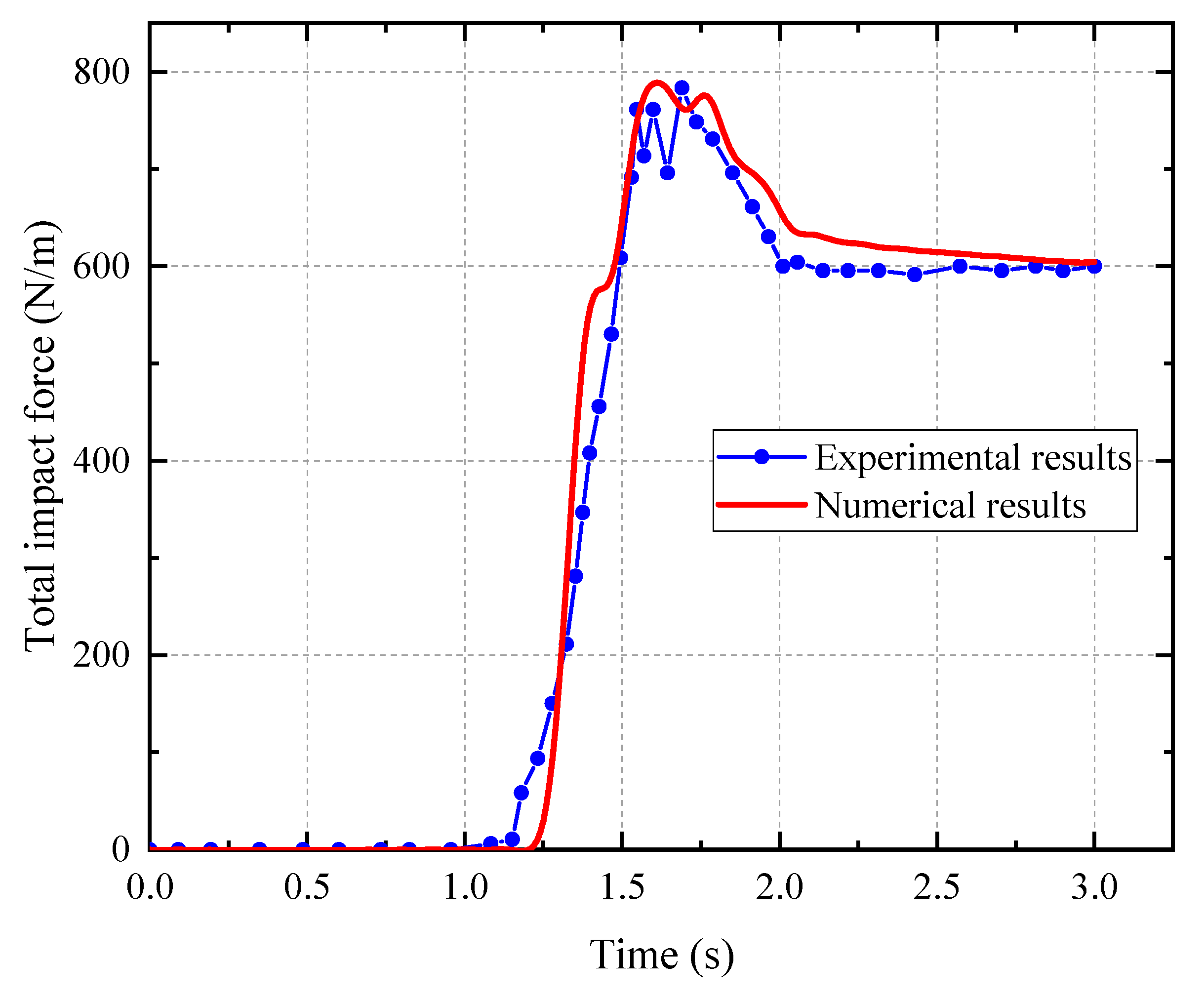
2. Materials and Methods
3. Results and Interpretation
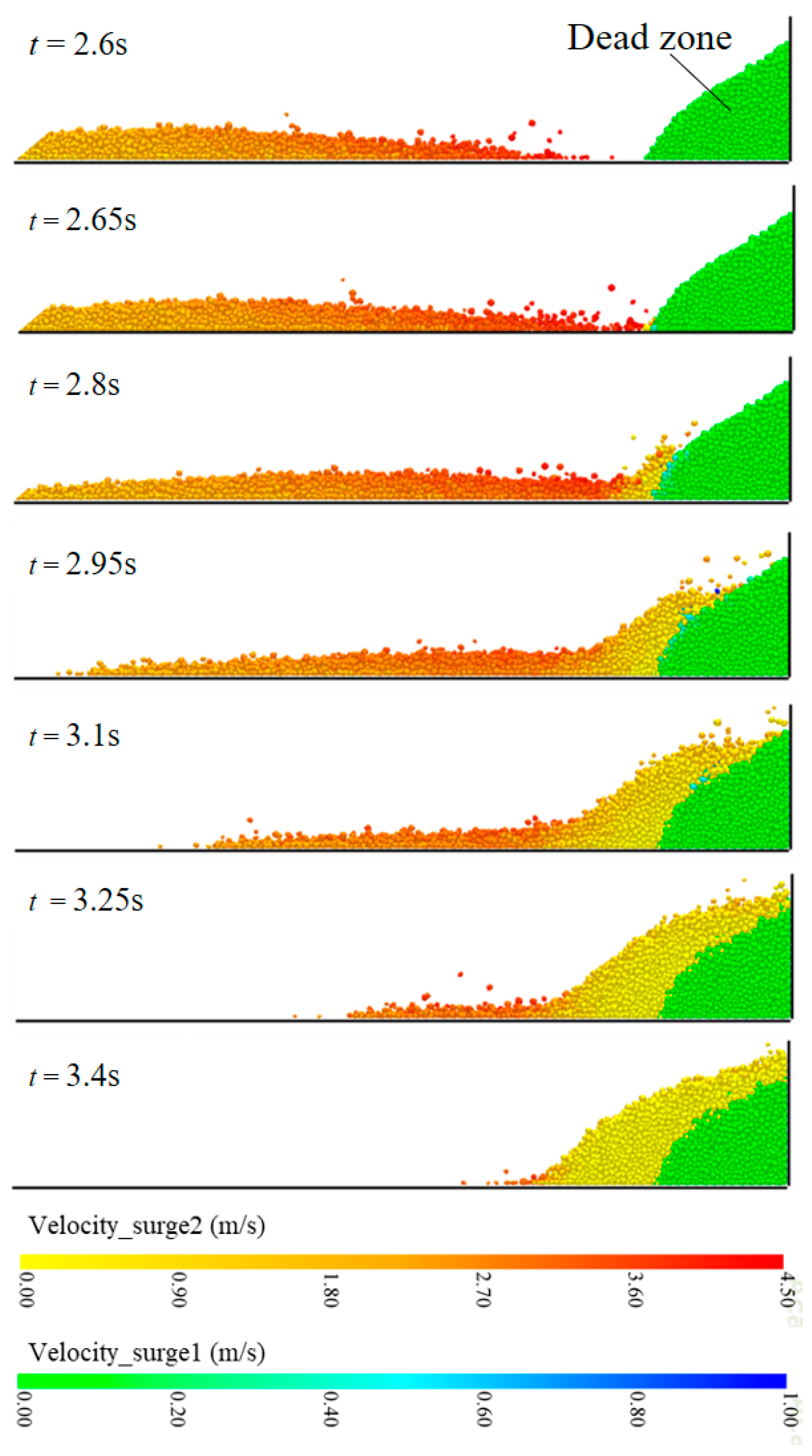
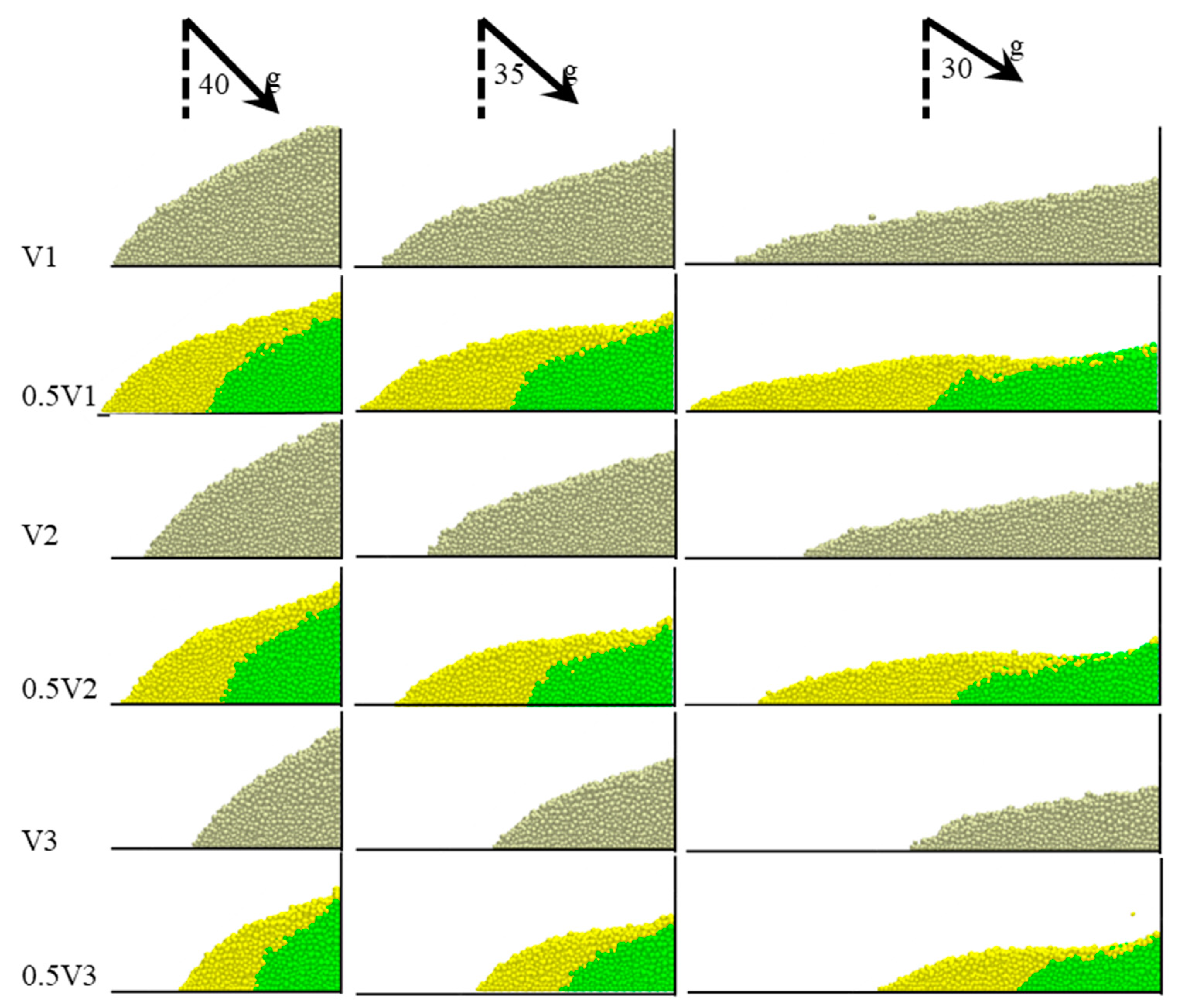
3.1. Flow–Dead-Zone Interaction Mechanism
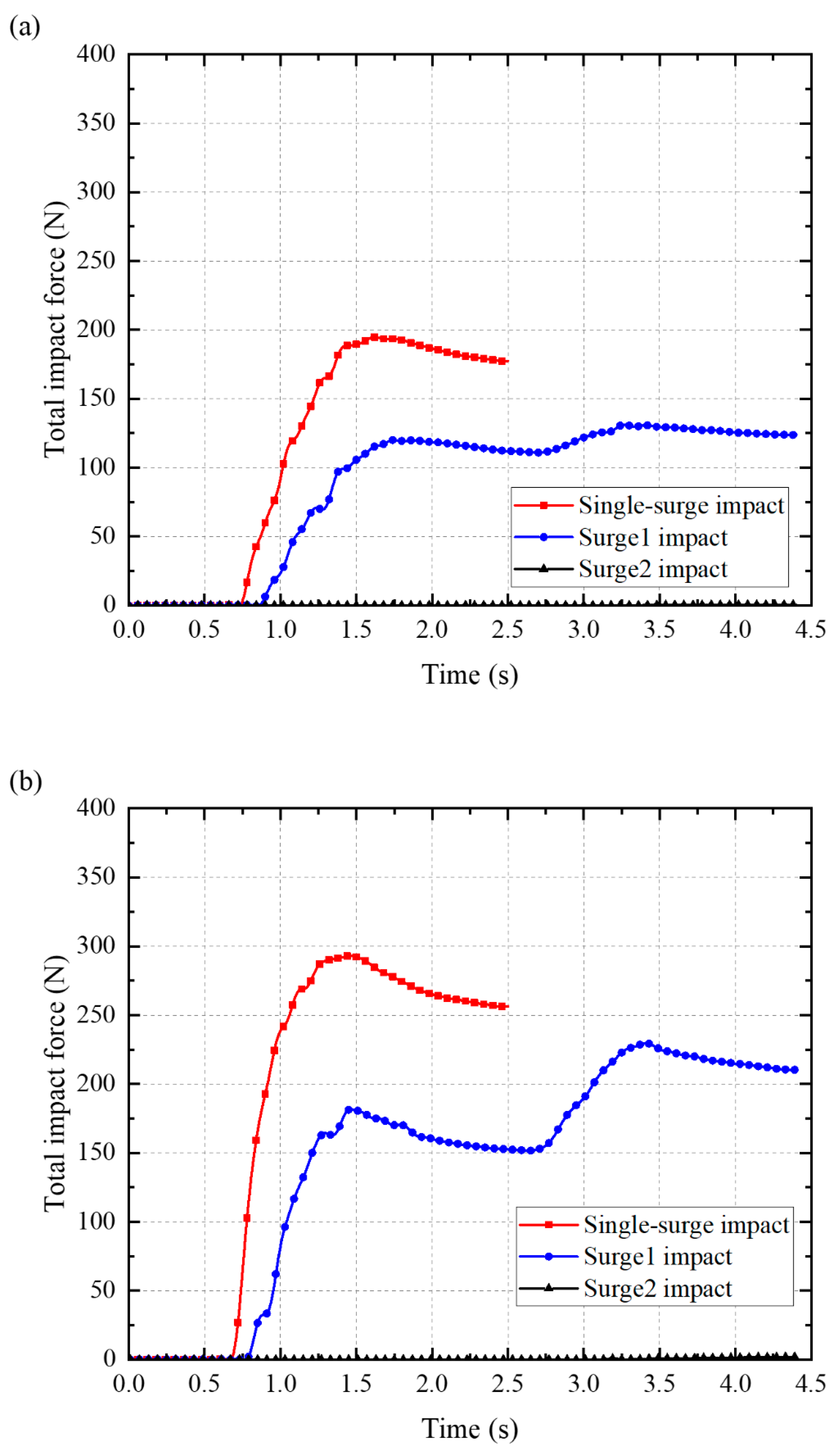
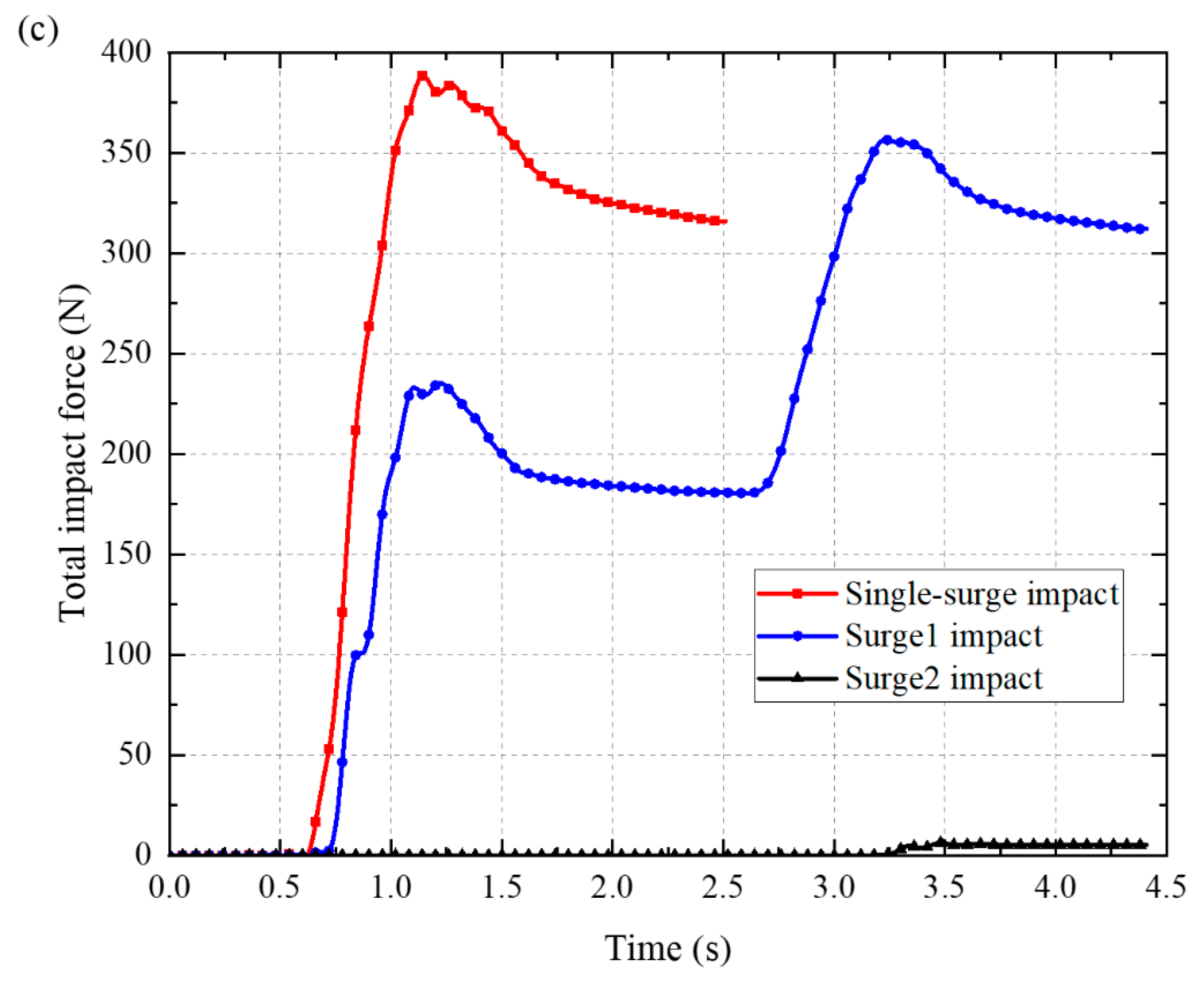
3.2. Impact Dynamics
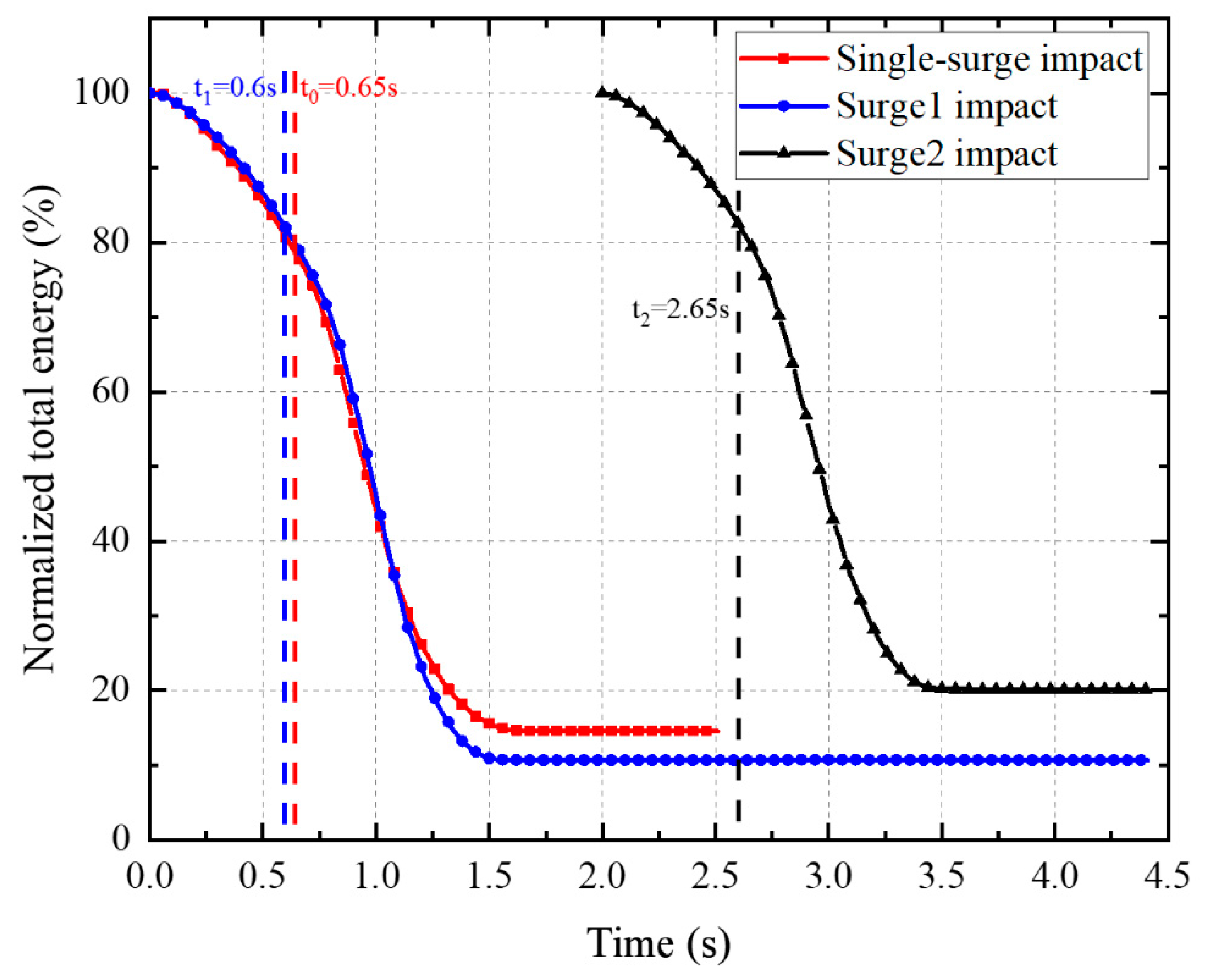
3.3. Energy Evolution
4. Discussion
4.1. Prediction of Multiple-Surge Impact Forces
4.2. Engineering Implications and Limitations
5. Conclusions
- (1)
- For cases in which the total volume of flow material is the same, the barrier is safer under double-surge impact than under single-surge impact, as the deposition spreading distance is extended by 6%~20% and the impact force is reduced by 6%~30%.
- (2)
- Compared with single-surge impact, the energy dissipated by particle–particle interaction during double-surge impact is enhanced by 20% because of the effect of the dead zone.
- (3)
- After the first surge is deposited and the dead zone is formed, the second surge arrives, and a large portion of the energy is dissipated when the second surge interacts with the dead zone. The second flow then impacts the barrier, generating a negligible impact force. The momentum of the subsequent surge is transmitted to the barrier mainly through the dead zone. Thus, the dead zone serves as an effective cushioning layer that protects the barrier.
- (4)
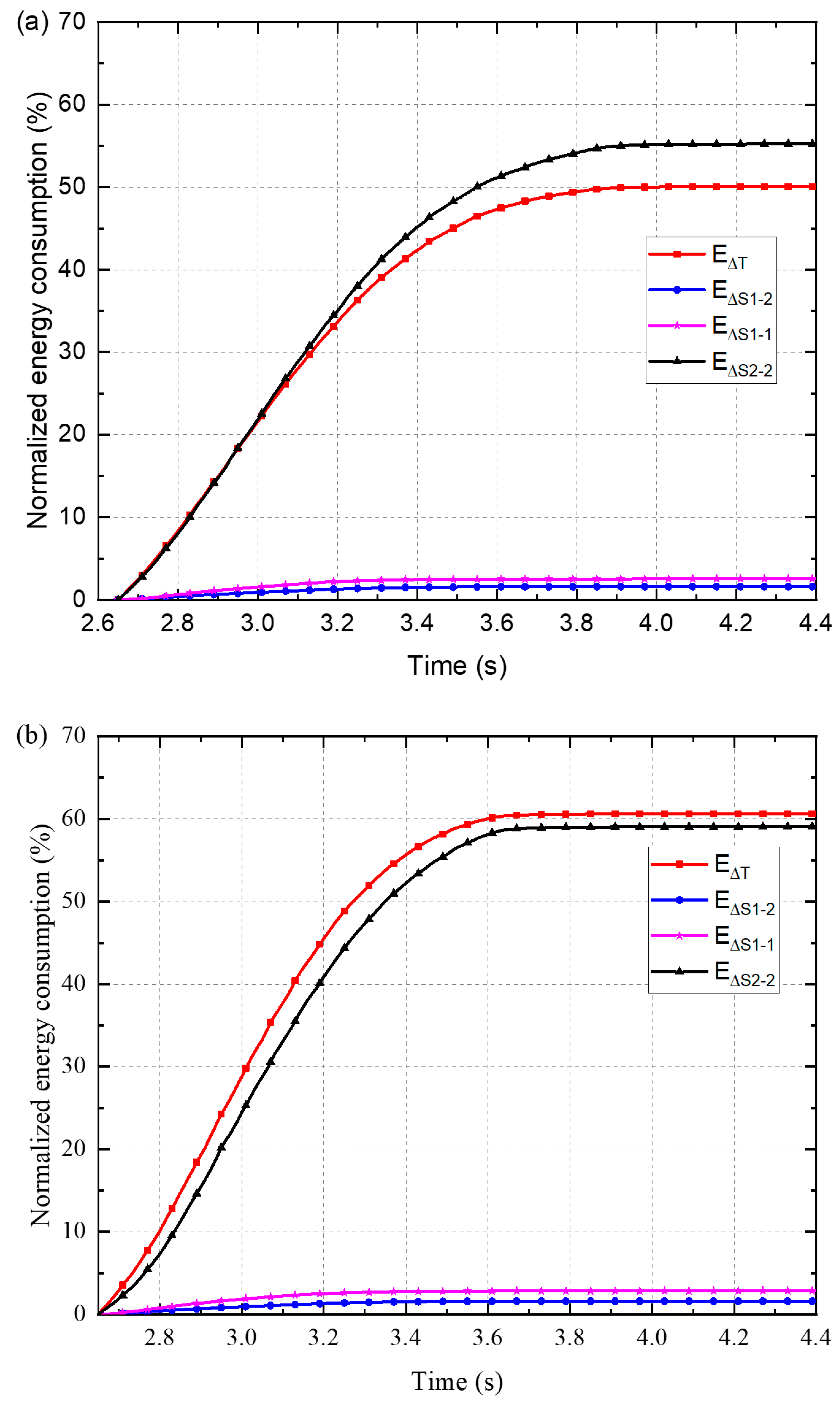
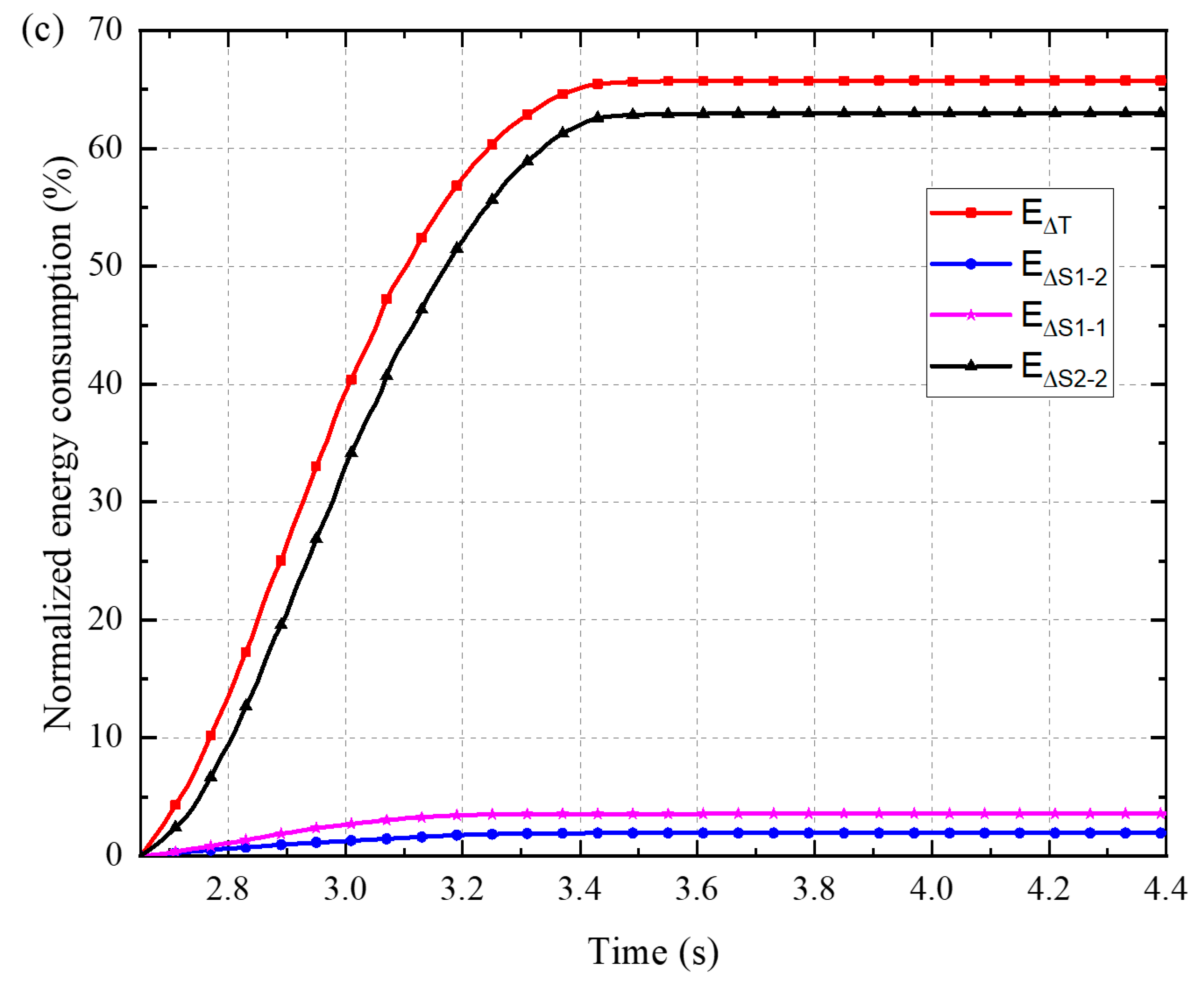
- Multiple-surge impact is a complex process. During the interaction between subsequent surges and the dead zone, three energy consumption mechanisms were identified: (1) friction and penetration at the interaction surface between surge2 and the dead zone, (2) inelastic deformation of the dead zone and (3) inter-particle interaction within surge2. These three mechanisms account for about 2%, 3% and 63% of the total energy loss, respectively.
- (5)
- The depth-averaged model based on granular jump theory may be a promising solution for predicting the multiple-surge impact force on the barrier. However, the performance of the original version is less satisfactory due to the dead zone shape effect, the cushion effect and the dead zone transition, leading to deformation not being reasonably addressed.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
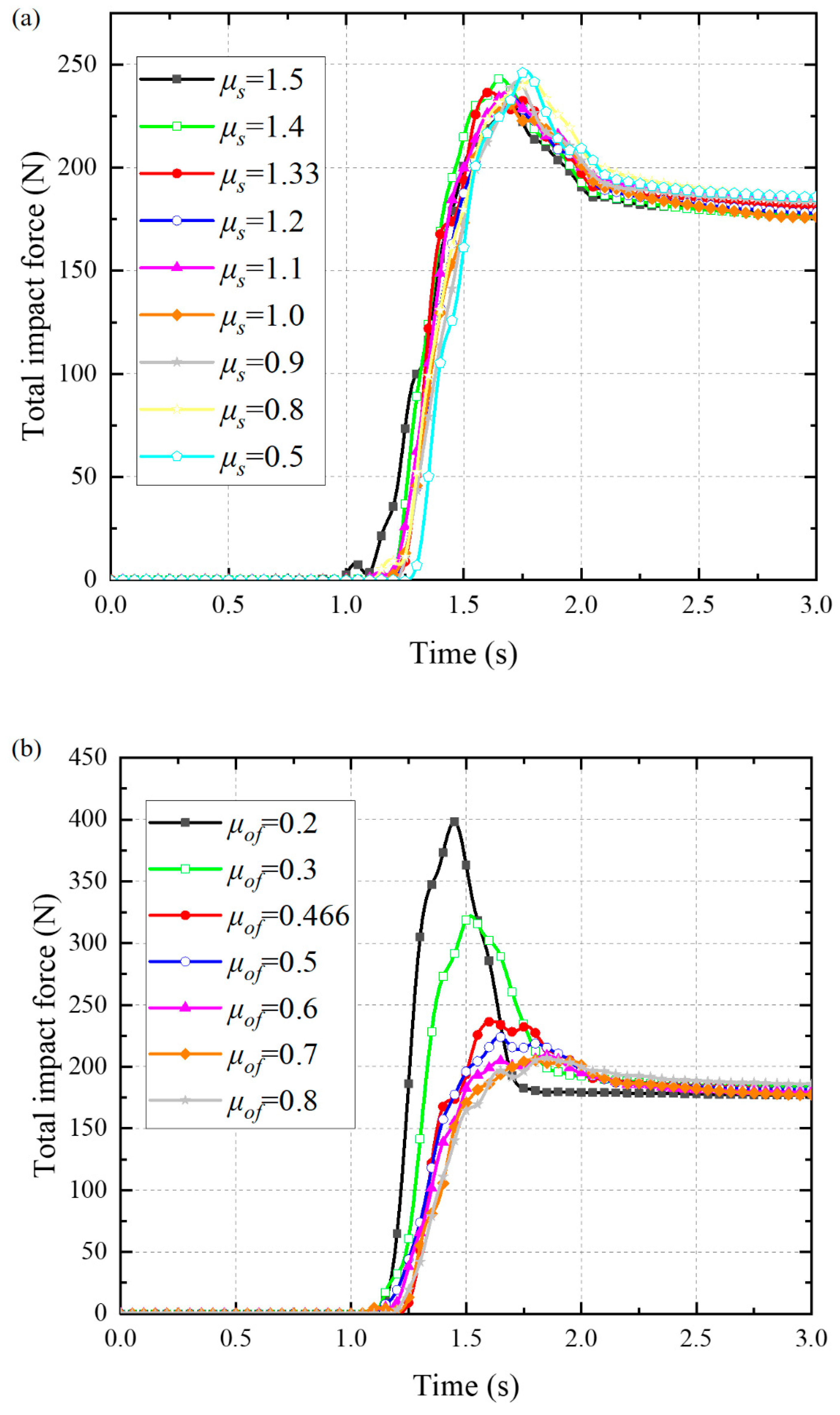
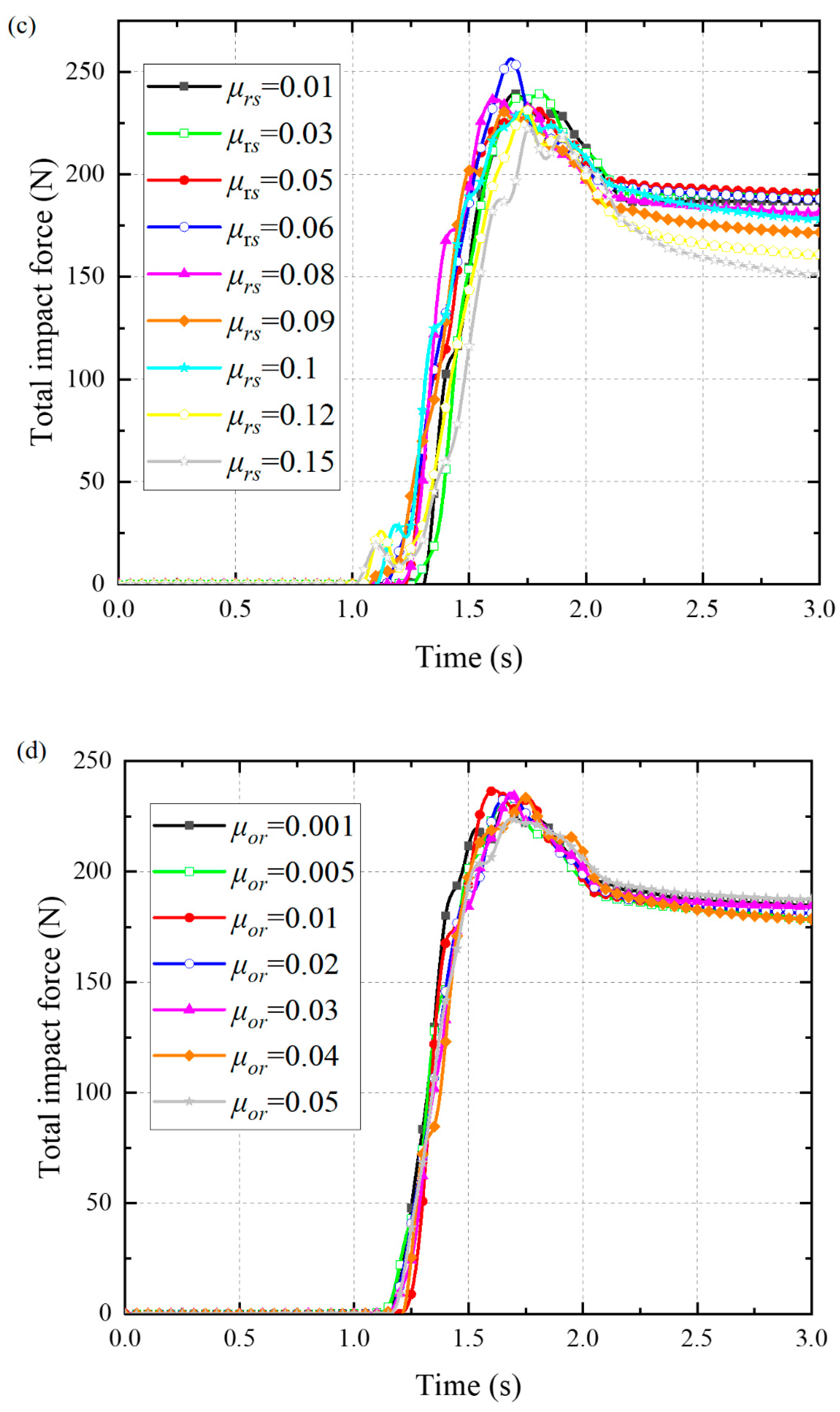
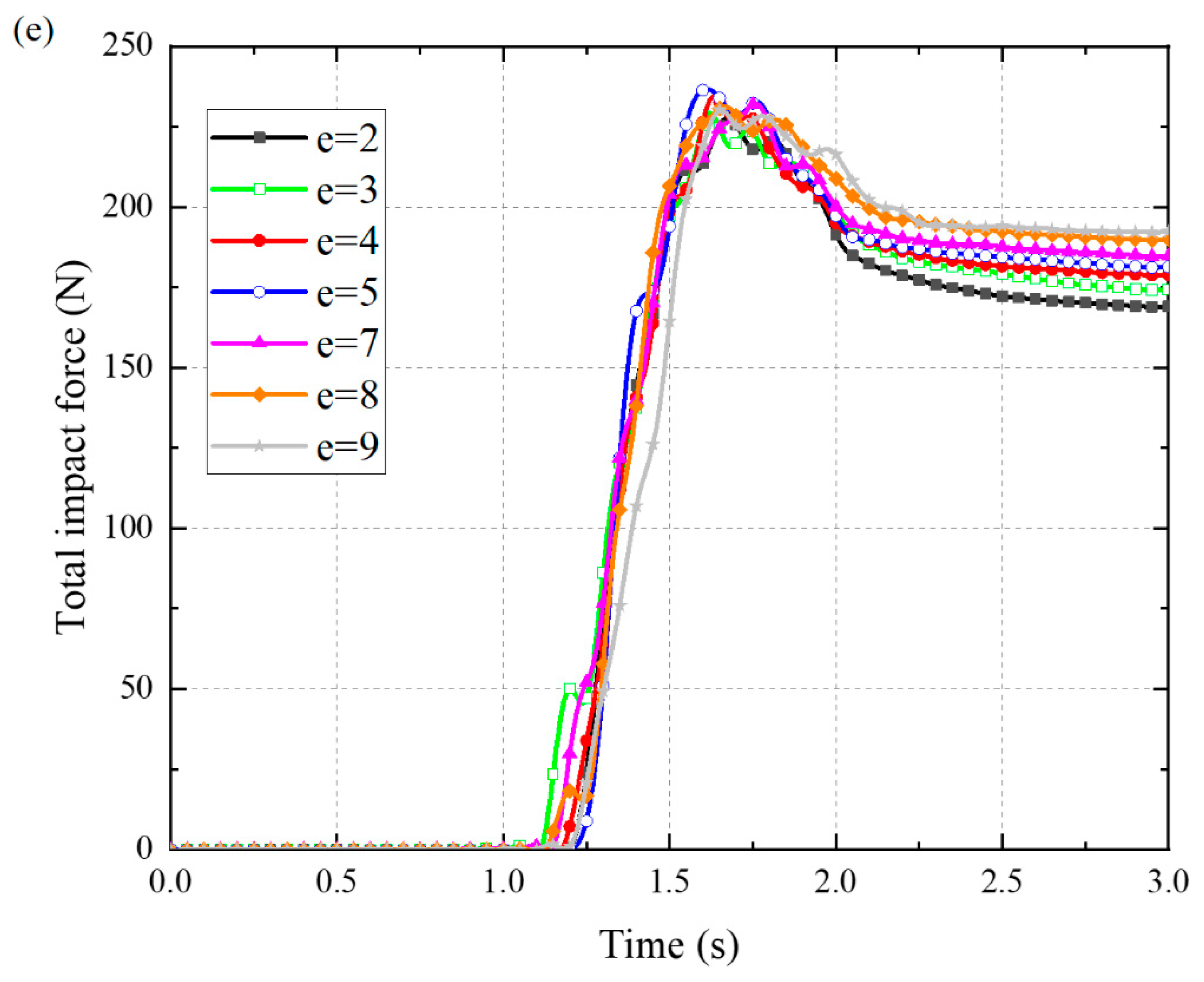
References
- Li, Y.; Ma, C.; Wang, Y. Landslides and debris flows caused by an extreme rainstorm on 21 July 2012 in mountains near Beijing, China. Bull. Eng. Geol. Environ. 2017. [Google Scholar] [CrossRef]
- Thouret, J.C.; Antoine, S.; Magill, C.; Ollier, C. Lahars and debris flows: Characteristics and impacts. Earth-Sci. Rev. 2020, 201, 103003. [Google Scholar] [CrossRef]
- Dai, Z.L.; Huang, Y.; Cheng, H.L.; Xu, Q. SPH model for fluid–structure interaction and its application to debris flow impact estimation. Landslides 2017, 14, 917–928. [Google Scholar] [CrossRef]
- Wang, D.P.; Li, Q.Z.; Bi, Y.Z.; He, S.M. Effects of new baffles system under the impact of rock avalanches. Eng. Geol. 2020, 264. [Google Scholar] [CrossRef]
- Bi, Y.Z.; He, S.M.; Du, Y.J.; Sun, X.P.; Li, X.P. Effects of the configuration of a baffle–avalanche wall system on rock avalanches in Tibet Zhangmu: Discrete element analysis. Bull. Eng. Geol. Environ. 2018, 78, 2267–2282. [Google Scholar] [CrossRef]
- Song, D.; Zhou, G.G.D.; Xu, M.; Choi, C.E.; Li, S.; Zheng, Y. Quantitative analysis of debris-flow flexible barrier capacity from momentum and energy perspectives. Eng. Geol. 2019, 251, 81–92. [Google Scholar] [CrossRef]
- Tan, D.Y.; Yin, J.H.; Qin, J.Q.; Zhu, Z.H.; Feng, W.Q. Experimental study on impact and deposition behaviours of multiple surges of channelized debris flow on a flexible barrier. Landslides 2020. [Google Scholar] [CrossRef]
- Leonardi, A.; Goodwin, G.R.; Pirulli, M. The force exerted by granular flows on slit dams. Acta Geotech. 2019, 14, 1949–1963. [Google Scholar] [CrossRef]
- Zhou, G.G.D.; Du, J.H.; Song, D.R.; Choi, C.E.; Hu, H.S.; Jiang, C. Numerical study of granular debris flow run-up against slit dams by discrete element method. Landslides 2020, 17, 585–595. [Google Scholar] [CrossRef]
- Rossi, G.; Armanini, A. Impact force of a surge of water and sediments mixtures against slit check dams. Sci. Total Environ. 2019, 683, 351–359. [Google Scholar] [CrossRef]
- Vagnon, F. Design of active debris flow mitigation measures: A comprehensive analysis of existing impact models. Landslides 2020, 17, 313–333. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Choi, C.E.; Koo, R.C.H.; Goodwin, G.R.; Song, D.; Kwan, J.S.H. Dry granular flow interaction with dual-barrier systems. Geotechnique 2018, 68, 386–399. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Song, D.; Choi, C.E.; Liu, L.H.D.; Kwan, J.S.H.; Koo, R.C.H.; Pun, W.K. Impact mechanisms of granular and viscous flows on rigid and flexible barriers. Can. Geotech. J. 2016, 54, 188–206. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Towhata, I. Experimental Study of Dry Granular Flow and Impact Behavior Against a Rigid Retaining Wall. Rock Mech. Rock Eng. 2013, 46, 713–729. [Google Scholar] [CrossRef]
- Tan, D.Y.; Yin, J.H.; Zhu, Z.H.; Qin, J.Q.; Chan, H.C.M. Fast Door-Opening Method for Quick Release of Rock Boulder or Debris in Large-Scale Physical Model. Int. J. Geomech. 2020, 20. [Google Scholar] [CrossRef]
- Luo, H.Y.; Zhang, L.M. Earth Pressure Buildup in Impacting Earth Flow behind a Barrier. Int. J. Geomech. 2020, 20. [Google Scholar] [CrossRef]
- Gao, G.; Meguid, M.A. Modeling the Impact of a Falling Rock Cluster on Rigid Structures. Int. J. Geomech. 2018, 18. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Wang, Z.Z.; Song, Y.; Xiao, S.Y. Cushion Layer Effect on the Impact of a Dry Granular Flow against a Curved Rock Shed. Rock Mech. Rock Eng. 2018, 51, 2191–2205. [Google Scholar] [CrossRef]
- Faug, T.; Lachamp, P.; Naaim, M. Experimental investigation on steady granular flows interacting with an obstacle down an inclined channel: Study of the dead zone upstream from the obstacle. Application to interaction between dense snow avalanches and defence structures. Nat. Hazards Earth Syst. Sci. 2002, 2, 187–191. [Google Scholar] [CrossRef]
- Jiang, R.; Fei, W.P.; Zhou, H.W.; Huo, M.; Zhou, J.W.; Wang, J.M.; Wu, J.J. Experimental and numerical study on the load and deformation mechanism of a flexible net barrier under debris flow impact. Bull. Eng. Geol. Environ. 2020. [Google Scholar] [CrossRef]
- Albaba, A.; Lambert, S.; Kneib, F.; Chareyre, B.; Nicot, F. DEM Modeling of a Flexible Barrier Impacted by a Dry Granular Flow. Rock Mech. Rock Eng. 2017, 50, 3029–3048. [Google Scholar] [CrossRef]
- He, S.; Liu, W.; Li, X. Prediction of impact force of debris flows based on distribution and size of particles. Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
- Koo, R.C.H.; Kwan, J.S.H.; Ng, C.W.W.; Lam, C.; Choi, C.E.; Song, D.; Pun, W.K. Velocity attenuation of debris flows and a new momentum-based load model for rigid barriers. Landslides 2016, 14, 617–629. [Google Scholar] [CrossRef]
- Shen, W.G.; Zhao, T.; Dai, F.; Jiang, M.J.; Zhou, G.G.D. DEM analyses of rock block shape effect on the response of rockfall impact against a soil buffering layer. Eng. Geol. 2019, 249, 60–70. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Su, Y.; Choi, C.E.; Song, D.; Lam, C.; Kwan, J.S.H.; Chen, R.; Liu, H. Comparison of Cushioning Mechanisms between Cellular Glass and Gabions Subjected to Successive Boulder Impacts. J. Geotech. Geoenvironmental Eng. 2018, 144, 04018058. [Google Scholar] [CrossRef]
- Soga, K.; Alonso, E.; Yerro, A.; Kumar, K.; Bandara, S. Trends in large-deformation analysis of landslide mass movements with particular emphasis on the material point method. Géotechnique 2015, 66, 248–273. [Google Scholar] [CrossRef]
- Huang, Y.; Cheng, H.L.; Dai, Z.L.; Xu, Q.; Liu, F.; Sawada, K.; Moriguchi, S.; Yashima, A. SPH-based numerical simulation of catastrophic debris flows after the 2008 Wenchuan earthquake. Bull. Eng. Geol. Environ. 2015, 74, 1137–1151. [Google Scholar] [CrossRef]
- Albaba, A.; Lambert, S.; Faug, T. Dry granular avalanche impact force on a rigid wall: Analytic shock solution versus discrete element simulations. Phys. Rev. E 2018, 97, 052903. [Google Scholar] [CrossRef]
- Bi, Y.; He, S.; Li, X.; Ouyang, C.; Wu, Y. Effects of segregation in binary granular mixture avalanches down inclined chutes impinging on defending structures. Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
- Zhou, G.G.D.; Song, D.; Choi, C.E.; Pasuto, A.; Sun, Q.C.; Dai, D.F. Surge impact behavior of granular flows: Effects of water content. Landslides 2018, 15, 695–709. [Google Scholar] [CrossRef]
- Shen, W.G.; Zhao, T.; Zhao, J.D.; Dai, F.; Zhou, G.G.D. Quantifying the impact of dry debris flow against a rigid barrier by DEM analyses. Eng. Geol. 2018, 241, 86–96. [Google Scholar] [CrossRef]

| Material Parameters | Value | Source |
|---|---|---|
| Particle diameter (mm) | 10–20 | [14] |
| Particle density (kg/m3) | 2550 | Lime stone |
| Young’s modulus of particle (MPa) | 100 | [14] |
| Particle Poisson’s ratio | 0.25 | Lime stone |
| Barrier/flume density (kg/m3) | 7900 | Steel material |
| Young’s modulus of barrier/flume (GPa) | 200 | Steel material |
| Poisson’s ratio of barrier/flume | 0.3 | Steel material |
| Coefficient of restitution | 0.5 | Calibration |
| Particle friction coefficient | 1.33 | [14] |
| Particle rolling friction coefficient | 0.08 | Calibration |
| Flume friction coefficient | 0.466 | [14] |
| Barrier friction coefficient | 0.384 | [14] |
| Flume/barrier rolling friction coefficient | 0.01 | Calibration |
| Case Number | Surge Number | Initial Deposition Volume/L | Slope Angle |
|---|---|---|---|
| 1 | Single surge | V1:39.6 | 30°, 35°, 40° |
| 2 | Surge1 and surge2 | 0.5V1:19.8 | |
| 3 | Single surge | V2:31.68 | |
| 4 | Surge1 and surge2 | 0.5V2:15.84 | |
| 5 | Single surge | V3:19.8 | |
| 6 | Surge1 and surge2 | 0.5V3:9.9 |
| Slope Angle | Block Volume1 | Block Volume2 | Block Volume3 |
|---|---|---|---|
| 30° | 12.58% | 18.59% | 17.62% |
| 35° | 6.80% | 12.98% | 9.32% |
| 40° | 6.48% | 11.07% | 10.00% |
| Slope Angle | Block Volume1 | Block Volume2 | Block Volume3 |
|---|---|---|---|
| 40° | 7.43% | 17.84% | 12.51% |
| 35° | 21.48% | 24.02% | 15.15% |
| 30° | 32.65% | 31.38% | 22.93% |
| Slope Angle | Block Volume | |||
|---|---|---|---|---|
| 40 | V1 | 1.94% | 3.59% | 62.99% |
| V2 | 2.06% | 3.69% | 62.83% | |
| V3 | 2.27% | 3.73% | 62.19% | |
| 35 | V1 | 1.61% | 2.85% | 59.04% |
| V2 | 1.75% | 2.83% | 59.53% | |
| V3 | 1.99% | 2.95% | 58.86% | |
| 30 | V1 | 1.60% | 2.54% | 55.24% |
| V2 | 1.64% | 2.48% | 55.97% | |
| V3 | 2.53% | 4.01% | 87.12% |
| Slope Angle | 40° | 35° | 30° | |
|---|---|---|---|---|
| DEM results | First impact/N | 235.22 | 181.71 | 120.00 |
| Second impact/N | 359.59 | 230.10 | 131.12 | |
| Estimated results with = 1 | First impact/N | 160.34 | 113.06 | 109.40 |
| Error | −31.84% | −37.78% | −8.83% | |
| Second impact/N | 306.70 | 202.78 | 145.33 | |
| Error | −14.71% | −11.87% | 10.83% | |
| Estimated results with = 1.3 for the slope angle of 40 and with = 1.2 for the slope angle of 35 | First impact/N | 190.98 | 131.46 | / |
| Error | −18.81% | −27.66% | / | |
| Second impact/N | 376.87 | 264.37 | / | |
| Error | 4.80% | 14.89% | / | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Huang, Y.; Lu, P.; Li, C. Numerical Investigation of Multiple-Impact Behavior of Granular Flow on a Rigid Barrier. Water 2020, 12, 3228. https://doi.org/10.3390/w12113228
Zhang B, Huang Y, Lu P, Li C. Numerical Investigation of Multiple-Impact Behavior of Granular Flow on a Rigid Barrier. Water. 2020; 12(11):3228. https://doi.org/10.3390/w12113228
Chicago/Turabian StyleZhang, Bei, Yu Huang, Ping Lu, and Chunxiang Li. 2020. "Numerical Investigation of Multiple-Impact Behavior of Granular Flow on a Rigid Barrier" Water 12, no. 11: 3228. https://doi.org/10.3390/w12113228
APA StyleZhang, B., Huang, Y., Lu, P., & Li, C. (2020). Numerical Investigation of Multiple-Impact Behavior of Granular Flow on a Rigid Barrier. Water, 12(11), 3228. https://doi.org/10.3390/w12113228






