Regional Parameter Estimation of the SWAT Model: Methodology and Application to River Basins in the Peruvian Pacific Drainage
Abstract
:1. Introduction
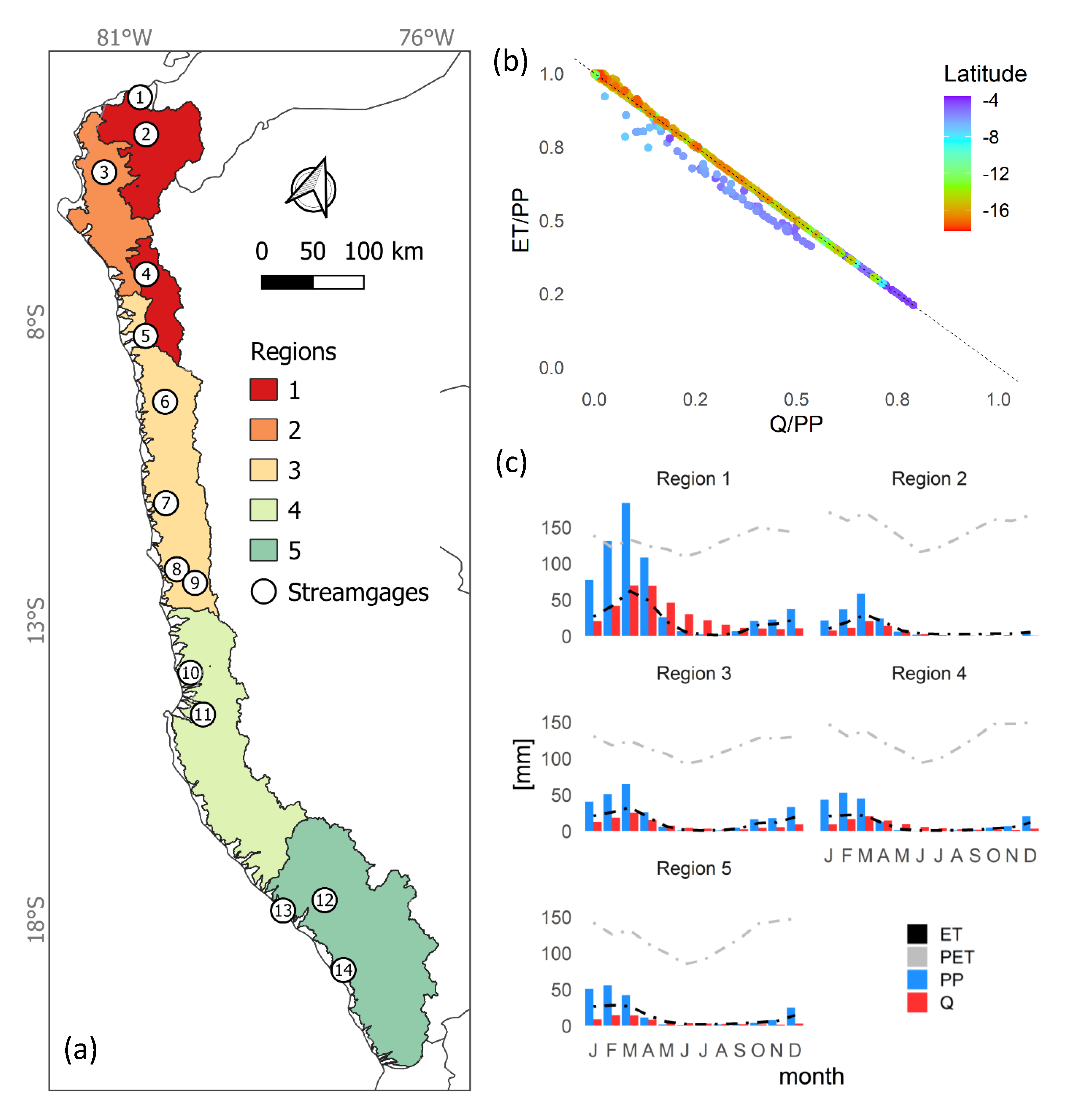
2. Study Area
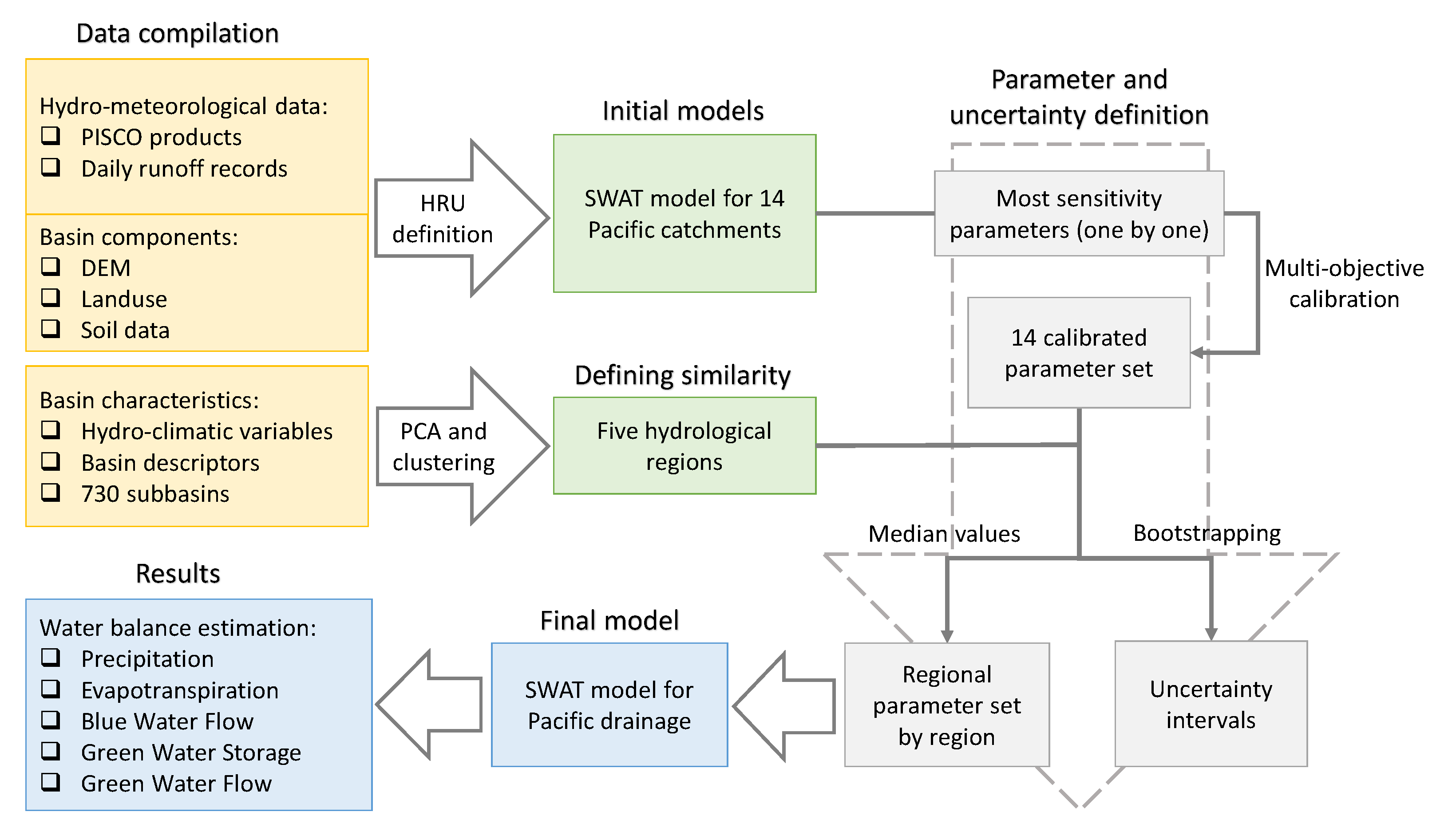
3. Materials and Methods
3.1. Hydrological Modelling Platform
3.2. Model Input
- The rainfall and temperature data were obtained from the product PISCO (Peruvian Interpolated data of Senamhi’s Climatological and Hydrological Observations). The daily rainfall database corresponded to version 2.1 [57], while the daily temperature database (maximum and minimum) was version 1.1 [58]. Both products are available from January 1981 to December 2016 and have a spatial resolution of 0.1 degree ( ). These databases are available on the IRI Climate Data Library website (http://iridl.ldeo.columbia.edu/SOURCES/.SENAMHI/.HSR/.PISCO/index.html?Set-Language=es).
- The 450-m digital elevation model (DEM) was obtained from HydroSHEDS (Hydrological data and maps base on SHuttle Elevation Derivatives at multiple Scales). This product is based on high-resolution elevation data obtained from SRTM (Shuttle Radar Topography Mission) [59].
- The 300-m land-use map used corresponds to 2015 and was obtained from the ESA CCI-LC (European Space Agency and Climate Change Initiative-Land Cover) project [60].
- The 8 km soil type map was obtained from FAO-UNESCO. The map for Volume IV South America [61] was taken, which gridded data was released in 2006.
3.3. Model Setup
3.4. Model Calibration
3.4.1. Evaluation Metrics
- Overall performance: KGE is a comprehensive metric, a weighted average of the Pearson product-moment correlation coefficient (r), the ratio between the mean of the simulated values and the mean of the observed ones (), and variability ratio (), which is computed using the standard deviation of simulated and observed (Equation (1)). Kling–Gupta efficiencies range from –Infinity to 1. The closer to 1, the more precise the model is.
- Low flows: By taking the log of simulated (log S) and observed (log O) before calculating the NSE, the influence of (missing) peak flows is reduced and more emphasis is placed on the base flow (the criticism of the standard NSE is that it is overly sensitive to the magnitude and timing of peak flows (Equation (2)).
3.4.2. Multiobjective Calibration Algorithm
- Step 1: For each i∈P, set = 0 and = Ø.
- Step 2: For all j ≠ i and j ∈ P, if i dominates j, Add j to the set of solutions dominated by i: = U j. Otherwise, increment the domination count of i: = +1.
- Step 3: If = 0, keep i in the first non-dominated front and set the front counter k = 1.
- Step 4: While ≠ Ø, initialize Q = Ø for storing the next non-dominated solutions.
- Step 5: For each i∈ and for each j∈, update = – 1. If = 0, j belongs to the next front and update Q = Q U j.
- Step 6: Set k = k +1 and = Q, go to Step 4.
3.5. Regionalization Using the Physical Similarity Approach
3.5.1. Clustering Dataset
3.5.2. Parameter Transfer Scheme
3.6. Uncertainty Analysis
4. Results
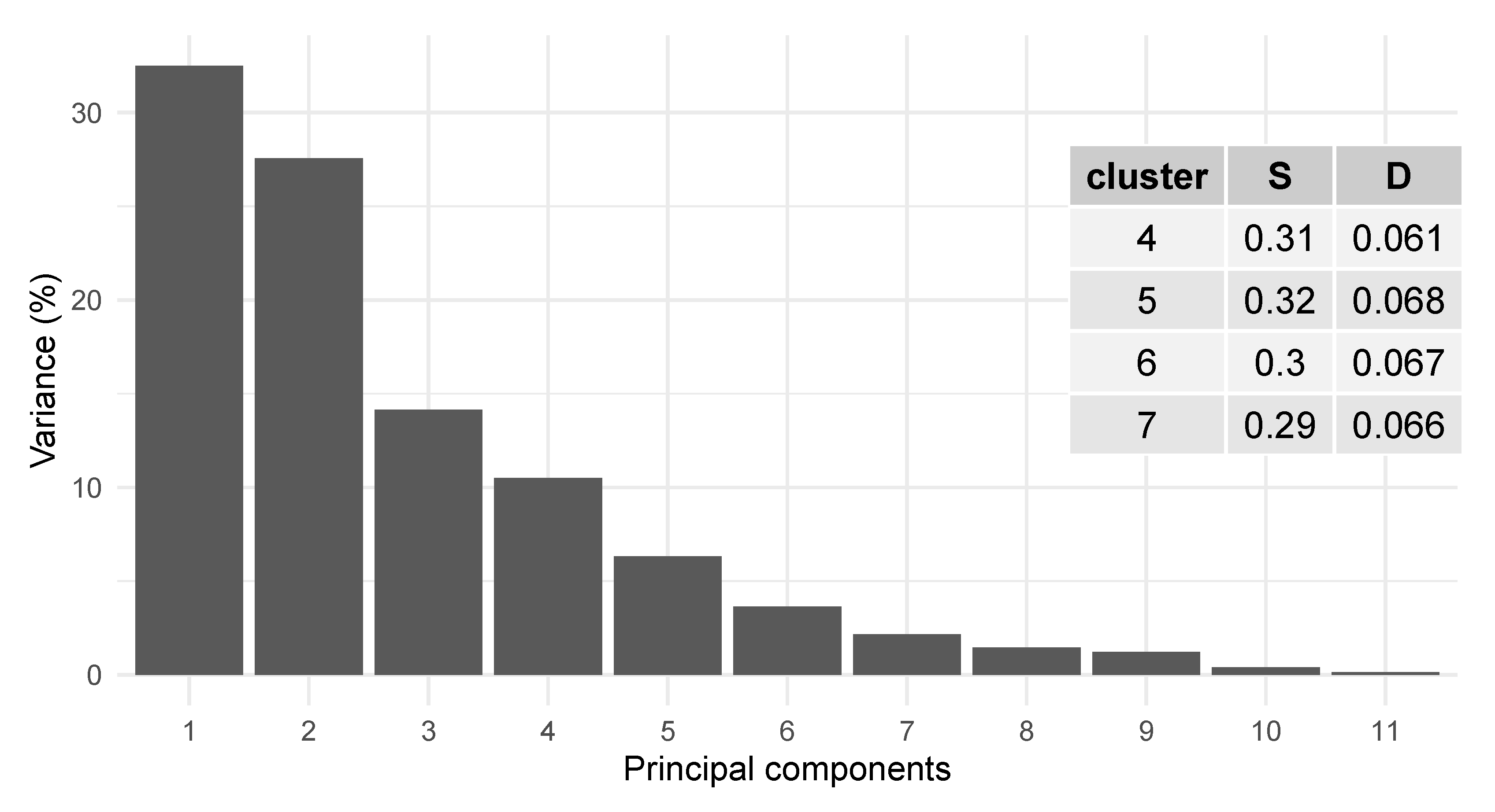
4.1. Defining Similarity by Clustering
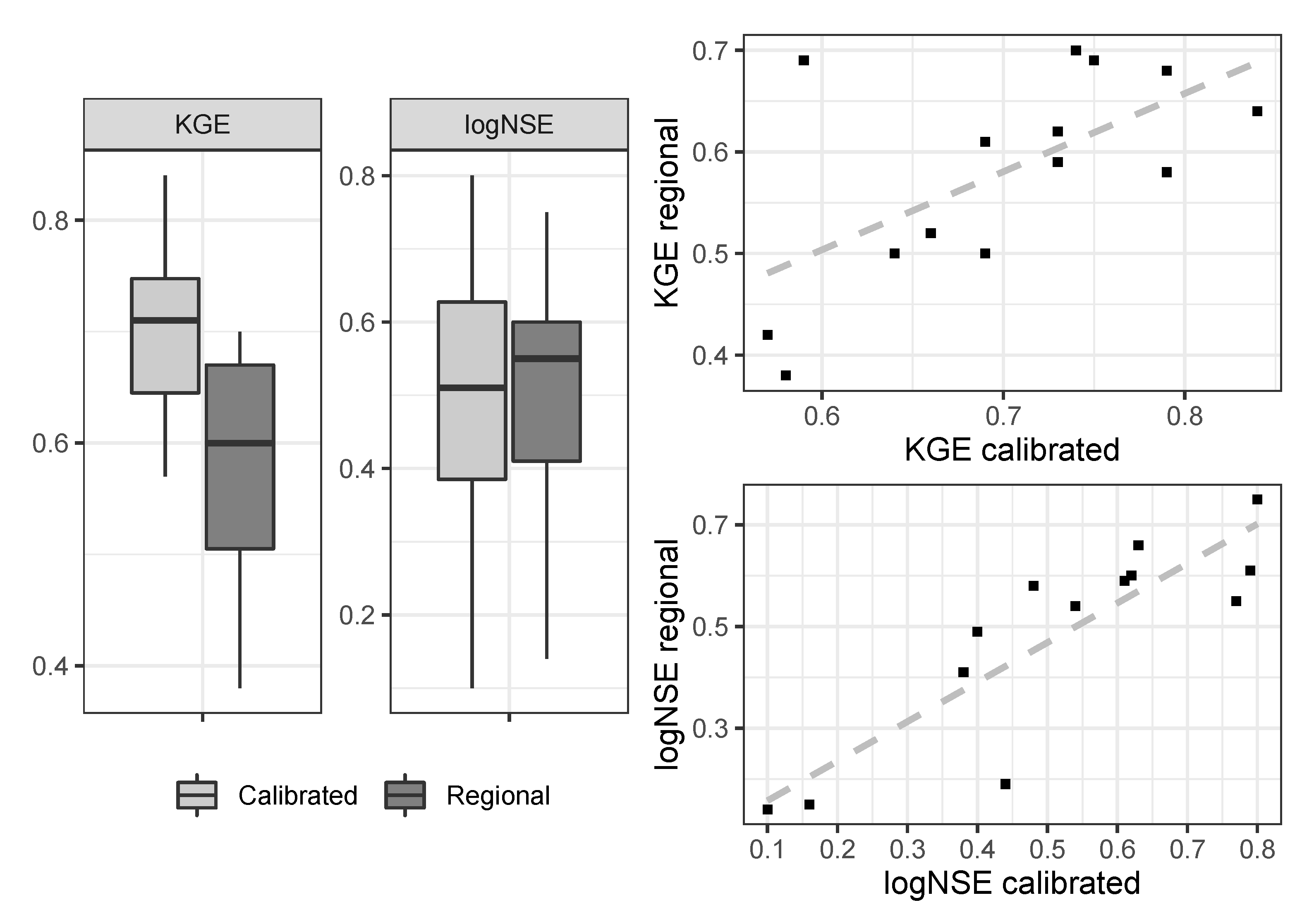
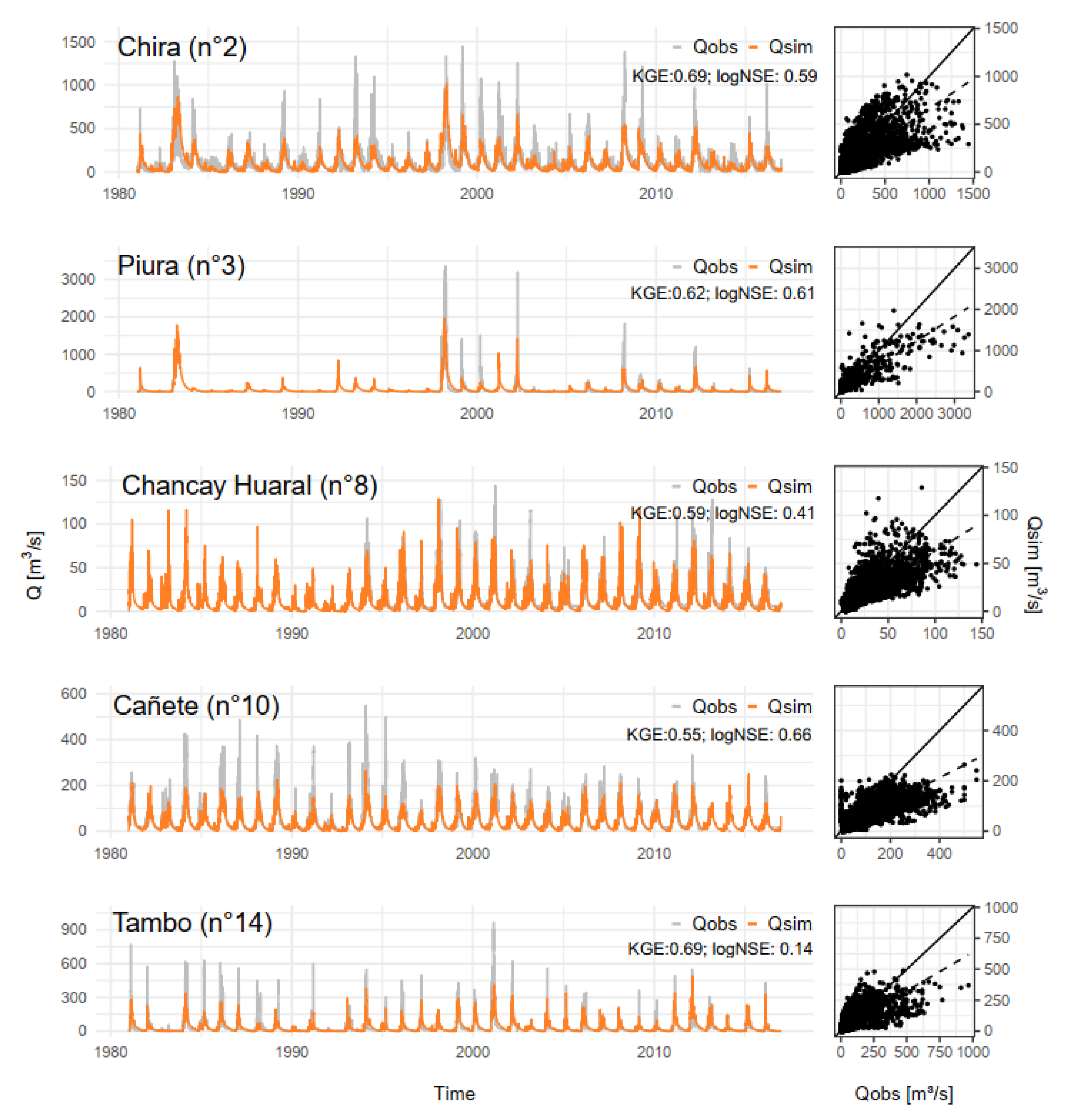
4.2. Regional Runoff Model Performance
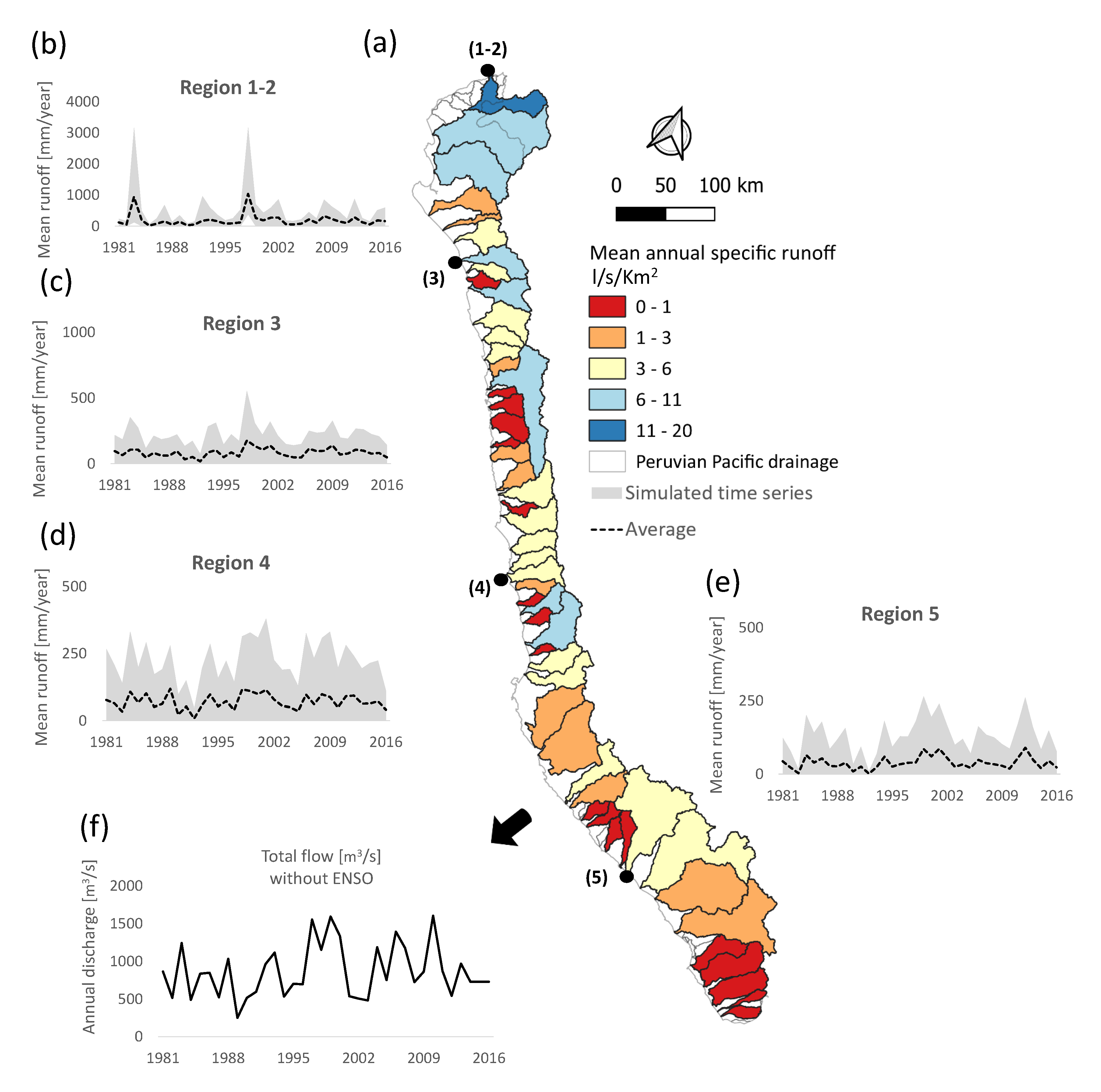
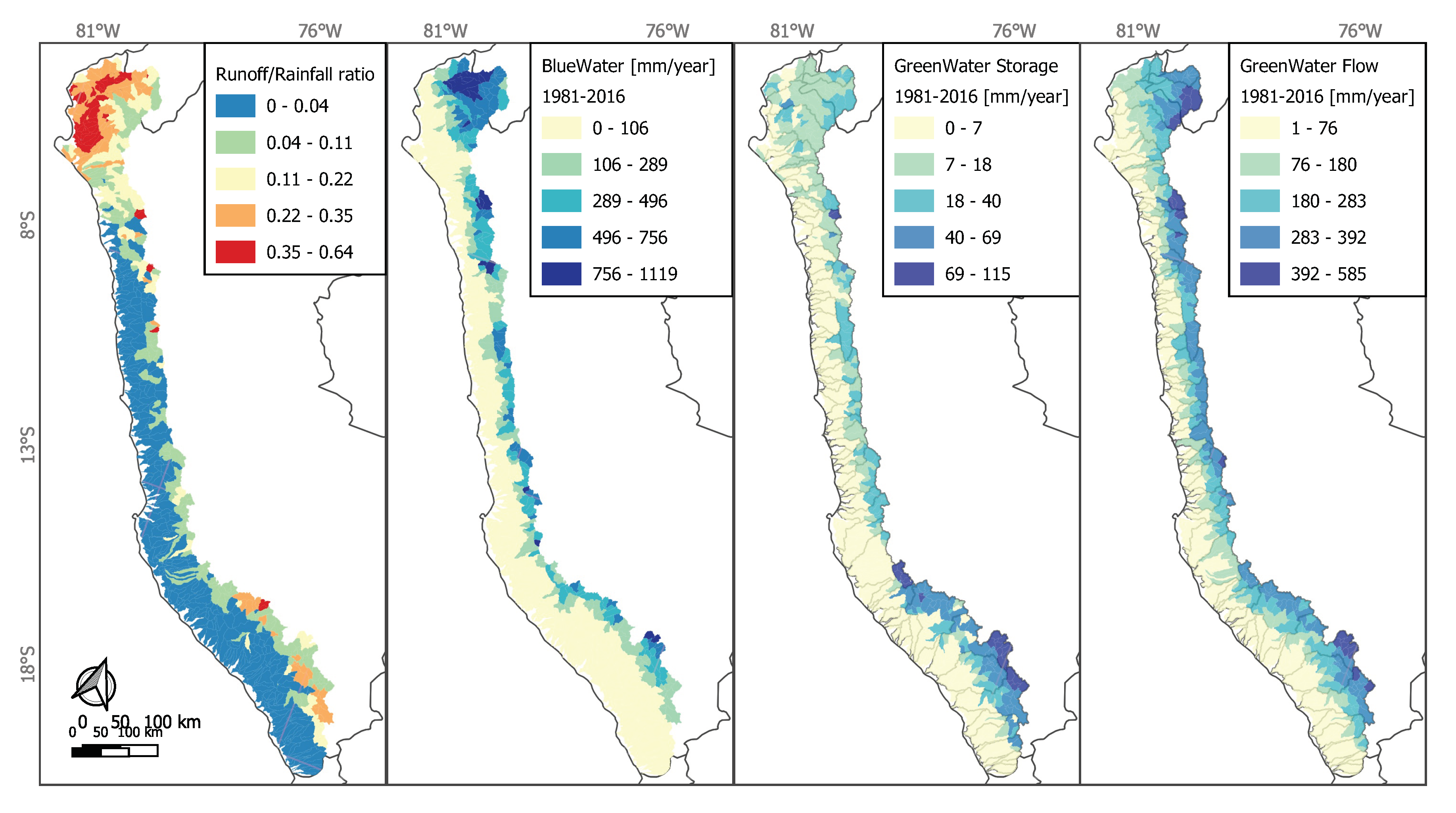
4.3. Quantification of Water Resources and Water Balance
4.4. Performance of the Uncertainty Bands at Streamgages
5. Discussion
5.1. Subjectivity in the Physical Similarity Approach by Clustering
5.2. Physical Implications of the Regional Parameter Set
5.3. Conditionality of the SWAT Calibrated Model and Its Applicability
6. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Garreaud, R.; Vuille, M.; Compagnucci, R.; Marengo, J. Present-day South American climate. Paleogeogr. Palaeoclimatol. Paleoecol. 2009, 281, 180–195. [Google Scholar] [CrossRef]
- Ruiz, R.; Torres, H.; Aguirre, M. Delimitación y Codificación de Unidades Hidrográficas del Perú; Autoridad Nacional del Agua—Ministerio de Agricultura: Lima, Perú, 2008.
- ANA. Recursos Hídricos en el Perú; Technical Report; Ministerio de Agricultura: Lima, Perú, 2012.
- PRB. World Population Data Sheet (Population Reference Bureau); PRB: Washington, DC, USA, 2020. [Google Scholar]
- FAO. FAO Statistical Yearbook 2013: World Food and Agriculture; FAO: Rome, Italy, 2013. [Google Scholar]
- Lavado, W.S.; Ronchail, J.; Labat, D.; Espinoza, J.C.; Guyot, J.L. Basin-scale analysis of rainfall and runoff in Peru (1969–2004): Pacific, Titicaca and Amazonas drainages. Hydrol. Sci. J. 2012, 57, 625–642. [Google Scholar] [CrossRef] [Green Version]
- Rau, P.; Bourrel, L.; Labat, D.; Melo, P.; Dewitte, B.; Frappart, F.; Lavado, W.; Felipe, O. Regionalization of rainfall over the Peruvian Pacific slope and coast. Int. J. Climatol. 2017, 37, 143–158. [Google Scholar] [CrossRef]
- Rau, P.; Bourrel, L.; Labat, D.; Ruelland, D.; Frappart, F.; Lavado, W.; Dewitte, B.; Felipe, O. Assessing multidecadal runoff (1970–2010) using regional hydrological modelling under data and water scarcity conditions in Peruvian Pacific catchments. Hydrol. Process. 2019, 33, 20–35. [Google Scholar] [CrossRef] [Green Version]
- Seiller, G.; Anctil, F.; Perrin, C. Multimodel evaluation of twenty lumped hydrological models under contrasted climate conditions. Hydrol. Earth Syst. Sci. 2012, 16, 1171–1189. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.E.; van Dijk, A.I.; De Roo, A.; Miralles, D.G.; McVicar, T.R.; Schellekens, J.; Bruijnzeel, L.A. Global-scale regionalization of hydrologic model parameters. Water Resour. Res. 2016, 52, 3599–3622. [Google Scholar] [CrossRef] [Green Version]
- Oudin, L.; Kay, A.; Andréassian, V.; Perrin, C. Are seemingly physically similar catchments truly hydrologically similar? Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Perrin, C.; Michel, C.; Le Moine, N. Spatial proximity, physical similarity, regression and ungaged catchments: A comparison of regionalization approaches based on 913 French catchments. Water Resour. Res. 2008, 44, 1–15. [Google Scholar] [CrossRef]
- Stoll, S.; Weiler, M. Explicit simulations of stream networks to guide hydrological modelling in ungauged basins. Hydrol. Earth Syst. Sci. 2010, 14, 1435–1448. [Google Scholar] [CrossRef] [Green Version]
- Samuel, J.; Coulibaly, P.; Metcalfe, R.A. Estimation of continuous streamflow in Ontario ungauged basins: Comparison of regionalization methods. J. Hydrol. Eng. 2011, 16, 447–459. [Google Scholar] [CrossRef]
- Parajka, J.; Viglione, A.; Rogger, M.; Salinas, J.; Sivapalan, M.; Blöschl, G. Comparative assessment of predictions in ungauged basins–Part 1: Runoff hydrograph studies. Hydrol. Earth Syst. Sci. Discuss. 2013, 10. [Google Scholar] [CrossRef]
- Razavi, T.; Coulibaly, P. Streamflow Prediction in Ungauged Basins: Review of Regionalization Methods. J. Hydrol. Eng. 2013, 18, 958–975. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. Regionalisation of catchment model parameters. J. Hydrol. 2004, 287, 95–123. [Google Scholar] [CrossRef] [Green Version]
- Parajka, J.; Merz, R.; Blöschl, G. A comparison of regionalisation methods for catchment model parameters. Hydrol. Earth Syst. Sci. 2005, 9, 157–171. [Google Scholar] [CrossRef] [Green Version]
- McIntyre, N.; Lee, H.; Wheater, H.; Young, A.; Wagener, T. Ensemble predictions of runoff in ungauged catchments. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef] [Green Version]
- Bárdossy, A. Calibration of hydrological model parameters for ungauged catchments. Eur. Geosci. Union 2007, 11, 703–710. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Chiew, F.H. Relative merits of different methods for runoff predictions in ungauged catchments. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G.; Parajka, J.D. Regionalization methods in rainfall-runoff modelling using large catchment samples. IAHS Publ. 2006, 307, 117. [Google Scholar]
- Arsenault, R.; Brissette, F.P. Continuous streamflow prediction in ungauged basins: The effects of equifinality and parameter set selection on uncertainty in regionalization approaches. J. Am. Water Resour. Assoc. 2014, 50, 6135–6153. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef] [Green Version]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development 1. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Gitau, M.W.; Chaubey, I. Regionalization of SWAT model parameters for use in ungauged watersheds. Water 2010, 2, 849–871. [Google Scholar] [CrossRef]
- Swain, J.B.; Patra, K.C. Streamflow estimation in ungauged catchments using regionalization techniques. J. Hydrol. 2017, 554, 420–433. [Google Scholar] [CrossRef]
- Van Liew, M.W.; Mittelstet, A.R. Comparison of three regionalization techniques for predicting streamflow in ungaged watersheds in nebraska, USA using SWAT model. Int. J. Agric. Biol. Eng. 2018, 11, 110–119. [Google Scholar] [CrossRef] [Green Version]
- Choubin, B.; Solaimani, K.; Rezanezhad, F.; Habibnejad Roshan, M.; Malekian, A.; Shamshirband, S. Streamflow regionalization using a similarity approach in ungauged basins: Application of the geo-environmental signatures in the Karkheh River Basin, Iran. Catena 2019, 182, 104128. [Google Scholar] [CrossRef]
- Pagliero, L.; Bouraoui, F.; Diels, J.; Willems, P.; McIntyre, N. Investigating regionalization techniques for large-scale hydrological modelling. J. Hydrol. 2019, 570, 220–235. [Google Scholar] [CrossRef]
- Molina, L.A.U. Validacion del Modelo Hidrologico SWAT, con interfaz Arcview, en la cuenca alta del rio Chama, estado Merida. Rev. For. Venez. 2005, 49, 105–106. [Google Scholar]
- Stehr, A.; Debels, P.; Romero, F.; Alcayaga, H. Hydrological modelling with SWAT under conditions of limited data availability: Evaluation of results from a Chilean case study. Hydrol. Sci. J. 2008, 53, 588–601. [Google Scholar] [CrossRef]
- Stehr, A.; Debels, P.; Arumi, J.L.; Romero, F.; Alcayaga, H. Combining the Soil and Water Assessment Tool (SWAT) and MODIS imagery to estimate monthly flows in a data-scarce Chilean Andean basin. Hydrol. Sci. J. 2009, 54, 1053–1067. [Google Scholar] [CrossRef]
- Barrios, A.G.; Urribarri, L.A. Aplicación del modelo Swat en los Andes venezolanos: Cuenca alta del río Chama. Rev. Geográfica Venez. 2010, 51, 11–29. [Google Scholar]
- Alarcon, V.J.; Alcayaga, H.; Álvarez, E. Hydrological modeling of an ungauged watershed in Southern Andes. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2015; Volume 1702, p. 190003. [Google Scholar]
- Yacoub, C.; Pérez-Foguet, A. Assessment of terrain slope influence in SWAT modeling of Andean watersheds. EGUGA 2009, 11, 6381. [Google Scholar]
- Uribe, N.; Quintero, M.; Valencia, J. Aplicación del Modelo Hidrológico SWAT (Soil and Water Assessment Tool) a la Cuenca del Río Cañete (SWAT); Technical Report; International Center for Tropical Agriculture: Cali, Colombia, 2013. [Google Scholar]
- Lavado Casimiro, W.S.; Labat, D.; Guyot, J.L.; Ardoin-Bardin, S. Assessment of climate change impacts on the hydrology of the Peruvian Amazon–Andes basin. Hydrol. Process. 2011, 25, 3721–3734. [Google Scholar] [CrossRef]
- Andres, N.; Vegas Galdos, F.; Lavado Casimiro, W.S.; Zappa, M. Water resources and climate change impact modelling on a daily time scale in the Peruvian Andes. Hydrol. Sci. J. 2014, 59, 2043–2059. [Google Scholar] [CrossRef] [Green Version]
- Zulkafli, Z.; Buytaert, W.; Manz, B.; Rosas, C.V.; Willems, P.; Lavado-Casimiro, W.; Guyot, J.L.; Santini, W. Projected increases in the annual flood pulse of the Western Amazon. Environ. Res. Lett. 2016, 11, 014013. [Google Scholar] [CrossRef]
- Olsson, T.; Kämäräinen, M.; Santos, D.; Seitola, T.; Tuomenvirta, H.; Haavisto, R.; Lavado-Casimiro, W. Downscaling climate projections for the Peruvian coastal Chancay-Huaral Basin to support river discharge modeling with WEAP. J. Hydrol. Reg. Stud. 2017, 13, 26–42. [Google Scholar] [CrossRef]
- Lavado Casimiro, W.S.; Labat, D.; Guyot, J.L.; Ronchail, J.; Ordonez, J. TRMM rainfall data estimation over the Peruvian Amazon-Andes basin and its assimilation into a monthly water balance model. In New Approaches to Hydrological Prediction in Datasparse Regions, Proceedings of Symposium HS; IAHS Press: Hyderabad, India, 2009; Volume 2, pp. 207–216. [Google Scholar]
- Zulkafli, Z.; Buytaert, W.; Onof, C.; Manz, B.; Tarnavsky, E.; Lavado, W.; Guyot, J.L. A comparative performance analysis of TRMM 3B42 (TMPA) versions 6 and 7 for hydrological applications over Andean–Amazon river basins. J. Hydrometeorol. 2014, 15, 581–592. [Google Scholar] [CrossRef]
- Zubieta, R.; Getirana, A.; Espinoza, J.C.; Lavado, W. Impacts of satellite-based precipitation datasets on rainfall–runoff modeling of the Western Amazon basin of Peru and Ecuador. J. Hydrol. 2015, 528, 599–612. [Google Scholar] [CrossRef]
- Strauch, M.; Kumar, R.; Eisner, S.; Mulligan, M.; Reinhardt, J.; Santini, W.; Vetter, T.; Friesen, J. Adjustment of global precipitation data for enhanced hydrologic modeling of tropical Andean watersheds. Clim. Chang. 2017, 141, 547–560. [Google Scholar] [CrossRef] [Green Version]
- Satgé, F.; Ruelland, D.; Bonnet, M.P.; Molina, J.; Pillco, R. Consistency of satellite precipitation estimates in space and over time compared with gauge observations and snow-hydrological modelling in the lake Titicaca region. Hydrol. Earth Syst. Sci. 2018, 1–41. [Google Scholar] [CrossRef]
- De Reparaz, G. Los Ríos de la Zona árida Peruana; Universidad de Piura: Piura, Perú, 2013. [Google Scholar]
- Rau, P.; Bourrel, L.; Labat, D.; Frappart, F.; Ruelland, D.; Lavado, W.; Dewitte, B.; Felipe, O. Hydroclimatic change disparity of Peruvian Pacific drainage catchments. Theor. Appl. Climatol. 2018, 134, 139–153. [Google Scholar] [CrossRef]
- Lavado, W.; Espinoza, J.C. Impactos de El Niño y La Niña en las lluvias del Perú (1965–2007). Rev. Bras. Meteorol. 2014, 29, 171–182. [Google Scholar] [CrossRef] [Green Version]
- Bourrel, L.; Rau, P.; Dewitte, B.; Labat, D.; Lavado, W.; Coutaud, A.; Vera, A.; Alvarado, A.; Ordoñez, J. Low-frequency modulation and trend of the relationship between ENSO and precipitation along the northern to centre Peruvian Pacific coast. Hydrol. Process. 2015, 29, 1252–1266. [Google Scholar] [CrossRef]
- Sanabria, J.; Bourrel, L.; Dewitte, B.; Frappart, F.; Rau, P.; Solis, O.; Labat, D. Rainfall along the coast of Peru during strong El Niño events. Int. J. Climatol. 2018, 38, 1737–1747. [Google Scholar] [CrossRef]
- Vargas, P. El Cambio Climático y sus Efectos en el Perú; Banco Central de Reserva del Perú: Lima, Perú, 2009.
- Arnold, J.; Allen, P. Estimating hydrologic budgets for three Illinois watersheds. J. Hydrol. 1996, 176, 57–77. [Google Scholar] [CrossRef]
- Neitsch, S.; Arnold, J.; Kiniry, J.; Williams, J. Soil & Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resour Inst.: Forney, TX, USA, 2011; pp. 1–647. [Google Scholar]
- Chaplot, V. Impact of DEM mesh size and soil map scale on SWAT runoff, sediment, and NO3–N loads predictions. J. Hydrol. 2005, 312, 207–222. [Google Scholar] [CrossRef]
- Bormann, H.; Breuer, L.; Gräff, T.; Huisman, J.; Croke, B. Assessing the impact of land use change on hydrology by ensemble modelling (LUCHEM) IV: Model sensitivity to data aggregation and spatial (re-) distribution. Adv. Water Resour. 2009, 32, 171–192. [Google Scholar] [CrossRef]
- Aybar, C.; Fernández, C.; Huerta, A.; Lavado, W.; Vega, F.; Felipe-Obando, O. Construction of a high-resolution gridded rainfall dataset for Peru from 1981 to the present day. Hydrol. Sci. J. 2019, 65, 770–785. [Google Scholar] [CrossRef]
- Huerta, A.; Aybar, C.; Lavado, W. PISCO Tem-Perature v.1.1.; Technical Report; SENAMHI: Lima, Perú, 2018.
- Lehner, B.; Verdin, K.; Jarvis, A. New global hydrography derived from spaceborne elevation data. Eos Trans. Am. Geophys. Union 2008, 89, 93–94. [Google Scholar] [CrossRef]
- Bontemps, S.; Defourny, P.; Radoux, J.; Van Bogaert, E.; Lamarche, C.; Achard, F.; Mayaux, P.; Boettcher, M.; Brockmann, C.; Kirches, G.; et al. Consistent global land cover maps for climate modelling communities: Current achievements of the ESA’s land cover CCI. In Proceedings of the ESA Living Planet Symposium, Edimburgh, UK, 9–13 September 2013; pp. 9–13. [Google Scholar]
- FAO-UNESCO. Soil Map of the World; Technical Report South America; FAO-UNESCO: Rome, Italy, 1971. [Google Scholar]
- Dile, Y.T.; Daggupati, P.; George, C.; Srinivasan, R.; Arnold, J. Introducing a new open source GIS user interface for the SWAT model. Environ. Model. Softw. 2016, 85, 129–138. [Google Scholar] [CrossRef]
- Luo, Y.; Su, B.; Yuan, J.; Li, H.; Zhang, Q. GIS techniques for watershed delineation of SWAT model in plain polders. Procedia Environ. Sci. 2011, 10, 2050–2057. [Google Scholar] [CrossRef] [Green Version]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather. Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Monteith, J. Evaporation and environment. The state and movement of water in living organisms. In Symposium of the Society of Experimental Biology; Cambridge Univ. Press: Cambridge, UK, 1965; Volume 19, pp. 205–234. [Google Scholar]
- Aouissi, J.; Benabdallah, S.; Chabaane, Z.L.; Cudennec, C. Evaluation of potential evapotranspiration assessment methods for hydrological modelling with SWAT—Application in data-scarce rural Tunisia. Agric. Water Manag. 2016, 174, 39–51. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.; Van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Vaghefi, S.A.; Srinivasan, R. A Guideline for Successful Calibration and Uncertainty Analysis for Soil and Water Assessment: A Review of Papers from the 2016 International SWAT Conference. Water 2017, 10, 6. [Google Scholar] [CrossRef] [Green Version]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Chilkoti, V.; Bolisetti, T.; Balachandar, R. Multi-objective autocalibration of SWAT model for improved low flow performance for a small snowfed catchment. Hydrol. Sci. J. 2018, 63, 1482–1501. [Google Scholar] [CrossRef]
- Saraiva, A.M.; Masih, I.; Uhlenbrook, S.; Jewitt, G.P.; Van der Zaag, P. Improved process representation in the simulation of the hydrology of a meso-scale semi-arid catchment. Water 2018, 10, 1549. [Google Scholar] [CrossRef] [Green Version]
- Siderius, C.; Biemans, H.; Kashaigili, J.J.; Conway, D. Going local: Evaluating and regionalizing a global hydrological model’s simulation of river flows in a medium-sized East African basin. J. Hydrol. Reg. Stud. 2018, 19, 349–364. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M. hydroGOF: Goodness-of-Fit Functions for Comparison of Simulated and Observed Hydrological Time Series R Package Version 0.4-0. 2020. Available online: https://cran.r-project.org/web/packages/hydroGOF/hydroGOF.pdf (accessed on 4 May 2020).
- Confesor, R.B.; Whittaker, G. Multi-Objective Automatic Calibration of a Semi-Distributed Watershed Model using Pareto Ordering Optimization and Genetic Algorithm. In Proceedings of the 2006 ASAE Annual Meeting. American Society of Agricultural and Biological Engineers, Portland, OR, USA, 9–12 July 2006; p. 1. [Google Scholar]
- Zhang, Z.; Wagener, T.; Reed, P.; Bhushan, R. Reducing uncertainty in predictions in ungauged basins by combining hydrologic indices regionalization and multiobjective optimization. Water Resour. Res. 2008. [Google Scholar] [CrossRef]
- Ercan, M.B.; Goodall, J.L. Design and implementation of a general software library for using NSGA-II with SWAT for multi-objective model calibration. Environ. Model. Softw. 2016, 84, 112–120. [Google Scholar] [CrossRef] [Green Version]
- Ching-Shih Tsou. nsga2R: Elitist Non-dominated Sorting Genetic Algorithm Based on R. 2013. Available online: https://cran.r-project.org/web/packages/nsga2R/nsga2R.pdf (accessed on 25 May 2020).
- Hannah, D.M.; Kansakar, S.R.; Gerrard, A.; Rees, G. Flow regimes of Himalayan rivers of Nepal: Nature and spatial patterns. J. Hydrol. 2005, 308, 18–32. [Google Scholar] [CrossRef]
- Ward, J.H. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Rao, A.R.; Srinivas, V. Regionalization of watersheds by hybrid-cluster analysis. J. Hydrol. 2006, 318, 37–56. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Xiong, H.; Gao, X.; Wu, J. Understanding of internal clustering validation measures. In Proceedings of the 2010 IEEE International Conference on Data Mining, ICDM; IEEE: New York, NY, USA, 2010; pp. 911–916. [Google Scholar] [CrossRef]
- Chavoshi, S.; Azmin Sulaiman, W.; Saghafian, B.; Sulaiman, M.N.; Latifah, A. Soft and hard clustering methods for delineation of hydrological homogeneous regions in the southern strip of the Caspian Sea W atershed. J. Flood Risk Manag. 2012, 5, 282–294. [Google Scholar] [CrossRef]
- Brock, G.; Pihur, V.; Datta, S.; Datta, S.; Brock, M.G.; Biobase, S. clValid, an R package for cluster validation. J. Stat. Softw. 2020, 25, 1–22. [Google Scholar]
- Xie, Z.; Yuan, F.; Duan, Q.; Zheng, J.; Liang, M.; Chen, F. Regional Parameter Estimation of the VIC Land Surface Model: Methodology and Application to River Basins in China. J. Hydrometeorol. 2007, 8, 447–468. [Google Scholar] [CrossRef] [Green Version]
- Efron, B. Bootstrap methods: Another look at the jackknife. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 569–593. [Google Scholar]
- Bourgin, F.; Andréassian, V.; Perrin, C.; Oudin, L. Transferring global uncertainty estimates from gauged to ungauged catchments. Hydrol. Earth Syst. Sci. 2015, 19, 2535–2546. [Google Scholar] [CrossRef]
- Bock, A.R.; Farmer, W.H.; Hay, L.E. Quantifying uncertainty in simulated streamflow and runoff from a continental-scale monthly water balance model. Adv. Water Resour. 2018, 122, 166–175. [Google Scholar] [CrossRef]
- Levin, S.; Farmer, W. Evaluation of Uncertainty Intervals for Daily, Statistically Derived Streamflow Estimates at Ungaged Basins Across the Continental U.S. Water 2020, 12, 1390. [Google Scholar] [CrossRef]
- Milliman, J.D.; Farnsworth, K.L. River Discharge to the Coastal Ocean: A Global Synthesis; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Falkenmark, M.; Rockström, J. The new blue and green water paradigm: Breaking new ground for water resources planning and management. J. Water Resour. Plan. Manag. 2006, 132, 129–132. [Google Scholar] [CrossRef]
- Reichl, J.; Western, A.; McIntyre, N.; Chiew, F. Optimization of a similarity measure for estimating ungauged streamflow. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef] [Green Version]
- Merz, R.; Blöschl, G. Flood frequency regionalisation—spatial proximity vs. catchment attributes. J. Hydrol. 2005, 302, 283–306. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G.; Parajka, J. Spatio-temporal variability of event runoff coefficients. J. Hydrol. 2006, 331, 591–604. [Google Scholar] [CrossRef]
- Sood, A.; Muthuwatta, L.; McCartney, M. A SWAT evaluation of the effect of climate change on the hydrology of the Volta River basin. Water Int. 2013, 38, 297–311. [Google Scholar] [CrossRef]
- Chu, T.; Shirmohammadi, A. Evaluation of the SWAT model’s hydrology component in the piedmont physiographic region of Maryland. Trans. ASAE 2004, 47, 1057. [Google Scholar] [CrossRef]
- Pfannerstill, M.; Guse, B.; Fohrer, N. A multi-storage groundwater concept for the SWAT model to emphasize nonlinear groundwater dynamics in lowland catchments. Hydrol. Process. 2014, 28, 5599–5612. [Google Scholar] [CrossRef]
- Luo, Y.; Arnold, J.; Allen, P.; Chen, X. Hydrology and Earth System Sciences Baseflow simulation using SWAT model in an inland river basin in Tianshan Mountains, Northwest China. Hydrol. Earth Syst. Sci. 2012, 16, 1259–1267. [Google Scholar] [CrossRef] [Green Version]
- Izady, A.; Davary, K.; Alizadeh, A.; Ziaei, A.N.; Akhavan, S.; Alipoor, A.; Joodavi, A.; Brusseau, M.L. Conceptualisation et modélisation hydrogéologique de la plain semi-aride et agricole de Neishaboor (Iran) en utilisant le modèle distribué SWAT. Hydrogeol. J. 2014, 23, 47–68. [Google Scholar] [CrossRef]
- Dowlatabadi, S.; Ali Zomorodian, S.M. Conjunctive simulation of surface water and groundwater using SWAT and MODFLOW in Firoozabad watershed. KSCE J. Civ. Eng. 2016, 20, 485–496. [Google Scholar] [CrossRef]
- Shao, G.; Zhang, D.; Guan, Y.; Xie, Y.; Huang, F. Application of SWAT model with a modified groundwater module to the semi-arid Hailiutu River catchment, northwest China. Sustainability 2019, 11, 2031. [Google Scholar] [CrossRef] [Green Version]
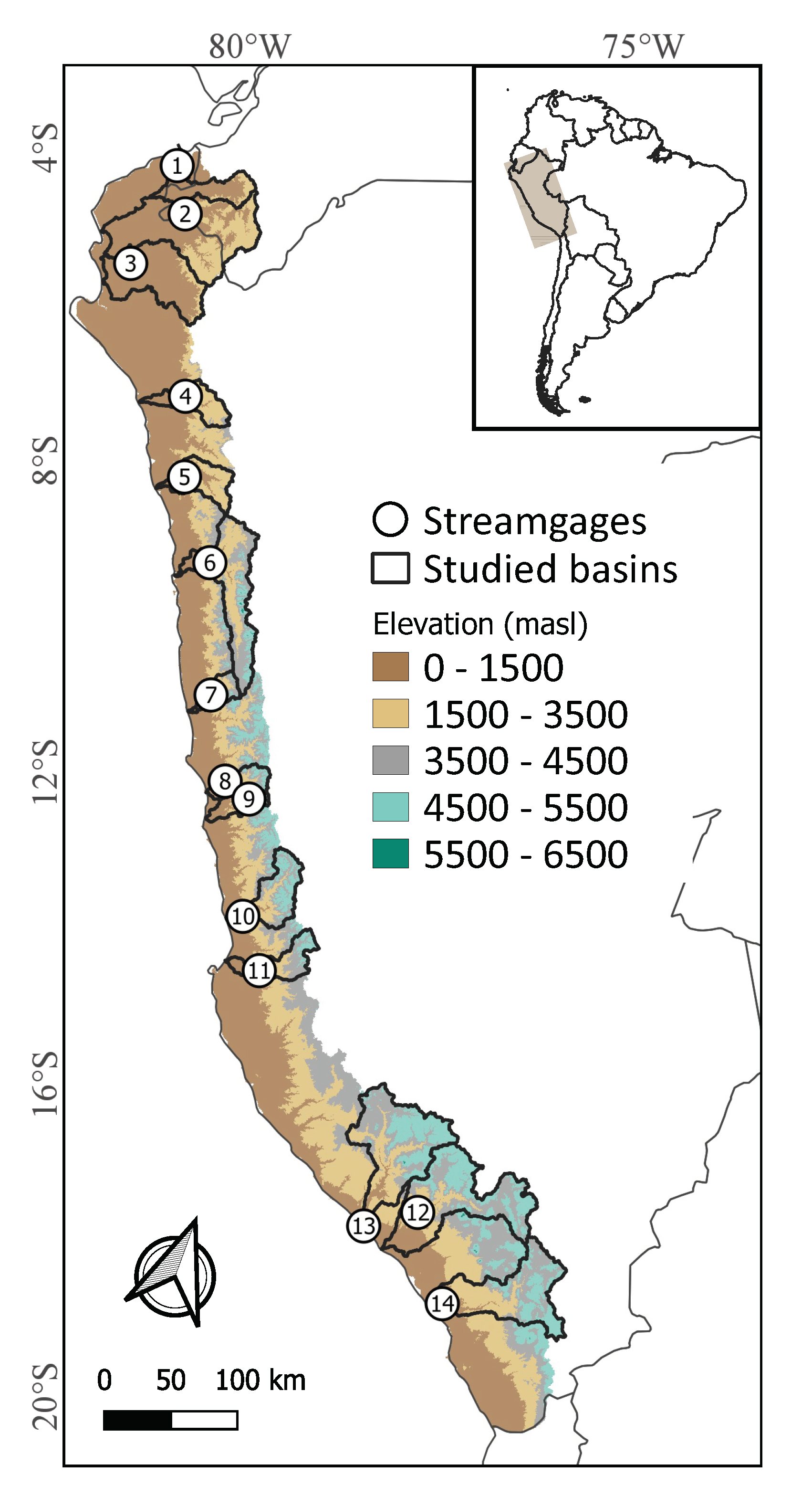
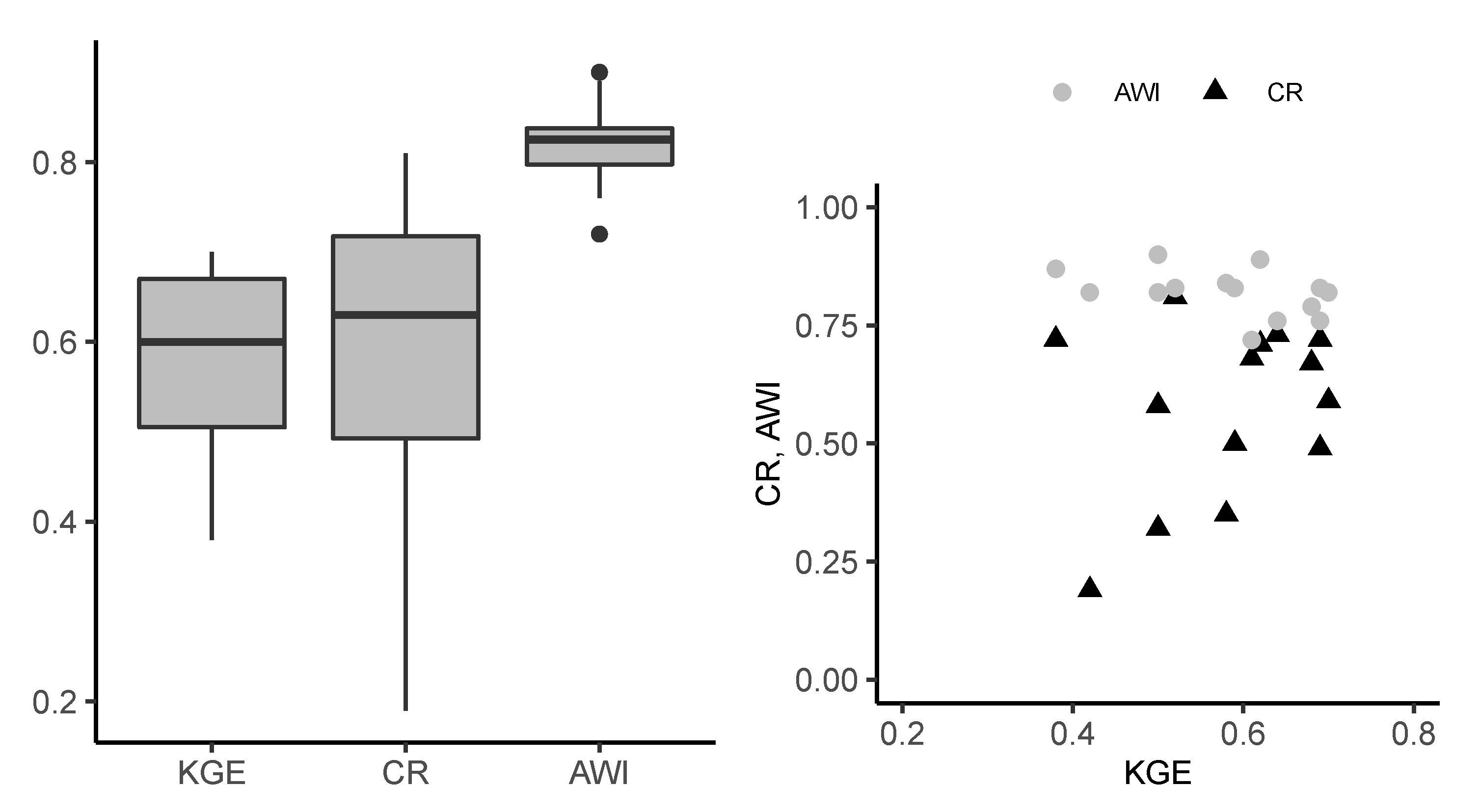
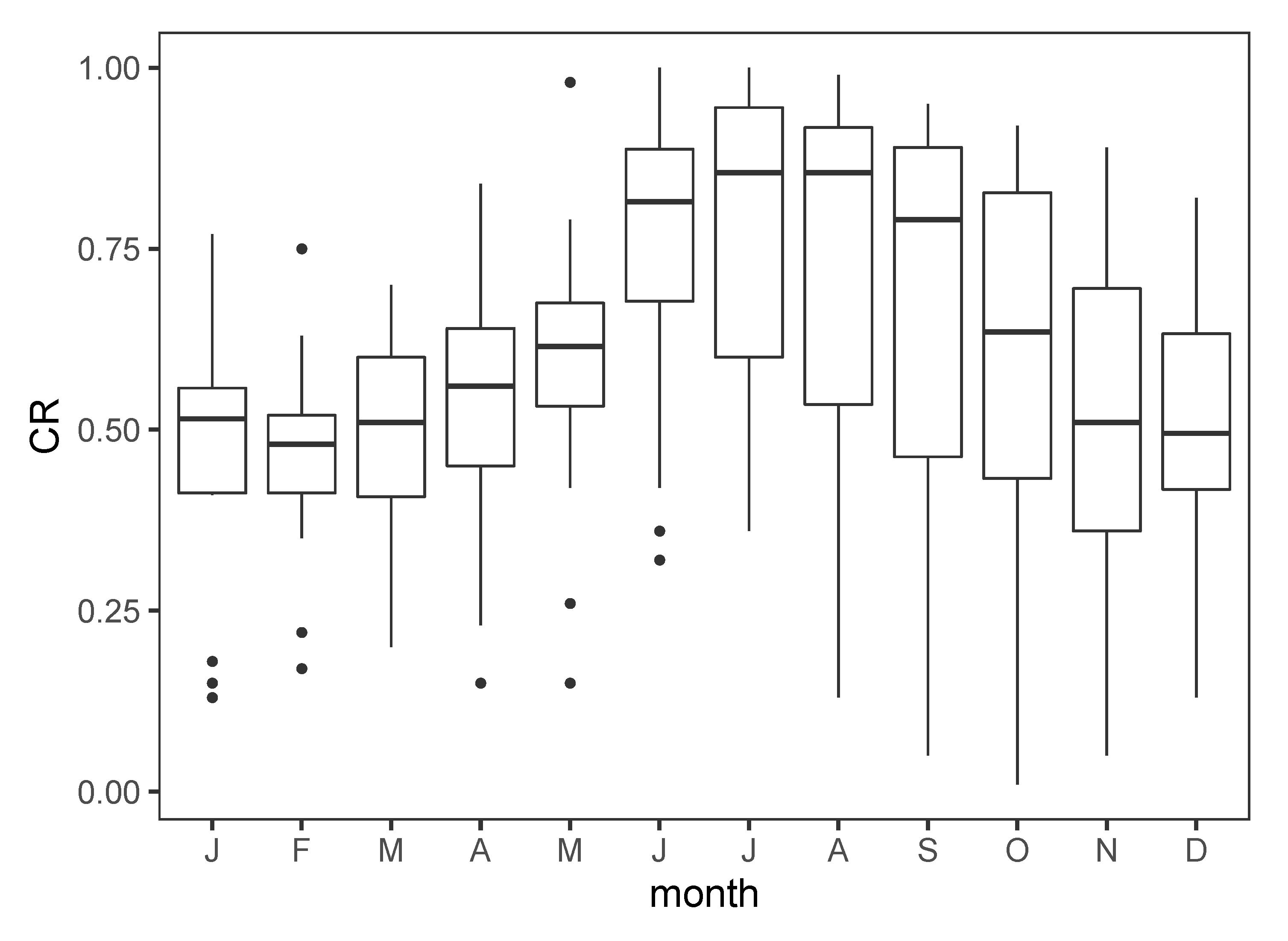
| no | River Basin | Streamgage (Data Period) | Calibration Period | Ab () | Rm (mm) | Qm (mm) | Rc (Qm/Rm) | Soil Composition | Land Cover Type | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Clay (%) | Silt (%) | Sand (%) | PAST (%) | FRST (%) | BARR (%) | Other (%) | ||||||||
| 1 | Tumbes | El Tigre (1981–2016) | January 1981–December 2003 | 5007 | 861 | 746 | 0.87 | 34 | 35 | 31 | 0 | 99 | 0 | 0.71 |
| 2 | Chira | El Ciruelo (1981–2016) | January 1981–December 2003 | 7050 | 796 | 476 | 0.60 | 35 | 34 | 31 | 0 | 88 | 12 | 0 |
| 3 | Piura | Puente Sánchez Cerro (1997–2016) | January 1990–December 2008 | 7575 | 510 | 180 | 0.35 | 28 | 23 | 49 | 0 | 63 | 37 | 0 |
| 4 | Chancay Lambayeque | Racarrumi (1981–2016) | January 1981–December 2003 | 2371 | 768 | 460 | 0.60 | 27 | 35 | 38 | 0 | 81 | 19 | 0 |
| 5 | Chicama | Salinar (1981–2016) | January 1981–December 2003 | 3671 | 477 | 206 | 0.43 | 23 | 31 | 46 | 0 | 81 | 19 | 0 |
| 6 | Santa | Condorcerro (1981–2016) | January 1981–December 2003 | 10,404 | 576 | 413 | 0.72 | 24 | 35 | 41 | 48 | 45 | 0 | 7 |
| 7 | Fortaleza | Malvados (2000–2016) | January 1997–December 2009 | 1317 | 304 | 134 | 0.44 | 30 | 36 | 34 | 0 | 78 | 22 | 0 |
| 8 | Chancay Huaral | Santo Domingo (1994–2016) | January 1991–December 2007 | 1851 | 429 | 273 | 0.64 | 27 | 37 | 37 | 27 | 54 | 19 | 0 |
| 9 | Chillón | Obrajillo (1997–2016) | January 1994–December 2008 | 486 | 705 | 333 | 0.47 | 24 | 37 | 39 | 40 | 14 | 46 | 0 |
| 10 | Cañete | Socsi (1981–2016) | January 1981–December 2003 | 5789 | 385 | 281 | 0.73 | 25 | 37 | 38 | 54 | 42 | 4 | 0 |
| 11 | Pisco | Letrayoc (1981–2016) | January 1981–December 2003 | 3088 | 494 | 247 | 0.50 | 24 | 37 | 40 | 61 | 6 | 33 | 0 |
| 12 | Camaná | Huatiapa (1998–2016) | January 1994–December 2008 | 12,845 | 458 | 184 | 0.40 | 18 | 37 | 46 | 47 | 17 | 36 | 0 |
| 13 | Ocoña | Puente Ocoña (2006–2016) | January 2004–December 2011 | 15,972 | 367 | 170 | 0.46 | 17 | 37 | 47 | 36 | 26 | 38 | 0.02 |
| 14 | Tambo | Puente Santa Rosa (1981–2016) | January 1981–December 2003 | 12,891 | 254 | 73 | 0.29 | 18 | 38 | 44 | 18 | 4 | 78 | 0 |
| Basin Characteristics | Notation (Unit) | Min | 25th Percentile | Median | 75th Percentile | Max |
|---|---|---|---|---|---|---|
| Hydro-Climatic Characteristics | ||||||
| Mean annual rainfall | Rm (mm/year) | 0.53 | 21 | 143 | 470 | 1219 |
| Mean annual potential evapotranspiration | Em (mm/year) | 1064 | 1326 | 1511 | 1679 | 2768 |
| Mean annual flow | Qm (mm/year) | 0 | 0.1 | 14 | 108 | 588 |
| Runoff coefficient | Qm/Rm (-) | 0 | 0.01 | 0.08 | 0.28 | 0.61 |
| Descriptors Used | ||||||
| Basin area | Ab ( ) | 0.56 | 222 | 321 | 495 | 1735 |
| Basin slope | Sb (-) | 0 | 0.08 | 0.17 | 0.26 | 0.55 |
| Mean basin altitude | Zb (m) | 0 | 536 | 1753 | 3460 | 4868 |
| Drainage density | dc (-) | 0.001 | 0.035 | 0.057 | 0.09 | 0.75 |
| Fraction of forest cover | fc (-) | 0 | 0.06 | 0.26 | 0.56 | 0.99 |
| Latitude | lat (-) | −18.2 | −15.6 | −12.8 | −6.9 | −3.5 |
| Longitude | long (-) | −81.2 | −79.2 | −76 | −72.7 | −69.9 |
| Original Variables | Principal Components | ||||
|---|---|---|---|---|---|
| PC1 | PC2 | PC3 | PC4 | PC5 | |
| Rm | −0.457 | −0.105 | 0.221 | −0.040 | 0.147 |
| Em | 0.163 | 0.460 | 0.025 | 0.173 | 0.038 |
| Qm | −0.416 | −0.011 | 0.385 | 0.022 | 0.194 |
| Rc | −0.399 | 0.108 | 0.395 | 0.089 | −0.032 |
| Ab | −0.085 | −0.148 | −0.242 | 0.639 | −0.202 |
| Sb | −0.152 | −0.316 | −0.481 | −0.276 | 0.191 |
| Zb | −0.155 | −0.514 | 0.091 | −0.024 | −0.096 |
| dc | 0.098 | 0.151 | 0.167 | −0.656 | −0.339 |
| fc | −0.348 | 0.031 | −0.452 | −0.215 | 0.222 |
| lat | −0.321 | 0.407 | −0.188 | 0.011 | 0.006 |
| long | 0.253 | −0.433 | 0.250 | −0.005 | 0.016 |
| Eigenvalues | 3.816 | 3.036 | 1.571 | 1.155 | 0.815 |
| Variance (%) | 31.8 | 25.3 | 13.1 | 9.6 | 6.8 |
| Cumulative variance (%) | 31.8 | 57.1 | 70.2 | 79.8 | 86.6 |
| No. | River Basin | Initial a | Calibration a | Validation b | Whole Period (1981–2016) | Regional (1981–2016) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| KGE | logNSE | KGE | logNSE | KGE | logNSE | KGE | logNSE | KGE | logNSE | ||
| 1 | Tumbes | 0.33 | −3.41 | 0.63 | 0.44 | 0.58 | 0.66 | 0.64 | 0.44 | 0.5 | 0.19 |
| 2 | Chira | 0.37 | −3.85 | 0.72 | 0.62 | 0.7 | 0.64 | 0.75 | 0.61 | 0.69 | 0.59 |
| 3 | Piura | 0.53 | 0.87 | 0.78 | 0.83 | 0.53 | 0.74 | 0.73 | 0.79 | 0.62 | 0.61 |
| 4 | Chancay Lambayeque | 0.33 | −3.19 | 0.81 | 0.76 | 0.85 | 0.79 | 0.84 | 0.77 | 0.64 | 0.55 |
| 5 | Chicama | 0.18 | 0.26 | 0.63 | 0.81 | 0.4 | 0.77 | 0.66 | 0.8 | 0.52 | 0.75 |
| 6 | Santa | 0.14 | −7.92 | 0.57 | 0.24 | 0.59 | 0.13 | 0.57 | 0.16 | 0.42 | 0.15 |
| 7 | Fortaleza | −0.18 | −0.03 | 0.8 | 0.33 | 0.59 | 0.49 | 0.74 | 0.4 | 0.7 | 0.49 |
| 8 | Chancay Huaral | 0.06 | −3.51 | 0.72 | 0.54 | 0.74 | 0 | 0.73 | 0.38 | 0.59 | 0.41 |
| 9 | Chillón | 0.53 | −4.06 | 0.62 | 0.48 | 0.72 | 0.63 | 0.69 | 0.54 | 0.61 | 0.54 |
| 10 | Cañete | 0.15 | −1.8 | 0.6 | 0.72 | 0.71 | 0.41 | 0.69 | 0.63 | 0.5 | 0.66 |
| 11 | Pisco | 0.14 | 0.52 | 0.53 | 0.72 | 0.67 | 0.35 | 0.58 | 0.62 | 0.38 | 0.6 |
| 12 | Ocoña | 0.63 | −8.01 | 0.77 | 0.3 | 0.72 | 0.3 | 0.79 | 0.31 | 0.58 | −2 |
| 13 | Camaná | 0.71 | −5.27 | 0.82 | 0.55 | 0.76 | 0.4 | 0.79 | 0.48 | 0.68 | 0.58 |
| 14 | Tambo | 0.65 | −0.68 | 0.71 | 0.25 | 0.1 | −0.2 | 0.59 | 0.1 | 0.69 | 0.14 |
| Parameter Name | Parameter Description [54] | Regional Parameters | ||||
|---|---|---|---|---|---|---|
| Region 1 | Region 2 | Region 3 | Region 4 | Region 5 | ||
| GWQMN | Threshold depth of water in the shallow aquifer required for return flow to occur | 542.70 | 773.14 | 469.32 | 524.16 | 503.31 |
| RCHRG_DP | Deep aquifer percolation fraction | 0.82 | 0.05 | 0.85 | 0.45 | 0.87 |
| SOL_AWC r | Available water capacity of the soil layer | −86.47 | −41.00 | −83.34 | −85.37 | −12.50 |
| SOL_BD r | Soil bulk density | 22.59 | 0 | 51.67 | 19.91 | 0 |
| SURLAG | Surface runoff lag coefficient | 0.40 | 1.75 | 2 | 2 | 1.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asurza-Véliz, F.A.; Lavado-Casimiro, W.S. Regional Parameter Estimation of the SWAT Model: Methodology and Application to River Basins in the Peruvian Pacific Drainage. Water 2020, 12, 3198. https://doi.org/10.3390/w12113198
Asurza-Véliz FA, Lavado-Casimiro WS. Regional Parameter Estimation of the SWAT Model: Methodology and Application to River Basins in the Peruvian Pacific Drainage. Water. 2020; 12(11):3198. https://doi.org/10.3390/w12113198
Chicago/Turabian StyleAsurza-Véliz, Flavio Alexander, and Waldo Sven Lavado-Casimiro. 2020. "Regional Parameter Estimation of the SWAT Model: Methodology and Application to River Basins in the Peruvian Pacific Drainage" Water 12, no. 11: 3198. https://doi.org/10.3390/w12113198
APA StyleAsurza-Véliz, F. A., & Lavado-Casimiro, W. S. (2020). Regional Parameter Estimation of the SWAT Model: Methodology and Application to River Basins in the Peruvian Pacific Drainage. Water, 12(11), 3198. https://doi.org/10.3390/w12113198






