Spatial and Temporal Evaluation of the Latest High-Resolution Precipitation Products over the Upper Blue Nile River Basin, Ethiopia
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Datasets
2.3. Data Comparison
2.4. Performance Indices
3. Results and Discussions
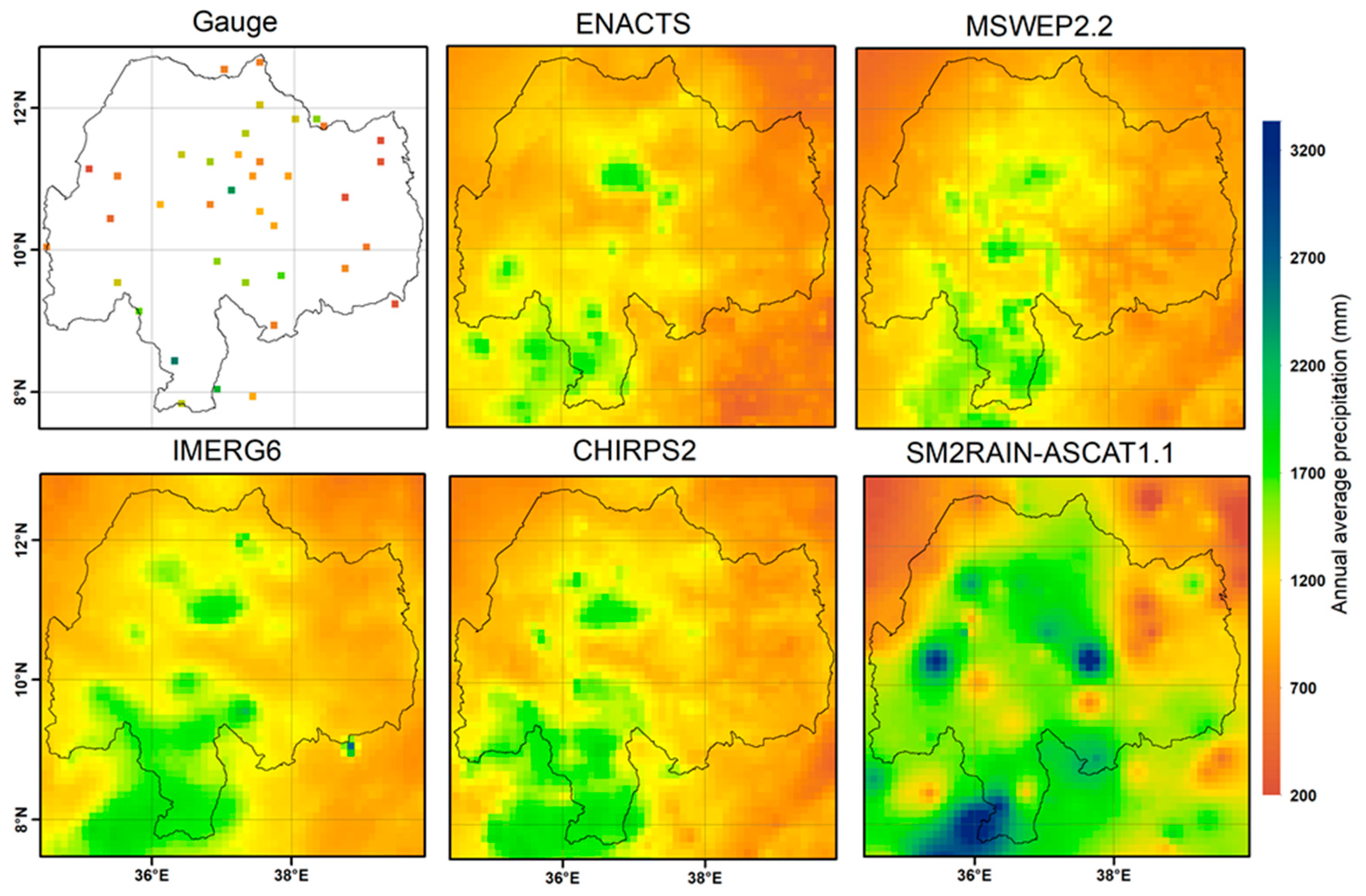
3.1. Representation of Spatial Variability
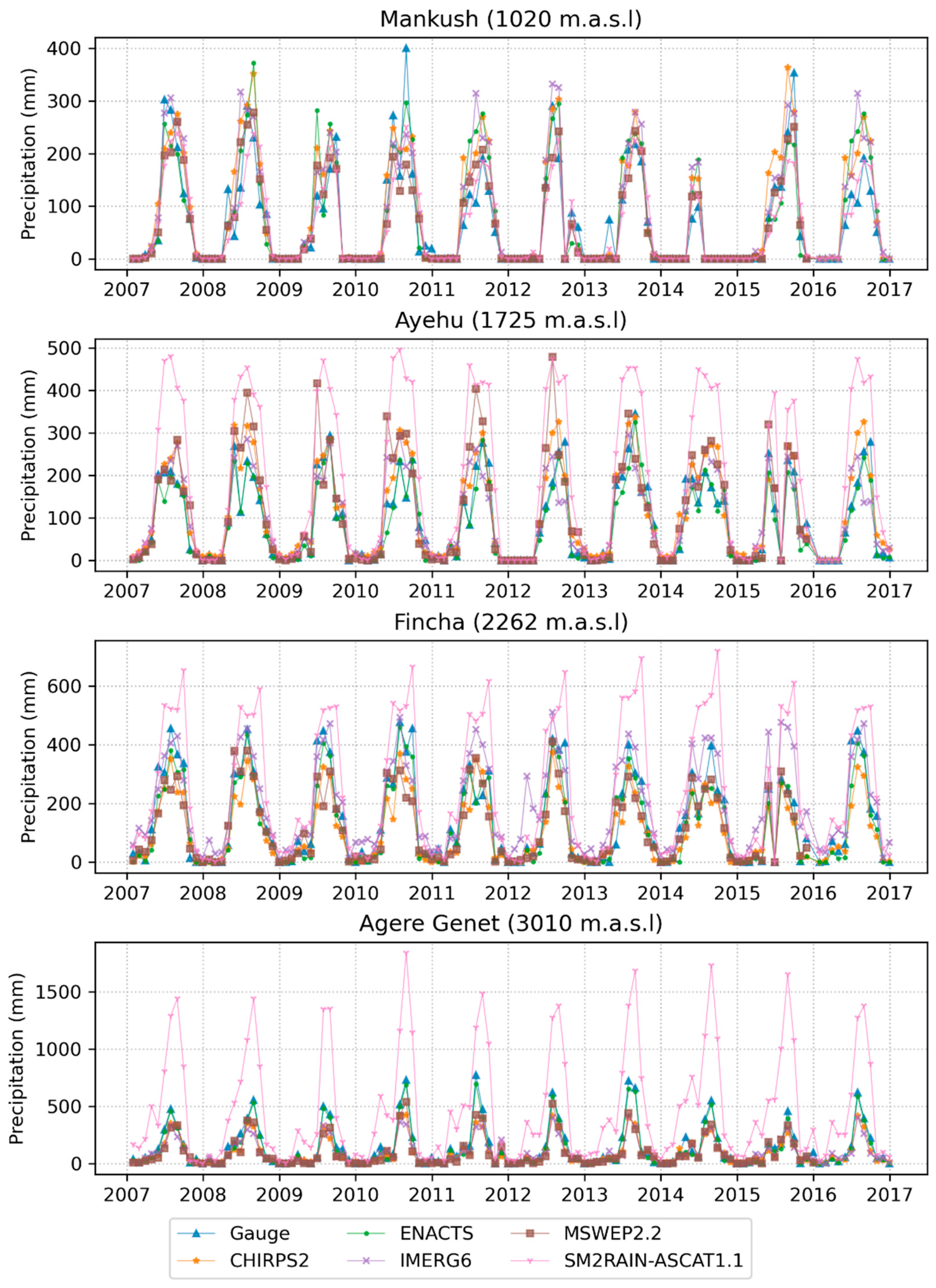
3.2. Representation of Temporal Variability
3.3. Representation of Different Intensities
4. Conclusions
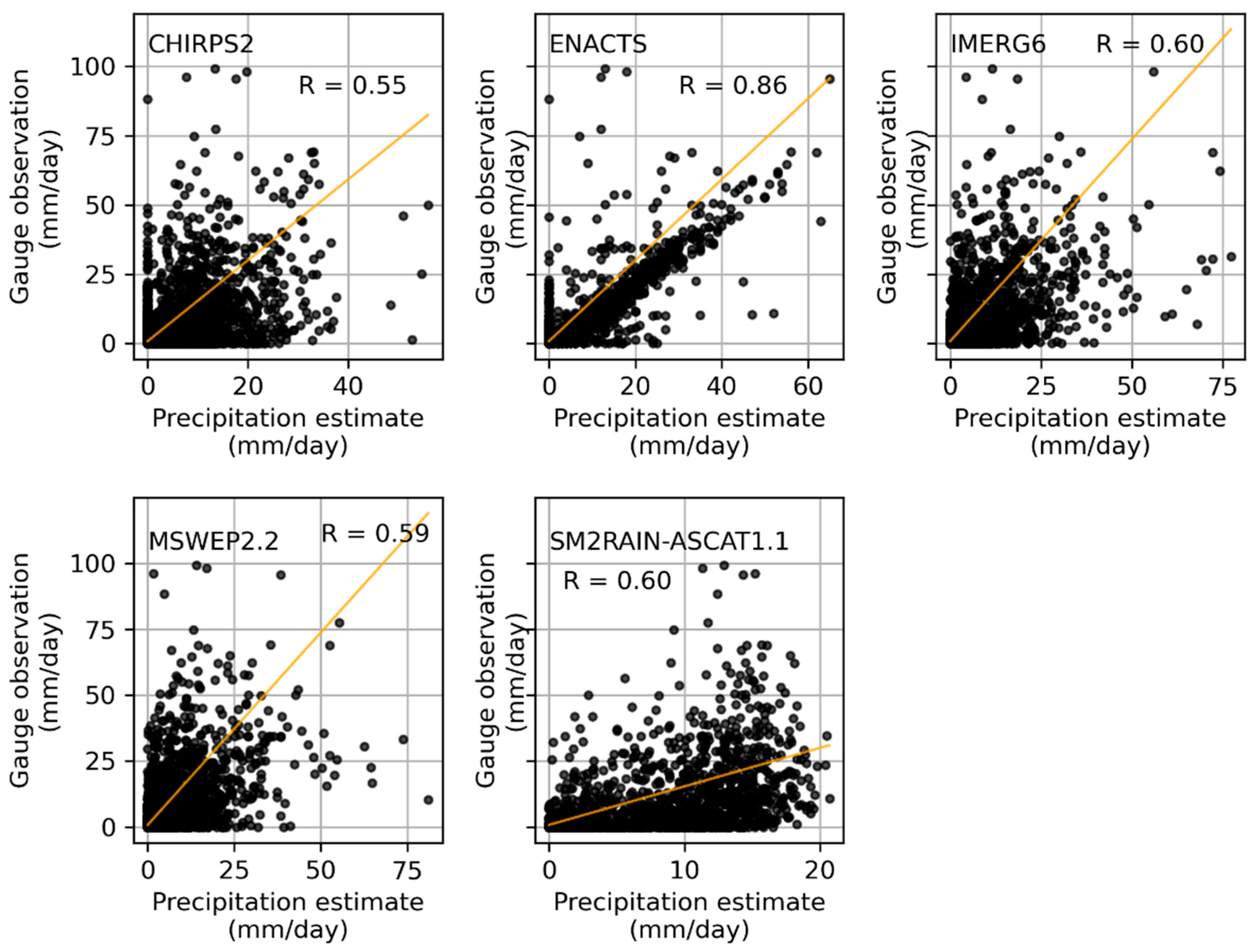
- CHIRPS2, IMERG6, and MSWEP2.2 precipitations exhibit good agreement with the average annual rainfall from ENACTS and the gauge dataset.
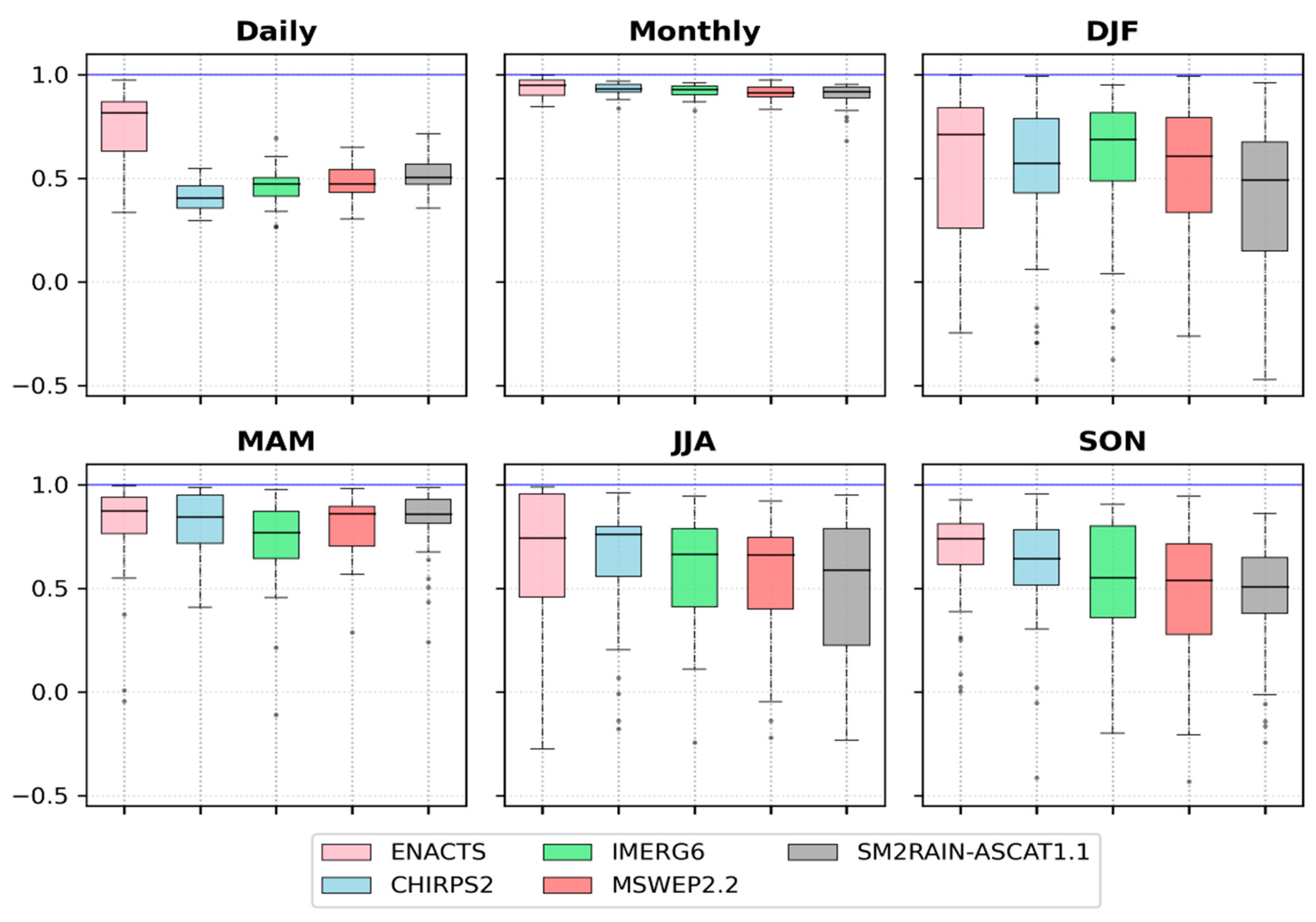
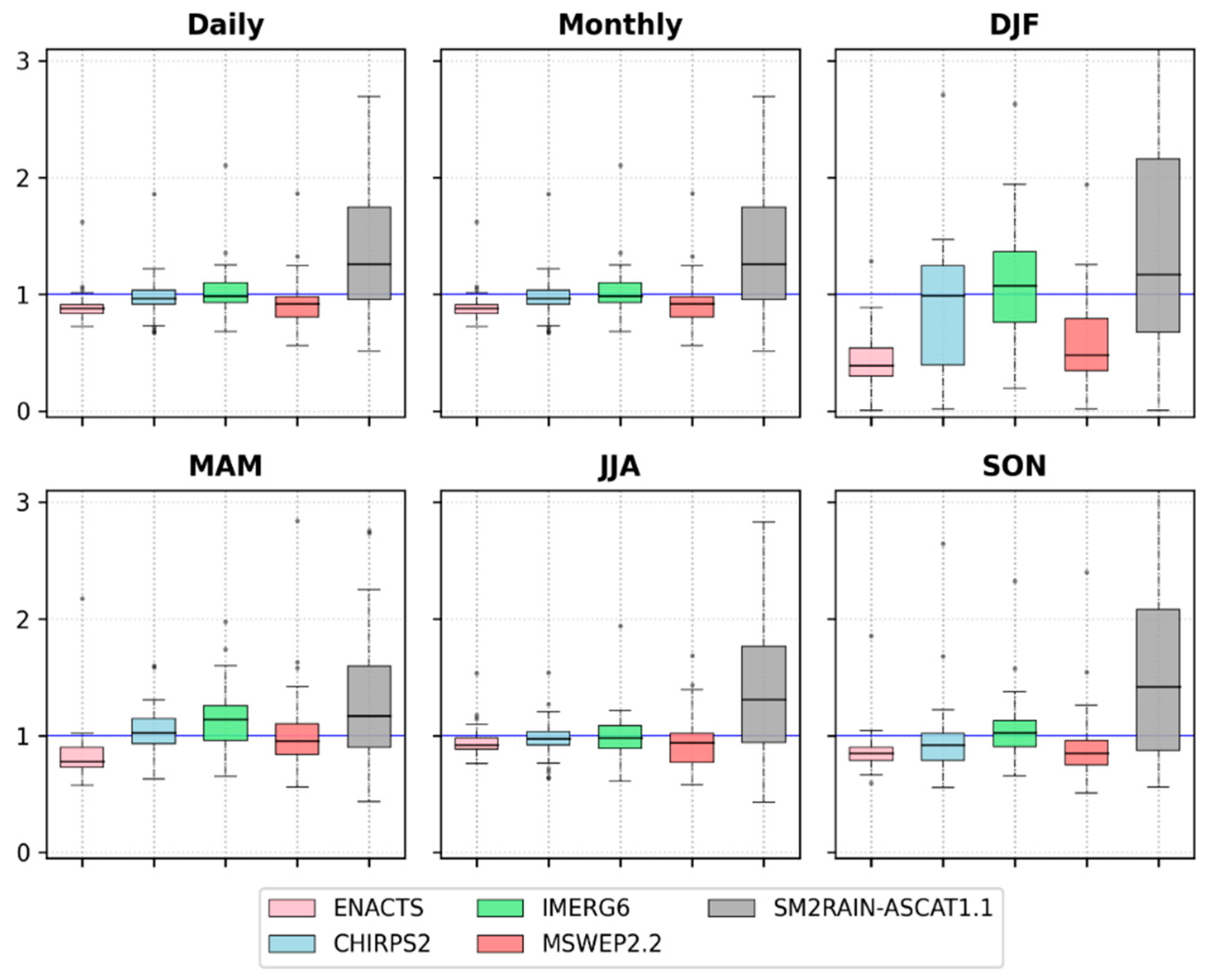
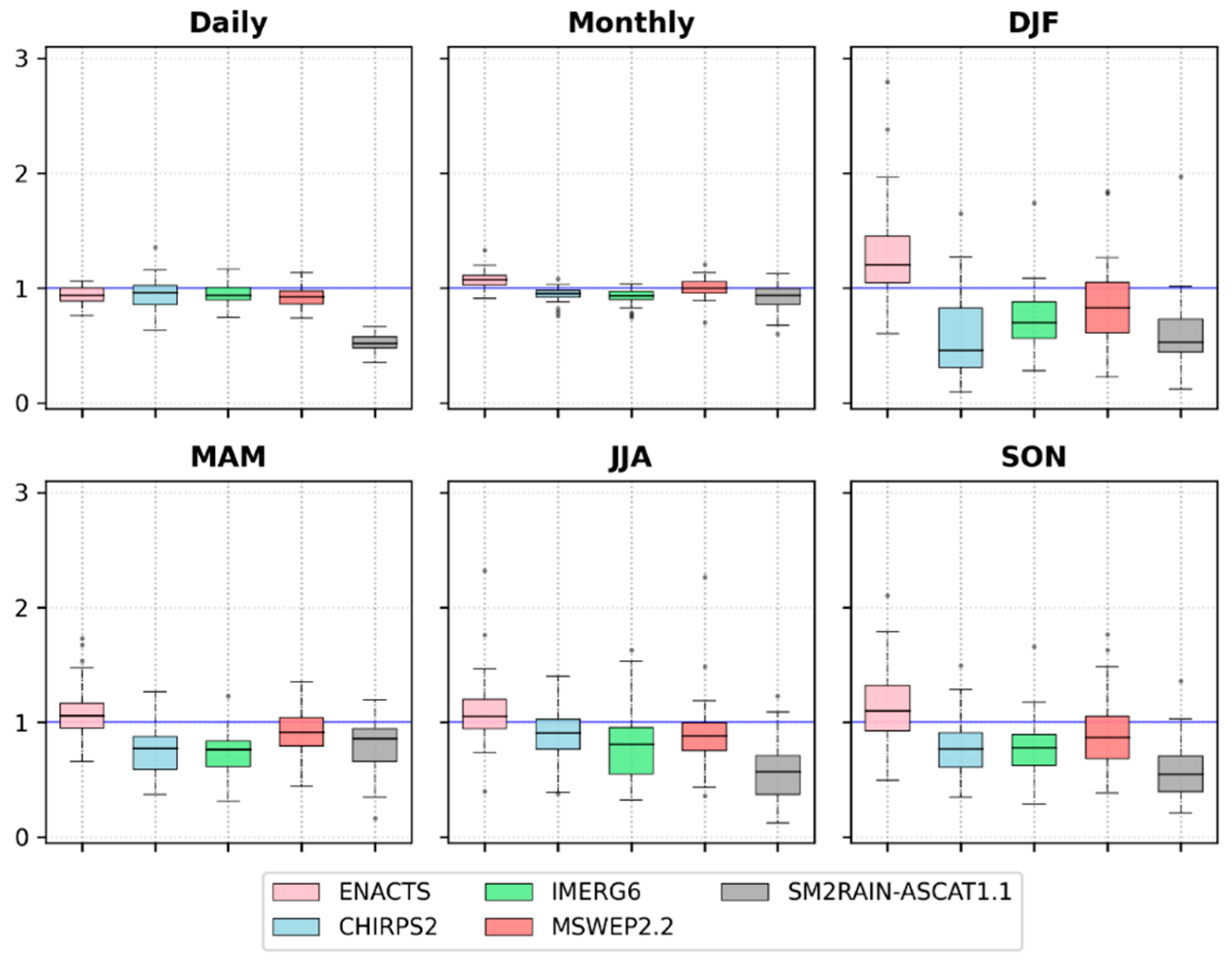
- All datasets provided better linear correlation (median r > 0.5) for monthly and seasonal time scales with the best correlation at the monthly time step (median r > 0.9).
- All datasets except SM2RAIN-ASCAT1.1 were nearly unbiased at all time scales except the dry season (DJF). SM2RAIN-ASCAT1.1 consistently and significantly overestimated the precipitation compared to gauge observations.
- All datasets captured precipitation variability on daily and monthly scales despite SM2RAIN-ASCAT1.1′s relatively low skill on a daily scale. A similar underestimation of precipitation variability has been observed at MAM, JJA, and SON seasons by all datasets. ENACTS, in contrast, showed a slight overestimation.
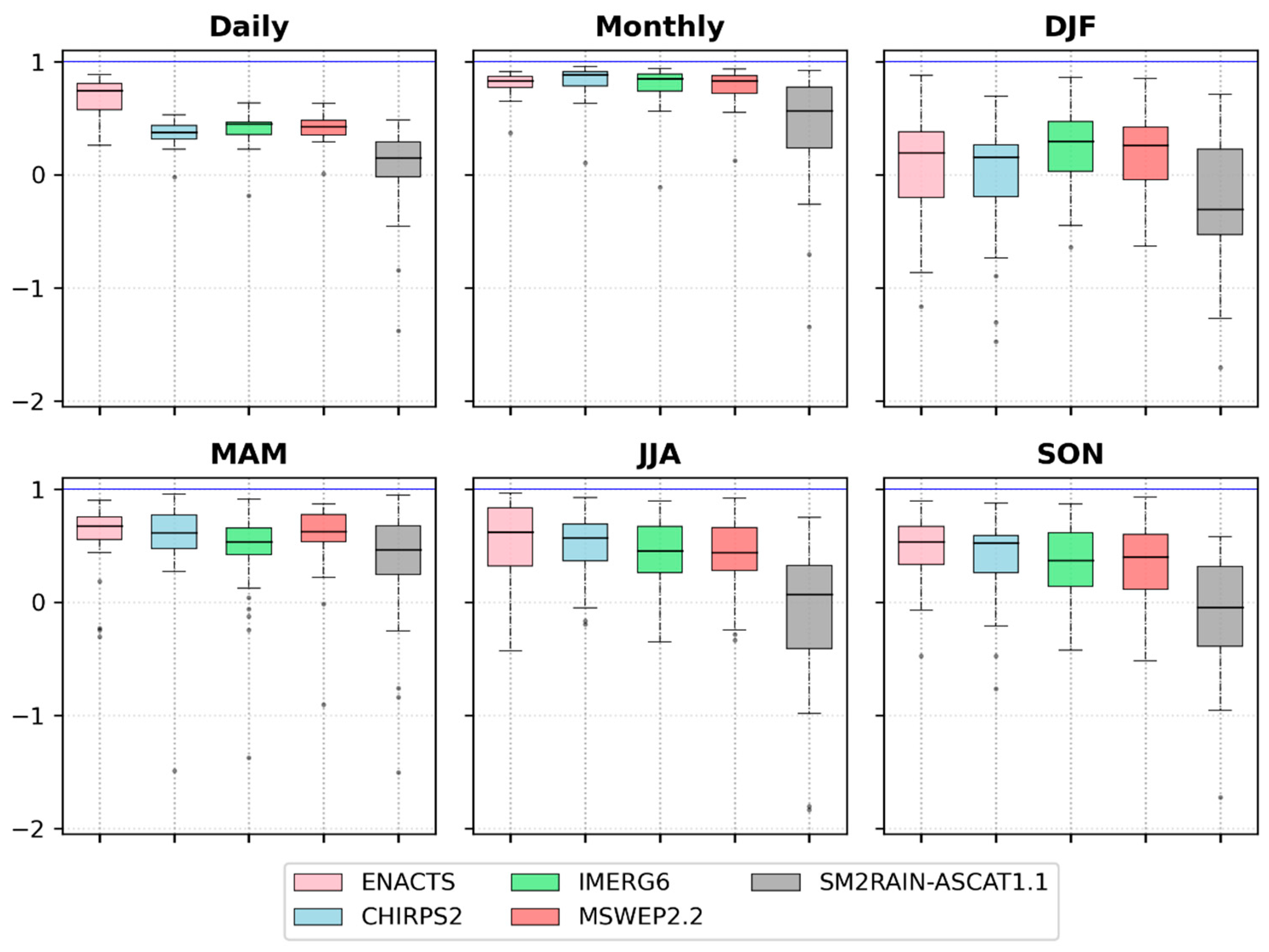
- Based on KGE’, all datasets had the best skill on a monthly time scale. On the remaining times, the overall performance was poor.
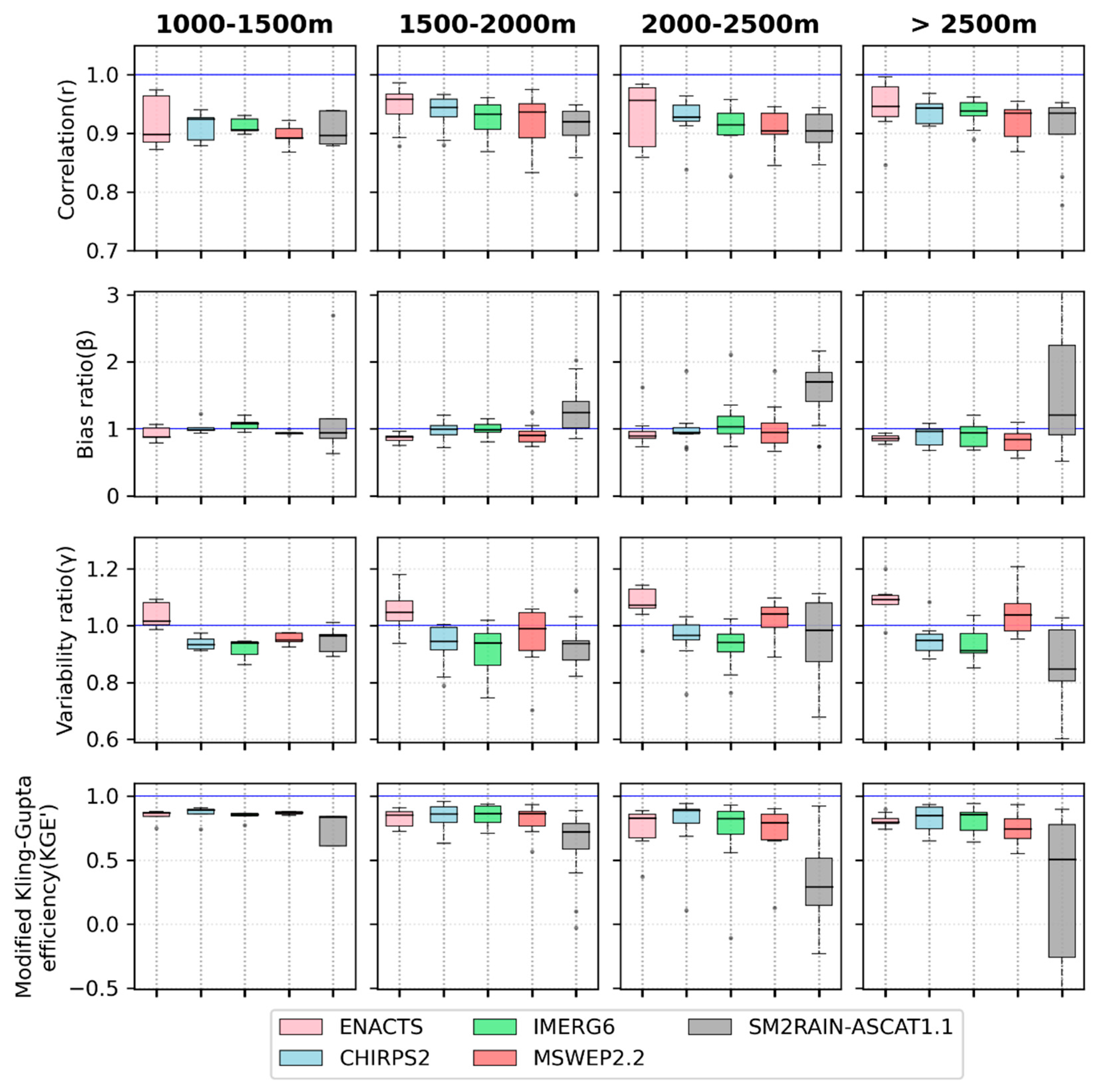
- ENACTS, MSWEP2.2, and IMERG6 showed better success (CSI > 0.6) in detecting precipitation at different elevations. As evidenced by all categorical measures, the resistance of MSWEP2.2 and IMERG6 to the influence of elevation variation shows their strength in correctly representing the area’s local climate features.
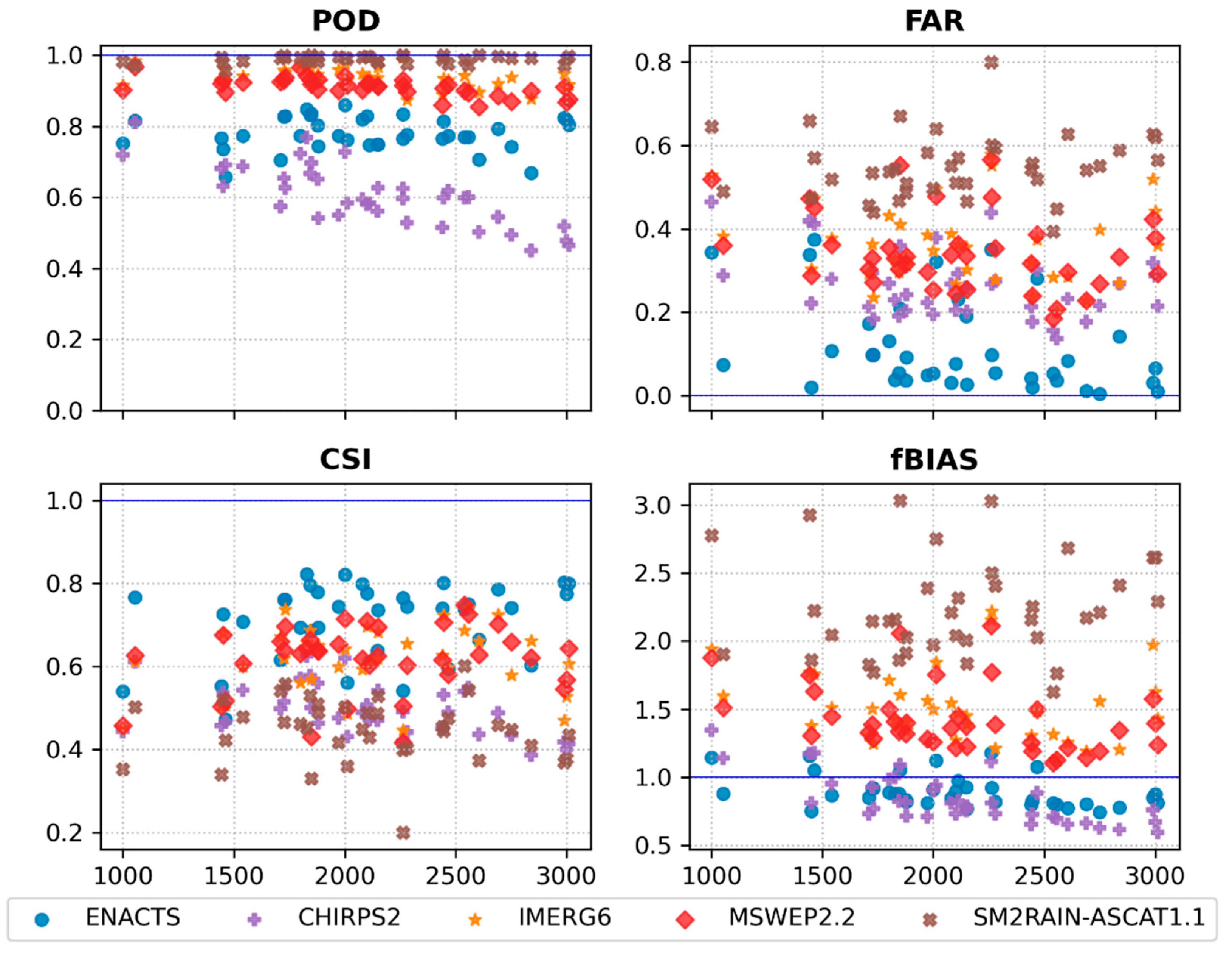
- All datasets correctly identified the occurrence of no-rain events (<1 mm/day). However, for higher intensities, they presented a low and deteriorating skill with an increase in intensity.
- Considering the scarcity of gauged datasets over UBNRB, IMERG6 and MSWEP2.2 could be considered to be valuable datasets for hydro-climatic analysis, particularly where gauging density is low. SM2RAIN-ASCAT1.1, on the other hand, needs a critical correction to treat its apparent wet biases before use.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Continuous and Categorical Indices Used for Evaluation
- Continuous indices
- Modified Kling-Gupta efficiency (KGE’)
- Pearson correlation coefficient (r)
- Bias ratio (β)
- Variability ratio (γ)where x = gauge observation, y = estimated precipitation, n = number of observations, = average gauge observation, = average estimated precipitation, sx = standard deviation of gauge observations, sy = standard deviation of estimated precipitations.
- Categorical indices
- e.
- Probability of detection (POD)
- f.
- False alarm ratio (FAR)
- g.
- Critical success index (CSI)
- h.
- Frequency bias (fBIAS)where H = hit (number of gauge observations correctly detected by datasets), M = miss (number of gauge observations which are not correctly detected by datasets), FA = false alarm (number of false precipitations recorded by datasets but not at the gauge).
References
- Beven, K.J. Rainfall-Runoff Modelling: The Primer, 2nd ed.; Wiley-Blackwell: Chichester, West Sussex, UK; Hoboken, NJ, USA, 2012; ISBN 978-0-470-71459-1. [Google Scholar]
- Artan, G.; Gadain, H.; Smith, J.L.; Asante, K.; Bandaragoda, C.J.; Verdin, J.P. Adequacy of satellite derived rainfall data for stream flow modeling. Nat. Hazards 2007, 43, 167–185. [Google Scholar] [CrossRef]
- Behrangi, A.; Khakbaz, B.; Jaw, T.C.; AghaKouchak, A.; Hsu, K.; Sorooshian, S. Hydrologic evaluation of satellite precipitation products over a mid-size basin. J. Hydrol. 2011, 397, 225–237. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Acharya, S.C.; Nathan, R.; Wang, Q.J.; Su, C.-H.; Eizenberg, N. An evaluation of daily precipitation from a regional atmospheric reanalysis over Australia. Hydrol. Earth Syst. Sci. 2019, 23, 3387–3403. [Google Scholar] [CrossRef]
- Ayehu, G.T.; Tadesse, T.; Gessesse, B.; Dinku, T. Validation of new satellite rainfall products over the Upper Blue Nile Basin, Ethiopia. Atmospheric Meas. Tech. 2018, 11, 1921–1936. [Google Scholar] [CrossRef]
- Dinku, T.; Chidzambwa, S.; Ceccato, P.; Connor, S.J.; Ropelewski, C.F. Validation of high-resolution satellite rainfall products over complex terrain. Int. J. Remote Sens. 2008, 29, 4097–4110. [Google Scholar] [CrossRef]
- Gebremichael, M.; Bitew, M.M.; Hirpa, F.A.; Tesfay, G.N. Accuracy of satellite rainfall estimates in the Blue Nile Basin: Lowland plain versus highland mountain. Water Resour. Res. 2014, 50, 8775–8790. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Nauditt, A.; Birkel, C.; Verbist, K.; Ribbe, L. Temporal and spatial evaluation of satellite-based rainfall estimates across the complex topographical and climatic gradients of Chile. Hydrol. Earth Syst. Sci. 2017, 21, 1295–1320. [Google Scholar] [CrossRef]
- Conway, D.; Mould, C.; Bewket, W. Over one century of rainfall and temperature observations in Addis Ababa, Ethiopia. Int. J. Clim. 2004, 24, 77–91. [Google Scholar] [CrossRef]
- Abera, W.; Brocca, L.; Rigon, R. Comparative evaluation of different satellite rainfall estimation products and bias correction in the Upper Blue Nile (UBN) basin. Atmospheric Res. 2016, 471–483. [Google Scholar] [CrossRef]
- Lakew, H.B.; Moges, S.; Asfaw, D.H. Hydrological Evaluation of Satellite and Reanalysis Precipitation Products in the Upper Blue Nile Basin: A Case Study of Gilgel Abbay. Hydrology 2017, 4, 39. [Google Scholar] [CrossRef]
- Dinku, T.; Connor, S.; Ceccato, P. Evaluation of Satellite Rainfall Estimates and Gridded Gauge Products over the Upper Blue Nile Region. In Nile River Basin; Melesse, A.M., Ed.; Springer: Dordrecht, The Netherlands, 2011; pp. 109–127. ISBN 978-94-007-0688-0. [Google Scholar]
- Fenta, A.A.; Rientjes, T.; Haile, A.T.; Reggiani, P. Satellite Rainfall Products and Their Reliability in the Blue Nile Basin. In Nile River Basin; Melesse, A.M., Abtew, W., Setegn, S.G., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 51–67. ISBN 978-3-319-02719-7. [Google Scholar]
- Lakew, H.B.; Moges, S.A.; Asfaw, D.H. Hydrological performance evaluation of multiple satellite precipitation products in the upper Blue Nile basin, Ethiopia. J. Hydrol. Reg. Stud. 2020, 27, 100664. [Google Scholar] [CrossRef]
- Worqlul, A.W.; Maathuis, B.; Adem, A.A.; Demissie, S.S.; Langan, S.; Steenhuis, T.S. Comparison of rainfall estimations by TRMM 3B42, MPEG and CFSR with ground-observed data for the Lake Tana basin in Ethiopia. Hydrol. Earth Syst. Sci. 2014, 18, 4871–4881. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS satellite rainfall estimates over eastern Africa. Q. J. R. Meteorol. Soc. 2018, 144, 292–312. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. Algorithm Theoretical Basis Document (ATBD) Version 6 for the NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (IMERG) GPM Project, Greenbelt, MD. 2019. Available online: https://gpm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V06.pdf (accessed on 30 October 2020).
- Beck, H.E.; Wood, E.F.; Pan, M.; Fisher, C.K.; Miralles, D.G.; Van Dijk, A.I.J.M.; McVicar, T.R.; Adler, R.F. MSWEP V2 Global 3-Hourly 0.1° Precipitation: Methodology and Quantitative Assessment. Bull. Am. Meteorol. Soc. 2019, 100, 473–500. [Google Scholar] [CrossRef]
- Brocca, L.; Filippucci, P.; Hahn, S.; Ciabatta, L.; Massari, C.; Camici, S.; Schüller, L.; Bojkov, B.; Wagner, W. SM2RAIN–ASCAT (2007–2018): Global daily satellite rainfall data from ASCAT soil moisture observations. Earth Syst. Sci. Data 2019, 11, 1583–1601. [Google Scholar] [CrossRef]
- Conway, D. The Climate and Hydrology of the Upper Blue Nile River. Geogr. J. 2000, 166, 49–62. [Google Scholar] [CrossRef]
- Conway, D. From headwater tributaries to international river: Observing and adapting to climate variability and change in the Nile basin. Glob. Environ. Chang. 2005, 15, 99–114. [Google Scholar] [CrossRef]
- Abtew, W.; Melesse, A.M.; Dessalegne, T. Spatial, inter and intra-annual variability of the Upper Blue Nile Basin rainfall. Hydrol. Process. 2009, 23, 3075–3082. [Google Scholar] [CrossRef]
- Samy, A.; Ibrahim, M.G.; Mahmod, W.E.; Fujii, M.; Eltawil, A.; Daoud, W. Statistical Assessment of Rainfall Characteristics in Upper Blue Nile Basin over the Period from 1953 to 2014. Water 2019, 11, 468. [Google Scholar] [CrossRef]
- Kim, U.; Kaluarachchi, J.J.; Smakhtin, V.U. Generation of Monthly Precipitation Under Climate Change for the Upper Blue Nile River Basin, Ethiopia1. JAWRA J. Am. Water Resour. Assoc. 2008, 44, 1231–1247. [Google Scholar] [CrossRef]
- Searcy, J.K.; Hardison, C.H.; Langbein, W.B. Double-Mass Curves, with a Section Fitting Curves to Cyclic Data; U.S. Government Printing Office: Washington, DC, USA, 1960.
- Dinku, T.; Block, P.; Sharoff, J.; Hailemariam, K.; Osgood, D.; Del Corral, J.; Cousin, R.; Thomson, M.C. Bridging critical gaps in climate services and applications in africa. Earth Perspect. 2014, 1, 15. [Google Scholar] [CrossRef]
- Bayissa, Y.; Tadesse, T.; Demisse, G.; Shiferaw, A. Evaluation of Satellite-Based Rainfall Estimates and Application to Monitor Meteorological Drought for the Upper Blue Nile Basin, Ethiopia. Remote Sens. 2017, 9, 669. [Google Scholar] [CrossRef]
- Baez-Villanueva, O.M.; Zambrano-Bigiarini, M.; Ribbe, L.; Nauditt, A.; Giraldo-Osorio, J.D.; Thinh, N.X. Temporal and spatial evaluation of satellite rainfall estimates over different regions in Latin-America. Atmospheric Res. 2018, 213, 34–50. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Hossain, F. Understanding the Dependence of Satellite Rainfall Uncertainty on Topography and Climate for Hydrologic Model Simulation. IEEE Trans. Geosci. Remote Sens. 2012, 51, 704–718. [Google Scholar] [CrossRef]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; Levizzani, V.; De Roo, A. Validation of Satellite-Based Precipitation Products over Sparsely Gauged African River Basins. J. Hydrometeorol. 2012, 13, 1760–1783. [Google Scholar] [CrossRef]
- Su, J.; Lü, H.; Zhu, Y.; Cui, Y.; Wang, X. Evaluating the hydrological utility of latest IMERG products over the Upper Huaihe River Basin, China. Atmospheric Res. 2019, 225, 17–29. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 264–277. [Google Scholar] [CrossRef]
- Haile, A.T.; Rientjes, T.; Gieske, A.; Gebremichael, M. Rainfall Variability over Mountainous and Adjacent Lake Areas: The Case of Lake Tana Basin at the Source of the Blue Nile River. J. Appl. Meteorol. Clim. 2009, 48, 1696–1717. [Google Scholar] [CrossRef]
- Melesse, A.M.; Abtew, W.; Setegn, S.G.; Dessalegne, T. Hydrological Variability and Climate of the Upper Blue Nile River Basin. In Nile River Basin; Melesse, A.M., Ed.; Springer: Dordrecht, The Netherlands, 2011; pp. 3–37. ISBN 978-94-007-0688-0. [Google Scholar]
- Brocca, L.; Ciabatta, L.; Massari, C.; Moramarco, T.; Hahn, S.; Hasenauer, S.; Kidd, R.; Dorigo, W.; Wagner, W.; Levizzani, V. Soil as a natural rain gauge: Estimating global rainfall from satellite soil moisture data: Using the soil as a natural raingauge. J. Geophys. Res. Atmos. 2014, 119, 5128–5141. [Google Scholar] [CrossRef]

| Dataset | Data Source | Spatial Coverage | Spatial Resolution | Temporal Resolution | References | Description |
|---|---|---|---|---|---|---|
| ENACTS | Gauge and Satellite | Selected developing countries | 0.0375° | daily | [28] | The estimation procedure involves integrating quality-controlled station data with satellite rainfall estimates and other proxies such as elevation information. |
| CHIRPS2 | Gauge and Satellite | Global | 0.05° | daily, pentad, monthly | [17] | Data is built by blending Climate Hazard Group’s Infrared Precipitation (CHIRP) with in situ gauge observations. |
| IMERG6 | Gauge and Satellite | Global | 0.1° | half-hourly, daily, monthly | [19] | Data is generated by merging passive microwave (PMW) and infrared (IR) precipitations using state of the art calibration and interpolation schemes. |
| MSWEP2.2 | Gauge, Satellite and Reanalysis | Global | 0.1° | three-hourly, daily | [20] | Estimation follows necessary bias corrections applications, and merging and gauge corrections to selected reanalysis and satellite precipitation estimates. |
| SM2RAIN-ASCAT1.1 | Gauge precipitation and Satellite Soil Moisture | Global | 0.1° | daily | [21] | The estimation procedure follows the interpolation and filtering of ASCAT observations, followed by applying the soil moisture to rain (SM2RAIN) algorithm and gauge corrections. |
| Elevation | Dataset | Correlation (r) | Bias Ratio (β) | Variability Ratio (γ) | KGE’ |
|---|---|---|---|---|---|
| 1000–1500 m.a.s.l. (5) | ENACTS | 0.610 | 0.878 | 0.907 | 0.537 |
| CHIRPS2 | 0.352 | 0.984 | 0.726 | 0.318 | |
| IMERG6 | 0.343 | 1.074 | 0.861 | 0.289 | |
| MSWEP2.2 | 0.424 | 0.935 | 0.819 | 0.382 | |
| SM2RAIN-ASCAT1.1 | 0.472 | 0.943 | 0.503 | 0.154 | |
| 1500–2000 m.a.s.l. (12) | ENACTS | 0.811 | 0.879 | 0.902 | 0.743 |
| CHIRPS2 | 0.412 | 0.994 | 0.866 | 0.398 | |
| IMERG6 | 0.455 | 0.985 | 0.900 | 0.443 | |
| MSWEP2.2 | 0.453 | 0.904 | 0.881 | 0.430 | |
| SM2RAIN-ASCAT1.1 | 0.497 | 1.244 | 0.490 | 0.174 | |
| 2000–2500 m.a.s.l. (12) | ENACTS | 0.794 | 0.898 | 0.954 | 0.759 |
| CHIRPS2 | 0.397 | 0.952 | 0.981 | 0.373 | |
| IMERG6 | 0.481 | 1.032 | 0.938 | 0.456 | |
| MSWEP2.2 | 0.476 | 0.948 | 0.936 | 0.387 | |
| SM2RAIN-ASCAT1.1 | 0.506 | 1.706 | 0.521 | 0.042 | |
| >2500 m.a.s.l. (9) | ENACTS | 0.823 | 0.858 | 1.007 | 0.749 |
| CHIRPS2 | 0.430 | 0.963 | 1.083 | 0.391 | |
| IMERG6 | 0.504 | 0.944 | 0.995 | 0.468 | |
| MSWEP2.2 | 0.523 | 0.840 | 0.983 | 0.462 | |
| SM2RAIN-ASCAT1.1 | 0.585 | 1.204 | 0.569 | 0.247 |
| Intensity | Dataset | POD | FAR | CSI | fBIAS |
|---|---|---|---|---|---|
| No rain | ENACTS | 0.94 | 0.07 | 0.89 | 1.01 |
| CHIRPS2 | 0.85 | 0.19 | 0.72 | 1.06 | |
| IMERG6 | 0.82 | 0.11 | 0.75 | 0.92 | |
| MSWEP2.2 | 0.83 | 0.12 | 0.75 | 0.92 | |
| SM2RAIN-ASCAT1.1 | 0.59 | 0.03 | 0.58 | 0.61 | |
| Light rain | ENACTS | 0.71 | 0.20 | 0.62 | 0.92 |
| CHIRPS2 | 0.14 | 0.77 | 0.10 | 0.62 | |
| IMERG6 | 0.53 | 0.64 | 0.27 | 1.58 | |
| MSWEP2.2 | 0.52 | 0.63 | 0.27 | 1.45 | |
| SM2RAIN-ASCAT1.1 | 0.76 | 0.86 | 0.13 | 5.27 | |
| Moderate rain | ENACTS | 0.89 | 0.10 | 0.83 | 1.02 |
| CHIRPS2 | 0.57 | 0.41 | 0.38 | 0.96 | |
| IMERG6 | 0.75 | 0.34 | 0.54 | 1.11 | |
| MSWEP2.2 | 0.73 | 0.35 | 0.53 | 1.11 | |
| SM2RAIN-ASCAT1.1 | 0.97 | 0.46 | 0.54 | 1.77 | |
| Heavy rain | ENACTS | 0.92 | 0.03 | 0.90 | 0.96 |
| CHIRPS2 | 0.38 | 0.47 | 0.30 | 0.74 | |
| IMERG6 | 0.74 | 0.37 | 0.50 | 1.09 | |
| MSWEP2.2 | 0.63 | 0.34 | 0.47 | 0.93 | |
| SM2RAIN-ASCAT1.1 | 0.17 | 0.96 | 0.04 | 0.50 | |
| Violent rain | ENACTS | 0.80 | 0.00 | 0.79 | 0.85 |
| CHIRPS2 | 0.03 | 0.94 | 0.02 | 0.35 | |
| IMERG6 | 0.41 | 0.55 | 0.27 | 1.00 | |
| MSWEP2.2 | 0.19 | 0.50 | 0.16 | 0.50 | |
| SM2RAIN-ASCAT1.1 | 0.00 | 1.00 | 0.00 | 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abebe, S.A.; Qin, T.; Yan, D.; Gelaw, E.B.; Workneh, H.T.; Kun, W.; Liu, S.; Dong, B. Spatial and Temporal Evaluation of the Latest High-Resolution Precipitation Products over the Upper Blue Nile River Basin, Ethiopia. Water 2020, 12, 3072. https://doi.org/10.3390/w12113072
Abebe SA, Qin T, Yan D, Gelaw EB, Workneh HT, Kun W, Liu S, Dong B. Spatial and Temporal Evaluation of the Latest High-Resolution Precipitation Products over the Upper Blue Nile River Basin, Ethiopia. Water. 2020; 12(11):3072. https://doi.org/10.3390/w12113072
Chicago/Turabian StyleAbebe, Sintayehu A., Tianling Qin, Denghua Yan, Endalkachew B. Gelaw, Habtamu T. Workneh, Wang Kun, Shanshan Liu, and Biqiong Dong. 2020. "Spatial and Temporal Evaluation of the Latest High-Resolution Precipitation Products over the Upper Blue Nile River Basin, Ethiopia" Water 12, no. 11: 3072. https://doi.org/10.3390/w12113072
APA StyleAbebe, S. A., Qin, T., Yan, D., Gelaw, E. B., Workneh, H. T., Kun, W., Liu, S., & Dong, B. (2020). Spatial and Temporal Evaluation of the Latest High-Resolution Precipitation Products over the Upper Blue Nile River Basin, Ethiopia. Water, 12(11), 3072. https://doi.org/10.3390/w12113072





