Study of the Sediment Transport Law in a Reverse-Slope Section of a Pressurized Pipeline
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Design
2.2. Experimental Design
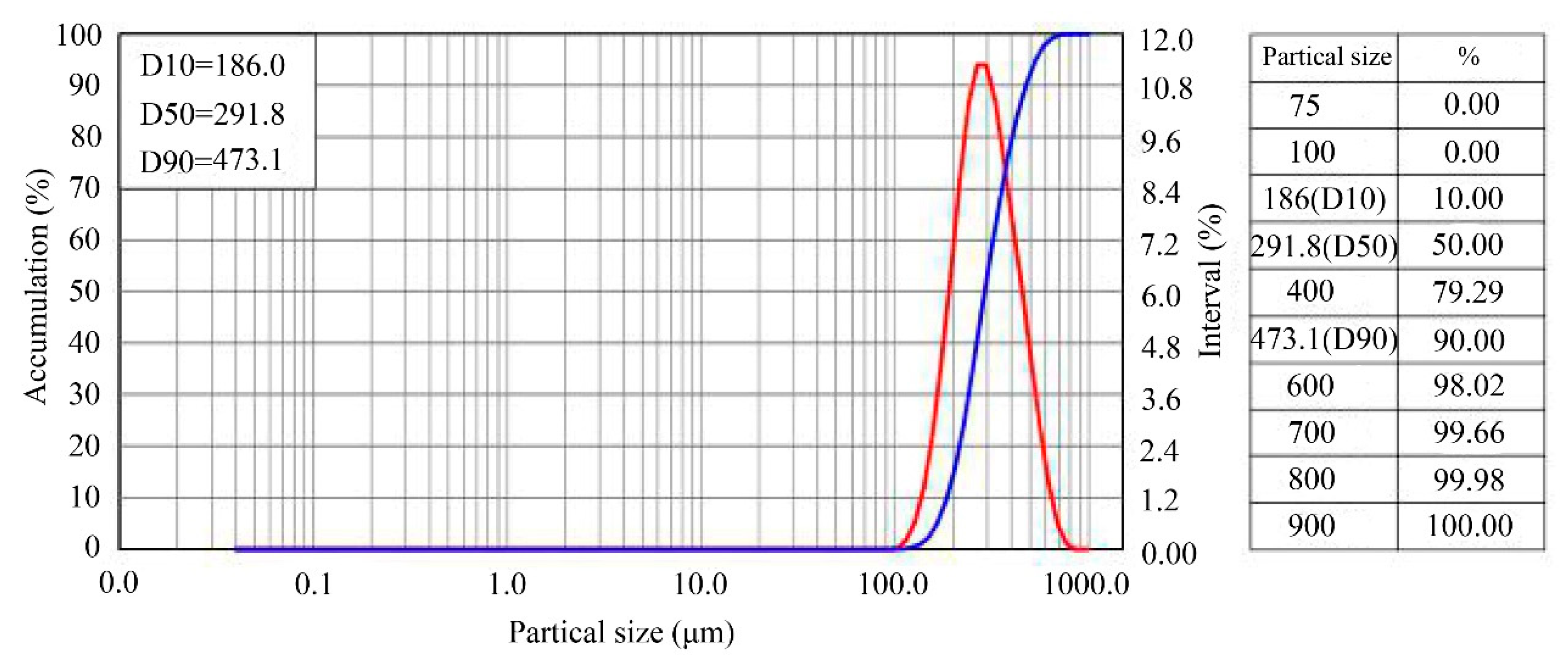
2.2.1. Test Sand
2.2.2. Experimental Arrangement
- (1)
- Prior to the experiment, the appropriate amount of sand was added, the blender was started, and the mixture was stirred for half an hour. This ensured that the sediment content in all portions of the mixer reached the same level.
- (2)
- The valve was then opened, and the motor (to drive the pump) was started. This flushed the silt into the glass tube, and then the motor and valve were closed.
- (3)
- Because a siphon formed in a section behind the highest point, the hose was loosened at the upper portion of channel 8. Note, however, that the highest point of the water level had to be higher than the position of channel 7.
- (4)
- The DHDAS system was opened, and the upper hose of channel 8 was closed after the pressure was cleared at each measuring point in the tube.
- (5)
- At the same time, the motor and valve were opened to produce a large flow rate so that the sediment in the measuring section of the pipe would not accumulate. Photos were taken, and the phenomenon and flow rate were recorded. The sediment concentration was measured using a specific gravity bottle, and the DHDAS system was used to measure the pressure at each channel in the pipe.
- (6)
- The motor was adjusted, and the flow rate was reduced to only one test section deposition, two depositions, and three depositions in the tube; step (5) was then repeated.
- (7)
- The motor was turned off, the mixer was turned off, the video and data were backed up, and the tests were transferred to a hard disk.
2.3. Data Analysis
3. Results and Discussion
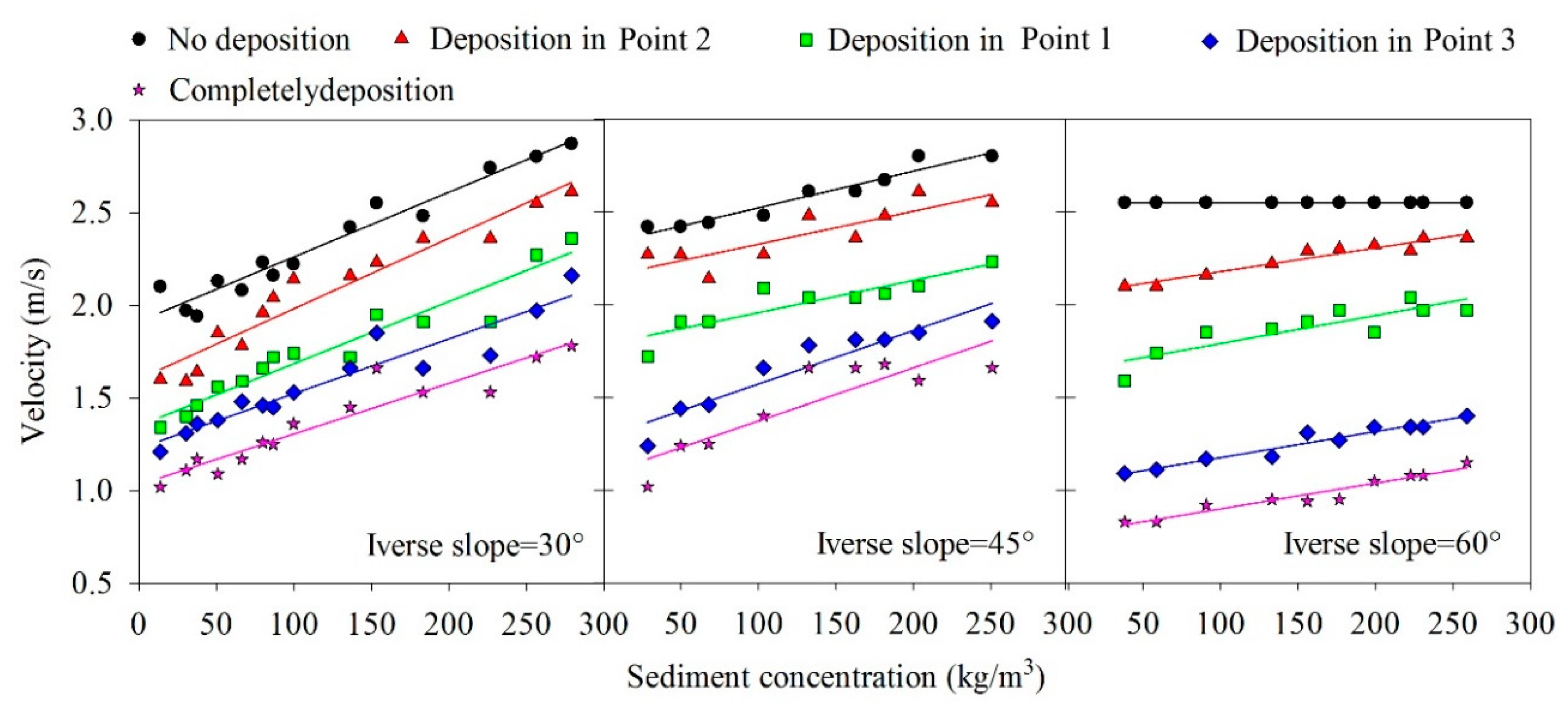
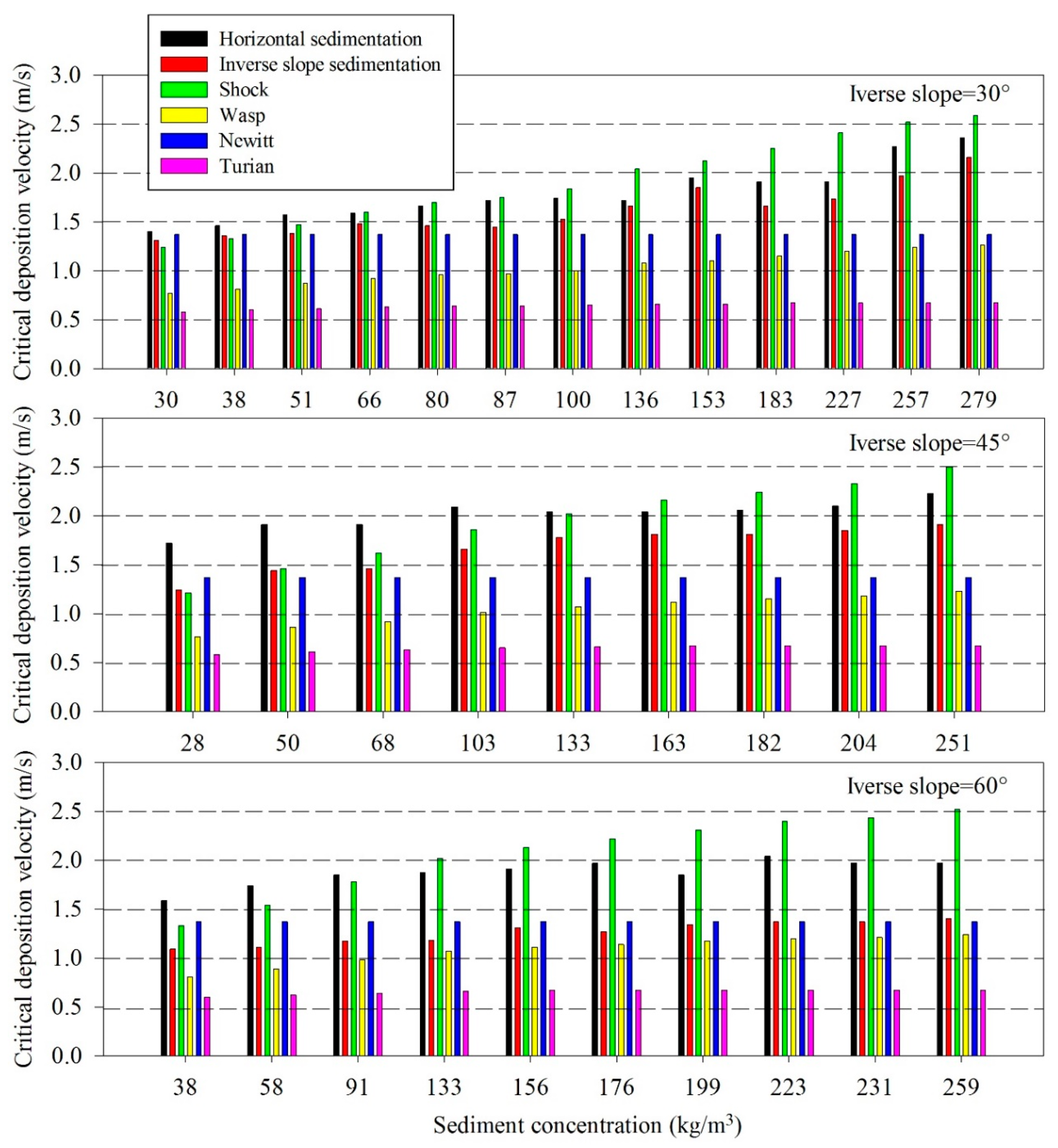
3.1. Influence Factors of the Critical Deposition Rate
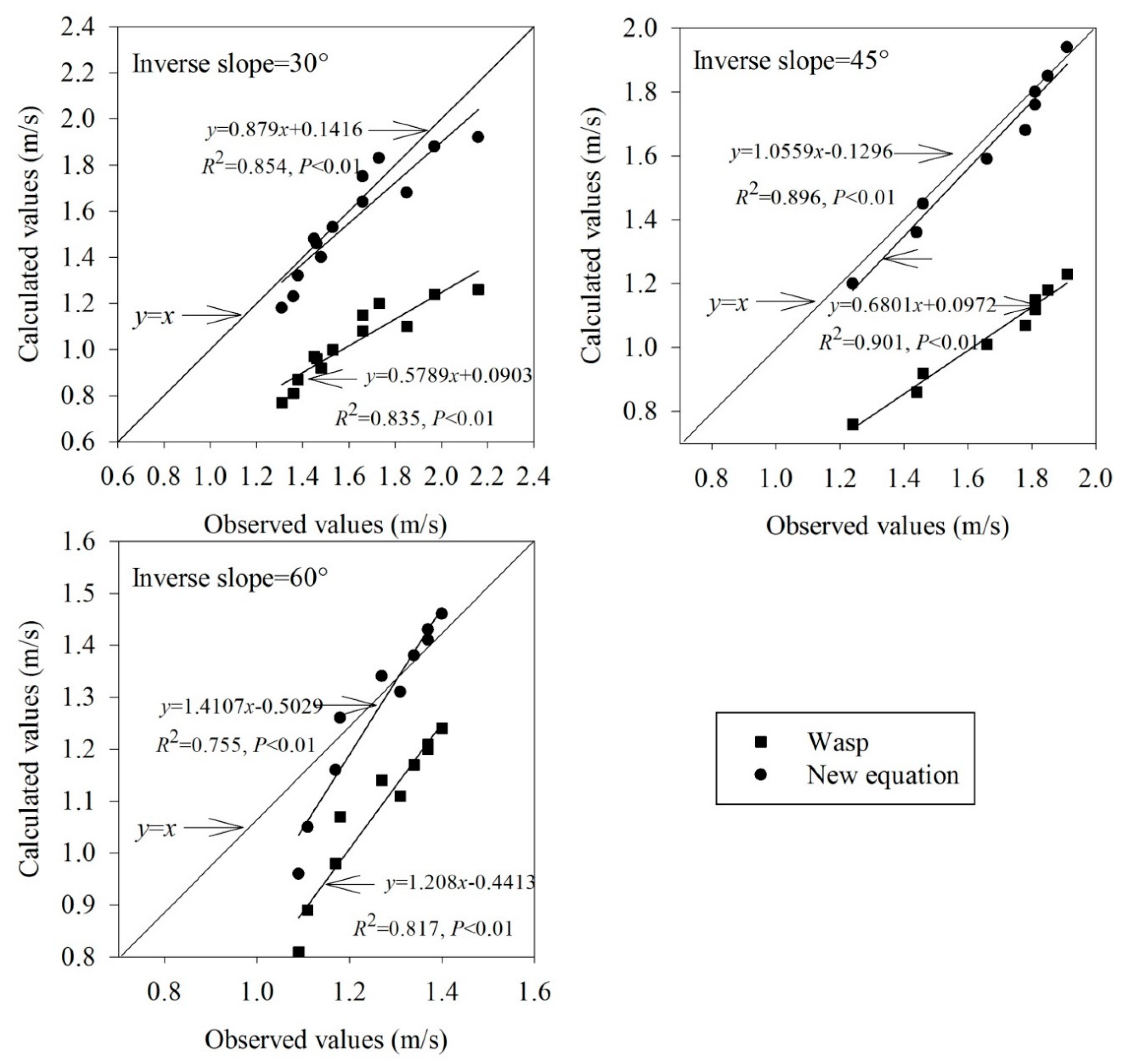
3.2. The Calculation of the Critical Deposition Rate
3.3. Critical Deposition Velocity of Reverse Slope Section
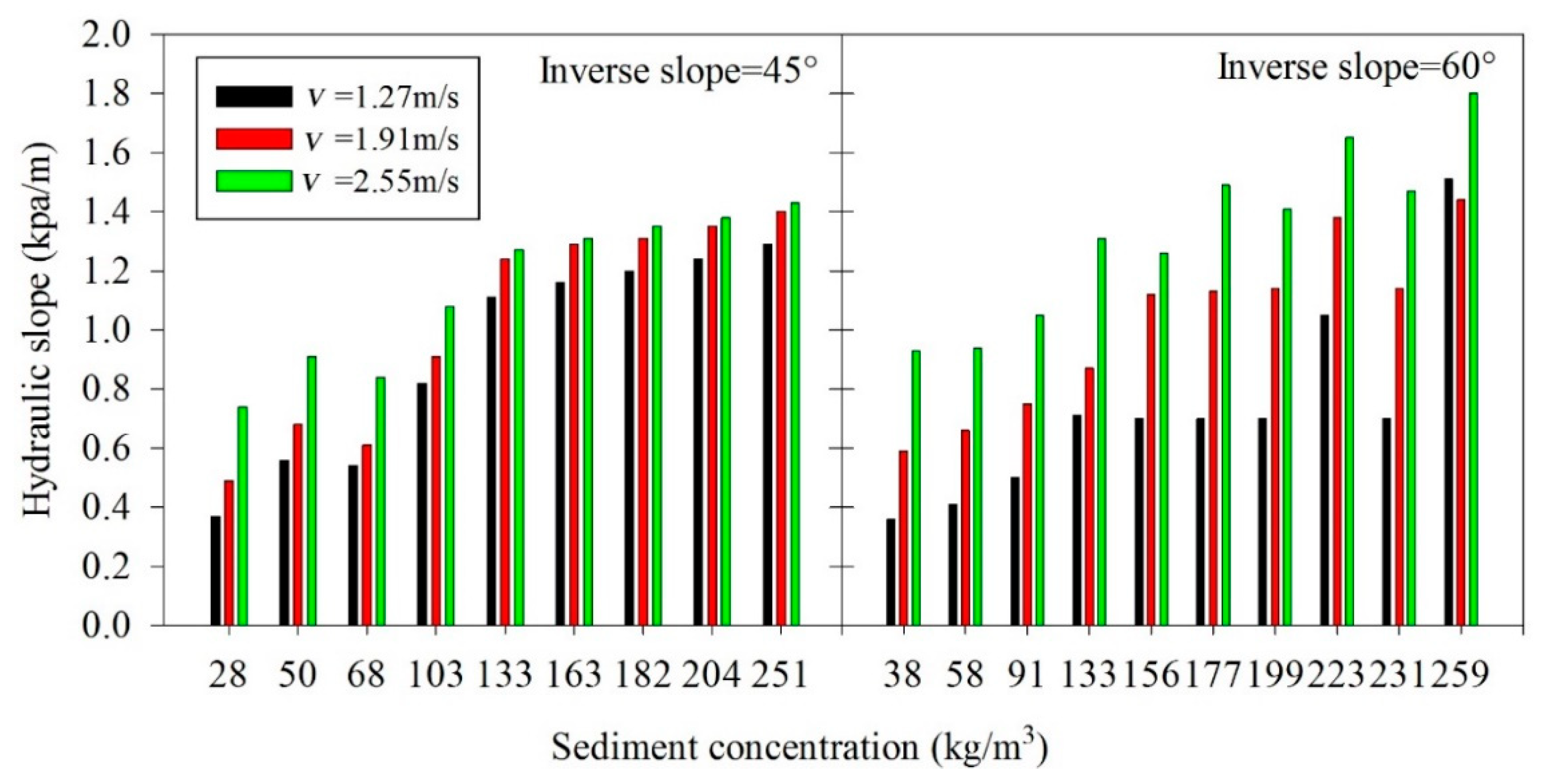
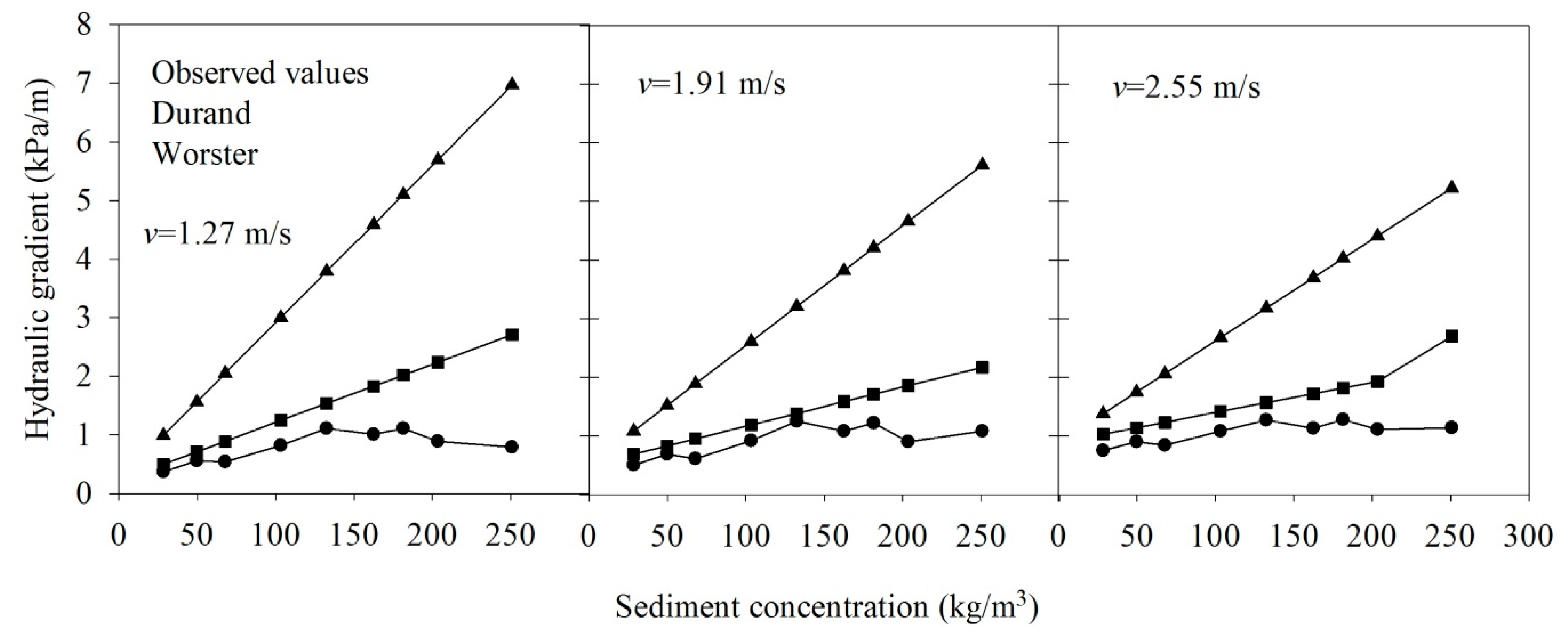
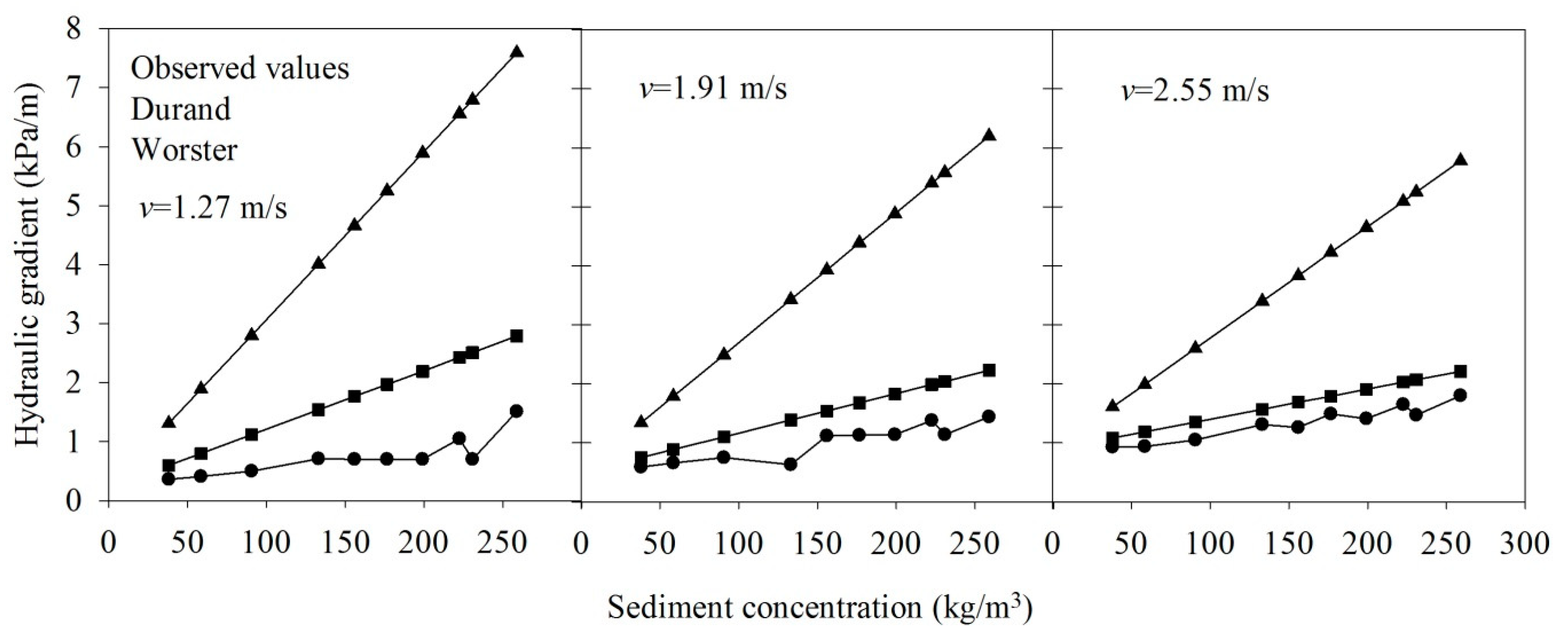
3.4. Influence Factors of the Head Loss in Pipe Sand Transportation
3.5. Calculation of the Reverse Slope Pipe Head Loss
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ellis, S.; Pecher, I.; Kukowski, N.; Xu, W.; Henrys, S.; Greinert, J. Testing proposed mechanisms for seafloor weakening at the top of gas hydrate stability on an uplifted submarine ridge (Rock Garden). N. Z. Mar. Geol. 2010, 272, 127–140. [Google Scholar] [CrossRef]
- Hadley, C.; Peters, D.; Vaughan, A.; Bean, D. Gumusut-Kakap project: Geohazard characterisation and impact on field development plans. In International Petroleum; Technology Conference: Dubai, The United Arab Emirates, 2008; Volume 15. [Google Scholar]
- Harbitz, C. Model simulations of tsunamis generated by the Storegga slides. Mar. Geol. 1992, 105, 1–21. [Google Scholar] [CrossRef]
- Hyodo, M.; Yoneda, J.; Yoshimoto, N.; Nakata, Y. Mechanical and dissociation properties of methane hydrate-bearing sand in deep seabed. Soils Found. 2013, 53, 299–314. [Google Scholar] [CrossRef]
- Jiang, M.; Konrad, J.; Leroueil, S. An efficient technique for generating homogeneous specimens for DEM studies. Comput. Geotech. 2003, 30, 579–597. [Google Scholar] [CrossRef]
- Jiang, M.; Sun, Y.; Xiao, Y. An experimental investigation on the mechanical behavior between cemented granules. Astm Geotech. Test. J. 2012, 35, 678–690. [Google Scholar] [CrossRef]
- Jiang, M.; Sun, C.; Zhang, W.; Liu, F. Coupled CFD–DEM simulations of submarine landslide induced by thermal dissociation of methane hydrate. In Proceedings of the International Symposium on Geomechanics from Micro to Macro, Cambridge, UK, 1–3 September 2014. [Google Scholar]
- Jung, W.; Vogt, P. Effects of bottom water warming and sea level rise on Holocene hydrate dissociation and mass wasting along the Norwegian-Barents Continental Margin. J. Geophys. Res. Solid Earth 2004, 109, 102–116. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, S.; Jin, Y.; Baranov, B.; Obzhirov, A.; Salomatin, A.; Shoji, H. The stability of gas hydrate field in the northeastern continental slope of Sakhalin Island, Sea of Okhotsk, as inferred from analysis of heat flow data and its implications for slope failures. Mar. Pet. Geol. 2013, 45, 198–207. [Google Scholar] [CrossRef]
- Locat, J.; Lee, H. Submarine landslides: Advances and challenges. Can. Geotech. J. 2002, 39, 193–212. [Google Scholar] [CrossRef]
- Luo, M.; Wang, H.; Yang, S.; Chen, D. Research advancement of natural gas hydrate n South China Sea. Bull. Mineral. Petrol. Geochem. 2013, 32, 56–69. [Google Scholar]
- Qiu, L.; Wu, C. Gravitational sedimentation and separation of particles in a iquid: A 3D DEM/CFD study. In Proceedings of the International Symposium on discrete Element Modelling of Particulate Media, University of Birmingham, Birmingham, UK, 28–30 March 2012. [Google Scholar]
- Yu, F.; Song, Y.; Liu, W.; Li, Y.; Zhao, J. Study on shear strength of artificial methane hydrate. In ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering; American Society of Mechanical Engineers: New York, NY, USA, 2010. [Google Scholar]
- Zhang, L.; Luan, X. Stability of submarine slopes in the northern South China Sea: A numerical approach. Chin. J. Oceanol. Limnol. 2013, 31, 146–158. [Google Scholar] [CrossRef]
- Zhao, J.; Shan, T. Coupled CFD–DEM simulation of fluid–particle interaction in geomechanics. Powder Technol. 2013, 239, 248–258. [Google Scholar] [CrossRef]
- Wu, N.; Zhang, H.; Yang, S.; Zhang, G.; Liang, J.; Lu, J.; Su, X.; Schultheiss, P.; Holland, M.; Zhu, Y. Gas hydrate system of Shenhu area, northern South China Sea: Geochemical results. J. Geol. Res. 2011, 2011, 1–10. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, J.; Gao, G. Desilting laws of precipitation washout test in Xiaolangdi reservoir. In International Forum on Energy, Environment Science and Materials; Atlantis Press: Paris, France, 2015; pp. 1538–1543. [Google Scholar]
- Winters, W.; Waite, W.; Mason, D.; Gilbert, L.; Pecher, I. Methane gas hydrate effect on sediment acoustic and strength properties. J. Pet. Sci. Eng. 2007, 56, 127–135. [Google Scholar] [CrossRef]
- Valdes, J.; Santamarina, J. Particle transport in a nonuniform flow field: Retardation and clogging. Appl. Phys. Lett. 2007, 90, 244101. [Google Scholar] [CrossRef]
- Sultan, N.; Garziglia, S.; Colliat, J. Gas hydrate occurrences and seafloor deformation: Investigation of strain-softening of gas-hydrate bearing sediments and its consequence in terms of submarine slope instabilities. In Offshore Technology Conference; Offshore Technology Conference: Houston, TX, USA, 2011; pp. 1–18. [Google Scholar]
- Zhang, Y.; Li, Y.; Yang, J.; Liu, D. Statistical particle stress in aeolian sand movement-derivation and validation. Powder Technol. 2011, 209, 147–151. [Google Scholar] [CrossRef][Green Version]
- Shook, C. Pipelining Solids: The design of short distance pipelines. In Symposium on Pipeline Transport of solids, Canadian Society for Chemical Engineering; Offshore Technology Conference: Vancouver, BC, Canada, 1969. [Google Scholar]
- Wasp, E.; Kenny, J.; Gandhi, R. Solid liquid flow—Slurry pipeline transportation. Trans. Tech. Publ. Rockport MA. 1977, 43, 101–109. [Google Scholar]
- Newitt, D.; Richardson, J. Hydraulic conveying of solids in horizontal pipes. Trans. Inst. Chem. Engrs. 1955, 33, 149–163. [Google Scholar]
- Turian, R. Estimation of the critical velocity in pipeline flow of slurries. Powder Technol. 1987, 51, 35–47. [Google Scholar] [CrossRef]
- Durand, R. The hydraulic transportation of coal and other materials in pipes. Colloa Natl. Coal Board Lond. 1952, 51, 39–52. [Google Scholar]
- Worster, R.; Denny, D. The hydraulic transport of solid material in pipes. In Proceedings of the Institution of Mechanical Engineers, London, UK, 7–9 November 1995. [Google Scholar]
- Xu, Z.; Jiang, W. Effect of slurry particle size conveying pressure loss of slurry pipeline. J. Liaoning Tech. Uni. 2014, 33, 1617–1619, (In Chinese with English abstract). [Google Scholar]
- Zhang, Y.; Yang, J.; Liu, D.; Wei, X.; Yu, L. Sand storms: CFD analysis of Reynolds stress and collision stress of particles near sand bed. Particuology 2010, 8, 325–331. [Google Scholar] [CrossRef]
- Lu, Y.; Huang, J.; Zheng, P. Fluid hydrodynamic characteristics in supercritical water fluidized bed: A DEM simulation study. Chem. Eng. Sci. 2014, 117, 283–292. [Google Scholar] [CrossRef]
- Brosh, T.; Kalman, H.; Levy, A. DEM simulation of particle attrition in dilute-phase pneumatic conveying. Granul Mat. 2011, 13, 175–181. [Google Scholar] [CrossRef]
- Markauskas, D.; Kacianauskas, R.; Dziugys, A.; Navakas, R. Investigation of adequacy of multi-sphere approximation of elliptical particles for DEM simulations. Granul. Mat. 2010, 12, 107–123. [Google Scholar] [CrossRef]
- Cao, B. Study on hydraulic transmission mechanism of granular materials under complex conditions. Minzu Univ. China 2013, 44, 221–234, (In Chinese with English abstract). [Google Scholar]
- Ning, D. Study on hydraulie gradient of settling slurry inclined pipeline. Liaoning Tech. Univ. 2002, 3, 47–49, (In Chinese with English abstract). [Google Scholar]
- Zhao, L. Study on friction loss of settling slurry inclined pipe. Liaoning Tech. Univ. 2004, 4, 39–45, (In Chinese with English abstract). [Google Scholar]
- Arolla, S.; Desjardins, O. Transport modeling of sedimenting particles in a turbulent pipe flow using euler–lagrange large eddy simulation. Int. J. Multiph. Flow 2015, 75, 1–11. [Google Scholar] [CrossRef]
- Capecelatro, J.; Desjardins, O. An Euler–Lagrange strategy for simulating particle laden flows. J. Comput. Phys. 2013, 238, 1–31. [Google Scholar] [CrossRef]
- Schmeeckle, M. Numerical simulation of turbulence and sediment transport of medium sand. J. Geophys. Res. Earth Surf. 2014, 119, 1240–1262. [Google Scholar] [CrossRef]
- Sun, R.; Xiao, H. Sedi Foam: A general-purpose, open-source CFD-DEM solver for particle laden flow with emphasis on sediment transport. Comput. Geosci UK 2016, 89, 207–219. [Google Scholar] [CrossRef]
- Xiao, H.; Young, Y.; Prévost, J. Hyro- and morpho-dynamic modeling of breaking solitary waves over sand beach. Part II: Numerical simulation. Mar. Geol. 2010, 269, 119–131. [Google Scholar] [CrossRef]
- Yu, X.; Hsu, T.; Jenkins, J.; Liu, P. Predictions of vertical sediment flux in oscillatory flows using a two-phase, sheet-flow model. Adv. Water Resour. 2012, 48, 2–17. [Google Scholar] [CrossRef]
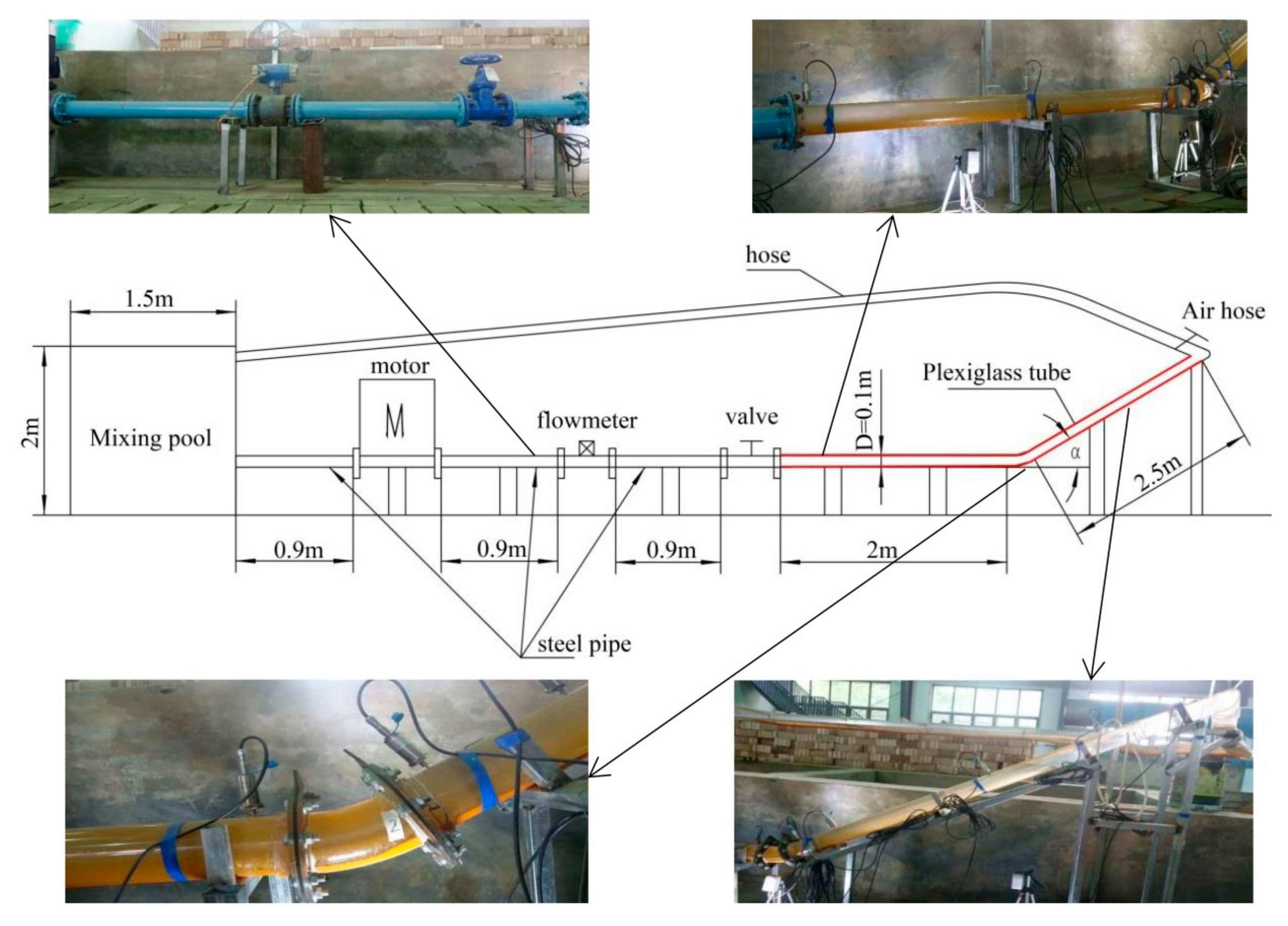
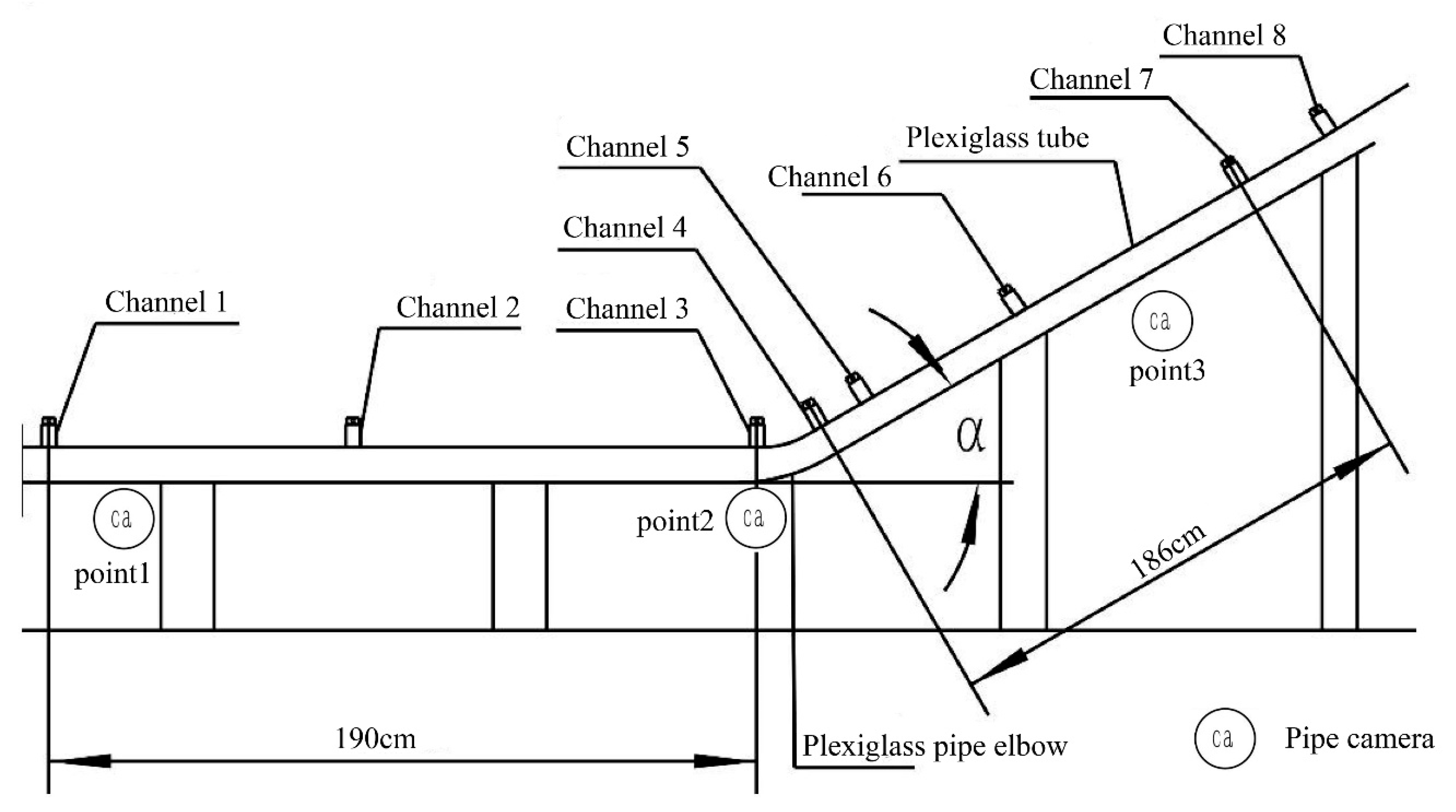
| Items | Materials and Equipment |
|---|---|
| Steel pipe | Inner diameter of 100 mm, and three steel tubes (0.9 m) |
| Hose | Inner diameter of 80 mm and length of 10 m |
| Plexiglass tube | Inner diameter of 100 mm, the length of two glass tubes: 2 m and 2.5 m, and the elbow angle: 30°, 45°, and 60° |
| Flow control | Frequency converter and valve |
| Filming equipment | Video recorder, video camera |
| Flow meter | Electromagnetic flow meter |
| Slope control | Plexiglass pipe elbow |
| Slope | Sediment Concentration (kg/m3) | Test Groups |
|---|---|---|
| 30°, 45°, 60° | 0 | Three repetitions |
| 30 | ||
| 60 | ||
| 90 | ||
| 120 | ||
| 150 | ||
| 180 | ||
| 210 | ||
| 240 | ||
| 270 |
| Reference | Particle Size (mm) | Pipe Diameter (mm) | Equation | Parameters |
|---|---|---|---|---|
| Shook (1969) [22] | 0.2–5.25 | 80–580 | Cv—volume concentration CD—drag coefficient g—9.8 m/s2 D—pipe diameterρw—liquid density ds—particle size ρs—solid density | |
| Wasp (1977) [23] | 0.25–2.04 | 26.7–139.7 | ||
| Newitt (1955) [24] | 0.208–3.81 | -- | ||
| Turian (1987) [25] | 0.02–2.2 | 58–101.6 |
| Slope | Observed (m/s) | Simulated (m/s) | Root Mean Square Error (RMSE) | ||
|---|---|---|---|---|---|
| New Formula | Wasp | New Formula | Wasp | ||
| 30° | 1.62 | 1.56 | 1.03 | 3% | 37% |
| 45° | 1.66 | 1.63 | 1.03 | 2% | 38% |
| 60° | 1.26 | 1.28 | 10.8 | 1% | 14% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Li, Y.; Pan, L.; Lai, Z.; Jian, S. Study of the Sediment Transport Law in a Reverse-Slope Section of a Pressurized Pipeline. Water 2020, 12, 3042. https://doi.org/10.3390/w12113042
Wang J, Li Y, Pan L, Lai Z, Jian S. Study of the Sediment Transport Law in a Reverse-Slope Section of a Pressurized Pipeline. Water. 2020; 12(11):3042. https://doi.org/10.3390/w12113042
Chicago/Turabian StyleWang, Jiayi, Yitian Li, Li Pan, Zhiqiang Lai, and Shengqi Jian. 2020. "Study of the Sediment Transport Law in a Reverse-Slope Section of a Pressurized Pipeline" Water 12, no. 11: 3042. https://doi.org/10.3390/w12113042
APA StyleWang, J., Li, Y., Pan, L., Lai, Z., & Jian, S. (2020). Study of the Sediment Transport Law in a Reverse-Slope Section of a Pressurized Pipeline. Water, 12(11), 3042. https://doi.org/10.3390/w12113042




