Prediction of Streamflow Based on Dynamic Sliding Window LSTM
Abstract
1. Introduction
- (1)
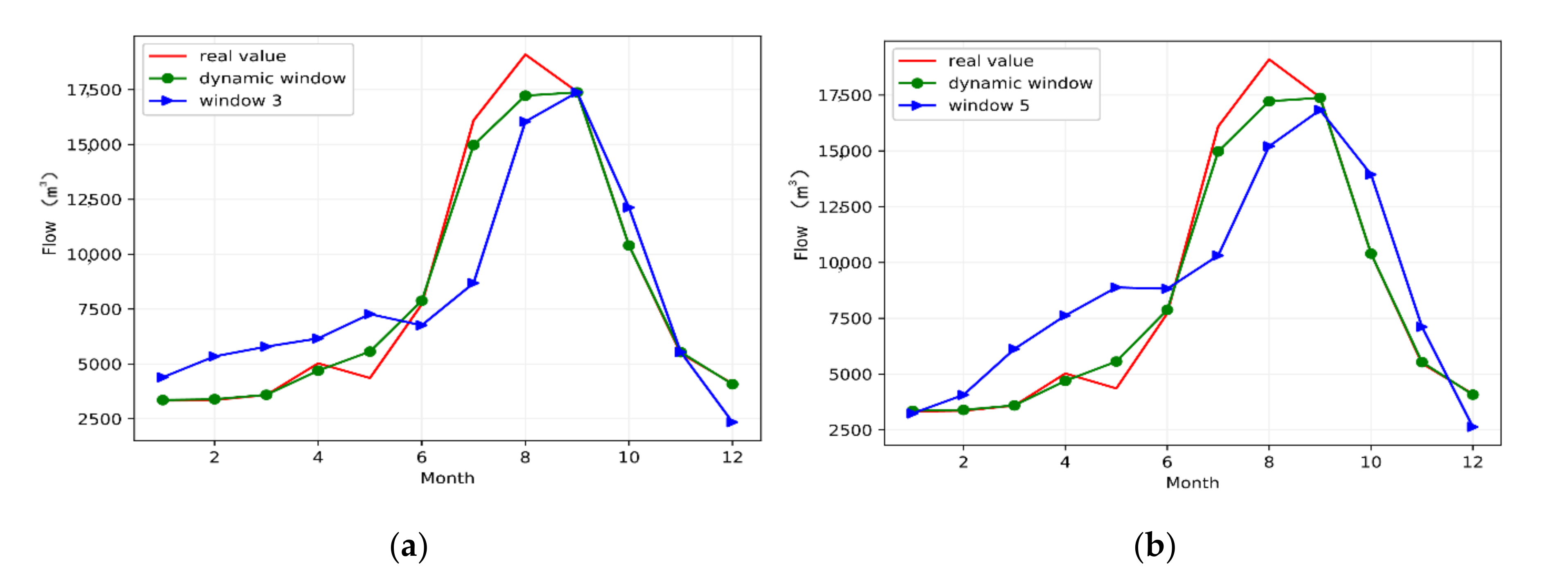
- the reconstruction of the time series data based on the dynamic slide window method to select the optimal window dimension, so the problem that the fixed sliding window cannot obtain the optimal data window and data dimension can be addressed. This approach can not only reflect the correlation between time series data, but also can reflect the periodicity characteristics of the data of different months, thus guaranteeing the successful selection of the optimal window dimension.
- (2)
- Based on the dynamic sliding window method, the nonlinear approximation ability of the LSTM neural network is exploited. Consequently, the dynamic sliding window LSTM is proposed to establish a medium- and long-term streamflow prediction model. The experimental verification was carried out using the streamflow data recorded by the Zhutuo hydrological station.
2. Streamflow Prediction Method Based on LSTM
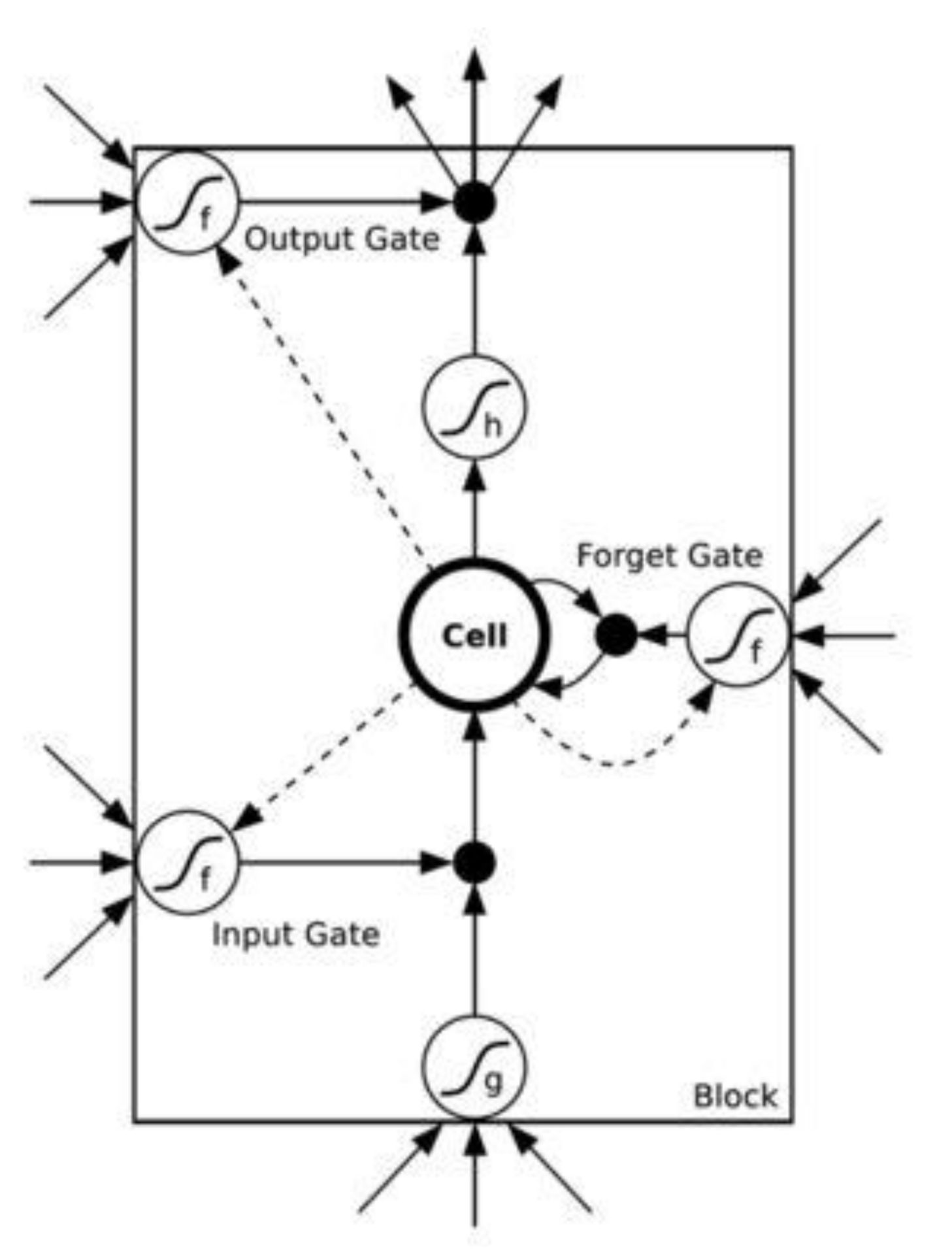
2.1. Principles of RNN and LSTM
2.2. Streamflow Prediction Method Based on LSTM
3. Verification of Flow Prediction
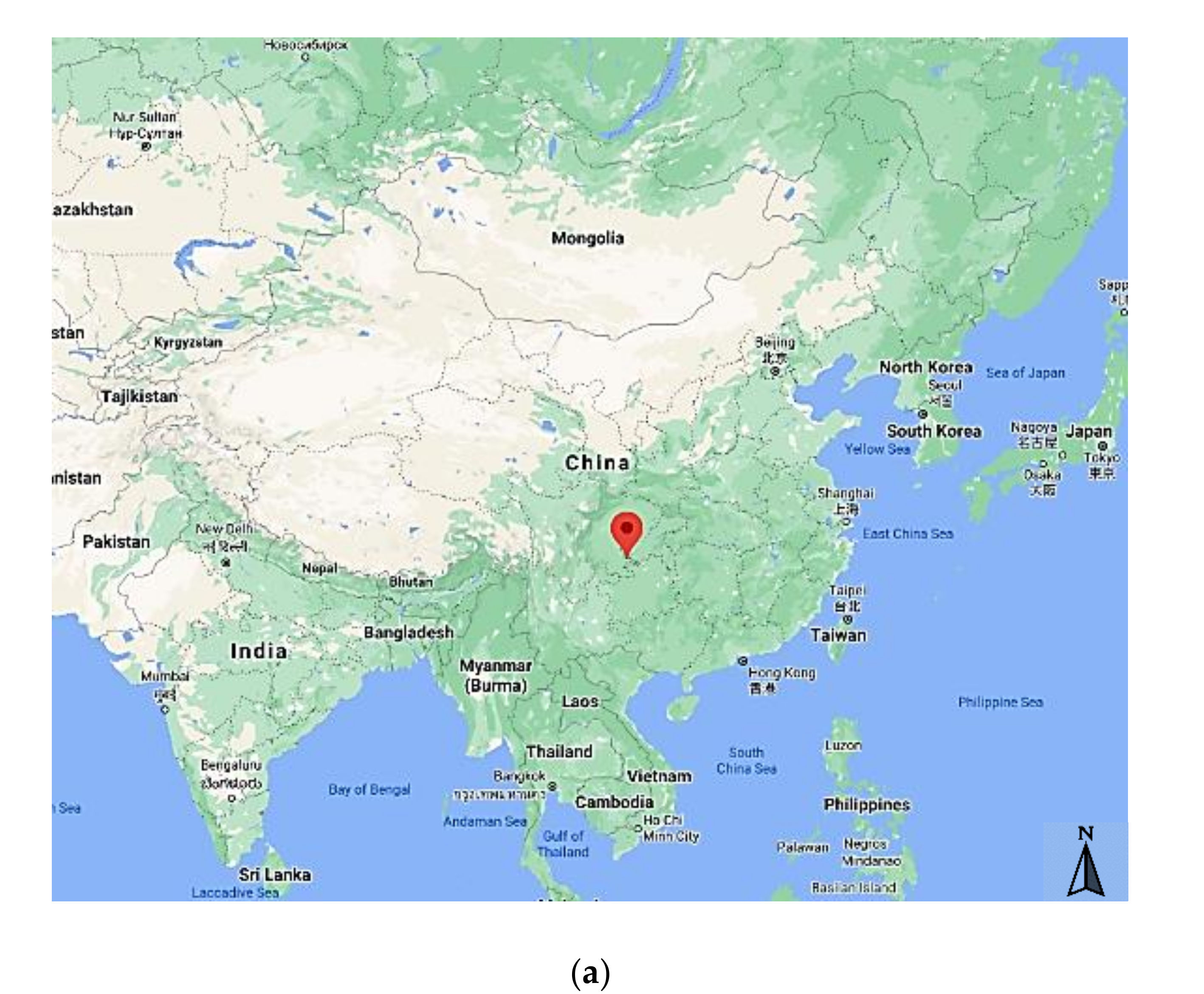
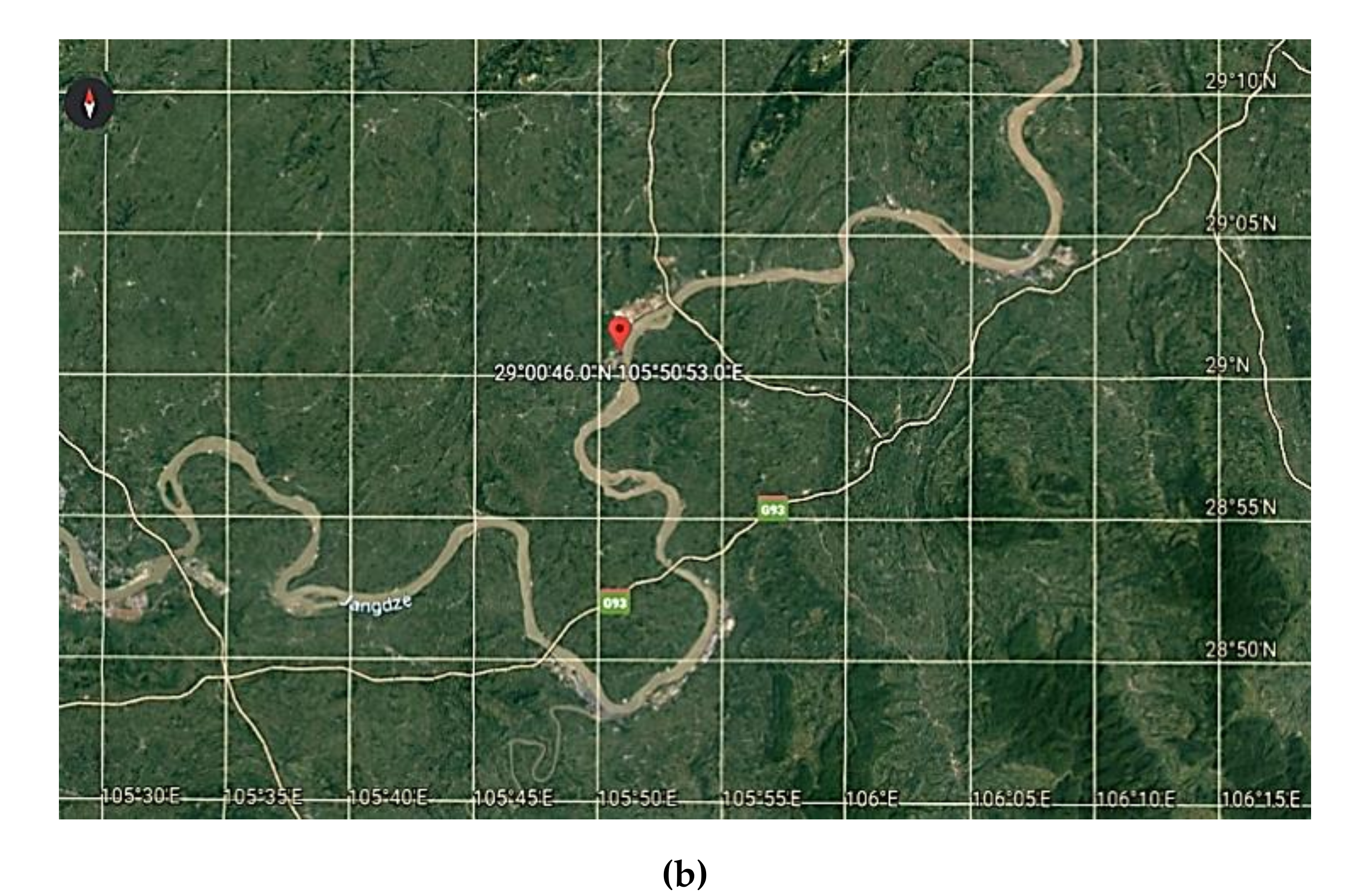
3.1. Overview of Hydrological Station
3.2. Data Source
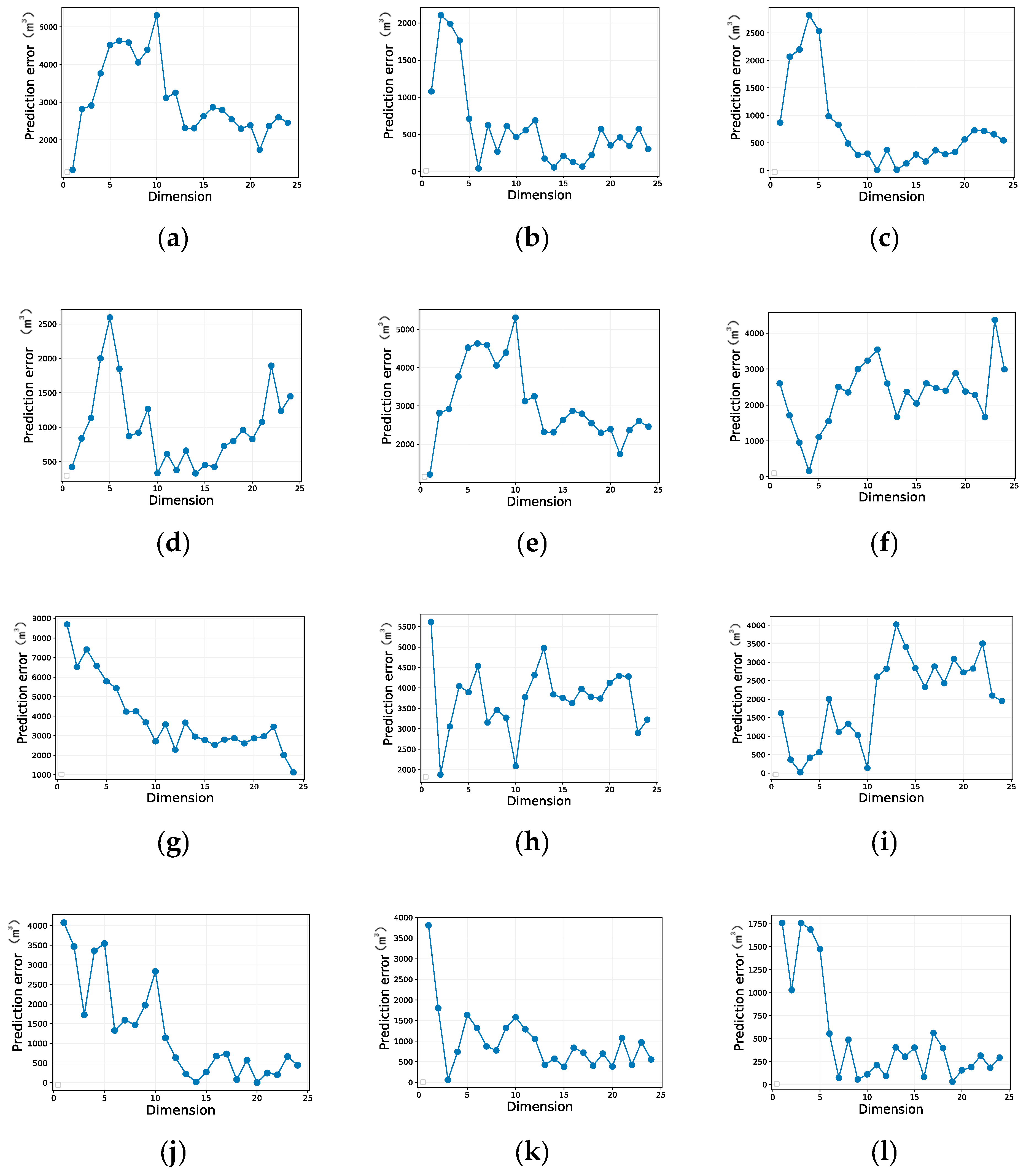
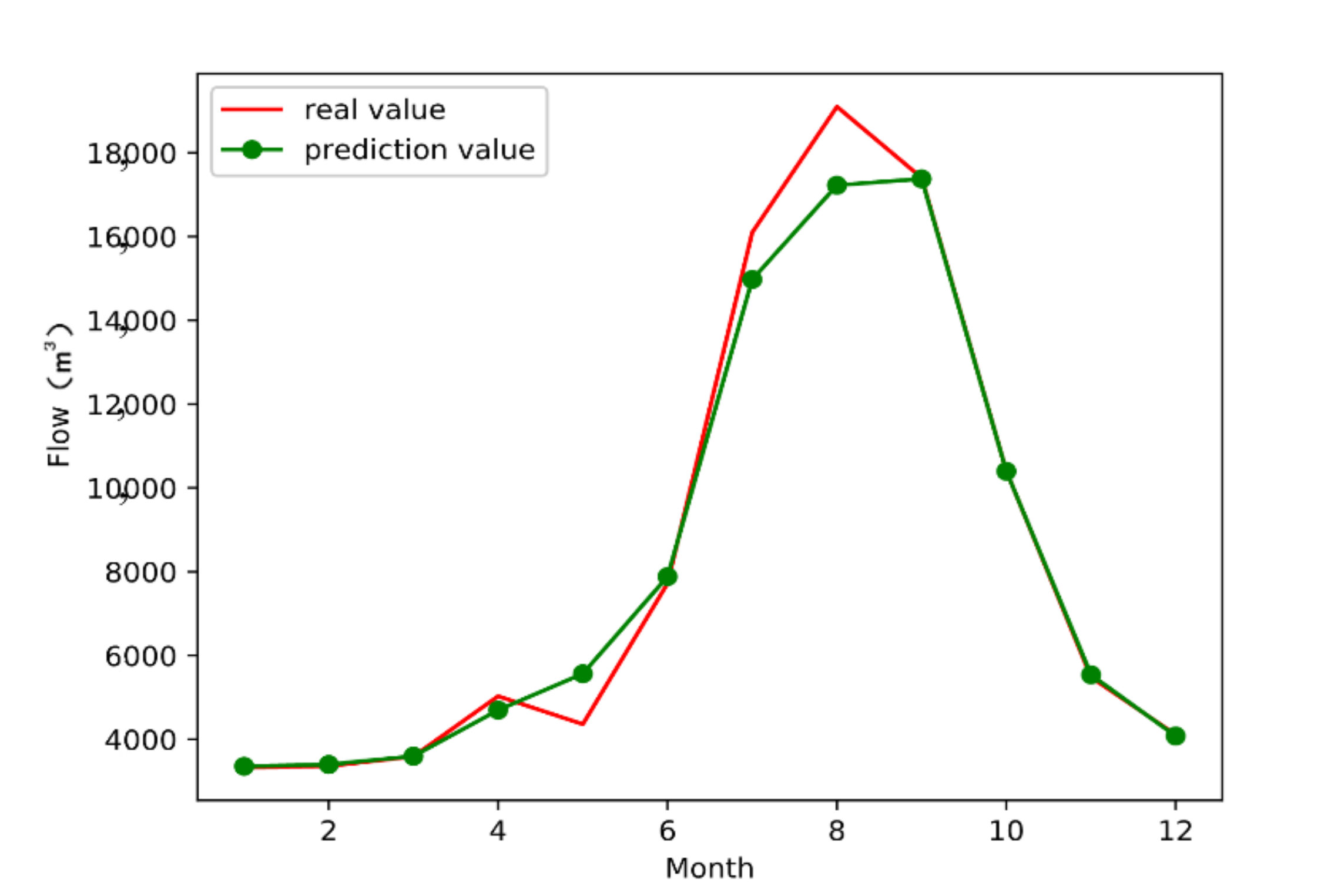
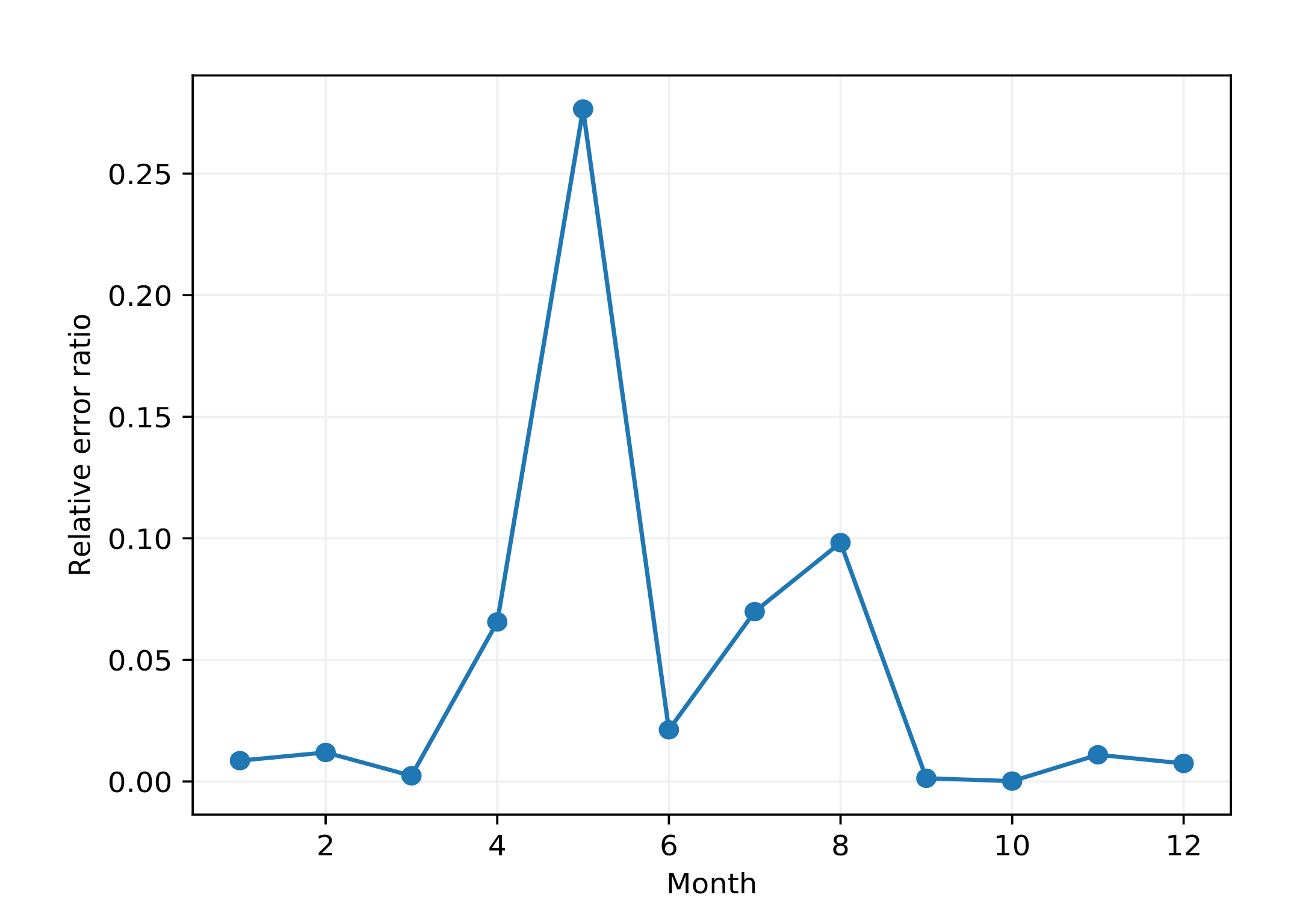
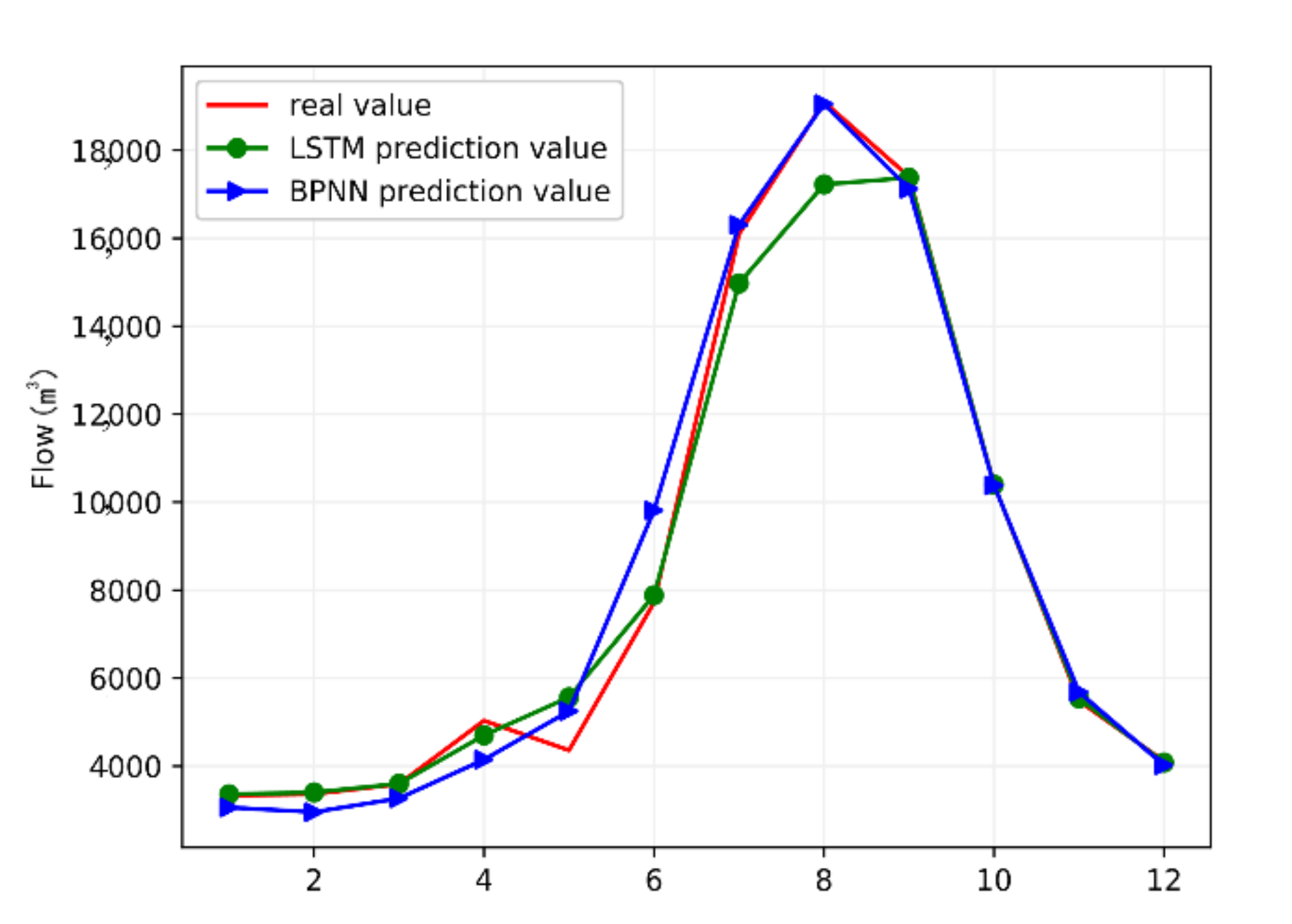
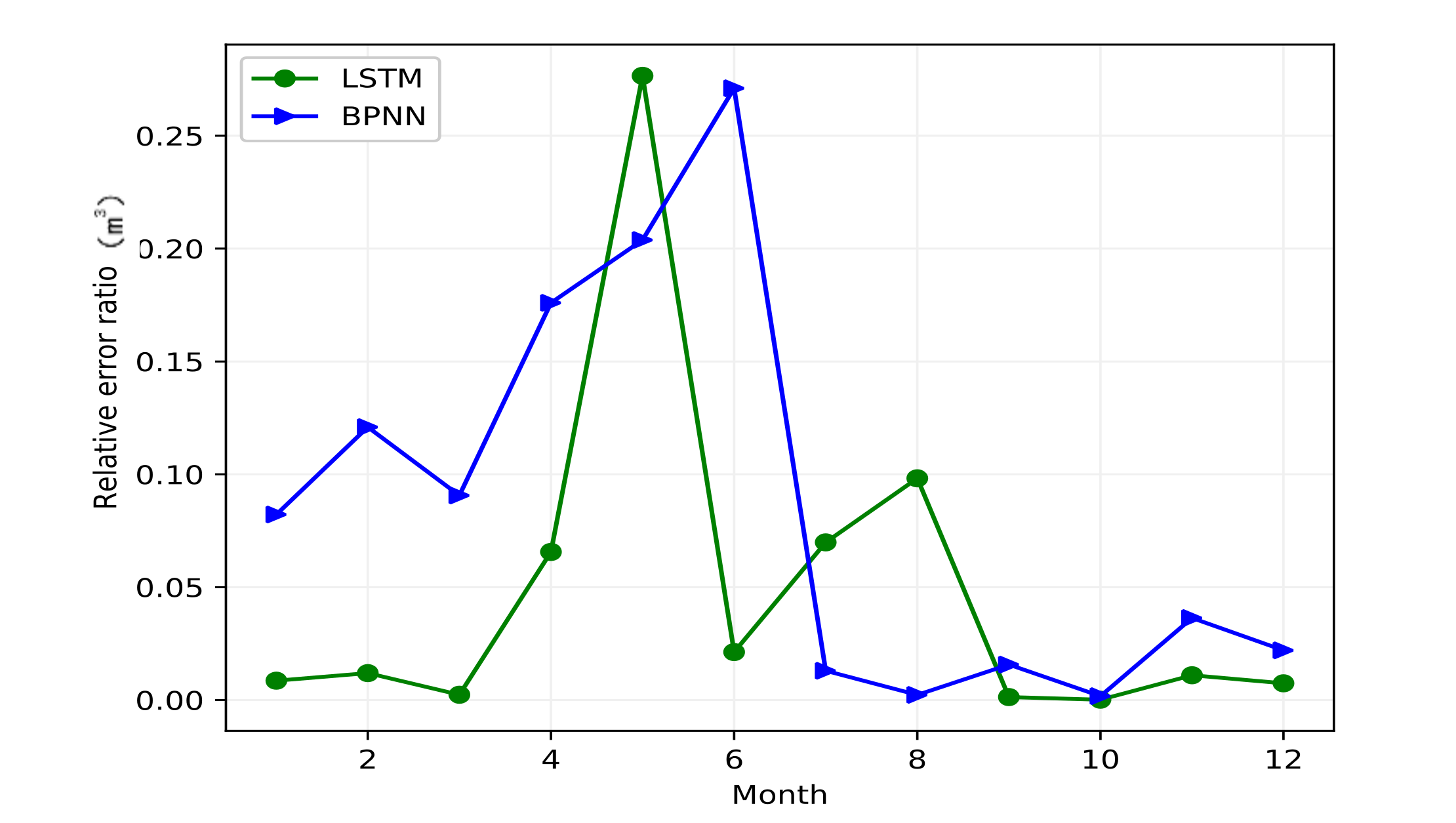
3.3. Model Simulation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Poff, N.L.; Zimmerman, J.K.H. Ecological responses to altered flow regimes: A literature review to inform the science and management of environmental flows. Freshw. Biol. 2010, 55, 194–205. [Google Scholar] [CrossRef]
- Loucks, D.P.; van Beek, E. Water Resources Planning and Management: An Overview. In Water Resource Systems Planning and Management; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Okewu, E.; Misra, S.; Maskeliunas, R.; Damaşeviçius, R.; Fernandez-Sanz, L. Optimizing green computing awareness for environmental sustainability and economic security as a stochastic optimization problem. Sustainability 2017, 9, 1857. [Google Scholar] [CrossRef]
- Pagano, T.C.; Wood, A.W.; Ramos, M.-H.; Cloke, H.L.; Pappenberger, F.; Clark, M.P.; Cranston, M.; Kavetski, D.; Mathevet, T.; Sorooshian, S.; et al. Challenges of Operational River Forecasting. J. Hydrometeorol. 2014, 15, 1692–1707. [Google Scholar] [CrossRef]
- Fotovatikhah, F.; Herrera, M.; Shamshirband, S.; Chau, K.W.; Ardabili, S.F.; Piran, J. Survey of computational intelligence as basis to big flood management: Challenges, research directions and future work. Eng. Appl. Comput. Fluid Mech. 2018, 12, 411–437. [Google Scholar] [CrossRef]
- Han, P.; Wang, X. Using ABCD model to predict the response of river basin hydrology to extreme climate. Yellow River 2016, 38, 16–22. [Google Scholar]
- Li, B.L.; Li, J.L.; Zan, M.J.; Li, Z.Q. R/S Grey Prediction of River Annual Runoff. Hydrology 2015, 35, 44–48. [Google Scholar]
- Zhu, B.; Zhao, L.L.; Li, M. Application of T-S-K fuzzy logic algorithm in Fuhe hydrological forecast. Hydrology 2015, 3, 53–58. [Google Scholar]
- Geng, Y.B.; Wang, Y.C. Prediction of river runoff variation based on BP neural network. Water Resour. Hydropower Northeast China 2016, 34, 29–30. [Google Scholar]
- Xing, B.F. Analysis of runoff prediction method based on wavelet neural network. Technol. Innov. Appl. 2012, 31, 41. [Google Scholar]
- Li, L. Application Research of BP Neural Network in Hydrological Data. Ph.D. Thesis, Shanxi University of Finance and Economics, Shanxi, China, 2011. [Google Scholar]
- Wang, L. Research on Runoff Forecast Based on BP Network. Ph.D. Thesis, Kunming University of Science and Technology, Kunming, China, 2015. [Google Scholar]
- Xingjian, S.H.I.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the NIPS’15 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2015; pp. 802–810. [Google Scholar]
- Wang, H.R.; Liu, X.H.; Tang, Q.; He, L. Support vector machine hydrological process prediction based on wavelet transform. J. Tsinghua Univ. Nat. Sci. Ed. 2010, 9, 1378–1382. [Google Scholar]
- Huang, Q.L.; Su, X.L.; Yang, J.T. Regression prediction model of daily runoff support vector machine based on wavelet decomposition. J. Northwest A F Univ. Nat. Sci. Ed. 2016, 44, 211–217. [Google Scholar]
- Sang, Y.F.; Singh, V.P.; Sun, F.; Chen, Y. Wavelet-Based Hydrological Time Series Forecasting. J. Hydrol. Eng. 2016, 21, 06016001. [Google Scholar] [CrossRef]
- Liu, H.Y.; Zhou, C.K. Prediction of the annual runoff of Guijiang River based on Markov chain. Trade News 2014, 50, 161. [Google Scholar]
- Sidekerskienė, T.; Woźniak, M.; Damaševičius, R. Nonnegative matrix factorization based decomposition for time series modelling. In Proceedings of the 16th IFIP International Conference on Computer Information Systems and Industrial Management (CISIM), Bialystok, Poland, 16–18 June 2017; pp. 604–613. [Google Scholar] [CrossRef]
- Sidekerskienė, T.; Damaševičius, R.; Woźniak, M. Zerocross density decomposition: A novel signal decomposition method. In Data Science: New Issues, Challenges and Applications; Springer International Publishing: Basel, Switzerland, 2020; pp. 235–252. [Google Scholar] [CrossRef]
- Xia, S.; Wang, G.; Chen, Z.; Duan, Y.; Liu, Q. Complete Random Forest based Class Noise Filtering Learning for Improving the Generalizability of Classifiers. IEEE Trans. Knowl. Data Eng. 2019, 31, 2063–2078. [Google Scholar] [CrossRef]
- Delafrouz, H.; Ghaheri, A.; Ghorbani, M.A. A novel hybrid neural network based on phase space reconstruction technique for daily river flow prediction. Soft Comput. 2018, 22, 2205–2215. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Khatibi, R.; Karimi, V.; Yaseen, Z.M.; Zounemat-Kermani, M. Learning from multiple models using artificial intelligence to improve model prediction accuracies: Application to river flows. Water Resour. Manag. 2018, 32, 4201–4215. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Fu, M.; Wang, C.; Mohtar, W.H.M.W.; Deo, R.C.; El-shafie, A. Application of the hybrid artificial neural network coupled with rolling mechanism and grey model algorithms for streamflow forecasting over multiple time horizons. Water Resour. Manag. 2018, 32, 1883–1899. [Google Scholar] [CrossRef]
- Fathian, F.; Mehdizadeh, S.; Kozekalani Sales, A.; Safari, M.J.S. Hybrid models to improve the monthly river flow prediction: Integrating artificial intelligence and non-linear time series models. J. Hydrol. 2019, 575, 1200–1213. [Google Scholar] [CrossRef]
- Meng, E.; Huang, S.; Huang, Q.; Fang, W.; Wu, L.; Wang, L. A robust method for non-stationary streamflow prediction based on improved EMD-SVM model. J. Hydrol. 2019, 568, 462–478. [Google Scholar] [CrossRef]
- Liang, C.; Li, H.; Lei, M.; Du, Q. Dongting Lake Water Level Forecast and Its Relationship with the Three Gorges Dam Based on a Long Short-Term Memory Network. Water 2018, 10, 1389. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, Y.-P.; Yang, Z.; Wang, G.; Zhu, Q. Integration of a Parsimonious Hydrological Model with Recurrent Neural Networks for Improved Streamflow Forecasting. Water 2018, 10, 1655. [Google Scholar] [CrossRef]
- De Melo, A.G.; Sugimoto, D.N.; Tasinaffo, P.M.; Moreira Santos, A.H.; Cunha, A.M.; Vieira Dias, L.A. A new approach to river flow forecasting: LSTM and GRU multivariate models. IEEE Latin Am. Trans. 2019, 17, 1978–1986. [Google Scholar] [CrossRef]
- Meshram, S.G.; Ghorbani, M.A.; Shamshirband, S.; Karimi, V.; Meshram, C. River flow prediction using hybrid PSOGSA algorithm based on feed-forward neural network. Soft Comput. 2019, 23, 10429–10438. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. LSTM can Solve Hard Long Time Lag Problems. In Proceedings of the Conference: Advances in Neural Information Processing Systems 9, NIPS, Denver, CO, USA, 2–5 December 1997. [Google Scholar]
- Pineda, F.J. Generalization of back-propagation to recurrent neural networks. Phys. Rev. Lett. 1987, 59, 2229–2232. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Xia, S.; Peng, D.; Meng, D.; Zhang, C.; Wang, G.; Giem, E.; Wei, W.; Chen, Z. A Fast Adaptive k-means with No Bounds. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 1. [Google Scholar] [CrossRef]
- Xia, S.; Zhang, Z.; Li, W.; Wang, G.; Giem, E.; Chen, Z. GBNRS: A Novel Rough Set Algorithm for Fast Adaptive Attribute Reduction in Classification. IEEE Trans. Knowl. Data Eng. 2020, 1. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, L.; Fang, D.; Wang, X.; Wei, W.; Damaševičius, R.; Scherer, R.; Woźniak, M. Prediction of Streamflow Based on Dynamic Sliding Window LSTM. Water 2020, 12, 3032. https://doi.org/10.3390/w12113032
Dong L, Fang D, Wang X, Wei W, Damaševičius R, Scherer R, Woźniak M. Prediction of Streamflow Based on Dynamic Sliding Window LSTM. Water. 2020; 12(11):3032. https://doi.org/10.3390/w12113032
Chicago/Turabian StyleDong, Limei, Desheng Fang, Xi Wang, Wei Wei, Robertas Damaševičius, Rafał Scherer, and Marcin Woźniak. 2020. "Prediction of Streamflow Based on Dynamic Sliding Window LSTM" Water 12, no. 11: 3032. https://doi.org/10.3390/w12113032
APA StyleDong, L., Fang, D., Wang, X., Wei, W., Damaševičius, R., Scherer, R., & Woźniak, M. (2020). Prediction of Streamflow Based on Dynamic Sliding Window LSTM. Water, 12(11), 3032. https://doi.org/10.3390/w12113032





