Simulation of Titicaca Lake Water Level Fluctuations Using Hybrid Machine Learning Technique Integrated with Grey Wolf Optimizer Algorithm
Abstract
:1. Introduction
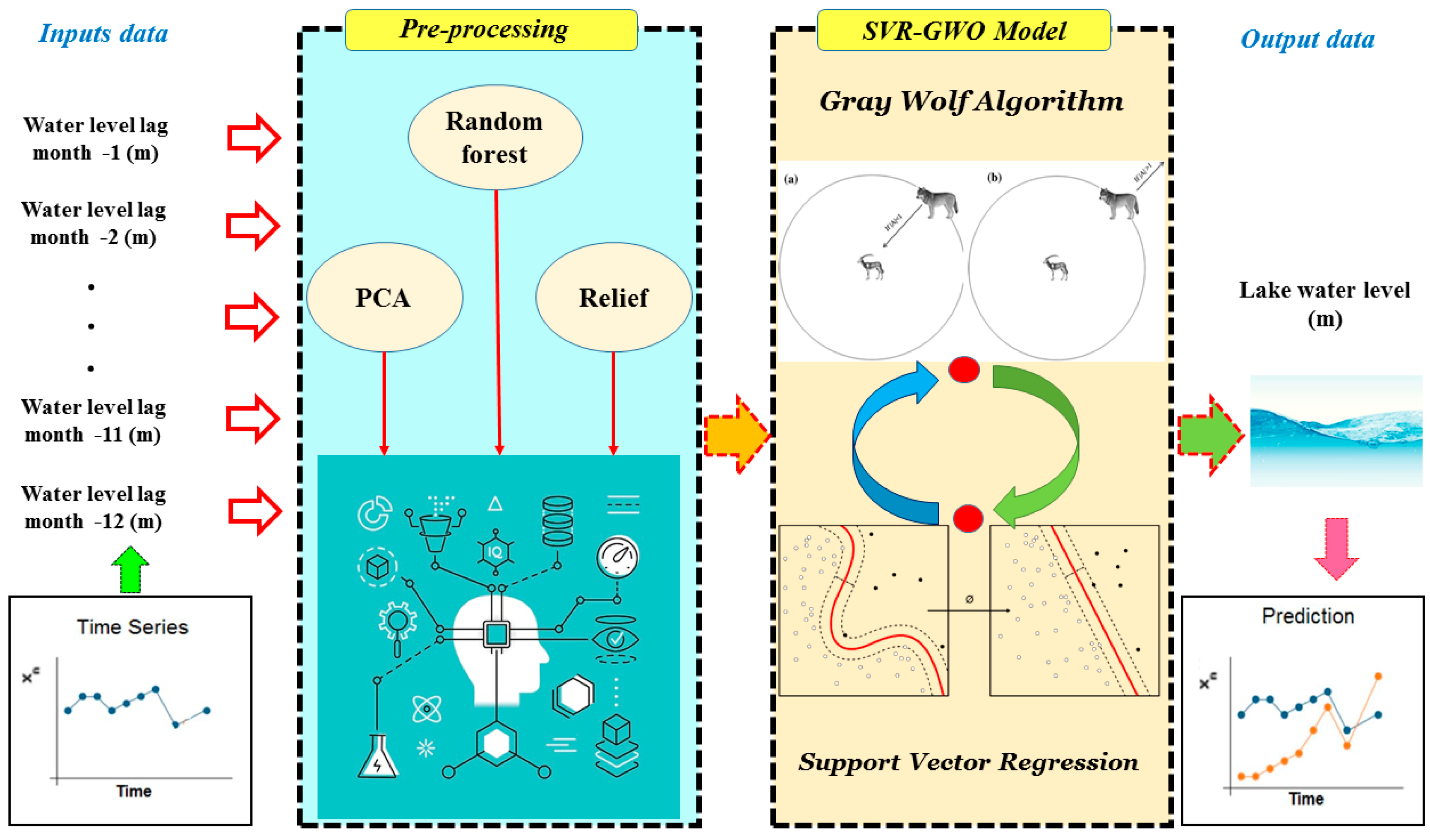
2. Materials and Methods
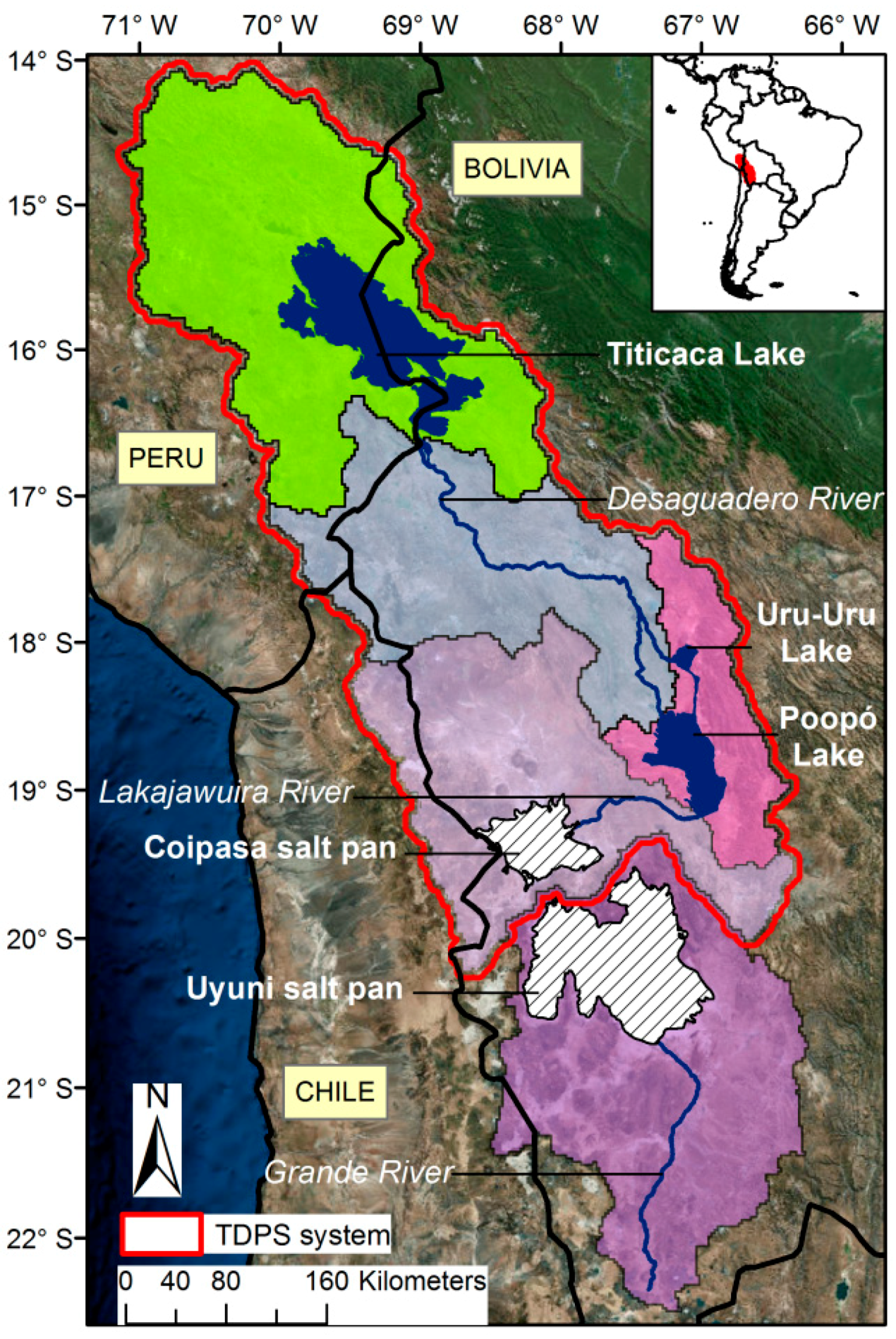
2.1. Study Area
2.2. Data Used
2.3. Preprocessing Methods
2.3.1. Principal Component Analysis (PCA)
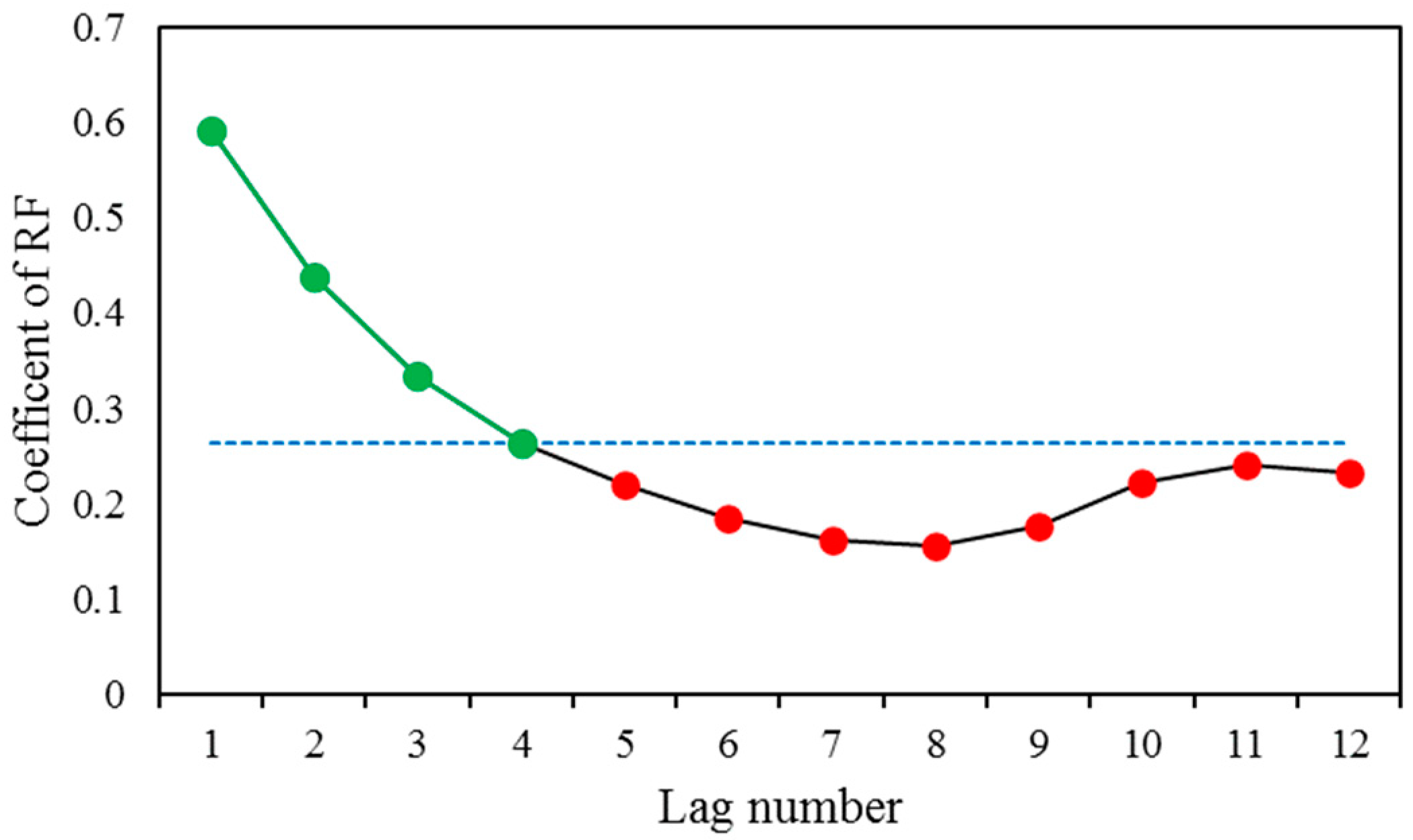
2.3.2. Random Forest (RF)
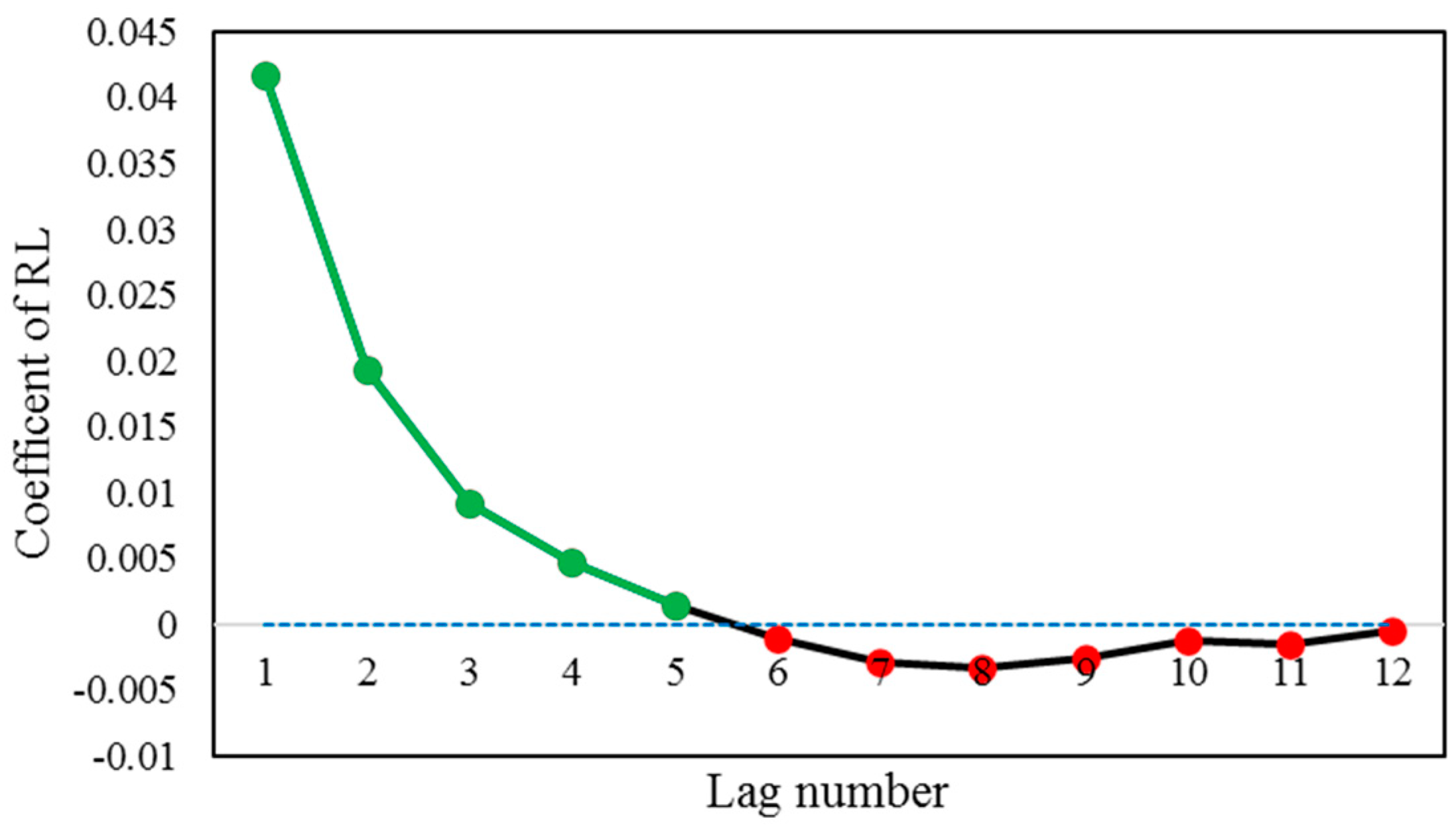
2.3.3. Relief (RL)
2.4. Predictor Methods
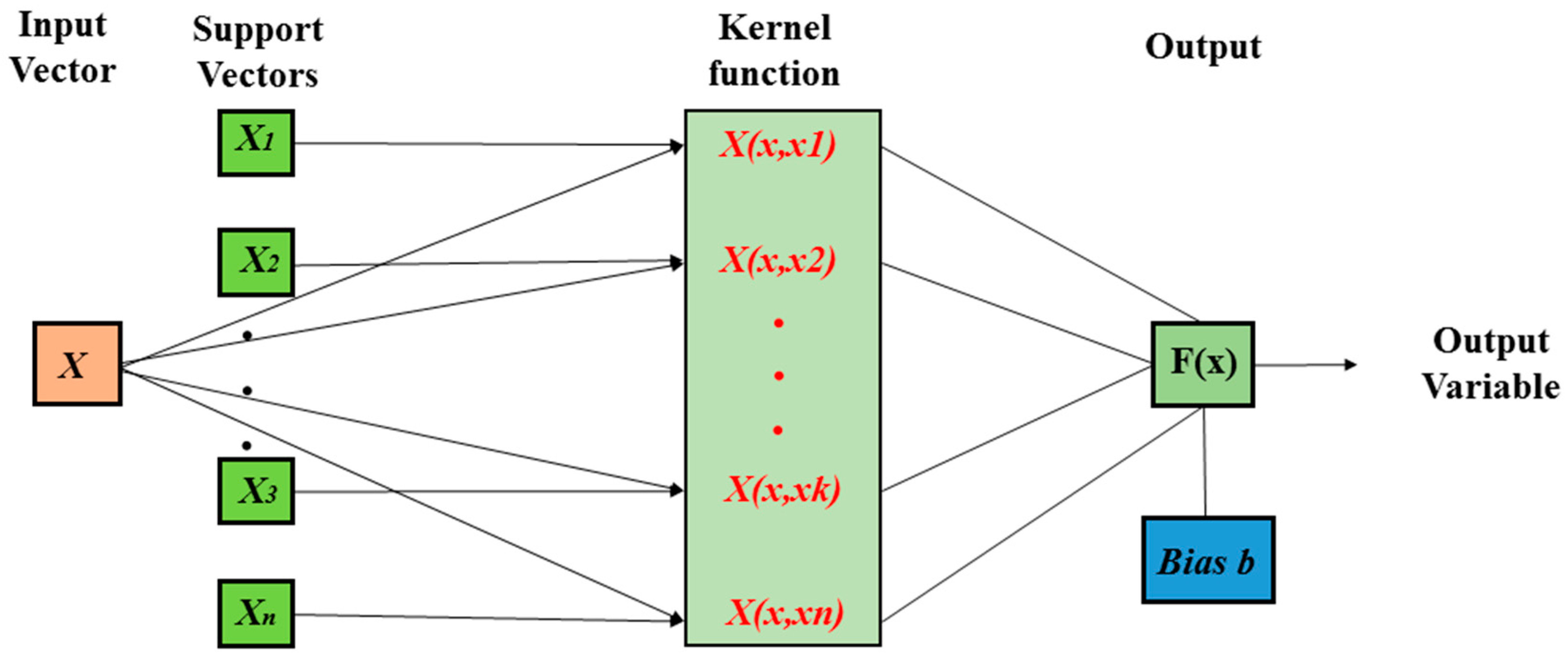
2.4.1. Support Vector Regression
2.4.2. Grey Wolf Optimizer
2.4.3. Hybrid SVR-GWO Model
2.5. Performance Indexes
3. Results and Discussion
3.1. Implementation of the Preprocessing Methods
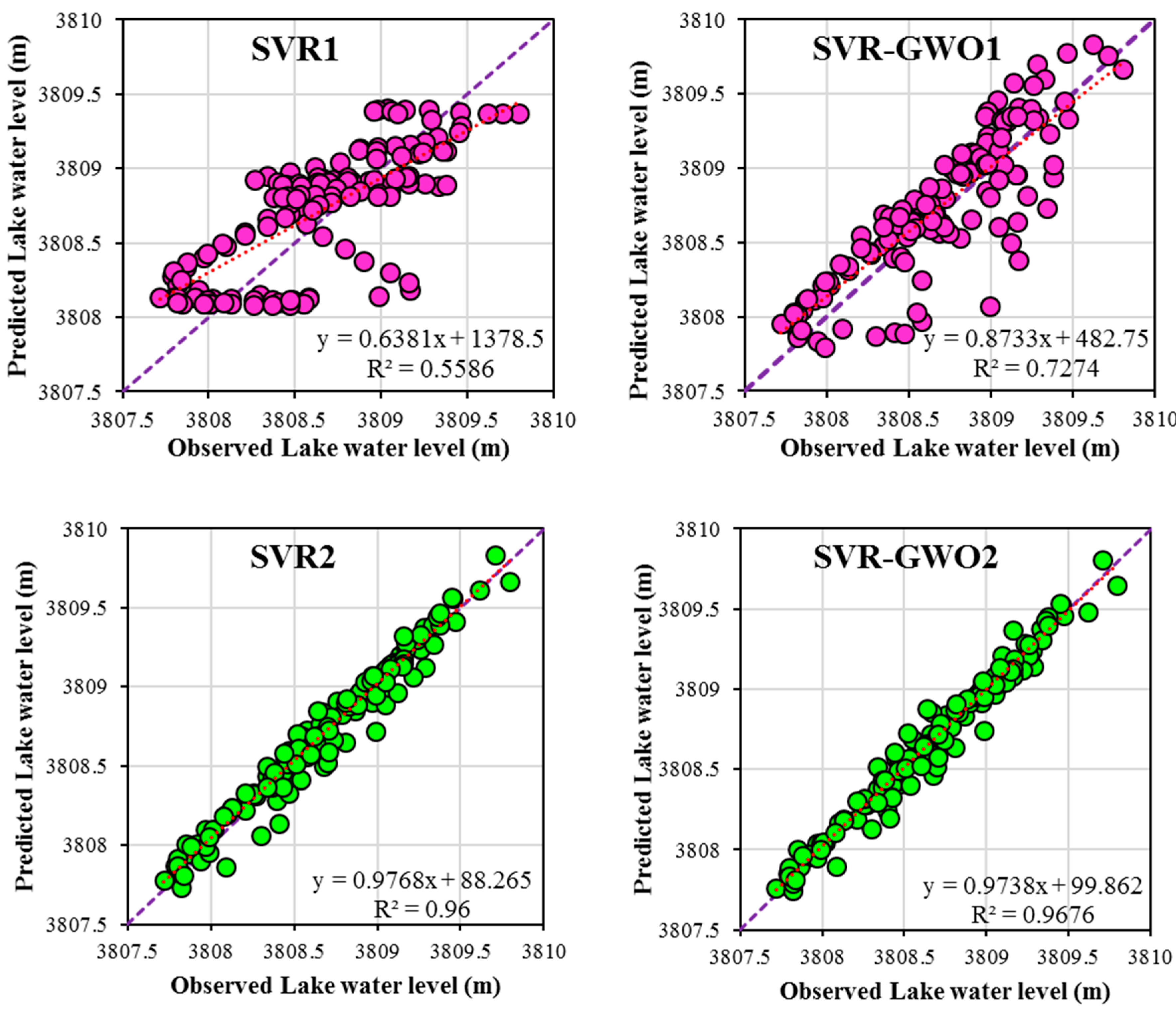
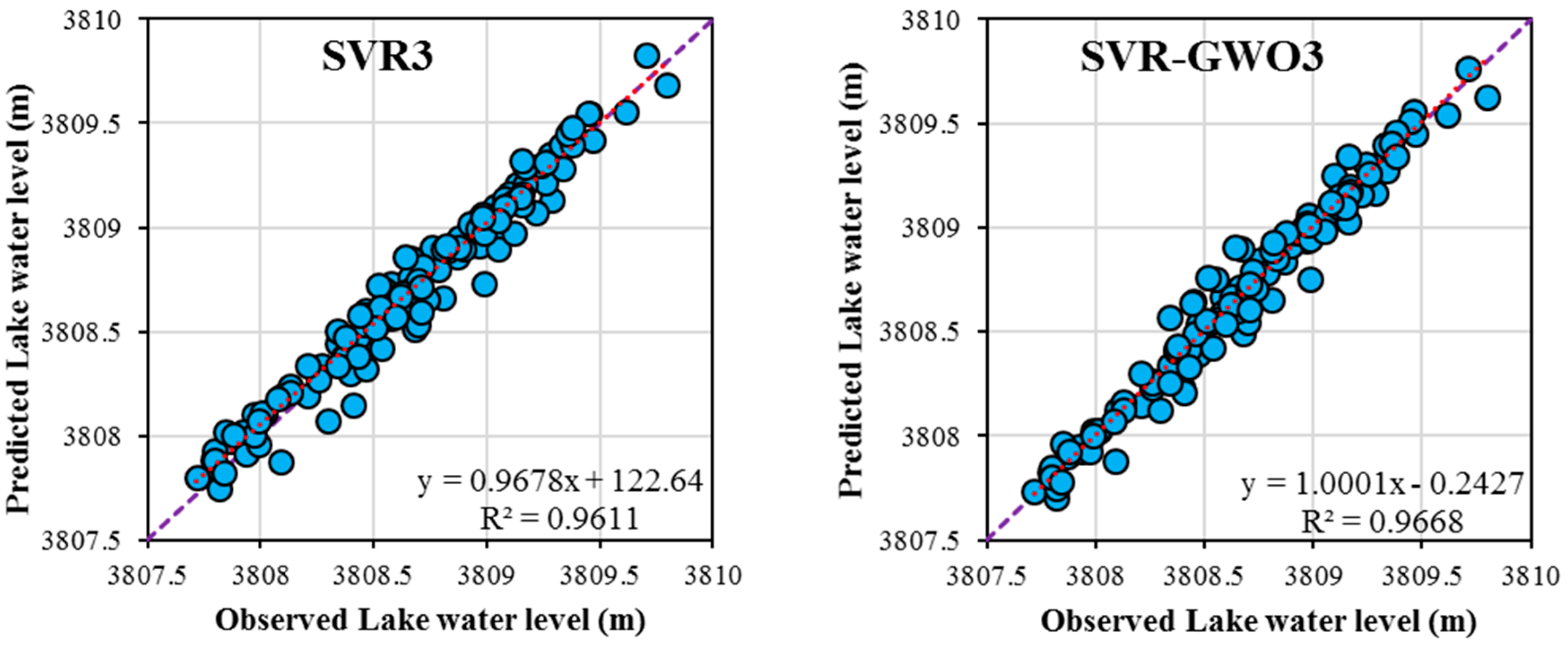
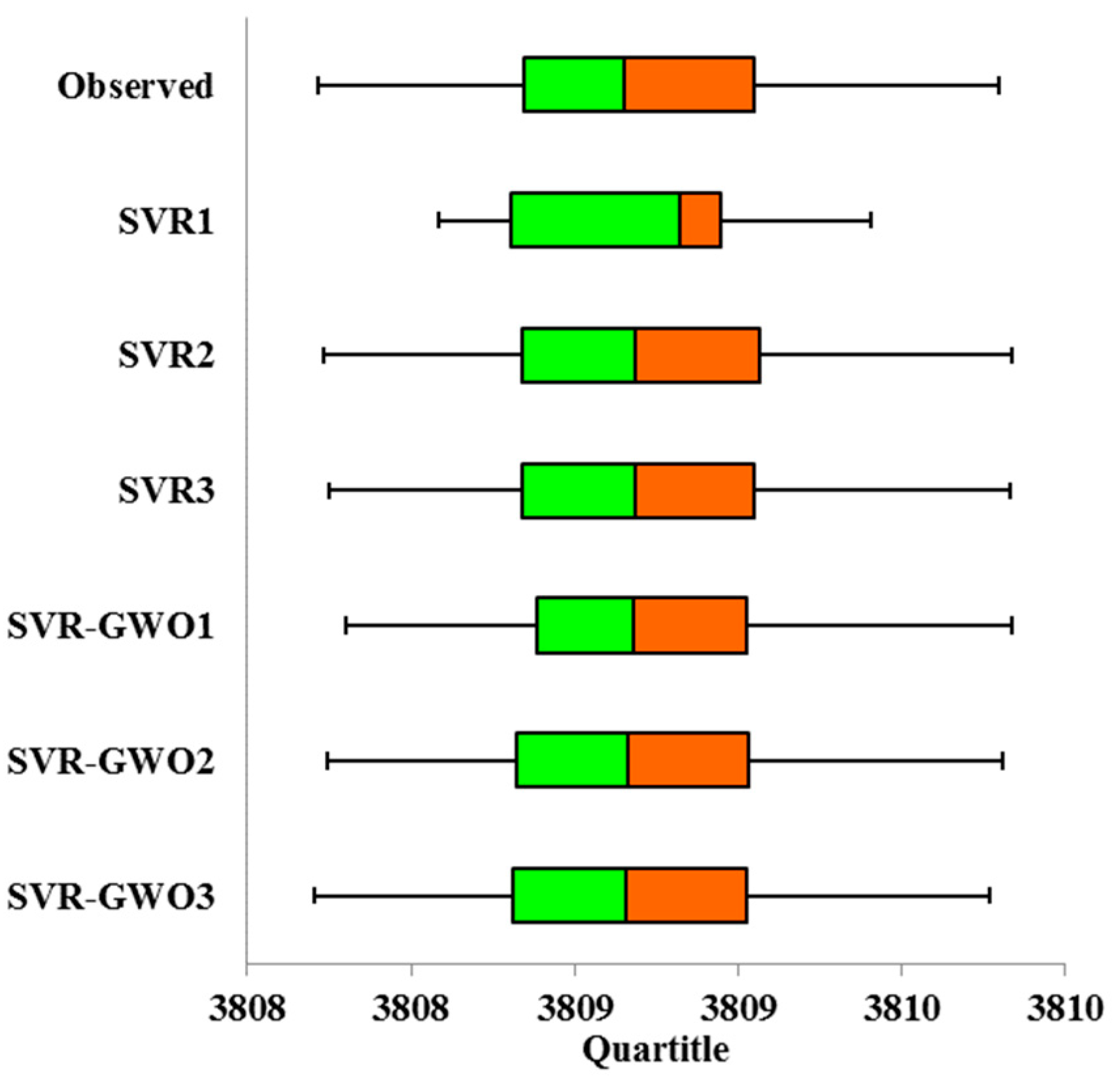
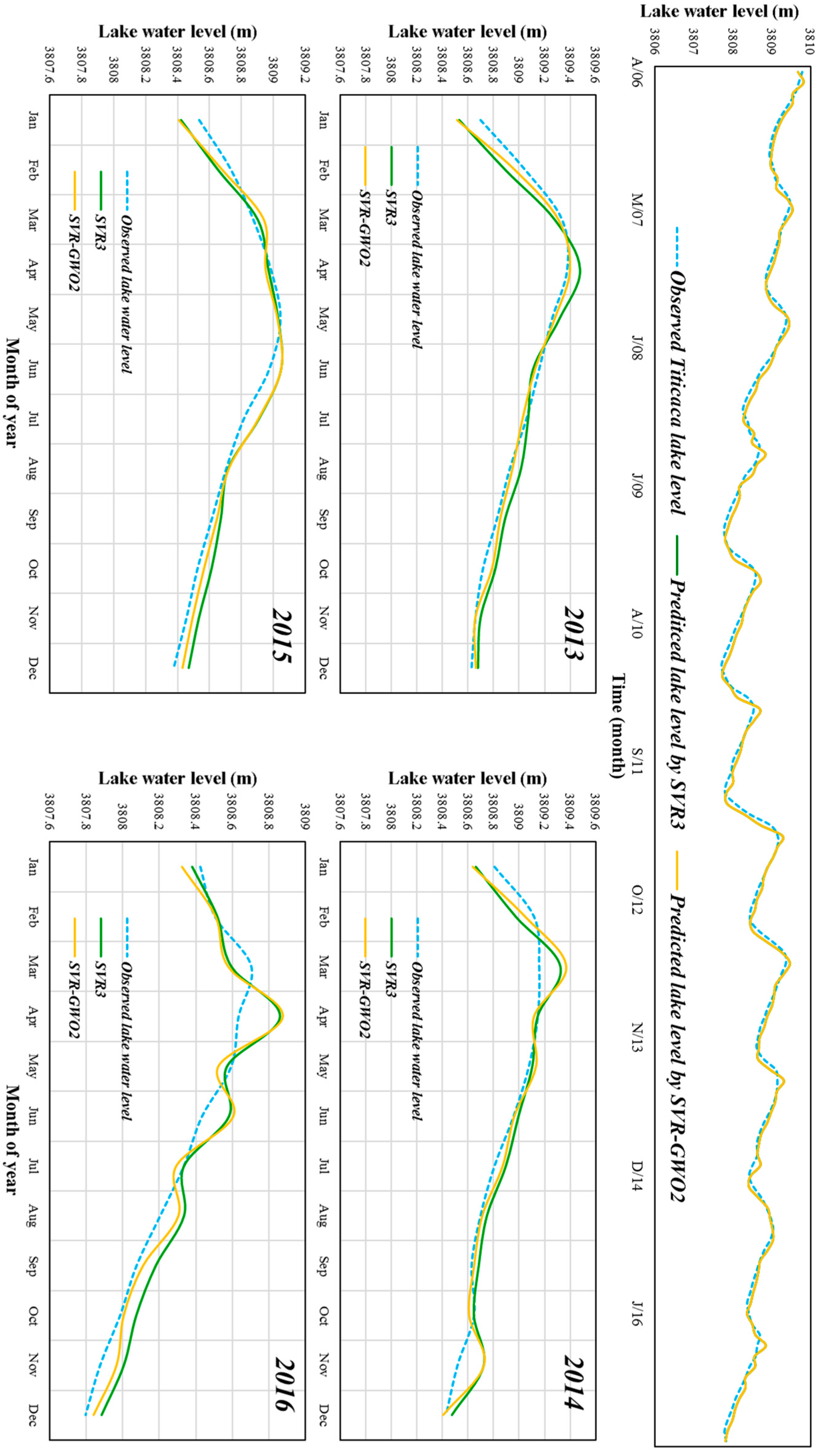
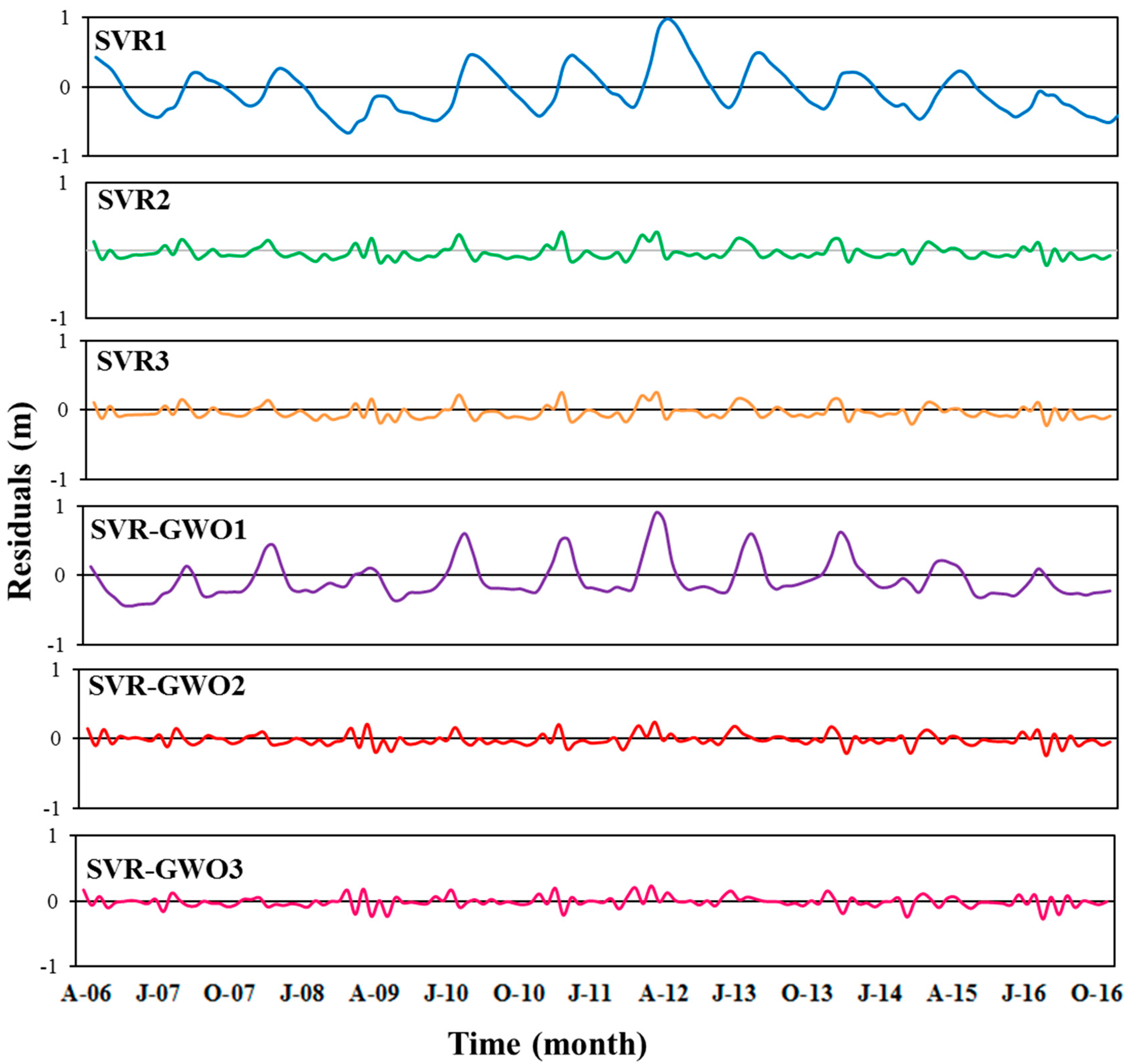
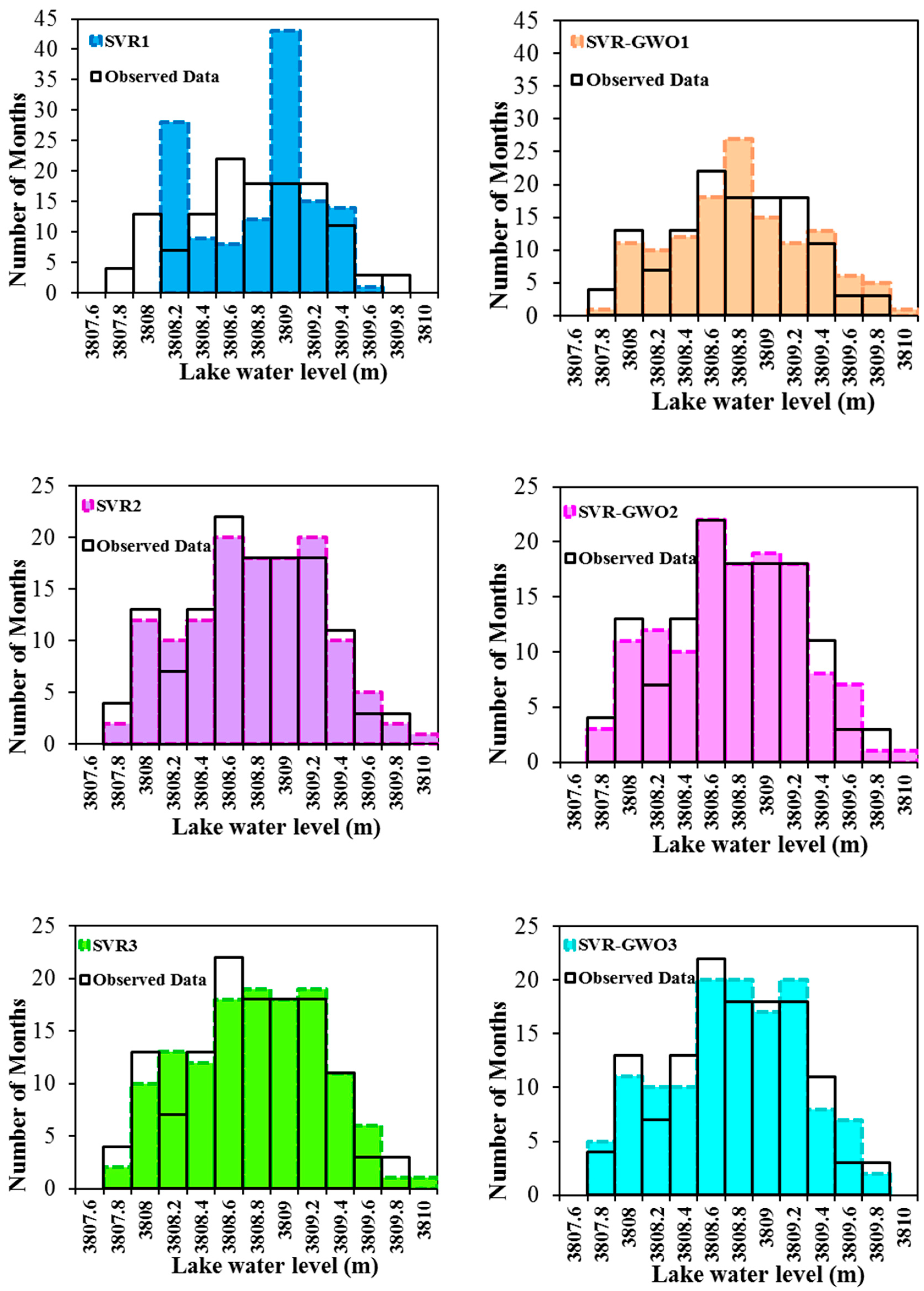
3.2. Performances of the SVR and SVR-GWO Models
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ebtehaj, I.; Bonakdari, H.; Gharabaghi, B. A reliable linear method for modeling lake level fluctuations. J. Hydrol. 2019, 570. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S.; Kisi, O.; Singh, V.P. Daily water level forecasting using wavelet decomposition and artificial intelligence techniques. J. Hydrol. 2015, 520. [Google Scholar] [CrossRef]
- Hu, T.; Mao, J.; Pan, S.; Dai, L.; Zhang, P.; Xu, D.; Dai, H. Water level management of lakes connected to regulated rivers: An integrated modeling and analytical methodology. J. Hydrol. 2018, 562. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Deo, R.C.; Karimi, V.; Yaseen, Z.M.; Terzi, O. Implementation of a hybrid MLP-FFA model for water level prediction of Lake Egirdir, Turkey. Stoch. Environ. Res. Risk Assess. 2018, 32. [Google Scholar] [CrossRef]
- Rajurkar, M.P.; Kothyari, U.C.; Chaube, U.C. Modeling of the daily rainfall-runoff relationship with artificial neural network. J. Hydrol. 2004, 285. [Google Scholar] [CrossRef]
- Croke, B.F.W.; Andrews, F.; Jakeman, A.J.; Cuddy, S.M.; Luddy, A. IHACRES Classic Plus: A redesign of the IHACRES rainfall-runoff model. Environ. Model. Softw. 2006, 21. [Google Scholar] [CrossRef]
- Bicknell, B.R.; Imhoff, J.C.; Kittle, J.L., Jr.; Donigan, A.S., Jr.; Johanson, R.C.; Barnwell, T.O. Hydrological Simulation Program-Fortran User’s Manual for Release 11; U.S. Environ. Prot. Agency: Washington, DC, USA, 1996.
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34. [Google Scholar] [CrossRef]
- Privalsky, V.E. Modeling long term lake variations by physically based stochastic dynamic models. Stoch. Hydrol. Hydraul. 1988, 2. [Google Scholar] [CrossRef]
- Mohammadi, B.; Mehdizadeh, S. Modeling daily reference evapotranspiration via a novel approach based on support vector regression coupled with whale optimization algorithm. Agric. Water Manag. 2020, 237. [Google Scholar] [CrossRef]
- Misra, D.; Oommen, T.; Agarwal, A.; Mishra, S.K.; Thompson, A.M. Application and analysis of support vector machine based simulation for runoff and sediment yield. Biosyst. Eng. 2009, 103. [Google Scholar] [CrossRef]
- Emamgholizadeh, S.; Demneh, R.K. A comparison of artificial intelligence models for the estimation of daily suspended sediment load: A case study on the telar and kasilian rivers in Iran. Water Sci. Technol. Water Supply 2019, 19. [Google Scholar] [CrossRef] [Green Version]
- Emamgholizadeh, S.; Moslemi, K.; Karami, G. Prediction the groundwater level of bastam plain (Iran) by Artificial Neural Network (ANN) and Adaptive Neuro-Fuzzy Inference System (ANFIS). Water Resour. Manag. 2014, 28. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Xue, Y. M5 model trees and neural networks: Application to flood forecasting in the upper reach of the Huai River in China. J. Hydrol. Eng. 2004, 9. [Google Scholar] [CrossRef]
- Emamgholizadeh, S.; Bahman, K.; Bateni, S.M.; Ghorbani, H.; Marofpoor, I.; Nielson, J.R. Estimation of soil dispersivity using soft computing approaches. Neural Comput. Appl. 2017, 28. [Google Scholar] [CrossRef]
- Aghelpour, P.; Bahrami-Pichaghchi, H.; Kisi, O. Comparison of three different bio-inspired algorithms to improve ability of neuro fuzzy approach in prediction of agricultural drought, based on three different indexes. Comput. Electron. Agric. 2020, 170. [Google Scholar] [CrossRef]
- Aghelpour, P.; Varshavian, V. Evaluation of stochastic and artificial intelligence models in modeling and predicting of river daily flow time series. Stoch. Environ. Res. Risk Assess. 2020, 34. [Google Scholar] [CrossRef]
- Guan, Y.; Mohammadi, B.; Pham, Q.B.; Adarsh, S.; Balkhair, K.S.; Rahman, K.U.; Linh, N.T.T.; Tri, D.Q. A novel approach for predicting daily pan evaporation in the coastal regions of Iran using support vector regression coupled with krill herd algorithm model. Theor. Appl. Climatol. 2020, 142. [Google Scholar] [CrossRef]
- Aghelpour, P.; Mohammadi, B.; Biazar, S.M. Long-term monthly average temperature forecasting in some climate types of Iran, using the models SARIMA, SVR, and SVR-FA. Theor. Appl. Climatol. 2019, 138. [Google Scholar] [CrossRef]
- Buyukyildiz, M.; Tezel, G.; Yilmaz, V. Estimation of the change in lake water level by artificial intelligence methods. Water Resour. Manag. 2014, 28. [Google Scholar] [CrossRef]
- Moazenzadeh, R.; Mohammadi, B.; Shamshirband, S.; Chau, K. Coupling a firefly algorithm with support vector regression to predict evaporation in northern Iran. Eng. Appl. Comput. Fluid Mech. 2018, 12, 584–597. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zhou, P.; Zhang, Y. A probabilistic wavelet-support vector regression model for streamflow forecasting with rainfall and climate information input. J. Hydrometeorol. 2015, 16. [Google Scholar] [CrossRef]
- Niu, M.; Wang, Y.; Sun, S.; Li, Y. A novel hybrid decomposition-and-ensemble model based on CEEMD and GWO for short-term PM2.5 concentration forecasting. Atmos. Environ. 2016, 134. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69. [Google Scholar] [CrossRef] [Green Version]
- Dehghani, M.; Seifi, A.; Riahi-Madvar, H. Novel forecasting models for immediate-short-term to long-term influent flow prediction by combining ANFIS and grey wolf optimization. J. Hydrol. 2019, 576. [Google Scholar] [CrossRef]
- Zolá, R.P.; Bengtsson, L. Long-term and extreme water level variations of the shallow Lake Poopó, Bolivia. Hydrol. Sci. J. 2006, 51. [Google Scholar] [CrossRef] [Green Version]
- Hastenrath, S.; Kutzbach, J. Late Pleistocene climate and water budget of the south American Altiplano. Quat. Res. 1985, 24. [Google Scholar] [CrossRef]
- Zolá, R.P.; Bengtsson, L.; Berndtsson, R.; Martí-Cardona, B.; Satgé, F.; Timouk, F.; Bonnet, M.P.; Mollericon, L.; Gamarra, C.; Pasapera, J. Modelling Lake Titicaca’s daily and monthly evaporation. Hydrol. Earth Syst. Sci. 2019, 23. [Google Scholar] [CrossRef] [Green Version]
- Choubin, B.; Malekian, A. Combined gamma and M-test-based ANN and ARIMA models for groundwater fluctuation forecasting in semiarid regions. Environ. Earth Sci. 2017, 76. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313. [Google Scholar] [CrossRef] [Green Version]
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88. [Google Scholar] [CrossRef]
- Díaz-Uriarte, R.; de Andrés, S.A. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kira, K.; Rendell, L.A. Feature selection problem: Traditional methods and a new algorithm. In Proceedings of the Tenth National Conference on Artificial Intelligence, San Jose, CA, USA, 12–16 July 1992. [Google Scholar]
- Faris, H.; Aljarah, I.; Al-Betar, M.A.; Mirjalili, S. Grey wolf optimizer: A review of recent variants and applications. Neural Comput. Appl. 2018, 30. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.D.S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47. [Google Scholar] [CrossRef]
- Mohammadi, B.; Ahmadi, F.; Mehdizadeh, S.; Guan, Y.; Pham, Q.B.; Linh, N.T.T.; Tri, D.Q. Developing novel robust models to improve the accuracy of daily streamflow modeling. Water Resour. Manag. 2020, 34. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Mohammadi, B.; Pham, Q.B.; Khoi, D.N.; Linh, N.T.T. Implementing novel hybrid models to improve indirect measurement of the daily soil temperature: Elman neural network coupled with gravitational search algorithm and ant colony optimization. Meas. J. Int. Meas. Confed. 2020, 165. [Google Scholar] [CrossRef]
- Mohammadi, B.; Aghashariatmadari, Z. Estimation of solar radiation using neighboring stations through hybrid support vector regression boosted by Krill Herd algorithm. Arab. J. Geosci. 2020, 13. [Google Scholar] [CrossRef]
- Mohammadi, B.; Linh, N.T.T.; Pham, Q.B.; Ahmed, A.N.; Vojteková, J.; Guan, Y.; Abba, S.I.; El-Shafie, A. Adaptive neuro-fuzzy inference system coupled with shuffled frog leaping algorithm for predicting river streamflow time series. Hydrol. Sci. J. 2020, 65. [Google Scholar] [CrossRef]
- Vaheddoost, B.; Guan, Y.; Mohammadi, B. Application of hybrid ANN-whale optimization model in evaluation of the field capacity and the permanent wilting point of the soils. Environ. Sci. Pollut. Res. 2020, 27. [Google Scholar] [CrossRef]
- Moazenzadeh, R.; Mohammadi, B. Assessment of bio-inspired metaheuristic optimisation algorithms for estimating soil temperature. Geoderma 2019, 353. [Google Scholar] [CrossRef]
- Li, B.; Yang, G.; Wan, R.; Dai, X.; Zhang, Y. Comparison of random forests and other statistical methods for the prediction of lake water level: A case study of the Poyang Lake in China. Hydrol. Res. 2016, 47. [Google Scholar] [CrossRef] [Green Version]
- Tikhamarine, Y.; Souag-Gamane, D.; Kisi, O. A new intelligent method for monthly streamflow prediction: Hybrid wavelet support vector regression based on grey wolf optimizer (WSVR–GWO). Arab. J. Geosci. 2019, 12. [Google Scholar] [CrossRef]
- Aghelpour, P.; Guan, Y.; Bahrami-Pichaghchi, H.; Mohammadi, B.; Kisi, O.; Zhang, D. Using the MODIS Sensor for Snow Cover Modeling and the Assessment of Drought Effects on Snow Cover in a Mountainous Area. Remote Sens. 2020, 12, 3437. [Google Scholar] [CrossRef]
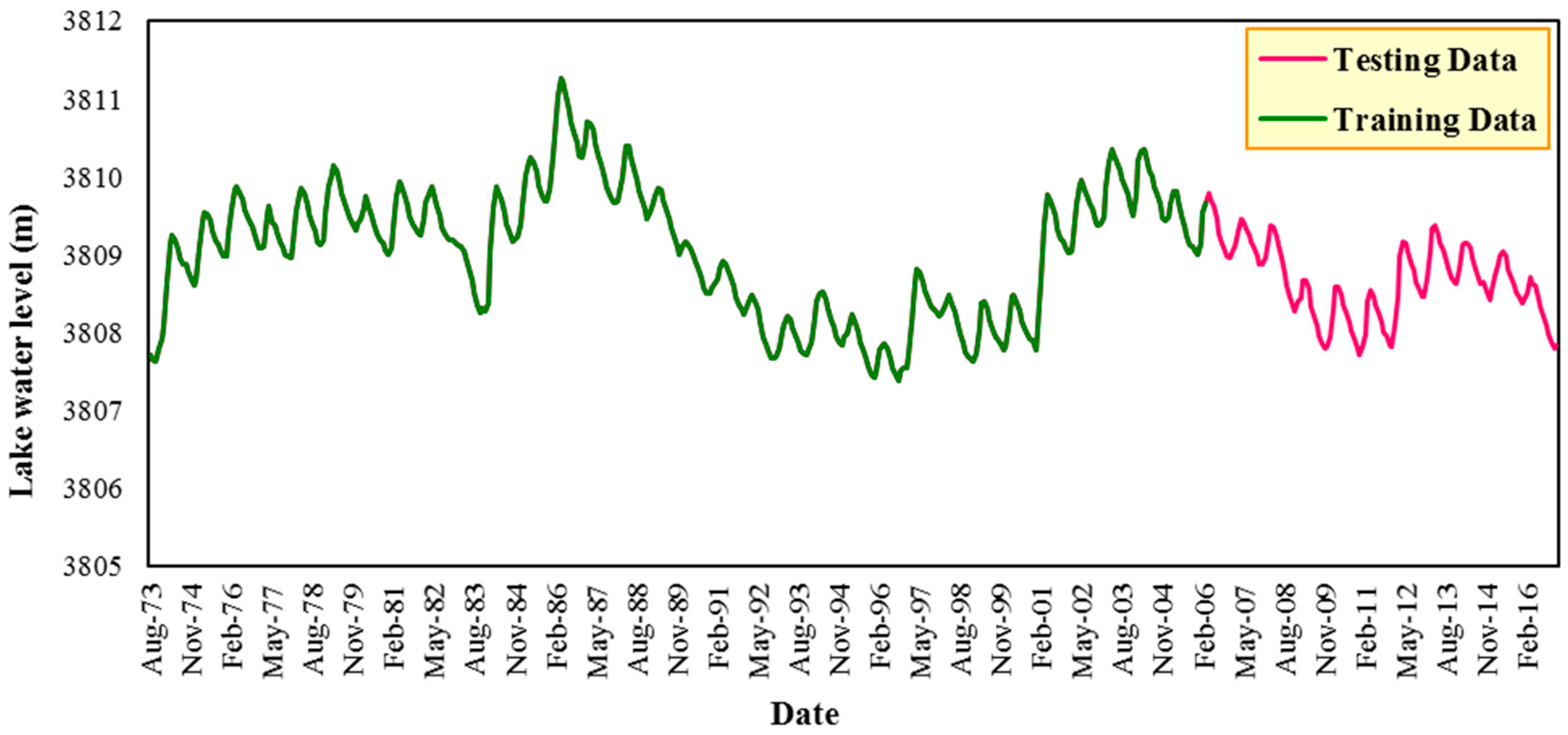
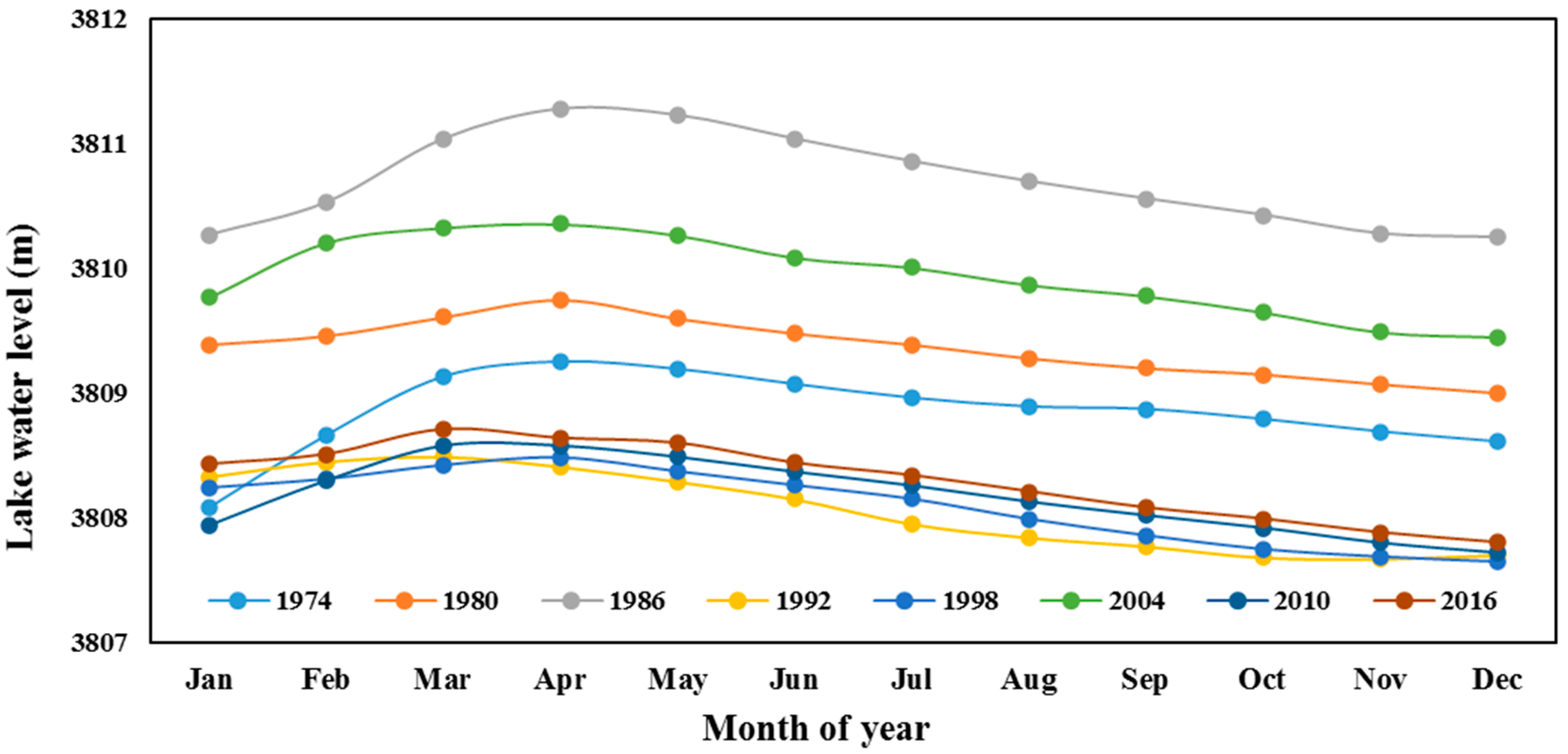
| Dataset | Min (m) | Max (m) | Mean (m) | SD (m) | Skewness (m) | Kurtosis (m) | Confidence Level (95%) |
|---|---|---|---|---|---|---|---|
| Total | 3807.387 | 3811.277 | 3808.959 | 0.781 | 0.11 | −0.584 | 0.067 |
| Training | 3807.387 | 3811.277 | 3809.059 | 0.834 | −0.101 | −0.743 | 0.082 |
| Testing | 3807.717 | 3809.797 | 3808.658 | 0.483 | −0.054 | −0.701 | 0.083 |
| Component | % of Variance | Cumulative % |
|---|---|---|
| 1 | 84.98 | 84.98 |
| 2 | 8.05 | 93.03 |
| 3 | 5.24 | 98.27 |
| 4 | 1.05 | 99.32 |
| 5 | 0.38 | 99.7 |
| 6 | 0.18 | 99.88 |
| 7 | 0.05 | 99.93 |
| 8 | 0.03 | 99.96 |
| 9 | 0.01 | 99.97 |
| 10 | 0.01 | 99.98 |
| 11 | 0.01 | 99.99 |
| 12 | 0.01 | 100 |
| No. | Preprocessing Method | Input Combinations | Model Designation | |
|---|---|---|---|---|
| SVR | SVR-GWO | |||
| 1 | Principal component analysis | PCA1 | SVR1 | SVR-GWO1 |
| 2 | Random forest | L (t − 1), L (t − 2), L (t − 3), L (t − 4) | SVR2 | SVR-GWO2 |
| 3 | Relief | L (t − 1), L (t − 2), L (t − 3), L (t − 4), L (t − 5) | SVR3 | SVR-GWO3 |
| Partition | Models Name | RMSE (m) | MAE (m) | R2 |
|---|---|---|---|---|
| Train phase | SVR1 | 0.395 | 0.312 | 0.774 |
| SVR2 | 0.11 | 0.082 | 0.982 | |
| SVR3 | 0.108 | 0.08 | 0.983 | |
| SVR-GWO1 | 0.304 | 0.208 | 0.877 | |
| SVR-GWO2 | 0.084 | 0.06 | 0.989 | |
| SVR-GWO3 | 0.079 | 0.052 | 0.99 | |
| Test phase | SVR1 | 0.329 | 0.276 | 0.558 |
| SVR2 | 0.101 | 0.084 | 0.96 | |
| SVR3 | 0.1 | 0.082 | 0.961 | |
| SVR-GWO1 | 0.27 | 0.223 | 0.727 | |
| SVR-GWO2 | 0.087 | 0.066 | 0.967 | |
| SVR-GWO3 | 0.089 | 0.064 | 0.966 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammadi, B.; Guan, Y.; Aghelpour, P.; Emamgholizadeh, S.; Pillco Zolá, R.; Zhang, D. Simulation of Titicaca Lake Water Level Fluctuations Using Hybrid Machine Learning Technique Integrated with Grey Wolf Optimizer Algorithm. Water 2020, 12, 3015. https://doi.org/10.3390/w12113015
Mohammadi B, Guan Y, Aghelpour P, Emamgholizadeh S, Pillco Zolá R, Zhang D. Simulation of Titicaca Lake Water Level Fluctuations Using Hybrid Machine Learning Technique Integrated with Grey Wolf Optimizer Algorithm. Water. 2020; 12(11):3015. https://doi.org/10.3390/w12113015
Chicago/Turabian StyleMohammadi, Babak, Yiqing Guan, Pouya Aghelpour, Samad Emamgholizadeh, Ramiro Pillco Zolá, and Danrong Zhang. 2020. "Simulation of Titicaca Lake Water Level Fluctuations Using Hybrid Machine Learning Technique Integrated with Grey Wolf Optimizer Algorithm" Water 12, no. 11: 3015. https://doi.org/10.3390/w12113015
APA StyleMohammadi, B., Guan, Y., Aghelpour, P., Emamgholizadeh, S., Pillco Zolá, R., & Zhang, D. (2020). Simulation of Titicaca Lake Water Level Fluctuations Using Hybrid Machine Learning Technique Integrated with Grey Wolf Optimizer Algorithm. Water, 12(11), 3015. https://doi.org/10.3390/w12113015







